Black Hole Solution in f(R,G) Gravitational Theory Coupled with Scalar Field

Abstract

In this work, we explore a class of spherically symmetric black hole (BH) solutions within the framework of modified gravity, focusing on a non-ghost-free $f(R,G)$ theory coupled to a scalar field. We present a novel black hole geometry that arises as a deformation of the Schwarzschild solution and analyze its physical and thermodynamic properties. Our results show that the model satisfies stability conditions, with the Ricci scalar R, as well as its first and second derivatives, remaining positive throughout the spacetime. The solution admits multiple horizons and exhibits strong curvature singularities compared to those in general relativity. Furthermore, it supports a non-trivial scalar field potential. A comprehensive thermodynamic analysis is performed, including evaluations of the entropy, temperature, heat capacity, and quasi-local energy. We find that the black hole exhibits thermodynamic stability within certain ranges of model parameters. In addition, we investigate geodesic deviation and derive the conditions necessary for stability within the $f(R,G)$ gravitational framework.

1. Introduction

The General Theory of Relativity (GR) has demonstrated exceptional success in describing gravitational phenomena across a wide range of physical scales. Over the past century, it has withstood extensive experimental scrutiny, including recent landmark confirmations such as the direct detection of gravitational waves by the LIGO and VIRGO collaborations [1,2,3,4]. Another major milestone is the imaging of superheated plasma orbiting the supermassive black hole at the center of the galaxy M87, as well as similar observations of the compact object at the center of our own Milky Way galaxy [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

Despite its successes, GR faces significant challenges, particularly regarding its reconciliation with quantum mechanics and its inability to fully explain the nature of dark matter and dark energy. These components were introduced to account for various astrophysical and cosmological observations, such as the accelerating expansion of the universe [20,21,22], anomalous galactic rotation curves, and the mass discrepancies observed in galaxy clusters. However, a comprehensive and universally accepted theoretical explanation for these phenomena remains elusive. Consequently, considerable efforts have been directed toward formulating modifications and extensions to GR, with the goal of addressing these open problems in both cosmology and high-energy physics [23,24]. A large amount of observational data supports the view that our universe is currently experiencing an accelerated expansion. To account for this, two main approaches have been proposed. The first, within the standard GR framework, involves positing a mysterious form of dark energy with repulsive gravitational effects, uniformly distributed across space. The second approach considers modifying the Einstein–Hilbert action by adding higher-order curvature invariants, such as the Ricci scalar R, Ricci and Riemann tensors, and their derivatives. This has led to a broad class of modified gravity models including Lovelock gravity, braneworld scenarios, scalar–tensor theories like Brans–Dicke, and $f\left(R\right)$ gravity models. For comprehensive reviews of dark energy models, see [25,26].

It has been demonstrated that $f\left(R\right)$ gravity is capable of reproducing the entire history of cosmic evolution, from the early inflationary epoch to the current phase of accelerated expansion [27,28,29,30,31,32,33,34,35,36], as supported by a wide range of theoretical developments and observational data [33,37,38,39,40,41]. Among the various extensions of $f\left(R\right)$ gravity, particular attention has been devoted to $f(R,G)$ theories, where G is the Gauss–Bonnet invariant, defined as

$$\mathcal{G}\equiv R^2-4R^{\alpha \beta }{R}_{\alpha \beta }+R^{\alpha \beta \mu \nu }{R}_{\alpha \beta \mu \nu },.$$

(1)

This extension incorporates higher-order curvature terms and has been widely studied for its rich phenomenology and theoretical appeal [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. In this context, a variety of black hole (BH) solutions have been constructed and analyzed [63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81]. Moreover, the Gauss–Bonnet framework has been employed in holographic studies, addressing processes such as thermalization via Wilson loops and entanglement entropy [82,83,84].

Obtaining black hole solutions with primary scalar hair remains significantly more challenging than those with secondary hair. Recently, the first black hole solution exhibiting primary scalar hair was discovered within a shift-symmetric subclass of Beyond Horndeski theories [85], sparking several generalizations and follow-up studies [86,87]. In these models, the existence of a conserved scalar charge stems from the underlying shift symmetry, allowing the scalar field to possess symmetries that differ from those of the spacetime geometry. This decoupling facilitates the construction of exact analytical solutions [88].

The physical implications of black hole configurations with primary scalar hair remain an active area of research. Recent efforts have primarily focused on their thermodynamic properties [85] and the weak gravitational lensing they induce [89]. However, the shadow cast by such black holes has yet to be thoroughly investigated, presenting a promising direction for future exploration. From a thermodynamic perspective, it is also crucial to understand how the presence of primary hair affects the stability of these solutions. In this work, we present and analyze the first black hole solution with primary scalar hair in the shift-symmetric sector of Beyond Horndeski gravity, with particular attention given to its thermodynamic behavior and physical characteristics.

The structure of this paper is organized as follows. In Section 2, we provide an overview of the gravitational framework based on $f(R,G)$ gravity. Section 3 applies the corresponding field equations to a spherically symmetric spacetime described by a single metric potential. In Section 3, we present the explicit form of this metric potential and outline the derived quantities relevant to the $f(R,G)$ theory, which are also documented in the supplementary computational notebook accompanying this work. Section 4 investigates the physical implications of the obtained solution, analyzing curvature invariants and the asymptotic behavior of key physical quantities. In Section 5, we explore the thermodynamic properties of the black hole, including its temperature profile, entropy, and heat capacity, while varying a parameter that distinguishes our solution from the classical Schwarzschild case. Section 5 addresses the presence of multiple horizons and examines their associated thermodynamic features, demonstrating consistency with established results. Section 6 further investigates the stability of the solution through a detailed analysis of geodesic deviation. Finally, the concluding section summarizes the main results and discusses potential implications and directions for future research.

Throughout this study, we employ geometric units with $8\pi G=\hslash ={\ell }_p=c=1$, adopt the sign convention $(-,+,+,+)$, and use primes to denote derivatives with respect to the radial coordinate.

2. Summary of $\mathit{f}(\mathit{R},\mathit{G})$ Gravity Coupled with Scalar Field

In this section, we examine the action of $f(R,G)$ gravity, where $f(R,G)$ represents an arbitrary function of the Ricci scalar R and the Gauss–Bonnet scalar G. It is crucial to emphasize that $f(R,G)$ gravity constitutes a modification of GR, aligning with Einstein’s GR at lower orders, specifically when $f(R,G)=R+G$. However, the theory becomes different from GR when $f\left(R\right)\ne R+G$.

We commence with the action of $f(R,G)$ gravity in D-dimensions, expressed as follows: (For this study, we assume that $f(R,G)=f\left(R\right)+f_1\left(G\right)$; to ensure the model is free from ghost instabilities, we reformulate $f_1\left(G\right)$ in terms of a scalar field $\psi$, expressing it as ${\rm Y}\left(\psi \right)G$. For a more comprehensive understanding, please see [90,91,92]).

$$\begin{array}{c}\hfill \mathcal{S}=\int d^{D}x\sqrt{-g}\left\{{\displaystyle \frac{1}{2{\chi }^2}}f\left(R\right)-{\displaystyle \frac{1}{2}}{\partial }_{\mu }\psi {\partial }^{\mu }\psi +\Phi \left(\psi \right)+{\rm Y}\left(\psi \right)\mathcal{G}\right\}.\end{array}$$

(2)

In this context, $\psi$ represents the scalar field, and $\Phi \left(\psi \right)$ denotes the potential associated with $\psi$, while ${\rm Y}\left(\psi \right)$ is another function dependent on $\psi$. Additionally, G signifies the Gauss–Bonnet invariant, defined as

$$\begin{array}{c}\hfill G=R^2-4R_{\alpha \beta }{R}^{\alpha \beta }+R_{\alpha \beta \rho \sigma }{R}^{\alpha \beta \rho \sigma }.\end{array}$$

(3)

Even though the Gauss–Bonnet invariant becomes a total derivative and hence a topological invariant without dynamical significance in four dimensions (D = 4), its coupling with ${\rm Y}\left(\psi \right)$ enables it to make non-trivial contributions to the field equations of the system. This coupling ensures that the Gauss–Bonnet term influences the dynamics despite its typical nature in four dimensions. We further assume that the matter fields do not interact with the scalar field $\psi$, a condition that may prevent the emergence of a fifth force. This assumption simplifies the model by decoupling the scalar field from matter interactions, focusing solely on its gravitational effects.

Upon varying the action (2) with respect to the scalar field $\psi$, we obtain the following equation:

$$\begin{array}{c}\hfill {\nabla }^2\psi -{\Phi }^{\prime }\left(\psi \right)+{{\rm Y}}^{\prime }\left(\psi \right)G=0.\end{array}$$

(4)

Alternatively, when we vary the action (denoted as (2)) in relation to the metric tensor $g_{\mu \nu }$, we derive the ensuing equations:

$$\begin{array}{cc}\hfill 0=& -{\displaystyle \frac{1}{2{\chi }^2}}\left(R_{\mu \nu }{f}_R-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }f\left(R\right)+[g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }]f_R\right)+{\displaystyle \frac{1}{2}}{\partial }^{\mu }\psi {\partial }^{\nu }\psi -{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\partial }_{\rho }\psi {\partial }^{\rho }\psi +{\displaystyle \frac{1}{2}}{g}^{\mu \nu }[{\rm Y}\left(\psi \right)G-\Phi \left(\psi \right)]+2{\rm Y}\left(\psi \right)R{R}^{\mu \nu }\hfill \\ \hfill & +2{\nabla }^{\mu }{\nabla }^{\nu }\left({\rm Y}\left(\psi \right)R\right)-2g^{\mu \nu }{\nabla }^2\left({\rm Y}\left(\psi \right)R\right)+8{\rm Y}\left(\psi \right){R^{\mu }}_{\rho }{R}^{\nu \rho }-4{\nabla }_{\rho }{\nabla }^{\mu }\left({\rm Y}\left(\psi \right)R^{\nu \rho }\right)-4{\nabla }_{\rho }{\nabla }^{\nu }\left({\rm Y}\left(\psi \right)R^{\mu \rho }\right)+4{\nabla }^2\left({\rm Y}\left(\psi \right)R^{\mu \nu }\right)\hfill \\ \hfill & +4g^{\mu \nu }{\nabla }_{\rho }{\nabla }_{\sigma }\left({\rm Y}\left(\psi \right)R^{\rho \sigma }\right)-2{\rm Y}\left(\psi \right)R^{\mu \rho \sigma \tau }{R^{\nu }}_{\rho \sigma \tau }+4{\nabla }_{\rho }{\nabla }_{\sigma }\left({\rm Y}\left(\psi \right)R^{\mu \rho \sigma \nu }\right).\hfill \end{array}$$

(5)

By employing the following Bianchi identities, which are fundamental relations in differential geometry:

$$\begin{array}{cc}\hfill & {\nabla }^{\rho }{R}_{\rho \tau \mu \nu }={\nabla }_{\mu }{R}_{\nu \tau }-{\nabla }_{\nu }{R}_{\mu \tau },{\nabla }^{\rho }{R}_{\rho \mu }={\displaystyle \frac{1}{2}}{\nabla }_{\mu }R,{\nabla }_{\rho }{\nabla }_{\sigma }{R}^{\mu \rho \nu \sigma }={\nabla }^2{R}^{\mu \nu }-{\displaystyle \frac{1}{2}}{\nabla }^{\mu }{\nabla }^{\nu }R+R^{\mu \rho \nu \sigma }{R}_{\rho \sigma }-{R^{\mu }}_{\rho }{R}^{\nu \rho },\hfill \\ \hfill & {\nabla }_{\rho }{\nabla }^{\mu }{R}^{\rho \nu }+{\nabla }_{\rho }{\nabla }^{\nu }{R}^{\rho \mu }={\displaystyle \frac{1}{2}}\left({\nabla }^{\mu }{\nabla }^{\nu }R+{\nabla }^{\nu }{\nabla }^{\mu }R\right)-2R^{\mu \rho \nu \sigma }{R}_{\rho \sigma }+2{R^{\mu }}_{\rho }{R}^{\nu \rho },{\nabla }_{\rho }{\nabla }_{\sigma }{R}^{\rho \sigma }={\displaystyle \frac{1}{2}}\square R,\hfill \end{array}$$

(6)

in Equation (5), we get the following simplified equations:

$$\begin{array}{cc}\hfill 0=& -{\displaystyle \frac{1}{2{\chi }^2}}\left(R_{\mu \nu }{f}_R-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }f\left(R\right)+[g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }]f_R\right)+\left({\displaystyle \frac{1}{2}}{\partial }^{\mu }\psi {\partial }^{\nu }\psi -{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\partial }_{\rho }\psi {\partial }^{\rho }\psi \right)+{\displaystyle \frac{1}{2}}{g}^{\mu \nu }\left[{\rm Y}\left(\psi \right)G-\Phi \left(\psi \right)\right]\hfill \\ \hfill & -2{\rm Y}\left(\psi \right)R{R}^{\mu \nu }+4{\rm Y}\left(\psi \right){R^{\mu }}_{\rho }{R}^{\nu \rho }-2{\rm Y}\left(\psi \right)R^{\mu \rho \sigma \tau }{R^{\nu }}_{\rho \sigma \tau }-4{\rm Y}\left(\psi \right)R^{\mu \rho \sigma \nu }{R}_{\rho \sigma }+2\left({\nabla }^{\mu }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R-2g^{\mu \nu }\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R\hfill \\ \hfill & -4\left({\nabla }_{\rho }{\nabla }^{\mu }{\rm Y}\left(\psi \right)\right)R^{\nu \rho }-4\left({\nabla }_{\rho }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R^{\mu \rho }+4\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R^{\mu \nu }+4g^{\mu \nu }\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\rho \sigma }-4\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\mu \rho \nu \sigma }.\hfill \end{array}$$

(7)

In the specific case of four dimensions, i.e., when the dimension $N=4$, Equation (7) simplifies to the following form:

$$\begin{array}{cc}\hfill {\mathcal{I}}_{\mu \nu }=& -{\displaystyle \frac{1}{2{\chi }^2}}\left(R_{\mu \nu }{f}_R-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }f\left(R\right)+[g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }]f_R\right)+\left({\displaystyle \frac{1}{2}}{\partial }^{\mu }\psi {\partial }^{\nu }\psi -{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\partial }_{\rho }\psi {\partial }^{\rho }\psi \right)-{\displaystyle \frac{1}{2}}{g}^{\mu \nu }\Phi \left(\psi \right)\hfill \\ \hfill & +2\left({\nabla }^{\mu }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R-2g^{\mu \nu }\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R-4\left({\nabla }_{\rho }{\nabla }^{\mu }{\rm Y}\left(\psi \right)\right)R^{\nu \rho }-4\left({\nabla }_{\rho }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R^{\mu \rho }+4\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R^{\mu \nu }\hfill \\ \hfill & +4g^{\mu \nu }\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\rho \sigma }-4\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\mu \rho \nu \sigma }=0.\hfill \end{array}$$

(8)

The trace of the field Equations (8) can be expressed in the following manner:

$$\begin{array}{c}\hfill \mathcal{I}=3\square f_R+R{f}_R-2f\left(R\right)+{\displaystyle \frac{1}{2}}{\partial }^{\rho }\psi {\partial }_{\rho }\psi +2\Phi \left(\psi \right)+2\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R-4\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\rho \sigma }\equiv 0.\end{array}$$

(9)

From Equation (9), one can derive the expression for the function $f\left(R\right)$ in the following form: (Given the focus of our current investigation on obtaining a vacuum solution, we will adopt relativistic units, which allow us to set the constant $2{\chi }^2=1$. This simplification is beneficial for our calculations).

$$\begin{array}{c}\hfill f\left(R\right)={\displaystyle \frac{1}{2}}\left[3\square f_R+R{f}_R+{\displaystyle \frac{1}{2}}{\partial }^{\rho }\psi {\partial }_{\rho }\psi +2\Phi \left(\psi \right)+2\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R-4\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\rho \sigma }\right].\end{array}$$

(10)

Using Equation (10) in Equation (8) we get:

$$\begin{array}{cc}\hfill & {\mathcal{I}}_{\mu \nu }=R_{\mu \nu }{f}_R-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }R{f}_R+{\displaystyle \frac{1}{4}}{g}_{\mu \nu }\square f_R-{\nabla }_{\mu }{\nabla }_{\nu }{f}_R+{\displaystyle \frac{1}{8}}{g}_{\mu \nu }{\partial }^{\rho }\psi {\partial }_{\rho }\psi -{\displaystyle \frac{1}{2}}{\partial }_{\mu }\psi {\partial }_{\nu }\psi -2\left({\nabla }^{\mu }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R+{\displaystyle \frac{3}{2}}{g}^{\mu \nu }\left({\nabla }^2{\rm Y}\left(\psi \right)\right)\\ & +4\left({\nabla }_{\rho }{\nabla }^{\mu }{\rm Y}\left(\psi \right)\right)R^{\nu \rho }+4\left({\nabla }_{\rho }{\nabla }^{\nu }{\rm Y}\left(\psi \right)\right)R^{\mu \rho }-4\left({\nabla }^2{\rm Y}\left(\psi \right)\right)R^{\mu \nu }-3g^{\mu \nu }\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\rho \sigma }+4\left({\nabla }_{\rho }{\nabla }_{\sigma }{\rm Y}\left(\psi \right)\right)R^{\mu \rho \nu \sigma }=0.\end{array}$$

(11)

It is well known that in four dimensions, the Gauss–Bonnet invariant acts as a total derivative. Consequently, if the function ${\rm Y}$ is a constant, then the term involving the Gauss–Bonnet invariant does not contribute to Equation (11). In the following section, we will apply the field Equation (11) to a spherically symmetric spacetime. Our goal is to derive analytical solutions for the resulting differential equations.

3. BH Solution with Spherical Symmetry in $\mathit{f}(\mathit{R},\mathit{G})$

To analyze the equations of motion (11) and derive general expressions for the arbitrary functions $f\left(R\right)$ and ${\rm Y}\left(\psi \right)$ without imposing any specific constraints on the Ricci scalar R or ${\rm Y}\left(\psi \right)$, we utilize a spacetime characterized by spherical symmetry. This spacetime involves one unknown function, $B\left(r\right)$, and is represented by the metric

$$\begin{array}{ccc}\hfill & & d{s}^2=-B\left(r\right)d{t}^2+{\displaystyle \frac{d{r}^2}{B\left(r\right)}}+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),\hfill \end{array}$$

(12)

The Ricci scalar, R, of the metric (12) is calculated to be

$$\begin{array}{c}\hfill \mathit{R}\left(r\right)=-{\displaystyle \frac{r^2{B}^{\prime \prime }+4r{B}^{\prime }+2B-2}{r^2}},\end{array}$$

(13)

where $B\equiv B\left(r\right)$, $B^{\prime }={\displaystyle \frac{dB}{dr}}$, $B^{\prime \prime }={\displaystyle \frac{d^{2}B}{d{r}^2}}$. Upon substituting Equations (10) and (11) into the metric (12), and utilizing the expression for the Ricci scalar R from Equation (13), we obtain

$$\begin{array}{cc}\hfill & {{\mathcal{I}}_t}^t={\displaystyle \frac{1}{8r^3}}\left[56{{\rm Y}}^{\prime }{B}^{\prime 2}{r}^2-16{{\rm Y}}^{\prime }{B}^{\prime }r-48{{\rm Y}}^{\prime }B+{\psi }^{2}B{r}^3+12{{\rm Y}}^{\prime }{B}^{\prime }{r}^3{B}^{\prime \prime }+96{{\rm Y}}^{\prime }{B}^{\prime }rB+12{{\rm Y}}^{\prime \prime }B{r}^3{B}^{\prime \prime }+56{{\rm Y}}^{\prime \prime }B{r}^2{B}^{\prime }\right.\hfill \\ \hfill & \left.+32{{\rm Y}}^{\prime }B{B}^{\prime \prime }{r}^2-2r^3{F}^{\prime }{B}^{\prime }+2r^3{F}^{\prime \prime }B+4r^2{F}^{\prime }B-4Fr-2F{r}^3{B}^{\prime \prime }+4FrB+48{{\rm Y}}^{\prime }{B}^2+12r^3{{\rm Y}}^{\prime }{B}^{\prime }+12r^3{{\rm Y}}^{\prime \prime }+24r^2{{\rm Y}}^{\prime }B\right]=0,\hfill \\ \hfill & {{\mathcal{I}}_r}^r={\displaystyle \frac{1}{8r^3}}\left[56{{\rm Y}}^{\prime }{B}^{\prime 2}{r}^2-16{{\rm Y}}^{\prime }{B}^{\prime }r-32{{\rm Y}}^{\prime \prime }Br-48{{\rm Y}}^{\prime }B-3{\psi }^{\prime 2}B{r}^3+12{{\rm Y}}^{\prime }{B}^{\prime }{r}^3{B}^{\prime \prime }+96{{\rm Y}}^{\prime }{B}^{\prime }rB+12{{\rm Y}}^{\prime \prime }B{r}^3{B}^{\prime \prime }-6r^3{F}^{\prime \prime }B\right.\hfill \\ \hfill & +12r^3{B}^{\prime }-4Fr+{{\rm Y}}^{\prime \prime }\{56B{r}^2{B}^{\prime }+12r^{3}B+32B^{2}r\}-2r^3{F}^{\prime }{B}^{\prime }+4r^2{F}^{\prime }B-2F{r}^3{B}^{\prime \prime }+4FrB+{{\rm Y}}^{\prime }\left\{48B^2+32B{B}^{\prime \prime }{r}^2\right.\hfill \\ \hfill & \left.\left.+24r^{2}B\right\}\right]=0,\hfill \\ \hfill & {{\mathcal{I}}_{\theta }}^{\theta }={{\mathcal{I}}_{\varphi }}^{\varphi }={\displaystyle \frac{1}{8r^3}}\left[40{{\rm Y}}^{\prime }{B}^{\prime 2}{r}^2-32{{\rm Y}}^{\prime }{B}^{\prime }r-32{{\rm Y}}^{\prime \prime }Br-48{{\rm Y}}^{\prime }B+{\psi }^{\prime 2}B{r}^3+12{{\rm Y}}^{\prime }{B}^{\prime }{r}^3{B}^{\prime \prime }+144{{\rm Y}}^{\prime }{B}^{\prime }rB+12{{\rm Y}}^{\prime \prime }B{r}^3{B}^{\prime \prime }\right.\hfill \\ \hfill & +2r^3{F}^{\prime }{B}^{\prime }+4{{\rm Y}}^{\prime \prime }\{10B{r}^2{B}^{\prime }+3r^{3}B+8B^{2}r\}+2r^3{F}^{\prime \prime }B-4r^2{F}^{\prime }B+2F\{2r+r^3{B}^{\prime \prime }-2rB\}+4{{\rm Y}}^{\prime }\left\{12B^2+3r^3{B}^{\prime }\right.\hfill \\ \hfill & \left.\left.+4B{B}^{\prime \prime }{r}^2+6r^{2}B\right\}\right]=0,\hfill \\ \hfill & \mathcal{I}=-{\displaystyle \frac{1}{2r^2}}\left[8{{\rm Y}}^{\prime }{B}^{\prime 2}r-8{{\rm Y}}^{\prime }{B}^{\prime }-8{{\rm Y}}^{\prime \prime }B+4f{r}^2-\Phi r^2-{\psi }^{\prime 2}B{r}^2+24{{\rm Y}}^{\prime }B{B}^{\prime }+8{{\rm Y}}^{\prime \prime }Br{B}^{\prime }+8{{\rm Y}}^{\prime }B{B}^{\prime \prime }r-6r^2{F}^{\prime }{B}^{\prime }-6r^2{F}^{\prime \prime }B\right.\hfill \\ \hfill & \left.-12F^{\prime }Br-4F+2F{r}^2{B}^{\prime \prime }+8Fr{B}^{\prime }+4FB+8{{\rm Y}}^{\prime \prime }{B}^2\right]=0,\hfill \end{array}$$

(14)

where $F\equiv F\left(r\right)=f_R={\displaystyle \frac{df\left(R\right(r\left)\right)}{dR\left(r\right)}}$, $F^{\prime }={\displaystyle \frac{dF\left(r\right)}{dr}}$, $F^{\prime \prime }={\displaystyle \frac{d^{2}F\left(r\right)}{d{r}^2}}$, $F^{\prime \prime \prime }={\displaystyle \frac{d^{3}F\left(r\right)}{d{r}^3}}$. Given the context of spherical symmetry, we express $f\left(R\right)$ as $f\left(r\right)$, where R is a function of the radial coordinate r. It is noteworthy that the system of differential equations derived from Equation (14) matches those presented in [91,93] when ${\rm Y}\left(r\right)=1$. Specifically, if $F\left(r\right)=1$ and ${\rm Y}\left(r\right)$ is a constant, it can be demonstrated that the set of Equation (14), excluding the trace equation, reduces to two independent equations (for further details, refer to [40,94]).

However, if ${\rm Y}\left(r\right)$ is not constant and $F\left(r\right)\ne 1$, the system of equations expands to include three differential equations (again, excluding the trace equation). These equations involve four unknown quantities: B, F, H, and $\psi$. To fully determine the system and find a solution, we require one additional condition or constraint.

This highlights the complexity of solving such systems in modified gravity theories, particularly in $f(R,G)$ gravity, where the introduction of new functions and the relaxation of certain assumptions lead to richer dynamics but also necessitate a more nuanced approach to finding solutions. From Equation (14), particularly focusing on the trace equation, we observe that setting $F={\rm Y}\left(r\right)=\Phi \left(r\right)=0$ results in $f\left(R\right)=R$. This indicates that the functions F and ${\rm Y}\left(r\right)$ significantly influence the study only when they are non-zero.

Now, let us assume $B\left(r\right)$ is an arbitrary function and aim to derive the forms of F, ${\rm Y}\left(r\right)$, and $\varphi \left(r\right)$. By manipulating Equation (14), specifically subtracting the third equation from the first, we arrive at

$$\begin{array}{cc}\hfill & F\left(r\right)={\displaystyle \frac{1}{\aleph }}\left[\int {\displaystyle \frac{4\left\{B\left(2-2B+B^{\prime }r\right){{\rm Y}}^{\prime \prime }+{{\rm Y}}^{\prime }\left[B{B}^{\prime \prime }r+B^{\prime }\left(B^{\prime }r+1-3B\right)\right]\right\}\aleph }{r\left(B^{\prime }r-2B\right)}}dr+c_1\right],\hfill \end{array}$$

(15)

where $\aleph \equiv \aleph \left(r\right)$ is defined as

$$\begin{array}{c}\hfill \aleph \left(r\right)=exp\int {\displaystyle \frac{2+r^2{B}^{\prime \prime }-2B}{r\left(B^{\prime }r-2B\right)}}dr.\end{array}$$

(16)

Given the relation $F\left(r\right)\equiv f_R={\displaystyle \frac{\partial f}{\partial r}}{\displaystyle \frac{\partial r}{\partial R}}$, we can derive the form of $f\left(R\right)\equiv f\left(r\right)$ as follows:

$$\begin{array}{cc}\hfill & f\left(r\right)=\int {\displaystyle \frac{1}{\aleph \left(r\right)r^3}}\left[4\int {\displaystyle \frac{\left(2{{\rm Y}}^{\prime \prime }{B}^2-2{{\rm Y}}^{\prime \prime }B-{{\rm Y}}^{\prime \prime }Br{B}^{\prime }-{{\rm Y}}^{\prime }B{B}^{\prime \prime }r-{{\rm Y}}^{\prime }{B}^{\prime 2}r-{{\rm Y}}^{\prime }{B}^{\prime }+3{{\rm Y}}^{\prime }B{B}^{\prime }\right)\aleph \left(r\right)}{r\left(2B-B^{\prime }r\right)}}dr+c_1\right]\hfill \\ \hfill & \times \left[2B^{\prime }r-B^{\prime \prime \prime }{r}^3-4r^2{B}^{\prime \prime }-4+4B\right]dr+c_2.\hfill \end{array}$$

(17)

From Equation (14), combining the first equation with 1/3 times the second equation results in the following expression:

$$\begin{array}{cc}\hfill & {\rm Y}\left(r\right)=\int {\displaystyle \frac{1}{2{\aleph }_1}}\left[\int {\displaystyle \frac{{\aleph }_1\left(2F^{\prime }Br-F{r}^2{B}^{\prime \prime }-r^2{F}^{\prime }{B}^{\prime }-2F+2FB\right)}{\left(3r^2-2+2B+14B^{\prime }r+3r^2{B}^{\prime \prime }\right)B}}dr-2c_1\right]dr+c_2,\hfill \end{array}$$

(18)

where ${\aleph }_1\equiv {\aleph }_1\left(r\right)$ is defined as

$$\begin{array}{cc}\hfill & {\aleph }_1=exp\int {\displaystyle \frac{8r^2{B}^{\prime \prime }B+3r^3{B}^{\prime \prime }{B}^{\prime }+14B^{\prime 2}{r}^2+24B{B}^{\prime }r-4B^{\prime }r+3B^{\prime }{r}^3+12B^2-12B+6B{r}^2}{r\left(3r^2-2+2B+14B^{\prime }r+3r^2{B}^{\prime \prime }\right)B}}dr.\hfill \end{array}$$

(19)

Finally, from Equation (14), subtracting the first equation from the second equation results in

$$\begin{array}{cc}\hfill & \psi =\pm \int {\displaystyle \frac{\sqrt{8{{\rm Y}}^{\prime \prime }B-8{{\rm Y}}^{\prime \prime }-2r^2{F}^{\prime \prime }}}{r}}dr+c_1.\hfill \end{array}$$

(20)

Equation (20) indicates that the expression under the square root must be positive, otherwise we will get a ghost. This condition is crucial for the equation to be valid and to ensure that the solutions derived from it are physically meaningful within the context of the problem being studied. Ensuring positivity helps avoid complex or non-real solutions that may not have a clear interpretation in the physical domain.

To maintain this positivity, certain constraints or conditions on the variables and parameters involved in the expression under the square root must be satisfied. These conditions might restrict the range of values these variables and parameters can take, directly influencing the applicability and scope of the solutions obtained from Equation (20).

Given the constants of integration $c_1$ and $c_2$ from Equations (15), (18) and (20), and substituting these into the trace equation from Equation (14), we derive the potential in the form

$$\begin{array}{cc}\hfill & \Phi ={\displaystyle \frac{1}{r^2}}\left[4f{r}^2+8{{\rm Y}}^{\prime }{B}^{\prime 2}r-{\psi }^{\prime 2}B{r}^2+24{{\rm Y}}^{\prime }B{B}^{\prime }+8{{\rm Y}}^{\prime \prime }Br{B}^{\prime }+8{{\rm Y}}^{\prime }B{B}^{\prime \prime }r-6r^2{F}^{\prime }{B}^{\prime }-6r^2{F}^{\prime \prime }B-12F^{\prime }Br-4F+2F{r}^2{B}^{\prime \prime }\right.\hfill \\ \hfill & \left.+8Fr{B}^{\prime }+4FB+8{{\rm Y}}^{\prime \prime }{B}^2-8{{\rm Y}}^{\prime }{B}^{\prime }-8{{\rm Y}}^{\prime \prime }B\right].\hfill \end{array}$$

(21)

In the subsequent subsection, we will explore specific form of the ansatz B that modify the Schwarzschild solution. This approach involves examining how alterations to the traditional Schwarzschild metric can lead to new solutions that potentially describe more complex or exotic spacetime geometries.

Altered Schwarzschild Solution

In this investigation, we will adopt a specific form for the ansatz (B) that alters the Schwarzschild spacetime, resulting in the following structure: [95,96] (Using the extended gravitational decoupling approach, the study presented in [95,96] investigated the emergence of hairy black holes resulting from matter surrounding the central source described by the Schwarzschild metric. By requiring that the solution consistently admits a well-defined event horizon, they derived the hairy black hole solution presented in Equation (22)).

$$\begin{array}{c}\hfill B=1-{\displaystyle \frac{2\mathcal{M}}{r}}+\alpha e^{-{\displaystyle \frac{r}{\mathcal{M}-\frac{\alpha \Xi }{2}}}}.\end{array}$$

(22)

Here, $\alpha$ serves as the coupling constant, and $\Xi$ is introduced as a new parameter possessing dimensions of length. This parameter $\Xi$ is tied to a fundamental feature, often referred to as a “hair” of the BH. The mass of the BH, denoted by $\mathcal{M}$, is related to the Schwarzschild mass M through a specific relationship:

$$\begin{array}{c}\hfill \mathcal{M}=M+{\displaystyle \frac{\alpha \Xi }{2}}.\end{array}$$

(23)

The influence of the parameters $\alpha$ and $\Xi$ on various physical phenomena, including geodesic motion, gravitational lensing, energy extraction processes, and the thermodynamics of BHs, has been examined in the literature [97,98]. These studies explore how these parameters modify the traditional behaviors predicted by GR, offering insights into potential observable effects and theoretical implications within extended theories of gravity or modified spacetime metrics. Applying Equation (22) to Equations (15), (18) and (20), we derive extensive expressions for $F\left(r\right)$, ${\rm Y}\left(r\right)$, $f\left(r\right)$, and others. The explicit formulations of these terms are listed in the accompanying notebook for this research. Here, we will detail the asymptotic behavior of these expressions, which results in

$$\begin{array}{cc}\hfill & F{\left(r\right)}_{r\to 0}={f_R}_{r\to 0}\approx -{\displaystyle \frac{1}{9}}{\displaystyle \frac{\left(7+2\alpha \right)c_2}{{\mathcal{M}}^{2}r}}-{\displaystyle \frac{5}{3}}{\displaystyle \frac{c_2}{\mathcal{M}{r}^2}}-{\displaystyle \frac{4c_2}{r^3}},\hfill \\ \hfill & {\rm Y}{\left(r\right)}_{r\to 0}\approx c_1+{\displaystyle \frac{c_{2}ln\left(r\right)}{2\mathcal{M}}}+{\displaystyle \frac{c_{2}r(1+\alpha )}{4{\mathcal{M}}^2}}+{\displaystyle \frac{c_2[2\mathcal{M}(1+{\alpha }^2)-\alpha {(1+\alpha )}^2\Xi ]r^2}{32{\mathcal{M}}^3{\mathcal{M}}_1}},\hfill \\ \hfill & f{\left(r\right)}_{r\to 0}\approx {\displaystyle \frac{8\alpha }{27{\mathcal{M}}^2{\mathcal{M}}_1{r}^3}}\left[\left(\mathcal{M}-{\displaystyle \frac{7\Xi }{4}}\right)\alpha -{\displaystyle \frac{{\alpha }^2\Xi }{2}}-{\displaystyle \frac{31}{4}}\mathcal{M}\right]c_2-{\displaystyle \frac{13c_2\alpha }{3}}{\displaystyle \frac{\left(\mathcal{M}+\frac{5}{26}\alpha \Xi \right)}{\mathcal{M}{\mathcal{M}}_1{r}^4}}+{\displaystyle \frac{16}{5}}{\displaystyle \frac{c_2\alpha }{r^5}},\hfill \\ \hfill & \psi {\left(r\right)}_{r\to \infty }=c_1+{\displaystyle \frac{\alpha \sqrt{2c_2}}{M\sqrt{r}}}-{\displaystyle \frac{4\sqrt{2c_2}}{3\sqrt{r^3}}},\Phi {\left(r\right)}_{r\to 0}\approx c_3+{\displaystyle \frac{c_4}{r}}+{\displaystyle \frac{c_5}{r^2}}.\hfill \end{array}$$

(24)

It is important to note that, using the solution provided by Equation (22), the scalar field $\psi \left(r\right)$ of Equation (20), whose asymptotic form given by Equation (24) will exhibit a positive behavior when the constant $c_2>0$. If $c_2<0$, the scalar field would become ghostly. In this study, we assume that $c_2>0$, a condition that is consistently applied throughout the analysis, as demonstrated by the plots presented in this work. Ultimately, by utilizing Equation (22), we derive the explicit expressions for the Ricci scalar and Gauss–Bonnet term as follows:

$$\begin{array}{cc}\hfill & R=-{\displaystyle \frac{2\alpha e^{\frac{-r}{{\mathcal{M}}_1}}\left[{\alpha }^2{\Xi }^2-4\Xi \left(\mathcal{M}-r\right)\alpha +4{\mathcal{M}}^2-8r\mathcal{M}+2r^2\right]}{4r^2{\left(2\mathcal{M}-\alpha \Xi \right)}^2}}, \hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & G={\displaystyle \frac{32{\alpha }^2{e}^{\frac{-2r}{{\mathcal{M}}_1}}{r}^4-16\alpha \left[{\alpha }^2{\Xi }^2-2\Xi \left(2\mathcal{M}+r\right)\alpha +2r^2+4{\mathcal{M}}^2+4r\mathcal{M}\right]r\mathcal{M}{e}^{\frac{-r}{{\mathcal{M}}_1}}+192{{\mathcal{M}}_1}^2{\mathcal{M}}^2}{2r^6{{\mathcal{M}}_1}^2}},\hfill \end{array}$$

(26)

where ${\mathcal{M}}_1$ is figured out as

$$\begin{array}{c}\hfill {\mathcal{M}}_1=\left(\mathcal{M}-{\displaystyle \frac{\alpha \Xi }{2}}\right).\end{array}$$

(27)

Equation (27) indicates that setting $\alpha$ to zero results in ${\mathcal{M}}_1$ equating to $\mathcal{M}$, which in turn equals the gravitational mass of Schwarzschild, i.e., M. The dynamics of the scalar field, as described by Equation (24), is illustrated in Figure 1a, demonstrating a positive pattern.

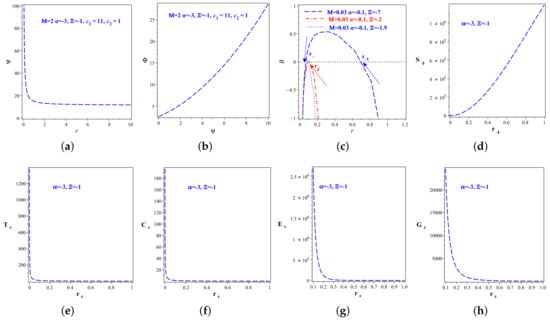
Figure 1. Illustrative diagrams of the thermodynamic properties for the BH solution (22) include: (a) a representation of the scalar field $\psi \left(r\right)$, demonstrating a positive trend; (b) the relationship between the potential $v\left(\psi \right)$ and $\psi$, showcasing its behavior; (c) graphical depiction of the ansatz function $B\left(r\right)$ as outlined in Equation (22); (d) an illustration of the horizon entropy’s typical behavior, indicating that S increases quadratically with $r_{+}$, ensuring a consistently positive entropy; (e) the characteristic behavior of the horizon temperature (42), highlighting its positive values; (f) the heat capacity (45) graph, showing a positive value that suggests the BH’s stability; (g) a visual representation of the quasi-local energy pattern; (h) a depiction of the Gibb’s free energy of the horizon, indicating that $G_{+}$ remains positive, thus affirming the stability of the presented model. These plots collectively provide insights into the thermodynamic stability and characteristics of the BH solution under consideration: (a) the scalar field $\psi$ in relation to the radial coordinate r; (b) the potential V as a function of the scalar field $\psi$; (c) the behavior of the metric (38); (d) the Bekenstein–Hawking entropy; (e) the Hawking temperature; (f) the heat capacity; (g) the quasi-local energy; (h) the Gibbs free energy.

In the following section, we will delve into the physical characteristics of the BH as defined by Equation (22), alongside an exploration of its thermodynamic quantities.

4. Physics of the Black Hole (22)

To delve into the physics of the BH characterized by Equation (22), we will express its significant scalar quantities, such as the Kretschmann scalar and Ricci tensor, at the limits where r approaches infinity and zero. Upon performing these calculations, we obtain

$$\begin{array}{cc}\hfill & R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }\equiv K{\left(r\right)}_{r\to \infty }\approx {\displaystyle \frac{48{{\mathcal{M}}_1}^2}{r^6}},\hfill \\ & K{\left(r\right)}_{r\to 0}\approx {\displaystyle \frac{{\alpha }^2}{{{\mathcal{M}}_1}^4}}+{\displaystyle \frac{8{\alpha }^2}{{{\mathcal{M}}_1}^{3}r}}-{\displaystyle \frac{4{\alpha }^2}{{{\mathcal{M}}_1}^2{r}^2}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & R_{\mu \nu }{R}^{\mu \nu }\equiv R_t{\left(r\right)}_{r\to 0}\approx {\displaystyle \frac{{\alpha }^2}{2{{\mathcal{M}}_1}^4}}-{\displaystyle \frac{2{\alpha }^2}{{{\mathcal{M}}_1}^{3}r}}+{\displaystyle \frac{4{\alpha }^2}{{{\mathcal{M}}_1}^2{r}^2}}-{\displaystyle \frac{4{\alpha }^2}{{\mathcal{M}}_1{r}^3}}, \hfill \end{array}$$

$$\begin{array}{cc}\hfill & R_{r\to 0}\approx {\displaystyle \frac{\alpha r}{{{\mathcal{M}}_1}^3}}-{\displaystyle \frac{5\alpha }{{{\mathcal{M}}_1}^2}}+{\displaystyle \frac{6\alpha }{\mathcal{M}r}},\hfill \\ \hfill & G{\left(r\right)}_{r\to 0}\approx -4{\displaystyle \frac{\left(10\mathcal{M}\alpha -5\Xi {\alpha }^2+\mathcal{M}\right)\alpha }{5{{\mathcal{M}}_1}^5}}-{\displaystyle \frac{\left(16\Xi \mathcal{M}{\alpha }^2-4{\Xi }^2{\alpha }^3+\mathcal{M}\left(\Xi -16\mathcal{M}\right)\alpha -2{\mathcal{M}}^2\right)\alpha }{{\mathcal{M}}^{5}r}}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{\left[18\mathcal{M}{\alpha }^3{\Xi }^2-3{\alpha }^4{\Xi }^3+8\mathcal{M}\left(3{\mathcal{M}}^2-\Xi \mathcal{M}\right)\alpha -2\left(18{\mathcal{M}}^2-\Xi \mathcal{M}\right)\Xi {\alpha }^2+{\mathcal{M}}^3\right]\alpha }{3{\mathcal{M}}^5{r}^2}}. \hfill \end{array}$$

(29)

Equation (29) demonstrates that as r approaches infinity, the Kretschmann scalar remains finite. However, when r approaches zero, these quantities are not well-defined, indicating the presence of singularities. Nonetheless, these singularities are generally much softer compared to those found in BHs within the framework of GR. This suggests that the solution presented by Equation (22) diverges from GR, with its singularities being less severe than those in GR. Additionally, it is important to note that the solution provided by Equation (22) aligns with GR predictions when $\alpha =0$. Under this condition, the invariants derived from Equation (29) also coincide with those of the Schwarzschild geometry.

Upon incorporating Equation (22), the line element (12) transforms into the following expression:

$$\begin{array}{c}\hfill d{s}^2=-\left(1-{\displaystyle \frac{2\mathcal{M}}{r}}+\alpha e^{-{\displaystyle \frac{r}{M-\frac{\alpha \Xi }{2}}}}\right)d{t}^2+{\displaystyle \frac{d{r}^2}{1-\frac{2\mathcal{M}}{r}+\alpha e^{-\frac{r}{M-\frac{\alpha \Xi }{2}}}}}+r^2(d{\theta }^2+{sin}^{2}d{\varphi }^2).\end{array}$$

(30)

The line element (30) asymptotically approaches the following form:

$$\begin{array}{c}\hfill B{\left(r\right)}_{r\to 0}\approx (1+\alpha )-{\displaystyle \frac{2\mathcal{M}}{r}}-{\displaystyle \frac{\alpha r}{{\mathcal{M}}_1}}+{\displaystyle \frac{\alpha r^2}{2{{\mathcal{M}}_1}^2}}.\end{array}$$

(31)

This form does not align with the Schwarzschild spacetime, primarily due to the influence of the parameter $\alpha$. We hypothesize that this parameter is linked to the higher-order curvature terms within the $f(R,G)$ framework and is also affected by the contributions from ${\rm Y}\left(\psi \right)$. It can be readily verified that setting $\alpha =0$ allows for a seamless transition back to the Schwarzschild spacetime, as discussed in [99]. Equation (28) illustrates that for a non-zero value of the parameter $\alpha$, the Ricci scalar assumes a non-trivial value. This is attributed to the contributions from higher-order curvature terms and the Gauss–Bonnet term. Conversely, when $\alpha$ is set to zero, the Ricci scalar simplifies to a trivial value, aligning with the predictions for a BH in GR. The asymptotic behavior of $f\left(r\right)$, is given by

$$f\left(r\right)\approx {\displaystyle \frac{\left(5\alpha \Xi +26\mathcal{M}\right)c_2\alpha }{6{\mathcal{M}}_1\mathcal{M}{r}^4}}+{\displaystyle \frac{16\mathcal{M}{\mathcal{M}}_1{c}_2\alpha }{5{\mathcal{M}}_1\mathcal{M}{r}^5}}.$$

(32)

Using Equation (28) we get

$$\begin{array}{c}\hfill r\left(R\right)\approx {\displaystyle \frac{\left[R{\alpha }^2{\Xi }^2-4RM\alpha \Xi +20\alpha +4R{{\mathcal{M}}_1}^2\pm \sqrt{16{{\mathcal{M}}_1}^4{R}^2+160\alpha {{\mathcal{M}}_1}^{2}R+16{\alpha }^2}\right]{\mathcal{M}}_1}{8\alpha }}.\end{array}$$

(33)

By substituting Equation (33) into Equation (32), we obtain

$$\begin{array}{ccc}\hfill & & f{\left(R\right)}_{R\to 0}\approx \mp {\displaystyle \frac{\left(200{\alpha }^3\Xi +656{\alpha }^2\mathcal{M}\right)c_2}{3840\alpha {{\mathcal{M}}_1}^5\mathcal{M}}}\mp {\displaystyle \frac{\left(1440{\alpha }^2{\mathcal{M}}^2\Xi -2240\alpha {\mathcal{M}}^3+240{\alpha }^3\mathcal{M}{\Xi }^2-200{\alpha }^4{\Xi }^3\right)c_{2}R}{3840\alpha {{\mathcal{M}}_1}^5\mathcal{M}}}\hfill \\ & & \mp {\displaystyle \frac{\left(2320{\mathcal{M}}^3{\alpha }^2{\Xi }^2-3760{\mathcal{M}}^4\alpha \Xi -440{\mathcal{M}}^2{\alpha }^3{\Xi }^3-70\mathcal{M}{\alpha }^4{\Xi }^4+25{\alpha }^5{\Xi }^5+2080{\mathcal{M}}^5\right)c_2{R}^2}{3840\alpha {{\mathcal{M}}_1}^5\mathcal{M}}}\mp \dots ,\hfill \\ & & f{\left(R\right)}_{r\to 0}\approx {\displaystyle \frac{4{\alpha }^6{c}_2\left(-4{\mathcal{M}}^2\alpha \Xi +\mathcal{M}{\alpha }^2{\Xi }^2+4{\mathcal{M}}^3\right)}{5{{\mathcal{M}}_1}^{17}\mathcal{M}{R}^5}}+{\displaystyle \frac{4{\alpha }^6{c}_2\left(25{\alpha }^2\Xi +30\alpha M\right)}{5{{\mathcal{M}}_1}^{17}\mathcal{M}{R}^6}}+\dots \hfill \end{array}$$

(34)

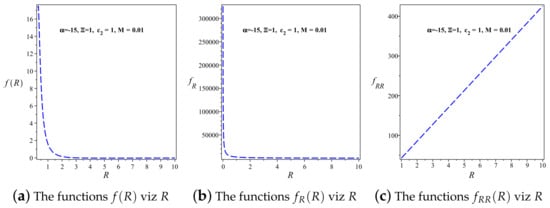
Using Equation (34), it is easy to find the first and second derivatives of $f\left(R\right)$ with respect to R to show if the model under consideration is stable or not. We show this behavior in Figure 2. The plots in Figure 2 demonstrate that the solution given by Equation (22) in the frame of $f\left(R\right)$ is stable due to the conditions $f\left(R\right)>0$, $f_R\left(R\right)>0$, and $f_{RR}\left(R\right)>0$ [100]. (The violation of the condition $f_{RR}>0$ gives rise to the negative mass squared $M^2$ for the scalaron field. Hence we require that $f_{RR}>0$ to avoid a tachyonic instability. The condition $f_R\equiv \partial f/\partial R>0$ is also required to avoid the appearance of ghosts. Thus, viable $f\left(R\right)$ dark energy models need to satisfy [37]). Furthermore, from Equation (24), we can derive $r\left(\psi \right)$ in the following form:

$$f_R>0,f_{RR}>0,\mathrm{for}R\ge R_0(>0).$$

(35)

$$\begin{array}{c}\hfill r\left(\psi \right)\approx 2{\displaystyle \frac{{\alpha }^2{c}_2}{{\mathcal{M}}^2{c_1}^2}}+4{\displaystyle \frac{{\alpha }^2{c}_2\psi }{{\mathcal{M}}^2{c_1}^3}}+\mathcal{O}\left({\psi }^2\right).\end{array}$$

(36)

By applying Equation (36) to Equation (24), we obtain

$$\begin{array}{c}\hfill {\rm Y}{\left(\psi \right)}_{\psi \to \infty }=c_6+c_7\psi +\mathcal{O}\left({\psi }^2\right),\Phi {\left(\psi \right)}_{\psi \to 0}=2c_8-c_9\psi +\mathcal{O}\left({\psi }^2\right),\end{array}$$

(37)

Here, the constants $c_6\dots c_9$, are derived from the combinations of the parameters $\alpha$, $c_1$, and $\mathcal{M}$. The nature of Equation (37) is illustrated in Figure 1b, demonstrating a positive trend.

Figure 2. Schematic diagrams: (a) f(R); (b) $f_R\left(R\right)$; (c) $f_{RR}\left(R\right)$ viz Ricci scalar R for the solution (22).

5. Thermodynamics of the BH

The metric potential for the temporal component of Equation (30) is expressed as follows:

$$\begin{array}{ccc}\hfill & & B\left(r\right)=1-{\displaystyle \frac{2\mathcal{M}}{r}}+\alpha e^{-{\displaystyle \frac{r}{\mathcal{M}-\frac{\alpha \Xi }{2}}}}.\hfill \end{array}$$

(38)

The dynamics of the line element as specified by Equation (30) are illustrated in Figure 1c. This figure suggests that the BH may have two horizons, determined by the roots of the equation $B\left(r\right)=0$. These horizons are denoted as $r_{-}$, representing the inner Cauchy horizon of the BH, and $r_{+}$, signifying the outer event horizon. Figure 1c demonstrates that for a parameter value of $\Xi =-7$, two distinct horizons are observed. When $\Xi =-2$, the two horizons merge into a single horizon, known as the degenerate horizon, where $r_{-}=r_{+}=r_d$. Finally, adjusting $\Xi$ to −1.9 shifts us into a parameter space where no horizons exist, leading to a naked singularity at the core.

The total mass enclosed within the event horizon (r) is determined by setting $B\left(r\right)=0$. Subsequently, the relationship between the mass and the radius of the horizon can be derived as follows:

$$\begin{array}{ccc}\hfill & & \mathcal{M}={\displaystyle \frac{1}{4}}\alpha r+{\displaystyle \frac{1}{4}}\alpha \Xi +{\displaystyle \frac{1}{4}}r\pm {\displaystyle \frac{1}{4}}\sqrt{{\alpha }^2{r}^2-2{\alpha }^{2}r\Xi -6\alpha r^2+{\alpha }^2{\Xi }^2-2r\alpha \Xi +r^2}.\hfill \end{array}$$

(39)

In the context of $f(R,G)$ gravity theory, the entropy is expressed as follows [101,102]:

$$S\left(r_{+}\right)={\displaystyle \frac{1}{4}}A(1+f_R),$$

(40)

where A denotes the area and $f_R$ represents the first derivative of $f\left(R\right)$ concerning the Ricci scalar. By substituting Equation (2), presented in the notebook, into Equation (40), we obtain the entropy of the BH described by Equation (30) as follows:

$$\begin{array}{cc}\hfill & {S_{+}}_{Equation\left(30\right)}=-{\displaystyle \frac{\pi \left(-30{\mathcal{M}}^2{r_{+}}^5+15\mathcal{M}{r_{+}}^5\alpha \Xi +25c_2{\alpha }^2{r}_{+}\Xi +130c_2\alpha r_{+}\mathcal{M}-96{\mathcal{M}}^2{c}_2\alpha +48\mathcal{M}{c}_2{\alpha }^2\Xi \right)}{30{r_{+}}^3{\mathcal{M}}_1\mathcal{M}}}.\hfill \end{array}$$

(41)

The above equation suggests that the entropy is influenced by the higher-order curvature terms. The behavior of Equation (41) is depicted in Figure 1d, demonstrating a positive value for entropy.

The Hawking temperature is typically defined in the following manner for cases where the metric ansatz functions are not identical [103,104,105,106]:

$$T_{+}={\displaystyle \frac{\kappa }{2\pi }}={\displaystyle \frac{1}{4\pi }}{\left({\displaystyle \frac{d{g}_{tt}}{dr}}\right)}_{r\to r_{+}},$$

(42)

where $\kappa$ represents the surface gravity of the BH. By applying Equation (30) to Equation (42), we derive the Hawking temperature as follows:

$$\begin{array}{ccc}\hfill & & T_{+}={\displaystyle \frac{1}{2\pi }}\left({\displaystyle \frac{M}{{r_{+}}^2}}-{\displaystyle \frac{\alpha e^{-2\frac{r_{+}}{2{\mathcal{M}}_1}}}{2{\mathcal{M}}_1}}\right)\approx {\displaystyle \frac{1}{4\pi }}\left({\displaystyle \frac{2M}{{r_{+}}^2}}-{\displaystyle \frac{\alpha }{{\mathcal{M}}_1}}+{\displaystyle \frac{\alpha r_{+}}{{{\mathcal{M}}_1}^2}}-{\displaystyle \frac{\alpha {r_{+}}^2}{2{{\mathcal{M}}_1}^3}}+{\displaystyle \frac{\alpha {r_{+}}^3}{6{{\mathcal{M}}_1}^4}}-{\displaystyle \frac{\alpha {r_{+}}^4}{24{{\mathcal{M}}_1}^5}}+{\displaystyle \frac{\alpha {r_{+}}^5}{120{{\mathcal{M}}_1}^6}}\right),\hfill \end{array}$$

(43)

The characteristics of the Hawking temperature, as described by Equation (43), are illustrated in Figure 1e. This figure demonstrates that $T_{+}$ maintains a positive value throughout.

Additionally, examining the stability of the BH solution is a crucial subject that can be explored both dynamically and through perturbative analysis [107,108,109]. To assess the thermodynamic stability of BHs, it is necessary to derive the formula for the heat capacity, $H\left(r_{+}\right)$, at the event horizon, which has the form [110,111,112]

$$H_{+}={\displaystyle \frac{\partial M_{+}}{\partial T_{+}}}={\displaystyle \frac{\partial M_{+}}{\partial r_{+}}}{\left({\displaystyle \frac{\partial T_{+}}{\partial r_{+}}}\right)}^{-1}.$$

(44)

A BH is considered thermodynamically stable if its heat capacity, $H_{+}$, is positive. Conversely, it is deemed unstable if $H_{+}$ is negative. By substituting Equations (39) and (43) into Equation (44), we derive the heat capacity as follows:

$$\begin{array}{cc}\hfill & {H_{+}}_{Equation\left(\right)}={\displaystyle \frac{\frac{\alpha e^{-\frac{r}{{\mathcal{M}}_1}}}{2\pi {{\mathcal{M}}_1}^2}-\frac{M}{r^3}}{\pi \left(\frac{2M}{r^2}-{\frac{\alpha }{\mathcal{M}}}_1+\frac{\alpha r}{{{\mathcal{M}}_1}^2}\right)}}\approx {\displaystyle \frac{1}{\pi \left(\frac{2M}{r^2}-{\frac{\alpha }{\mathcal{M}}}_1+\frac{\alpha r}{{{\mathcal{M}}_1}^2}\right)}}\left[{\displaystyle \frac{\alpha }{{{\mathcal{M}}_1}^2}}-{\displaystyle \frac{4M}{r^3}}-{\displaystyle \frac{\alpha r}{{{\mathcal{M}}_1}^3}}+{\displaystyle \frac{\alpha r^2}{2{{\mathcal{M}}_1}^4}}-{\displaystyle \frac{\alpha r^3}{6{{\mathcal{M}}_1}^5}}+{\displaystyle \frac{\alpha r^4}{24{{\mathcal{M}}_1}^6}}\right].\hfill \end{array}$$

(45)

Equation (45) indicates that $H_{+}$ does not exhibit any local divergence. The behavior of the heat capacity is illustrated in Figure 1f, demonstrating a positive trend, which implies that the BH described by Equation (30) is stable.

The quasi-local energy is calculated as cited in [101,102,103,104,105,106]:

$${\displaystyle E\left(r_{+}\right)=\frac{1}{4}\int \left[2f_R\left(r_{+}\right)+{r_{+}}^2\left\{f\left(R\left(r_{+}\right)\right)-R\left(r_{+}\right)f_R\left(r_{+}\right)\right\}\right]d{r}_{+}.}$$

(46)

By applying Equation (30) to Equation (46), we obtain the quasi-local energy as follows:

$$\begin{array}{cc}\hfill & E_{+}={\displaystyle \frac{1}{2880{\mathcal{M}}^2{r}^2{{\mathcal{M}}_1}^4}}\left[\left(1440{\mathcal{M}}^6-2640r^3{\alpha }^2\Xi {\mathcal{M}}^2-1440r^3{\alpha }^3\Xi {\mathcal{M}}^2+720r^3{\alpha }^4{\Xi }^2\mathcal{M}+720r^3{\alpha }^3{\Xi }^2\mathcal{M}+680r^4{\alpha }^2\Xi \mathcal{M}\right.\right.\hfill \\ \hfill & +480r^4{\alpha }^3\Xi \mathcal{M}+960{\mathcal{M}}^3{r}^3{\alpha }^2+5760{\mathcal{M}}^3{r}^3\alpha -120r^4{\alpha }^4{\Xi }^2-420r^3{\alpha }^4{\Xi }^3-420r^4{\alpha }^3{\Xi }^2-120r^3{\alpha }^5{\Xi }^3-1480r^4\alpha {\mathcal{M}}^2\hfill \\ \hfill & -480r^4{\alpha }^2{\mathcal{M}}^2-11760\alpha r{\mathcal{M}}^5-2880{\mathcal{M}}^5\alpha \Xi +108{\Xi }^4{\mathcal{M}}^2{\alpha }^5-560ln\left(r\right){\mathcal{M}}^4{r}^2+1020{\Xi }^3{\alpha }^{4}r{\mathcal{M}}^2-600{\Xi }^3{\alpha }^{3}r{\mathcal{M}}^2\hfill \\ \hfill & -7920{\Xi }^2{\alpha }^{3}r{\mathcal{M}}^3+1800{\Xi }^2{\alpha }^{2}r{\mathcal{M}}^3+17040\Xi {\alpha }^{2}r{\mathcal{M}}^4-2400\Xi \alpha r{\mathcal{M}}^4+1200r{\mathcal{M}}^5+75{\Xi }^4{\alpha }^{5}r\mathcal{M}+75{\Xi }^4{\alpha }^{4}r\mathcal{M}-3456\Xi {\mathcal{M}}^5{\alpha }^2\hfill \\ \hfill & +2592{\Xi }^2{\mathcal{M}}^4{\alpha }^3-864{\Xi }^3{\mathcal{M}}^3{\alpha }^4-840ln\left(r\right){\alpha }^3{\Xi }^2{r}^2{\mathcal{M}}^2-480ln\left(r\right){\alpha }^4{\Xi }^2{r}^2{\mathcal{M}}^2+160ln\left(r\right){\alpha }^5{\Xi }^3{r}^2\mathcal{M}+640ln\left(r\right){\alpha }^3{\mathcal{M}}^3\Xi r^2\hfill \\ \hfill & -260ln\left(r\right){\alpha }^4{\Xi }^3{r}^2\mathcal{M}+9040ln\left(r\right){\alpha }^2{\mathcal{M}}^3\Xi r^2+280{\Xi }^3{\alpha }^{3}ln\left(r\right)r^2\mathcal{M}-840{\Xi }^2{\alpha }^{2}ln\left(r\right)r^2{\mathcal{M}}^2+1120\Xi \alpha ln\left(r\right)r^2{\mathcal{M}}^3\hfill \\ \hfill & -35{\Xi }^4{\alpha }^{4}ln\left(r\right)r^2-320ln\left(r\right){\alpha }^2{M}^4{r}^2-11360ln\left(r\right)\alpha {\mathcal{M}}^4{r}^2-20ln\left(r\right){\alpha }^6{\Xi }^4{r}^2-80ln\left(r\right){\alpha }^5{\Xi }^4{r}^2+90{\mathcal{M}}^2{\alpha }^4{\Xi }^4\hfill \\ \hfill & \left.\left.-720{\mathcal{M}}^3{\alpha }^3{\Xi }^3+2160{\mathcal{M}}^4{\alpha }^2{\Xi }^2+1728{\mathcal{M}}^6\alpha \right)c_2\right].\hfill \end{array}$$

(47)

The behavior of the quasi-local energy is depicted in Figure 1g, illustrating a positive value for $E_{+}$. The Gibb’s free energy is defined as follows, as per [102,113]:

$$G\left(r_{+}\right)=M\left(r_{+}\right)-T\left(r_{+}\right)S\left(r_{+}\right).$$

(48)

The terms $M\left(r_{+}\right)$, $T\left(r_{+}\right)$, and $S\left(r_{+}\right)$ represent the mass, temperature, and entropy at the event horizon, respectively. By substituting Equations (39), (41), and (43) into Equation (48), we obtain

$$\begin{array}{cc}\hfill & {G_{+}}_{Equation\left(30\right)}={\displaystyle \frac{-64c_2}{40{{\mathcal{M}}_1}^3\mathcal{M}{r}^5}}\left[-{\displaystyle \frac{{\Xi }^2}{8}}\left\{{\mathcal{M}}^2\Xi -{\displaystyle \frac{3r}{8}}\left(r^2\Xi -{\displaystyle \frac{8r}{3}}-{\displaystyle \frac{25}{18}}\Xi \right)\mathcal{M}-{\displaystyle \frac{25}{96}}{r}^3\left(\Xi r-2\right)\right\}{\alpha }^4+{\displaystyle \frac{3}{4}}\left(\Xi {\mathcal{M}}^3-{\displaystyle \frac{3}{8}}\left({\displaystyle \frac{5}{18}}\Xi -{\displaystyle \frac{16}{9}}r\right.\right.\right.\hfill \\ \hfill & \left.\left.+r^2\Xi \right)r{\mathcal{M}}^2+{\displaystyle \frac{65}{96}}\left(\Xi r-{\displaystyle \frac{176}{195}}+{\displaystyle \frac{{\Xi }^2}{13}}\right)r^3\mathcal{M}+\left({\displaystyle \frac{25}{576}}{\Xi }^2-{\displaystyle \frac{25}{144}}\right)r^4\right)\Xi {\alpha }^3-3/2\left(\Xi {\mathcal{M}}^3-3/8r\left(-{\displaystyle \frac{8}{9}}r+r^2\Xi +{\displaystyle \frac{35}{18}}\Xi \right){\mathcal{M}}^2\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{155}{96}}{r}^3\left(\Xi r-{\displaystyle \frac{226}{465}}+{\displaystyle \frac{3}{31}}{\Xi }^2\right)\mathcal{M}+{\displaystyle \frac{25}{192}}{r}^4\left({\displaystyle \frac{356}{75}}+{\Xi }^2\right)\right)\mathcal{M}{\alpha }^2+\left({\mathcal{M}}^3+\left(-3/8r^3-{\displaystyle \frac{65}{48}}r\right){\mathcal{M}}^2+{\displaystyle \frac{245}{96}}{r}^3\left(r+{\displaystyle \frac{9}{49}}\Xi \right)\mathcal{M}\right.\hfill \\ \hfill & \left.\left.+{\displaystyle \frac{25}{64}}\Xi r^4\right){\mathcal{M}}^2\alpha -{\displaystyle \frac{5}{16}}\left(\mathcal{M}+5/6r\right)r^3{\mathcal{M}}^3\right].\hfill \end{array}$$

(49)

We illustrate the Gibb’s free energy of Equation (49) in Figure 1h. This figure demonstrates that the Gibb’s energy consistently maintains a positive value.

Multi-Horizons Spacetime

In this section we discuss if the spacetime (30) can create a multi-horizon or not. As we discussed in Section 5, we can reproduce two horizons when we give fixed values for the gravitational mass and the dimensionless parameter $\alpha$ and solve for $\Xi$. From this calculation we show that if $\Xi <-2$ we can create two horizons, if $\Xi =-2$ then the two horizons coincide, and if $\Xi >-2$ then the naked singularity region appears. Now we follow another procedure by assuming certain values of M and $\Xi$ and solving for the dimensionless parameter $\alpha$. In this case, as Figure 3 shows, if $\alpha >11.5$ we can get three horizons, if $\alpha =11.5$ two of these horizons coincide, and for $\alpha <11.5$ we only have one horizon. It is worth noting that this case, multi-horizon, differs from the first case, two horizons, in that we have only obtained one critical value for $\Xi$. It is important to stress that if we use the numerical values of the multi-horizon spacetime, i.e., $M=1,\Xi =0.1,\mathrm{and}\alpha =13$, we can create similar behavior for the thermodynamic quantities presented in Section 5.

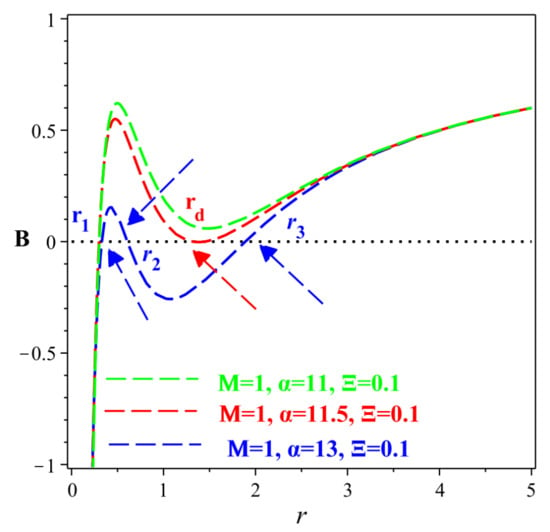
Figure 3. Multi-horizons for the spacetime (30).

6. Geodesic and Geodesic Deviation

The paths followed by a particle within a gravitational field are determined by

$${\displaystyle \frac{d^2{x}^{\sigma }}{d{\tau }^2}}+\left\{\begin{array}{c}\sigma \hfill \\ \mu \nu \hfill \end{array}\right\}{\displaystyle \frac{d{x}^{\mu }}{d\tau }}{\displaystyle \frac{d{x}^{\nu }}{d\tau }}=0,$$

(50)

where $\tau$ represents an affine parameter along the geodesic.

Now let us discuss the geodesic of the line element (30). To this end, we use the line element (30) and assuming the motion to be in the equatorial plane ($\theta =\pi /2$) without loss of generality. The Lagrangian for a test particle is then

$$\begin{array}{c}\hfill \mathcal{L}={\displaystyle \frac{1}{2}}\left[-B\left(r\right){\dot{t}}^2+{\displaystyle \frac{1}{B\left(r\right)}}{\dot{r}}^2+r^2{\dot{\varphi }}^2\right],\end{array}$$

(51)

where the dot denotes derivative with respect to proper time $\tau$. Due to the time translation and rotational symmetries, we have two conserved quantities:

$$\begin{array}{c}\hfill E=B\left(r\right)\dot{t},L=r^2\dot{\varphi },\end{array}$$

(52)

corresponding to the energy and angular momentum per unit mass, respectively. The normalization condition for a timelike geodesic ($u^{\mu }{u}_{\mu }=-1$) leads to

$$\begin{array}{c}\hfill -B\left(r\right){\dot{t}}^2+{\displaystyle \frac{1}{B\left(r\right)}}{\dot{r}}^2+r^2{\dot{\varphi }}^2=-1.\end{array}$$

(53)

Using the conserved quantities, we obtain

$$\begin{array}{c}\hfill {\dot{r}}^2+V_{\mathrm{eff}}\left(r\right)=0,\end{array}$$

(54)

where the effective potential $V_{\mathrm{eff}}\left(r\right)$ includes terms depending on $B\left(r\right)$ and L.

For circular orbits, we require

$$\begin{array}{c}\hfill \dot{r}=0,{\displaystyle \frac{d{V}_{\mathrm{eff}}}{dr}}=0.\end{array}$$

(55)

These conditions allow us to solve for L and E as functions of r and to determine the orbital angular velocity:

$$\begin{array}{c}\hfill \Omega ={\displaystyle \frac{d\varphi }{dt}}={\displaystyle \frac{\dot{\varphi }}{\dot{t}}}={\displaystyle \frac{L/r^2}{E/B\left(r\right)}}={\displaystyle \frac{B\left(r\right)L}{E{r}^2}}.\end{array}$$

(56)

Using the geodesic equations, this ultimately gives

$$\begin{array}{c}\hfill {\Omega }^2={\displaystyle \frac{B^{\prime }\left(r\right)}{2r}},\end{array}$$

(57)

which yields the orbital period:

$$\begin{array}{c}\hfill T={\displaystyle \frac{2\pi }{\Omega }},\Rightarrow T^2={\displaystyle \frac{4{\pi }^2}{{\Omega }^2}}={\displaystyle \frac{8{\pi }^{2}r}{B^{\prime }\left(r\right)}}.\end{array}$$

(58)

In the weak-field limit where $B\left(r\right)1-{\displaystyle \frac{2\mathcal{M}}{r}}+\alpha e^{-{\displaystyle \frac{r}{\mathcal{M}-\frac{\alpha \Xi }{2}}}}$, we recover the classical Kepler’s third law:

$$\begin{array}{c}\hfill T^2\propto r^3+\mathcal{O}\left(r^5\right).\end{array}$$

(59)

However, in our modified gravity model, the functional form of $B\left(r\right)$ deviates from the Schwarzschild form, leading to corrections to the Keplerian relation. These corrections are direct consequences of the modified field equations and can, in principle, be linked to the total energy of the system. Such deviations could serve as observational signatures distinguishing our model from general relativity.

Equation (50) outlines the geodesic equations, and their deviation is expressed as [114]

$${\displaystyle \frac{d^2{\eta }^{\sigma }}{d{\tau }^2}}+2\left\{\begin{array}{c}\sigma \hfill \\ \mu \nu \hfill \end{array}\right\}{\displaystyle \frac{d{x}^{\mu }}{d\tau }}{\displaystyle \frac{d{\eta }^{\nu }}{ds}}+{\left\{\begin{array}{c}\sigma \hfill \\ \mu \nu \hfill \end{array}\right\}}_{,\rho }{\displaystyle \frac{d{x}^{\mu }}{d\tau }}{\displaystyle \frac{d{x}^{\nu }}{d\tau }}{\eta }^{\rho }=0,$$

(60)

where ${\eta }^{\rho }$ denotes the deviation 4-vector. By incorporating Equations (50) and (60) into the line element (12), we obtain

$${\displaystyle \frac{d^{2}t}{d{\tau }^2}}=0,{\displaystyle \frac{1}{2}}{B}^{\prime }\left(r\right){\left({\displaystyle \frac{dt}{d\tau }}\right)}^2-r{\left({\displaystyle \frac{d\varphi }{d\tau }}\right)}^2=0,{\displaystyle \frac{d^2\theta }{d{\tau }^2}}=0,{\displaystyle \frac{d^2\varphi }{d{\tau }^2}}=0,$$

(61)

and for Equation (60) we get

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d^2{\eta }^1}{d{\tau }^2}}+B\left(r\right)B^{\prime }\left(r\right){\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{d{\eta }^0}{d\tau }}-2rB\left(r\right){\displaystyle \frac{d\varphi }{d\tau }}{\displaystyle \frac{d{\eta }^3}{d\tau }}+\left[{\displaystyle \frac{1}{2}}\left(B^{\prime 2}\left(r\right)+B\left(r\right)B^{\prime \prime }\left(r\right)\right){\left({\displaystyle \frac{dt}{d\tau }}\right)}^2-\left(B\left(r\right)+r{B}^{\prime }\left(r\right)\right){\left({\displaystyle \frac{d\varphi }{d\tau }}\right)}^2\right]{\eta }^1=0,\hfill \\ & & {\displaystyle \frac{d^2{\eta }^0}{d{\tau }^2}}+{\displaystyle \frac{B^{\prime }\left(r\right)}{B\left(r\right)}}{\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{d{\zeta }^1}{d\tau }}=0,{\displaystyle \frac{d^2{\eta }^2}{d{\tau }^2}}+{\left({\displaystyle \frac{d\varphi }{d\tau }}\right)}^2{\eta }^2=0,{\displaystyle \frac{d^2{\eta }^3}{d{\tau }^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{d\varphi }{d\tau }}{\displaystyle \frac{d{\eta }^1}{d\tau }}=0,\hfill \end{array}$$

(62)

where $B\left(r\right)$ is defined by Equation (30). Equations (61) and (62) represent the geodesic and geodesic deviation equations, respectively. Considering the circular orbit:

$$\theta ={\displaystyle \frac{\pi }{2}},{\displaystyle \frac{d\theta }{d\tau }}=0,{\displaystyle \frac{dr}{d\tau }}=0,$$

(63)

we get

$${\left({\displaystyle \frac{d\varphi }{d\tau }}\right)}^2={\displaystyle \frac{B^{\prime }\left(r\right)}{r[2B\left(r\right)-r{B}^{\prime }\left(r\right)]}},{\left({\displaystyle \frac{dt}{d\tau }}\right)}^2={\displaystyle \frac{2}{2B\left(r\right)-r{B}^{\prime }\left(r\right)}}.$$

(64)

Equation (62) can be reformulated as follows:

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d^2{\eta }^1}{d{\varphi }^2}}+B\left(r\right)B^{\prime }\left(r\right){\displaystyle \frac{dt}{d\varphi }}{\displaystyle \frac{d{\eta }^0}{d\varphi }}-2rB\left(r\right){\displaystyle \frac{d{\eta }^3}{d\varphi }}+\left[{\displaystyle \frac{1}{2}}\left(B^{\prime 2}\left(r\right)+B\left(r\right)B^{\prime \prime }\left(r\right)\right){\left({\displaystyle \frac{dt}{d\varphi }}\right)}^2-\left(B\left(r\right)+r{B}^{\prime }\left(r\right)\right)\right]{\zeta }^1=0,\hfill \\ & & {\displaystyle \frac{d^2{\eta }^2}{d{\varphi }^2}}+{\eta }^2=0,{\displaystyle \frac{d^2{\eta }^0}{d{\varphi }^2}}+{\displaystyle \frac{B^{\prime }\left(r\right)}{B\left(r\right)}}{\displaystyle \frac{dt}{d\varphi }}{\displaystyle \frac{d{\eta }^1}{d\varphi }}=0,{\displaystyle \frac{d^2{\eta }^3}{d{\varphi }^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{d{\eta }^1}{d\varphi }}=0.\hfill \end{array}$$

(65)

The second Equation in (65) indicates that it exhibits simple harmonic motion, implying a stable trajectory. For the remaining part of Equation (65), we can propose a solution in the form of

$${\eta }^0={\zeta }_1{e}^{i\sigma \varphi },{\eta }^1={\zeta }_2{e}^{i\sigma \varphi },and{\eta }^3={\zeta }_3{e}^{i\sigma \varphi },$$

(66)

where ${\zeta }_1,{\zeta }_2$, and ${\zeta }_3$ are constants and $\varphi$ should be determined. Substituting (66) in (65), we get

$${\displaystyle \frac{3B{B}^{\prime }-{\omega }^2{B}^{\prime }-2r{B}^{\prime 2}+rB{B}^{\prime \prime }}{B^{\prime }}>0.}$$

(67)

The stability condition, originally expressed in Equation (67) for the BH (30), can be re-expressed in a clearer form as follows:

$$\begin{array}{cc}\hfill & \left[-48\left(-1/6\alpha \left(1/4M{\alpha }^2{\Xi }^2-\Xi \left(7/2rM-3/4r^2+M^2\right)\alpha +7r{M}^2+M^3-5/2r^{2}M+1/2r^3\right)r{e}^{2{\displaystyle \frac{r}{-2M+\alpha \Xi }}}\right.\right.\hfill \\ \hfill & {\left.\left.+1/4{\alpha }^2{r}^3\left(M-1/2\alpha \Xi +1/3r\right)e^{4{\displaystyle \frac{r}{-2M+\alpha \Xi }}}+{\left(M-1/2\alpha \Xi \right)}^{2}M\left(M-1/6r\right)\right)\left(-1/2\alpha e^{2{\displaystyle \frac{r}{-2M+\alpha \Xi }}}{r}^2+{\mathcal{M}}_{1}M\right)r^{-5}\right]}^{1/2}\hfill \\ \hfill & r^2{{\mathcal{M}}_1}^{-1/2}{\left(2{\mathcal{M}}_1\mathcal{M}-\alpha e^{{\displaystyle \frac{-r}{{\mathcal{M}}_1}}}{r}^2\right)}^{-1}>0,\hfill \end{array}$$

(68)

This represents the stability criterion for the solution given in (30) as shown in Figure 4. Specifically, when $\alpha =0$, the condition simplifies to $r>6M$, which corresponds to the stability condition for Schwarzschild spacetime, as referenced in [99].

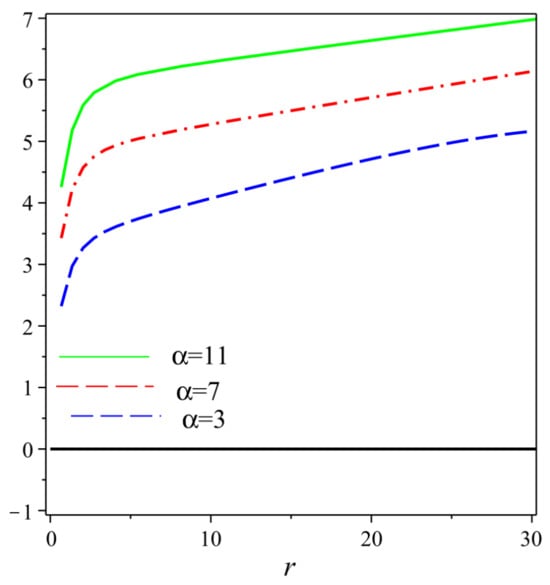
Figure 4. The stability conditions for different values of $\alpha$.

7. Discussion and Conclusions

The increasing interest in $f\left(G\right)$ gravity is largely driven by its ability to explain the observed late-time cosmic acceleration without the need for exotic matter with negative pressure. Within this broader framework, $f(R,G)$ gravity, where both the Ricci scalar R and the Gauss–Bonnet term G contribute to the gravitational action, has gained significant attention. Previous studies have demonstrated that certain functional forms of $f(R,G)$ can effectively describe the transition from a decelerated to an accelerated phase of cosmic expansion, offering viable alternatives to the standard cosmological paradigm [115,116].

In this work, we investigate a novel class of spherically symmetric black hole solutions within the framework of $f(R,G)$ gravity coupled to a scalar field. Our analysis reveals that these black holes possess multiple horizons and exhibit significantly weakened curvature singularities compared to their counterparts in general relativity. These distinctive features not only enrich the phenomenology of black hole solutions in modified gravity theories but also highlight the versatility of $f(R,G)$ models in addressing fundamental challenges in gravitational physics.

Our study primarily focuses on the thermodynamic properties of these solutions. We have shown that the derived black holes comply with the laws of black hole thermodynamics, consistent with established results, thereby underscoring the universality of thermodynamic principles across modified theories of gravity. We examined essential thermodynamic quantities, such as entropy, temperature, heat capacity, and quasi-local energy, and identified the conditions under which these solutions remain thermodynamically stable.

A notable feature of our solution is its multi-horizon structure, akin to that of charged or rotating black holes like Reissner–Nordström and Kerr. In addition to thermodynamic analysis, we examined the dynamics by studying geodesic deviation and stability conditions for circular orbits. Our results indicate subtle but significant departures from the Schwarzschild scenario.

These results establish $f(R,G)$ gravity coupled with scalar fields as a robust framework for generating physically consistent and theoretically rich black hole solutions. Future work should extend this framework to rotating and dynamic spacetime, investigating observational signatures such as gravitational lensing, shadow morphology, and quasi-normal mode spectra. Such studies will deepen insight into strong-field gravity and may guide the development of a more comprehensive theory beyond GR.