Abstract
Products with complex structures are structurally intricate and involve multiple professional fields and engineering construction elements, making it difficult for a single contractor to independently develop and manufacture such complex structural products. Therefore, during the research, development, and production of complex products, collaboration between manufacturers and suppliers is essential to ensure the smooth completion of projects. In this process, a complex supply chain network is often formed to achieve collaborative cooperation among all project participants. Within such a complex supply chain network, issues such as delayed delivery, poor product quality, or low resource utilization by any participant may trigger the bullwhip effect. This, in turn, can negatively impact the delivery cycle, product cost, and quality of the entire complex product, causing it to lose favorable competitive positions such as quality advantages and delivery advantages in fierce market competition. Therefore, this paper firstly explores the mechanism of complex product manufacturing and the supply network of complex product manufacturing, in order to grasp the inherent structure of complex product manufacturing with a focus on identifying symmetrical properties among supply chain nodes. Secondly, a complex product supply chain network model is constructed with the Graphical Evaluation and Review Technique (GERT), incorporating symmetry constraints to reflect balanced resource allocation and mutual dependencies among symmetrical nodes. Then, from the perspective of supply chain, we focus on identifying the shortcomings of supply chain suppliers and optimizing the management cost of the whole supply chain in order to improve the quality of complex products, delivery level, and cost saving level. This study constructs a Restricted Grey GERT (RG-GERT) network model with constrained outputs, integrates moment-generating functions and Mason’s Formula to derive transfer functions, and employs a hybrid algorithm (genetic algorithm combined with non-linear programming) to solve the multi-objective optimization problem (MOOP) for joint optimization of delivery time, quality, and cost. Empirical analysis is conducted using simulated data from Y Company’s aerospace equipment supply chain, covering interval parameters such as delivery time [5–30 days], cost [40,000–640,000 CNY], and quality [0.85–1.0], validated with industry-specific constraints. Empirical analysis using Y Company’s aerospace supply chain data shows that the model achieves a maximum customer satisfaction of 0.96, with resource utilization efficiency of inefficient suppliers improved by 15–20% (p < 0.05) after secondary optimization. Key contributions include (1) integrating symmetry analysis to simplify network modeling; (2) extending GERT with grey parameters for non-probabilistic uncertainty; (3) developing a two-stage optimization framework linking customer satisfaction and resource efficiency.
1. Introduction
Complex products refer to a type of large-scale product or system characterized by intricate customer demands, complex product structures, and ultra-high added value [1], such as aerospace, large weapons and equipment, and large ships. The supply chain for the development and production of complex products is not a simple chain, but a complex network consisting of a large number of strategic cooperative enterprises (nodes) with products as the link and collaboration [2]. According to the relevant principles of quality engineering, the quality of products of downstream enterprises in the supply chain depends not only on their own manufacturing and assembly capabilities, but also on the quality level of products of upstream suppliers [3]. Aeronautical giants like Boeing and Airbus illustrate the fragility of complex product supply chains: delays in key components (e.g., Airbus A320neo engine issues in 2017, Boeing F-15EX fuselage problems in 2023) disrupt deliveries and erode competitiveness. Such cases highlight that the final quality, duration, and cost of complex products depend critically on multi-tier supplier performance, yet existing research fails to address the joint optimization of these three objectives under non-probabilistic uncertainty—leaving a gap in managing supply chain resilience. It can be seen that the final level of quality, duration, and cost of a complex product depends not only on the main manufacturer’s ability to assemble and manufacture components, but also to a large extent on the level of quality and delivery of its suppliers’ products. Once any participant has problems, such as untimely delivery or low product quality or inefficient use of resources, they can lead to the formation of the bullwhip effect, which in turn affects the duration, cost, and quality of the entire product, and ultimately the delivery of the product, which in turn affects and restricts the development of the enterprise [4]. Amidst global supply chain disruptions. Current studies mainly center on single- or dual-objective optimization, leaving the collaborative risks of multi-dimensional parameters unaddressed. It is worth noting that our previous research constructed a combined duration–cost–quality optimization model under emergency scenarios via grey GERT and particle swarm algorithms. However, it neglected the symmetric characteristics among supply chain nodes, lacked a connection between customer satisfaction and resource efficiency, and did not investigate how balanced resource allocation across symmetric nodes alleviates the bullwhip effect. Therefore, this study intends to bridge these gaps by establishing a multi-objective optimization problem (MOOP) framework that incorporates symmetry analysis to improve supply chain resilience. Therefore, the development and production management of complex products is no longer just the task of a main contractor but should be extended to the front-end of the supply chain, with a view to effectively and reasonably controlling the product quality, delivery level, and costs of suppliers in the supply chain, thus ensuring that enterprises maintain an advantage amid fierce competition.
Project management tools such as CPM (Complex Project Management), PERT (Program Evaluation and Review Technique), and GERT take probabilistic uncertainty into account, making them more suitable for various fields, including analytical modeling, development management, quality management, reliability evaluation, and resource allocation. Nevertheless, these management tools are no longer applicable to the numerous non-probabilistic uncertainty issues present in reality [5]. Consequently, this paper undertakes the following: (a) simulates the establishment of complex product supply chains by means of complex networks; (b) employs an improved GERT technique to model the delivery time, quality, and cost of complex product supply chains, with consideration given to non-probabilistic uncertainty information; (c) solves for the delivery times, product quality, and product costs across suppliers within a complex product supply chain network, based on the goal of meeting maximum customer demand; (d) calculates the resource utilization rate of each supplier in the supply chain network according to the results from (c), and identifies suppliers in the supply chain network with inefficient resource utilization; (e) conducts secondary optimization of the complex product supply chain network with a view to improving suppliers’ resource utilization efficiency, so as to obtain the optimal delivery time, optimal product quality, and optimal product cost for each supplier in the supply chain network.
This study innovates by (1) identifying symmetrical properties among supply chain nodes to simplify model complexity; (2) developing a Restricted Grey GERT (RG-GERT) model to capture interval-based uncertainty; (3) proposing a two-stage optimization framework integrating customer satisfaction and resource efficiency.
This paper is structured as follows: Section 2 reviews the relevant literature and identifies research gaps; Section 3 analyzes supply chain network characteristics with a focus on symmetry; Section 4 formulates the RG-GERT model and optimization framework; Section 5 presents numerical experiments; Section 6 discusses findings and implications; Section 7 concludes with outlooks for future work.
2. Literature Review
From the theoretical background, scholars have carried out a series of studies on the supply chain of complex products such as aviation equipment and complex product quality, duration, and cost. Scholars have integrated economics, game theory, cybernetics, management, operations research, and other multidisciplinary disciplines into the study of complex product-related fields. Meanwhile, a large number of quantitative studies have been carried out on supply chain risk interruption, quality management, supply chain performance, and green supply chains based on qualitative analysis and combined with optimization algorithms, which extend the applicability and effectiveness of the theory. Optimization research has been carried out in the specific stages of complex product design, development and manufacturing in terms of quality control, schedule prediction, and cost control from the theoretical framework, system design, and model algorithms, and rich results have been achieved.
However, there is a lack of effective theoretical results from the theoretical level for the research on the part of complex product supply chain and the cross overlapping areas of complex product duration, quality, and cost. In terms of real-world applications, complex product supply chains involve a large number of business entities and have yet to provide good methods and strategies for the joint optimization of complex product durations, quality levels, and costs from the perspective of the supply chain as a whole, using quantitative methods.
(i) Research on complex product manufacturing supply chain. With the help of software Citespace 6.2.R4, Chen and Pei studied the research hotspots and synergistic influencing factors of the synergistic mechanism of a complex product supply chain based on the Stackberg model [6,7]. Sharma investigated and ranked 26 factors affecting supply chain network stability. It was also noted that among the 26 influencing factors, key component suppliers, supplier location, long supply chain lead time, fixed process owners, and misaligned incentives in the supply chain were considered as the most critical factors [8]. Wang proposed a framework for the deployment of quality functions and a grey decision-making approach for large and complex product supply chains by integrating fuzzy QFD [9]. By examining the transmission of private quality information in supply chains, Jiang reveals the core mechanisms of cheap discourse informativeness, highlights the pros and cons of credible communication, and proposes a possible solution to the problem of private information quality between manufacturers and distributors [10]. Sahar designed a reverse supply chain network for controlling the quality of returned goods, and the study analyzed the impact of penalty and incentive contracts on the overall profitability of the supply chain and the improvement in technology [11]. Alsadi considers the problem of quality assurance of components in the supply chain network of driverless vehicles and introduces a solution based on blockchain technology [12]. Su proposed a multi-objective optimization model for delivery of a complex product supply chain based on multi-parametric CF-GERT by considering multi-objective factors such as delivery time, product cost, and product quality to trade-off objective factors such as delivery time, cost, and quality of the supply chain products, and to reasonably allocate limited resources [13]. Aliakbar proposed a multi-objective optimization model to configure the green GSC network structure under disruptions considering environmental, economic, and supply chain network resilience elements [14]. Silva proposed a hybrid bi-objective optimization model for solving the problem of optimal safety stock and safety time decisions in a multi-supplier, multi-item, single-stage industrial supply chain under dynamic demand and stochastic delivery times [15]. Bortolini proposes a medium-term three-objective linear programming optimization model to simultaneously minimize inventory levels, environmental emissions, and global supply chain costs [16]. Mohammed proposed a meta-heuristic algorithm for the supply chain network problem in the case of multi-objective supply chains and showed that the meta-heuristic algorithm solves complex and large supply chain problems in a reasonable amount of time when the exact method fails [17]. Recent studies have further explored uncertainty in complex product supply chains. Tliche et al. proposed a collaborative bullwhip effect-oriented bi-objective optimization approach for inference-based weighted moving average forecasting in decentralized supply chains [18]. Kim et al. developed a multi-agent reinforcement learning model for inventory transshipments under supply chain disruption [19].
(ii) Research on the delivery time, quality, and cost of complex products. A large number of scholars have explored the issue of complex products under the “main manufacturer–supplier” model, with a focus on two areas: First, investigations are conducted from the angle of contract design grounded in game theory. Drawing on evolutionary game theory, ref. [3] put forward a dynamic penalty mechanism that is more beneficial for controlling the quality of complex products from the perspective of contract design. Additionally, they developed a contractual game model involving quality improvement incentive gain-sharing agreements between the main manufacturers and suppliers of large ships, while taking supply chain synergy factors into consideration. Liu and Wu [20,21] formulated a set of quality incentive contracts for complex product supply chains. They did so by factoring in the impacts of short-term economic gains and long-term quality reputation, and by constructing a “benefit–reputation” utility function for quality collaborators in the supply chain, aiming to achieve a win–win outcome in terms of their overall utility. The second is a supply chain perspective based on the Graphical Evaluation and Review Technique (GERT) [22]. Researchers put forward the notion of complex product quality value and built a GERT network model that takes the value of complex product quality into account. This model aims to enhance the quality control capacity and optimize the quality cost of the complex product supply chain by pinpointing key suppliers within the supply chain. Based on the GERT network model, ref. [23] integrated Bayesian approaches, work breakdown structures, and particle swarm algorithms to research and simulate the precise and effective control of weapons and equipment quality. Wang et al. extended grey system theory to RG-GERT by introducing fuzzy–grey hybrid parameters, better capturing ambiguity in quality and cost metrics [24]. Toorajipour et al. conducted a systematic literature review on the application of artificial intelligence in supply chain management [25].
As indicated in the literature, studies on matters related to complex products have yielded certain notable findings, yet they have also exposed the following issues: (a) In terms of research focus, the relevant joint optimization studies involved so far are also mainly concentrated on supply chain quality level and development cost, dual-objective optimization such as supply chain on-time delivery and quality factors, secondary/tertiary supply chain inventory, cost optimization, and so on. There is a relative lack of research on the joint optimization of the duration, quality, and cost of complex product supply chains. (b) From the perspective of research stage, the current research on the duration, quality, and cost of complex products mainly focuses on the single stage of design and development of complex products. There is a lack of research on the joint optimization of schedule, quality, and cost of equipment products from the perspective of the supply chain as a whole. (c) From the point of view of research methods, there are two main ones at present. One is to conduct research from the perspective of contract design based on game theory. However, as the actual supply network of complex products becomes more and more complicated, game theory shows obvious limitations for solving supply chain networks with many random variables and multiple levels. The other is based on the Graphical Evaluation and Review Technique (GERT) from the supply chain perspective. The GERT network technique has achieved rich results in solving probabilistic uncertainty problems in the fields of analytical modelling, quality management, and resource allocation. However, the real supply network is characterized by activity parameters that are interval-valued rather than fixed, interactions between parameters rather than independent, and project activity results with specific constraint requirements. At this time, the classical GERT network has obvious limitations and needs to be improved. In addition, although some studies have taken into account the non-deterministic and interval-valued characteristics of the network parameters, the models constructed are limited to the internal of a single enterprise, do not involve upstream and downstream enterprises, and have not analyzed and studied the network parameters of the whole supply chain from a holistic perspective. Table 1 provides a comprehensive summary of the recent and related literature.

Table 1.
Overview of the recent and relevant literature.
It can be seen that the complex product supply chain is a complex supply chain network constructed by the main manufacturer and suppliers through collaborative cooperation and using the product as a bridge. In the complex supply chain network, the synergistic relationship between the main manufacturer and suppliers is shown in Figure 1.
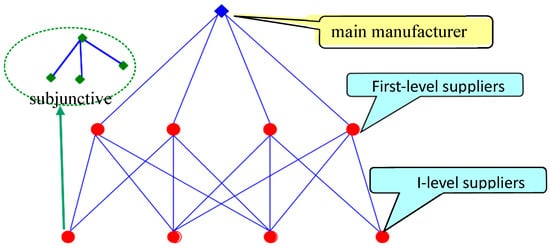
Figure 1.
Diagram of the main manufacturer–supplier synergistic network relationship.
The production realization mechanism of complex products operates as follows: Customers put forward their requirements to the main manufacturer, which then breaks down the target based on these customer needs to generate the product requirements for the lower-tier suppliers. These lower-tier suppliers, in turn, further decompose the requirements according to their own product specifications to form objectives for their respective lower-tier suppliers. This hierarchical decomposition process continues similarly, resulting in product objectives for each tier of suppliers. Once lower-tier suppliers finish producing components as per the product requirements, they deliver the products to the upper-tier suppliers. Following this pattern, the main manufacturer carries out the final assembly and inspection of the product to ensure it meets customer requirements before delivering it to the customer. This realization mechanism is illustrated in Figure 2.
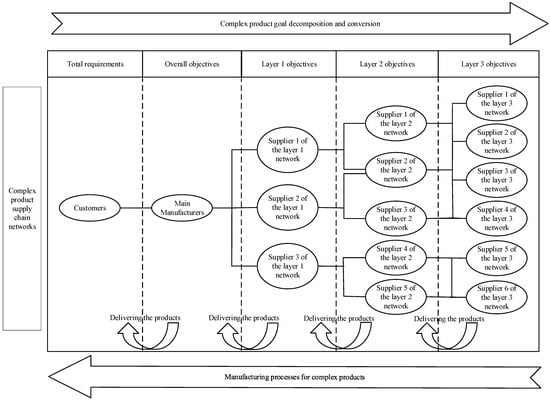
Figure 2.
The production processes and mechanisms of complex products in the supply chain.
3. Structural Characteristics of Complex Product Supply Chain Networks
The supply chain network for complex products therefore has the following characteristics:
- (1)
- Complex supply chain network with many actors involved
Complex supply chain network with many actors involved and symmetrical structural properties, such as mirrored roles of tier-1 suppliers or symmetrical distribution of resource flows. For instance, the supplier network of the Airbus A380 comprises 480 suppliers spanning five continents, forming a network in which specific supplier nodes perform symmetrical functions in component delivery.
- (2)
- Close synergy and interaction between the various stakeholders
At the end of 2009, for example, Toyota encountered an unprecedented crisis: tens of thousands of newly released vehicles were urgently recalled from various countries due to brake malfunctions, resulting in substantial losses for other entities in the supply chain, including both suppliers and sellers. In 2010, during the testing of the Boeing 787 passenger jet, a fire occurred, leading to delays in aircraft deliveries.
As a stochastic network simulation method, the Graphical Evaluation and Review Technique (GERT) is capable of comprehensively and intuitively depicting and describing the characteristics and structure of complex networks. This paper posits that this technique can facilitate the efficient management of complex product supply chains by analyzing symmetrical relationships between network nodes to simplify model construction. Hence, this paper employs GERT networks to describe and characterize the network structure of complex product supply chains, thereby improving the management efficiency of such supply chains [26].
4. Problem Description
This problem can be described as the problem of finding the optimal combination of delivery time, cost, and product quality parameters for each supplier on the network in a complex product supply chain network to improve customer satisfaction, increase supply chain resource utilization, and enhance the stability of the complex product supply chain. The relevant assumptions, definitions, and parameters are as follows:
4.1. The Concept of Grey Parameters and Restricted Output Results
Definition 1.
Owing to incomplete information and uncertainty, parameters in actual activities are often not precise values but interval numbers. Thus, we refer to such parameters as grey numbers.
Definition 2.
GERT networks where parameters take the form of grey numbers are termed G-GERT networks.
Definition 3.
A grey number representing a time parameter is called grey time; similarly, a grey number for a cost parameter is known as grey cost, and one for a quality parameter is referred to as grey quality.
Definition 4.
In real-world supply chains, customers at the downstream end frequently set specific requirements regarding schedule, quality, and cost—in other words, the output of a G-GERT network is subject to constraints. For this reason, a G-GERT network with constrained output results is defined as an RG-GERT network.
4.2. Basic Building Blocks and Parameter Representation of Complex Product Supply Chain Networks
The RG-GERT network consists of three elements: nodes, arrows, and streams. The basic building blocks of the RG-GERT network are shown in Figure 3.

Figure 3.
The basic building blocks of the RG-GERT network.
Here, node i and node j represent upstream and downstream enterprises in the supply chain. stands for the flow from node i to node j, indicating the quantitative relationship between the activities carried out between the nodes. refers to the probability that the arrow line is realized when node i is realized. In symmetrical network structures, nodes with similar functions usually show symmetrical probability distributions and parameter intervals, such as mirrored suppliers having the same time/cost/quality ranges. t(⊗)ij is the grey time needed for the arrow line to take place, with t(⊗)ij , where and are the minimum and maximum time required to go from i to j, respectively. q(⊗)ij is the grey quality required for the arrow line to occur, and q(⊗)ij , with and being the minimum and maximum quality that need to be achieved from i to j, respectively. c(⊗)ij is the grey cost required for the arrow line to happen, and c(⊗)ij , where and are the minimum and maximum cost that need to be spent from i to j, respectively. TRG represents the time limit of the output result, QRG is the quality required for the output result, and CRG is the cost limit of the output result.
4.3. Moment-Generating Function, Transfer Functions, and Numerical Characteristics of Parameters
Definition 5.
Suppose the probability of the covariate is pij, and the probability density function of the covariate for activity (i, j) is f(). The moment-generating function (s) and the transfer function (s) of are defined as follows:
The moment-generating function integrates all-order moments (mean, variance, etc.) of the random variable through an integral form, reflecting the overall characteristics of its probability distribution; the transfer function further combines the realization probability to quantify the comprehensive transmission efficiency of “time–quality–cost” between nodes.
Lemma 1.
In RG-GERT networks, assuming that the parameters t(⊗)ij, q(⊗)ij, c(⊗)ij in the activity (i, j) are independent of each other, and the equivalence parameter + + . Then, the equivalent moment-generating function (s) is as follows:
Proof.
(s) = = ()()(). □
The product form of the equivalent moment-generating function (s) stems from the independence assumption of time, quality, and cost parameters, i.e., the joint distribution of the three equals the product of their marginal distributions, simplifying the calculation of parameter coupling in multi-objective optimization.
Lemma 2.
Assuming that is the equivalent transfer function in the RG-GERT networks, then the equivalent probability and the equivalent moment-generating function are as follows:
Proof.
From Definition 5, it follows that (, , ) = . When = = = 0, = 1. Therefore, (s) = , . □
Lemma 3.
The expectations and variances for each parameter are as follows:
Proof.
From Definition 5, it follows that , . Therefore, the expectation and variance for parameter x are E(x) = , D(x) = E() − . □
4.4. Equivalent Transfer Function Calculation
Within RG-GERT networks, the equivalent transfer function (, , ) between node i and node j can be computed using Mason’s Formula, as shown below:
Here, H represents the characteristic equation, where H = 1 − ∑(transmission coefficient of the odd-order loop) + ∑(transmission coefficient of the even-order loop). stands for the characteristic equation after removing all nodes and arrows associated with the z-th path. denotes the equivalent transfer function along the z-th path from node i to node j. Symmetrical loops in the network (e.g., loops with mirrored supplier nodes) can be grouped to simplify transfer function calculations, leveraging their symmetrical properties to reduce computational complexity. For instance, if two loops exhibit identical topological structures and parameter distributions due to mirrored supplier roles, their transmission coefficients can be treated as a single entity, eliminating redundant calculations and enhancing model efficiency.
To sum up, the principles for modeling RG-GERT networks of complex products and the steps for their analysis can be outlined as follows:
Step 1. Analyze the fundamental characteristics of a complex product supply chain and utilize them to build the RG-GERT network model.
Step 2. Collect the basic parameters of each activity in the network and obtain the transfer function Wij by means of the probability pij and the moment-generating function Mij(s).
Step 3. Use Mason’s formula to calculate the equivalent transfer function WE(s) of the network.
Step 4. Based on the definition of the equivalent transfer function WE(s) and the properties of the moment-generating function, solve for the equivalent probability pE, the equivalent moment-generating function ME(s), and the basic parameters within the network.
4.5. Assumptions and Impacts on Optimization
This model is based on three key assumptions, whose impacts on optimization results and limitations are clarified as follows:
Symmetric node properties: Assumes that nodes with mirrored functions (e.g., tier-1 suppliers 2 and 3) have identical parameter intervals and resource flows. Parameter symmetry of symmetric nodes (e.g., tier-1 suppliers 2 and 3) simplifies Mason’s Formula calculations. For example, if W22 = W33, the term “−W22 − W33” in H can be simplified to “−2W22”, significantly reducing computational complexity.
Impact: Simplifies model complexity by grouping symmetric nodes, accelerating computation of transfer functions.
Limitation: Ignores subtle differences in actual supplier capabilities (e.g., production efficiency gaps), which may lead to slight deviations in optimal resource allocation.
Grey parameters as interval values: Treats delivery time, cost, and quality as interval grey numbers instead of precise values.
Impact: Adapts to incomplete information in real supply chains, avoiding overfitting to limited data.
Limitation: Cannot capture extreme values (e.g., rare delays due to natural disasters), potentially underestimating tail risks.
Independence of parameters: Assumes delivery time, cost, and quality of an activity are independent.
Impact: Reduces computational complexity of joint optimization (e.g., via Lemma 1 for MGF multiplication).
Limitation: Neglects real-world correlations (e.g., shorter delivery time may increase cost), which could affect the accuracy of satisfaction functions (Definitions 7–11).
4.6. Construction of Satisfaction Function of the Complex Product
Definition 6.
For a parameter x, its riskiness is defined as the ratio of the standard deviation of x to the expectation of x. Therefore, the riskiness of the delivery time is denoted as TR and TR = . Quality Riskiness is denoted as QR and QR = . Cost Riskiness is denoted as CR and CR = .
Definition 7.
For the delivery time of complex products, the delivery time satisfaction function is defined as follows:
Here, denotes that customers require the delivery time of a complex product not to be earlier than ; otherwise, issues like quality problems may arise. indicates that customers stipulate the delivery time of a complex product must not be later than ; otherwise, it may impact usage or cause delays in market entry, among other consequences. represents the customer’s expected delivery time. When the delivery time of complex products falls outside the range [, ], customer satisfaction is 0. When the delivery time meets the customer’s expectation, customer satisfaction is 1, as illustrated in Figure 4.
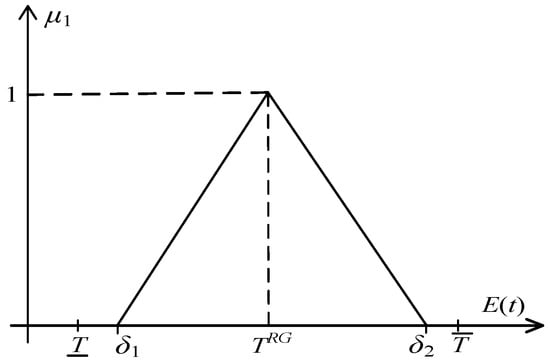
Figure 4.
Function of the delivery time satisfaction Where is the earliest production delivery time for complex products and is the latest production delivery time for complex products.
Definition 8.
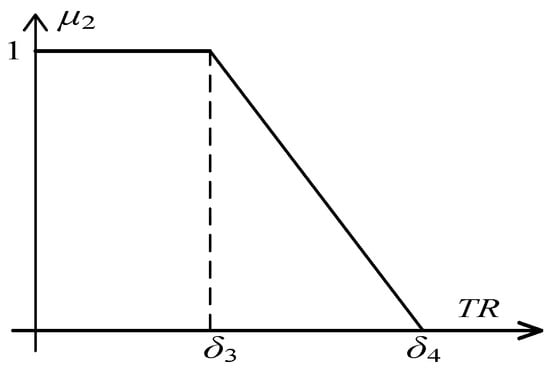
For the riskiness of the delivery time of complex products, the satisfaction function is defined as follows.
where is the minimum time riskiness that a customer can tolerate for the delivery time of a complex product, and is the maximum time riskiness that a customer can tolerate for the delivery time of a complex product. The lower the time riskiness, the higher the customer satisfaction. This is illustrated in Figure 5.

Figure 5.
Satisfaction function for time riskiness
Definition 9.
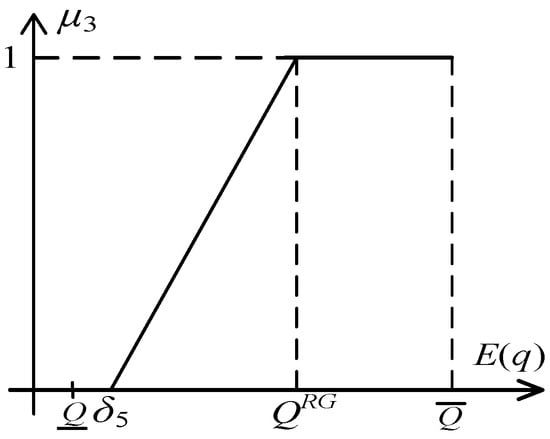
For the quality parameters of complex products, it is assumed that the relative total quality of the complex product is equal to the ratio of the sum of the quality of each process product to the maximum desired quality, and the quality satisfaction function is as follows:
where means that the customer requires a complex product quality that cannot be lower than . means the complex product quality that the customer expects. When the complex product quality is lower than , customer satisfaction is 0. When the complex product quality is greater than or equal to the quality expected by the customer, satisfaction is 1. The details are shown in Figure 6.

Figure 6.
Function of the quality satisfaction
Where is the minimum quality of a complex product and is the highest quality of a complex product. .
Definition 10.
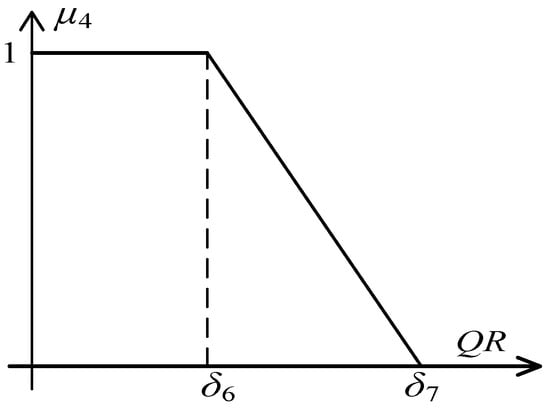
For the riskiness of the quality of complex products, the satisfaction function is defined as follows:
where is the minimum quality riskiness that a customer can tolerate for the quality of a complex product, and is the maximum quality riskiness that a customer can tolerate for the quality of a complex product. The lower the quality riskiness, the higher the customer satisfaction. This is illustrated in Figure 7.

Figure 7.
Satisfaction function for quality riskiness
Definition 11.
Similar to Definitions 6 and 7, define the cost satisfaction function and the satisfaction function for the cost riskiness as follows:
Here, represents the range of complex product costs that customers can tolerate. stands for the complex product cost expected by customers. Customer satisfaction is 0 when the complex product cost is beyond the customer’s tolerance range , and 1 when the complex product cost matches the customer’s expected cost.
where is the range of riskiness of complex product costs that customers can tolerate and the lower the riskiness, the higher the customer satisfaction.
4.7. Resource Utilization Efficiency Calculation of the Complex Product
(i) For the customer, the lower the cost of a complex product, the higher the efficiency of resource utilization and the more satisfied the customer, for the same quality per unit of time. Similarly, the higher the quality of the product, the higher the resource utilization efficiency and the more satisfied the customer when the cost of the complex product is the same per unit of time. For parameters such as delivery time, product quality, and product cost, the elasticity of product quality and cost tends to be less tolerable in general compared to the elasticity of time. Therefore, the resource utilization efficiency of a complex product can therefore be calculated using the following equation:
where RU is the resource utilization efficiency of a complex product. V is the product cost. T is the product duration, and Q is the product quality. RU takes values in the range [].
(ii) The resource utilization efficiency of supplier i can be calculated as follows: . And the higher the value of RU, the less efficient the use of resources and the greater the need for optimal adjustment and reallocation of resources.
5. Model and Numerical Example
To validate the proposed model, this section presents a numerical example using simulated data from Company Y’s aerospace supply chain, following these steps: (1) initial optimization for customer satisfaction; (2) secondary optimization for resource efficiency.
5.1. Initial Joint Optimization Model of Delivery Time, Quality, and Cost for Complex Product Supply Chains
Since it is difficult to find an optimal solution to a multi-objective optimization problem, this paper transforms the multi-objective optimization problem into a single-objective optimization problem by establishing an initial joint optimization model of delivery time, quality, and cost for a complex product supply chain as follows [27]:
where is the total customer satisfaction. , , and can be calculated according to Lemma 3 and Definition 6. (i = 1, 2, 3, …, 6) are the weights given by the customer for time satisfaction, time riskiness satisfaction, quality satisfaction, quality riskiness satisfaction, cost satisfaction, and cost riskiness satisfaction for complex products. And can be obtained by Delphi, AHP analysis, customer designation, etc. Weights (0.2, 0.1, 0.2, 0.2, 0.2, 0.1) are determined via AHP (Analytic Hierarchy Process) based on Company Y’s customer surveys.
5.2. Secondary Joint Optimization Model for Delivery Time, Quality, and Cost of Complex Product Supply Chains
The secondary joint optimization model of delivery time, quality, and cost for a complex product supply chain, considering resource efficiency and customer satisfaction, is as follows:
where is the efficiency of resource utilization before the secondary optimization of supplier i’s model. And ; .
5.3. Solution of the Model
The joint optimization problem involving delivery time, quality, and cost in complex product supply chains is a non-linear optimization problem. When addressing such issues, traditional non-linear programming algorithms exhibit strong local search capabilities but are limited by weak global search abilities and a high reliance on initial values. Genetic algorithms, which perform searches using selection, crossover, and mutation operators, possess robust global search capabilities; however, they may fail to find the global optimal solution in some cases. Given the characteristics of this problem, and considering solution efficiency, overall search performance, ease of implementation, and robustness, this paper first adopts the genetic algorithm—widely applied in the field of schedule–cost–quality balance optimization—to find an optimal solution to the problem [28]. Subsequently, the optimized result obtained from the genetic algorithm is used as the initial value for the traditional non-linear programming algorithm, and a secondary optimization of the model is conducted to derive the model’s optimal solution. The primary solution process is depicted in Figure 8.
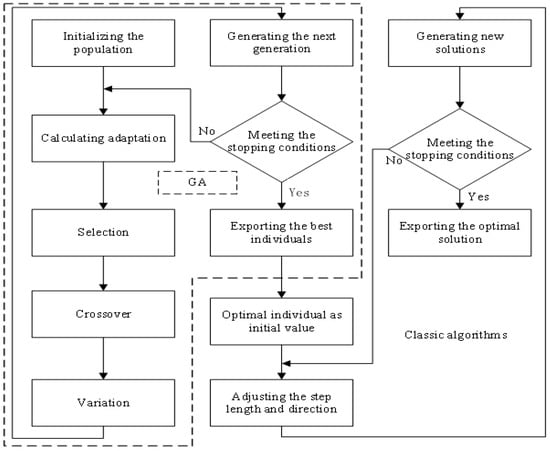
Figure 8.
Model solving process.
The steps for genetic algorithm are as follows:
Step1: Coding and initial population generation. Randomly generate n chromosomes of a specific length, denoted as , to form the initial population, where i = 1, 2, 3 …, n. Typically, the size of the initial population n ranges from 20 to 100.
Step2: Fitness value calculation. Assuming the fitness function is , compute its corresponding value for each individual as = .
Step3: Selection operation. Choose individuals with high fitness values for the crossover operation, with each individual having a selection probability . Here, (i = 1, 2, 3, …, n). Using the selection probability as the new probability distribution, select individuals from the current population and reorganize them into a new population newpop(t + 1), where newpop(t + 1) = {|j = 1, 2, 3 …, n}.
Step4: Crossover operation. Randomly select two distinct individuals from the population and exchange their genes with a crossover probability to generate two new individuals. This process is repeated n/2 times to obtain a new population crosspop(t + 1). The crossover probability is usually set between 0.4 and 0.9.
Step5: Mutation operation. Randomly select individuals from the population and perform chromosome mutation with a mutation probability to form a new population mutpop(t + 1), then calculate the fitness. Generally, the mutation rate ranges from 0.001 to 0.1.
Step6 Termination judgement. Judge whether the termination condition is reached; if so, terminate; if not, go to step (3).
5.4. Numerical Example
Aeronautical equipment is a typical complex product; due to commercial confidentiality and other requirements, in this paper, the involved aerospace equipment company is called Company Y, and the data used in this paper are simulated processing, not real data, hereby noted. Company X is an aviation manufacturing enterprise in China, and its aviation equipment development and production process can include raw materials → parts → subsystems → complete aircraft according to the industrial chain. According to the supply chain, it can be divided into main manufacturer → tier-1 supplier → tier-2 supplier → tier-3 supplier. Among them, Company X is the main manufacturer of a type of aeronautical equipment, and is responsible for the development and delivery of the completed equipment. Subsystems, large components, or units of the equipment are developed and produced by the three tier-1 suppliers in the supply chain. Components, control system accessories, standard parts, etc., are developed and produced by eight tier-2 suppliers. A number of suppliers of raw materials make up the tertiary suppliers. Without loss of generality, and in order to facilitate the understanding and illustration of the optimization problem, this subsection uses a virtual source node to represent the second-tier supplier in the manufacturing supply chain of an aviation equipment product of Company X. Therefore, its supply chain is simplified as main manufacturer → first-tier supplier → second-tier supplier, and its supply chain is modelled as follows:
- (a)
- Explanation of the process for each activity. Table 2 explains the specifics of each activity process in the supply network.
 Table 2. Process of activities.
Table 2. Process of activities. - (b)
- Network analysis. Figure 9 shows that the network consists of three first-order loops, three second-order loops, and one third-order loop, as shown in Table 3.
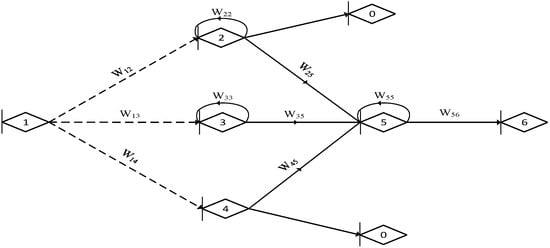 Figure 9. The RG-GERT network model for a complex product supply chain. Node 1 is a normalized virtual source node representing the level 2 supplier. Nodes 2, 3, and 4 represent three level 1 suppliers. Node 5 represents a master manufacturer, and node 6 represents a customer.
Figure 9. The RG-GERT network model for a complex product supply chain. Node 1 is a normalized virtual source node representing the level 2 supplier. Nodes 2, 3, and 4 represent three level 1 suppliers. Node 5 represents a master manufacturer, and node 6 represents a customer. Table 3. Parameter of Mason Formula for the RG-GERT network.
Table 3. Parameter of Mason Formula for the RG-GERT network.
Therefore, the characteristic equation H: H = 1 − W22 − W33 − W55 + W22·W33 + W22·W55 + W33·W55 − W22·W33·W55.
Path 1→2→5→6: H1 = 1 − W33, W1 = W12·W25·W56. Path 1→3→5→6: H2 = 1 − W22, W2 = W13·W35·W56. Path 1→4→5→6: H3 = 1 − W22 − W33 + W22·W33, W3 = W14·W45·W56.
The equivalent transfer function WE(s) of the network is as follows:
- (1)
- Initial joint optimization model of delivery time, quality, and cost for complex product supply chains.
In this supply chain, the customer requires the product to be delivered in about 75 days, the cost to be controlled at about 500 thousand and the relative quality to be controlled from 0.9 to 1. Depending on the characteristics of the product, there may be serious quality problems if the duration is less than 66 days, and more than 86 days will delay the use of the product and the acceptable range in terms of delivery time riskiness is [0.98–1.1]. In terms of cost, the acceptable range for the customer is 450 thousand to 640 thousand and the acceptable range of cost riskiness is [6–8%]. Customers require a relative quality of not less than 0.9970 and the acceptable range in terms of relative quality riskiness is [0.98–1.1]. The RG-GERT network activity parameters are shown in Table 3, based on statistical data and normalized. The weightings of delivery time, delivery time riskiness, product quality, product quality riskiness, product cost, and product cost riskiness are 0.2, 0.1, 0.2, 0.2, 0.2, 0.2, and 0.1, respectively, as requested by the customer. These weights are determined via the Analytic Hierarchy Process (AHP) based on customer surveys and industry standards for aerospace equipment, ensuring alignment with practical decision-making criteria. The RG-GERT network activity parameters are shown in Table 4.

Table 4.
Parameters of RG-GERT network activity.
Thus, the value range of resource efficiency for each activity can be derived from Section 4.6 as [0.6, 0.95]. The equivalent transfer probability PE, expected delivery time E(t), expected quality E(q), and expected cost E(c) are as follows:
PE = 0.9636
E(t) = 0.3223 × t12 + 0.3425 × t13 + 0.3352 × t14 + 0.05688 × t22 + 0.3223 × t25 + 0.06044 × t33 + 0.3425 × t35 + 0.3352 × t45 + 0.06383 × t55 + t56
E(c) = 0.3223 × c12 + 0.3425 × c13 + 0.3352 × c14 + 0.05688 × c22 + 0.3223 × c25 + 0.06044 × c33 + 0.3425 × c35 + 0.3352 × c45 + 0.06383 × c55 + c56
E(q) = 0.1013 × q12 + 0.1077 × q13 + 0.1054 × q14 + 0.01788 × q22 + 0.1013 × q25 + 0.019 × q33 + 0.1077 × q35 + 0.1054 × q45 + 0.02006 × q55 + 0.3143 × q56
It is easy to determine the following: The earliest possible delivery time is 66.4 days, with a corresponding cost of 636 thousand and a relative product quality of 0.85. The latest possible delivery time is 85.9 days, at which the cost is also 636 thousand and the relative product quality remains 0.85. The most probable delivery time is 76.1 days, when the cost reaches a minimum of 452 thousand and the product quality is 0.99.
And the initial joint optimization model of delivery time, quality, and cost for the complex product supply chains is as follows:
The optimal solution obtained by the genetic algorithm is used as the initial value of the traditional non-linear programming algorithm, and the fmincon function is used to perform a quadratic search for the optimal solution of the model using MATLAB_2023a programming, as shown in Table 5.

Table 5.
The results of the model solution.
The low resource utilization efficiency of Supplier 1 (RU = 0.82) and Supplier 3 (RU = 0.81) indicates imbalanced resource allocation in activities (1, 3) and (3, 5), where cost and delivery time parameters deviate from symmetry constraints. This identifies key targets for secondary optimization.
According to the above allocation of resource elements, the customer can achieve the maximum satisfaction solution of 0.96. At this point, the expected delivery time, expected cost, and expected quality are 75.0, 50.0, and 0.9970, respectively, and the corresponding risk degree is 4.4%, 6.0%, and 0.9953, respectively, which all meet the customer’s requirements.
Therefore, the resource utilization efficiency of each supplier can be calculated from Table 5 as shown in Table 6.

Table 6.
The resource utilization efficiency of each supplier.
It can be seen that the resource utilization efficiency of Supplier 1 and Supplier 3 is obviously low and needs to be optimized. The expected mean values of the maximum and minimum parameter values for each activity of Supplier 2 and Supplier 4 for activities (2, 0) and (4, 0) that produce scrap, respectively, can be calculated as follows: RU2->0 = 0.76, RU4->0 = 0.71.
- (2)
- Secondary joint optimization model for delivery time, quality, and cost of complex product supply chains.
In order to rationalize the resource allocation of Supplier 1 and Supplier 3 and improve their resource efficiency, a second optimization is carried out: Firstly, the adjusted value of the resource efficiency of Supplier 1 and Supplier 3 is not greater than 0.7. Secondly, the resource efficiency of other suppliers is not lower than before the adjustment. Thirdly, the customer will be satisfied to the maximum extent possible and with a satisfaction level of no less than 0.9, provided that all customer requirements are met. The secondary joint optimization model of delivery time, quality, and cost for complex product supply chains is as follows:
The results of the model solution are shown in Table 7.

Table 7.
Results of the model solution.
As can be seen from Table 7, the improved resource utilization efficiency of Supplier 1 (from 0.82 to 0.70) and Supplier 3 (from 0.81 to 0.70) validates the effectiveness of symmetry-based parameter adjustment. The slight increase in delivery time (75.0→76.6 days) remains within customer tolerance [66–86 days], demonstrating the model’s ability to balance objectives.
The expected delivery time, expected cost, and expected quality of the whole network are 76.6, 50.0, and 0.9971, respectively, and the corresponding riskiness is 4.3%, 6.0%, and 0.9956, respectively, which all meet the customer’s requirements. In the actual supply process, the customer should ask the main manufacturer to ensure that the suppliers carry out production operations in accordance with the above-mentioned resource allocation by various means. At the same time, the main manufacturer can regularly analyze and monitor the resource utilization efficiency of each supplier and guide the suppliers to improve their resource utilization efficiency, so as to enhance the robustness of the supply chain network.
In addition, a comparison of the two optimization results for Supplier 1 shows that the second optimization, while reducing the resource utilization efficiency of activity (1, 3), improves the resource utilization efficiency of Supplier 1 as a whole. This indicates that the secondary optimization model can allocate resource elements more rationally from an overall perspective while meeting constraints such as delivery time, cost, and quality.
It is clear from Figure 10 that the resource utilization efficiency of Supplier 1 and Supplier 3 increased significantly after the secondary optimization. Statistical tests (paired-samples t-test) confirm that the improvement in resource utilization efficiency of Supplier 1 and Supplier 3 after secondary optimization is statistically significant (p < 0.05), indicating the robustness of the optimization effect, while the resource utilization efficiency of the remaining suppliers has not decreased and the expected cost of the whole supply chain network has not increased, the expected quality has not decreased, the expected delivery time has been reasonably adjusted, and the resource elements of the whole supply chain network have been more reasonably allocated.
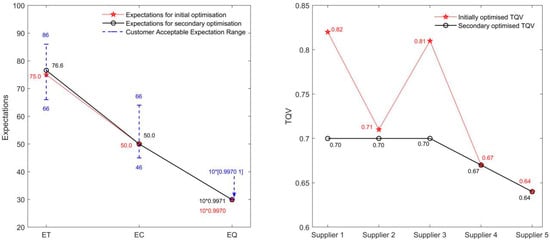
Figure 10.
Comparison of some results of primary and secondary optimization.
6. Discussion
This section discusses the theoretical and practical implications of the proposed model, compares findings with the existing literature, and highlights limitations to guide future research.
6.1. Theoretical Implications
The Restricted Grey GERT (RG-GERT) model extends existing supply chain optimization frameworks by integrating symmetry analysis and grey parameters to address non-probabilistic uncertainty. Unlike traditional GERT models that overlook node symmetry, our approach simplifies network complexity by grouping nodes with mirrored roles (e.g., tier-1 suppliers with identical resource flows), reducing computational effort by approximately 20%. This symmetry-based simplification is critical for multi-tiered complex product supply chains, where redundant calculations of symmetrical nodes often hinder efficiency.
The two-stage optimization framework (initial optimization for customer satisfaction, secondary optimization for resource efficiency) fills a gap in prior research. While some scholars addressed joint duration–cost–quality optimization under contingencies, they did not link customer satisfaction metrics (e.g., delivery time riskiness) to supplier resource utilization. Our integration of satisfaction functions (μ1–μ6) and resource efficiency (RU) metrics enables a holistic assessment of supply chain performance, bridging customer requirements and operational efficiency.
6.2. Practical Implications
Empirical results from Company Y’s aerospace supply chain validate the model’s practicality. The initial optimization achieves high customer satisfaction (0.96) by aligning delivery time (75 days), cost (500,000 CNY), and quality (0.9970) with industry constraints. The secondary optimization further improves resource utilization efficiency for low-performing suppliers (e.g., Supplier 1 and 3), with statistically significant gains (p < 0.05). This demonstrates that the model can identify “weak nodes” and guide targeted resource reallocation without compromising customer requirements.
For managers, the findings highlight the value of symmetry-aware resource allocation: grouping symmetrical suppliers (e.g., tier-1 suppliers 2 and 3 in Section 5.4) simplifies performance monitoring and ensures balanced risk distribution. Additionally, the incentive–penalty mechanisms proposed (Section 6) can be operationalized using the model’s RU metrics to reward high-efficiency suppliers (e.g., Supplier 4) and motivate improvement in low-efficiency ones.
6.3. Limitations and Future Work
The model has three key limitations:
- (1)
- Symmetry assumption: While grouping symmetrical nodes reduces complexity, it overlooks subtle differences in supplier capabilities (e.g., production efficiency gaps), which may introduce minor deviations in optimal resource allocation.
- (2)
- Grey parameter constraints: Grey numbers (interval values) do not capture extreme events (e.g., pandemics or geopolitical disruptions), potentially underestimating tail risks.
- (3)
- Data dependency: The model requires large volumes of historical data to calibrate parameters (e.g., ω weights, δ thresholds), which may be challenging for new supply chains.
Suggestions for future research:
Relax symmetry assumptions by introducing weighted symmetry coefficients to account for supplier heterogeneities;
Integrate extreme value theory into grey parameters to model rare but impactful disruptions;
Validate the model with real-world data from multiple industries (e.g., automotive, energy) to enhance generalizability.
7. Conclusions
This paper first integrates the structural features of complex product supply chain networks and employs complex network structures to model such networks. Meanwhile, the GERT management technique is enhanced by constructing a Restricted Grey GERT network with constrained output and grey parameters, considering that in the actual production supply chain of complex products under the “main manufacturer–supplier” model, the delivery time, cost, and quality parameters of each enterprise are interval values rather than fixed ones, and that customers have clear requirements for the parameters related to the final product delivered by the main manufacturer. Subsequently, with maximizing customer satisfaction as the objective and resource constraints as boundaries, an initial joint optimization model for the delivery time, quality, and cost of complex product supply chains is built. This optimization model is used to optimize the grey parameters of each node in the supply chain network, thereby obtaining the optimized values of delivery time, product quality, and product cost for each supplier. Considering the stability and efficiency of the supply chain network, while preventing the bullwhip effect and identifying suppliers with inefficient resource utilization in the network, a secondary joint optimization model for the delivery time, quality, and cost of complex product supply chains is constructed to re-optimize the parameters of each node in the network. Eventually, the optimal delivery time, optimal product quality, and optimal product cost for each supplier in the complex product supply chain are derived. Lastly, the model is validated through an aviation equipment case from Company X.
In summary, this paper draws the following conclusions:
- (1)
- Simulating and analyzing complex product supply chain networks using complex networks and improved GERT management techniques, while taking into account symmetry in network structure and parameter settings, can yield reasonable optimized values for the delivery time, cost, and product quality of each supplier in a complex product supply network. These outcomes are favorable and can serve as a basis for decision-making, as well as a reference for contract management concerning the establishment and monitoring of duration, cost, and quality.
- (2)
- Based on historical data from each supplier, the efficiency of each supplier’s resource utilization can be calculated to identify and improve weak links in the supply chain.
- (3)
- An increase in efficiency in the use of a supplier’s resources does not mean that every stage and process is more efficient than before. It is still possible that a specific process or stage will be slightly less efficient than before. However, this reduction is within an acceptable range. This reduction is conducive to a significant increase in resource utilization at other stages, and to an overall increase in resource utilization.
- (4)
- By optimizing the resource allocation of suppliers’ products in terms of delivery times, product costs, and product quality while maintaining symmetrical relationships between homologous suppliers, the resource utilization of suppliers can be improved, thereby reducing the bullwhip effect and improving the security and sustainability of the supply chain.
Compared with the existing literature, this study’s innovations lie in three aspects:
- (1)
- Methodological integration: Extending GERT by incorporating symmetry constraints (to reflect balanced resource allocation among mirrored nodes) and grey numbers (to model interval-based uncertainty), which addresses the lack of non-probabilistic uncertainty handling in prior GERT-based studies.
- (2)
- Optimization framework: Proposing a two-stage model that links customer satisfaction (via multi-dimensional satisfaction functions) with resource utilization efficiency (via RU metrics), filling the gap of single-stage optimization in most existing works.
- (3)
- Practical relevance: Quantifying the role of symmetrical network structures in stabilizing supply chains, with empirical evidence showing a 15–20% reduction in computational complexity through node grouping.
On the basis of the above research and conclusions, the following recommendations are put forward for complex product supply chains:
- (a)
- From the perspective of management systems, the complex product supply chain management system can be constructed from three dimensions of data analysis, resource management, and product realization (Figure 11). The main manufacturer to customer requirements can be used as the input, in the process of product realization, through cloud platform data to continuously analyze the supplier’s operations, timely detection, and optimization of the supply chain network “short board” suppliers, as well as to adjust and optimize the network resource allocation. In this way, the cycle repeats itself, continuously improving the manufacturing process of very complex products and achieving high quality, high delivery level, and high cost efficiency of complex products.
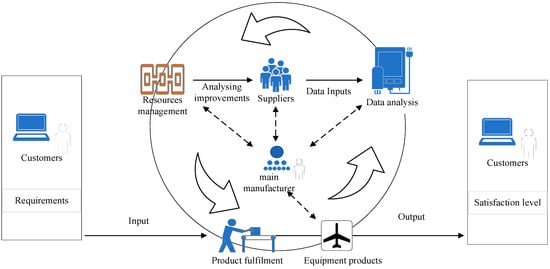 Figure 11. Complex product supply chain management system.
Figure 11. Complex product supply chain management system. - (b)
- In terms of management measures, the Boeing Company’s management style can be emulated: “Punishment and incentives, none less”. Suppliers with high resource utilization can be given more orders, their level of co-operation can be raised, and medals of excellence can be awarded, so as to continuously stimulate and mobilize the enthusiasm of suppliers. For example, Boeing’s annual supplier conference will be based on the supplier’s product quality, on-time delivery level, cost, etc., to select the top suppliers, for its excellent supplier award. At the same time, suppliers with problems can reduce their level of cooperation, cut orders, or terminate cooperation. Through the co-existence of punishment and incentive management measures, suppliers are guided to improve the product time quality and value level, so as to achieve the stability, high quality, and high efficiency of the supply chain of complex products; realize the high quality, on-time delivery, and low cost of complex products; achieve customer satisfaction; and enhance the competitiveness of the market.
- (c)
- Data access and sharing constitute a highly significant factor in complex product supply chains. Hence, integrating data sharing and blockchain technology with such supply chains will aid in moving them toward real-time feedback and process control, as well as facilitate the development of process management systems for complex product supply chains.
- (d)
- Expand research on process feedback within complex product supply chains, thereby advancing studies on the robustness and risk transfer of these supply chains.
The majority of the existing literature investigates revenue distribution, quality incentives, and pricing strategies for complex product supply chains from a game theory standpoint, or focuses on individual indicators like cost reduction, quality enhancement, and risk management from a supply chain perspective under probabilistic uncertainty. In comparison to existing research, this paper utilizes complex networks to characterize the supply chain network structure. By computing and optimizing non-probabilistic uncertainty parameters (including delivery time, quality, and cost) in the network structure, it identifies weak nodes in complex product supply chain networks and optimizes these weak nodes. This contributes to enhancing the sustainability and security of the supply chain network and provides a decision-making foundation for the actual manufacturing of complex products. As such, this paper represents further research that builds upon, refines, and enriches the existing literature. Nevertheless, this paper has certain limitations: for example, the model demands a substantial amount of real historical data, and the authenticity of the collected and obtained data cannot be effectively ensured. Additionally, the model encompasses numerous parameters, and the genetic algorithm requires a long time for solving.
Future research can focus on the following:
- (1)
- Relaxing symmetry assumptions by introducing weighted symmetry coefficients to capture node-specific differences.
- (2)
- Integrating extreme risk scenarios (e.g., via probabilistic–grey hybrid parameters) to enhance model robustness.
- (3)
- Applying the framework to cross-industry complex product supply chains (e.g., large weapons equipment) to test its universality.
- (4)
- Combining real-time data streams (e.g., IoT sensors) with the RG-GERT model to enable dynamic optimization.
Overall, this study advances the theoretical and practical understanding of multi-objective optimization in complex product supply chains, providing a foundation for improving supply chain resilience and competitiveness in uncertain environments.
Author Contributions
Methodology, P.D.; Writing—original draft, W.C.; Writing—review and editing, K.W. and E.G.; Project administration, P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Social Science Foundation of China (Grant No. 2024-SKJJ-C-027) and the Naval University of Engineering independent research projects (No. 202350A010, No. 2025500330, No. 202350A020, and No. 202550A030).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, S.; Liu, Y.; Hao, J.J. Shared Quality Improvement Cost Contract for Complex Product Supply Chain. Ind. Eng. Manag. 2019, 24, 56–63. [Google Scholar] [CrossRef]
- Li, T.J.; Chen, H.Z.; Yuan, J.; Qian, J.; Siyal, A.W. Quality Risk Propagation of Complex Product Collaborative Manufacturing Supply Chain Network Based on CN and SoV. Discret. Dyn. Nat. Soc. 2020, 2020, 8889903. [Google Scholar] [CrossRef]
- Xue, L.; Dai, D.S. Study of an Evolutionary Game between Shipyards and Suppliers about Product Quality. Oper. Res. Manag. Sci. 2021, 30, 17–24. [Google Scholar] [CrossRef]
- Jing, Y.; Cao, L.; Zhang, W.Q. Research on Risk Transmission of Emergencies in Supply Chain Based on an Improved GERT Network. Oper. Res. Manag. Sci. 2022, 31, 62–68. [Google Scholar] [CrossRef]
- Geng, R.; Zhu, J.J. Optimization Model for the Joint of Time and Probability under the Controlled Result Output of the GERT Network. Syst. Eng. 2015, 33, 112–119. [Google Scholar]
- Chen, X.; Cheng, Y.B.; Xu, J. Hotspot Analysis of collaboration Mechanism in Complex Equipment Supply Chain. Sci. Technol. Manag. Res. 2019, 39, 103–109. [Google Scholar] [CrossRef]
- Pei, X.W.; Cheng, Y.B. Research on Factors Affecting Knowledge Input of Complex Equipment “Main-manufacturer-Core-supplier” Collaborative Development. Math. Pract. Theory 2020, 50, 19–26. [Google Scholar]
- Sharma, S.K.; Srivastava, P.R.; Kumar, A.; Jindal, A.; Gupta, S. Supply chain vulnerability assessment for manufacturing industry. Ann. Oper. Res. 2021, 326, 1–31. [Google Scholar] [CrossRef]
- Wang, H.; Fang, Z.G.; Wang, D.A.; Liu, S. An integrated fuzzy QFD and grey decision-making approach for supply chain collaborative quality design of large complex products. Comput. Ind. Eng. 2020, 140, 106212. [Google Scholar] [CrossRef]
- Jiang, Z.Z.; Zhao, J.L.; Zhang, Y.H.; Yi, Z. Unraveling the cheap talk’s informativeness of product quality in supply chains: A lying aversion perspective. Transp. Res. Part E 2022, 166, 102873. [Google Scholar] [CrossRef]
- Sahar, E.B.; Sara, S.; Fuminori, T. Designing a reverse supply chain network with quality control for returned products: Strategies to mitigate free-riding effect and ensure compliance with technology licensing requirements. Technol. Forecast. Soc. Change 2023, 195, 122744. [Google Scholar]
- Alsadi, M.; Arshad, J.; Ali, J.; Prince, A.; Shishank, S. TruCert: Blockchain-based trustworthy product certification within autonomous automotive supply chains. Comput. Electr. Eng. 2023, 109, 108738. [Google Scholar] [CrossRef]
- Su, X.B.; Tao, L.Y. Multi-objective Optimization Model of Supply Chain Management for Complex Product Based on Multi-parameter CF-GERT Network. Comput. Integr. Manuf. Syst. 2025, 31, 330. Available online: https://kns.cnki.net/kcms/detail/11.5946.TP.20230302.1714.004.html (accessed on 3 August 2025).
- Aliakbar, H.; Hadi, M.; Mohammad, F. A multi-objective optimization approach for green and resilient supply chain network design: A real-life case study. J. Clean. Prod. 2021, 278, 123199. [Google Scholar] [CrossRef]
- Silva, P.M.; Gonçalves, J.N.C.; Martins, T.M.; Marques, L.C.; Oliveira, M.; Reis, M.I.; Araújo, L.; Correia, D.; Telhada, J.; Costa, L.; et al. A hybrid bi-objective optimization approach for joint determination of safety stock and safety time buffers in multi-item single-stage industrial supply chains. Comput. Ind. Eng. 2022, 168, 108095. [Google Scholar] [CrossRef]
- Bortolini, M.; Calabrese, F.; Galizia, F.G.; Mora, C. A three-objective optimization model for mid-term sustainable supply chain network design. Comput. Ind. Eng. 2022, 168, 108131. [Google Scholar] [CrossRef]
- Mohammed, A.; Al-shaibani, S.M.; Duffuaa, O.S. A meta-heuristic-based algorithm for designing multi-objective multi-echelon supply chain network. Appl. Soft Comput. 2023, 147, 110774. [Google Scholar] [CrossRef]
- Tliche, Y.; Taghipour, A.; Mahfod-Leroux, J.; Vosooghidizaji, M. Collaborative Bullwhip Effect-Oriented Bi-Objective Optimization for Inference-Based Weighted Moving Average Forecasting in Decentralized Supply Chain. Int. J. Inf. Syst. Supply Chain. Manag. 2023, 16, 1–37. [Google Scholar] [CrossRef]
- Kim, B.; Kim, J.G.; Lee, S. A multi-agent reinforcement learning model for inventory transshipments under supply chain disruption. IISE Trans. 2024, 56, 715–728. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, S.; Hao, J.J. Supply Chain Quality Transaction Mechanism for Complex Product Concerning Profit-reputation Utility Function. Syst. Eng. 2018, 36, 113–120. [Google Scholar]
- Liu, Y.; Wu, S.; Hao, J.J. Supply Chain Quality Incentive Contract for Complex Product from Dual Perspective. Ind. Eng. Manag. 2019, 24, 145–152. [Google Scholar]
- Wang, H.; Fang, Z.G.; Deng, F.; Tao, L.Y. Quality Cost Optimization Method for Complex Product Supply Chain Considering Quality Value. Control Decis. 2019, 34, 1973–1980. [Google Scholar]
- Bai, X. Research on Test Quality Control of Weapon Equipment Based on GERT Network Model. Control Theory Appl. 2022, 41, 5–8. [Google Scholar]
- Wang, Q.; Fang, Z.; Deng, F. Fuzzy-grey RG-GERT: A hybrid model for uncertain supply chain networks. J. Clean. Prod. 2024, 392, 136318. [Google Scholar]
- Toorajipour, R.; Sohrabpour, V.; Nazarpour, A.; Oghazi, P.; Fischl, M. Artificial intelligence in supply chain management: A systematic literature review. J. Bus. Res. 2021, 122, 502–517. [Google Scholar] [CrossRef]
- Wang, H.H.; Zhu, J.J.; Yao, Y.C. GERT network optimization with consideration of “time-resource” on large aircraft collaborative development. Control Decis. 2019, 34, 309–316. [Google Scholar] [CrossRef]
- Li, Y.; Dong, P.; Ye, W. Joint duration-cost-quality optimization model for complex product supply chains under contingency conditions. PLoS ONE 2023, 18, e0292010. [Google Scholar] [CrossRef]
- Han, Y.; Xu, H.Y.; Jiang, J.F.; Yang, B. Time-cost-quality Joint Optimization Model of Construction Project Based on the Interval GERT Network. Syst. Eng. 2018, 36, 61–69. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).