Abstract
This work investigates the intricate dynamics of the Carreau hybrid nanofluid’s inclined magnetohydrodynamic (MHD) flow, exploring both active and passive control modes. The study incorporates critical factors, including Arrhenius activation energy across a stretched sheet, chemical interactions, and nonlinear thermal radiation. The formulation of the boundary conditions and governing equations is inherently influenced by symmetric considerations in the physical geometry and flow assumptions. Such symmetry-inspired modeling facilitates dimensional reduction and numerical tractability. The analysis employs realistic boundary conditions, including convective heat transfer and control of nanoparticle concentration, which are solved numerically using MATLAB’s bvp5c solver. Findings indicate that an increase in activation energy results in a steeper concentration boundary layer under active control, while it flattens in passive scenarios. An increase in the Biot number () and relaxation parameter () enhances heat transfer and thermal response, leading to a rise in temperature distribution in both cases. Additionally, the 3D surface plot illustrates elevation variations from the surface at low inclination angles, narrowing as the angle increases. The Nusselt number demonstrates a contrasting trend, with thermal boundary layer thickness increasing with higher radiation parameters. A graphical illustration of the average values of skin friction, Nusselt number, and Sherwood number for both active and passive scenarios highlights the impact of each case. Under active control, the Brownian motion’s effect diminishes, whereas it intensifies in passive control. Passive techniques, such as zero-flux conditions, offer effective and low-maintenance solutions for systems without external regulation, while active controls, like wall heating and setting a nanoparticle concentration, maximize heat and mass transfer in shear-thinning Carreau fluids.
Keywords:
arrhenius activation energy; inclined MHD nanofluid flow; nonlinear thermal radiation; carreau model MSC:
00-01; 99-00
1. Introduction
Nanofluids, consisting of nanoparticles suspended in base fluids, have gained attention for their enhanced thermophysical properties and heat transfer performance compared to conventional fluids. However, despite promising results in academic research, challenges remain for widespread industrial implementation. As nanotechnology, surface science, and colloidal chemistry advance, nanofluids are expected to play a significant role in future heat transfer applications. Ongoing research focuses on understanding nanofluid behavior and exploring their potential applications in various fields, including solar collectors, electronics cooling, automobile radiators, nuclear reactors, and space technology [1,2,3]. Hayat et al. [4] investigated the melting point shift of nanofluids near a stretched surface under the influence of heat generation/absorption, nonlinear thermal radiation, and a magnetic field, and obtained a convergent series solution using the homotopy technique.
Algehyne et al. [5] found that increasing nonlinear thermal radiation and source/sink factors augmented temperature profiles, while chemical reaction factors adversely affected concentration profiles. Prasad et al. [6] investigated the influence of magnetic fields, radiation, heat sources, and porosity on hybrid nanofluid flow characteristics. Vijaya et al. [7] reported that exponential heat source parameters increased temperature profiles, while variable viscosity decreased fluid velocity. They also noted that magnetic fields reduced skin friction coefficients. Mabood et al. [8] investigated the effects of radiation. They found that temperature profile increases with the radiation parameter. Kumar et al. [9] studied the impact of irregular heat sources with nonlinear radiation, along with the influence of Arrhenius activation energy on electro-magnetohydrodynamic hybrid nanofluid flow.
A quasi-linearization analysis was conducted by Ali et al. [10,11] for entropy generation in the MHD mixed-convection flow of a Casson nanofluid over a nonlinear stretching sheet with Arrhenius activation energy. Kalaivanan et al. [12] analyzed the Arrhenius activation energy associated with nanofluid flow under both active and passive control of nanomaterials. Their results showed that the local Nusselt number increased with the activation energy and decreased with elastic deformation and the exponential fitted rate. The study [13] noted that increased reaction rate and activation energy reduced the local Nusselt number and increased the local Sherwood number.
The optimization of entropy in both passive and active liquid hydrogen flow based on nanoliquid transport via a curved stretching sheet was studied by Khan et al. [14]. Duari et al. [15] detected that, in the presence of active and passive control, the thermal energy profile showed a decreasing behavior with the fluctuating parameter; however, the concentration profile exhibited a dual nature under passive control. Kumar et al. [16,17] examined MHD nanofluid flow over a stretching sheet with nonlinear thermal radiation and a non-uniform heat source, revealing that temperature profiles intensified with higher temperature ratios and thermal radiation under active and passive controls. Their study focused on the flow characteristics and mass–heat distribution of a steady MHD nanofluid stream over an axially moving thin needle with passive and active nanoparticle controls. The model under consideration was based on a second-grade nanofluid with two types of nanoparticle controls: active and passive. In recent years, various researchers have conducted studies on second-grade nanofluids [18,19,20,21,22]. Mumtaz et al. [23] found that higher-order chemical reactions increased fluid density under active control but decreased it under passive control, while velocity slip raised drag friction and reduced heat transport; active control also enhanced heat transfer with stronger chemical reactions, unlike passive control. Yasmin et al. [24] conducted a numerical study on the hybrid nanofluid flow over an extended sheet under convective conditions using magnetized water, considering both active and passive nanoparticle controls.
The effects of parameters like porosity, heat source, chemical reaction, and Biot number on flow velocity and temperature in the boundary-layer flow of Carreau nanofluids over a nonlinearly stretched sheet were studied in [25]. The Biot number and thermal radiation parameters were found to significantly influence temperature profiles, with increasing values leading to higher thermal distributions [26,27]. Shah et al. [28] investigated bioconvection effects on Prandtl hybrid nanofluid flow, finding that velocity profiles increased with Prandtl parameters. Increasing Biot number has been found to enhance heat transfer rates and thermal efficiency in various configurations, including flow past orthogonal plates and over exponentially shrinking sheets. Several studies have investigated hybrid nanofluids composed of different nanoparticles, such as Cu-TiO2 in water (El-Hakiem et al. [29]) and Fe3O4-Go in water (Madhukesh et al. [30]). The Biot number also positively influences temperature profiles in hybrid nanofluid flows.
The behavior of hybrid nanofluids under various conditions, particularly in the presence of inclined magnetic fields, has also been investigated. Hybrid nanofluids, consisting of multiple types of nanoparticles suspended in a base fluid, demonstrate enhanced heat transfer capabilities compared to single-component nanofluids, as studied by Algehyne et al. [31]. The thermodynamics of a Carreau nanoliquid thin film containing graphene nanoparticles across a stretched sheet was investigated by Choudhary et al. [32] in the presence of an inclined magnetic field with a heat source. There have also been studies investigating natural and mixed convection in different geometries, including inclined needles, nonlinear stretching sheets, and enclosures with circular heaters (e.g., Rajamani et al. [33]).These effects significantly influence heat and mass transfer in hybrid nanofluids, which consist of hybrid nanoparticles dispersed in a base fluid [34,35].
The abovementioned studies discuss heat transfer in hybrid nanofluids under various conditions, such as nonlinear sheets, and explore the impact of parameters like radiation, magnetic field, and heat source. Also, they employ different conditions like convective boundary condition, activation energy, and active and passive cases. Although various authors have explored the effect of an inclined magnetic field, there remains a gap regarding the parallel inclined MHD effect with different conditions in the presence of nonlinear radiation, heat source, activation energy, and convective boundary conditions. The present article extends the above investigations to examine the simultaneous effects of an inclined magnetic field on different parameters such as nonlinear radiation, heat source, activation energy, and convective boundary conditions, including activation energy and Weissenberg number on the flow of Carreau hybrid nanofluids over a stretching sheet with active and passive controls. The simultaneous effect of MHD is shown in different profiles, skin friction, and Nusselt number, with the use of various parameters highlighting the novelty and different outcomes of this article. Although symmetry is not the central focus of the current study, it plays an implicit role in the formulation of the mathematical model. The assumptions of a steady, two-dimensional, laminar boundary-layer flow over a stretching sheet inherently introduce geometric and flow symmetries that enable the reduction in the governing equations using similarity transformations. Such symmetric simplifications are widely employed in fluid mechanics to derive dimensionless forms that capture the essence of the physical phenomena while maintaining analytical and numerical tractability. Furthermore, the analysis of control strategies, both active and passive, often relies on the assumption of the symmetrical distribution of thermal and concentration fields along the transverse direction. These underlying symmetric aspects justify the inclusion of the study within the broader context of symmetry-based modeling in complex fluid dynamics. Also, both active and passive cases are analyzed, with detailed discussions on 3D graphs of the Nusselt number as well as comprehensive tables. Furthermore, average number graphs are presented to elucidate the numerical simulation of heat transfer in hybrid nanofluids. This extension has significant implications for diverse applications, showcasing the efficacy of numerical analysis in understanding complex heat transfer phenomena in nanofluids.
2. Physical Pattern and Interpretation
- The study investigates two-dimensional, laminar, and incompressible inclined magnetohydrodynamic (MHD) flow of a Carreau hybrid nanofluid over a nonlinear radiative stretching surface (as shown in Figure 1 [12]).
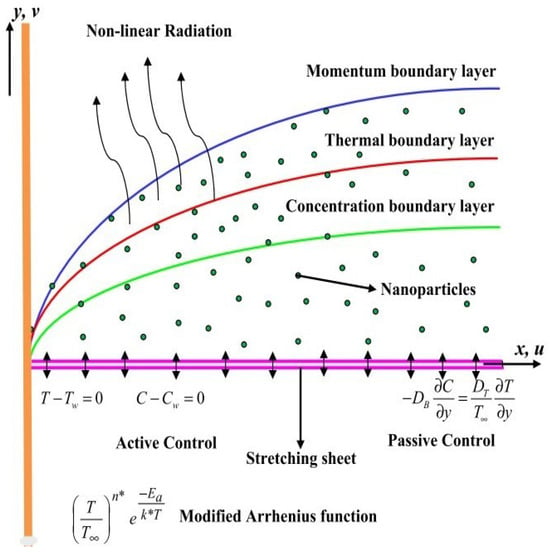 Figure 1. Graphical representation of the model.
Figure 1. Graphical representation of the model. - The hybrid nanofluid is water-based and contains copper (Cu) and iron oxide (Fe3O4) nanoparticles.
- The analysis includes the effects of Brownian motion, thermophoresis, magnetic field effects, surface chemical reaction rate (), activation energy (E), thermal radiation, and internal heat generation.
- A hot working fluid at temperature convectively heats the nanofluid through the stretching surface; a zero mass flux condition is considered; and as , the temperature and concentration approach their ambient values and , respectively.
The governing equations for the Carreau hybrid nanofluid flow under these conditions, based on the boundary layer approximation, are presented in the works of [11,36,37].
According to the problem’s geometry, the boundary conditions can be divided into the preceeding classes:
Here, velocity components along axes x and y are denoted by u and v, respectively; is the kinematic viscosity; is the base fluid’s density; n is the power-law index; the fluid’s thermal conductivity is denoted by ; is the thermal diffusivity with being the specific heat at constant pressure; K is the permeability of the porous medium; the coefficient of dimensional heat production and absorption is denoted by ; is the diffusion coefficient of Brownian; and is the diffusion coefficient for thermophoresis. Thermal relaxation is represented by , chemical reaction parameter by , strength of the magnetic field by , activation energy by , and relaxation parameter by . Consistent properties are maintained, with the exception of density variations that provide a thermal buoyancy force. Here, and m* stand for the Stefan–Boltzmann constant and the average absorption factor, respectively. Table 1 and Table 2 gives the thermo-physical and physical properties of hybrid nano fluid.

Table 1.
Thermophysical Properties [38,39,40].

Table 2.
Physical Properties [41,42].
Here, represents a stretching (if ) or shrinking (if ) surface along the x-direction. The term allows for a nonlinear variation in stretching rate along the surface. When , no penetration through the wall can occur, and so fluid does not enter or leave the surface. The boundary condition for convective heat transfer at the surface is set. The concentration of nanoparticles on the wall is fixed at . Consider a zero net mass flux condition, where the total mass flux is zero at the wall. These are far-field conditions indicating that the influence of the wall vanishes at large distances. The fluid becomes stationary as . The temperature and concentration approach ambient values and , respectively. It is necessary to incorporate the following non-dimensional variables in order to simplify the detailed problem:
where f, , and are the self-similar velocity, temperature, and concentration, respectively; also, is a scaled boundary layer coordinate and is the stream function. Ordinary differential equations (ODEs) are finally obtained using similarity transformation by substituting Equation (6) in partial differential Equations (2)–(5):
Moreover, the modified boundary limitations are expressed as
3. Physical Quantities
The various factors involved in Equations (7) to (10) are as follows: Prandtl number , magnetic parameter , Weissenberg number , relaxation parameter , Brownian parameter , thermophoresis parameter , radiation parameter (), Ecart number (), Biot number (), inclination parameter (), heat source parameter (), and temperature ratio parameter ().
4. Engineering Quantities
The essential facets of engineering include the skin friction factor , local Sherwood number , and local Nusselt number . The following equation is specifically of interest to this study:
where is the wall shear stress and and are the wall heat and mass fluxes, respectively. By utilizing the above similarity transformations, the following quantities can be calculated as
Here, is the local Reynold’s number.
5. Execution of Methodology
Considering the impact of key active physical parameters, this study utilizes the bvp5c method to solve the governing equations for MHD Carreau hybrid nanofluid flow over a stretching surface. The simulations were carried out using MATLAB 2021 as the computational platform. The highly nonlinear coupled system of ordinary differential equations, along with the boundary conditions (Equation (10)) and Equations (7)–(9), was solved using MATLAB’s bvp5c function. The bvp5c method adaptability allows for an effective balance between computational efficiency and accuracy. The solution was iteratively improved by updating the initial guesses for the unknown boundary values using the model’s residuals. When the desired accuracy, specified by an error tolerance of is reached, the final solution is obtained, providing the values of the dependent variables throughout the domain. MATLAB computational environment supports efficient implementation and analysis of the numerical method, enabling organized computations and clear visualization of the model outcomes. The bvp5c solver in MATLAB is a collocation-based method that uses a fifth-order finite-difference scheme with a fourth-order error estimate to solve boundary value problems accurately. It ensures solution accuracy through adaptive mesh refinement and residual control, which allow it to concentrate computational effort where needed. Convergence is achieved via a Newton-like iterative method applied to the discretized system until a specified tolerance is met. The solver’s implicit formulation and capacity to handle stiff equations contribute to its numerical stability, even in problems with sharp gradients. By continuously monitoring the residual error, bvp5c adapts the solution until both absolute and relative error criteria are satisfied.
The boundary conditions for the active control case are
The boundary conditions for the passive control case are
The infinity boundary condition is rescaled to . The accuracy of the numerical method is verified through a detailed comparison with previously published results, as presented in Table 3.

Table 3.
Validation of the Proposed Model with Existing Studies.
To verify the accuracy of the proposed problem, the computed results are validated against previous studies, as shown in Table 3.
6. Results and Discussion
The effects of various physical parameter values—such as , and —on the velocity profile , temperature profile , and concentration profile of nanoparticles for fixed values of , , and have been discussed in order to learn about the problem physically. The numerical analysis of these parameters is illustrated through various figures and tables, reflecting their impact on the flow field. A range of physical parameters has been evaluated, and Table 4, Table 5 and Table 6 specifically present numerical data for local skin friction, Nusselt number, and Sherwood number, respectively, across different inclination angles () for both active and passive nanoparticle management strategies.

Table 4.
The variation in the skin friction coefficient for different values of M, , , , , and while other parameters remain fixed in active and passive cases.

Table 5.
The variation in the Nusselt number for different values of M, , , , , and while other parameters remain fixed in active and passive cases.

Table 6.
The variation in Sherwood number for different values of M, , , , , and while other parameters remain fixed in active and passive cases.
Figure 2 illustrates the variation in velocity profiles influenced by the Weissenberg number () and the relaxation parameter (). It is observed that increasing either or leads to a decrease in fluid velocity, highlighting the physical connection between relaxation time and time-dependent expansion. As the Weissenberg number increases, it enhances the relaxation effects (), resulting in greater resistance from viscous forces and thus reducing the fluid’s velocity. This decline in velocity with rising values is clearly depicted in Figure 2. Due to the dominant influence of viscosity, fluid particles exhibit increased resistance to motion.
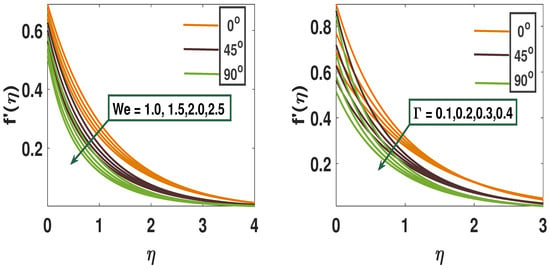
Figure 2.
A pictorial representation of velocity profile using parameters We and .
Figure 3 demonstrates that the temperature profile rises with an increase in the Biot number (). Physically, a higher indicates a greater ratio of convective heat transfer to thermal conductivity, leading to elevated temperature within the fluid. When the Biot number is low (), the internal thermal resistance of the solid is negligible compared to surface resistance, resulting in a nearly uniform solid temperature, and making enhancements to the surface convection (such as fins or increased fluid flow) is the most effective design strategy. When the Biot number is high (), internal thermal resistance dominates, causing significant temperature gradients within the solid and making it essential to enhance internal thermal conductivity—such as by using materials with higher k, like metals or nanocomposites—for effective heat transfer. In convective cooling design, selecting high-conductivity materials is vital for high-Biot-number systems to reduce internal temperature gradients, while reducing characteristic length can lower Biot number and shift resistance to the surface. Enhancing surface convection is most effective in low-Biot-number scenarios, and identifying whether conduction or convection limits performance is key to optimizing the overall cooling strategy. Figure 3 illustrates that the temperature distribution increases as the relaxation parameter () becomes larger. An increase in the relaxation parameter reduces fluid temperature by delaying heat flux, which slows heat conduction. This reflects the system’s resistance to sudden thermal changes, resulting in lower temperatures than those predicted by classical conduction models. In high-frequency heating or laser applications, or in nanoscale flows where Fourier’s law fails, the relaxation parameter is vital for accurately modeling thermal behavior, as a higher relaxation time indicates slower thermal response, which is beneficial for designing materials with controlled heat transfer or insulation.
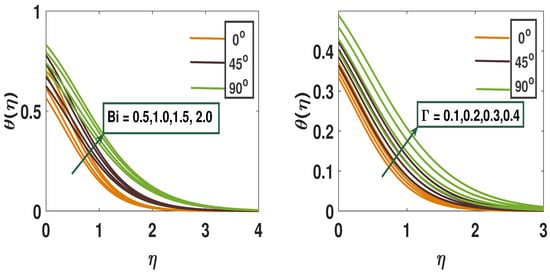
Figure 3.
A pictorial representation of temperature profile using parameters Bi and .
Figure 4 presents the influence of the thermophoresis parameter () and the heat source parameter () on the temperature field. As increases, the temperature rises due to the stronger response of particles to thermal gradients, causing them to accumulate in hotter regions and altering the fluid’s heat transfer characteristics. The heat source parameter () represents the rate of thermal energy addition or removal, playing a crucial role in analyzing energy transfer and understanding the interaction between temperature distribution and fluid motion. Figure 4 clearly illustrates how the inclination angle and the exponentially space-dependent heat source () influence the temperature profile in both active and passive control scenarios, showing that increasing enhances the thermal boundary layer and increases its thickness.
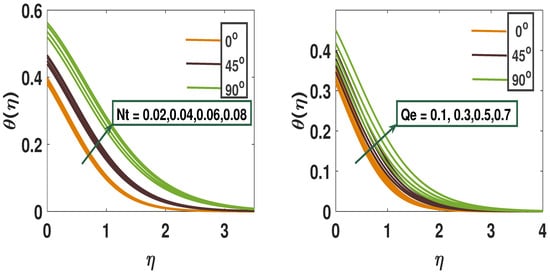
Figure 4.
A pictorial representation of the temperature profile using parameters Nt and Qe.
Figure 5 show that increasing the radiation parameter and the wall temperature parameter leads to a rise in the nanofluid temperature profile. Physically, while conductive heat transfer dominates over radiative transfer, reducing the thermal boundary layer thickness and buoyancy effects, radiation also contributes by breaking water molecules to generate hydrogen. In high-temperature settings such as combustion chambers, solar collectors, or nuclear reactors, the radiation parameter is crucial for accurately modeling the significant role of radiative heat transfer in temperature distribution. Additionally, as increases, the temperature profile continues to rise, a trend consistently observed across all inclination angles .
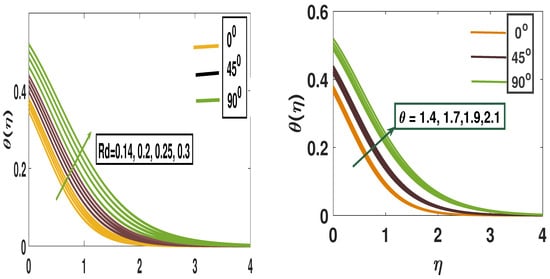
Figure 5.
A pictorial representation of the temperature profile using parameters Rd and .
Figure 6 illustrates the temperature profile’s response to variations in the Weissenberg number , showing that an increase in leads to a rise in fluid temperature due to longer particle relaxation times and increased fluid collisions. Figure 6 highlights the contrasting effects on the concentration profile: it decreases concentration in the active control scenario, while it enhances concentration in the passive case. Figure 7 displays the boundary layer thickness as a function of the Biot number () under both active and passive control scenarios. Since the Biot number is inversely related to surface heat resistance, a higher leads to an increase in the concentration profile for both cases, indicating enhanced convection due to reduced thermal resistance. Conversely, Figure 7 shows that the parameter produces an opposite effect, where its increase leads to greater heat conduction in both active and passive control scenarios through fluid accumulation.
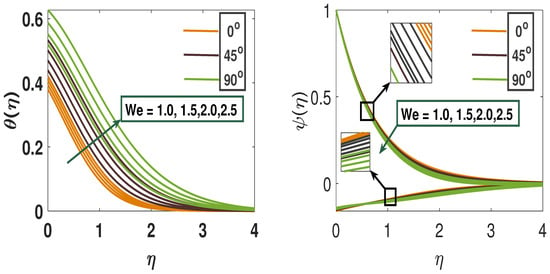
Figure 6.
A pictorial representation of the temperature profile and concentration profile using parameter We.
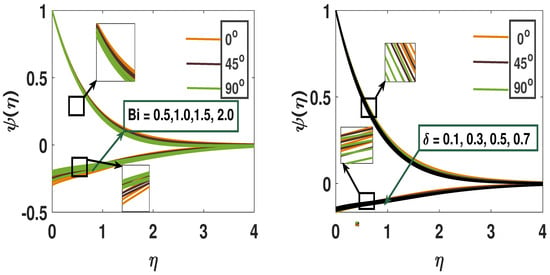
Figure 7.
A pictorial representation of concentration profile using parameters Bi and .
Figure 8 illustrates the impact of the chemical reaction parameter on the concentration profile under active and passive control scenarios. In the passive case, increasing and the inclination angle () leads to a decrease in concentration, while in the active case, higher values of these parameters result in an increased volume fraction. Similarly, Figure 8 shows that the concentration profile rises with increasing thermophoresis parameter and inclination angle in both control scenarios. Figure 9 presents the behavior of the concentration field influenced by the Eckert number () and the inclination angle (), showing that concentration increases with both parameters. Physically, the presence of activation energy enhances molecular interactions, accelerating chemical reactions, which in turn boosts the concentration profile in both active and passive scenarios. Activation energy critically influences reaction rates in reactive flows. High slows down species consumption, leading to elevated concentration levels, while lower enhances reaction rates, causing sharper declines in species concentration; therefore, its inclusion is vital for accurate modeling of mass transfer and conversion in reactive systems. Figure 9 illustrates the effect of the Brownian motion parameter (), where increased particle agitation causes wider dispersion. This results in a reduced concentration profile under active control but an increase in the passive case, as the concentration field becomes more uniformly distributed throughout the fluid. The velocity and temperature profiles exhibit variations in response to different values of the inclination angle (). As increases, the velocity boundary layer becomes thinner due to a reduction in fluid velocity within the flow region. Conversely, a higher inclination angle tends to increase the thermal boundary layer thickness, as it resists fluid motion and promotes greater thermal diffusion.
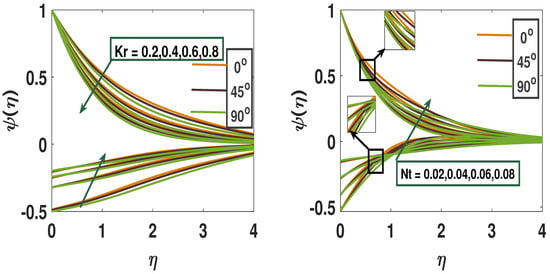
Figure 8.
A pictorial representation of the concentration profile using parameters Kr and Nt.
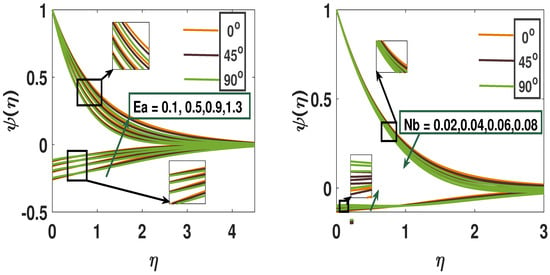
Figure 9.
A pictorial representation of the concentration profile using parameters Ea and Nb.
Figure 10 present 3D surface plots of skin friction in both active and passive control cases, showing its variation with increasing radiation parameter () and Weissenberg number . The plots indicate that skin friction values are more dispersed at lower inclination angles but converge at higher inclinations. As increases, skin friction generally rises due to the added resistance from fluid elasticity. In contrast, higher tends to reduce skin friction by elevating the temperature and lowering the fluid’s viscosity. In a 3D surface plot, skin friction is expected to increase along the Weissenberg number () axis and decrease along the radiation parameter () axis. This behavior is crucial in applications involving heat transfer and viscoelastic fluids, where the interaction between and can lead to complex flow dynamics, as shown in Figure 11. Notably, the Nusselt number displays an opposite trend to that of skin friction in the corresponding plots. The Weissenberg number () reflects the fluid’s elasticity, with higher values indicating stronger elastic effects. Increased elasticity typically resists convective heat transfer, leading to reduced heat transfer rates and lower Nusselt numbers. In contrast, a higher radiation parameter enhances energy transport, thereby increasing the Nusselt number and improving heat transfer performance. At very high values of the radiation parameter (), radiation can dominate over convection, significantly altering the relationship between the Nusselt number and the Weissenberg number . In a 3D surface plot of the Nusselt number versus and , the surface typically decreases along the axis and increases along the axis. The combined effect of these parameters is influenced by the flow regime, boundary conditions, and fluid properties. Understanding these effects is essential for optimizing heat transfer in industrial applications such as radiative heat transfer systems, cooling technologies, and polymer processing. Figure 12 illustrate the average values of skin friction, Nusselt number, and Sherwood number in both active and passive control scenarios. The 3D plots show that skin friction values are more spread out at lower inclination angles but converge as inclination increases, while the Nusselt number displays the opposite trend to skin friction. Similar trends in Nusselt number, Sherwood number, and velocity or temperature profiles can be seen in [11,16].
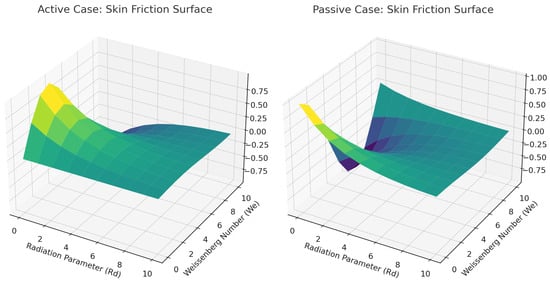
Figure 10.
A pictorial representation of the skin friction using parameters and Rd with active and passive cases.
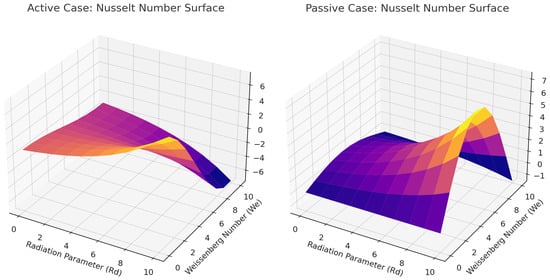
Figure 11.
A pictorial representation of the Nusselt number using parameters and Rd with active and passive cases.
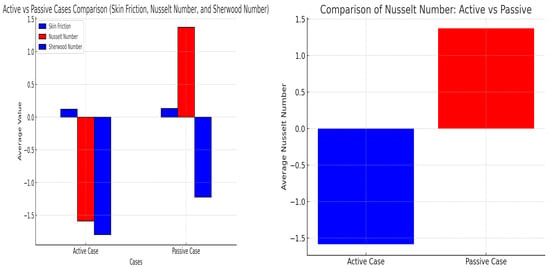
Figure 12.
A pictorial representation of the average value of skin friction, Nusselt and Sherwood numbers in active and passive cases.
As the radiation parameter () increases, skin friction decreases while the Nusselt number rises in both active and passive control scenarios. However, the Sherwood number exhibits contrasting behavior: it increases with in the active case but decreases in the passive case. Additionally, as the Weissenberg number () increases, the Eckert number () and Nusselt number also increase, while skin friction decreases. A stronger magnetic field generates a Lorentz force that resists fluid motion, thereby increasing wall drag and enhancing skin friction. The opposing Lorentz force slows the fluid near the boundary, reducing velocity gradients and thickening the boundary layer with a more uniform velocity profile. As the Weissenberg number increases, enhanced fluid elasticity resists shear deformation, reducing the near-wall velocity gradient and consequently lowering the wall shear stress. Elastic effects delay the fluid’s response to applied forces, causing a more gradual development of velocity near the wall, which reduces the velocity gradient and thus decreases the skin friction coefficient. In active control (surface heating), boundary conditions can be directly manipulated, allowing the elastic effects of higher Weissenberg numbers to be harnessed for drag reduction or flow control in applications like polymer processing and cooling systems. In contrast, passive control (zero flux) depends on natural system responses, where increased elasticity passively reduces skin friction and energy loss, making it advantageous for low-maintenance systems such as microfluidic devices or coating flows. Notably, with higher , both skin friction and Sherwood number rise, whereas the Nusselt number declines across both control modes. For higher values of the Brownian motion parameter (), the Sherwood number shows an increasing trend in active control cases, while the opposite is observed in passive scenarios. Similarly, as the Biot number increases, the Nusselt number rises in both active and passive cases. However, the Sherwood number behaves differently—rising in the active case but decreasing in the passive one.
7. Numerical Outcomes
This section presents the numerical results for skin friction, Nusselt number, and Sherwood number in relation to various parameters and the inclination angle . The computed values are summarized in Table 4, Table 5 and Table 6, corresponding to skin friction, Nusselt number, and Sherwood number, respectively. As the magnetic parameter increases from , an inverse relationship with skin friction is observed. The rising magnetic field strength reduces the velocity gradient near the wall, leading to a lower skin friction coefficient. This indicates a decrease in wall shear stress due to a stronger damping of the flow close to the surface. As the radiation parameter values are , skin friction decreases. This is because higher radiation enhances radiative heat transfer during forced convection, leading to a thicker thermal boundary layer. Consequently, the momentum boundary layer gradient weakens, reducing wall shear stress and lowering skin friction. In contrast, increasing the Weissenberg number from results in higher skin friction due to stronger elastic effects in the fluid. As the inclination angle increases from , the buoyant driving force weakens, resulting in slower fluid motion near the surface. This reduction in velocity leads to lower wall shear stress and, consequently, a decrease in skin friction. As the inclination angle increases from , the surface gravity component decreases, leading to a reduced buoyant force that weakens the flow and consequently lowers both the Nusselt number and convective heat transfer in active and passive scenarios. A higher Biot number reflects stronger surface convection relative to internal conduction, which enhances heat transfer and results in an increased Nusselt number. As the radiation parameter increases from , and the Biot number from , the Nusselt number correspondingly rises in both cases. Additionally, increasing values of the radiation parameter , Weissenberg number , Brownian motion parameter , and Biot number lead to a rise in the Sherwood number. However, an opposite trend is observed with increasing values of the Eckert number and thermophoresis parameter , which cause a reduction in the Sherwood number. Furthermore, as the inclination angle increases from 0 90, the Sherwood number increases in the active control scenario but decreases in the other control case.
7.1. How Boundary Conditions Differ Between Active and Passive Situations
In this study, the primary distinction between active and passive nanoparticle concentration control stems from the type of boundary condition applied at the wall. Under active control, the wall concentration is fixed at , implying that nanoparticles are externally maintained or injected at a constant level. This enforces a strong concentration gradient near the surface, promoting higher mass transfer rates and leading to an increase in the Sherwood number. Conversely, passive control employs a zero mass flux condition:
which allows the wall concentration to naturally adjust based on the interplay of Brownian diffusion and thermophoresis, without direct intervention. As a result, the concentration gradient can become weaker or even reverse, often resulting in a decrease or reversal in the Sherwood number trend compared to the active case. This difference is more than theoretical; it has important practical implications. Active systems, such as drug delivery platforms or nanofluid-based thermal devices, offer precise and responsive control over mass transfer performance through controlled nanoparticle input. In contrast, passive systems, like microfluidic setups or self-regulating thermal coatings, leverage natural thermophoretic and diffusive behaviors to achieve maintenance-free operation, though with limited control over concentration profiles. A clear understanding of how these boundary conditions influence mass transfer is essential for the effective design and optimization of nanofluid applications.
7.2. Engineering Applications or Implications in Thermal Systems or Reactor Designs
This study provides engineering strategies to enhance heat and mass transfer using magnetic fields, hybrid nanofluids, and radiation control. Magnetic field application improves flow regulation in systems like nuclear reactors and MHD pumps, while hybrid nanofluids enhance thermal conductivity, making them ideal for heat exchangers and microchannel cooling. Active controls (wall heating) offer precision, whereas passive methods (zero flux) suit low-maintenance systems like spacecraft insulation. Nonlinear thermal radiation and inclined magnetic fields further refine thermal management in high-temperature environments, enabling accurate temperature prediction and optimized flow behavior. These insights support improved design and efficiency in advanced thermal systems.
8. Concluding Remarks
The current study examines the two-dimensional, incompressible, water-based Carreau nanofluid flow with active and passive controls over a nonlinearly stretched sheet, taking into account nonlinear thermal radiation, Arrhenius activation energy, and inclined MHD effects. The governing PDEs are reduced to ODEs using similarity transformations. The bvp5c solver is employed to obtain numerical results. This research offers several fascinating observations which, due to the intricate mechanisms involved, are summarized below in terms of the quantities affected by the influencing parameters:
- In both the active and passive control scenarios, the skin friction is decreased with increasing values of magnetic field (M) and Weissenberg ().
- An increase in the Biot number () and relaxation parameter () enhances heat transfer and thermal response, leading to a rise in temperature distribution in both cases.
- With increasing Biot number (), the concentration profile reduces in the active case but improves in the passive case.
- With growing values of inclination (), skin friction on the 3D surface reaches near the surface, but a reverse effect can be seen in the case of a Nusselt number 3D surface plot.
- When we increase the radiation parameter from and Biot number from < < , we see that the Sherwood number also increases.
- As the inclination rises from , the Nusselt number and convective heat transfer in both active and passive cases reduce.
- The Sherwood number likewise rises in the case of active control but falls in the case of passive control for increasing values of inclination from .
- A graphical illustration of the average values of skin friction, Nusselt number, and Sherwood number for both active and passive scenarios is presented, highlighting the impact of each case.
- This study provides valuable engineering insights into enhancing heat and mass transfer through active control methods—such as fixed nanoparticle concentration and wall heating—that are crucial for applications ranging from electromagnetic pumps and nuclear reactors to microelectronic cooling and solar collectors.
- The accuracy of the Carreau model in capturing the complete rheological complexity of nanofluids is limited by its dependence on a fixed functional form, even if it is a useful tool for capturing shear-thinning, particularly when shear rates or time-dependent behaviors are high.
- Symmetry is prominently exhibited across various parameters and profiles as a function of the angle .
This successful computational study has properly elucidated the parametric influences on the dynamics of inclined magnetohydrodynamic Carreau nanofluid flow with activation energy and multiple slip boundary conditions. This study may be extended to include Maxwell dusty nanofluid, Casson nanofluid, and hybrid nanofluid.
Author Contributions
Conceptualization, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Methodology, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Software, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Validation, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Formal analysis, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Writing—original draft, P.K. (Praveen Kumari), H.P., P.K. (Pardeep Kumar) and M.A.; Project administration, M.A.; Funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The first author acknowledges with thanks the Department of Mathematics and Statistics, for their technical support at Haryana Agricultural University.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
The following abbreviations are used in this manuscript:
| Symbol | Quantity (Unit) |
| Fluid velocity components () | |
| Uniform magnetic field () | |
| f | Non-dimensional radial velocity component () |
| a | Reference velocity (m/s) |
| l | Characteristic length (m) |
| R | Radius of the cylinder (m) |
| Cylindrical coordinates | |
| Reynolds number | |
| Ambient temperature (K(Kelvin)) | |
| T | Fluid temperature (K(Kelvin)) |
| Fluid temperature at the cylinder (K(Kelvin)) | |
| C | Fluid concentration |
| Ambient nanoparticle concentration | |
| n | Power-law index |
| Nanoparticle concentration at the disc | |
| Brownian diffusivity | |
| Thermophoretic diffusion | |
| Prandtl number | |
| M | Magnetic field parameter |
| Local drag coefficient | |
| Local Nusselt number | |
| Local Sherwood number | |
| Curvature parameter | |
| Heat source | |
| Weissenberg number | |
| Chemical reaction parameter | |
| Greek symbols | |
| Non-dimensional temperature | |
| Density (kg) | |
| Dimensionless variable | |
| k | Thermal conductivity () |
| Specific heat capacity () | |
| Viscosity () | |
| Boltzmann’s constant ( | |
| Kinematic Viscosity () | |
| Time material constant (s) | |
| Electrical conductivity ( ) |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Gholinia, M.; Pourfallah, M.; Chamani, H. Numerical investigation of heat transfers in the water jacket of heavy duty diesel engine by considering boiling phenomenon. Case Stud. Therm. Eng. 2018, 12, 497–509. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Khan, M.I.; Alsaedi, A. Theoretical investigation of Ree–Eyring nanofluid flow with entropy optimization and Arrhenius activation energy between two rotating disks. Comput. Methods Programs Biomed. 2019, 177, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Shafiq, A. Inclined magnetic field and heat source/sink aspects in flow of nanofluid with nonlinear thermal radiation. Int. J. Heat Mass Transf. 2016, 103, 99–107. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Lone, S.A.; Raizah, Z.; Eldin, S.M.; Saeed, A.; Galal, A.M. Chemically reactive hybrid nanofluid flow past a Riga plate with nonlinear thermal radiation and a variable heat source/sink. Front. Mater. 2023, 10, 1132468. [Google Scholar]
- Fatima, K.; Prasad, J.R. Effect of Inclined Magnetic Field and Chemical Reaction on Radiative Hybrid Nanofluid Flow Through an Exponentially Stretched Porous Surface in the Presence of Heat Source. J. Mech. Contin. Math. Sci. 2025, 20, 4. [Google Scholar] [CrossRef]
- Sreenivasulu, M.; Bhuvana Vijaya, R. Influence of exponential heat source, variable viscosity and shape factor on a hybrid nanofluid flow over a flat plate when thermal radiation and chemical reaction are significant. Mod. Phys. Lett. B 2024, 38, 2450102. [Google Scholar] [CrossRef]
- Mabood, F.; Shafiq, A.; Khan, W.A.; Badruddin, I.A. MHD and nonlinear thermal radiation effects on hybrid nanofluid past a wedge with heat source and entropy generation. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 120–137. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Areekara, S.; Sabu, A.; Mathew, A.; Ali, L. Significance of irregular heat source and Arrhenius energy on electro-magnetohydrodynamic hybrid nanofluid flow over a rotating stretchable disk with nonlinear radiation. Numer. Heat Transf. Part Appl. 2024, 85, 1866–1888. [Google Scholar] [CrossRef]
- Ali, K.; Faridi, A.A.; Ahmad, S.; Jamshed, W.; Hussain, S.M.; Tag-Eldin, E.S.M. Quasi-linearization analysis for entropy generation in MHD mixed-convection flow of Casson nanofluid over nonlinear stretching sheet with Arrhenius activation energy. Symmetry 2022, 14, 1940. [Google Scholar] [CrossRef]
- Bilal, S.; Shah, I.A.; Rashid, M.; Khan, I. Impact of activation energy on carreau nanofluid flow over non-linear stretching surface. Heliyon 2024, 10, e23934. [Google Scholar] [CrossRef]
- Kalaivanan, R.; Ganesh, N.V.; Al-Mdallal, Q.M. An investigation on Arrhenius activation energy of second grade nanofluid flow with active and passive control of nanomaterials. Case Stud. Therm. Eng. 2020, 22, 100774. [Google Scholar] [CrossRef]
- Ramesh, G. Analysis of active and passive control of nanoparticles in viscoelastic nanomaterial inspired by activation energy and chemical reaction. Phys. Stat. Mech. Its Appl. 2020, 550, 123964. [Google Scholar] [CrossRef]
- Khan, S.A.; Hayat, T.; Alsaedi, A. Entropy optimization in passive and active flow of liquid hydrogen based nanoliquid transport by a curved stretching sheet. Int. Commun. Heat Mass Transf. 2020, 119, 104890. [Google Scholar] [CrossRef]
- Duari, P.R.; Das, K. Active-passive controls on magneto CNTs nanofluid flow over a wavy rotating disc. Int. J. Model. Simul. 2023, 43, 1–16. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L. Insight into the dynamics of active and passive controls over the measurement of thermal conductivity of nanofluids subject to magnetic field and thermal radiation through the stretching surface. Numer. Heat Transf. Part Appl. 2025, 86, 651–666. [Google Scholar] [CrossRef]
- Bag, R.; Kundu, P.K. Aspects of active-passive controls of nanoparticles of chemically reactive and radiative nanofluid flow past a frequently moving thin needle with thermal and velocity slip: A numerical framework. Numer. Heat Transf. Part Appl. 2024, 85, 3714–3734. [Google Scholar] [CrossRef]
- Hakeem, A.A.; Kalaivanan, R.; Ganga, B.; Ganesh, N.V. Nanofluid slip flow through porous medium with elastic deformation and uniform heat source/sink effects. Comput. Therm. Sci. Int. J. 2019, 11, 269–283. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A.; Mustafa, M. On magnetohydrodynamic flow of second grade nanofluid over a convectively heated nonlinear stretching surface. Adv. Powder Technol. 2016, 27, 1992–2004. [Google Scholar] [CrossRef]
- Hakeem, A.; Kalaivanan, R.; Ganga, B.; Ganesh, N.V. Effect of elastic deformation on nano-second grade fluid flow over a stretching surface. Front. Heat Mass Transf. 2018, 10, 20. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.; Imran, M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Hayat, T.; Khan, S.A.; Alsaadi, F.E.; Khan, M.I. Investigation of physical aspects of cubic autocatalytic chemically reactive flow of second grade nanomaterial with entropy optimization. Comput. Methods Programs Biomed. 2020, 183, 105061. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, M. Hydrothermal dynamics of darcy Forchheimer ternary hybrid nanofluid flow past bended surface with active—Passive controls. Adv. Mech. Eng. 2024, 16, 16878132241293958. [Google Scholar] [CrossRef]
- Yasmin, H.; Al-Essa, L.A.; Bossly, R.; Alrabaiah, H.; Lone, S.A.; Saeed, A. A numerical investigation of the magnetized water-based hybrid nanofluid flow over an extending sheet with a convective condition: Active and passive controls of nanoparticles. Nanotechnol. Rev. 2024, 13, 20240035. [Google Scholar] [CrossRef]
- Eid, M.R.; Mahny, K.; Dar, A.; Muhammad, T. Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. Phys. Stat. Mech. Its Appl. 2020, 540, 123063. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Liu, D.; Abid, M.; Imran, M.; Muhammad, T. Heat transfer analysis of hybrid nanofluid flow with thermal radiation through a stretching sheet: A comparative study. Int. Commun. Heat Mass Transf. 2022, 138, 106303. [Google Scholar] [CrossRef]
- Aly, E.H.; Roşca, A.V.; Roşca, N.C.; Pop, I. Convective heat transfer of a hybrid nanofluid over a nonlinearly stretching surface with radiation effect. Mathematics 2021, 9, 2220. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Din, E.M.T.E.; Gamaoun, F.; Awan, A.U.; Ali, B. Bio-convection effects on prandtl hybrid nanofluid flow with chemical reaction and motile microorganism over a stretching sheet. Nanomaterials 2022, 12, 2174. [Google Scholar] [CrossRef]
- EL-Hakiem, A.; Zaki, A.S.; EL-Zahar, E.R.; Rashad, A.M. Heat Transfer in Hybrid Nanofluid Flow Past an Infinite Orthogonal Plate with Biot Number and Velocity Slip Effects. J. Nanofluids 2024, 13, 65–72. [Google Scholar] [CrossRef]
- Madhukesh, J.; Ramesh, G.; Alsulami, M.; Prasannakumara, B. Characteristic of thermophoretic effect and convective thermal conditions on flow of hybrid nanofluid over a moving thin needle. Waves Random Complex Media 2024, 34, 5773–5795. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Al-Bossly, A.; Alduais, F.S.; Almusawa, M.Y.; Saeed, A. Significance of the inclined magnetic field on the water-based hybrid nanofluid flow over a nonlinear stretching sheet. Nanotechnology 2023, 34, 215401. [Google Scholar] [CrossRef]
- Choudhary, S.; Mehta, R.; Mehta, T. A comparative analysis: Heat transfer in thermally stratified MHD Carreau ternary (Cu-Al2O3-TiO2) hybrid nanofluid flow across an inclined vertical cylinder in presence of radiation. J. Therm. Anal. Calorim. 2025, 1–14. [Google Scholar] [CrossRef]
- Priya, S.; Rajamani, G.R.; Ganga, B.; Hakeem, A.K.A.; Ragupathi, P. Analysing entropy generation of MHD (50: 50) slip flow over an inclined needle. Mech. Eng. Adv. 2023, 1, 106. [Google Scholar] [CrossRef]
- Jat, K.; Sharma, K.; Soni, P.; Choudhary, P. Numerical analysis of heat and mass transport of hybrid nanofluid over a nonlinear stretchable sheet with magnetic field in presence of Soret and dufour Effect. J. Phys. Conf. Ser. 2024, 2844, 012019. [Google Scholar] [CrossRef]
- Rafique, K.; Mahmood, Z.; Ansari, M.A.; Kumar, A.; Khan, U. Investigating Soret–Dufour effects and discharge concentration on accelerating hybrid nanofluid flow over radiative disk embedded in porous media under convective conditions. Can. J. Phys. 2025. [Google Scholar] [CrossRef]
- Ghobadi, A.H.; Hassankolaei, M.G. Numerical treatment of magneto Carreau nanofluid over a stretching sheet considering Joule heating impact and nonlinear thermal ray. Heat Transf. Res. 2019, 48, 4133–4151. [Google Scholar] [CrossRef]
- Mohamed, R.; Abo-Dahab, S.; Soliman, M. Effects of nonlinear thermal radiation and heat generation/absorption on magnetohydrodynamic (MHD) Carreau nanofluid flow on a nonlinear stretching surface through a porous medium. J. Nanofluids 2022, 11, 845–856. [Google Scholar] [CrossRef]
- Reddy, R.R.; Reddy, P.B.A.; Chamkha, J. Influence of Soret and Dufour effects on unsteady 3D MHD slip flow of Carreau nanofluid over a slendering stretchable sheet with chemical reaction. Nonlinear Anal. Model. Control 2019, 24, 853–869. [Google Scholar] [CrossRef]
- Raju, S.S.K.; Babu, M.J.; Raju, C. Irreversibility analysis in hybrid nanofluid flow between two rotating disks with activation energy and cross-diffusion effects. Chin. J. Phys. 2021, 72, 499–529. [Google Scholar] [CrossRef]
- Neethu, T.S.; Areekara, S.; Mathew, A. Statistical approach on 3D hydromagnetic flow of water-based nanofluid between two vertical porous plates moving in opposite directions. Heat Transf. 2021, 50, 5170–5197. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D. Investigation on thermophysical properties of Tio2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Gholinia, M.; Hoseini, M.; Ganji, D. Natural convection MHD flow due to MoS2–Ag nanoparticles suspended in C2H6O2H2O hybrid base fluid with thermal radiation. J. Taiwan Inst. Chem. Eng. 2019, 97, 12–23. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Sabu, A.S.; Areekara, S.; Mathew, A. Effects of multislip and distinct heat source on MHD Carreau nanofluid flow past an elongating cylinder using the statistical method. Heat Transf. 2021, 50, 5652–5673. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).