Strong-Field Interaction of Molecules with Linearly Polarized Light: Pathway to Circularly Polarized Harmonic Generation
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
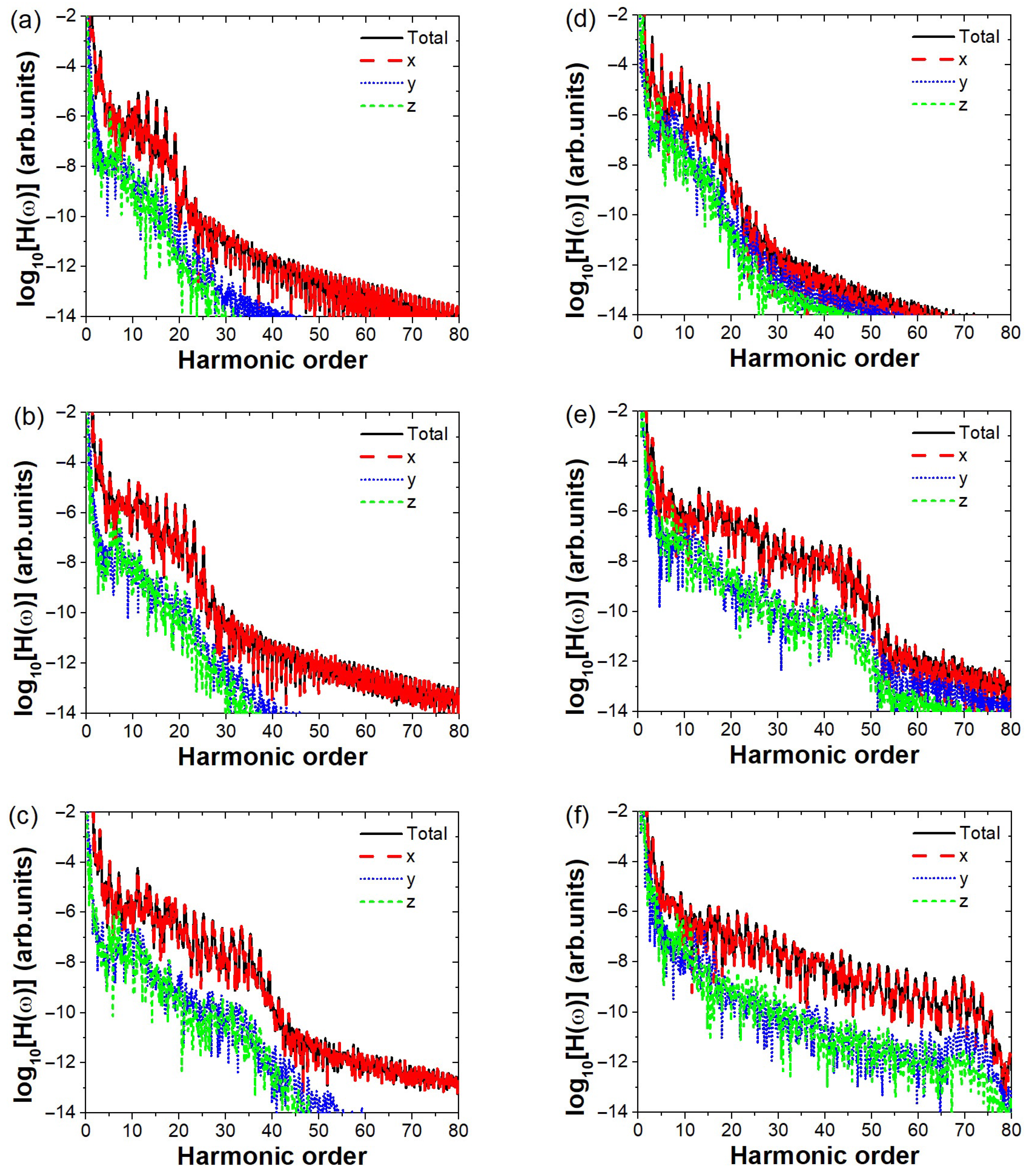
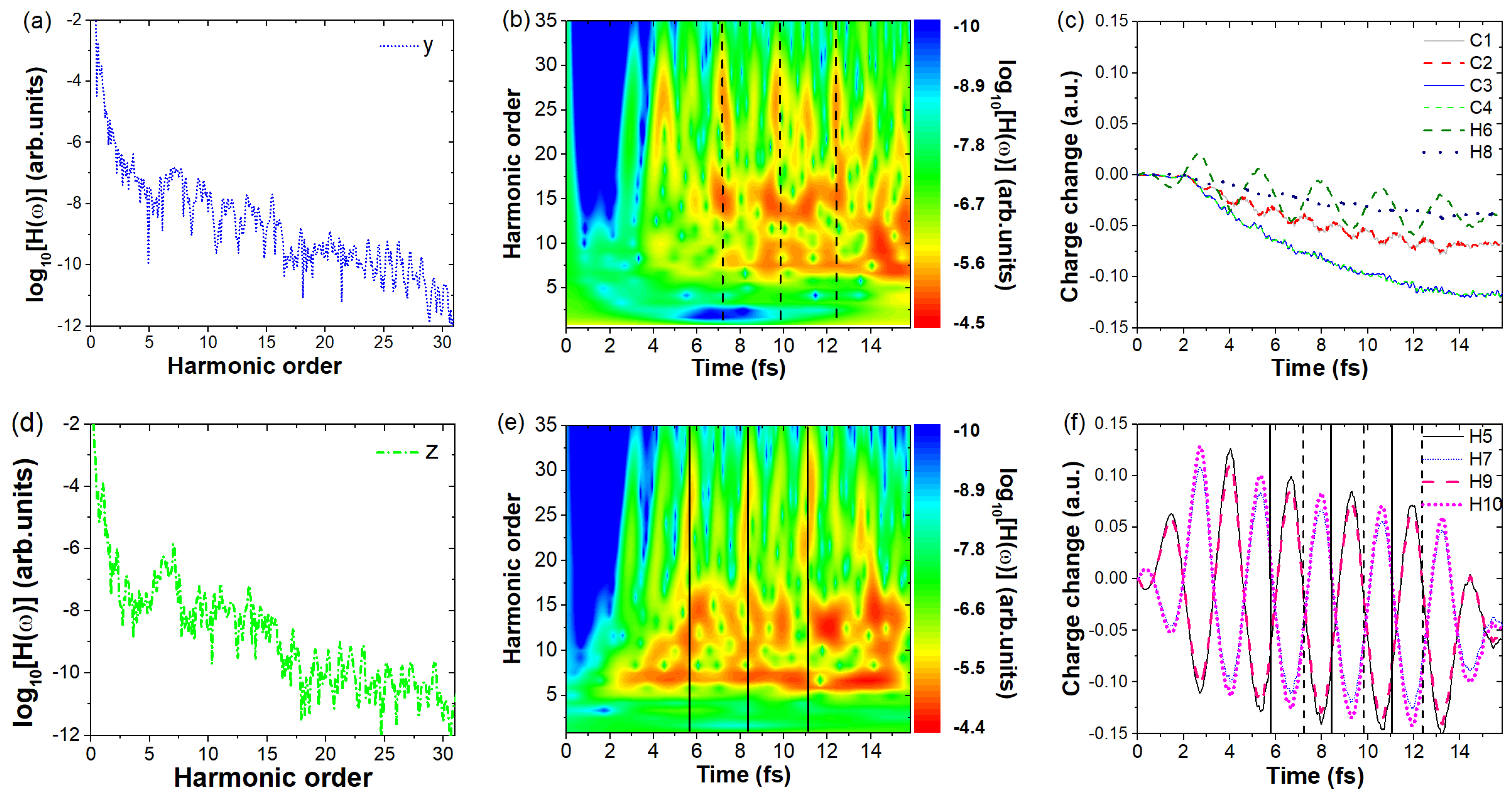
3.1. High-Harmonic Generation of a C4H6 Molecule in a Linearly Polarized Laser Field
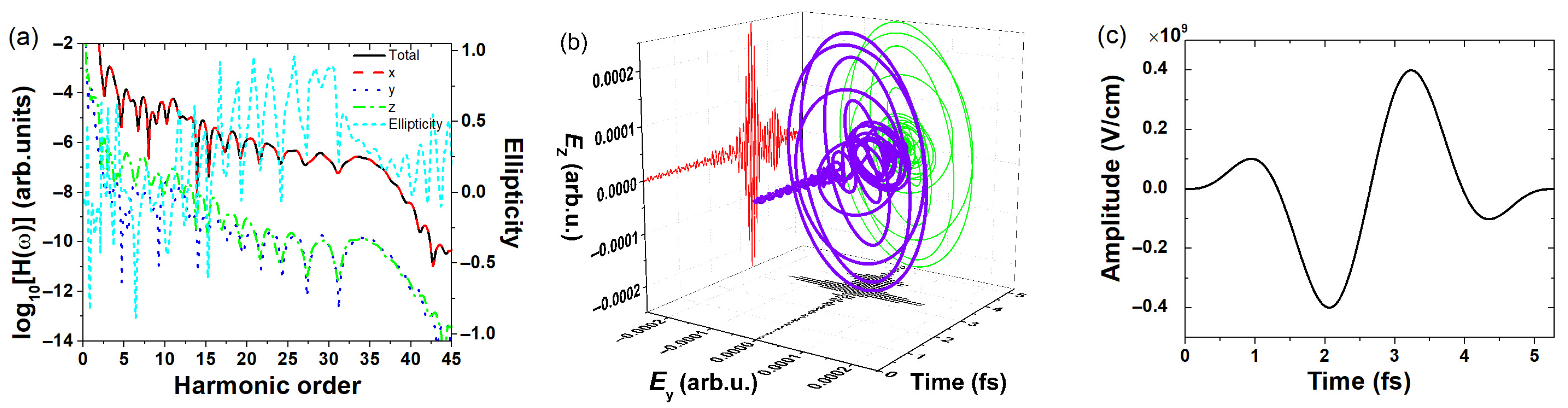
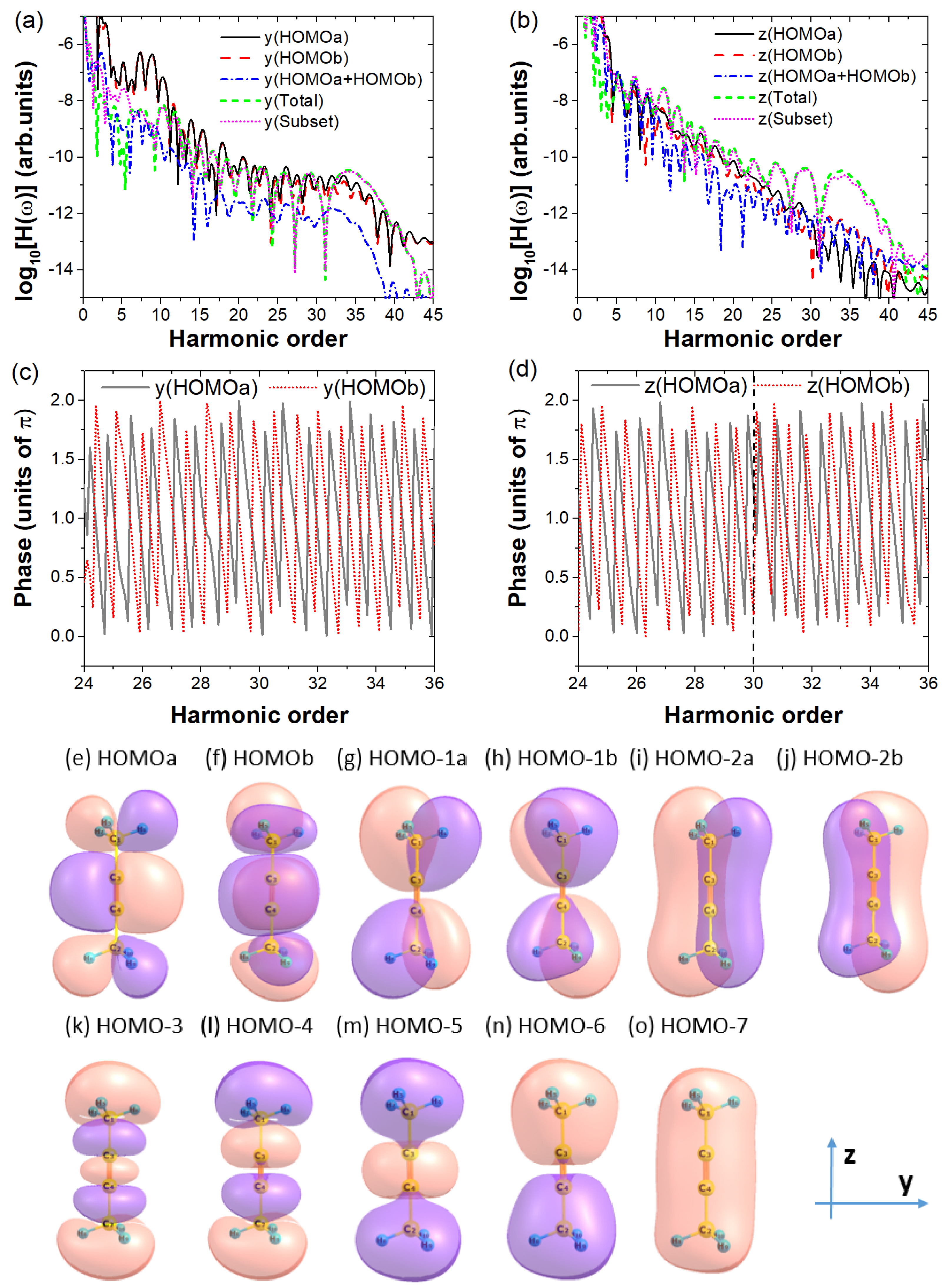
3.2. Synthesis of Circularly Polarized Attosecond Pulses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Yanovsky, V.; Chvykov, V.; Kalinchenko, G.; Rousseau, P.; Planchon, T.; Matsuoka, T.; Maksimchuk, A.; Nees, J.; Cheriaux, G.; Mourou, G.; et al. Ultra-high intensity- 300-TW laser at 0.1 Hz repetition rate. Opt. Express 2008, 16, 2109–2114. [Google Scholar] [CrossRef]
- Schenkel, B.; Biegert, J.; Keller, U.; Vozzi, C.; Nisoli, M.; Sansone, G.; Stagira, S.; Silvestri, S.D.; Svelto, O. Generation of 3.8-fs pulses from adaptive compression of a cascaded hollow fiber supercontinuum. Opt. Lett. 2003, 28, 1987–1989. [Google Scholar] [CrossRef] [PubMed]
- Wirth, A.; Hassan, M.T.; Grguraš, I.; Gagnon, J.; Moulet, A.; Luu, T.T.; Pabst, S.; Santra, R.; Alahmed, Z.A.; Azzeer, A.M.; et al. Synthesized Light Transients. Science 2011, 334, 195–200. [Google Scholar] [CrossRef]
- Baltuška, A.; Fuji, T.; Kobayashi, T. Visible pulse compression to 4 fs by optical parametric amplification and programmable dispersion control. Opt. Lett. 2002, 27, 306–308. [Google Scholar] [CrossRef]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Gordon, A.; Kärtner, F.X. Scaling of keV HHG photon yield with drive wavelength. Opt. Express 2005, 13, 2941–2947. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, S.; Jiang, W.; Guo, F.; Wang, J.; Chen, J.; Yang, Y. Modulation of harmonics from solids by laser pulses with a small chirp. Phys. Rev. A 2025, 111, 013501. [Google Scholar] [CrossRef]
- Xu, N.; Zhou, S.S.; Wang, Y. Regulation of helium atom higher harmonic emission and attosecond pulse angle in inhomogeneous fields. Results Phys. 2025, 72, 108190. [Google Scholar] [CrossRef]
- Tong, X.M. Multiscale simulation of high-order harmonic generation: From microscopic to macroscopic. Phys. Rev. A 2023, 108, 023118. [Google Scholar] [CrossRef]
- Ding, Z.W.; Wang, Y.B.; Li, Z.L.; Bian, X.B. High-order harmonic generation in liquids in bicircularly polarized laser fields. Phys. Rev. A 2023, 107, 013503. [Google Scholar] [CrossRef]
- Li, M.; Xie, M.F.; Wang, H.; Jia, L.; Li, J.; Wang, W.; Cai, J.; Hong, X.; Shi, X.; Lv, Y.; et al. Observation of Laser-Assisted Dynamic Interference by Attosecond Controlled Photoelectron Spectroscopy. Phys. Rev. Lett. 2024, 133, 253201. [Google Scholar] [CrossRef]
- Chang, Z. Single attosecond pulse and xuv supercontinuum in the high-order harmonic plateau. Phys. Rev. A 2004, 70, 043802. [Google Scholar] [CrossRef]
- Li, J.B.; Zhang, X.; Yue, S.J.; Wu, H.M.; Hu, B.T.; Du, H.C. Enhancement of the second plateau in solid high-order harmonic spectra by the two-color fields. Opt. Express 2017, 25, 18603–18613. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Iravani, H.; Madsen, L.B. Crystal-momentum-resolved contributions to multiple plateaus of high-order harmonic generation from band-gap materials. Phys. Rev. A 2020, 102, 033105. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Gibson, G.; Luk, T.S.; Rhodes, C.K. Tunneling ionization in the multiphoton regime. Phys. Rev. A 1990, 41, 5049–5052. [Google Scholar] [CrossRef] [PubMed]
- Augst, S.; Strickland, D.; Meyerhofer, D.D.; Chin, S.L.; Eberly, J.H. Tunneling ionization of noble gases in a high-intensity laser field. Phys. Rev. Lett. 1989, 63, 2212–2215. [Google Scholar] [CrossRef]
- Sørngård, S.A.; Simonsen, S.I.; Hansen, J.P. High-order harmonic generation from graphene: Strong attosecond pulses with arbitrary polarization. Phys. Rev. A 2013, 87, 053803. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef]
- Chen, F.; Luo, J.; Luo, F. Single circularly polarized attosecond pulse generation by spatially inhomogeneous fields from atoms with nonvanishing angular quantum number. Opt. Commun. 2015, 342, 68–72. [Google Scholar] [CrossRef]
- Hernández-García, C.; Durfee, C.G.; Hickstein, D.D.; Popmintchev, T.; Meier, A.; Murnane, M.M.; Kapteyn, H.C.; Sola, I.J.; Jaron-Becker, A.; Becker, A. Schemes for generation of isolated attosecond pulses of pure circular polarization. Phys. Rev. A 2016, 93, 043855. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Guo, J.; Yuan, K.J. Circularly polarized attosecond pulse generation and applications to ultrafast magnetism. J. Opt. 2017, 19, 124016. [Google Scholar] [CrossRef]
- Shao, R.; Zhai, C.; Zhang, Y.; Sun, N.; Cao, W.; Lan, P.; Lu, P. Generation of isolated circularly polarized attosecond pulses by three-color laser field mixing. Opt. Express 2020, 28, 15874–15884. [Google Scholar] [CrossRef]
- Zhong, C.; Qiao, B.; Zhang, Y.; Zhang, Y.; Li, X.; Wang, J.; Zhou, C.; Zhu, S.; He, X. Production of intense isolated attosecond pulses with circular polarization by using counter-propagating relativistic lasers. New J. Phys. 2021, 23, 063080. [Google Scholar] [CrossRef]
- Brooks, N.J.; de las Heras, A.; Wang, B.; Binnie, I.; Serrano, J.; San Román, J.; Plaja, L.; Kapteyn, H.C.; Hernández-García, C.; Murnane, M.M. Circularly Polarized Attosecond Pulses Enabled by an Azimuthal Phase and Polarization Grating. ACS Photonics 2025, 12, 495–504. [Google Scholar] [CrossRef]
- Svoboda, V.; Waters, M.D.J.; Zindel, D.; Wörner, H.J. Generation and complete polarimetry of ultrashort circularly polarized extreme-ultraviolet pulses. Opt. Express 2022, 30, 14358–14367. [Google Scholar] [CrossRef]
- Han, M.; Ji, J.B.; Ueda, K.; Wörner, H.J. Attosecond metrology in circular polarization. Optica 2023, 10, 1044–1052. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, H.; Wang, F.; Song, J.; Zhao, Y.; Yang, C.; Ou, T.; Zhang, R.; Chang, Q.; Sun, Y. The Generation of Circularly Polarized Isolated Attosecond Pulses with Tunable Helicity from CO Molecules in Polarization Gating Laser Fields. Photonics 2024, 11, 464. [Google Scholar] [CrossRef]
- Sun, N.; Zhu, X.; Wang, B.; Wang, D.; Shao, R.; Lan, P.; Lu, P. Near-circularly-polarized attosecond pulse generation from carbon monoxide molecules with a combination of linearly and circularly polarized fields. Phys. Rev. A 2020, 101, 053437. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Q.; Guo, F.; Wang, J.; Chen, J.; Yang, Y. High-order harmonic generation of benzene molecules irradiated by circularly polarized laser pulses. Chem. Phys. 2021, 545, 111147. [Google Scholar] [CrossRef]
- Pan, C.; Wang, J.; Luan, S.; Zhao, Y.; Leng, Y.; Li, R. Circularly polarized attosecond pulses generation from laser interaction with magnetized sub-critical plasmas. Plasma Phys. Control. Fusion 2023, 65, 065006. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, Y.; Liu, Y.; Zhang, K.; Kang, S.; Li, Z.; Wu, F.; Dong, X.; Cheng, X.; Li, Y.; et al. Near-circularly polarized isolated attosecond pulse generation from gas mixture with two-color multicycle laser fields. Results Phys. 2024, 58, 107518. [Google Scholar] [CrossRef]
- Zhai, C.; Zhu, X.; Li, Y.; Tang, Q.; Yu, B.; Lan, P.; Lu, P. Helicity-selected near-circularly polarized attosecond pulses generated from mixed He-Ne gases. Phys. Rev. A 2025, 111, 043519. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Mücke, O.D.; Kärtner, F.X.; Rubio, A. Impact of the Electronic Band Structure in High-Harmonic Generation Spectra of Solids. Phys. Rev. Lett. 2017, 118, 087403. [Google Scholar] [CrossRef]
- Zhou, S.S.; Yang, Y.J.; Guo, F.M.; Chen, J.G.; Wang, J. Multielectron Effect for High-Order Harmonic Generation From Molecule Irradiated by Bichromatic Counter-Rotating Circularly Polarized Laser Pulses. IEEE J. Quantum Electron. 2020, 56, 1–7. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Kleinman, L.; Bylander, D.M. Efficacious Form for Model Pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]
- Castro, A.; Marques, M.A.; Rubio, A. Propagators for the time-dependent Kohn-Sham equations. J. Chem. Phys. 2004, 121, 3425–3433. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Wang, H.; Yu, D.; Xu, N.; Hu, M. Enhancing High-Order Harmonic Generation Efficiency Through Molecular Size and Orientation Effects: A Pathway to Ultrafast Chemical Dynamics Studies. Molecules 2025, 30, 2133. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, H.; Hu, M.; Sun, Y.; Zhao, X. Review of the Generation, Regulation, and Applications of High-Order Harmonic Generation in Gases Studied Using Time-Dependent Density Functional Theory. Symmetry 2025, 17, 359. [Google Scholar] [CrossRef]
- Xing, M.; Wang, J.; Zhao, X.; Zhou, S. The Role of Multi-Electron and Multi-Orbital Effects in High-Order Harmonic Generation of Benzonitrile Molecules. Chin. Phys. Lett. 2025, 42, 043201. [Google Scholar] [CrossRef]
- Giovannini, U.D.; Larsen, A.H.; Rubio, A. Modeling electron dynamics coupled to continuum states in finite volumes with absorbing boundaries. Eur. Phys. J. B 2015, 88, 56. [Google Scholar] [CrossRef]
- Burnett, K.; Reed, V.C.; Cooper, J.; Knight, P.L. Calculation of the background emitted during high-harmonic generation. Phys. Rev. A 1992, 45, 3347–3349. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 61, 063403. [Google Scholar] [CrossRef]
- Chini, M.; Zhao, K.; Chang, Z. The generation, characterization and applications of broadband isolated attosecond pulses. Nat. Photonics 2014, 8, 178–186. [Google Scholar] [CrossRef]
- Franklin, J.L.; Field, F.H. The Ionization Potentials of Substituted Acetylenes by Electron Impact. J. Am. Chem. Soc. 1954, 76, 1994–1997. [Google Scholar] [CrossRef]
- Schwell, M.; Bénilan, Y.; Fray, N.; Gazeau, M.C.; Es-Sebbar, E.; Gaie-Levrel, F.; Champion, N.; Leach, S. Ionization photophysics and Rydberg spectroscopy of diacetylene. Mol. Phys. 2012, 110, 2843–2856. [Google Scholar] [CrossRef]
- Peter, M.; Daniel, D. High-order harmonic generation from highly excited states in acetylene. Phys. Rev. A 2018, 97, 043428. [Google Scholar] [CrossRef]
- BiÉmont, E.; FrÉmat, Y.; Quinet, P. Ionization Potentials of Atoms and Ions from Lithium to Tin (Z = 50). At. Data Nucl. Data Tables 1999, 71, 117–146. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. J. Exp. Theor. Phys. 1965, 20, 1307–1314. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Wang, H.; Xu, N.; Wu, D.; Hu, M. Strong-Field Interaction of Molecules with Linearly Polarized Light: Pathway to Circularly Polarized Harmonic Generation. Symmetry 2025, 17, 1329. https://doi.org/10.3390/sym17081329
Zhou S, Wang H, Xu N, Wu D, Hu M. Strong-Field Interaction of Molecules with Linearly Polarized Light: Pathway to Circularly Polarized Harmonic Generation. Symmetry. 2025; 17(8):1329. https://doi.org/10.3390/sym17081329
Chicago/Turabian StyleZhou, Shushan, Hao Wang, Nan Xu, Dan Wu, and Muhong Hu. 2025. "Strong-Field Interaction of Molecules with Linearly Polarized Light: Pathway to Circularly Polarized Harmonic Generation" Symmetry 17, no. 8: 1329. https://doi.org/10.3390/sym17081329
APA StyleZhou, S., Wang, H., Xu, N., Wu, D., & Hu, M. (2025). Strong-Field Interaction of Molecules with Linearly Polarized Light: Pathway to Circularly Polarized Harmonic Generation. Symmetry, 17(8), 1329. https://doi.org/10.3390/sym17081329





