Abstract
To offer a viewpoint on convexity and connectedness inside intuitionistic fuzzy graphs (IFGs), the paper is devoted to the study of intuitionistic fuzzy geodetic convexity. The paper introduces an algorithm for precise identification and characterization of geodetic pathways in IFGs, supported by a Python program. Various properties of IF-geodetic convex sets such as IF-internal and IF-boundary vertices are obtained. Furthermore, this work introduces and characterizes the concepts of geodetic IF-cover, geodetic IF-basis, and geodetic IF-number. Additionally, the study develops the IF-geodetic Wiener index. The scope of the work explores the application of IF-geodetic cover in wireless mesh networks, focusing on the identification of gateway nodes, where symmetry in connectivity patterns enhances network efficiency. A practical implementation of the IF-geodetic Wiener index method in global human trading analysis underscores the real-world implications of the developed concepts, where the efficiency and interpretability of fuzzy geodetic measures are improved by symmetry in network topologies and trade patterns.
1. Introduction
The concept of fuzzy sets was introduced by Lotfi A. Zadeh [1] in 1965 and addresses ambiguity and imprecision in set theory. Zadeh [2] explored fuzzy relations and their underlying mechanisms. His objective was to create a theory that could deal with the ambiguity and impreciseness of human reasoning, particularly in the areas of abstraction, information technology, and communication. In their study, Zadeh challenged a basic concept of probability theory. Each element in the universal set is assigned a value of 1 or 0 by the characteristic function in the crisp set. A generalization of this characteristic function is fuzzy set theory, in which the membership grade of each item in the universal set is indicated by a value assigned within a predefined range. Subsequently, this function is referred to as a membership function, and the set that is produced is known as a fuzzy set. The membership function has a range of values from 0 to 1.
Rosenfeld [3] is credited with organizing and developing the concept of fuzzy graphs. Yeh and Bang also independently contributed to the development. Rosenfeld deduced the fuzzy equivalents of multiple concepts in graph theory. Fuzzy graphs have found widespread application in various domains, including cluster analysis, group structure, pattern categorization, networking, management, and others, demonstrating their broad range of applications, especially where symmetry and uncertainty play significant roles. Numerous other authors, like P.S. Nair [4], Sunil Mathew and J.N. Mordeson [5,6], Sunitha and Vijayakumar [7], and R. Rajeshkumar and A. M. Anto [8], have conducted groundbreaking studies in this area.
Atanassov [9] introduced a number of concepts related to intuitionistic fuzzy graphs (IFGs). The field of intuitionistic fuzzy sets has seen exponential growth in both theoretical development and practical application. This idea now encompasses the fields of information technology as well as traditional mathematics. As a specific instance of those defined by Shannon and Atanassov [10], Parvathy and Karunambigai [11,12] developed the idea and related characteristics of IFGs, including aspects of symmetry. Additionally, Nagoor Gani covered a few more features of IFGs in [13]. In [14], Akram et al. offered various concepts and provided a precise definition of IFGs. Anto A.M. and Rajeshkumar R. [15] introduced the idea of IFGs having independent dominances. Motivated by the growing need to analyze complex networks under uncertainty, this paper investigates new structures in IFGs that incorporate both membership and non-membership values. The inspiration for this work is drawn from the foundational studies by Mordeson and Mathew on distances and convexity in fuzzy graphs [6], as well as from the work of Binu, Mathew, and Mordeson on the Wiener index in fuzzy graphs and its application to illegal immigration networks [16]. Additionally, significant insights presented in [17,18,19,20] have served as a motivation for the present study. Despite significant progress in the development of IFGs, there are still a number of important structural aspects that remain underexplored. The main contribution of this paper lies in addressing a research gap where the notions of geodetic convexity and its associated structural parameters, although well studied in classical and fuzzy graph theory, have yet to be defined and explored within the framework of IFGs. Furthermore, intuitionistic fuzzy environments have not yet been subjected to the concept of a geodetic block, which is essential to comprehending connection and decomposition in graphs. In this paper, we introduce and formalize the notions of intuitionistic fuzzy geodetic convexity and intuitionistic fuzzy geodetic block to fill these research gaps.
This paper is organized as outlined below. This article begins with a brief overview of the fundamentals of IFGs, as discussed in [11,14,15,21,22,23,24]. In Section 3, building on a metric established for IFGs in [22], this study proposes novel metric-based approaches that contribute significantly to the structural analysis of IFGs. We introduce the concept of intuitionistic fuzzy geodetic convexity, which offers deeper insights into convexity and connectivity within these graphs. To complement the theoretical framework, Section 4 details a Python program and associated techniques for accurately identifying and describing geodetic pathways in IFGs. Section 5 examines the structure of intuitionistic fuzzy geodetic blocks, while Section 6 investigates IF-internal and IF-boundary vertices within IF-geodetic convex sets. In Section 7, we define the concepts of geodetic IF-basis and geodetic IF-number. We also propose the notion of the minimal IF-geodetic subgraph, providing its characterizations and offering new tools for analyzing IFG structures. Finally, Section 8 highlights a key innovation of this research, the intuitionistic fuzzy geodetic Wiener index (), a robust metric that extends the classical Wiener index introduced in [25] to the IFG context. Unlike traditional approaches, incorporates both membership and non-membership degrees, enabling a more comprehensive measurement of geodetic distances under uncertainty. Finally, as a practical application, the concept of the IF-geodetic cover is applied to wireless mesh networks to identify optimal gateway nodes, thereby demonstrating its potential in enhancing connectivity and optimizing node placement. In addition, the method is also employed to analyze global human trading networks [26].
2. Preliminaries
Intuitionistic fuzzy graphs and intuitionistic fuzzy relations were first introduced by Atanassov [9,10]. Parvathi and Karunambigai [11] provided a definition of intuitionistic fuzzy graphs as a special case of those defined by Shannon and Atanassov [10]. In this work, we follow the notion of intuitionistic fuzzy graphs (IFGs) discussed by Muhammad Akram and Bijan Davvaz [14]. This section includes foundational definitions.
Definition 1
([14]). An IFG is a pair = where = is the vertex set, and represent the membership degree and the non-membership degree of each element , respectively, and varies in the range [0, 1] for all . , where and are given by , and . Here, varies in the range [0, 1] for all .
Example 1.
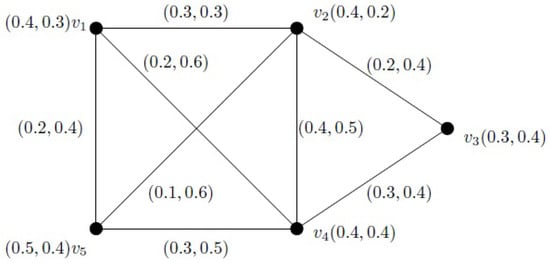
Figure 1 illustrates the above definition.

Figure 1.
An intutionistic fuzzy graph.
Definition 2
([11]). Let and be two IFGs, such that and . We call an IF-subgraph of .
Definition 3
([12]). In an IFG, a path is defined as a chain of distinct vertices which satisfies any one of the following three conditions: (a) and for some i and j; (b) and for some i and j; (c) Both and are greater than zero for some i and j ().
Definition 4
([12]). The μ-strength and γ-strength of a path are defined as and , respectively. The strength of a path is the value of an edge with both the values of μ-strength and γ-strength, and it is denoted as .
Example 2.
Let us consider a path = in Figure 1. Here, = = min{0.3, 0.2, 0.3} = 0.2, and . Therefore, the strength of the path , , is .
Definition 5
([21]). represents the μ-strength of connectedness, and represents the γ-strength of connectedness among all possible paths.
Definition 6
([22]). An IFG is complete if = and = .
Example 3.
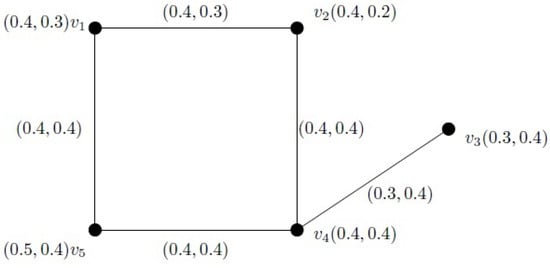
The illustration in Figure 2 supports the above definition.

Figure 2.
A complete intutionistic fuzzy graph.
Definition 7
([23]). A connected IFG is an intuitionistic fuzzy tree if it has an intuitionistic fuzzy spanning subgraph that is a tree, where for all arcs not in , and .
Definition 8
([24]). In an IFG, the weight of a vertex u is defined as = , and the weight of an edge is defined as = .
Definition 9
([21]). In an IFG, the distance between two of its vertices is the length of the shortest path between them, i.e., = , where each summation represents the total weight of a possible path connecting and . The minimum is taken over all such paths. The function d is called an intuitionistic fuzzy graph metric on .
The key symbols, notations and abbreviations employed throughout this paper are summarized in Table 1.

Table 1.
Symbols, notations and abbreviations.
3. Intuitionistic Fuzzy Geodetic Convexity
In classical fuzzy graph theory, geodetic convexity deals with the set of all vertices lying on the shortest paths between pairs of vertices. In the context of intuitionistic fuzzy graphs (IFGs), extending this idea reflects a more flexible structure, which naturally captures uncertainty and partial truth. In this context, we introduce the concept of intuitionistic fuzzy geodetic convexity. Furthermore, we define related measures such as the IF-geodetic eccentricity and IF-geodetic diameter, and we explore their basic properties.
Definition 10.
Let and be any two vertices in a connected IFG = . A path is called an IF geodesic if = , where = .
Definition 11.
Given any two vertices and in a connected IFG = , the IF-geodetic closed set is defined to be the set that contains all the vertices in all IF-geodesics together with and , and it is denoted by .
Definition 12.
In a connected IFG = , the IF-geodetic closure of is defined by the union of all IF-geodetic closed sets over each pair of vertices and is denoted as .
Definition 13.
Let ρ be a subset of in a connected IFG . ρ is said to be IF-geodetic convex if its IF-geodetic closure equals ρ, i.e., .
Definition 14.
IF-geodetic eccentricity is defined by . of a vertex in an IFG is defined as
Definition 15.
The IF-geodetic radius of an IFG is given by = , and the IF-geodetic diameter of is defined by .
Definition 16.
A vertex is a mid-vertex if . Similarly, a vertex is a geodetic IF-peripheral vertex if .
Example 4.
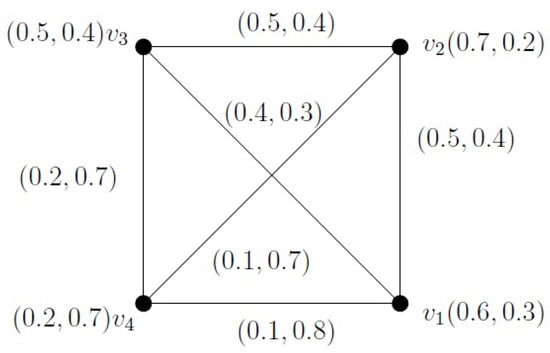
Consider the following IFG given in Figure 3.

Figure 3.
Intutionistic fuzzy graph in Example 4.
Here, let be an IF-geodetic convex set since . Similarly, and are IF-geodetic convex sets. The IF-geodetic eccentricity of a vertex is = . Also, = 0.25 and = 0.45.
The observations mentioned in the following proposition are generally considered obvious.
Proposition 1.
Let = be an IFG. Then, the set of entire vertices, all singleton sets of vertices, and the null set are IF-geodetic convex.
Theorem 1.
For an IFG = , the intersection between two IF-geodetic convex sets is again IF-geodetic convex.
Proof.
Let ∈. This means that both and are in both X and Y, which satisfy IF-geodetic convexity. This leads to the conclusion that all the vertices in each IF-geodesics are both in X and Y, and hence in . Therefore, is an IF-geodetic convex set. □
Theorem 2.
If = is an IF-tree, there exists an IF-spanning subgraph and a finite collection of nested sets = , where each is IF-geodetic convex.
Proof.
Assume that is an IF tree from the definition with an IF-spanning subgraph, where = exists, which is itself a tree. Thus, there exists a unique path between any pair of vertices. Therefore, the path connecting any pair of vertices in is the unique IF-geodesic between them. Hence, the union of all vertices in every geodetic path is an IF-geodetic convex. Let be a subgraph of that is obtained from the set by removing a terminal vertex from . The induced IF-subgraph remains a tree, implying that is IF-geodetic convex. Repeating this process yields a finite nested sequence = . □
4. Algorithm to Compute Geodetic Path of IFGs
Let = be an IFG with n vertices. In the literature of graph theory, various algorithms are available to compute the geodetic path between pairs of nodes. In this part, we created an algorithm for determining the geodetic path of an IFG and, more specifically, we offered a Python program for identifying all geodetic paths of IFGs. The software environment used is Python 3.x with standard scientific libraries.
4.1. Geodesic Path Identification Algorithm
The step-by-step pseudocode provides a concise and formal description of the algorithm’s logic and workflow.
Input: List of vertices (e.g., A_B_C_D).
Output: Geodesic paths and distances between all vertex pairs.
- Read the vertices as a single string and split it using underscores to create a list of vertices.
- Generate all unique unordered source–destination vertex pairs (e.g., A_B_C_D, etc.).
- For each source–destination pair:
- (a)
- Prompt the user to enter the number of known paths between the pair.
- (b)
- For each known path:
- Prompt the user to input the full path sequence (e.g., A_B_C).
- Store these paths in a dictionary: PATH_SUBPATHS[src_dest] = [list of paths].
- For each path corresponding to each source–destination pair:
- (a)
- Initialize the path weight to 0.
- (b)
- Determine the number of edges in the path.
- (c)
- For each edge in the path:
- Prompt the user to input the values of and .
- Compute the edge weight using the formula: .
- Add the edge weight to the total path weight.
- Store all computed weights in a dictionary: CALCULATED_PATHS[main_path][subpath].
- For each source–destination pair:
- (a)
- Identify the path with the minimum weight (i.e., the geodesic path).
- (b)
- Store the result in FINAL_GEODETIC_PATHS.
- Display the geodesic paths and their corresponding total weights.
Figure 4 presents the flowchart of the proposed geodesic path identification algorithm, as discussed.
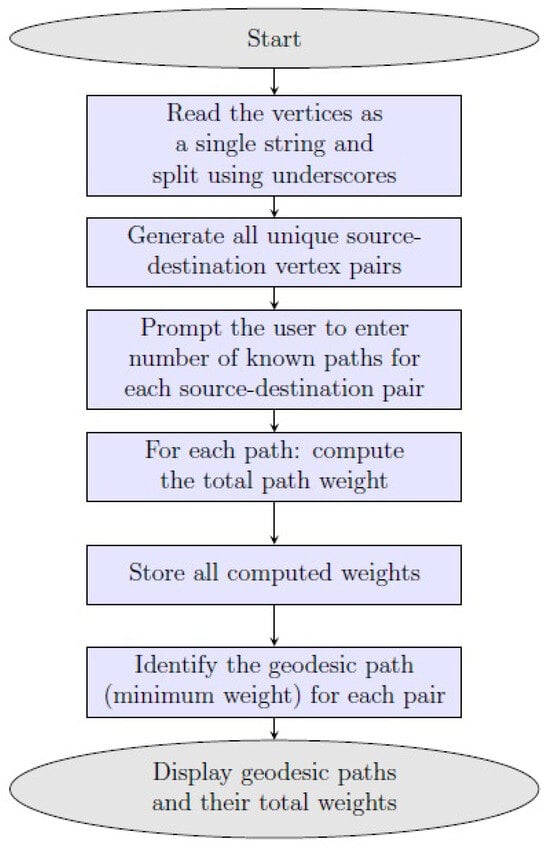
Figure 4.
Flowchart of geodesic path identification algorithm.
4.2. Limitations
The following are some limitations of the algorithm:
- The user manually inputs paths and edges present in IFGs. Thus, the algorithm assumes that all entered paths are valid.
- The algorithm assumes an undirected graph; modifications are needed for directed graphs. The storage of all geodetic paths in nested dictionaries increases memory usage for large graphs.
Therefore, the proposed algorithm is well suited for exploratory and user-controlled applications. The complete Python program, presented in Section 4.3.
4.3. Python Program for Identifying All Geodetic Paths of IFGs
# Program to find Geodesic Paths in an Intuitionistic Fuzzy Graph.
# INPUT ALL THE VERTICES (EXAMPLE INPUT = A_B_C_D
#use "_" for seperating each vertices from one another
vertices = str(input("Enter the vertices : "))
vertices = vertices.split("_") # seperate all vertices
def path_finder(vertices):
"""Find all the possible source to destinations"""
# We will do simple multiplication among the vertices itself and
# remove all start to start paths. For example, if vertices = [A,B,C]
# we can imagine if there exist all possible paths A_B, A_C
and B_C but not A_A,B_B and C_C
# the output of this function will be path = [A_B,A_C,B_C]
for the above example.
ver1, ver2 = vertices, vertices
paths = []
for v in ver1:
for v_ in ver2:
if v != v_:
path_ = str(v)+"_"+str(v_)
if path_ in paths or str(v_)+"_"+str(v) in paths:
pass
else:
paths.append(path_)
#print(paths)
return paths
source_dest = path_finder(vertices)
PATH_SUBPATHS = {}
#store source-destination : [path1,path2,path3…]
for src_des in source_dest:
# for each source to destination there may exist so many ways for
# ariving once destination these paths can be manually given. It will
# be asking to enter the no of paths available to travel and then we
# need to enter the paths one by one.
v1,v2 = src_des.split("_")
print("Enter paths btwn ’{v1}’ and ’{v2}’".format(v1=v1,v2=v2))
num_path = int(input(":=> "))
sub_path_list = []
for i in range(num_path):
sub_path = str(input("Enter path {path} : ".format(path = i)))
sub_path_list.append(sub_path)
PATH_SUBPATHS[src_des] = sub_path_list
#PATH_SUBPATH is a dictionary where key is the source and destination
#value is a list of subpaths
print(PATH_SUBPATHS)
CALCULATED_PATHS = {}
#{MAIN_PATH1:{PATH:distance}, MAIN_PATH2: {PATH:distance}}
class Distance:
"""A class for distance calculation"""
def __init__(self):
pass
def get_weight(self,mu2,gama2):
# A function to calculate weigth
weight = (1+mu2-gama2)/2
return weight
def distance(self,path):
# A function to do the weight calculation on subpath (edge)
num_edges = len(path.split("_")) - 1
# Num.of edges in the path
weight_sum = 0
# a variable to store weight value
print("Enter the edges of subpath "+ path + " accordingly")
for i in range(num_edges):
edge = input("Enter the edge "+ str(i+1) + " : ")
edge = tuple(float(num) for num in edge.split())
weight = self.get_weight(mu2 = edge[0], gama2 = edge[1])
# calculating the weight
weight_sum += weight
return weight_sum
# weight of that particular subpath
for MAIN_PATH in PATH_SUBPATHS.keys():
paths_mainpath = PATH_SUBPATHS[MAIN_PATH]
dist = Distance()
CALCULATED_PATHS[MAIN_PATH] = {}
for path in paths_mainpath:
CALCULATED_PATHS[MAIN_PATH][path] = dist.distance(path)
print(CALCULATED_PATHS)
FINAL_GEODETICS_PATHS = {}
#{MAIN_PATH:{"GEODESIC_PATH":value}}
for MAIN_PATH in CALCULATED_PATHS.keys():
distances = list(CALCULATED_PATHS[MAIN_PATH].values())
keys = list(CALCULATED_PATHS[MAIN_PATH].keys())
min_distance = sorted(distances)[0] # Minimum distance
min_index = distances.index(min_distance)
Gdesic_path = keys[min_index]
FINAL_GEODETICS_PATHS[MAIN_PATH] ={}
FINAL_GEODETICS_PATHS[MAIN_PATH][Gdesic_path] = min_distance
print("====================GEODESIC PATHS======================")
print(FINAL_GEODETICS_PATHS)
5. Intuitionistic Fuzzy Geodetic Blocks
In intuitionistic fuzzy graphs, the idea of blocks was established by Muhammad Akram and N. O. Akshehri in [23]. In this section, we present the notion of intuitionistic fuzzy geodetic blocks and some of its characterization.
Definition 17.
A connected intuitionistic fuzzy subgraph of is called an intuitionistic fuzzy geodetic block (IFGB) if there does not exist a path such that .
It follows directly from the definition that for an IFGB, there is a unique IF-geodetic path between any pair of nodes. In the case of a complete IF-subgraph, each edge acts as a unique IF-geodetic path.
Example 5.
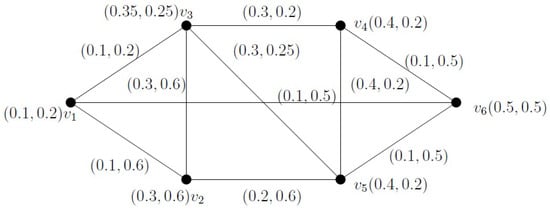
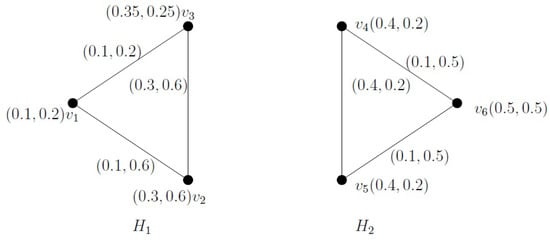
To illustrate Definition 17, an example is presented. We now examine the IFG illustrated in Figure 5 along with its subgraphs in Figure 6. Here, the IF-subgraph is an IFGB. However, on the other hand, is not an IFGB, since there exists more than one IF-geodetic path between the vertices and .

Figure 5.
Intutionistic fuzzy graph in Example 5.

Figure 6.
IF-subgraphs and of in Example 5.
Theorem 3.
If = is a complete IF-subgraph of a connected IFG , then is an IFGB if and only if is IF-geodetic convex for any .
Proof.
Assume that is an IFGB. Since is complete, there exists a direct edge between every pair . In an IFGB, the geodesic between any two vertices is unique, and due to completeness, this geodesic must be a direct edge. Hence, is IF-geodetic convex.
Conversely, suppose that is IF-geodetic convex for every . Assume, for contradiction, that there exists more than one IF-geodetic path between some pair in . Let one such alternate path have edges. However, since is complete, the direct edge must exist and constitutes a geodetic path. Thus for will exceed , contradicting the assumption of uniqueness and convexity of geodesic sets. Therefore, the assumption is false, and must be an IFGB. □
Theorem 4.
Let = be a complete IF-subgraph of a connected IFG . If is an IFGB, then is an IF-geodetic convex.
Proof.
Assume that is a complete IF-subgraph of and that is an IFGB. Since is complete, every pair of vertices is connected by a direct edge. Moreover, as is an IFGB, the direct edge is the IF-geodesic between and . Hence, the only vertices lying on the IF-geodesic between and are and themselves. Therefore, for all , the IF-geodesic between them lies entirely within , and no intermediate vertices are involved. This implies that contains all vertices lying on IF-geodesics between any two elements in , which completes this proof. □
Theorem 5.
Let be a complete IF-subgraph of a connected IFG . If is an IF-geodetic block (IFGB), then for any vertex , the induced IF-subgraph is also an IFGB.
Proof.
Since is a complete IF-subgraph and also an IFGB, there exists exactly one IF-geodesic between every pair of vertices in . Thus, for any pair of vertices in , the unique geodesic is the direct edge connecting them. Let , and consider the induced subgraph . Because is complete, the removal of does not affect the existence or uniqueness of geodesics between the remaining vertices; all such geodesics remain as direct edges. Hence, retains the property of being a complete IF-subgraph, and the geodetic property is preserved. Therefore, is also an IFGB. □
6. Geodetic Intuitionistic Fuzzy Boundary and Internal Vertices
In this section, we define the geodetic IF-boundary and IF-internal vertices of IF-geodetic convex sets and discuss some of their properties.
Definition 18.
Given a connected IFG = , and with ρ being a non-empty subset of , which is an IF-geodetic convex, a node is called a geodetic IF-boundary vertex of ρ if is an IF-geodetic convex. Otherwise, is referred to as a geodetic IF-internal vertex of ρ.
Example 6.
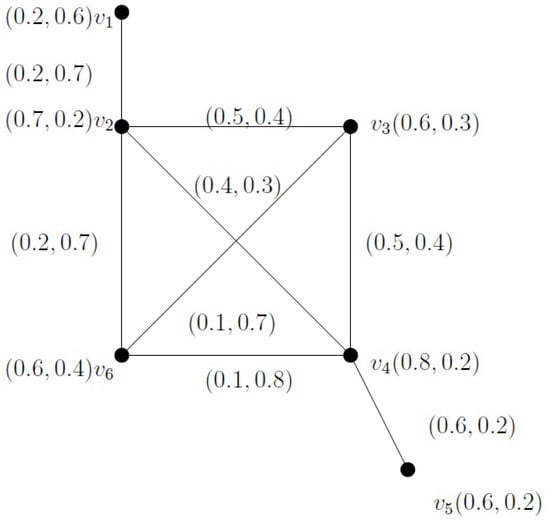
Consider the IFG depicted in Figure 7.

Figure 7.
Intuitionistic fuzzy graph with geodetic IF-boundary and geodetic IF-internal vertices.
Note that the direct edge is an IF-geodesic, and the path is also an IF-geodesic connecting and . Let , which is an IF-geodetic convex set since . Similarly, the set is also an IF-geodetic convex set. Now, consider the set , which remains IF-geodetic convex. Therefore, the vertex is a geodetic IF-boundary vertex of ρ, whereas the vertex is a geodetic IF-internal vertex.
Example 7.
Referring to Example 4, let . This is an IF-geodetic convex set. Similarly, the sets and are also IF-geodetic convex. In this case, the vertices and are geodetic IF-boundary vertices.
The subsequent theorems presents characterizations of geodetic IF-boundary and geodetic IF-internal vertices.
Theorem 6.
Let be an IF-geodetic convex set in a connected IFG. A vertex is a geodetic IF-boundary vertex of ρ if and only if does not lie on any IF-geodesic between any pair of distinct vertices .
Proof.
Assume that is a geodetic IF-boundary vertex of . Then, by definition, the set is also an IF-geodetic convex set. Let . Since is IF-geodetic convex, every IF-geodesic between and lies entirely within . Hence, does not lie on any IF-geodesic between such vertex pairs.
Conversely, suppose that does not lie on any IF-geodesic between any pair of vertices . We must show that is an IF-geodetic convex set. Since all IF-geodesics between and (for ) are independent of , it follows that all vertices on these geodesics are contained in . Therefore, by Definition 18, is IF-geodetic convex, and thus is a geodetic IF-boundary vertex of . □
Theorem 7.
Let be an IF-geodetic convex set in a connected IFG. A vertex is a geodetic IF-internal vertex of ρ if and only if lies on at least one IF-geodesic between some pair of vertices .
Proof.
Assume that is a geodetic IF-internal vertex of . By definition, the set is not IF-geodetic convex. Then, there exist vertices such that at least one IF-geodesic between and contains . Since , it follows that lies on an IF-geodesic between and , as required.
Conversely, suppose that lies on an IF-geodesic between some pair of vertices . Then, the geodesic cannot be fully contained in , which implies that fails to be an IF-geodetic convex set. Therefore, by definition, is a geodetic IF-internal vertex of . □
Theorem 8.
Let be a complete IF-subgraph of a connected IFG . If is an IFGB, then every vertex of is a geodetic IF-boundary vertex of .
Proof.
Assume that is an IFGB. Let be an arbitrary vertex. We aim to show that is a geodetic IF-boundary vertex of . By definition, it is sufficient to prove that the set is IF-geodetic convex. By Theorem 3, is IF-geodetic convex for any . Since was arbitrary, it follows that every vertex in is a geodetic IF-boundary vertex of . □
7. Minimal IF-Geodetic Subgraph
There is no end to the remarkable characteristics of IF-geodesics. This section focuses on key concepts related to IF-geodesics, including the geodetic IF-cover, geodetic IF-basis, and geodetic IF-number of an IFG. We also introduce the notion of the minimal IF-geodetic subgraph and present its characterizations.
Definition 19.
A subset ρ of in a connected IFG = is said to be a geodetic IF-cover of if .
Definition 20.
A geodetic IF-basis for = is any of with the fewest vertices, and the number of vertices in it is termed as the geodetic IF-number and denoted by .
Example 8.
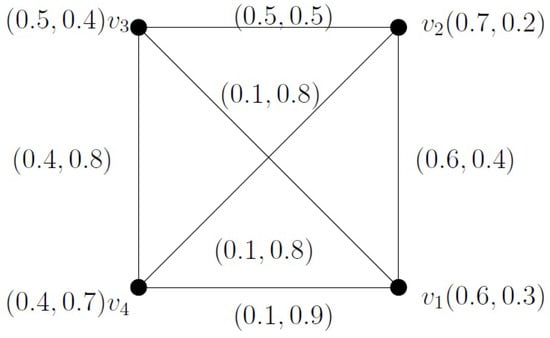
To become acquainted with the above definitions, consider , as shown in Figure 8. Here, the path is an IF – geodesic. Let . Then, ; therefore, is an . Observe that . Also, serves the role of an .

Figure 8.
IFG in Example 8.
Theorem 9.
In a complete IFG, the full set of vertices is the only of .
Proof.
For a complete IFG, each edge between a pair of vertices serves as the sole IF-geodetic path. Hence, the result follows immediately. □
An immediate corollary to Theorem 9 is as follows:
Corollary 1.
For a complete IFG , .
Theorem 10.
If is an IF-tree, then there exists an IF-subgraph that spans a unique consisting of its end nodes.
Proof.
As observed from Theorem 2, there exists an IF-spanning subgraph with a finite collection of nested sets that are IF-geodetic convex. By the construction of such a collection, it follows that there exists a unique for consisting of its end vertices. □
Based on the definitions and the findings presented thus far, the lower and upper bounds for can be determined as follows.
Theorem 11.
Consider any non-trivial IFG with n vertices. Then, .
Proof.
In a non-trivial IFG , any must consist of at least two vertices. Thus, . Also, the full vertex set of is an of ; thus, clearly, . This completes the proof. □
Definition 21.
An IF-graph = is called a minimal IF-geodetic subgraph if there exists an IF-graph containing such that .
Example 9.
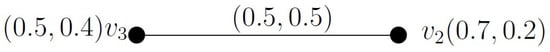
To get a sense of the above definition, let us once again refer to Figure 8 in Example 8. Here, we consider the IF-subgraph of , as given in Figure 9. Clearly, is a minimal IF-geodetic subgraph of , since for , we have . Thus, is an , and at the same time, , with .
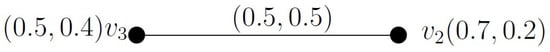
Figure 9.
A minimal IF-geodetic subgraph of in Figure 8.
Here, , , and . Therefore, and are geodetic IF-peripheral vertices of .
The next theorem follows directly from the previous results.
Theorem 12.
Let be a minimal IF-geodetic subgraph of with . Then, every vertex is a geodetic IF-peripheral vertex of .
Theorem 13.
If is a minimal IF-geodetic subgraph of with n vertices, then
Proof.
Let be a non-trivial IF-subgraph of , where . By Theorem 11, we have
Since is a minimal IF-geodetic subgraph of , we have . Therefore, , and it follows that
Finally, by Theorem 11, we conclude that
□
Theorem 14.
The only minimal IF-geodetic subgraph of a complete IFG is itself.
Proof.
To justify this, we refer to Theorem 9. In a complete IFG, each edge between a pair of vertices serves as the sole IF-geodetic path. Hence, the is the entire vertex set. Therefore, , which completes the proof. □
8. Intuitionistic Fuzzy Geodetic Wiener Index
The Wiener index is a widely used metric in areas such as telecommunications, facility localization, chemical graph theory, networking, analyzing the symmetry, and so on. A connected intuitionistic fuzzy graph (IFG) can effectively represent various real-world systems. In this section, we extend the classical Wiener index from [25] by introducing the intuitionistic fuzzy geodetic Wiener index (IFgWI), a robust metric for IFGs that is formulated based on IF-geodesics. The formal definition is presented below.
Definition 22.
Let be a path in an intuitionistic fuzzy graph (IFG) . The intuitionistic fuzzy geodetic Wiener index is defined as
where denotes the IF-geodetic distance between the vertices and .
Example 10.
Let be an IFG, as shown in Figure 3. The direct edges , , and are IF-geodesics. The paths , , and are also IF-geodesics. Therefore,
Removing a node from a graph typically results in a subgraph of the original graph. Consequently, the nature of the graph determines whether the intuitionistic fuzzy geodetic Wiener index, , will increase, decrease, or remain unchanged. In most cases, this index tends to decrease. The effect of removing a bridge on will be examined in the following scenario.
Example 11.
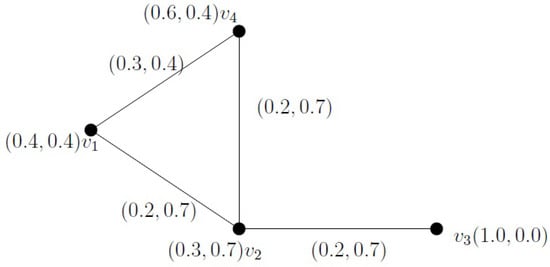
In Figure 10, the paths and have strengths and , respectively. Here, the edge joining and serves as both a bridge and a geodesic. In this case, , but .

Figure 10.
IFG with an edge that is both a bridge and a geodesic.
The above case will be generalized by the following theorem.
Theorem 15.
If a bridge is removed from an IFG, then increases only if the bridge is an edge of some geodesic.
Proof.
Assume that there exists a bridge in an IFG, say . We consider two cases:
Case 1: Suppose that itself is a geodesic between and . Then, . The deletion of the edge increases the geodetic distance between and , i.e., increases. Hence, by the definition of , its value increases.
Case 2: Suppose that is part of a geodetic path between some pair of vertices. Deleting modifies the structure of such geodesic paths, resulting in longer alternative paths. Thus, there is an increase in the total geodetic distances, and consequently, in .
In both cases, increases if the removed bridge is a part of any geodesic. □
Theorem 16.
The of two isomorphic IFGs are equal.
Proof.
Let = and = be two isomorphic IFGs. Then, there exists a bijective map such that for every and for every and . This ensures that edge weights and vertex weights are preserved under the isomorphism. Now, for every pair of vertices , there exists a corresponding pair such that
Since geodesic distances are preserved, the intuitionistic fuzzy geodetic Wiener index of is given by
as required. □
9. Applications
9.1. Application of in Wireless Mesh Network
In 2015, mesh networking for small networks made its debut with the promise of resolving Wi-Fi issues through increased coverage, faster networks, and less issues. In order to prevent inactive and weak spots, it also claimed to eliminate the requirement for base stations to be placed precisely across a house or small workplace. Mesh networks also offer help in figuring out where to locate units. The symmetry in node distribution contributes to more effective coverage and reliable connectivity. Mesh networks have the ability to scale effortlessly by incorporating additional nodes without requiring substantial alterations to the network infrastructure, making them well suited to extend coverage over expansive areas. In general, wireless mesh networks provide a robust and decentralized networking solution that is applicable in numerous scenarios where traditional wired networks are not viable or feasible.
For instance, in a hypothetical university campus environment, setting up a wireless mesh network can help increase network coverage and efficiency. Every node in a wireless mesh network communicates with other nodes in the area, creating a scalable and self-healing network. For stability and to prevent wireless congestion, certain nodes could still require a wired Ethernet connection to the main router to accomplish this. In order to plan and configure a wireless mesh network (WMN), follow these general steps. The first step is to survey the area, where we identify areas that need Wi-Fi coverage and make note of any obstacles, such as walls and other structural constraints. The second factor, node location, guarantees that the wireless mesh is strategically placed and that the entire region is adequately covered. Symmetry in node placement can enhance signal strength and network efficiency. Lastly, the types of nodes are crucial in designating specific nodes as “gateway” nodes that provide a direct Ethernet connection to the main router. The remaining nodes will be “mesh” nodes that establish wireless connections with both the gateway and other nodes. Use Ethernet connections to link gateway nodes to the main router. In a wireless mesh network, not all nodes necessarily need a wired connection. We need to identify gateway nodes or the nodes that need to be linked to the cable in order to cover the entire area. With the help of geodetic IF-cover, we can now tackle the issue. To make computations easier, we have taken . Take a look at the fuzzified WMN model shown in Figure 11.
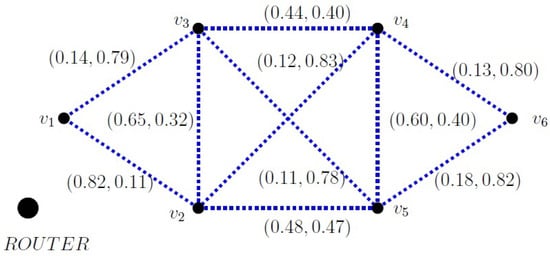
Figure 11.
A fuzzified WMN model of a hypothetical university campus.
Consider the vertices and . The possible paths between them, and the corresponding sum of weights computed as , are listed below:
- : = = 0.855.
- : = = 0.175 + 0.665 = 0.84.Similarly,
- : 0.175 + 0.52 + 0.145 = 0.84.
- : 0.175 + 0.165 + 0.60 + 0.145 = 1.085.
- : 0.175 + 0.165 + 0.505 = 0.845.
- : 0.175 + 0.52 + 0.165 + 0.18 + 0.505 = 1.545.
- : 0.175 + 0.52 + 0.60 + 0.505 = 1.78.
- : 0.175 + 0.165 + 0.18 + 0.165 + 0.145 = 0.83.
Therefore, = = 0.83. Thus, from the above-listed pathways, we identify that is an IF geodesic, and we denote this path as .
In a similar manner, the paths connecting and are as follows:
And corresponding sums of weights are 0.175, 1.52, 1.52, 2.48, 1.765, 1.525, 1.51, and 2.225, respectively. Thus, = = 0.175. Therefore, we identify the direct path as the geodetic path connecting and , and we denote this geodetic path as .
In a similar way, we can determine the IF-geodetic distance between other pairs of vertices, leading to the construction of the IF-geodetic distance matrix corresponding to the network shown in Figure 11, as presented below.
Thus, we identify a total of 15 geodetic pathways in the network, as listed below.
| : | : |
| : | : |
| : | : |
| : | : |
| : | : |
| : | : |
| : | : |
| : . |
Let . Then, . Thus, by Definition 19, is an for the network shown in Figure 11.
Similarly, the set is also an since it covers all vertices in . We can perform similar verifications for other possible subsets. However, in this case, the only subset with the minimum number of vertices that still covers is .
Therefore, to reduce wired connections in our wireless mesh network (WMN), we may designate and as the gateway nodes, as they can effectively cover the entire network.
Finally, Figure 12 depicts the finalized structure of a wireless mesh network, where gateway nodes are highlighted in red, mesh nodes are identified with green labels, dotted lines in the figure symbolize wireless connections, and solid lines in black color without breaks indicate wired connections with the router.
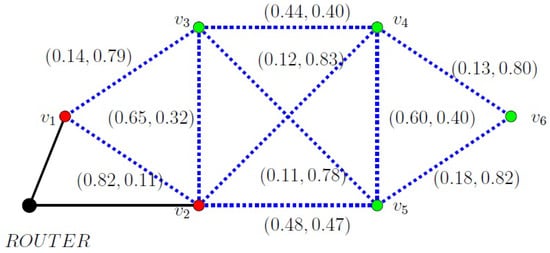
Figure 12.
WMN configuration with gateway and mesh nodes.
Note that depending on the hardware and software solutions selected for your wireless mesh network (WMN), there may be variations in the specific processes and required equipment. Expanding and enhancing a WMN to form a more complex and sophisticated network configuration can lead to increased coverage, improved connectivity, and enhanced overall network capabilities.
9.2. Application of in Global Human Trading
Human trading often involves intricate networks of individuals and organizations. Taking into account the ambiguity and uncertainty in the connections, IFG theory can be used to examine and visualize these networks. In this paper, we use the major illegal human trade routes to the United States as mentioned in [17,19]. We assess the suitability of the intuitionistic fuzzy geodetic Wiener index as a comparative metric against the existing fuzzy graph Wiener index discussed in reference [16].
The Global Slavery Index in [26] provides a comprehensive evaluation of population-level vulnerability to modern slavery across 160 countries. Over the past two decades, international organizations such as the United Nations Office on Drugs and Crime (UNODC) and the International Labour Organization (ILO) have made significant progress in measuring modern slavery globally. Several approaches were applied to fuzzy graphs to assess the likelihood of illegal immigration along various routes from the countries of origin to the United States. Binu et al. [16] investigated the Wiener index on fuzzy graphs to study illegal immigration pathways, presenting a valuable approach to understanding human trafficking networks. Their model effectively captured migration flows and network centralities within fuzzy relational contexts. Building on this foundation, the present study adopts the same fuzzy graph structure used by Binu et al. for testing the applicability and correctness through the intuitionistic fuzzy geodetic Wiener index . This new index enhances the analytical power by incorporating degrees of membership and non-membership, thus allowing for a more refined understanding of uncertainty in human trafficking routes.
We interpret the membership degree as the level of government measures taken to prevent inflow into the country, while the non-membership degree reflects the effectiveness of these measures in controlling internal transit. Despite these efforts, some flow from the source to the destination may still occur. Accordingly, denotes the intensity of outflow, and indicates the effectiveness of measures taken to combat this movement. Figure 11 in [16] is considered as the underlying model of a directed intuitionistic fuzzy graph (IFG). The normalized data for government response and vulnerability ratings of the countries are compiled based on the information reported in [16], while the data normalization process itself—employing t-norms and t-conorms—follows the methodology discussed in detail in [17,18]. Accordingly, Table 2 presents the graph data corresponding to the mentioned figure.

Table 3.
Intuitionistic fuzzy parameters reflecting vulnerability and government response measures across selected countries.
It is important to note that lower values of indicate higher effectiveness of a path in preventing trafficking. For instance, the path from India to the United States yields . Along the route from Somalia, two distinct pathways are observed: one via Guatemala with and another through Mexico from Colombia with . The route originating from China results in an index of 1.37. From Nigeria, two routes are identified: one via Guatemala with and a more direct path through Colombia and Mexico with . The pathway from Ethiopia to the United States yields an index of 1.84.
Route vulnerability to illicit human movement is assessed using the introduced metric, the intuitionistic fuzzy geodetic Wiener index (), derived through the application of intuitionistic fuzzy graph principles. Three fuzzy graph-based techniques were employed to evaluate the likelihood of illegal immigration along specific routes from source countries to the United States. The findings of this study are consistent with those reported in [16,17,19], all of which identify Somalia as the origin of the most vulnerable pathway. Nigeria is identified as the second most susceptible source country. The proposed method demonstrates improved accuracy, as it accounts for internal and outflow control. A comparison between the average Wiener index [16] in fuzzy graphs and the values obtained in this study confirms the enhanced precision of the proposed approach.
9.3. Summary Comparison Table
To further clarify the conceptual and computational distinctions between the classical fuzzy Wiener index and the proposed intuitionistic fuzzy geodetic Wiener index , a comparison table is presented in Table 3.

Table 4.
Comparison of classical fuzzy Wiener index and IF-geodetic Wiener index .
10. Conclusions
This article presents a comprehensive study on intuitionistic fuzzy geodetic convexity within the framework of IFG metrics. Core contributions include the formalization of IF-geodetic eccentricity, IF-geodetic diameter, and the novel intuitionistic fuzzy geodetic Wiener index (). Structural elements such as IF-boundary vertices, IF-internal vertices, geodetic IF-cover, and geodetic IF-number are defined and characterized, with established upper and lower bounds. A Python-based algorithm was developed for efficiently identifying geodetic paths, particularly suitable for small-scale and user-guided environments.
The utility of these developments was demonstrated through two significant applications. First, we employed the concept of IF-geodetic cover to optimize gateway node placement in a wireless mesh network. Second, the introduction of the intuitionistic fuzzy geodetic Wiener index () has demonstrated practical utility in the domain of global human trading analysis. Specifically, it was employed to assess the vulnerability of trafficking routes to the United States, with findings that not only support earlier studies but also offer improved precision by incorporating internal and outflow control over illicit human movements.
Despite its strengths, this study has limitations. Constructing IFGs requires detailed, reliable data, which may not be available in all domains. Additionally, storing all geodetic paths in nested dictionaries increases memory usage, limiting scalability of the algorithm for large-scale graphs. Incorporating optimization methods, automated graph construction, dynamic models, or hybrid approaches may improve efficiency and applicability.
Future research may extend IF-geodetic convexity to dynamic intuitionistic fuzzy networks with evolving topologies. Additionally, applying this concept to other fuzzy frameworks—such as intuitionistic fuzzy bipolar or Pythagorean fuzzy graphs—could offer deeper insights into complex and uncertain systems. The definitions of IF-boundary and IF-internal vertices were introduced to support the theoretical development of IF-geodetic convexity in intuitionistic fuzzy graph structures. While primarily conceptual, these notions hold potential for practical applications—such as identifying exit–entry or weakly connected nodes in a network—which may be explored in future studies.
Author Contributions
Conceptualization, A.M.A., R.R., L.E.P. and V.M.M.R.; methodology, A.M.A., R.R. and L.E.P.; writing—original draft preparation, A.M.A., R.R. and L.E.P.; writing—review and editing, A.M.A., R.R., L.E.P. and V.M.M.R.; supervision, A.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in this article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the reviewers for their valuable suggestions in improving the quality of this paper.
Conflicts of Interest
The authors of this paper declare that they have no conflicts of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Fu, K.S.; Shimura, M. Fuzzy Sets and Their Applications; Academic Press: Cambridge, MA, USA, 1975; pp. 125–149. [Google Scholar]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Applications of Fuzzy Graphs. In Fuzzy Graphs and Fuzzy Hypergraphs; Physica-Verlag: Heidelberg, Germany, 2000; pp. 83–133. [Google Scholar] [CrossRef]
- Mathew, S.; Mordeson, J.N.; Malik, D.S. Connectivity in Fuzzy Graphs Theory. In Fuzzy Graph Theory; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 85–116. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Mathew, S. Distances and Convexity in Fuzzy Graphs. In Advanced Topics in Fuzzy Graph Theory; Springer: Cham, Switzerland, 2019; pp. 93–126. [Google Scholar] [CrossRef]
- Sunitha, M.S.; Vijayakumar, A. Complement of a fuzzy graph. Indian J. Pure Appl. Math. 2002, 33, 1451–1464. [Google Scholar]
- Rajeshkumar, R.; Anto, A.M. Fuzzy Detour Convexity and Fuzzy Detour Covering in Fuzzy Graphs. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 2170–2175. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. In Intuitionistic Fuzzy Sets: Theory and Applications; Physica-Verlag HD: Heidelberg, Germany, 1999; pp. 1–137. [Google Scholar] [CrossRef]
- Shannon, A.; Atanassov, K. A first step to a theory of the intuitionistic fuzzy graphs. In Proceedings of the First Workshop on Fuzzy Based Expert Systems, Sofia, Bulgaria, 28–30 September 1994; pp. 59–61. [Google Scholar]
- Parvathy, R.; Karunambigai, M.G. Intuitionistic Fuzzy Graphs. In Computational Intelligence, Theory and Applications, Proceedings of the International Conference 9th Fuzzy Days in Dortmund, Germany, 18–20 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 139–150. [Google Scholar] [CrossRef]
- Karunambigai, M.G.; Parvathi, R.; Buvaneswari, R. Arcs in intuitionistic fuzzy graphs. Notes Intuitionistic Fuzzy Sets 2011, 17, 37–47. [Google Scholar]
- Gani, A.N.; Begum, S.S. Degree, Order and Size in Intuitionistic Fuzzy Graphs. Int. J. Algorithms Comput. Math. 2010, 3, 11–16. [Google Scholar]
- Akram, M.; Davvaz, B. Strong intuitionistic fuzzy graphs. Filomat 2012, 26, 177–196. Available online: http://www.jstor.org/stable/24895720 (accessed on 4 August 2025). [CrossRef]
- Rajeshkumar, R.; Anto, A.M. Some domination parameters in intuitionistic fuzzy graphs. AIP Conf. Proc. 2022, 2516, 200016. [Google Scholar] [CrossRef]
- Binu, M.; Mathew, S.; Mordeson, J.N. Wiener index of a fuzzy graph and application to illegal immigration networks. Fuzzy Sets Syst. 2020, 384, 132–147. [Google Scholar] [CrossRef] [PubMed]
- Mordeson, J.N.; Mathew, S.; Malik, D.S. Generalized Fuzzy Relations. New Math. Nat. Comput. 2018, 14, 187–202. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Mathew, S. t-Norm fuzzy graphs. New Math. Nat. Comput. 2018, 14, 129–143. [Google Scholar] [CrossRef]
- Darabian, E.; Borzooei, R.A. Results on vague graphs with applications to human trafficking. New Math. Nat. Comput. 2018, 14, 37–52. [Google Scholar] [CrossRef]
- Guan, H.; Khan, W.A.; Saleem, S.; Arif, W.; Shafi, J.; Khan, A. Some Connectivity Parameters of Interval-Valued Intuitionistic Fuzzy Graphs with Applications. Axioms 2023, 12, 1120. [Google Scholar] [CrossRef]
- Mohamed, S.Y.; Mohamed Ali, A. Intuitionistic fuzzy graph metric space. Int. J. Pure Appl. Math. 2018, 118, 67–74. [Google Scholar]
- Naeem, T.; Gumaei, A.; Kamran Jamil, M.; Alsanad, A.; Ullah, K. Connectivity Indices of Intuitionistic Fuzzy Graphs and Their Applications in Internet Routing and Transport Network Flow. Math. Probl. Eng. 2021, 2021, 4156879. [Google Scholar] [CrossRef]
- Akram, M.; Alshehri, N.O. Intuitionistic fuzzy cycles and intuitionistic fuzzy trees. Sci. World J. 2014, 2014, 305836. [Google Scholar] [CrossRef] [PubMed]
- Tanev, D. On an intuitionistic fuzzy norm. Notes Intuitionistic Fuzzy Sets 1995, 1, 25–26. [Google Scholar]
- Zahid, H.; Dinar, J.; Shahid, Z.; Shams, U.R. Wiener index for an intuitionistic fuzzy graph and its application in water pipeline network. Ain Shams Eng. J. 2023, 14, 101826. [Google Scholar] [CrossRef]
- Walk Free Global Slavery Index. Available online: https://www.walkfree.org/global-slavery-index/2016 (accessed on 12 January 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).