Abstract
Cloud computing has witnessed widespread adoption across numerous sectors, primarily due to its substantial storage capacity and powerful computational resources. In this context, secure data sharing in cloud environments is critically important. Identity-based broadcast proxy re-encryption (IB-BPRE) has emerged as a promising solution; however, existing IB-BPRE schemes lack dynamic functionality—specifically, the ability to support user revocation and addition without updating re-encryption keys. Consequently, data owners must frequently reset and distribute these keys in response to user membership changes, leading to increased system complexity and communication overhead. In this paper, we propose an identity-based broadcast proxy re-encryption scheme with dynamic functionality (IB-BPRE-DF) to address this challenge. The proposed scheme utilizes a symmetric design of re-encryption keys to enable dynamic user updates while preserving a constant re-encryption key size. Furthermore, IB-BPRE-DF is constructed under the -GDDHE assumption and achieves semantic security in the random oracle model. Performance evaluations demonstrate that IB-BPRE-DF significantly reduces both the communication overhead (by maintaining a constant size for the re-encryption key and re-encrypted ciphertext) and the computational burden (with near-zero computational cost for generating the re-encryption key) for resource-constrained users. This work provides a practical and scalable cryptographic solution for secure and efficient data sharing in dynamic cloud environments.
1. Introduction
Cloud computing, with its powerful computational capabilities and massive storage capacity, has become widely adopted for large-scale data processing and efficient data management, particularly in personal information systems to enhance data sharing. However, data transmitted over public networks is vulnerable to eavesdropping, and stored data may be accessed by unauthorized users. Public key encryption protects data by converting it into ciphertext, preventing unauthorized access during transmission and storage. To support secure and efficient data sharing in the cloud, systems must also ensure flexibility and fine-grained access control. Proxy re-encryption (PRE) [1] offers a promising solution by enabling secure data sharing while supporting delegated access control. In addition to cloud data sharing [2,3], PRE has also been applied in areas such as email forwarding [4] and distributed file systems [5,6].
Green and Ateniese [7] first introduced identity-based proxy re-encryption (IB-PRE), combining proxy re-encryption with identity-based encryption [8] to simplify public key infrastructure and enable flexible access control. While IB-PRE supports secure data sharing, it is inefficient in cloud scenarios involving multiple receivers. Specifically, for n receivers, the sender must generate n re-encryption keys, and the proxy must produce n ciphertexts. To overcome this limitation, Xu et al. [9] proposed identity-based broadcast proxy re-encryption (IB-BPRE), which allows a single re-encryption key to support multiple receivers, thereby reducing overhead and improving efficiency.
Dynamic user revocation and addition are common in cloud-based data sharing, requiring timely updates to user access permissions. Although identity-based broadcast proxy re-encryption (IB-BPRE) reduces the computational and communication overhead associated with generating multiple re-encryption keys, it still requires re-encryption keys to be updated whenever user membership changes. This creates a burden for data owners, who must remain online to generate new keys, especially in scenarios with frequent updates. Moreover, existing IB-BPRE schemes lack key security guarantees—if a re-encryption key is leaked, any holder can perform re-encryption. To ensure confidentiality, each updated key must be securely transmitted, further increasing overhead. Thus, dynamic user updates still incur considerable computational and communication costs due to the need for frequent key updates.
To address the aforementioned challenges, we propose an identity-based broadcast proxy re-encryption scheme with dynamic functionality (IB-BPRE-DF) that enables flexible and secure data sharing in cloud environments. The proposed scheme introduces a novel re-encryption key generation mechanism, departing from traditional designs by deriving the re-encryption key from the delegator’s private value. This results in a symmetric key structure that maintains a constant key size, regardless of dynamic changes in user membership. This approach significantly reduces computational and communication overhead while supporting efficient and secure dynamic user updates.
Contributions
As previously discussed, user revocation and addition represent common requirements in cloud-based data sharing. Considering the limited resources of user devices, operations for achieving dynamic functionality must be lightweight. In data-sharing systems, user revocation and addition can be achieved without updating or re-encrypting keys, which is our primary design objective. Specifically, the contributions of this research can be summarized as follows:
- The proposed IB-BPRE-DF scheme ensures both flexibility and efficiency in cloud-based data sharing by maintaining a constant re-encryption key size, even under frequent user revocation and addition.
- The proposed IB-BPRE-DF scheme employs a symmetric key structure derived from the delegator’s private value to maintain a constant key size in dynamic settings, while a dual-agent mechanism improves fault tolerance and security.
- We provide a comprehensive security analysis of IB-BPRE-DF and conduct a detailed performance comparison with existing BPRE schemes. The results highlight the practical applicability and efficiency of the proposed scheme.
2. Related Work
2.1. Proxy Re-Encryption
Proxy re-encryption (PRE) was first introduced by Blaze et al [1]. To address the issue of costly certificate management in public key infrastructure (PKI) systems, Green and Ateniese [7] proposed the identity-based proxy re-encryption, which integrates the concept of identity-based encryption with PRE. Since its inception, extensive research [10,11,12,13] has been dedicated to constructing proxy re-encryption schemes with diverse properties to satisfy varying application requirements. However, traditional PRE schemes often encounter challenges in efficiently delegating authority to multiple receivers. Specifically, the number of re-encryption keys and re-encryption ciphertexts grows with the number of receivers.
2.2. Broadcast Proxy Re-Encryption
Broadcast encryption is a cryptographic primitive that allows a sender to encrypt a message for a subset S of authorized receivers over a broadcast channel, such that only receivers in the subset S can decrypt the broadcast using their respective private keys [14]. Building on this concept [15,16], Chu et al. [17] proposed conditional broadcast proxy re-encryption, enabling a sender to delegate decryption rights to a specific subset of users. In this scheme, the proxy cannot re-encrypt ciphertexts without the sender’s explicit authorization. Xu et al. [9] subsequently proposed a conditional identity-based broadcast proxy re-encryption scheme with constant-length re-encrypted ciphertexts, which is well suited for cloud email systems. Building on this, Sun et al. [18] designed a broadcast proxy re-encryption scheme tailored for cloud computing environments (e.g., cloud data sharing) and proved its security against chosen-ciphertext attacks. Existing broadcast proxy re-encryption schemes [9,18] enable the delegation of decryption rights to a subset of receivers at a specific time. However, these schemes impose substantial computational burdens on resource-constrained mobile devices. To address this limitation, Sumana et al. [19] proposed a privacy-preserving identity-based broadcast proxy re-encryption scheme aimed at reducing decryption overhead. More recently, Zhang et al. [20] introduced an IB-BPRE scheme tailored for flexible data sharing in VANETs. The work in [21] introduced identity-based threshold BPRE to incorporate multiple proxies, thereby effectively resisting single-point attacks. Subsequently, the studies in [22,23] proposed pairing-free BPRE for application in vehicular networks and cloud data-sharing environments, respectively, thereby enhancing data-sharing efficiency. Although the aforementioned BPRE schemes have achieved improvements in terms of efficiency and security, they exhibit limited flexibility. This limitation stems primarily from their design for static environments, without adequately addressing user revocation and addition in dynamic settings.
2.3. Revocable Proxy Re-Encryption
Ge et al. [24] proposed a revocable identity-based broadcast proxy re-encryption scheme for cloud-based data sharing, enabling the proxy to revoke a subset of receivers authorized by the delegator. However, the scheme imposes significant computational overhead on receivers, particularly those operating on resource-constrained mobile devices. Maiti et al. [25] proposed a coalitional game-based BPRE scheme that efficiently updates re-encryption keys for an optimal number of users in dynamic environments. Nevertheless, the recipient set needs to be predetermined prior to the generation of re-encryption keys. Recently, the study in [26] achieved efficient computation and communication among multiple sets of broadcast receivers by introducing a multi-channel BPRE scheme. However, to enable ciphertext transformation among different sets of broadcast receivers, it is necessary to configure multiple re-encryption keys, which introduces additional computational overhead. Subsequently, Chen et al. [27] designed a conditional identity-based broadcast proxy re-encryption scheme with anonymity and revocation, which is capable of simultaneously optimizing multiple performance metrics. Nevertheless, this scheme also encounters the challenge of re-encryption key updates. It is worth noting that existing BPRE and revocable (or dynamic) BPRE schemes demonstrate limitations when applied to data sharing in dynamic environments. The primary reason is that, with frequent user updates, the data owner must remain continuously online to update re-encryption keys in real time, thereby achieving dynamic functionality. This requirement substantially increases system overhead and diminishes the practical feasibility of the scheme in real-world scenarios.
This paper is organized as follows: Section 2 presents the related work. Section 3 offers a rigorous definition of bilinear maps and computational complexity, along with the formal definition and security model of the IB-BPRE-DF scheme. Section 4 elaborates on the concrete construction of the proposed IB-BPRE-DF scheme. Section 5 and Section 6 provide the security proof and performance analysis, respectively. Finally, Section 7 concludes this paper and outlines potential future research directions.
3. Preliminaries
We first give a strict definition of the bilinear map and then elaborate on the complexity assumption relied upon for the security proofs in detail.
3.1. Bilinear Map
For cyclic groups , and of the large prime order p, a bilinear pairing is a function that maps pairs of elements in () to elements of the group . The map e must satisfy the following properties:
- Bilinear: For all , and , it holds that .
- Non-degenerate: There exist and such that .
- Computable: The map e is efficiently computable and so are the group operations in , and .
There are two forms of pairings used in the cryptography literature [28]. In the symmetric setting, it holds that , whereas in the asymmetric setting, . The IB-BPRE-DF scheme adopts a symmetric bilinear pairing , fully exploiting the characteristics of its symmetric form. Bilinear pairings provide the mathematical foundation for designing the IB-BPRE-DF structure, enabling the implementation of complex access control and authorization mechanisms.
3.2. Complexity Assumption
The -GDDHE) assumption [29] is explained as follows: Let = ( ) be a bilinear map group system and let f and g be two coprime polynomials with pairwise distinct roots of respective orders t and n. Let be a generator of and be a generator of . Solving the -GDDHE problem, vector is
and ; non-probabilistic polynomial-time adversary can decide whether T is equal to or to some random element of with a non-negligible advantage. The -GDDHE assumption underpins the scheme’s security by preventing attackers without legitimate keys from recovering plaintext or private keys from ciphertext or re-encryption keys, thus ensuring data confidentiality during proxy re-encryption.
3.3. Definition and Security Model
As illustrated in Figure 1, the IB-BPRE-DF scheme is applied to cloud-based data sharing involving three primary entities: data owners, data users, and proxies. The process proceeds as follows: the data owner first encrypts the data and outsources the ciphertext to the cloud server to preserve data confidentiality. To enforce access control, the data owner then generates the re-encryption key. The proxies use the re-encryption key and the original ciphertext to produce a re-encrypted ciphertext, which authorized users can decrypt to access the data. In dynamic settings, when user updates occur, the same re-encryption key allows the proxies to transfer the ciphertext into the re-encryption ciphertext for authorized updated users, eliminating the need for frequent key regeneration and thus supporting efficient dynamic access control. The definition of IB-BPRE-DF, along with its correctness and security, is elaborated upon below.
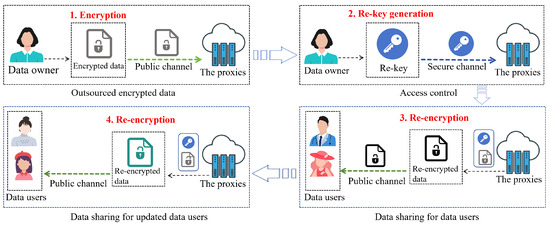
Figure 1.
IB-BPRE-DF applied to data sharing in the cloud.
3.3.1. Definition of IB-BPRE-DF
Definition 1
(IB-BPRE-DF). An IB-BPRE-DF scheme comprises the following algorithms: the setup algorithm, the key extract algorithm, the encryption algorithm (abbreviated as Enc), the re-encryption key generation algorithm (abbreviated as RKeyGen), the re-encryption algorithm (abbreviated as Re-Enc), and the decryption algorithms (abbreviated as Dec1 and Dec2). These algorithms are formally defined as follows:
- Setup . The trusted key generation center (KGC) executes the setup algorithm to establish the master secret key () and the master public key (). It takes as inputs a system security parameter and the maximum number n of broadcast receivers allowed in a single re-encryption process and outputs a key pair .
- Extract . The KGC executes the extract algorithm to generate the secret key for the user . It takes as inputs the master public key , the master secret key , and the identity and outputs the corresponding secret key .
- Enc . The delegator executes the Enc algorithm to generate the ciphertext for the message m. It takes as the input the master public key , an identity , and the message m and outputs the ciphertext c along with the secret value (note that the secret value is selected and stored by the delegator during the initial execution of the encryption algorithm).
- RKeyGen . The delegator performs the RKeyGen algorithm to generate the re-encryption key . It takes as inputs the master public key and the secret value of the delegator and outputs the re-encryption key .
- ReEnc . Proxies execute the ReEnc algorithm to transform the ciphertext under the delegator into the ciphertext , associated with the set of broadcast receivers, for , where ℓ denotes the number of dynamic user updates. The algorithm takes as inputs the master public key , the re-encryption key , and the ciphertext corresponding to the delegator and outputs the ciphertext corresponding to the receiver set .
- Dec1. The delegator executes the Dec1 algorithm to decrypt the ciphertext . Upon input of the master public key , the delegator’s secret key , and a ciphertext , if the ciphertext is valid, the algorithm returns the message m; otherwise, it outputs an error symbol ⊥.
- Dec2. The receiver in the receiver set , where , executes the Dec2 algorithm to decrypt the ciphertext . It takes as inputs the master public key , the ciphertext associated with the receiver set , and the private key of the receiver in the receiver set . If the re-encryption ciphertext is valid, the algorithm returns the message m; otherwise, it outputs an error symbol ⊥.
Correctness. We say that the IB-BPRE-DF scheme is correct if it satisfies the following two equations:
- , where , .
- , where , .
3.3.2. Security Model
We formally define the indistinguishability under the chosen-plaintext attack (CPA) security of the IB-BPRE-DF system against a probabilistic polynomial-time adversary . This security notion is captured through a game played between the adversary and a challenger . In this game, simulates the execution environment for the IB-BPRE-DF scheme and provides responses to queries issued by :
- Init. The adversary selects a challenge identity set , with ; .
- Setup. The challenger generates the system public parameters and subsequently provides it to the adversary .
- Query phase 1. At this stage, the adversary’s capabilities are formally defined, including the allowable queries for key extraction and re-encryption key generation. The adversary makes the following queries:For an extraction query , subject to the constraint that , the challenger executes the extract algorithm to generate the secret key . Subsequently, provides the secret key to the adversary .For a re-encryption key query , upon receiving an identity , the challenger executes the re-encryption key generation algorithm to generate the re-encryption key . Subsequently, provides the re-encryption key to the adversary .
- Challenge. The adversary outputs two messages . Subsequently, the challenger selects a random bit and encrypts the message under the challenge set . The resulting re-encryption ciphertext is then provided to the adversary . During the challenge phase of the IND-CPA game, the challenger generates a ciphertext that is computationally indistinguishable from a real ciphertext, ensuring the adversary cannot distinguish between the two with a non-negligible advantage.
- Query phase 2. continues making queries as in query phase 1. Note that cannot make query for . In query phase 2, the adversary is explicitly allowed to continue making queries even after receiving the challenge ciphertext.
- Guess. The adversary outputs a guess and succeeds in the game if . Let denote the advantage of an adversary in winning the game, defined as follows:
Definition 2.
The IB-BPRE-DF scheme is said to be semantically secure under the IND-CPA notion if the advantage is negligible.
4. Proposed IB-BPRE-DF
In this section, we formally define the concrete construction of the proposed IB-BPRE-DF scheme and provide a rigorous correctness analysis. The overall architecture and the high-level interactions among the participating entities are depicted in Figure 2. In the IB-BPRE-DF scheme, the key generation, encryption, and decryption algorithm are largely consistent with those of existing BPRE schemes. The novelty of IB-BPRE-DF lies in the use of two cooperating proxies for re-encryption and a distinctive re-encryption key management approach. Specifically, the delegator generates a re-encryption key and splits it into two components, and , which are distributed to proxy 1 and proxy 2, respectively. Proxy 1 uses to compute a partial re-encryption ciphertext , which is then forwarded to proxy 2. Upon receiving , proxy 2 combines it with to compute the re-encryption ciphertext , which can be correctly decrypted by authorized users to recover the plaintext m.
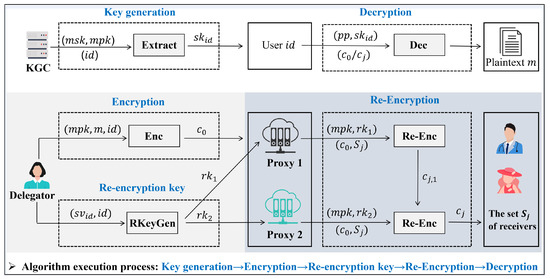
Figure 2.
High level interactions in the concrete construction.
4.1. Our Techniques
In contrast to existing IB-BPRE schemes [18,19,20,24], which necessitate re-encryption key updates for user revocation or addition, the dynamic mechanism introduced in this paper enables seamless user updates without altering the re-encryption key. In this section, we provide a concise overview of our primary implementation techniques. Consider the re-encryption ciphertext , corresponding to a broadcast receiver set , which includes the term . Similarly, the re-encryption ciphertext , associated with an updated receiver set , includes the term . In this context, the proxies and assist in generating these components by leveraging their respective partial re-encryption keys and , such that the re-encryption key is defined as . This construction ensures that ciphertexts corresponding to different receiver sets can be generated in a consistent format using the same re-encryption key while preserving data privacy—since neither proxy gains access to sensitive information.
4.2. Construction
We formally present the construction of IB-BPRE-DF with constant-size re-encryption keys, which comprises the following algorithms:
- Setup algorithm. The key generation center, acting as the trusted party, generates the master secret key and public key pair by executing the setup algorithm.Setup . It takes as inputs the system’s security parameter and the maximum number n of receivers in a single re-encryption and outputs a pair of master keys . Given a bilinear map parameter and a cryptographically secure function modeled as a random oracle for security analysis, it randomly selects two generators and , as well as a secret value . The master secret key is defined as , and the master public key is defined as , where and .
- Extract algorithm. The KGC generates the secret key for the user by executing the extract algorithm.Extract . It takes as inputs the master secret key and the identity and outputs the corresponding secret key:
- Encryption algorithm. The delegator encrypts the message m by executing the encryption algorithm.Enc . The delegator randomly selects , , and from , sets the secret value , and computes the ciphertext and as the public parameter, whereNote that ciphertext mainly consists of four parts and , each of which is calculated by the client.
- Re-encryption key algorithm. The delegator performs the re-encryption key algorithm to set the re-encryption key.RKeyGen . Given the secret value of the delegator , it partitions into and such that , and sets the re-encryption key , where and . Finally, the delegator transmits and to proxies and , respectively, via the secure channel.
- Re-encryption algorithm. The proxies and generate the re-encryption ciphertext via executing the re-encryption algorithm.ReEnc . Assume for notational simplicity that , where and . The proxy randomly selects and computes partial re-encryption ciphertext , whereand sends it to the proxy . After receiving partial re-encryption ciphertext , the proxy randomly chooses and computes the re-encryption ciphertext , whereWe have and , where .
- Decryption algorithm. The users (i.e., the delegator and receivers) perform the decryption algorithm to recover the plaintext m.Dec1. For a ciphertext , the delegator with the corresponding private key computesthen computes and .Dec2. For the re-encryption ciphertext , the receiver with identity in and the corresponding private key computeswiththen computes and .
In the dynamic setting, the IB-PRE-DF scheme employs a symmetric form of re-encryption keys. Specifically, if data owner Alice intends to share data with the broadcast receiver set and the updated set , she can generate the re-encryption key for and the re-encryption key for , where . This symmetric form of re-encryption keys effectively minimizes the computational overhead associated with re-encryption key generation in dynamic settings.
4.3. Correctness
- (1)
- For the ciphertext , the delegator computes
In the decryption algorithm, the entire decryption process is systematically divided into three steps. For Equation (1), the parameter K is obtained by combining the secret key , the ciphertexts and , and the public parameter h and then computing
For Equation (2), based on the intermediate parameter K and the public parameter , further operations are performed to calculate . We have
For Equation (3), the data m is finally recovered by using the ciphertext and the parameter obtained by Equation (2).
- (2)
- For the re-encryption ciphertext , the receiver with identity in computes
In the decryption algorithm of re-encryption ciphertext , the entire decryption process is divided into three steps. For Equation (4), the parameter K is obtained by combining the secret key , the ciphertexts and , and the public parameter and then computing
For Equation (5), based on the intermediate parameter K and the public parameter , further operations are performed to calculate . We have
For Equation (6), the data m is finally recovered by using the ciphertext and the parameter obtained by Equation (5).
From the above verification procedure, we conclude that the IB-BPRE-DF scheme satisfies the correctness property, as all operations produce the expected outputs under the defined system parameters and algorithms.
5. Security Proof
In this section, we formally prove that the IB-BPRE-DF scheme achieves CPA security. The detailed security analysis and proof are provided below to rigorously demonstrate the security of the IB-BPRE-DF scheme.
Theorem 1.
The IB-BPRE-DF scheme proposed in Section 4 is provably secure against chosen-plaintext attacks. Specifically, it achieves CPA security for re-encryption ciphertexts under the decisional -GDDHE assumption, within the random oracle model.
Proof of Theorem 1.
Suppose there exists a probabilistic polynomial-time adversary that can attack the IB-BPRE-DF scheme described in Section 3 with a non-negligible advantage . We build a adversary that uses as a subroutine to solve the -GDDHE assumption in with advantage . Let n be the maximum number of receivers included in a single re-encryption operation, and let t be the total number of queries made by , including key extraction, hash, and re-encryption key queries. Algorithm is provided with a bilinear group system and a decisional -GDDHE challenge instance defined as follows:
- -
- for .
- -
- for and , which is a polynomial of degree .
- -
- for and , which is a polynomial of degree .
These notations , , and are mainly used to construct simulation schemes, thereby making the simulation schemes indistinguishable from the real ones in terms of functionality and performance.
The above process first assumes that adversary has certain capabilities (i.e., it can break the proposed scheme IB-BPRE-DF with a non-negligible advantage ). Based on this, adversary takes a decisional -GDDHE challenge instance as the input to simulate the scheme and interact with . If succeeds, can solve the -GDDHE problem, thereby establishing the security of IB-BPRE-DF under this assumption.
- Init. The adversary outputs a set of identities that they intend to attack, where .
- Setup. To generate the system parameters , formally sets (i.e., without computing it) and randomly selects and then setsdefines the system parameters as . Subsequently, sends and to , where is a random oracle controlled by and is described below.
- Hash queries. At any point during the game, the adversary may issue a hash query to the random oracle on an identity , up to a total of times, where and denote the number of key extraction and re-encryption key queries, respectively. To respond to these queries, maintains a list of tuples of the form . Initially, this list includes
- where “∗” denotes an empty entry. Upon receiving a hash query for an identity , the challenger proceeds as follows:
- 1.
- If already exists in the list sets the corresponding value .
- 2.
- Otherwise, sets , appends to , and returns to the adversary.
- Query phase 1.Extraction query . Upon receiving an extraction query for an identity , the challenger proceeds as follows:
- -
- If an extraction query for has already been made, returns the corresponding private key from the list .
- -
- If a hash query has been previously issued for , retrieves the corresponding and computes the private key asWe use a random oracle to simulate the generation of private keys, ensuring that no real key is leaked.Re-encryption key generation query . When issues a re-encryption key generation query, performs the RKeyGen algorithm to set the re-encryption key , where the value is uniformly sampled from .
- Challenge. When decides that phase 1 is over, algorithm computes the encrypt algorithm to obtain , as shown below:with . One can verify thatWe observe that is a valid challenge ciphertext when . When T is a random value in , the challenge ciphertext appears independent of b from the adversary’s view. The challenge ciphertext constructed by adversary either conforms to the ciphertext structure of the proposed scheme or is generated at random, making it indistinguishable from adversary under the given security assumptions.
- Query phase 2. continues to make queries as in query phase 1 while strictly adhering to the constraints imposed by the indistinguishable game.
- Guess. In the guessing phase, the adversary ’s success probability in distinguishing the challenge ciphertext is used to derive a non-negligible advantage in solving the underlying hard problem (the decisional -GDDHE), thereby reinforcing the security reduction. outputs a guess . If outputs 1, this indicates that ; otherwise outputs 0, indicating that T is a random element in . This concludes the simulation. We now analyze the probability that the adversary solves the decisional -GDDHE assumption. If , the view of is independent of the bit b, implying that . Conversely, if , the adversary s output is dependent on s behavior, yielding . Consequently, the advantage of in solving the decisional -GDDHE assumption is . This concludes the proof of Theorem 1, thereby establishing the IB-BPRE-DF is CPA secure.
□
6. Performance Analysis
This section presents a comprehensive performance analysis of the proposed scheme from both theoretical and experimental perspectives.
6.1. Theoretical Analysis
A Comparison of the IB-BPRE-DF and IB-BPRE Schemes in [18,19,20,24]. Firstly, we define the notations used in Table 1, Table 2, Table 3 and Table 4 and align with those introduced in [19,24]. Let , , , and denote the sizes of the public parameter, ciphertext, re-encryption key, and re-encryption ciphertext, respectively. The variables n, k, and denote the maximum number of receivers in a single re-encryption, the number of revoked users, and the size of a broadcast receiver set S, respectively. Denote , , and as the computational costs for a modular exponentiation, a bilinear pairing operation, and a hash operation, respectively. , , and represent the bit lengths of an element in , , and , respectively. To simplify the discussion, we uniformly represent all groups involved in the schemes [18,19,20,24] by the symbol , all prime fields by the symbol , and all hash functions by the symbol .

Table 1.
Function comparison.

Table 2.
Computation overhead comparison.

Table 3.
Storage overhead comparison.
Feature Comparisons of IB-BPRE Schemes. Table 1 provides a summary of the feature metrics for the proposed IB-BPRE-DF scheme. These metrics are compared with those of relevant schemes [18,19,20,24]. The results indicate that the IB-BPRE-DF scheme achieves distinctive properties such as dynamic functionality, revocation functionality, and maintaining constant-size re-encryption keys. In contrast, some existing schemes struggle to effectively maintain these properties simultaneously. For instance, the BPRE schemes in [18,19,20] fail to support dynamic functionality while keeping re-encryption keys of a constant size. Additionally, the BPRE schemes in [24] require the proxy to achieve revocation by updating re-encryption keys.
Efficiency Comparisons of IB-BPRE Schemes. In Table 2 and Table 3, we present a comprehensive comparison between the IB-BPRE-DF scheme and related works [18,19,20,24] in terms of communication and computation overheads.
Communication costs encompass data transmission via private channels and broadcast channels, whereas computational costs primarily focus on the burden associated with private channels. System public parameters, ciphertexts, and re-encrypted ciphertexts are public information and do not require transmission to the user through private channels. Consequently, this paper emphasizes the communication burden imposed by re-encryption keys. The IB-BPRE-DF scheme exhibits a significant advantage in the setting of re-encryption keys compared to other schemes [18,19,20,24]. Specifically, this scheme only requires selecting one element from the domain as the re-encryption key, and its selection process is independent of the number of broadcast receivers. By contrast, the number of re-encryption keys in other schemes is typically directly proportional to the number of receivers.
Computational costs primarily stem from key extraction, encryption, re-encryption key generation, re-encryption operations, and the decryption of both original and re-encrypted ciphertexts. Key extraction and re-encryption algorithms are handled by the key generation center and proxy server, respectively, both assumed to have ample computational resources. This study focuses on the computational costs borne by terminal users with constrained computing capabilities. As shown in Table 3, in the IB-BPRE-DF scheme, the delegator incurs no computational overhead for setting up the re-encryption key, whereas schemes [18,19,20,24] require at least exponentiations, which imposes a significant burden on users with constrained computing power. During the decryption of the original ciphertext, the computational overhead of IB-BPRTE-DF is comparable to that in [19,24], but users in [18,20] bear higher computational costs. In the stage of decrypting the re-encrypted ciphertext, the computational overhead of this scheme is similar to that in [18,20,24]. However, although the scheme [19] requires users to bear only a small amount of computational overhead, it struggles to flexibly and efficiently adapt to frequent data-sharing scenarios in cloud environments.
6.2. Experimental Results
We utilized the Java Pairing-Based Cryptography (JPBC) Library [30] to implement the IB-BPRE-DF scheme and related works on personal computers. Specifically, the smartphone was employed to represent users with resource-constrained mobile devices.
Experiment settings. In the experiment, the smartphone operated on the Android 11 platform with specifications of 8 GB RAM and an 8-core 64-bit CPU processor running at 3072 MHz. The type A elliptic curve in the PBC library [30], with a 160-bit group order, was selected for conducting experiments. The elliptic curve had the form and was defined over the finite field . Two groups, and , were introduced, both of which had an order p and were subgroups of . Specifically, bits and bits in the binary system. Additionally, we let bits and bits.
Experiment results. Figure 2 and Table 3 illustrate the implementation of the algorithms presented in [24] (referred to as BPRE-1), in [20] (referred to as BPRE-2), and the proposed IB-BPRE-DF scheme. To provide a clearer visualization, Figure 3 employs a non-uniform axis. As illustrated in Figure 4 (with ), the encryption time of the proposed IB-BPRE-DF scheme is approximately 93.433 ms, which is lower than that of [24] (123.36 ms) and comparable to [20] (93.523 ms). Figure 3 shows that the re-encryption key generation in IB-BPRE-DF incurs only 1.347 ms (with ), in stark contrast to the 1558.7 ms and 1559.724 ms required by [24] and [20], respectively. This significant reduction greatly alleviates the computational burden on resource-constrained mobile devices. According to Table 4 and Figure 5 (for ), the decryption times for original ciphertexts in [20,24] and IB-BPRE-DF are 403.234 ms, 436.86 ms, and 401.352 ms, respectively. For re-encrypted ciphertexts, the decryption time of IB-BPRE-DF is comparable to [20]. Although [24] requires slightly less computation during decryption, it lacks dynamic support for user revocation and addition. The experimental results shown in Figure 4, Figure 5 and Figure 6 and Table 4 demonstrate that the IB-BPRE-DF scheme provides a notable efficiency advantage for algorithms executed on resource-constrained mobile devices.
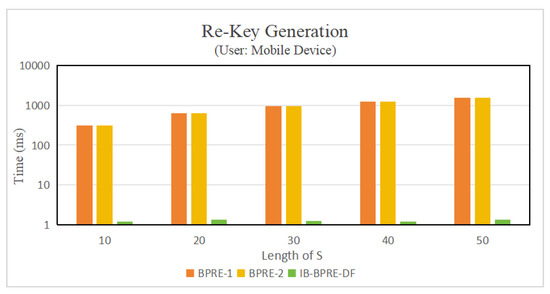
Figure 3.
Re-key generation time.
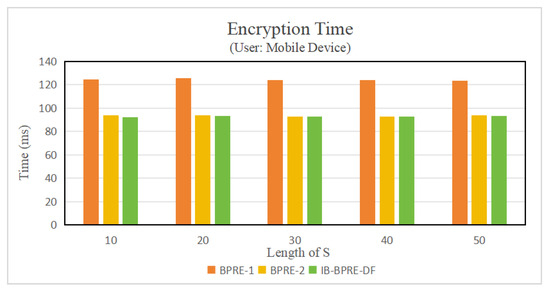
Figure 4.
Encryption time.
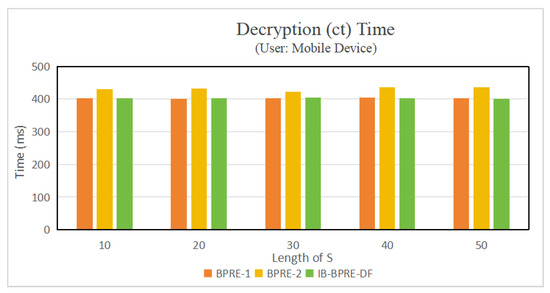
Figure 5.
Decryption () time.
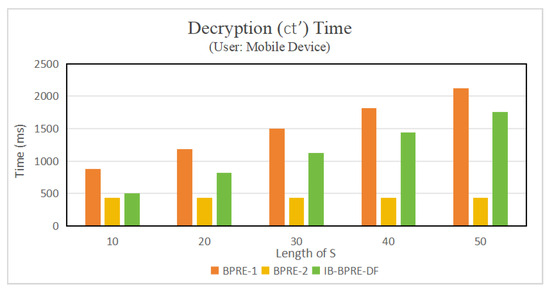
Figure 6.
Decryption () time.

Table 4.
Execution time.
Table 4.
Execution time.
| Algorithms | Enc | Re-Key | Dec() | Dec() |
|---|---|---|---|---|
| ms | ms | ms | ms | |
| ms | ms | ms | ms | |
| ms | ms | ms | ms | |
| ms | ms | ms | ms | |
| ms | ms | ms | ms |
7. Conclusions
We presented an identity-based broadcast proxy re-encryption scheme with dynamic functionality (IB-BPRE-DF) designed to facilitate secure and efficient data sharing in cloud environments. The proposed scheme supported dynamic user revocation and addition without requiring updates to the re-encryption key, thereby maintaining a constant key size. This design eliminated the need for repeated reconfiguration and distribution of re-encryption keys by the data owner in response to changes in user membership, which significantly improved system flexibility and reduced communication overhead. Furthermore, performance evaluations demonstrated that IB-BPRE-DF achieved communication and computational efficiency compared to existing BPRE schemes, particularly in reducing the computational burden on resource-constrained users.
Although the proposed identity-based broadcast proxy re-encryption scheme with dynamic functionality (IB-BPRE-DF) effectively reduced computational and communication overhead in dynamic environments, several limitations remained to be addressed. First, the current design did not consider resistance to quantum attacks. Second, while the computational cost of encrypting and decrypting the original ciphertext had been reduced, the decryption of re-encrypted ciphertext still imposed a considerable burden on resource-constrained users.
Future work will focus on integrating quantum-resistant cryptographic techniques, including lattice-based cryptography and hash-based cryptography, into the broadcast proxy re-encryption framework, thereby enhancing its resilience against quantum adversaries. In particular, we aim to design a lattice-based BPRE scheme that preserves dynamic functionality while ensuring security under post-quantum assumptions. To improve computational efficiency, we will investigate lightweight lattice constructions and optimize key and ciphertext sizes using structured lattices such as Ring-LWE. Moreover, we will investigate secure outsourcing mechanisms that delegate the decryption of re-encrypted ciphertext to third-party servers with substantial computational capabilities while preserving both the correctness of the decryption process and the confidentiality of the underlying data.
Author Contributions
Writing—original draft preparation, H.H.; writing—review and editing, H.H. and H.J.; formal analysis, H.H., C.L. and H.J.; resources, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the National Natural Science Foundation of China (Grant No. U1705264) and the Fuzhou Science and Technology Planning Projects (Project Nos. 2024-Y-013, 2024-SG-005, 2024H6008, 2023-ZD-003, and 2022-ZD-022).
Data Availability Statement
The data is contained within the article.
Conflicts of Interest
Author Huasong Jin was employed by the company Fujian Zhong Xin Network Security Information Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence ofany commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Advances in Cryptology-EUROCRYPT-98; Springer: Berlin/Heidelberg, Germany, 1998; pp. 127–144. [Google Scholar]
- Luo, F.; Wang, H.; Susilo, W.; Yan, X.; Zheng, X. Public trace-and-revoke proxy re-encryption for secure data sharing in clouds. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2919–2934. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, Y.; Cui, J.; He, D.; Zhong, H. Efficient fine-grained data sharing based on proxy re-encryption in IIoT. IEEE Trans. Dependable Secur. Comput. 2024, 21, 5797–5809. [Google Scholar] [CrossRef]
- Liu, G.; Xie, H.; Wang, W.; Huang, H. A secure and efficient electronic medical record data sharing scheme based on blockchain and proxy re-encryption. J. Cloud Comput. 2024, 13, 44. [Google Scholar] [CrossRef]
- Rawal, B.S.; Manogaran, G.; Hamdi, M. Multi-tier stack of block chain with proxy re-encryption method scheme on the internet of things platform. ACM Trans. Internet Technol. (TOIT) 2021, 22, 1–20. [Google Scholar] [CrossRef]
- Lin, S.; Cui, L.; Ke, N. End-to-end encrypted message distribution system for the Internet of Things based on conditional proxy re-encryption. Sensors 2024, 24, 438. [Google Scholar] [CrossRef] [PubMed]
- Green, M.; Ateniese, G. Identity-based proxy re-encryption. In Applied Cryptography and Network Security: Proceedings of the 5th International Conference, ACNS 2007, Zhuhai, China, 5–8 June 2007; Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2007; pp. 288–306. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Xu, P.; Jiao, T.; Wu, Q.; Wang, W.; Jin, H. Conditional identity-based broadcast proxy re-encryption and its application to cloud email. IEEE Trans. Comput. 2015, 65, 66–79. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, H.; Zhao, Y. AP-PRE: Autonomous path proxy re-encryption and its applications. IEEE Trans. Dependable Secur. Comput. 2017, 16, 833–842. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, S.; Han, S.; Zhang, H. Fine-grained proxy re-encryption: Definitions and constructions from LWE. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Guangzhou, China, 4–8 December 2023; Springer Nature: Singapore, 2023; pp. 199–231. [Google Scholar]
- Zhou, Y.; Liu, S.; Han, S. Multi-hop fine-grained proxy re-encryption. In Proceedings of the IACR International Conference on Public-Key Cryptography, Sydney, Australia, 15–17 April 2024; Springer: Cham, Switzerland, 2024; pp. 161–192. [Google Scholar]
- Pei, H.; Yang, P.; Li, W.; Du, M.; Hu, Z. Proxy re-encryption for secure data sharing with blockchain in internet of medical things. Comput. Netw. 2024, 245, 110373. [Google Scholar] [CrossRef]
- Fiat, A.; Naor, M. Broadcast encryption. In Advances in Cryptology-CRYPTO’93; Springer: Berlin/Heidelberg, Germany, 1994; pp. 480–491. [Google Scholar]
- Boneh, D.; Gentry, C.; Waters, B. Collusion resistant broadcast encryption with short ciphertexts and private keys. In Advances in Cryptology-CRYPTO 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 258–275. [Google Scholar]
- Boneh, D.; Gentry, C.; Waters, B. Identity-based broadcast encryption with constant size ciphertexts and private keys. In Advances in Cryptology-ASIACRYPT 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 200–215. [Google Scholar]
- Chu, C.K.; Weng, J.; Chow, S.S.M.; Zhou, J.; Deng, R.H. Conditional proxy broadcast re-encryption. In Proceedings of the 14th Australasian Conference on Information Security and Privacy, Brisbane, Australia, 1–3 July 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 327–342. [Google Scholar]
- Sun, M.; Ge, C.; Fang, L.; Wang, J. A proxy broadcast re-encryption for cloud data sharing. Multimed. Tools Appl. 2018, 77, 10455–10469. [Google Scholar] [CrossRef]
- Maiti, S.; Misra, S. P2B: Privacy preserving identity-based broadcast proxy re-encryption. IEEE Trans. Veh. Technol. 2020, 69, 5610–5617. [Google Scholar] [CrossRef]
- Zhang, J.; Su, S.; Zhong, H.; Cui, J.; He, D. Identity-based broadcast proxy re-encryption for flexible data sharing in VANETs. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4830–4842. [Google Scholar] [CrossRef]
- Liu, X.; Song, H.; Li, Z.; Yin, Y.; Han, G.; Liu, S. Identity-Based Threshold Broadcast Proxy Re-encryption Plus Scheme. In Proceedings of the International Conference on Frontiers in Cyber Security, Chongquing, China, 26–28 July 2024; Springer Nature: Singapore, 2024; pp. 396–412. [Google Scholar]
- Li, B.; Deng, L.; Mou, Y. A Pairing-Free Identity-Based Broadcast Proxy Re-Encryption Scheme for the Cloud. In Proceedings of the 2024 14th International Conference on Information Technology in Medicine and Education (ITME), Guiyang, China, 13–15 September 2024; pp. 521–528. [Google Scholar]
- Li, B.; Deng, L.; Liu, H.; Mou, Y.; Qu, Y.; Wang, N. A CCA-Secure Pairing-Free Broadcast Proxy Re-Encryption Scheme for VANETs. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar]
- Ge, C.; Liu, Z.; Xia, J.; Fang, L. Revocable identity-based broadcast proxy re-encryption for data sharing in clouds. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1214–1226. [Google Scholar] [CrossRef]
- Maiti, S.; Misra, S.; Mondal, A. CBP: Coalitional-Game-Based Broadcast Proxy Re-Encryption in IoT. IEEE Internet Things J. 2023, 10, 15642–15651. [Google Scholar] [CrossRef]
- Maiti, S.; Misra, S.; Mondal, A. MBP: Multi-channel broadcast proxy re-encryption for cloud-based IoT devices. Comput. Commun. 2024, 214, 57–66. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Li, J. Conditional Identity-Based Broadcast Proxy Re-Encryption With Anonymity and Revocation. IEEE Trans. Reliab. 2025; early access. [Google Scholar]
- Galbraith, S.D.; Paterson, K.G.; Smart, N.P. Pairings for cryptographers. Discret. Appl. Math. 2008, 156, 3113–3121. [Google Scholar] [CrossRef]
- Boneh, D.; Boyen, X.; Goh, E.J. Hierarchical identity based encryption with constant size ciphertext. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 440–456. [Google Scholar]
- Lynn, B. On the Implementation of Pairing-Based Cryptosystems. Available online: http://crypto.stanford.edu/pbc (accessed on 7 May 2014).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).