Abstract
With the dramatic growth in dataset size, active learning has become one of the effective methods to deal with large-scale unlabeled data. However, most of the existing active learning methods are inefficient due poor target models and lack the ability to utilize the feature similarity between labeled and unlabeled data. Furthermore, data leakage is a serious threat to data privacy. In this paper, considering the features of the data itself, an augmented graph convolutional network is proposed which acts as a sampler for data selection in active learning, avoiding the involvement of the initial poor target model. Then, by applying the proposed GCN as a substitute for the initial poor target model, this paper proposes an active learning model based on augmented GCNs, which is able to select more representative data, enabling the active learning model to achieve better classification performance with limited labeled data. Finally, this paper proposes a homomorphic encryption-based federated active learning model to improve the data utilization and enhance the security of private data. Experiments were conducted on three datasets, Cora, CiteSeer and PubMed, and achieved accuracy rates of 94.47%, 92.86% and 91.51%, respectively, while providing provable security guarantees. Furthermore, the highest malicious user detection accuracy was 88.07%, and the global model test accuracy reached 88.42%, 84.22% and 81.46%, under a model poisoning attack.
1. Introduction
In today’s digital era, graph-structured data are widely used in social networks, transportation networks, and biological networks [1,2,3,4,5]. These graph-structured data usually have complex topologies and contain rich hidden information. However, effective analysis and learning of large-scale graph-structured data usually requires a large amount of labeled data to train machine learning models. Obtaining labeled data is often challenging due to issues such as the scarcity of labeled data and the high cost of labeling. In the field of machine learning, feature selection is one of the key methods to optimize model performance and reduce the risk of overfitting [6,7,8,9,10,11,12,13,14,15]. However, with the high dimensionality of data and complex feature space, traditional feature selection methods lose important feature information, especially in the context of active learning. It is especially critical to select the most informative features to improve model performance.
Graph Convolutional Networks (GCNs) are a specialized class of deep learning models designed for processing graph-structured data. They extend the capabilities of traditional Convolutional Neural Networks (CNNs) to enable direct feature learning and prediction on non-Euclidean spaces (e.g., graphs, social networks, molecular structures) [16,17,18,19,20,21,22,23]. The core concept revolves around local information aggregation to extract feature representations of nodes and their neighborhoods within the graph. In recent years, research on feature selection and active learning based on Graph Convolutional Networks (GCNs) has attracted lots of attention [24,25,26,27]. In 2016, Kipf and Welling first proposed a semi-supervised classification method based on GCNs [12]. The method significantly improved the performance of the semi-supervised learning task by utilizing the relationship information between nodes in graph-structured data. In 2022, Zhang et al. proposed a graph convolutional network method based on node feature convolution [15]. By introducing the node feature convolution mechanism in GCNs, the method captured more nonlinear relationships between node features, improving the modeling capability of graph-structured data. In 2023, Chen et al. proposed a graph convolutional network-based feature selection method specifically for processing high-dimensional low-data-volume data [28]. The method selected the most representative subset of features through the graph structure information transfer mechanism of GCNs, improving the performance and the generalization ability of the model.
Federated Learning (FL) is a distributed machine learning framework that enables multiple clients, such as mobile devices and medical institutions, to collaboratively train a shared model using their local data without directly exchanging raw data [29,30,31]. Its core principle lies in transmitting only model parameters (e.g., gradients) instead of the underlying data, thereby preserving data privacy. Meanwhile, a central server aggregates local updates from participating clients to construct a global model.
In federated learning, how to effectively select data for training local models poses a significant challenge. Furthermore, data leakage and misuse may occur during the processes of data transmission and aggregation [29]. In addition to these privacy and security concerns, the decentralized nature of FL also makes it vulnerable to poisoning attacks. In model poisoning attacks, adversaries manipulate local model parameters and upload carefully crafted malicious updates to the server, aiming to compromise the integrity of the global model [32,33,34,35,36,37,38,39]. Such compromised participants are referred to as malicious users.
Based on the above problem analysis, our technical approach consists of three key modules:
First, the integration of active learning with Graph Convolutional Networks (GCNs) not only facilitates the selection of the most representative and informative samples for labeling, but also allows dynamic adjustment of the data selection strategy according to varying data distributions and task-specific characteristics during the learning process.
Second, homomorphic encryption techniques enable computations on encrypted data without requiring decryption, thereby providing strong guarantees for data security. This ensures that data remain encrypted throughout the entire lifecycle (including transmission, storage, and processing), effectively preventing data leakage and unauthorized use.
Third, a Key Generation Center (KGC) is employed to verify user-submitted updates and detect malicious users. The KGC has the capability to decrypt user ciphertexts. After the server performs model aggregation, the KGC uses the global model parameters to validate each client’s update, identifying and filtering out any potentially malicious contributions. Subsequently, the KGC uploads only the parameters from legitimate users back to the server for further aggregation. This mechanism ensures that the final global model does not incorporate any parameters from malicious users, thereby effectively defending against model poisoning attacks.
The main contributions of this paper are as below.
Firstly, this paper proposes a graph convolutional network model based on feature enhancement. By averaging the feature vectors output from multiple convolutional layers, the multi-level features of nodes can be better captured. The feature similarity between labeled and unlabeled data is utilized so that the unlabeled data that are more different from the labeled data can be selected to obtain more representative data.
Secondly, by applying the proposed GCNs as a substitute for the initial poor target model, this paper proposes an active learning model based on augmented GCNs, which is able to select more representative data, enabling the active learning model to achieve better classification performance with limited labeled data.
Thirdly, this paper proposes a homomorphic encryption-based federated active learning model to improve the data utilization and enhance the security of private data. In the federated active learning model, Client is employed as the proposed active learning based on augmented GCNs, to achieve privacy protection and improve the performance of the active learning model.
2. Preliminaries
2.1. Definition of the Problem
GCNs are deep learning models specialized in processing graph-structured data and incorporating active learning methods to select the most informative nodes for labeling. In GCNs, we let the graph contain nodes, denoted as , where denotes the set of nodes and denotes the set of edges. Each node i has a feature representation h_i, and these node features can be combined into a feature matrix , where , and denotes the feature dimension of each node. The graph structure can be represented by an adjacency matrix , , where denotes whether node to node is connected by an edge. The node representation of each layer is updated by aggregating the information of its neighboring nodes, denoted as , where denotes the node representation of the th layer, f denotes the aggregation function, and is the adjacency matrix. And in the first layer of GCNs, the input node feature matrix is usually directly used as the initial node representation matrix , i.e., . By stacking multiple layers, the node representations can be gradually updated for tasks such as node classification, graph classification, etc. The core idea of GCNs is to utilize the connectivity information between the nodes in the graph structure to enhance the capability of representation learning so that it can effectively handle graph data tasks.
In active learning, there is a collection of unlabeled nodes and a collection of labeled nodes , where the concatenation of and constitutes the entire collection of nodes, i.e., . The goal of active learning is to select the most informative nodes for labeling so as to maximize the model performance. In this process, the active learning algorithm selects the most valuable nodes for labeling based on the current model state and the information of the unlabeled nodes.
Combining GCNs and active learning, by training GCNs as samplers for active learning, it is possible to select the most informative nodes for labeling, thus improving the performance of the active learning model.
2.2. Graph Convolutional Network
Graph Convolutional Networks (GCNs) bridge the gap between graph-structured data and convolutional neural networks (CNNs) by adapting the powerful feature extraction capabilities of CNNs to non-Euclidean domains. Graph Convolutional Networks (GCNs) are a specialized class of deep learning models designed for processing graph-structured data. denotes an undirected graph, and represents the sets of edges that connect different nodes of set . An adjacency matrix describes the connectivity between nodes in the graph. Typically, is a sparse matrix, where indicates whether there is an edge or connection between node i and node j. In GCNs, the adjacency matrix is used to propagate the feature information of the nodes and realize the information interaction between nodes. In GCNs, the relationship between nodes is represented by the adjacency matrix of the graph, and the information propagation and feature extraction of the graph structure are achieved by updating the representation of the nodes by aggregating the information of their neighboring nodes. The feature matrix propagation in GCNs is shown in Equation (1):
is the node identity matrix of layer , is the symmetric adjacency matrix formed by adding the self-connections to the adjacency matrix , is the degree matrix of , is the weight matrix of layer , and is the activation function, where .
The propagation rule Equation (1) is derived from spectral graph theory [12], where ensures each node aggregates its own features. symmetrically normalizes the adjacency matrix to avoid numerical instability and maintain scale-invariant features. The weight matrix learns layer-specific transformations. This formulation approximates a first-order Chebyshev polynomial filter on the graph Laplacian, balancing local feature aggregation and computational efficiency.
GCNs achieve efficient processing of graph data by defining convolution operations on the nodes of the graph structure. In GCNs, each node exchanges information with its neighboring nodes and updates its own feature representation. Through multi-layered graph convolution operations, GCNs are able to utilize the connectivity between nodes to learn the node representations, thus enabling feature extraction and prediction on graph data.
2.3. Homomorphic Encryption
Homomorphic encryption is a cryptographic method that allows specific types of algebraic operations to be performed on ciphertext, producing an encrypted result that, when decrypted, matches the result of performing the same operations on the corresponding plaintext. In other words, this technology enables operations such as retrieval and comparison to be carried out directly on encrypted data, yielding correct results, without the need to decrypt the data throughout the entire processing process. A homomorphic encryption scheme consists of four probabilistic polynomial time algorithms: public key and key generation algorithm, encryption algorithm, decryption algorithm, and ciphertext evaluation algorithm.
- KeyGen (): Input security parameter , output public key evk for ciphertext evaluation and secret key sk.
- Enc (pk, m): Input public key pk and message m, output ciphertext c.
- Dec (sk, c): Input ciphertext c and secret key sk, output message m.
- Eval (evk, f, ): Input ciphertexts , public key evk for ciphertext evaluation and a function f, where f: . Input ciphertexts into function f using evk, output ciphertext .
2.4. Federated Learning
In federated learning, a central server aggregates locally computed models from clients to train a global model. There are n clients, and each client has its own dataset . The central server has initial model . After receiving the model from the server, client uses to compute the gradient, where and D is the cost function. Client computes the local model and sends it to the server. Then the server carries out aggregation to derive the global model as follows: . The iterative training process does not terminate until the model converges.
3. Our Methodology
3.1. Feature Enhancement-Based GCNs
The original GCN merely learned the feature information of nodes through the feature matrix. This paper further incorporates the similarity matrix and adjacency matrix based on the feature matrix. The addition of these matrices can enhance the feature learning ability of GCN. Moreover, by using a multi-layer feature fusion method, the ability of GCN to extract features is further strengthened. In this section, we propose a feature enhancement-based graph convolutional network model, which acts as a sampler for data selection, making the selected data more representative. The feature enhancement in the proposed model works in three aspects. Firstly, by combining the feature similarity and adjacency matrix of labeled and unlabeled nodes, the unlabeled nodes with the least correlation with the labeled nodes are selected. Secondly, the representation of nodes is improved by aggregating the node feature information output from different convolutional layers and combining local and global information. Finally, the feature similarity between labeled and unlabeled data is utilized to enable the graph convolutional network to predict whether the input data are labeled or not, so that the unlabeled data which are more different compared to the labeled data can be selected to ensure that the selected data are more representative. The graph convolutional network model based on feature enhancement is shown in Figure 1.
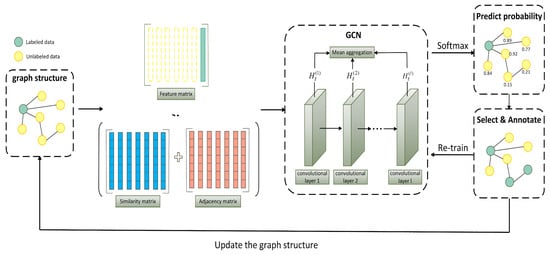
Figure 1.
Feature enhancement-based graph convolutional network.
3.1.1. Node Feature Similarity
In GCNs, the adjacency matrix describes the connectivity between nodes in the graph. Typically, is a sparse matrix, where indicates whether there is an edge or connection between node i and node j. In GCNs, the adjacency matrix is used to propagate the feature information of the nodes and realize the information interaction between nodes.
Node features are vectors describing the attributes or characteristics of a node in a graph, which are usually used to represent information on various attributes of a node in the graph. Node feature vectors can provide more key information about the nodes themselves, which can help distinguish the feature differences between different nodes and help the model learn the relationships between nodes in the graph data.
Although the adjacency matrix can reflect the connection relationship between nodes, when calculating node correlation, not only the adjacency matrix is needed, but also the similarity of node features. The node feature vector reflects the attribute information of the nodes, which can help distinguish the feature differences between different nodes, while the adjacency matrix describes the connectivity relationship between nodes, which can reveal the topology between nodes.
Traditional GCNs rely solely on the adjacency matrix A to propagate node information, which may fail to capture latent relationships between semantically similar but topologically distant nodes. To address this, we introduce a feature similarity matrix S computed via cosine similarity (Equation (2)), as the cosine metric is robust to high-dimensional sparse features. The combined correlation matrix C = αA + βS leverages both topological connectivity and feature semantics. Our ablation study shows that combining A and S improves accuracy by 5.3% compared to using A alone, validating the necessity of the similarity matrix.
We assume that the feature matrix of labeled nodes is and the feature matrix of unlabeled nodes is , where is the number of labeled nodes, is the number of unlabeled nodes, and is the dimensionality of the feature vectors. can be computed by cosine similarity as shown in Equation (2):
where denotes the feature vector of labeled node i and denotes the feature vector of unlabeled node j. By cosine similarity calculation, we can get a similarity value ranging between [−1, 1], where 1 means completely similar and −1 means not similar at all. The feature similarity matrix is shown in Equation (3):
The adjacency matrix represents the adjacency between nodes, , where is the total number of nodes. The correlation calculation is shown in Equation (4):
where and are weight parameters to balance the effects of feature similarity and adjacency in the correlation calculation. is the feature similarity term, which represents the similarity between the feature vector of the labeled node i and the feature vector of the unlabeled node j. is the adjacency term, which represents the adjacency relationship between the labeled node and the unlabeled node . The graph convolutional network feature matrix propagation in this paper’s method is conducted as shown in Equation (1):
The feature matrix is computed through layer-wise propagation, where the adjacency matrix is normalized by to avoid numerical instability. The weight matrix is initialized using Xavier initialization, and ReLU is chosen as the activation function due to its effectiveness in mitigating vanishing issues in deep GNNs.
By combining feature similarity and adjacency, the degree of association between labeled and unlabeled nodes is determined through correlation, which in turn, selects the unlabeled nodes that are least relevant to the labeled nodes. This approach mines potential relationships between nodes in the graph and helps to select the unlabeled nodes that have the greatest feature differences from the labeled nodes.
3.1.2. Multi-Layer Feature Fusion
In GCNs, the aggregation of node features is a key process that aims to integrate a node’s own features and the features of its neighboring nodes in order to update the node’s representation. By continuously aggregating information from neighboring nodes, the representation of a node gradually incorporates more information about its surrounding structure and context, thus improving the node feature representation. Nodes throughout the graph go through this aggregation process, allowing each node’s representation to learn global structural information.
In the traditional node feature aggregation process, after multiple information transfers, the node will learn more information about its neighboring nodes, resulting in the loss of key feature information about the node itself. In this paper, we propose a multi-layer feature fusion approach to improve the representation of nodes by aggregating the node feature information output from different convolutional layers and combining local and global information. The feature vector of node in the th round and th layer is calculated as shown in Equation (5):
where denotes the eigenvector of node at round , layer l. and denote the eigenvector of node , node at round , and layer . is the weight matrix at round , and layer . is the set of neighbors of node . denotes the correlation between node and node . is the activation function. The process of multi-layer feature fusion is shown in Equation (6):
where is the feature vector of node i in the tth round, is the feature vector of node in the th round and th convolutional layer, and denotes the number of convolutional layers. When all the (i = 1, 2, …, n) are obtained, the feature matrix after the average aggregation at round can be obtained. The feature matrix after the average aggregation at round is shown in Equation (7):
By averaging the feature vectors of nodes at different convolutional layers, the feature information learned by each node at different convolutional layers is actually being aggregated. This operation enables the model to synthesize multi-layered feature representations from different convolutional layers, combining local and global information and improving the performance of the model for node feature extraction.
The advantage of the multi-layer feature fusion approach is that by combining the feature information learned from different convolutional layers, the model is able to better capture the complex relationships and structural features of the graph data. By integrating local and global information, the multi-layer feature fusion approach can enhance the model’s ability to model node features, thereby improving the model’s performance in the node classification task.
3.2. Active Learning Based on Augmented GCNs
The feature-enhanced graph convolutional network model based on features, instead of the target model, acts as a sampler for data selection, and the active learning can select representative nodes more efficiently, which makes the model pay more attention to those nodes that have an important impact on model parameter updating during the training process, and thus improves the performance of the model. By predicting the nodes based on their feature similarity, representative nodes can be better selected and the efficiency of node selection can be improved. Then, the active learning model is trained based on the graph-structured data selected by this augmented graph convolutional network model, and the active learning model based on an augmented graph convolutional network is proposed, which achieves the maximization of the classification performance of the active learning model on graph-structured data with less labeled data. The active learning model based on an augmented graph convolutional network is shown in Figure 2.
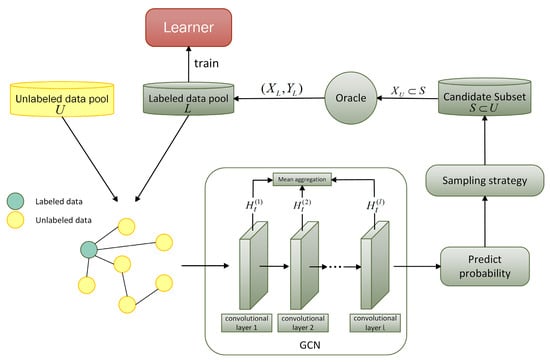
Figure 2.
Active learning based on augmented GCNs.
The node classification objective function is shown in Equation (8):
where and are the real labels of node and node , is the set of labeled nodes, is the set of unlabeled nodes, and and are the prediction results of whether node and node are labeled or not. The node feature objective function is shown in Equation (9):
where is the aggregated feature vector of labeled node , and is the aggregated feature vector of unlabeled node . By combining Equations (8) and (9), the complete objective function for training the graph convolutional network model can be obtained as shown in Equation (10):
where and are hyperparameters that determine whether the graph convolutional network effectively distinguishes between nodes with and without labels.
In this approach, the classification layer of the graph convolutional network is binary, where nodes with features similar to those of the labeled data are likely to be predicted as labeled nodes, while the opposite case will be predicted as unlabeled nodes. The cost of labeling nodes is reduced by selecting nodes that need to be manually labeled through the confidence level of the graph convolutional network model on the nodes. Based on the predicted probability to determine whether a node has labeled data or not, the nodes with the smallest probability value of being predicted as unlabeled nodes are selected to be manually labeled and the labeled nodes are added to the set of labeled nodes .
For the classification task, the active learning model is trained using the set of labeled nodes . The loss function is shown in Equation (11):
where is the number of samples in the training set; is the number of categories; denotes the parameters of the active learning model; is the true label value of the th category of the th node; and is the prediction probability of the model for the th category of the th sample. By minimizing the cross-entropy loss function, the prediction result of the active learning model can be made as close as possible to the true label, thus improving the classification accuracy of the active learning model.
3.3. Homomorphic Encryption Algorithm Based on Identity Authentication
To protect the client’s private data from leakage, we introduce homomorphic encryption to resist against model poisoning attacks in federated learning. The legitimacy of the client needs to be verified. In this paper, we propose a homomorphic encryption algorithm based on authentication using the Paillier algorithm. The algorithm can verify the functionality of client legitimacy, while KGC is a trusted third party. Identity authentication acts to verify whether participants in federated learning are legitimate users or malicious adversaries. By calculating the mean, median and standard deviation of the first-round gradient data, abnormal data can be identified, and then the source of malicious users can be identified. The identified malicious users will be isolated in the following submitting stages, achieving the purpose of identity authentication. Eventually, a homomorphic encryption algorithm based on identity authentication is implemented. In the proposed homomorphic encryption algorithm, only data from honest users are aggregated and decrypted, which ensures the isolating of malicious data, preserving the client’s private data from leakage. The proposed homomorphic encryption scheme consists of five core algorithms: Key Generation, Encryption, Verification, Aggregation, and Decryption. The homomorphic encryption algorithm based on authentication is shown in Figure 3. The detailed homomorphic encryption algorithm is as follows.
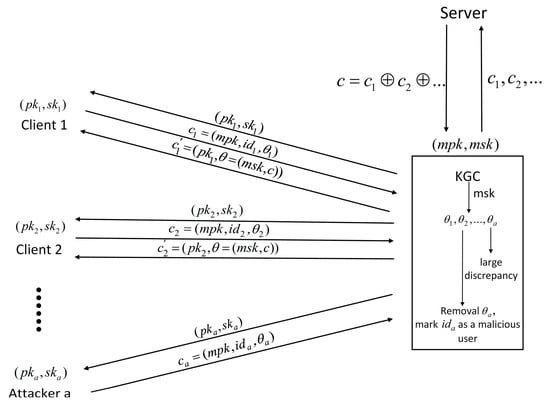
Figure 3.
Homomorphic encryption algorithm based on identity authentication.
Key generation: KGC selects two large prime numbers and and calculates ; then it calculates , where denotes the least common multiple; it then randomly selects an integer , , and calculates , where . The master key pair for generating the KGC can be represented as follows: master public key , master private key . For each client , a large integer is randomly generated and ensures that is mutually prime with . The client public key is obtained by performing a computation on the client private key (. The key pair for each client can be expressed as follows: private key , public key .
Encryption: Each client uses the master public key to encrypt its locally trained model parameters to obtain the ciphertext model parameter . The encryption process can be expressed as follows: , where is a random number.
Verification: KGC uploads the first round of received directly to the server, which obtains the encrypted global model parameter by the homomorphic encryption algorithm and sends it down to KGC. KGC decrypts the global model parameter of the first round by using the master private key , and the decryption process can be expressed as follows: . KGC decrypts using the master private key to obtain the model parameter for each client, and the decryption process can be expressed as follows: . It then calculates the cosine similarity of the model parameters to the global model parameters for all clients. The mean (), median () and standard deviation () of the cosine similarity of all legitimate clients are then calculated. If , the cosine similarity value will be lower than for most potentially illegitimate clients. If , client is illegitimate, and is a hyper-parameter.
Aggregation: Starting from the second iteration loop, KGC removes the model parameters uploaded by illegitimate clients and uploads the remaining ciphertext model parameters to the server, which performs aggregation by homomorphic encryption and sends the aggregated ciphertext global model parameters to KGC.
Decryption: The KGC decrypts using the master private key to obtain the global model parameters. Then it encrypts and sends it down using the legitimate client’s public key , and client decrypts it using its own private key to obtain the plaintext global model parameters to update the local model.
3.4. Homomorphic Encryption-Based Federated Active Learning
Federated learning allows multiple participants to train models at the same time, which solves the problem of data sharing but also carries the risk of privacy breaches. Homomorphic encryption allows computations to be performed on encrypted data without the need to decrypt the data. This means that in federated learning, participants can share encrypted data or model parameters without exposing the original data, thus realizing privacy protection. Combining homomorphic encryption algorithms with federated learning can further enhance data privacy and security.
In this section, active learning privacy protection is realized for graph-structured data, and a federated active learning system based on homomorphic encryption is proposed by designing a homomorphic encryption algorithm based on authentication, as shown in Figure 4. When handling graph-structured data, the system employs an active learning model based on augmented graph convolutional networks to enhance training efficiency and model performance while ensuring data privacy.
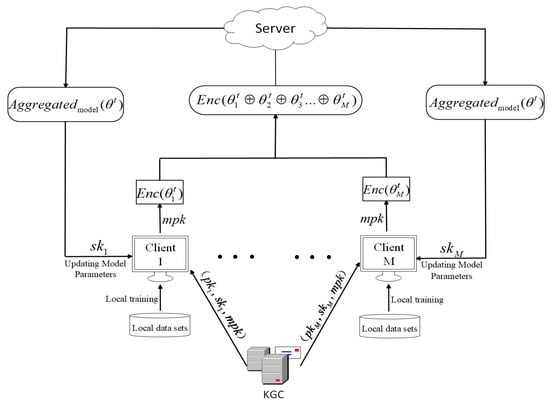
Figure 4.
Federated active learning system based on homomorphic encryption.
Specifically, for the graph-structured data, federated active learning is implemented on datasets, Cora, CiteSeer, and PubMed, respectively. The specific process includes the active learning training phase, encryption phase, authentication phase, federation aggregation phase, and decryption phase.
Active Learning Training Phase: There are clients, and each client trains an active learning model by a feature-enhanced graph convolutional network using the structural dataset of this graph-structured data to obtain the local model parameters .
Encryption phase: client encrypts the local model parameters of the t th round of their respective training using the master public key to obtain , respectively, and uploads the encrypted local model parameters to KGC.
Authentication phase: The KGC verifies the legitimacy of client according to the homomorphic encryption algorithm based on authentication and uploads the cipher model parameters of the legitimate client to the server.
Federated Aggregation Phase: The server takes the cipher model parameters uploaded by KGC received in the th round and aggregates them against the cipher model parameters of legitimate client .
Decryption phase: The server sends the aggregated encrypted model parameters to KGC, which decrypts the global model parameter using the master private key . KGC encrypts the encrypted global model parameters using the public key of the legitimate client and sends it to the legitimate client , which decrypts the encrypted global model parameters using the private key and obtains the global model parameters in plaintext.
Active Learning Model Parameter Update Phase: Legitimate clients use the decrypted global model parameters to update the local model parameters and improve the local active learning model performance.
Since client data are encrypted using the homomorphic algorithm during the federated learning process, the ciphertext remains encrypted both during transmission and while stored on the server. This prevents the leakage of information related to gradients. Before the ciphertext is submitted to the server for computation, the key generation center performs authentication, which can identify non-compliant data and malicious users. As a result, this mechanism effectively defends against poisoning attacks.
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets
As shown in Table 1, Cora, Citeseer and PubMed are three commonly used academic citation network datasets widely used in the field of graph neural network research [8,9,12,15,19]. The Cora dataset consists of 2708 papers in the field of machine learning, and each paper is represented by an eigenvector containing word-frequency statistics, and the edges indicate the citation relationships between papers. It is mainly used for the node classification task, by categorizing the papers into seven categories according to their research areas, namely, “Case_Based”, “Genetic_Algorithms”, “Neural_Networks”, “Probabilistic_Methods”, “Reinforcement_ Learning”, “Rule_Learning”, and “Theory”. Edges denote citation relationships between papers, i.e., if a paper cites another paper, then there is an edge between the corresponding nodes. The Citeseer dataset contains 3327 academic papers and also covers citation relationships between papers. Each paper is represented by a feature vector with dimension 3703. Citeseer is also widely used for node classification tasks and is categorized into six categories based on different research areas in computer science, namely, “CS.CC”, “CS.DS”, “CS.GL”, “CS.IR”, “CS.LG”, and “CS.NE”. Similar to the Cora dataset, edges indicate citation relationships between papers. The PubMed dataset consists of 19,717 biomedical articles, each with a feature vector of dimension 500, with a total of three categories: “Cardiovascular_Diseases”, “Cancer_Research”, and “Neurology”. The edges represent citation relationships between documents, which are mainly used for node classification and document relationship mining tasks. Researchers can utilize PubMed datasets to study literature relationships in the biomedical field, infer correlations between literature and classify topics, and provide useful references and insights for medical research. The characteristics and size of these three datasets make them important benchmark datasets for studying graph neural network models and algorithms.

Table 1.
Statistics of three datasets.
4.1.2. Baselines
Random: Random method is a simple baseline method for decision making or experimentation by random selection.
Entropy-based method [11]: Information entropy-based methods utilize the concept of information entropy for decision making or selection and are commonly used for feature selection and decision tree construction.
Coreset [10]: Coreset method is a data sampling technique that preserves the main features of the original dataset by selecting representative samples.
Degree: Degree methods are commonly used in graph theory for iterative labeling of nodes based on their degree and are used to measure the importance of nodes.
AGE [8]: AGE is a method used to learn causal relationships in graphs, inferring causal relationships between variables through greedy algorithms and equivalence classes.
ANRMAB [9]: ANRMAB is a multi-armed gaming machine algorithm for decision making problems in non-smooth environments by dynamically adapting to changes in the environment.
4.1.3. Assessment Indicators
In machine learning and classification problems, there is a close relationship between accuracy, precision, recall, specificity and F1 score, which are important metrics for evaluating the performance of a classifier. Accuracy is the ratio of the total number of samples correctly predicted by the classifier to the total number of samples, and is a measure of the overall performance of the classifier. Precision rate is the ratio of the number of samples predicted by the classifier as positive categories and correct to the number of samples predicted as positive categories, which emphasizes the accuracy of the classifier in predicting positive categories. Recall is the ratio of the number of samples correctly predicted as positive categories by the classifier to the number of samples that are actually positive categories, which evaluates the ability of the classifier to recognize positive categories. The F1 score combines the precision and recall and is the reconciled average of the precision and recall, which is used to evaluate the performance of the classifier in a comprehensive manner. Sensitivity is the proportion of samples that are actually positive categories that are correctly recognized as positive categories by the classifier, also known as true instance rate or check all rate. Specificity is the proportion of samples that are actually negative categories that are correctly recognized as negative categories by the classifier, and evaluates the ability of the classifier to recognize on negative categories.
4.2. Results and Analysis
Based on the experimental results, it can be seen that there is a difference in the performance of the model on the three different datasets. As shown in Table 2, the best results are achieved with the Cora dataset in terms of accuracy, precision, recall, specificity and F1 score, showing its superiority on the classification task. This may be due to the fact that the Cora dataset has a clearer distribution of categories and higher quality data, which makes it easier for the model to learn and generalize to new data. The slightly lower recall and F1 scores of CiteSeer may be affected by the imbalance of categories in the dataset, which results in the model’s poor performance on a few categories. The PubMed dataset, on the other hand, has relatively low specificity and accuracy, possibly due to poor data quality or feature selection.

Table 2.
Classification performance on three datasets.
These results suggest the importance of data characteristics that need to be considered when designing models for different datasets. In practical applications, careful analysis and preprocessing of datasets, and selection of appropriate feature engineering methods, as well as model tuning strategies, can help improve model performance and generalization. Comprehensive consideration of data quality, feature selection, model complexity, and training strategies can be targeted to improve model performance on different datasets and increase the accuracy of the classification task.
4.2.1. Classification Experiment
Based on the analysis of the experimental results, it can be observed that on the Cora, CiteSeer and PubMed datasets, this paper’s method is able to achieve a high level of accuracy when only 40% labeled data are used. As shown in Figure 5, as the amount of labeled data increases from 10% to 40%, the accuracy of the model on each dataset gradually improves and finally reaches a high level in the case of 40% labeled data. The accuracy increased from 48.15% to 94.47% on the Cora dataset, from 55.22% to 92.48% on the CiteSeer dataset, and from 53.16% to 91.51% on the PubMed dataset. This indicates that the model is able to select more representative data on these datasets, thus achieving higher classification accuracy. This suggests that the data selection by the method in this paper helps the model learn more representative features and improves generalization to unlabeled data. This approach not only improves the accuracy, but also highlights the model’s generalization ability and learning effect on different datasets, which provides an effective solution to address the situation where labeled data are scarce or costly to label.
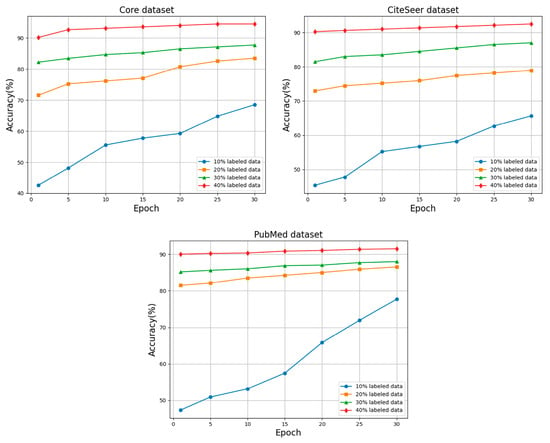
Figure 5.
Accuracy analysis of 10%, 20%, 30%, and 40% labeled data.
4.2.2. Ablation Experiment
When performing ablation experiments on Cora, CiteSeer and PubMed datasets with different numbers of GCN convolutional layers, some clear trends were found. As shown in Figure 6, on the Cora dataset, as the number of GCN convolutional layers increases, the F1 score is highest at GCN 3 convolutional layers, with the highest value of 94.05%, showing that increasing the number of convolutional layers helps the model to better understand the complex relationships between the data. Similarly, the highest F1 score of 91.78% was achieved with the GCN 3-layer convolutional layer on the CiteSeer dataset, with the three-layer convolutional layer performing better for the model compared to fewer or more convolutional layers. The results on the PubMed dataset show a similar trend, with the highest F1 score of 91.26% for the GCN three-layer convolutional layer, showing that increasing the number of convolutional layers to three helps to improve the model’s classification performance. Comprehensively analyzing these experimental results, it can be concluded that choosing a three-layer GCN convolutional layer may be a more appropriate choice on the Cora, CiteSeer, and PubMed datasets. The three-layer GCN convolutional layer shows better performance on these datasets, and is able to achieve higher F1 scores on different datasets. This suggests that increasing the number of convolutional layers to three in these cases helps the model to learn the complexity of the data better, improves the classification performance of the model, and exhibits better generalization ability.
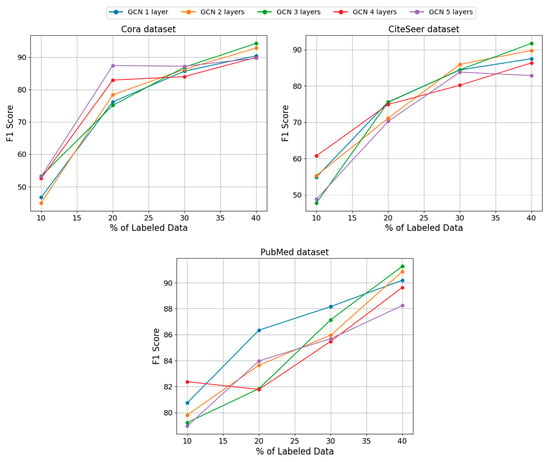
Figure 6.
F1 scores for different numbers of convolutional layers.
4.2.3. Comparison Experiment
According to the experimental results, the F1 scores of seven different methods on Cora, CiteSeer and PubMed datasets are analyzed. As shown in Figure 7, on the Cora dataset, it is observed that the F1 scores of this paper’s methods gradually increase from 10.33% to 94.05% under different labeled data ratios, showing a significant growth trend. For the CiteSeer dataset, it is observed that the performance of the different methods also improves with the increase in the labeled data ratio. Specifically, the F1 score of this paper’s method on this dataset increased from 15.56% to 91.78%, showing a high growth rate. On the PubMed dataset, the F1 scores of the different methods similarly show an increasing trend with the increase in the proportion of labeled data. The performance of the method in this paper is also highlighted again by the F1 scores, which increase from 30.18% to 91.26%, demonstrating a clear advantage. Other methods such as AGE, ANRMAB, Degree, Entropy-based method, Coreset, and Random also show an increasing trend with the increase in the proportion of labeled data, but among these methods, the method in this paper has the highest performance on the Cora, CiteSeer, and PubMed datasets. Combining the experimental results of the three datasets, this paper’s method performs well on Cora, CiteSeer and PubMed datasets, and relative to the other six methods, this paper’s method achieves higher F1 scores with different labeled data proportions. Therefore, based on the presented data, it can be concluded that the method proposed in this paper performs best under these experimental conditions and has better generalization performance and stability.
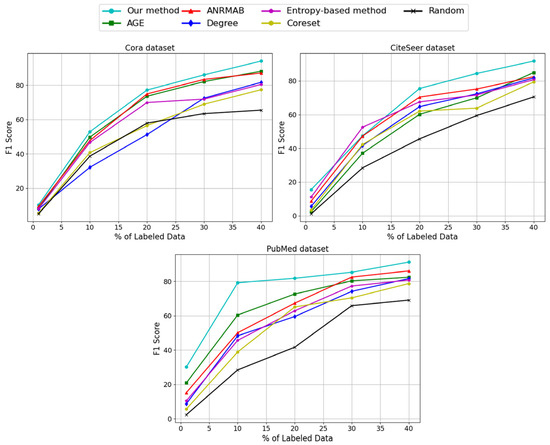
Figure 7.
Comparison of F1 scores of different methods on three datasets.
4.2.4. Precision, Recall, Specificity Analysis
Based on the experimental results, we can analyze the performance of the method in this paper using three evaluation metrics: precision, recall and specificity. The datasets include Cora, CiteSeer and PubMed. As shown in Figure 8, we can see that for the precision (precision) on the three datasets, the performance of this paper’s method is 93.99% (Cora), 92.64% (CiteSeer) and 91.9% (PubMed). Precision measures the proportion of all samples classified as positive classes in which the model is truly positive, so high precision indicates that the model is highly accurate in classifying positive classes. Based on the data, this paper’s method performs best on the Cora dataset, while also maintaining a high level of accuracy on the CiteSeer and PubMed datasets. Recall evaluates the ability of the classifier to recognize positive categories. The recall performance of this paper’s method on the three datasets is 94.29% (Cora), 91.29% (CiteSeer) and 90.79% (PubMed). Sensitivity measures the model’s ability to correctly identify positive class samples, i.e., the proportion of all true positive class samples that are correctly identified as positive. The data show that this paper’s method has the highest sensitivity on the Cora dataset, while it also performs well on the CiteSeer and PubMed datasets. The experimental results show that the specificity (specificity) performance of this paper’s method on the three datasets is 99.08% (Cora), 98.56% (CiteSeer), and 95.48% (PubMed), respectively. The specificity metric measures the model’s ability to correctly identify negative class samples, i.e., the proportion of all true negative class samples that are correctly identified as negative. According to the data, this paper’s method has the highest specificity on the Cora dataset, while it also has a high level of specificity on the CiteSeer and PubMed datasets. In summary, this paper’s method performs well on the Cora, CiteSeer and PubMed datasets in the three evaluation metrics of accuracy, sensitivity and specificity. Specifically, on the Cora dataset, the method performs best in terms of accuracy, sensitivity and specificity; while on the CiteSeer and PubMed datasets, it maintains a high level of overall performance, albeit with slight differences.
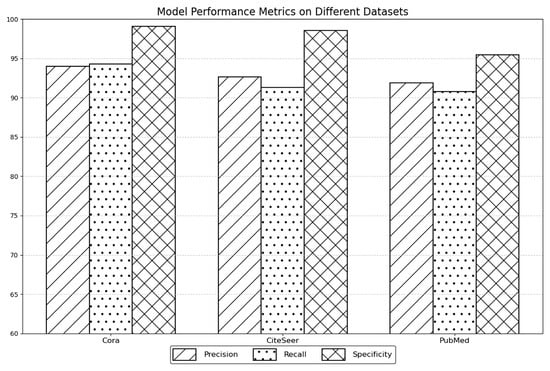
Figure 8.
Analysis of the precision, recall and specificity of the proposed method.
4.2.5. Malicious User Detection Rate
According to the experimental results, the method proposed in this subsection shows a high malicious user detection accuracy in terms of using graph-structured data when 10 clients are involved and each of them contains 5 malicious clients. As shown in Figure 9, during the federated learning process, a significant improvement in malicious user detection accuracy is achieved as the number of training sessions increases. When using graph-structured datasets, the highest malicious user detection accuracy is 88.07% for the Cora dataset, 83.9% for the CiteSeer dataset, and 81.74% for the PubMed dataset. Similarly, the malicious user detection accuracy when dealing with graph-structured data shows a significant growth trend as the number of trainings increases. These experimental results demonstrate that the method proposed in this subsection exhibits high accuracy in detecting malicious users, achieving satisfactory results when graph-structured data are used. This further validates the effectiveness and practicality of the homomorphic encryption algorithm based on authentication proposed in this subsection, which provides a reliable and efficient solution for malicious user detection in federated learning systems.
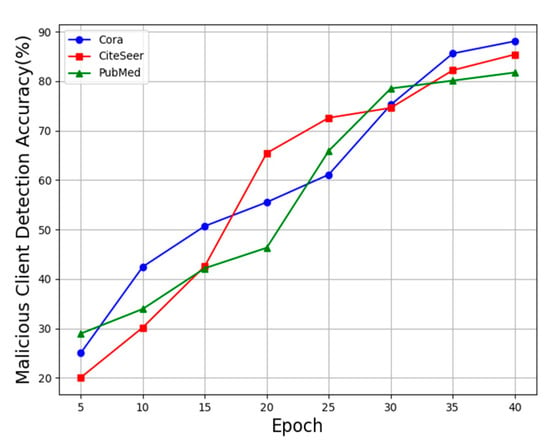
Figure 9.
Accuracy of malicious user detection on graph-structured data.
4.2.6. Global Model Performance Analysis
Based on the analysis of the experimental results, the method proposed in this subsection performs well in processing graph-structured data (e.g., Cora, CiteSeer, and PubMed). In the case of malicious clients using model poisoning attacks, the accuracy of the global model test is significantly improved, demonstrating the ability of the method in this subsection against malicious attacks. As shown in Figure 10, on the graph-structured data, the global model test accuracy for Cora, CiteSeer and PubMed datasets shows a significant increase from 29.06%, 27.03% and 24.86% to 88.42%, 84.22% and 81.46%, respectively. The effectiveness of the homomorphic encryption algorithm based on authentication is verified, with the algorithm successfully detecting and defending against attacks from malicious clients and ensuring the stable performance of the global model. When dealing with graph-structured data, the methods proposed in this subsection perform well, showing a wide range of applicability and robustness. Despite five malicious clients using the model poisoning attack, the test accuracy of the global model is still significantly improved, confirming that the method proposed in this subsection can effectively filter the interference of malicious clients and guarantee the security and performance of the federated learning system. In summary, the method proposed in this subsection achieves satisfactory results in processing graph-structured data, effectively counteracts attacks from malicious clients, and ensures the security and performance of the federated learning system.
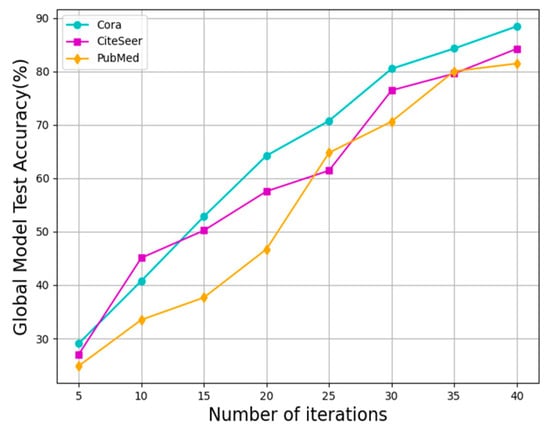
Figure 10.
Accuracy of global model test under model poisoning attack.
5. Conclusions
Considering the features of the data itself, an augmented graph convolutional network is proposed and acts as a sampler for data selection in active learning, avoiding the involvement of the initial poor target model. The proposed GCNs not only fully utilize the feature similarity between labeled and unlabeled data, but also solve the problem of unrepresentative selected data, significantly improving the model performance in active learning. By applying the active learning model based on enhancement graph convolutional network into federated learning, this paper proposes a homomorphic encryption-based federated active learning. Experimental results on multiple datasets show that the method performs well in terms of accuracy, sensitivity and specificity, especially in the node classification task, to achieve significant performance improvement. Our experiments reveal that the computation of the feature matrix significantly impacts model performance. Proper normalization (e.g., symmetric normalization) not only stabilizes training but also enhances the model’s ability to capture long-range dependencies in the graph. The proposed homomorphic encryption-based federal active learning not only guarantees the data security, but also improves the data utilization and the classification performance of the active learning model. In future work, we will extend the proposed model to image data to widen its application prospects.
Author Contributions
Methodology, X.H., Z.S. and H.J.; Validation, Z.S.; Formal analysis, X.H., D.Z. and Q.M.; Investigation, Q.M.; Writing—original draft, Z.S.; Writing—review & editing, D.Z. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Research Project of Weinan Science and Technology Bureau grant number NO. ZWGX2003-1.
Data Availability Statement
Data available on request due to restrictions.
Acknowledgments
Thank all the authors for their efforts and cooperation. Thank all the reviewers and editors for their assistance and contributions to the improvement of this paper. This work is financially supported by the Science Research Project of Weinan Science and Technology Bureau (NO. ZWGX2003-1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caramalau, R.; Bhattarai, B.; Kim, T.K. Sequential graph convolutional network for active learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9583–9592. [Google Scholar]
- Tong, Z.; Liang, Y.; Sun, C. Directed graph convolutional network. arXiv 2020, arXiv:2004.13970. [Google Scholar]
- Wu, Y.; Xu, Y.; Singh, A. Active learning for graph neural networks via node feature propagation. arXiv 2019, arXiv:1910.07567. [Google Scholar]
- Li, X.; Wu, Y.; Rakesh, V. Smartquery: An active learning framework for graph neural networks through hybrid uncertainty reduction. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 4199–4203. [Google Scholar]
- Hu, S.; Xiong, Z.; Qu, M. Graph policy network for transferable active learning on graphs. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2020; Volume 33, pp. 10174–10185. [Google Scholar]
- Zhang, Y.; Tong, H.; Xia, Y. Batch active learning with graph neural networks via multi-agent deep reinforcement learning. Proc. AAAI Conf. Artif. Intell. 2022, 36, 9118–9126. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Y.; Li, Y. Alg: Fast and accurate active learning framework for graph convolutional networks. In Proceedings of the 2021 International Conference on Management of Data, Xi’an, China, 20–25 June 2021; pp. 2366–2374. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. Active learning for graph embedding. arXiv 2017, arXiv:1705.05085. [Google Scholar]
- Gao, L.; Yang, H.; Zhou, C. Active discriminative network representation learning. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Sener, O.; Savarese, S. Active learning for convolutional neural networks: A core-set approach. arXiv 2017, arXiv:1708.00489. [Google Scholar]
- Joshi, A.J.; Porikli, F.; Papanikolopoulos, N. Multi-class active learning for image classification. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA; pp. 2372–2379. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S. Graph Neural Networks: A Review of Methods and Applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Chen, C.; Weiss, S.T.; Liu, Y.Y. Graph convolutional network-based feature selection for high-dimensional and low-sample size data. Bioinformatics 2023, 39, btad135. [Google Scholar] [CrossRef]
- Zhang, L.; Song, H.; Aletras, N. Node-feature convolution for graph convolutional networks. Pattern Recognit. 2022, 128, 108661. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef]
- Wu, F.; Souza, A.; Zhang, T. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Chen, M.; Wei, Z.; Huang, Z. Simple and deep graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Vienna, Austria, 13–18 July 2020; pp. 1725–1735. [Google Scholar]
- Gao, H.; Wang, Z.; Ji, S. Large-scale learnable graph convolutional networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1416–1424. [Google Scholar]
- Manessi, F.; Rozza, A.; Manzo, M. Dynamic graph convolutional networks. Pattern Recognit. 2020, 97, 107000. [Google Scholar] [CrossRef]
- Yao, L.; Mao, C.; Luo, Y. Graph convolutional networks for text classification. Proc. AAAI Conf. Artif. Intell. 2019, 33, 7370–7377. [Google Scholar] [CrossRef]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the 15th International Conference, ESWC 2018, Heraklion, Greece, 3–7 June 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 593–607. [Google Scholar]
- Ma, Y.; Wang, S.; Aggarwal, C.C. Graph convolutional networks with eigenpooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 723–731. [Google Scholar]
- Yu, P.; Fu, C.; Yu, Y. Multiplex heterogeneous graph convolutional network. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 2377–2387. [Google Scholar]
- Gao, C.; Zhu, J.; Zhang, F. A novel representation learning for dynamic graphs based on graph convolutional networks. IEEE Trans. Cybern. 2022, 53, 3599–3612. [Google Scholar] [CrossRef] [PubMed]
- Gan, J.; Hu, R.; Mo, Y. Multigraph fusion for dynamic graph convolutional network. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 196–207. [Google Scholar] [CrossRef]
- Xie, Y.; Lv, S.; Qian, Y. Active and semi-supervised graph neural networks for graph classification. IEEE Trans. Big Data 2022, 8, 920–932. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, L.; Yao, J. Learnable graph convolutional network and feature fusion for multi-view learning. Inf. Fusion 2023, 95, 109–119. [Google Scholar] [CrossRef]
- Kurniawan, H.; Mambo, M. Homomorphic Encryption-Based Federated Privacy Preservation for Deep Active Learning. Entropy 2022, 24, 1545. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, S.; Xia, J.Z. Batchcrypt: Efficient homomorphic encryption for cross-silo federated learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 2020), Boston, MA, USA, 15–17 July 2020. [Google Scholar]
- Angulo, E.; Marquez, J.; Villanueva-Polanco, R. Training of Classification Models via Federated Learning and Homomorphic Encryption. Sensors 2023, 23, 1966. [Google Scholar] [CrossRef]
- Awan, S.; Luo, B.; Li, F.J. Contra: Defending against poisoning attacks in federated learning. In Proceedings of the Computer Security—ESORICS 2021: 26th European Symposium on Research in Computer Security, Darmstadt, Germany, 4–8 October 2021; Part I 26. Springer International Publishing: Cham, Switzerland, 2021; pp. 455–475. [Google Scholar]
- Gao, X.Y.; Gong, N.Z.Q. Mpaf: Model poisoning attacks to federated learning based on fake clients. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 3396–3404. [Google Scholar]
- Zhou, X.C.; Xu, M.; Wu, Y.M.; Zheng, N. Deep model poisoning attack on federated learning. Future Internet 2021, 13, 73. [Google Scholar] [CrossRef]
- Almutairi, A.; Barnawi, A. A comprehensive analysis of model poisoning attacks in federated learning for autonomous vehicles: A benchmark study. Results Eng. 2024, 24, 103295. [Google Scholar] [CrossRef]
- Kolasa, D.; Pilch, K.; Mazurczyk, M. Federated learning secure model: A framework for malicious clients detection. SoftwareX 2024, 27, 101765. [Google Scholar] [CrossRef]
- Ma, H.; Li, Q.; Zheng, Y.F.; Zhang, Z.; Liu, X.N. MUD-PQFed: Towards Malicious User Detection on model corruption in Privacy-preserving Quantized Federated learning. Comput. Secur. 2023, 133, 103406. [Google Scholar] [CrossRef]
- Xia, G.M.; Chen, J.; Yu, C.D. Poisoning Attacks in Federated Learning: A Survey. IEEE Access 2023, 11, 10708–10722. [Google Scholar] [CrossRef]
- Feng, Y.; Gao, Y.; Hou, Y. A survey of security threats in federated learning. Complex Intell. Syst. 2025, 11, 165. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).