Investigation of General Sombor Index for Optimal Values in Bicyclic Graphs, Trees, and Unicyclic Graphs Using Well-Known Transformations
Abstract
1. Introduction
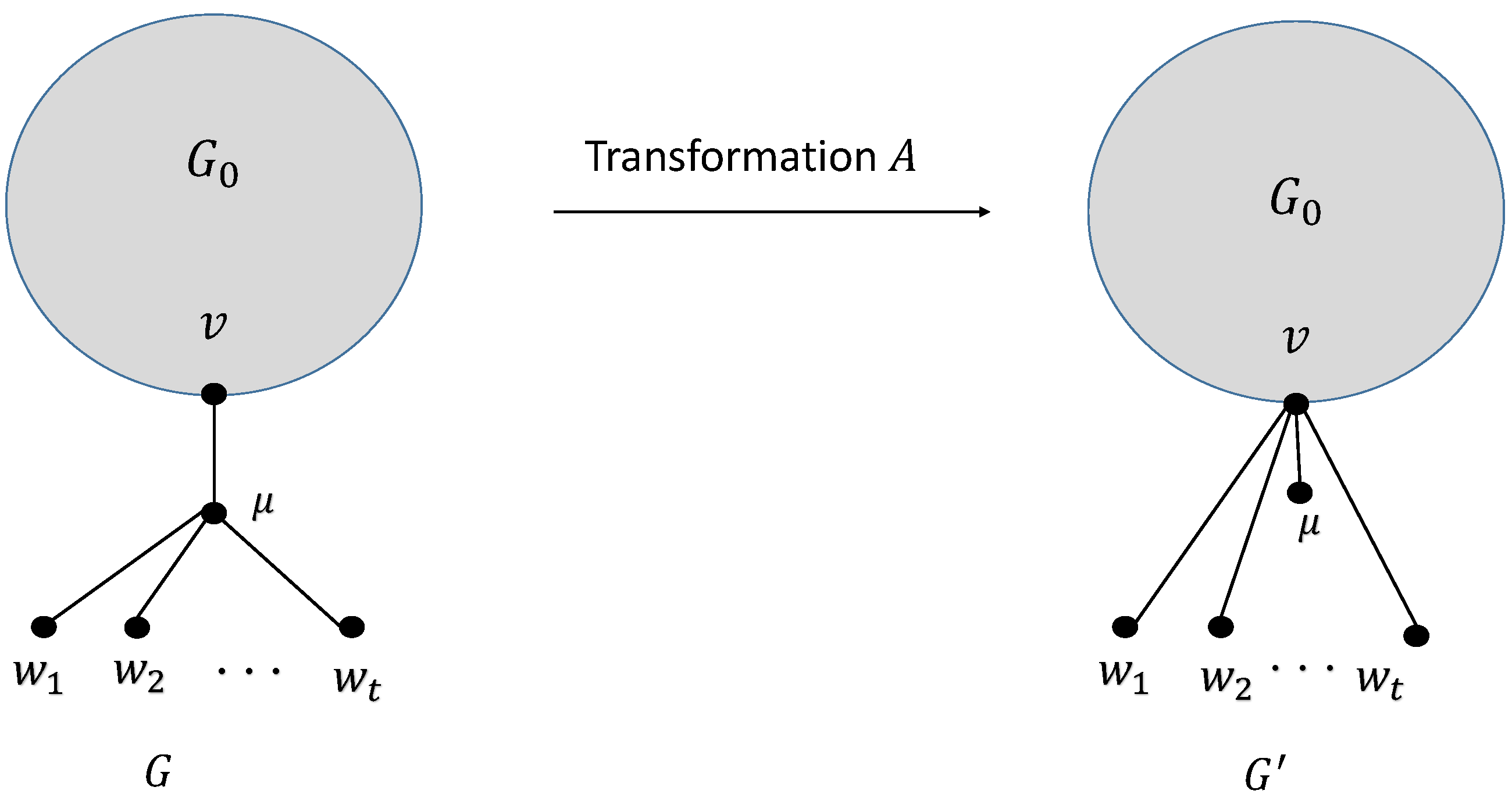
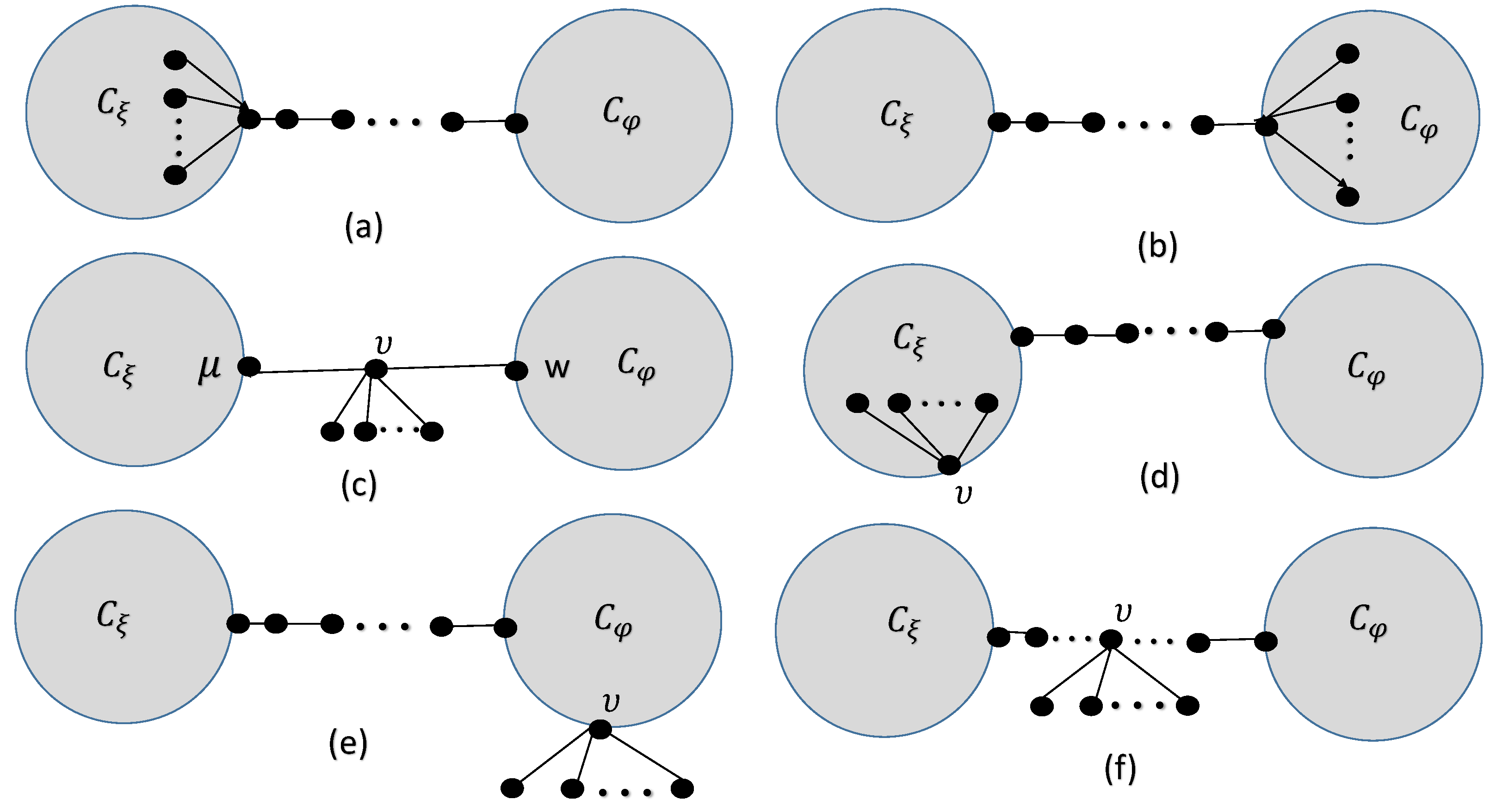
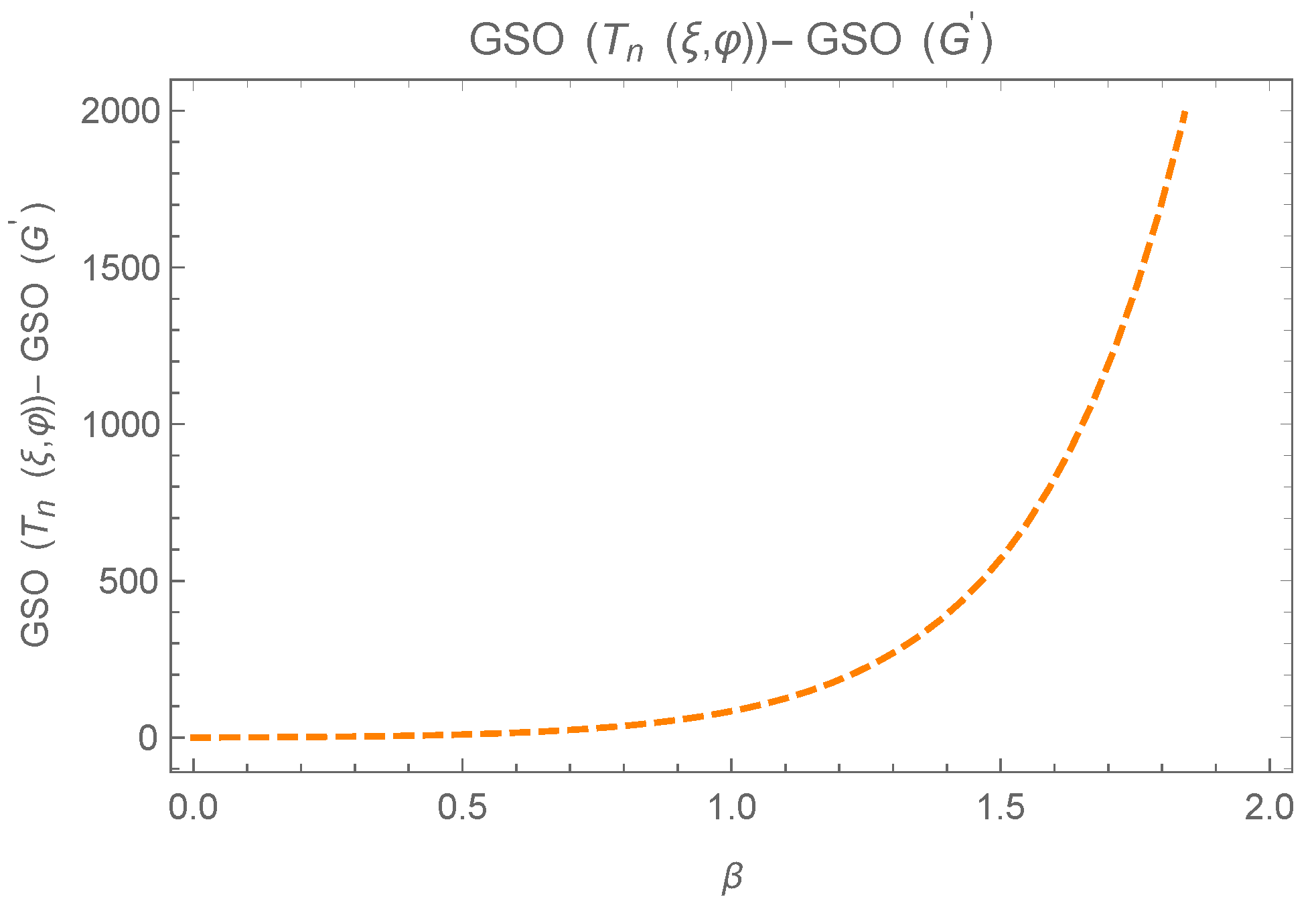
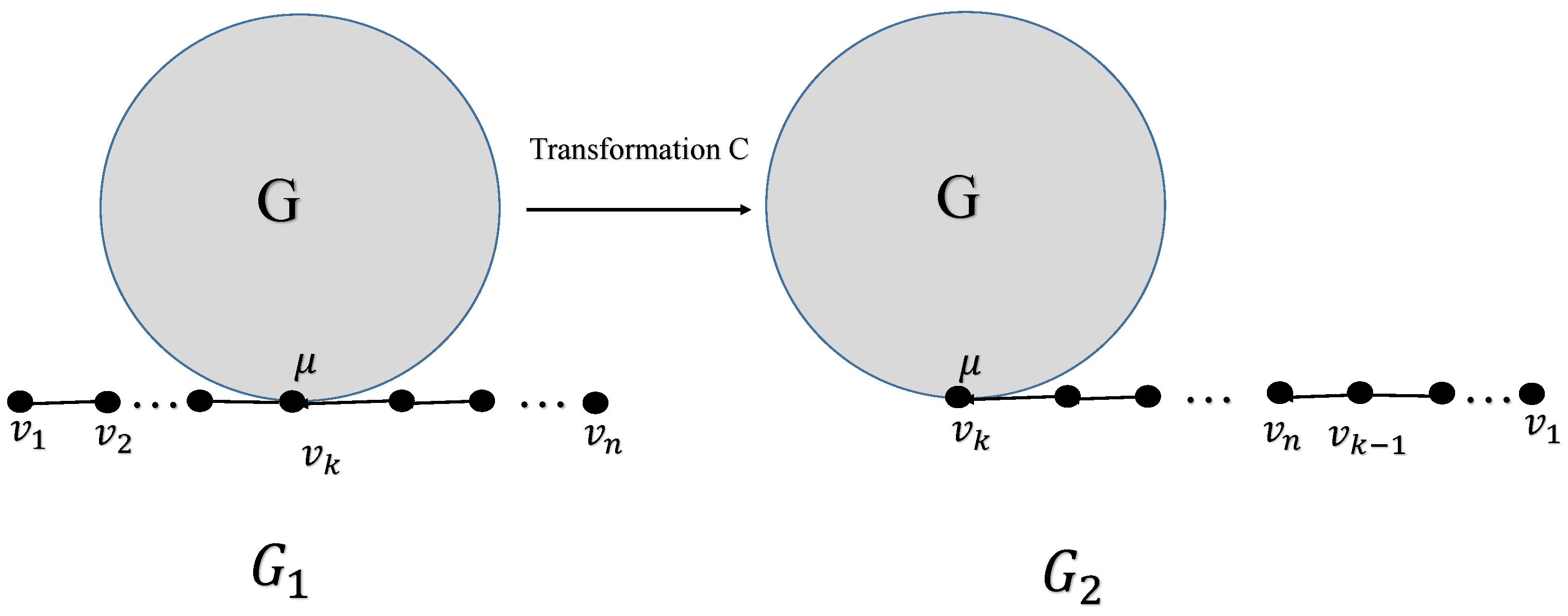
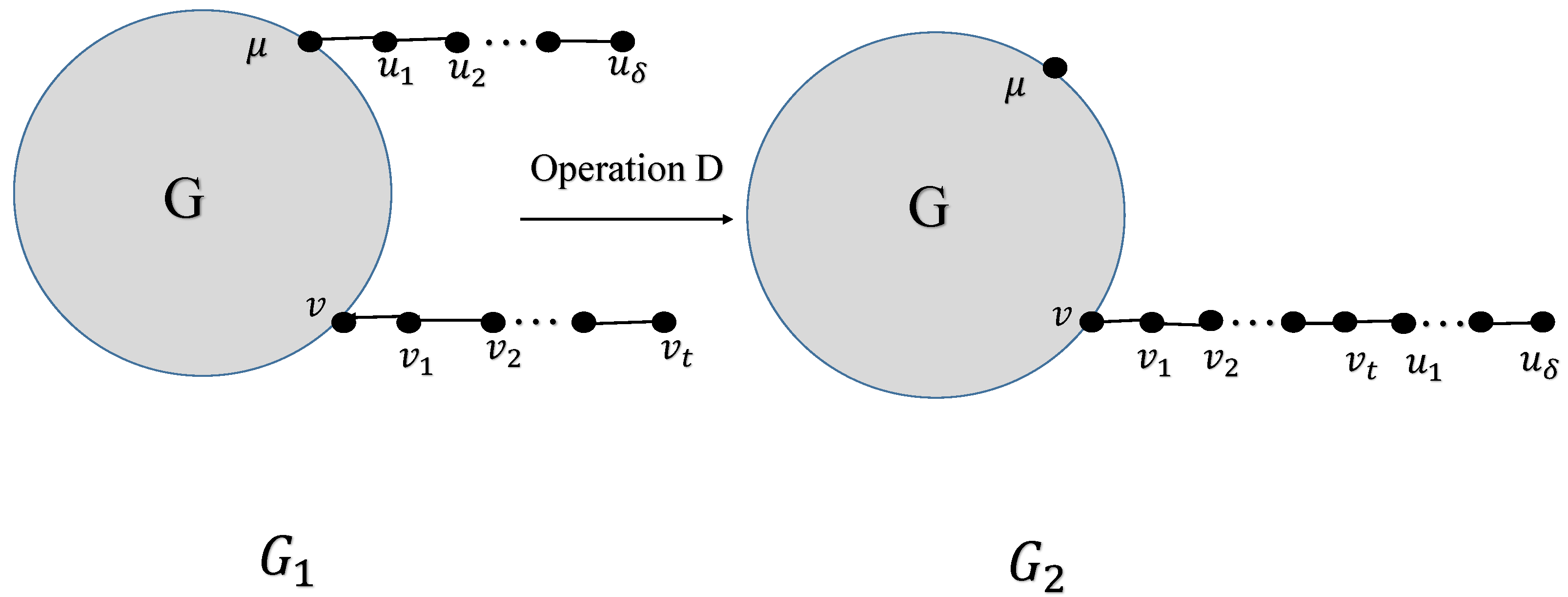
2. Transformation for Greatest Value of Generalized Sombor Index
- Case 1. Consider G, if v and are not connected directly by an edge, then for we haveConsider , then is given byTaking , then is in the followingSuppose and , we consider the followingNow , if the following holdsIf then , we have the following for this
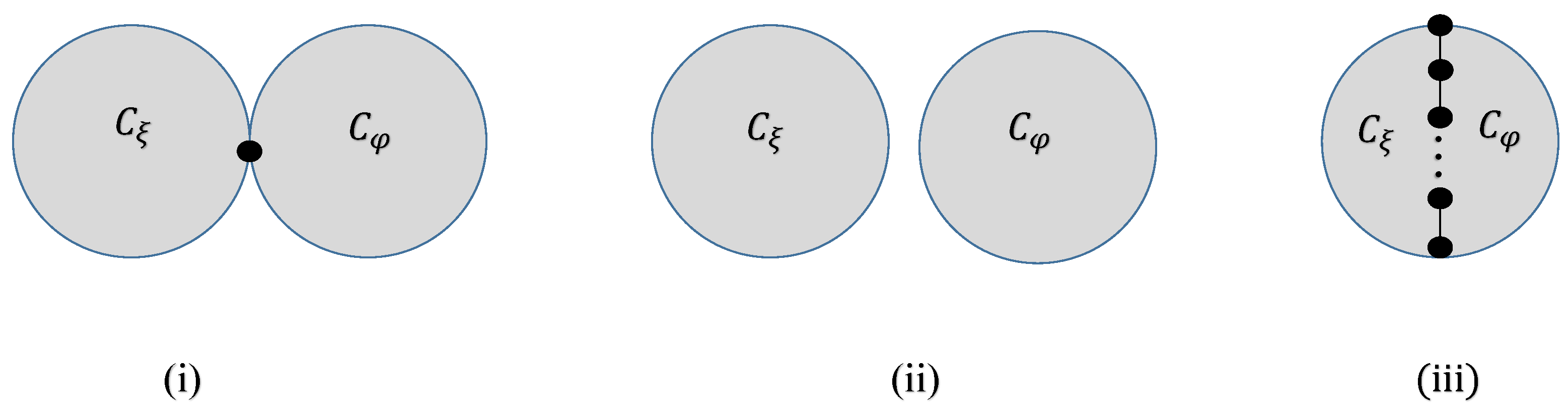
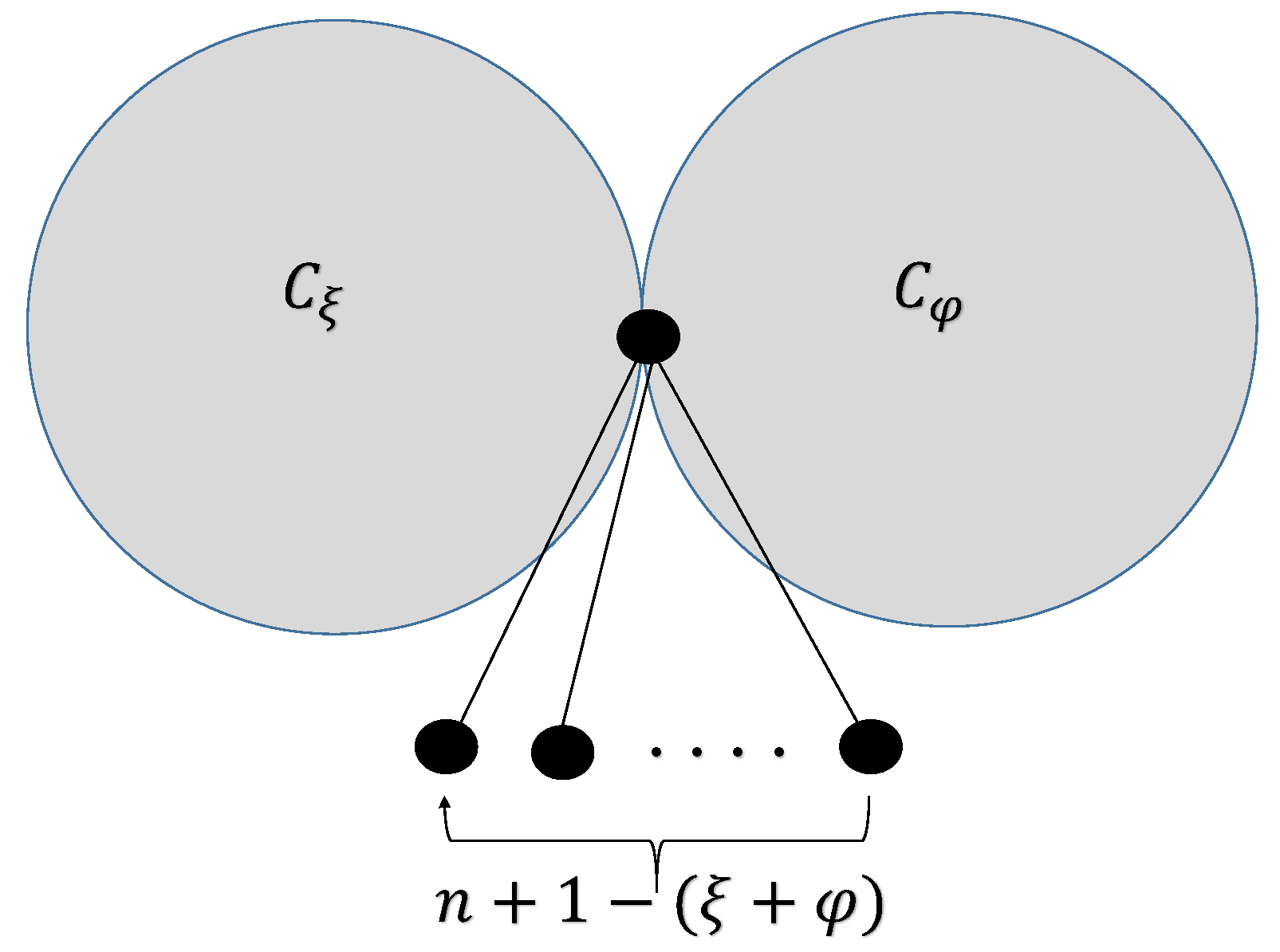
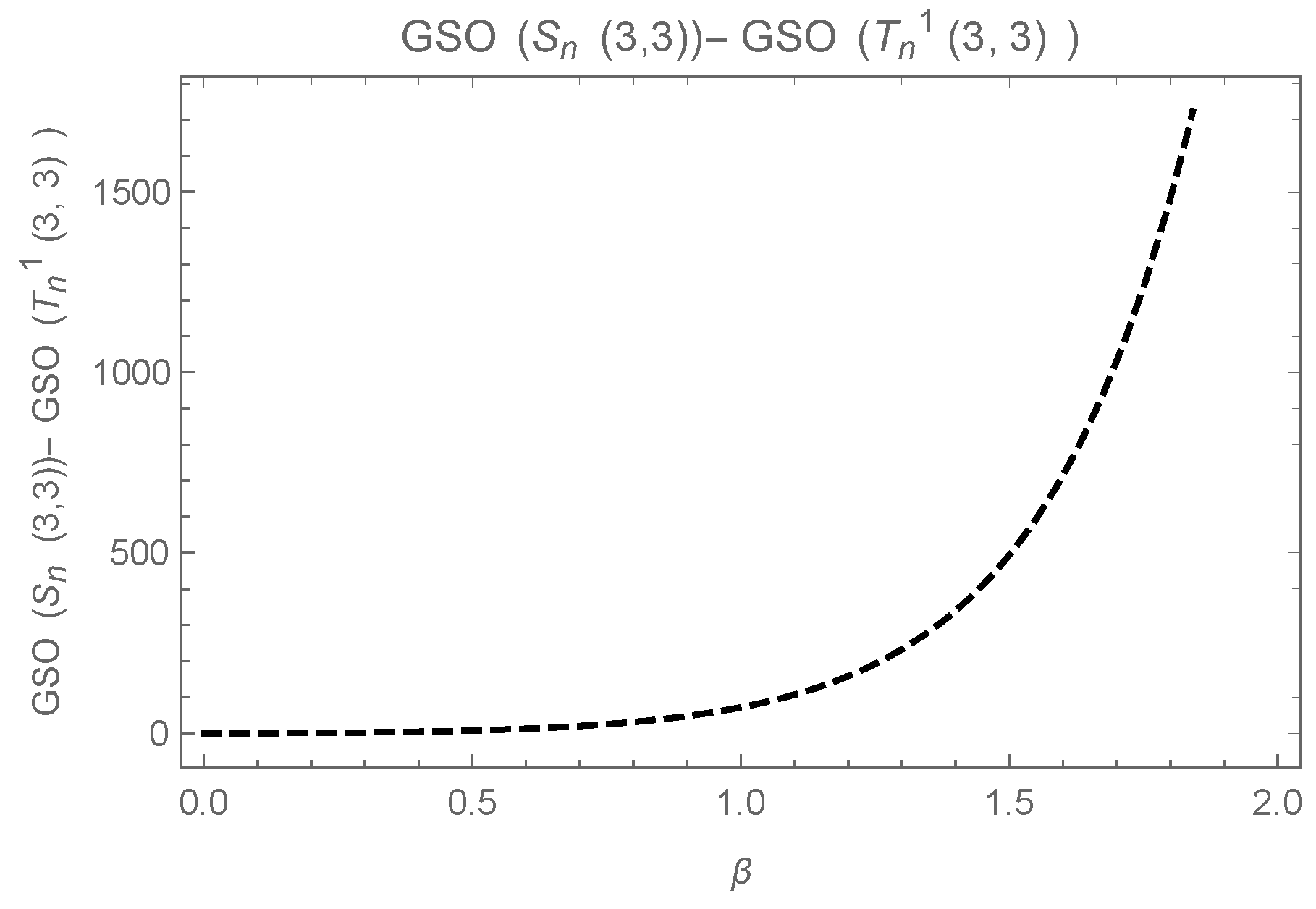
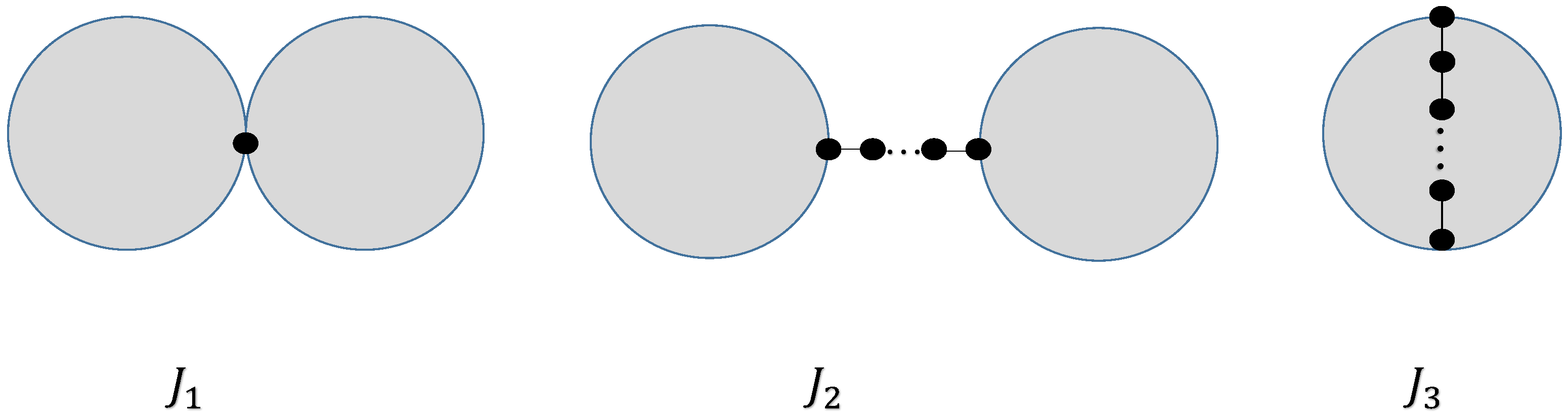
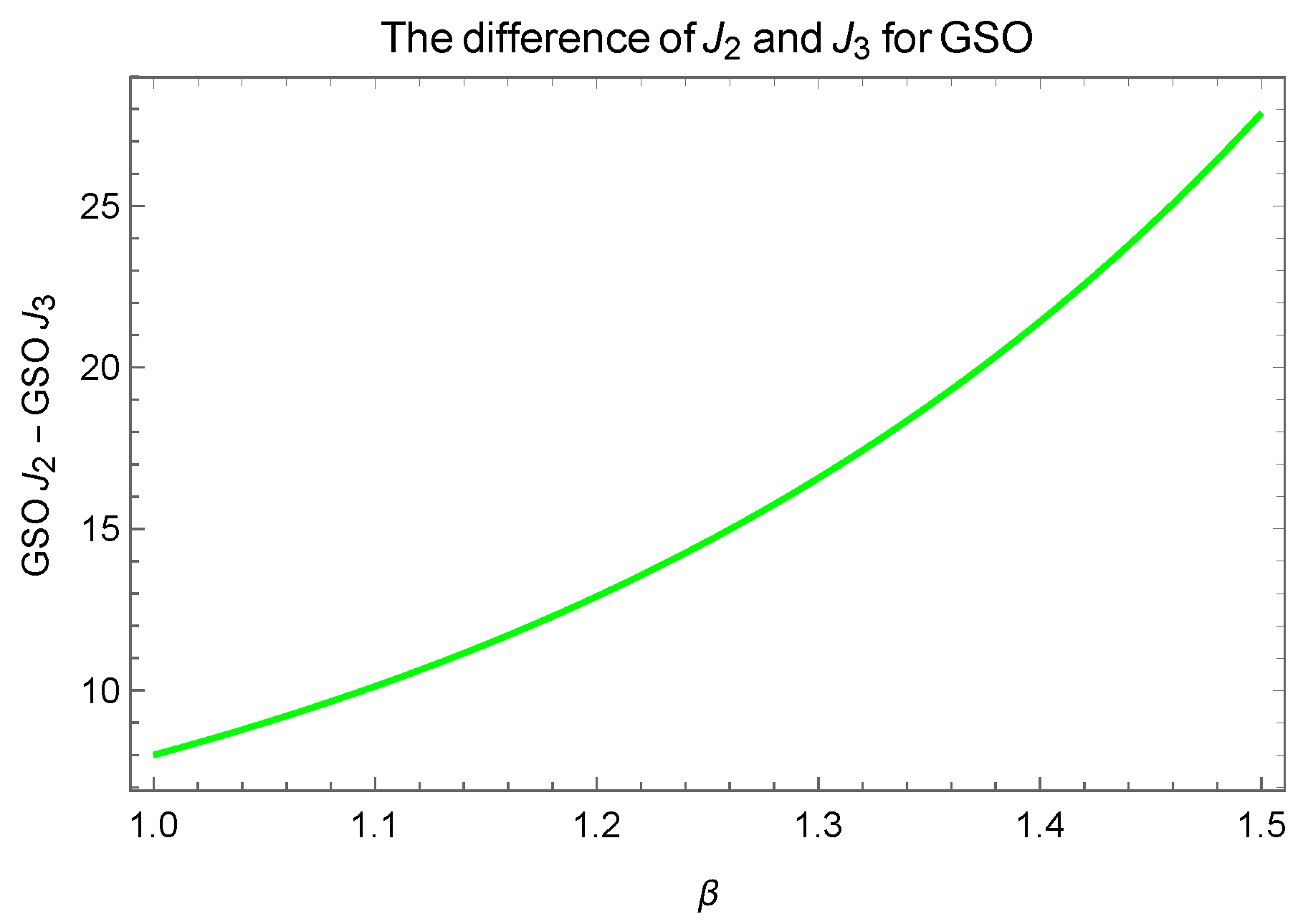
3. for Greatest Values
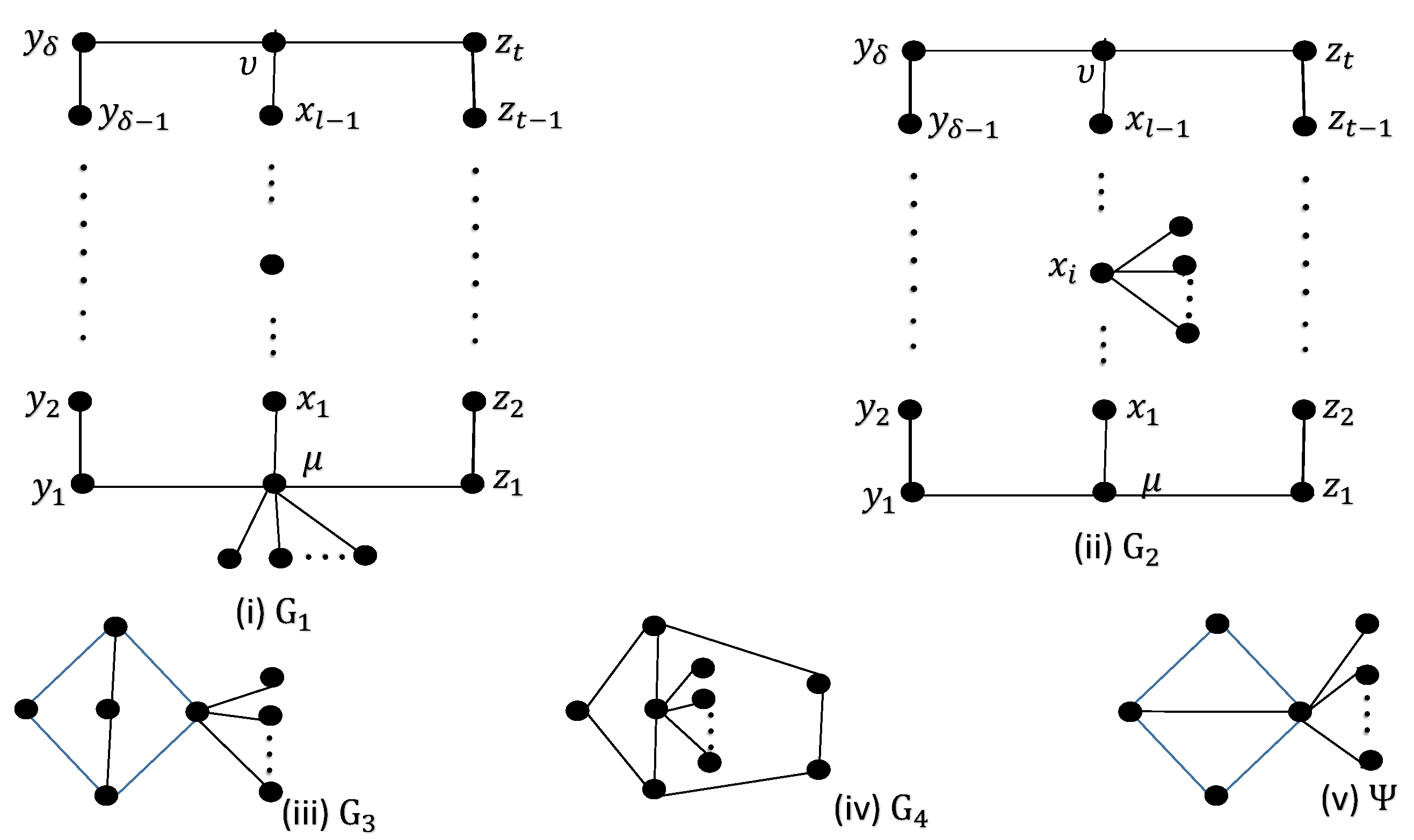
- (I)
- consists of , where and share one vertex in common.
- (II)
- consists of , where and share no common vertex.
- (III)
- contains , where the cycles and are connected by a common path of length l.
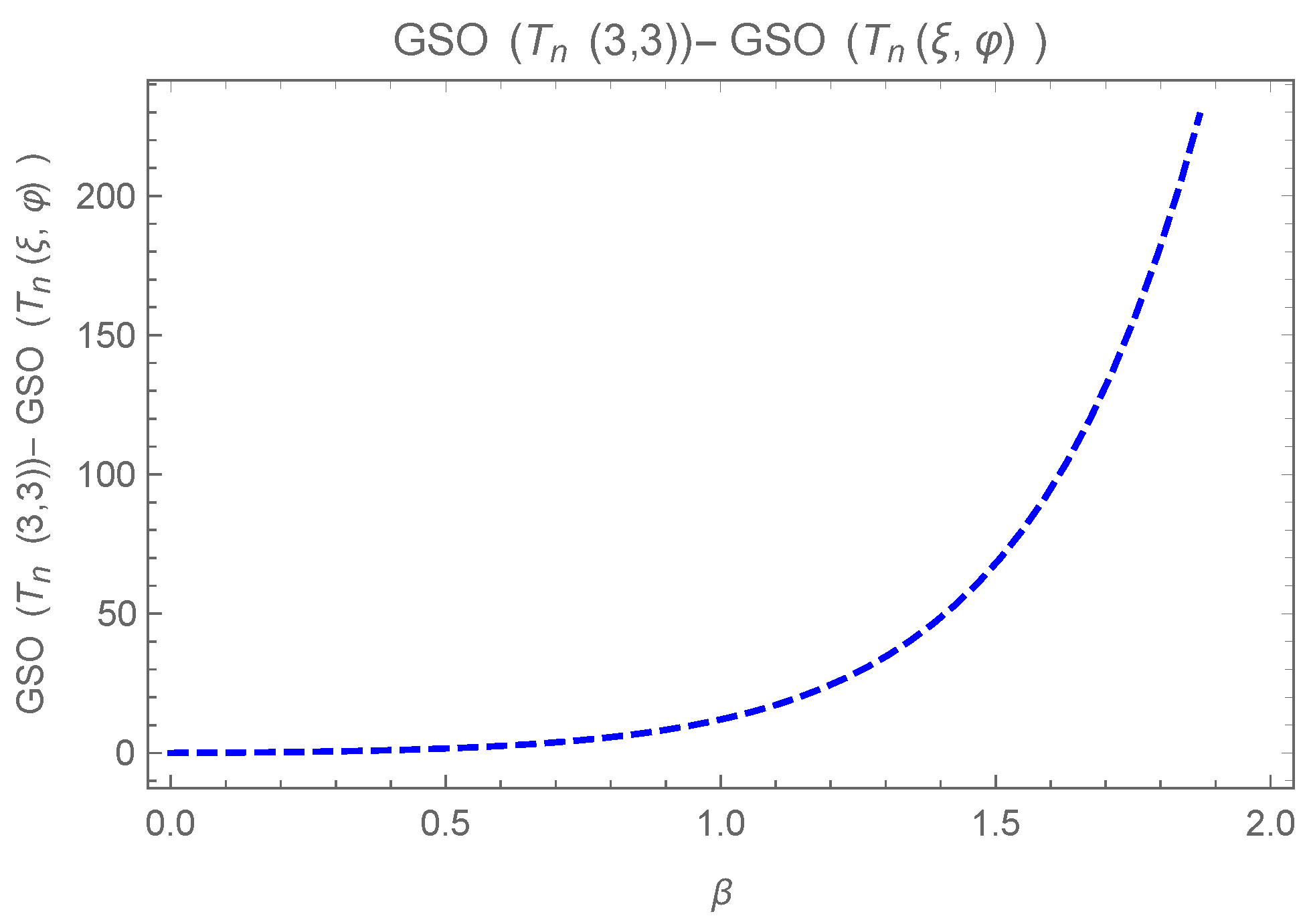
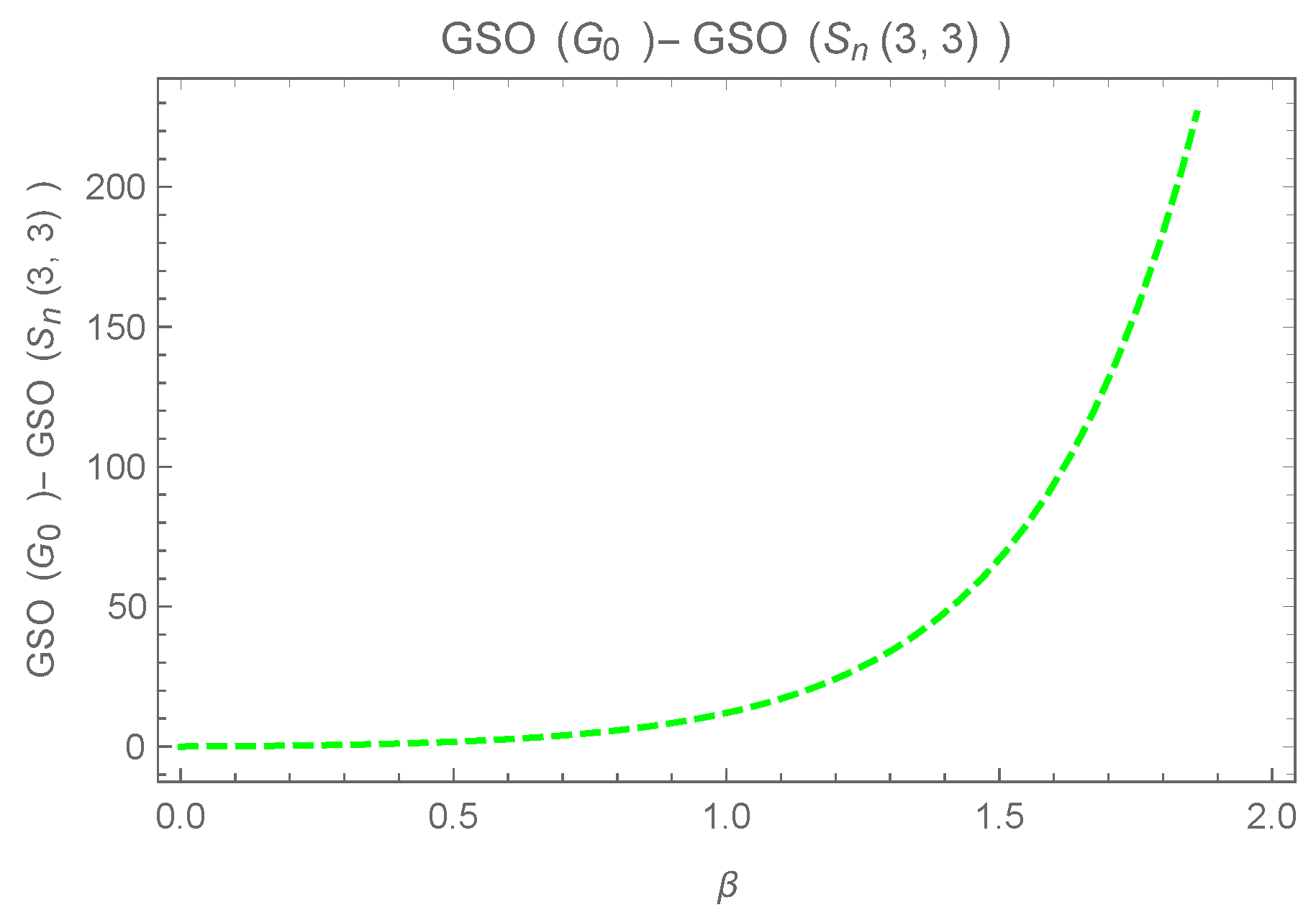
4. Greatest in the Family
- Case 1. Consider that v and are not adjacent, the following is consideredfor , is considered in the followingConsider the following differenceHere, equality holds iff .
- Case 2. Consider that v and are connected directly by an edge in . Then,The following difference is consideredWhile equality holds iff .
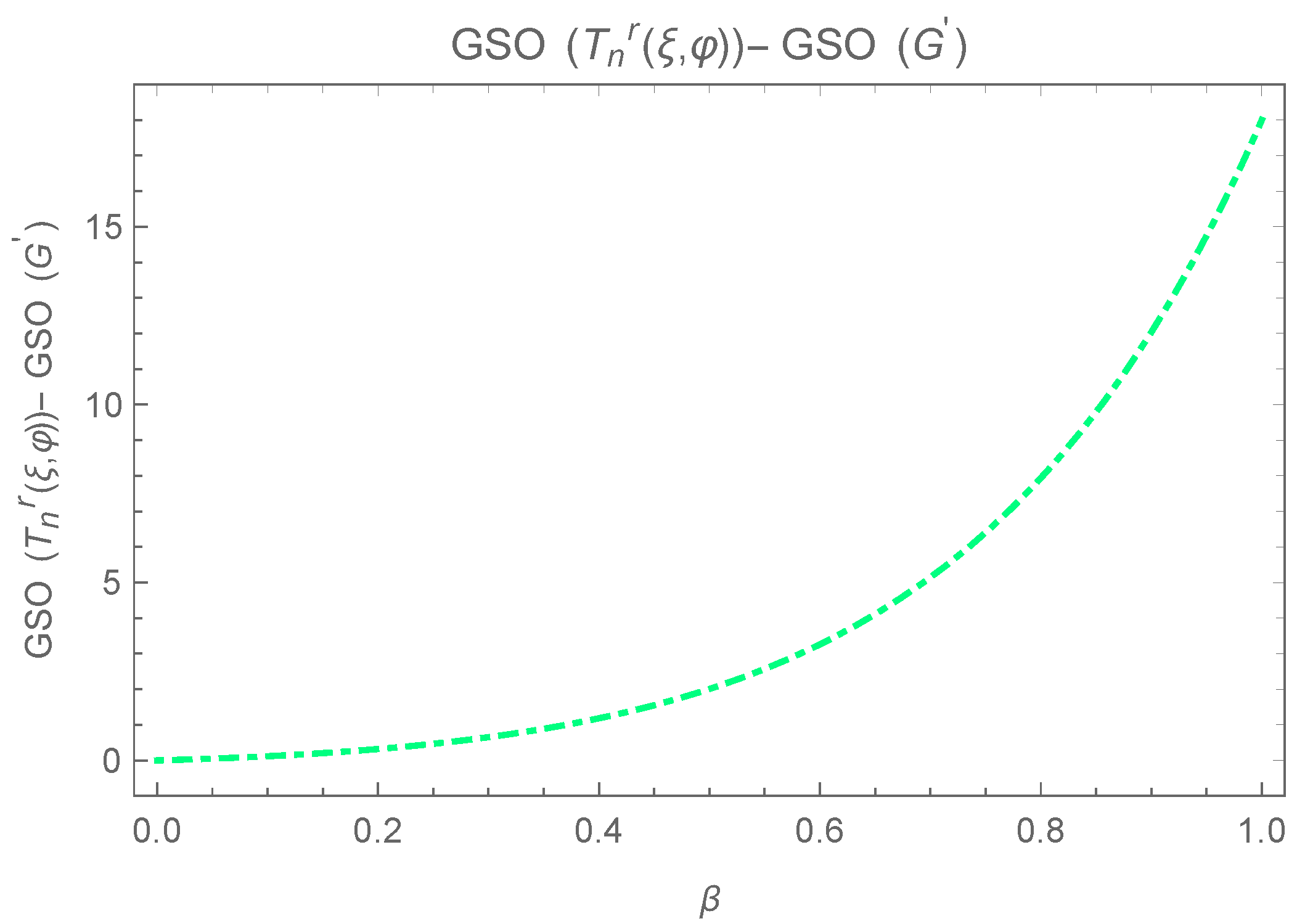
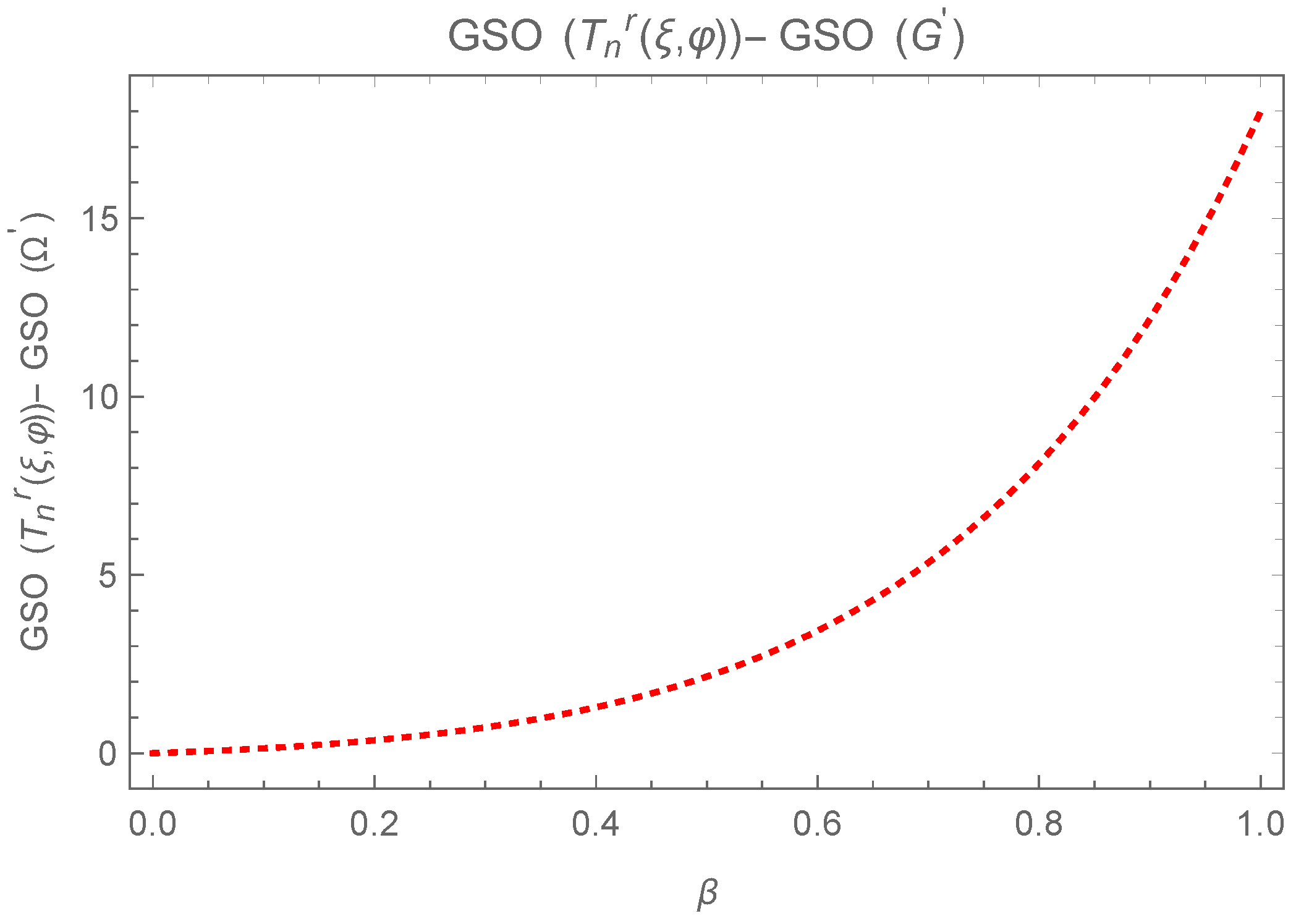
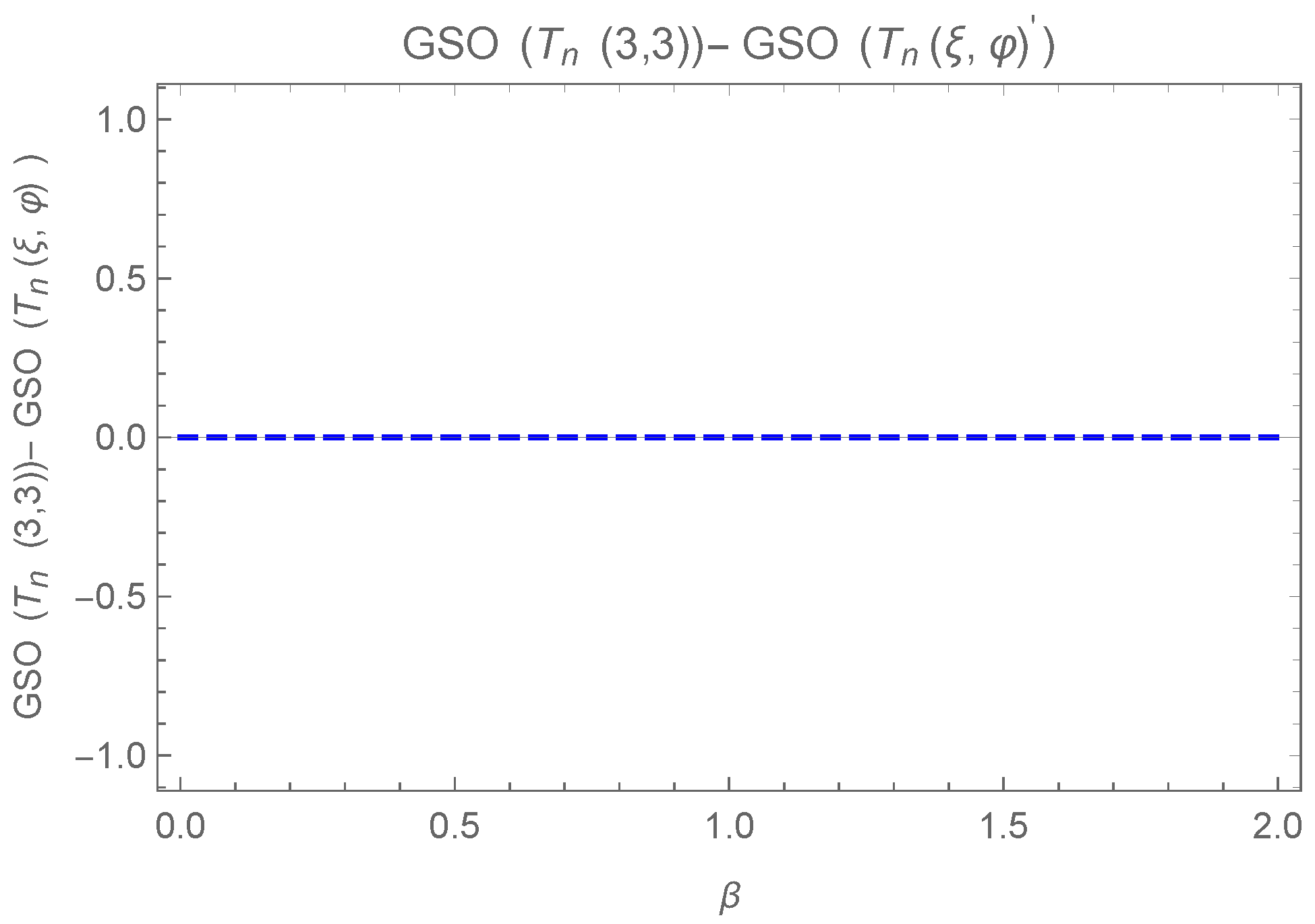
5. for Greatest Values in
6. Greatest in
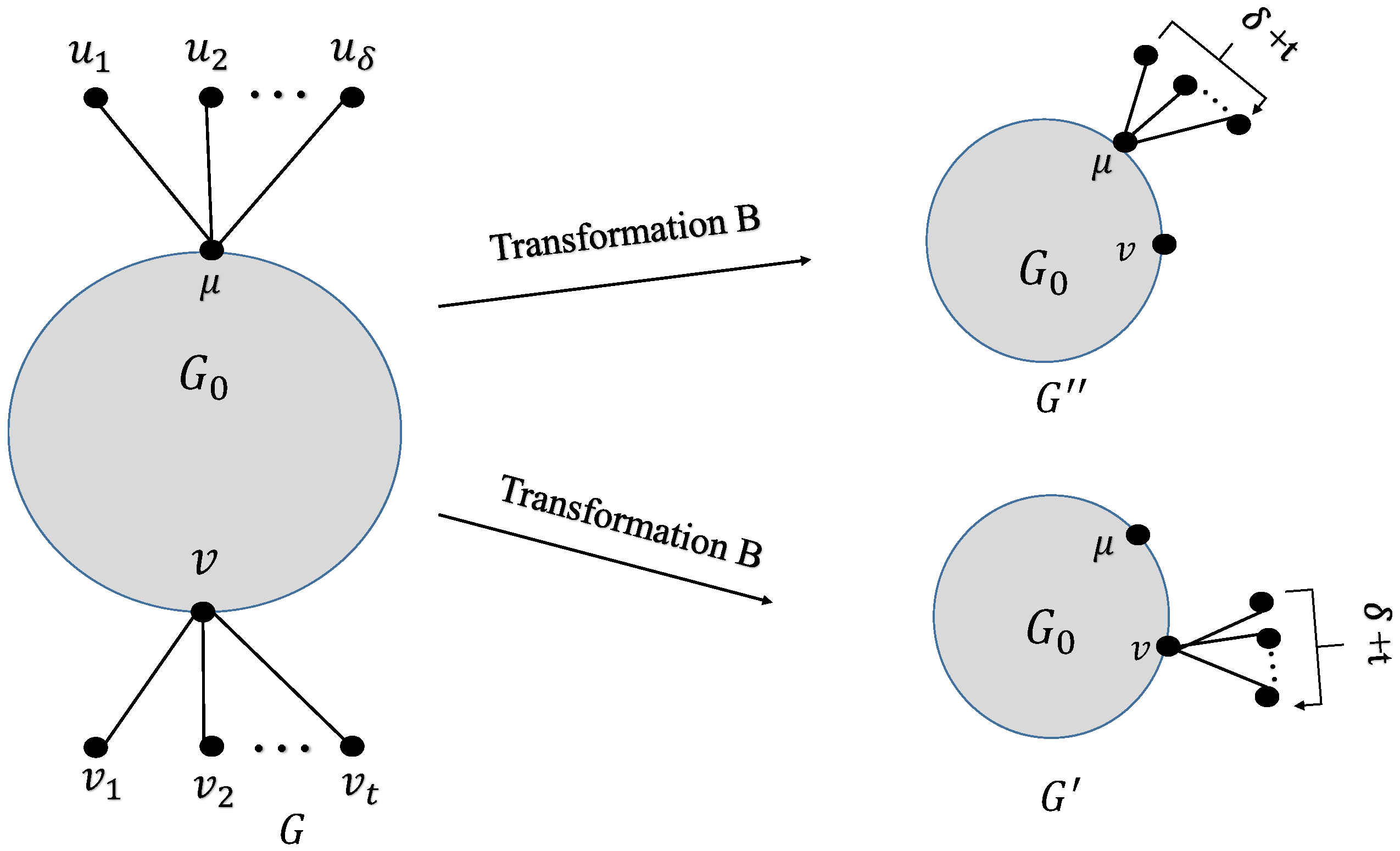
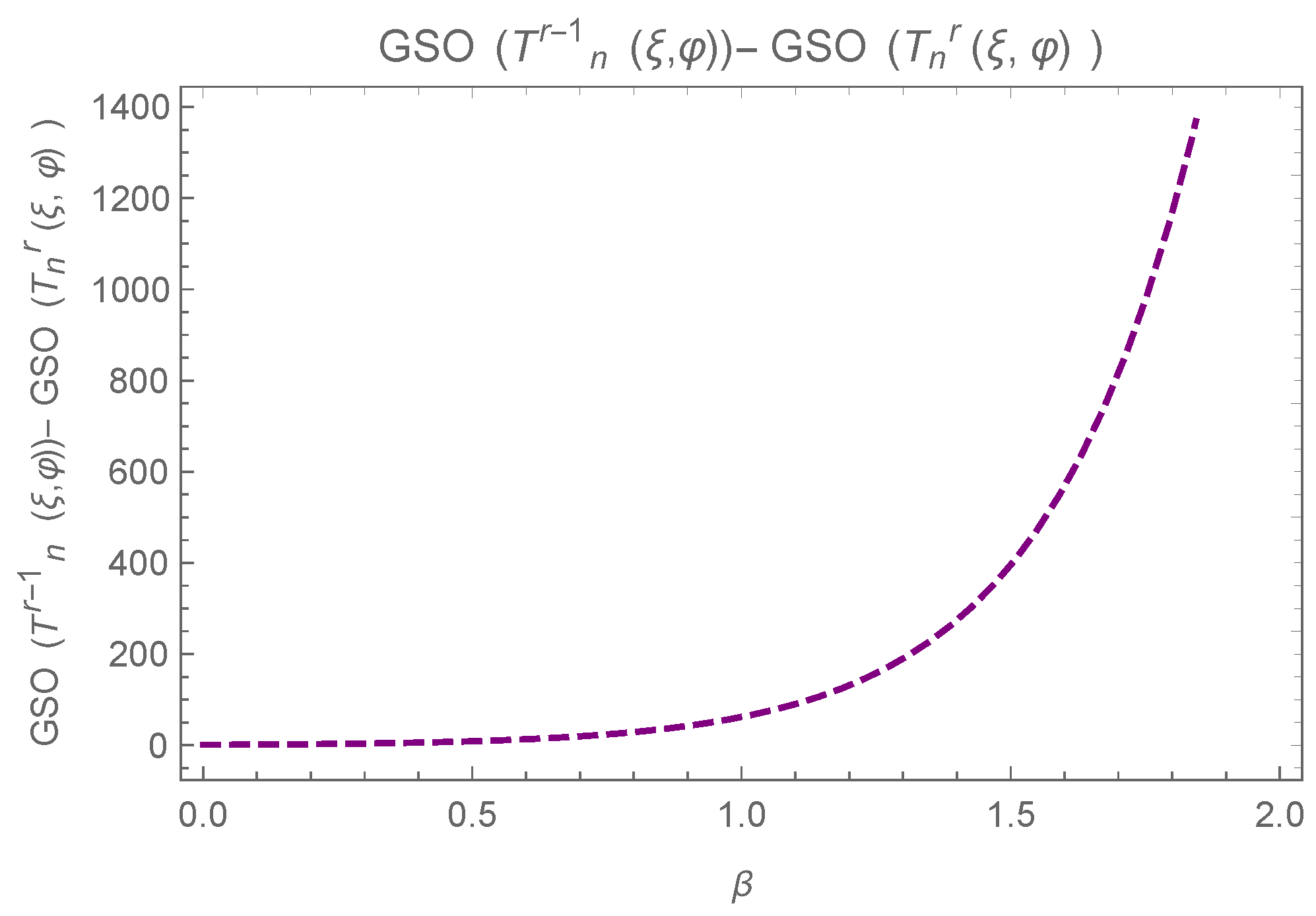
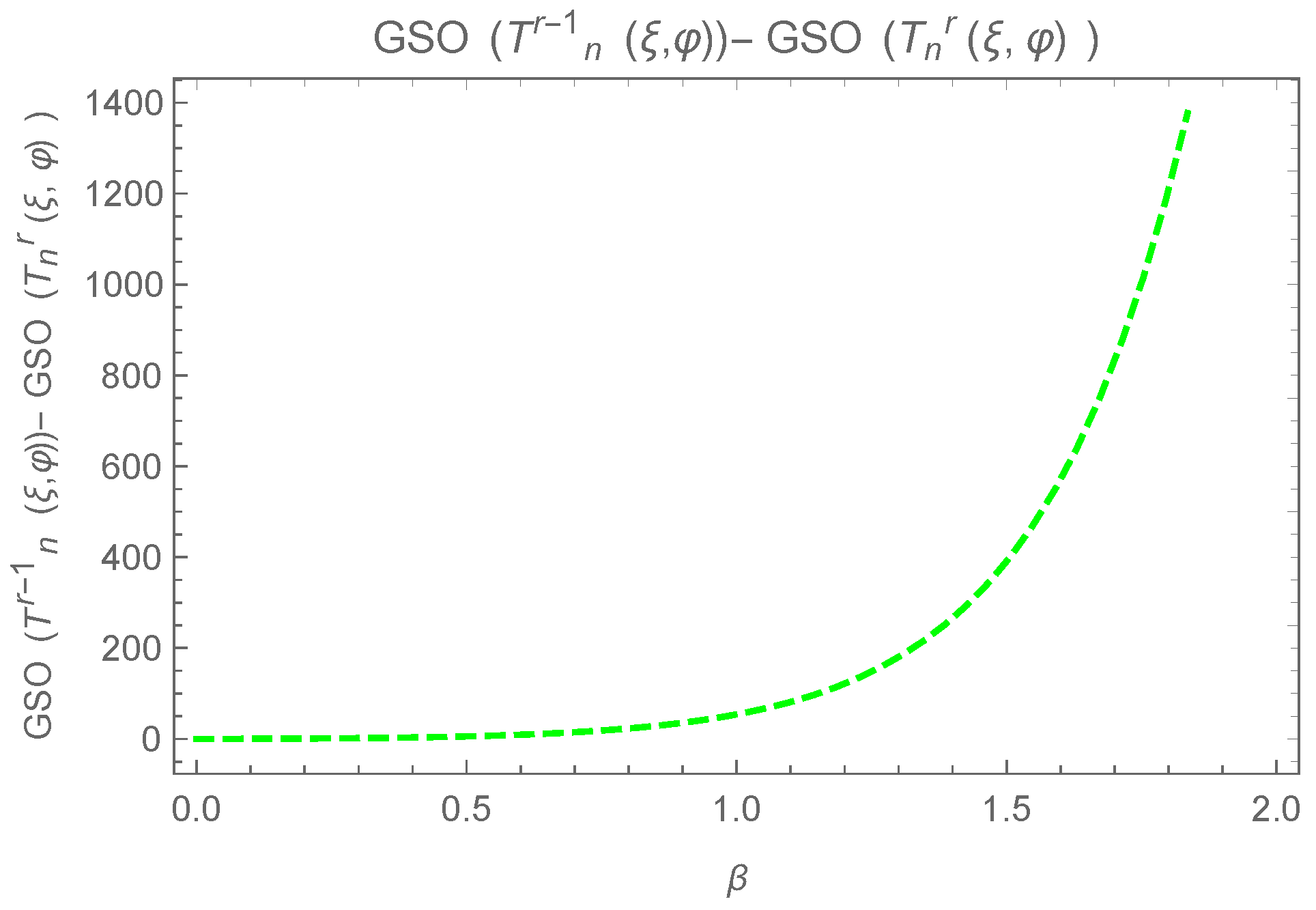
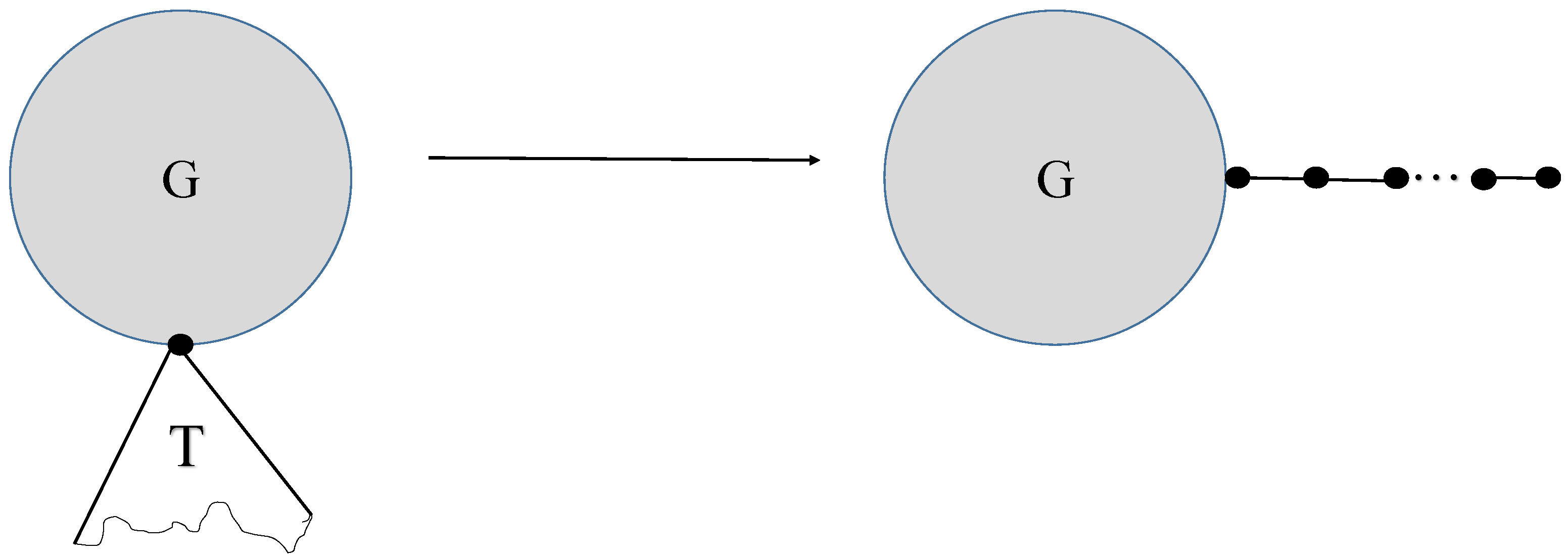
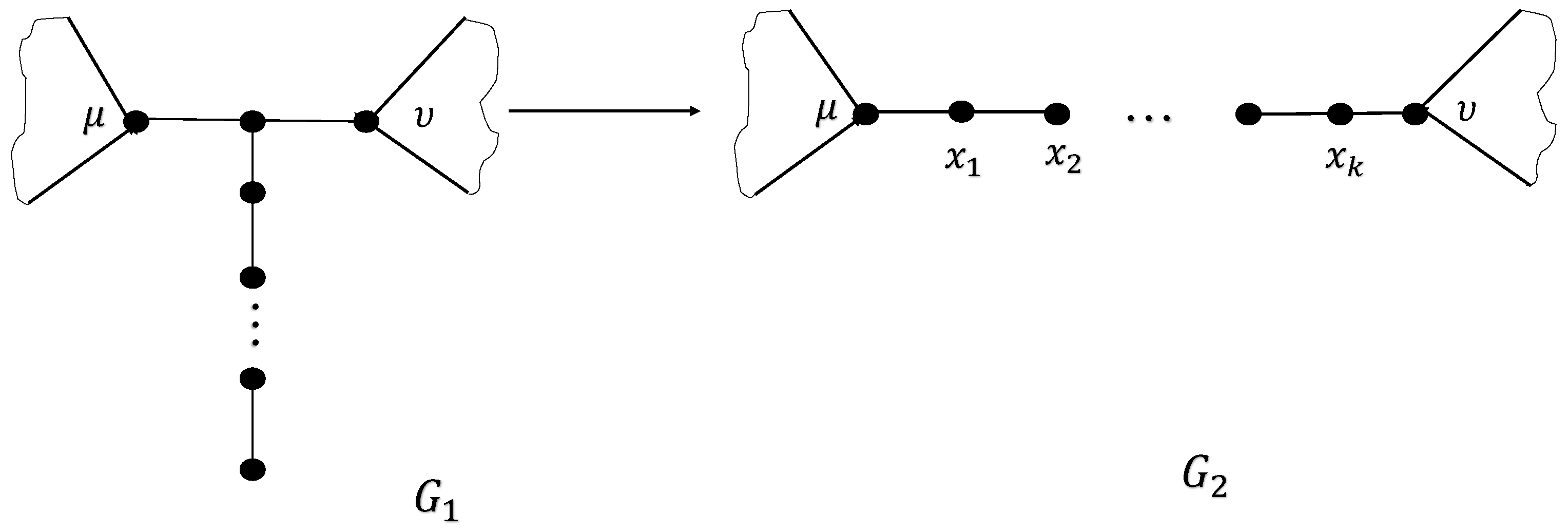
7. Transformation for Decreasing
- Case 1: If and .
- In the considered case, the following value is considered:for is given byis considered in the following:Comparing terms of the above last inequality, we obtain .
- Case 2: If and .The following value is considered:for is given byThe difference of and is given in the followingComparing terms of the above last inequality we obtain that .
- Case 3: Consider and .The following value is considered:for is given in the following:The difference of and is considered in the following:Term by term comparison provided that , hence .
- Case 4: Consider and .In the desired case, the following value is consideredis considered in the following:The difference of and is considered in the following:Term by term comparison provided that . Hence it follows that .
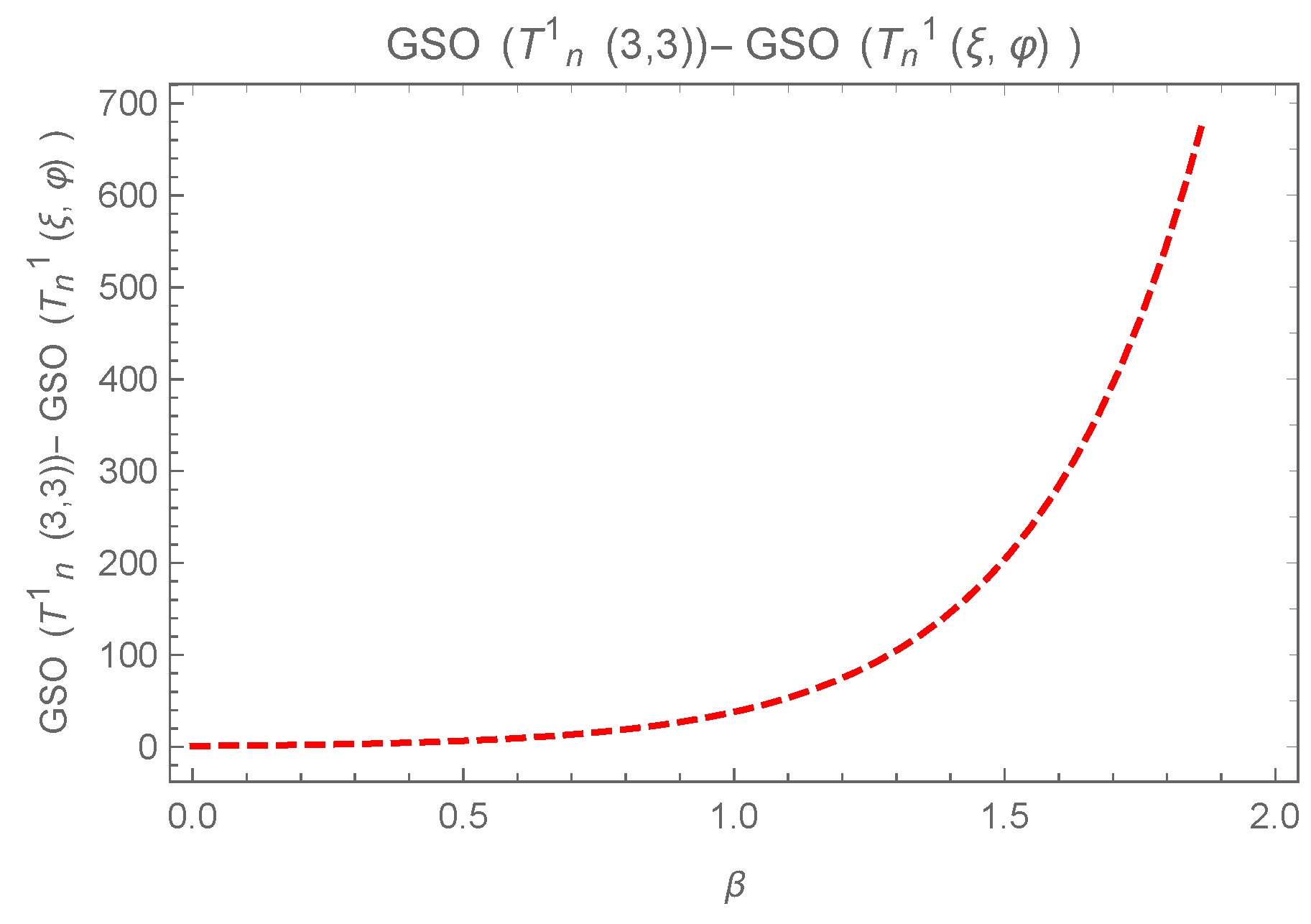
- (i)
- For , we have ;
- (ii)
- For and , we have .
- Case 1. For and .In the considered case, for we have the following:is considered in the following:The difference of and is considered in the followingHence .
- Case 2. If and .In the considered case, we have in the followingis considered in the following:is considered in the following:Hence .
- Case 3. If and .In the considered case, is given byThe value of is considered belowis considered in the following:Here we have .
- Case 4. If and .In the considered case, is given byis considered in the following:The following difference is consideredHence and .(ii). For and , if v and are adjacent then the following is considered:is considered below.is considered in the following:The above inequality provided that .If v and are adjacent, thenFor , it follows thatis considered in the following:Hence and .
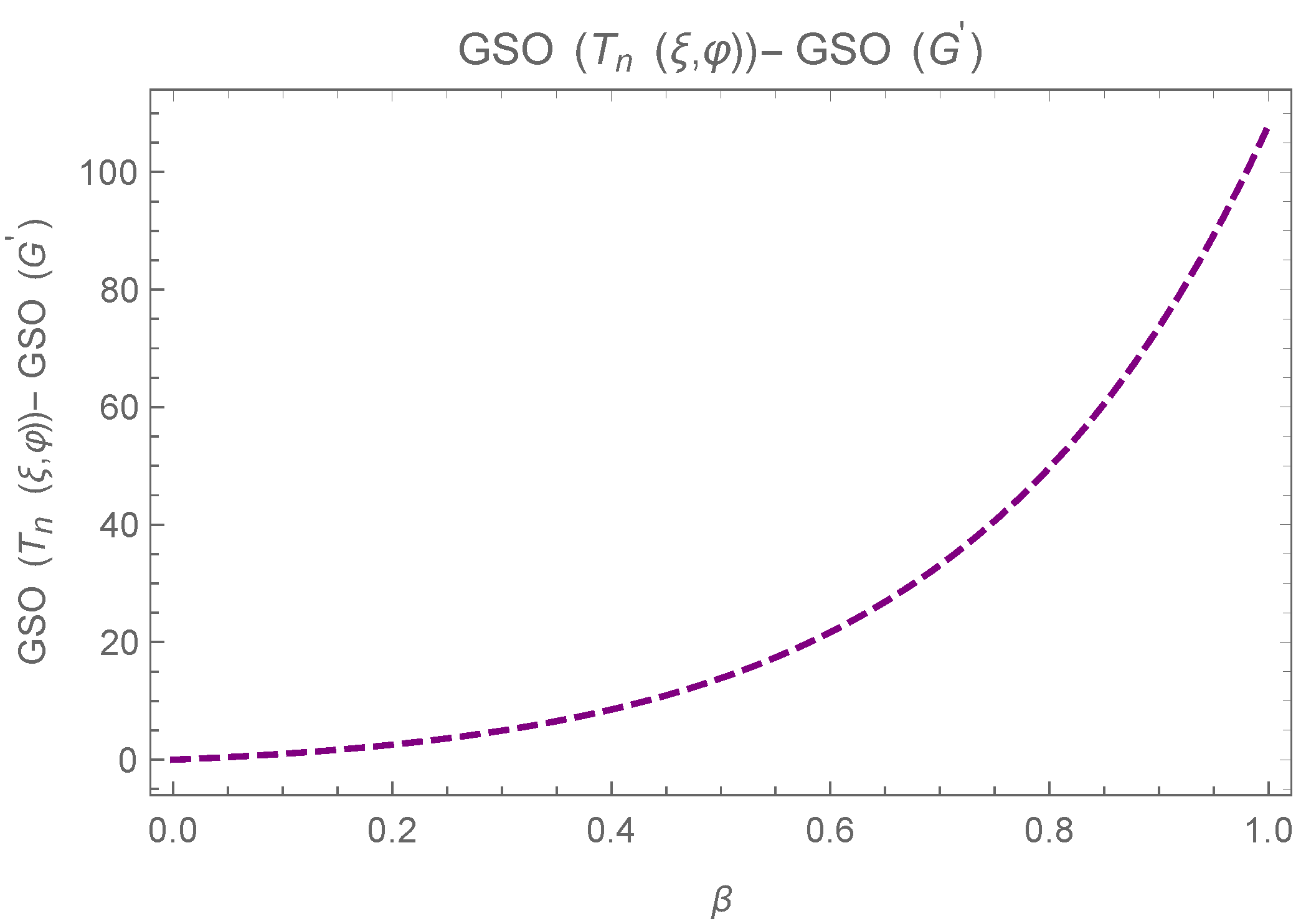
8. The Smallest in Trees, Unicyclic, and Bicyclic Graphs
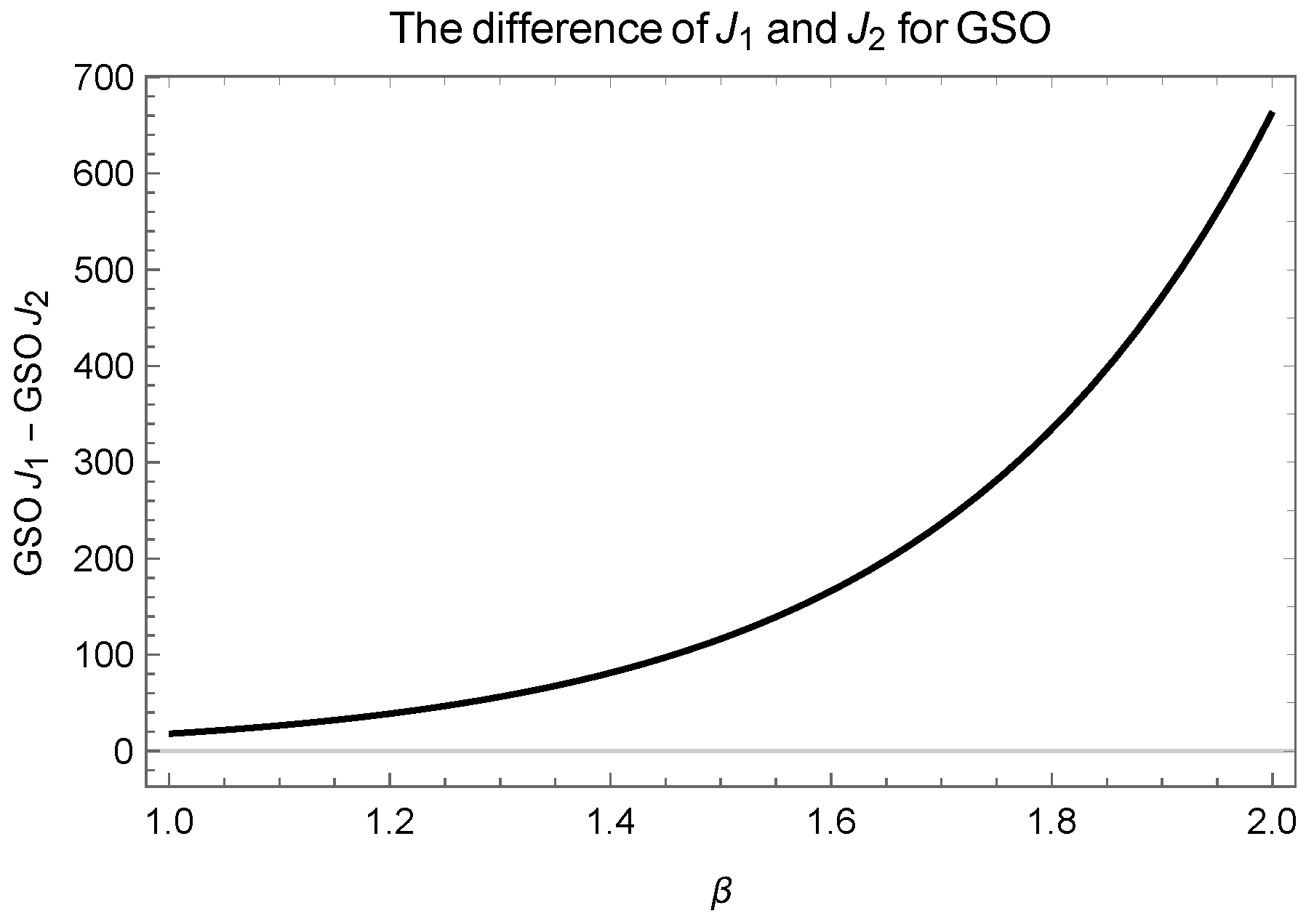
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Balakrishnan, V.K. Schaum’s Outline of Theory and Problems of Graph Theory; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Khan, M.Y.; Ali, G.; Popa, I.L. Optimization of General Power-Sum Connectivity Index in Uni-Cyclic Graphs, Bi-Cyclic Graphs and Trees by Means of Operations. Axioms 2024, 13, 840. [Google Scholar] [CrossRef]
- Khan, M.Y.; Ali, G.; Popa, I.L. Optimization in Symmetric Trees, Unicyclic Graphs, and Bicyclic Graphs with Help of Mappings Using Second Form of Generalized Power-Sum Connectivity Index. Symmetry 2025, 17, 122. [Google Scholar] [CrossRef]
- Diudea, M.V.; Gutman, I.; Jantschi, L. Molecular Topology; Nova Science Publishers: Huntington, NY, USA, 2001. [Google Scholar]
- Mahasinghe, A.C.; Erandi, K.K.W.H.; Perera, S.S.N. Optimizing Wiener and Randić Indices of Graphs. Adv. Oper. Res. 2020, 2020, 3139867. [Google Scholar] [CrossRef]
- Gutman, I.; Mohar, B. The quasi-Wiener and the Kirchhoff indices coincide. J. Chem. Inf. Comput. Sci. 1996, 36, 982–985. [Google Scholar] [CrossRef]
- Otte, E.; Rousseau, R. Social network analysis: A powerful strategy, also for the information sciences. J. Inf. Sci. 2002, 28, 441–453. [Google Scholar] [CrossRef]
- Imran, M.; Hayat, S.; Mailk, M.Y.H. On topological indices of certain interconnection networks. Appl. Math. Comput. 2014, 244, 936–951. [Google Scholar] [CrossRef]
- Kier, L.B. Indexes of molecular shape from chemical graphs. Med. Res. Rev. 1987, 7, 417–440. [Google Scholar] [CrossRef] [PubMed]
- Camarda, K.V.; Maranas, C.D. Optimization in polymer design using connectivity indices. Ind. Eng. Chem. Res. 1999, 38, 1884–1892. [Google Scholar] [CrossRef]
- Matamala, A.R.; Estrada, E. Generalised topological indices: Optimisation methodology and physico-chemical interpretation. Chem. Phys. Lett. 2005, 410, 343–347. [Google Scholar] [CrossRef]
- Preuß, M.; Dehmer, M.; Pickl, S.; Holzinger, A. On terrain coverage optimization by using a network approach for universal graph-based data mining and knowledge discovery. In Brain Informatics and Health, Proceedings of the International Conference, BIH 2014, Warsaw, Poland, 11–14 August 2014; Proceedings; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 564–573. [Google Scholar]
- Che, Z.; Chen, Z. Lower and upper bounds of the forgotten topological index. MATCH Commun. Math. Comput. Chem. 2016, 76, 635–648. [Google Scholar]
- Monsalve, J.; Rada, J. Sharp upper and lower bounds of VDB topological indices of digraphs. Symmetry 2021, 13, 1903. [Google Scholar] [CrossRef]
- Martínez-Pérez, Á.; Rodríguez, J.M. New bounds for topological indices on trees through generalized methods. Symmetry 2020, 12, 1097. [Google Scholar] [CrossRef]
- Martínez-Pérez, Á.; Rodríguez, J. M Upper and lower bounds for topological indices on unicyclic graphs. Topol. Its Appl. 2023, 339, 108591. [Google Scholar] [CrossRef]
- Wei, C.C.; Salman, M.; Ali, U.; Rehman, M.U.; Khan, M.A.A.; Chaudary, M.H.; Ahmad, F. Some topological invariants of graphs associated with the group of symmetries. J. Chem. 2020, 2020, 6289518. [Google Scholar] [CrossRef]
- Chu, P.; Li, Y.; He, Z.; Li, E.; Ozgun, O.; Venbosch, G.A.; Zheng, X. A group theory based topology optimization scheme for the design of inhomogeneous waveguides with dihedral group symmetries. Eng. Anal. Bound. Elem. 2024, 166, 105845. [Google Scholar] [CrossRef]
- Öztürk Sözen, E.; Alsuraiheed, T.; Abdioğlu, C.; Ali, S. Computing topological descriptors of prime ideal sum graphs of commutative rings. Symmetry 2023, 15, 2133. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological indices, graph spectra, entropies, Laplacians, and matching polynomials of n-dimensional hypercubes. Symmetry 2023, 15, 557. [Google Scholar] [CrossRef]
- Kosaka, I.; Swan, C.C. A symmetry reduction method for continuum structural topology optimization. Comput. Struct. 1999, 70, 47–61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.; Khan, M.Y.; Ali, G.; Popa, I.-L. Investigation of General Sombor Index for Optimal Values in Bicyclic Graphs, Trees, and Unicyclic Graphs Using Well-Known Transformations. Symmetry 2025, 17, 968. https://doi.org/10.3390/sym17060968
Khan M, Khan MY, Ali G, Popa I-L. Investigation of General Sombor Index for Optimal Values in Bicyclic Graphs, Trees, and Unicyclic Graphs Using Well-Known Transformations. Symmetry. 2025; 17(6):968. https://doi.org/10.3390/sym17060968
Chicago/Turabian StyleKhan, Miraj, Muhammad Yasin Khan, Gohar Ali, and Ioan-Lucian Popa. 2025. "Investigation of General Sombor Index for Optimal Values in Bicyclic Graphs, Trees, and Unicyclic Graphs Using Well-Known Transformations" Symmetry 17, no. 6: 968. https://doi.org/10.3390/sym17060968
APA StyleKhan, M., Khan, M. Y., Ali, G., & Popa, I.-L. (2025). Investigation of General Sombor Index for Optimal Values in Bicyclic Graphs, Trees, and Unicyclic Graphs Using Well-Known Transformations. Symmetry, 17(6), 968. https://doi.org/10.3390/sym17060968







