Abstract
State evaluation of relay protection equipment constitutes a crucial component in ensuring the stable, secure, and symmetric operation of power systems. Current methodologies predominantly encompass fuzzy-rule-based control systems and data-driven machine learning approaches. The former relies on manual experience for designing fuzzy rules and membership functions and exhibits limitations in high-dimensional data integration and analysis. The latter predominantly formulates state evaluation as a classification task, which demonstrates its ineffectiveness in identifying equipment at boundary states and faces challenges in model parameter selection. To address these limitations, this paper proposes a quantitative state evaluation method for relay protection equipment based on a two-stage artificial protozoa optimizer (two-stage APO) optimized improved Conformer (two-stage APO-IConf) model. First, we modify the Conformer architecture by replacing pre-layer normalization (Pre-LN) in residual networks with post-batch normalization (post-BN) and introducing dynamic weighting coefficients to adaptively regulate the connection strengths between the first and second feed-forward network layers, thereby enhancing the capability of the model to fit relay protection state evaluation data. Subsequently, an improved APO algorithm with two-stage optimization is developed, integrating good point set initialization and elitism preservation strategies to achieve dynamic equilibrium between global exploration and local exploitation in the Conformer hyperparameter space. Experimental validation using operational data from a substation demonstrates that the proposed model achieves a RMSE of 0.5064 and a MAE of 0.2893, representing error reductions of 33.6% and 35.0% compared to the baseline Conformer, and 9.1% and 15.2% error reductions over the improved Conformer, respectively. This methodology can provide a quantitative state evaluation and guidance for developing maintenance strategies for substations.
1. Introduction
In the development of new power systems, the symmetry equilibrium of grid structures faces critical challenges due to the large-scale integration of high-penetration renewable energy [1,2], power electronic devices [3], and heterogeneous loads [4], leading to escalating topological complexity and heightened risks for secure and stable operation. In January 2022, China’s National Development and Reform Commission and National Energy Administration issued the 14th Five-Year Plan for Modern Energy Systems, explicitly proposing the promotion of the construction of new power systems, accelerating the digital transformation of power systems, and enhancing grid intelligence [5]. During the development of digital twin models for smart substation protection systems, the state evaluation of relay protection equipment is critically important. As a safety barrier for power grids, the health status of relay protection equipment directly affects the maintenance of the operational symmetry and dynamic stability of power systems. When asymmetric faults occur, negative- and zero-sequence components emerge in the system, potentially leading to severe accidents. Healthy relay protection devices can correctly monitor these components and facilitate the restoration of the grid symmetry. Therefore, an accurate status evaluation and timely detection of potential faults in these devices are critical for preserving the symmetric characteristics of power grids.
Traditional methods for evaluating the state of relay protection equipment often rely on manual periodic inspections, which depend heavily on workers’ empirical judgments, leading to inefficiency, subjectivity, and an inability to meet modern grid demands for real-time and precise evaluations. To improve maintenance efficiency and reduce resource waste, early researchers developed mathematical models for reliability assessment based on the failure rates of relay protection systems and introduced stochastic failure indicators [6] for model correction. However, these early approaches could only predict binary failure states (functional or failed) without quantifying specific health conditions.
Advancements in information technology and equipment upgrades have enabled substations to collect and analyze multi-source data, including operational telemetry, historical maintenance records, and familial device data, leading to increasingly diversified evaluation criteria. To characterize device health, researchers typically define four states: normal, attention, abnormal, and critical [7,8,9]. Subsequent studies incorporated analog/digital signals and power module data, while references [10,11,12] expanded the considerations to channel testing results, operational lifespan, fault alarms, environmental temperature, and voltage levels. These works gradually established small-scale expert rule libraries, where the device status is scored based on predefined rules for each indicator and aggregated for final evaluation. Reference [13] specifically addressed the temperature impacts by proposing an overheating analysis framework. However, these studies only partially incorporated the aforementioned factors and failed to establish a comprehensive evaluation system. To integrate multi-dimensional state features, reference [14] adopted entropy-based weight assignment, while references [15,16] utilized the fuzzy analytical hierarchy process (FAHP) to determine indicator weights and reference [17] combined entropy and FAHP method. Reference [18] applied Bayesian theory, and reference [19] integrated Bayesian networks with FAHP to achieve more objective and reasonable weight allocations. Based on FAHP-derived weights, reference [20] implemented fuzzy control methods with various membership functions for comprehensive fuzzy evaluations of relay protection devices.
The aforementioned methods, expert rule libraries, FAHP, and fuzzy control, overemphasize subjective human judgment. For instance, FAHP pairwise comparison matrices and fuzzy control membership functions rely on expert-defined rules, neglecting data-driven statistical patterns. Furthermore, fuzzy control struggles with high-dimensional data due to the complex rule limitations. Recent advances in intelligent technologies [21] have shifted the focus to data-driven and AI-based evaluation methods. Reference [22] demonstrated the feasibility of AI for power system fault analysis. Reference [23] employed back propagation (BP) neural networks for health assessment but showed poor accuracy for degraded devices. Reference [24] enhanced evaluation precision using least-squares support vector machines (LSSVM) and Bayesian network decision trees (BNDT). Addressing data imbalance, reference [8] achieved over 96% accuracy by combining generative adversarial networks (GAN) for data augmentation with random forest classifiers. Reference [25] validated the superiority of data-driven methods using CNN-BiGRU models with scenario-simulated sample-balancing. However, due to constraints in maintenance, most substations currently still rely on the four-state qualitative classification (normal, attention, abnormal, and critical) to assess equipment status, implementing uniform maintenance for devices deemed abnormal and critical. Driven by the need to build smart grids and develop digital twin models, substation operators now seek a more detailed understanding of equipment conditions rather than merely determining whether maintenance is required. The use of continuous numerical values to precisely reflect equipment conditions is a good approach. This would enable preventive maintenance strategies for devices in critical transitional states between attention and abnormalities.
Current mainstream data-driven approaches [8,23,24,25] primarily formulate state evaluation as classification tasks, where neural networks directly assign discrete labels like “normal” or “attention”. Although these methods achieve high accuracy, they fail to quantify the boundary states. For example, two devices labeled “attention” with scores of 89 and 80 cannot be differentiated, limiting precise maintenance guidance. Conventional models (e.g., MLP and CNN) have limitations in extracting complex patterns from high-dimensional heterogeneous data sources. This paper aims to address the limitations stated above. Recent advances in Conformer models, which integrate the multi-head self-attention (MHSA) mechanism of Transformers with depthwise separable convolutional layers of CNNs, have demonstrated superior capabilities in synergistic global-local feature modeling across domains, such as speech recognition. Inspired by these developments, this study proposes an improved Conformer architecture specifically designed for the multi-dimensional and heterogeneous nature of relay protection device state data, which encompasses fundamental condition evaluation data, operational condition evaluation data, maintenance condition evaluation data, and ancillary factor evaluation data. Owing to the synergistic design of Transformer and CNN, this architecture efficiently captures both local characteristics and global features of the device state data, thereby improving the accuracy of the state quantification evaluation. Furthermore, the proposed framework incorporates a two-stage APO strategy to learn discriminative multi-dimensional features from device state data, enabling precise state quantification rather than categorical labels. Granular quantification provides critical guidance for formulating data-driven maintenance strategies.
The differences between the method proposed in this paper and conventional methods are shown in Table 1.

Table 1.
Comparative analysis of the proposed method and previous methods.
The principal contributions of this study are summarized as follows:
- (1)
- Architectural improvement of the Conformer model: An improved Conformer architecture tailored for the quantitative state evaluation of relay-protection equipment is proposed. By replacing pre-layer normalization with post-batch normalization in residual networks and introducing dynamic weighting coefficients to adaptively regulate the connectivity between the first and second feed-forward network segments, the model significantly enhances its capability to fit relay protection state evaluation data, achieving superior fitting accuracy compared to traditional machine learning models.
- (2)
- Enhancement of the optimization algorithm: A two-stage APO algorithm is developed, incorporating good point set initialization and elitism preservation strategies. This innovation synergistically strengthens global search and local optimization while mitigating stochastic interference.
- (3)
- Model-algorithm co-optimization: The two-stage APO algorithm is integrated to optimize the hyperparameters of the improved Conformer model. By harmonizing the APO’s global search capabilities with Conformer’s hybrid architectural features, a dynamic equilibrium between exploitation and exploration is achieved in the hyperparameter space, effectively resolving the parameter selection challenges in relay protection state evaluation models.
- (4)
- Experimental validation: Experimental validation conducted on the PyCharm platform demonstrates the efficacy of the proposed methodology. The results show a RMSE of 0.5064 and a MAE of 0.2893. These outcomes can provide a quantitative state evaluation and guidance for developing maintenance strategies for substations.
The rest of this paper is organized as follows: Section 2 elaborates on the quantitative state evaluation methodology for relay protection equipment, including the state indicator system and evaluation workflow; Section 3 details the structural improvements of the Conformer model and the operational principles of the two-stage APO algorithm; Section 4 describes the model training procedures and performance evaluation metrics; Section 5 validates the effectiveness of the proposed method through practical case studies; Section 6 concludes the research.
2. Quantitative State Evaluation Methodology for Relay Protection Equipment
2.1. State Evaluation Indicator System
Currently, state evaluation data for relay protection equipment primarily originate from three sources: offline file imports, online acquisition via relay protection master stations, and manual entry. Offline imported files mainly include equipment ledger files that contain device models, commissioning dates, and other metadata. Relay protection master stations can acquire data online, such as analog signal verification results, real-time operational anomalies, alerts, homologous data comparison results, device communication rates, and trip operation records. For data that are unobtainable through online or offline means, manual collection and entry are employed, including familial defect records, secondary circuit insulation defects, periodic inspection completion status, corrective action implementation status, spare parts inventory status, and equipment production status (discontinued/active).
Based on the available data, the state evaluation indicator system categorizes data into four classes: fundamental condition evaluation data, operational condition evaluation data, maintenance condition evaluation data, and ancillary factor evaluation data. The data are organized as listed in Table 2.

Table 2.
State evaluation indicator system for relay protection equipment.
In the evaluation metric parameters listed above, most of the recorded data pertain to the occurrence frequencies. Under basic information, the commissioning date and record generation timestamp document the equipment’s operational start date and the record’s creation date, respectively, which are converted into the device’s actual operational duration. The standard version compliance adopts a binary yes/no value to indicate whether the device is included in the standardized equipment list. The device model and device name/ID are textual fields in which identical models or names share uniform encoding to differentiate the device identities.
In real-time analog verification, the system logs the count of analog signal over-limit alarms (amplitude/phase) during an inspection cycle, including zero-sequence current over-limit alarms, differential current alarms for line/transformer protection, current/voltage sampling over-limit alarms, device temperature alarms, and DC voltage over-limit alarms.
Real-time operational alerts track tier-2 and tier-3 operational anomaly alarm quantities within the evaluation period.
For operational parameter verification, the active setting zone verification status reflects whether the current setting zone number operates normally or not. Setting deviation values from baseline quantifies entries deviating from predefined benchmarks, while the remaining metrics count discrepancy alarms for soft plates, hard plates, and clock synchronization.
Homologous data comparisons arise from multiple measurement points on the same device. Data inconsistency alarms are triggered when faulty measurement points or device malfunctions cause discrepancies between homologous data sources.
Online risk identification records the frequencies of anomalies in the communication channels (fiber-optic/high-frequency), CT-N/PT-N wire disconnections, analog sampling disconnections, single-bit alarms, and frequent tier II-V signal alarms.
Process-level secondary virtual circuits document failure counts in data transmission links such as GOOSE link disconnections, optical port signal anomalies, and network port frame loss/CRC errors.
The device communication rate is expressed as a percentage. For legacy devices lacking sampling capabilities, this value defaults to 100% based on expert consensus.
Familial defects quantify failures using same-model device defect frequencies (current cycle or lifecycle).
The secondary circuit insulation counts insulation defect alarms in secondary circuits.
Action history validation and misoperation/refusal records quantify historical errors through incorrect protection/breaker operations, fault zone misidentifications, and misoperation/refusal events.
The periodic inspection status uses yes/no to indicate the completion of scheduled inspections. Corrective action status evaluates historical corrective measures based on their implementation frequency. Manufacturer support factors indicate whether the device is discontinued and spare parts are available.
Due to space constraints of the table, a single indicator may encompass multiple types of captured data. For instance, metrics involving “alarm counts” can include both the number of monitoring points that trigger alarms within an evaluation cycle and the total number of alarm occurrences across all monitoring points.
In the table above, the equipment operation time data are converted into floating-point years; status information such as maintenance status and spare parts status are quantized into binary states 0 or 1; continuous variables like device communication rate are converted into decimals; and abnormal alarm information is quantized into analog limit-exceeding counts and abnormal alarm counts, respectively. Furthermore, analog parameters are acquired and validated by analog signal monitoring modules, which detect over-limit conditions and generate the corresponding over-limit alarm counts. This approach significantly reduces the amount of analog data required to evaluate equipment status. Normalize the alarm count data to the range of 0–1 to eliminate differences in feature scales, facilitating the subsequent model learning of features.
It should be noted that the indicators in this paper do not directly incorporate the action time data of relay protection devices. If devices fail to operate correctly or timely due to faults, relevant failure alarm information (e.g., misoperation counts and refusal counts) can be collected. These records are then used to train the models. Once trained, the model can immediately generate quantified health scores for devices based on the collected data, including both online data collection and automatic offline data import. The time required for scoring is negligible.
2.2. Quantitative State Evaluation Workflow
The quantitative state evaluation process for relay protection equipment based on the aforementioned indicator system operates as follows.
Grid experts initially scored the equipment within a range of 0–100 using existing technical specifications and scoring rule databases. However, because these specifications and rules are predominantly derived from engineering experience with inherent subjectivity and single rules cannot accurately evaluate diverse equipment states, field technicians must physically inspect the equipment and iteratively adjust scores through expert consultation to obtain final ratings.
The two-stage APO-IConf model learns expert scoring logic and field adjustment patterns from historical data patterns, enabling direct score generation on newly acquired inspection data. This approach replaces multi-round empirical adjustments by maintenance personnel, thereby enhancing evaluation objectivity and efficiency. Compared to direct classification methods, quantifying equipment scores allows technicians to precisely discern device conditions, particularly for equipment near critical state boundaries, facilitating proactive maintenance planning to prevent severe failures.
3. Two-Stage APO-IConf-Based Quantitative State Evaluation Method for Relay Protection Equipment
3.1. Standard Conformer Encoder Architecture
The Conformer model was initially proposed by Google Research in 2020 [30] to address the limitations of Transformer models in capturing local features. Designed to synergize the Transformer’s global modeling capabilities with CNN’s local feature extraction strengths, the Conformer architecture enhances model performance. The standard Conformer model comprises both encoder and decoder layers. However, in quantitative state evaluation tasks for relay protection equipment, where text/audio outputs are unnecessary, the decoder layer is omitted, retaining only the encoder structure, as shown in Figure 1.
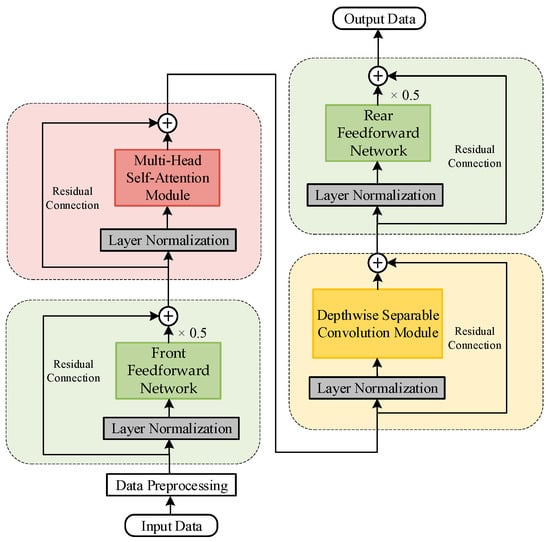
Figure 1.
Standard Conformer encoder architecture.
The feed-forward network (FFN) in the Conformer model inherits the core design principles of traditional Transformers while enhancing the representational capacity through modular enhancements and parameter optimization. Each Conformer encoder block contains two FFN modules positioned before and after the multi-head self-attention layer and the convolutional module, respectively. This architectural design facilitates a two-phase non-linear transformation process that enables a progressive feature refinement. The FFN employs swish activation functions, which demonstrate marginally superior performance compared to ReLU functions [31].
The front-end FFN performs preliminary feature enhancement on the input to supply richer contextual information for the self-attention layer, while the rear-end FFN processes the local features output by the convolutional module through global integration and recalibration. Applying identical 0.5 coefficients to both front-end FFN and rear-end FFN modules enhances accuracy when stacking multiple encoder layers while maintaining implementation balance and reducing model complexity.
The multi-head self-attention mechanism module employs relative positional encoding, which enhances the learning and generalization capabilities for variable-length input sequences. The input sequence undergoes linear transformations to generate three vector sets: Query (Q), Key (K), and Value (V). Relative positional encoding replaces absolute positional encoding [32] with its mathematical formulation given in Equation (1). Here, indices i and j denote positional coordinates of the target () and contextual () elements respectively, while represents the dimensionality of the vectors.
By partitioning the , , and vectors into h independent heads, where the vector dimensionality of the model is defined as , each head attains a dimensionality of (with and h being appropriately chosen to ensure integer dimensionality). This configuration enabled parallel feature learning across distinct subspaces.
where , , are learnable parameter matrices. Each head performs scaled dot-product attention, which incorporates relative positional encoding [33].
The relative positional offset P enhances the perception of local temporal relationships. The outputs from all heads are concatenated and linearly transformed to produce the final multi-head attention output, where denotes the fusion weight matrix.
The convolutional layer in the Conformer employs a gated depthwise separable convolution, which differs from standard CNN layers through the combination of depthwise and pointwise convolutions. This architecture offers several advantages, including a reduced parameter count and enhanced computational efficiency. The workflow can be summarized as follows, with a schematic diagram of the Conformer convolutional layer provided in Figure 2. The depthwise separable convolution process begins with pointwise convolution to reduce the channel dimensions for parameter efficiency, followed by GLU to selectively filter features. Depthwise convolution processes spatial features per channel independently. Batch normalization stabilizes training, while the swish activation enhances non-linear capabilities with smoother gradients. A second pointwise convolution adjusts the channel dimensions, and dropout regularizes the model by randomly deactivating the neurons.

Figure 2.
Schematic of the Conformer convolutional layer.
Depthwise convolution independently performs single-channel convolution on each input channel, extracting spatial features without altering the channel count, thereby significantly reducing the parameter quantity. Pointwise convolution employs convolutional kernels primarily for adjusting channel numbers or cross-channel feature fusion. By linearly combining information across different channels, it modifies the feature map depth while preserving the spatial resolution while maintaining high computational efficiency. Figure 3 shows a schematic of the depthwise and pointwise convolutions. Where H represents the convolution height, W denotes the convolution width, is the number of input channels, K specifies the convolution kernel size, and indicates the number of output channels.
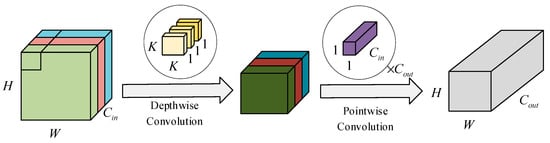
Figure 3.
Schematic diagram of depthwise and pointwise convolutions.
3.2. Improved Conformer Encoder
This study introduces architectural improvements to the Conformer encoder for the quantitative state evaluation of relay protection equipment. The key modifications are as follows:
- (1)
- Replacement of layer normalization with batch normalization;
- (2)
- Repositioning the pre-normalization layer in each residual network to post-residual connections;
- (3)
- Implementation of dynamic weighting coefficients to adaptively adjust contributions from front-end and rear-end feed-forward networks.
Vaswani et al. [34] proposed the original Transformer architecture for natural language processing (NLP) tasks, and its derivative Conformer model optimized for speech sequences utilizes layer normalization to handle variable-length inputs without padding alignment while preserving temporal dependencies. However, relay protection state data exhibit fixed-dimensional characteristics and lack intra-sample temporal relationships. Batch normalization is more effective in this context by mitigating gradient vanishing/explosion issues and enhancing the model training stability, thereby improving the prediction accuracy.
While pre-normalization facilitates gradient propagation through direct input pathways and reduces attenuation through non-linear transformations, it becomes redundant for shallow neural networks in our application. Repositioning normalization layers after residual connections stabilize the training convergence in such architectures.
Conventional implementations fix the front/rear feed-forward network weights at 0.5. Given that the model structure for relay protection state evaluation tasks does not require stacking multiple encoder layers to significantly increase complexity like NLP models, our innovation employs trainable coefficients () to dynamically balance their contributions, strengthening the model’s non-linear fitting capacity.
The architecture of the improved Conformer encoder is shown in Figure 4.
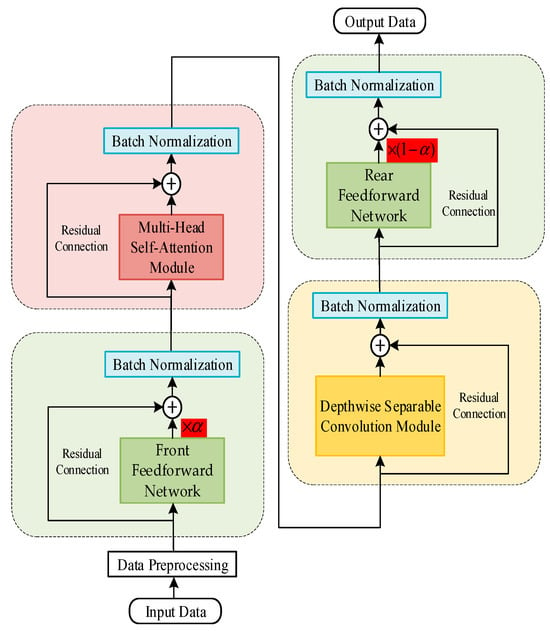
Figure 4.
Improved Conformer encoder architecture.
3.3. APO Algorithm
This study employs a novel artificial protozoa optimizer (APO) [35] for the hyperparameter optimization of the model. Inspired by natural protozoan behaviors, the algorithm simulates their survival mechanisms through foraging, dormancy, and reproductive behaviors. The APO categorizes foraging behavior into autotrophic and heterotrophic modes. The foraging process facilitates local optimization, dormancy resets individuals, and reproduction induces minor variations.
Initially, a population of n protozoa is randomly generated, where n denotes the population size (number of individuals) and represents the protozoan index. The mathematical representation of is given in Equation (5).
In the above equation, denotes the dimensionality of the vector. Each must satisfy the constraint , where the upper and lower bounds and are defined as follows:
where and denote the upper and lower bounds of the element in the i-th dimension, respectively.
Following the initialization of all protozoa individuals, the objective function is utilized to calculate fitness values. This function can be designed for maximization (e.g., profit, throughput) or minimization (e.g., cost, error). A ranking function is defined under the minimization paradigm, which sorts individuals in ascending order of their objective function values such that superior solutions occupy leading positions in ascending order of their fitness values, as formalized in Equation (8).
The APO employs three key parameters to differentiate the survival mode of each protozoan individual.
In Equation (9)–(11), represents the proportional fraction of protozoa engaged in dormancy and reproduction within the population, while 1- denotes the proportion allocated to foraging (i.e., autotrophic and heterotrophic). The parameter is compared against a system-generated random number rand to determine whether a protozoan adopts autotrophic or heterotrophic behavior. Similarly, is evaluated against rand to trigger dormancy or reproduction. Here, rand denotes a uniformly distributed random number within the interval [0, 1], t and T represent the current and maximum iteration counts, respectively, and i and n indicate the individual index and population size.
If , the protozoa individuals are foraging in an autotrophic mode, otherwise in a heterotrophic mode. If , the protozoa individuals are in dormancy, otherwise in reproduction. As shown in Equations (10) and (11), is the decreasing function of t, while is the increasing function of i. Therefore, decreases with the increase of t, so protozoa individuals tend to be more inclined toward heterotrophic mode as the iterative process proceeds. increases with the increase of i, so lower-ranked protozoa individuals tend to be more inclined toward dormancy mode. Finally, the higher-ranked individuals have significantly reduced errors after multiple rounds of iterative optimization. The following sections detail the four protozoan behaviors in the APO.
3.3.1. Autotrophic Behavior
For autotrophic behavior, individuals are updated using Equation (12):
In Equation (12), represents the updated individual while denotes a randomly selected j-th protozoan. Equations (13)–(16) provide supplementary specifications to Equation (12), where f is the foraging factor, indicates the number of neighbor pairs with a maximum limit , refers to a protozoan randomly chosen from neighbor pairs with indices , and corresponds to a protozoan selected from neighbor pairs with indices . Boundary conditions dictate that if is , defaults to , and if is , defaults to . The weighting factor governs autotrophic behavior, eps (2.2204 × 10−16) is a minimal constant, and denotes the fitness function. The operator ⊙ signifies the Hadamard product (element-wise multiplication), is a binary search-oriented mapping vector of size with elements 0 or 1, and represents the dimension index within .
3.3.2. Heterotrophic Behavior
For heterotrophic behavior, individuals are updated using Equation (17):
Equations (18)–(20) provide the supplementary specifications for Equation (17). Here, denotes a position in the vicinity of , where the ± notation indicates that can be sampled in different directions relative to the i-th protozoan. represents the protozoan with index i − k selected from the k-th neighbor pair, while corresponds to the protozoan with index i + k. Boundary conditions ensure that if is , defaults to , and if is , defaults to . The weighting factor governs heterotrophic behavior, and Rand denotes a random vector with elements uniformly distributed in [0, 1].
3.3.3. Dormancy Behavior
For dormancy behavior, the model is defined as follows:
where and denote the upper and lower bound vectors, respectively.
3.3.4. Reproductive Behavior
For reproductive behavior, the model is defined using the following equation:
where is a mapping vector of size , with each element being either 0 or 1.
Autotrophic behavior and heterotrophic behavior are two different methods of local optimization. Dormancy behavior is equivalent to randomly resetting individuals and directly discarding the current solution in order to escape from local optima. Reproductive behavior is similar to mutation in genetic algorithms, causing significant changes in the current solution and also helping to escape from local optima.
The APO algorithm primarily involves parameters including population size (n), number of neighbor pairs for protozoa (), maximum proportion fraction for dormancy and reproduction (), and maximum iteration count (T). To balance the model training accuracy and training time, the population size is set to 50 and the maximum iteration count to 50. The number of neighbor pairs for protozoa influences the randomness of individual updates during autotrophic and heterotrophic behaviors. For example, in autotrophic behavior, individuals are randomly selected from the current individual’s neighboring pairs; a smaller number of neighbor pairs reduces randomness during selection, thereby enhancing the algorithm stability and accelerating convergence. The maximum proportion fraction for dormancy and reproduction determines the maximum proportion of individuals entering dormancy and reproductive states during iterations. A larger parameter improves the algorithm’s global optimization capability but may weaken the local refinement searchability. Based on empirical evidence from the original references, we set the number of neighbor pairs to 1 and the maximum proportion fraction for dormancy and reproduction to 0.1.
3.4. Two-Stage APO Algorithm
The existing APO algorithm demonstrates strong exploration capabilities in the solution space, yet its probabilistic behavior selection mechanism risks the non-deterministic dormancy of high-quality individuals, thereby compromising exploitation performance. To address this imbalance, this study introduces an improved APO algorithm that integrates three strategic refinements. First, a good point set theory-driven initialization method is adopted to minimize the performance fluctuations caused by random initialization. Second, a two-stage optimization framework is established, explicitly separating global exploration during the initial iterations from intensified local exploitation in the convergence stages. Finally, an elite retention strategy is incorporated in the later optimization stages to refine the convergence precision. Collectively, these improvements aim to harmonize exploration-exploitation dynamics while mitigating initialization-induced stochastic disturbances. The technical specifications of these improvements are elaborated below:
- (1)
- Good point set initialization: Based on the good point set theory proposed by Hua, L. K. et al. [36], the initial population is constructed within the s-dimensional unit cube . Let be a good point. When the discrepancy function satisfies (where is a constant dependent only on and an arbitrary positive ), the good point set is defined as:Specifically, the parameter is selected as , where is the smallest prime number satisfying . This construction method rigorously ensures a uniform spatial distribution of the initial population in the solution space.Figure 5 shows the comparison results between the good point set initialization and random initialization visualized using two-dimensional free variables. The figure reveals that the points generated by good point set initialization are uniformly distributed, while random initialization samples exhibit significant local clustering and sparse spatial regions. These results indicate that a good point set initialization strategy effectively mitigates the incomplete spatial coverage issue inherent in traditional random sampling.
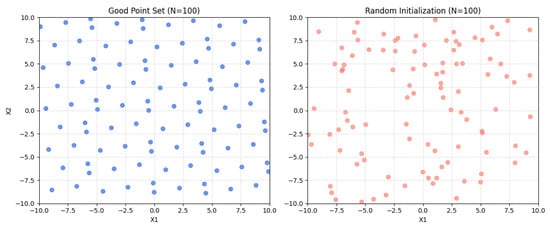 Figure 5. Comparison of results between good point set initialization and random initialization.
Figure 5. Comparison of results between good point set initialization and random initialization. - (2)
- Two-stage optimization: The iterative process is partitioned into two stages with distinct selection strategies demarcated by the median iteration count as a threshold. During the second stage, an exponential probability distribution replaces the original uniform distribution to select individuals undergoing “dormancy or reproduction”. The probability density function is defined aswhere is the progression factor (c > 1), denotes a protozoan individual, represents the individual’s ranked index, and is the population size. For moderate population sizes (e.g., ), is recommended to avoid exponential explosion risks.The selection probabilities are computed via this exponential distribution and executed using a roulette wheel strategy. When duplicate selections occur, priority is given to replacing duplicates with the suboptimal nearest-neighbor individual. If suboptimal candidates are exhausted, global reselection is triggered until the required number of individuals is selected.
- (3)
- Elitism preservation strategy: During the second optimization stage, a fixed percentage of the fittest individuals is retained and exempted from resetting.
For a fair comparison, the parameters of the two-stage APO are consistent with the APO, and the selected parameters remain unchanged.
The optimization flowchart of the two-stage APO employed in this study is shown in Figure 6.
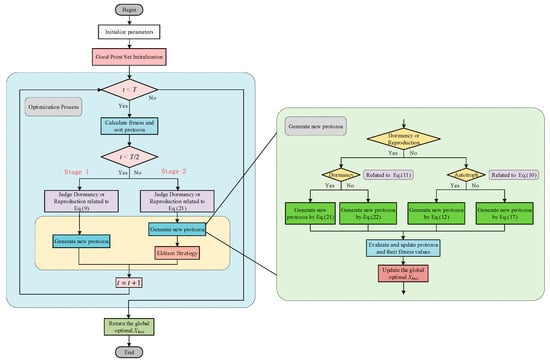
Figure 6.
Flowchart of two-stage APO algorithm.
The following table shows the pseudocode for the two-stage APO algorithm (Algorithm 1).
| Algorithm 1: Pseudo code of the proposed two-stage APO algorithm | |
| Input: Initialize parameters , , , , and Output: The global optima and | |
| 1: | while do |
| 2: | ), i = 1, 2, …, n; // sort positions by fitness in ascending order |
| 3: | ; // proportion fraction |
| 4: | if then |
| 5: | ; |
| 6: | else |
| 7: | is selected by Equation (25) and roulette wheel strategy |
| 8: | end if |
| 9: | for do |
| 10: | if i is in then |
| 11: | if then |
| 12: | Calculate using Equation (21); // dormancy |
| 13: | else |
| 14: | Calculate using Equation (22); // reproduction |
| 15: | end if |
| 16: | else |
| 17: | if then |
| 18: | Calculate using Equation (12); // foraging in an autotroph |
| 19: | else |
| 20: | Calculate using Equation (17); // foraging in a heterotroph |
| 21: | end if |
| 22: | Get the current new position. |
| 23: | if then |
| 24: | if then |
| 25: | ; |
| 26: | else |
| 27: | |
| 28: | end if |
| 29: | else |
| 30: | Select the top m individuals with the best fitness as elites; Merge them with the new population to form a candidate pool of size n + m; Choose the top n individuals from this pool as the next generation. |
| 31: | end if |
| 32: | end for |
| 33: | |
| 34: | end while |
| 35: | return and |
4. Model Training and Evaluation Metrics
4.1. Model Training
The training procedure for the relay protection equipment state quantification evaluation model consists of the following steps:
- (1)
- Dataset processing: Given that the majority of data in the original relay protection equipment state evaluation dataset comprise high-score samples, synthetic low-score data were algorithmically generated to mitigate imbalance, while irrelevant feature columns with insufficient training samples were pruned. The processed dataset retained 42 feature columns and one device score column, partitioned into training, validation, and test sets in an 8:1:1 ratio.
- (2)
- Model architecture: An improved Conformer model was constructed (detailed architecture in Figure 4), where the input data underwent feature projection via a fully connected layer followed by flattening. The model leverages multi-head attention mechanisms and depthwise separable convolutional modules within the Conformer blocks to capture cross-dimensional feature interactions, enhanced by two feed-forward networks for non-linear fitting capacity, culminating in a single-neuron FC layer for regression-based state score prediction.
- (3)
- Training model: Training hyperparameters included a batch size of 128, 50 epochs, and an Adam optimizer with a dynamic learning rate (initial = 0.001; halved after five epochs of stagnant validation loss) using mean squared error (MSE) loss. The APO algorithm optimizes the Conformer hyperparameters via training and validation sets and then merges these sets for final model training, with the performance evaluated on the test set.
4.2. Model Evaluation Metrics
This study employs root mean square error (RMSE), mean absolute error (MAE), coefficient of determination (), and adjusted to evaluate model performance. The mathematical formulations of these metrics are defined as follows:
where n denotes the number of samples and k represents the number of features in the dataset.
The RMSE amplifies the difference between the predicted and true values through squaring, making it sensitive to large errors. The numerical units align with the original data, directly reflecting the absolute deviation level of the model predictions. MAE calculates the mean absolute value of prediction errors, demonstrating strong robustness to outliers. quantifies the model’s ability to explain variance in the dependent variable while adjusted penalizes the number of independent variables to eliminate inflation effects caused by model complexity on R2, making it more suitable for multiple regression analysis.
5. Case Study and Results Analysis
5.1. Data Sources and Preprocessing
This study utilizes the monitoring data from relay protection devices at substations in a southern Chinese region in the Year 2024, encompassing fundamental condition evaluation data, operational condition evaluation data, maintenance condition evaluation data, and ancillary factor evaluation data. Invalid feature columns with insufficient data were removed, and 42 valid features were retained to construct the dataset. To address the predominance of high-score samples in substation-provided data, synthetic low-score data were generated through rule-based guided corrections and expert knowledge integration. The final dataset contained 16,489 samples covering multiple device models within substations. In the complete dataset, there were 10,897 high-score samples accounting for 66.1%, corresponding to equipment normal status; 3198 attention-status samples accounting for 19.4%; abnormal-status and severe-abnormal sample numbers 1349 and 1276, accounting for 8.2% and 7.7%, respectively. Because substation monitoring data contain extremely few abnormal and severe-abnormal samples, small-sample generation algorithms are unsuitable for synthesis. Manual synthesis is employed to generate most of the data for sample construction. The entire dataset is randomly divided into training, validation, and test sets at an 8:1:1 ratio. All data are normalized to the range of 0–1 to eliminate differences in feature scales based on the features of the training set for model training. The divided validation and test sets each contained 1649 samples, maintaining a consistent data distribution across all three datasets. Each column of the data is normalized according to the characteristics of the corresponding column in the training set.
5.2. Parameter Optimization
The two-stage APO optimization algorithm is employed to optimize four hyperparameters in the improved Conformer encoder model: the number of neurons in the feed-forward network, the number of convolutional kernels in the convolutional layer, neuron dropout rate, and weight coefficient of the feed-forward network. Training hyperparameters include a batch size of 128 and 50 epochs and the Adam optimizer with a dynamic learning rate (initial = 0.001; halved after five epochs with stagnant validation loss). The APO configurations set the population size to 50, with 10 experimental trials conducted to select the optimal values. The optimized parameters are as follows: neurons: 351, convolutional kernels: 31, dropout rate: 0.1573, weight coefficient: 0.6903.
5.3. Method Validation and Result Analysis
The optimized model was retrained using the merged training set (combining the original training and validation sets) and evaluated on the test set. The test results are shown in Figure 7 and Figure 8. Figure 7 presents the training and testing loss curves, while Figure 8 demonstrates the difference between the predicted and actual scores for 100 randomly selected test samples. During the initial training stages, both the training and testing losses decreased rapidly, converging to similar values as the iterations progressed, indicating effective model training. The observed error in training loss (occasionally exceeding testing loss) arises from dropout regularization during training, which is normal behavior.
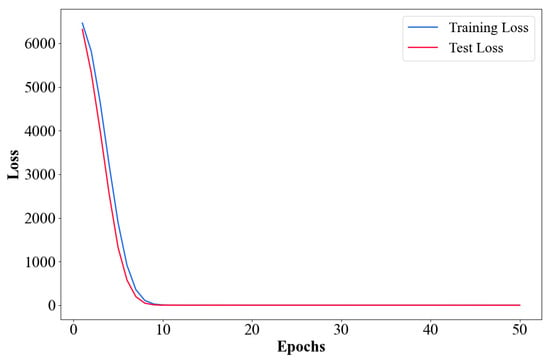
Figure 7.
Training loss curves of the two-stage APO-IConf model.
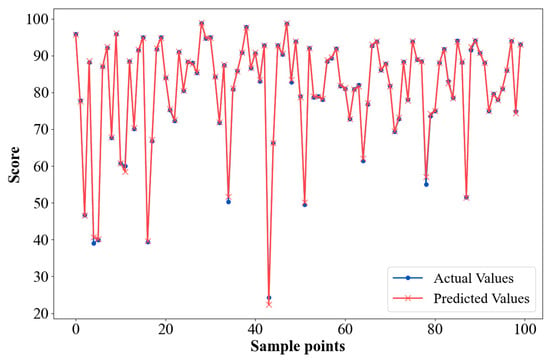
Figure 8.
State quantification score prediction results.
Figure 7 shows the training and testing loss curves. The curves demonstrate that the two-stage APO method proposed in this paper achieves a rapid convergence speed and stable convergence behavior when optimizing the relay protection state quantification evaluation model. During the initial training stages, both the training and testing losses decreased rapidly, converging to similar values as the iterations progressed, indicating effective model training. The observed error in training loss (occasionally exceeding testing loss) arises from dropout regularization during training, which is normal behavior.
Figure 8 shows the difference between the predicted and actual scores for 100 randomly selected test samples. In the prediction results, due to differences in data distribution, the prediction scores for most devices are concentrated in the high-score range, with only a very small number of devices scoring below 60. The graph shows that high-score data exhibit smaller deviations between predicted and actual values, while low-score data (below 60) demonstrate certain prediction errors, indicating that the model is more accurate in identifying the status of normal equipment.
To validate the performance superiority of the proposed improved model, comparative experiments were conducted against normal deep learning models: CNN, MLP, CNN-BiGRU, CNN-BiLSTM, and a standard Transformer. The entire experiment was repeated ten times with the mean and best prediction metrics from each model selected for comparison. Figure 9 illustrates the mean prediction error across the machine learning approaches, and detailed performance parameter comparisons are summarized in Table 3. Table 4 shows the significance test results for the models in Table 3. Using a two-tailed Welch’s t-test with a significance level of 0.05, pairwise comparisons are conducted between the model proposed in this paper and each model in Table 3.
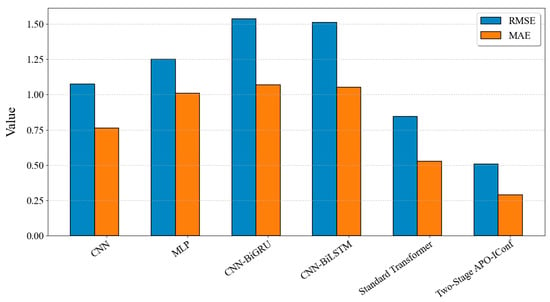
Figure 9.
Mean prediction error across normal machine learning models.

Table 3.
Performance comparison with normal machine learning models.

Table 4.
Welch’s t-test results with the proposed mode as the baseline.
Welch’s t-test is a statistical method for comparing whether there is a significant difference between the means of two independent samples. It does not assume equal variances between samples, making it more broadly applicable than the traditional t-test. The test yields a test statistic and p-value, which represents the ratio of the between-group mean difference to the sample variability, where larger absolute values indicate more pronounced group differences. The p-value denotes the probability of observing the current data or more extreme cases under the assumption of no difference between samples, with smaller values providing stronger evidence of statistically significant group differences.
As demonstrated by the experimental results, the two-stage APO-IConf model achieves significant advantages in the quantitative evaluation of the relay protection equipment state. Compared to the standard Transformer, it reduces the mean RMSE by 40.1% (from 0.8455 to 0.5064) and mean MAE by 45.2% (from 0.5277 to 0.2893) while attaining optimal performance in both R2 (Best: 0.9988) and adjusted R2 (Best: 0.9988) metrics. The model also shows substantial improvements over traditional methods, reducing the RMSE by 52.8% compared to CNN (Mean: 1.0733) and 59.5% compared to MLP (Mean: 1.2516). Both the mean and best values significantly outperform hybrid architectures like CNN-BiGRU and CNN-BiLSTM, demonstrating superior training efficacy across all evaluation metrics.
In Table 4, the proposed model has a very small p-value for all models, indicating statistically significant performance differences from the traditional machine learning baselines. This confirms that the performance improvement is attributable to model efficacy rather than to random factors.
To thoroughly validate the effectiveness of each component in the proposed method, experiments are conducted and compared with other Conformer models. Model 1 is the standard Conformer; Model 2 is the dynamic weighting coefficients Conformer, which adopts dynamic weighting coefficients on the standard Conformer architecture; Model 3 is post-BN-Conformer, which replaces the Pre-LN structure with a post-BN structure in the standard Conformer architecture; Model 4 is Improved Conformer; Model 5 is APO-Conformer; Model 6 is Two-Stage APO-Conformer; Model 7 is APO-IConformer; Model 8 is Two-Stage APO-IConformer. Standard Conformer serves as the baseline. This systematic evaluation quantifies the incremental contributions of architectural modifications to the final performance in the quantitative state evaluation of relay protection equipment. Figure 10 illustrates the prediction error across the other Conformer models, and detailed performance parameter comparisons are summarized in Table 5. Table 6 displays the significance test results for the models listed in Table 5. The testing process is the same as before, except that a standard Conformer (Model 1) is used as the baseline. Bold results indicate that the model shows no significant superiority over the benchmark.
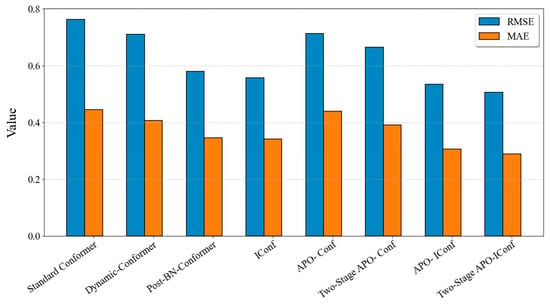
Figure 10.
Predictive mean error across other Conformer models.

Table 5.
Performance comparison with other Conformer models.

Table 6.
Welch’s t-test results with standard Conformer (Model 1) as the baseline.
This experiment demonstrates that the proposed two-stage APO-IConf (Model 8) achieves comprehensive superiority in the quantitative evaluation of relay protection equipment state, reducing mean RMSE by 33.6% (from 0.7626 to 0.5064) and mean MAE by 35.0% (from 0.4449 to 0.2893) compared to the baseline standard Conformer (Model 1) while improving the mean metric from 0.9965 to 0.9985.
Models 1 through 4 form a controlled experimental group, where Model 2 and Model 3 represent single-aspect improvements over Model 1, and Model 4 combines both modifications. The experimental data demonstrate that both improvement methods (post-BN structure and dynamic weighting coefficient) enhance the model performance. Notably, the performance gain from implementing the post-BN structure was more substantial than that from adjusting the dynamic weighting coefficients. This indicates that post-BN modification serves as an effective enhancement approach, contributing more significantly to overall performance improvements than dynamic weighting coefficient optimization. While single-aspect modifications yield statistically insignificant improvements, the enhanced Conformer demonstrates significant gains.
Relative to the single-modification IConf (Model 4), the integration of the two-stage APO optimization strategy further reduces the mean RMSE by 9.1% (from 0.5572 to 0.5064) and mean MAE by 15.2% (from 0.3413 to 0.2893), validating the necessity of algorithm-architecture co-design. When compared to optimized variants, the proposed two-stage APO-IConf (Model 8) exhibits a 23.9% mean RMSE reduction (from 0.6654 to 0.5064) and 26.2% mean MAE reduction (from 0.3918 to 0.2893) over Two-Stage APO-Con (Model 6), as well as a 5.2% mean RMSE reduction (from 0.5342 to 0.5064) and 5.6% mean MAE reduction (from 0.3063 to 0.2893) against APO-IConf (Model 7), confirming that the synergistic combination of the improved Conformer architecture and two-stage APO strategy drives performance breakthroughs, as structural deficiencies in Model 6 and non-staged optimization in Model 7 result in significantly higher errors.
As shown in Table 6, the proposed model demonstrates the strongest statistical significance, followed by Model 4. Both exhibit the largest absolute values of the test statistics and smallest p-values, indicating robust significance. While Model 2 and Model 5 show improvements in both mean and best values, their statistical significance remains weak, potentially lacking statistical significance.
The two-stage APO-IConf achieves optimal RMSE (0.4857), MAE (0.2754), (0.9988), and adjusted (0.9988), providing quantitative state evaluation and guidance for developing maintenance strategies for substations.
6. Conclusions
To address the challenges of ambiguous status boundaries and hyperparameter selection in relay protection equipment evaluation, this study proposes a state quantification method based on a two-stage APO-optimized improved Conformer model. Experimental validation using real-world datasets confirms the effectiveness of the method. Key conclusions are:
- (1)
- This paper proposes an improved Conformer architecture by replacing pre-layer normalization with post-batch normalization and introducing dynamic weight coefficients to regulate feed-forward network connectivity, which significantly improves the feature fusion capability and fitting accuracy for relay protection data.
- (2)
- The two-stage APO algorithm integrates good point set initialization and elitism preservation strategies, achieving dynamic equilibrium between global exploration and local exploitation in the hyperparameter space of the Conformer, which effectively resolves traditional parameter selection difficulties.
- (3)
- The two-stage APO-IConf model exhibits a 23.9% mean RMSE reduction (from 0.6654 to 0.5064) and 26.2% mean MAE reduction (from 0.3918 to 0.2893) over the Two-Stage APO-Con (Model 6), as well as a 5.2% mean RMSE reduction (from 0.5342 to 0.5064) and 5.6% mean MAE reduction (from 0.3063 to 0.2893) compared to APO-IConf (Model 7), confirming that the synergistic combination of the improved Conformer architecture and two-stage APO strategy drives performance breakthroughs.
- (4)
- The two-stage APO-IConf model autonomously learns expert rule-based scoring patterns and field adjustment logic from data, enabling objective and rapid state evaluation without manual intervention in new inspection scenarios.
Existing device data already include dozens of substation protection devices, such as busbar and differential protection devices. In the future, testing can be conducted in actual substations to apply the research work to substations. For example, it can be combined with digital twin models of substations to perform online state evaluations, thereby improving the accuracy.
This paper still has the following limitations. First, the training data relies on expert scoring, which inherently embodies the subjective quantification of domain priors and may be influenced by experts’ cognitive frameworks, knowledge blind spots, and evaluation criteria. Such implicit biases may be assimilated by the model, causing its scoring results to deviate from the objective truth condition. Second, although RMSE and MAE eliminate the state boundary problem in traditional classification methods and instead use continuous scores to evaluate the state of devices, these metrics are unable to distinguish the direction of error and are unable to reflect the error distribution. Therefore, the next stage of research will focus on other relevant metrics and whether we can train the corresponding models for devices with different score ranges.
Author Contributions
Y.L. led the conceptualization, methodology, and original draft preparation. Validation was carried out by Y.L., M.Z. and S.Z., while formal analysis was performed by Y.L. and M.Z.; S.Z. managed the investigation, and resources were provided by S.Z. and Y.Z.; Y.Z. was responsible for data curation. Writing—review and editing involved Y.L., M.Z. and Y.Z., with visualization by M.Z. and Y.Z. Supervision was provided by Y.L. and S.Z., project administration by Y.L. and Y.Z., and funding acquisition by Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the grant from China Southern Power Grid Co., Ltd. (Project No. 030100KC23110037).
Data Availability Statement
Data are contained in the article.
Conflicts of Interest
Authors Yanhong Li, Min Zhang, and Shaofan Zhang were employed by the Guangzhou Power Supply Bureau of Guangdong Power Grid Co., Ltd. Author Yifan Zhou was employed by the company NR Engineering Co., Ltd. The authors declare that this study received funding from China Southern Power Grid Co., Ltd. (Project No. 030100KC23110037). The funder was not involved in the study design, collection, analysis, interpretation of data, writing of this article, or the decision to submit it for publication.
Abbreviations
The following abbreviations are used in this manuscript:
| APO | Artificial protozoa optimize |
| APO-Conf | Artificial protozoa optimize-Conformer |
| APO-IConf | Artificial protozoa optimize-improved Conformer |
| BNDT | Bayesian network decision trees |
| BP | Back propagation |
| CNN | Convolutional neural network |
| CNN-BiGRU | Convolutional neural network-bidirectional gated recurrent unit |
| CNN-BiLSTM | Convolutional neural network-bidirectional long short term memory network |
| CRC | Cyclic redundancy check |
| CT-N wire | Current transformer neutral wire |
| FAHP | Fuzzy analytical hierarchy process |
| FFN | Feed-forward network |
| GAN | Generative adversarial networks |
| GOOSE | Generic object oriented substation event |
| IConf | Improved Conformer |
| LSSVM | Least squares support vector machines |
| MHSA | Multi-head self-attention |
| MLP | Multilayer perceptron |
| NLP | Nature language processing |
| Post-BN | Post-batch normalization |
| Pre-LN | Pre-layer normalization |
| PT-N wire | Potential transformer neutral wire |
| Two-stage APO | Two-stage artificial protozoa optimizer |
| Two-stage APO-Conf | Two-stage artificial protozoa optimizer-Conformer |
| Two-stage APO-IConf | Two-stage artificial protozoa optimizer-improved Conformer |
References
- Kang, C.; Yao, L. Key Scientific Issues and Theoretical Research Framework for Power Systems with High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2017, 41, 2–11. [Google Scholar]
- Ou, K.; Gao, S.; Wang, Y.; Zhai, B.; Zhang, W. Assessment of the Renewable Energy Consumption Capacity of Power Systems Considering the Uncertainty of Renewables and Symmetry of Active Power. Symmetry 2024, 16, 1184. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, M.; Chi, Y.; Ju, P. Basic Challenges of and Technical Roadmap to Power-electronized Power System Dynamics Issues. Proc. CSEE 2022, 42, 1904–1916. [Google Scholar]
- Qiu, Y.; Lu, S.; Lu, H.; Luo, E.; Gu, W.; Zhuang, W. Flexibility of Integrated Energy System: Basic Connotation, Mathematical Model and Research Framework. Autom. Electr. Power Syst. 2022, 46, 16–43. [Google Scholar]
- National Development and Reform Commission; National Energy Administration. The 14th Five-Year Plan for Building a Modern Energy System (2021–2025). Available online: https://www.gov.cn/zhengce/zhengceku/2022-03/23/content_5680759.htm (accessed on 26 April 2025).
- Wang, L.; Zhang, J.; Zeng, Z.; Yu, H.; Zheng, X. Research and Application of the Random Failure Indicators in Status Evaluation of Relay Protection. Electr. Power 2013, 46, 87–90. [Google Scholar]
- Wang, Y.; Liao, H.; Yuan, X.; Chen, J.; Xu, Z.; Luo, C. Development and application of relay protection condition evaluation system based on fault information processing system. Power Syst. Prot. Control. 2014, 42, 134–139. [Google Scholar]
- Zhang, L.; Wang, G.; Cao, L.; Dai, Z.; Kou, B. Smart status evaluation and early warning approach for highly-reliable protection systems based on GAN model and random forest algorithm. J. Electr. Power Sci. Technol. 2021, 36, 104–112. [Google Scholar]
- Wang, L.; Guo, P.; Kang, Y.; Yan, Z. Research on Relay Protection Equipment Maintenance Decision-Making Method Based on Risk Assessment. In Proceedings of the 2023 IEEE PES GTD International Conference and Exposition (GTD), Istanbul, Turkiye, 22–25 May 2023; pp. 231–235. [Google Scholar]
- Zheng, S.; Yang, X.; Du, J.; Dong, P.; Li, Y.; Guo, P. Indexes and Methods of Multi-Dimensional Comprehensive Evaluation of Relay Protection. In Proceedings of the 2022 4th International Conference on System Reliability and Safety Engineering (SRSE), Guangzhou, China, 15–18 December 2022; pp. 307–311. [Google Scholar]
- Dong, Z.; Li, H.; Tang, Y.; Yin, H.; Yin, J. Research and Application of Intelligent Diagnosis of Health Status of Relay Protection Equipment. In Proceedings of the 2022 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Hengyang, China, 26–27 March 2022; pp. 847–853. [Google Scholar]
- Hu, H.; Kang, Y.; Zhang, Y.; Ye, X.; Guo, P.; Yan, Z. A Relay Protection State Evaluation Method with Multiple Influencing Factors. In Proceedings of the 2023 IEEE Sustainable Power and Energy Conference (iSPEC), Chongqing, China, 28–30 November 2023; pp. 1–5. [Google Scholar]
- Jin, L.; Zhou, Z.; Zhan, R.; Yang, G.; Zhang, Y. Optimal Layout and Overheat Monitoring for Components of Highly Reliable Relay Protection Equipment. IEEE Access 2023, 11, 85615–85625. [Google Scholar] [CrossRef]
- Fu, H.; Liu, Q.; Wang, Y.; Zhou, S.; Wang, K.; Wang, C.; Song, W.; Li, Y. Fuzzy Assessment of Hierarchical State of Relay Protection Equipment in Intelligent Substation Based on Entropy Weight DSmT. In Proceedings of the 2023 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Xi’an, China, 2–4 November 2023; pp. 1–6. [Google Scholar]
- Sun, H.; Zhang, G.; Gao, B.; Wang, Y.; Li, Y.; Li, Y. Fuzzy Comprehensive Evaluation of Relay Protection Equipment Status in Intelligent Substations Based on Combination Weighting Method. Electr. Meas. Instrum. 2020, 57, 23–28. [Google Scholar]
- Xu, C.; Wang, Y.; Zhao, L.; Gao, J.; Huang, L.; Ying, L. Fuzzy comprehensive evaluation of intelligent substation relay protection system state based on information trend prediction and combination weighting. Electr. Power Autom. Equip. 2018, 38, 162–168. [Google Scholar]
- Zhang, J.; Xue, A.; Zhang, L.; Zhou, Z.; Yang, G.; Zhang, H.; Wang, W.; Wang, Z. Research on Health Status Evaluation of Relay Protection Based on Combinatorial Weighting Model. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 618–622. [Google Scholar]
- Xu, C.; Ying, L.; Luo, X.; Zhao, L.; Gao, J.; Huang, L.; Tan, J. Method of weight updating for state evaluation of relay protection equipment based on Bayesian theory. Eng. J. Wuhan Univ. 2017, 50, 738–744. [Google Scholar]
- Zhao, X.; Yu, Z.; Zhang, X. Fuzzy comprehensive state evaluation method of variable weight of relay protection based on variable membership degree. Power Syst. Prot. Control. 2017, 45, 22–29. [Google Scholar]
- Zhou, Y.; Ou, R.; Li, D.; Liao, X.; Yang, Y. Health status assessment of secondary equipment based on interval PCA and fuzzy comprehensive evaluation. Manuf. Autom. 2023, 45, 104–109. [Google Scholar]
- Alaerjan, A.; Jabeur, R.; Ben, H.; Karray, M.; Ksantini, M. Improvement of Smart Grid Stability Based on Artificial Intelligence with Fusion Methods. Symmetry 2024, 16, 459. [Google Scholar] [CrossRef]
- Kezunovic, M.; Baembitov, R.; Mohamed, T. No Silver Bullet: Artificial Intelligence Is Not a Panacea, but It Works for Fault Analysis and Outage Management. IEEE Power Energy Mag. 2024, 22, 78–88. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, W.; Liu, H.; Wang, Q.; Wang, T.; Zhao, Z. Research on State Warning of Relay Protection Device Based on BP Neural Network. Mod. Sci. Instrum. 2022, 39, 195–201. [Google Scholar]
- Jia, Y.; Ying, L.; Wang, D.; Zhang, J. Defect Prediction of Relay Protection Systems Based on LSSVM-BNDT. IEEE Trans. Ind. Inform. 2020, 17, 710–719. [Google Scholar] [CrossRef]
- Zhou, D. Research on Digital Twin of Relay Protection Simulation Deduction and State Prediction Technology in the Intelligent Substation. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Liu, Y. Research on Reliability Evaluation Method of Protective Equipment and Software Design. Master’s Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar]
- Dong, Y. State Evaluation and Fault Prediction of Protection System Based on Digital Twin. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Zhu, Q.; Xu, Z.; Wang, L. Analysis and Comparison of Corporation Control Activities Assessment Based on Fuzzy Comprehensive Method and BP Neural Network Method. Manag. Rev. 2013, 25, 113–123. [Google Scholar]
- Wang, F. A Comparative Study of Speed Control Schemes of PMSM Based on Fuzzy PID Control and BP Neural Network PID Control. Micromotors 2020, 53, 103–107. [Google Scholar]
- Gulati, A.; Qin, J.; Chiu, C.C.; Parmar, N.; Zhang, Y.; Yu, J.; Han, W.; Wang, S.; Zhang, Z.; Wu, Y. Conformer: Convolution-Augmented Transformer for Speech Recognition. arXiv 2020, arXiv:2005.08100. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-Xl: Attentive Language Models beyond a Fixed-Length Context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-Attention with Relative Position Representations. arXiv 2018, arXiv:1803.02155. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html (accessed on 5 May 2025).
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.S.; Kong, L.; Shehadeh, H.A. Artificial Protozoa Optimizer (APO): A Novel Bio-Inspired Metaheuristic Algorithm for Engineering Optimization. Knowl.-Based systems 2024, 295, 111737. [Google Scholar] [CrossRef]
- Hua, L.K.; Wang, Y. Applications of Number Theory to Numerical Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 3-642-67829-7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).