Symmetries in High-Temperature Lattice QCD with (u, d, s, c, b) Optimal Domain-Wall Quarks

Abstract

We investigate the spatial z-correlators of meson operators in $N_f=2+1+1+1$ lattice QCD with optimal domain-wall quarks across eight temperatures ranging from 325 to 3250 MeV. The meson operators include a complete set of Dirac bilinears for ten flavor combinations. Our findings reveal a hierarchical restoration of chiral symmetry in QCD with $(u,d,s,c,b)$ quarks, progressing sequentially from $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ to $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$, then to $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$, and finally to $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ as the temperature increases. Additionally, we explore the emergence of the $SU{\left(2\right)}_{CS}$ chiral-spin symmetry and compare the temperature windows for all flavor combinations. Our results indicate that the temperature windows for the emergent $SU{\left(2\right)}_{CS}$ symmetry are primarily dominated by the $\overline{u}b$ and $\overline{s}b$ sectors.

1. Introduction

Understanding the symmetries of high-temperature QCD is a crucial first step in determining the properties and dynamics of matter under extreme conditions. These studies are essential for gaining insight into the mechanisms governing matter creation in the early universe and for interpreting the results of relativistic heavy-ion collision experiments, such as those conducted at the LHC and RHIC, as well as future electron–ion collision experiments at planned electron–ion colliders. Lattice QCD provides a nonperturbative framework to explore the symmetries of high-temperature QCD from first principles. Since 1987 [1,2], numerous lattice studies have utilized the screening masses of meson z-correlators to investigate the effective restoration of $U{\left(1\right)}_A$ and $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetries of u and d quarks in high-temperature QCD (see ref. [3] and references therein). However, the hierarchical restoration of chiral symmetry in high-temperature QCD has not been discussed or studied in the literature, with the exception of refs. [4,5].

In $N_f=2+1+1+1$ QCD with nonzero quark masses, the theory does not exhibit $SU{\left(N\right)}_L\times SU{\left(N\right)}_R\times U{\left(1\right)}_A$ chiral symmetry for any integer N from 2 to 5, due to the explicit symmetry breaking induced by the quark masses. However, as the temperature T increases, each quark gains thermal energy on the order of $\pi T$, and eventually its rest mass energy becomes negligible when $\pi T\gg m_q$. Given that quark masses span from a few MeV to several GeV, chiral symmetry is restored in a hierarchical manner as the temperature rises: first, the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ symmetry of $(u,d)$ quarks is restored, followed by the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ symmetry of $(u,d,s)$ quarks, then the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ symmetry of $(u,d,s,c)$ quarks, and finally the $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ symmetry of $(u,d,s,c,b)$ quarks. This hierarchical pattern was first pointed out in ref. [4]. It is important to note that the top quark can be neglected in QCD, as it is extremely short-lived, decaying into a W-boson and a b-quark (most frequently), or an s- or d-quark (the rarest) before it can interact with gluons. Furthermore, since the QCD action with nonzero quark masses does not possess exact chiral symmetries, the term “hierarchical restoration of chiral symmetry” should be regarded as “hierarchical emergence of chiral symmetry”.

In ref. [5], the hierarchical restoration of chiral symmetry was first observed in $N_f=2+1+1$ lattice QCD with $(u,d,s,c)$ domain-wall quarks at the physical point. The restoration progresses sequentially from $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ to $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$, and subsequently to $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ as the temperature increases from 190 MeV to 1540 MeV. While this observation provides strong evidence supporting the hierarchical restoration of chiral symmetry in QCD, it remains incomplete, as the emergence of $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ symmetry for $(u,d,s,c,b)$ quarks has not yet been verified. This limitation motivates the present study, which aims to complete the picture of hierarchical chiral symmetry restoration in $N_f=2+1+1+1$ lattice QCD.

However, simulating $N_f=2+1+1+1$ lattice QCD with $(u,d,s,c,b)$ quarks at the physical point remains a grand challenge as discussed in Ref. [6]. To control both discretization and finite volume errors, the constraints $a\lesssim 0.03$ fm and $M_{\pi }L>4$ must be satisfied, which necessitate a lattice size larger than ${180}^3\times N_t$, exceeding the capabilities of current lattice computations.

Since our primary objective is to observe the emergence of $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ symmetry in QCD with $(u,d,s,c,b)$ quarks at temperatures $T\ge T_{c1}^{\overline{b}b}>T_{c1}^{\overline{c}c}$ (see the definition of $T_{c1}^{\overline{q}Q}$ in (2)) after the restoration of $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ symmetry for $(u,d,s,c)$ quarks at the lower temperature $T_{c1}^{\overline{c}c}$, this problem can be qualitatively addressed in lattice QCD with physical $(s,c,b)$ quarks but unphysically heavy $u/d$ quarks (e.g., with $M_{\pi }$∼700 MeV). Under these conditions, simulations can be conducted on ${40}^3\times (64,20,16,12,10,8,6,4,2)$ lattices using a modest GPU cluster. The “zero” temperature ensemble for the ${40}^3\times 64$ lattice has already been generated in ref. [6], along with the basic physical properties of mesons with flavor contents $\overline{b}b$, $\overline{b}c$, $\overline{b}s$, and $\overline{c}c$. In this exploratory study, we generate eight ensembles at finite temperatures, summarized in Table 1. Details of the simulation algorithms, the determination of the lattice spacing a, the $(s,c,b)$ physical quark masses, and the residual masses of $(u/d,s,c,b)$ quarks have been given in ref. [6] and the references therein. It is important to note that any results derived from these ensembles are subject to systematic uncertainties arising from unphysically heavy $u/d$ quarks, as well as discretization and finite volume effects. These uncertainties cannot be quantified within the present study, as the gauge ensembles include only a single unphysical $u/d$ quark mass, one spatial volume, and a single lattice spacing. Our goal here is not to provide a precise determination of the temperatures for the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ lattice QCD but rather to offer a qualitative picture of the hierarchical restoration of chiral symmetry in this system. This work represents a first step toward more precise determinations of $T_{c1}^{\overline{q}Q}$ with controlled systematics in future lattice studies, which will require simulations at the physical point and sufficiently large spatial volumes, with lattice sizes exceeding ${180}^3\times N_t$.

Table 1. The lattice parameters and statistics of the eight gauge ensembles for computing the meson correlators. The HMC simulations are performed with the Wilson plaquette gauge action [7] at $\beta =6/g^2=6.70$, the two-flavor optimal domain-wall fermion action for $u/d$ quarks [8,9], and the exact one-flavor optimal domain-wall fermion action for s, c, and b quarks [10,11]. The lattice spacing $a=0.0303\left(2\right)$ fm is determined by Wilson flow [12,13] with the condition $⟨t^{2}E\left(t\right)⟩{|}_{t=t_0}=0.3$ and input $\sqrt{t_0}=0.1416\left(8\right)$ fm [14]. The bare quark masses are $(m_{u/d},m_s,m_c,m_b)a=(0.010,0.015,0.200,0.850)$, where $m_s$, $m_c$, and $m_b$ are at the physical point, while the $u/d$ quarks are at the unphysical point with $M_{\pi }$∼700 MeV. The last four columns are the residual masses [15] of $u/d$, s, c, and b quarks.

${\mathit{N}}_{\mathit{x}}$	${\mathit{N}}_{\mathit{t}}$	T [MeV]	${\mathit{N}}_{\mathbf{confs}}$	${\left({\mathit{m}}_{\mathit{u}/\mathit{d}}\mathit{a}\right)}_{\mathbf{res}}$	${\left({\mathit{m}}_{\mathit{s}}\mathit{a}\right)}_{\mathbf{res}}$	${\left({\mathit{m}}_{\mathit{c}}\mathit{a}\right)}_{\mathbf{res}}$	${\left({\mathit{m}}_{\mathit{b}}\mathit{a}\right)}_{\mathbf{res}}$
40	20	325	306	8.21(33) $\times {10}^{-7}$	8.22(33) $\times {10}^{-7}$	8.70(33) $\times {10}^{-7}$	9.74(36) $\times {10}^{-7}$
40	16	406	382	9.35(28) $\times {10}^{-7}$	9.42(28) $\times {10}^{-7}$	9.82(28) $\times {10}^{-7}$	1.09(31) $\times {10}^{-6}$
40	12	524	380	9.46(28) $\times {10}^{-7}$	9.46(28) $\times {10}^{-7}$	9.74(28) $\times {10}^{-7}$	1.08(31) $\times {10}^{-7}$
40	10	650	260	9.12(33) $\times {10}^{-7}$	9.12(33) $\times {10}^{-7}$	9.25(34) $\times {10}^{-7}$	1.01(36) $\times {10}^{-8}$
40	8	813	337	1.03(3) $\times {10}^{-6}$	1.02(3) $\times {10}^{-6}$	1.04(3) $\times {10}^{-6}$	1.12(3) $\times {10}^{-6}$
40	6	1084	411	1.03(3) $\times {10}^{-6}$	1.03(3) $\times {10}^{-6}$	1.02(3) $\times {10}^{-6}$	1.07(3) $\times {10}^{-6}$
40	4	1626	337	1.13(4) $\times {10}^{-6}$	1.13(4) $\times {10}^{-6}$	1.12(4) $\times {10}^{-6}$	1.13(4) $\times {10}^{-6}$
40	2	3252	727	1.7(5) $\times {10}^{-7}$	1.7(5) $\times {10}^{-7}$	1.9(5) $\times {10}^{-7}$	2.3(5) $\times {10}^{-7}$

In this study, we adopt the same strategy as in refs. [4,5] to examine the hierarchical restoration of chiral symmetry in high-temperature QCD by analyzing the splittings of meson z-correlators within symmetry multiplets. In general, the meson z-correlator, $C_{\Gamma }\left(zT\right)$, of the meson interpolator $\overline{q}\Gamma Q$ is expressed as a function of the dimensionless variable:

$$\begin{array}{c}\hfill zT={\displaystyle \frac{n_{z}a}{N_{t}a}}={\displaystyle \frac{n_z}{N_t}},\end{array}$$

(1)

where $T={\displaystyle \frac{1}{N_{t}a}}$ is the temperature. For the classification of meson operators, along with their names and notations, we refer to Table II in ref. [5]. Additionally, we adopt the symmetry-breaking parameters as defined in ref. [5], following the same conventions and notations used therein. For the convenience of the reader, we summarize our conventions and notations in Appendix A.

We also recall the following notation introduced in ref. [5]:

$$T_{c1}^{\overline{q}Q}\equiv max(T_c^{\overline{q}Q},T_1^{\overline{q}Q}),$$

(2)

where $T_c^{\overline{q}Q}$ and $T_1^{\overline{q}Q}$ represent the temperatures at which the restoration of $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ and $U{\left(1\right)}_A$ chiral symmetries occurs, respectively, as determined via meson z-correlators with flavor content $\overline{q}Q$. For $T>T_{c1}^{\overline{q}Q}$, the theory exhibits the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry in the $\overline{q}Q$ sector.

Besides the hierarchical restoration of chiral symmetry, we are also interested in the emergence of symmetries that are not inherent to the full QCD action but apply only to specific components of it. One such example is the $SU{\left(2\right)}_{CS}$ chiral-spin symmetry (with $U{\left(1\right)}_A$ as a subgroup) [16,17], which is a symmetry of the chromoelectric part of the quark–gluon interaction and the color charge. Since free fermions and the chromomagnetic part of the quark–gluon interaction do not possess $SU{\left(2\right)}_{CS}$ symmetry, its emergence in high-temperature QCD suggests the possible existence of hadronlike objects predominantly bound by chromoelectric interactions. The first indication of approximate $SU{\left(2\right)}_{CS}$ symmetry was observed in the multiplets of z-correlators of vector mesons at temperatures T∼220–500 MeV in $N_f=2$ lattice QCD with domain-wall fermions [18]. In ref. [4], we investigated the emergence of $SU{\left(2\right)}_{CS}$ symmetry in $N_f=2+1+1$ lattice QCD with optimal domain-wall quarks at the physical point. Our findings indicated that $SU{\left(2\right)}_{CS}$ symmetry breaking in the $\overline{u}d$ sector of $N_f=2+1+1$ lattice QCD is larger than that in $N_f=2$ lattice QCD at the same temperature, for both z-correlators and t-correlators of vector mesons composed of u and d quarks. In ref. [5], our study was extended to all flavor combinations ($\overline{u}d$, $\overline{u}s$, $\overline{s}s$, $\overline{u}c$, $\overline{s}c$, and $\overline{c}c$), revealing that the temperature windows for the emergence of $SU{\left(2\right)}_{CS}$ symmetry are predominantly dominated by $\overline{u}c$ and $\overline{s}c$ sectors. In this work, we further extend our investigation to $N_f=2+1+1+1$ lattice QCD with physical $(s,c,b)$ quarks but unphysically heavy $u/d$ quarks, with $M_{\pi }\sim 700$ MeV.

The outline of this paper is as follows. In Section 2, we present the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ QCD, progressing from $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ to $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$, then to $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$, and finally to $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$. In Section 3, we estimate the approximate temperature windows for the emergent $SU{\left(2\right)}_{CS}$ symmetry across ten flavor combinations. Our findings indicate that the $SU{\left(2\right)}_{CS}$ symmetry is predominantly governed by the $\overline{u}b$ and $\overline{s}b$ sectors. In Section 4, we summarize our findings and provide concluding remarks. The appendices contain supplementary details. Appendix A summarizes the notations and conventions used in this paper. Appendix B estimates the variation of $\sqrt{t_0}$ as $M_{\pi }$ changes from 700 MeV to 140 MeV (the physical point). Appendix C tabulates the numerical values of ${\kappa }_{VA}$, ${\kappa }_{TX}$, $\kappa$, and ${\kappa }_{CS}$ for $zT=1$, 2, and 3 in each flavor sector. Appendix D provides the corresponding numerical values for $N_f=2+1+1$ lattice QCD at the physical point [5] at $zT=0.5$, 1, and 2.

2. Hierarchical Restoration of Chiral Symmetry

First, we recall the general features of symmetry-breaking parameters as discussed in ref. [5].

In general, the degeneracy of any two meson z-correlators $C_{{\Gamma }_A}\left(zT\right)$ and $C_{{\Gamma }_B}\left(zT\right)$ with flavor content $\overline{q}Q$ can be measured by the symmetry-breaking parameter

$$\begin{array}{c}\hfill {\kappa }_{AB}\left(zT\right)={\displaystyle \frac{\left|C_{{\Gamma }_A}\left(zT\right)-C_{{\Gamma }_B}\left(zT\right)\right|}{C_{{\Gamma }_A}\left(zT\right)+C_{{\Gamma }_B}\left(zT\right)}},z>0.\end{array}$$

(3)

If $C_{{\Gamma }_A}$ and $C_{{\Gamma }_B}$ are exactly degenerate at T, then ${\kappa }_{AB}=0$ for any z, and the symmetry is effectively restored at T. On the other hand, if there is any discrepancy between $C_A$ and $C_B$ at any z, then ${\kappa }_{AB}$ is nonzero at this z, and the symmetry is not exactly restored at T. Here, the denominator of (3) serves as (re)normalization and the value of ${\kappa }_{AB}$ is bounded between zero and one. Obviously, this criterion is more stringent than the equality of the ground-state screening masses, $m_A^{scr}=m_B^{scr}$, which are extracted from $C_{{\Gamma }_A}$ and $C_{{\Gamma }_B}$ at large z.

For example, the effective restoration of $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetry for any $\overline{q}Q$ implies that the correlators of the vector and axial-vector mesons are identical at all distances, i.e., $C_{V_k}\left(zT\right)=C_{A_k}\left(zT\right),(k=1,2,4)$ for any z at fixed T. Since each correlator consists of contributions from both the ground state and excited states, the equality of these correlators implies that the screening masses of the vector and axial-vector mesons are identical for the ground state as well as for each excited state. Similarly, the effective restoration of $U{\left(1\right)}_A$ symmetry for any $\overline{q}Q$ implies that the correlators of the pseudoscalar and scalar mesons are equal at all distances, $C_P\left(zT\right)=C_S\left(zT\right)$ for any z at fixed T. As with the vector and axial-vector correlators, this equality indicates that the screening masses of the pseudoscalar and scalar mesons are degenerate for both the ground state and each excited state.

Therefore, examining the degeneracy of the correlators of symmetry partners at any $z<N_z/2$ (accounting for the periodic boundary condition in the z direction) provides a more rigorous test of symmetry restoration than focusing solely on the degeneracy of the ground-state screening masses at large distances. Consequently, the symmetry-breaking parameters presented in this work offer more reliable insights into chiral symmetry breaking and restoration compared to approaches that rely only on the degeneracy of ground-state screening masses of symmetry partners.

The $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ symmetry breaking for any $\overline{q}Q$ sector can be measured by

$$\begin{array}{c}\hfill {\kappa }_{VA}\left(zT\right)={\displaystyle \frac{\left|C_{V_k}\left(zT\right)-C_{A_k}\left(zT\right)\right|}{C_{V_k}\left(zT\right)+C_{A_k}\left(zT\right)}},z>0,(k=1,2,4).\end{array}$$

(4)

In principle, any component of (4) can serve as the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ symmetry-breaking parameter. Due to the $S_2$ symmetry of the z-correlators, the $k=1$ and $k=2$ components are identical. To enhance the statistics, we average over $k=1$ and $k=2$ components to measure the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ symmetry breaking.

In general, to determine to what extent the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetry is restored, it is necessary to examine whether ${\kappa }_{VA}$ is sufficiently small. To this end, we use the following criterion for the manifestation of $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetry at T for a fixed $zT$:

$$\begin{array}{c}\hfill {\kappa }_{VA}\left(zT\right)\le {ϵ}_{VA},\end{array}$$

(5)

where ${ϵ}_{VA}$ is a small parameter which defines the precision of the chiral symmetry. For fixed $zT$ and ${ϵ}_{VA}$, the temperature $T_c$ is the lowest temperature satisfying (5), i.e.,

$$\begin{array}{c}\hfill {\kappa }_{VA}\left(zT\right)<{ϵ}_{VA}\mathrm{for}T>T_c.\end{array}$$

(6)

The $U{\left(1\right)}_A$ symmetry breaking for any $\overline{q}Q$ sector can be measured by the z-correlators in the pseudoscalar and scalar channels, with

$${\kappa }_{PS}\left(zT\right)={\displaystyle \frac{\left|C_P\left(zT\right)-C_S\left(zT\right)\right|}{C_P\left(zT\right)+C_S\left(zT\right)}},z>0,$$

(7)

as well as in the tensor vector and axial–tensor vector channels, with

$$\begin{array}{c}\hfill {\kappa }_{TX}\left(zT\right)={\displaystyle \frac{\left|C_{T_k}\left(zT\right)-C_{X_k}\left(zT\right)\right|}{C_{T_k}\left(zT\right)+C_{X_k}\left(zT\right)}},z>0,(k=1,2,4).\end{array}$$

(8)

In principle, (7) and any component of (8) can serve as the $U{\left(1\right)}_A$ symmetry-breaking parameter. In the following, we use (8) with $k=4$ to measure the $U{\left(1\right)}_A$ symmetry breaking. The reason for choosing the $k=4$ component is for consistency since the $k=4$ component of (8) is also needed to measure the $U{\left(1\right)}_A$ symmetry breaking in the multiplet $\{C_{A_1},C_{T_4},C_{X_4}\}$ of the $SU{\left(2\right)}_{CS}$ chiral-spin symmetry which contains $U{\left(1\right)}_A$ as a subgroup. (See the discussion in Section 3 and our notatations and conventions in refs. [4,5].)

Similar to (5), we use the following criterion for the manifestation of $U{\left(1\right)}_A$ symmetry at T for a fixed $zT$:

$$\begin{array}{c}\hfill {\kappa }_{TX}\left(zT\right)\le {ϵ}_{TX},\end{array}$$

(9)

where ${ϵ}_{TX}$ is a small parameter which defines the precision of $U{\left(1\right)}_A$ symmetry. For fixed $zT$ and ${ϵ}_{TX}$, the temperature $T_1$ is the lowest temperature satisfying (9), i.e.,

$$\begin{array}{c}\hfill {\kappa }_{TX}\left(zT\right)<{ϵ}_{TX}\mathrm{for}T>T_1.\end{array}$$

(10)

Next, consider QCD with $N_f$ quarks $(q_1,q_2,\cdots ,q_{N_f})$ where $N_f\ge 2$. As discussed in ref. [5], upon neglecting the disconnected diagrams in the meson z-correlators, the $SU{\left(N\right)}_L\times SU{\left(N\right)}_R$ chiral symmetry of N ($2\le N\le N_f$) quarks is manifested by the degeneracies of meson z-correlators in the vector and axial-vector channels, $C_{V_k}^{{\overline{q}}_i{q}_j}\left(z\right)=C_{A_k}^{{\overline{q}}_i{q}_j}\left(z\right)$, $(k=1,2,4)$, for all flavor combinations of N quarks (${\overline{q}}_i{q}_j$, $i,j=1,\cdots ,N$). Thus, to determine the temperature $T_c$ for the manifestation of the $SU{\left(N\right)}_L\times SU{\left(N\right)}_R$ chiral symmetry of N quarks, it needs to measure ${\kappa }_{VA}^{{\overline{q}}_i{q}_j}$ for all flavor combinations of N quarks, and check whether they all satisfy (6) for fixed $zT$ and ${ϵ}_{VA}$. This amounts to finding the largest $T_c^{{\overline{q}}_i{q}_j}$ satisfying (6) among all flavor combinations of N quarks, i.e.,

$$\begin{array}{c}\hfill T_c^N=max(T_c^{{\overline{q}}_i{q}_j},i,j=1,2,\cdots ,N).\end{array}$$

(11)

Similarly, about the $U{\left(1\right)}_A$ symmetry of N ($2\le N\le N_f$) quarks, upon neglecting the disconnected diagrams in the meson z-correlators, it is manifested by the degeneracies of meson z-correlators in the pseudoscalar and scalar channels, $C_P^{{\overline{q}}_i{q}_j}\left(z\right)=C_S^{{\overline{q}}_i{q}_j}\left(z\right)$, as well as in the tensor vector and axial–tensor vector channels, $C_{T_k}^{{\overline{q}}_i{q}_j}\left(z\right)=C_{X_k}^{{\overline{q}}_i{q}_j}\left(z\right)$, $(k=1,2,4)$, for all flavor combinations of N quarks (${\overline{q}}_i{q}_j$, $i,j=1,\cdots ,N$). To determine the temperature $T_1$ for the manifestation of $U{\left(1\right)}_A$ symmetry via the tensor vector and axial–tensor vector channels, it needs to measure ${\kappa }_{TX}^{{\overline{q}}_i{q}_j}$ for all flavor combinations of N quarks, and check whether they all satisfy (10) for fixed $zT$ and ${ϵ}_{TX}$. This amounts to finding the largest $T_1^{{\overline{q}}_i{q}_j}$ satisfying (10) among all flavor combinations of N quarks, i.e.,

$$\begin{array}{c}\hfill T_1^N=max(T_1^{{\overline{q}}_i{q}_j},i,j=1,2,\cdots ,N).\end{array}$$

(12)

Then, for the ${ϵ}_{VA}$ and ${ϵ}_{TX}$ specified in (6) and (10), the $SU{\left(N\right)}_L\times SU{\left(N\right)}_R\times U{\left(1\right)}_A$ chiral symmetry is effectively restored at

$$\begin{array}{c}\hfill T_{c1}^N=max(T_c^N,T_1^N).\end{array}$$

(13)

At this point, we recall that, in QCD with $N_f>2$ massless quarks, meson z-correlators for the flavor singlet and nonsinglet states with the same quantum numbers (i.e., scalar, pseudoscalar, vector, or axial-vector) become equal at temperatures above $T_c$ [19,20,21,22]. This equality implies that disconnected diagrams are suppressed in meson z-correlators for QCD with $N_f>2$ massless quarks at $T>T_c$. However, to what extent this suppression persists in QCD with $N_f=2+1+1+1$ massive quarks remains unknown. We aim to address this question through noise estimation of all-to-all quark propagators, an analysis that is currently underway.

2.1. Results of ${\kappa }_{VA}$ and ${\kappa }_{TX}$

Now we proceed to investigate the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ lattice QCD with physical s, c and b quarks but unphysically heavy $u/d$ quarks (with $M_{\pi }$∼700 MeV).

First, we compute two sets of quark propagators with periodic and antiperiodic boundary conditions in the z-direction while keeping the boundary conditions in the $(x,y,t)$-directions the same—periodic in $(x,y)$ and antiperiodic in t. Each set of quark propagators is independently used to construct the z-correlators according to Equation (A1), and their average is taken to obtain the final z-correlators. This procedure effectively cancels the contributions of unphysical meson states at large distances [4].

Using these refined z-correlators, we compute the chiral symmetry-breaking parameters ${\kappa }_{VA}\left(zT\right)$ and ${\kappa }_{TX}\left(zT\right)$, plotting them as functions of T for $zT=(1,2,3)$ as shown in Figure 1, Figure 2 and Figure 3. The numerical values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ are provided in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 of Appendix C for each flavor sector: $(\overline{u}d,\overline{u}s,\overline{s}s,\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b,\overline{c}c,\overline{c}b,\overline{b}b)$. The statistical errors of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ are estimated using the jackknife method with a bin size of ∼10–15 configurations of which the error saturates.

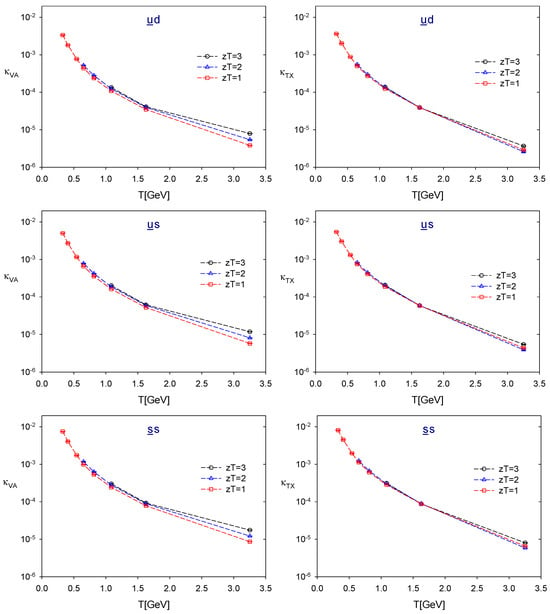
Figure 1. The chiral symmetry-breaking parameters $({\kappa }_{VA},{\kappa }_{TX})$ in the $(\overline{u}d,\overline{u}s,\overline{s}s)$ sectors.

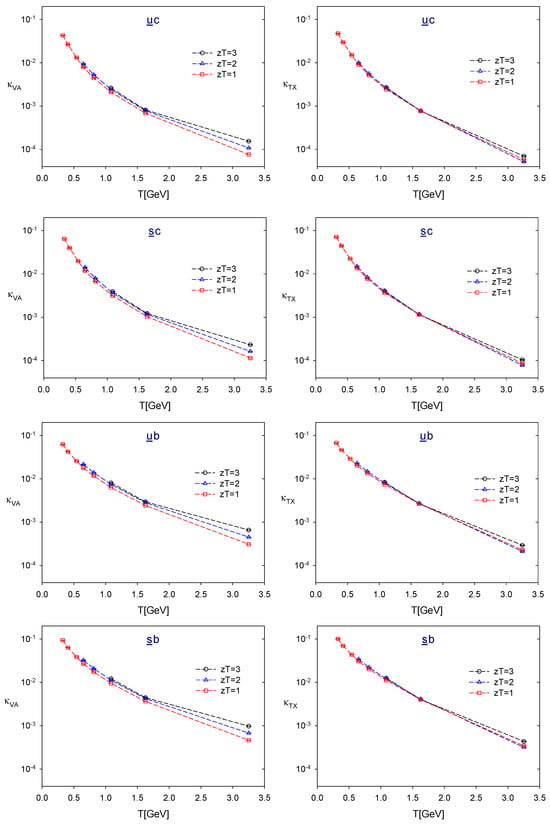
Figure 2. The chiral symmetry-breaking parameters $({\kappa }_{VA},{\kappa }_{TX})$ in the $(\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b)$ sectors.

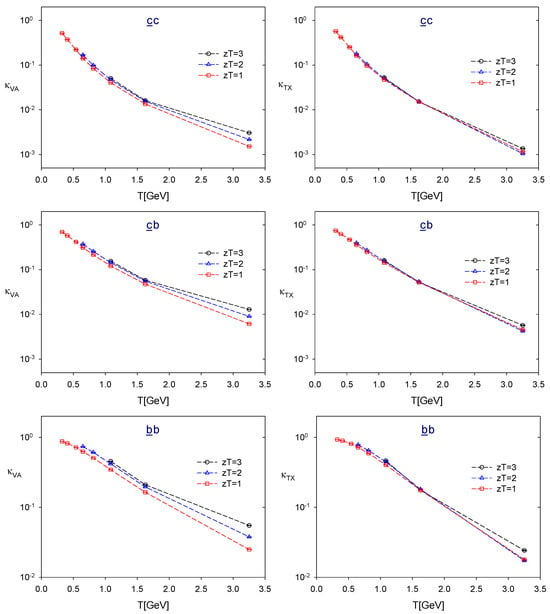
Figure 3. The chiral symmetry-breaking parameters $({\kappa }_{VA},{\kappa }_{TX})$ in the $(\overline{c}c,\overline{c}b,\overline{b}b)$ sectors.

For the z-correlators, the possible values of $zT$ at $T=1/\left(N_{t}a\right)$ are given by $\{n_z/N_t\mid n_z=1,2,\dots ,N_z/2\}$. Thus, for $N_z=40$ and $N_t=(20,16,12,10,8,6,4,2)$, the number of available temperature points is $(8,5,3)$ for $zT=(1,2,3)$, respectively, as illustrated in Figure 1, Figure 2 and Figure 3 and Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 of Appendix C.

First, for each flavor content, ${\kappa }_{VA}\left(zT\right)$ and ${\kappa }_{TX}\left(zT\right)$ at fixed $zT$ is a monotonic decreasing function of T. At each T, and for fixed $zT$, the chiral symmetry breakings due to the quark masses of the meson operator can be seen clearly from ${\kappa }_{VA}$ and ${\kappa }_{TX}$, in the order of

$$\begin{array}{c}\hfill {\kappa }_{\alpha }^{\overline{u}d}<{\kappa }_{\alpha }^{\overline{u}s}<{\kappa }_{\alpha }^{\overline{s}s}<{\kappa }_{\alpha }^{\overline{u}c}<{\kappa }_{\alpha }^{\overline{s}c}<{\kappa }_{\alpha }^{\overline{u}b}<{\kappa }_{\alpha }^{\overline{s}b}<{\kappa }_{\alpha }^{\overline{c}c}<{\kappa }_{\alpha }^{\overline{c}b}<{\kappa }_{\alpha }^{\overline{b}b},{\kappa }_{\alpha }={\kappa }_{VA},{\kappa }_{TX}.\end{array}$$

(14)

It follows that for any ${ϵ}_{VA}$ in (6) and any ${ϵ}_{TX}$ in (10), the flavor dependence of $T_c$ and $T_1$ is in the order of

$$\begin{array}{ccc}& & T_c^{\overline{u}d}<T_c^{\overline{u}s}<T_c^{\overline{s}s}<T_c^{\overline{u}c}<T_c^{\overline{s}c}<T_c^{\overline{u}b}<T_c^{\overline{s}b}<T_c^{\overline{c}c}<T_c^{\overline{c}b}<T_c^{\overline{b}b},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}& & T_1^{\overline{u}d}<T_1^{\overline{u}s}<T_1^{\overline{s}s}<T_1^{\overline{u}c}<T_1^{\overline{s}c}<T_1^{\overline{u}b}<T_1^{\overline{s}b}<T_1^{\overline{c}c}<T_1^{\overline{c}b}<T_1^{\overline{b}b}.\hfill \end{array}$$

(16)

This immediately gives

$$\begin{array}{c}\hfill T_{c1}^{\overline{u}d}<T_{c1}^{\overline{u}s}<T_{c1}^{\overline{s}s}<T_{c1}^{\overline{u}c}<T_{c1}^{\overline{s}c}<T_{c1}^{\overline{u}b}<T_{c1}^{\overline{s}b}<T_{c1}^{\overline{c}c}<T_{c1}^{\overline{c}b}<T_{c1}^{\overline{b}b},\end{array}$$

(17)

and the hierarchic restoration of chiral symmetry in $N_f=2+1+1+1$ QCD, i.e., from the restoration of $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d)$ quarks at $T>T_{c1}^{\overline{u}d}$ to the the restoration of $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks at $T>T_{c1}^{\overline{s}s}$, then to the restoration of $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks at $T>T_{c1}^{\overline{c}c}$, and finally to $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c,b)$ quarks at $T>T_{c1}^{\overline{b}b}$.

Thus, with the result of (17), our primary objective in this exploratory study (see the discussion in Section 1)—to observe the emergence of $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ symmetry in QCD with $(u,d,s,c,b)$—has been fulfilled. It is important to emphasize that our goal is to provide a qualitative understanding of the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ lattice QCD rather than to precisely determine the temperatures associated with this restoration.

In the following, we aim to estimate approximate values of $T_c$ and $T_1$ for each flavor sector by solving Equations (6) and (10) through interpolation or extrapolation of the data points for ${\kappa }_{VA}$ and ${\kappa }_{TX}$.

For example, at $zT=1$, if we impose ${ϵ}_{VA}={ϵ}_{TX}$∼0.025 as the criterion for chiral symmetry restoration, then the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ for the $\overline{b}b$ sector, as well as other flavor contents, are all below 0.025 at T∼3252 MeV as shown in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12. Consequently, the $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c,b)$ quarks is restored at $T_{c1}^{\overline{b}b}$∼$3252\left(10\right)$ MeV, in accordance with Equation (13).

The next step is to determine $T_{c1}^{\overline{c}c}$, at which the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks is restored. From Table A6, Table A7 and Table A10, the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ for the $(\overline{u}c,\overline{s}c,\overline{c}c)$ sectors decrease to approximately 0.025 at three different temperatures: $406<T_{c1}^{\overline{u}c}<542$ MeV, $406<T_{c1}^{\overline{s}c}<542$ MeV, and $1084<T_{c1}^{\overline{c}c}<1626$ MeV, following the hierarchy $T_{c1}^{\overline{u}c}<T_{c1}^{\overline{s}c}<T_{c1}^{\overline{c}c}$ in (17). Consequently, the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks is restored at $T_{c1}^{\overline{c}c}\sim 1385\left(50\right)$ MeV, estimated via piecewise linear interpolation of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ between 1084 MeV and 1626 MeV. The uncertainty in $T_c$ ($T_1$) is estimated by comparing results from two different schemes: piecewise linear interpolation of ${\kappa }_{VA}$ (${\kappa }_{TX}$) and piecewise linear interpolation of $\log \left({\kappa }_{VA}\right)$ ($\log \left({\kappa }_{TX}\right)$).

Similarly, from Table A3, Table A4 and Table A5 for the $(\overline{u}d,\overline{u}s,\overline{s}s)$ sectors, the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ fall below 0.025 at $T\sim 325$ MeV, the lowest temperature among the eight gauge ensembles listed in Table 1. This indicates that the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks has been restored at $T<325$ MeV. By applying piecewise linear extrapolation of $\log \left({\kappa }_{VA}\right)$ and $\log \left({\kappa }_{TX}\right)$, we estimate $T_{c1}^{\overline{s}s}\sim 167\left(8\right)$ MeV. Here, the logarithmic scale is preferred due to the observed linear behavior of $\log \left({\kappa }_{VA}\right)$ and $\log \left({\kappa }_{TX}\right)$ versus T for the three lowest temperature data points at $T=(325,406,542)$ MeV. Therefore, the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks is restored at $T_{c1}^{\overline{s}s}\sim 167\left(8\right)$ MeV, implying that the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d)$ quarks should be restored at $T_{c1}^{\overline{u}d}<167$ MeV. However, we do not attempt to estimate $T_{c1}^{\overline{u}d}$ via extrapolation, given the unphysically heavy $u/d$ quarks used in this study.

To summarize the hierarchical restoration of chiral symmetry for ${ϵ}_{VA}={ϵ}_{TX}\sim 0.025$ and $zT=1$, we give the following:

• First, the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d)$ quarks is expected to be restored at $T_{c1}^{\overline{u}d}<167$ MeV, but its precise determination is beyond the scope of this study.
• As the temperature increases, the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks is restored at $T_{c1}^{\overline{s}s}\sim 167\left(8\right)$ MeV.
• With further temperature increase, the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks is restored at $T_{c1}^{\overline{c}c}\sim 1385\left(50\right)$ MeV.
• Finally, the $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c,b)$ quarks is restored at $T_{c1}^{\overline{b}b}\sim 3252\left(10\right)$ MeV.

It should be emphasized that our results for $T_{c1}^{\overline{q}Q}$ are subject to systematic uncertainties arising from unphysically heavy $u/d$ quarks, as well as discretization and finite volume effects. These uncertainties cannot be quantified in the present study, as the available gauge ensembles include only a single unphysical $u/d$ quark mass, one spatial volume, and a single lattice spacing. Our goal is not to provide a precise determination of $T_c$ (or $T_1$) for each flavor content in $N_f=2+1+1+1$ lattice QCD but rather to offer a qualitative picture of the hierarchical restoration of chiral symmetry in the $N_f=2+1+1+1$ lattice QCD as demonstrated above. This work represents a first step toward more precise determinations of $T_{c1}$ with controlled systematics in future lattice studies, which will require simulations at the physical point and sufficiently large spatial volumes (i.e., >${180}^3\times N_t$).

Next, we demonstrate how $T_c$ and $T_1$ depend on ${ϵ}_{VA}$ and ${ϵ}_{TX}$ in (6) and (10). Since ${\kappa }_{VA}^{{\overline{q}}_1{q}_2}$ (${\kappa }_{TX}^{{\overline{q}}_1{q}_2}$) at fixed $zT$ is a monotonically decreasing function of T, it follows that $T_c$ ($T_1$) increases as ${ϵ}_{VA}$ (${ϵ}_{TX}$) decreases (i.e., the precision of chiral symmetry improves).

For example, consider the case at $zT=1$ when both ${ϵ}_{VA}$ and ${ϵ}_{TX}$ are decreased from 0.025 to 0.015. According to Table A3, Table A4 and Table A5, at $T=325$ MeV (the lowest temperature of the gauge ensembles), the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ for the $(\overline{u}d,\overline{u}s,\overline{s}s)$ sectors are all significantly below 0.015. This suggests that the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks must have been restored at $T<325$ MeV. Using the piecewise linear extrapolation of $\log \left({\kappa }_{VA}\right)$ and $\log \left({\kappa }_{TX}\right)$, we estimate $T_{c1}^{\overline{s}s}\sim 240\left(10\right)$ MeV. The choice of using logarithmic values instead of linear ones follows the same reasoning as in the case where ${ϵ}_{VA}={ϵ}_{TX}\sim 0.025$ at $zT=1$. Thus, the restoration of $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry occurs at $T_{c1}^{\overline{s}s}\sim 240\left(10\right)$ MeV.

At higher temperatures, Table A6, Table A7, and Table A10 show that the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ for the $(\overline{u}c,\overline{s}c,\overline{c}c)$ sectors decrease to approximately 0.015 at temperatures $T_{c1}^{\overline{u}c}\sim 542$ MeV, 542 MeV $<T_{c1}^{\overline{s}c}<$ 650 MeV, and $T_{c1}^{\overline{c}c}\sim 1626$ MeV. Consequently, the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks is restored at $T_{c1}^{\overline{c}c}\sim 1626\left(20\right)$ MeV.

Turning to the $\overline{b}b$ sector, Table A12 indicates that for $zT=1$, the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ remain above 0.015 even at $T=3252$ MeV, the highest temperature among the eight gauge ensembles studied. This implies that the $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c,b)$ quarks is restored only at $T_{c1}^{\overline{b}b}>3252$ MeV. Using the piecewise linear extrapolation of ${\kappa }_{VA}$ and ${\kappa }_{TX}$, we estimate $T_{c1}^{\overline{b}b}\sim 3370\left(50\right)$ MeV.

This analysis demonstrates the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ QCD for ${ϵ}_{VA}={ϵ}_{TX}\sim 0.015$ and $zT=1$, progressing from the restoration of $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ for $(u,d,s)$ quarks at $T_{c1}^{\overline{s}s}\sim 240\left(10\right)$ MeV, to $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ for $(u,d,s,c)$ quarks at $T_{c1}^{\overline{c}c}\sim 1626\left(20\right)$ MeV, and finally to $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ for $(u,d,s,c,b)$ quarks at $T_{c1}^{\overline{b}b}\sim 3370\left(50\right)$ MeV.

Clearly, regardless of how small ${ϵ}_{VA}$ and ${ϵ}_{TX}$ become, the hierarchical restoration of chiral symmetry in QCD with $(u,d,s,c,b)$ quarks will occur at progressively higher temperatures.

2.2. Comparison with $N_f=2+1+1$ Lattice QCD at the Physical Point

Now we compare the chiral symmetry-breaking parameters, ${\kappa }_{VA}$ and ${\kappa }_{TX}$, in $N_f=2+1+1+1$ lattice QCD with those in $N_f=2+1+1$ lattice QCD at the physical point [5]. The numerical values for $N_f=2+1+1+1$ QCD are presented in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12, while those for $N_f=2+1+1$ QCD can be found in Table A13, Table A14, Table A15, Table A16, Table A17 and Table A18. Figure 4 and Figure 5 show the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ at $zT=1$ for both lattice setups.

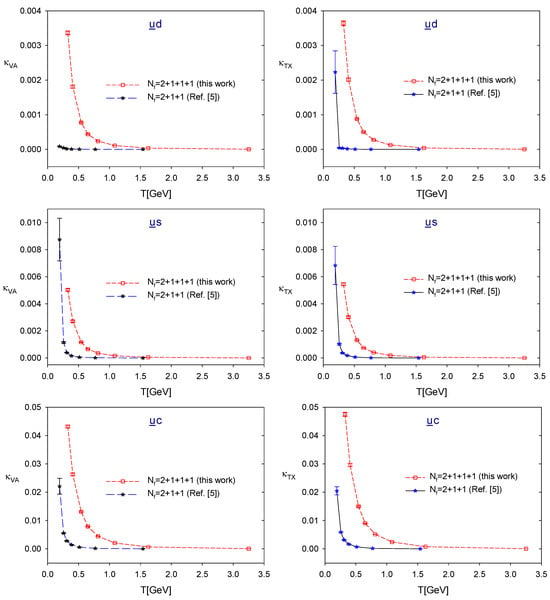
Figure 4. Comparison of the chiral symmetry-breaking parameters, ${\kappa }_{VA}$ and ${\kappa }_{TX}$, in the $(\overline{u}d,\overline{u}s,\overline{u}c)$ sectors for lattice QCD with $N_f=2+1+1+1$ (this work) and $N_f=2+1+1$ at the physical point [5].

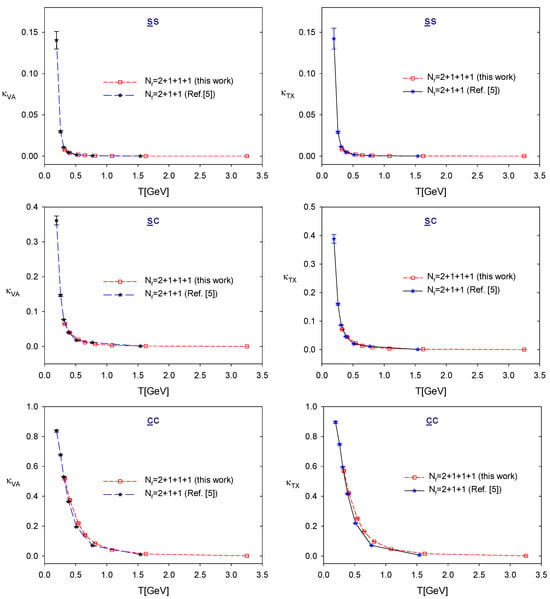
Figure 5. Comparison of the chiral symmetry-breaking parameters, ${\kappa }_{VA}$ and ${\kappa }_{TX}$, in the $(\overline{s}s,\overline{s}c,\overline{c}c)$ sectors for lattice QCD with $N_f=2+1+1+1$ (this work) and $N_f=2+1+1$ at the physical point [5].

For the $(\overline{u}d,\overline{u}s,\overline{u}c)$ sectors, significant discrepancies are observed, which can be attributed to the unphysically heavy $u/d$ quarks contributing to both the valence quark propagators and the vacuum fluctuations in the sea.

For the $\overline{s}s$ and $\overline{s}c$ sectors, the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ in $N_f=2+1+1+1$ lattice QCD are in good agreement with those in $N_f=2+1+1$ lattice QCD at the physical point, despite the presence of unphysically heavy $u/d$ quarks in the sea.

For the $\overline{c}c$ sector, the values of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ in $N_f=2+1+1+1$ lattice QCD are in reasonable agreement with those in $N_f=2+1+1$ lattice QCD at the physical point. However, discrepancies in the temperature range $T\sim 400$–1200 MeV are more pronounced compared to those in the $\overline{s}s$ and $\overline{s}c$ sectors. At a fixed temperature, ${\kappa }_{VA}$ and ${\kappa }_{TX}$ in the $N_f=2+1+1+1$ lattice QCD are consistently larger than those in $N_f=2+1+1$ lattice QCD. Due to the limited number of data points in both lattice setups, precisely quantifying these discrepancies remains challenging. Since both setups are subject to discretization and finite volume uncertainties, these effects are likely the primary sources of the observed differences. A more thorough understanding would require taking the continuum and infinite volume limits for both lattice setups, which is beyond the scope of this paper.

Next, we compare $T_c$ ($T_1$) between the two lattice setups for a given ${ϵ}_{VA}$ (${ϵ}_{TX}$). This generally requires interpolation or extrapolation ${\kappa }_{VA}$ (${\kappa }_{TX}$) to solve Equation (6) or (10), which may introduce significant uncertainties due to the limited number of data points in both setups.

This issue becomes particularly severe when ${ϵ}_{VA}$ or ${ϵ}_{TX}$ falls below 0.01, as the approximate solutions for $T_c$ and $T_1$ extend into or beyond the range of the two highest-temperature data points: $(770,1540)$ MeV for $N_f=2+1+1$ QCD and $(1626,3252)$ MeV for $N_f=2+1+1+1$ QCD. Consequently, the interpolation or extrapolation of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ may introduce large uncertainties, leading to discrepancies of approximately 100–300 MeV in the estimated values of $T_c$ and $T_1$. Furthermore, these two highest-temperature data points correspond to the smallest values of $N_t=4$ and 2, which can introduce significant discretization errors and distort the z-correlators, thereby affecting ${\kappa }_{VA}$ and ${\kappa }_{TX}$. In other words, interpolation or extrapolation using only the two highest-temperature data points in each lattice setup is prone to large systematic errors. As a result, the discrepancies in $T_c$ and $T_1$ between the two lattice setups may increase as ${ϵ}_{VA}$ and ${ϵ}_{TX}$ decrease—that is, as higher precision in chiral symmetry is pursued.

In view of the above discussion, we set ${ϵ}_{VA}$ and ${ϵ}_{TX}$ to 0.1 and 0.05 (both smaller than 0.01) and estimate approximate values of $T_c$ and $T_1$ in the ($\overline{s}s,\overline{s}c,\overline{c}c)$ sectors for two lattice setups.

In Table 2 and Table 3, we compare $T_c$ and $T_1$ for the $(\overline{s}s,\overline{s}c,\overline{c}c)$ sectors in two lattice setups at $zT=1$, with ${ϵ}_{VA}={ϵ}_{TX}=0.1$ and 0.05. The values of $T_c$ and $T_1$ are obtained by solving Equations (6) and (10) through the interpolation or extrapolation of ${\kappa }_{VA}$ and ${\kappa }_{TX}$. The uncertainty in each $T_c$ ($T_1$) is estimated by comparing results from two different schemes: piecewise linear interpolation/extrapolation of ${\kappa }_{VA}$ (${\kappa }_{TX}$) and piecewise linear interpolation/extrapolation of $\log \left({\kappa }_{VA}\right)$ ($\log \left({\kappa }_{TX}\right)$).

Table 2. Comparison of $T_c^{\overline{s}s}$, $T_c^{\overline{s}c}$, and $T_c^{\overline{c}c}$ between $N_f=2+1+1$ and $N_f=2+1+1+1$ lattice QCD, for $zT=1$ and ${ϵ}_{VA}=0.1$ and 0.05, respectively.

	${\mathit{N}}_{\mathit{f}}=2+1+1$ [5]		${\mathit{N}}_{\mathit{f}}=2+1+1+1$ (This Work)
${\mathit{ϵ}}_{\mathit{VA}}$	0.1	0.05	0.1	0.05
$T_c^{\overline{s}s}$ [MeV]	210(5)	240(10)	<325	<325
$T_c^{\overline{s}c}$ [MeV]	285(10)	360(10)	250(40)	370(10)
$T_c^{\overline{c}c}$ [MeV]	710(30)	965(50)	760(20)	1010(20)

Table 3. Comparison of $T_1^{\overline{s}s}$, $T_1^{\overline{s}c}$, and $T_1^{\overline{c}c}$ between $N_f=2+1+1$ and $N_f=2+1+1+1$ lattice QCD, for $zT=1$ and ${ϵ}_{TX}=0.1$ and 0.05, respectively.

	${\mathit{N}}_{\mathit{f}}=2+1+1$ [5]		${\mathit{N}}_{\mathit{f}}=2+1+1+1$ (This Work)
${\mathit{ϵ}}_{\mathit{TX}}$	0.1	0.05	0.1	0.05
$T_1^{\overline{s}s}$ [MeV]	210(5)	240(10)	<325	<325
$T_1^{\overline{s}c}$ [MeV]	295(10)	370(10)	270(30)	380(10)
$T_1^{\overline{c}c}$ [MeV]	720(30)	1020(30)	800(50)	1060(20)

First, consider the $\overline{s}s$ sector. For ${ϵ}_{VA}={ϵ}_{TX}=0.1$ and 0.05, $T_c$ and $T_1$ of $N_f=2+1+1+1$ lattice QCD cannot be determined using any of the two extrapolation schemes mentioned above, as the values fall well below 325 MeV (the lowest temperature of the gauge ensembles in this study). Consequently, a comparison in this case is not possible.

Next, consider the $\overline{s}c$ and $\overline{c}c$ sectors. For ${ϵ}_{VA}={ϵ}_{TX}=0.1$ and 0.05, the values of $T_c$ ($T_1$) from $N_f=2+1+1+1$ and $N_f=2+1+1$ lattice QCD are in good agreement, within the uncertainties due to interpolation.

Overall, the reasonable agreement of ${\kappa }_{VA}$ and ${\kappa }_{TX}$ as well as $T_c$ and $T_1$ between $N_f=2+1+1+1$ lattice QCD and $N_f=2+1+1$ lattice QCD at the physical point [5] for the $(\overline{s}s,\overline{s}c,\overline{c}c)$ sectors highlights the consistency between these two lattice setups for the physical s and c quarks.

3. $\mathit{SU}{\left(\mathbf{2}\right)}_{\mathit{CS}}$ Chiral-Spin Symmetry

In this section, we explore the emergence of approximate $SU{\left(2\right)}_{CS}$ chiral-spin symmetry in $N_f=2+1+1+1$ lattice QCD. Our results are subject to systematic uncertainties arising from unphysically heavy $u/d$ quarks, as well as discretization and finite volume effects. These uncertainties cannot be quantified within this study, as the gauge ensembles include only a single unphysical $u/d$ quark mass, one spatial volume, and a single lattice spacing. Rather than precisely determining the temperatures at which approximate $SU{\left(2\right)}_{CS}$ chiral-spin symmetry emerges in each flavor sector, our aim is to provide a qualitative picture of its behavior in $N_f=2+1+1+1$ lattice QCD.

First, we recall the $S{U}_{CS}$ symmetry-breaking and -fading parameters $({\kappa }_{CS},\kappa )$ as defined in ref. [5], following the same notations and conventions.

In general, to examine the emergence of $SU{\left(2\right)}_{CS}$ symmetry, it needs to measure the splittings in the $S{U}_{CS}\left(2\right)$ multiplet $(A_1,T_4,X_4)$. Since the splitting of $T_4$ and $X_4$ has been measured by the $U{\left(1\right)}_A$ symmetry-breaking parameter ${\kappa }_{TX}$ (8) with $k=4$, it remains to measure the splitting of $A_1$ and $X_4$ with

$$\begin{array}{c}\hfill {\kappa }_{AX}\left(zT\right)={\displaystyle \frac{\left|C_{A_1}\left(zT\right)-C_{X_4}\left(zT\right)\right|}{C_{A_1}\left(zT\right)+C_{X_4}\left(zT\right)}},z>0,\end{array}$$

(18)

then taking the maximum of ${\kappa }_{AT}$ and ${\kappa }_{TX}$ as the $SU{\left(2\right)}_{CS}$ symmetry-breaking parameter,

$$\begin{array}{c}\hfill {\kappa }_{CS}=max({\kappa }_{AX},{\kappa }_{TX}).\end{array}$$

(19)

Note that ${\kappa }_{AX}$ in (18) is exactly the same as ${\kappa }_{AT}$ in ref. [5]. Here, we just change the subscript from $AT$ to $AX$ for consistency since it refers to the splitting of the axial vector $A_1$ and the axial–tensor vector $X_4$.

As the temperature T is increased, the separation between the multiplets of $SU{\left(2\right)}_{CS}$ and $U{\left(1\right)}_A$ is decreased. Therefore, at sufficiently high temperatures $T>T_c^{\overline{q}Q}$, the $U{\left(1\right)}_A$ multiplet $M_0=(P,S)$ and the $SU{\left(2\right)}_{CS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ multiplet $M_2=(V_1,A_1,T_4,X_4)$ merge together, then the $SU{\left(2\right)}_{CS}$ symmetry becomes washed out, and only the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry remains. Note that the $SU{\left(2\right)}_{CS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ multiplet $M_4=(V_4,A_4,T_1,X_1)$ never merges with $M_0$ and $M_2$ even in the limit $T\to \infty$, as discussed in Ref. [4]. Thus, $M_4$ is irrelevant to the fading of the $SU{\left(2\right)}_{CS}$ symmetry. Following Ref. [5], we use $\kappa \left(zT\right)$ to measure the fading of the $SU{\left(2\right)}_{CS}$ symmetry:

$$\begin{array}{c}\hfill \kappa \left(zT\right)=\left|{\displaystyle \frac{C_{A_1}\left(zT\right)-C_{X_4}\left(zT\right)}{C_{M_0}\left(zT\right)-C_{M_2}\left(zT\right)}}\right|,z>0,\end{array}$$

(20)

where

$$\begin{array}{ccc}& & C_{M_0}\left(zT\right)\equiv {\displaystyle \frac{1}{2}}\left[C_P\left(zT\right)+C_S\left(zT\right)\right],\hfill \\ & & C_{M_2}\left(zT\right)\equiv {\displaystyle \frac{1}{4}}\left[C_{V_1}\left(zT\right)+C_{A_1}\left(zT\right)+C_{T_4}\left(zT\right)+C_{X_4}\left(zT\right)\right].\hfill \end{array}$$

Thus, to determine to what extent the $SU{\left(2\right)}_{CS}$ symmetry is manifested in the z-correlators, it is necessary to examine whether both $\kappa \left(zT\right)$ and ${\kappa }_{CS}\left(zT\right)$ are sufficiently small. For a fixed $zT$, the following condition

$$\begin{array}{c}\hfill \left({\kappa }_{CS}\left(zT\right)<{ϵ}_{cs}\right)\wedge \left(\kappa \left(zT\right)<{ϵ}_{fcs}\right)\end{array}$$

(21)

serves as a criterion for the $SU{\left(2\right)}_{CS}$ symmetry in the z-correlators, where ${ϵ}_{cs}$ is for the $SU{\left(2\right)}_{CS}$ symmetry-breaking, while ${ϵ}_{fcs}$ for the $SU{\left(2\right)}_{CS}$ symmetry fading. For fixed $zT$, (21) gives a window of T for the $SU{\left(2\right)}_{CS}$ symmetry. Obviously, the size of this window depends on ${ϵ}_{cs}$ and ${ϵ}_{fcs}$. That is, larger ${ϵ}_{cs}$ or ${ϵ}_{fcs}$ gives a wider window of T, and conversely, smaller ${ϵ}_{cs}$ or ${ϵ}_{fcs}$ gives a narrower window of T.

3.1. Results of ${\kappa }_{CS}$ and $\kappa$

We now proceed to study the $SU{\left(2\right)}_{CS}$ symmetry in $N_f=2+1+1+1$ lattice QCD, incorporating physical s, c, and b quarks but unphysically heavy $u/d$ quarks ($M_{\pi }\sim 700$ MeV).

To this end, we first compute the z-correlators following the procedure outlined in Section 2. We then evaluate the $SU{\left(2\right)}_{CS}$ symmetry-breaking parameter (${\kappa }_{CS}$) and the symmetry-fading parameter ($\kappa$) and plot them as functions of temperature T for $zT=(1,2,3)$ as shown in Figure 6, Figure 7 and Figure 8. The numerical values of ${\kappa }_{CS}$ and $\kappa$ for each flavor sector $(\overline{u}d,\overline{u}s,\overline{s}s,\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b,\overline{c}c,\overline{c}b,\overline{b}b)$ are tabulated in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 in Appendix C. The statistical error for each ${\kappa }_{CS}$ or $\kappa$ is estimated using the jackknife method with a bin size of ∼$10–15$ configurations, of which the statistical error saturates.

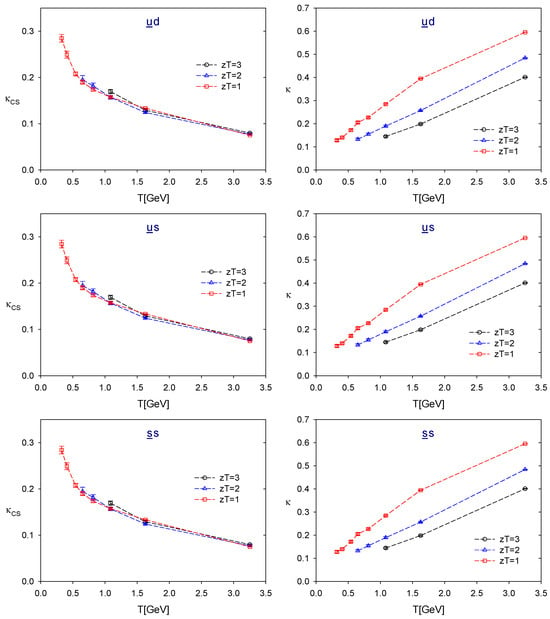
Figure 6. The chiral-spin symmetry-breaking and -fading parameters of the $(\overline{u}d,\overline{u}s,\overline{s}s)$ sectors.

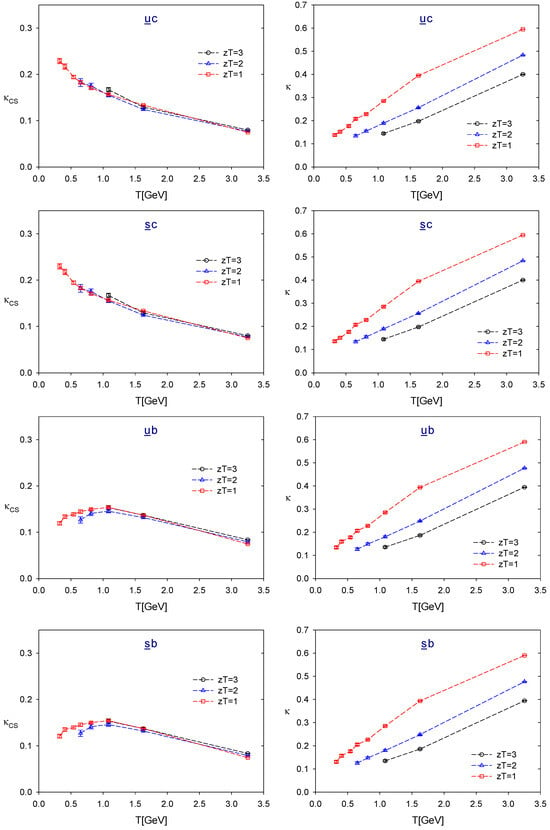
Figure 7. The chiral-spin symmetry-breaking and -fading parameters of the $(\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b)$ sectors.

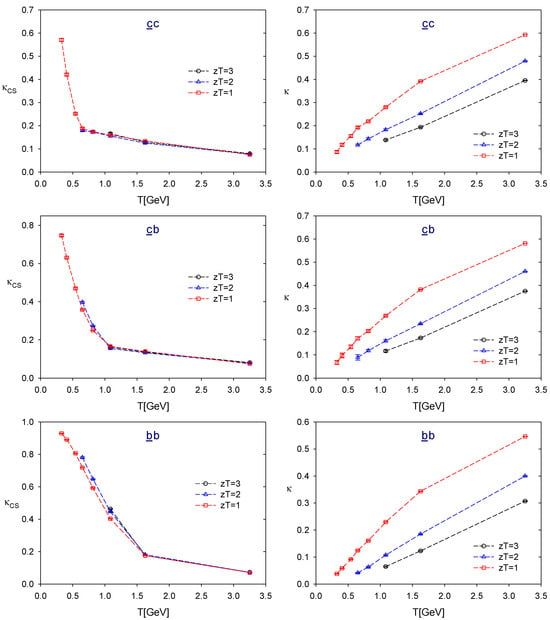
Figure 8. The chiral-spin symmetry-breaking and -fading parameters of the $(\overline{s}c,\overline{s}b,\overline{c}b)$ sectors.

For the z-correlators, the possible values of $zT$ at $T=1/\left(N_{t}a\right)$ are

$$\left\{{\displaystyle \frac{n_z}{N_t}}\mid n_z=1,2,\dots ,{\displaystyle \frac{N_z}{2}}\right\}.$$

Thus, for $N_z=40$ and $N_t=(20,16,12,10,8,6,4,2)$, the number of available temperature points is $(8,5,3)$ for $zT=(1,2,3)$, respectively, as illustrated in Figure 6, Figure 7 and Figure 8 and Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12.

For the $(\overline{u}d,\overline{u}s,\overline{s}s,\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b)$ sectors, we find that

$${\kappa }_{AX}\left(zT\right)>{\kappa }_{TX}\left(zT\right)\mathrm{for}\mathrm{all}zT\mathrm{at}\mathrm{the}\mathrm{same}T.$$

Thus, (19) gives ${\kappa }_{CS}={\kappa }_{AX}$. However, for the $(\overline{c}c,\overline{c}b,\overline{b}b)$ sectors, we observe that

$${\kappa }_{AX}\left(zT\right)<{\kappa }_{TX}\left(zT\right)$$

at low temperatures, while ${\kappa }_{AX}\left(zT\right)>{\kappa }_{TX}\left(zT\right)$ at high temperatures. Thus, (19) gives ${\kappa }_{CS}={\kappa }_{TX}$ at low temperatures but ${\kappa }_{CS}={\kappa }_{AX}$ at high temperatures. This results in an abrupt transition at some intermediate temperature. This transition is evident in the left panels of Figure 8.

In general, for any flavor content and at fixed $zT$, $\kappa$ is a monotonically increasing function of T, while ${\kappa }_{CS}$ is a monotonically decreasing function of T, except for the $\overline{u}b$ and $\overline{s}b$ sectors as seen in Figure 7. Thus, for any given ${ϵ}_{cs}$ and ${ϵ}_{fcs}$, we can determine the temperature window satisfying the criterion (21) for each flavor content. Moreover, as ${ϵ}_{cs}$ or ${ϵ}_{fcs}$ decreases, the window of T narrows and eventually vanishes.

We estimate the approximate T-window for each flavor sector by solving (21) through interpolation or extrapolation of the available data points for ${\kappa }_{CS}$ and $\kappa$, as tabulated in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 in Appendix C. For $zT=1,2,$ and 3, we estimate the temperature windows for all ten flavor sectors, as presented in Table 4, Table 5 and Table 6, across all values of ${ϵ}_{cs}$ and ${ϵ}_{fcs}$, sampled from (0.1, 0.15, 0.20). Each T-window is expressed in MeV, with uncertainties of approximately 10–20 MeV on both ends, combining statistical and interpolation/extrapolation uncertainties in quadrature. If the lower bound of a T-window cannot be reliably determined by extrapolation below 325 MeV, it is denoted as “<325 MeV”. Likewise, temperatures that cannot be reliably extrapolated below 650 MeV are represented as “<650 MeV”.

Table 4. The approximate ranges of T satisfying the criterion (21) at $zT=1$ for ten flavor contents. The table lists all nonzero windows of T for all values of ${ϵ}_{cs}$ and ${ϵ}_{fcs}$ sampling from $(0.1,0.15,0.20)$. Each T window is in units of MeV, with uncertainties ∼10–20 MeV on both ends of the window.

${\mathit{ϵ}}_{\mathit{cs}}$	${\mathit{ϵ}}_{\mathit{fcs}}$	$\overline{\mathit{u}}\mathit{d}$	$\overline{\mathit{u}}\mathit{s}$	$\overline{\mathit{s}}\mathit{s}$	$\overline{\mathit{u}}\mathit{c}$	$\overline{\mathit{s}}\mathit{c}$	$\overline{\mathit{u}}\mathit{b}$	$\overline{\mathit{s}}\mathit{b}$	$\overline{\mathit{c}}\mathit{c}$	$\overline{\mathit{c}}\mathit{b}$	$\overline{\mathit{b}}\mathit{b}$
0.20	0.20	590–635	590–635	590–635	510–620	510–625	<325-625	<325–630	<650–700	NULL	NULL
0.20	0.15	NULL	NULL	NULL	NULL	NULL	<325–375	<325–385	NULL	NULL	NULL
0.15	0.20	NULL	NULL	NULL	NULL	NULL	<325–625	<325–630	NULL	NULL	NULL
0.15	0.15	NULL	NULL	NULL	NULL	NULL	<325–375	<325–385	NULL	NULL	NULL
0.10	0.20	NULL	NULL	NULL	NULL	NULL	<325–625	<325–630	NULL	NULL	NULL
0.10	0.15	NULL	NULL	NULL	NULL	NULL	<325–375	<325–385	NULL	NULL	NULL
0.10	0.10	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL

Table 5. Same as Table 4 except for $zT=2$.

${\mathit{ϵ}}_{\mathit{cs}}$	${\mathit{ϵ}}_{\mathit{fcs}}$	$\overline{\mathit{u}}\mathit{d}$	$\overline{\mathit{u}}\mathit{s}$	$\overline{\mathit{s}}\mathit{s}$	$\overline{\mathit{u}}\mathit{c}$	$\overline{\mathit{s}}\mathit{c}$	$\overline{\mathit{u}}\mathit{b}$	$\overline{\mathit{s}}\mathit{b}$	$\overline{\mathit{c}}\mathit{c}$	$\overline{\mathit{c}}\mathit{b}$	$\overline{\mathit{b}}\mathit{b}$
0.20	0.20	<650–1170	<650–1170	<650–1170	<650–1170	<650–1170	<325–1240	<325–1245	<650–1220	980–1375	1590–1740
0.20	0.15	<650–780	<650–780	<650–780	<650–780	<650–780	<325–825	<325–830	<650–860	980–1020	NULL
0.20	0.10	NULL	NULL	NULL	<650–385	<650–390	<325–450	<325–460	NULL	NULL	NULL
0.15	0.20	NULL	NULL	NULL	NULL	NULL	<325–1240	<325–1245	1175–1220	1190–1375	NULL
0.15	0.15	NULL	NULL	NULL	NULL	NULL	<325–825	<325–830	NULL	NULL	NULL
0.15	0.10	NULL	NULL	NULL	NULL	NULL	<325–450	<325–460	NULL	NULL	NULL
0.10	0.20	NULL	NULL	NULL	NULL	NULL	<325–340	<325–335	NULL	NULL	NULL
0.10	0.15	NULL	NULL	NULL	NULL	NULL	<325–340	<325–335	NULL	NULL	NULL
0.10	0.10	NULL	NULL	NULL	NULL	NULL	<325–340	<325–335	NULL	NULL	NULL

Table 6. Same as Table 4 except for $zT=3$.

${\mathit{ϵ}}_{\mathit{cs}}$	${\mathit{ϵ}}_{\mathit{fcs}}$	$\overline{\mathit{u}}\mathit{d}$	$\overline{\mathit{u}}\mathit{s}$	$\overline{\mathit{s}}\mathit{s}$	$\overline{\mathit{u}}\mathit{c}$	$\overline{\mathit{s}}\mathit{c}$	$\overline{\mathit{u}}\mathit{b}$	$\overline{\mathit{s}}\mathit{b}$	$\overline{\mathit{c}}\mathit{c}$	$\overline{\mathit{c}}\mathit{b}$	$\overline{\mathit{b}}\mathit{b}$
0.20	0.20	675–1640	675–1640	675–1640	610–1650	610–1650	<325–1730	<325–1735	<650–1680	980–1850	1580–2310
0.20	0.15	675–1140	675–1140	675–1140	610–1140	610–1140	<325–1235	<325–1240	<650–1200	980–1410	1580–1870
0.15	0.20	1345–1640	1345–1640	1345–1640	1330–1650	1330–1650	1190–1730	1190–1735	1315–1680	1315–1850	2030–2310
0.20	0.10	NULL	NULL	NULL	610–630	610–630	<325–705	<325–710	<650–710	NULL	NULL
0.15	0.15	NULL	NULL	NULL	NULL	NULL	1190–1235	1190–1240	NULL	1315–1410	NULL
0.15	0.10	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL
0.10	0.10	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL	NULL

Table 4, Table 5 and Table 6 show that as $({ϵ}_{cs},{ϵ}_{fcs})$ decrease from (0.20, 0.20) to (0.15, 0.15), and further to (0.10, 0.10), the T-windows for all flavor sectors progressively shrink and eventually vanish, except for the $\overline{u}b$ and $\overline{s}b$ sectors, which retain nonzero T-windows. This indicates that the T-windows of the emergent $SU{\left(2\right)}_{CS}$ symmetry are primarily dominated by the $\overline{u}b$ and $\overline{s}b$ sectors, composed of the heaviest b quark and the light quarks of the system.

Notably, in lattice QCD with $(u,d,s,c)$ quarks, the T-windows of the emergent $SU{\left(2\right)}_{CS}$ symmetry are predominantly governed by the $\overline{u}c$ and $\overline{s}c$ sectors, composed of the heaviest c quark and the light quarks of the system, as reported in ref. [5]. Comparing these two lattice setups suggests an important universal feature of any QCD system: the T-windows of the emergent chiral-spin symmetry are primarily dominated by the sectors involving the heaviest quark and the light quarks of the system.

The results in Table 4, Table 5 and Table 6 also indicate that the most favorable channels for detecting the emergence of $SU{\left(2\right)}_{CS}$ symmetry in QCD with $(u,d,s,c,b)$ quarks are in vector mesons with flavor contents $\overline{u}b$ ($\overline{d}b$) and $\overline{s}b$. This finding may have phenomenological implications for observing $SU{\left(2\right)}_{CS}$ symmetry in relativistic heavy-ion collisions at experiments such as the LHC and RHIC.

Moreover, this suggests that hadron-like objects, particularly vector mesons with flavor contents $\overline{s}b$ and $\overline{u}b$ ($\overline{d}b$), are more likely to be predominantly bound by chromoelectric interactions into color singlets at temperatures within their respective T-windows of the emergent $SU{\left(2\right)}_{CS}$ symmetry. This is notable because neither the chromomagnetic part of the quark–gluon interaction nor the noninteracting theory with free quarks possesses any $SU{\left(2\right)}_{CS}$ symmetry.

It is important to note that since the $u/d$ quarks are unphysical and the gauge ensembles are limited to a single lattice spacing and spatial volume, we cannot determine the T windows of any flavor sector in the physical limit. However, we expect that, in the physical limit, the vector mesons in the $\overline{s}b$ sector will remain one of the most favorable channels for detecting the emergent $SU{\left(2\right)}_{CS}$ chiral-spin symmetry, and these hadron-like objects will predominantly be bound by chromoelectric interactions into color singlets.

3.2. Comparison with $N_f=2+1+1$ Lattice QCD at the Physical Point

In the following, we compare the $SU{\left(2\right)}_{CS}$ symmetry-breaking and -fading parameters (${\kappa }_{CS}$ and $\kappa$), as well as the temperature windows for the emergent $SU{\left(2\right)}_{CS}$ chiral-spin symmetry, between $N_f=2+1+1+1$ QCD (this work) and $N_f=2+1+1$ QCD at the physical point [5].

The numerical values of ${\kappa }_{CS}$ and $\kappa$ for $N_f=2+1+1+1$ QCD are provided in Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 of Appendix C, while those for $N_f=2+1+1$ QCD can be found in Table A13, Table A14, Table A15, Table A16, Table A17 and Table A18 of Appendix D.

As an example, we compare the $SU{\left(2\right)}_{CS}$ symmetry-breaking and -fading parameters (${\kappa }_{CS}$ and $\kappa$) at $zT=1$ for both lattice setups as shown in Figure 9 and Figure 10.

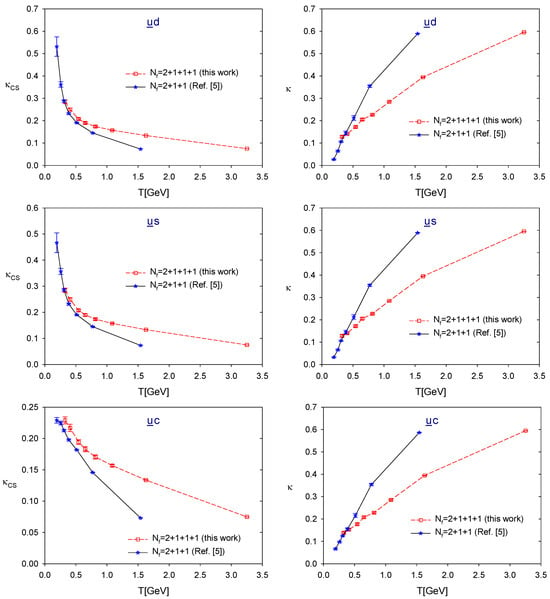
Figure 9. Comparison of the ${SU\left(2\right)}_{CS}$ chiral-spin symmetry-breaking and -fading parameters $({\kappa }_{CS},\kappa )$ at $zT=1$, for the $(\overline{u}d,\overline{u}s,\overline{u}c)$ sectors of lattice QCD with $N_f=2+1+1+1$ (this work) and $N_f=2+1+1$ at the physical point [5].

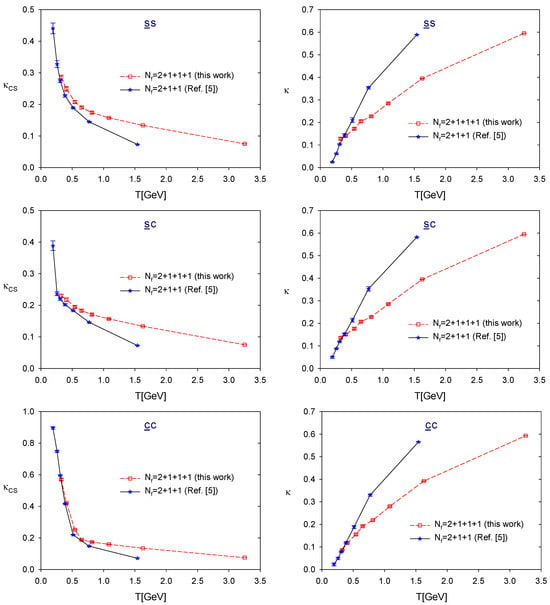
Figure 10. Comparison of the ${SU\left(2\right)}_{CS}$ chiral-spin symmetry-breaking and -fading parameters $({\kappa }_{CS},\kappa )$ at $zT=1$, for the $(\overline{s}s,\overline{s}c,\overline{c}c)$ sectors of lattice QCD with $N_f=2+1+1+1$ (this work) and $N_f=2+1+1$ at the physical point [5].

First, we observe that for any flavor sector with $T>325$ MeV, ${\kappa }_{CS}$ in $N_f=2+1+1+1$ QCD is larger than in $N_f=2+1+1$ QCD, while $\kappa$ in $N_f=2+1+1+1$ QCD is smaller than in $N_f=2+1+1$ QCD. Since ${\kappa }_{CS}$ is a monotonically decreasing function of T, while $\kappa$ is a monotonically increasing function of T, it follows that for any given ${ϵ}_{cs}$ and ${ϵ}_{fcs}$ in (21), both the lower and upper bounds of each T-window for the emergent $SU{\left(2\right)}_{CS}$ symmetry in $N_f=2+1+1+1$ QCD occur at higher temperatures than those in $N_f=2+1+1$ QCD.

For instance, for ${ϵ}_{CS}={ϵ}_{FCS}=0.20$, the corresponding results are summarized in Table 7. The lower and upper bounds of each T-window, along with their uncertainties, are estimated through piecewise linear interpolation of ${\kappa }_{CS}$ and $\kappa$. Clearly, for any flavor sector, the T-window in $N_f=2+1+1+1$ QCD shifts to a higher temperature range compared to that in $N_f=2+1+1$ QCD, while also expanding in size.

Table 7. Comparison of the approximate temperature windows for the $SU{\left(2\right)}_{CS}$ emergent symmetry between $N_f=2+1+1$ and $N_f=2+1+1+1$ lattice QCD, for $zT=1$ and ${ϵ}_{cs}={ϵ}_{fcs}=0.20$. All temperatures are given in MeV.

Flavor Content	${\mathit{N}}_{\mathit{f}}=2+1+1$ [5]	${\mathit{N}}_{\mathit{f}}=2+1+1+1$ (This Work)
$\overline{u}d$	485(10)–490(20)	590(20)–635(15)
$\overline{u}s$	485(10)–490(20)	590(20)–635(15)
$\overline{u}c$	370(10)–480(20)	510(20)–620(15)
$\overline{s}s$	475(10)–495(20)	590(20)–635(15)
$\overline{s}c$	400(20)–485(15)	510(20)–625(15)
$\overline{c}c$	NULL	630(10)–700(20)

To better understand this behavior, we compare the T-window for the emergent $SU{\left(2\right)}_{CS}$ symmetry in the $\overline{u}d$ sector between $N_f=2+1+1$ lattice QCD at the physical point [5] and $N_f=2$ lattice QCD near the physical point [18].

Specifically, for ${ϵ}_{cs}={ϵ}_{fcs}=0.2$ at $zT=2$, the T-window in $N_f=2$ lattice QCD spans approximately 320–500 MeV, whereas in $N_f=2+1+1$ lattice QCD, it shifts to $610\left(15\right)$–$730\left(15\right)$ MeV. This indicates that the presence of dynamical s and c quarks, which are significantly heavier than the light u and d quarks, raises both the lower and upper bounds of the T-window in the $\overline{u}d$ sector while also reducing its size.

Synthesizing these findings with our earlier discussions, we obtain a universal feature of the emergent chiral-spin symmetry in any QCD system:

Increasing the number of dynamical heavy quarks shifts the T-windows for $SU{\left(2\right)}_{CS}$ symmetry to higher temperature ranges, and these windows are primarily dominated by the sectors involving the heaviest quark and the light quarks of the system.

This constitutes one of the interesting findings of our study.

However, given the different lattice spacings in the $N_f=2/2+1+1/2+1+1+1$ ensembles and the associated discretization errors—as well as the unphysical $u/d$ quark masses in the $N_f=2+1+1+1$ lattices—it remains an open question whether this feature persists in the physical limit; that is, with $(u,d,s,c,b)$ quarks at the physical point across all lattice setups, in the continuum and infinite volume limits. If confirmed, this would reflect a nontrivial realization of nonperturbative QCD dynamics of increasing the number of heavy dynamical quarks at high temperatures. This effect is revealed through changes of the splitting in the $SU{\left(2\right)}_{CS}$ multiplet $(A_1,T_4,X_4)$ as measured by the $SU{\left(2\right)}_{CS}$ symmetry-breaking parameter ${\kappa }_{AX}$ (18), and the ratio of the splitting to the distance between the $U{\left(1\right)}_A$ multiplet $M_0=(P,S)$ and the $SU{\left(2\right)}_{CS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ multiplet $M_2=(V_1,A_1,T_4,X_4)$ as measured by the $SU{\left(2\right)}_{CS}$ symmetry-fading parameter $\kappa$ (20).

3.3. Comparison Between ${\kappa }_{VA}$ and ${\kappa }_{CS}$

Finally, we compare the precision of symmetry between the $SU{\left(2\right)}_{CS}$ chiral-spin symmetry and the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetry. This comparison provides critical insights into the interplay of chiral and chiral-spin symmetry manifestations in lattice QCD.

To this end, we compute the ratio of their symmetry-breaking parameters, ${\kappa }_{VA}/{\kappa }_{CS}$, for all flavor contents as shown in Figure 11 for $zT=1$, 2, and 3. Notably, for each flavor content, the ratio ${\kappa }_{VA}/{\kappa }_{CS}$ decreases monotonically with T and remains nearly constant across all $zT$ at a fixed T. This behavior strongly suggests the emergence of an $SU{\left(2\right)}_{CS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ symmetry once the $SU{\left(2\right)}_{CS}$ symmetry arises within the temperature windows satisfying the criterion (21). Furthermore, this observation hints at the possible manifestation of a larger $SU\left(4\right)$ symmetry, which contains $SU{\left(2\right)}_{CS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ as a subgroup [16,17].

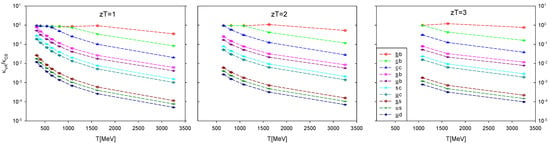
Figure 11. The ratio of the chiral symmetry-breaking parameter ${\kappa }_{VA}$ and the chiral-spin symmetry breaking parameter ${\kappa }_{CS}$ as a function of T, for all flavor combinations and $zT=1$, 2, and 3, respectively.

To fully investigate the $SU\left(4\right)$ symmetry, it is necessary to examine the degeneracies of $SU\left(4\right)$ multiplets, including flavor singlets of $J=1$ mesons. However, the z-correlators for these multiplets involve disconnected diagrams, which are not included in this study. Instead, we will address this by analyzing the degeneracies in the chiral susceptibilities of the multiplets using all-to-all quark propagators estimated with $Z_2$ noise.

Moreover, the hierarchy of the ratio $R\equiv {\kappa }_{VA}/{\kappa }_{CS}$ follows the same order as (15) and (16), i.e.,

$$\begin{array}{c}\hfill R^{\overline{u}d}<R^{\overline{u}s}<R^{\overline{s}s}<R^{\overline{u}c}<R^{\overline{s}c}<R^{\overline{u}b}<R^{\overline{s}b}<R^{\overline{c}c}<R^{\overline{c}b}<R^{\overline{b}b},\end{array}$$

(22)

for all $zT$ at fixed T. However, this hierarchy does not necessarily imply that the emergence of $SU{\left(2\right)}_{CS}$ symmetry follows the same order, as the fading of $SU{\left(2\right)}_{CS}$ symmetry must also be considered. This is evident from the temperature windows for the emergence of $SU{\left(2\right)}_{CS}$ symmetry as detailed in Table 4, Table 5 and Table 6.

If we compare ${\kappa }_{CS}$ and ${\kappa }_{VA}$ on an equal footing, Figure 11 reveals that the $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ chiral symmetry (as well as $U{\left(1\right)}_A$ since ${\kappa }_{TX}\simeq {\kappa }_{VA}$) is significantly more precise than the $SU{\left(2\right)}_{CS}$ chiral-spin symmetry in the $(\overline{u}d,\overline{u}s,\overline{s}s)$ sectors involving light quarks, with ${\kappa }_{VA}/{\kappa }_{CS}\lesssim {10}^{-2}$. In the heavy–light quark sectors $(\overline{u}c,\overline{s}c,\overline{u}b,\overline{s}b)$, the chiral symmetry remains slightly more precise than the chiral-spin symmetry, with ${\kappa }_{VA}/{\kappa }_{CS}\lesssim 0.5$. In contrast, for sectors containing only heavy quarks $(\overline{c}c,\overline{c}b,\overline{b}b)$, the precision of the chiral and chiral-spin symmetries becomes comparable as indicated by ${\kappa }_{VA}/{\kappa }_{CS}\lesssim 1$. This provides a qualitative picture of how the relative strength of the chiral-spin symmetry versus the chiral symmetry varies with quark content.

4. Concluding Remarks

In this study, we have generated eight gauge ensembles of $N_f=2+1+1+1$ lattice QCD with physical $(s,c,b)$ quarks but unphysically heavy $u/d$ quarks with $M_{\pi }\sim 700$ MeV, on the ${40}^3\times (20,16,12,10,8,6,4,2)$ lattices with lattice spacing $a\sim 0.03$ fm, for temperatures in the range of 325–3250 MeV as summarized in Table 1.

Using these eight gauge ensembles, we computed the meson z-correlators for the complete set of Dirac bilinears (scalar, pseudoscalar, vector, axial vector, tensor vector, and axial–tensor vector), and each for ten combinations of quark flavors ($\overline{u}d$, $\overline{u}s$, $\overline{s}s$, $\overline{u}c$, $\overline{s}c$, $\overline{u}b$, $\overline{s}b$, $\overline{c}c$, $\overline{c}b$, $\overline{b}b$). Then, we used (6) and (10) to determine $T_c$ and $T_1$ for each flavor combination and obtain the hierarchy of restoration of chiral symmetry, in the order of

$$\begin{array}{c}\hfill T_{c1}^{\overline{u}d}<T_{c1}^{\overline{u}s}<T_{c1}^{\overline{s}s}<T_{c1}^{\overline{u}c}<T_{c1}^{\overline{s}c}<T_{c1}^{\overline{u}b}<T_{c1}^{\overline{s}b}<T_{c1}^{\overline{c}c}<T_{c1}^{\overline{c}b}<T_{c1}^{\overline{b}b},T_{c1}\equiv max(T_c,T_1),\end{array}$$

which immediately gives the hierarchical restoration of chiral symmetry in $N_f=2+1+1+1$ QCD, i.e., from the restoration of $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d)$ quarks at $T_{c1}^{\overline{u}d}$ to the $SU{\left(3\right)}_L\times SU{\left(3\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s)$ quarks at $T_{c1}^{\overline{s}s}$, then to the $SU{\left(4\right)}_L\times SU{\left(4\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c)$ quarks at $T_{c1}^{\overline{c}c}$, and finally to the $SU{\left(5\right)}_L\times SU{\left(5\right)}_R\times U{\left(1\right)}_A$ chiral symmetry of $(u,d,s,c,b)$ quarks at $T_{c1}^{\overline{b}b}$.

One of the key phenomenological outcomes of the hierarchical restoration of chiral symmetry is the sequential pattern of hadron dissolution as the temperature is increased successively, resulting in a hierarchy in both the dissolution of hadrons and their suppression within the quark–gluon plasma. This can be seen as follows. Theoretically, a meson with quark content $\overline{q}Q$ dissolves entirely when $\overline{q}$ and Q become deconfined. This occurs when the screening mass of the meson exceeds that of the corresponding noninteracting theory with free quarks of the same masses of q and Q. It is expected that $m_{\mathrm{scr}}^{\overline{q}Q}\ge m_{\mathrm{scr}}^{\overline{q}Q\left(\mathrm{free}\right)}$ at a temperature $T_d^{\overline{q}Q}\gtrsim T_{c1}^{\overline{q}Q}$, where the chiral symmetry $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_A$ of $\overline{q}\Gamma Q$ has been effectively restored. For $N_f=2+1+1+1$ lattice QCD, this implies that the hierarchy of meson dissolution is exactly the same as that of chiral symmetry restoration (17), i.e.,

$$\begin{array}{c}\hfill T_d^{\overline{u}d}<T_d^{\overline{u}s}<T_d^{\overline{s}s}<T_d^{\overline{u}c}<T_d^{\overline{s}c}<T_d^{\overline{u}b}<T_d^{\overline{s}b}<T_d^{\overline{c}c}<T_d^{\overline{c}b}<T_d^{\overline{b}b}.\end{array}$$

(23)

This hierarchy predicts the gradual suppression of mesons within the quark–gluon plasma, potentially observable in relativistic heavy-ion collision experiments, such as those conducted at the LHC and RHIC. This notion builds on the pioneering work [23], which proposed that the dissolution of $J/\psi$ mesons in the quark–gluon plasma would manifest as suppressed production in heavy-ion collision experiments.

Regarding the emergent $SU{\left(2\right)}_{CS}$ chiral-spin symmetry, it is intriguing to observe that the temperature windows meeting the criterion (21) are dominated by the channels of heavy vector mesons with flavor contents $\overline{u}b$ and $\overline{s}b$ as indicated by Table 4, Table 5 and Table 6. These results represent the first findings in lattice QCD and suggest that, within their respective temperature windows, hadronlike states—especially $\overline{u}b$ and $\overline{s}b$ vector mesons-are likely bound into color singlets by chromoelectric interactions. This is notable because neither the chromomagnetic part of the quark–gluon interaction nor the noninteracting theory with free quarks possesses any $SU{\left(2\right)}_{CS}$ symmetry. Furthermore, these findings offer valuable insights for exploring the emergent $SU{\left(2\right)}_{CS}$ symmetry in relativistic heavy-ion collision experiments, such as those conducted at the LHC and RHIC, by focusing on meson channels with $\overline{u}b$, $\overline{d}b$ and $\overline{s}b$ quark contents.

By comparing the T-windows for the emergent $SU{\left(2\right)}_{CS}$ symmetry across different lattice QCD setups, we obtained a universal feature of chiral-spin symmetry in any QCD system. Specifically, we analyzed the following:

• The $\overline{u}d$ sector in $N_f=2$ lattice QCD near the physical point [18] versus $N_f=2+1+1$ lattice QCD at the physical point [5].
• The $(\overline{u}d,\overline{u}s,\overline{u}c,\overline{s}s,\overline{s}c,\overline{c}c)$ sectors in $N_f=2+1+1$ lattice QCD at the physical point [5] versus $N_f=2+1+1+1$ lattice QCD in this work.

From these comparisons, we deduce the following universal feature of chiral-spin symmetry in any QCD system: Increasing the number of dynamical heavy quarks shifts the T-windows for $SU{\left(2\right)}_{CS}$ symmetry to higher temperature ranges, with these windows being primarily dominated by the sectors involving the heaviest quark and the light quarks of the system. However, given the different lattice spacings in the $N_f=2/2+1+1/2+1+1+1$ ensembles and the associated discretization errors—as well as the unphysical $u/d$ quark masses in the $N_f=2+1+1+1$ lattices—it remains an open question whether this feature persists in the physical limit; that is, with $(u,d,s,c,b)$ quarks at the physical point across all lattice setups, in the continuum and infinite volume limits.

To understand the nature of mesonlike states in the $J=1$ channels (i.e., $V_k$, $A_k$, $T_k$, and $X_k$) which are relevant to the emergent $SU{\left(2\right)}_{CS}$ symmetry, it is essential to analyze the behavior of their spectral functions as the temperature increases. If bound-state peaks are found within the temperature ranges where the $SU{\left(2\right)}_{CS}$ symmetry holds, and these peaks gradually broaden and eventually vanish as T rises beyond these ranges, it would suggest that the degrees of freedom in these mesonlike objects correspond to color-singlet mesons, as opposed to deconfined quarks and gluons. To investigate this, one could consider extending the method used in refs. [24,25,26] for $J=0$ mesons to the $J=1$ mesons. Additionally, it is necessary to compute the spatial z-correlators of vector mesons to high precisions, free of the contribution of unphysical meson states even at large distances, in order to reliably extract the damping factor for each $J=1$ meson channel. The prescription used in ref. [4] (to compute two sets of quark propagators with periodic and antiperiodic boundary conditions in the z direction) provides an effective way to eliminate the contribution of unphysical meson states to the z-correlators and offers a promising way to achieve this goal.