Comment on Ghali et al. Mathematical Entropy Analysis of Natural Convection of MWCNT—Fe3O4/Water Hybrid Nanofluid with Parallel Magnetic Field via Galerkin Finite Element Process. Symmetry 2022, 14, 2312

Asterios Pantokratoras

doi:10.3390/sym17020237

School of Engineering, Democritus University of Thrace, 67100 Xanthi, Greece

Symmetry2025, 17(2), 237;https://doi.org/10.3390/sym17020237

Version Notes

Order Reprints

Abstract

A serious error and many typographical errors exist in the above paper.

Serious Error

The horizontal and vertical momentum Equations (2) and (3) in [1] are as follows

u \frac{\partial u}{\partial x} + υ \frac{\partial u}{\partial y} = - \frac{1}{ρ_{h n f}} \frac{\partial P}{\partial x} + ν_{h n f} (\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}})

(1)

u \frac{\partial υ}{\partial x} + υ \frac{\partial υ}{\partial y} = - \frac{1}{ρ_{h n f}} \frac{\partial P}{\partial y} + ν_{h n f} (\frac{\partial^{2} υ}{\partial x^{2}} + \frac{\partial^{2} υ}{\partial y^{2}}) + β_{h n f} g (T - T_{a v g}) + \frac{σ_{h n f}}{ρ_{h n f}} B_{0}^{2} υ

(2)

where

u, υ

are the horizontal and vertical fluid velocities and

B_{0}

is the magnetic flux density. In Figure 1a in [1] it is shown that the magnetic field is parallel to the horizontal x-axis and perpendicular to the vertical y-axis. This is also mentioned in the title in [1]. In order to check the correctness of the magnetic force in Equations (1) and (2) we present the following momentum equations from reference [2]. The horizontal and vertical momentum equations in [2] are as follows

ρ u \frac{\partial u}{\partial x} = - \frac{\partial p}{\partial x} + \frac{\partial}{\partial x} (\frac{4}{3} μ \frac{\partial u}{\partial x}) - σ (E + u B \sin χ_{b} - υ B c o s χ_{b}) B \sin χ_{b}

(3)

ρ u \frac{\partial υ}{\partial x} = - \frac{\partial p}{\partial y} + \frac{\partial}{\partial x} (\frac{4}{3} μ \frac{\partial υ}{\partial x}) + σ (E + u B \sin χ_{b} - υ B c o s χ_{b}) B \cos χ_{b}

(4)

In Equations (3) and (4) the magnetic field is inclined and

χ_{b}

is the angle between the magnetic field and horizontal axis

x

(Figure 1). If the magnetic field in Equations (3) and (4) becomes horizontal, as happens in Equations (1) and (2), the angle

χ_{b}

is zero, the

\sin χ_{b}

is zero and the

\cos χ_{b}

is equal to 1. The electric field

E

in [1] is zero. Then, the magnetic term in Equation (3) is

- σ (u B \sin χ_{b} - υ B c o s χ_{b}) B \sin 0 = 0

and the magnetic term in Equation (4) is

+ σ (u B \sin χ_{b} - υ B c o s χ_{b}) B \cos χ_{b} = + σ (u B \sin 0 - υ B c o s 0) B \cos 0 = - σ (υ B) B = - σ B^{2} υ

. It is clear that the magnetic term in the vertical momentum in Equation (4) is

- σ B^{2} υ

whereas the magnetic term in the vertical momentum in Equation (2) is

+ \frac{σ_{h n f}}{ρ_{h n f}} B_{0}^{2} υ

; that is, it is positive instead of negative.

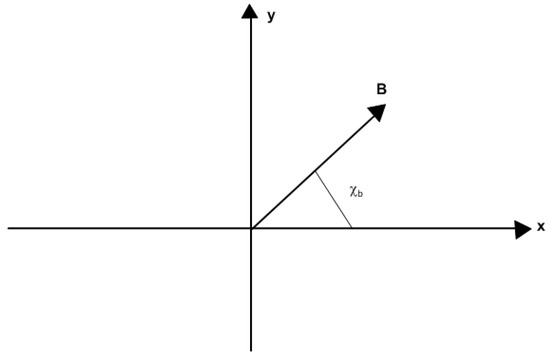
Figure 1. Flow configuration and coordinate system in [2].

Another argument that the magnetic term in Equation (2) must be negative is included in the NACA technical report 3971 ([3], Equation (47)). The Equation (47) in NACA [3] is as follows

u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = ν \frac{\partial^{2} u}{\partial y^{2}} - \frac{σ B_{0}^{2}}{ρ} (u - u_{\infty})

(5)

where the velocity

u

is horizontal and the magnetic field acts transversely to

u

. In the above Equation (5),

u_{\infty}

is the free stream velocity which is zero in [1].

The correct negative term is shown also in Equation ((5.32), page 151) in [4] as follows

- \frac{\partial p}{\partial x} + ρ ν \frac{\partial^{2} u}{\partial y^{2}} - σ B^{2} u = 0

(6)

The wrong positive term

+ \frac{σ_{h n f}}{ρ_{h n f}} B_{0}^{2} υ

in Equation (2) appears also in Equation (19) in [1] and as

+ \frac{σ_{f}}{σ_{h n f}} \frac{ρ_{f}}{ρ_{h n f}} \frac{\Pr H_{a}^{2}}{ε \sqrt{R a}} V

in the transformed Equation (28) in [1] where Ha is the dimensionless Hartmann number which represents the magnetic field.

Typographical Errors

In the nomenclature it is written that U,V are dimensional velocity components. However, U,V are dimensionless.
In the nomenclature it is written that the units of dynamic viscosity $μ$ are $W \cdot m^{- 1} \cdot K^{- 1} = k g \cdot m \cdot s^{- 3} \cdot K^{- 1}$ . However, the units of $μ$ are $k g \cdot m^{- 1} \cdot s^{- 1}$ .
In the nomenclature it is written that the units of electrical conductivity $σ$ are $Ω \cdot M$ . However, the units of $σ$ are $Ω^{- 1} \cdot m^{- 1} = {(O h m)}^{- 1} {(l e n g t h)}^{- 1}$ .
In the nomenclature it is written that $λ$ is the length of the baffle. However, in Figure 1 in [1] no baffle with length $λ$ appears.
In the dimensional Equations (2), (3), (18) and (19) in [1] the pressure P is dimensional, whereas in Equation (21) in [1], the pressure P (same symbol) is dimensionless.
In Equation (21) in [1] appears an unknown parameter $g_{y}$ .
Above Equation (29) in [1] it is written that “The following formula is the energy equation for normal convection inside a porous region, with σ the thermal capacity ratio”. However, no parameter σ exists in Equation (29) in [1]. In addition, σ is the electrical conductivity.
Between Equations (33) and (34) in [1] are presented the boundary conditions concerning the dimensional velocities and temperatures. The corresponding boundary conditions for dimensionless quantities do not exist in [1].
In the dimensionless Figures 3, 8, 12, 15 and 17, for the isotherms, the symbol T (Kelvin) is presented. The correct term is $θ (\dim e n s i o n l e s s)$ .
The caption of Figure 5 says. “Variation of $N u_{a v g}$ with Ra for different Da at Ha = 0, $ϕ = 0.02$ , and $ε = 0.4$ ”. However, in the figure there is a different $ϕ$ , not a different Da.
The caption of Figure 6 says. “Variation of $N u_{a v g}$ with Ra for different $ϕ$ at Da = 0.01, Ha = 0, and $ε = 0.4$ ”. However, in the figure there is a different Da, not a different $ϕ$ .
In the caption of Figure 9 $ε = 0$ and on the figure $ε = 0.4$ .
In the caption of Figure 10 $ε = 0$ and on the figure $ε = 0.4$ .
In the caption of Figure 11 it is written that Ha = 0 whereas the Ha in the horizontal axis varies between 0 and 100.
In Figure 28 the $ϕ$ varies between 0.02 and 0.08, whereas in the caption it is written that $ϕ = 0.02$ .
In the problem description in [1] it is written that “NF is power-law non-Newtonian”. However, no NF power-law non-Newtonian exists in [1].
The entropy generation is presented in Equation (36) in [1]. Above Equation (36) is written “Non-Dimensional Entropy Generation” and exactly below it is written “The dimensional local entropy produced is represented by equation (36)”. In Equation (36) $k_{m}, T_{a v g}, μ_{n f}, K, σ_{n f}, B$ are dimensional and $U, V, X, Y, θ$ are dimensionless. Therefore, Equation (36) in [1] is neither dimensional nor dimensionless.

Conflicts of Interest

The author declares no conflict of interest.

References

Ghali, D.; Redouane, F.; Abdelhak, R.; Belhadj Mahammed, A.; Zineb, C.D.; Jamshed, W.; Eid, M.R.; Eldin, S.M.; Musa, A.; Mohd Nasir, N.A.A. Mathematical Entropy Analysis of Natural Convection of MWCNT—Fe₃O₄/Water Hybrid Nanofluid with Parallel Magnetic Field via Galerkin Finite Element Process. Symmetry 2022, 14, 2312. [Google Scholar] [CrossRef]
Berton, R.P.H. Analytic model of a resistive magnetohydrodynamic shock without Hall effect. J. Fluid Mech. 2018, 842, 273–322. [Google Scholar] [CrossRef]
Rossow, V.J. On Flow of Electrically Conducting Fluids over a Flat Plate in the Presence of a Transverse Magnetic Field; Technical Note 3971; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1957.
Davidson, P.A. An Introduction to Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Comment on Ghali et al. Mathematical Entropy Analysis of Natural Convection of MWCNT—Fe₃O₄/Water Hybrid Nanofluid with Parallel Magnetic Field via Galerkin Finite Element Process. Symmetry 2022, 14, 2312

Abstract

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics