1. Introduction
A graph is a mathematical structure comprising a non-empty set of vertices V and a set of edges E connecting pairs of vertices. In this study, we exclusively consider finite and undirected simple graphs. The vertex and edge sets constitute the graph’s elements. The degree of an element x (vertex or edge) is denoted by . If x is a vertex, then represents the number of edges incident to x. If x is an edge, then represents the number of edges adjacent to x (i.e., the number of edges sharing a common vertex with x). The order and size of a graph G are defined as the number of vertices and number of edges, respectively. A graph G is called k-regular if every vertex in G is incident to exactly k edges. The line graph of a graph G is a new graph that models the adjacency relationships between the edges of G. The vertex set of corresponds to the edge set of G, and two vertices in are adjacent if and only if the corresponding edges in G share a common vertex (adjacent).
For a comprehensive overview of the notations and definitions employed in this work, consult [
1,
2]. Path, cycle, and complete graphs with
n vertices are known as
and
, respectively. A bipartite graph is a graph with a vertex set that can be partitioned into two disjoint and independent sets, often denoted by
X and
Y, such that no two vertices within the same set are adjacent. A complete bipartite graph is a bipartite graph in which every vertex in set
X is adjacent to every vertex in set
Y, and is denoted by
, where
and
. The Cartesian product of two graphs
and
, denoted by
, has vertex set
; two distinct vertices
and
of
are adjacent if either
and
or
and
. The join of two graphs
G and
H, denoted
, is a graph operation where every vertex of
G is connected to every vertex of
H. A wheel
is the join of
and
. A helm graph, denoted by
, is a graph with
vertices obtained from a wheel graph
by adjoining a pendant edge at each vertex of the cycle. A gear graph is a wheel graph with a vertex added between each pair of adjacent graph vertices of the outer cycle. A tadpole graph
is obtained by joining a cycle
and a path
by a bridge, where
. A book graph
is defined as the graph Cartesian product
. A stacked book graph
is defined as the graph Cartesian product
, where
is a star graph and
is the path graph.
Topological indices are numerical representations derived from molecular graphs. These indices capture the structural features of molecules, with atoms represented as vertices and bonds as edges. The underlying symmetry of these molecular graphs plays a crucial role in determining their topological properties. By exploiting the inherent symmetries, efficient algorithms can be developed to calculate these indices and correlate them with various physicochemical properties. These indices are valuable tools for predicting the properties of novel compounds and optimizing drug design for specific desired characteristics [
3]. By understanding the relationship between molecular structure and properties, researchers can accelerate the discovery and development of new materials and pharmaceuticals. Topological indices date back to 1947, when a scientist named Wiener created the first topological index, known as the Wiener index [
4], to search for boiling points. The Wiener index is defined as
, where
is the set of vertices in graph
G and
is the shortest path distance between vertices
u and
v. In 1972, Gutman and Trinajstić [
5] introduced the first and second Zagreb indices. These degree-based topological indices were utilized to determine the total
-electron energy of molecules, and are defined as follows:
The first general Zagreb index, introduced in [
6], is defined as
where
is a real number that is not equal to zero or one. In [
7], a specific case of this index was investigated. This particular case is denoted as
and defined as
.
Inspired by these advancements, numerous mathematicians and chemists have developed a wide range of topological indices to explore the diverse chemical properties of molecular graphs (structures); see [
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Among distance-based topological indices, the Gutman index and degree distance index are particularly prominent and widely applied [
19,
20]. The forgotten topological index
is defined in [
21] as the sum of the cubes of the degrees of the vertices of a graph
G, meaning that
In [
21], Furtula and Gutman observed that the predictive power of the forgotten index is comparable to that of the first Zagreb index, particularly for acentric factor and entropy, with both indices achieving correlation coefficients exceeding
. This suggests that the the forgotten index could be a valuable tool for assessing the chemical and pharmacological properties of drug molecules. In [
22], Sun et al. explored the fundamental properties of the forgotten index and demonstrated its potential to complement the predictive capabilities of the Zagreb indices regarding physicochemical properties. More recently, Gao et al. [
23] applied the forgotten index to analyze the structural features of significant drug molecules.
In 2018, Alwardi, A. et al. [
24] introduced the first and second entire Zagreb topological index, as follows:
Note that in the expressions for the first and second entire Zagreb indices, the variable
x can correspond to either a vertex or an edge. When
x represents a vertex,
signifies the degree of that vertex in the graph
G. Conversely, when
x denotes an edge,
refers to the degree of
x in the line graph
. The same interpretation applies to the variable
y. The entire Zagreb indices are receiving a great deal of attention from many authors; for example, see [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34].
In [
33], the forgotten index was the subject of an initial study in which it was defined as
In this research, we introduce a novel topological index called the modified entire forgotten index, which incorporates both vertex and edge contributions to provide a more comprehensive representation of molecular structure. This index is computationally efficient even for large and complex molecules. Furthermore, we demonstrate its strong correlation with various physicochemical properties, surpassing the performance of both the forgotten index and entire forgotten index. This potential makes it a valuable tool for predicting molecular properties and aiding in the design of new molecules. We anticipate that this index will find widespread applications in fields such as chemistry, biology, and materials science, including drug design, protein structure prediction, and materials development
2. Entire Forgotten and Entire Modified Forgotten Zagreb Indices for Some Standard Graphs
This section formally introduces our novel graph invariant called the modified entire forgotten Zagreb index. We subsequently establish explicit formulas for its computation on significant classes of graphs alongside the entire forgotten Zagreb index. Throughout the proofs of the theorems and propositions, we utilize the notation to denote the set of vertices v incident to edge e, where and represent the degrees of vertex u and edge e, respectively, with the condition that u is incident to e.
Definition 1. For any graph G, the modified entire forgotten Zagreb index is denoted by and defined asAnalogously, we define the modified entire forgotten Zagreb co-index as follows: Proposition 1. Let G be a graph with n vertices, and suppose that it is a k regular graph.
Proof. Consider a
k-regular graph
G with
n vertices. In this case, graph
G contains
edges. It is worth noting that all edges have the same degree equal to
; consequently, after performing straightforward calculations, we obtain
Similarly,
□
Corollary 1. For the complete graph and the cycle graph , we have
- i
,
- ii
,
- iii
,
- iv
.
Proposition 2. For any path with vertices, we have
- i
,
- ii
.
Proof. We label the vertices and edges of the path from left to right, as follows: = and . Then, the degrees of all elements of are equal to 2 except for the elements , which all have degree 1. Thus, and . □
Proposition 3. Let be a complete bipartite graph of order and size . Then,
- i
,
- ii
.
Proof. Let
be a complete bipartite graph. There are
a vertices of degree
b and
b vertices of degree
a. There are also
edges of degree
. Therefore,
By simple calculation, we obtain
For the entire forgotten index,
□
Proposition 4. For a wheel graph of vertices, we have
- i
- ii
Proof. Let
be a wheel graph. There are
a vertices of degree 3, one vertex of degree
a,
a edges of degree four, and
a edges of degree
. Thus,
For the modified entire forgotten index,
By applying the partition of the vertices incident with the edges, as in
Table 1, we obtain
□
Thanks to their advantageous properties, wheel graphs and their generalizations find applications across diverse domains such as wireless sensor networks and network vulnerability analysis. Notably, from the perspective of the central hub vertex, all other vertices and edges are located within its immediate one-hop neighborhood. This proximity simplifies information dissemination and control within the network, making it valuable for modeling various network structures.
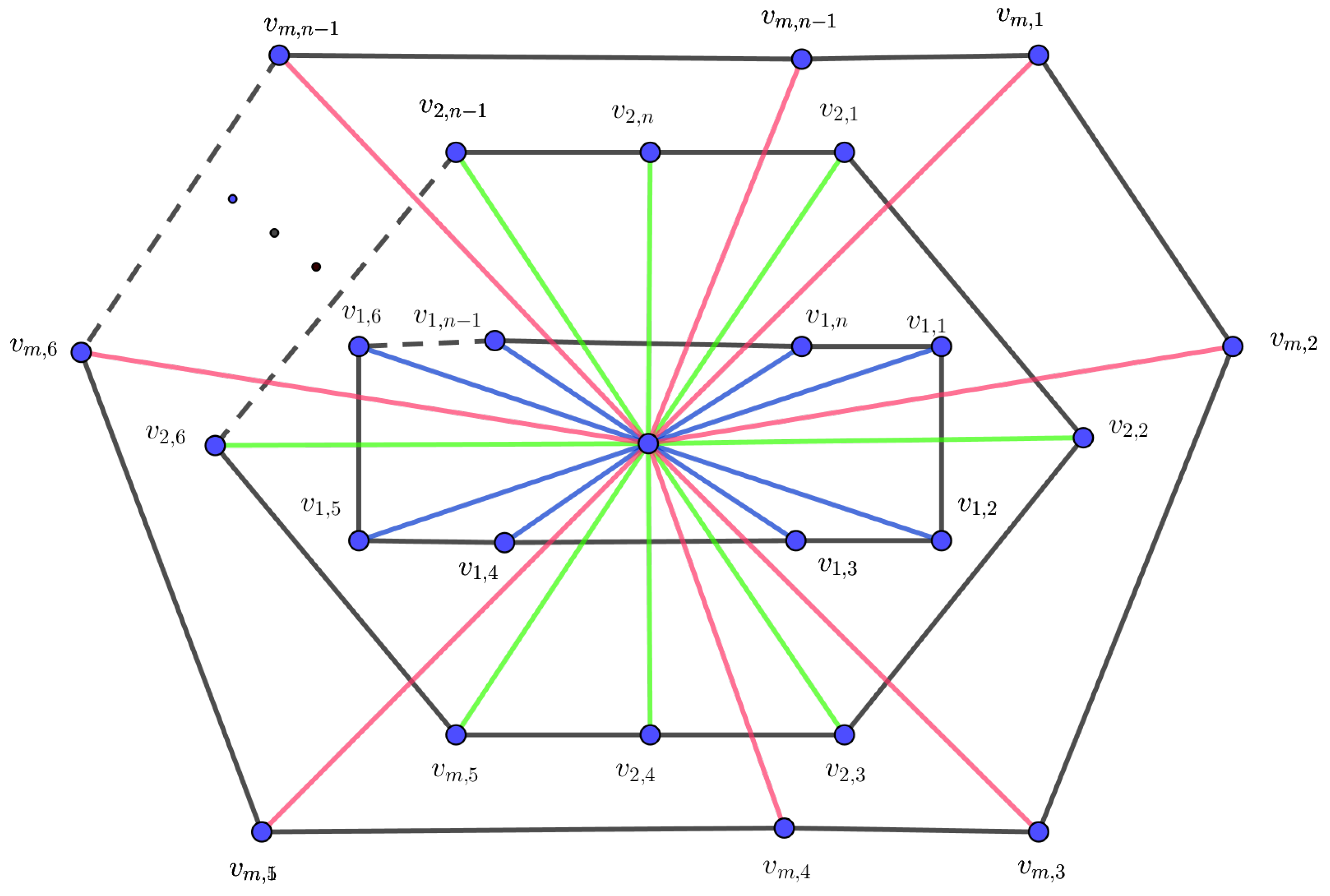
The m-wheel graph, denoted by , is a graph constructed by connecting m copies of a cycle graph to a single central vertex v. Each vertex in each cycle is adjacent to the central vertex.
Theorem 1. Let be an m-level wheel graph. Then,
- i
- ii
Proof. Let
G be an
m-level graph, as in
Figure 1. Obviously, all the vertices are of degree 3 except the center vertex, which is of degree
. Thus,
By using the entire forgotten formula for the m-level wheel graph and the partition in
Table 2, we obtain
□
Theorem 2. Let G be a helm graph . Then,
- i
- ii
Proof. Let G be the helm graph . There are a vertices of degree one, a vertices of degree four, and the center vertex with degree a. For the edges, there are a edges of degree 3, a edges of degree 6, and a edges of degree .
Therefore,
To obtain the formula of the modified entire forgotten index, we have
Using the partition in
Table 3, we obtain
□
Proposition 5. For the gear graph , we obtain
- i
- ii
Proof. For the gear graph, there are edges of degree 3 and p edges of degree . In addition, there are p vertices of degree 2, p vertices of degree 3, and one vertex of degree p.
Therefore,
To obtain the modified forgotten index, we can use the result of the entire forgotten index and apply the vertex edge partitions in
Table 4, obtaining the following result:
□
Theorem 3. Let G be a -kite graph with . Then,
- i
,
- ii
Proof. For the
-kite graph, there are
vertices of degree 2, one vertex of degree 3, and one vertex of degree one. In addition, there are
edges of degree 2, one edge of degree one, and 3 edges of degree 3. Thus,
In addition to the result of the entire forgotten index, using
Table 5 we obtain
□
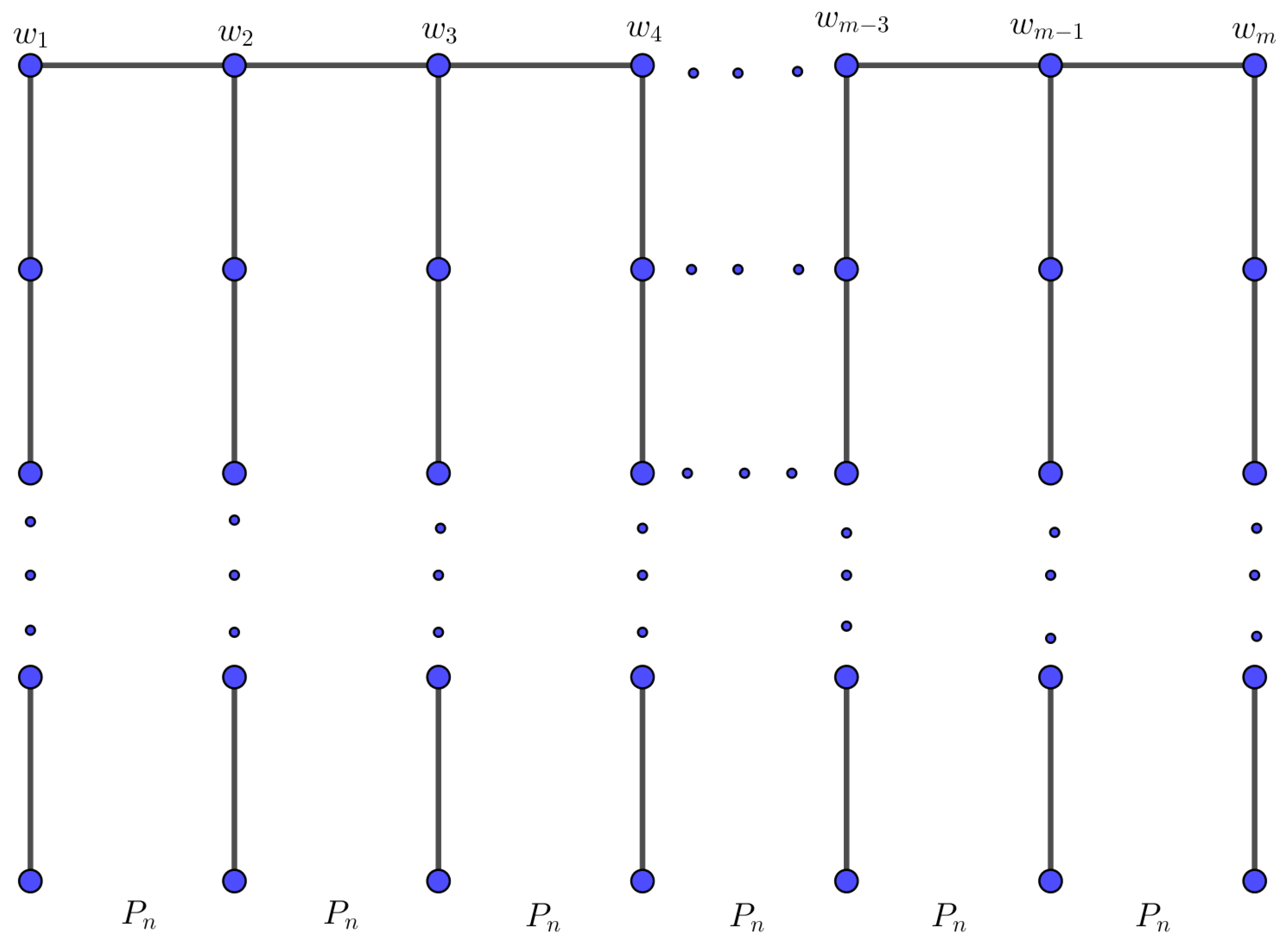
Let
be a set of finite pairwise disjoint graphs with
The bridge graph
of
with respect to the vertices
is the graph obtained from graphs
by connecting vertices
and
by an edge for all
; see
Figure 2.
Theorem 4. Let G be a bridge graph over path , . Then,
- i
,
- ii
Proof. Let
G be a bridge graph over path
with
, as in
Figure 2. There are
m vertices of degree one,
vertices of degree three, and
vertices of degree two. For the edges, there are
m edges of degree one,
of degree four,
m edges of degree three, and
of degree two. Therefore,
By applying the partition in
Table 6 and the value of entire forgotten index, we obtain
□
Theorem 5. Let G be the m-bridge graph on cycle , . Then,
- i
,
- ii
Proof. As
G is the
m-bridge over a cycle
, there are 2 vertices of degree 3,
vertices of degree four, and
vertices of degree two. In addition, there are two edges of degree five,
edges of degree six, four edges of degree three,
edges of degree four, and
edges of degree two. Therefore,
The vertex edge partition can be written as shown in
Table 7.
By applying the partition in
Table 7 and the value of entire forgotten index we obtain
□
Theorem 6. Let G be the m-bridge graph on a complete graph , where . Then,
- i
,
- ii
Proof. Let
G be the
m-bridge over a complete graph
. The graph
G then has
vertices and
edges with the following degrees: 2 vertices of degree
n,
vertices of degree
, and
of degree
. For the edges, there are two edges of degree
,
edges of degree
,
edges of degree
,
edges of degree
, and
edges of degree 2n-4
. Therefore,
The vertex edge partition can be written as in
Table 8.
By applying the partition in
Table 8 and the value of entire forgotten index, we obtain
□
A graph which has been derived from a graph G by a sequence of edge subdivision operations is called a subdivision graph of G, and is denoted by .
Theorem 7. Let G be any graph of n vertices and m edges, and let H be the subdivision of G. Then,
- i
,
- ii
.
Proof. Let
G be any graph of
m edges and let
H be the subdivision of
G. Then,
Through a rigorous analysis of the subdivision graph definition and subsequent calculations, we determined that
To determine the formula of the modified entire forgotten index, we have
Hence,
□
Theorem 8. Let G be a graph of n vertices and m edges, and let H be its central graph. Then,
- i
- ii
Proof. Consider that
G is a graph of
n vertices and
m edges with
H as its central graph. Then, there are two type of vertices in
H, namely,
m vertices of degree two and
n vertices of degree
. In addition, there are
edges of degree
and
edges of degree
. Thus,
To obtain the expression of the modified entire forgotten index, we have
Hence,
□
Theorem 9. For any book graph , where ,
- i
- ii
Proof. Obviously, from the definition of the book graph
, there are
vertices with degree 2, two vertices of degree
m,
edges of degree
m, one edge of degree
, and
m edges of degree
. Therefore,
Furthermore, employing
Table 9, it can be observed that
□
Theorem 10. Let with be a stacked book graph. Then,
- i
- ii
Proof. Let
H be the stacking book graph
. It is not difficult to see that the graph
possesses 2 vertices of degree
a,
vertices of degree
,
vertices of degree 2, and
vertices of degree 3. Regarding the edges, there are
edges of degree
a,
edges of degree
,
edges of degree 3,
edges of degree 4, two edges of degree
, and
edges of degree
. Consequently,
Hence,
Based on the partition of vertices incident with edges delineated in
Table 10, we deduce that
Hence, after some calculations, we have
□
Definition 2. [35] A firefly graph, denoted by , is a connected graph with a unique central vertex from which emanate x pendant edges, y pendant paths of length 2, and z triangles. The graph has vertices and edges, where x, y, and z are positive integers. Theorem 11. Consider , which is a firefly graph. Then,
- i
- ii
Proof. The firefly graph H has the following properties: for vertices, vertices of degree 1, vertices of degree 2, and one vertex of degree ; for edges, b edges of degree 1, z edges of degree 2, x edges of degree , and edges of degree .
Therefore,
From the analysis of the vertex partition incident with the edges outlined in
Table 11, after some calculations we can conclude that
□
3. Utility in Predicting Molecular Properties
This section employs the Quantitative Structure–Property Relationship (QSPR) methodology to evaluate the efficacy of the newly introduced modified entire forgotten topological index in characterizing molecular structural features. We emphasize the significance of the index by investigating its correlations with a diverse array of chemical and physical properties, including the acentric factor (AF), enthalpy of vaporization (HVAP), entropy (S), heat capacity at constant pressure (CP), motor octane number (MON), density (DENS), and molar volume (MV). For more information about these chemical and physical concepts and their values, see [
36,
37].
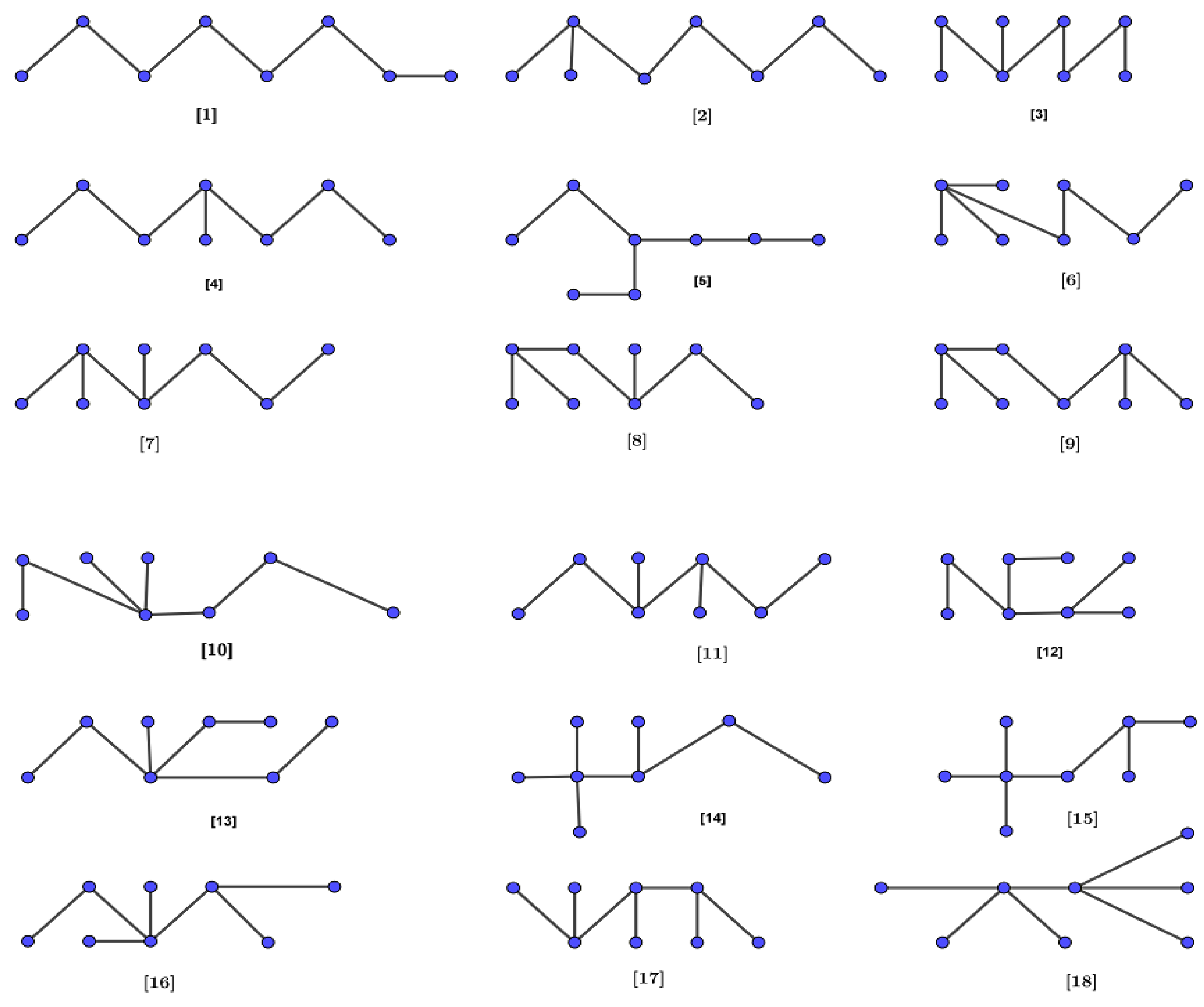
The dataset corresponds to octane isomers and is derived from [
36,
37,
38,
39], as shown in
Figure 3. Using SPSS software, we analyzed and determined the correlations between the modified entire forgotten topological index and the previously mentioned physicochemical properties of octane isomers. The results of these correlations are detailed in
Table 12 and
Table 13. By employing a linear model, we determined the correlation between the modified entire forgotten topological index and various chemical and physical properties of 18 octane isomers. The results indicate strong correlations, as presented in
Table 14 and
Table 15.
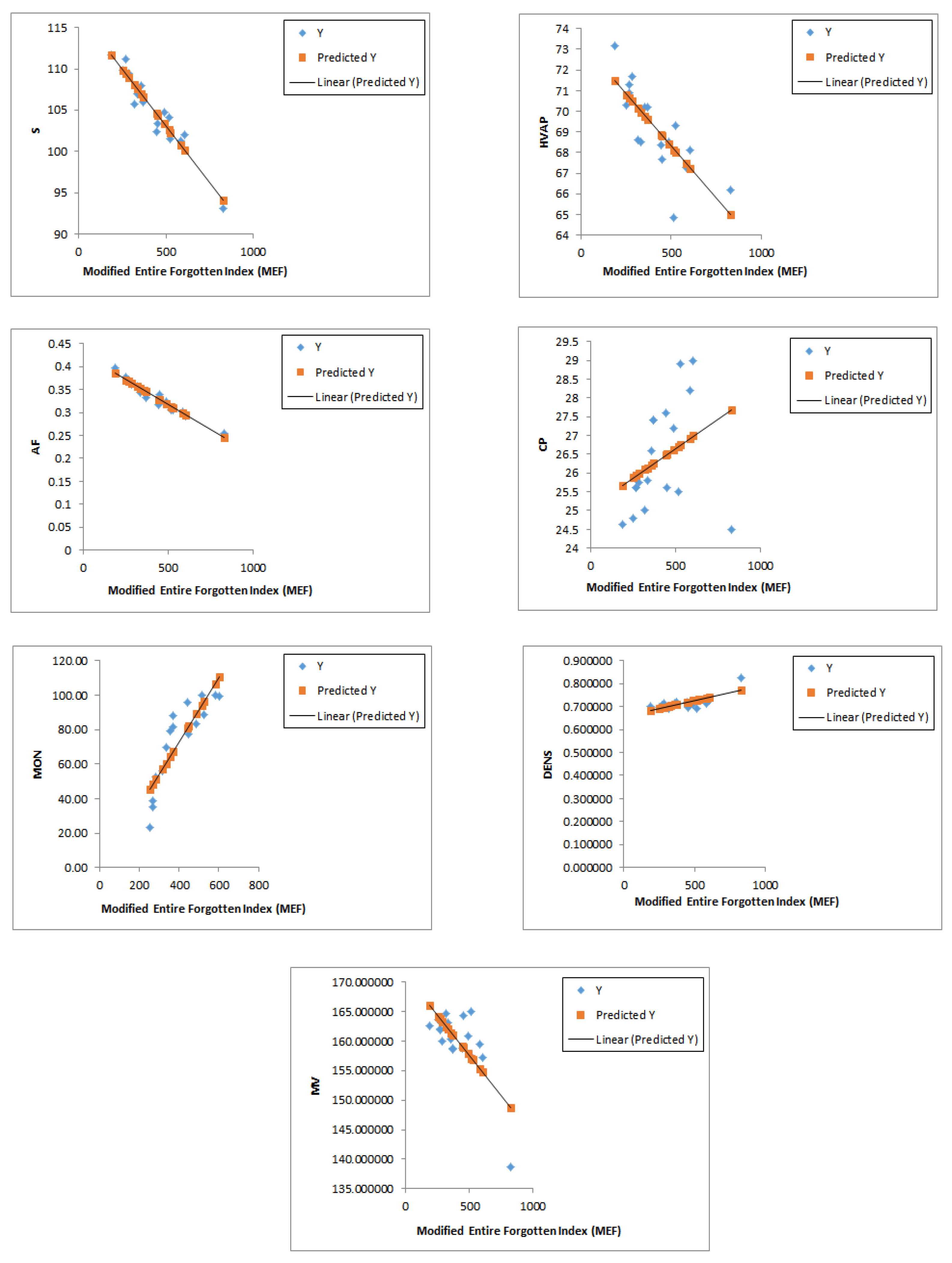
A comparison of the correlations between the modified entire forgotten index
, the forgotten index
, and the entire forgotten index
with respect to the properties of the octane isomers (acentric factor (AF), enthalpy of vaporization (HVAP), entropy (S), heat capacity at constant pressure (CP), motor octane number (MON), density (DENS), and molar volume (MV)) reveals that
exhibits stronger correlations with almost all of the proprieties compared to the other two indices, as demonstrated in corr1,SYMM2.
Figure 4 illustrates the correlations between the modified entire forgotten index and the physicochemical properties of octane isomers.
This finding underscores the superior predictive power of our newly introduced index in characterizing molecular properties.
We obtained the following regression equations:
To further validate the predictive power of the new index, we investigated its correlation with the properties of benzenoid hydrocarbons. We explored the relationship between the experimentally determined boiling point (BP),
-electron energy, molecular weight (MW), polarizability (P), and molar refractivity (MR) of 21 lower benzenoid hydrocarbons. The molecular structures of these compounds are depicted in
Figure 5. The forgotten, entire forgotten, and modified entire forgotten indices were calculated using established mathematical formulas. The experimental property values were sourced from [
36,
37,
38] and are tabulated in
Table 16.
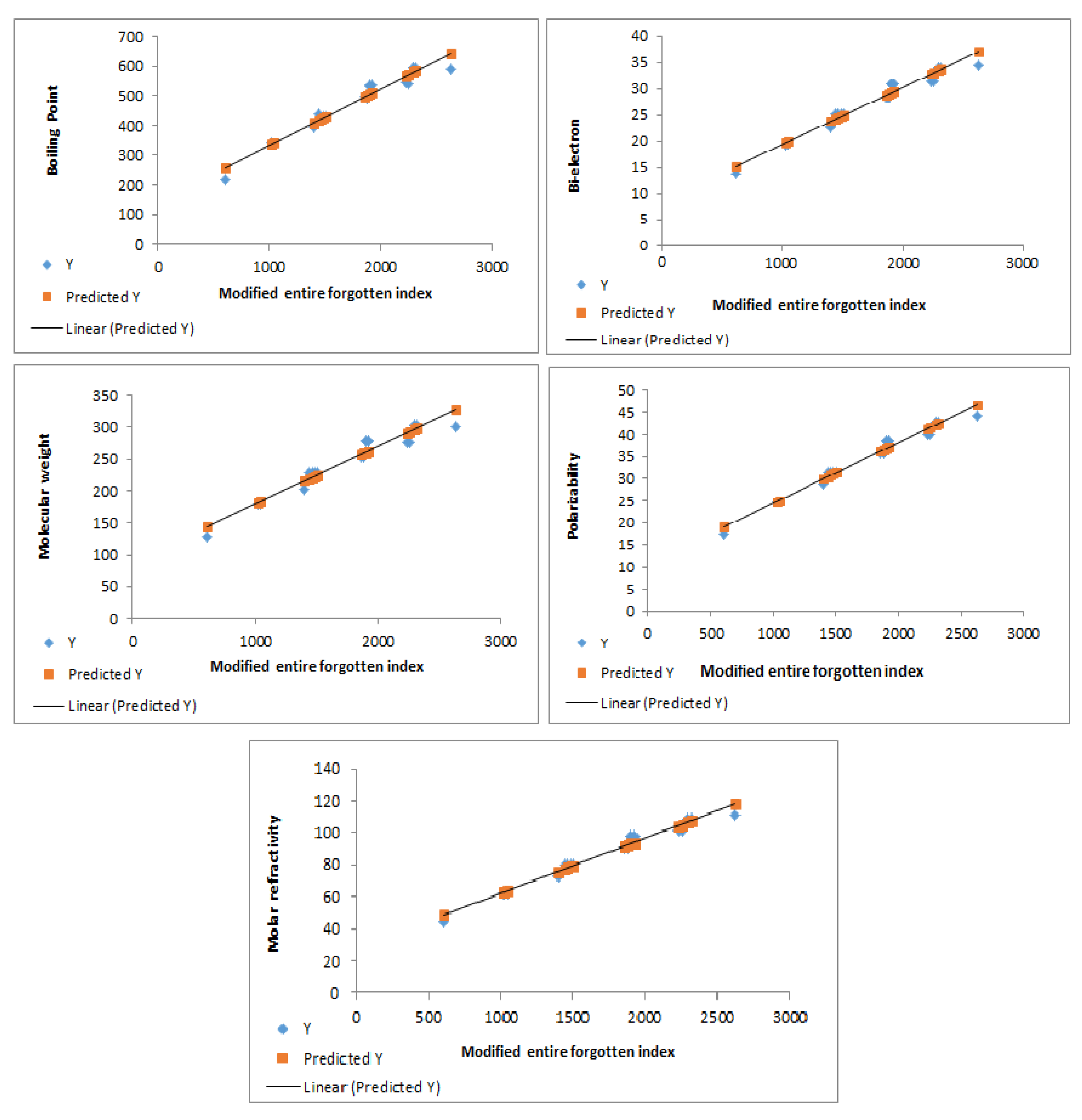
The modified entire forgotten index exhibits excellent correlations with various properties, as shown in
Table 17.
Figure 6 illustrates the strong correlations between the modified entire forgotten index and the physicochemical properties of benzenoid hydrocarbons.
Linear regression analysis was employed to establish quantitative relationships between the modified entire forgotten index and the experimental boiling point (BP), -electron energy, molecular weight (MW), polarizability (P), and molar refractivity (MR) of 21 lower benzenoid hydrocarbons, as follows:
4. Conclusions
This study introduces the modified forgotten entire index, a novel topological descriptor that incorporates vertex and edge degrees while considering adjacency and incidence relationships within molecular graphs. By capitalizing on the inherent symmetries found in these systems, we have developed efficient algorithms for its computation, particularly for large and complex molecular structures.
The predictive power of the entire and modified entire forgotten indices was evaluated by analyzing their correlations with key physicochemical properties of octane isomers and lower benzenoid hydrocarbons. The observed strong correlations demonstrate the potential of our new index as a valuable tool for Quantitative Structure–Property Relationship (QSPR) modeling in various domains, including computational chemistry and biology. Furthermore, we have derived explicit formulas for these indices in several important graph families, providing a solid foundation for further theoretical investigations and applications.
Potential avenues for future research include extending the applicability of the entire and modified entire forgotten indices as well as investigating their predictive power for a wider range of molecular properties and biological activities, such as toxicity, drug-likeness, and protein–ligand interactions.
In addition, QSPR models can be further developed by utilizing the entire and modified entire forgotten indices as key descriptors in machine learning algorithms to build predictive models for various molecular properties.
Applying the entire and modified entire forgotten indices to specific applications could provide a new a way of exploring drug design, materials science, and other relevant fields by developing specific applications and case studies.
Finally, investigating the mathematical properties of the entire and modified entire forgotten indices could help to further explore their respective mathematical properties, such as their bounds and relationships with other graph invariants.