Explicit Analytical Form for the Average Run Length of Double-Modified Exponentially Weighted Moving Average Control Charts Through the MA(q) Process and Applications

Abstract

The Statistical Process Control (SPC) approach using mathematical modeling proves effective for correlated data, with applications in healthcare, finance, and technology to enhance quality and efficiency. Here, we provide a novel SPC method using mathematical modeling and discuss its use in simulation tests to assess its applicability for tracking processes containing correlated data operating on sophisticated control charts. Particularly, an approach for detecting small shifts in the mean of a process running on the double-modified exponentially weighted moving average (DMEWMA) control chart, which is symmetric about the center line with upper and lower control limits, is of special interest. The computations showed exceptional accuracy, with ARL from the explicit formula closely matching that from the NIE method. Simulation tests assess its applicability in detecting small mean shifts and compare its performance with exponentially weighted moving average (EWMA) and modified exponentially weighted moving average (MEWMA) control charts across various scenarios. For several values of the design parameters, the performances of these three control charts are also compared in terms of the relative average index and relative standard deviation index. The results show that the DMEWMA chart outperforms others for several process mean shifts. The method’s practical use is demonstrated with stock data, highlighting its superior effectiveness in enhancing process monitoring.

1. Introduction

Statistical Process Control (SPC) is a methodological framework that employs statistical techniques to monitor and control manufacturing processes, ensuring efficiency and quality. Symmetry is essential in SPC, especially for designing and interpreting control charts. Control charts are fundamental instruments in SPC for monitoring process stability and variability across time. The development of these charts is underpinned by the assumption of symmetry, which is frequently based on the normal distribution of process data. The concept of SPC was pioneered by Shewhart [1] in 1926 and has since evolved into a critical aspect of operational excellence. Its notable application in the manufacturing sector has significantly reduced variability, enhanced product quality, and minimized waste. The methodology’s versatility extends beyond manufacturing, finding utility in healthcare, where it aids in managing patient care processes, and in financial services, where it improves compliance and service delivery [2]. A comprehensive review of research on the limitations and advantages of Statistical Process Control (SPC) in enhancing healthcare system quality is available in [3,4]. Additionally, Saravanan and Nagaragan [5] provide a comparative analysis of SPC and various control charts employed in the manufacturing industry.

There are two techniques to describe symmetry in control charts. First, control limits are symmetrically positioned around the process mean in traditional Shewhart control charts, like the $\overline{\mathrm{X}}$-chart. The process data are assumed to have a normal distribution in this design, meaning that departures from the mean are equally likely to occur. Process shifts or anomalies can be easily detected thanks to its symmetry. Second, the assumption that process data are regularly distributed is necessary for symmetrical control limits to be effective. Effective monitoring and quality control are made possible when this assumption is true because the control limits appropriately represent the anticipated process variability [6,7].

Control charts, also known as Shewhart charts, are fundamental tools in SPC that visualize how a process changes over time. They consist of data points representing a statistic from a process, plotted in chronological order, with three key components: a central line (average), an upper control limit (UCL), and a lower control limit (LCL) [2]. These charts are used to monitor process stability, detect out-of-control conditions, and investigate variations that may affect quality [3]. The Shewhart chart is a memoryless chart that only considers the most current process observations, ignoring any previous outcomes. In looking for modest fluctuations in process parameters, the cumulative sum (CUSUM) control chart recommended by Page [8] and the exponentially weighted moving average (EWMA) control chart suggested by Roberts [9] outperform the Shewhart-type control chart. Since then, numerous studies have been conducted to improve the performance of EWMA charts for minor process changes. For example, Shamma [10] proposed double exponentially weighted moving average (DEWMA); adaptive exponentially weighted moving average (AEWMA) was introduced by Capizzi and Masarotto [11]; Zhou et al. developed the weighted exponentially weighted moving average (WEWMA) chart for identifying changes in a Poisson incidence rate [12]; Patel and Divecha suggested the modified exponentially weighted moving average (MEWMA) [13]; and Naveed et al. devised extended exponentially weighted moving average (EEWMA) [14]. Alevizakos et al. proposed a triple exponentially weighted moving average (TEWMA), a hybrid of EWMA in 2021, and reported that it was more efficient than the EWMA control chart [15]. They also proposed a double-modified exponentially weighted moving average (DMEWMA), which is a hybrid of the two MEWMA control charts [16].

One tool that is frequently used in control chart measurement is Average Run Length (ARL). The Average Run Length (ARL) is the average number of observations or samples collected before a control chart indicates a potential shift in the process. When discussing symmetry, the focus is frequently on how symmetric and asymmetric alterations in process parameters (e.g., mean or variance) affect ARL and the comparative performance of various control charts [7]. Several common control charts, such as Shewhart charts, make the assumption that the process data are distributed symmetrically, much like the normal distribution. Both in-control (IC) and out-of-control (OOC) statuses are used to compute ARL. Consistent ARL performance for equal-sized deviations in both directions is guaranteed by symmetry [17]. Numerous techniques can be used to calculate the ARL; in particular, numerical integration equations (NIE) based on different quadrature methods can be used [18]. The solution of second-order Fredholm IEs is necessary to determine the explicit form of the ARL [19]. One benefit of using quadrature rules with the NIE technique is that it offers an accurate and computationally efficient means of estimating the ARL [20]. As a result, it can be used for the comparative analysis of exact solutions.

While traditional control charts like EWMA, MEWMA, and DMEWMA are typically designed with symmetric two-sided control limits, real-world applications may require one-sided limits. Additionally, processes exhibiting autocorrelation, where past data points influence current values, can undermine the effectiveness of standard control charts. In such cases, specialized charts or adjustments are necessary to accurately monitor and analyze these processes.

Stochastic processes that rely on time-space or time series are frequently the source of observations or data used in real-world scenarios. In other words, the models developed using econometric models are sometimes expressed in time-series models. The observations in an econometrics time-series model are made up of autoregressive (AR) and moving average (MA) elements. Identifying movement patterns of time-series observations in MA models is simple, and seasonal factors can easily be treated as seasonal moving averages (SMAs). Modeling should take into the difference between the exact and approximated values, often known as error. A smaller inaccuracy indicates higher accuracy. A smaller inaccuracy indicates higher accuracy. The error of a time-series model, known as white noise, often follows a normal distribution; however, another type of time-series model with auto-correlated observations is exponential white noise [21,22,23,24].

According to the literature review, DMEWMA charts have not been provided in any method other than the AR process [25]. Recently, Neammai et al. [26] compared DMEAMA on the MA(q) process utilizing only the NIE approach. However, no exact solution has been discovered and compared to other charts. As a result, the primary focus of this study was on constructing an ARL for monitoring change in a time series using an MA model order q. In various circumstances, this approach is based on the DMEWMA control chart with underlying exponential white noise. An explicit formula was used to calculate the ARL. The control charts for EWMA and MEWMA continue for comparison. Furthermore, their ARL is extended to compare processes with the AMC entertainment stock datasets.

2. Materials and Methods

2.1. Exponentially Weighted Moving Average, EWMA

The exponentially weighted moving average (EWMA) is a statistical analysis technique that progressively averages data, assigning less weight to observations as they move further from the current measurement in time [9]. The EWMA statistic is calculated recursively using individual data points providing a dynamic and responsive measure of process behavior.

$$E{W}_t=\lambda X_t+\left(1-\lambda \right)E{W}_{t-1}$$

(1)

where $E{W}_t$ is the EWMA statistic at time t, $\lambda$ is an exponential smoothing parameter such that $0\le \lambda \le 1$ and $X_t$ is the observation at time t. The mean is $E\left(E{W}_t\right)={\mu }_0$, and the variance of the EWMA control chart is $Var\left(E{W}_t\right)=\lambda {\sigma }^2/\left(2-\lambda \right)$. The center line (CL) for the control chart is the average of historical data. The upper (UCL) and lower (LCL) control limits of the EWMA control charts are determined by

$$CL={\mu }_0,$$

$$UCL/LCL={\mu }_0\pm W_E\sigma \sqrt{{\displaystyle \frac{\lambda }{2-\lambda }}}$$

where ${\mu }_0$ and $\sigma$ are the mean and standard deviation, respectively, and $W_L$ is the width of the control limit.

2.2. Modified Exponentially Weighted Moving Average, MEWMA

The MEWMA control chart is an attempt to improve the conventional EWMA chart’s performance. The constant case is taken into account in a revised MEWMA control chart [13]. The following is a description of the MEWMA statistic control chart:

$$M_t=\lambda X_t+(1-\lambda )M_{t-1}+c(X_t-X_{t-1})$$

(2)

where $\lambda$ is an exponential smoothing parameter such that $0\le \lambda \le 1$, $M_t$ is a MEWMA statistic at time t, with $M_0$ as the initial value and $X_t$ as the observation at time t; $c$ is an additional parameter in case $c=0$ turns to an EWMA control chart. The mean of $M_t$ is $E\left(E{W}_t\right)={\mu }_0$, and for large values of t, the variance of the statistic $M_t$ is approximately equal to $Var\left(M_t\right)=\left(\lambda +2c\left(\lambda +c\right)\right){\sigma }^2/\left(2-\lambda \right)$. The center line (CL) for the control chart is the average of historical data. The upper (UCL) and lower (LCL) control limits of the EWMA control charts are determined by

$$CL={\mu }_0,$$

$$UCL/LCL={\mu }_0\pm W_M\sigma \sqrt{{\displaystyle \frac{\lambda +2c\left(\lambda +c\right)}{2-\lambda }}}$$

where ${\mu }_0$ and $\sigma$ are the mean and standard deviation, respectively, and $W_M$ is the width of the control limit.

2.3. Double-Modified EWMA Control Chart, DMEWMA

The DMEWMA control chart is a smoothed variant of the modified EWMA control chart, which allows the control chart to detect small shifts more easily [16]. The system of Equation (3) can be used to calculate the DMEWMA statistics.

$$\begin{array}{l}D{M}_t={\lambda }_2{M}_t+(1-{\lambda }_2)D{M}_{t-1}+c_2(M_t-M_{t-1}),\\ M_t={\lambda }_1{X}_t+(1-{\lambda }_1)M_{t-1}+c_1(X_t-X_{t-1}),\end{array}$$

(3)

where $D{M}_t,M_t$ are DMEWMA and MEWMA statistics at time $t$, $X_t$ is the observed value of the process at time $t,$ $0\le {\lambda }_1,{\lambda }_2\le 1$ are the smoothing parameters, $c_1,c_2$ are constants, and the starting values $D{M}_0=M_0=X_0={\mu }_0.$ The calculations for the proposed DMEWMA chart are too complex because it includes four parameters, ${\lambda }_1,{\lambda }_2,c_1,$ and $c_2.$ To enhance the implementation and decrease the computational complexity, we take into account ${\lambda }_1={\lambda }_2=\lambda$ and $c_1=c_2=c.$ The control chart performs best when $c=-\lambda /2$ and $c=-\lambda /4$ are configured [16].

For a DMEWMA chart, the mean value is generally assumed to be the process mean in the absence of shifts. This is because the chart is designed to detect shifts from a stable process, so in the normal state, the chart’s value should be centered around the mean of the process. The mean $D{M}_t$ is equal to $E\left(D{M}_t\right)={\mu }_0$.

For a DMEWMA chart, the variance can be more complex and will generally be a function of both the smoothing constant $\lambda$ and the time horizon over which the control chart is monitored. However, for large values of t, the variance can be approximated as

$${\displaystyle \frac{Var\left(D{M}_t\right)}{{\sigma }^2}}={\left(c+\lambda \right)}^4+4{\lambda }^2{\left(c+\lambda \right)}^2{\left(c+\lambda -1\right)}^2+{\displaystyle \frac{4{\lambda }^2{\left(c+\lambda \right)}^2{\left(c+\lambda -1\right)}^2{\left(1-\lambda \right)}^2}{1-{\left(1-\lambda \right)}^2}}$$

$$-{\displaystyle \frac{4{\lambda }^3\left(c+\lambda \right){\left(c+\lambda -1\right)}^3\left(1-\lambda \right)}{{\left(1-{\left(1-\lambda \right)}^2\right)}^2}}+{\lambda }^4{\left(c+\lambda -1\right)}^4{\displaystyle \frac{1+{\left(1-\lambda \right)}^2}{{\left(1-{\left(1-\lambda \right)}^2\right)}^3}}$$

Following (1), the centerline (CL), the upper control limit (UCL), and the lower control limit (LCL) of the proposed DMEWMA control chart are given by

$$CL={\mu }_0,$$

$$UCL/LCL={\mu }_0\pm W_D\sigma \sqrt{Var\left(D{M}_t\right)}$$

where ${\mu }_0$ and $\sigma$ are the mean and standard deviation of the process, and $W_D$ is the width of the control limit.

The DMEWMA control chart’s stopping time is represented as follows:

$${\tau }_b=\inf \left\{t>0:D{M}_t>b\right\},\mathrm{for} b\ge u$$

where the constant parameter $b$ represents the upper control limit and $u$ is the initial value of $D{M}_0.$

2.4. Analytical Explicit Formula of ARL for the MA Model

In the case of exponential white noise, the observations equation for the moving average for the order q model ($MA(q)$) where q is the number of lags, or past values is specified as

$$X_t=\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{t-i}+{\epsilon }_t}$$

(4)

where $\mu$ is the mean of the MA process, $\left|{\theta }_i\right|<1$ are the coefficients of the process, and ${\epsilon }_t~Exp\left(\beta \right)$ is the exponential white noise. The DMEWMA statistics based on $MA(q)$ can be written as

$$D{M}_t=\left({\lambda }_1{\lambda }_2+c_1{\lambda }_2+c_2{\lambda }_1+c_1{c}_2\right)\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{t-i}+{\epsilon }_t}\right)-({\lambda }_2+c_2)c_1{X}_{t-1}+\left({\lambda }_2-{\lambda }_1{\lambda }_2-c_2{\lambda }_1\right)M_{t-1}+(1-{\lambda }_2)D{M}_{t-1}$$

Consider $t=1$ with initial value $D{M}_0=u,$ $X_0=v,$ $X_{-1}=e,$ $M_{-1}=d$ and define $A={\lambda }_1{\lambda }_2+c_1{\lambda }_2+c_2{\lambda }_1+c_1{c}_2$ and $B=-({\lambda }_2+c_2)c_{1}v+\left({\lambda }_2-{\lambda }_1{\lambda }_2-c_2{\lambda }_1\right)\left({\lambda }_{1}e+\left(1-{\lambda }_1\right)d+c_1\left(v-e\right)\right).$

Thus, the DMEWMA statistics for $MA(q)$ at $t=1$ can be described as

$$D{M}_1=A{\epsilon }_1+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)+B+(1-{\lambda }_2)u$$

(5)

In the control process, the interval of $D{M}_1$ between the lower and upper bound control limits is expressed as $a$ and $b,$ as shown below.

$$a\le D{M}_1=A{\epsilon }_1+(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)\le b$$

Subsequently, the control limit is moved to the exponential residual term in the following form:

$${\displaystyle \frac{a-(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\le {\epsilon }_1\le {\displaystyle \frac{b-(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}$$

The integral equation representing the ARL of the DMEWMA control chart (denoted by ${\phi }_{EF}(u)$)

$${\phi }_{EF}(u)=1+{\displaystyle \underset{\left[a-(1-{\lambda }_2)u+B\right]/A+\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\overset{\left[b-(1-{\lambda }_2)u+B\right]/A+\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\int }}\phi \left[Aw+(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)\right]f\left(w\right)dw}$$

(6)

Let $y=Aw+(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right),$; then, $dw={\displaystyle \frac{1}{A}}dy.$ It can be rewritten as follows when the variable in (6) is changed:

$${\phi }_{EF}(u)=1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}$$

Since ${\epsilon }_t~Exp\left(\beta \right)$ so $f\left(x\right)={\displaystyle \frac{1}{\beta }}{e}^{-\frac{x}{\beta }};x\ge 0$. Then,

$${\phi }_{EF}(u)=1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)\frac{e^{\frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)-y}{\beta A}}}{\beta }dy}=1+{\displaystyle \frac{1}{\beta A}}{\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)e^{\frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}-\frac{y}{\beta A}}dy}$$

After that, we define $L\left(u\right)=e^{{\displaystyle \frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}$ and $I={\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)e^{-\frac{y}{\beta A}}dy}$. We obtain

$${\phi }_{EF}(u)=1+{\displaystyle \frac{L\left(u\right)}{\beta A}}I$$

(7)

Additionally, the solution to $C$ is as follows:

$$I={\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)e^{-\frac{y}{\beta A}}dy}={\displaystyle \underset{a}{\overset{b}{\int }}\left(1+\frac{L\left(y\right)}{\beta A}I\right)e^{-\frac{y}{\beta A}}dy}={\displaystyle \underset{a}{\overset{b}{\int }}{e}^{-\frac{y}{\beta A}}dy}+{\displaystyle \frac{I{e}^{\frac{B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{\beta A}}{\displaystyle \underset{a}{\overset{b}{\int }}{e}^{-\frac{{\lambda }_{2}y}{\beta A}}dy}$$

Then,

$$I={\displaystyle \frac{-\beta A\left(e^{-\frac{b}{\beta A}}-e^{-\frac{a}{\beta A}}\right)}{1+\frac{e^{\frac{B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{{\lambda }_2}\left(e^{-\frac{{\lambda }_{2}b}{\beta A}}-e^{-\frac{{\lambda }_{2}a}{\beta A}}\right)}}$$

(8)

Ultimately, the explicit ARL formula on a two-sided DMEWMA control chart for the MA(q) model can be found by substituting Equation (8) into Equation (7).

$${\phi }_{EF}(u)=1+{\displaystyle \frac{e^{\frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{\beta A}}\left[{\displaystyle \frac{-\beta A\left(e^{-\frac{b}{\beta A}}-e^{-\frac{a}{\beta A}}\right)}{1+\frac{e^{\frac{B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{{\lambda }_2}\left(e^{-\frac{{\lambda }_{2}b}{\beta A}}-e^{-\frac{{\lambda }_{2}a}{\beta A}}\right)}}\right]$$

$${\phi }_{EF}(u)=1-{\displaystyle \frac{e^{\frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}\left(e^{-\frac{b}{\beta A}}-e^{-\frac{a}{\beta A}}\right)}{1+\frac{e^{\frac{B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{{\lambda }_2}\left(e^{-\frac{{\lambda }_{2}b}{\beta A}}-e^{-\frac{{\lambda }_{2}a}{\beta A}}\right)}}$$

(9)

The process is in control ($AR{L}_{in}$) when the exponential parameter $\beta ={\beta }_0,$ but out of control ($AR{L}_{out}$) when the exponential parameter $\beta ={\beta }_1,$ which ${\beta }_1=\left(1+\delta \right){\beta }_0,$ where $\delta$ is the shift size in the mean.

2.5. The Existence and Uniqueness of Explicit Formula via Banach’s Fixed Point Theorem and Hölder Inequality

To verify that the ARL solution illustrates that the integral equation for an exact formula appears only once. To demonstrate the proof, we will use Banach’s fixed point theorem and Hölder inequality. The connection between Banach’s fixed-point theorem and Hölder’s inequality lies in their combined utility in solving problems involving the existence and uniqueness of solutions. The Banach fixed-point theorem is often applied to demonstrate the existence of solutions to integral equations, while Hölder’s inequality aids in establishing bounds necessary for these proofs [27,28].

For each class of continuous functions described by, let $\phi$ represent a function operation.

$$T\left({\phi }_{EF}(u)\right)=1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}$$

(10)

Theorem 1.

(Banach’s Fixed-point): Suppose that $X$ is a continuous function and $T:X\to X$ satisfying the following assumption:

(H0): $‖T\left({\phi }_1\right)-T\left({\phi }_2\right)‖\le \delta ‖{\phi }_1-{\phi }_2‖,$ for ${\phi }_1,{\phi }_2\in \left[a,b\right],$ with ${‖\phi ‖}_{\infty }=\underset{u\in [a,b]}{\sup }\left|\phi \left(u\right)\right|$. If $\delta ={\displaystyle \frac{{\left(b-a\right)}^{\sigma }}{A}}{\left[e^{{\displaystyle \frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A\left(1-\sigma \right)}}}\left(e^{{\displaystyle \frac{-a}{\beta A\left(1-\sigma \right)}}}-e^{{\displaystyle \frac{-b}{\beta A\left(1-\sigma \right)}}}\right)\right]}^{1-\sigma }<1,$ where $\sigma \in \left(0,1\right)$ and $\beta >0,$; then, the formula has a unique solution.

Proof of Theorem 1.

Let $T$ be the contraction mapping for $u,v\in \left(\left[0,T\right],ℝ\right)$ and for each $t\in \left[0,T\right]$; then,

$$\begin{array}{l}‖T\left({\phi }_1\left(u\right)\right)-T\left({\phi }_2\left(u\right)\right)‖\\ =\underset{u\in [a,b]}{\sup }\left|\left(1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}{\phi }_1\left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}\right)-\left(1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}{\phi }_2\left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}\right)\right|\end{array}$$

$$=\underset{u\in [a,b]}{\sup }\left|{\displaystyle \frac{1}{A}}\left({\displaystyle \underset{a}{\overset{b}{\int }}{\phi }_1\left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}-{\displaystyle \underset{a}{\overset{b}{\int }}{\phi }_2\left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}\right)\right|$$

$$\le {\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}\left|{\phi }_1-{\phi }_2\right|\left|f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)\right|dy}$$

$$\le {\displaystyle \frac{1}{A}}‖{\phi }_1-{\phi }_2‖{\displaystyle \underset{a}{\overset{b}{\int }}\left|f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)\right|dy}$$

□

Theorem 2.

(Hölder’s inequality) Let $\left(S,\sum ,\mu \right)$ be the measure space, and let $p,q\in \left[1,\infty \right]$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1.$ Then, for all measurable real-valued function $f$ and $g$ on $S,$ Hölder’s inequality is

$$\left(\mathrm{H}1\right): {\displaystyle \underset{S}{\int }\left|f\left(x\right)g\left(x\right)\right|}dx\le {\left({{\displaystyle \underset{S}{\int }\left|f\left(x\right)\right|}}^{p}dx\right)}^{{\displaystyle \frac{1}{p}}}{\left({{\displaystyle \underset{S}{\int }\left|g\left(x\right)\right|}}^{q}dx\right)}^{{\displaystyle \frac{1}{q}}}$$

Proof of Theorem 2.

Given Hölder’s inequality, we have

$$‖T\left({\phi }_1\left(u\right)\right)-T\left({\phi }_2\left(u\right)\right)‖\le {\displaystyle \frac{1}{A}}‖{\phi }_1-{\phi }_2‖{\left[{\displaystyle \underset{a}{\overset{b}{\int }}\left|f{\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)}^{\frac{1}{1-\sigma }}\right|dy}\right]}^{1-\sigma }{\left[{\displaystyle \underset{a}{\overset{b}{\int }}{\left|1\right|}^{\frac{1}{\sigma }}dy}\right]}^{\sigma }$$

$$\le {\displaystyle \frac{1}{A}}‖{\phi }_1-{\phi }_2‖{\left[{\displaystyle \frac{1}{\beta A}}{e}^{{\displaystyle \frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A}}}{\displaystyle \underset{a}{\overset{b}{\int }}{\left(e^{\frac{-y}{\beta A}}\right)}^{\frac{1}{1-\sigma }}dy}\right]}^{1-\sigma }{\left[b-a\right]}^{\sigma }$$

$$={\displaystyle \frac{{\left(b-a\right)}^{\sigma }}{A}}‖{\phi }_1-{\phi }_2‖{\left[{\displaystyle \frac{1}{\beta A\left(1-\sigma \right)}}{e}^{{\displaystyle \frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A\left(1-\sigma \right)}}}\left(-\beta A\left(1-\sigma \right)\right)\left(e^{{\displaystyle \frac{-b}{\beta A\left(1-\sigma \right)}}}-e^{{\displaystyle \frac{-a}{\beta A\left(1-\sigma \right)}}}\right)\right]}^{1-\sigma }$$

$$={\displaystyle \frac{{\left(b-a\right)}^{\sigma }}{A}}‖{\phi }_1-{\phi }_2‖{\left[e^{{\displaystyle \frac{(1-{\lambda }_2)u+B+A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{\beta A\left(1-\sigma \right)}}}\left(e^{{\displaystyle \frac{-a}{\beta A\left(1-\sigma \right)}}}-e^{{\displaystyle \frac{-b}{\beta A\left(1-\sigma \right)}}}\right)\right]}^{1-\sigma }=\delta ‖{\phi }_1-{\phi }_2‖$$

It follows that $T$ is a contraction mapping. Hence, Banach’s fixed point theorem implies that $T$ has a unique point, which is the unique solution to problem (10). This completes the proof. □

2.6. Approximate Numerical Integral Equation of ARL for the MA Model

The explicit formula’s accuracy is verified using the ARL’s numerical integral equation approach (NIE method). The midpoint quadrature rule, designated ${\phi }_{NIE}(u)$, are used to determine the estimated ARL using the NIE approach.

A form that represents the solution to an integral equation for calculating the ARL is provided as

$$\phi (u)=1+{\displaystyle \frac{1}{A}}{\displaystyle \underset{a}{\overset{b}{\int }}\phi \left(y\right)f\left(\frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}\right)dy}$$

The approximation for an integral is evaluated using the quadrature rule as follows:

$${\displaystyle {\int }_a^{b}f(x)}dx\approx {\displaystyle \sum _{l=1}^n{w}_l}f(a_l)$$

where $a_l=\left(l-{\displaystyle \frac{1}{2}}\right)w_l$ is a point, and $w_l={\displaystyle \frac{b}{m}}$ $;l=1,2,\dots ,m$ is a weight that is determined by the midpoint quadrature rule.

Using the midpoint quadrature formula, the result of the system of $m$ linear equations is as follows:

$${\phi }_{NIE}(a_f)=1+{\displaystyle \frac{1}{A}}{\displaystyle \sum _{l=1}^m{w}_l}\phi \left(a_l\right)f\left({\displaystyle \frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right),f=1,2,\dots ,m$$

$${\phi }_{NIE}(a_1)=1+{\displaystyle \frac{1}{A}}{\displaystyle \sum _{l=1}^m{w}_l}\phi \left(a_l\right)f\left({\displaystyle \frac{a_l-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right)$$

$${\phi }_{NIE}(a_2)=1+{\displaystyle \frac{1}{A}}{\displaystyle \sum _{l=1}^m{w}_l}\phi \left(a_l\right)f\left({\displaystyle \frac{a_l-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right)$$

$${\phi }_{NIE}(a_m)=1+{\displaystyle \frac{1}{A}}{\displaystyle \sum _{l=1}^m{w}_l}\phi \left(a_l\right)f\left({\displaystyle \frac{a_l-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right)$$

The system of m linear equations can be shown as ${\phi }_{m\times 1}=1_{m\times 1}+R_{m\times m}{\phi }_{m\times 1}.$ If the inverse ${\left({\phi }_m-R_{m\times m}\right)}^{-1}$ exists, the distinct resolution appears as

$${\phi }_{m\times m}={\left(I_m-R_{m\times m}\right)}^{-1}{1}_{m\times 1}$$

where ${\phi }_{m\times 1}={[{\phi }_{NIE}(a_1),{\phi }_{NIE}(a_2),\dots ,{\phi }_{NIE}(a_m)]}^{\prime },$ $I_m=diag\left(1,1,\dots ,1\right),$ $1_{m\times 1}={\left(1,1,\dots ,1\right)}^{\prime },$ and $R_{m\times m}$ is a matrix. The $\left(m,m^{th}\right)$ elements of the R matrix are defined as

$$\left[R_{fl}\right]\approx {\displaystyle \frac{1}{A}}{w}_{l}f\left({\displaystyle \frac{y-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right)$$

Finally, an approximation of the numerical integral for the function ${\phi }_{NIE}(u)$ is

$${\phi }_{NIE}(u)=1+{\displaystyle \frac{1}{A}}{\displaystyle \sum _{l=1}^m{w}_l}\phi \left(a_l\right)f\left({\displaystyle \frac{a_l-(1-{\lambda }_2)u-B-A\left(\mu -{\displaystyle \sum _{i=1}^q{\theta }_i{\epsilon }_{1-i}}\right)}{A}}\right)$$

(11)

where $a_l=\left(l-{\displaystyle \frac{1}{2}}\right)w_l$ and $w_l={\displaystyle \frac{b}{m}}$ $;l=1,2,\dots ,m$ are a point and a weight that is determined by the midpoint quadrature rules, respectively.

3. Evaluation of Performance

Statistical performance was evaluated using simulation. All computations are repeated 1000 times. There are some criteria for evaluating the performance of a control chart. The most popular ARL has been chosen as the performance indicator for our suggestions. To determine the accuracy of the ARL solution between the proposed explicit form and the NIE method, the relative percentage change (RPC) [29] is used to compare the results of the two techniques, as seen below.

$$RPC=\left|{\displaystyle \frac{{\phi }_{EF}(u)-{\phi }_{NIE}(u)}{{\phi }_{EF}(u)}}\right|\times 100\%$$

Several researchers also defend other criteria, such as the median run length (MRL), which relates to the run length at the middle, and the standard deviation of run length (SDRL), which is a beneficial statistic used to examine the spreading [30]. Thus, the MRL and SDRL are estimated for the schemes described.

The in-control ARL, MRL, and SDRL are defined as

$$AR{L}_{in}=1/\alpha , SDR{L}_{in}=\sqrt{\left(1-\alpha \right)/{\alpha }^2}, MR{L}_{in}=\log \left(0.5\right)/\log \left(1-\alpha \right),$$

for $\alpha =1-P\left(LCL<Y<UCL|\mu \right)$ where $Y$ is the result of the process, and $\mu$ is the mean. While the out-of-control are given by

$$AR{L}_{out}=1/\left(1-\beta \right), SDR{L}_{out}=\sqrt{\beta /{\left(1-\beta \right)}^2}, MR{L}_{out}=\log \left(0.5\right)/\log \left(\beta \right),$$

for $\beta =P\left(LCL<Y<UCL|{\mu }_{sh}\right)$ where ${\mu }_{sh}$ is the shifted mean proportion parameter.

However, these criteria measure the performance of a control chart for a specific shift. To measure the overall performance, the relative mean index (RMI) and relative standard deviation index (RSDI) were proposed by Han and Tsung [31].

The RMI and RSDI measures are calculated as

$$RMI={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{AR{L}_{out}\left(r_i\right)-AR{L}_{out}^{*}\left(r_i\right)}{AR{L}_{out}^{*}\left(r_i\right)}},$$

$$RSDI={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{SDR{L}_{out}\left(r_i\right)-SDR{L}_{out}^{*}\left(r_i\right)}{SDR{L}_{out}^{*}\left(r_i\right)}},$$

where $n$ is an amount of shift size considered, $AR{L}_{out}\left(r_i\right)$ and $SDR{L}_{out}\left(r_i\right)$ are the $AR{L}_{out}$ and $SDR{L}_{out}$ values of control charts for the specific shift $r_i$, and $AR{L}_{out}^{*}\left(r_i\right)$ and $SDR{L}_{out}^{*}\left(r_i\right)$ are the smallest of $AR{L}_{out}$ and $SDR{L}_{out}$ values found in all of the charts proposed to detect the shift $r_i$, receptively. Control schemes with the lowest RMI and RSDI values detect shifts more swiftly and robustly. It should be noted that in this article, SDRL values equal to zero are not considered in the computation of RSDI, and this index is calculated by the range of shifts with SDRL greater than zero. To start the monitoring action, we consider a specific in-control ARL. The control chart methods in this article have been developed to have an in-control ARL of around 370.

3.1. Simulation Results

The study is divided into two parts: comparing the proposed approach to numerical methods and determining whether the proposed method performs better. The criteria utilized is the relative percentage change. The other part is to look at the performance of the proposed method by comparing it with previously studied charts, namely the EWMA chart and the DMEWMA chart. This analysis was carried out using simulations in Wolfram Mathematica 8, which were conducted 1000 times each. The relative standard deviation index (RSDI) and relative mean index (RMI) are used to compare how well these three approaches perform. The selection of the optimal method is determined by two crucial factors minimizing the values of indicators RSDI and RMI. In this research, we study the performance of the control chart to detect only the mean by fixing the variation. Therefore, the performance of the proposed control chart will challenge only detecting the mean. The process mean shifts from ${\beta }_0$ to ${\beta }_1,$ where ${\beta }_1=(1+\delta ){\beta }_0,$ indicating an out-of-control condition. The in-control condition is characterized by exponential white noise with mean ${\beta }_0=1$. The results are as follows: $\delta$ = 0.001, 0.003, 0.005, 0.01, 0.03, 0.05, 0.1, 0.3, 0.5, and 1, where $\delta =0$ and, respectively, imply that the process is under control and out of control, respectively. These processes are denoted as $AR{L}_{in}$ and $AR{L}_{out}.$

We performed simulation research to assess the efficacy of explicit formulas, and NIE approaches for the ARL of an MA(q) process running on the DMEWMA control chart using the steps detailed below.

Step 1: Setting up the control limit for the MA(q) process:

i.

Define the exponential white noise (${\beta }_0$) and smoothing parameters for the in-control process.

ii.

Define the initial values for the MA(q) process and the DMEWMA statistic.

iii.

Select acceptable values for ARL_out and the shift sizes ($\delta$).

iv.

Compute the upper control limit (b) that gives the desired ARL for the control process by using (9).

Step 2: For the in-control ARL:

i.

Compute ARL_in using (9) when given the upper control limit (b) from Step 1.

ii.

Approximate the value of ARL_in Via the NIE method by using (11).

iii.

If necessary, change the value of b according to the desired ARL_in value (Here, we set ARL0 = 370).

Step 3: For the out-of-control ARL:

i.

Compute ARL_out for various shift sizes and ${\beta }_1=(1+\delta ){\beta }_0,$ using (9) and the value of b from Step 1.

ii.

Approximate ARL_out Via the NIE method by using (6).

iii.

Compare the ARL values obtained using the explicit formulas and NIE methods.

When examining the exact and numerical approaches’ relative percentage change (RPC) values. Table 1 and Table 2 present the results of the simulation, which show that the relative percentage change (RPC) produces relatively modest numbers. This indicates that there is no difference between the two approaches’ average values. This is relevant even though the $c$ value adjusts, and the process mean shifts grow.

Table 1. The ARL values for MA(q) models on the DMEWMA control chart with the initial $c_1=1$ and $c_2=-{\lambda }_2/2$, where $\theta ={\theta }_1={\theta }_2={\theta }_3$ with $AR{L}_0=370$.

$\mathit{\theta }$	$\mathit{\delta }$	MA(1)			MA(2)			MA(3)
		λ1 = 0.05, λ2 = 0.1			λ1 = 0.1, λ2 = 0.1			λ1 = 0.2, λ2 = 0.1
		${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC	${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC	${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC
		0.00000004651			0.0000001415			0.0000008574
0.2	0	370.06599099	370.06599097	5.40 × 10−9	370.18643108	370.18643108	0	370.00929403	370.00929403	0
	0.001	362.45882162	362.45882160	5.52 × 10−9	362.96195047	362.96195046	2.76 × 10−9	363.40862560	363.40862560	0
	0.003	347.75381070	347.75381068	5.75 × 10−9	348.97443935	348.97443935	0	350.59608759	350.59608759	0
	0.005	333.70070787	333.70070786	2.99 × 10−9	335.57860543	335.57860543	0	338.28350065	338.28350065	0
	0.007	320.26834537	320.26834538	3.12 × 10−9	322.74736297	322.74736297	0	326.44961922	326.44961922	0
	0.01	301.21941228	301.21941227	3.32 × 10−9	304.50311477	304.50311478	3.28 × 10−9	309.55227925	309.55227925	0
	0.03	202.00490775	202.00490774	4.95 × 10−9	208.40989177	208.40989176	4.80 × 10−9	218.92831272	218.92831272	0
	0.07	95.14833819	95.14833819	0	101.97977703	101.97977703	0	113.91462707	113.91462707	0
	0.1	56.22040234	56.22040234	0	61.85815712	61.85815712	0	72.09160881	72.09160881	0
	0.5	1.32943633	1.32943633	0	1.47010967	1.47010967	0	1.83226459	1.83226459	0
	1	1.00904094	1.00904094	0	1.01540939	1.01540939	0	1.03630688	1.03630688	0
−0.2		0.0000000312			0.00000006355			0.0000002582
	0	370.34322939	370.34322941	5.40 × 10−9	370.01220717	370.01220717	0	369.94837505	369.94837505	0
	0.001	362.58582492	362.58582493	2.76 × 10−9	362.50209909	362.50209909	0	362.91462183	362.91462183	0
	0.003	347.59935947	347.59935945	5.75 × 10−9	347.97894841	347.97894840	2.87 × 10−9	349.28590317	349.28590317	0
	0.005	333.28869070	333.28869072	6.00 × 10−9	334.09229235	334.09229235	0	336.22028669	336.22028669	0
	0.007	319.62099445	319.62099443	6.26 × 10−9	320.81202222	320.81202223	3.12 × 10−9	323.69254849	323.69254849	0
	0.01	300.25739039	300.25739040	3.33 × 10−9	301.96646003	301.96646002	3.31 × 10−9	305.85725787	305.85725787	0
	0.03	199.82590714	199.82590713	5.00 × 10−9	203.53715931	203.53715932	4.91 × 10−9	211.40745707	211.40745707	0
	0.07	92.78547011	92.78547012	1.08 × 10−8	96.78542929	96.78542929	0	105.37132431	105.37132431	0
	0.1	54.28843940	54.28843941	1.84 × 10−8	57.56243250	57.56243249	1.74 × 10−8	64.73310077	64.73310077	0
	0.5	1.28853032	1.28853032	0	1.35989959	1.35989959	0	1.55778367	1.55778367	0
	1	1.00740765	1.00740765	0	1.01032433	1.01032433	0	1.01992212	1.01992212	0

Table 2. The ARL values for MA(q) models on the DMEWMA control chart with the initial $c_1=1$ and $c_2=-{\lambda }_2/4$, where $\theta ={\theta }_1={\theta }_2={\theta }_3$ with $AR{L}_0=370$.

$\mathit{\theta }$	$\mathit{\delta }$	MA(1)			MA(2)			MA(3)
		λ1 = 0.05, λ2 = 0.1			λ1 = 0.1, λ2 = 0.1			λ1 = 0.2, λ2 = 0.1
		${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC	${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC	${\mathit{\phi }}_{\mathit{E}\mathit{F}}$(u)	${\mathit{\phi }}_{\mathit{N}\mathit{I}\mathit{E}}$(u)	RPC
		0.00003971			0.00009038			0.0003278
0.2	0	369.60789426	369.60789426	0	370.02499526	370.02499526	0	369.99003541	369.99003541	0
	0.001	364.30292869	364.30292869	0	364.99421498	364.99421498	0	365.39203261	365.39203261	0
	0.003	353.95053168	353.95053168	0	355.16553942	355.16553942	0	356.39289257	356.39289257	0
	0.005	343.93126915	343.93126915	0	345.63850270	345.63850270	0	347.64924562	347.64924562	0
	0.007	334.23326838	334.23326838	0	336.40280558	336.40280558	0	339.15295737	339.15295737	0
	0.01	320.26379426	320.26379426	0	323.07393700	323.07393700	0	326.85522884	326.85522884	0
	0.03	242.45417948	242.45417948	0	248.21716517	248.21716517	0	256.90323168	256.90323168	0
	0.07	143.34883729	143.34883729	0	150.88465547	150.88465547	0	163.00000264	163.00000264	0
	0.1	99.13343094	99.13343094	0	106.38127708	106.38127708	0	118.41130164	118.41130164	0
	0.5	3.72430968	3.72430968	0	4.52857694	4.52857694	0	6.25355254	6.25355254	0
	1	1.21528610	1.21528610	0	1.31727410	1.31727410	0	1.57707711	1.57707711	0
−0.2		0.00002665			0.0000406			0.00009861
	0	370.07773148	370.07773148	0	370.04167628	370.04167628	0	369.99862427	369.99862427	0
	0.001	364.62005491	364.62005491	0	364.71780281	364.71780281	0	364.95619628	364.95619628	0
	0.003	353.97606978	353.97606978	0	354.32910088	354.32910088	0	355.10543180	355.10543180	0
	0.005	343.68287666	343.68287666	0	344.27546445	344.27546445	0	345.55783898	345.55783898	0
	0.007	333.72769914	333.72769914	0	334.54492499	334.54492499	0	336.30303199	336.30303199	0
	0.01	319.40200743	319.40200743	0	320.52988600	320.52988600	0	322.94803234	322.94803234	0
	0.03	239.95081009	239.95081009	0	242.49761512	242.49761512	0	247.97850968	247.97850968	0
	0.07	139.83626953	139.83626953	0	143.20503022	143.20503022	0	150.60020440	150.60020440	0
	0.1	95.73861116	95.73861116	0	98.95530495	98.95530495	0	106.12358527	106.12358527	0
	0.5	3.38680948	3.38680948	0	3.70094125	3.70094125	0	4.51244738	4.51244738	0
	1	1.17645526	1.17645526	0	1.21255789	1.21255789	0	1.31596286	1.31596286	0

Table 3 compares lambda values on the DMEWMA chart in $MA(2)$ and $MA(3)$ processes for ${\lambda }_2={\lambda }_1$ and ${\lambda }_2>{\lambda }_1$. In this case, giving the lower $AR{L}_{out}$ values is used in the control chart comparison phase. The results demonstrate that ${\lambda }_2>{\lambda }_1$ produces a lower $AR{L}_{out}$ value (the bold fonts indicate the $AR{L}_{out}$ lower values for a specific shift, and each value of $\lambda$) in the case of $c$ being small (lower than 5), obviously, but when $c$ is large, ${\lambda }_2={\lambda }_1$ gives a lower $AR{L}_{out}$ value, but when considered carefully in this situation, the values are not much different. So, in this study, we put ${\lambda }_2>{\lambda }_1$ to compare the charts in the following step.

Table 3. Comparison of ARL values for DMEWMA control charts under varying $\lambda$. Conditions $(1):{\lambda }_1={\lambda }_2=0.05$ and $(2):{\lambda }_2>{\lambda }_1;{\lambda }_1=0.05,{\lambda }_2=0.1$.

MA(2)
$\mathit{\delta }$	C1 = C2 = 0.5		C1 = C2 = 1		C1 = 1, C2 = 3		C1 = C2 = 3		C1 = C2 = 5		C1 = C2 = 7
	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)
	1.19125	0.68373	1.677663	1.20412	2.91761	2.47904	6.40976	6.19054	15.6465	15.8183	29.3889	30.0861
0	369.946	369.961	370.000	370.047	370.369	370.197	369.980	370.108	369.928	370.223	370.078	370.036
0.001	359.475	349.640	306.447	286.245	258.359	246.724	231.324	227.951	220.193	221.110	216.893	219.025
0.003	340.129	314.903	228.127	197.083	161.192	148.224	132.508	129.208	122.002	122.775	118.986	120.914
0.005	322.656	286.303	181.722	150.329	117.282	106.086	93.033	90.342	84.577	85.180	82.186	83.709
0.01	285.580	232.919	120.521	94.458	69.992	62.239	53.588	51.831	48.147	48.522	46.631	47.593
0.03	193.342	131.564	51.512	38.212	27.250	23.915	20.393	19.670	18.212	18.354	17.611	17.988
0.05	144.125	90.316	32.871	24.099	17.200	15.078	12.900	12.442	11.543	11.628	11.170	11.402
0.1	85.078	48.963	17.414	12.717	9.269	8.150	7.065	6.821	6.371	6.411	6.181	6.297
0.3	27.870	15.255	6.378	4.769	3.784	3.386	3.063	2.972	2.834	2.843	2.771	2.807
0.5	15.248	8.451	4.138	3.177	2.670	2.423	2.250	2.191	2.114	2.118	2.077	2.097
1	6.690	3.926	2.495	2.020	1.833	1.703	1.633	1.600	1.567	1.568	1.549	1.558
MA(3)
$\mathit{\delta }$	C1 = C2 = 0.5		C1 = C2 = 1		C1 = 1, C2 = 3		C1 = C2 = 3		C1 = C2 = 5		C1 = C2 = 7
	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)
	1.23761	0.72789	1.83392	1.37127	3.35807	2.94963	7.65116	7.54494	19.00647	19.46550	35.90100	37.13110
0	370.135	370.419	369.872	369.884	369.901	370.228	370.063	369.964	369.936	370.183	370.587	369.902
0.001	359.131	349.236	305.571	287.899	260.532	252.211	236.817	235.495	227.172	229.531	224.545	227.654
0.003	328.890	313.268	226.789	199.555	163.936	154.247	137.966	136.655	128.532	130.733	125.900	128.999
0.005	320.705	283.882	180.347	152.763	119.749	111.254	97.529	96.446	89.824	91.595	87.682	90.202
0.01	282.422	229.569	119.367	96.421	71.780	65.804	56.564	55.844	51.533	52.672	50.143	51.776
0.03	188.921	128.339	50.968	39.222	28.081	25.468	21.650	21.343	19.606	20.059	19.044	19.701
0.05	140.016	87.826	32.554	24.793	17.757	16.083	13.711	13.512	12.435	12.714	12.085	12.493
0.1	82.204	47.579	17.303	13.130	9.595	8.702	7.513	7.401	6.858	6.998	6.678	6.886
0.3	26.990	14.974	6.409	4.958	3.937	3.609	3.250	3.202	3.031	3.074	2.971	3.038
0.5	14.863	8.375	4.188	3.312	2.781	2.573	2.378	2.344	2.248	2.272	2.212	2.251
1	6.609	3.948	2.546	2.103	1.905	1.792	1.711	1.690	1.648	1.658	1.630	1.649

Table 4 presents a comparison of the $\theta$ scenarios for equal and unequal Zeta values. In the case of $MA(2)$, when ${\theta }_1={\theta }_2$ the ARL value is slightly lower, particularly when the mean undergoes small to moderate changes. Similarly, for $MA(3),$ ${\theta }_1={\theta }_2={\theta }_3$ results in a noticeably lower ARL value under small to moderate mean shifts. However, the difference is not substantial enough to impact the analysis significantly. Hence, for chart comparisons, the scenario where $\theta$ values are equal is selected for simulation.

Table 4. Comparison of ARL values for DMEWMA control charts under varying $\theta$. Conditions $(1):{\theta }_1={\theta }_2={\theta }_3=0.2$ and $(2):{\theta }_1=0.2,{\theta }_2=0.3,{\theta }_3=0.5$.

$\mathit{\delta }$	MA(2): for θ1, θ2				MA(3): for θ1, θ2, θ3
	C1 = 0.5, C2 = 1		C1 = 3, C2 = 5		C1 = 0.5, C2 = 1		C1 = 3, C2 = 5
	(1)	(2)	(1)	(2)	(1)	(2)	(1)	(2)
	b= 0.285341	0.31621	8.70184	9.64651	0.35053	0.53124	10.69735	16.246
0	370.00410	369.66375	369.85936	369.96074	370.20447	369.86214	370.07235	370.28991
0.001	313.39718	315.03276	218.07332	221.95416	317.35045	325.43850	226.04914	245.58710
0.003	239.81202	243.00997	120.08458	123.61481	246.71736	262.28665	127.42626	147.04708
0.005	194.07388	197.65861	83.05387	85.86232	201.67451	219.55192	88.92141	105.14325
0.01	131.14285	134.51258	47.17362	48.96813	138.21413	155.76894	50.93950	61.69997
0.03	56.40056	58.36532	17.81168	18.54302	60.51030	71.36048	19.35152	23.85669
0.05	35.52137	36.86424	11.28574	11.75174	38.33003	45.86147	12.26730	15.14393
0.1	18.06242	18.80236	6.22934	6.48188	19.60991	23.79975	6.76114	8.31130
0.3	5.80729	6.06211	2.77480	2.87531	6.34012	7.77954	2.98612	3.58787
0.5	3.50075	3.64982	2.07356	2.14097	3.81255	4.65230	2.21520	2.61326
1	1.98438	2.05395	1.54293	1.58269	2.13006	2.52223	1.62647	1.85809

The performance comparison of the EWMA, MEWMA, and DMEWMA control charts with varying $c_1$ and $c_2$ utilizing the ARL at ${\lambda }_1=0.05,{\lambda }_2=0.1$ for the $MA(2)$ and $MA(3)$ models, respectively, is displayed in Table 5 and Table 6. When the shift in the process means becomes bigger, these ARL data clearly demonstrate that the average run length of the DMEWMA approach is less than that of MEWMA and EWMA. If the $c$ values are the same, the MEWMA and DMEWMA approaches are comparable. Table 5 and Table 6 demonstrate that the additional parameters in the DMEWMA chart enhance detection speed, resulting in lower ARL values. Notably, when c is set to match the MEWMA, the chart achieves reduced ARL values. Similarly, keeping $c_1$ in the DMEWMA equal to $c$ in the MEWMA ensures that $c_2$ in the DMEWMA also yields lower ARL values. For example, In Table 5, at $\delta =0.001$, the EWMA chart yields an ARL_out of 364.6455. When $c=0.5$ is applied in the MEWMA chart, the ARL_out reduces to 335.9040. Further, in the DMEWMA chart, with $c_1=c=0.5$ fixed and set $c_2=0.5$, the ARL_out decreases to 308.9601, demonstrating a consistent trend across all cases. This clearly shows that the DMEWMA chart is superior.

Table 5. The ARL, SDRL, and MRL values for two-sided control charts on $MA(2)$ when ${\lambda }_1=0.05,{\lambda }_2=0.1$ ${\theta }_1={\theta }_2=0.2,$ and $\left[0.1,b\right]$ with $AR{L}_0=370$.

$\mathit{\delta }$	Chart	EWMA	MEWMA (c)				DMEWMA (c1, c2)
			0.5	1	3	10	0.5, 0.5	1, 1	1, 3	3, 3	10, 10
		b = 0.10000379	0.80751	0.65675	0.959455	2.34905	1.64661	6.32246	9.7581	29.189	86.4675
0.001	ARLout	364.6455	335.9040	276.2000	217.4547	215.3046	308.9601	231.5981	224.7168	216.9983	214.3852
	SDRLout	364.1452	335.4037	275.6995	216.9541	214.8040	308.4596	231.0975	224.2162	216.4978	213.8846
	MRLout	252.4063	232.4842	191.1004	150.3812	148.8909	213.8080	160.1847	155.4150	150.0649	148.2537
0.003	ARLout	352.9561	283.7107	183.2607	119.5263	117.4893	232.3062	132.7764	126.1784	119.0332	116.7953
	SDRLout	352.4558	283.2103	182.7600	119.0252	116.9883	231.8057	132.2754	125.6774	118.5322	116.2942
	MRLout	244.3038	196.3065	126.6798	82.5022	81.0903	160.6756	91.6865	87.1131	82.1605	80.6093
0.005	ARLout	341.6854	245.4477	137.1517	82.6188	80.9325	186.1505	93.2524	87.9109	82.2149	80.4684
	SDRLout	341.1850	244.9472	136.6508	82.1173	80.4309	185.6499	92.7510	87.4095	81.7134	79.9668
	MRLout	236.4915	169.7846	94.7193	56.9197	55.7508	128.6828	64.2904	60.5880	56.6398	55.4291
0.01	ARLout	315.2342	183.2973	84.2463	46.9103	45.7227	124.4193	53.7310	50.2750	46.6462	45.5538
	SDRLout	314.7338	182.7966	83.7448	46.4076	45.2200	123.9183	53.2286	49.7725	46.1435	45.0511
	MRLout	218.1569	126.7051	58.0478	32.1679	31.3447	85.8938	36.8958	34.5003	31.9849	31.2277
0.03	ARLout	230.1697	90.1858	33.2579	17.7268	17.2096	53.6114	20.4513	19.0594	17.6160	17.1874
	SDRLout	229.6691	89.6844	32.7541	17.2195	16.7021	53.1091	19.9451	18.5527	17.1087	16.6799
	MRLout	159.1946	62.1648	22.7043	11.9373	11.5788	36.8129	13.8263	12.8613	11.8605	11.5633
0.05	ARLout	170.0919	59.2364	20.8099	11.2447	10.9225	34.2623	12.9363	12.0696	11.1728	10.9072
	SDRLout	169.5912	58.7343	20.3037	10.7331	10.4105	33.7586	12.4263	11.5588	10.6611	10.3952
	MRLout	117.5518	40.7120	14.0749	7.4423	7.2188	23.4005	8.6156	8.0144	7.3924	7.2082
0.1	ARLout	83.8687	31.2683	10.8799	6.2226	6.0564	18.1471	7.0834	6.6404	6.1822	6.0467
	SDRLout	83.3672	30.7643	10.3679	5.7007	5.5339	17.6400	6.5644	6.1200	5.6602	5.5241
	MRLout	57.7861	21.3251	7.1893	3.9565	3.8410	12.2288	4.5545	4.2467	3.9284	3.8342
0.3	ARLout	39.1365	10.2073	4.0399	2.7886	2.7315	6.6076	3.0695	2.9231	2.7711	2.7261
	SDRLout	38.6333	9.6945	3.5044	2.2333	2.1747	6.0871	2.5204	2.3709	2.2154	2.1692
	MRLout	26.7793	6.7227	2.4373	1.5608	1.5205	4.2240	1.7583	1.6554	1.5485	1.5167
0.5	ARLout	22.4532	6.0078	2.7021	2.0892	2.0544	4.2655	2.2531	2.1668	2.0770	2.0503
	SDRLout	21.9475	5.4850	2.1446	1.5085	1.4718	3.7322	1.6803	1.5901	1.4956	1.4674
	MRLout	15.2142	3.8072	1.4998	1.0642	1.0392	2.5947	1.1815	1.1198	1.0554	1.0362
1	ARLout	6.0837	3.1175	1.7578	1.5569	1.5392	2.5503	1.6348	1.5931	1.5494	1.5363
	SDRLout	5.5613	2.5693	1.1542	0.9311	0.9110	1.9884	1.0187	0.9720	0.9226	0.9077
	MRLout	3.8600	1.7920	0.8238	0.6742	0.6608	1.3925	0.7327	0.7015	0.6685	0.6586

Table 6. The ARL, SDRL, and MRL values for two-sided control charts on $MA(3)$ when ${\lambda }_1=0.05,{\lambda }_2=0.1$ ${\theta }_1={\theta }_2={\theta }_3=0.2,$ and $\left[0.1,b\right]$ with $AR{L}_0=370$.

$\mathit{\delta }$	Chart	EWMA	MEWMA (c)				DMEWMA (c1, c2)
			0.5	1	3	10	0.5, 0.5	1, 1	1, 3	3, 3	10, 10
		b = 0.15143	0.97119	0.782202	1.15148	1.62678	1.79576	3.25073	18.83	51.2787	80.035
0.001	ARLout	367.6157	342.3886	281.8298	221.5179	207.3860	307.9553	262.0984	227.5443	220.7706	201.5782
	SDRLout	367.1154	341.8882	281.3294	221.0173	206.8853	307.4549	261.5980	227.0438	220.2700	201.0775
	MRLout	254.4651	236.9790	195.0028	153.1977	143.4021	213.1116	181.3260	157.3749	152.6797	139.3765
0.003	ARLout	362.8827	297.5887	190.8726	123.2368	110.6148	230.7788	165.7873	128.6869	122.3759	103.2890
	SDRLout	362.3823	297.0882	190.3720	122.7358	110.1137	230.2782	165.2865	128.1859	121.8749	102.7878
	MRLout	251.1844	205.9260	131.9559	85.0742	76.3252	159.6168	114.5681	88.8519	84.4775	71.2473
0.005	ARLout	358.2276	263.0402	144.3368	85.5768	75.5907	184.5699	121.3882	89.9171	84.4821	75.4170
	SDRLout	357.7272	262.5397	143.8360	85.0753	75.0890	184.0692	120.8871	89.4157	83.9806	74.9153
	MRLout	247.9577	181.9788	99.6997	58.9700	52.0481	127.5872	83.7928	61.9786	58.2113	51.9277
0.01	ARLout	346.9212	203.5693	89.7391	48.8102	42.4215	123.0718	72.9440	51.5778	48.3852	42.1341
	SDRLout	346.4209	203.0687	89.2377	48.3076	41.9185	122.5708	72.4423	51.0753	47.8825	41.6311
	MRLout	240.1207	140.7566	61.8552	33.4849	29.0564	84.9598	50.2136	35.4033	33.1903	28.8572
0.03	ARLout	306.0328	105.7627	35.8594	18.5175	15.8245	52.9551	28.5889	19.6195	18.3440	15.5245
	SDRLout	305.5324	105.2615	35.3559	18.0106	15.3163	52.4527	28.0844	19.1130	17.8370	15.0162
	MRLout	211.7790	72.9620	24.5076	12.4856	10.6183	36.3580	19.4677	13.2496	12.3653	10.4103
0.05	ARLout	271.1569	70.6712	22.5106	11.7585	9.9808	33.8713	18.0788	12.4429	11.0979	9.7613
	SDRLout	270.6564	70.1694	22.0049	11.2474	9.4676	33.3675	17.5717	11.9324	10.5861	9.2478
	MRLout	187.6048	48.6382	15.2539	7.7987	6.5655	23.1295	12.1814	8.2733	7.3405	6.4132
0.1	ARLout	203.9691	37.7609	11.8021	6.5131	5.4747	17.9980	9.7609	6.8621	6.4827	5.3127
	SDRLout	203.4685	37.2576	11.2910	5.9922	4.9495	17.4909	9.2474	6.3424	5.9618	4.7866
	MRLout	141.0337	25.8257	7.8289	4.1583	3.4365	12.1254	6.4129	4.4007	4.1372	3.3238
0.3	ARLout	79.9738	12.2468	4.3800	2.9177	2.4258	6.6284	3.9912	3.0326	2.8990	2.3155
	SDRLout	79.4722	11.7361	3.8476	2.3654	1.8598	6.1079	3.4552	2.4827	2.3463	1.7453
	MRLout	55.0863	8.1373	2.6744	1.6517	1.3043	4.2384	2.4033	1.7324	1.6385	1.2259
0.5	ARLout	39.5154	7.1083	2.9152	2.1814	1.8224	4.3105	2.8127	2.2489	2.1731	1.7908
	SDRLout	39.0122	6.5893	2.3629	1.6053	1.2242	3.7775	2.2580	1.6759	1.5967	1.1900
	MRLout	27.0419	4.5717	1.6499	1.1303	0.8711	2.6260	1.5777	1.1784	1.1243	0.8480
1	ARLout	12.1688	3.5780	1.8698	1.6159	1.3837	2.5993	1.9199	1.6483	1.6085	1.3793
	SDRLout	11.6581	3.0371	1.2753	0.9977	0.7286	2.0388	1.3290	1.0337	0.9893	0.7233
	MRLout	8.0833	2.1146	0.9057	0.7186	0.5404	1.4271	0.9421	0.7428	0.7131	0.5369

Additionally, Table 7’s summarized findings for each control chart are compared using the RMI and RSDI values, which were calculated so that the DMEWMA control chart’s RMI and RSDI values are lower than those of the EMMA and MEWMA at the same $c_1$ and $c_2$. Furthermore, greater capacity and lower ARL and RMI values are shown by the DMEWMA control charts with large $c_1$ and $c_2$ values.

Table 7. On the EWMA, MEWMA, and DMEWMA control charts, the RMIs and RSDI from the simulated data fitted to the $MA(2),$ $MA(3)$ models from Table 5 and Table 6.

Control Charts	C1	C2	MA(2)		MA(3)
			RMI	RSDI	RMI	RSDI
EWMA	-	-	7.801	9.005	15.963	19.501
MEWMA	0.5	-	2.562	2.876	3.591	4.181
	1	-	0.600	0.657	0.900	1.036
	3	-	0.024	0.027	0.186	0.234
	10	-	0.003	0.003	0.025	0.029
DMEWMA	0.5	0.5	1.390	1.567	1.655	1.942
	1	1	0.139	0.157	0.646	0.768
	1	3	0.080	0.091	0.238	0.294
	3	3	0.019	0.021	0.172	0.218
	10	10	0.000	0.000	0.000	0.000

3.2. Empirical Applications

In this section, the ARL formula has been applied to real data using the following steps.

• Estimate parameters from relevant data, such as stock prices, ensuring the inclusion of an MA mode by using the SPSS program.
• Estimate the parameter of exponentially distributed residuals using the one-sample Kolmogorov–Smirnov goodness-of-fit test.
• Use the parameter values from steps 1 and 2 to calculate the ARL using Equation (9).
• Compare performance by evaluating the ARL obtained in step 3 with the EWMA and MEWMA control charts.
• Detect changes in the process mean by determining the UCL value using the equation in (9) and applying it to data for computation.

To accomplish the primary goal of this study, we present experiments with real data to observe how the results align with the results of synthetic data. The real data used is the stock of AMC Entertainment (AMC), an American entertainment corporation provided by https://th.investing.com/equities/amc-entertat-hld (accessed on 10 October 2024). From these data, we have 52 total weekly price histories ranging from 17 September 2023 to 8 September 2024.

Before comparing the performance of EWMA, MEWMA, and DMEWMA control charts, we check the compatibility between the real data and the MA models, namely $MA(1),$ $MA(2),$ and $MA(3)$, by taking into account the following values: R-squared, Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and Mean Absolute Error (MAE), as shown in Table 8. The following shows the parameter $\theta$ values and Kolmogorov–Smirnov goodness-of-fit test that were obtained by fitting the model using SPSS. For dataset, it was fitted to the $MA(3)$ because, as a result, the $MA(3)$ has the highest R-square and the lowest RMSE, MAPE, and MAE, indicating that it is the best model, as illustrated in bold letters in Table 8. Apply the Kolmogorov–Smirnov Test to ensure that white noise conforms to the exponential mean presented in Table 9. The parameters of this prediction model can be assigned as follows:

$$X_t=5.606+1.119{\epsilon }_{t-1}+0.974{\epsilon }_{t-2}+0.397{\epsilon }_{t-3}+{\epsilon }_t; {\epsilon }_t\sim \exp \left(0.7647\right).$$

Table 8. The MA estimates for AMC Entertainment stock price and model fit.

Model	Model Parameters				Model Statistics
	Constant	Lag1	Lag2	Lag3	R2	RMSE	MAPE	MAE
MA(1)	5.535	−0.732	-	-	0.554	1.270	17.821	0.956
MA(2)	5.550	−0.993	−0.633	-	0.728	1.003	13.247	0.728
MA(3)	5.606	−1.119	−0.974	−0.397	0.774	0.922	11.185	0.625

Table 9. Exponential white noise of residual using the one-sample Kolmogorov–Smirnov goodness of fit test.

Model	Exponential Parameter	Sig
MA(3)	0.7647	0.157

Table 10 summarizes the results of the explicit formula technique used to compare the ARL, SDRL, and MRL values for $MA(3)$ on the EWMA, MEWMA, and DMEWMA control charts. It can be seen that the results are clearly consistent with Table 5. The table shows that the DMEWMA control chart has lower ARL, SDRL, and MRL values than EWMA and MEWMA, as shown in Figure 1. Here, we compare MEWMA and DMEWMA in terms of looking at the c value (i.e., the c value in MEWMA is equal to the c₁ value in DMEWMA is compared), and if we look at the trend of ARL values when c in MEWMA increases, the ARL value decreases. At the same time, when c₁ in DMEWMA increases, the ARL value decreases significantly. Overall, when all the models are compared in terms of each process mean shifts, DMEWMA has the lowest value. This also resulted in the lowest RMI and RSDI of all mean process changes, as shown in Figure 2.

Table 10. The ARL, SDRL, and MRL values for two-sided control charts on $MA(3)$ when $\mu =5.606,{\theta }_1=-1.119,{\theta }_2=-0.974,{\theta }_3=-0.397,$ and $\left[0.1,b\right]$.

$\mathit{\delta }$	Charts	EWMA	MEWMA (c)				DMEWMA (c1, c2)
			0.5	1	3	10	0.5, 0.5	1, 1	3, 3	10, 10
		b = 0.12398	2.02348	2.011	2.00206	1.9621	1.47694	3.99586	28.4216	90.1302
0	ARLin	369.91654	369.99253	370.15477	370.72015	369.9703	370.2553	370.0693	369.9847	370.0226
	SDRLin	369.4162	369.4922	369.6544	370.2198	369.4700	369.7550	369.5689	369.4844	369.5222
	MRLin	256.0599	256.1125	256.2250	256.6169	256.0971	256.2947	256.1657	256.1071	256.1334
0.001	ARLout	368.77143	368.64605	364.89692	359.15517	350.1337	360.9612	351.9256	314.7130	299.0203
	SDRLout	368.2711	368.1457	364.3966	358.6548	349.6333	360.4609	351.4252	314.2126	298.5198
	MRLout	255.2661	255.1792	252.5805	248.6007	242.3474	249.8525	243.5895	217.7957	206.9183
0.003	ARLout	366.49964	365.94901	354.69450	337.81776	315.8523	351.3734	324.6360	253.6623	247.0180
	SDRLout	365.9993	365.4487	354.1941	337.3174	315.3519	350.8730	324.1356	253.1618	246.5175
	MRLout	253.6915	253.3098	245.5088	233.8107	218.5854	243.2067	224.6737	175.4785	170.8731
0.005	ARLout	364.25214	363.24699	344.89113	318.58003	287.2715	326.7858	225.3434	178.0265	175.3567
	SDRLout	363.7518	362.7466	344.3908	318.0796	286.7711	326.2855	224.8428	177.5258	174.8560
	MRLout	252.1336	251.4369	238.7136	220.4761	198.7747	226.1639	155.8493	123.0517	121.2011
0.007	ARLout	362.02860	360.54052	335.46576	301.15003	263.0832	290.1986	185.0478	125.7999	118.4053
	SDRLout	361.5283	360.0402	334.9654	300.6496	262.5827	289.6982	184.5471	125.2989	117.9043
	MRLout	250.5924	249.5609	232.1804	208.3945	182.0086	200.8036	127.9185	86.8508	81.7253
0.01	ARLout	358.73747	356.47370	321.99390	277.88039	233.0584	243.3182	129.5987	78.9768	72.1781
	SDRLout	358.2371	355.9733	321.4935	277.3799	232.5578	242.8177	129.0978	78.4752	71.6764
	MRLout	248.3111	246.7420	222.8424	192.2652	161.1969	168.3085	89.4840	54.3952	49.6827
0.03	ARLout	338.07575	329.27247	248.85699	177.58718	127.1687	158.4546	76.4265	50.5188	47.7907
	SDRLout	337.5754	328.7721	248.3565	177.0865	126.6677	157.9538	75.9249	50.0163	47.2880
	MRLout	233.9895	227.8875	172.1477	122.7472	87.7996	109.4854	52.6275	34.6692	32.7782
$\mathit{\delta }$	Charts	EWMA	MEWMA (c)				DMEWMA (c1, c2)
			0.5	1	3	10	0.5, 0.5	1, 1	3, 3	10, 10
		B = 0.12398	2.02348	2.011	2.00206	1.9621	1.819064	4.37942	32.2921	88.978
0.05	ARLout	319.43208	302.28887	196.67406	125.01030	83.2433	116.5744	54.9317	34.9291	31.9074
	SDRLout	318.9317	301.7885	196.1734	124.5093	82.7418	116.0733	54.4294	34.4255	31.4034
	MRLout	221.0667	209.1839	135.9772	86.3035	57.3526	80.4562	37.7281	23.8628	21.7681
0.07	ARLout	302.55307	275.99674	158.18133	93.10998	59.5376	87.6432	38.1022	21.6339	20.2366
	SDRLout	302.0527	275.4963	157.6805	92.6086	59.0355	87.1418	37.5988	21.1280	19.7303
	MRLout	209.3670	190.9596	109.2960	64.1917	40.9208	60.4024	26.0623	14.6462	13.6774
0.1	ARLout	280.08034	238.69328	117.10408	63.97491	39.55221	58.5818	27.7200	10.9154	8.5243
	SDRLout	279.5799	238.1928	116.6030	63.4729	39.0490	58.0797	27.2154	10.4034	8.0087
	MRLout	193.7901	165.1028	80.8233	43.9965	27.0675	40.2582	18.8654	7.2139	5.5548
0.3	ARLout	185.51563	81.75042	26.83266	24.90194	13.4499	35.5645	14.6515	7.7634	4.5832
	SDRLout	185.0150	81.2489	26.3279	24.3968	12.9402	35.0610	14.1426	7.2462	4.0524
	MRLout	128.2428	56.3178	18.2502	16.9118	8.9717	24.3032	9.8050	5.0266	2.8160
0.5	ARLout	138.36034	30.82622	15.94643	10.18304	8.3159	21.0450	7.7915	4.6546	3.0417
	SDRLout	137.8594	30.3221	15.4383	9.6701	7.7999	20.5389	7.2744	4.1244	2.4920
	MRLout	95.5571	21.0186	10.7029	6.7058	5.4102	14.2379	5.0462	2.8658	1.7388
0.7	ARLout	110.41873	16.65663	8.56165	7.86115	6.1066	8.6037	2.6817	2.3524	2.0872
	SDRLout	109.9176	16.1489	8.0461	7.3441	5.5843	8.0882	2.1237	1.7836	1.5064
	MRLout	76.1893	11.1953	5.5807	5.0945	3.8759	5.6099	1.4854	1.2521	1.0628
1	ARLout	83.44615	8.58630	5.96060	4.79052	4.4676	4.1556	1.9847	1.4316	1.0352
	SDRLout	82.9446	8.0708	5.4377	4.2613	3.9360	3.6213	1.3980	0.7861	0.1908
	MRLout	57.4932	5.5978	3.7744	2.9604	2.7355	2.5180	0.9890	0.5781	0.2049
RMI		28.419	10.202	5.280	3.469	2.230	3.830	1.155	0.249	0.000
RSDI		67.603	14.531	7.954	5.525	4.040	5.729	1.793	0.55232	0

Figure 1. Graphical display of out-of-control ARL values of each control chart occur when the shift size values vary.

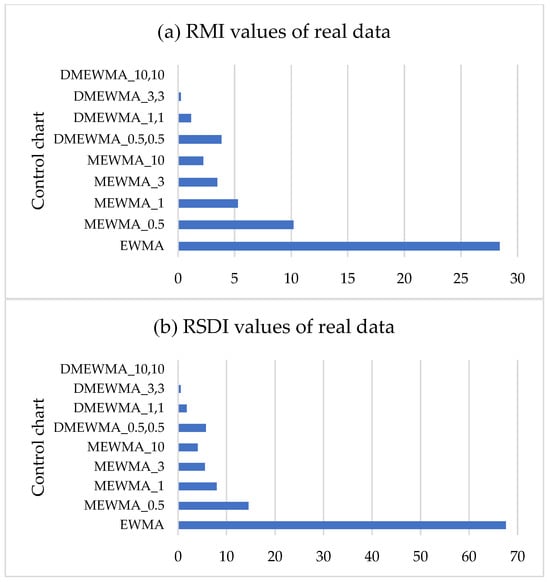
Figure 2. Comparing (a) RMI and (b) RSDI values across EWMA, MEWMA, and DMEWMA control charts.

Figure 3 has been applied to real data through the following steps:

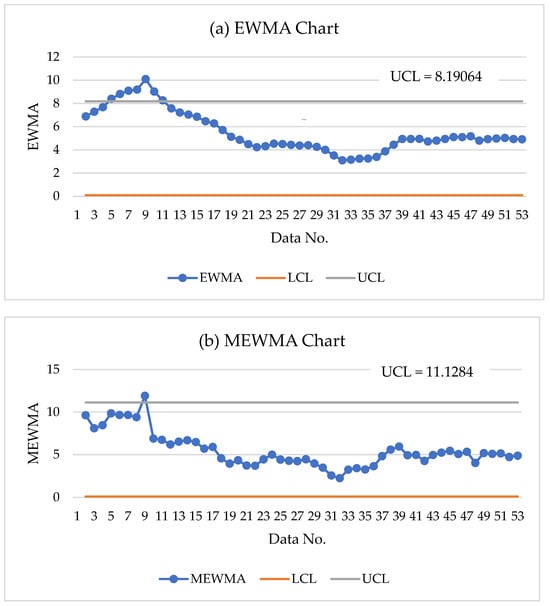
Figure 3. The AMC Entertainment stock price fitted to an $MA(3)$ process running on (a) EWMA chart, (b) MEWMA chart, and (c) DMEWMA chart.

• Import AMC Entertainment ($X_t$) stock price data.
• Set initial values and parameters.
• Calculate the statistics for the three control charts using Equations (1)–(3) with the data from step 1.
• Set the upper control limit (UCL) to 0.1.
• Determine the lower control limit (LCL) using Equation (9).
• Plot the graph using the results from steps 3, 4, and 5, and identify any values that exceed the control limits.

Control charts for stock prices as a statistical tool used to monitor fluctuations and identify atypical trends based on Statistical Process Control (SPC) methodologies. While traditional SPC charts are designed for stable industrial processes, applying them to stock prices can still provide insights, particularly for detecting unusual price movements or volatility spikes. This chart enables traders and analysts to detect significant deviations from expected price movements, facilitating informed decision-making and risk management. Figure 3, the EWMA, MEWMA, and DMEWMA statistics for AMC Entertainment’s stock price are analyzed to assess variability and detection efficiency, determining which control chart identifies changes most rapidly. The findings indicate that the DMEWMA control chart detects the change at the first observation, whereas the EWMA and MEWMA charts identify changes at the fifth and ninth observations, respectively. This suggests that, for this real dataset, the DMEWMA control chart exhibits a shorter initial detection time compared to the other two methods. Consequently, the results highlight the superior detection speed of the DMEWMA control chart, demonstrating its enhanced performance in adapting to process variations relative to the EWMA and MEWMA control charts.

4. Discussion and Conclusions

The theoretical computations revealed exceptional accuracy, with the ARL calculated from the explicit formula closely matching the ARL obtained using the NIE method, indicating a relative percentage error of less than 0.00001. Furthermore, the existence and uniqueness of the ARL derivation based on the explicit formulas were proved. The explicit formula and NIE method were applied to derive and evaluate ARL values for an MA process with exponential white noise operating under the DMEWMA control chart that features symmetric two-sided control limits. While the literature highlights the EWMA and MEWMA control charts for their similarities to the DMEWMA chart, the DMEWMA chart—an advanced iteration of the MEWMA—was chosen for comparative analysis. Its performance against EWMA and MEWMA charts underscores its refined design and superior efficacy. Our analysis of the DMEWMA chart focused on the critical parameter $\left(\lambda \right)$, revealing that assigning greater weight to ${\lambda }_2$ compared to ${\lambda }_1$ (the parameter of MEWMA) results in a lower ARL value. The proposed method evaluated the ARL, SDRL, and MRL values for MA processes on EWMA, MEWMA, and DMEWMA control charts, comparing their performances across varying mean shift sizes. Additionally, these charts were assessed using RMIs and RSDIs for different design parameter values. Experimental results using AMC stock price data aligned closely with theoretical computations, affirming the DMEWMA control chart’s superior ability to detect small process shifts. This validates the assertion that while MEWMA, an enhancement of EWMA, is highly effective at detecting small changes, DMEWMA, built upon MEWMA, achieves even greater performance. Notably, the DMEWMA chart identified out-of-control values faster than both the EWMA and MEWMA charts. The findings of this study align with the research of Phanthuna et al. [25], who analyzed the DMEWMA chart in the context of the AR model and similarly concluded that the DMEWMA control chart outperformed the comparison chart.

This research not only validates the DMEWMA control chart’s efficacy but also highlights its practical utility in financial strategies, enabling the detection of shifts in stock price movements because the DMEWMA control chart is a variant of the EWMA control chart that is well-suited for monitoring systems that exhibit dynamic or non-stationary behavior. Its application to stock data has important consequences because financial markets are inherently unpredictable and non-stationary [6]. Such detections can serve as actionable buy or sell signals for investors, underscoring the chart’s potential in optimizing investment decisions. In summary, the DMEWMA control chart outperformed EWMA and MEWMA charts for all change magnitudes, with results validated using AMC Entertainment stock data. However, the proposed explicit formula derivation for the ARL can be applied to other scenarios.

The limitations of this research are that it only considers scenarios using exponential white noise and the MA(q) model. To increase detection efficiency, we can differentiate between detected changes for real shifts and random variations. For data with other white noise patterns, alternative approaches, such as the Markov Chain Method, may be required to calculate the ARL value. Furthermore, using other models such as ARMA, ARIMA, or ARFIMA in conjunction with the DMEW-MA control chart may result in more comprehensive solutions for real-world applications.