Mathematical Entropy Analysis of Natural Convection of MWCNT—Fe₃O₄/Water Hybrid Nanofluid with Parallel Magnetic Field via Galerkin Finite Element Process

Abstract

Heat transfer in a symmetrical cavity with two semi-cylinders was explored in this study. Several parameters, such as (${10}^3\le Ra\le {10}^6$), (${10}^{-5}\le Da\le {10}^{-2}$), ($0.02\le \varphi \le 0.08$), ($0.2\le \epsilon \le 0.8$), and ($0\le Ha\le 100$) were selected and evaluated in this research. The outcome of the magnetic field and the temperature gradient on the nanofluid flow is considered. The geometric model is therefore described using a symmetry technique. The flow issue for the governing equations has been solved using the Galerkin finite element method (G-FEM), and these solutions are presented in dimensionless form. The equations for energy, motion, and continuity were solved using the application of the COMSOL Multiphysics^® software computer package. According to the results, there is a difference in the occurrence of the magnetic parameter and an increase in heat transmission when the right wall is recessed inward. The heat transmission is also significantly reduced when the right wall is exposed to the outside. The number of Nusselt grows directly proportional to the number of nanofluids in the environment. In contrast, all porous media with low Darcy and Hartmann numbers, high porosity, and low volume fraction have high Nusselt numbers. It is found that double streamlines for the hot side and single cooling for Darcy, Rayleigh, and Hartmann numbers. A cold isotherm at various physical parameters is needed in the top cavity. Rayleigh’s number and a solid volume fraction raise Darcy’s number, increasing heat transmission inside the cavity and thermal entropy determines entropy components.

1. Introduction

In recent years, experts have been intrigued by Magnetohydrodynamics (MHD) heat transfer due to its vast application in various industries. Boilers, cooling systems, thermal energy, and numerous technological applications are examples [1,2,3,4]. Furthermore, the most effective technique is to enhance the thermal characteristics of the system’s operating fluid. As a result, many studies have been conducted to improve heat transfer performance by inventing novel materials, including nanofluids and hybrid nanofluids [5,6,7,8,9,10].

The belongings of thermal radiation and viscidness dissipative on natural convective nano liquid flowing beyond a vertical surface were investigated by Kumar et al. [11]. As the Grashof number increased, they saw an increase in the velocity dispersion. On the other hand, it was growing magnetic forces with lower velocity distributions. Because of this, they found a rise in the flow distributions as the radiation factor increased. Applying the finite element methodology, Selimefendigil and Chamkha [12] deliberated the convection flowing of Ag–MgO/water hybridity nano liquid inner a triangular enclosure with a porous layer. Magnetic field toughness and tilt influence the flow and thermal patterns. Larger inclination angles reduce average heat transfer, but higher Hartmann numbers dwindle it. Heat transmission and fluid flow properties were strongly influenced by the presence of a porous media and the capacity to modify its size. Permeability increases as the distance between the heated wall and the porous medium’s vertex increases, resulting in an escalation in the average Nusselt number.

Al₂O₃–Cu water-based hybrid nanofluid mixed convection in a wave-shaped canal with a spherical cylinder was inspected by Hussain et al. [13]. The Galerkin finite element method was adopted to discretize a two-dimensional system of partial differential equations. In fluid flow and heat transfer studies, the Reynolds number is crucial. The fluid’s speed changes when the Reynolds number is increased. The velocity rises with each hump, and the local Nusselt number on the wavy lowermost wall is immensely enriched. By Fares et al., triangular cavities were used to study the convection of a TiO₂–SiO₂/water-based hybrid nanofluid [14]. When the Richardson number $Ri$ is more significant than 1, the importance of mixed convection flow behavior is demonstrated.

Al-Farhany et al. [15] directed mathematical research in analyzing the unforced convection in laminar condition nanofluid inside a porous half-heated chamber. Nusselt’s average decreases as the Hartman number is amplified. Increases in the Rayleigh number, nanoparticle concentration, Darcy number, hot fins length, and partially heated wall length can all result in higher heat transfer rates. Fares et al. [16] discovered that the entropy formed in a porous square-shaped container filled with Ag/Water nanofluid progressively increased. The Lorentz force law and the Darcy–Forchheimer model have both mathematically represented porosity. According to the researchers, consistent magnetization reduced the nanofluid flow upward into the cavity. Concerning hydrodynamic and thermal fields, increasing the Hartmann number has consequences. A side effect of this rise has been an expansion of the temperature and velocity gradients along the active wall. As the Darcy number grows, the total entropy also rises, which is linked to the porosity of the porous enclosure. The unrestricted convective heat transport of Ag–water nano liquid permeable absorbent C-shaped cavity fortified with a cold rippled perplex was premeditated numerically by Belhadj et al. [17]. They discovered that growing the Ra value improves heat transmission. Thermal efficiency is enhanced, and nanofluid circulation is accelerated by increasing buoyancy forces. In addition, the results revealed that adding a horizontal baffle to the investigated design improved heat transmission. Changing the undulation number, on the other hand, had little effect. Magnetohydrodynamic flow across a stretched layer in the existence of a magnetic field was considered by Bayones et al. [18]. Physical parameters such as the Prandtl number and the stretching parameter were examined in their research. Their findings show an improvement in axial velocity and a reduction in temperature with an increased Hartmann number. They also found that when the velocity ratio parameter is raised, the extending speed becomes quicker than the unrestricted stream velocity, resulting in lower temperature profiles when the ratio is increased.

Entropy production and convection heat transfer in the trapezoidal crater occupied with Cu-Al₂O₃/Water hybrid nanofluid were studied numerically by Mebarek-Oudina et al. [19]. The results discovered that increasing the volume percentage of the hybrid nano-liquid is essential when free convection is poor. It is due to the internal heat generation rate increases; conductive and convective thermal transfer are both enhanced. A spongy compartment occupied with Fe₃O₄-CuO hybrid nanofluid was the setting for Qin’s [20] investigation of the influence of the Lorentz force. The MHD and porous medium source terms were combined, and the vorticity formulation was used to simplify the equations. There is evidence that MHD leads to less convection and more noticeable conduction, which reduces heat transfer. As a result, transporting nanomaterials becomes more accessible and faster when greater buoyant force is taken into account. Due to an increase in convection, the isothermal fluctuation rises. There is a rise in entropy-generating levels as the Rayleigh number upsurges. Due to the reduction in nanoparticle velocity, the Hartmann number escalations while the temperature gradient diminutions.

The heat transmission behavior of a triangle chamber comprising an Ag-MgO water-based hybridity nano-liquid with a spinning spherical blockade and a quarter-circle absorbent medium at the right-angled angle was deliberate by Belhadj et al. [21]. The outcomes revealed that the Rayleigh number had a boosting effect and that the magnetic parameter regulated heat transfer. Researchers found that the accumulative sponginess and permeability of the spongy zone substantially impacted heat transfer efficiency. The heat transference and fluid flowing parameters of an Al₂O₃–Cu/H₂O nano-liquid rectangular cavity with various configurations of a grooved directing dense were studied by Tayebi and Chamkha [22]. With the finite volume discretization approach, governing equations were numerically solved with nanoparticle Brownian motion incorporated in the computations. Abu-Libdeh et al. [23] implemented the finite element approach to solve the heat transference response of Ag-MgO H₂O-based hybrid nanoliquids in a spongy chamber under continuous magnetic stresses. The results suggest that the magnetic field may be utilized as a heat transference regulator, as the heat transition rate reduces while the Ha number increases. Thermal conductance was examined by Brahimi et al. [24] in an insertion dominated with an Ag-MgO water-based nano liquid beneath a constant magnetic field. Because the box’s construction sources the flow to ramble above the cliff bars, this exceptional liquid undertaking decelerates the flowing at the surrounding, allowing the molecules to transmit heat more effectively. In addition, the enclosure’s restrictions are based on fluidity. Every aspect of this undertaking had a considerable impact. The fluidity of the meandering box is enhanced by increasing $Ra$, $Da$, or porosity, whereas nanoparticle volume fraction and $Ha$ tend to resist it.

The fascinating characteristics of carbon nanotube-magnetite nanocomposites, particularly at the nanoscale [25,26,27], have sparked a recent upsurge in interest. In a square-shaped cavity, Sajjadi et al. [28] used the MWCNT–Fe₃O₄/water hybrid nanofluid to explore MHD-free convective utilizing the dual MRT lattice Boltzmann technique. It is thought that MWCNTs, Fe₃O₄ nano-solids, and water are all Newtonian working fluids. The Rayleigh number was increased by adding MWCNT and Fe₃O₄ nanoparticles, whereas increasing the magnetic field had the opposite effect, as demonstrated by the results. Several nanofluids, including MWCNT-Fe₃O₄ hybrid nanofluids, were compared in a study by Saghir et al. [29]. The hybrid performed better in all temperatures, according to the data. Other nanofluids were also examined, and the MWCNT-Fe₃O₄ combination was shown to perform better than the others. The inspiration of magnetics on the performance of MWCNT/Fe₃O₄ hybrid nanofluid by Shin et al. [30] was studied in order to advance photo-thermal energy alteration presentation. Investigators are using an MWCNT/Fe₃O₄ hybrid nanofluid with varying magnetic strengths to experiment with the impact of external magnetic forces on photo-thermal energy conversion proficiency. Thermal conductivity and photo-thermal energy alteration were studied using Fe₃O₄ and MWCNT nanofluids [31]. Zafar et al. employed a multilayer perceptron coupled to an artificial neural network to investigate the thermophysical characteristics and stability of H₂O-based hybrid nanofluids covered with multi-walled carbon nanotubes. It was able to accurately replicate the circumstances of the experiments, regardless of the temperature or concentration. MWCNT/Fe₃O₄ nanofluids were tested as a plate heat exchanger coolant by Alklaibi et al. [32]. Several parameters showed that MWCNT + Fe₃O₄/water nanofluids improved plate heat exchanger performance. Increases in coolant flow velocity and nanoparticle concentration both contribute to amplification.

The focal independent of our study is to scrutinize the symmetrical cavity with two semi-cylinders. Additionally, this paper investigates nanofluids’ natural convective heat transfer (MWCNT-Fe₃O₄/H₂O). The effect of various control variables such as $Ra$, $Da$, $Ha$, $\varphi ,$ and porous amounts on the flowing characteristics and heat transition was investigated. The equations for energy, motion, and continuity were solved using the application of the COMSOL Multiphysics^® software computer package.

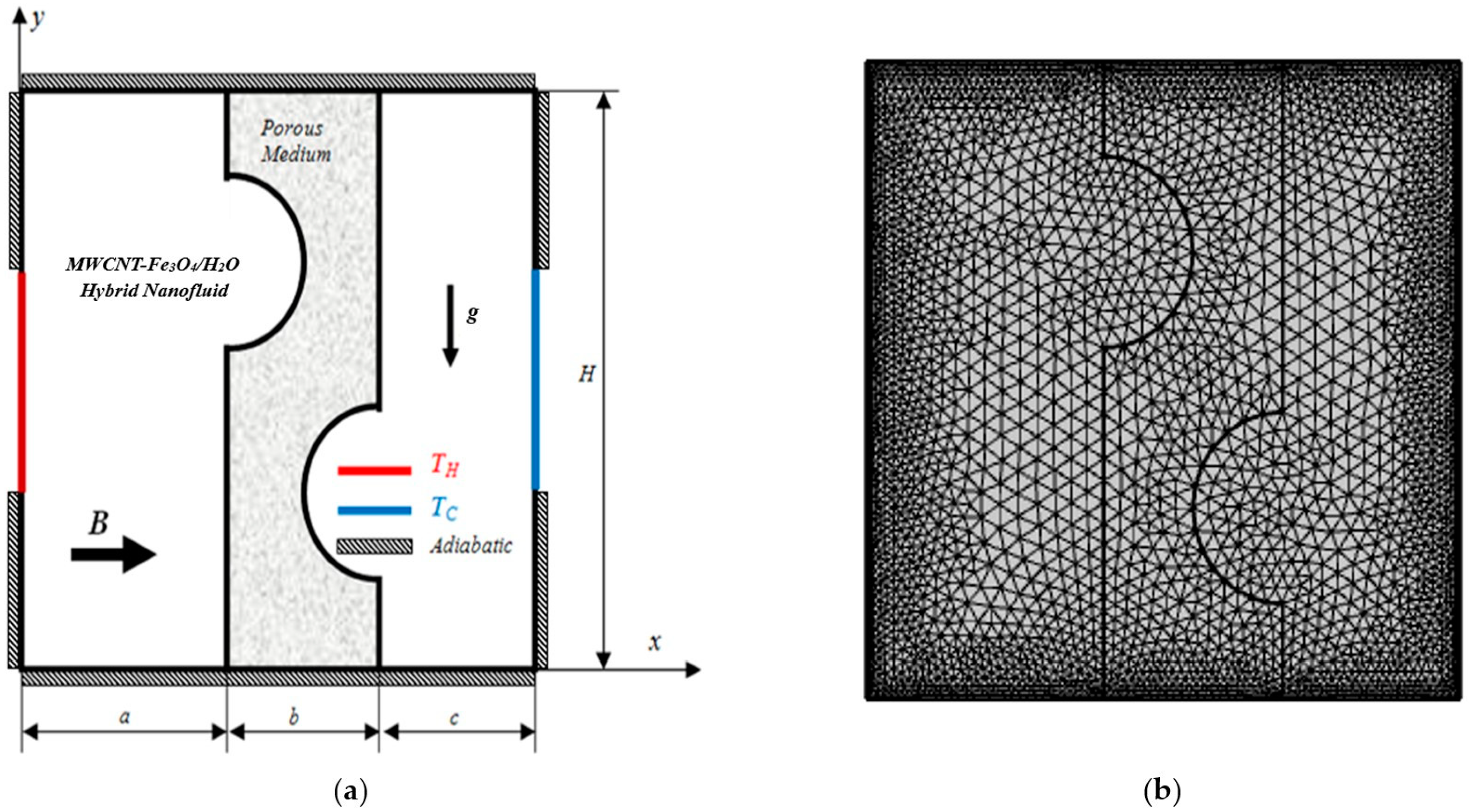
2. Problem Description

In this single-phase case, the temperature and velocity fields in the square cavity of Figure 1 were obtained by solving the continuity, Navier-Stokes, and energy equations. Therefore, the governing equations are simplified by using the following assumptions:

• ▪ The flow is incompressible, and NF is power-law non-Newtonian.
• ▪ Relative movement between fluid and Fe₃O₄, MWCNT particles is zero, and thermal equilibrium exists between them.
• ▪ The temperature and velocity fields are laminar, steady state, and 2D.
• ▪ The effects of radiation and viscous dissipation are neglected.

In the two-dimensional system, Newtonian Nano liquid media are used to fill a square cavity with a two-semicircle enclosure. Secondary geometry is reduced by the form L × H and the diameter of ($2r$) cylinders. (MWCNT-Fe₃O₄/H₂O) nanofluid fills the inside of the domain. Additionally, it is assumed that the uniform magnetic field $\left(B=B_x{e}_x+B_y{e}_y\right)$ of constant magnitude $(B=\sqrt{B_x^2+B_y^2})$ is applied, where ${\overrightarrow{e}}_x$ and ${\overrightarrow{e}}_y$ are unit vectors in the Cartesian coordinate system. The electric current $J$ and the electromagnetic force $F$ are defined by $J=\sigma (\overrightarrow{V}\times \overrightarrow{B})$ and $F=\sigma (\overrightarrow{V}\times \overrightarrow{B})\times \overrightarrow{B}$, respectively. Figure 1 illustrates a graphical issue with the enclosure’s fundamental geometric characteristics. Semi-cylinders are adiabatic, with the left wall being hot and the right wall being cool.

Table 1. Thermophysical properties of MWCNT-Fe₃O₄/H₂O (50%/50%) [33].

Material	$C_p \left(J/kg·K\right)$	$k \left(W/m·k\right)$	$\rho \left(kg/m^3\right)$	$\beta \times {10}^{-5} \left(K^{-1}\right)$	$\sigma \left(s/m\right)$
Water	4179	0.613	997.1	21	5.5 × 10−6
Fe3O4	670	6	5810	1.3	2.5 × 104
MWCNT	711	3000	2100	4.2	1.9 × 10−4

demonstrates the main thermos-physical possessions of the essential liquid (H₂O) and the nano molecules.

3. Mathematical Model

For numerical modeling of porous media, the Darcy–Brinkman–Forchheimer model is utilized. The governing equations (continuity, momentum, and energy equations) and definitions of dimensionless variables can be introduced as follows based on the above assumptions [34,35].

In the hybrid-nanofluid:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\rho }_{hnf}}\frac{\partial P}{\partial x}+{\nu }_{hnf}\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right),$$

(2)

$$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{{\rho }_{hnf}}\frac{\partial P}{\partial y}+{\nu }_{hnf}\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)+{\beta }_{hnf}g\left(T-T_{avg}\right)+\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}_0^{2}v,$$

(3)

$${(\rho c_p)}_{hnf}\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k_{hnf}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right),$$

(4)

To solve the governing equations for single-phase modeling, the nanofluid effective properties are required and can be calculated as a single phase by the following equations

$$\varphi ={\varphi }_{MWCNT}+{\varphi }_{F{e}_3{O}_4}$$

(5)

$${\rho }_{np}=\frac{{\varphi }_{MWCNT}{\rho }_{MWCNT}+{\varphi }_{F{e}_3{O}_4}{\rho }_{F{e}_3{O}_4}}{\varphi }$$

(6)

$${(c_p)}_{np}=\frac{{\varphi }_{MWCNT}{(c_p)}_{MWCNT}+{\varphi }_{F{e}_3{O}_4}{(c_p)}_{F{e}_3{O}_4}}{\varphi }$$

(7)

$${\beta }_{np}=\frac{{\varphi }_{MWCNT}{\beta }_{MWCNT}+{\varphi }_{F{e}_3{O}_4}{\beta }_{F{e}_3{O}_4}}{\varphi }$$

(8)

$$k_{np}=\frac{{\varphi }_{MWCNT}{k}_{MWCNT}+{\varphi }_{F{e}_3{O}_4}{k}_{F{e}_3{O}_4}}{\varphi }$$

(9)

$${\sigma }_{np}=\frac{{\varphi }_{F{e}_3{O}_4}{\sigma }_{F{e}_3{O}_4}+{\varphi }_{MWCNT}{\sigma }_{MWCNT}}{\varphi }$$

(10)

The thermal conductivity, heat capacity, and density of the nanofluid can be calculated as follows:

$${\sigma }_{hnf}=\left(1-\varphi \right){\sigma }_{bf}+\varphi {\sigma }_{np}$$

(11)

$${\rho }_{hnf}=\left(1-\varphi \right){\rho }_{bf}+\varphi {\rho }_{np}$$

(12)

$${\left(\rho \beta \right)}_{hnf}=\left(1-\varphi \right){\left(\rho \beta \right)}_{bf}+\varphi {\left(\rho \beta \right)}_{np}$$

(13)

$${\left(\rho c_p\right)}_{hnf}=\left(1-\varphi \right){\left(\rho c_p\right)}_{bf}+\varphi {\left(\rho c_p\right)}_{np}$$

(14)

$${\alpha }_{hnf}=\frac{k_{hnf}}{{\left(\rho c_p\right)}_{hnf}}$$

(15)

$k_{hnf}$, ${\mu }_{hnf},$ and ${\rho }_{hnf}$ represent the thermal conductivity, viscosity, and density of the nanofluid, respectively. Additionally, ${\beta }_{hnf}$ is the nanofluid thermal expansion coefficient and ${\left(c_p\right)}_{hnf}$ is the nanofluid heat capacity [16].

In this case, the Hamilton equation is applied to calculate the thermal conductivity of the nanofluids, and it can be shown that for spherical nanoparticles $n=3$:

$$\frac{k_{hnf}}{k_{bf}}=\frac{k_{np}+\left(n-1\right)k_{bf}-\left(n-1\right)\left(k_{bf}-k_{np}\right)\varphi }{k_{np}+\left(n-1\right)k_{bf}+\left(k_{bf}-k_{np}\right)\varphi }$$

(16)

Following the generalized Darcy–Brinkman–Forchheimer equation, the formulas that control the porous region are specified as:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(17)

$$\frac{1}{{\epsilon }^2}\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{1}{{\rho }_{hnf}}\frac{\partial P}{\partial x}+\frac{{\nu }_{hnf}}{\epsilon }\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)-{\nu }_{hnf}\frac{u}{K}-\frac{1.75}{\sqrt{150}{\epsilon }^{\frac{3}{2}}}\frac{1}{\sqrt{K}}u\sqrt{u^2+v^2},$$

(18)

$$\frac{1}{{\epsilon }^2}\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{1}{{\rho }_{hnf}}\frac{\partial P}{\partial y}+\frac{{\nu }_{hnf}}{\epsilon }\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)-{\nu }_{hnf}\frac{v}{K}-\frac{1.75}{\sqrt{150}{\epsilon }^{3/2}}\frac{1}{\sqrt{K}}v\sqrt{u^2+v^2}+{\beta }_{hnf}g\left(T-T_{avg}\right)+\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}_0^{2}v,$$

(19)

$${(\rho c_p)}_{hnf}\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k_{hnf}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right).$$

(20)

where $\epsilon$ is its porosity and $K=\frac{{\epsilon }^3{d}_m^2}{150{\left(1-\epsilon \right)}^2}$ is the permeability, described as follows [36,37].

The following variables managed to device the preceding major formulas into non-dimensional ones

$$\begin{array}{c}X=\frac{x}{L},Y=\frac{y}{L},U=\frac{uL}{{\alpha }_{bf}},V=\frac{vL}{{\alpha }_{bf}}, \theta =\frac{T-T_f}{T_h-T_f},P=\frac{\left(p+{\rho }_{bf}{g}_y\right)L^2}{{\rho }_{bf}{\alpha }_{bf}^2},\\ Ra=\frac{{\beta }_{bf}g\left(T_h-T_f\right)L^3}{{\alpha }_{bf}{v}_{bf}},Ha=L{B}_0\sqrt{\frac{{\sigma }_{bf}}{{\mu }_{bf}}}, Da=\frac{K}{L^2},Pr=\frac{v_{bf}}{{\alpha }_{bf}}. \end{array}\}$$

(21)

In the hybrid-nanofluid area, the non-dimensional formulas are as follows:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0,$$

(22)

$$U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+\mathrm{Pr}\frac{{\rho }_f}{{\rho }_{hnf}}\frac{{\mu }_{hnf}}{{\mu }_f}\left(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2}\right),$$

(23)

$$U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+\mathrm{Pr}\frac{{\rho }_f}{{\rho }_{hnf}}\frac{{\mu }_{hnf}}{{\mu }_f}\left(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2}\right)-Ra Pr\frac{{\rho }_f}{{\rho }_{hnf}}\left[1-\varphi +\varphi \frac{{\left(\rho \beta \right)}_{hnf}}{{\left(\rho \beta \right)}_f}\right]\theta ,$$

(24)

$$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\frac{{\alpha }_{hnf}}{{\alpha }_{bf}}\left(\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2}\right).$$

(25)

Porous area non-dimensional equations can be expressed in this manner:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0,$$

(26)

$$\frac{1}{{\epsilon }^2}\frac{{\rho }_{hnf}}{{\rho }_{bf}}\left(U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}\right)=-\frac{\partial P}{\partial X}+\frac{1}{\epsilon }\frac{{\nu }_{hnf}}{{\nu }_{bf}}\mathrm{Pr}(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2})-\frac{{\nu }_{hnf}}{{\nu }_{bf}}\frac{Pr}{Da}-\frac{1.75}{\sqrt{150}{\epsilon }^{\frac{3}{2}}}\frac{1}{\sqrt{Da}}\sqrt{U^2+V^2}U$$

(27)

$$\begin{gathered} \frac{1}{{\epsilon }^2}\frac{{\rho }_{hnf}}{{\rho }_f}\left(U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}\right)=-\frac{\partial P}{\partial Y}+\frac{1}{\epsilon }\frac{{\nu }_{hnf}}{{\nu }_f}Pr\left(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2}\right)-\frac{{\nu }_{hnf}}{{\nu }_f}\frac{Pr}{Da}V-\frac{1.75}{\sqrt{150}{\epsilon }^{3/2}}\frac{1}{\sqrt{Da}}\sqrt{U^2+V^2}V+ \\ \frac{{\beta }_{hnf}}{{\beta }_f}Pr.Ra\theta +\frac{{\sigma }_f}{{\rho }_{hnf}}\frac{{\rho }_f}{{\rho }_{hnf}}\frac{PrH{a}^2}{\epsilon \sqrt{Ra}}V, \end{gathered}$$

(28)

The following formula is the energy equation for normal convection inside a porous region, with σ the thermal capacity ratio

$$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\frac{{\alpha }_{hnf}}{{\alpha }_{bf}}\left(\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2}\right).$$

(29)

The velocity and the stream function are linked by [38].

$$\begin{array}{c}U=\frac{\partial \psi }{\partial Y}, \\ V=-\frac{\partial \psi }{\partial X}\end{array}\}$$

(30)

Then the single equation can be written by,

$$\frac{{\partial }^2\psi }{\partial X^2}+\frac{{\partial }^2\psi }{\partial y^2}=\frac{\partial U}{\partial Y}-\frac{\partial V}{\partial X},$$

(31)

Based on the Brinkman mode, the effective dynamical viscosity and the conducting of the hybridity nano liquid are:

$${\mu }_{hnf}=\frac{{\mu }_{bf}}{{\left(1-\varphi \right)}^{2.5}},$$

(32)

$$\frac{{\sigma }_{hnf}}{{\sigma }_{bf}}=1+\frac{3\left({\sigma }_{np}-{\sigma }_{bf}\right)\varphi }{\left({\sigma }_{np}+2{\sigma }_{bf}\right)-\left({\sigma }_{np}-{\sigma }_{bf}\right)\varphi }.$$

(33)

Boundary conditions relating to the cavity’s walls are presented as follows:

• The hot wall:

$$u=v=0, T=T_h$$

• The cold wall:

$$u=v=0, T=T_c$$

• The insolated walls:

$$u=v=0,\frac{\partial T}{\partial n}=0.$$

The local and average Nusselt numbers along the heated wall can be defined as:

$$N{u}_{loc}=-\frac{k_h{}_{nf}}{k_{bf}}\frac{\partial \theta }{\partial X},$$

(34)

$$N{u}_{avg}={{\displaystyle \int }}_0^{L}N{u}_{local}dY,$$

(35)

Non-Dimensional Entropy Generation

The dimensional local entropy produced is represented by equation (36) given by Woods [39] with the convective process, the magnetic field, and the dimensional local entropy (DLE):

$$S_{tot}=\frac{k_m}{{\left(T_{avg}\right)}^2}\left[{\left(\frac{\partial \theta }{\partial X}\right)}^2+{\left(\frac{\partial \theta }{\partial Y}\right)}^2\right]+\frac{{\mu }_{nf}}{T_{avg}}\left[\frac{{\epsilon }_p}{K}\left(U^2+V^2\right)+2{\left(\frac{\partial U}{\partial X}\right)}^2+2{\left(\frac{\partial V}{\partial Y}\right)}^2+{\left(\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)}^2\right]+\frac{{\sigma }_{nf}}{T_{avg}}{B}^{2}V,$$

(36)

when $T_{avg}=\frac{T_H+T_C}{2}$.

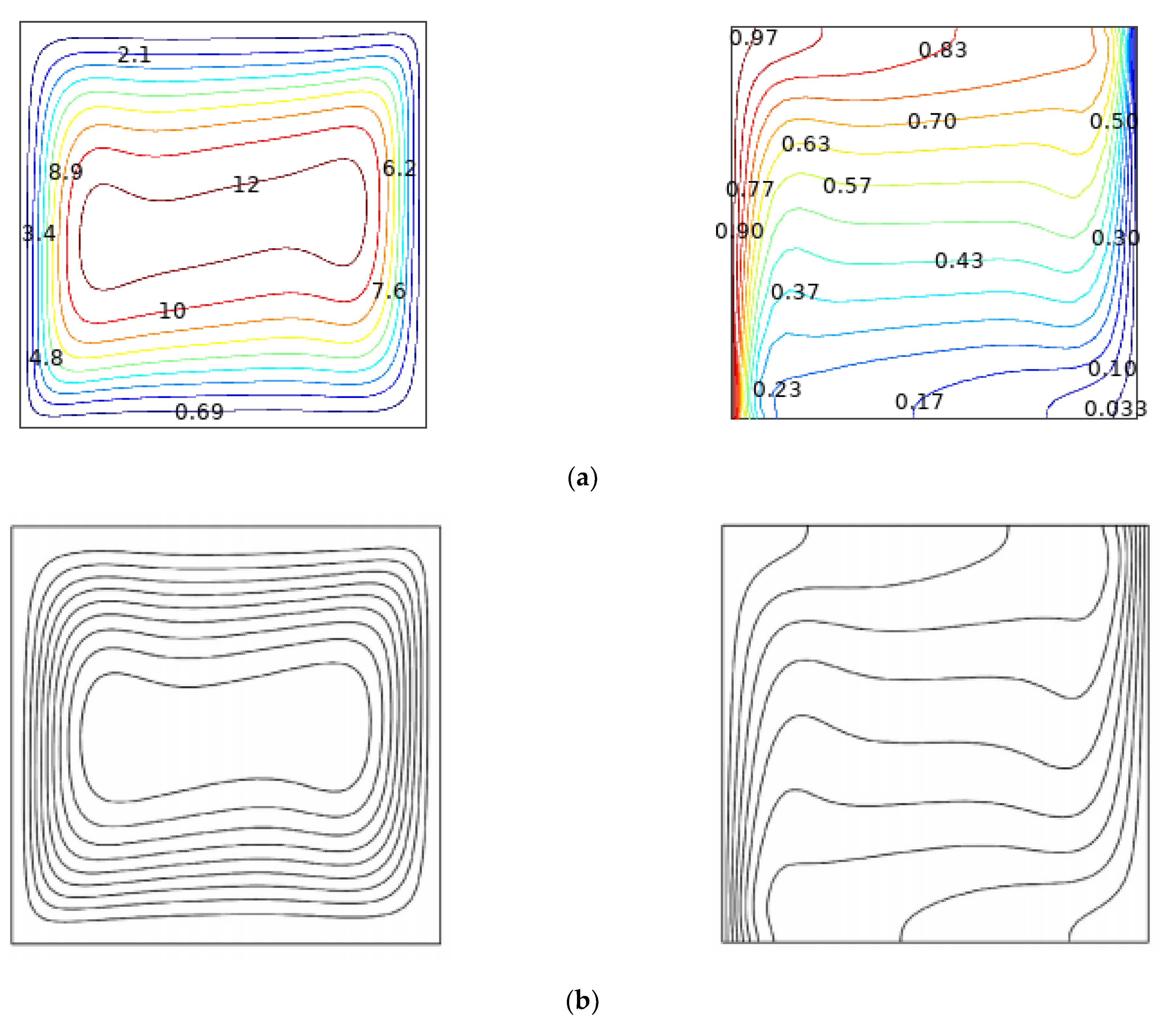
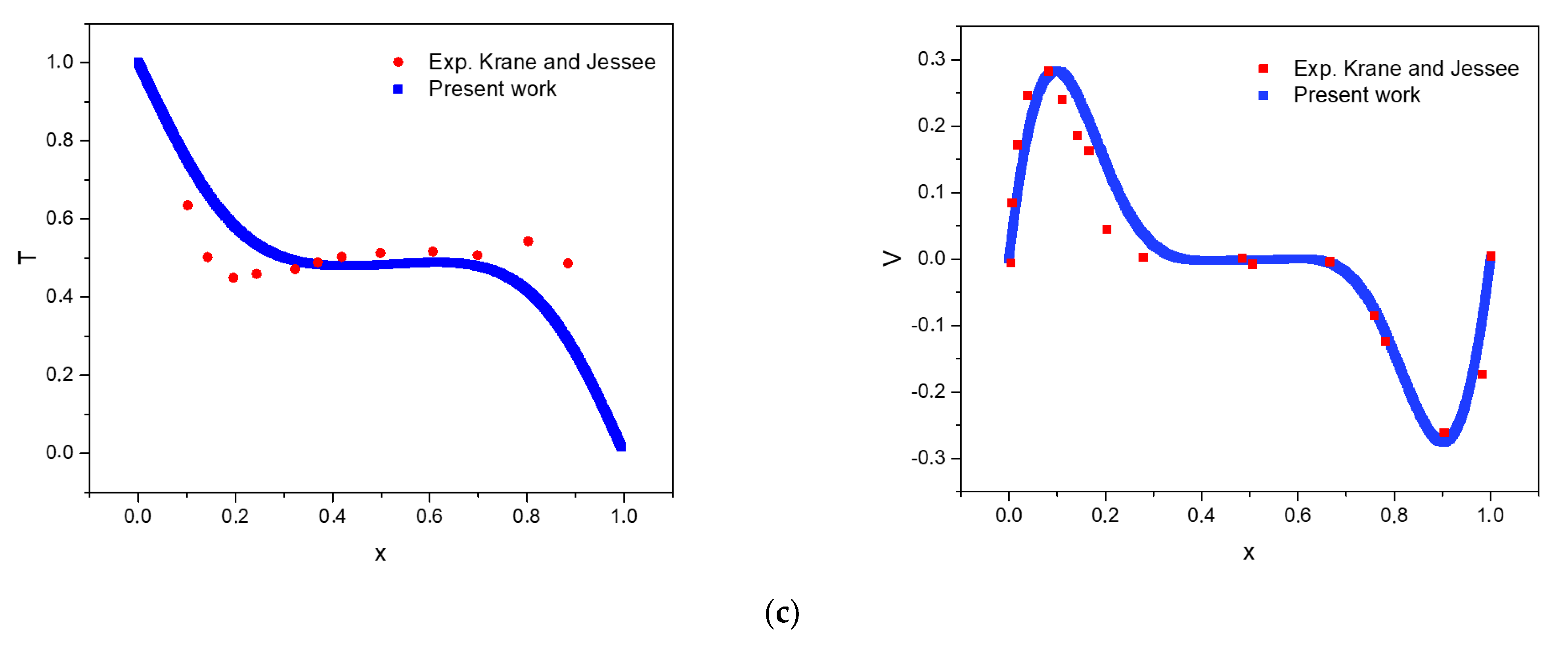
4. Authentication and Grid Independence Evaluation

Seven distinct grids were utilized to ensure the consequences were independent between them.

Table 2. Variation of $N{u}_{avg},{\psi }_{max}$, Max ($S_{tot}$ ) with mesh elements number at $Ra={10}^5$, $\varphi =0.02$, $Ha=0$, $Da=0.01$, and $\epsilon =0.4$.

Number of elements	604	1092	1642	2660	5852	15,886	26,098
$N{u}_{avg}$	6.219	6.320	6.564	6.427	6.564	6.667	6.668
${\psi }_{max}$	0.471	0.471	0.457	0.462	0.457	0.455	0.453
$\mathrm{Max} \left(S_{tot}\right)$ in the porous medium	1.644	1.644	2.042	1.993	2.042	2.219	2.220

shows the $N{u}_{avg}$, stream function, and max ($S_{tot}$) as measures of flow and heat flow independence from grid count. The sixth grid (15,886) was chosen as the final grid due to the disparity in results. How many elements are necessary for a model to ensure that the outcomes of an investigation are unaffected by altering the mesh size is determined by mesh converging. With diminishing element size, system response (stress and deformation) will converge to a reproducible solution.

In order to verify the validity of the findings, researchers compared their findings to previous research. Figure 2a represents the current outcomes, while Figure 2b illustrates the results from Corcione et al. [40]. Meanwhile, Figure 2c depicts the present numerical results compared with Krane [41]. The two figures in particular (Figure 2a,b) showed excellent settlement with each other.

It should be noted that the above-mentioned governing equations, along with the boundary conditions, are solved using the finite element method by using COMSOL Multiphysics [42]. Triangular elements make up the discretizing computational domain. Each flowing parameters inside the computational domain is represented by a set of triangular Lagrange finite elements of various orders. The approximations are then substituted into the regulating formulas to get the residuals for each conservation equation. Using a Newton-Raphson iteration approach, the non-linear components in the impetus equation were made simpler. When the relative errors for each of the parameters fulfills the essential converging criterion, the converging of the solution is presumed: Where I stand for the iterations and is the converging criteria, the expression is $\left|\frac{{\Gamma }^{i+1}-{\Gamma }^i}{{\Gamma }^i}\right|\le \eta$. The convergence criteria for this investigation were set at $\eta ={10}^{-6}$.

5. Results and Discussion

Five parameters related to streamlines, isotherms, and universal entropy are presented. Those parameters signify Darcy’s quantity (${10}^{-5}\le Da\le {10}^{-2}$), nanoparticle volume fraction ($0\le \varphi \le 0.08$), the porosity ($0.2\le {\epsilon }_p\le 0.8$), Rayleigh quantity (${10}^3\le Ra\le {10}^6$), and Hartmann quantity ($0\le Ha\le 100$). The thermophysical properties, base fluid (water), and solids (MWCNT and Fe₃O₄) are illustrated in Table 1. The fallouts are classified into the subsequent four subdivisions. The values of all parameters used are based on previous research [40,43].

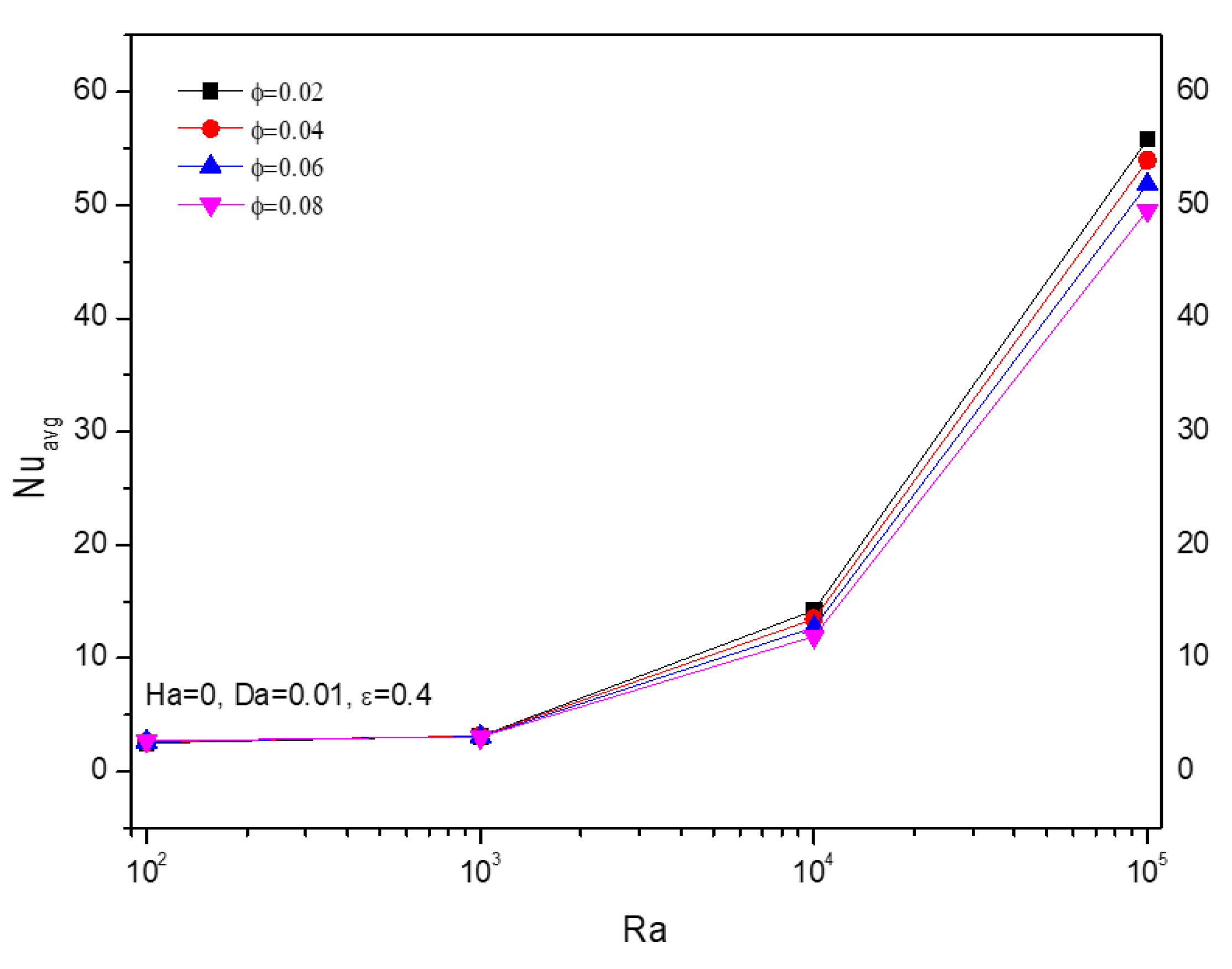
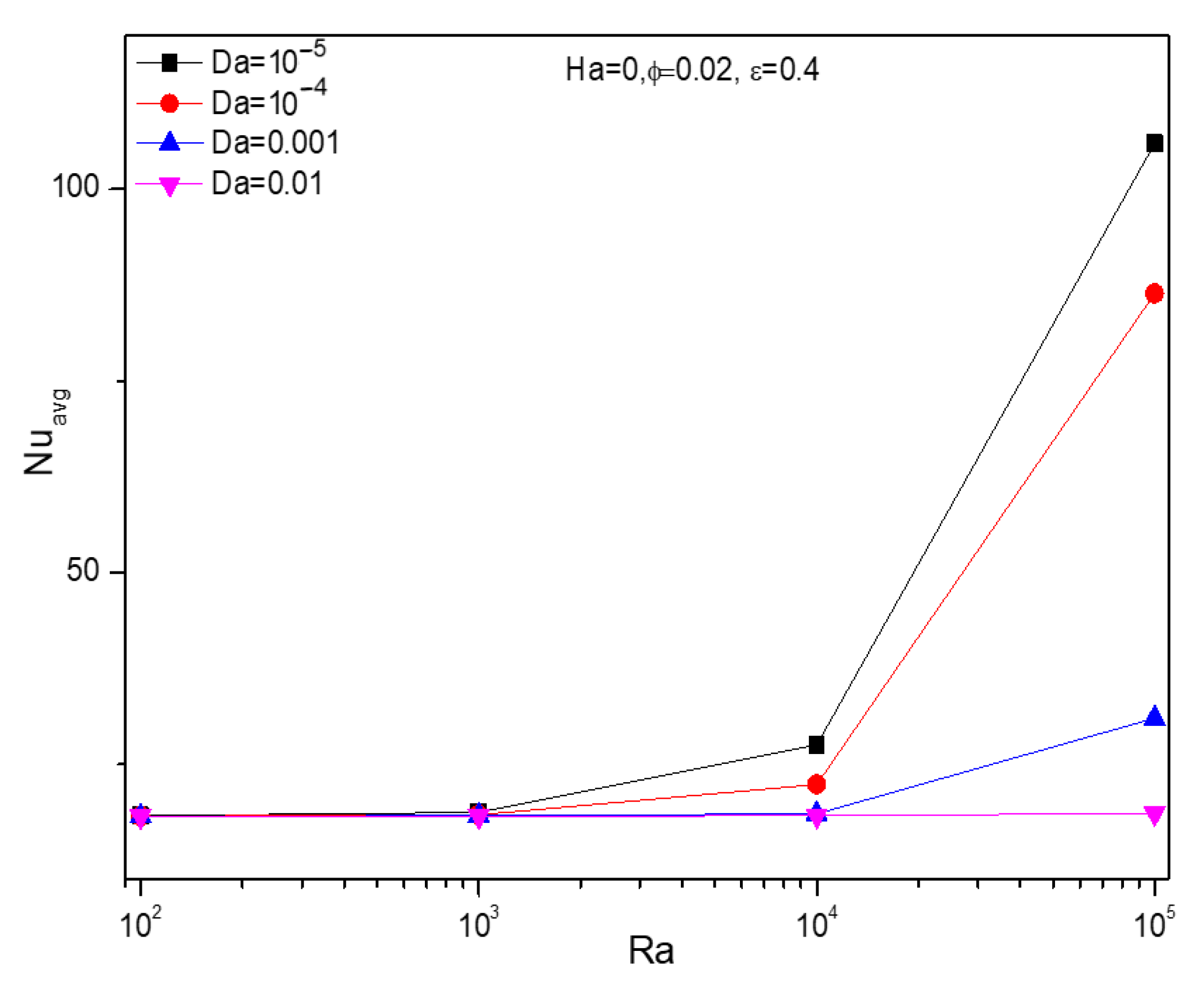
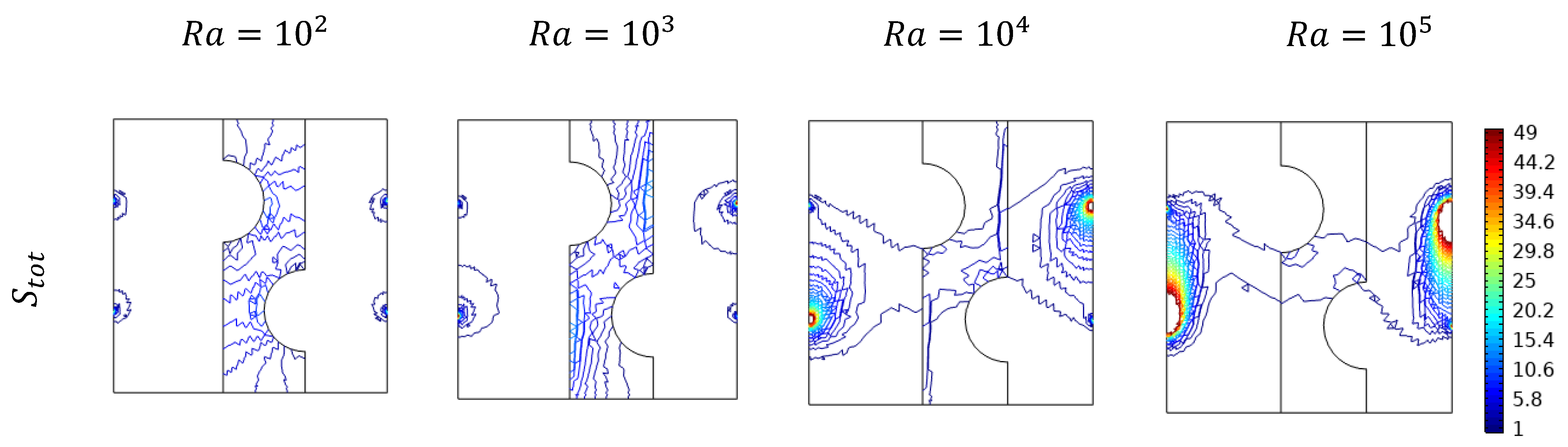
5.1. Effect of Rayleigh Number

Figure 3 demonstrates the changing of streamlines and isotherms with diverse Rayleigh numbers $Ra$, ($Da=0.01$, $Ha=0$, $\varphi =0.02$ and $\epsilon =0.4$). The effects of Rayleigh numbers inside the cavity filled with MWCNT–Fe₃O₄/water are shown on streamlines and isotherm. In Rayleigh’s initial values. Laminar currents flashed and faded on the hot side end to end with the upstream currents. The latter drew thick lines at the first bend, accompanied by a moderate field at the lower end. It is noticeable when the moment of the Rayleigh number increases, a fluctuation in the stream state. This phenomenon leads to the occurrence of the middle contour. In addition, it is seen that the currents are driven toward the scorching end of the solid. It proves that the flow phases were observed at higher Rayleigh values in the transition to turbulence. The heated isotherm extends to the edge of the cooled wall. At the same time, the coolant isotherm turns to the other end. It leads to a diminution in density due to the heat in the cavity fluid.

Figure 4 shows that $N{u}_{avg}$ improves with $Ra$. This process was conducted after considering all $Ha$ values. The velocity of the liquid in the bounded area rises as it rises to enhance $Ra$ number. This occurrence is due to an upsurge in buoyancy force. Hence, its diminutions $N{u}_{avg}$. However, when the Lorentz force and $Ha$ built up, the $N{u}_{avg}$ diminished. The formation of vortices stops due to the Lorentz force. Consequently, the rapidity of the liquid in the cavity declines, and so does the level of $N{u}_{avg}$.

Figure 5 and Figure 6 illustrate the variation of Nu_avg over Ra pour ($Da=0.01$, $Ha=0$, $\epsilon =0.4$). For all values of $Da$, $N{u}_{avg}$ improves with $Ra$. However, the heat transfer and Nusselt number are enhanced for greater $Ra$ values. The result of the conductive heat will not affect the lower values of $Ra$. In contrast, small bands show apparent escalations (enlarged by 23$\%$). Additionally, $N{u}_{avg}$ improved Rayleigh’s number to less than 10³. In the lower ranges, the improvement of fluid movement is of greater importance. The porous parameter $\epsilon$ is exposed in Figure 7. The Nusselt number improves to a higher value and keeps improving. The flow and diffusion of nanoparticles are less accessible, facilitating the heat transfer process. $\epsilon$ enhanced with the improvement of $Ra$ does not affect the improvement of $N{u}_{avg}$. The isothermal behavior is due to the convergence between convection and thermal conductivity. At high values of $Ra$, we notice a significant improvement in heat transfer rates.

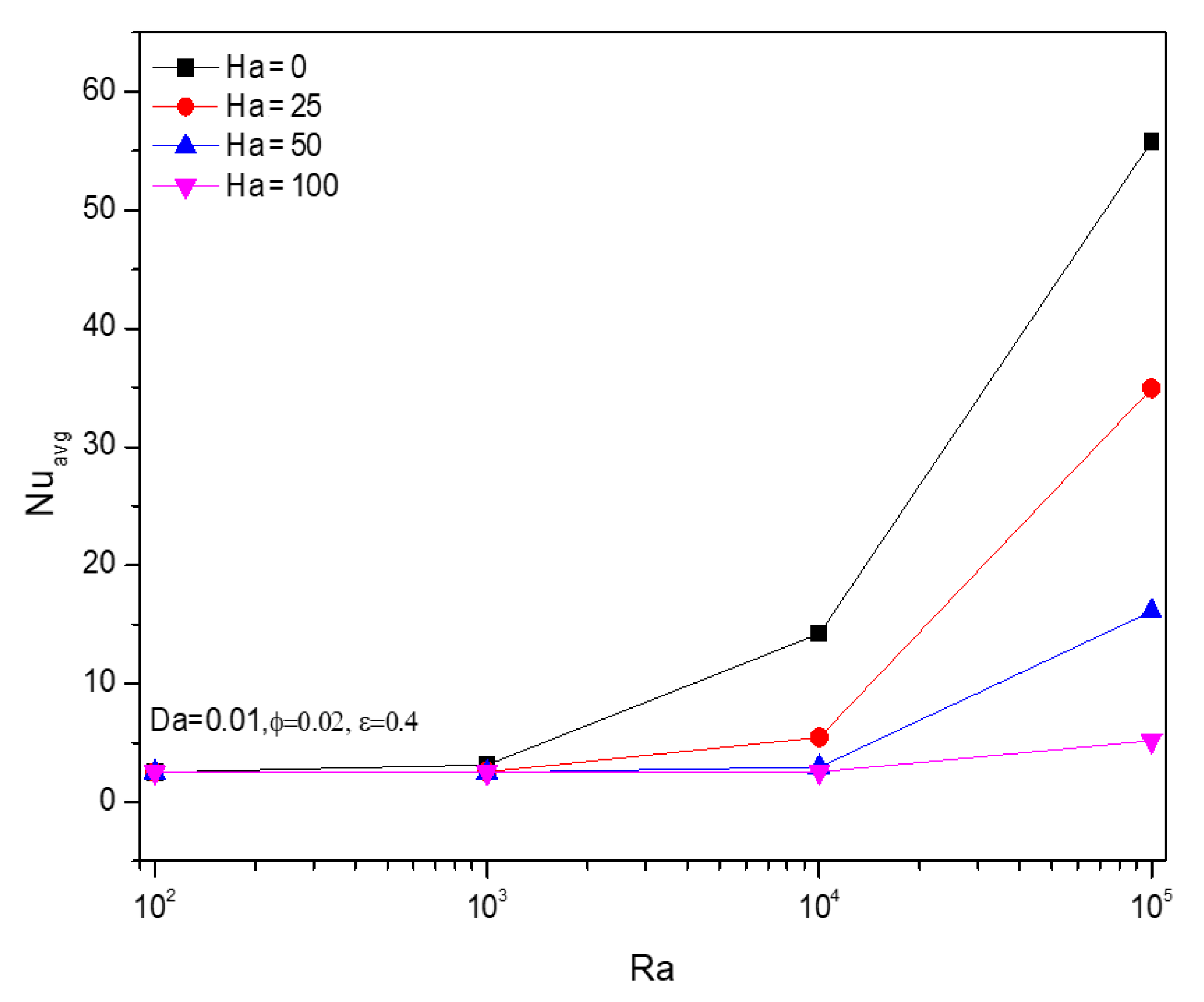
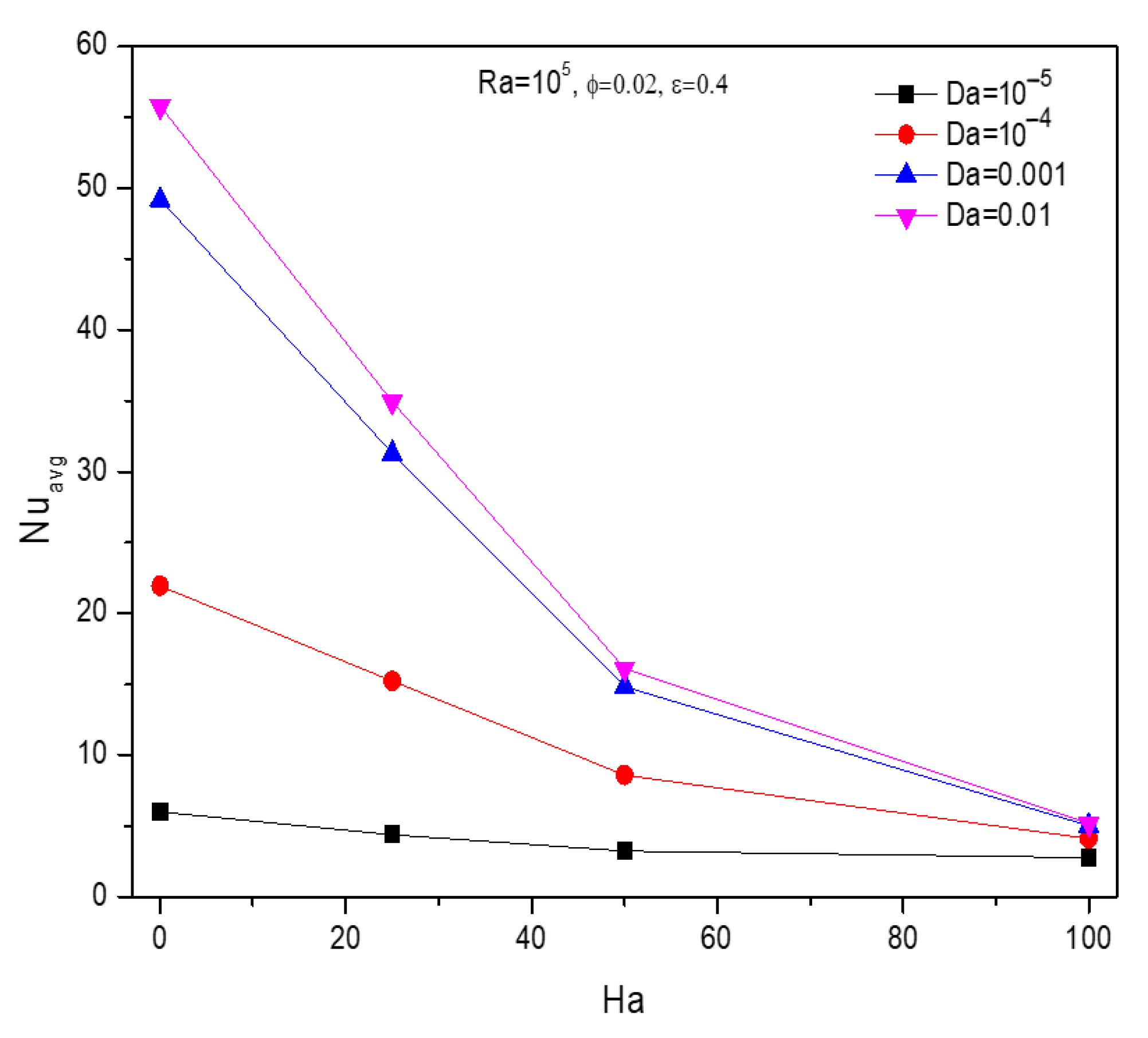
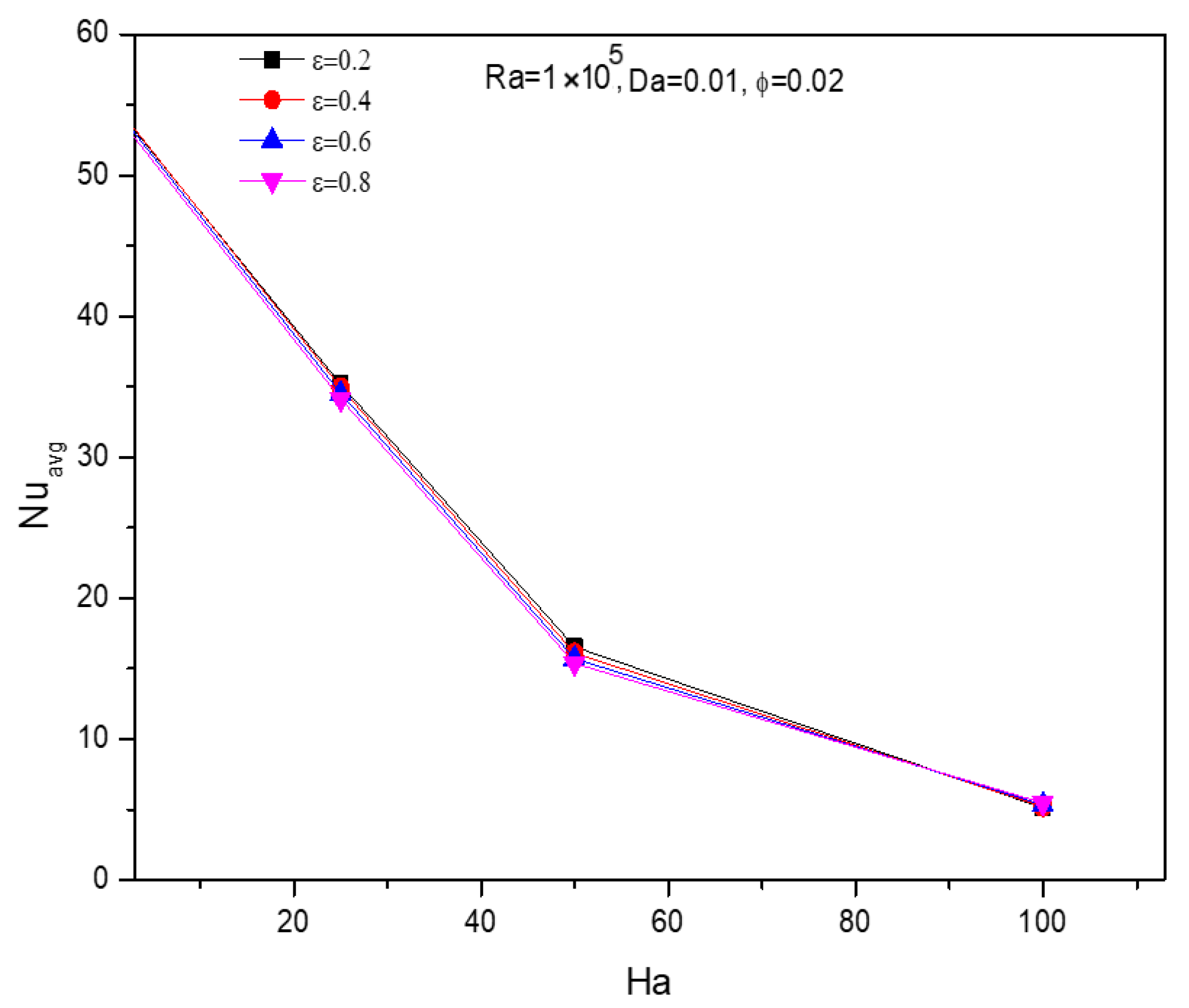
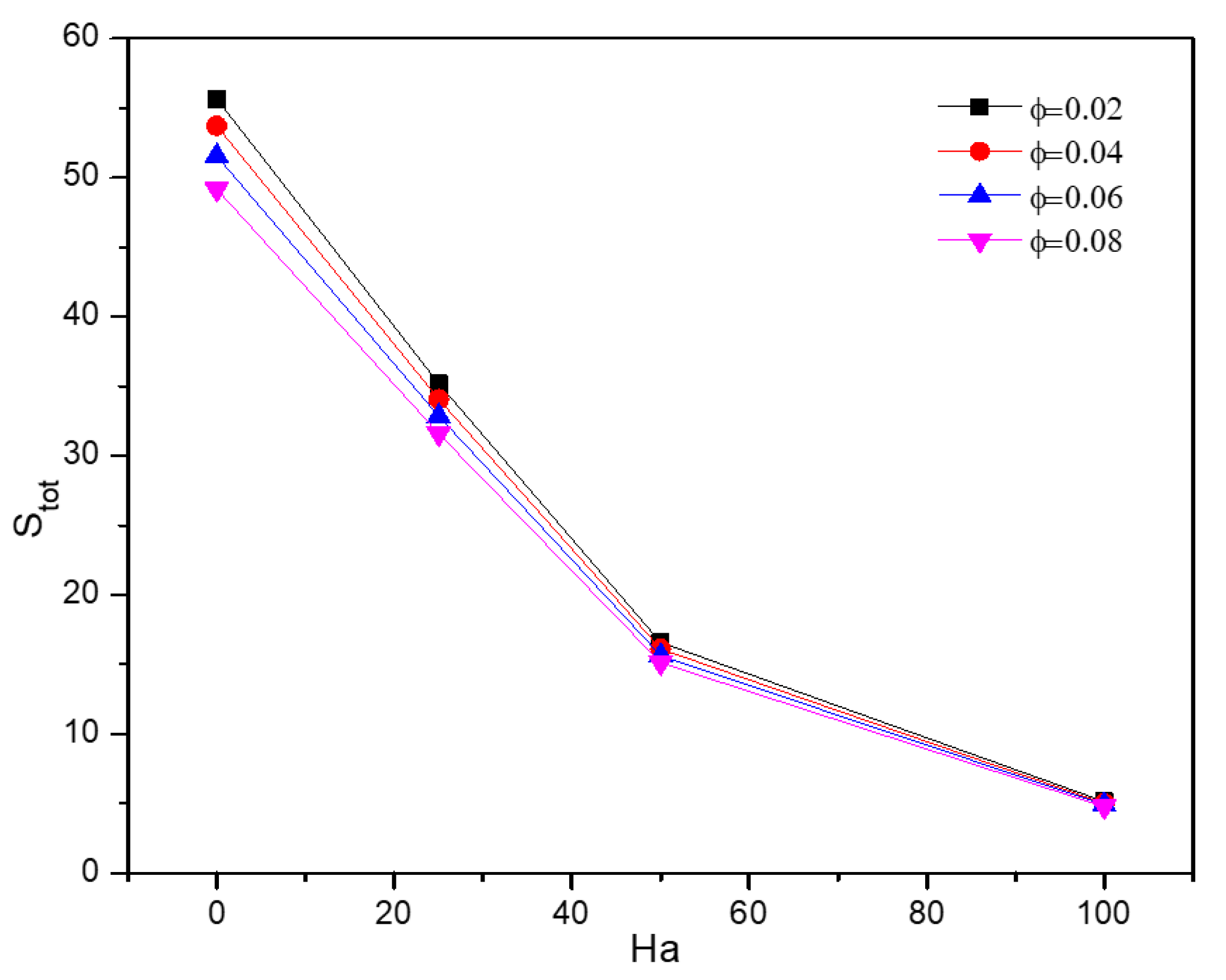
5.2. Effect of Hartmann Number

Figure 8 illustrates changing of streamlines and isotherms with diverse $Ha$ ($Da=0.01$, $Ra={10}^5$, $\varphi =0.02$, $\epsilon =0$). The streamline and isotherm appear within a cavity in the presence of temperature variations exposed to the magnetic field. In the beginning, when there was no magnetic field ($Ha=0$), the streamline formed one contour from the cold side, together with the circumference on the hot side. Secondly, there is resistance to flow at high Hartmann numbers, as the intensity of these lines’ changes down the bore. The magnetically limited flow of the fluid in the cavity dissipates the temperature in both directions.

Figure 9, Figure 10 and Figure 11 provide a clear justification for the variance of $Ha$. $Da$ affects heat transition, as demonstrated by Figure 9. Moreover, the improvement in $Ha$ leads to a shrinkage in the movement of the fluid and, therefore, the efficiency of the heat transfer displays reductions. It is necessary to realize that the heat transference is not impacted by the variation of the particle size values of solid nanoparticles between 0.02 and 0.08 with $Ra$ and $Da$ in each $Ha$ preparation, as shown in Figure 10. In addition, $\epsilon$ affects $N{u}_{avg}$ by a significant amount. At low values of $Ha$, it gives the highest values of $N{u}_{avg}$ as well as declines to approach zero at high values of $Ha$, as shown in Figure 11. The previous conclusions confirmed that the intensification in the value of $Ha$ reduces the heat transfer process. The new deduction is that $N{u}_{avg}$ is affected by the Hartmann number in the improvement of $\epsilon$. The reduction in the magnetic field leads to the improved fluid movement and, thus, better heat transfer.

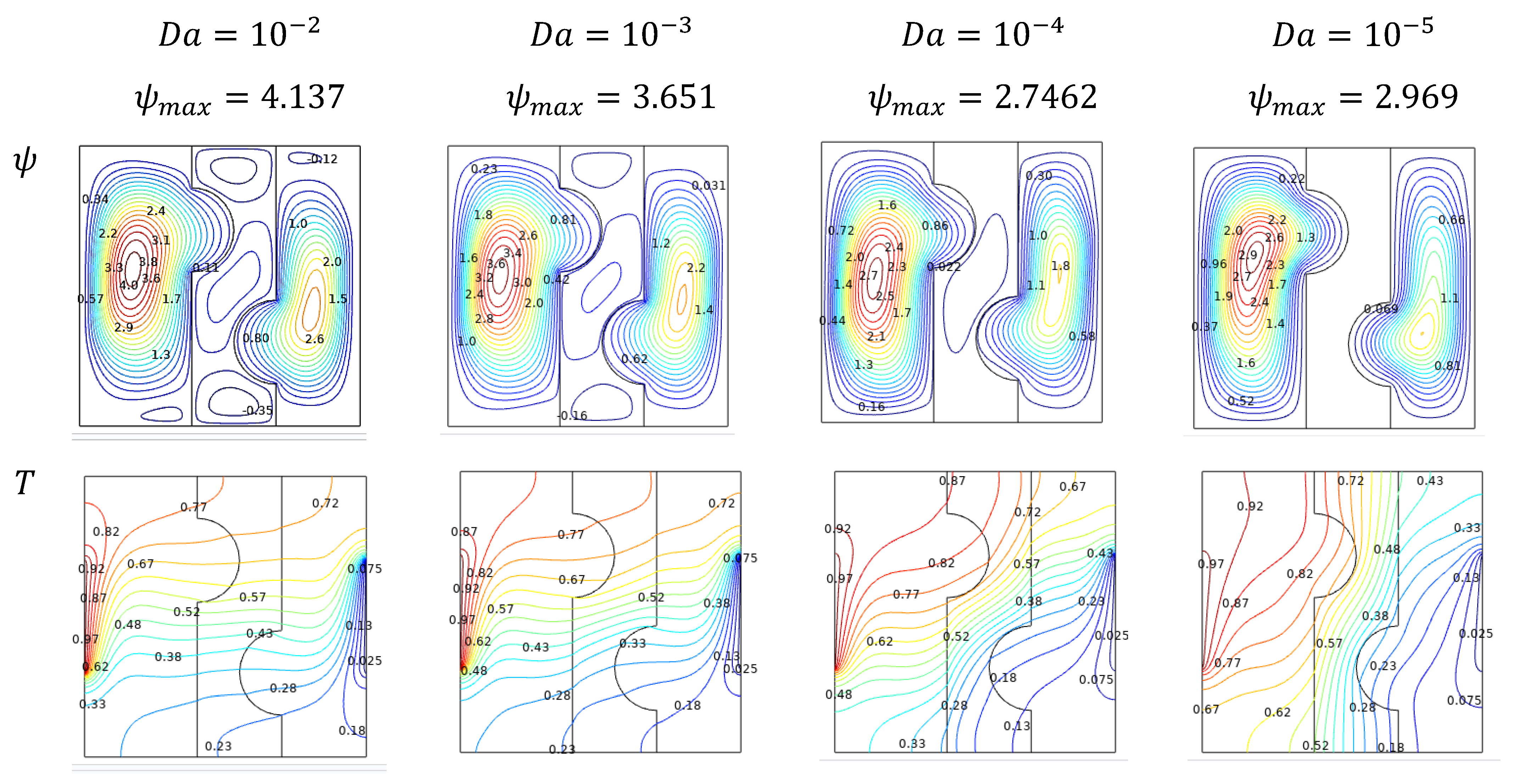
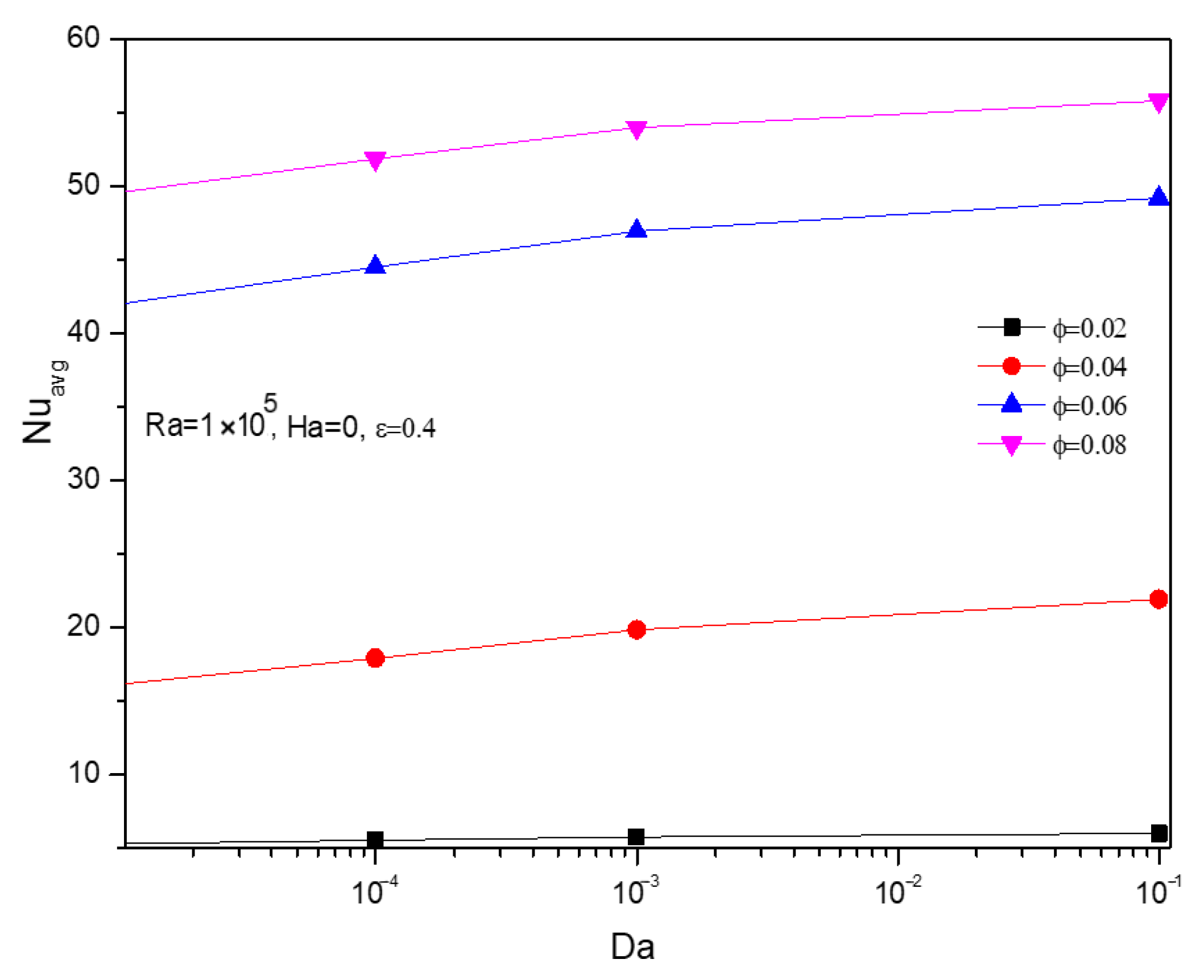
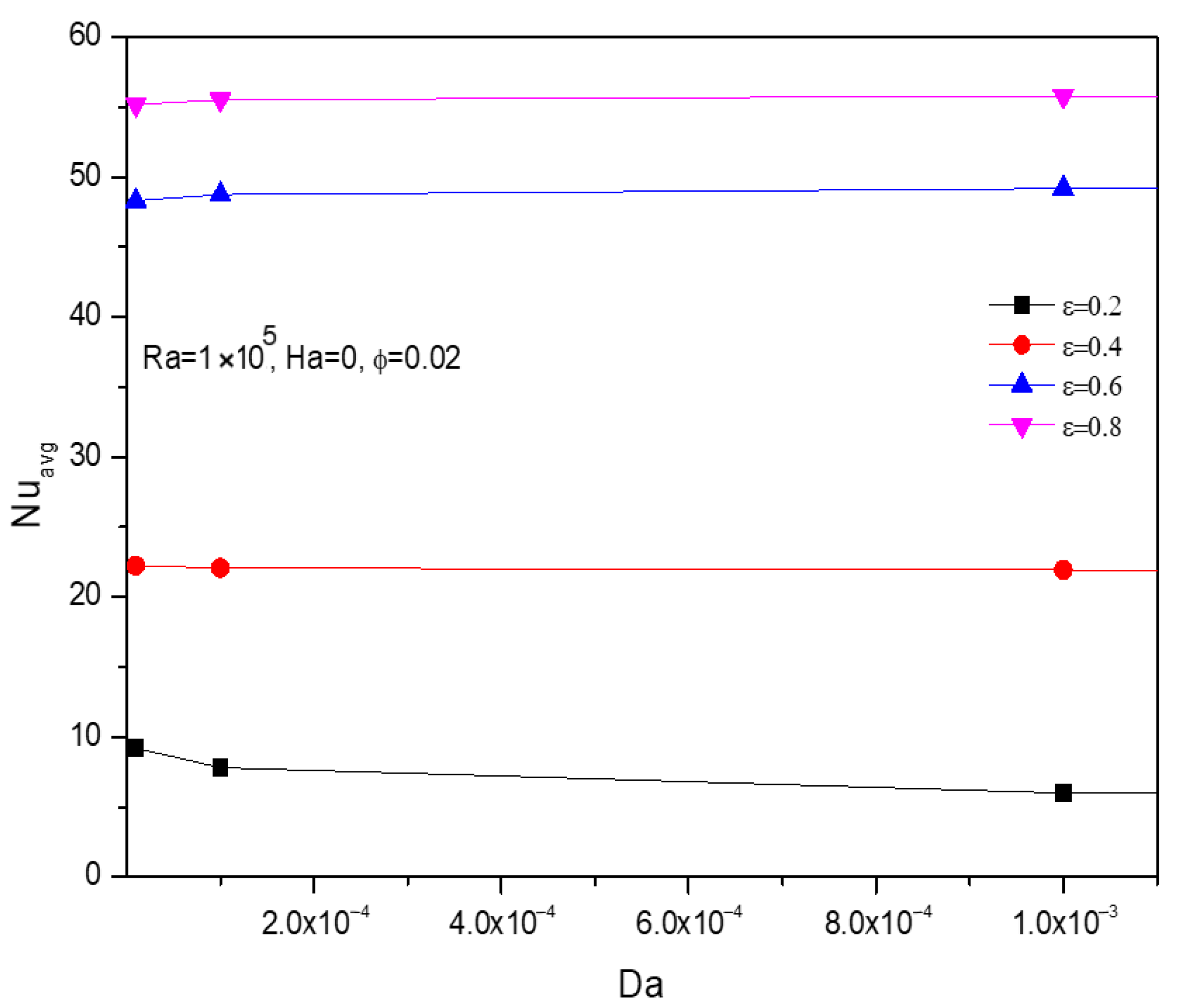
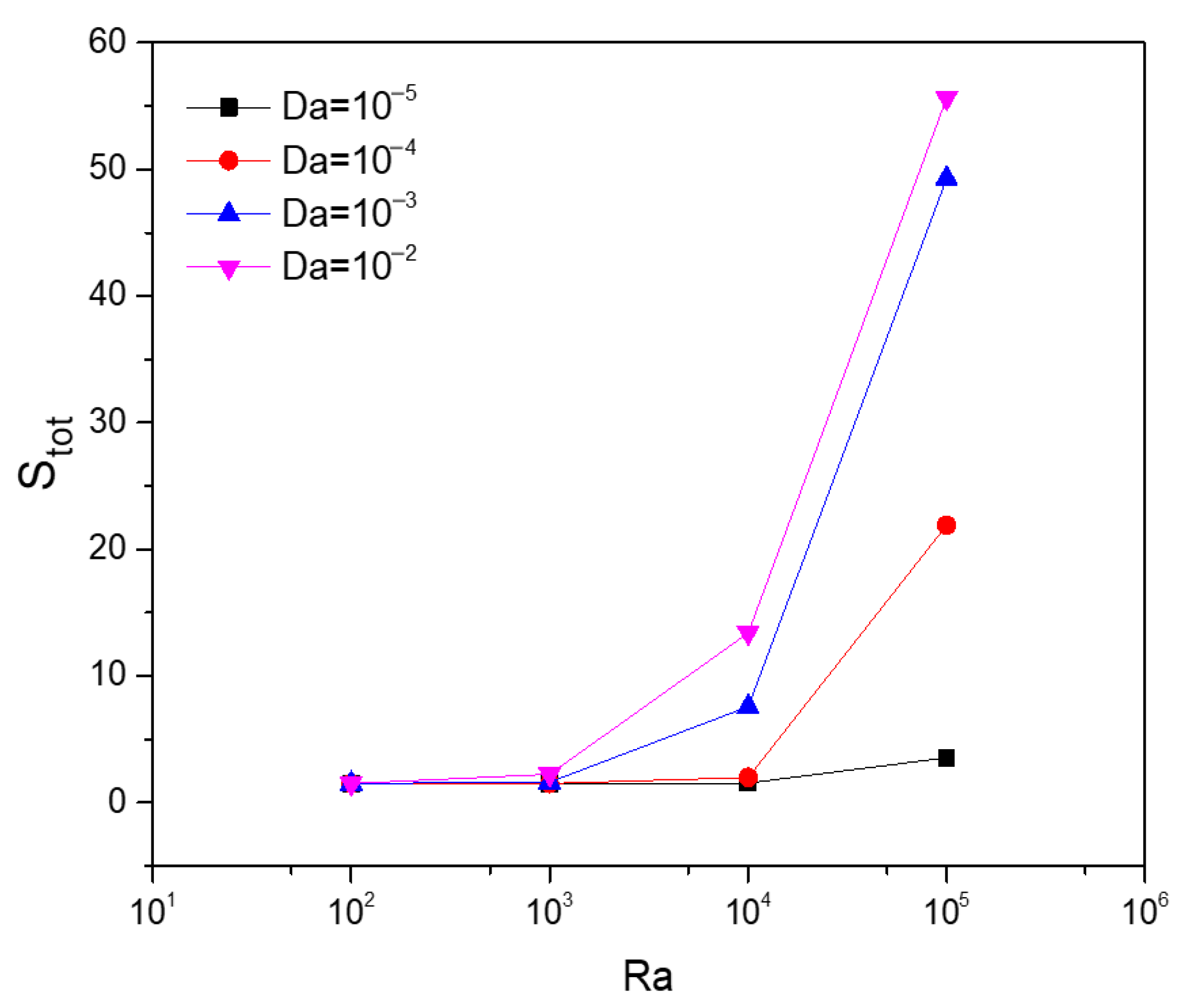
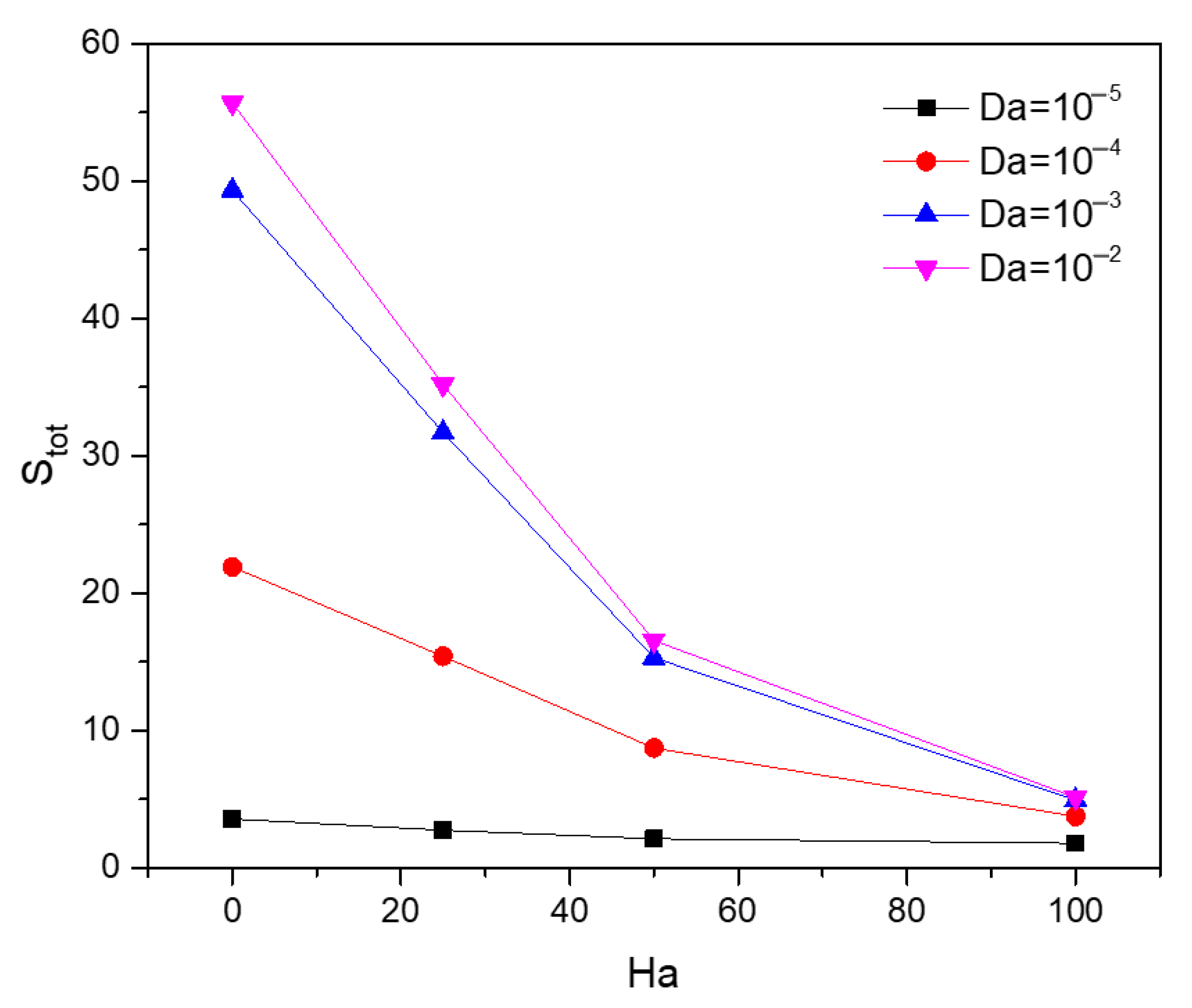
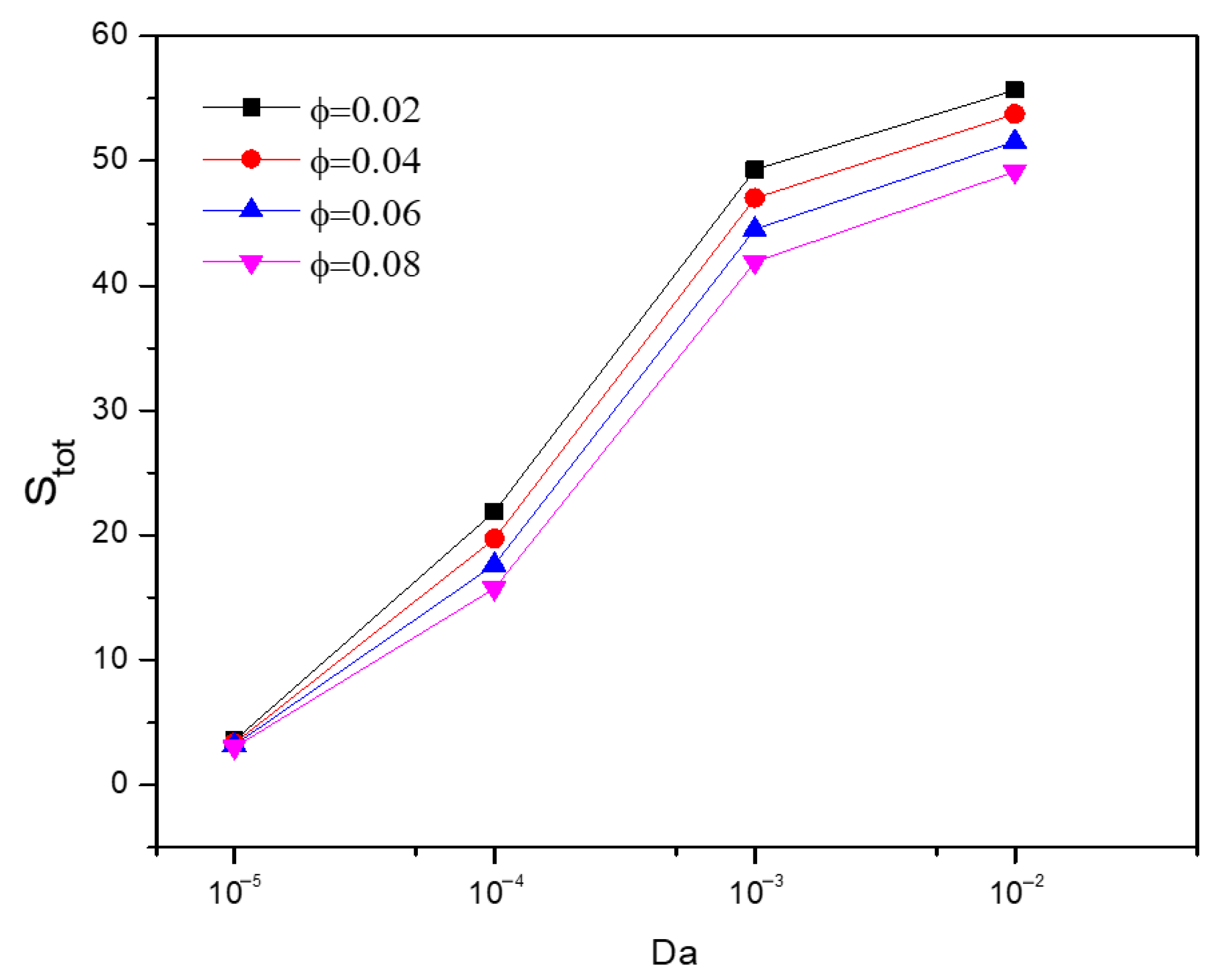
5.3. Effect of Darcy’s Number

Figure 12 illustrates changing of streamlines and isotherms with diverse Darcy-number ($Ra={10}^5$, $Ha=0$, $\varphi =0.02$, $\epsilon =0$). The porous structure is significantly affected by $Da$. The surface’s penetrability improves with the number of Darcy, allowing flow to it. The streamline accumulates at both ends of the porous medium and then flows to give high Darcy values. The cold end has a severe circumference compared to the hot end. This circumference is due to the slow permeability of the coolant. The results are shown in Figure 12. The temperature in the porous medium’s periphery and the cavity’s middle region equals the temperature above the Darcy number. This phenomenon happens because the liquid enters through the porous medium to raise the value of Darcy’s number.

Figure 13 shows the excellent effect of $Da$ for all $\varphi$ values. On the contrary, its effect is virtually constant on all ε values, as shown in Figure 14, where the dominance of the impact of porosity $\epsilon$ on the divergent differences of $Da$. This occurrence is due to the porosity of the surface. The in-field movement of nanoparticles is caused by a growth in the average Nusselt number.

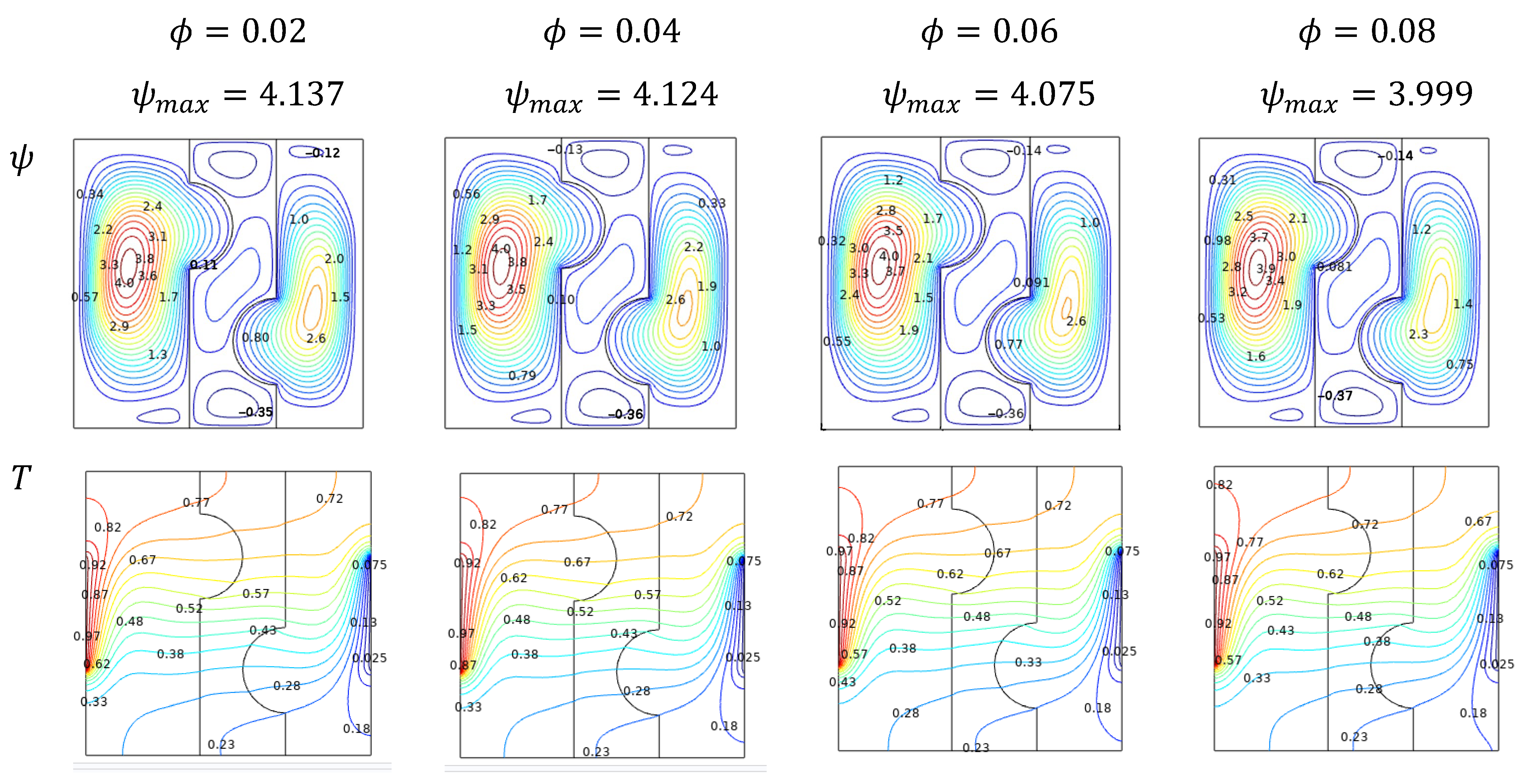
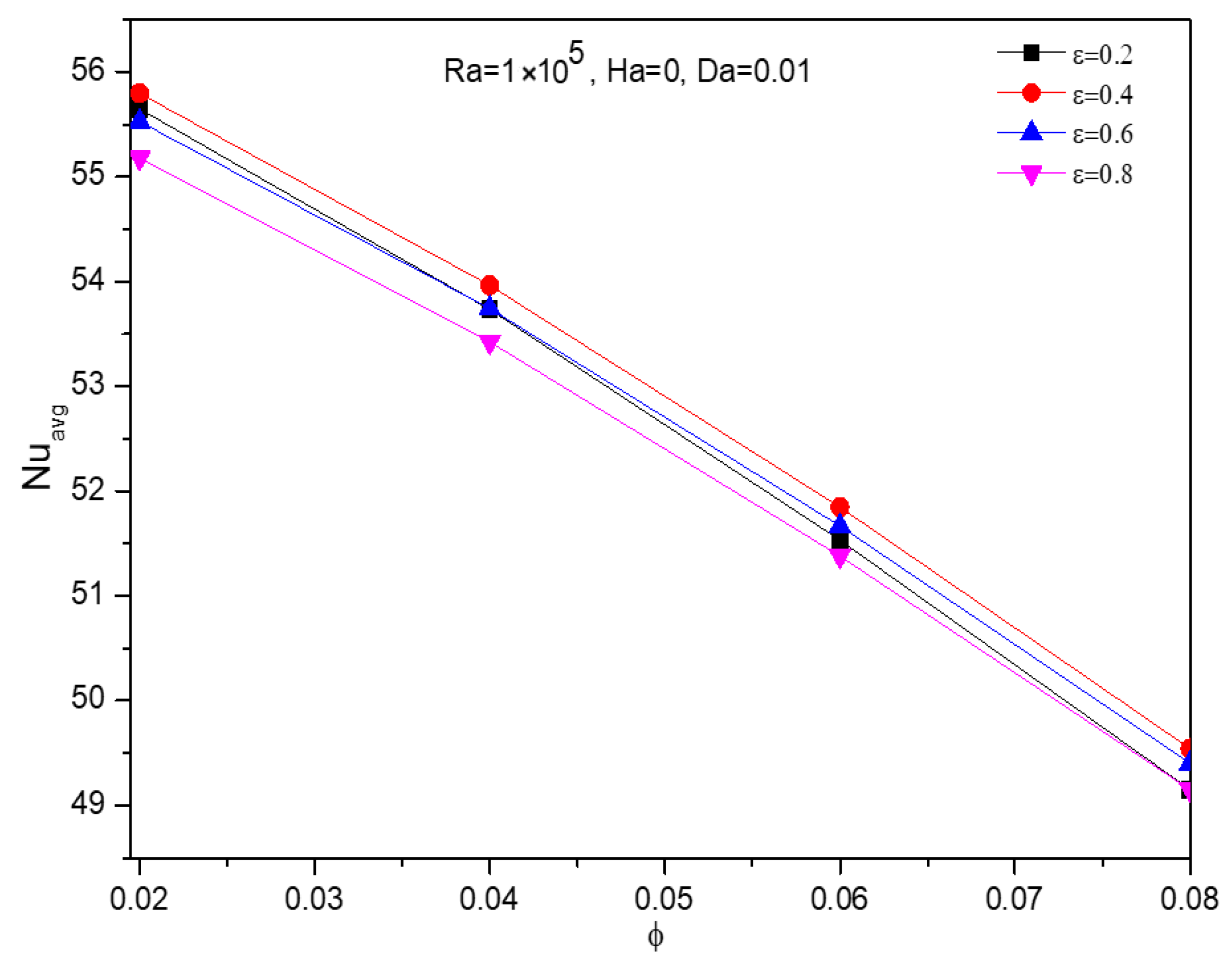
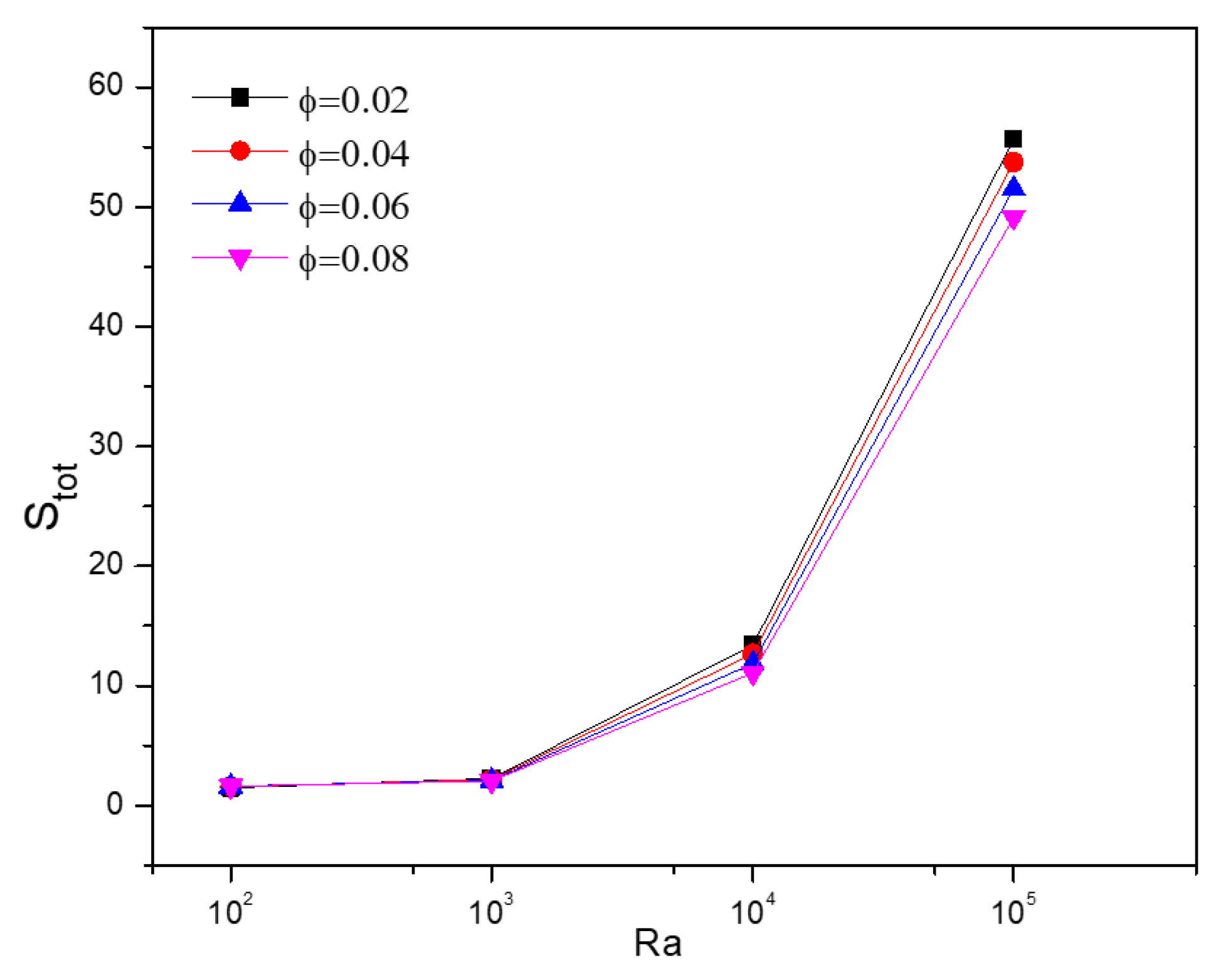
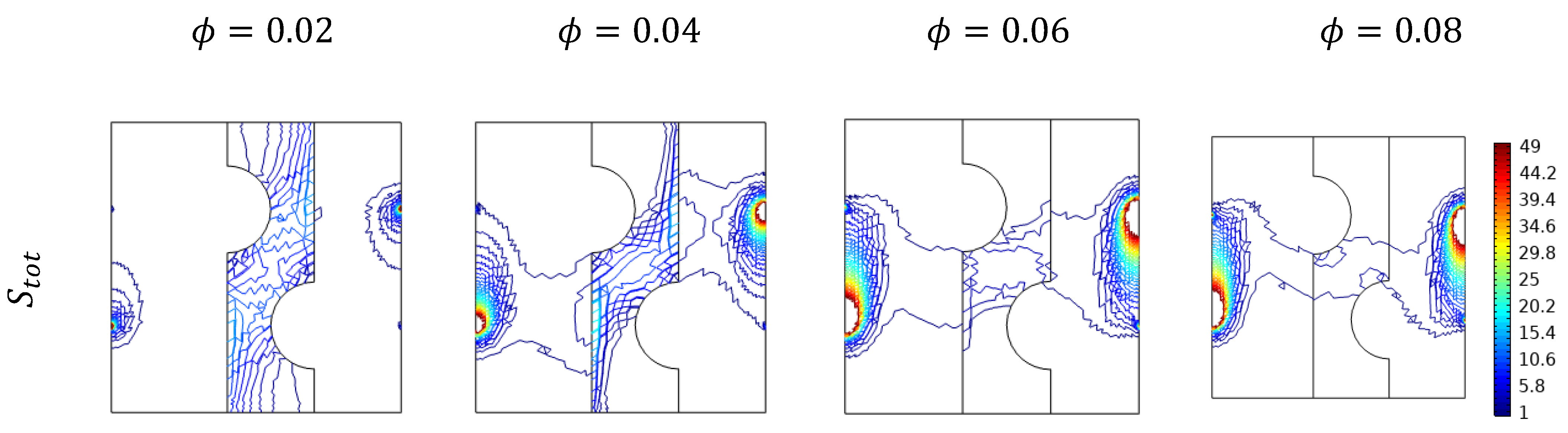
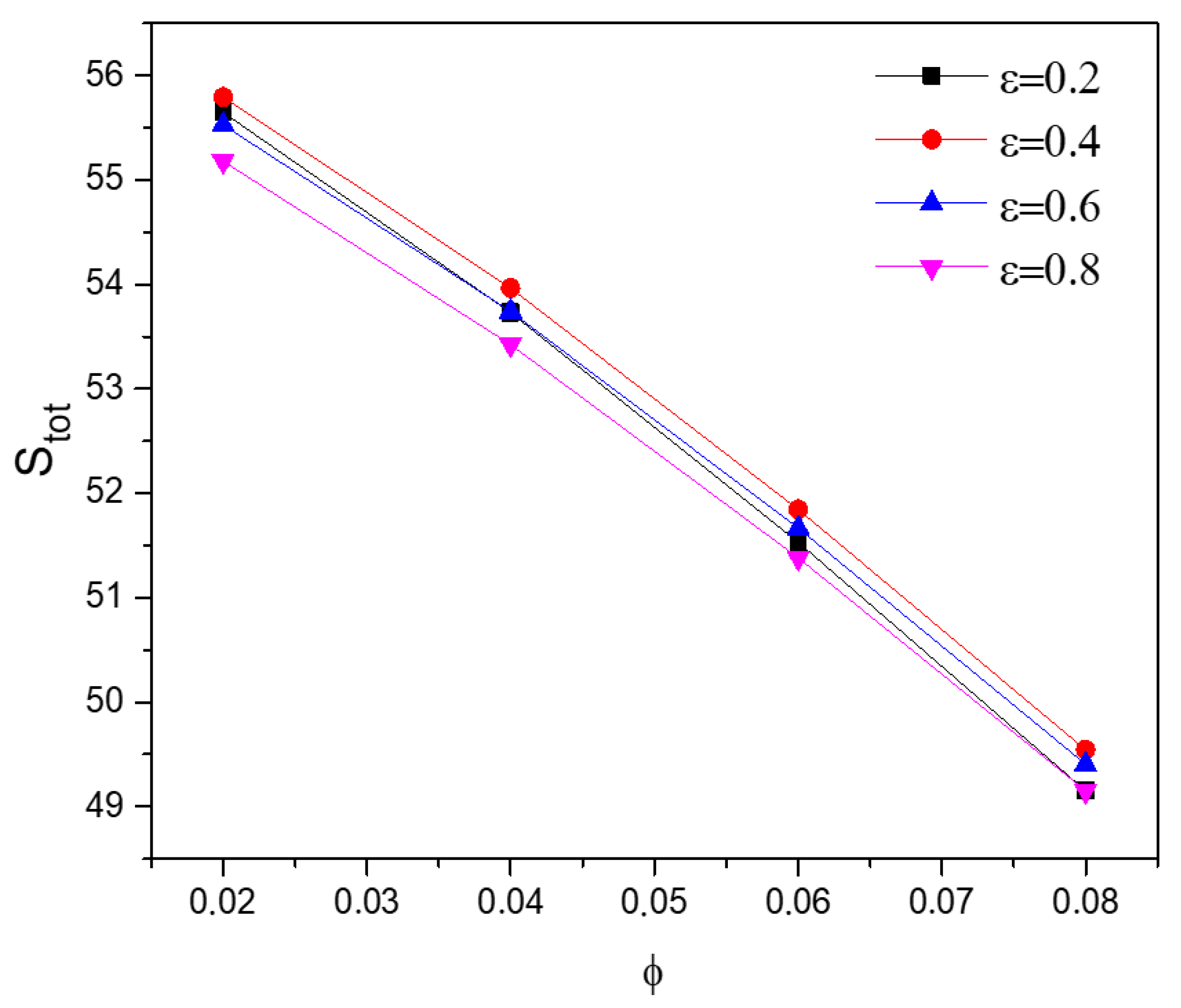
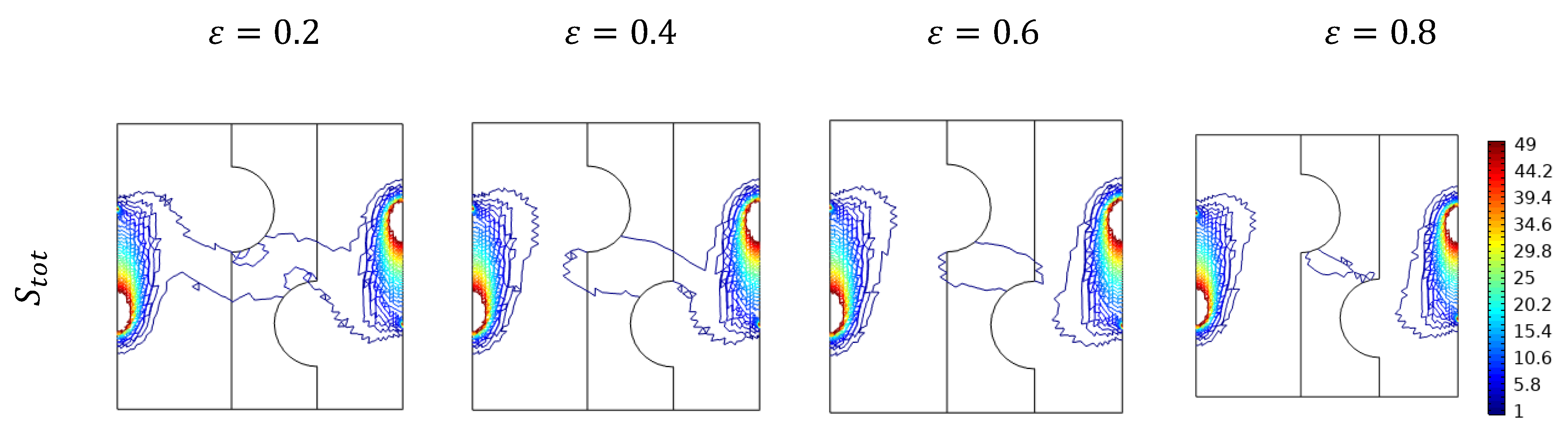
5.4. Effect of Nanofluid Loading

Figure 15 illustrates changing of streamlines and isotherms with varied $\varphi$ at ($Da=0.01$, $Ra={10}^5$, $Ha=0$, $\epsilon =0$). The quality of nanofluids is reflected in the volume fraction concentration in terms of thermal efficiency and fluidity. Variations in the solid volume fraction affect the streamlines. The features of the streamlines are scattered in the height of the substantial volume fraction caused by the lateness created in the cavity by the additional molecules’ fractional size. Figure 16 presents the adaptation of $N{u}_{avg}$ with $\varphi$ for varied $\epsilon$ at ($Ra={10}^5$, $Ha=0$, $Da=0.01$). The solid volume fraction shows a dwindling temperature in the hot region. $\epsilon$ oppositely affects $N{u}_{avg}$ as the solid volume fraction proliferates, a diminution in $N{u}_{avg}$. An intensification in $\epsilon$ reduces heat transition in the cavity. In addition, more heat transfer tends to exacerbate.

5.5. Effect of Porosity

Figure 17 illustrates changing of streamlines and isotherms with diverse Porosity ($Ra={10}^5$, $Da=0.01$, $Ha=0$, $\varphi =0.02$). Compared to normal liquids in a porous medium, porosity is critical when flowing nanofluids. This circumference is due to the nature of suspended nanoparticles. In addition, to the causes of $Da$. The porousness $\epsilon$ is due to lines gathered around the porous media but to a lesser extent. The streamlines change due to the amplified porosity that simplifies the flow through the cavity. For isotherms, porosity has a common effect. It can be observed that there are no significant changes or improvements in the graphs.

5.6. Effect of General Entropy of Different Numbers

Recently, parametric-level entropy studies have been incorporated into the flow and thermal studies to identify energy loss and minimize it with the necessary efforts. Figure 18 represents the entropy formation on the enclosure filled with hybrid fluid MWCNT-Fe₃O₄/H₂O for collective amounts of $Ra$. For lower amounts, the flow claims to be laminar; under these conditions, the entropy formation was at the emergent stage, which can be found mainly near the lower corrugated wall. As it propagates into a turbulent phase of higher Rayleigh number ($Ra$) values, entropy formation is also augmented from significant parts of the enclosure. In particular, the diagonal dominance trend can be visualized for the more significant Rayleigh number ($Ra$).

Figure 18 represents the entropy formation on the enclosure filled with hybrid fluid MWCNT-Fe₃O₄/H₂O for snowballing amounts of $Ra$. For lower quantities, the flow claims to be laminar. Under these conditions, the entropy formation was at the emergent stage, which can be found mainly near the bottom wall. This result showed that $Ra$ disturbed the entropy system in the flow. Figure 19, Figure 20 and Figure 21 present the variation of entropy on Rayleigh function for varied $Da$, notable that the entropy varied proportionally by $Ra$ as well as the descending $Da$ and volume fraction and Hartmann number to diminish.

Figure 22 represents entropy formation on the enclosure filled with hybrid fluid MWCNT-Fe₃O₄/H₂O for accumulative values of the Hartman number $Ha$. For higher values, the flow pretends to be laminar. Under these conditions, the entropy formation was augmented in the porous medium and lessened in the non-porous medium.

Figure 23 and Figure 24 contemporaneous discuss the variation of entropy on the Hartmann function and are noteworthy that the Darcy number and the fractional size are fixed. The entropy varied inversely by the number of the Hartmann volume fraction as well as the descending Darcy and volume fraction. It is worth mentioning that the magnetic convection in the flow disturbed the entropy system, and the permeability will enhance the entropy generation in the flow.

Figure 25 represents the formation of entropy on the enclosure filled with hybrid fluid MWCNT-Fe₃O₄/H₂O for accumulative amounts of $Da$. For lower amounts, the flow claims to be laminar. Under these conditions, entropy formation dwindled in the porous medium and rose in the nanofluid medium.

Figure 26 offerings the variation of entropy on Darcy function for different volume fractions. Noticeably, the entropy varied proportionally by the Hartmann volume fraction and the descending volume fraction.

Figure 27 represents entropy formation on the enclosure filled with hybrid nanofluid MWCNT-Fe₃O₄/H₂O for increasing values of volume fraction $\varphi$. For lower values, the flow pretends to be laminar; consequently, the propagation of heating and randomness in the porousness surface by diminishing volume fraction $\varphi$ and stabilizing so that the volume fraction $\varphi$ intensifications in the opposite way for the no-porous medium.

Figure 28 shows the variation of entropy as a function of the fractional size for varied porosities. It is noted that the entropy varied inversely with volume fraction and the porosity decreasing.

Figure 29 represents the formation of entropy on the enclosure filled with hybrid nanofluid MWCNT-Fe₃O₄/H₂O for aggregate values of porosity $\epsilon .$ For lower values, the flow pretends to be laminar. Therefore, the propagation of heat and randomness in a porous medium decreases porosity and stabilizes; hence, porosity increases in the opposite way for the non-porous medium.

6. Conclusions

The parametric regulation was studied in the hybrid nanofluid MWCNT–Fe₃O₄/water packed in the porous cavity medium in layers and under a magnetic field. Then, the problem studied is solved using the finite element method. The validation is conducted by comparing with existing results. The results will be benefits technological applications. Thus, the numerical results are extracted from the following.

• Activation of double streamlines for the hot side and single cooling for smaller amounts of Darcy numbers, Rayleigh numbers, and more significant amounts of Hartmann numbers.
• In the upper part of the cavity, a cold isotherm is required below it at varying values of physical parameters.
• At low values of Darcy and Hartmann number, Rayleigh number, high porosity, and lower volume fraction dominated by high $N{u}_{avg}$ in all porous mediums.
• The high heat transfer rate inside the cavity is due to a rise in Darcy’s number with $Ra$ and a solid volume fraction. These results are reflected when Hartmann is elevated.
• Thermal entropy production determines the entropy components.

The FEM approach could be applied to a variety of physical and technical challenges in the future [44,45,46,47,48,49,50].