Diversity of Optical Soliton Solutions of Akbota Models in the Application of Heisenberg Ferromagnet

Abstract

This paper explores the integrability of the Akbota equation with various types of solitary wave solutions. This equation belongs to a class of Heisenberg ferromagnet-type models. The model captures the dynamics of interactions between atomic magnetic moments, as governed by Heisenberg ferromagnetism. To reveal its further physical importance, we calculate more solutions with the applications of the logarithmic transformation, the M-shaped rational solution method, the periodic cross-rational solution technique, and the periodic cross-kink wave solution approach. These methods allow us to derive new analytical families of soliton solutions, highlighting the interplay of discrete and continuous symmetries that govern soliton formation and stability in Heisenberg-type systems. In contrast to earlier studies, our findings present notable advancements. These results hold potential significance for further exploration of similar frameworks in addressing nonlinear problems across applied sciences. The results highlight the intrinsic role of symmetry in the underlying nonlinear structure of the Akbota equation, where integrability and soliton formation are governed by continuous and discrete symmetry transformations. The derived solutions provide original insights into how symmetry-breaking parameters control soliton dynamics, and their novelty is verified through analytical and computational checks. The interplay between these symmetries and the magnetic spin dynamics of the Heisenberg ferromagnet demonstrates how symmetry-breaking parameters control the diversity and stability of optical solitons. Additionally, the outcomes contribute to a deeper understanding of fluid propagation and incompressible fluid behavior. The solutions obtained for the Akbota equation are original and, to the best of our knowledge, have not been previously reported. Several of these solutions are illustrated through 3-D, contour, and 2-D plots by using Mathematica software. The validity and accuracy of all solutions we present here are thoroughly verified.

1. Introduction

Most real-world systems exhibit nonlinear behavior and evolve dynamically over time. Given that time varies continuously, accurately modeling such systems presents significant challenges and often necessitates the use of mathematical formulations expressed as nonlinear partial differential equations (NLPDEs). These equations offer a robust mathematical model for characterizing the diverse dynamics and multifaceted phenomena inherent in complex systems. Scientists’ interest in comprehending and successfully resolving these complex nonlinear models has grown in recent decades. Curiosity arises from the desire to understand dynamic processes and their impact in diverse fields of science [1]. Nonlinear partial differential equations (NLPDEs) play a significant role in various scientific disciplines. This impact is noticeable in a variety of fields, including mathematical biology, chemical physics, optical fibers, mechanics, hydrodynamics, and others. NLPDEs are essential for understanding the intricate aspects of these fields [2,3].

A wide range of effective analytical and semi-analytical techniques have been developed to solve nonlinear partial differential equations. These methods include the exponential function method [4], Hirota’s bilinear method [5,6], Bäcklund transformations [7,8], the homogeneous balance method [9], the tanh–coth method [10], the variational iteration method [11], the modified Jacobi elliptic expansion method [12], the improved F-expansion method [13], the Riccati projective equation method [14], the inverse scattering transform [15], the modified sub-equation method [16], and the Sardar sub-equation method [17,18], among others [19,20,21,22,23,24,25].

Diverse soliton structures have been identified and discussed in the scientific literature. One such example is the homoclinic breather, characterized by a localized energy concentration and an oscillatory profile. Other well-known solitonic structures include breather waves and rogue waves, both of which exhibit strong localization in space and time [26,27,28]. Rogue waves—also known as freak or killer waves—can attain amplitudes three to five times larger than those of the surrounding waves [29]. Breathers, in contrast, are typically described by their dual spatial and temporal localization properties. The rogue wave and breather solutions are closely related, often transforming into one another under specific conditions [30,31]. Notable types of breather solutions include the Akhmediev breather [32], the generalized breather [33], and the Kuznetsov–Ma breather [34].

Rizvi acquired multi-wave and breather solitons for the Hunter–Saxton model [35]. The M-shaped rational solution and additional solutions [36] were obtained by Seadawy through their study of the perturbed Fokas–Lenells problem. Rizvi investigated various nonlinear wave structures, including periodic-kink solutions, homoclinic breathers, rogue waves, M-shaped rational solutions, and multi-wave solutions, within the framework of nonlinear differential equations [37].

In this manuscript, we focus on (1 + 1)-dimensional Akbota equation (AE). The Akbota equation [38] has the following form:

$$\begin{array}{c}\hfill i{P}_t+\alpha P_{xx}+\beta P_{xt}+\mu \gamma P=0,\\ \hfill {\mu }_x-2\varpi \left({\alpha \left|P\right|}_x^2+\beta {\left|P\right|}_t^2\right)=0,\varpi =\pm 1.\end{array}$$

(1)

where $\mu =\mu (x,t)$ is a real value function, $P=P(x,t)$ is a complex function, and $\alpha ,\beta ,\gamma ,\varpi$ are arbitrary constants that represents the linear dispersion, nonlinearity, high-order dispersion and frequency respectively. The Akbota equation can also be considered as a general form of two other well-known equations. Specifically,

• If $\beta =0$, the Akbota equation reduces to the Nonlinear Schrödinger equation.
• If $\alpha =0$, the Akbota equation reduces to the Kuralay equation.

The Akbota equation, a Heisenberg ferromagnetic-type equation, is fundamental to studying nonlinear processes in magnetism, optics, and curve and surface differential geometry. This integrable equation admits several important reductions, including the Kuralay equation and the nonlinear Schrödinger equation, which play a significant role in understanding the behavior of solitons and other nonlinear wave phenomena. The Akbota equation has been employed to study the dynamics of breather, rogue, and semi-rational solutions, which play a crucial role in understanding the behavior and interactions of optical solitons in optical fibers and related applications [39].

The Akbota equation has numerous applications in various scientific areas; hence, analytical solutions are required to gain deep insights into this model. Analytical solutions allow us to completely understand the underlying behavior of the system described by the equations. The clear and concise depiction of the interactions between variables and parameters allows for a more in-depth understanding of the core ideas governing the system.

Symmetry plays a fundamental role in nonlinear dynamical systems and soliton theory. The integrability of the Akbota model, like many soliton-bearing equations, relies on its inherent symmetry properties, such as invariance under translation, phase rotation, and gauge transformations. In the context of the Heisenberg ferromagnet, these symmetries correspond to spin rotation and conservation laws. Understanding how these symmetries are preserved or broken leads to deeper insight into the diversity and stability of optical soliton solutions. Therefore, the present work contributes to the study of symmetry and its manifestations in nonlinear spin and optical systems. Previous studies on the Akbota equation primarily focused on specific types of solitary wave solutions. While these works provided valuable insights into certain dynamical behaviors, they did not explore the full diversity of solution families or systematically analyze the role of discrete and continuous symmetries in soliton formation. In contrast, the present study derives new analytical families of soliton solutions, including M-shaped rational, periodic cross-rational, and periodic cross-kink wave solutions, using bilinear and rational transformation methods. Moreover, our approach explicitly examines how symmetry-breaking parameters influence solution stability and diversity, offering a more comprehensive understanding of the nonlinear dynamics in Heisenberg-type systems. This positions our work as a significant extension and generalization of prior Akbota-related research.

This manuscript presents a detailed investigation of the M-shaped rational solution, periodic cross-rational solutions, and periodic cross-kink wave solutions of the Akbota equation. Importantly, this study addresses a gap not explored in the current literature. Our main focus is to establish various kinds of solitons using M-shaped rational solution, periodic cross-rational solution and periodic cross-kink wave solution methods. However, in terms of future research, this control framework is quite significant. In the future perspective, N-soliton solutions can be developed using the Darboux transformation in the framework discussed in [40,41] with its non-commutative analogs.

In this paper, Section 2 is devoted to the derivation of the ordinary differential equation (ODE) and its corresponding bilinear form. Section 3, Section 4 and Section 5 presents various analytical solutions, including the M-shaped rational solutions, periodic cross-kink wave solutions, and periodic cross-rational solutions. Section 6 offers a detailed analysis of the graphical analysis, while Section 7 concludes the study by summarizing the key findings.

2. Reduction of Governing Model

The following traveling wave transformation is employed to convert the partial differential equation into an ordinary differential equation, thereby simplifying the analytical investigation.

$$P(x,t)=V\left(\mathrm{\Omega }\right)e^{\iota \eta },\mu (x,t)=\chi \left(\mathrm{\Omega }\right),$$

(2)

where $\mathrm{\Omega }=x-\delta t$ and $\eta =-\kappa x+\omega t$. $\delta$ is the speed, $V\left(\mathrm{\Omega }\right)$ represents the amplitude and $\eta$ shows the phase transition. By inserting Equation (2) into Equation (1), we obtain

$$\left({\kappa }^2\alpha -\omega +\kappa \beta \omega +\gamma \chi \left(\mathrm{\Omega }\right)\right)\mathbb{V}\left(\mathrm{\Omega }\right)+\left(\alpha -\beta \delta \right){\mathbb{V}}^{″}\left(\mathrm{\Omega }\right)=0,$$

(3)

Separating the real and imaginary components, the following equations are obtained.

$$(-2\kappa \alpha -\delta +\kappa \beta \delta +\beta \omega )V^{\prime }\left(\mathrm{\Omega }\right)=0,$$

(4)

$$-4\varpi (\alpha -\beta \delta )\mathbb{V}\left(\mathrm{\Omega }\right){\mathbb{V}}^{\prime }\left(\mathrm{\Omega }\right)+{\chi }^{\prime }\left(\mathrm{\Omega }\right)=0.$$

(5)

Now, integrating Equation (5) with respect to $\mathrm{\Omega }$, we have

$$\chi \left(\mathrm{\Omega }\right)=2\varpi (\alpha -\beta \delta ){\mathbb{V}}^2\left(\mathrm{\Omega }\right).$$

(6)

Now, using Equations (4) and (6) in Equation (3), we obtain the following ODE:

$$(-\delta +\kappa (\beta \kappa -2)(\alpha -\beta \delta ))\mathbb{V}\left(\mathrm{\Omega }\right)+2\beta \gamma \varpi (\alpha -\beta \delta ){\mathbb{V}}^3\left(\mathrm{\Omega }\right)+\beta c{\mathbb{V}}^{\prime }\left(\mathrm{\Omega }\right)=0.$$

(7)

where $(\alpha -\beta \delta )\ne 0$.

Bilinear Form

The following transformation is employed to construct various rational solutions, where the bilinear form provides a systematic framework to simplify the nonlinear equation and uncover the symmetries governing soliton dynamics.

$$V\left(\xi \right)=2{\partial }_{\xi }(logf\left(\xi \right)),$$

(8)

where $f\left(\xi \right)$ is a generating function for soliton solutions and $\xi$ is the transformed coordinate. This formulation simplifies the nonlinear structure, reveals underlying symmetries, and ensures that the solutions are transparent and reproducible. Using Equation (8) in Equation (7), we have

$$\begin{array}{cc}\hfill & -2f^2\delta f_{\xi }-4f^2\alpha \kappa f_{\xi }+2f^2\alpha \beta {\kappa }^2{f}_{\xi }-2f^2{\beta }^2\delta {\kappa }^2{f}_{\xi }\hfill \\ \hfill & +4\beta \delta \kappa f^2{f}_{\xi }-4{\beta }^2\delta f_{\xi \xi \xi }+16\alpha \beta \gamma \delta \varpi f_{\xi \xi \xi }-16{\beta }^2\gamma \delta \varpi f_{\xi \xi \xi }\hfill \\ \hfill & +2\alpha \beta f^2{f}_{\xi \xi \xi }-2f^2{\beta }^2\delta f_{\xi \xi \xi }-6\alpha \beta f_{\xi \xi }{f}_{\xi }+6{\beta }^2\delta f_{\xi \xi }{f}_{\xi }\hfill \\ \hfill & +4\alpha \beta f_{\xi \xi \xi }=0.\hfill \end{array}$$

(9)

The equation consists of a sum of algebraic and differential terms set to zero. It combines the function f, its square $f^2$, and its first ($f_{\xi }$), second ($f_{\xi \xi }$), and third ($f_{\xi \xi \xi }$) derivatives. In D-operator form, it can be written as

$$\begin{array}{cc}\hfill & \left(-\delta -2\alpha \kappa +\alpha \beta {\kappa }^2-{\beta }^2\delta {\kappa }^2+2\beta \delta \kappa \right)D_{\xi }f·f\hfill \\ \hfill & +\left(-2{\beta }^2\delta +8\alpha \beta \gamma \delta \varpi -8{\beta }^2\gamma \delta \varpi +2\alpha \beta -2{\beta }^2\delta +4\alpha \beta \right)D_{\xi }^{3}f·f=0,\hfill \end{array}$$

(10)

where the Hirota D-operator is defined as

$$D_{\xi }^{n}f·g={\left({\displaystyle \frac{\partial }{\partial \xi }}-{\displaystyle \frac{\partial }{\partial {\xi }^{\prime }}}\right)}^{n}f\left(\xi \right)g\left({\xi }^{\prime }\right){|}_{{\xi }^{\prime }=\xi }.$$

3. M-Shaped Rational Solution

In this section, we investigate M-shaped rational solutions composed of quadratic functions. The purpose of studying M-shaped rational solutions is to describe double-peak localized wave structures that arise from nonlinear dispersion effects. These solutions help explain energy splitting within a pulse and provide valuable analytical benchmarks for understanding complex wave dynamics in nonlinear systems. To derive the M-shaped soliton, the following transformation is applied [42].

$$f={(b_1\xi +b_2)}^2+{(b_3\xi +b_4)}^2+b_5.$$

(11)

All $b_i(1\le i\le 5)$ are constants to be determined. Using Mathematica, insert Equation (11) in Equation (9) and calculate the coefficient of all powers of $\xi$. We derive an equation that yields the following parameter values.

Case 1:

$$b_3=b_3;b_2=-i{b}_4;b_5=b_5,$$

(12)

inserting Equation (12) in Equation (11), we have the following expression:

$$f={\xi }^2{b}_1^2+{\xi }^2{b}_3^2-2i\xi b_1{b}_4+2\xi b_3{b}_4+b_5,$$

(13)

using Equation (13) in Equation (8), we obtain

$$V={\displaystyle \frac{4\left(\xi b_1^2-i{b}_1{b}_4+b_3\left(\xi b_3+b_4\right)\right)}{{\xi }^2{b}_1^2+{\xi }^2{b}_3^2-2i\xi b_1{b}_4+2\xi b_3{b}_4+b_5}},$$

(14)

now, substituting Equation (14) in Equation (2), we obtain M-shaped solution of Equation (1).

$$P={\displaystyle \frac{e^{-xi\kappa +ti\omega }\left(4(x-t\delta )\left(b_1^2+b_3^2\right)+4(-i{b}_1+b_3)b_4\right)}{(x-t\delta )\left((x-t\delta )\left(b_1^2+b_3^2\right)+2(-i{b}_1+b_3)b_4\right)+b_5}}.$$

(15)

And $\mu$ can be calculated from Equation (6) as

$$\mu =2\varpi (\alpha -\beta \delta )P^2.$$

(16)

inserting Equation (15) in Equation (16), we obtain

$$\mu ={\displaystyle \frac{2e^{-2x\iota \kappa +2t\iota \omega }\varpi (\alpha -\beta \delta ){\left[4(x-t\delta )\left(b_1^2+b_3^2\right)+4(-i{b}_1+b_3)b_4\right]}^2}{{\left[(x-t\delta )\left((x-t\delta )(b_1^2+b_3^2)+2(-i{b}_1+b_3)b_4\right)+b_5\right]}^2}}.$$

(17)

Case 2:

$$b_2=b_2,b_4=i{b}_2,b_5=b_5.$$

(18)

substituting Equation (18) in Equation (11), we obtain

$$f={\xi }^2{b}_1^2+2\xi b_1{b}_2+2i\xi b_2{b}_3+{\xi }^2{b}_3^2+b_5.$$

(19)

using this f expression in Equation (8), we obtain

$$V={\displaystyle \frac{4(b_1+i{b}_3)(\xi b_1+b_2-i\xi b_3)}{{\xi }^2{b}_1^2+2\xi b_1{b}_2+2i\xi b_2{b}_3+{\xi }^2{b}_3^2+b_5}}.$$

(20)

in order to obtain the M-shaped rational solution, we substitute Equation (20) into Equation (2).

$$P={\displaystyle \frac{e^{-x\iota \kappa +t\iota \omega }\left(4b_1\left((x-t\delta )b_1+b_2\right)+4i{b}_2{b}_3+4(x-t\delta )b_3^2\right)}{(x-t\delta )\left(2b_2+(x-t\delta )(b_1-i{b}_3)\right)(b_1+i{b}_3)+b_5}}.$$

(21)

$\mu$ can be obtained by inserting the above expression in Equation (16).

$$\mu ={\displaystyle \frac{2e^{-2x\iota \kappa +2t\iota \omega }\varpi (\alpha -\beta \delta ){\left(4b_1\left((x-t\delta )b_1+b_2\right)+4i{b}_2{b}_3+4(x-t\delta )b_3^2\right)}^2}{{\left((x-t\delta )\left(2b_2+(x-t\delta )(b_1-i{b}_3)\right)(b_1+i{b}_3)+b_5\right)}^2.}}$$

(22)

4. Periodic Cross-Rational Solution

We now consider the periodic cross-rational solution, which involves a combination of quadratic, trigonometric, and hyperbolic trigonometric functions, along with arbitrary coefficients. A periodic cross-rational solution describes a waveform generated by the interaction of a periodic background with a rationally localized structure, producing a characteristic cross-shaped pattern. Such solutions capture the combined effects of periodic modulation and algebraic localization, and are useful for modeling interference-driven wave patterns in nonlinear systems. To construct this solution, we employ the following transformation [42]:

$$f={(z_1\xi +z_2)}^2+{(z_3\xi +z_4)}^2+(z_1\xi +z_2)cos(a_1\xi +a_2)+(z_3\xi +z_4)cosh(a_3\xi +a_4)+z_5.$$

(23)

where $z_i(1\le i\le 5)$ and $a_i(1\le i\le 4)$ are all parameters to be determined. By substituting Equation (23) into Equation (9) and equating the coefficients of like terms involving powers of $\xi$, as well as the functional combinations such as $\xi sin(a_2+a_1\xi ){sinh}^2(a_4+a_3\xi )$, $sin(a_2+a_1\xi ){sinh}^2(a_4+a_3\xi )$, ${\xi }^2{sinh}^2(a_4+a_3\xi )$, $\xi {sinh}^2(a_4+a_3\xi )$, ${sinh}^2(a_4+a_3\xi )$, ${sin}^2(a_2+a_1\xi )sinh(a_4+a_3\xi )$, and ${\xi }^2{sin}^2(a_2+a_1\xi )sinh(a_4+a_3\xi )$, among others, we obtain a system of equations that determines the values of the unknown coefficients.

$$a_3=0,z_3=-\mathrm{i}{z}_1,z_4=-\mathrm{i}{z}_2.$$

(24)

substituting these coefficient values into Equation (23), we obtain the following expression.

$$f=z_5+{(-\mathrm{i}{z}_2-\mathrm{i}{z}_1\xi )}^2+{(z_2+z_1\xi )}^2+(z_2+z_1\xi )cos(a_2+a_1\xi )+(-\mathrm{i}{z}_2-\mathrm{i}{z}_1\xi )cosh\left(a_4\right).$$

(25)

by incorporating Equation (25) in Equation (8), the resulting analytical expression is obtained.

$$V=-{\displaystyle \frac{2\left(-z_{1}cos(a_2+a_1\xi )+\mathrm{i}{z}_{1}cosh\left(a_4\right)+a_1(z_2+z_1\xi )sin(a_2+a_1\xi )\right)}{z_5+(z_2+z_1\xi )cos(a_2+a_1\xi )-\mathrm{i}(z_2+z_1\xi )cosh\left(a_4\right)}}$$

(26)

By substituting Equation (26) into Equation (2), we obtain the periodic cross-rational solution corresponding to Equation (1).

$$P=-{\displaystyle \frac{2e^{-\mathrm{i}x\kappa +\mathrm{i}t\omega }\left(-z_{1}cos(a_2+a_{1}x-a_{1}t\delta )+\mathrm{i}{z}_{1}cosh\left(a_4\right)+a_1(x{z}_1+z_2-t{z}_1\delta )sin(a_2+a_{1}x-a_{1}t\delta )\right)}{z_5+(x{z}_1+z_2-t{z}_1\delta )cos(a_2+a_{1}x-a_{1}t\delta )-\mathrm{i}(x{z}_1+z_2-t{z}_1\delta )cosh\left(a_4\right)}}.$$

(27)

To compute $\mu$, we substitute the above expression into Equation (16).

$$\mu ={\displaystyle \frac{8e^{-2x\iota \kappa +2t\iota \omega }\varpi (\alpha -\beta \delta ){\left(-z_{1}cos(a_2+a_{1}x-a_{1}t\delta )+\mathrm{i}{z}_{1}cosh\left(a_4\right)+a_1(x{z}_1+z_2-t{z}_1\delta )sin(a_2+a_{1}x-a_{1}t\delta )\right)}^2}{{\left[z_5+(x{z}_1+z_2-t{z}_1\delta )cos(a_2+a_{1}x-a_{1}t\delta )-\mathrm{i}(x{z}_1+z_2-t{z}_1\delta )cosh\left(a_4\right)\right]}^2}}.$$

(28)

Case 2:

$$a_3=0,z_3=i{z}_1,\kappa ={\displaystyle \frac{\alpha -\beta \delta +\sqrt{{\alpha }^2-\alpha \beta \delta }}{\alpha \beta -{\beta }^2\delta }}.$$

(29)

upon substituting Equation (29) in Equation (23), we obtain the following expression.

$$f=z_5+{(z_4+i{z}_1\xi )}^2+{(z_2+z_1\xi )}^2+(z_2+z_1\xi )cos(a_2+a_1\xi )+(z_4+i{z}_1\xi )cosh\left(a_4\right),$$

(30)

Inserting the above expression in Equation (8), we obtain

$$V={\displaystyle \frac{4z_1{z}_2+4i{z}_1{z}_4+2z_{1}cos(a_2+a_1\xi )+2i{z}_{1}cosh\left(a_4\right)-2a_1{z}_{2}sin(a_2+a_1\xi )-2a_1{z}_1\xi sin(a_2+a_1\xi )}{z_2^2+z_4^2+z_5+2z_1{z}_2\xi +2i{z}_1{z}_4\xi +(z_2+z_1\xi )cos(a_2+a_1\xi )+(z_4+i{z}_1\xi )cosh\left(a_4\right),}}$$

(31)

The periodic cross-rational solution is derived by substituting Equation (31) into Equation (2).

$$\begin{array}{c}\hfill P={\displaystyle \frac{e^{\mathrm{i}\left[{\displaystyle \frac{x\left(\alpha -\beta \delta +\sqrt{\alpha (\alpha -\beta \delta )}\right)}{\beta (-\alpha +\beta \delta )}}+t\omega \right]}\begin{array}{c}\left\{4z_1{z}_2+4\mathrm{i}{z}_1{z}_4+2z_{1}cos\left(a_2+a_1(x-t\delta )\right)+2\mathrm{i}{z}_{1}cosh\left(a_4\right)\right\}\hfill \\ -2a_1{z}_{2}sin\left(a_2+a_1(x-t\delta )\right)-2a_1{z}_1(x-t\delta )sin\left(a_2+a_1(x-t\delta )\right)\hfill \end{array}}{\begin{array}{cc}\hfill & z_2^2+z_4^2+z_5+2z_1{z}_2(x-t\delta )+2\mathrm{i}{z}_1{z}_4(x-t\delta )\hfill \\ \hfill & +(x{z}_1+z_2-t{z}_1\delta )cos\left(a_2+a_1(x-t\delta )\right)+(z_4+\mathrm{i}{z}_1(x-t\delta ))cosh\left(a_4\right)\hfill \end{array}}}\end{array}$$

(32)

$\mu$ is obtained by substituting Equation (32) into Equation (16), yielding the following expression:

$$\mu =2\varpi (\alpha -\beta \delta )e^{2\iota \left({\displaystyle \frac{x(\alpha -\beta \delta +\sqrt{\alpha (\alpha -\beta \delta )})}{\beta (-\alpha +\beta \delta )}}+t\omega \right)}{\left({\displaystyle \frac{N(A,\varphi )}{D(A,\varphi )}}\right)}^2,$$

(33)

where

$$\begin{array}{cc}\hfill A& =x-t\delta ,\hfill \\ \hfill \varphi & =a_2+a_{1}A,\hfill \\ \hfill N(A,\varphi )& =4z_1{z}_2+4\iota z_1{z}_4+2z_{1}cos\varphi +2\iota z_{1}cosh{a}_4-2a_1{z}_{2}sin\varphi -2a_1{z}_{1}Asin\varphi ,\hfill \\ \hfill D(A,\varphi )& =z_2^2+z_4^2+z_5+2z_1{z}_{2}A+2\iota z_1{z}_{4}A+(z_{1}A+z_2)cos\varphi +(z_4+\iota z_{1}A)cosh{a}_4.\hfill \end{array}$$

5. Periodic Cross-Kink Wave Solution

In this section, we investigate the periodic cross-kink wave solution, which incorporates hyperbolic trigonometric, trigonometric, and exponential functions, along with free coefficients. A periodic cross-kink solution represents the interaction between a kink-type wave and an underlying periodic background, resulting in a distinct cross-shaped structure. This solution captures the combined effects of topological transitions and periodic modulation, providing insight into complex nonlinear wave interactions. To facilitate this analysis, we employ the following transformation [42].

$$\begin{array}{cc}\hfill f& =e^{-{\eta }_1}+{\eta }_1{e}^{{\eta }_1}+{\eta }_{2}cos\left({\eta }_2\right)+{\eta }_{3}cosh\left({\eta }_3\right)+a_7,\hfill \\ \hfill {\eta }_1& =a_1\xi +a_2,{\eta }_2=a_3\xi +a_4,{\eta }_3=a_5\xi +a_6.\hfill \end{array}$$

(34)

where $a_i$ for $1\le i\le 7$ and ${\eta }_i$ for $i=1,2,3$ denote constants. By substituting Equation (34) into Equation (9) and comparing coefficients of terms such as $e^{-2a_2-2a_1\xi }$, $e^{-a_2-a_1\xi }$, $\xi e^{-a_2-a_1\xi }$, $\xi e^{a_2+a_1\xi }$, etc., we obtain a set of algebraic expressions that determine the values of the coefficients.

Case 1:

$$\begin{array}{cc}\hfill a_4& =0,a_3=0,a_1=0,\hfill \\ \hfill a_6& =-\left({\displaystyle \frac{i\sqrt{2}{a}_5\sqrt{\alpha \beta -{\beta }^2\delta +4\alpha \beta \gamma \delta \varpi -4{\beta }^2\gamma \delta \varpi }}{\sqrt{-\delta -2\alpha \kappa +2\beta \delta \kappa +\alpha \beta {\kappa }^2-{\beta }^2\delta {\kappa }^2}}}\right).\hfill \end{array}$$

(35)

inserting Equation (35) in Equation (34), we obtain

$$f=a_7+e^{-a_2}+a_2{e}^{a_2}+\left(-{\displaystyle \frac{i\sqrt{2}{a}_5\sqrt{\alpha \beta -{\beta }^2\delta +4\varpi \alpha \beta \gamma \delta -4\varpi {\beta }^2\gamma \delta }}{\sqrt{-\delta -2\alpha \kappa +2\beta \delta \kappa +\alpha \beta {\kappa }^2-{\beta }^2\delta {\kappa }^2}}}+a_5\xi \right)cos\left({\displaystyle \frac{\sqrt{2}{a}_5\sqrt{\alpha \beta -{\beta }^2\delta +4\varpi \alpha \beta \gamma \delta -4\varpi {\beta }^2\gamma \delta }}{\sqrt{-\delta -2\alpha \kappa +2\beta \delta \kappa +\alpha \beta {\kappa }^2-{\beta }^2\delta {\kappa }^2}}}+i{a}_5\xi \right)$$

(36)

Using Equation (36) in Equation (8), we obtain

$$\begin{array}{c}\hfill V={\displaystyle \frac{2a_5{e}^{a_2}\left(\sqrt{A}cos\left(\frac{a_5\sqrt{B}}{\sqrt{A}}+i{a}_5\xi \right)-a_5\left(\sqrt{B}+i\sqrt{A}\xi \right)sin\left(\frac{a_5\sqrt{B}}{\sqrt{A}}+i{a}_5\xi \right)\right)}{(1+a_7{e}^{a_2}+a_2{e}^{2a_2})\sqrt{A}+a_5{e}^{a_2}\left(-i\sqrt{B}+\sqrt{A}\xi \right)cos\left(\frac{a_5\sqrt{B}}{\sqrt{A}}+i{a}_5\xi \right)}}\end{array}$$

(37)

where

$$\begin{array}{cc}\hfill A& =\alpha \kappa (-2+\beta \kappa )-\delta {(-1+\beta \kappa )}^2,\hfill \\ \hfill B& =2\alpha \beta -2({\beta }^2-4\varpi \alpha \beta \gamma +4\varpi {\beta }^2\gamma )\delta .\hfill \end{array}$$

Inserting Equation (37) in Equation (2), we obtain the periodic cross-kink wave solution to Equation (1):

$$\begin{array}{c}\hfill P={\displaystyle \frac{2a_5{e}^{a_2-x\iota \kappa +t\iota \omega }\left[Rcosh\left(\frac{a_5(x-t\delta )-i{a}_5\mathrm{\Lambda }}{R}\right)-i{a}_5\left(\mathrm{\Lambda }+i(x-t\delta )R\right)sinh\left(\frac{a_5(x-t\delta )-i{a}_5\mathrm{\Lambda }}{R}\right)\right]}{(1+a_7{e}^{a_2}+a_2{e}^{2a_2})R+a_5{e}^{a_2}\left(-i\mathrm{\Lambda }+(x-t\delta )R\right)cosh\left(\frac{a_5(x-t\delta )-i{a}_5\mathrm{\Lambda }}{R}\right)}}\end{array}$$

(38)

where

$$\begin{array}{cc}\hfill R& =\sqrt{\alpha \kappa (-2+\beta \kappa )-\delta {(-1+\beta \kappa )}^2},\hfill \\ \hfill \mathrm{\Lambda }& =\sqrt{2\alpha \beta -2\delta \left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)}.\hfill \end{array}$$

Now, $\mu$ is obtained by substituting Equation (38) in Equation (16).

$$\begin{array}{c}\hfill \mu ={\displaystyle \frac{8a_5^2{e}^{2a_2-2x\iota \kappa +2t\iota \omega }·\varpi (\alpha -\beta \delta ){\left(\sqrt{\mathcal{R}}cosh\left(\frac{\mathcal{Z}}{\sqrt{\mathcal{R}}}\right)-i{a}_5\left(\sqrt{\mathcal{S}}+i(x-t\delta )\sqrt{\mathcal{R}}\right)sinh\left(\frac{\mathcal{Z}}{\sqrt{\mathcal{R}}}\right)\right)}^2}{{\left[(1+a_7{e}^{a_2}+a_2{e}^{2a_2})\sqrt{\mathcal{R}}+a_5{e}^{a_2}\left(-i\sqrt{\mathcal{S}}+(x-t\delta )\sqrt{\mathcal{R}}\right)cosh\left(\frac{\mathcal{Z}}{\sqrt{\mathcal{R}}}\right)\right]}^2}}\end{array}$$

(39)

where

$$\begin{array}{cc}\hfill \mathcal{R}& =\alpha \kappa (-2+\beta \kappa )-\delta {(-1+\beta \kappa )}^2,\hfill \\ \hfill \mathcal{S}& =2\alpha \beta -2\delta \left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right),\hfill \\ \hfill \mathcal{X}& =a_5(x-t\delta ),\mathcal{Y}=i{a}_5\sqrt{\mathcal{S}},\mathcal{Z}=\mathcal{X}-\mathcal{Y}.\hfill \end{array}$$

Case 2:

$$\begin{array}{cc}\hfill a_5& =-\left({\displaystyle \frac{\mathrm{i}{a}_6\sqrt{\delta +2\alpha \kappa -2\beta \delta \kappa -\alpha \beta {\kappa }^2+{\beta }^2\delta {\kappa }^2}}{\sqrt{-2\alpha \beta +2{\beta }^2\delta -8\varpi \alpha \beta \gamma \delta +8\varpi {\beta }^2\gamma \delta }}}\right),\hfill \\ \hfill a_4& =0,a_3=0,a_1=0.\hfill \end{array}$$

(40)

Inserting Equation (40) in Equation (34),

$$\begin{array}{cc}\hfill f=& a_7+e^{-a_2}+a_2{e}^{a_2}\hfill \\ \hfill & +\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6\sqrt{\delta +2\alpha \kappa -2\beta \delta \kappa -\alpha \beta {\kappa }^2+{\beta }^2\delta {\kappa }^2}\xi }{\sqrt{-2\alpha \beta +2{\beta }^2\delta -8\varpi \alpha \beta \gamma \delta +8\varpi {\beta }^2\gamma \delta }}}\right)\hfill \\ \hfill & \times cosh\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6\sqrt{\delta +2\alpha \kappa -2\beta \delta \kappa -\alpha \beta {\kappa }^2+{\beta }^2\delta {\kappa }^2}\xi }{\sqrt{-2\alpha \beta +2{\beta }^2\delta -8\varpi \alpha \beta \gamma \delta +8\varpi {\beta }^2\gamma \delta }}}\right)\hfill \end{array}$$

(41)

Substituting Equation (41) in Equation (8), we obtain the following expression.

$$\begin{array}{c}\hfill V={\displaystyle \frac{a_{6}R\left[2\mathrm{i}Gcosh\left(H\right)+a_6\left(2\mathrm{i}G+\sqrt{2}R\xi \right)sinh\left(H\right)\right]}{\sqrt{2}\left(\alpha \beta -\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta \right)\left[a_7+{\mathrm{e}}^{-a_2}+a_2{\mathrm{e}}^{a_2}+Hcosh\left(H\right)\right]}}\end{array}$$

(42)

where

$$\begin{array}{cc}\hfill R& =\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(-1+\beta \kappa )}^2}\hfill \\ \hfill G& =\sqrt{-\alpha \beta +\left({\beta }^2-4\varpi \alpha \beta \gamma +4\varpi {\beta }^2\gamma \right)\delta }\hfill \\ \hfill H& =a_6-{\displaystyle \frac{\mathrm{i}{a}_{6}R\xi }{\sqrt{-2\alpha \beta +2\left({\beta }^2-4\varpi \alpha \beta \gamma +4\varpi {\beta }^2\gamma \right)\delta }}}\hfill \end{array}$$

In order to obtain the periodic cross-kink wave solution to Equation (1), Equation (42) is substituted into Equation (2).

$$\begin{array}{c}\hfill P={\displaystyle \frac{a_6{e}^{-x\iota \kappa +t\iota \omega }\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(-1+\beta \kappa )}^2}\left[2\mathrm{i}\sqrt{\mathrm{\Lambda }}cosh\left(a_6-\frac{\mathrm{i}{a}_6(x-t\delta )M}{S}\right)+a_6\left(2\mathrm{i}\sqrt{\mathrm{\Lambda }}+\sqrt{2}(x-t\delta )M\right)sinh\left(a_6-\frac{\mathrm{i}{a}_6(x-t\delta )M}{S}\right)\right]}{\sqrt{2}·D\left[a_7+e^{-a_2}+a_2{e}^{a_2}+\left(a_6-\frac{\mathrm{i}{a}_6(x-t\delta )M}{S}\right)cosh\left(a_6-\frac{\mathrm{i}{a}_6(x-t\delta )M}{S}\right)\right]}}\end{array}$$

(43)

where

$$\begin{array}{cc}\hfill M& =\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(-1+\beta \kappa )}^2}\hfill \\ \hfill S& =\sqrt{-2\alpha \beta +2(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma ))\delta }\hfill \\ \hfill \mathrm{\Lambda }& =-\alpha \beta +(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma ))\delta \hfill \\ \hfill D& =\alpha \beta -(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma ))\delta \hfill \end{array}$$

$\mu$ can be calculated by substituting Equation (43) in Equation (16).

$$\begin{array}{cc}\hfill \mu =& a_6^2{e}^{-2x\mathrm{i}\kappa +2t\mathrm{i}\omega }\varpi (\alpha -\beta \delta )\left(\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2\right)\hfill \\ \hfill & \times \{2\mathrm{i}\sqrt{-\alpha \beta +\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }cosh\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6(x-t\delta )\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2}}{\sqrt{-2\alpha \beta +2\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }}}\right)\hfill \\ \hfill & +a_6\left(2\mathrm{i}\sqrt{-\alpha \beta +\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }+\sqrt{2}(x-t\delta )\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2}\right)\hfill \\ \hfill & \times sinh\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6(x-t\delta )\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2}}{\sqrt{-2\alpha \beta +2\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }}}\right){\}}^2\hfill \\ \hfill & /[{\left(\alpha \beta -\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta \right)}^2\hfill \\ \hfill & \times (a_7+e^{-a_2}+a_2{e}^{a_2}\hfill \\ \hfill & +\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6(x-t\delta )\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2}}{\sqrt{-2\alpha \beta +2\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }}}\right)\hfill \\ \hfill & \times {cosh}^2\left(a_6-{\displaystyle \frac{\mathrm{i}{a}_6(x-t\delta )\sqrt{\alpha \kappa (2-\beta \kappa )+\delta {(1-\beta \kappa )}^2}}{\sqrt{-2\alpha \beta +2\left(-4\varpi \alpha \beta \gamma +{\beta }^2(1+4\varpi \gamma )\right)\delta }}}\right)\left)\right].\hfill \end{array}$$

(44)

6. Graphical Analysis

The findings of the present study on the Akbota equation carry significant physical implications. The derived soliton solutions describe nonlinear wave structures that maintain their shape during propagation—an essential characteristic for understanding the dynamics of optical solitons in telecommunication systems. Moreover, the M-shaped rational solution, periodic cross-kink wave solution, and periodic cross-rational solution—analytical methods commonly utilized in the study of physical systems—provide new perspectives on the intricate dynamics of nonlinear phenomena.

To highlight the physical relevance of the model, we presented a comprehensive set of visualizations, including contour plots, as well as two-dimensional and three-dimensional graphical representations of the obtained results. These visualizations are meticulously generated using Mathematica, with careful selection of parameter values to ensure clarity and interpretability. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 illustrate the effectiveness of the proposed techniques and provide a compelling depiction of the underlying dynamics, thereby enhancing our understanding of the modeled nonlinear processes.

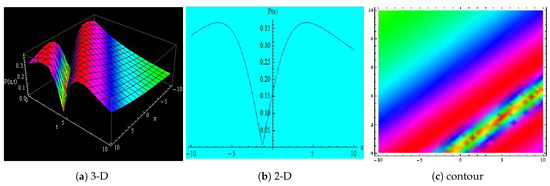
Figure 1. Depicts the 3-D, 2-D and contour representation of Equation (15) for $b_1$ = 0.002, $b_3$ = 0.04, $\delta$ = 2.5, $\omega$ = 0.07, $\kappa$ = 0.09, $b_4$ = 0.05, $b_5$ = 0.05, x = −10 to 10 and t = 0 to 10.

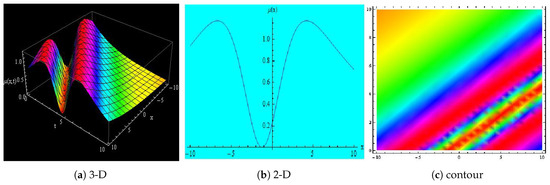
Figure 2. Depicts the 3-D, 2-D and contour representation of Equation (17) for $b_1=0.002$, $b_3=0.04$, $\delta =2.5$, $\omega =0.07$, $\kappa =0.09$, $b_4=0.05$, $b_5=0.05$, $\varpi =1$, $\alpha =5$, $\beta =0.07$, x = −10 to 10 and t = 0 to 10.

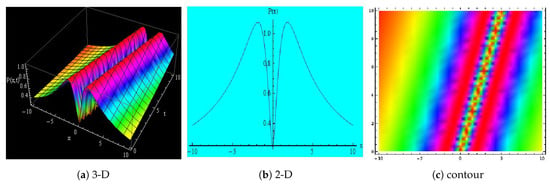
Figure 3. Depicts the 3-D, 2-D and contour representations of Equation (21) for $b_1=0.02$, $b_3=0.24$, $\delta =0.5$, $\omega =0.06$, $\kappa =0.08$, $b_2=0.05$, $b_5=0.2$, x = −10 to 10 and t = 0 to 10.

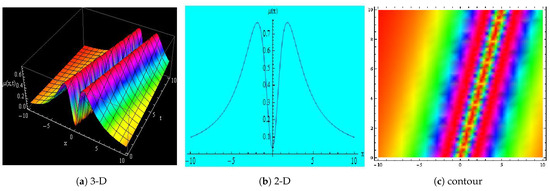
Figure 4. Depicts the 3-D, 2-D and contour representations of Equation (22) for $b_1=0.02$, $b_2=0.05$, $b_3=0.24$, $b_5=0.2$, $\delta =0.5$, $\omega =0.06$, $\kappa =0.08$, $\varpi =1$, $\alpha =0.9$, $\beta =0.7$, x = −10 to 10 and t = 0 to 10.

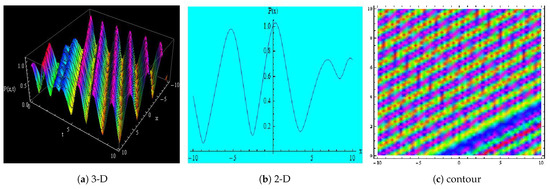
Figure 5. Depicts the 3-D, 2-D and contour representations of Equation (27) for $z_1=0.1$, $a_1=0.5$, $a_2=0.09$, $a_4=0.04$, $\delta =3.5$, $\kappa =0.9$, $z_2=0.03$, $z_5=0.4$,$\omega =0.7$, $x=-10$ to 10 and $t=0$ to 10.

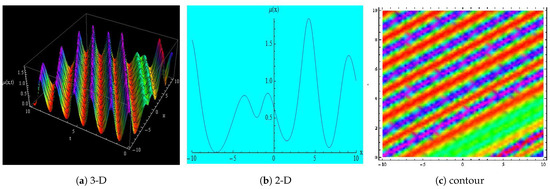
Figure 6. Depicts the 3-D, 2-D and contour representation of Equation (28) for $z_1=0.1$, $z_2=0.03$, $z_5=0.4$, $a_1=0.5$, $a_2=0.09$, $a_4=0.04$, $\delta =3.5$, $\kappa =0.9$, $\omega =0.7$, $\alpha =0.03$, $\beta =0.08$, $\varpi =1$, x = −10 to 10 and t = 0 to 10.

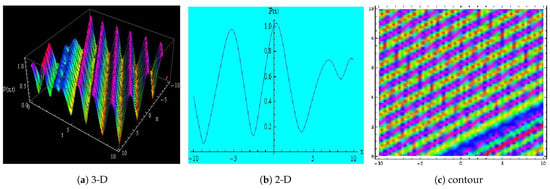
Figure 7. Depicts the 3-D, 2-D and contour representations of Equation (32) for $z_1=0.1$, $a_1=0.6$, $a_2=0.9$, $a_4=0.6$, $\delta =0.9$, $z_2=0.03$, $z_4=0.03$, $z_5=0.4$, $\omega =0.07$, $\alpha =0.3$, $\beta =0.04$, x = −10 to 10 and t = 0 to 10.

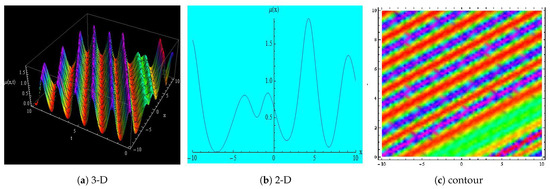
Figure 8. Depicts the 3-D, 2-D and contour representations of Equation (33) for $z_1=0.1$; $a_1=0.6$; $a_2=0.9$; $a_4=0.6$; $\delta =0.9$; $\iota =\sqrt{-1}$; $z_2=0.03$; $z_4=0.03$; $z_5=0.4$; $\omega =0.07$; $\alpha =0.3$; $\beta =0.04$; $\varpi =1$, x = −10 to 10 and t = 0 to 10.

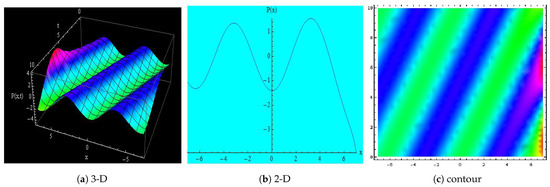
Figure 9. Depicts the 3-D, 2-D and contour representations of Equation (38) for $a_5=0.6$, $\delta =0.02$, $\kappa =0.99$, $\omega =0.6$, $\alpha =1$, $\beta =2$, $\gamma =0.3$, $\varpi =1$, $a_2=0.8$, $a_7=0.7$, x = −6 to 6 and t = 0 to 10.

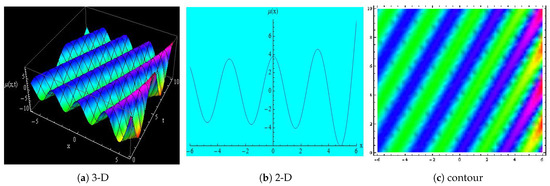
Figure 10. Depicts the 3-D, 2-D and contour representations of Equation (39) for $a_5=0.6$, $\delta =0.02$, $\kappa =0.99$, $\omega =0.6$, $\alpha =1$, $\beta =2$, $\gamma =0.3$, $\varpi =1$, $a_2=0.8$, $a_7=0.7$, x = −5 to 5 and t = 0 to 10.

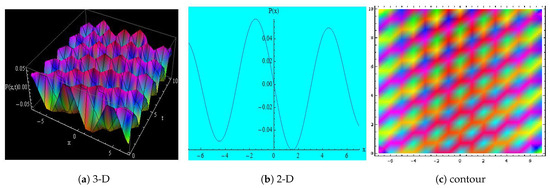
Figure 11. Depicts the 3-D, 2-D and contour representation of Equation (43) for $a_6=0.3$, $\delta =0.04$, $\kappa =0.98$, $\omega =2.9$, $\alpha =0.99$, $\beta =2.5$, $\gamma =0.32$, $\varpi =1$, $a_2=0.88$, $a_7=0.6$, x = −6 to 6 and t = 0 to 10.

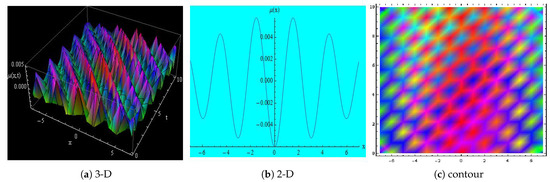
Figure 12. Depicts the 3-D, 2-D and contour representations of Equation (44) for $a_6=0.3$, $\delta =0.04$, $\kappa =0.98$, $\omega =2.9$, $\alpha =0.99$, $\beta =2.5$, $\gamma =0.32$, $\varpi =1$, $a_2=0.88$, $a_7=0.6$, x = −6 to 6 and t = 0 to 10.

The analytical solutions derived in this work are complex-valued. In physical applications such as nonlinear optics and wave propagation, the modulus $\left|u\right(x,t\left)\right|$ corresponds to the observable field intensity. Therefore, throughout the manuscript we plot the modulus of the complex solutions for clarity and physical relevance. The graphical results vividly demonstrate how variations in key parameters influence soliton amplitude, width, and phase, revealing transitions between localized and periodic wave patterns. The 3-D surface plots, in particular, capture the evolution and interaction of wave peaks, confirming the equation’s stability characteristics and integrable nature. The contour maps further highlight the symmetry and periodic modulation patterns associated with the cross-rational and cross-kink solutions, providing deeper insight into the role of symmetry-breaking effects in soliton propagation. The distinct geometrical structures observed in the plots reflect the sensitivity of the system to parameter changes, emphasizing the physical realism of the obtained solutions. Overall, the graphical exploration not only validates the analytical findings but also bridges the theoretical model with observable physical behaviors relevant to optical, magnetic, and fluid systems.

7. Conclusions

The main results of our work presented here are M-shaped rational solutions, periodic cross-rational solutions, and periodic cross-kink wave solutions of the Akbota equation. Furthermore, we provide detailed visual representations of these solutions through three-dimensional, two-dimensional, and contour plots. The analysis reveals that the arbitrary parameters play a key role in governing the propagation characteristics of solitons. The solutions obtained are novel and hold potential for application in areas such as nonlinear optical fibers, differential geometry of surfaces, and the geometric study of curves. Moreover, the methodology employed enables the derivation of a diverse range of exact solutions.

The results underscore the potential for manipulating wave propagation in nonlinear media. Specifically, periodic soliton solutions, which exhibit recurring wave structures, are particularly relevant for systems with periodic boundary conditions. M-shaped rational solutions, on the other hand, are effective in capturing sharp, localized phenomena within nonlinear systems. These solutions represent different aspects of localized wave dynamics: M-shaped rational solutions describe sharply peaked, isolated structures, while periodic solutions characterize oscillatory, spatially localized behavior. Both types of solutions contribute significantly to the modeling of complex physical phenomena such as energy localization and nonlinear wave interactions.

All analytical results have been verified using Mathematica, ensuring the reliability and accuracy of the derived solutions. These findings are expected to facilitate further investigations into the dynamics of the Akbota equation and related nonlinear models. A detailed stability analysis of the obtained M-shaped rational solution is an important direction for future research and will be pursued in our upcoming work.