Symmetric Discrete Distributions on the Integer Line: A Versatile Family and Applications

Abstract

We introduce the Symmetric-$\mathbb{Z}$ (Sy-$\mathbb{Z}$) family, a unified class of symmetric discrete distributions on the integers obtained by multiplying a three-point symmetric sign variable by an independent non-negative integer-valued magnitude. This sign-magnitude construction yields interpretable, zero-centered models with tunable mass at zero and dispersion balanced across signs, making them suitable for outcomes, such as differences of counts or discretized return increments. We derive general distributional properties, including closed-form expressions for the probability mass and cumulative distribution functions, bilateral generating functions, and even moments, and show that the tail behavior is inherited from the magnitude component. A characterization by symmetry and sign–magnitude independence is established and a distinctive operational feature is proved: for independent members of the family, the sum and the difference have the same distribution. As a central example, we study the symmetric Poisson model, providing measures of skewness, kurtosis, and entropy, together with estimation via the method of moments and maximum likelihood. Simulation studies assess finite-sample performance of the estimators, and applications to datasets from finance and education show improved goodness-of-fit relative to established integer-valued competitors. Overall, the Sy-$\mathbb{Z}$ framework offers a mathematically tractable and interpretable basis for modeling symmetric integer-valued outcomes across diverse domains.

1. Introduction

Many discrete datasets encountered in practice take values on the non-negative integers that are routinely modeled using standard families, such as the Poisson or geometric distributions. In contrast, there are important situations where the natural support is the whole set of integers $\mathbb{Z}$, most notably when observations are signed differences of counts or other zero-centered measurements. Canonical examples include score differences in sports, day-to-day changes in transaction counts or sales, inter-rater differences in clinical tallies, and discretized (symmetric) return increments in finance. For such problems, modeling directly on $\mathbb{Z}$ with distributions that respect symmetry around zero is both natural and desirable.

Several integer-valued distributions on $\mathbb{Z}$ have been proposed. Prominent instances include the Skellam distribution [1], obtained as the difference of two independent Poisson variables; the discrete Laplace distribution [2], along with related skew/asymmetric variants [3,4]; the discrete normal distribution [5]; and, recently, perturbed Laplace–type models [6]. Applications of signed count differences appear in medical and reliability studies [7,8] and in sports analytics, such as goal differences [9]. For general background on count modeling and discrete distributions, see refs. [10,11]. In addition, substantial probability mass at zero frequently arises in practice, creating links with the zero-inflated literature [12].

Beyond these classical constructions, there has been a notable increase in recent work on flexible integer-valued distributions supported on $\mathbb{Z}$, including several models explicitly designed to capture symmetry and tunable dispersion. For example, ref. [13] introduced the discrete skew logistic distribution, which can accommodate symmetric and asymmetric count data and provides a useful reference for tail-shape control. Two recent contributions by refs. [14,15] developed new symmetric and perturbation-based distributions on the integers, with applications to stock exchange and hydrological data. In parallel, ref. [6] proposed a general perturbation of the discrete Laplace distribution, demonstrating improvements in financial and health datasets. More broadly, ref. [16] reviewed Skellam-type models and related integer-supported families, while ref. [17] provided an up-to-date survey on models for integer-valued data, highlighting the importance of distributions supported on $\mathbb{Z}$ in modern applications. These recent works underscore the need for simple, interpretable, and analytically tractable symmetric models on $\mathbb{Z}$, a gap that the present Sy-$\mathbb{Z}$ family aims to fill. These recent developments further motivate the need for a symmetric decomposition-based model with explicit identifiability and analytical tractability, such as the Sy-$\mathbb{Z}$ and Sy-$\mathcal{P}$ formulations proposed in this work.

This paper introduces a unified and tractable framework for symmetric integer-valued data on $\mathbb{Z}$, named the Sy-$\mathbb{Z}$ family. The construction separates a three-point symmetric sign component from a non-negative magnitude: a data-generating sign takes values in $\{-1,0,1\}$ with a tunable mass at zero and is multiplied by an independent, non-negative integer-valued variable. This sign–magnitude representation yields zero-centered, exactly symmetric models with interpretable control of the atom at zero while allowing the analyst to inherit tail behavior, dispersion, and computational convenience from the chosen baseline magnitude distribution.

We develop a coherent set of distributional results for the family: closed-form probability mass functions and cumulative distribution functions, bilateral probability generating functions, and moment identities. Symmetry implies vanishing odd moments, whereas even moments factor through the baseline magnitude. We also establish a characterization by symmetry and independence: an integer-valued distribution belongs to the proposed family if and only if it is symmetric and its sign is independent of the magnitude with a three-point symmetric distribution. Beyond these foundations, we study general consequences of the product structure, including tail transfer from the magnitude, conditions for unimodality or bimodality, and simple obstructions to infinite divisibility.

A distinctive feature of this framework is a strong symmetry property for operations on independent variables, where for two independent members of the family, the sum and the difference have the same distribution. This identity is a direct consequence of the bilateral generating function symmetry and does not generally hold for standard two-sided competitors, such as Skellam [1], discrete Laplace [2], perturbed Laplace [6], or extended Poisson models [18].

As a central example, we particularize the family with a Poisson magnitude, thereby obtaining the symmetric Poisson model. We derive distributional formulas (including entropy), discuss the induced zero mass in relation to zero-inflated counts [12], and develop estimation via the method of moments and maximum likelihood. Simulation studies assess finite-sample behavior, and applications to datasets from finance and education illustrate a competitive or improved fit relative to established alternatives supported on $\mathbb{Z}$.

The remainder of the paper is organized as follows. Section 2 introduces the Sy-$\mathbb{Z}$ family, detailing the construction from a symmetric modified Bernoulli sign and an independent non-negative magnitude. Section 3 develops core distributional results for the family, including closed-form probability mass function (PMF) and cumulative distribution function (CDF) identities, bilateral generating functions, characterization by symmetry and sign–magnitude independence, tail transfer from the magnitude, modality conditions, criteria precluding infinite divisibility, the quantile function, and the median, as well as a discussion of first-order stochastic dominance for $\left|Z\right|$. Section 4 specializes in the Sy–Poisson model, deriving the moment generating function (MGF) and probability generating function (PGF), closed-form even moments (via Touchard polynomials), skewness, kurtosis, and Shannon entropy. Section 5 presents inference for Sy–Poisson: method-of-moments estimation (with asymptotic variance via the delta method), likelihood-based estimation, and both observed and expected Fisher information. Section 6 reports a simulation study evaluating the finite-sample bias and mean squared error of the maximum likelihood estimators. Section 7 provides two empirical applications (finance and education) comparing Sy–Poisson with established competitors on $\mathbb{Z}$. A concluding section summarizes implications and outlines directions for future research.

2. The Sy-$\mathbb{Z}$ Family: Construction and Basic Setup

A key building block of the Sy-$\mathbb{Z}$ family is a three-point symmetric distribution on $\{-1,0,1\}$ that combines a random sign with a controllable mass at zero. This distribution will serve as the canonical sign mechanism in our sign–magnitude representation of Z. We refer to it as the symmetric modified Bernoulli distribution.

Definition 1.

Let $\theta \in (0,1/2)$. A discrete random variable X is said to follow the symmetric modified Bernoulli distribution with parameter θ, denoted $\mathrm{SMB}\left(\theta \right)$, if its PMF is

$$\begin{array}{c}\hfill \mathbb{P}(X=k)={(1-2\theta )}^{1-\left|k\right|}{\theta }^{\left|k\right|},k\in \{-1,0,1\}.\end{array}$$

(1)

Proposition 1.

Let $V_1\sim \mathrm{Bernoulli}\left(2\theta \right)$ and $V_2\sim \mathrm{Bernoulli}(1/2)$ be independent random variables. Define

$$X=V_1\left(2V_2-1\right).$$

Then $X\sim \mathrm{SMB}\left(\theta \right)$ with support $\{-1,0,1\}$ and $\theta \in (0,1/2)$.

Proof. 

Write $W=2V_2-1$, so $\mathbb{P}(W=1)=\mathbb{P}(W=-1)=1/2$ and $W\perp V_1$, where ⊥ denotes independence between random variables. Then, we obtain

$$\mathbb{P}(X=0)=\mathbb{P}(V_1=0)=1-2\theta ,\mathbb{P}(X=\pm 1)=\mathbb{P}(V_1=1)\mathbb{P}(W=\pm 1)=\left(2\theta \right){\displaystyle \frac{1}{2}}=\theta ,$$

which matches the symmetric modified Bernoulli distribution with parameter $\theta$.    □

To facilitate simulation and highlight the structural symmetry of $\mathrm{SMB}\left(\theta \right)$, we present it in Appendix A two equivalent stochastic constructions for generating $X\sim \mathrm{SMB}\left(\theta \right)$. These representations are convenient for both algorithmic sampling and concise derivations of basic properties.

2.1. Stochastic Representation

Definition 2.

Let $X\sim \mathrm{SMB}\left(\theta \right)$ be as defined in Definition 1, and let Y be a discrete random variable with support ${\mathbb{N}}_0$. Assume X and Y are independent. We say that a discrete random variable Z belongs to the Sy-$\mathbb{Z}$ family if it admits the stochastic representation

$$Z\stackrel{d}{=}XY.$$

(2)

Proposition 2.

Let $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$, let Y be an independent ${\mathbb{N}}_0$-valued random variable, and set $Z=XY$. Then:

(i) 

Moments of X. For every odd integer r, $\mathbb{E}\left(X^r\right)=0$. For every even integer $q\ge 2$, $\mathbb{E}\left(X^q\right)=2\theta$. In particular, $\mathbb{E}\left(X\right)=0$, $\mathrm{Var}\left(X\right)=2\theta$, and $\sqrt{\mathrm{Var}\left(X\right)}=\sqrt{2\theta }$.

(ii) 

Moments of $Z=XY$. If $\mathbb{E}\left(Y^{2m}\right)<\infty$, then for all $m\ge 0$, $\mathbb{E}\left(Z^{2m+1}\right)=0$, and for all $m\ge 1$,

$$\mathbb{E}\left(Z^{2m}\right)=\mathbb{E}\left(X^{2m}\right)\mathbb{E}\left(Y^{2m}\right)=2\theta \mathbb{E}\left(Y^{2m}\right).$$

In particular, $\mathbb{E}\left(Z\right)=0$ and $\mathrm{Var}\left(Z\right)=\mathbb{E}\left(Z^2\right)=2\theta \mathbb{E}\left(Y^2\right)$.

Proof. 

For $X\sim \mathrm{SMB}\left(\theta \right)$, $\mathbb{P}(X=0)=1-2\theta$, and $\mathbb{P}(X=\pm 1)=\theta$. Hence $\mathbb{E}\left(X^r\right)=\theta (1^r+{(-1)}^r)$ for $r\ge 1$, which is 0 for odd r and $2\theta$ for even r; the variance follows since $\mathbb{E}\left(X\right)=0$ and $\mathbb{E}\left(X^2\right)=2\theta$. For $Z=XY$ with $X\perp Y$, we have $\mathbb{E}\left(Z^k\right)=\mathbb{E}\left(X^k\right)\mathbb{E}\left(Y^k\right)$ whenever the moments exist; the claims for odd and even powers follow by substituting the moments of X obtained above.    □

2.2. Characterization by Symmetry and Independence

We show that the Sy-$\mathbb{Z}$ family is exactly the class of symmetric integer-valued distributions for which the sign is independent of the magnitude and is represented by the symmetric modified Bernoulli distribution.

Theorem 1.

Let Z be an integer-valued random variable with $\mathbb{P}(Z=0)<1$. The following statements are equivalent:

(i) 

Z belongs to the Sy-$\mathbb{Z}$ family; that is, there exist $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$ and an independent $Y\in {\mathbb{N}}_0$ such that $Z\stackrel{d}{=}XY$.

(ii) 

Z is symmetric about zero, i.e.,  $\mathbb{P}(Z=k)=\mathbb{P}(Z=-k)$ for all $k\in \mathbb{Z}$, and there exist random variables S and W such that $S\sim \mathrm{SMB}\left(\theta \right)$ for some $\theta \in (0,1/2)$, $W\in {\mathbb{N}}_0$, S, and W are independent, and $Z\stackrel{d}{=}SW$.

Proof. 

(i) ⇒ (ii). Suppose $Z\stackrel{d}{=}XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$, $\theta \in (0,1/2)$, and $Y\in {\mathbb{N}}_0$ independent of X. Then Z is symmetric because

$$\mathbb{P}(Z=k)=\mathbb{P}(XY=k)=\mathbb{P}(X=1,Y=k)=\mathbb{P}(X=-1,Y=k)=\mathbb{P}(Z=-k),k>0.$$

Set $S:=X$ and $W:=Y$. By construction, $S\sim \mathrm{SMB}\left(\theta \right)$, $W\in {\mathbb{N}}_0$, $S\perp W$, and $Z\stackrel{d}{=}SW$. Thus (ii) holds. (ii) ⇒ (i). Conversely, suppose (ii) holds. Take $X:=S$ and $Y:=W$. Then $X\sim \mathrm{SMB}\left(\theta \right)$, $Y\in {\mathbb{N}}_0$, and $X\perp Y$, with $Z\stackrel{d}{=}XY$. Hence Z belongs to the Sy-$\mathbb{Z}$ family, so (i) holds.    □

Remark 1.

Theorem 1 establishes that Definition 2 is not merely a constructive scheme but a complete characterization of the class: symmetry, together with sign–magnitude independence and a three-point symmetric sign distribution, is equivalent to membership in Sy-$\mathbb{Z}$. This validates the use of $\mathrm{SMB}\left(\theta \right)$ (Definition 1) as the canonical mechanism for the sign component.

Further analytical properties of the Sy-$\mathbb{Z}$ distribution, including its moment generating function and characteristic function, are provided in Section 3.

3. Main Properties of the Sy-$\mathbb{Z}$ Family Distributions

Proposition 3.

Let $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$ and support $\{-1,0,1\}$, and let $Y\in {\mathbb{N}}_0$ be independent of X. Define $Z=XY$. Then Z belongs to the Sy-$\mathbb{Z}$ family, and its PMF is

$$\mathbb{P}(Z=k)=\left\{\begin{array}{cc}\theta \mathbb{P}(Y=|k\left|\right),\hfill & \mathit{if}k\in \mathbb{Z}\setminus \left\{0\right\},\hfill \\ (1-2\theta )+2\theta \mathbb{P}(Y=0),\hfill & \mathit{if}k=0.\hfill \end{array}\right.$$

(3)

Proof. 

Since X and Y are independent and $Y\ge 0$, consider three cases:

For $k>0$. Then

$$\mathbb{P}(Z=k)=\mathbb{P}(XY=k)=\mathbb{P}(X=1,Y=k)=\mathbb{P}(X=1)\mathbb{P}(Y=k)=\theta \mathbb{P}(Y=k).$$

For $k<0$. Writing $k=-m$ with $m>0$,

$$\mathbb{P}(Z=k)=\mathbb{P}(XY=-m)=\mathbb{P}(X=-1,Y=m)=\mathbb{P}(X=-1)\mathbb{P}(Y=-k)=\theta \mathbb{P}(Y=-k).$$

For $k=0$. The event $\{Z=0\}$ occurs if $X=0$ (regardless of Y) or if $Y=0$ with $X\in \{\pm 1\}$. By independence,

$$\begin{array}{ccc}\hfill \mathbb{P}(Z=0)& =& \mathbb{P}(X=0)+\mathbb{P}(Y=0,X\ne 0)\hfill \\ & =& (1-2\theta )+\mathbb{P}(X\ne 0)\mathbb{P}(Y=0)\hfill \\ & =& (1-2\theta )+2\theta \mathbb{P}(Y=0).\hfill \end{array}$$

Combining the three cases yields the result. Normalization follows since   

$$\begin{array}{ccc}\hfill \sum _{k\in \mathbb{Z}}\mathbb{P}(Z=k)& =& \mathbb{P}(Z=0)+\sum _{k\ge 1}(\mathbb{P}(Z=k)+\mathbb{P}(Z=-k))\hfill \\ & =& (1-2\theta )+2\theta \mathbb{P}(Y=0)+\sum _{k\ge 1}(\theta \mathbb{P}(Y=k)+\theta \mathbb{P}(Y=-k))\hfill \\ & =& (1-2\theta )+2\theta \mathbb{P}(Y=0)+2\theta \sum _{k\ge 1}\mathbb{P}(Y=k)\hfill \\ & =& (1-2\theta )+2\theta \underset{1}{\underbrace{\sum _{k\ge 0}\mathbb{P}(Y=k)}}=1.\hfill \end{array}$$

   □

Corollary 1.

Let Z be an integer-valued random variable and define $W=\left|Z\right|$. Then W has support $\mathbb{N}$, and its PMF is

$$\mathbb{P}(W=k)=\left\{\begin{array}{cc}\mathbb{P}(Z=k)+\mathbb{P}(Z=-k)=2\theta \mathbb{P}(Y=k),\hfill & \mathit{if}k\in \mathbb{N}\setminus \left\{0\right\},\hfill \\ \mathbb{P}(Z=0)=(1-2\theta )+2\theta \mathbb{P}(Y=0),\hfill & \mathit{if}k=0.\hfill \end{array}\right.$$

Moreover, we have

$$\mathbb{E}\left(\left|Z\right|\right)=2\theta \mathbb{E}\left(Y\right)andVar\left(\right|Z\left|\right)=2\theta Var\left(Y\right)+2\theta \left(1-2\theta \right){\left(\mathbb{E}\left(Y\right)\right)}^2.$$

(4)

3.1. Identifiability Within Sy-$\mathbb{Z}$

Let $Z=XY$, where $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$ and $Y\in {\mathbb{N}}_0$ is independent of X. Denote $p_Z\left(k\right)=\mathbb{P}(Z=k)$ and $p_Y\left(k\right)=\mathbb{P}(Y=k)$ for $k\in {\mathbb{N}}_0$. The PMF of Z is

$$p_Z\left(0\right)=(1-2\theta )+2\theta p_Y\left(0\right),p_Z\left(k\right)=\theta p_Y\left(\right|k\left|\right)\mathrm{for}k\ne 0.$$

(5)

Proposition 4.

From the marginal distribution $p_Z(·)$ alone, the pair $(\theta ,p_Y(·))$ is not identifiable in the model class

$$\mathcal{M}=\left\{(\theta ,p_Y(·)):\theta \in (0,1/2),p_Y(·)aPMFon{\mathbb{N}}_0\right\}.$$

More precisely, for any fixed $p_Z(·)$, there exist infinitely many pairs $(\theta ,p_Y(·))\in \mathcal{M}$ satisfying (5).

Proof. 

Fix $p_Z(·)$. From (5) and the constraint $0<\theta <1/2$, we have for $k\ge 1$

$$\theta p_Y\left(k\right)=p_Z\left(k\right).$$

Thus, whenever $\theta$ is chosen, the off-zero masses of Y must satisfy $p_Y\left(k\right)=p_Z\left(k\right)/\theta$ for $k\ge 1$. Using normalization,

$$1=\sum _{k\ge 0}{p}_Y\left(k\right)=p_Y\left(0\right)+\sum _{k\ge 1}{\displaystyle \frac{p_Z\left(k\right)}{\theta }}=p_Y\left(0\right)+{\displaystyle \frac{1-p_Z\left(0\right)}{\theta }},$$

which yields

$$p_Y\left(0\right)=1-{\displaystyle \frac{1-p_Z\left(0\right)}{\theta }}.$$

(6)

On the other hand, the zero-mass identity in (5) gives

$$p_Z\left(0\right)=(1-2\theta )+2\theta p_Y\left(0\right)=(1-2\theta )+2\theta \left(1-{\displaystyle \frac{1-p_Z\left(0\right)}{\theta }}\right)=p_Z\left(0\right),$$

so (6) is consistent for any $\theta$ that makes $p_Y\left(0\right)\in [0,1]$ and $p_Y\left(k\right)\ge 0$ for $k\ge 1$. For all such $\theta$, we obtain a valid PMF $p_Y(·)$ producing the same $p_Z(·)$. Hence, the mapping $(\theta ,p_Y(·))\mapsto p_Z(·)$ is not one-to-one on $\mathcal{M}$, proving non-identifiability.    □

Proposition 5.

Suppose Y belongs to a parametric family $\{p_Y(·;\lambda ):\lambda \in \Lambda \}$ with $p_Y(0;\lambda )$ known as a function of λ, and such that for every λ, the map $k\mapsto p_Y(k;\lambda )$ is injective in λ on a set of indices with nonzero $p_Y(·;\lambda )$. Then the parameter pair $(\theta ,\lambda )$ is identifiable from $p_Z(·)$.

Proof. 

From (5), for any $k\ge 1$,

$$p_Z\left(k\right)=\theta p_Y(k;\lambda ).$$

If $({\theta }_1,{\lambda }_1)$ and $({\theta }_2,{\lambda }_2)$ produce the same $p_Z$, then $p_Z\left(k\right)$ agrees for all $k\ge 1$, and hence

$${\theta }_1{p}_Y(k;{\lambda }_1)={\theta }_2{p}_Y(k;{\lambda }_2)\mathrm{for}\mathrm{all}k\ge 1.$$

If ${\lambda }_1\ne {\lambda }_2$, the injectivity of $k\mapsto p_Y(k;\lambda )$ in $\lambda$ implies that the ratio $p_Y(k;{\lambda }_1)/p_Y(k;{\lambda }_2)$ cannot be constant in k on any set of indices with positive mass; thus, the equality above cannot hold for all $k\ge 1$ unless ${\lambda }_1={\lambda }_2$. Therefore ${\lambda }_1={\lambda }_2$, and then ${\theta }_1={\theta }_2$ follows from any single $k\ge 1$. Finally, $p_Z\left(0\right)=(1-2\theta )+2\theta p_Y(0;\lambda )$ is automatically satisfied, so $(\theta ,\lambda )$ is identifiable.    □

Corollary 2.

(i) 

If $Y\sim \mathrm{Poisson}\left(\lambda \right)$, then $(\theta ,\lambda )$ is identifiable.

(ii) 

If $Y\sim \mathrm{Geometric}\left(q\right)$, then $(\theta ,q)$ is identifiable.

Proof. 

For Poisson, $p_Y(k;\lambda )=e^{-\lambda }{\lambda }^k/k!$ and $p_Y(0;\lambda )=e^{-\lambda }$; distinct $\lambda$ produce non-proportional sequences ${\left\{p_Y(k;\lambda )\right\}}_{k\ge 1}$, so the injectivity condition holds. For geometric distributions with success probabilities q, $p_Y(k;q)={(1-q)}^{k}q$, and $p_Y(0;q)=q$; distinct q once again yield non-proportional sequences on $k\ge 1$. Proposition 5 applies in both cases.    □

Corollary 3.

If θ is known (such as from external calibration), then $p_Y(·)$ is recovered from $p_Z(·)(·)$ via

$$p_Y\left(0\right)={\displaystyle \frac{p_Z\left(0\right)-(1-2\theta )}{2\theta }},p_Y\left(k\right)={\displaystyle \frac{p_Z\left(k\right)}{\theta }}\mathrm{for}k\ge 1,$$

(7)

and this defines a valid PMF provided $p_Z(·)$ arises from a Sy-$\mathbb{Z}$ model with the given θ.

Proof. 

Equations (7) are a direct rearrangement of (5). Nonnegativity and normalization follow from the fact that $p_Z(·)$ is generated by the Sy-$\mathbb{Z}$ structure with $\theta$.    □

Proposition 4 clarifies that, without additional structure on the magnitude Y, the sign parameter $\theta$, and the zero mass $p_Y\left(0\right)$ are confounded through $p_Z\left(0\right)=(1-2\theta )+2\theta p_Y\left(0\right)$, while only the products $\theta p_Y\left(k\right)$ and $k\ge 1$ are determined by ${\left\{p_Z\left(k\right)\right\}}_{k\ne 0}$. Imposing a parametric family for Y restores identifiability (Proposition 5), as illustrated by Sy-Poisson and Sy-Geometric (Corollary 2). When $\theta$ is externally known, $p_Y$ is uniquely reconstructed from $p_Z$ (Corollary 3).

3.2. Tail Behaviour

Proposition 6.

Under the assumptions of Proposition 3, for all $k\ge 0$,

$$\mathbb{P}\left(\right|Z|>k)=2\theta \mathbb{P}(Y>k).$$

Consequently, $\left|Z\right|$ is tail-equivalent to Y up to factor $2\theta$: if $\mathbb{P}(Y>k)\sim cg\left(k\right)$ as $k\to \infty$ for some reference function g, then $\mathbb{P}\left(\right|Z|>k)\sim \left(2\theta c\right)g\left(k\right)$.

Proof. 

By (3), for $k\ge 0$,

$$\mathbb{P}\left(\right|Z|>k)=\sum _{j>k}\left[\mathbb{P}(Z=j)+\mathbb{P}(Z=-j)\right]=\sum _{j>k}2\theta \mathbb{P}(Y=j)=2\theta \mathbb{P}(Y>k).$$

The asymptotic equivalence follows immediately.    □

Remark 2.

If Y has exponential (light) tails (for example, Poisson, binomial, geometric), then so does $\left|Z\right|$; if Y has regularly varying (power-distribution) tails, then so does $\left|Z\right|$ with the same index. The parameter θ scales tail probabilities but does not change their rate.

3.3. Unimodality and Number of Modes

Proposition 7.

Let $Z=XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$, $\theta \in (0,1/2)$, and $Y\in {\mathbb{N}}_0$ be independent. Define the off-zero mode of Y by

$$m_{+}\in arg\underset{k\ge 1}{max}\mathbb{P}(Y=k)(\mathit{choose}\mathit{the}\mathit{smallest}\mathit{such}\mathit{index}).$$

Then:

(i) 

For $k\ge 1$, $\mathbb{P}(Z=k)=\mathbb{P}(Z=-k)=\theta \mathbb{P}(Y=k)$. Hence, the positive (and negative) sides of Z are proportional copies of the PMF of Y restricted to $\{1,2,\dots \}$, and $m_{+}$ is the (unique smallest) mode on the positive side of Z as well as the mode of $\left|Z\right|$ on $\{1,2,\dots \}$.

(ii) 

The global modes of Z are determined by comparing the mass at zero with the peak on the positive side:

$$\left\{\begin{array}{cc}\mathit{single}\mathit{mode}\mathit{at}0\hfill & \mathit{if}\mathbb{P}(Z=0)>\theta \mathbb{P}(Y=m_{+}),\hfill \\ \mathit{three}\mathit{modes}\mathit{at}0,\pm m_{+}\hfill & \mathit{if}\mathbb{P}(Z=0)=\theta \mathbb{P}(Y=m_{+}),\hfill \\ \mathit{two}\mathit{symmetric}\mathit{modes}\mathit{at}\pm m_{+}\hfill & \mathit{if}\mathbb{P}(Z=0)<\theta \mathbb{P}(Y=m_{+}).\hfill \end{array}\right.$$

In particular, using $\mathbb{P}(Z=0)=(1-2\theta )+2\theta \mathbb{P}(Y=0)$,

$$(1-2\theta )+2\theta \mathbb{P}(Y=0)\ge \theta \underset{k\ge 1}{max}\mathbb{P}(Y=k)⟹Z\mathit{is}\mathit{unimodal}\mathit{at}0.$$

Proof. 

Part (i) is immediate from the Sy-$\mathbb{Z}$ PMF: for $k\ge 1$, $\mathbb{P}(Z=\pm k)=\theta \mathbb{P}(Y=k)$, so the positive and negative sides inherit the shape of Y on $\{1,2,\dots \}$. For (ii), because both sides are scaled copies of ${\left\{\mathbb{P}(Y=k)\right\}}_{k\ge 1}$, the only competitors for the global maximum are $k=0$ and $k=\pm m_{+}$. Comparing $\mathbb{P}(Z=0)$ with $\theta \mathbb{P}(Y,m_{+})$ yields three cases.    □

Corollary 4.

If Y is unimodal with a mode at $m=0$ (such as, geometric or binomial with $p\ge 1/2$), then Z is unimodal at 0 for all $\theta \in (0,1/2)$. More generally, if Y is log-concave on ${\mathbb{N}}_0$, then Z is either unimodal at 0 or bimodal at $\pm m_{+}$, depending on the inequality in Proposition 7 (ii); no additional modes can appear.

3.4. Cumulative Distribution Function

Proposition 8.

Let $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$, $Y\in {\mathbb{N}}_0$ be a random variable with CDF $F_Y(·)$, independent of X and $Z=XY$. The CDF of Z is

$$F_Z\left(k\right)=\left\{\begin{array}{cc}\theta \left(1-F_Y\left(\right|k|-1)\right),\hfill & \mathit{if}k\le -1,\hfill \\ (1-\theta )+\theta \mathbb{P}(Y=0),\hfill & \mathit{if}k=0,\hfill \\ (1-\theta )+\theta F_Y\left(k\right),\hfill & \mathit{if}k\ge 1.\hfill \end{array}\right.$$

Proof. 

From the given PMF, $\mathbb{P}(Z=m)=\theta \mathbb{P}(Y=|m\left|\right)\mathrm{for}m\ne 0,m\in \mathbb{Z}$, and $\mathbb{P}(Z=0)=(1-2\theta )+2\theta \mathbb{P}(Y=0)$.

For $k\le -1$,

$$F_Z\left(k\right)=\sum _{m=-\infty }^k\mathbb{P}(Z=m)=\sum _{j=\left|k\right|}^{\infty }\theta \mathbb{P}(Y=j)=\theta \mathbb{P}(Y\ge |k\left|\right)=\theta \left(1-F_Y\left(\right|k|-1)\right).$$

For $k=0$,

$$\begin{array}{cc}\hfill F_Z\left(0\right)& =\sum _{m\le -1}\mathbb{P}(Z=m)+\mathbb{P}(Z=0)\hfill \\ & =\theta \mathbb{P}(Y\ge 1)+(1-2\theta )+2\theta \mathbb{P}(Y=0)\hfill \\ & =(1-\theta )+\theta \mathbb{P}(Y=0).\hfill \end{array}$$

For $k\ge 1$,

$$\begin{array}{cc}\hfill F_Z\left(k\right)& =\sum _{m\le -1}\mathbb{P}(Z=m)+\mathbb{P}(Z=0)+\sum _{m=1}^k\mathbb{P}(Z=m)\hfill \\ & =(1-\theta )+\theta \mathbb{P}(Y=0)+\theta \sum _{m=1}^k\mathbb{P}(Y=m)\hfill \\ & =(1-\theta )+\theta F_Y\left(k\right).\hfill \end{array}$$

This completes the proof.    □

Corollary 5.

Under the assumptions of Proposition 8, let $S_Z\left(k\right)=\mathbb{P}(Z>k)=1-F_Z\left(k\right)$ denote the survival function of Z. Then

$$S_Z\left(k\right)=\left\{\begin{array}{cc}1-\theta S_Y\left(\right|k|-1),\hfill & \mathit{if}k\le -1,\hfill \\ \theta S_Y\left(k\right),\hfill & \mathit{if}k\ge 0,\hfill \end{array}\right.$$

where $S_Y\left(k\right)=1-F_Y\left(k\right)$ denotes the survival function of Y.

3.5. First-Order Stochastic Dominance

We say that A dominates B in the first-order sense if $F_A\left(z\right)\le F_B\left(z\right)$ holds for all $z\in \mathbb{Z}$. For Sy-$\mathbb{Z}$ distributions $Z=XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$ and $Y\in {\mathbb{N}}_0$ being independent, write

$$T_Y\left(k\right):=\mathbb{P}(Y\ge k),k\in \mathbb{N}.$$

From Proposition 8, for any $k\ge 1$,

$$F_Z(-k)=\theta T_Y\left(k\right),F_Z\left(k\right)=1-\theta T_Y(k+1).$$

(8)

Theorem 2.

Let $Z_i=X_i{Y}_i$ with $X_i\sim \mathrm{SMB}\left({\theta }_i\right)$, $Y_i\in {\mathbb{N}}_0$, and $X_i\perp Y_i$ ($i=1,2$). If $F_{Z_1}\left(z\right)\le F_{Z_2}\left(z\right)$ for all $z\in \mathbb{Z}$, then $F_{Z_1}\left(z\right)=F_{Z_2}\left(z\right)$ for all $z\in \mathbb{Z}$. In particular, strict first-order dominance cannot occur between two distinct members of the Sy-$\mathbb{Z}$ family.

Proof. 

Assume $F_{Z_1}(·)\le F_{Z_2}(·)$ pointwise. For every $k\ge 1$,

$$F_{Z_1}(-k)\le F_{Z_2}(-k)\Rightarrow {\theta }_1{T}_{Y_1}\left(k\right)\le {\theta }_2{T}_{Y_2}\left(k\right),$$

and

$$F_{Z_1}(k-1)\le F_{Z_2}(k-1)\Rightarrow 1-{\theta }_1{T}_{Y_1}\left(k\right)\le 1-{\theta }_2{T}_{Y_2}\left(k\right)\Rightarrow {\theta }_1{T}_{Y_1}\left(k\right)\ge {\theta }_2{T}_{Y_2}\left(k\right).$$

Hence ${\theta }_1{T}_{Y_1}\left(k\right)={\theta }_2{T}_{Y_2}\left(k\right)$ for all $k\ge 1$. Using (8) this yields $F_{Z_1}(·)=F_{Z_2}(·)$ on $\mathbb{Z}$.    □

Remark 3.

Classical first-order dominance is too restrictive on symmetric two-sided supports. A more informative comparison works on magnitudes. Since $\mathbb{P}\left(\right|Z|>k)=2\theta \mathbb{P}(Y>k)$,

$$|Z_1|\mathit{dominates}|Z_2|\mathit{in}\mathit{the}\mathit{first-}\mathit{order}\mathit{sense}⟺{\theta }_1\mathbb{P}(Y_1>k)\le {\theta }_2\mathbb{P}(Y_2>k)\mathit{for}\mathit{all}k\ge 0.$$

This provides a practical dominance notion for dispersion comparisons and for tail–probability assessments based on $\left|Z\right|$.

Remark 4.

Other stochastic orders can still distinguish members of the family. In particular, the convex order and increasing–convex order separate distributions with the same mean (zero by symmetry) but different tail weights. For Sy-$\mathbb{Z}$, many such comparisons reduce to corresponding orders on $\left|Z\right|$ (or on Y) via the product representation; a systematic treatment is left for future work.

3.6. Generating Function

Proposition 9.

Under the assumptions of Proposition 8, let $M_Y\left(t\right)=\mathbb{E}\left(e^{tY}\right)$ denote the MGF of Y, and $G_Y\left(s\right)=\mathbb{E}\left(s^Y\right)$ its PGF. Then, for all t,

$$M_Z\left(t\right)=\mathbb{E}\left(e^{tZ}\right)=(1-2\theta )+\theta (M_Y\left(t\right)+M_Y(-t))=(1-2\theta )+\theta (G_Y\left(e^t\right)+G_Y\left(e^{-t}\right)).$$

(9)

Proof. 

By independence and conditioning on X,

$$\begin{array}{ccc}\hfill M_Z\left(t\right)& =& \mathbb{E}\left(\mathbb{E}(e^{tXY}\mid X)\right)=\mathbb{E}\left(M_Y\left(tX\right)\right)\hfill \\ & =& \mathbb{P}(X=0)M_Y\left(0\right)+\mathbb{P}(X=1)M_Y\left(t\right)+\mathbb{P}(X=-1)M_Y(-t).\hfill \end{array}$$

Since $\mathbb{P}(X=0)=1-2\theta$ and $\mathbb{P}(X=\pm 1)=\theta$, we obtain

$$M_Z\left(t\right)=(1-2\theta )+\theta M_Y\left(t\right)+\theta M_Y(-t),$$

which proves the first identity. The second follows from $M_Y\left(t\right)=G_Y\left(e^t\right)$ for integer $Y\ge 0$. The stated domain requires simultaneous finiteness of $M_Y\left(t\right)$ and $M_Y(-t)$.    □

Corollary 6.

If $M_Y^{″}\left(0\right)<\infty$, then $\mathbb{E}\left(Z\right)=0$ and $\mathrm{Var}\left(Z\right)=2\theta \mathbb{E}\left(Y^2\right)$.

Proof. 

Differentiating at $t=0$: $M_Z^{\prime }\left(0\right)=\theta M_Y^{\prime }\left(0\right)-\theta M_Y^{\prime }(-0)=0$, and $M_Z^{″}\left(0\right)=\theta M_Y^{″}\left(0\right)+\theta M_Y^{″}\left(0\right)=2\theta \mathbb{E}\left(Y^2\right)$.    □

3.7. Quantile Function and Median

Let $p_k=\mathbb{P}(Y=k)$, $p_0=\mathbb{P}(Y=0)$, $F_Y\left(k\right)=\mathbb{P}(Y\le k)$, and $T_Y\left(k\right)=\mathbb{P}(Y\ge k)$ be such that $Y\in {\mathbb{N}}_0$. From Proposition 8, for integers $k\ge 1$,

$$F_Z(-k)=\theta T_Y\left(k\right),F_Z\left(0\right)=1-\theta +\theta p_0,F_Z\left(k\right)=1-\theta +\theta F_Y\left(k\right).$$

Equivalently, for $k\ge 0$,

$$\mathbb{P}\left(\right|Z|>k)=2\theta \mathbb{P}(Y>k),\mathbb{P}\left(\right|Z|\le k)=1-2\theta \mathbb{P}(Y>k).$$

Proposition 10.

Let $Q_Z\left(u\right):=inf\{z\in \mathbb{Z}:F_Z\left(z\right)\ge u\}$ denote the (left-continuous) quantile function. Set

$$a_{-}:=F_Z(-1)=\theta (1-p_0),a_0:=F_Z\left(0\right)=1-\theta +\theta p_0.$$

Then, for $u\in (0,1)$,

$$Q_Z\left(u\right)=\left\{\begin{array}{cc}-k^{-}\left(u\right),\hfill & 0<u\le a_{-},\hfill \\ 0,\hfill & a_{-}<u\le a_0,\hfill \\ k^{+}\left(u\right),\hfill & a_0<u<1,\hfill \end{array}\right.$$

where $k^{-}\left(u\right),k^{+}\left(u\right)\in \{1,2,\dots \}$ are obtained from Y via

$$k^{-}\left(u\right)=min\{k\ge 1:\theta T_Y\left(k\right)\ge u\},k^{+}\left(u\right)=min\{k\ge 1:1-\theta +\theta F_Y\left(k\right)\ge u\}.$$

Proof. 

The direct inversion of the three pieces above, using that $T_Y$ is non-increasing and $F_Y(·)$ is non-decreasing on ${\mathbb{N}}_0$.    □

3.8. Median

Corollary 7.

Every Sy-$\mathbb{Z}$ distribution has 0 as a median. Moreover, if $\theta \in (0,1/2)$, then 0 is the unique median.

Proof. 

Since $F_Z(-1)=\theta (1-p_0)\le \theta <1/2$ and $F_Z\left(0\right)=1-\theta +\theta p_0>1/2$, we have $F_Z(-1)<1/2\le F_Z\left(0\right)$, so 0 is the unique integer m with $F_Z(m-1)\le 1/2\le F_Z\left(m\right)$.    □

3.9. Distribution of Sums and Differences

We now characterize the distribution of sums and differences of independent Sy-$\mathbb{Z}$ variables, showing that they share the same law and admit explicit convolution formulas for their PMFs.

Proposition 11.

Let $Z_i=X_i{Y}_i$, $X_i\sim \mathrm{SMB}\left({\theta }_i\right)$, ${\theta }_i\in (0,1/2)$, and $Y_i\in {\mathbb{N}}_0$ be independent of $X_i$, and $(Z_1,Z_2)$ be independent. Write $p_i\left(k\right)=\mathbb{P}(Y_i=k)$ and $G_{Y_i}\left(s\right)={\sum }_{k\ge 0}{p}_i\left(k\right)s^k$ for the one–sided PGF of $Y_i$. Then, for $k\ge 1$,

$$\mathbb{P}(Z_i=\pm k)={\theta }_i{p}_i\left(k\right),\mathbb{P}(Z_i=0)=(1-2{\theta }_i)+2{\theta }_i{p}_i\left(0\right),$$

the following holds:

(i) 

The bilateral PGF of $Z_i$ is

$$G_{Z_i}\left(s\right)=(1-2{\theta }_i)+{\theta }_i\left(G_{Y_i}\left(s\right)+G_{Y_i}(1/s)\right),s>0,$$

so $G_{Z_i}\left(s\right)=G_{Z_i}(1/s)$ for all $s>0$. Consequently, for the sum $S:=Z_1+Z_2$ and the difference $D:=Z_1-Z_2$,

$$G_S\left(s\right)=G_{Z_1}\left(s\right)G_{Z_2}\left(s\right),G_D\left(s\right)=G_{Z_1}\left(s\right)G_{Z_2}(1/s)=G_{Z_1}\left(s\right)G_{Z_2}\left(s\right)=G_S\left(s\right),$$

and therefore $D\stackrel{d}{=}S$.

(ii) 

Let $S:=Z_1+Z_2$. For $k>0$,

$$\begin{array}{cc}\hfill \mathbb{P}(S=k)=& \underset{Z_1=0,Z_2=k}{\underbrace{\mathbb{P}(Z_1=0){\theta }_2{p}_2\left(k\right)}}+\underset{Z_2=0,Z_1=k}{\underbrace{\mathbb{P}(Z_2=0){\theta }_1{p}_1\left(k\right)}}+\underset{Z_1>0,Z_2>0}{\underbrace{{\theta }_1{\theta }_2\sum _{j=1}^{k-1}{p}_1\left(j\right)p_2(k-j)}}\hfill \\ \hfill & +\underset{Z_1=-u,Z_2=k+u}{\underbrace{{\theta }_1{\theta }_2\sum _{u=1}^{\infty }{p}_1\left(u\right)p_2(k+u)}}+\underset{Z_2=-u,Z_1=k+u}{\underbrace{{\theta }_1{\theta }_2\sum _{u=1}^{\infty }{p}_2\left(u\right)p_1(k+u)}}.\hfill \end{array}$$

(10)

For $k=0$,

$$\mathbb{P}(S=0)=\mathbb{P}(Z_1=0)\mathbb{P}(Z_2=0)+2{\theta }_1{\theta }_2\sum _{u=1}^{\infty }{p}_1\left(u\right)p_2\left(u\right),$$

(11)

and by symmetry $\mathbb{P}(S=-k)=\mathbb{P}(S=k)$ for all $k\ge 1$. By part (i), the same formulas hold for D.

Proof. 

For $Z=XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$ and $Y\in {\mathbb{N}}_0$ independent of X, we have

$$s^Z=\left\{\begin{array}{cc}1,\hfill & X=0,\hfill \\ s^Y,\hfill & X=1,\hfill \\ s^{-Y},\hfill & X=-1,\hfill \end{array}\right.$$

thus, using independence and $\mathbb{P}(X=0)=1-2\theta$, $\mathbb{P}(X=\pm 1)=\theta$,

$$G_Z\left(s\right)=(1-2\theta )+\theta G_Y\left(s\right)+\theta G_Y(1/s),$$

which yields $G_Z\left(s\right)=G_Z(1/s)$ for all $s>0$. For independent $Z_1,Z_2$,

$$G_S\left(s\right)=G_{Z_1}\left(s\right)G_{Z_2}\left(s\right),G_D\left(s\right)=G_{Z_1}\left(s\right)G_{Z_2}(1/s).$$

Since $G_{Z_2}(1/s)=G_{Z_2}\left(s\right)$, we obtain $G_D\left(s\right)=G_S\left(s\right)$, and hence $D\stackrel{d}{=}S$.

On the other hand, let $S=Z_1+Z_2$ and $k>0$. By independence,

$$\mathbb{P}(S=k)=\sum _{z\in \mathbb{Z}}\mathbb{P}(Z_1=z)\mathbb{P}(Z_2=k-z).$$

Splitting the sum into the disjoint cases $z=0$, $z=k$, $z=j\in \{1,\dots ,k-1\}$, $z=-u$, and $z=k+u$ with $u\ge 1$, and using $\mathbb{P}(Z_i=0)$ and $\mathbb{P}(Z_i=\pm m)={\theta }_i{p}_i\left(m\right)$ for $m\ge 1$ yields

$$\begin{array}{cc}\hfill \mathbb{P}(S=k)& =\mathbb{P}(Z_1=0){\theta }_2{p}_2\left(k\right)+\mathbb{P}(Z_2=0){\theta }_1{p}_1\left(k\right)+{\theta }_1{\theta }_2\sum _{j=1}^{k-1}{p}_1\left(j\right)p_2(k-j)\hfill \\ \hfill & +{\theta }_1{\theta }_2\sum _{u\ge 1}{p}_1\left(u\right)p_2(k+u)+{\theta }_1{\theta }_2\sum _{u\ge 1}{p}_2\left(u\right)p_1(k+u),\hfill \end{array}$$

which is (10).

For $k=0$,

$$\mathbb{P}(S=0)=\mathbb{P}(Z_1=0,Z_2=0)+2\sum _{u\ge 1}\mathbb{P}(Z_1=u,Z_2=-u),$$

and substituting the same probabilities gives (11). The symmetry of each $Z_i$ implies $\mathbb{P}(S=-k)=\mathbb{P}(S=k)$ for $k\ge 1$, and by part (i) the same formulas hold for D.    □

Remark 5.

Equations (10) and (11) decompose the mass of the sum S into three types of contributions: first, cases where one addend is zero; second, positive–positive convolution over $\{1,\dots ,k-1\}$; and third, positive–negative cross terms with unbalanced magnitudes (tails). This partition is useful both for theoretical bounds (for example, tail comparisons driven by the $Y_i$) and for stable numerical evaluation. If some $Y_i$ has finite support, the infinite sums truncate automatically. By Proposition 11, the same decomposition applies to the difference D.

4. Special Case: The Sy-Poisson Distribution

In this subsection, we particularize the Sy-$\mathbb{Z}$ family by taking the mixing variable Y to be Poisson. Recall the set-up in Definition 2 (and Proposition 8): $X\sim \mathrm{SMB}\left(\theta \right)$ with $\theta \in (0,1/2)$, $Y\perp X$ takes values in $\mathbb{N}$, and $Z=XY$.

Definition 3.

Let $Y\sim \mathcal{P}\left(\lambda \right)$ with $\lambda >0$ and $X\sim \mathrm{SMB}\left(\theta \right)$, $\theta \in (0,1/2)$, be independent. The random variable $Z=XY$ is said to follow a Sy-Poisson distribution, denoted $Z\sim S\mathit{y-}\mathcal{P}(\theta ,\lambda )$. Its PMF, inherited from the Sy-$\mathbb{Z}$ construction, is

$$\mathbb{P}(Z=k)=\left\{\begin{array}{cc}{\displaystyle \theta e^{-\lambda }\frac{{\lambda }^{\left|k\right|}}{\left|k\right|!},}\hfill & k\in \mathbb{Z}\setminus \left\{0\right\},\hfill \\ (1-2\theta )+2\theta e^{-\lambda },\hfill & k=0.\hfill \end{array}\right.$$

(12)

Consequently, the CDF of Z is obtained from Proposition 8 by replacing $F_Y(·)$ with the Poisson CDF.

It is useful to contrast the proposed Sy–Poisson specification with classical symmetric models on $\mathbb{Z}$. The Skellam distribution, obtained as the difference of two independent Poisson variables, is symmetric but couples the zero mass and tail decay through a single intensity parameter. Similarly, symmetric negative binomial variants provide heavier tails but still link dispersion and central mass through a common shape parameter. Zero-inflated symmetric count models allow for additional mass at zero but do not preserve exact symmetry unless extra constraints are imposed. In contrast, the Sy–Poisson model separates the sign and magnitude mechanisms, offering exact bilateral symmetry, independent control of the zero mass via $\theta$, and inherited Poisson-type tail behavior through $\lambda$. This decomposition makes the model both flexible and analytically tractable, and it ensures identifiability under mild parametric assumptions, providing advantages over the alternatives above.

Proposition 12.

Let $Z=XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$, $\theta \in (0,1/2)$, $Y\sim \mathcal{P}\left(\lambda \right)$, and $\lambda >0$ be independent. Then the CDF of $Z\sim Sy-\mathcal{P}(\theta ,\lambda )$ is

$$F_Z\left(k\right)=\mathbb{P}(Z\le k)=\left\{\begin{array}{cc}{\displaystyle \theta (1-H(\left|k\right|,\lambda \left)\right),}\hfill & k\le -1,\hfill \\ (1-\theta )+\theta e^{-\lambda },\hfill & k=0,\hfill \\ (1-\theta )+\theta H(k+1,\lambda ),\hfill & k\ge 1,\hfill \end{array}\right.$$

(13)

where $H(m,\lambda )=\mathbb{P}(Y\le m-1)$ for $m\ge 1$, $H(a,x)=\mathbf{\Gamma }(a,x)/\Gamma \left(a\right)$, and $\mathbf{\Gamma }(a,z)$ denotes the incomplete gamma function defined by ${\int }_z^{\infty }{t}^{a-1}{e}^{-t}dt$.

Proof. 

Apply Proposition 8 with $F_Y(·)$ equal to the $\mathcal{P}\left(\lambda \right)$ CDF: $F_Y\left(k\right)=e^{-\lambda }{\sum }_{j=0}^k{\lambda }^j/j!=H(k+1,\lambda )$ for $k\ge 0$, and $1-F_Y\left(\right|k|-1)=e^{-\lambda }{\sum }_{j=\left|k\right|}^{\infty }{\lambda }^j/j!=1-H\left(\right|k|,\lambda )$ for $k\le -1$.    □

Remark 6.

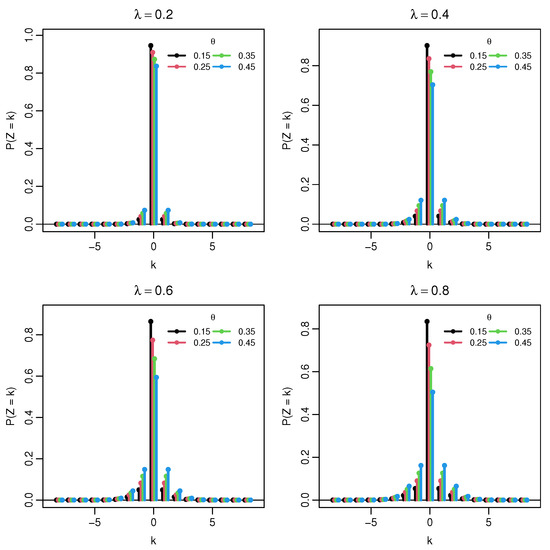
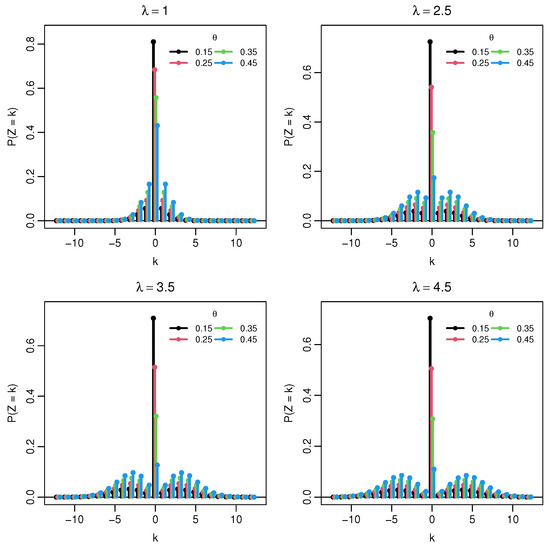
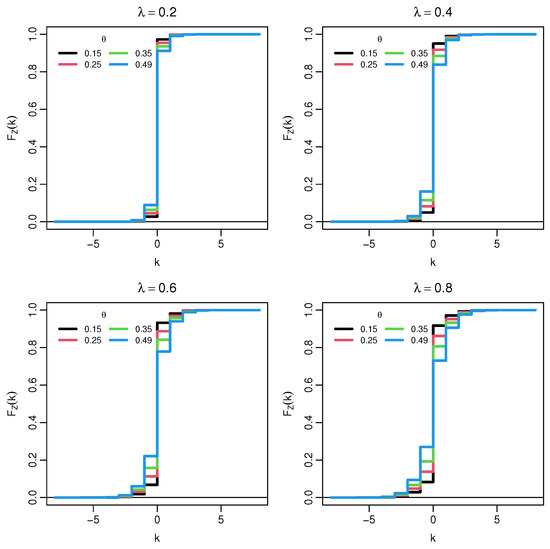
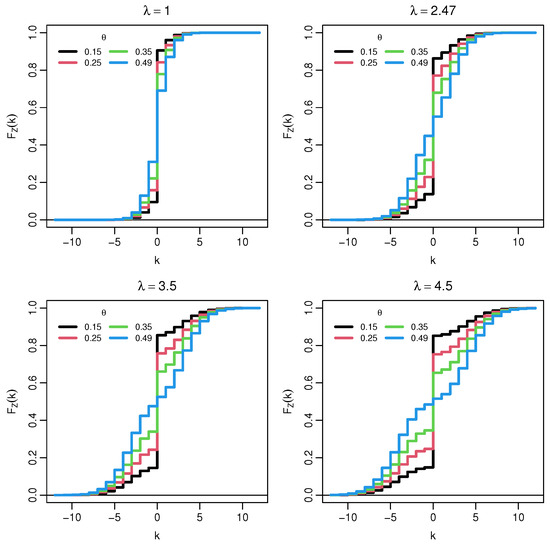
The distribution $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ is symmetric about 0 and zero–inflated, with $\mathbb{P}(Z=0)=(1-2\theta )+2\theta e^{-\lambda }$. For small λ, most of the mass is concentrated at 0, so the PMF is sharply unimodal at the origin. As λ increases, the Poisson component spreads out, and two symmetric shoulders emerge on the positive and negative sides; for moderate and large λ, the central mode at 0 is flanked by two lighter side peaks, yielding an overall three–bump shape. In the limit $\theta \to 1/2$, the point mass at 0 tends to $e^{-\lambda }$, and the side peaks become more pronounced, whereas when $\theta \to 0$, the concentration at 0 dominates for any fixed λ. These behaviors are illustrated by the PMF in Figure 1 and Figure 2, and the corresponding CDF in Figure 3 and Figure 4.

Figure 1. Probability mass function of $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Each panel fixes $0<\lambda <1$.

Figure 2. Probability mass function of $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Each panel fixes $\lambda \ge 1$.

Figure 3. Cumulative distribution function of $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Each panel fixes $0<\lambda <1$.

Figure 4. Cumulative distribution function of $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Each panel fixes $\lambda \ge 1$.

4.1. Generating Functions

Proposition 13.

Let $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ with $\theta \in (0,1/2)$ and $\lambda >0$, constructed as $Z=XY$ where $X\sim \mathrm{SMB}\left(\theta \right)$ and $Y\sim \mathcal{P}\left(\lambda \right)$ are independent. Then:

$$\begin{array}{ccc}\hfill M_Z\left(t\right)& =& (1-2\theta )+\theta exp\left\{\lambda (e^t-1)\right\}+\theta exp\left\{\lambda (e^{-t}-1)\right\},t\in \mathbb{R},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill G_Z\left(s\right)& =& (1-2\theta )+\theta exp\left\{\lambda (s-1)\right\}+\theta exp\left\{\lambda (1/s-1)\right\},s>0.\hfill \end{array}$$

(15)

Moreover, $G_Z\left(s\right)=G_Z(1/s)$ for all $s>0$, reflecting the exact symmetry of Z.

Proof. 

Condition on X. Since $Y\sim \mathcal{P}\left(\lambda \right)$, $\mathbb{E}\left(e^{tY}\right)=exp\left\{\lambda (e^t-1)\right\}$, and $\mathbb{E}\left(s^Y\right)=exp\left\{\lambda (s-1)\right\}$. Use $\mathbb{P}(X=0)=1-2\theta$, $\mathbb{P}(X=\pm 1)=\theta$, and the independence of X and Y.    □

Corollary 8.

All odd raw moments vanish, $\mathbb{E}\left(Z^{2m+1}\right)=0$ for $m\ge 0$. For $m\ge 1$,

$$\mathbb{E}\left(Z^{2m}\right)=\mathbb{E}\left(X^{2m}{Y}^{2m}\right)=2\theta \mathbb{E}\left(Y^{2m}\right)=2\theta T_{2m}\left(\lambda \right),$$

where $T_r\left(\lambda \right)$ is the r-th Touchard polynomial [10] (raw moment of a Poisson$\left(\lambda \right)$). In particular,

$$\mathbb{E}\left(Z^2\right)=2\theta \lambda (1+\lambda ),\mathbb{E}\left(Z^4\right)=2\theta \lambda (1+7\lambda +6{\lambda }^2+{\lambda }^3).$$

Hence $\mathrm{Var}\left(Z\right)=2\theta \lambda (1+\lambda )$.

Corollary 9.

Skewness is 0 due to symmetry, and the (non–excess) kurtosis is

$$\kappa ={\displaystyle \frac{\mathbb{E}\left(Z^4\right)}{{\left(\mathrm{Var}\left(Z\right)\right)}^2}}={\displaystyle \frac{1+7\lambda +6{\lambda }^2+{\lambda }^3}{2\theta \lambda {(1+\lambda )}^2}},$$

and the excess kurtosis equals $\kappa -3$.

Remark 7.

(i) The identities (14) and (15) yield derivatives at $t=0$ (or $s=1$) that recover the even moments without resorting to series expansions. (ii) The symmetry $G_Z\left(s\right)=G_Z(1/s)$ implies that the distributions of $Z_1+Z_2$ and $Z_1-Z_2$ coincide for independent Sy–Poisson variables; see Section 3.9.

4.2. The Total Time on Test Transform

The total time on test (TTT) transform is a standard tool in reliability analysis and quality-control methodology for assessing distributional shape and aging properties. For a non-negative random variable X with distribution function F and survival function $S\left(x\right)=1-F\left(x\right)$, the  TTT transform is defined by

$$T\left(u\right)={\displaystyle \frac{1}{\mathbb{E}\left(X\right)}}{\int }_0^{F^{-1}\left(u\right)}S\left(x\right)dx,0\le u\le 1,$$

where $F^{-1}$ denotes the (generalized) quantile function of F. The function $T\left(u\right)$ is increasing in u, and its curvature reveals information about the underlying failure rate behavior: concave curves indicate a decreasing failure rate (DFR), convex curves indicate an increasing failure rate (IFR), and curves close to the diagonal $T\left(u\right)=u$ correspond to approximately exponential or memoryless behavior.

In practice, the TTT transform is implemented through its discrete empirical version. For ordered non-negative observations $X_{\left(1\right)}\le \cdots \le X_{\left(n\right)}$, the empirical TTT values are computed as

$$T_i={\displaystyle \frac{1}{{\sum }_{j=1}^n{X}_{\left(j\right)}}}\left(\sum _{j=1}^i{X}_{\left(j\right)}+(n-i)X_{\left(i\right)}\right),i=1,\dots ,n,$$

and the TTT plot is obtained by graphing $T_i$ against $u_i=i/n$. The diagonal line $T\left(u\right)=u$ serves as a natural reference: empirical curves lying above the diagonal suggest DFR behavior, while those below the diagonal suggest IFR behavior.

In our setting, we apply the TTT transform to the non-negative magnitudes $\left|Z\right|$ (equivalently, to the Y component in the Sy-$\mathbb{Z}$ representation), and we compare the empirical TTT plot with the TTT curve implied by the fitted $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ model as a diagnostic tool; see Section 6.

4.3. Shannon Entropy

Proposition 14.

Under the assumptions of Proposition 13, the Shannon entropy $H\left(Z\right)=-{\sum }_{k\in \mathbb{Z}}\mathbb{P}(Z=k)log\left(\mathbb{P}(Z=k)\right)$ (natural logarithm) admits an exact representation

$$H\left(Z\right)=-p_{0}log\left(p_0\right)-2\theta \left((log\left(\theta \right)-\lambda )(1-e^{-\lambda })+\lambda log\left(\lambda \right)-{\mathbb{E}}_Y\left(log(Y!)\right)\right),$$

(16)

where $p_0=(1-2\theta )+2\theta e^{-\lambda }$ and $Y\sim \mathcal{P}\left(\lambda \right)$. In base-2 units, replace $H\left(Z\right)$ with $H\left(Z\right)/log\left(2\right)$.

Proof. 

By symmetry, write $p_0=\mathbb{P}(Z=0)$ and, for $n\ge 1$, $p_{\pm n}=\mathbb{P}(Z=\pm n)=\theta e^{-\lambda }{\lambda }^n/n!$. Then

$$H\left(Z\right)=-p_{0}log\left(p_0\right)-2\sum _{n=1}^{\infty }{p}_{n}log\left(p_n\right),p_n=\theta e^{-\lambda }{\displaystyle \frac{{\lambda }^n}{n!}}.$$

Using $log\left(p_n\right)=log\left(\theta \right)-\lambda +nlog\left(\lambda \right)-log(n!)$ and factoring out $2\theta e^{-\lambda }$,

$$\begin{array}{cc}\hfill H\left(Z\right)& =-p_{0}log\left(p_0\right)-2\theta e^{-\lambda }\sum _{n=1}^{\infty }{\displaystyle \frac{{\lambda }^n}{n!}}\left(log\left(\theta \right)-\lambda +nlog\left(\lambda \right)-log(n!)\right)\hfill \\ & =-p_{0}log\left(p_0\right)-2\theta [(log\left(\theta \right)-\lambda )\underset{1-e^{-\lambda }}{\underbrace{e^{-\lambda }\sum _{n=1}^{\infty }{\displaystyle \frac{{\lambda }^n}{n!}}}}+log\left(\lambda \right)\underset{\lambda }{\underbrace{e^{-\lambda }\sum _{n=1}^{\infty }{\displaystyle \frac{n{\lambda }^n}{n!}}}}\hfill \\ & -\underset{{\mathbb{E}}_Y(log(Y!))}{\underbrace{e^{-\lambda }\sum _{n=1}^{\infty }{\displaystyle \frac{{\lambda }^n}{n!}}log(n!)}}].\hfill \end{array}$$

This yields (16).    □

Corollary 10.

Using Stirling’s expansion [19] $log(n!)=nlog\left(n\right)-n+\frac{1}{2}log\left(2\pi n\right)+O(1/n)$ and taking expectations for $Y\sim \mathcal{P}\left(\lambda \right)$,

$$\mathbb{E}(log(Y!))=\lambda (log\left(\lambda \right)-1)+\frac{1}{2}log\left(2\pi \lambda \right)+O\left({\lambda }^{-1}\right),$$

so that

$$H\left(Z\right)=-p_{0}log\left(p_0\right)-2\theta \left((log\left(\theta \right)-\lambda )(1-e^{-\lambda })+\lambda -\frac{1}{2}log\left(2\pi \lambda \right)\right)+O\left({\lambda }^{-1}\right).$$

(17)

5. The Statistical Inference of the Model

5.1. Method of Moments Estimation (MoM)

Consider an i.i.d. sample $z=(z_1,\dots ,z_n)$ from $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ with $\theta \in (0,1/2)$ and $\lambda >0$. From Section 4.1 we have

$$\mathbb{E}\left(\right|Z\left|\right)=2\theta \lambda ,\mathbb{E}\left(Z^2\right)=2\theta \lambda (1+\lambda ).$$

Let the empirical moments be

$${\overline{m}}_1={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|z_i\right|,{\overline{m}}_2={\displaystyle \frac{1}{n}}\sum _{i=1}^n{z}_i^2.$$

Matching ${\overline{m}}_1$ and ${\overline{m}}_2$ to their population counterparts yields a closed form solution. If ${\overline{m}}_1>0$ and ${\overline{m}}_2>{\overline{m}}_1$, the MoM are

$${\widehat{\lambda }}_{\mathrm{M}}={\displaystyle \frac{{\overline{m}}_2}{{\overline{m}}_1}}-1,{\widehat{\theta }}_{\mathrm{M}}={\displaystyle \frac{{\overline{m}}_1}{2{\widehat{\lambda }}_{\mathrm{M}}}}={\displaystyle \frac{{\overline{m}}_1^2}{2({\overline{m}}_2-{\overline{m}}_1)}}.$$

(18)

The feasibility conditions ${\overline{m}}_1>0$ and ${\overline{m}}_2>{\overline{m}}_1$ ensure ${\widehat{\lambda }}_{\mathrm{M}}>0$ and ${\widehat{\theta }}_{\mathrm{M}}>0$. If ${\widehat{\theta }}_{\mathrm{M}}\ge 1/2$, the estimate lies outside the parameter space; in practice, one may either declare the MoM fit infeasible or project to $1/2-\epsilon$ for a small $\epsilon >0$ and use the projected value as initialization for maximum likelihood.

5.2. Asymptotic Distribution and Standard Errors (Delta Method)

Let ${\mu }_1=\mathbb{E}\left(\right|Z\left|\right)=2\theta \lambda$ and ${\mu }_2=\mathbb{E}\left(Z^2\right)=2\theta \lambda (1+\lambda )$. From the closed-form moments,

$$\mathrm{Var}\left(\right|Z\left|\right)=2\theta \lambda +2\theta (1-2\theta ){\lambda }^2,\mathbb{E}\left(Z^4\right)=2\theta \lambda (1+7\lambda +6{\lambda }^2+{\lambda }^3),$$

so

$$\mathrm{Var}\left(Z^2\right)=\mathbb{E}\left(Z^4\right)-{\mu }_2^2=2\theta \lambda (1+7\lambda +6{\lambda }^2+{\lambda }^3)-{\left\{2\theta \lambda (1+\lambda )\right\}}^2.$$

Using ${\mathbb{E}\left(\right|Z|}^3)=2\theta \lambda (1+3\lambda +{\lambda }^2)$,

$$\mathrm{Cov}\left(\right|Z|,Z^2{)=\mathbb{E}(\left|Z\right|}^3)-{\mu }_1{\mu }_2=2\theta \lambda \left[1+3\lambda +{\lambda }^2-4\theta \lambda (1+\lambda )\right].$$

A multivariate central limit theorem [20] yields

$$\sqrt{n}\left({({\overline{m}}_1,{\overline{m}}_2)}^{\top }-{({\mu }_1,{\mu }_2)}^{\top }\right)\stackrel{d}{\to }\mathcal{N}\left(0,\Sigma \right),\Sigma =\left(\begin{array}{cc}\mathrm{Var}\left(\right|Z\left|\right)& \mathrm{Cov}\left(\right|Z|,Z^2)\\ \mathrm{Cov}\left(\right|Z|,Z^2)& \mathrm{Var}\left(Z^2\right)\end{array}\right).$$

Define the transformation $g({\overline{m}}_1,{\overline{m}}_2)=(\lambda ,\theta )$ by $\lambda ={\overline{m}}_2/{\overline{m}}_1-1$ and $\theta ={\overline{m}}_1^2/\left(2({\overline{m}}_2-{\overline{m}}_1)\right)$. The Jacobian at $({\mu }_1,{\mu }_2)$ is

$$K=\left(\begin{array}{cc}-{\displaystyle \frac{{\mu }_2}{{\mu }_1^2}}& {\displaystyle \frac{1}{{\mu }_1}}\\ {\displaystyle \frac{{\mu }_1(2{\mu }_2-{\mu }_1)}{2{({\mu }_2-{\mu }_1)}^2}}& -{\displaystyle \frac{{\mu }_1^2}{2{({\mu }_2-{\mu }_1)}^2}}\end{array}\right)=\left(\begin{array}{cc}-{\displaystyle \frac{1+\lambda }{2\theta \lambda }}& {\displaystyle \frac{1}{2\theta \lambda }}\\ {\displaystyle \frac{1+2\lambda }{2{\lambda }^2}}& -{\displaystyle \frac{1}{2{\lambda }^2}}\end{array}\right).$$

By the delta method,

$$\sqrt{n}\left({({\widehat{\lambda }}_{\mathrm{M}},{\widehat{\theta }}_{\mathrm{M}})}^{\top }-{(\lambda ,\theta )}^{\top }\right)\stackrel{d}{\to }\mathcal{N}\left(0,V\right),V=K\Sigma K^{\top },$$

with a practical plug-in estimator of V obtained by replacing $(\theta ,\lambda )$ with $({\widehat{\theta }}_{\mathrm{M}},{\widehat{\lambda }}_{\mathrm{M}})$.

5.3. Algorithm for MoM Estimation

To facilitate the practical implementation of the inference method, we summarize the computational procedure below, by the Algorithm 1 that outlines the step-by-step calculation of the moment-based estimates.

Remark 8.

The closed form pair $({\overline{m}}_1,{\overline{m}}_2)$ provides stable initialization for maximum likelihood, typically improving convergence and reducing sensitivity to local optima. In very small samples, the method of moments may yield ${\widehat{\theta }}_{\mathrm{M}}$ close to $1/2$; in that case, it is advisable to compare the implied modality (see Proposition 7) using the empirical shape as a diagnostic check.

Algorithm 1 Computation of MoM estimates

1: Compute ${\overline{m}}_1={\sum }_i\left|z_i\right|/n$ and ${\overline{m}}_2={\sum }_i{z}_i^2/n$. 2: If ${\overline{m}}_1\le 0$ or ${\overline{m}}_2\le {\overline{m}}_1$, declare the MoM fit infeasible and proceed with likelihood-based estimation. 3: Else, compute $({\widehat{\lambda }}_{\mathrm{M}},{\widehat{\theta }}_{\mathrm{M}})$ via (18). 4: Optionally report delta-method standard errors using the plug-in estimate of V.

5.4. Likelihood-Based Inference

Given an i.i.d. sample $\mathit{z}=(z_1,\dots ,z_n)$ from $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ with $\theta \in (0,1/2)$ and $\lambda >0$, let $n_0=\#\{i:z_i=0\}$ and $n_1=n-n_0$ be the numbers of zeros and nonzeros, respectively. Writing $p_0=\mathbb{P}(Z=0)=(1-2\theta )+2\theta e^{-\lambda }=1-2\theta (1-e^{-\lambda })$, the likelihood factorizes as

$$L(\theta ,\lambda \mid \mathit{z})=p_0^{n_0}{\theta }^{n_1}{e}^{-\lambda n_1}{\displaystyle \frac{{\lambda }^{{\sum }_{i:z_i\ne 0}\left|z_i\right|}}{{\prod }_{i:z_i\ne 0}\left|z_i\right|!}},$$

(19)

so that the log-likelihood is

$$\mathcal{\ell }(\theta ,\lambda )=n_{0}log\left(p_0\right)+n_{1}log\left(\theta \right)-\lambda n_1+log\left(\lambda \right)\sum _{i:z_i\ne 0}|z_i|-\sum _{i:z_i\ne 0}log\left(\right|z_i|!).$$

The score equations are obtained from

$${\displaystyle \frac{\partial \mathcal{\ell }}{\partial \theta }}=-{\displaystyle \frac{2n_0(1-e^{-\lambda })}{p_0}}+{\displaystyle \frac{n_1}{\theta }},{\displaystyle \frac{\partial \mathcal{\ell }}{\partial \lambda }}=-{\displaystyle \frac{2\theta n_0{e}^{-\lambda }}{p_0}}-n_1+{\displaystyle \frac{{\sum }_{i:z_i\ne 0}\left|z_i\right|}{\lambda }},$$

The maximum likelihood estimators (MLEs) solve $\partial \mathcal{\ell }/\partial \theta =0$ and $\partial \mathcal{\ell }/\partial \lambda =0$ numerically (no closed form in general). For numerical maximization of the log-likelihood, we used the quasi-Newton BFGS algorithm [21], which provides stable performance for smooth two-parameter models such as $\mathrm{Sy-}\mathcal{P}$. The optimization was initialized at $({\theta }^{\left(0\right)},{\lambda }^{\left(0\right)})=({\overline{p}}_0/2,max\{{\overline{Z}}^2,{10}^{-3}\})$, where ${\overline{p}}_0$ is the empirical proportion of zeros, and ${\overline{Z}}^2$ is the empirical second moment. A convergence tolerance of ${10}^{-8}$ on both the absolute and relative change in the objective value was imposed. To guard against potential local maxima, the optimization was repeated from five random starting points generated uniformly over $(0,0.5)\times (0,10)$. The algorithm converged to identical estimates, indicating that the likelihood is well behaved for the $\mathrm{Sy-}\mathcal{P}$ model. These implementation details ensure reproducibility and support the observed numerical stability of the MLE.

5.5. Score Derivatives and Information Matrices

Hessian (second derivatives).

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\mathcal{\ell }}{\partial {\theta }^2}}& =-{\displaystyle \frac{4n_0{(1-e^{-\lambda })}^2}{p_0^2}}-{\displaystyle \frac{n_1}{{\theta }^2}},\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\mathcal{\ell }}{\partial \theta \partial \lambda }}& ={\displaystyle \frac{{\partial }^2\mathcal{\ell }}{\partial \lambda \partial \theta }}=-{\displaystyle \frac{2n_0{e}^{-\lambda }}{p_0^2}},\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\mathcal{\ell }}{\partial {\lambda }^2}}& ={\displaystyle \frac{2\theta n_0{e}^{-\lambda }(1-2\theta )}{p_0^2}}-{\displaystyle \frac{{\sum }_{i:z_i\ne 0}\left|z_i\right|}{{\lambda }^2}}.\hfill \end{array}$$

5.6. Observed Information

The observed information matrix is $J(\theta ,\lambda )=-{\nabla }^2\mathcal{\ell }(\theta ,\lambda )$:

$$J(\theta ,\lambda )=\left[\begin{array}{cc}{\displaystyle \frac{4n_0{(1-e^{-\lambda })}^2}{p_0^2}}+{\displaystyle \frac{n_1}{{\theta }^2}}& {\displaystyle \frac{2n_0{e}^{-\lambda }}{p_0^2}}\\ {\displaystyle \frac{2n_0{e}^{-\lambda }}{p_0^2}}& {\displaystyle \frac{{\sum }_{i:z_i\ne 0}\left|z_i\right|}{{\lambda }^2}}-{\displaystyle \frac{2\theta n_0{e}^{-\lambda }(1-2\theta )}{p_0^2}}\end{array}\right].$$

An asymptotically consistent covariance estimator for $(\widehat{\theta },\widehat{\lambda })$ is $J{(\widehat{\theta },\widehat{\lambda })}^{-1}$.

5.7. Expected Fisher Information

Let $q=1-p_0=2\theta (1-e^{-\lambda })$. Using $\mathbb{E}\left(N_0\right)=n{p}_0$, $\mathbb{E}\left(N_1\right)=nq$, and  $\mathbb{E}({\sum }_{i:z_i\ne 0}|Z_i\left|\right)=\mathbb{E}({\sum }_{i=1}^n|Z_i\left|\right)=n\mathbb{E}\left(\right|Z\left|\right)=n\left(2\theta \lambda \right)$, the expected (per-observation) Fisher information is

$$i(\theta ,\lambda )={\displaystyle \frac{1}{n}}\mathbb{E}\left[J(\theta ,\lambda )\right]=\left[\begin{array}{cc}{\displaystyle \frac{4{(1-e^{-\lambda })}^2}{p_0}}+{\displaystyle \frac{q}{{\theta }^2}}& {\displaystyle \frac{2e^{-\lambda }}{p_0}}\\ {\displaystyle \frac{2e^{-\lambda }}{p_0}}& {\displaystyle \frac{2\theta }{\lambda }}-{\displaystyle \frac{2\theta e^{-\lambda }(1-2\theta )}{p_0}}\end{array}\right],I(\theta ,\lambda )=ni(\theta ,\lambda ).$$

Remark 9.

The observed Fisher information matrix for the $\mathrm{Sy-}\mathcal{P}$ model is positive definite whenever $(\theta ,\lambda )$ belongs to the interior of the parameter space $(0<\theta <0.5,\lambda >0)$. This follows from the strict concavity of the log-likelihood in both parameters: the sign component induces a strictly negative second derivative in θ, while the Poisson magnitude contributes a negative curvature in λ for all $\lambda >0$. Consequently, the Hessian matrix is negative definite, and the observed information and its negative remain positive definite away from the boundary. Loss of positive definiteness can only occur near the boundary limits $\theta \to 0$, $\theta \to 0.5$, or $\lambda \to 0$, where the model collapses to a degenerate or nearly degenerate form, and classical asymptotic theory is no longer applicable. Thus, for all practical estimation scenarios in the interior region, the observed information matrix provides a valid and reliable approximation to the asymptotic covariance.

Hence, under standard regularity conditions,

$$\sqrt{n}\left((\widehat{\theta },\widehat{\lambda })-(\theta ,\lambda )\right)\stackrel{d}{\to }\mathcal{N}\left(\mathbf{0},i{(\theta ,\lambda )}^{-1}\right),$$

and a large-sample covariance estimator is $I{(\widehat{\theta },\widehat{\lambda })}^{-1}={\left(ni(\widehat{\theta },\widehat{\lambda })\right)}^{-1}$.

5.8. Percentile Estimators

Percentile estimators provide a robust and intuitive alternative to likelihood and moment based procedures. Because the $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ distribution is defined through a symmetric, zero-centered mixture structure, its shape is largely determined by its quantiles, particularly those away from the median. Percentile estimators, therefore, offer a way to capture the distributional form using direct CDF inversion, without relying on the smoothness of the likelihood or long-tailed moments. Percentile estimators are obtained by matching the empirical and model based percentiles at two symmetric quantiles, namely the 25th and 75th percentiles. Let $F(z;\theta ,\lambda )$ be the $\mathrm{Sy-}\mathcal{P}$ CDF, and let $Q\left(p\right)$ denote the population p-th percentile, given as $Q(p;\theta ,\lambda )=F^{-1}(p;\theta ,\lambda )$.

Given empirical percentiles $\tilde{Q}\left(p_1\right)$ and $\tilde{Q}\left(p_2\right)$, which are the sample percentiles at level p, the goal of percentile estimation is to find parameter values $(\theta ,\lambda )$ such that the model percentiles match the data percentiles. We thus define the percentile estimators $(\widehat{\theta },\widehat{\lambda })$ as the solution of

$$Q(p_1;\theta ,\lambda )=\tilde{Q}\left(p_1\right)\mathrm{and}Q(p_2;\theta ,\lambda )=\tilde{Q}\left(p_2\right).$$

These two non-linear equations can be solved numerically to obtain the estimators. The practical utility of the proposed percentile estimators is illustrated in Section 6, where they are applied to both empirical datasets alongside the MLE estimators. The comparison highlights the robustness of percentile-based estimation, especially in settings with moderate tails or irregular zero concentrations.

6. Simulation Study

To evaluate the finite-sample properties of the proposed estimators for $Z\sim \mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$, we performed a comprehensive Monte Carlo experiment. This simulation mechanism follows directly from Proposition 1, which characterizes any Sy-$\mathbb{Z}$ random variable as the product of an independent symmetric sign and a non-negative magnitude. Specifically, the representation

$$Z=V_1(2V_2-1)Y$$

The constructive form is associated with the probability mass function given in Equation (12): $V_1$ determines whether $Z=0$ or $Z\ne 0$ applies, $V_2$ selects the sign when $Z\ne 0$, and Y supplies the magnitude. Thus, the generative steps above reproduce exactly the $\mathrm{Sy-}\mathcal{P}$ distribution implied by the theoretical results. For each parameter configuration, 10,000 independent samples of size $n\in \{10,20,\dots ,200\}$ were drawn under the true parameters $(\theta ,\lambda )=(0.3,3)$. This parameter configuration is representative of many practical scenarios: $\theta =0.3$ yields a moderate zero mass in the $\mathrm{Sy-}\mathcal{P}$ model, while $\lambda =3$ produces a magnitude distribution with moderate dispersion. Together, these values generate datasets whose symmetry, central concentration, and tail behavior closely resemble those encountered in empirical applications, making them well suited for assessing estimation accuracy in realistic settings. The log-likelihood $\mathcal{\ell }(\theta ,\lambda )$ was maximized numerically to obtain MLEs, and MoM estimators were computed from the first two empirical moments. The Algorithm 2 below provides a concise summary of the exact data-generation procedure used in all Monte Carlo experiments. This step-by-step formulation clarifies how independent draws from the $\mathrm{Sy-}\mathcal{P}$ model are produced and ensures full reproducibility of the simulation design.

Algorithm 2 Generation of an i.i.d. sample ${\left\{Z_i\right\}}_{i=1}^n$ from $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$

1: for  $i=1,\dots ,n$  do 2:        Draw $V_{1i}\sim \mathrm{Bernoulli}\left(2\theta \right)$. If $V_{1i}=0$, set $Z_i\leftarrow 0$ and continue. 3:        Draw $V_{2i}\sim \mathrm{Bernoulli}(1/2)$ and set $S_i\leftarrow 2V_{2i}-1\in \{-1,1\}$. 4:        Draw $Y_i\sim \mathcal{P}\left(\lambda \right)$ and set $Z_i\leftarrow S_i{Y}_i$. 5: end for

6.1. Comparison of MLE and MoM Estimators

For each n, bias and mean-squared error (MSE) were calculated as

$${\mathrm{Bias}}_n\left(\widehat{\eta }\right)={\displaystyle \frac{1}{R}}\sum _{r=1}^R({\widehat{\eta }}_r-\eta ),{\mathrm{MSE}}_n\left(\widehat{\eta }\right)={\displaystyle \frac{1}{R}}\sum _{r=1}^R{({\widehat{\eta }}_r-\eta )}^2,$$

with $\eta \in \{\theta ,\lambda \}$. Figure 5 plots Monte Carlo estimates of ${\mathrm{Bias}}_n$ against n, whereas Figure 6 plots Monte Carlo estimates of ${\mathrm{MSE}}_n$ against n.

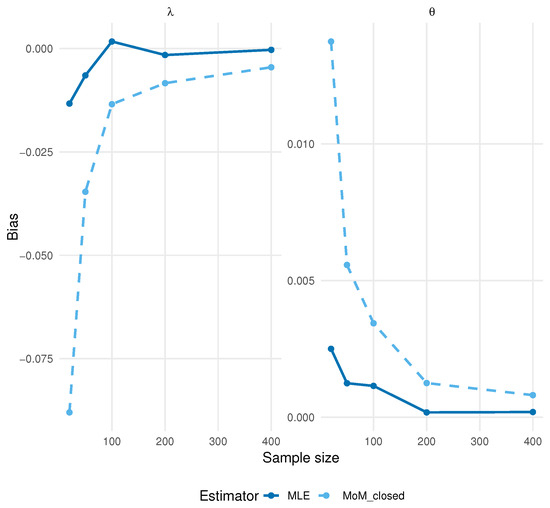
Figure 5. Bias of $\widehat{\lambda }$ and $\widehat{\theta }$ under $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Curves compare MLE and MoM estimators across sample sizes.

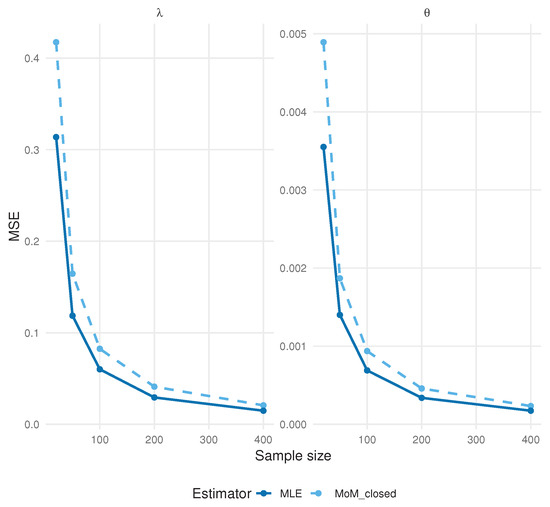
Figure 6. MSE of $\widehat{\lambda }$ and $\widehat{\theta }$ under $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$. Curves compare MLE and MoM estimators across sample sizes.

Both MLEs and MoM estimators show rapidly vanishing bias and MSE as the sample size increases, consistent with standard asymptotic theory. The MoM estimator displays a slightly higher MSE for small n compared to the MLE, but its performance converges to that of the MLE as $n\to 200$.

Across the grid of n, $\widehat{\theta }$ shows a mild positive bias, while $\widehat{\lambda }$ tends to underestimate the true value. Moreover, ${\mathrm{MSE}}_n(\widehat{\lambda })$ remains larger than ${\mathrm{MSE}}_n(\widehat{\theta })$, reflecting the higher sampling variability of the rate parameter. These bias patterns are consistent with the structure of the log-likelihood and the Fisher information described in Section 5.8. The information for $\theta$ is primarily driven by the zero and near zero observations, where the curvature of the likelihood is pronounced; this yields relatively strong identifiability for $\theta$ and explains the small positive finite-sample bias. In contrast, the information for $\lambda$ depends on the dispersion of the magnitude component: when many observations fall at or near zero, the effective information about $\lambda$ is reduced, leading to a mild tendency toward underestimation. As the sample size increases, both information components scale linearly with n, causing the biases in $\widehat{\theta }$ and $\widehat{\lambda }$ to diminish, in agreement with the asymptotic theory.

6.2. Standard-Error Accuracy and Confidence-Interval Coverage

To assess standard-error accuracy and validate asymptotic normality, we formed observed Wald confidence intervals using the inverse Hessian at the MLE, as given by $\widehat{\mathrm{Var}}(\widehat{\theta },\widehat{\lambda })=J{(\widehat{\theta },\widehat{\lambda })}^{-1}$. For each replication and parameter, we constructed two-sided Wald intervals at the 90%, 95%, and 99% nominal levels and recorded empirical coverage along with the average interval length. Figure 7 reports the CI coverage, whereas Figure 8 shows the average CI length as functions of n.

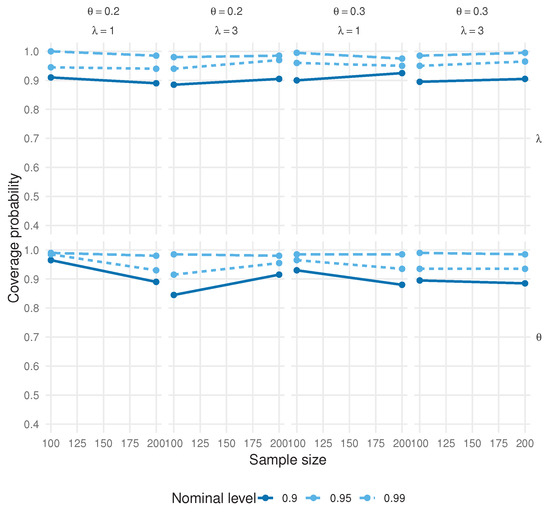
Figure 7. Empirical coverage probabilities of the observed Wald confidence intervals for $\widehat{\theta }$ and $\widehat{\lambda }$ as a function of n.

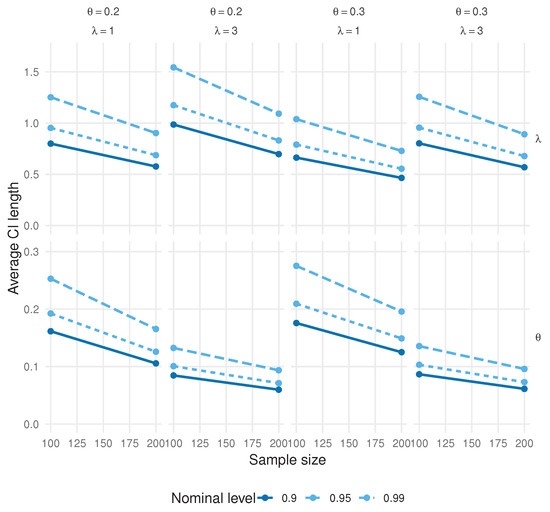
Figure 8. Average lengths of the observed Wald confidence intervals for $\widehat{\theta }$ and $\widehat{\lambda }$ as a function of n.

The observed Wald intervals show coverage approaching nominal levels as n increases, with noticeable gains between small and moderate sample sizes. In cases of small $\lambda$, the intervals can be slightly conservative for very small n, but accuracy improves quickly with n, and the average lengths decrease at the expected $n^{-1/2}$ rate, consistent with the asymptotic theory for the MLE.

A further point of reassurance concerns the use of Wald confidence intervals in a discrete setting. Although discrete models sometimes induce irregular likelihood shapes and poor Wald performance, the $\mathrm{Sy-}\mathcal{P}$ model benefits from a smooth and strictly concave log-likelihood in both parameters. The independence between the symmetric sign and the Poisson magnitude yields well-behaved score functions and a Fisher information matrix that remains finite and positive for all admissible $(\theta ,\lambda )$. These properties ensure that the MLEs lie well within the interior of the parameter space and satisfy standard differentiability conditions, so Wald intervals inherit the usual asymptotic validity even in finite samples. This explains why the simulation results show accurate coverage levels despite the inherent discreteness of the data-generating process. The observed coverage behavior can be directly linked to the analytical form of the Fisher information derived in Section 5.8. When the zero mass $p_0=(1-2\theta )+2\theta e^{-\lambda }$ is large, the term $q/{\theta }^2$ in the information matrix (where $q=2\theta (1-e^{-\lambda })$) dominates, yielding high curvature of the log-likelihood with respect to $\theta$ and, therefore, tighter confidence intervals. Conversely, the information component associated with $\lambda$ depends on both $\theta$ and $\lambda$ through $2\theta /\lambda -2\theta e^{-\lambda }(1-2\theta )/p_0$, which can be relatively flat for small $\lambda$. This explains why the empirical coverage for $\lambda$ tends to be slightly conservative in small samples, whereas the coverage for $\theta$ rapidly approaches nominal levels. As the sample size increases, both components of the Fisher information scale linearly with n, leading to asymptotic normality and the near-exact coverage observed for $n\ge 100$.

7. Practical Data Analysis

We illustrate the applicability of the proposed $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ model using two real-life datasets. After first-differencing (day-to-day or session-to-session changes), the outcomes lie on $\mathbb{Z}$, matching the model’s support.

7.1. PTT Stock Price Increments (Thailand, 2014)

The first dataset, previously analyzed in ref. [4], consists of daily closing prices for the Petroleum Authority of Thailand (PTT), recorded from 1 April 2014 to 20 October 2014 (Stock Exchange of Thailand). For completeness, the data are as follows:

-12, -11, -9, -8, -7, -6, -6, -5, -5, -5, -5, -5, -5, -5, -5, -4, -4, -4,

-4, -4, -4, -4, -4, -4, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -2, -2,

-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -1, -1, -1, -1, -1, -1, -1, -1,

-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1,

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3,

3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7,

7, 7, 8, 8, 9, 9, 9, 10, 14

According to ref. [4], we model price increments; that is, the day-to-day change in the closing price is measured in integer Baht. A Mann–Kendall test against a monotonic trend yields a p-value of $0.9467$, providing no evidence of such a trend and supporting the i.i.d. working assumption for the increment series.

We fit $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ by maximum likelihood, obtaining $(\widehat{\theta },\widehat{\lambda })=(0.45,3.71)$. A Kolmogorov–Smirnov (K–S) test gives $p=0.47$, indicating an adequate fit. Furthermore, we also find the percentile estimators by fixing $p_1=0.25,p_2=0.75$ of the parameters, which are given by $(\widehat{\theta },\widehat{\lambda })=(0.37,3.43)$. Figure 9 overlays the fitted probability mass function on the empirical frequencies. Figure 10 contains the total time on test (TTT) plot, as described in Section 4.2. The empirical TTT curve was compared to the TTT curve implied by the fitted $\mathrm{Sy-}\mathcal{P}$ model. A close alignment of the curves indicates an adequate fit.

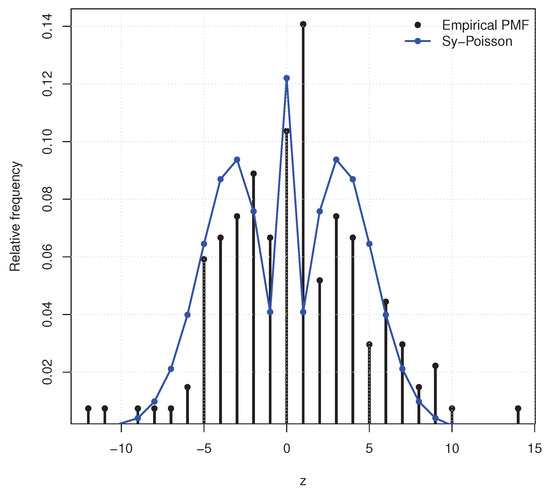
Figure 9. Empirical PMF and fitted $\mathrm{Sy-}\mathcal{P}(\widehat{\theta },\widehat{\lambda })$ for PTT price increments.

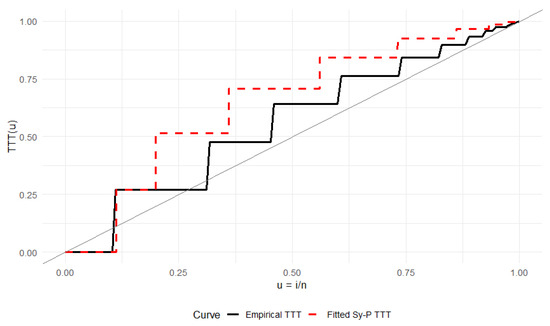
Figure 10. TTT plot for PTT price increments comparing the empirical curve with the fitted $\mathrm{Sy-}\mathcal{P}$ model. The diagonal line represents the exponential distribution reference.

For benchmarking, we also fit the perturbed discrete Laplace $PDL(p,\alpha )$ [6], the discrete Laplace $DL\left(p\right)$, the discrete normal $DN(\mu ,\sigma )$ [5], and the discrete asymmetric Laplace $DALD(\mu ,\beta ,\lambda )$ [4]. Table 1 reports log-likelihood, AIC, and BIC. The $\mathrm{Sy-}\mathcal{P}$ model attains the smallest AIC/BIC, and, following ref. [22], the BIC differences relative to competitors exceed 2, providing positive evidence in favor of $\mathrm{Sy-}\mathcal{P}$. This good empirical fit is consistent with the theoretical properties of the $\mathrm{Sy-}\mathcal{P}$ model. The financial return increments are nearly symmetric and exhibit a pronounced central mass at zero; the $\mathrm{Sy-}\mathcal{P}$ structure accommodates both features naturally through its symmetric sign component and the tunable zero probability governed by $\theta$. Moreover, the inherited Poisson tail behavior aligns well with the moderate dispersion observed in the positive and negative increments, explaining the improved information-criteria performance over classical competitors.

Table 1. Model comparison for PTT price increments.

Model	Fitted Parameters	Log-Likelihood	AIC	BIC
$PDL(p,\alpha )$	$\widehat{p}=0.74,\widehat{\alpha }=0.67$	$-388.17$	780.35	786.15
$DL\left(p\right)$	$\widehat{p}=0.59$	$-391.52$	785.04	792.85
$DN(\mu ,\sigma )$	$\widehat{\mu }=0.32,\widehat{\sigma }=1.71$	$-412.15$	828.29	834.11
$DALD(\mu ,\beta ,\lambda )$	$\widehat{\mu }=1,\widehat{\beta }=0.73,\widehat{\lambda }=0.72$	$-409.67$	825.34	834.05
$\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$	$\widehat{\theta }=0.45,\widehat{\lambda }=3.71$	−385.32	772.64	778.91

Remark 10.

The $\mathrm{Sy-}\mathcal{P}$ fit closely tracks competitors while imposing exact symmetry around zero and supporting closed-form manipulations for sums and differences (Section 3.9).

7.2. Attendance Increments in a Marketing Course (Lyon, 2012–2013)

We revisit a dataset previously analyzed in ref. [18], where the extended Poisson model was introduced. The data record attendance counts for 60 consecutive marketing sessions in the Bachelor program at IDRAC International Management School (Lyon, France), between 1 September 2012 and 1 April 2013. For completeness, the exact dataset is as given below:

-5, -5, -5, -4, -4, -4, -3, -3, -3, -3, -3, -3, -2, -2, -2, -2, -2, -2,

-2, -2, -2, -2, -2, -2, -2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0,

0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3,

3, 3, 3, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 7, 8

As documented in ref. [18], we analyze first differences between consecutive sessions, yielding $n=59$ integer-valued observations ranging from $-5$ to 7. This transformation centers the process and produces signed counts, providing a natural benchmark for two-sided discrete models.

As a preliminary diagnostic, the runs test reported in ref. [18] indicates that while the raw series is not random (p-value $=0$), the differenced series behaves as an approximately random sample (p-value $=0.7077$), supporting independent-sample modeling at the differenced scale. We fit the symmetric Poisson model $\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$ by maximum likelihood and compare it with standard competitors: discrete Laplace $DL\left(p\right)$, perturbed discrete Laplace $PDL(p,\alpha )$ [6], discrete normal $DN(\mu ,\sigma )$ [5], and the extended Poisson $\mathrm{E-}\mathcal{P}(p,\lambda )$ introduced in ref. [18]. Model fit is assessed via log-likelihood and information criteria (AIC/BIC), using grouped frequencies consistent with ref. [18] for the goodness-of-fit evaluation.

Figure 11 displays the fitted probability mass functions, whereas Figure 12 contains the Total Time on Test (TTT) plot. The empirical TTT curve was compared to the TTT curve implied by the fitted $\mathrm{Sy-}\mathcal{P}$ model. A close alignment of the curves indicates an adequate fit. Table 2 reports the numerical comparisons. The symmetric Poisson achieves the best (smallest) AIC and BIC, marginally improving upon the extended Poisson while preserving explicit symmetry around zero. The estimated parameters for $\mathrm{Sy-}\mathcal{P}$ are $\widehat{\theta }=0.49$ and $\widehat{\lambda }=2.47$, consistent with a zero-centered, moderately dispersed pattern with a high concentration of probability near the origin. Further, we also find the percentile estimators by fixing $p_1=0.25,p_2=0.75$ of the parameters, which are given by $(\widehat{\theta },\widehat{\lambda })=(0.41,2.87)$. The favorable fit obtained for attendance differences directly reflects the strengths of the $\mathrm{Sy-}\mathcal{P}$ specification. These data are balanced around zero and moderately dispersed; the $\mathrm{Sy-}\mathcal{P}$ model captures these patterns through exact symmetry, flexible control of the zero mass via $\theta$, and tail heredity from the Poisson magnitude. Such theoretical features translate into practical performance, as confirmed by the reduced AIC/BIC values relative to other symmetric alternatives.

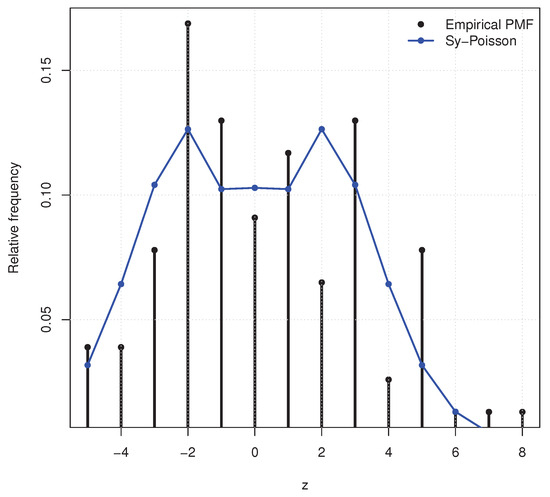
Figure 11. Empirical PMF and fitted $\mathrm{Sy-}\mathcal{P}(\widehat{\theta },\widehat{\lambda })$ for attendance increments.

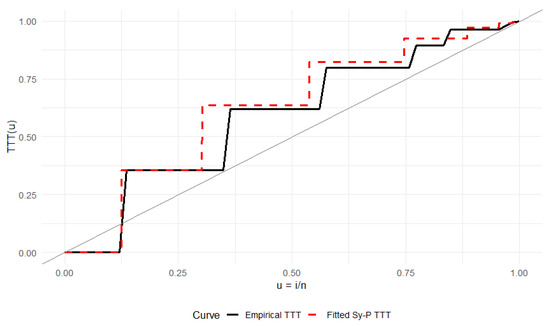
Figure 12. TTT plot for attendance increments comparing the empirical curve with the fitted $\mathrm{Sy-}\mathcal{P}$ model. The diagonal line represents the exponential distribution reference.

Table 2. Model comparison for attendance increments (IDRAC, Lyon, 2012–2013).

Model	Fitted Parameters	Log-Likelihood	AIC	BIC
$DL\left(p\right)$	$\widehat{p}=0.73$	$-203.54$	409.08	411.43
$PDL(p,\alpha )$	$\widehat{p}=0.65,\widehat{\alpha }=0.49$	$-202.94$	409.89	414.57
$DN(\mu ,\sigma )$	$\widehat{\mu }=0.31,\widehat{\sigma }=1.73$	$-195.10$	394.21	398.88
$\mathrm{E-}\mathcal{P}(p,\lambda )$	$\widehat{p}=0.51,\widehat{\lambda }=2.45$	$-193.64$	391.28	395.96
$\mathrm{Sy-}\mathcal{P}(\theta ,\lambda )$	$\widehat{\theta }=0.49,\widehat{\lambda }=2.47$	−193.62	391.25	395.93

Remark 11.

(i) The $\mathrm{Sy-}\mathcal{P}$ fit closely tracks the extended Poisson while enforcing exact symmetry and offering closed-form tools for sums/differences (Section 3.9). (ii) The estimate $\widehat{\theta }=0.49$ lies near the upper boundary $1/2$, aligning with pronounced concentration at zero and balanced tails; convergence diagnostics were stable under maximum likelihood with MoM initialization.

8. Concluding Remarks

In this paper, we introduce the Sy-$\mathbb{Z}$ family, a unified and tractable framework for symmetric integer-valued modeling based on a simple sign-magnitude decomposition. Writing $Z=XY$ with $X\sim \mathrm{SMB}\left(\theta \right)$ and $Y\in {\mathbb{N}}_0$ as independent variables yields models that are exactly symmetric around zero, allowing for interpretable control of the atom at zero and inheriting tail behavior and dispersion from the chosen magnitude distribution. Within this framework, we derived closed-form expressions for the PMF and CDF, bilateral generating functions, and even-order moments; established a characterization by symmetry and sign-magnitude independence; and studied tail transfer, modality, and the equality in law between sums and differences of independent Sy-$\mathbb{Z}$ variables.

Specializing in a Poisson magnitude leads to the Sy-Poisson model, for which we obtained explicit generating functions, moment identities, and entropy, and developed both method-of-moments and likelihood-based inference. Monte Carlo simulations showed that the maximum likelihood estimators exhibit small finite-sample bias and accurate Wald confidence-interval coverage, while the TTT plots and empirical applications in finance and education confirmed that Sy-Poisson can match or improve upon classical two-sided competitors on $\mathbb{Z}$. Beyond these case studies, the sign-magnitude structure suggests further applications in quality-control contexts, where signed deviations from target defect levels or specification limits arise naturally. Promising directions for future work include regression extensions, dependence modeling and time-series formulations, multivariate constructions, and the development of Sy-$\mathbb{Z}$ based monitoring tools for quality-control problems.