A Utilization of Liouville–Caputo Fractional Derivatives for Families of Bi-Univalent Functions Associated with Specific Holomorphic Symmetric Function

Abstract

In this investigation, two new subfamilies of bi-univalent functions defined on the open unit disk are presented using Liouville–Caputo fractional derivatives. We determine bounds on the initial Maclaurin coefficients $|a_2|$ and $|a_3|,$ as well as Fekete–Szegö inequality results based on the bonds of $a_2$ and $a_3$ for functions belonging to certain bi-univalent function subfamilies. Additionally, some novel subfamilies are inferred that have not yet been examined within the context of Liouville–Caputo fractional derivatives.

1. Introduction

Let $\mathbf{U}$ denote the family of holomorphic functions of the form:

$$f\left(z\right)=z+\sum _{v=2}^{\infty }{a}_v{z}^v,\mathrm{\Delta }=\left\{z:\left|z\right|<1\right\}.$$

(1)

Further, the family of all functions in $\mathbf{U}$ that are univalent in the symmetric domain $\mathrm{\Delta }$ is denoted by $\mathcal{W}$. Therefore, every function $f\in \mathcal{W}$ has an inverse $f^{-1}$, defined by

$$f^{-1}\left(f\left(z\right)\right)=z(z\in \mathrm{\Delta })$$

and

$$f\left(f^{-1}\left(w\right)\right)=w(\left|w\right|<r_0\left(f\right);r_0\left(f\right)\ge {\displaystyle \frac{1}{4}})$$

where

$$G\left(w\right)=:f^{-1}\left(w\right)=w-a_2{w}^2+(2a_2^2-a_3)w^3-(5a_2^3-5a_2{a}_3+a_4)w^4+\dots .$$

If both $f\left(z\right)$ and $f^{-1}\left(z\right)$ are univalent in $\mathrm{\Delta }$, then a function $f\in \mathbf{U}$ is in the family $\mathbf{\Omega }$ (the family of bi-univalent functions in $\mathrm{\Delta })$.

For holomorphic functions f and J in $\mathrm{\Delta }$. The function f is subordinate to J, if there exists a holomorphic function w in $\mathrm{\Delta }$, such that $\left|w\left(z\right)\right|<1$, $w\left(0\right)=0$ and $f\left(z\right)=J\left(w\right(z\left)\right).$ Also, if J $\in \mathcal{W}$ in $\mathrm{\Delta }$, then $f\left(z\right)\prec J\left(z\right)$ iff $f\left(0\right)=J\left(0\right)$ and $f\left(\mathrm{\Delta }\right)\subset J\left(\mathrm{\Delta }\right).$

Operators have been used since the early development of complex function theory. They may yield new findings, especially those concerning the convexity and starlikeness of specific functions, and they have simplified the application of many established discoveries. New families of analytic functions are typically introduced as a result of operator-based research. In recent years, the use of operators to analyze bi-univalent functions has also become a common approach, as demonstrated by the latest results in refs. [1,2]. Getting Fekete–Szegö (Fekete and Szegö [3]) functional for special families is of particular interest, according to the most recent publication [4].

The investigation of non-integer-order integro-differential operators is known as fractional calculus (FC). This subject was initially brought up by Gottfried Wilhelm Leibniz in a 1695 letter addressed to Guillaume de L’Hospital. When he asked What happens if the order of a derivative is half, W. Leibniz replied that “it will lead to a paradox, from which one day a useful consequence will be drawn” (for more details, see ref. [5]). The literature claims that the Riemann–Liouville fractional integral and derivative play a major role in FC growth [6]. We used earlier concepts and their well-known extensions involving fractional derivatives (FDs) and fractional integrals (FIs). In 1984, Srivastava and Owa [7] introduced the operator $R^{\gamma }:\mathbf{U}\to \mathbf{U}$, defined by

$$R^{\gamma }f\left(z\right)=\mathrm{\Gamma }(2-\gamma )z^{\gamma }{\mathcal{I}}_z^{\gamma }f\left(z\right)=z+\sum _{v=2}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(v+1)\mathrm{\Gamma }(2-\gamma )}{\mathrm{\Gamma }(v+1-\gamma )}}{a}_v{z}^v=z+\sum _{v=2}^{\infty }\mathrm{\Lambda }(v,\gamma )a_v{z}^v,$$

where $\gamma \in \mathbb{R};\gamma \ne 2,3,4,\dots$.

Definition 1.

Let $f\in \mathbf{U}$ be defined on a simply connected region of the z-plane containing the origin. The fractional integral (FI) of f of order ρ is defined as follows:

$${\mathcal{I}}_z^{-\rho }f\left(z\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\rho \right)}}\underset{0}{\overset{z}{\int }}{\displaystyle \frac{f\left(y\right)}{{(z-y)}^{1-\rho }}}dy,\rho >0.$$

Additionally, the fractional derivatives (FD) of f of order ρ is defined as follows:

$${\mathcal{I}}_z^{\rho }f\left(z\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\rho )}}{\displaystyle \frac{d}{dz}}{\int }_0^z{\displaystyle \frac{f\left(y\right)}{{(z-y)}^{\rho }}}dy,0\le \rho <1,$$

where the multiplicity in the expressions ${(z-y)}^{\rho -1}$ and ${(z-y)}^{-\rho }$ is resolved by imposing that $log(z-y)$ be real for $z>y$.

Definition 2.

The FD of f of order $n+\rho$ is defined as follows:

$${\mathcal{I}}_z^{-n+\rho }f\left(z\right)={\displaystyle \frac{d^n}{d{z}^n}}{\mathcal{I}}_z^{\rho }f\left(z\right),0\le \rho <1,n\in {\mathbb{N}}_0.$$

The fractional-order derivative is defined in the sense of Liouville–Caputo [8], and it is assumed that

$${\mathcal{I}}^{\rho }f\left(z\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(v-\rho )}}\underset{a}{\overset{z}{\int }}{\displaystyle \frac{f^{\left(v\right)}\left(y\right)}{{(u-y)}^{\rho +1-v}}}dy$$

where $v-1<Re\left(\rho \right)\le v,v\in \mathbb{N},$ and $\rho \in \mathbb{C}$ is the initial value of $f.$

Additionally, Owa [9] proposed an operator that extends and unifies the Salagean derivative operator [10] and the Libera integral operator [11].

$${\mathrm{\Theta }}^{\varsigma }f\left(z\right)=\mathrm{\Gamma }(2-\varsigma )z^{\varsigma }{\mathcal{I}}^{\rho }f\left(z\right)=z+\sum _{v=2}^{\infty }{a}_v{z}^v,\varsigma \in \mathbb{R}.$$

Recently, Salah et al. in ref. [12] examined

$$\begin{array}{ccc}\hfill K_{\rho }^{\varsigma }f\left(z\right)& =& {\displaystyle \frac{\mathrm{\Gamma }(2+\varsigma -\rho )}{\mathrm{\Gamma }(\varsigma -\rho )}}{z}^{\rho -\varsigma }{\int }_0^z{\displaystyle \frac{{\mathrm{\Theta }}^{\varsigma }f\left(y\right)}{{(z-y)}^{\rho +1-\varsigma }}}dy,\hfill \\ \hfill (\varsigma & \in & \mathbb{R},\varsigma -1<\rho <\varsigma <2).\hfill \end{array}$$

Simple calculations yield

$$K_{\rho }^{\varsigma }f\left(z\right)=z+\sum _{v=2}^{\infty }{O}_v{a}_v{z}^v,z\in \mathrm{\Delta }$$

where

$$O_v={\displaystyle \frac{\mathrm{\Gamma }(2+\varsigma -\rho )\mathrm{\Gamma }(2-\varsigma ){\left(\mathrm{\Gamma }(v+1)\right)}^2}{\mathrm{\Gamma }(v-\varsigma +1)\mathrm{\Gamma }(v+\varsigma -\rho +1)}}.$$

(2)

Note that, $K_0^{0}f\left(z\right)=f\left(z\right)$ and $K_1^{1}f\left(z\right)=z{f}^{\prime }\left(z\right).$

We express

$$\begin{array}{ccc}\hfill K_{\rho }^{\varsigma }f\left(z\right)& =& z+O_2{a}_2{z}^2+O_3{a}_3{z}^3+\dots z\in \mathbf{U}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill K_{\rho }^{\varsigma }G\left(w\right)& =& w-O_2{a}_2{w}^2+O_3(2a_2^2-a_3)w^3+\dots w\in \mathbf{U}.\hfill \end{array}$$

(4)

Studying subfamilies by additional geometric or analytic criteria, such as starlike functions, convex functions, bi-starlike, bi-convex, highly starlike, quasi-convex functions, etc., provides insight into how analytic functions transform the unit disk; it is helpful for readers and researchers because it helps extend classical results such as coefficient bounds or distortion theorems for univalent functions that do not directly apply to bi-univalent ones. It also develops coefficient bounds and subfamilies enable applications in the applied sciences, better estimation, and comprehension of the features of inverse functions.

The investigation of coefficient estimates for functions belonging to specific special families traces back to the early development of univalent function theory. Gronwall’s Area Theorem, which was discovered in 1914 and is used to compute restrictions on the coefficients of the family of meromorphic functions, is a significant finding in the theory of univalent functions. Bieberbach’s well-known conjecture led to the development of numerous techniques in the geometric theory of functions of a complex variable, which was only confirmed in 1984, and his solution of an equivalent problem for the family $\mathcal{W}$ in 1916. Similar to the families Gronwall and Bieberbach looked at, the first two coefficients of Maclaurin are usually estimated when studying bi-univalent functions.

For each function in $\mathbf{\Omega }$ given by (1), Lewin [13] proved that $|a_2| <1.51$. Brannan and Clunie [14] then refined Lewin’s conclusion and postulated that $\left|a_2\right| \le \sqrt{2}$. Netanyahu [15] later proved that $\underset{f\in \mathbf{\Omega }}{\max }\left|a_2\right|={\displaystyle \frac{4}{3}}$. The challenge of estimating Maclaurin coefficient problem $|a_v|$ for $v\in \{4,5,6,\dots \}$ remains an open problem (for more information, see ref. [16]).

The concepts of quantum or fractional calculus are applied to develop new families of holomorphic functions. Consequently, one can investigate various useful results such as the Fekete–Szegö problem, coefficient estimations, and subordination features. This brings up important topics for scholars, such as radius challenges, convolution characteristics, distortion theorems, and closure theorems. These results can also be applied to meromorphic and multivalent functions, which are inspired by recent studies on bi-univalent functions, for example, [17,18], as well as by the methods previously employed (see refs. [19,20]).

The recurrence relation quantifies the traditional telephone numbers, often known as involution numbers

$$\chi \left(v\right)=\chi (v-1)+(v-1)\chi (v-2),v\ge 2$$

with initial conditions $\chi \left(0\right)=\chi \left(1\right)=1.$

Heinrich August Rothe connected these numbers over symmetric groups in 1800 and discovered that $\chi \left(v\right)$ is the number of involutions in the symmetric group (see, for instance, refs. [21,22]). It is true that the vth involution number is also the number of the Young tableaux on the set $1,2,\dots ,v$ since involutions resemble a typical Young tableaux (for more information, see ref. [23]). John Riordan claims that the number of construction patterns in a telephone system with n customers can be found using the above recurrence relation (see ref. [24]). Wlochand Wolowiec-Musial [25] introduced generalized telephone numbers $\chi (\mathcal{l},v)$, which are defined for integers $v\ge 0$ and $\mathcal{l}\ge 1$ by the following recursion:

$$\chi (\mathcal{l},v)=\mathcal{l}\chi (\mathcal{l},v-1)+(v-1)\chi (\mathcal{l},v-2)$$

with initial conditions $\chi (\mathcal{l},0)=1$ and $\chi (\mathcal{l},1)=\mathcal{l}.$

Bednarz and Wolowiec-Musial [26] have provided an easily accessible generalization of phone numbers by

$${\chi }_{\mathcal{l}}\left(v\right)={\chi }_{\mathcal{l}}(v-1)+\mathcal{l}(v-1){\chi }_{\mathcal{l}}(v-2),(\mathcal{l}\ge 1,v\ge 2)$$

with initial conditions ${\chi }_{\mathcal{l}}\left(0\right)={\chi }_{\mathcal{l}}\left(1\right)=1.$

Most recently, Deniz [27] derived the exponential generating function $\mathsf{Ϝ}\left(z\right)$ for ${\chi }_{\mathcal{l}}\left(v\right)$ with the domain $\mathrm{\Delta }$ as follows:

$$\begin{array}{ccc}\hfill \mathsf{Ϝ}\left(z\right)& =& e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}=\sum _{v=0}^{\infty }{\chi }_{\mathcal{l}}\left(v\right){\displaystyle \frac{z^v}{v!}}\hfill \\ & =& {\chi }_{\mathcal{l}}\left(0\right)+{\chi }_{\mathcal{l}}\left(1\right)z+{\displaystyle \frac{{\chi }_{\mathcal{l}}\left(2\right)}{2}}{z}^2+{\displaystyle \frac{{\chi }_{\mathcal{l}}\left(3\right)}{6}}{z}^3+{\displaystyle \frac{{\chi }_{\mathcal{l}}\left(4\right)}{24}}{z}^4+\dots \hfill \\ & \equiv & 1+z+{\displaystyle \frac{1+\mathcal{l}}{2}}{z}^2+{\displaystyle \frac{1+3\mathcal{l}}{6}}{z}^3+{\displaystyle \frac{3{\mathcal{l}}^2+6\mathcal{l}+1}{24}}{z}^4+\dots ,\mathcal{l}\ge 1,\hfill \end{array}$$

(5)

(see Deniz [27] for more information).

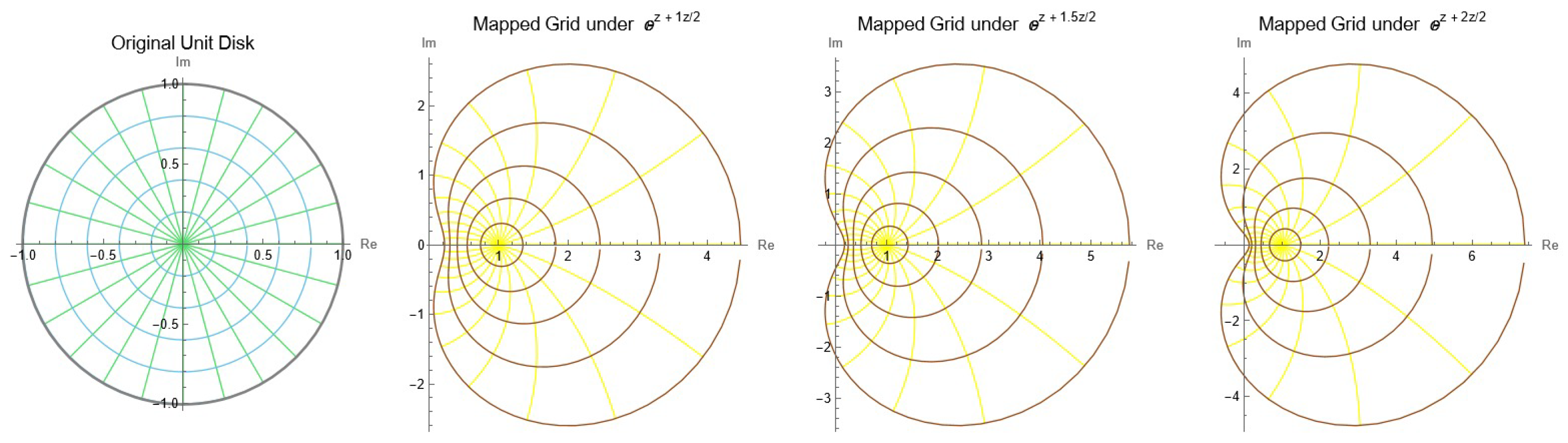
We note that $\mathsf{Ϝ}\left(z\right)$ is holomorphic in $\mathrm{\Delta }$ such that $\mathsf{Ϝ}\left(0\right)=1,$ ${\mathsf{Ϝ}}^{\prime }\left(0\right)>0$ and $\mathsf{Ϝ}$ maps $\mathrm{\Delta }$ onto a starlike region with respect to 1 and symmetric with respect to the real axis.

Figure 1 shows the image of the mapping $\mathsf{Ϝ}\left(z\right)=e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$ for special choices of parameter ℓ.

Figure 1. The image of the mapping $\mathsf{Ϝ}\left(z\right)=e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$.

Recently, many scholars have investigated different families of holomorphic and univalent functions by choosing appropriate special functions (see, for example, refs. [28,29,30]). In this work, we employ the function $\mathsf{Ϝ}\left(z\right)$ for this purpose.

Lemma 1 ([31]).

Let $M\in \mathcal{W}$ be a function of the form:

$$M\left(z\right)=1+m_{1}z+m_2{z}^2+m_3{z}^3+\dots (z\in \mathrm{\Delta }),$$

then $\left|m_v\right|\le 2,$ $v\in \mathbb{N}$.

In this work, according to the modified Liouville–Caputo fractional derivative operator $K_{\rho }^{\varsigma }$, we create two new families $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ and $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ in $\mathbf{\Omega }$, then we determine $|a_2|$ and $|a_3|$, as well as the Fekete–Szegö issue for functions in these new families with considering $z,w\in \mathrm{\Delta }$ and $G=f^{-1}$ unless otherwise stated.

2. The Main Results of Function Family $\mathcal{A}(\mathit{\kappa },\mathit{\epsilon };{\mathit{O}}_{\mathit{v}};\mathsf{Ϝ})$

In this section, we will provide the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ of holomorphic functions and then estimates for the coefficients $|a_2|$, $|a_3|,$ and the Fekete-Szegö functional $\left|a_3-{\rm Y}{a}_2^2\right|$ for functions in this family.

Definition 3.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ provided that it satisfies the following subordination conditions:

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }f\left(z\right)}{z}}+\kappa {\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\epsilon z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }G\left(w\right)}{w}}+\kappa {\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\epsilon w{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}$$

where $\kappa \ge 1$ and $\epsilon \ge 0.$

We may compute examples of functions in the aforementioned family using Mathematica, as demonstrated by the following example, which graphically illustrates this inclusion:

Example 1.

The family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ is not empty; for example, let $f_{\lambda }\left(z\right)={\displaystyle \frac{z}{1-\lambda z}}$. Then

$$K_{\rho }^{\varsigma }{f}_{\lambda }\left(z\right)=z+\sum _{v=2}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(2+\varsigma -\rho )\mathrm{\Gamma }(2-\varsigma ){\left(\mathrm{\Gamma }(v+1)\right)}^2}{\mathrm{\Gamma }(v-\varsigma +1)\mathrm{\Gamma }(v+\varsigma -\rho +1)}}{\lambda }^v{z}^v,$$

and hence

$$\mathbb{K}\left(z\right):=(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }{f}_{\lambda }\left(z\right)}{z}}+\kappa {\left(K_{\rho }^{\varsigma }{f}_{\lambda }\left(z\right)\right)}^{\prime }+\epsilon z{\left(K_{\rho }^{\varsigma }{f}_{\lambda }\left(z\right)\right)}^{″}$$

$$=1+\sum _{v=2}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(2+\varsigma -\rho )\mathrm{\Gamma }(2-\varsigma ){\left(\mathrm{\Gamma }(v+1)\right)}^2}{\mathrm{\Gamma }(v-\varsigma +1)\mathrm{\Gamma }(v+\varsigma -\rho +1)}}((1-\kappa )+\kappa v+\epsilon v(v-1)){\lambda }^v{z}^{v-1}.$$

(1) 

Taking $\varsigma =1$, $\rho =0$, $\epsilon =0$, $\kappa ={\displaystyle \frac{1}{2}}$, then

$${\mathbb{K}}_1\left(z\right)=1+\sum _{v=2}^{\infty }v{\lambda }^v{z}^{v-1}\prec e^{\left(z+0.9{\displaystyle \frac{z^2}{2}}\right)}\mathit{whenever}\left|\lambda \right|<0.6.$$

Therefore $f_{\lambda }\in \mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})\mathit{whenever}\left|\lambda \right|<0.6.$

(2) 

Taking $\varsigma ={\displaystyle \frac{3}{2}}$, $\rho ={\displaystyle \frac{1}{2}}$, $\epsilon ={\displaystyle \frac{1}{2}}$, $\kappa ={\displaystyle \frac{1}{2}}$, then

$${\mathbb{K}}_2\left(z\right)=1+\sum _{v=2}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }(v+1)(1+v^2)}{\mathrm{\Gamma }(v-\frac{1}{2})(v+1)}}{\lambda }^v{z}^{v-1}.\prec e^{\left(z+0.9{\displaystyle \frac{z^2}{2}}\right)}\mathit{whenever}\left|\lambda \right|<0.3.$$

Therefore $f_{\lambda }\in \mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})\mathit{whenever}\left|\lambda \right|<0.3.$

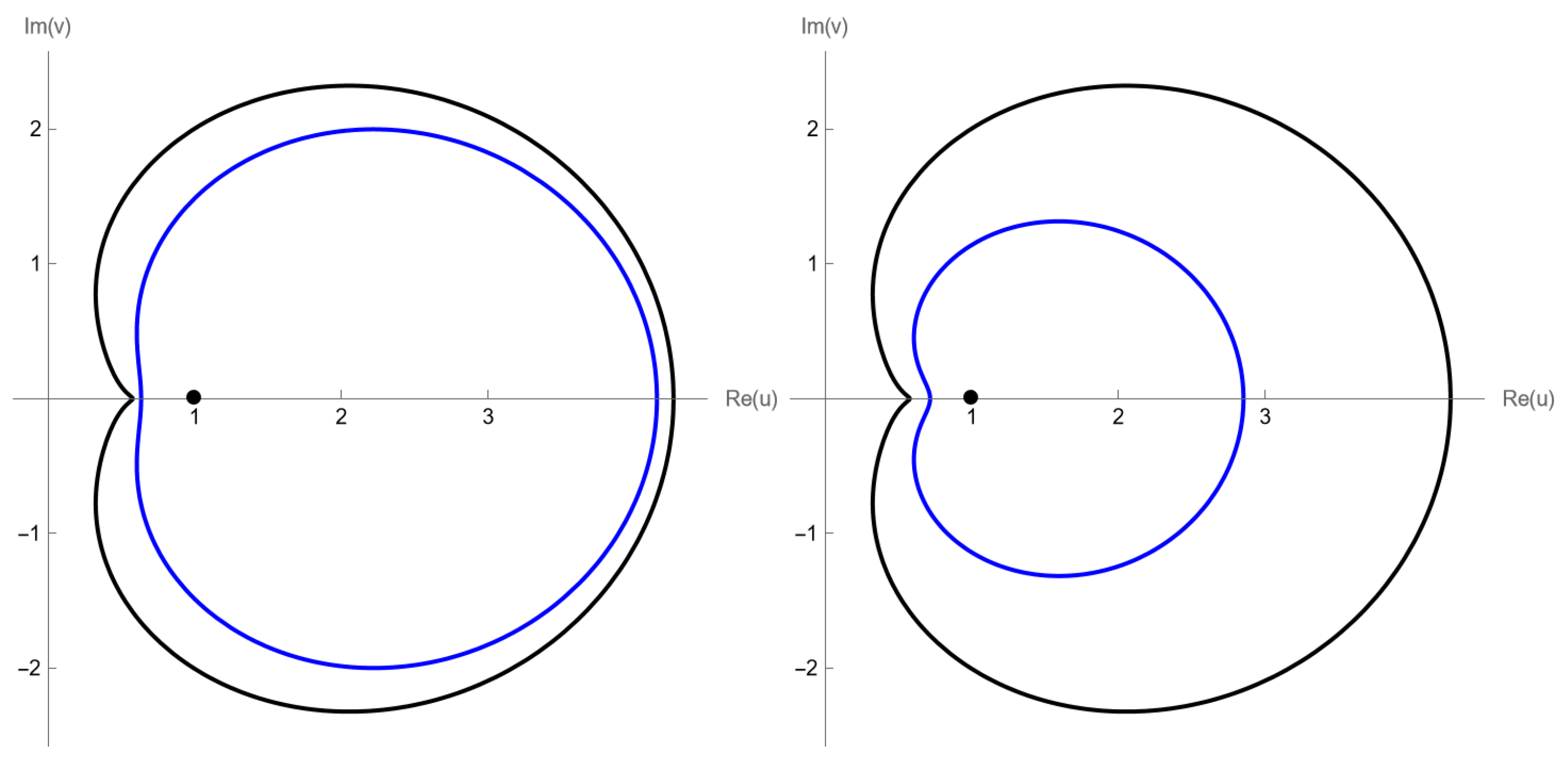
Figure 2 below illustrate the inclusion observed in the previous example. Readers can also explore numerous special cases by varying the parameter values and performing computations and plots using Mathematica 14.3.

Figure 2. The inclusion depicted in (1) is represented by the left figure, and the inclusion depicted in (2) is represented by the right figure.

The remaining examples will be special cases that come from the newly introduced family of functions. For $\kappa =1$, the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 2.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(1,\epsilon ;O_v;\mathsf{Ϝ})$ if

$${\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\epsilon z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$${\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\epsilon w{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}$$

where $\epsilon \ge 0.$

For $\epsilon =0$, the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 3.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(\kappa ,0;O_v;\mathsf{Ϝ})$ if

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }f\left(z\right)}{z}}+\kappa {\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }G\left(w\right)}{w}}+\kappa {\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}$$

where $\kappa \ge 1.$

For $\epsilon =0$ and $\kappa =1$, the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 4.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(1,0;O_v;\mathsf{Ϝ})$ if

$${\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$${\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}.$$

For $\epsilon =\varsigma =\rho =0$ and $\kappa =1$, the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 5.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(1,0;1;\mathsf{Ϝ})$ if

$$f^{\prime }\left(z\right)\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$G^{\prime }\left(w\right)\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right).}$$

For $\varsigma =\rho =0$, the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 6 ([32]).

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{A}(\kappa ,\epsilon ;1;\mathsf{Ϝ})$ if

$$(1-\kappa ){\displaystyle \frac{f\left(z\right)}{z}}+\kappa f^{\prime }\left(z\right)+\epsilon z{f}^{″}\left(z\right)\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$(1-\kappa ){\displaystyle \frac{G\left(w\right)}{w}}+\kappa G^{\prime }\left(w\right)+\epsilon w{G}^{″}\left(w\right)\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}$$

where $\kappa \ge 1$ and $\epsilon \ge 0.$

Theorem 1.

Let $\kappa \ge 1,$$\epsilon \ge 0$. If the function $f\left(z\right)$, defined by (1), is a member of the family $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{O_2\left|2\epsilon +\kappa +1\right|}},{\displaystyle \frac{2}{O_2\sqrt{\left|2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{O_3\left|6\epsilon +2\kappa +1\right|}}+{\displaystyle \frac{1}{O_3{\left|2\epsilon +\kappa +1\right|}^2}},{\displaystyle \frac{\mathcal{l}+1}{O_3\left|6\epsilon +2\kappa +1\right|}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{O_3(6\epsilon +2\kappa +1)}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{O_2^2\left[2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right]}}.$$

The bounds in Theorem 1 are not sharp.

Proof. 

Let $f\left(z\right)\in \mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ and $G=f^{-1}$. Then there are two holomorphic functions $\beta ,\alpha :\mathrm{\Delta }\to \mathrm{\Delta }$ with $\beta \left(0\right)=\alpha \left(0\right)=0,$ and satisfying the conditions:

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }f\left(z\right)}{z}}+\kappa {\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\epsilon z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}=\mathsf{Ϝ}\left(\beta \left(z\right)\right),z\in \mathrm{\Delta }$$

(6)

and

$$(1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }G\left(w\right)}{w}}+\kappa {\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\epsilon w{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}=\mathsf{Ϝ}\left(\alpha \left(w\right)\right),w\in \mathrm{\Delta }.$$

(7)

Define the functions C and B by

$$C\left(z\right)={\displaystyle \frac{1+\beta \left(z\right)}{1-\beta \left(z\right)}}=1+r_{1}z+r_2{z}^2+\dots$$

and

$$B\left(z\right)={\displaystyle \frac{1+\alpha \left(z\right)}{1-\alpha \left(z\right)}}=1+l_{1}z+l_2{z}^2+\dots .$$

It is clear that C and B are holomorphic in $\mathrm{\Delta }$ and $C\left(0\right)=B\left(0\right)=1$. Then the functions $\beta ,\alpha :\mathrm{\Delta }\to \mathrm{\Delta }$ are defined such that each of C and B has a positive real part in $\mathrm{\Delta }$, and we have

$$\beta \left(z\right)={\displaystyle \frac{C\left(z\right)-1}{C\left(z\right)+1}}={\displaystyle \frac{1}{2}}\left[r_{1}z+\left(r_2-{\displaystyle \frac{r_1^2}{2}}\right)z^2\right]+\dots (z\in \mathrm{\Delta })$$

(8)

and

$$\alpha \left(z\right)={\displaystyle \frac{B\left(z\right)-1}{B\left(z\right)+1}}={\displaystyle \frac{1}{2}}\left[l_{1}z+\left(l_2-{\displaystyle \frac{l_1^2}{2}}\right)z^2\right]+\dots (z\in \mathrm{\Delta }).$$

(9)

Substituting (8) into (6) and (9) into (7), and applying (5), we have

$$\begin{array}{}& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& (1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }f\left(z\right)}{z}}+\kappa {\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\epsilon z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}\hfill & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& \mathsf{Ϝ}\left(\beta \left(z\right)\right)=:e^{\left({\displaystyle \frac{r\left(z\right)-1}{r\left(z\right)+1}}+{\displaystyle \frac{\mathcal{l}}{2}}{\left({\displaystyle \frac{r\left(z\right)-1}{r\left(z\right)+1}}\right)}^2\right)}\hfill & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& 1+{\displaystyle \frac{1}{2}}{r}_{1}z+\left({\displaystyle \frac{r_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)r_1^2}{8}}\right)z^2+\dots \hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(10\right)\end{array}$$

and

$$\begin{array}{}& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& (1-\kappa ){\displaystyle \frac{K_{\rho }^{\varsigma }G\left(w\right)}{w}}+\kappa {\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\epsilon w{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}\hfill & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& \mathsf{Ϝ}\left(\alpha \left(w\right)\right)=:e^{\left({\displaystyle \frac{l\left(w\right)-1}{l\left(w\right)+1}}+{\displaystyle \frac{\mathcal{l}}{2}}{\left({\displaystyle \frac{l\left(w\right)-1}{l\left(w\right)+1}}\right)}^2\right)}\hfill & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& 1+{\displaystyle \frac{1}{2}}{l}_{1}w+\left({\displaystyle \frac{l_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)l_1^2}{8}}\right)w^2+\dots .\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(11\right)\end{array}$$

From (10) and (11), we get

$$\begin{array}{cc}\hfill (2\epsilon +\kappa +1)O_2{a}_2& ={\displaystyle \frac{r_1}{2}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill (6\epsilon +2\kappa +1)O_3{a}_3& ={\displaystyle \frac{r_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)r_1^2}{8}},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill -(2\epsilon +\kappa +1)O_2{a}_2& ={\displaystyle \frac{l_1}{2}},\hfill \end{array}$$

(14)

and

$$(6\epsilon +2\kappa +1)(2O_2^2{a}_2^2-O_3{a}_3)={\displaystyle \frac{l_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)l_1^2}{8}}.$$

(15)

From (12) and (14), we get

$$r_1=-l_1$$

(16)

and

$$8{(2\epsilon +\kappa +1)}^2{O}_2^2{a}_2^2=r_1^2+l_1^2.$$

(17)

By adding (13) with (15), we get

$$2(6\epsilon +2\kappa +1)O_2^2{a}_2^2={\displaystyle \frac{1}{2}}(r_2+l_2)+{\displaystyle \frac{(\mathcal{l}-1)}{8}}(r_1^2+l_1^2).$$

(18)

Substituting the value of $r_1^2+l_1^2$ from (17) in (18), we find that

$$a_2^2={\displaystyle \frac{r_2+l_2}{O_2^2\left[2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right]}}.$$

(19)

Using Lemma 1 for (17) and (19), we get

$$\left|a_2\right|\le {\displaystyle \frac{1}{O_2\left|2\epsilon +\kappa +1\right|}},\left|a_2\right|\le {\displaystyle \frac{2}{O_2\sqrt{\left|2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right|}}}.$$

Next, by subtracting (15) from (13) and using (16), we get $r_1^2=l_1^2,$ hence

$$2(6\epsilon +2\kappa +1)\left(O_3{a}_3-O_2^2{a}_2^2\right)={\displaystyle \frac{1}{2}}(r_2-l_2),$$

(20)

then by substituting the value of $a_2^2$ from (17) into (20), we have

$$O_3{a}_3={\displaystyle \frac{r_2-l_2}{4(6\epsilon +2\kappa +1)}}+{\displaystyle \frac{r_1^2+l_1^2}{8{(2\epsilon +\kappa +1)}^2}}.$$

Applying Lemma 1, we have

$$\left|a_3\right|\le {\displaystyle \frac{1}{O_3\left|6\epsilon +2\kappa +1\right|}}+{\displaystyle \frac{1}{O_3{\left|2\epsilon +\kappa +1\right|}^2}}.$$

Also, substituting the value of $a_2^2$ from (18) into (20), we have

$$O_3{a}_3={\displaystyle \frac{2r_2+\frac{1}{4}(\mathcal{l}-1)\left(r_1^2+l_1^2\right)}{4(6\epsilon +2\kappa +1)}}.$$

Applying Lemma 1, we have

$$\left|a_3\right|\le {\displaystyle \frac{\mathcal{l}+1}{O_3\left|6\epsilon +2\kappa +1\right|}}.$$

From (19) and (20), it follows that

$$\begin{array}{ccc}\hfill a_3-{\rm Y}{a}_2^2& =& {\displaystyle \frac{r_2-l_2}{4O_3(6\epsilon +2\kappa +1)}}+({\displaystyle \frac{O_2^2}{O_3}}-{\rm Y})a_2^2\hfill \\ & =& {\displaystyle \frac{r_2-l_2}{4O_3(6\epsilon +2\kappa +1)}}+{\displaystyle \frac{(\frac{O_2^2}{O_3}-{\rm Y})\left(r_2+l_2\right)}{O_2^2\left[2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right]}}\hfill \\ & =& \left[H({\rm Y})+{\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}}\right]r_2+\left[H({\rm Y})-{\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}}\right]l_2,\hfill \end{array}$$

where

$$H({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{O_2^2\left[2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right]}}.$$

According to Lemma 1, we get

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{O_3(6\epsilon +2\kappa +1)}}\mathrm{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}},\\ \\ 4\left|H({\rm Y})\right|\mathrm{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{4O_3(6\epsilon +2\kappa +1)}}.\end{array}\right.$$

□

By setting $\kappa =1$ in Theorem 1, we obtain.

Corollary 1.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{A}(1,\epsilon ;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{2O_2\left|\epsilon +1\right|}},{\displaystyle \frac{2}{O_2\sqrt{\left|6(2\epsilon +1)+4(1-\mathcal{l}){(\epsilon +1)}^2\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{3O_3\left|2\epsilon +1\right|}}+{\displaystyle \frac{1}{4O_3{\left|\epsilon +1\right|}^2}},{\displaystyle \frac{\mathcal{l}+1}{3O_3\left|2\epsilon +1\right|}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{3O_3(2\epsilon +1)}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{12O_3(2\epsilon +1)}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{12O_3(2\epsilon +1)}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{O_2^2\left[6(2\epsilon +1)+4(1-\mathcal{l}){(\epsilon +1)}^2\right]}}.$$

By setting $\epsilon =0$ in Theorem 1, we obtain.

Corollary 2.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{A}(\kappa ,0;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{O_2\left|\kappa +1\right|}},{\displaystyle \frac{2}{O_2\sqrt{\left|2(2\kappa +1)+(1-\mathcal{l}){(\kappa +1)}^2\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{O_3\left|2\kappa +1\right|}}+{\displaystyle \frac{1}{O_3{\left|\kappa +1\right|}^2}},{\displaystyle \frac{\mathcal{l}+1}{O_3\left|2\kappa +1\right|}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{O_3(2\kappa +1)}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{4O_3(2\kappa +1)}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{4O_3(2\kappa +1)}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{O_2^2\left[2(2\kappa +1)+(1-\mathcal{l}){(\kappa +1)}^2\right]}}.$$

By setting $\epsilon =0$ in Corollary 1 or $\kappa =1$ in Corollary 2, we get.

Corollary 3.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{A}(1,0;O_v;\mathsf{Ϝ})$.

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{2O_2}},{\displaystyle \frac{1}{O_2\sqrt{\left|\frac{5}{2}-\mathcal{l}\right|}}}\right\},\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{3O_3}}+{\displaystyle \frac{1}{4O_3}},{\displaystyle \frac{\mathcal{l}+1}{3O_3}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{3O_3}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{12O_3}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{12O_3}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{2O_2^2\left[5-2\mathcal{l}\right]}}.$$

By setting $\varsigma =\rho =0$ in Corollary 3, we obtain.

Corollary 4.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{A}(1,0;1;\mathsf{Ϝ})$.

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{\sqrt{\left|\frac{5}{2}-\mathcal{l}\right|}}}\right\},\left|a_3\right|\le min\left\{{\displaystyle \frac{7}{12}},{\displaystyle \frac{\mathcal{l}+1}{3}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{3}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{12}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{12}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{1-{\rm Y}}{10-4\mathcal{l}}}.$$

By setting $\varsigma =\rho =0$ in Theorem 1, we obtain.

Corollary 5 ([32]).

If $f\left(z\right)$ given by (1) and in the family $\mathcal{A}(\kappa ,\epsilon ;1;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{\left|2\epsilon +\kappa +1\right|}},{\displaystyle \frac{2}{\sqrt{\left|2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{\left|6\epsilon +2\kappa +1\right|}}+{\displaystyle \frac{1}{{\left|2\epsilon +\kappa +1\right|}^2}},{\displaystyle \frac{\mathcal{l}+1}{\left|6\epsilon +2\kappa +1\right|}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{6\epsilon +2\kappa +1}}\mathit{for}\left|H({\rm Y})\right|\le {\displaystyle \frac{1}{4(6\epsilon +2\kappa +1)}},\\ \\ 4\left|H({\rm Y})\right|\mathit{for}\left|H({\rm Y})\right|\ge {\displaystyle \frac{1}{4(6\epsilon +2\kappa +1)}},\end{array}\right.$$

where

$$H({\rm Y})={\displaystyle \frac{1-{\rm Y}}{2(6\epsilon +2\kappa +1)+(1-\mathcal{l}){(2\epsilon +\kappa +1)}^2}}.$$

3. The Main Results of Function Family $\mathcal{B}(\mathit{\xi };{\mathit{O}}_{\mathit{v}};\mathsf{Ϝ})$

In this section, we will present the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ of holomorphic functions and then provide estimates for the coefficients $|a_2|$, $|a_3|,$ and the Fekete-Szegö functional $\left|a_3-{\rm Y}{a}_2^2\right|$ for functions in this family.

Definition 4.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ if it meets the following subordinations

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }f\left(z\right)+\xi z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }}}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }G\left(w\right)+\xi z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }}}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}.$$

In accordance with Example 1, we leave it to the reader to use any program at their disposal to locate examples of functions that correspond to the aforementioned family.

We also include a number of examples below that give us notable special instances. For $\xi =1$, the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 7.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{B}(1;O_v;\mathsf{Ϝ})$ if

$$1+{\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}}{{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }}}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$1+{\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}}{{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }}}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}.$$

For $\xi =0$, the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 8.

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{B}(0;O_v;\mathsf{Ϝ})$ if

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }}{K_{\rho }^{\varsigma }f\left(z\right)}}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }}{K_{\rho }^{\varsigma }G\left(w\right)}}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}.$$

For $\varsigma =\rho =0$ and $\xi =1$, the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 9 ([33]).

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{B}(1;1;\mathsf{Ϝ})$ if

$$1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$$1+{\displaystyle \frac{z{G}^{″}\left(w\right)}{G^{\prime }\left(w\right)}}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right)}.$$

For $\varsigma =\rho =\xi =0$, the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ leads to the next subfamily.

Example 10 ([33]).

A function $f\left(z\right)\in \mathbf{\Omega }$ is said to belong to the family $\mathcal{B}(0;1;\mathsf{Ϝ})$ if

$${\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \mathsf{Ϝ}\left(z\right)=:e^{\left(z+\mathcal{l}{\displaystyle \frac{z^2}{2}}\right)}$$

and

$${\displaystyle \frac{z{G}^{\prime }\left(w\right)}{G\left(w\right)}}\prec \mathsf{Ϝ}\left(w\right)=:e^{\left(w+\mathcal{l}{\displaystyle \frac{w^2}{2}}\right).}$$

Theorem 2.

If the function $f\left(z\right)$, given by (1), is a member of the family $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{O_2\left|\xi +1\right|}},{\displaystyle \frac{\sqrt{2}}{O_2\sqrt{\left|2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{1}{2O_3\left|2\xi +1\right|}}+{\displaystyle \frac{1}{O_3{\left|\xi +1\right|}^2}},{\displaystyle \frac{1}{2O_3\left|2\xi +1\right|}}+{\displaystyle \frac{\mathcal{l}+1}{2O_3\left|2\xi -{\xi }^2+1\right|}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2O_3(2\xi +1)}}\mathit{for}\left|U({\rm Y})\right|\le {\displaystyle \frac{1}{8O_3(2\xi +1)}},\\ \\ 4\left|U({\rm Y})\right|\mathit{for}\left|U({\rm Y})\right|\ge {\displaystyle \frac{1}{8O_3(2\xi +1)}},\end{array}\right.$$

where

$$U({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{2O_2^2\left[2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right]}}.$$

The bounds in Theorem 2 are not sharp.

Proof. 

Let $f\left(z\right)\in \mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ and $G=f^{-1}$. Then there are two holomorphic functions $\beta ,\alpha :\mathrm{\Delta }\to \mathrm{\Delta }$ with $\beta \left(0\right)=\alpha \left(0\right)=0,$ satisfying the conditions:

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }f\left(z\right)+\xi z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }}}=\mathsf{Ϝ}\left(\beta \left(z\right)\right),z\in \mathrm{\Delta }$$

(21)

and

$${\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }G\left(w\right)+\xi z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }}}=\mathsf{Ϝ}\left(\alpha \left(w\right)\right),w\in \mathrm{\Delta },$$

(22)

where $\beta$ given by (8) and $\alpha$ given by (9).

Substituting the value of $\beta$ into (21) and the value of $\alpha$ into (22), and applying (5), we have

$$\begin{array}{}& \hfill {\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }f\left(z\right)+\xi z{\left(K_{\rho }^{\varsigma }f\left(z\right)\right)}^{\prime }}}& =& \mathsf{Ϝ}\left(\beta \left(z\right)\right)=:e^{\left({\displaystyle \frac{r\left(z\right)-1}{r\left(z\right)+1}}+{\displaystyle \frac{\mathcal{l}}{2}}{\left({\displaystyle \frac{r\left(z\right)-1}{r\left(z\right)+1}}\right)}^2\right)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left(23\right)& & =& 1+{\displaystyle \frac{1}{2}}{r}_{1}z+\left({\displaystyle \frac{r_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)r_1^2}{8}}\right)z^2+\dots \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

and

$$\begin{array}{}& \hfill {\displaystyle \frac{z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }+\xi z^2{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{″}}{(1-\xi )K_{\rho }^{\varsigma }G\left(w\right)+\xi z{\left(K_{\rho }^{\varsigma }G\left(w\right)\right)}^{\prime }}}& =& \mathsf{Ϝ}\left(\alpha \left(w\right)\right)=:e^{\left({\displaystyle \frac{l\left(w\right)-1}{l\left(w\right)+1}}+{\displaystyle \frac{\mathcal{l}}{2}}{\left({\displaystyle \frac{l\left(w\right)-1}{l\left(w\right)+1}}\right)}^2\right)}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(24\right)& & =& 1+{\displaystyle \frac{1}{2}}{l}_{1}w+\left({\displaystyle \frac{l_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)l_1^2}{8}}\right)w^2+\dots .\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

From (23) and (24), we get

$$\begin{array}{cc}\hfill (\xi +1)O_2{a}_2& ={\displaystyle \frac{r_1}{2}},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill 2(2\xi +1)O_3{a}_3-{(\xi +1)}^2{O}_2^2{a}_2^2& ={\displaystyle \frac{r_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)r_1^2}{8}},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill -(\xi +1)O_2{a}_2& ={\displaystyle \frac{l_1}{2}},\hfill \end{array}$$

(27)

and

$$-2(2\xi +1)O_3{a}_3-({\xi }^2-6\xi -3)O_2^2{a}_2^2={\displaystyle \frac{l_2}{2}}+{\displaystyle \frac{(\mathcal{l}-1)l_1^2}{8}}.$$

(28)

From (25) and (27), we get

$$r_1=-l_1$$

(29)

and

$$8{(\xi +1)}^2{O}_2^2{a}_2^2=r_1^2+l_1^2.$$

(30)

By adding (26) with (28), we have

$$2(2\xi -{\xi }^2+1)O_2^2{a}_2^2={\displaystyle \frac{1}{2}}(r_2+l_2)+{\displaystyle \frac{(\mathcal{l}-1)}{8}}(r_1^2+l_1^2).$$

(31)

Substituting the value of $r_1^2+l_1^2$ from (30) in (31), we get

$$a_2^2={\displaystyle \frac{r_2+l_2}{2O_2^2\left[2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right]}}.$$

(32)

Then, applying Lemma 1 for (30) and (32), we have

$$\left|a_2\right|\le {\displaystyle \frac{1}{O_2\left|\xi +1\right|}},\left|a_2\right|\le {\displaystyle \frac{\sqrt{2}}{O_2\sqrt{\left|2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right|}}}.$$

If we subtract (28) from (26) and use (29), we get $r_1^2=l_1^2,$ hence

$$4(2\xi +1)\left(O_3{a}_3-O_2^2{a}_2^2\right)={\displaystyle \frac{1}{2}}(r_2-l_2),$$

(33)

then by substituting the value of $a_2^2$ from (30) into (33), we have

$$O_3{a}_3={\displaystyle \frac{r_2-l_2}{8(2\xi +1)}}+{\displaystyle \frac{r_1^2+l_1^2}{8{(\xi +1)}^2}}.$$

Applying Lemma 1, we have

$$\left|a_3\right|\le {\displaystyle \frac{1}{2O_3\left|2\xi +1\right|}}+{\displaystyle \frac{1}{O_3{\left|\xi +1\right|}^2}}.$$

Also, substituting the value of $a_2^2$ from (31) into (33), we get

$$O_3{a}_3={\displaystyle \frac{r_2-l_2}{8(2\xi +1)}}+{\displaystyle \frac{r_2+l_2+\frac{1}{4}(\mathcal{l}-1)\left(r_1^2+l_1^2\right)}{4(2\xi -{\xi }^2+1)}}.$$

Applying Lemma 1, we have

$$\left|a_3\right|\le {\displaystyle \frac{1}{2O_3\left|2\xi +1\right|}}+{\displaystyle \frac{\mathcal{l}+1}{2O_3\left|2\xi -{\xi }^2+1\right|}}.$$

From (32) and (33), we have

$$\begin{array}{ccc}\hfill a_3-{\rm Y}{a}_2^2& =& {\displaystyle \frac{r_2-l_2}{8O_3(2\xi +1)}}+({\displaystyle \frac{O_2^2}{O_3}}-{\rm Y})a_2^2\hfill \\ & =& {\displaystyle \frac{r_2-l_2}{8O_3(2\xi +1)}}+{\displaystyle \frac{(\frac{O_2^2}{O_3}-{\rm Y})\left(r_2+l_2\right)}{2O_2^2\left[2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right]}}\hfill \\ & =& \left[U({\rm Y})+{\displaystyle \frac{1}{8O_3(2\xi +1)}}\right]r_2+\left[U({\rm Y})-{\displaystyle \frac{1}{8O_3(2\xi +1)}}\right]l_2,\hfill \end{array}$$

where

$$U({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{2O_2^2\left[2(2\xi -{\xi }^2+1)+(1-\mathcal{l}){(\xi +1)}^2\right]}}.$$

According to Lemma 1, we get

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2O_3(2\xi +1)}}\mathrm{for}\left|U({\rm Y})\right|\le {\displaystyle \frac{1}{8O_3(2\xi +1)}},\\ \\ 4\left|U({\rm Y})\right|\mathrm{for}\left|U({\rm Y})\right|\ge {\displaystyle \frac{1}{8O_3(2\xi +1)}}.\end{array}\right.$$

□

By settig $\xi =1$ in Theorem 2, we obtain.

Corollary 6.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{B}(1;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{2O_2}},{\displaystyle \frac{1}{O_2\sqrt{2\left|2-\mathcal{l}\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{5}{12O_3}},{\displaystyle \frac{3\mathcal{l}+5}{12O_3}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{6O_3}}\mathit{for}\left|U({\rm Y})\right|\le {\displaystyle \frac{1}{24O_3}},\\ \\ 4\left|U({\rm Y})\right|\mathit{for}\left|U({\rm Y})\right|\ge {\displaystyle \frac{1}{24O_3}},\end{array}\right.$$

where

$$U({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{8O_2^2\left[2-\mathcal{l}\right]}}.$$

By setting $\xi =0$ in Theorem 2, we have.

Corollary 7.

If $f\left(z\right)$ given by (1) and in the family $\mathcal{B}(0;O_v;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{O_2}},{\displaystyle \frac{\sqrt{2}}{O_2\sqrt{\left|3-\mathcal{l}\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{3}{2O_3}},{\displaystyle \frac{\mathcal{l}+2}{2O_3}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2O_3}}\mathit{for}\left|U({\rm Y})\right|\le {\displaystyle \frac{1}{8O_3}},\\ \\ 4\left|U({\rm Y})\right|\mathit{for}\left|U({\rm Y})\right|\ge {\displaystyle \frac{1}{8O_3}},\end{array}\right.$$

where

$$U({\rm Y})={\displaystyle \frac{\frac{O_2^2}{O_3}-{\rm Y}}{2O_2^2\left[3-\mathcal{l}\right]}}.$$

By setting $\varsigma =\rho =0$ in Corollary 6, we have.

Corollary 8 ([33]).

If $f\left(z\right)$ given by (1) and in the family $\mathcal{B}(1;1;\mathsf{Ϝ})$.

$$\left|a_2\right|\le min\left\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{\sqrt{2\left|2-\mathcal{l}\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{5}{12}},{\displaystyle \frac{3\mathcal{l}+5}{12}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{6}}\mathit{for}\left|{\rm Y}-1\right|\le {\displaystyle \frac{\left|2-\mathcal{l}\right|}{3}},\\ \\ {\displaystyle \frac{\left|{\rm Y}-1\right|}{2\left|2-\mathcal{l}\right|}}\mathit{for}\left|{\rm Y}-1\right|\ge {\displaystyle \frac{\left|2-\mathcal{l}\right|}{3}}.\end{array}\right.$$

By setting $\varsigma =\rho =0$ in Corollary 7, we have.

Corollary 9 ([33]).

If $f\left(z\right)$ given by (1) and in the family $\mathcal{B}(0;1;\mathsf{Ϝ})$. Then

$$\left|a_2\right|\le min\left\{1,{\displaystyle \frac{\sqrt{2}}{\sqrt{\left|3-\mathcal{l}\right|}}}\right\},$$

$$\left|a_3\right|\le min\left\{{\displaystyle \frac{3}{2}},{\displaystyle \frac{\mathcal{l}+2}{2}}\right\},$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2}}\mathit{for}\left|{\rm Y}-1\right|\le {\displaystyle \frac{\left|3-\mathcal{l}\right|}{4}},\\ \\ {\displaystyle \frac{2\left|{\rm Y}-1\right|}{\left|3-\mathcal{l}\right|}}\mathit{for}\left|{\rm Y}-1\right|\ge {\displaystyle \frac{\left|3-\mathcal{l}\right|}{4}},\end{array}\right.$$

Finally, we now offer particular numerical examples for the families $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ and $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ to demonstrate the efficacy and applicability of the theoretical results derived in this study.

Example 11.

Examine the subfamily $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ with $\epsilon =\varsigma =\rho =0$ and $\kappa =\mathcal{l}=1$ in Theorem 1 or the subfamily $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$ with $\xi =\varsigma =\rho =0$ and $\mathcal{l}=1$ in Theorem 2. The coefficient estimates yield

$$\left|a_2\right|\le {\displaystyle \frac{1}{2}}=0.25,\left|a_3\right|\le {\displaystyle \frac{7}{12}}\approx 0.583,$$

and

$$\left|a_3-{\rm Y}{a}_2^2\right|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{3}}\mathit{for}\left|1-{\rm Y}\right|\le {\displaystyle \frac{1}{2}},\\ \\ {\displaystyle \frac{2}{3}}\left|1-{\rm Y}\right|\mathit{for}\left|1-{\rm Y}\right|\ge {\displaystyle \frac{1}{2}}.\end{array}\right.$$

4. Conclusions

This work has established estimates for the Fekete–Szegő functional and the initial Maclaurin coefficients $|a_2|$ and $|a_3|$ for the new bi-univalent function families $\mathcal{A}(\kappa ,\epsilon ;O_v;\mathsf{Ϝ})$ and $\mathcal{B}(\xi ;O_v;\mathsf{Ϝ})$, along with their subfamilies detailed in Examples 2–10. The application of a specialized operator to generate these families underscores the novelty of our approach. Looking forward, this research opens avenues for further investigation, particularly the study of second- and third-order Hankel determinants and upper bounds related to the Zalcman conjecture within these families [34].

Ongoing research continues to elucidate the fundamental characteristics of these function classes, motivating the systematic exploration of new families. The consequent refinement of coefficient estimates and the pursuit of original findings remain primary drivers of progress in geometric function theory.