A Symmetrically Verifiable Outsourced Decryption Data Sharing Scheme with Privacy-Preserving for VANETs

Abstract

Frequent data sharing in Vehicular Ad Hoc Networks (VANETs) necessitates a robust foundation of secure access control to ensure data security. Existing ciphertext-policy attribute-based encryption schemes are constrained by the performance bottleneck of a single attribute authority. Furthermore, although many schemes adopt outsourced decryption, the verifiability of the decryption results is not guaranteed. Therefore, this paper proposes a Symmetrically Verifiable Outsourced Decryption Data Sharing Scheme with Privacy-Preserving for VANETs (VODDS). To balance the computational overhead across multiple authorities, VODDS introduces a distributed key distribution mechanism that organizes them into groups. Within each group, the key distribution credential is generated through a Group Key Agreement, with each round secured by a Byzantine consensus mechanism to achieve a balance between security and efficiency. User identities are converted into anonymous representations via hashing for embedding into the attribute keys. Furthermore, blockchain technology is used to record a hash commitment for the verification ciphertext. This enables the user to verify the outsourced result through a smart contract, which performs a symmetrical verification by matching the user’s locally computed hash against the on-chain record. Moreover, VODDS employs a linear secret sharing scheme to achieve policy hiding. We provide security analysis under the q-parallel Bilinear Diffie–Hellman Exponent and Decisional Diffie–Hellman assumptions, which proves the security of VODDS. In addition, VODDS exhibits higher efficiency compared to related schemes in the performance evaluation.

1. Introduction

Benefiting from the growing demand for wireless data exchange in transportation environments, Vehicular Ad Hoc Networks (VANETs) have attracted increasing attention [1]. As an emerging technology, VANETs enable vehicles to share information with other entities (e.g., vehicles, pedestrians, infrastructure) [2]. To ensure the security of shared data (e.g., vehicle speed, energy consumption, road conditions, weather), data encryption is essential [3,4,5].

Frequent data sharing in Vehicular Ad Hoc Networks (VANETs) demands robust and flexible cryptographic solutions. Traditional encryption schemes are often limited by single- or coarse-grained data sharing models. In contrast, Ciphertext-Policy Attribute-Based Encryption (CP-ABE) empowers data owners to define flexible access policies over encrypted data [6]. In CP-ABE, user decryption keys are bound to sets of attributes, and a ciphertext can only be decrypted if the user’s attributes satisfy the policy embedded within it. This fine-grained access control mechanism makes CP-ABE particularly suitable for the complex access control requirements of VANETs.

Nevertheless, a limitation of some CP-ABE schemes [7,8,9,10] is their reliance on a single Attribute Authority (AA) for key distribution. This centralized approach inevitably creates a performance bottleneck in large-scale VANET environments. Therefore, schemes with multiple attribute authorities have been designed. In these schemes [8,9,10], the authority for distributing attribute keys is delegated to specific AAs, which then operate independently. However, when certain attributes are popular and common, the corresponding keys are requested at a high frequency. This inevitably imposes a heavy computational overhead on the AA managing those attributes.

In addition, the storage of ciphertexts generated by CP-ABE encryption in VANETs is a significant challenge [11,12,13]. In recent years, cloud storage has been employed to store these massive ciphertexts. Then vehicles download the ciphertexts from the cloud and decrypt them locally [14]. However, this approach introduces substantial communication and computational overhead for data users, making it unfeasible for resource-constrained individuals and thereby hindering wide deployment.

To ensure secure data sharing and alleviate the user-side computational burden in VANETs, several outsourced decryption schemes have been proposed [13,15,16]. In such schemes, most decryption computations are offloaded to a cloud server. The user can then recover the data by performing only a lightweight operation on the result returned by the server. However, in this cloud-centric outsourcing model [17], the user must first send a request to the remote cloud and wait for a response. Subsequently, the user must submit the keys and parameters required for partial decryption. Only after receiving these essential components does the cloud perform the partial decryption and return the result to the user. This process involves multiple rounds of long-distance interaction, incurring substantial communication overhead and latency.

Due to the uncertainty of outsourced decryption, verification of outsourced decryption results is necessary. The schemes in [7,18] adopt a ciphertext-verification mechanism, in which the user compares a verification ciphertext with the outsourced decryption result and then decides whether to perform local decryption based on this comparison. However, integrity verification for the verification ciphertext has not yet been achieved. Concurrently, ciphertexts are vulnerable to malicious tampering, making integrity verification a critical challenge. Therefore, there is a pressing need for a cloud-based CP-ABE scheme that supports edge-assisted outsourced decryption to reduce user-side cost and provides a comprehensive verification mechanism for outsourced results to ensure their reliability.

Motivated by the problems of single-point performance bottlenecks in multi-authority key distribution, insufficient privacy protection, and the lack of reliable verification of outsourced decryption, we present our proposed scheme. The main contributions of this paper are summarized as follows:

(1)

We propose a Symmetrically Verifiable Outsourced Decryption Data Sharing Scheme with Privacy-Preserving for VANETs (VODDS). In VODDS, AAs are partitioned into groups, and a PBFT-style Byzantine protocol is introduced during the in-group negotiation of key-distribution credentials. This mechanism spreads computation across authorities while tolerating partial faults. Users derive hash-based pseudonyms that bind to attribute keys for key extraction, and access policies are concealed via an LSSS-based construction to protect private information.

(2)

VODDS leverages blockchain and smart contracts to enable a symmetrically verifiable outsourced decryption. A hash of the verification ciphertext, generated during encryption, is stored on the blockchain as a commitment. During verification, the smart contract performs a symmetric check by matching the hash computed by the user from the returned result against the on-chain commitment. This process reliably detects incorrect or tampered outsourced decryption results, establishing a trust anchor for secure data sharing.

(3)

We conduct a rigorous security analysis and a detailed performance evaluation of VODDS. The scheme’s security is formally proven under the q-parallel BDHE and DDH assumptions, complemented by an informal analysis; additionally, a comprehensive performance evaluation from both theoretical and experimental perspectives demonstrates its high efficiency through comparisons with existing schemes in terms of functionality, storage, and computational overhead.

The outline of this paper is as follows. Section 2 reviews the related work, and Section 3 introduces the preliminaries. Section 4 formulates the problem by presenting the system model, security model, and a formal definition of VODDS. The specific construction of VODDS is detailed in Section 5, followed by its security analysis in Section 6. Section 7 presents the performance evaluation. Finally, Section 8 concludes the paper and discusses future work.

2. Related Work

2.1. CP-ABE

Originally proposed by Sahai and Waters [19], the concept of ABE enables fine-grained access control to improve the efficiency of data sharing, and extensive research has subsequently been carried out on this basis. Goyal et al. [20] first introduced the concept of CP-ABE, which associates access policies with ciphertexts to achieve secure and flexible access control of outsourced data. Cheung and Newport [21] later presented the first provably secure CP-ABE scheme in the standard model, whose security is based on the Decisional Bilinear Diffie–Hellman (DBDH) assumption, where access policies are expressed by simple AND gates. This work attracted much attention due to its improved encryption efficiency and suitability for complex application scenarios such as cloud storage. Subsequently, Bethencourt et al. [22] proposed a CP-ABE scheme that employs a tree-based access structure, where access policies are represented as trees, attributes as nodes, and the branching structure encodes access control logic. Guo et al. [23] proposed an offline/online encryption technique for CP-ABE, which allows users to pre-compute some ciphertext components in advance, thereby reducing online computation and offering effective support for resource constrained entities.

2.2. Access Policy Hiding

As an important part of CP-ABE, the security of access policies is necessary. Boneh and Waters [24] proposed a CP-ABE scheme for hidden vector encryption, which hides the field names in the attribute vector to achieve anonymity. Nishide et al. [25] proposed a partial policy hiding scheme in CP-ABE, where attribute values are defined as secret values hidden in the access structure, but their AND gates structure limits the expression of access policies. In the scheme proposed by Hao et al. [26], the randomization technology is used to completely hide the attribute information in the access policy, and a fuzzy attribute localization mechanism based on garbled bloom filter is developed to help the authorized receiver efficiently locate its attributes and successfully decrypt the ciphertext. LSSS [27] provides a more expressive framework for representing access policies. A Poly-ABE scheme was proposed by Xue et al. [28], which uses LSSS expressing access policy and combines hidden vector encryption to achieve secure access control in multi-energy systems. Zhao et al. [2] proposes a CP-ABE scheme for VANETs that uses LSSS to express access policies and uses fog nodes to participate in the encryption process.

2.3. Outsourced Decryption of CP-ABE

The purpose of outsourced decryption is to reduce the computational burden on the user’s side. Green et al. [29] have long proposed an ABE scheme that supports outsourced decryption, which provides a transformation key to perform outsourced decryption in the cloud, reducing the user’s decryption overhead. Immediately afterwards, Li et al. [30] applied outsourced decryption to CP-ABE, and access control-related decryption operations were offloaded to a third party in their work. Guo et al. [7] put forward an outsourced decryption scheme applied in VANETs that uses validation ciphertext to help users confirm the correctness of partial decryption results. Ge et al. [31] proposed a verifiable outsourced decryption scheme and used smart contracts to improve the claim mechanism against the outsourced decryption party. Wang et al. [12] proposed a cloud-assisted partial decryption CP-ABE solution in which the cloud is assigned to perform partial decryption but cannot fully decrypt data because it does not have a user identity. Chen et al. [32] proposed an outsourced decryption plan to introduce smart contracts, which also formulated a reward and punishment mechanism for outsourced decryption parties.

2.4. Multi-Authority CP-ABE

The multi-authority [33] setting distributes the key distribution authority to AAs, which can distribute keys to users more efficiently than the single-authority setting. Ghorbel et al. [34] proposed an attribute-based cryptographic scheme for access management in cloud services using blockchain. Belguith et al. [35] proposed a CP-ABE scheme that relies on multi-attribute authority, which considers anti-collusion attacks. The decentralized CP-ABE scheme proposed by Zhang et al. [36] implements an adaptive and secure single-round distributed key generation protocol. Ren et al. [37] utilized blockchain nodes that act as trusted proxy entities to generate and distribute key fragments. In the proposal proposed by Lin et al. [38], load balancing of authorization in distributed systems is achieved based on the characteristic of multi-authority. Their specific nodes are equipped with cryptographic reverse firewalls to prevent information leakage.

3. Preliminaries

This section introduces the background knowledge used in VODDS, including the bilinear map, group key agreement, the Byzantine Agreement, and the Decisional q-parallel BDHE assumption. The descriptions of key symbols are summarized in Table 1.

Table 1. Symbols and their meanings.

Symbols	Meaning
$\mathbb{G},{\mathbb{G}}_T$	p-order cyclic groups with $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$
${\mathbb{Z}}_{\mathbb{p}}^{\ast }$	p-order finite field
g	Generator of group $\mathbb{G},{\mathbb{G}}_T$
$MS{K}_{TA}$	Master private key
$\mathcal{PP}$	Common parameter set
$aid$	Identifier of $AA$
$APK$	Public key of $AA$
$ASK$	Private key of $AA$
$uid$	Identifier of user
v	Secret value of user
$UPK$	Private key of user
$GPK$	Public key of the $AA$ group
$GSK$	Private key of the $AA$ group
S	Attribute set
m	Plaintext
C	Ciphertext
$IVC,CVC$	Verification ciphertext
$\psi$	Blinded key
$Enc$	Symmetric encryption algorithm
$TCT$	Outsource decryption results

3.1. Bilinear Map

Let $\mathbb{G}$ and ${\mathbb{G}}_T$ be multiplicative cyclic groups of prime order p. A bilinear map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ can be defined, with g denoting a generator of $\mathbb{G}$. The map e satisfies the following properties:

(1)

$Bilinearity$: For all $U,V\in \mathbb{G}$ and $a,b\in {\mathbb{Z}}_p$, it holds that $e(U^a,V^b)=e{(U,V)}^{ab}$.

(2)

$Non$-$degeneracy$: $e(g,g)\ne 1$ which ensures that the map is not trivially constant.

(3)

$Computability$: There exists an efficient algorithm to compute $e(U,V)$ for any $U,V\in \mathbb{G}$.

3.2. Group Key Agreement

Building upon the Group Key Agreement (GKA) protocol [39], we organize AAs into groups based on the attributes they manage. For each attribute, the corresponding AAs form a group responsible for issuing user-related keys, and the generation of key distribution certificate is participated by all AA collaborators within the group. The construction of the AAs grouping mechanism based on GKA is described as the following matrix.

$$\left(\begin{array}{ccccccc}& {\mathcal{AA}}_1\mathrm{knows}& {\mathcal{AA}}_2\mathrm{knows}& {\mathcal{AA}}_3\mathrm{knows}& \dots & {\mathcal{AA}}_n\mathrm{knows}& \mathrm{PK}\\ {\mathcal{AA}}_1\prec :& ◯& {\sigma }_{1,2}\left(ai{d}_2\right)& {\sigma }_{1,3}\left(ai{d}_3\right)& \dots & {\sigma }_{1,n}\left(ai{d}_n\right)& AP{K}_1\\ {\mathcal{AA}}_2\prec :& {\sigma }_{2,1}\left(ai{d}_1\right)& ◯& {\sigma }_{2,3}\left(ai{d}_3\right)& \dots & {\sigma }_{2,n}\left(ai{d}_n\right)& AP{K}_2\\ {\mathcal{AA}}_3\prec :& {\sigma }_{3,1}\left(ai{d}_1\right)& {\sigma }_{3,2}\left(ai{d}_2\right)& ◯& \dots & {\sigma }_{3,n}\left(ai{d}_n\right)& AP{K}_3\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ {\mathcal{AA}}_n\prec :& {\sigma }_{n,1}\left(ai{d}_1\right)& {\sigma }_{n,2}\left(ai{d}_2\right)& {\sigma }_{n,3}\left(ai{d}_3\right)& \dots & ◯& AP{K}_n\\ & \downarrow & \downarrow & \downarrow & \dots & \downarrow & \Downarrow \\ \mathrm{example}:& {\sigma }_1& {\sigma }_2& {\sigma }_3& \dots & {\sigma }_n& GPK\end{array}\right)$$

Our single-round GKA protocol is described as follows.

$PublicParameterGeneration$: When the system is initialized, $\lambda$ is used as input and outputs the common parameter set $\mathcal{PP}$.

$GroupSetup$: Take $\{A{A}_1,A{A}_2,\dots ,A{A}_n\}$ as a set of group members, and correspondingly, their identities $\{ai{d}_1,ai{d}_2,\dots ,ai{d}_n\}$.

$GroupKeyAgreement$: $A{A}_i$ generates its own public key $AP{K}_i$ and broadcasts its own signature line:

$${\sigma }_{i,1}\left(ai{d}_1\right),\dots ,{\sigma }_{i,i-1}\left(ai{d}_{i-1}\right),◯,{\sigma }_{i,i+1}\left(ai{d}_{i+1}\right),\dots ,{\sigma }_{i,n}\left(ai{d}_n\right),AP{K}_i,$$

for $1\le i,j\le n$, ${\sigma }_{i,j}\left(ai{d}_j\right)$ is the signature of $A{A}_i$ to $A{A}_j$, and ◯ represents ${\sigma }_{i,i}\left(ai{d}_i\right)$ is not public.

$GroupPublicKeyDerivation$: The group public key is:

$$pk=\underset{j=1}{\overset{n}{⨂}}p{k}_j.$$

$KeyDistributionCertificateDerivation$: $A{A}_i$ can calculate its key distribution certificate ${\sigma }_i$ from the corresponding column of the matrix:

$${\sigma }_i={\sigma }_{i,i}\left(ai{d}_i\right)\underset{\begin{array}{c}j=1\end{array}}{\overset{n,j\ne i}{⨀}}{\sigma }_{j,i}\left(ai{d}_i\right)=\underset{j=1}{\overset{n}{⨀}}{\sigma }_{j,i}\left(ai{d}_i\right).$$

3.3. Byzantine Agreement

In distributed systems, Byzantine Agreement refers to protocols that enable nodes to reach a collective decision, even when a subset of nodes fails or behaves arbitrarily. A Byzantine Agreement protocol must satisfy the following properties:

(1)

$Consistency$: All honest nodes must output the same value.

(2)

$Validity$: If all honest nodes propose the same value v, then any honest node’s output must be v.

(3)

$Fault$$Tolerance$: The protocol remains secure and functional as long as no more than t nodes exhibit arbitrary faulty behavior, where $t<{\displaystyle \frac{n}{3}}$ and n is the total number of nodes.

VODDS employs the Byzantine Agreement during the initialization of AA groups to ensure that each AA is reliably authenticated by all other members. This approach aims to enhance the reliability of the distributed key distribution process.

3.4. Decisional q-Parallel BDHE Assumption

Let $(\mathbb{G},{\mathbb{G}}_T)$ be a bilinear group pair of prime order p, with generator $g\in \mathbb{G}$ and bilinear map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$. Let q be a polynomial in the security parameter $\lambda$.

The challenger samples random elements $\gamma ,s\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p,$ and provides the following challenge tuple to the adversary:

$$\mathcal{P}=\left(g,g^{\gamma },g^{{\gamma }^2},\dots ,g^{{\gamma }^q},g^{{\gamma }^{q+2}},\dots ,g^{{\gamma }^{2q}},g^s,g^{\gamma s},g^{{\gamma }^{2}s},\dots ,g^{{\gamma }^{q}s}\right).$$

Additionally, the adversary receives an element $T\in {\mathbb{G}}_T$, which is either: $T=e{(g,g)}^{{\gamma }^{q+1}s}$ (real case), or  $T\stackrel{\$}{\leftarrow }{\mathbb{G}}_T$ (random case). The adversary’s goal, in the Decisional q-parallel BDHE problem, is to distinguish which of the two cases holds.

Definition: An adversary $\mathcal{A}$ has advantage $ϵ$ in solving the Decisional q-parallel BDHE problem if:

$${Adv}_{\mathcal{A}}^{q-\mathrm{BDHE}}=\left|Pr[\mathcal{A}(\mathcal{P},T=e{(g,g)}^{{\gamma }^{q+1}s})=1]-Pr[\mathcal{A}(\mathcal{P},T=R)=1]\right|\ge ϵ,$$

where $R\stackrel{\$}{\leftarrow }{\mathbb{G}}_T$ is a random element.

We say the Decisional q-parallel BDHE Assumption [40] holds if for any probabilistic polynomial-time (PPT) adversary $\mathcal{A}$, the advantage $Ad{v}_{\mathcal{A}}$ is negligible in the security parameter $\lambda$.

4. Problems Formulation

4.1. System Model

As shown in Figure 1, we employ blockchain technology to store the hash value of the verification ciphertext alongside the blinded keys generated prior to data encryption and upload, while cloud servers are responsible for the long-term storage of users’ encrypted data. The VODDS framework involves six entities: (1) Trusted Authority (TA); (2) AA; (3) Cloud Storage Server (CSS); (4) Road Side Unit (RSU); (5) Data Owner (DO); and (6) Data User (DU). The roles of these entities are described as follows.

Figure 1. System model of VODDS.

(1)

$TA$: TA is the fully trusted administrator of the system, responsible for system initialization and user registration with aa. In addition, TA also assists in constructing the AAs attribute group.

(2)

$AAs$: AAs are registered by TA authentication and are responsible for issuing attribute keys to users. They are semi-trusted, meaning they are “honest-but-curious”. While they execute assigned tasks honestly, they may attempt to extract private information from user identities or abuse their permissions by distributing keys to unauthorized users. Unlike most multi-AA key distribution schemes, in which each AA manages a different attribute or attribute set, VODDS assigns frequently used attributes to be jointly managed by multiple AAs. These AAs form a management group for the corresponding attribute. In addition, the allocation of the group is not static, and we support AA to join and exit a certain attribute group. Upon receiving a user request, AA generates attribute key for the user using the key distribution credential obtained from the group.

(3)

$CSS$: CSS stores the ciphertext uploaded by the user for a long time and sends the ciphertext in response to the RSU’s request. CSS does not store authentication ciphertext in our scenario. They are semi-credible.

(4)

$RSU$: RSUs are communication facilities deployed on the side of the road, honest but curious. They are responsible for receiving decryption requests from users and providing outsourced decryption.

(5)

$DO$: DO are the initiators of data sharing and gain legal status by registering with TAs. After obtaining the data collected by the vehicle’s sensors, DO can develop an access policy to encrypt the data to be shared and upload it to CSS.

(6)

$DU$: The DU is the recipient of data sharing and also must register with the TA. A DU may be a vehicle, a pedestrian, or an infrastructure node. The DU requests services from the RSU. Upon receiving the outsourced decryption results provided by the RSU, the DU verifies them through a verification mechanism. Ultimately, the DU can perform the decryption operation independently.

4.2. Security Model

The security of the VODDS scheme is under a comprehensive threat model that considers the following potential adversaries:

• Collusion DU: Multiple data users may collude by pooling their attribute keys in an attempt to access data that none of them could individually decrypt.
• Semi-Trusted AAs: A subset of AAs may be malicious and refuse to reach a consensus with other legitimate AAs during the credential generation process.
• Semi-Trusted CSS and RSU: The CSS and RSU are considered “honest-but-curious.” They will execute the protocol faithfully but may try to learn additional information from the ciphertexts or intermediate results they process.

Based on the above threat model, we present the formal security models for ciphertext semantic security and leak-free distributed key distribution.

1) Ciphertext Semantic Security: In the context of the selective model, the original ciphertext generated by this method is deemed to achieve semantic security if the adversary ${\mathcal{A}}^{\prime }$ s advantage in the corresponding game is proven to be negligible.

Init: $\mathcal{A}$ chooses an access structure $(m_{l^{\ast }\times n^{\ast }}^{\ast },{\rho }^{\ast })$. Each row of $m^{\ast }$ is mapped to an attribute by ${\rho }^{\ast }$. The attribute set is defined as $\mathcal{T}={\left\{{\rho }^{\ast }\left(i\right)\right\}}_{i\in \left[l^{\ast }\right]}$. Finally $\mathcal{A}$ sends $(m_{l^{\ast }\times n^{\ast }}^{\ast },{\rho }^{\ast })$ to challenger $\mathcal{C}$.

Setup: Prior to this phase, $\mathcal{A}$ submitted a portion of the corrupted $AA$ collection $S_c$ to $\mathcal{C}$. $\mathcal{C}$ runs the $TASetup\left(\lambda \right)$ algorithm, takes $\lambda$ as input, and then transmits the generated public parameters to $\mathcal{A}$, while retaining the master secret key secretly. For each attribute authority $A{A}_i$, if $A{A}_i\notin S_c$, only its attribute public key $AP{K}_i$ is revealed to $\mathcal{A}$. Otherwise, if $A{A}_i\in S_c$, both the attribute public key $AP{K}_i$ and the corresponding secret key $AS{K}_i$ are revealed to $\mathcal{A}$.

Query Phase 1: $\mathcal{A}$ is allowed to issue multiple private key queries. For each query, it submits an attribute set S and a user identity $id$ to the challenger. The challenger checks whether S satisfies the challenge access structure $(M^{\ast },{\rho }^{\ast },T^{\ast })$. If it does not satisfy the structure, the challenger proceeds to generate the corresponding private key $S{K}_{S,\mathsf{id}}$ by running the KeyGen algorithm and returns it to the adversary. Otherwise, the query is rejected.

Challenge Phase: Two equal-length messages, $K_0$ and $K_1$, are submitted by $\mathcal{A}$. $\mathcal{C}$ randomly flips a coin $h\in \{0,1\}$, and encrypts $K_h$ under the access structure $(m_{l^{\ast }\times n^{\ast }}^{\ast },{\rho }^{\ast })$, then sends the ciphertext $C{T}_h^{\ast }$ to $\mathcal{A}$.

Query Phase 2: This stage is identical to Query Phase 1. $\mathcal{A}$ may continue to submit attribute sets S associated with a user identity $id$ in order to obtain the corresponding private keys. These sets must also not satisfy the challenge access structure.

Guess phase: $\mathcal{A}$ outputs a guess $K_h^{\prime }$ of $K_h$.

The advantage of $\mathcal{A}$ in outputting $K_h$ rightly is:

$${Adv}_{\mathcal{A}}\left(\lambda \right)=\left|Pr[h^{\prime }=h]-1/2\right|.$$

If no PPT adversary can win the game with non-negligible advantage, then the VODDS scheme is IND-sCPA secure.

2) Leak-Free Distributed Key Distribution: Inspired by Zhang et al. [41], our distributed key extraction process takes into account information security in the key distribution process.

Leak-free is defined as a game between a challenger $\mathcal{C}$ and an attacker $\mathcal{A}$. $\mathcal{A}$ first submits the identity and attribute set. In the case of setting 0, $\mathcal{C}$ entrusts a third party to independently execute the initialization and key generation algorithm, and in the case of 1, $\mathcal{C}$ uses the identity and attribute set to interact with AA to obtain the real attribute key. $\mathcal{C}$ selects a bit $b\in \{0,1\}$, executes the algorithm, returns the key to $\mathcal{A}$. Then, $\mathcal{A}$ output guess b, its advantage is defined as:

$${Adv}_{\mathcal{A}}=\left|Pr[b^{\prime }=b]-1/2\right|.$$

If no PPT attacker can pass the game with the above advantages, then the distributed key distribution is leak-free.

4.3. Formal Definition of VODDS

In this section, we present the formal definition of VODDS. VODDS mainly includes the following ten algorithms.

$TASetup\left(\lambda \right)\to (\mathcal{PP},MS{K}_{TA})$: This algorithm is executed by the TA. On input the security parameter $\lambda$, it generates the public parameters $\mathcal{PP}$ and the master secret key $MS{K}_{TA}$.

$AAsRegistration\left(\mathcal{PP}\right)\to (AS{K}_i,AP{K}_i)$: This AA registration algorithm is performed by the TA. It takes the public parameters $\mathcal{PP}$ as input and outputs the private key $AS{K}_i$ and public key $AP{K}_i$ for $A{A}_i$.

$UsersRegistration\left(\mathcal{PP}\right)\to (ui{d}_k,v_k,UP{K}_k)$: This algorithm is executed by the TA. It takes the public parameters $\mathcal{PP}$ as input and outputs the user’s unique identifier $ui{d}_k$, secret value $v_k$, as well as the user’s public key $UP{K}_k=g^{v_k}$.

$AAGroupsConstruction(\mathcal{PP},a_u,s_1,s_2,\dots ,s_z,ai{d}_1,ai{d}_2,\dots ,ai{d}_z)\to \left({\sigma }_{a_u,1},{\sigma }_{a_u,2},\dots ,{\sigma }_{a_u,z}\right)$: This process is coordinated by the TA with the participation of AAs in group $G_{a_u}$. It takes as input $\mathcal{PP}$, an attribute $a_u$, a set of secret keys $s_i$ and identifiers $ai{d}_i$. The TA first computes the group private key $GS{K}_{a_u}={\sum }_{i=1}^z{s}_i$. Then, the AAs execute a Byzantine consensus protocol where each $A{A}_j$ generates a partial signature ${\sigma }_{a_u,j,i,0}=g^{ai{d}_i·s_j}$ for a claimant $A{A}_i$. Finally, the TA converts and aggregates these signatures to produce the final credential ${\sigma }_{a_u,i}={\gamma }^z·g^{ai{d}_i·GS{K}_{a_u}}$ for each $A{A}_i$.

$AttributeKeysGeneration(\mathcal{PP},x_{uid},S_k,GS{K}_{a_i},ai{d}_i,z)\to \left(S{K}_k\right)$: This algorithm is executed by $A{A}_i$. It takes as input the public parameters $\mathcal{PP}$, the user’s hashed identity $x_{uid}=H\left(uid\right)$, the user’s attribute set $S_k$, the group secret key $GS{K}_{a_i}$, the authority’s identifier $ai{d}_i$, and the group size z. For each attribute $a_u\in S_k$ assigned to this AA, it selects a random tag $e\in \mathbb{Z}p$ and random values $x,x_1,\dots ,x_t\in \mathbb{Z}p$, then computes the user’s attribute secret key $S{K}_k$ which includes components $K_0$, $K_1$, $K_2$, $K_3$, and for each attribute $a_i$, the components $K0,i$, $K1,i$, and $K_{2,i}$.

$OfflineEncryption(M,\rho ,v_k)\to \left(C{T}_0\right)$: This algorithm is executed by the data owner. It takes as input an access structure $(M,\rho )$ and the user’s secret value $v_k$. It randomly selects a secret $s\in \mathbb{Z}p$ and computes a vector $\overrightarrow{y}={(s,y_2,\dots ,y_n)}^T$. For each row i of M, it computes ${\lambda }_i=M_i·\overrightarrow{y}$ and generates the partial ciphertext $C{T}_0$ containing $(M,\rho )$, $C_0=g^s$, $C_1=g^{\mu /\eta }$, and ${Ci,1=g^{{\lambda }_i+c_i}}_{i\in \left[l\right]}$.

$OnlineEncryption(\mathcal{PP},C{T}_0,m,v_k)\to (C,IVC,CVC,C{T}_1)$: This algorithm is executed by the data owner. It takes as input the public parameters $\mathcal{PP}$, the partial ciphertext $C{T}_0$, the message m, and the user’s secret value $v_k$. It computes the main ciphertext $C=m·e{(g,g)}^{\alpha (\beta +s)}$, generates the integrity verification code $IVC=H\left(C\right)$, and computes additional ciphertext components $C{T}_1$ containing $C_2=g^{\alpha \mu }$ and for each row i, $C_{i,3}=g^{c_i/\alpha +s}$ and $C_{i,4}={\xi }^{c_i/\alpha }{a}_i{g}^{GS{K}_{a_i}/z}$. The final ciphertext $CT=C{T}_0,C,C{T}_1$ is uploaded to the CSS.

$CiphertextTransformation(\mathcal{PP},C{T}_0,C{T}_1)\to (CVC,C{T}_0^{\prime },C{T}_1^{\prime })$: This algorithm is executed by the data user. It takes as input the public parameters $\mathcal{PP}$ and ciphertext components $C{T}_0$, $C{T}_1$. It randomly selects $\psi \in {\mathbb{Z}}_p$ and transforms the ciphertext by computing $C{T}_0^{\prime }$ and $C{T}_1^{\prime }$ where all components are scaled by $1/\psi$ in the exponent. It then generates the correctness verification ciphertext $CVC=H\left(e{(g,g)}^{\alpha (\beta +s)/\psi }\right)$, uploads $H\left(IVC\right|\left|CVC\right)$ to the blockchain, and sends the transformed ciphertext $C{T}^{\prime }=C,C{T}_0^{\prime },C{T}_1^{\prime }$ to the CSS.

$OutsourceDecryption(C{T}^{\prime },UK)\to \left(TCT\right)$: This algorithm is executed by the RSU. It takes as input the transformed ciphertext $C{T}^{\prime }$ and the user’s attribute key $UK$. The RSU first computes the set of matching attributes I between the user’s attributes and the access policy, and calculates secret sharing coefficients ${\omega }_i$. It then performs a series of pairing operations to compute intermediate values Q, R, S, T, and D, ultimately deriving $B=e{(g,g)}^{\beta \alpha v_k^2/\psi }$ and $D=e{(g,g)}^{\alpha s_i/\psi }$. Finally, the RSU returns the transformed ciphertext $TCT=B,D,C^{\prime }$ to the data user.

$UserDecryption(TCT,v)\to \left(m\right)$: This algorithm is executed by the data user. It takes as input the transformed ciphertext $TCT$ and the user’s secret value v. The user first computes a hash value $h=H\left(H\left(D^{1/v}{B}^{1/v^2}\right)\right|H\left(C^{\prime }\right))$ and submits it to the smart contract for verification. If the verification passes, the contract returns $En{c}_{IVC}\left(\psi \right)$, which the user decrypts to obtain $\psi$. Finally, the user recovers the message by computing $m=C/(D^{\psi /v}·B^{\psi /v^2})$.

5. Specific Construction of VODDS

In this section, inspired by the work of Zheng et al. [42], we propose to decouple the storage of verification ciphertexts from the encrypted data directly uploaded to the Cloud Storage Server (CSS). To this end, a blockchain is deployed to store hashes of verification ciphertexts generated by DOs, enabling secure and verifiable outsourced decryption. Furthermore, to prevent unauthorized data injection or tampering, we employ smart contracts to regulate all data-writing operations on the blockchain. The overall construction process of the VODDS scheme is shown in Figure 2, and the implementation mechanism of each stage will be described in detail below.

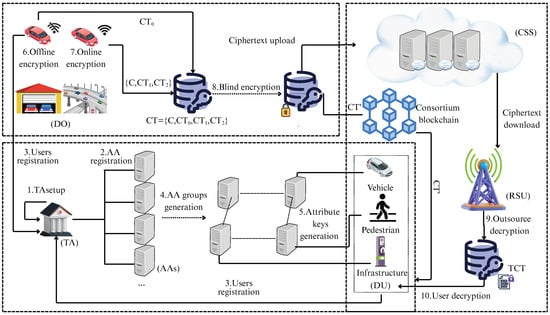
Figure 2. Architecture and workflow of VODDS.

5.1. System Initialization

1) $TASetup\left(\lambda \right)\to (\mathcal{PP},MS{K}_{TA})$: Given a security parameter $\lambda$, let g be a generator of the group $\mathbb{G}$, and let p be the order of multiplicative cyclic groups $\mathbb{G}$ and ${\mathbb{G}}_T$. Given a bilinear mapping $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ and a hash function $H:\{0,1\}\to \mathbb{G}$. Randomly select $\alpha ,\beta ,\gamma ,\mu ,\xi ,\eta \in {\mathbb{Z}}_p^{\ast }$. Finally, $TA$ exposes the parameters $\mathcal{PP}=\{\mathbb{G},{\mathbb{G}}_T,g,g^{\alpha },g^{\beta },\gamma ,\mu ,\xi ,\eta \}$ and keeps $MS{K}_{TA}=\{\alpha ,\beta \}$ private.

2) $AAsRegistration\left(\mathcal{PP}\right)\to (AS{K}_i,AP{K}_i)$: Let n denote the total number of AAs. Upon registration with the TA, each $A{A}_i$$(i\in [n\left]\right)$ is assigned a unique identifier $ai{d}_i\in {\mathbb{Z}}_p^{\ast }$, which is publicly known. Then, $A{A}_i$ randomly selects a secret value $s_i\in {\mathbb{Z}}_p^{\ast }$ as its private key: $AS{K}_i=s_i$. The corresponding public key is computed as $AP{K}_i=g^{ai{d}_i/s_i}$.

3) $UsersRegistration\left(\mathcal{PP}\right)\to (ui{d}_k,v_k,UP{K}_k)$: Each user $U_k$ registers with the $TA$ and obtains a unique identifier $ui{d}_k\in {\mathbb{Z}}_p^{\ast }$. Then, the $TA$ computes a secret value $v_k\in {\mathbb{Z}}_p^{\ast }$ for the user. The user’s public key is defined as $UP{K}_k=g^{v_k}$.

4) $AAGroupsConstruction(\mathcal{PP},a_u,\{s_1,s_2,\dots ,s_z\},\{ai{d}_1,ai{d}_2,\dots ,ai{d}_z\})\to \left(\{{\sigma }_{a_u,1},{\sigma }_{a_u,2},\dots ,{\sigma }_{a_u,z}\}\right)$: First, let m denote the number of attributes in the system. For any attribute $a_u\in \{a_1,a_2,\dots ,a_m\}$, the TA assigns appropriate AAs to manage $a_u$, thereby forming an attribute group $G_{a_u}=\{A{A}_1,A{A}_2,\dots ,A{A}_z\}$, where z is the number of members in $G_{a_u}$. The TA then computes the group private key as $GS{K}_{a_u}={\sum }_{i=1}^z{s}_i$, where $A{A}_i\in G_{a_u}$. The corresponding group public key is $GP{K}_{a_u}=a_u{g}^{GS{K}_{a_u}}$.

Within the group, each member derives a signature through the BLS-based consensus protocol. Any attribute authority $A{A}_i$ that intends to distribute a key for users must obtain identity signatures from other members $A{A}_j$ in the group.

We introduce the Byzantine consensus mechanism in the process of signature. Concretely, we instantiate the above BLS consensus as a PBFT-style five-phase protocol with a per-request timestamp $\tau \in \mathbb{N}$ that binds the distribution instance. Let $G_{a_u}=\{A{A}_1,\dots ,A{A}_z\}$ be the AA group for attribute $a_u$, where each $A{A}_j$ holds secret $s_j$ and public key $AP{K}_j=g^{s_j}$. For the claimant $A{A}_i$ with public identifier $ai{d}_i$, define $h_i=g^{ai{d}_i}$. The consensus process is shown in Figure 3.

Figure 3. Consensus mechanism for AAs group.

We use a PBFT-style consensus inside $G_{a_u}=\{A{A}_1,\dots ,A{A}_z\}$ with at most f Byzantine members and $z\ge 3f+1$. Let the current view be v with primary p. A request is:

$$m=⟨a_u,ai{d}_i,\tau ⟩,d=H\left(m\right),$$

we write ${⟨X⟩}_j$ for message X signed by $A{A}_j$ (BLS). Nodes log tuples $(v,n,d)$ with sequence number n.

Request: The claimant $A{A}_i$ sends ${⟨REQUEST,m,v⟩}_i$ to the primary. The primary checks the signature and that $\tau$ is unused.

Pre-Prepare: If valid, the primary chooses n and multicasts:

$${⟨PRE\_PREPARE,v,n,d,m⟩}_p,$$

A replica $A{A}_j$ accepts this if (1) the sender is the current primary, (2) $H\left(m\right)=d$, (3) $(v,n)$ not previously used, (4) $\tau$ is fresh. Upon acceptance it records $(v,n,d)$.

Prepare: Each accepting replica broadcasts:

$${⟨PREPARE,v,n,d⟩}_j,$$

Let $Q=2f+1$. A node is prepared for $(v,n,d)$ when it has one valid PRE_PREPARE and at least Q matching PREPARE messages from distinct members. At this point each honest $A{A}_j$ computes its claimant-bound partial signature:

$${\sigma }_{a_u,j,i,0}=g^{ai{d}_i·s_j},$$

and keeps it pending finalization.

Commit: Nodes then broadcast:

$${⟨COMMIT,v,n,d⟩}_j,$$

When a node collects at least Q matching COMMIT messages for $(v,n,d)$, the request is decided (finalized). Each honest $A{A}_j$ releases ${\sigma }_{a_u,j,i,0}$ to $A{A}_i$.

Reply: The claimant $A{A}_i$ accepts success after receiving valid responses from at least Q distinct members.

For each signature received by $A{A}_i$, the TA performs the transformation as follows: ${\sigma }_{a_u,j,i,1}=\gamma {\sigma }_{a_u,j,i,0}=\gamma g^{ai{d}_i·s_j}$. Then, TA aggregates the signatures to generate $A{A}_i$’s proof ${\sigma }_{a_u,i}=\left({\prod }_{j=1}^z\gamma ·g^{ai{d}_i·s_j}\right)={\gamma }^z{g}^{ai{d}_i·GS{K}_{a_u}}$. After obtaining the certificate, the attribute authority can independently distribute attribute keys to users.

5) $AttributeKeysGeneration(\mathcal{PP},x_{uid},S_k,GS{K}_{a_i},ai{d}_i,z)\to \left(S{K}_k\right)$: For a user $U_k$, let $x_{uid}=H\left(uid\right)$. The user’s attribute set is denoted as $S_k=\{a_1,a_2,\dots ,a_t\}$, where t is the number of attributes held by the user. For each attribute $a_u\in S_k$, an $A{A}_i\in G_{a_u}$ is selected to generate the attribute key of $a_u$ for the user. A value $e\in {\mathbb{Z}}_p$ is chosen as the tag used during attribute key distribution. Additionally, random values $x,x_1,x_2,\dots ,x_t\in {\mathbb{Z}}_p$ are chosen. The attribute key $UK$ corresponding to $a_u$ is:

$$\begin{array}{c}\hfill ⟨K_0=g^{\beta v_k^2/\mu +x_{uid}{v}_k/\eta },K_1=x_{uid},K_2=e,K_3=g^{e{v}_k\alpha },\\ \hfill {\left\{K_{0,i}={\left(\gamma \right)}^{z_{a_i}}{a}_i^{zai{d}_i}{g}^{GS{K}_{a_i}zai{d}_i},K_{1,i}=g^{v_k}{\xi }^{s_{aid}},K_{2,i}={\xi }^{v_k-s_{aid}}\right\}}_{i\in \left[t\right]}⟩.\end{array}$$

5.2. Data Uploads

1) $OfflineEncryption(M,\rho ,v_k)\to \left(C{T}_0\right)$: Given the public parameters $\mathcal{PP}$, an access structure $(M,\rho )$ is specified, where M is an $l\times n$ matrix and $\rho$ maps each row i to an attribute $\rho \left(i\right)$. Randomly select $s\in {\mathbb{Z}}_p$, and define a vector $\overrightarrow{y}={(s,y_2,y_3,\dots ,y_n)}^T\in {\mathbb{Z}}_p^n$ to embed the secret s. Let $M_i$ denote the i-th row of M, then compute ${\lambda }_i=M_i·\overrightarrow{y}\mathrm{for}\mathrm{all}i\in \left[l\right]$ For each row i, compute a blinding value $c_i\in {\mathbb{Z}}_p$, and generate ciphertext components as:

$$C{T}_0=⟨(M,\rho ),C_0=g^s,C_1=g^{\mu /\eta },{\{C_{i,1}=g^{{\lambda }_i+c_i}\}}_{i\in \left[l\right]}⟩.$$

2) $OnlineEncryption(\mathcal{PP},C{T}_0,m,v_k)\to (C,IVC,CVC,C{T}_1)$: In this stage, the data owner performs the following operations. First, compute ciphertext $C=me{(g,g)}^{\alpha (\beta +s)}.$ Then, generate the integrity verification ciphertext $IVC=H\left(me{(g,g)}^{\alpha (\beta +s)}\right).$ Next, compute the ciphertext component $C{T}_1$:

$$C{T}_1=⟨C_2=g^{\alpha \mu },{\left\{C_{i,3}=g^{c_i/\alpha +s},C_{i,4}={\xi }^{c_i/\alpha }{a}_i{g}^{GS{K}_{a_i}/z}\right\}}_{i\in \left[l\right]}⟩,$$

Finally, $CT=\{C{T}_0,C,C{T}_1\}$ is obtained and uploaded to CSS.

3) $CiphertextTransformation(\mathcal{PP},C{T}_0,C{T}_1)\to (CVC,C{T}_0^{\prime },C{T}_1^{\prime })$: The DU randomly chooses $\psi \in {\mathbb{Z}}_p$, then compute convert ciphertext as follows:

$$C{T}_0^{\prime }=⟨\left(M,\rho \right),C_0^{\prime }=g^{s/\psi },C_1^{\prime }=g^{\mu /\eta \psi },{\left\{C_{i,1}^{\prime }=g^{({\lambda }_i+c_i)/\psi }\right\}}_{i\in \left[l\right]}⟩,$$

$$C{T}_1^{\prime }=⟨C_2^{\prime }=g^{\alpha \mu /\psi },{\left\{C_{i,3}^{\prime }=g^{{\displaystyle \frac{c_i/\alpha +s}{\psi }}},C_{i,4}^{\prime }={\xi }^{c_i/\alpha }·GP{K}_{a_i}={\xi }^{c_i/\alpha }·g^{a_i^{GS{K}_{a_i}}}\right\}}_{i\in \left[l\right]}⟩,$$

Finally, generate the correctness verification ciphertext $CVC=H\left(e{(g,g)}^{\alpha (\beta +s)/\psi }\right)$. Upload $H\left(IVC\right|\left|CVC\right)$ to the blockchain and $C{T}^{\prime }=\{C,C{T}_0^{\prime },C{T}_1^{\prime }\}$ to CSS.

5.3. Data Download

1) $OutsourceDecryption(C{T}^{\prime },UK)\to \left(TCT\right)$: At this stage, the RSU obtains the attribute key of user and downloads the ciphertext from the CSS to perform outsourced decryption. Let the intersection between the user’s possessed attributes and the row-mapped attributes of the access structure matrix M be defined as $I={\{i\mid \rho \left(i\right)\in S_{uid}\}}_{i\in \left[l\right]}.$ Compute coefficients ${\omega }_i\in {\mathbb{Z}}_p$ such that: ${\sum }_{i\in I}{\omega }_i{M}_i=\{1,0,\dots ,0\},$ where $M_i$ is the i-th row of the access matrix M. Then, the secret value s is defined as $s={\sum }_{i\in I}{\omega }_i{\lambda }_i.$

For each $i\in \left[l\right]$, the RSU obtains the number of AAs in group $z_{a_i}$, the global constant $\gamma$, and the public identifiers $ai{d}_i$ of each $A{A}_i\in G_{a_i}$. Next, transform the ciphertext component:

$$C_{i,4}^{\prime }={\left({\displaystyle \frac{{\gamma }^{z_{a_i}}{\left(C_{i,4}\right)}^{zai{d}_i}}{K_{0,i}}}\right)}^{{\displaystyle \frac{1}{zai{d}_i}}}={\xi }^{c_i/\alpha }.$$

Then the RSU calculate:

$$\begin{array}{cc}\hfill Q& =\prod _{i\in \left[l\right]}e\left({K_3}^{\frac{1}{K_2}},{\left(C_{i,4}^{\prime }\right)}^{{\omega }_i}\right)e\left(K_{2,i},C_0^{\prime }\right)\hfill \\ & =\prod _{i\in \left[l\right]}e\left({\left(g^{e{v}_k\alpha }\right)}^{\frac{1}{e}},{\xi }^{c_i{\omega }_i/\alpha }\right)e\left({\xi }^{v_k-s_{aid}},g^{s/\psi }\right)\hfill \\ & =\prod _{i\in \left[l\right]}e{\left(g,\xi \right)}^{v_k{c}_i{\omega }_i}e{\left(\xi ,g\right)}^{v_{k}s/\psi -s_{aid}s/\psi }\hfill \\ & =\prod _{i\in \left[l\right]}e{\left(g,\xi \right)}^{v_k{c}_i{\omega }_i+v_{k}s/\psi -s_{aid}s/\psi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R& =\prod _{i\in \left[l\right]}{\displaystyle \frac{e\left({\left(K_{1,i}\right)}^{{\omega }_i},C_{i,1}^{\prime }\right)}{e(K_{1,i},C_0^{\prime })}}\hfill \\ & =\prod _{i\in \left[l\right]}{\displaystyle \frac{e\left(g^{v_k{\omega }_i}{\xi }^{s_{aid}{\omega }_i},g^{({\lambda }_i+c_i)/\psi }\right)}{e\left(g^{v_k},g^{s/\psi }\right)·e\left({\xi }^{s_{aid}},g^{s/\psi }\right)}}\hfill \\ & =\prod _{i\in \left[l\right]}{\displaystyle \frac{e\left(g^{v_k{\omega }_i},g^{({\lambda }_i+c_i)/\psi }\right)e\left({\xi }^{s_{aid}{\omega }_i},g^{({\lambda }_i+c_i)/\psi }\right)}{e\left(g^{v_k},g^{s/\psi }\right)e\left({\xi }^{s_{aid}},g^{s/\psi }\right)}}\hfill \\ & =\prod _{i\in \left[l\right]}{\displaystyle \frac{e{(g,g)}^{v_k{\omega }_i{\lambda }_i/\psi +v_k{\omega }_i{c}_i/\psi }e{(\xi ,g)}^{s_{aid}{\omega }_i{\lambda }_i/\psi +s_{aid}{\omega }_i{c}_i/\psi }}{e{(g,g)}^{v_{k}s/\psi }e{(\xi ,g)}^{s_{aid}s/\psi }}}\hfill \\ & =\prod _{i\in \left[l\right]}e{(g,g)}^{v_k{\omega }_i{c}_i/\psi }e{(\xi ,g)}^{s_{aid}{\omega }_i{c}_i/\psi }.\hfill \\ \hfill S& ={\displaystyle \frac{R}{Q}}\hfill \\ & =\prod _{i\in \left[L\right]}{\displaystyle \frac{e{\left(g,g\right)}^{v_k{\omega }_i{c}_i/\psi }e{\left(\xi ,g\right)}^{s_{aid}s/\psi +s_{aid}{\omega }_i{c}_i/\psi }}{e{\left(g,g\right)}^{v_{k}s/\psi }e{\left(\xi ,g\right)}^{s_{aid}s/\psi }}}\hfill \\ & =\prod _{i\in \left[L\right]}e{\left(g,g\right)}^{v_k{\omega }_i{c}_i/\psi }e{\left(\xi ,g\right)}^{s_{aid}{\omega }_i{c}_i/\psi }.\hfill \\ \hfill T& =e\left({\left(C_{i,3}^{\prime },C_0^{\prime }\right)}^{\alpha },K_3^{1/K_2}\right)=e{\left(g,g\right)}^{v_k\alpha c_i/\psi +\alpha s_i/\psi }.\hfill \\ \hfill D& ={\displaystyle \frac{T}{S}}={\displaystyle \frac{e{\left(g,g\right)}^{v_k\alpha c_i/\psi +\alpha s_i/\psi }}{e{\left(g,g\right)}^{v_k\alpha c_i/\psi }}}=e{\left(g,g\right)}^{\alpha s_i/\psi }.\hfill \\ \hfill \tilde{B}& ={\displaystyle \frac{e\left(K_0,{\left(C_2^{\prime }\right)}^{K_2}\right)}{e\left({\left(C_1^{\prime }\right)}^{K_1},K_3\right)}}\hfill \\ & ={\displaystyle \frac{e\left(g^{v_k^2\beta /\mu +v_k{x}_{uid}/\eta },g^{e\alpha \mu /\psi }\right)}{e\left(g^{x_{uid}\mu /\eta \psi },g^{e{v}_k\alpha }\right)}}\hfill \\ & ={\displaystyle \frac{e{(g,g)}^{\beta e\alpha v_k^2/\psi +v_k{x}_{uid}e\alpha \mu /\eta \psi }}{e{(g,g)}^{e{v}_k\alpha x_{uid}\mu /\eta \psi }}}\hfill \\ & =e{(g,g)}^{\beta e\alpha v_k^2/\psi }.\hfill \\ \hfill B& ={\left(\tilde{B}\right)}^{1/K_2}=e{\left(g,g\right)}^{\beta \alpha v_k^2/\psi }.\hfill \end{array}$$

Finally, the RSU returns $TCT=\{B,D,C^{\prime }\}$ to the DU.

2) $UserDecryption(TCT,v)\to \left(m\right)$: As the RSU is an entity requiring vigilance, users must verify the decryption results returned by the RSU prior to decryption. This verification encompasses validating the correctness of parameters B and D, as well as confirming the integrity of parameter $C^{\prime }$.

First, DU calculates a hash value h based on the acquired $TCT$, which is described as:

$$h=H\left(H\left(D_i^{1/v_i}{B}^{1/v_i^2}\right)\parallel H\left(C^{\prime }\right)\right).$$

Then, the DU submits h to the smart contract, which performs a symmetrical matching against the on-chain commitment. If a match is found, it indicates that $\mathrm{IVC}=C^{\prime }$, $\mathrm{CVC}=D_i^{1/v_i}{B}^{1/v_i^2}$. Next, the smart contract returns ${\mathrm{Enc}}_{\mathrm{IVC}}\left(\psi \right)$, and the user decrypts it with $IVC$ to obtain $\psi$. Finally, combined with user private $v_i$ (Here $v_k$ is the private holding value of the user $U_k$ that obtains the attribute key, and $v_i$ is the private holding value of $U_i$, for clarity, note that, we explain: $U_i$ and $U_K$ are the same user) the user computes:

$$\begin{array}{cc}\hfill {\displaystyle \frac{C}{D_i^{\psi /v_i}·B^{\psi /v_i^2}}}& ={\displaystyle \frac{me{(g,g)}^{\alpha (\beta +s)}}{{\left(e{(g,g)}^{\alpha s_i/\psi }\right)}^{\psi /v_i}·{\left(e{(g,g)}^{\beta \alpha v_k^2/\psi }\right)}^{\psi /v_i^2}}}\hfill \\ \hfill & ={\displaystyle \frac{me{(g,g)}^{\alpha (\beta +s)}}{e{(g,g)}^{\alpha s}·e{(g,g)}^{\beta \alpha }}}\hfill \\ \hfill & =m.\hfill \end{array}$$

6. Security Analysis

6.1. IND-sCPA Security

Theorem 1.

Under the Decisional q-parallel BDHE Assumption, no PPT adversary can win the game with a non-negligible advantage. Therefore, the proposed VODDS scheme achieves IND-sCPA security.

Proof. 

Assume, for contradiction, that a PPT adversary $\mathcal{A}$ wins the selective IND-sCPA game with advantage $ϵ={Adv}_{\mathcal{A}}^{\mathsf{IND}-\mathsf{sCPA}}\left(\lambda \right)$. We construct a simulator $\mathcal{S}$ and build an adversarial game that proves that $\mathcal{S}$ also has a non-negligible advantage in breaking the q-parallel BDHE Assumption thanks to the non-negligible advantages of $\mathcal{A}$. In the construction, $\mathcal{S}$ is given:

$$\left(g,g^{\gamma },g^{{\gamma }^2},\dots ,g^{{\gamma }^q},g^{{\gamma }^{q+2}},\dots ,g^{{\gamma }^{2q}},T\right)\in {\mathbb{G}}^{2q}\times {\mathbb{G}}_T,$$

where T is either $e{(g,g)}^{{\gamma }^{q+1}}$ (real) or a random element $R\in {\mathbb{G}}_T$ (random). Its goal is to decide which case holds.

1) Init: $\mathcal{A}$ commits to a target access structure $(M^{\ast },{\rho }^{\ast })$ with $M^{\ast }\in {\mathbb{Z}}_p^{{\ell }^{\ast }\times n^{\ast }}$ and ${\ell }^{\ast },n^{\ast }\le q$. $\mathcal{S}$ records the attribute rows $I_x=\{i\mid {\rho }^{\ast }\left(i\right)=x\}$ for each attribute x.

2) Setup: $\mathcal{S}$ picks ${\alpha }^{\prime },\beta ,v\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and defines $e{(g,g)}^{\alpha }=e{(g,g)}^{{\alpha }^{\prime }}·T$. So $\alpha ={\alpha }^{\prime }+{\gamma }^{q+1}$ is implicit. For every attribute x it programs a hash oracle $H_0:{\{0,1\}}^{\ast }\to \mathbb{G}$ as:

$$H_0\left(x\right)=\left\{\begin{array}{cc}{g}^{\tilde{x}}\hfill & I_x=⌀,\hfill \\ {\displaystyle g^{\tilde{x}}\prod _{i\in I_x}\prod _{j=1}^{n^{\ast }}{\left(g^{{\gamma }^j}\right)}^{M_{i,j}^{\ast }/o_i}}\hfill & I_x\ne ⌀,\hfill \end{array}\right.$$

where $\tilde{x},o_i\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$. For every AA_k: If corrupted, choose $s_k\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$, set $AP{K}_k=g^{ai{d}_k/s_k}$ and leak $AS{K}_k=s_k$ to $\mathcal{A}$. else, choose $t_k\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$, set $AP{K}_k=g^{t_k}$ (keep $t_k$ secret). Finally, publish the simulated public parameters:

$$PP=\left(g,g^{\beta },g^v,e{(g,g)}^{\alpha },{\left\{AP{K}_k\right\}}_k,H_0\right).$$

3) Key Query Phase 1: For every attribute set S queried by $\mathcal{A}$ with $S⊭(M^{\ast },{\rho }^{\ast })$, $\mathcal{S}$ returns a user secret key: it uses genuine keys for corrupted AAs and TA components, and simulates honest-AA components with the programmed $H_0$. Collusion resistance (user-specific factors $v_k$) prevents combining different keys to satisfy the policy.

4) Challenge: $\mathcal{A}$ submits $(m_0,m_1)$. $\mathcal{S}$ picks $b\stackrel{\$}{\leftarrow }\{0,1\}$ and $s\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$. Then, Message is calculated to:

$$C=m_b·e{(g,g)}^{\alpha (\beta +s)}=m_b·e{(g,g)}^{{\alpha }^{\prime }(\beta +s)}·T^{\beta +s},$$

Next, build $C{T}_0=(M^{\ast },{\rho }^{\ast },g^s,{\{C_{i,1}=g^{{\lambda }_i+c_i}\}}_i)$, where ${\lambda }_i=M_i^{\ast }·\tilde{y}$ and $c_i\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$. Construct other ciphertext components, for each row i, set $C_{i,3}=g^{c_i/(\alpha +s)},C_{i,4}={\xi }^{c_i/\alpha }{g}^{GS{K}_{a_u}ai{d}_i},$ consistent with the public keys (BDHE bases appear inside $H_0$ terms). Last, send $C{T}^{\ast }=\{C{T}_0,C\}$ to $\mathcal{A}$.

5) Key Query Phase 2: Identical to Phase 1 (queries still must miss the policy).

6) Guess: $\mathcal{A}$ outputs $b^{\prime }\in \{0,1\}$. $\mathcal{S}$ answers:

$$\mathrm{output}\mathrm{REAL}⟺b^{\prime }=b,$$

The overall advantage of $\mathcal{S}$ tackling the Decisional q-parallel BDHE Assumption is:

$${Adv}_{\mathcal{S}}^{q-\mathrm{BDHE}}=\left|Pr[b^{\prime }=b\mid T=e{(g,g)}^{{\gamma }^{q+1}}]-Pr[b^{\prime }=b\mid T=R]\right|=\left|\frac{1}{2}+ϵ-\frac{1}{2}\right|=ϵ.$$

As shown in the result, if a PPT adversary $\mathcal{A}$ could win the IND-sCPA security game with non-negligible advantage $ϵ$, then the simulator $\mathcal{S}$ would be able to solve the Decisional q-parallel BDHE problem with the same advantage.However, the q-parallel BDHE Assumption is believed to be hard. Therefore, according to Theorem 1, our proposed scheme achieves IND-sCPA security. □

6.2. Leak-Freeness of the Distributed Key Extraction

Inspired by [41], we conduct a security analysis of the distributed key extraction process based on the decisional Diffie–Hellman assumption.

Theorem 2

(Leak–Freeness). Under the decisional Diffie–Hellman assumption in the scheme’s bilinear groups, the multi-authority CP-ABE key-generation process is leak-free. Specifically, for any PPT adversary $\mathcal{A}$, the advantage ${\mathrm{Adv}}_{\mathcal{A}}^{\mathit{Leak}-\mathit{Free}}\left(\lambda \right)$ is negligible.

Proof. 

Let $\mathcal{PP}$ denote the public parameters, $x_{uid}$ the public tag bound to user $uid$, $UP{K}_k$ the set of public keys visible to $\mathcal{A}$, and $\mathcal{T}$ the transcript of all messages in the key-generation session. For $i\in \{0,1,2,3,4\}$, let ${\mathsf{View}}_{\mathcal{A}}^{G_i}\left(\lambda \right)$ denote the random variable equal to the view of $\mathcal{A}$ in Game $G_i$, and let $P_i$ be the event that $\mathcal{A}$ outputs the bit “Real” in $G_i$. We write $\mathrm{negl}\left(\lambda \right)$ for a negligible function in $\lambda$ (namely, for every polynomial p there exists N such that $\mathrm{negl}\left(\lambda \right)<1/p\left(\lambda \right)$ for all $\lambda >N$). Different occurrences of $\mathrm{negl}(·)$ may denote different negligible functions, their sum is still negligible.

The leak-freeness advantage is defined as:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Leak}-\mathrm{Free}}\left(\lambda \right)=\mid Pr[{\mathrm{Real}}_{\mathcal{A}}\left(\lambda \right)=1]-Pr[{\mathrm{Ideal}}_{\mathcal{A},\mathcal{S}}\left(\lambda \right)=1]\mid =\mid Pr[P_0=1]-Pr[P_4=1]\mid .$$

In the Real experiment, there is no extra trusted third party beyond the TA. In the Ideal experiment, the behaviors of the TA and the AAs are abstracted by an ideal functionality that, on input $(\mathcal{PP},x_{uid},S)$, returns a correctly distributed $S{K}_{uid,S}$ and nothing else. The simulator $\mathcal{S}$ is PPT and has black-box access to this functionality (equivalently, the master secrets); it answers $\mathcal{A}$’s queries and fabricates a transcript consistent with $(\mathcal{PP},x_{uid},UP{K}_k,S{K}_{uid,S})$ by replacing any blinded group element of the form $g^{\theta +r}$ with an independent uniform element in the prime-order group, simulating honest AAs’ BLS shares as $H{\left(uid\right)}^{s_{a,i}^{\prime }}$ for fresh $s_{a,i}^{\prime }\leftarrow {\mathbb{Z}}_p$, and recomputing all deterministic fields from public data and $S{K}_{uid,S}$, while maintaining a consistency table keyed by $(uid,S)$ to ensure identical answers across repeated queries.

Game ${\mathit{G}}_{\mathbf{0}}$ (Real protocol). All authorities run the genuine key-generation protocol with $\mathcal{A}$. The adversary’s view is ${\mathsf{View}}_{\mathcal{A}}^{G_0}\left(\lambda \right)=(\mathcal{PP},x_{uid},UP{K}_k,\mathcal{T},S{K}_{uid,S})$. By definition:

$$Pr[P_0=1]=Pr[{\mathrm{Real}}_{\mathcal{A}}\left(\lambda \right)=1].$$

Game ${\mathit{G}}_{\mathbf{1}}$ (Uniformizing random blindings). In $\mathcal{T}$, every term of the form $g^{\theta +r}$ (where r is sampled uniformly from ${\mathbb{Z}}_p$) is replaced by an independent uniform element of the prime-order group $\mathcal{G}=⟨g⟩$. Since adding a fixed $\theta$ permutes ${\mathbb{Z}}_p$, the exponent $\theta +r$ is uniform in ${\mathbb{Z}}_p$, hence $g^{\theta +r}$ is uniform in $\mathcal{G}$. Therefore the replacement preserves the joint distribution of $\mathsf{Tr}$, and:

$${\mathsf{View}}_{\mathcal{A}}^{G_1}\equiv {\mathsf{View}}_{\mathcal{A}}^{G_0}\Rightarrow Pr[P_1=1]=Pr[P_0=1].$$

Game ${\mathit{G}}_{\mathbf{2}}$ (Simulating BLS signature shares). For each honest AA, the BLS share $H{\left(uid\right)}^{s_{a,i}}$ that appears in $\mathsf{Tr}$ is replaced by $H{\left(uid\right)}^{s_{a,i}^{\prime }}$ where $s_{a,i}^{\prime }$ is chosen independently and uniformly from ${\mathbb{Z}}_p$ (H hashes to $\mathcal{G}$ and $s_{a,i}$ is the AA’s secret exponent). If a PPT distinguisher could tell the real shares from these simulated ones (given the corresponding public information), one would obtain a PPT algorithm that breaks the standard security of BLS-type signatures, which relies on Diffie–Hellman–type assumptions in bilinear groups (e.g., q-SDH). By a standard hybrid argument over all honest shares:

$$\mid Pr[P_2=1]-Pr[P_1=1]\mid \le \mathrm{negl}\left(\lambda \right).$$

Game ${\mathit{G}}_{\mathbf{3}}$ (Simulator with master secrets). A simulator $\mathcal{S}$ that knows all master secrets computes $S{K}_{uid,S}$ directly and fabricates a transcript $\tilde{\mathcal{T}}$ consistent with $(\mathcal{PP},x_{uid},UP{K}_k,S{K}_{uid,S})$: deterministic components are recomputed from public data and $S{K}_{uid,S}$. Blinded components are resampled uniformly in $\mathcal{G}$ as in $G_1$ and BLS shares follow the distribution enforced in $G_2$. Consequently:

$${\mathsf{View}}_{\mathcal{A}}^{G_3}\equiv {\mathsf{View}}_{\mathcal{A}}^{G_2}\Rightarrow Pr[P_3=1]=Pr[P_2=1].$$

Game ${\mathit{G}}_{\mathbf{4}}$ (Ideal world). The simulator outputs only $(\mathcal{PP},x_{uid},UP{K}_k,S{K}_{uid,S})$, omitting the transcript. There exists a PPT re-simulation procedure which, given $(\mathcal{PP},x_{uid},UP{K}_k,S{K}_{uid,S})$, reconstructs a transcript that is computationally indistinguishable from $\tilde{\mathcal{T}}$ in $G_3$: blinded parts are independent uniforms and the remaining parts are determined by public inputs and $S{K}_{uid,S}$. Hence removing the transcript changes the adversary’s success probability by at most a negligible amount:

$$\mid Pr[P_4=1]-Pr[P_3=1]\mid \le \mathrm{negl}\left(\lambda \right).$$

Combining the bounds by the triangle inequality yields:

$$\left|Pr[P_0=1]-Pr[P_4=1]\right|\le \sum _{i=0}^3\mid Pr[P_i=1]-Pr[P_{i+1}=1]\mid \le \mathrm{negl}\left(\lambda \right),$$

Since $G_0$ is the Real experiment and $G_4$ is the Ideal experiment, we obtain:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Leak}-\mathrm{Free}}\left(\lambda \right)=\mid Pr[{\mathrm{Real}}_{\mathcal{A}}\left(\lambda \right)=1]-Pr[{\mathrm{Ideal}}_{\mathcal{A},\mathcal{S}}\left(\lambda \right)=1]\mid \le \mathrm{negl}\left(\lambda \right),$$

namely, the protocol leaks no information. □

6.3. Collusion Resistance

The proposed VODDS scheme is resistant to collusion attacks, including both user collusion and AA collusion, under standard cryptographic assumptions.

(1)

Resistance to User Collusion

Each user is assigned a unique identity ${\mathit{uid}}_{\mathit{k}}\in {\mathbb{Z}}_p^{\ast }$ and a secret value $v_k\in {\mathbb{Z}}_p^{\ast }$, both generated by TA during registration. The user’s public key is computed as ${\mathit{UPK}}_k=g^{v_k}$, and the attribute secret keys include components such as:

$$K_0=g^{\beta v_k^2/\mu +x_{uid}{v}_k/\eta },K_3=g^{e{v}_k\alpha },$$

which embed both ${\mathit{uid}}_k$ and $v_k$ in the exponent. These values ensure that each user’s keys are uniquely bound to their identity and cannot be reused or recombined across users. Even if several users share their keys in an attempt to satisfy an access policy collectively, the cryptographic binding to ${\mathit{uid}}_k$ and $v_k$ makes such efforts ineffective. The attribute key components are not interoperable due to their user-specific structures, and thus the scheme inherently prevents collusion among users. This property holds under the hardness assumptions of the discrete logarithm and bilinear pairing problems.

(2)

Resistance to AA Collusion

To prevent collusion among AAs, the scheme introduces an Group Key Agreement mechanism to organize AAs into groups based on the attributes they manage. For each attribute group, the participating AAs jointly generate the group public key, and collaboratively distribute attribute credentials. Each AA contributes a partial signature on the attribute identifier $ai{d}_i$, and the full credential is constructed by aggregating these signatures:

$${\sigma }_{a_u,i}=\left(\prod _{j=1}^z\gamma ·g^{ai{d}_i·s_j}\right)={\gamma }^z{g}^{ai{d}_i·GS{K}_{a_u}},$$

where $GS{K}_{a_u}={\sum }_{j=1}^z{s}_j$ denotes the group private key, which is never reconstructed explicitly. Furthermore, the signature generation follows a Byzantine Agreement protocol that ensures consistency and fault tolerance within each AA group. Under this protocol, a credential is only accepted if it is confirmed by a quorum of honest AAs. The Byzantine consensus guarantees that the system remains secure even when up to $\lfloor \frac{n}{3}\rfloor$ AAs behave maliciously, where n is the total number of AAs in the group.

Since the signature generation requires participation from a majority of honest AAs, no subset of malicious or colluding AAs can forge valid credentials without authorization. Moreover, each AA’s private key is tied to its identity, and cannot be simulated or substituted by others.

Therefore, the proposed VODDS scheme achieves strong resistance to both user collusion and AA collusion attacks.

7. Performance Evaluation

7.1. Functional Comparison

In this section, we compare the proposed scheme with schemes [7,8,9,10,28,43,44]. As shown in Table 2, we analyze the schemes from eight aspects: privacy protection, multi-authority, distributed key distribution, access structure, anti-collusion for AAs, anti-collusion for DU, verifiability of outsourced decryption, and verifiability of ciphertext integrity. In the table, “✓” indicates support for the feature, “×” indicates no support, and “−” indicates either a single-AA architecture or that the scheme does not involve an AA setup.

Table 2. Functional comparison.

Scheme	Privacy Protection	Multi- Authority	Distributed Key Distribution	Access Structure	Anti- Collusion for AAs	Anti- Collusion for DU	Verifiability of Outsourced Decryption	Verifiability of Ciphertext Integrity
[8]	×	×	×	Tree	−	✓	✓	×
[9]	×	×	×	LSSS	−	×	✓	×
[10]	×	×	×	LSSS	−	✓	×	×
[43]	×	✓	✓	LSSS	×	✓	×	×
[44]	×	✓	×	LSSS	×	✓	×	×
[28]	✓	−	×	LSSS	−	×	×	×
[7]	✓	✓	×	LSSS	✓	✓	✓	×
Ours	✓	✓	✓	LSSS	✓	✓	✓	✓

Apart from the schemes in [7,28] and VODDS, the remaining schemes risk privacy leakage by exposing user identity or access policy. VODDS achieves privacy by encrypting user identities during distributed key distribution and employing an LSSS-based policy-hiding. Multi-authority is supported by most schemes, except for the single-AA architectures in [8,9,10] and the non-AA scheme in [28]. Consequently, AA collusion is not applicable to these four schemes, while it is actively supported in all others except [43,44], which lack this feature. Distributed key distribution is a distinctive feature, implemented only in [43] and VODDS. Regarding access structures, all schemes employ LSSS except [8], which uses a Tree structure. Resistance to user collusion is universally supported except in [9,28]. Verifiable outsourced decryption is another key differentiator; it is only supported in [7,8,9], and our work. Finally, VODDS is the sole one that provides reliable verification of ciphertext integrity.

7.2. Experimental Environment

To comprehensively evaluate the performance of VODDS against the advanced schemes [7,8,9,10,12,28,43,45], we conducted simulation tests to measure the computation overhead of each stage. The experiments were implemented in Java using the JPBC library, and the execution time of the main operations at each stage was recorded. Performance comparison charts were then plotted based on the results. The experimental environment is configured with an AMD Ryzen 7 7745HX @ 3.60 GHz CPU (Advanced Micro Devices, Inc., Santa Clara, CA, USA), Windows 11 Pro 24H2 (64 bit) operating system, and IntelliJ IDEA 2024.1.2 as the development platform. A Type A symmetric prime-order bilinear group was used, with curve parameters set to a 512-bit prime, resulting in $\left|Z_p\right|=512$ bits and $\left|G_1|=|G_T\right|\approx 1024$ bits. Each experimental result was averaged over 1000 independent runs to ensure stability and accuracy. Since the initialization phase is a single process, we only give the comparison on the table. We conducted a detailed comparison and test of the scheme’s encryption overhead, decryption overhead, key generation overhead and total overhead. In addition, since we have introduced the blockchain to the verification mechanism of outsourced decryption, we have experimentally tested the hash value of verifying ciphertext and the packaging and on-chain delay of blinded keys, blockchain throughput, and blinded key retrieval and download delay to express the performance of our blockchain.

The detailed configuration of our experimental environment is summarized in Table 3.

Table 3. Experimental Environment Configuration.

Category	Configuration
Hardware
CPU	AMD Ryzen 7 7745HX @ 3.60 GHz
Software
Operating System	Windows 11 Pro 24H2 (64-bit)
Development Platform	IntelliJ IDEA 2024.1.2
Cryptographic Library	JPBC
Cryptographic Parameters
Bilinear Group	Type A (Symmetric, Prime Order)
Prime (p) Size	512 bits ($|{\mathbb{Z}}_p|=512$ bits)
Group Element Size	$\left|\mathbb{G}\right|=|{\mathbb{G}}_T|\approx 1024$ bits
Experimental Method
Measurements per Point	1000 independent runs (results averaged)

Our experiments focus on functional correctness and core costs, namely storage and computation overhead comparisons, and the performance of the blockchain and the PBFT consensus. This isolates the cryptographic and protocol costs that dominate the design space and establishes a fair, reproducible baseline across schemes.

In VODDS, the number of communication rounds (for example, between the DU and the RSU, and when interacting with the blockchain) is kept as small as possible, and RSUs are placed close to the DU side. In real deployments, authorities in the same group can also be placed by geographic or network proximity to further reduce the network latency of group key agreement, which is flexible.

In our permissioned blockchain architecture, gas is used for accounting, and the cost of writing a commitment (a 32-byte hash plus minimal metadata) is negligible. Overall, while wide-area latency and gas pricing may introduce additional overhead in practice, our measurements show moderate per-event delay for commitment and lookup and predictable consensus scalability, supporting the applicability of our design.

7.3. Storage and Computation Overhead Comparison

This subsection compares VODDS to schemes [7,8,9,10,28,43] in terms of storage and computational overhead. The symbols used in the overhead expressions are defined in Table 4. A detailed comparison is separately summarized in Table 5 and Table 6.

Table 4. Notation for storage and computation overhead.

Symbols	Meaning
$\left|G\right|$	the length of the element in $\mathbb{G}$
$\left|G_T\right|$	the length of the element in ${\mathbb{G}}_T$
$\left|Z_p\right|$	the length of the element in $Z_p$
E	exponential operations in $\mathbb{G}$
$E_T$	exponential operations in ${\mathbb{G}}_T$
M	multiplication operation in $\mathbb{G}$
$M_T$	multiplication operation in ${\mathbb{G}}_T$
P	bilinear pairing
H	hash evaluation
m	total number of system attributes
n	number of attribute authorities
z	size of an attribute group
$\left|S\right|$	size of user’s attribute set
l	number of rows in the access matrix M
a	the number of attribute authority associated with the user attribute
N	number of system users

Table 5. Storage overhead comparison.

Scheme	Setup	Key	Ciphertext
[8]	$(5+2N)\left|G\right|+|G_T|+(2+N)\left|Z_p\right|$	$(2+2|S\left|\right)\left|G\right|+2|Z_p|+|G_T|$	$(2+2l)\left|G\right|+|G_T|$
[9]	$3\left|G\right|+\left|G_T\right|+H+N\left|S\right|\left|Z_p\right|$	$(2+|S\left|\right)\left|G\right|+\left|S\right|\left|Z_p\right|$	$(2+l+3|S\left|\right)\left|G\right|$
[10]	$(1+m)\left|G\right|+(1+mN)\left|Z_p\right|$	$\left(\right|S\left|\right|G|+|S\left|\right|Z_p\left|\right)$	$(1+2l)\left|G\right|+l\left|Z_p\right|$
[43]	$\left(\right|S|+3+n+N)\left|G\right|+5|Z_p|+(n+N)|Z_p|$	$(3+2|S\left|\right)\left|G\right|+\left|S\right|\left|Z_p\right|$	$(2+2l)\left|G\right|+\left|G_T\right|$
[28]	$\left|G\right|+(5m+1)|G_T|+(2+m)\left|Z_p\right|$	$\left(\right|S|+l+1\left)\right|Z_p|+9|G_T|$	$(4+2l)|G_T|+(1+l)|G|$
[7]	$(3n+4)\left|G\right|+|G_T|+|Z_p|$	$(4a+4|S|+2)\left|G\right|+3\left|Z_p\right|$	$(3l+2)\left|G\right|+|G_T|+Z_p$
Ours	$(6+m+n)\left|G\right|+|G_T|+(2+mz)|Z_p|$	$(2+2|S\left|\right)\left|G\right|+\left|Zp\right|$	$(3+2l)\left|G\right|+\left|G_T\right|$

Table 6. Computation overhead comparison.

Scheme	Setup	Keys Generation	Encryption	Decryption
[8]	$(2N+5)E+P$	$(4+5|S\left|\right)E+\left|S\right|H$	$3l\left|E\right|+(1+l)E_T+H$	$2E_T+M_T+2H$
[28]	$(2+5m)E$	$\left(3\right|S|+2)E+M$	$(4+5l)E+(1+l)M+H$	$(2l+3)P+(2l+1)M$
[9]	$2E+P+H$	$(4+|S\left|\right)E+M$	$(4+9l)E+lM$	$6P+6E$
[10]	$(m+N)M+H$	$(H+M)\left|S\right|+\left|S\right|E$	$(1+4l)E$	$(1+l)E$
[7]	$(n+7)M$	$\left(2\right|S|+3)E$	$(3l+1)E+2lM+P$	$M_T+E_T+H$
[43]	$(3+n+N)E+$ $(n+N+|S\left|\right)M$	$\left(2\right|S|+6)E+$ $(3+2|S\left|\right)M$	$\left(3\right|S|+1)E+E_T+$ $\left(\right|S|-1)M+M_T$	$\left(2\right|S|+1)P+\left|S\right|E_T+$ $\left|S\right|M+\left(2\right|S|-1)M_T$
Ours	$(4+n+mz+2m)E+P+E_T$	$(2+3|S\left|\right)E+H$	$(2+3l)E+P+H$	$2E_T+2M_{G_T}$

Table 5 compares the storage overhead of different schemes across three phases: system setup, key generation, and ciphertext size. The results indicate that the storage overhead of VODDS is comparable to most existing approaches. For instance, in the setup phase, our overhead of $(6+m+n)\left|G\right|+|G_T|+(2+mz)|Z_p|$ is within a similar range to other multi-authority schemes like [7,43]. Similarly, the private key and ciphertext sizes in VODDS remain competitive. It is worth noting that VODDS achieves a more comprehensive functionality and, as will be shown in the subsequent computation overhead comparison, also demonstrates superior performance.

Table 6 presents a comparative analysis of the computational overhead across different cryptographic phases. The results demonstrate that VODDS achieves highly competitive performance, particularly in the critical phases of encryption and decryption. For encryption, our overhead of $(2+3l)E+P+H$ is lower than that of several comparable schemes [8,9,28]. More notably, our decryption overhead of only $2E_T+2M_{G_T}$ is significantly more efficient than others, especially those requiring multiple pairing operations (e.g., [9,28,43]). This efficiency gain stems from our streamlined verification and decryption process. The slightly higher overhead in our setup phase, attributed to the distributed key generation and system initialization, is a one-time overhead that is justified by the enhanced security and functionality it enables.

From encryption to ciphertext storage and subsequent outsourced decryption, it is necessary to convert ciphertext or key to protect user privacy and data security. Table 7 compares the transformation overhead of our solution with existing schemes. The results demonstrate that VODDS incurs a transformation overhead of $(3+2l)E$, which depends linearly on the complexity of the access policy. In contrast, other schemes involve more costly operations, such as bilinear pairings in [8,12], or a higher number of exponentiations in [7]. This comparison clearly shows that our approach achieves a significant reduction in transformation overhead, contributing to the overall efficiency of the data sharing process.

Table 7. Ciphertext transformation overhead comparison.

Scheme	Transformation Overhead
[8]	$(2l+1)P+(1+l)E_T+\left(2l\right)M_T+E$
[7]	$(2+4l)E+2lM$
[12]	$2P\left|S\right|+H\left|S\right|+M\left|S\right|$
[45]	$(a+3|S\left|\right)E$
Ours	$(3+2l)E$

Figure 4a shows the key generation overhead of VODDS compared with the other six schemes. The number of attributes showed a clear positive correlation with the time overhead. Although the binding of attribute groups in our scheme introduces some computational overhead, its performance remains superior to that of schemes [8,28,43]. Scheme [10] key generation uses simple public parameters and a single-attribute authoritative private key as inputs, and the operation is lightweight. Scheme [8] has the highest overhead overhead due to the Group-KeyGen algorithm and the key transformation interaction of multiple entities. Within a multi-authority architecture, the key generation overhead of our scheme is competitive.

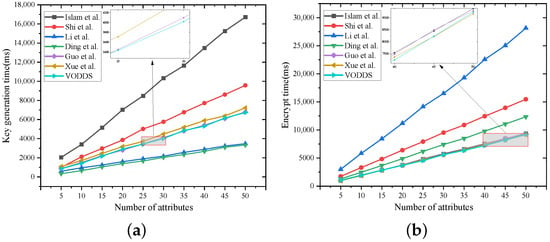
Figure 4. VODDS’s performance: (a) Key generation performance; (b) Encryption performance [7,8,9,10,28,43].

As shown in Figure 4b, the overhead of our solution is comparable to that of [7,8,43]. When the number of attributes reaches 40, however, the overhead of our solution is only 7242.518 ms, which is the lowest among all schemes. It is worth noting that our solution employs an offline/online encryption strategy, whereas [8,43] rely on conventional encryption. In contrast, the scheme in [9] requires collaborative encryption between the DU and ESP and introduces a large number of ciphertext components, resulting in relatively high computational overhead.

As an important part of the outsourced decryption or ciphertext storage architecture, the transformation of ciphertext or keys will also bring certain computational overhead. Based on Table 2, we perform a performance comparison with schemes [7,8,12,45]. As shown in Figure 5a, the scheme [7] requires exponential encryption of each ciphertext component at the RSU end and storing the result in the cloud, which leads to high overhead. Our solution only converts some ciphertext components related to user privacy and decryption security, thereby maintaining a relatively low computational overhead.

Figure 5. VODDS’s performance: (a) Ciphertext transformation performance; (b) Decryption performance [7,8,9,10,12,28,43,45].

For the comparison of decryption overhead, Figure 5b shows that, due to the use of outsourced decryption and a complete verification mechanism, the decryption overhead for our users remains lightweight. The scheme in [7] employs simpler bilinear exponentiation and approximation operations to restore the plaintext; however, our verification mechanism offers stronger reliability. In [43], the computational overhead introduced by decryption operations associated with the access policy is positively correlated with the number of attributes, which imposes a significant computational burden on the user.

In Figure 6, we present a comprehensive experimental comparison of the three key stages of the CP-ABE scheme: encryption, decryption, and key generation. In terms of total overhead, VODDS demonstrates a clear advantage. When the number of attributes ranges from 40 to 50, VODDS reduces the delay by approximately 500 ms compared with [7,10]. Overall, in all the given attribute number test points, VODDS consistently outperforms outstanding performance relative to the other schemes.

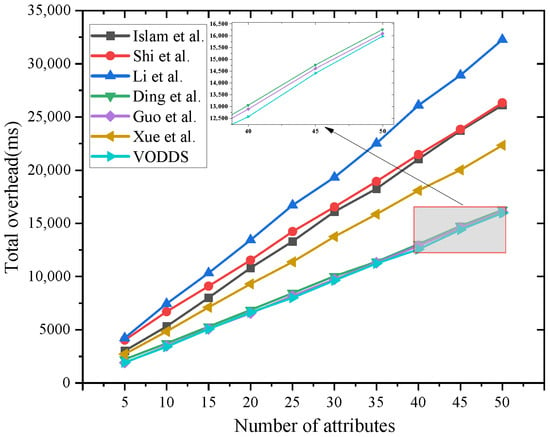
Figure 6. Comparison of total performance [7,8,9,10,28,43].

In addition to the above work, we evaluate the performance of the blockchain layer that records and verifies decryption commitments. In our architecture, the DO computes $h=(IVC\mid CVC)$ and $En{c}_{IVC}\left(\psi \right)$, and writes one on-chain commitment per decryption event (a 32-byte hash plus metadata) on an Ethereum-compatible, permissioned blockchain. When the DU receives the outsourced decryption result, it computes $h^{\prime }$, submits $h^{\prime }$ to the smart contract to retrieve $En{c}_{IVC}\left(\psi \right)$, and then completes the local verification/decryption upon receiving the on-chain response. We measure three metrics that directly affect this workflow: write throughput, confirmation latency for the commitment write, and key-retrieval latency for the DU lookup. Under our parameter settings (permissioned deployment with deterministic block generation), the write cost for one commitment is approximately 45,000 gas and the latency to confirm that write is about 150–200 ms; the key-retrieval latency ranges from 90 ms to 140 ms as the number of participating nodes increases from 1 to 25. Figure 7 shows how performance scales with the number of nodes: write throughput decreases gradually from about 870 transactions/s to about 770 transactions/s, while both the confirmation latency and the key-retrieval latency increase steadily (approximately 150→200 ms and 90→140 ms, respectively). These results indicate that, although additional nodes introduce communication and synchronization overhead—as expected—the system preserves relatively high throughput and keeps per-event delays in an acceptable range for VANET-scale data sharing.

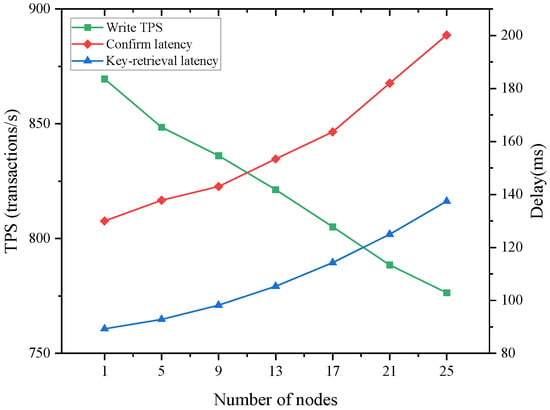
Figure 7. Blockchain performance.

To bootstrap each attribute group we run a PBFT-style Byzantine consensus when issuing the claimant’s group certificate. This provides strong consistency and fault tolerance for the key-distribution credentials and, in turn, underpins the security of the subsequent cryptographic workflow. We further evaluated the practical cost of this consensus by varying the number of attribute authorities and measuring network-wide communication and cumulative computation per decided round. As shown in Figure 8, communication grows predictably with the number of attribute authorities: from about 4.9 KB when there are 4 authorities to about 286 KB when there are 31 authorities. The cumulative computation exhibits a similar trend, rising from 92 ms to about 3.4 s across all nodes. These results match the quadratic profile expected from PBFT’s all-to-all Prepare/Commit phases and show that the overhead remains moderate for the group sizes we target, while providing the robustness needed for secure key distribution in VODDS.

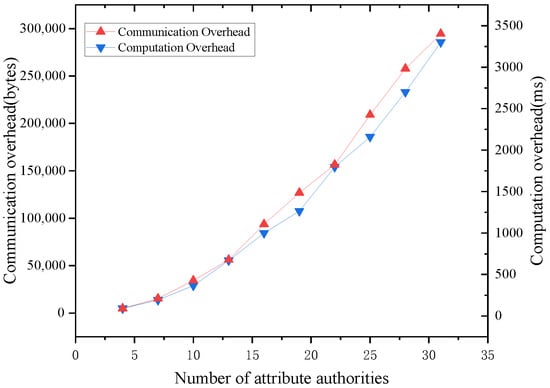
Figure 8. Overhead of the PBFT consensus.

8. Conclusions and Discussions

This paper presents VODDS, a symmetrically verifiable and privacy-preserving data sharing scheme for VANETs. Its main works are threefold: First, to address the single-point performance bottleneck in multi-authority systems, a distributed key distribution mechanism is introduced. This mechanism organizes attribute authorities into groups. Within each group, key distribution credentials are generated through a Group Key Agreement protocol, with each round secured by a Byzantine consensus. This approach effectively balances decentralized load balancing with robust security assurance. Second, the scheme implements a policy-hiding access control mechanism by leveraging the LSSS, which not only supports the flexible expression of complex access policies but also effectively conceals the policy information to protect user privacy. Third, a secure and reliable outsourced decryption framework is constructed based on blockchain and smart contracts. This framework records verification commitments on the blockchain and utilizes smart contracts for symmetrical verification—a process that symmetrically matches the outsourced decryption result against the on-chain commitment—thereby providing users with a trustworthy verification service for outsourced decryption in complex, low-latency vehicular environments. Security analysis demonstrates that VODDS achieves IND-sCPA security, leak-freeness, and collusion resistance. Finally, extensive performance evaluations and comparisons confirm the scheme’s superior efficiency and scalability.

In this paper, the term “symmetry” has a specific meaning. It refers to the structural equivalence between the verification ciphertext generated by the DO and the pseudo-verification ciphertext computed by the DU based on the outsourced decryption result. First, the DO creates a verification ciphertext and saves its hash on the blockchain. Then, the DU receives a result from the RSU and calculates a pseudo-verification ciphertext. The process is called symmetrical because if the RSU’s work is correct, the DU’s result will match the DO’s original in structure. The smart contract can then reliably compare these two values. It checks the DU’s result against the DO’s stored commitment. This is also the origin of the term “Symmetrically Verifiable Outsourced Decryption” in the title of this paper.

VODDS demonstrates strong theoretical suitability for VANETs that need frequent data sharing and flexible access control. Its practical efficiency in low-latency settings is achieved by offloading most decryption tasks to an outsourced mechanism. Nevertheless, some limitations require further investigation. Currently, the LSSS-based access structure in VODDS does not support dynamic policy updates. Implementing such updates would require the integration of mechanisms for proxy re-encryption, a process expected to introduce considerable overhead and latency. Moreover, the current design lacks a fully developed mechanism for tracing malicious users and attribute authorities.

We plan to augment VODDS with accountable anonymity via threshold openable group signatures. Users operate with unlinkable group signatures by default, so identities remain hidden in all honest interactions. Upon evidenced misbehavior, a quorum of independent trace authorities jointly executes an opening procedure to recover only the culprit’s enrollment identity with public verifiability. We will pair this with dynamic revocation such as accumulator-based blacklists and, where appropriate, verifiable encryption of identities under the same threshold escrow. This approach clarifies the inherent trade off: raising the opening threshold and using short-lived pseudonyms strengthens anonymity but slows or complicates tracing, whereas lowering the threshold and using longer-lived identifiers improves traceability and revocation efficiency but increases linkability risk.

In the near future, by incorporating support for dynamic policy updates and enhancing the traceability mechanism against malicious entities, VODDS is expected to be adopted in more complex and dynamic data-sharing scenarios, thereby broadening its practical applicability in intelligent transportation systems and beyond.