Global Sensitivity and Mathematical Modeling for Zoonotic Lassa Virus Transmission and Disability in Critical Cases in the Light of Fractional Order Model

Abstract

Lassa fever remains a significant zoonotic threat in West Africa, characterized by complex human-to-human and rodent-to-human transmission pathways and prolonged immune responses. Existing integer-order models often neglect the long-term memory and delayed recovery effects inherent to the disease. In this study, we develop and analyze a fractional-order Caputo model for Lassa fever transmission incorporating disability feedback among recovered individuals. The model captures memory-dependent infection and recovery dynamics, offering a more realistic description of epidemic persistence. The model is symmetric when the fractional approach to unity where it recovers its classical ODE counterpart. Analytical results establish the positivity, boundedness, existence, and uniqueness of solutions, while Picard stability and contraction mapping confirm well-posedness within the fractional framework. A Grünwald–Letnikov discretization scheme is constructed for numerical simulation, validated under varying fractional orders ($\lambda \in [0.7,1]$). The results reveal that decreasing the fractional order slows the infection decay rate and prolongs epidemic duration, highlighting the biological significance of memory effects. A global sensitivity analysis based on Latin Hypercube Sampling and Partial Rank Correlation Coefficients (LHS–PRCC) identifies the rodent-to-human transmission rate (${\kappa }_1$), human-to-human transmission rate (${\eta }_1$), and rodent interaction rate (${\xi }_r$) as the most influential parameters. These findings provide critical insight into the control and management of Lassa fever through rodent population control, improved recovery rates, and early human intervention. The fractional-order formulation thus extends existing models both mathematically and epidemiologically by capturing delayed dynamics and disability-induced feedback mechanisms.

1. Introduction

Lassa fever is a rodent-borne viral hemorrhagic disease caused by the Lassa virus, an arenavirus that is maintained in nature primarily by the multimammate rat Mastomys natalensis (MN). The disease was first recognized in Nigeria in 1969 [1] and is now endemic across several regions of West Africa. Although most infections are mild or asymptomatic, severe disease and fatal outcomes occur in a subset of patients. Human infection typically results from exposure to food or household items contaminated with the urine or feces of infected rodents, particularly the multimammate rat MN.

While MN is the principal reservoir host, field and molecular studies have identified additional rodent species such as Mastomys erythroleucus, Hylomyscus pamfi, and Mus baoulei as potential carriers. These findings, together with spatial risk-mapping analyses, indicate that rodent ecology, land use patterns, and local socio-environmental conditions strongly influence the risk of human spillover across West Africa [2,3,4,5].

Human-to-human transmission can also occur, most often in healthcare settings lacking adequate infection prevention and control measures, through contact with blood or other bodily fluids of infected individuals. Currently, no licensed vaccine is available, and although ribavirin has been used clinically, its efficacy and optimal dosing remain uncertain. Early supportive care, however, has been shown to improve survival outcomes [6].

Mathematical modeling in biological dynamics has gained a lot of interest from researchers in the current century [7,8,9,10]. Modeling works approach Lassa fever at different scales. Deterministic compartmental models caputre zoonotic spillover, limited human-to-human transmission, and seasonality. Recent work displays that seasonal forcing of rodent population dynamics reproduces Nigeria’s peaks in human cases [11]. Other various studies on Lassa fever are listed in [12,13,14]. Recently, Ramzan et al. devised a mathematical model for Lassa fever and its effect on the spinal cord and brain [15]. The authors have divided the total population into human and rodent subpopulations. Then, the human population was further divided into susceptible, mildly infected, infected, and recovered populations, while the rodent population was categorized only into susceptible and infected populations. They have investigated mathematical properties, control strategies and performed numerical simulations to show the dynamics of the disease.

The generalization of traditional calculus is known as fractional calculus [16]. The fractional order (FO) operators have the tendency to predict all previous information about physical process which is not attainable on integer order operators. Recently, scientists have frequently utilized FO operators to study more generalized dynamics of physical phenomen occurs in various fields of science. For instance, Li et al. investigated well-posedness and fractional dynamics of the delayed zooplankton–phytoplankton model [17]. Xu et al. characterized potential glycerol hydrogenolysis mechanisms by qualitatively analyzing, within a fractional-order DE framework, the kinetics of a catalytic model [18]. Xu et al. considered an RSV transmission model on a continuous human population, incorporating a superspreading infectious cohort under the FO system [19]. In the literature, Saifullah et al. investigated fractional dynamics of nonlinear waves governed by the generalized KdV equation [20]. The fractional order breast cancer model is studied in [21]. The Malaria disease model is studied in [22]. Similarly, the authors in [23] developed a fractional-order model for the Omicron variant of COVID-19 and showed that the fractional derivative framework better characterizes delayed immune responses and long-term infection persistence. Similarly, in [24], Ul Haq et al. analyzed the COVID-19 outbreak using the Caputo fractional derivative and established the stability conditions for disease-free and endemic equilibria. Furthermore, the authors in [25] formulated a fractional mathematical model incorporating isolation and social distancing effects, highlighting the role of nonlocal operators in accurately describing epidemic spread under mitigation measures. More applications of FO models are provided in [26,27,28]. Building upon these fractional modeling approaches, the present study extends the application of fractional calculus to the Lassa fever dynamics, capturing both human-to-human and rodent-to-human transmission processes with memory-dependent infection and recovery behaviors. Motivated by interesting applications of FO systems, we study the FO version of the model presented in [15]. The transmission of the Lassa fever is portrayed in Figure 1.

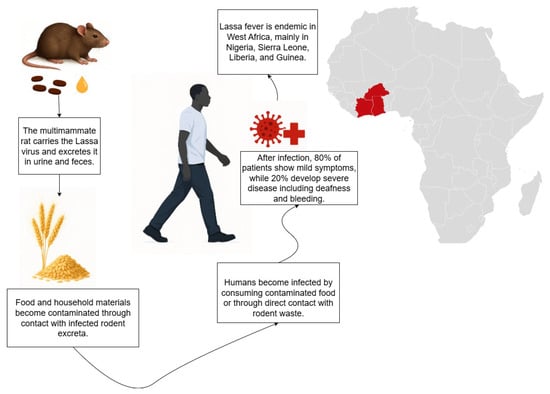
Figure 1. Picture of transmission of the considered disease.

Let the total human population is given by $N_h=\mathcal{S}+{\mathcal{I}}_m+{\mathcal{I}}_s+\mathcal{R}$, and the total rodent population by $N_r={\mathcal{S}}_r+{\mathcal{I}}_r$. The dynamics of Lassa fever spread under fractional order $\lambda \in (0,1]$ are modeled as

$$\begin{array}{cc}\hfill & D_t^{\lambda }\mathcal{S}={\Lambda }_h-{\eta }_1\mathcal{S}{\mathcal{I}}_m-{\eta }_2\mathcal{S}{\mathcal{I}}_s-({\kappa }_1+{\kappa }_2)\mathcal{S}{\mathcal{I}}_r-{\mu }_h\mathcal{S},\hfill \\ & D_t^{\lambda }{\mathcal{I}}_m={\eta }_1\mathcal{S}{\mathcal{I}}_m+{\kappa }_1\mathcal{S}{\mathcal{I}}_r-\delta {\mathcal{I}}_m-({\mu }_h+{\sigma }_1){\mathcal{I}}_m,\hfill \\ & D_t^{\lambda }{\mathcal{I}}_s={\eta }_2\mathcal{S}{\mathcal{I}}_s+{\kappa }_2\mathcal{S}{\mathcal{I}}_r+\delta {\mathcal{I}}_m-({\mu }_h+{\sigma }_2){\mathcal{I}}_s,\hfill \\ & D_t^{\lambda }\mathcal{R}={\sigma }_1{\mathcal{I}}_m+{\sigma }_2{\mathcal{I}}_s-{\mu }_h\mathcal{R},\hfill \\ & D_t^{\lambda }{\mathcal{S}}_r={\Lambda }_r-{\xi }_r{\mathcal{S}}_r{\mathcal{I}}_r-{\mu }_r{\mathcal{S}}_r,\hfill \\ & D_t^{\lambda }{\mathcal{I}}_r={\xi }_r{\mathcal{S}}_r{\mathcal{I}}_r-{\mu }_r{\mathcal{I}}_r.\hfill \end{array}$$

(1)

The parameter descriptions and their values are displayed in the Table 1 and Table 2.

Table 1. Parameter values for ${\mathcal{R}}_0>1$ (endemic case).

Parameter	Value	Biological Description	Source
${\Lambda }_h$	$8.5\times {10}^4$	Recruitment rate of humans (birth/immigration)	[15]
${\mu }_h$	$1.0\times {10}^{-4}$	Natural death rate of humans	[15]
${\eta }_1$	$9.0\times {10}^{-12}$	Human-to-human transmission rate (mild infection)	[15]
${\eta }_2$	$1.8\times {10}^{-11}$	Human-to-human transmission rate (severe infection)	[15]
${\kappa }_1$	$5.5\times {10}^{-9}$	Rodent-to-human transmission rate (mild infection)	[15]
${\kappa }_2$	$4.0\times {10}^{-15}$	Rodent-to-human transmission rate (severe infection)	[15]
$\delta$	$7.0\times {10}^{-5}$	Rate of progression from mild to severe infection	[15]
${\sigma }_1$	$6.5\times {10}^{-4}$	Recovery rate of mildly infected humans	[15]
${\sigma }_2$	$3.8\times {10}^{-5}$	Recovery rate of severely infected humans	[15]
${\Lambda }_r$	$1.1\times {10}^5$	Recruitment rate of rodents	[15]
${\xi }_r$	$8.0\times {10}^{-7}$	Transmission rate between infected and susceptible rodents	[15]
${\mu }_r$	$0.28$	Natural death rate of rodents	[15]

Table 2. Parameter values for ${\mathcal{R}}_0<1$ (disease-free case).

Parameter	Value	Biological Description	Source
${\Lambda }_h$	$8.5\times {10}^4$	Recruitment rate of humans (birth/immigration)	[15]
${\mu }_h$	$1.0\times {10}^{-4}$	Natural death rate of humans	[15]
${\eta }_1$	$4.5\times {10}^{-12}$	Reduced human-to-human transmission rate (mild)	[15]
${\eta }_2$	$8.5\times {10}^{-12}$	Reduced human-to-human transmission rate (severe)	[15]
${\kappa }_1$	$3.5\times {10}^{-9}$	Reduced rodent-to-human infection (mild)	[15]
${\kappa }_2$	$1.5\times {10}^{-15}$	Reduced rodent-to-human infection (severe)	[15]
$\delta$	$9.0\times {10}^{-5}$	Faster mild-to-severe progression	[15]
${\sigma }_1$	$8.0\times {10}^{-4}$	Increased recovery rate of mild infection	[15]
${\sigma }_2$	$4.5\times {10}^{-5}$	Increased recovery rate of severe infection	[15]
${\Lambda }_r$	$1.1\times {10}^5$	Recruitment rate of rodents	[15]
${\xi }_r$	$6.0\times {10}^{-7}$	Decreased rodent-to-rodent transmission rate	[15]
${\mu }_r$	$0.32$	Slightly higher natural rodent mortality	[15]

In the present model, the total human population is divided into four epidemiological classes: susceptible humans $\left(\mathcal{S}\right)$, mildly infected humans $\left({\mathcal{I}}_m\right)$, severely infected humans $\left({\mathcal{I}}_s\right)$, and recovered individuals $\left(\mathcal{R}\right)$, some of whom may experience post-infection disability. The rodent population is represented by susceptible rodents $\left({\mathcal{S}}_r\right)$ and infected rodents $\left({\mathcal{I}}_r\right)$. Disease transmission occurs through two primary pathways: human-to-human contact, represented by the coefficients ${\eta }_1$ and ${\eta }_2$ for mild and severe infections, respectively, and rodent-to-human contact, represented by ${\kappa }_1$ and ${\kappa }_2$. Rodent infection is governed by the transmission parameter ${\xi }_r$, which links susceptible and infected rodents within the rodent subsystem. The overall model structure is adapted from the integer-order Lassa fever framework proposed by Ramzan et al. [15], with two principal extensions: (i) the introduction of the Caputo fractional derivative to capture memory-dependent infection and recovery dynamics, and (ii) the inclusion of a disability feedback mechanism in the recovered class, reflecting the long-term health effects of Lassa fever and their influence on disease persistence.

2. Basic Concepts

Let $\mathcal{G}:[0,\infty )\to \mathbb{R}$ be sufficiently smooth and of exponential order.

Definition 1.

Riemann–Liouville fractional derivative of order $\lambda >0$. Let $n=\lceil \lambda \rceil$. Using the Riemann–Liouville fractional integral

$$\left(I_0^{\lambda }\mathcal{G}\right)\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}\mathcal{G}\left(\tau \right)d\tau \hspace{1em}(\lambda >0),$$

the Riemann–Liouville derivative is

$$\left(D_0^{\lambda }\mathcal{G}\right)\left(t\right)={\displaystyle \frac{d^n}{d{t}^n}}\left(I_0^{n-\lambda }\mathcal{G}\right)\left(t\right).$$

For $0<\lambda <1$, this reduces to

$$\left(D_0^{\lambda }\mathcal{G}\right)\left(t\right)={\displaystyle \frac{d}{dt}}{\displaystyle \frac{1}{\Gamma (1-\lambda )}}{\int }_0^t{(t-\tau )}^{-\lambda }\mathcal{G}\left(\tau \right)d\tau .$$

Definition 2.

Caputo fractional derivative of order $\lambda >0$. With the same $n=\lceil \lambda \rceil$,

$$\left({}^{C}D_0^{\lambda }\mathcal{G}\right)\left(t\right)=\left(I_0^{n-\lambda }{\mathcal{G}}^{\left(n\right)}\right)\left(t\right)={\displaystyle \frac{1}{\Gamma (n-\lambda )}}{\int }_0^t{(t-\tau )}^{n-\lambda -1}{\mathcal{G}}^{\left(n\right)}\left(\tau \right)d\tau .$$

For $0<\lambda <1$:

$$\left({}^{C}D_0^{\lambda }\mathcal{G}\right)\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\lambda )}}{\int }_0^t{(t-\tau )}^{-\lambda }{\mathcal{G}}^{\prime }\left(\tau \right)d\tau .$$

Definition 3.

Laplace transform of the Caputo derivative. Let ${\displaystyle \mathcal{L}\left\{\mathcal{G}\right\}\left(s\right)=\tilde{\mathcal{G}}\left(s\right)={\int }_0^{\infty }{e}^{-st}\mathcal{G}\left(t\right)dt}$ and $n=\lceil \lambda \rceil$. If ${\mathcal{G}}^{\left(k\right)}\left(0^{+}\right)$ exist for $k=0,\dots ,n-1$, then

$$\mathcal{L}\left\{{}^{C}D_0^{\lambda }\mathcal{G}\left(t\right)\right\}\left(s\right)=s^{\lambda }\tilde{\mathcal{G}}\left(s\right)-\sum _{k=0}^{n-1}{s}^{\lambda -1-k}{\mathcal{G}}^{\left(k\right)}\left(0^{+}\right).$$

3. Mathematical Analysis

Theorem 1 (Positivity and Boundedness).

Let state vector $x={(\mathcal{S},{\mathcal{I}}_m,{\mathcal{I}}_s,\mathcal{R},{\mathcal{S}}_r,{\mathcal{I}}_r)}^{\top }$. Assume the initial conditions are non-negative:

$$\mathcal{S}\left(0\right),{\mathcal{I}}_m\left(0\right),{\mathcal{I}}_s\left(0\right),\mathcal{R}\left(0\right),{\mathcal{S}}_r\left(0\right),{\mathcal{I}}_r\left(0\right)\ge 0.$$

Then, for all $t\ge 0$, the following hold

• The solution components $\mathcal{S}\left(t\right),{\mathcal{I}}_m\left(t\right),{\mathcal{I}}_s\left(t\right),\mathcal{R}\left(t\right),{\mathcal{S}}_r\left(t\right),{\mathcal{I}}_r\left(t\right)$ remain non-negative for all $t\ge 0$.
• The solutions of the system remain bounded, i.e.,

  $$0\le \mathcal{S}\left(t\right)\le {\displaystyle \frac{{\Lambda }_h}{{\mu }_h}},\hspace{1em}0\le {\mathcal{I}}_m\left(t\right)\le {\displaystyle \frac{{\Lambda }_h}{{\mu }_h}},\hspace{1em}0\le {\mathcal{I}}_s\left(t\right)\le {\displaystyle \frac{{\Lambda }_h}{{\mu }_h}},\hspace{1em}0\le \mathcal{R}\left(t\right)\le {\displaystyle \frac{{\Lambda }_h}{{\mu }_h}},$$

  $$0\le {\mathcal{S}}_r\left(t\right)\le {\displaystyle \frac{{\Lambda }_r}{{\mu }_r}},\hspace{1em}0\le {\mathcal{I}}_r\left(t\right)\le {\displaystyle \frac{{\Lambda }_r}{{\mu }_r}}.$$

Proof. 

• We begin by proving positivity. We will use the comparison principle for fractional DEs to show that the solution remains non-negative.
  Consider the equation for $\mathcal{S}$ as

  $$D_t^{\lambda }\mathcal{S}={\Lambda }_h-{\eta }_1\mathcal{S}{\mathcal{I}}_m-{\eta }_2\mathcal{S}{\mathcal{I}}_s-({\kappa }_1+{\kappa }_2)\mathcal{S}{\mathcal{I}}_r-{\mu }_h\mathcal{S}.$$
  At $\mathcal{S}=0$, the equation simplifies to

  $$D_t^{\lambda }\mathcal{S}{|}_{\mathcal{S}=0}={\Lambda }_h\ge 0.$$
  Thus, if $\mathcal{S}\left(t\right)=0$ at some time t, then $D_t^{\lambda }\mathcal{S}\left(t\right)={\Lambda }_h\ge 0$, meaning that $\mathcal{S}\left(t\right)$ cannot become negative. Since the fractional derivative $D_t^{\lambda }$ preserves the order (in the sense of non-negativity for cooperative systems), $\mathcal{S}\left(t\right)$ remains non-negative for all $t\ge 0$. Next, consider the equation for ${\mathcal{I}}_m$ as

  $$D_t^{\lambda }{\mathcal{I}}_m={\eta }_1\mathcal{S}{\mathcal{I}}_m+{\kappa }_1\mathcal{S}{\mathcal{I}}_r-\delta {\mathcal{I}}_m-({\mu }_h+{\sigma }_1){\mathcal{I}}_m.$$
  At ${\mathcal{I}}_m=0$, this simplifies to

  $$D_t^{\lambda }{\mathcal{I}}_m{|}_{{\mathcal{I}}_m=0}={\kappa }_1\mathcal{S}{\mathcal{I}}_r\ge 0,$$

  and thus ${\mathcal{I}}_m\left(t\right)$ cannot become negative.
  A similar analysis can be performed for the other variables, such as ${\mathcal{I}}_s$, $\mathcal{R}$, ${\mathcal{S}}_r$, and ${\mathcal{I}}_r$. In each case with aid of comparison principle, we find that the fractional derivative is non-negative when the corresponding variable is zero, and so each component of the solution vector remains non-negative for all $t\ge 0$.
• Now, we show that the solutions are bounded by deriving upper bounds for each population.
  The total human population is given by $N_h=\mathcal{S}+{\mathcal{I}}_m+{\mathcal{I}}_s+\mathcal{R}$. Summing the equations for $\mathcal{S}$, ${\mathcal{I}}_m$, ${\mathcal{I}}_s$, and $\mathcal{R}$, we obtain

  $$D_t^{\lambda }{N}_h={\Lambda }_h-{\mu }_h\mathcal{S}-({\mu }_h+{\sigma }_1){\mathcal{I}}_m-({\mu }_h+{\sigma }_2){\mathcal{I}}_s-{\mu }_h\mathcal{R}+{\sigma }_1{\mathcal{I}}_m+{\sigma }_2{\mathcal{I}}_s.$$
  We obtain the following

  $$D_t^{\lambda }{N}_h={\Lambda }_h-{\mu }_h{N}_h.$$
  The solution of the above linear fractional DE is given by

  $$N_h\left(t\right)=N_{h,\infty }+\left(N_h\left(0\right)-N_{h,\infty }\right)E_{\lambda }\left(-{\mu }_h{t}^{\lambda }\right),$$

  where $N_{h,\infty }={\displaystyle \frac{{\Lambda }_h}{{\mu }_h}}$, and $E_{\lambda }$ is the Mittag–Leffler function. Since $E_{\lambda }(-{\mu }_h{t}^{\lambda })$ is always between 0 and 1 for all $t\ge 0$, it follows that

  $$0\le N_h\left(t\right)\le N_{h,\infty }={\displaystyle \frac{{\Lambda }_h}{{\mu }_h}}.$$
  Similarly, define the total rodent population as $N_r={\mathcal{S}}_r+{\mathcal{I}}_r$. Summing the equations for ${\mathcal{S}}_r$ and ${\mathcal{I}}_r$, we obtain

  $$D_t^{\lambda }{N}_r={\Lambda }_r-{\mu }_r{N}_r.$$
  The solution to this equation is

  $$N_r\left(t\right)=N_{r,\infty }+\left(N_r\left(0\right)-N_{r,\infty }\right)E_{\lambda }\left(-{\mu }_r{t}^{\lambda }\right),$$

  where $N_{r,\infty }={\displaystyle \frac{{\Lambda }_r}{{\mu }_r}}$. Since $E_{\lambda }(-{\mu }_r{t}^{\lambda })$ is also always between 0 and 1, we conclude that

  $$0\le N_r\left(t\right)\le N_{r,\infty }={\displaystyle \frac{{\Lambda }_r}{{\mu }_r}}.$$
  Thus, the solutions for $\mathcal{S}\left(t\right),{\mathcal{I}}_m\left(t\right),{\mathcal{I}}_s\left(t\right),\mathcal{R}\left(t\right),{\mathcal{S}}_r\left(t\right),{\mathcal{I}}_r\left(t\right)$ are bounded above by ${\displaystyle \frac{{\Lambda }_h}{{\mu }_h}}$ for humans and ${\displaystyle \frac{{\Lambda }_r}{{\mu }_r}}$ for rodents. These upper bounds confirm that the solutions remain bounded for all $t\ge 0$.

□

3.1. Disease-Free and Endemic Equilibrium Points for Lassa Fever Model

This part presents the disease-free and endemic equilibrium points for Lassa fever model.

3.1.1. Disease-Free Equilibrium

The disease-free equilibrium (DFE) corresponds to the absence of infection in both the human and rodent populations, that is, $I_m=I_s=I_r=0.$ At steady state, all time derivatives vanish, so the right-hand sides of the governing equations satisfy

$$\begin{array}{cc}\hfill 0& ={\Lambda }_h-{\mu }_{h}S,\hfill \\ \hfill 0& ={\mu }_{h}R,\hfill \\ \hfill 0& ={\Lambda }_r-{\mu }_r{S}_r,\hfill \\ \hfill 0& ={\mu }_r{I}_r.\hfill \end{array}$$

Solving these equations yields the disease-free equilibrium point:

$$E_0=(S_0,I_m^0,I_s^0,R_0,S_r^0,I_r^0)=\left({\displaystyle \frac{{\Lambda }_h}{{\mu }_h}},0,0,0,{\displaystyle \frac{{\Lambda }_r}{{\mu }_r}},0\right).$$

3.1.2. Endemic Equilibrium (EE)

An EE occurs when there are non-zero numbers of infected individuals in both human and rodent populations. To find the EEs, we set the time derivatives equal to zero and solve the system of equations under the assumption that ${\mathcal{I}}_m,{\mathcal{I}}_s,{\mathcal{I}}_r\ne 0$. The system of equations for equilibrium is

$$\begin{array}{cc}\hfill {\Lambda }_h-{\eta }_1\mathcal{S}{\mathcal{I}}_m-{\eta }_2\mathcal{S}{\mathcal{I}}_s-({\kappa }_1+{\kappa }_2)\mathcal{S}{\mathcal{I}}_r-{\mu }_h\mathcal{S}& =0,\hfill \\ \hfill {\eta }_1\mathcal{S}{\mathcal{I}}_m+{\kappa }_1\mathcal{S}{\mathcal{I}}_r-\delta {\mathcal{I}}_m-({\mu }_h+{\sigma }_1){\mathcal{I}}_m& =0,\hfill \\ \hfill {\eta }_2\mathcal{S}{\mathcal{I}}_s+{\kappa }_2\mathcal{S}{\mathcal{I}}_r+\delta {\mathcal{I}}_m-({\mu }_h+{\sigma }_2){\mathcal{I}}_s& =0,\hfill \\ \hfill {\sigma }_1{\mathcal{I}}_m+{\sigma }_2{\mathcal{I}}_s-{\mu }_h\mathcal{R}& =0,\hfill \\ \hfill {\Lambda }_r-{\xi }_r{\mathcal{S}}_r{\mathcal{I}}_r-{\mu }_r{\mathcal{S}}_r& =0,\hfill \\ \hfill {\xi }_r{\mathcal{S}}_r{\mathcal{I}}_r-{\mu }_r{\mathcal{I}}_r& =0.\hfill \end{array}$$

Thus, the EE is given as

$$E_1=\left({\mathcal{S}}^{*},{\mathcal{I}}_m^{*},{\mathcal{I}}_s^{*},{\mathcal{R}}^{*},{\mathcal{S}}_r^{*},{\mathcal{I}}_r^{*}\right),$$

where

$${\mathcal{S}}^{*}={\displaystyle \frac{{\Lambda }_h}{{\eta }_1{\mathcal{I}}_m^{*}+{\eta }_2{\mathcal{I}}_s^{*}+({\kappa }_1+{\kappa }_2){\mathcal{I}}_r^{*}+{\mu }_h}},$$

$${\mathcal{I}}_m^{*}={\displaystyle \frac{{\eta }_1{\mathcal{S}}^{*}+{\kappa }_1{\mathcal{S}}^{*}}{\delta +{\mu }_h+{\sigma }_1}},$$

$${\mathcal{I}}_s^{*}={\displaystyle \frac{\delta {\mathcal{I}}_m^{*}}{{\eta }_2{\mathcal{S}}^{*}+{\kappa }_2{\mathcal{S}}^{*}+{\mu }_h+{\sigma }_2}},$$

$${\mathcal{R}}^{*}={\displaystyle \frac{{\sigma }_1{\mathcal{I}}_m^{*}+{\sigma }_2{\mathcal{I}}_s^{*}}{{\mu }_h}},$$

$${\mathcal{S}}_r^{*}={\displaystyle \frac{{\Lambda }_r}{{\mu }_r+{\xi }_r{\mathcal{I}}_r^{*}}},$$

$${\mathcal{I}}_r^{*}={\displaystyle \frac{{\xi }_r{\mathcal{S}}_r^{*}}{{\mu }_r}}.$$

3.2. Existence of Solution and Picard Stability

This part presents the existence of solution and the Picard stability analysis of the proposed model.

Theorem 2.

Let the fractional-order Lassa fever system be written as

$$D_t^{\lambda }x\left(t\right)=f\left(x\left(t\right)\right),\hspace{1em}x\left(0\right)=x_0,$$

where $x\left(t\right)={[S\left(t\right),I_m\left(t\right),I_s\left(t\right),R\left(t\right),S_r\left(t\right),I_r\left(t\right)]}^{\top }$ and $f:{\mathbb{R}}^6\to {\mathbb{R}}^6$ is continuous and satisfies a Lipschitz condition

$$\parallel f\left(x\right)-f\left(y\right)\parallel \le L\parallel x-y\parallel ,\hspace{1em}\forall x,y\in {\mathbb{R}}^6,$$

with constant $L>0$. Then, there exists a unique solution $x\left(t\right)$ in the Banach space $(C([0,T],{\mathbb{R}}^6),$ ${\parallel ·\parallel }_{\infty })$ and the solution is Picard stable if $L<{\displaystyle \frac{1}{\Gamma (\lambda +1)}}$.

Proof. 

We rewrite the system in its equivalent Volterra integral form:

$$x\left(t\right)=x_0+{\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}f\left(x\left(\tau \right)\right)d\tau .$$

Define the Picard operator

$$\left(\mathcal{F}x\right)\left(t\right)=x_0+{\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}f\left(x\left(\tau \right)\right)d\tau .$$

For any $x,y\in C([0,T],{\mathbb{R}}^6)$, we have

$$\begin{array}{cc}\hfill \parallel \left(\mathcal{F}x\right)\left(t\right)-\left(\mathcal{F}y\right)\left(t\right)\parallel & \le {\displaystyle \frac{L}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}\parallel x\left(\tau \right)-y\left(\tau \right)\parallel d\tau \hfill \\ \hfill & \le {\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}{\parallel x-y\parallel }_{\infty }.\hfill \end{array}$$

Hence,

$${\parallel \mathcal{F}x-\mathcal{F}y\parallel }_{\infty }\le K{\parallel x-y\parallel }_{\infty },K={\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}.$$

If $K<1$, i.e.,

$$L<{\displaystyle \frac{\Gamma (\lambda +1)}{T^{\lambda }}},$$

then $\mathcal{F}$ is a contraction mapping on $C([0,T],{\mathbb{R}}^6)$. By the Banach fixed-point theorem, there exists a unique fixed point $x\left(t\right)=\mathcal{F}x\left(t\right)$, which is the unique solution of the system. Moreover, since $\mathcal{F}$ is a contraction, small perturbations in initial conditions decay geometrically, ensuring Picard stability. □

Theorem 3.

Consider the fractional-order system

$$D_t^{\lambda }x\left(t\right)=f\left(x\left(t\right)\right),\hspace{1em}x\left(0\right)=x_0,\hspace{1em}0<\lambda \le 1,$$

with $x\left(t\right)={[S\left(t\right),I_m\left(t\right),I_s\left(t\right),R\left(t\right),S_r\left(t\right),I_r\left(t\right)]}^{\top }\in {\mathbb{R}}^6$. Assume $f:{\mathbb{R}}^6\to {\mathbb{R}}^6$ is continuous and Lipschitz on a convex set $\subset {\mathbb{R}}^6$ that contains the trajectory, i.e.,

$$\parallel f\left(u\right)-f\left(v\right)\parallel \le L\parallel u-v\parallel \hspace{1em}\mathit{for}\mathit{all}u,v\in \mathcal{D},$$

for some $L\ge 0$ and any fixed vector norm $\parallel ·\parallel$ on ${\mathbb{R}}^6$. Then, for any $T>0$ such that

$$K:={\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}<1,$$

there exists a unique solution $x\in C([0,T],{\mathbb{R}}^6)$, and the Picard sequence converges to it geometrically in the supremum norm. Moreover, the solution depends continuously on the initial data (Picard stability).

Proof. 

Step 1 (integral formulation and function space). For Caputo derivatives, the system is equivalent to the Volterra equation

$$x\left(t\right)=x_0+{\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}f\left(x\left(\tau \right)\right)d\tau .$$

Define the Banach space $X:=\left(C([0,T],{\mathbb{R}}^6),{\parallel ·\parallel }_{\infty }\right)$ with ${\parallel x\parallel }_{\infty }={sup}_{t\in [0,T]}\parallel x\left(t\right)\parallel$. Introduce the operator $\mathcal{F}:X\to X$ by

$$\left(\mathcal{F}x\right)\left(t\right):=x_0+{\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}f\left(x\left(\tau \right)\right)d\tau .$$

We also fix a closed, convex subset

$$\mathcal{B}:=\{x\in X:\parallel x-x_0{\parallel }_{\infty }\le M\}$$

with $M>0$ chosen so that $\mathcal{F}\left(\mathcal{B}\right)\subseteq \mathcal{B}$ (this is possible by continuity of f and small enough T; a standard growth bound shows $\parallel \mathcal{F}x-x_0{\parallel }_{\infty }\le T^{\lambda }{\parallel f\left(x\right)\parallel }_{\infty }/\Gamma (\lambda +1)$).

Step 2 (contraction estimate). For $x,y\in X$ and $t\in [0,T]$,

$$\parallel \left(\mathcal{F}x\right)\left(t\right)-\left(\mathcal{F}y\right)\left(t\right)\parallel \le {\displaystyle \frac{1}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}\parallel f\left(x\left(\tau \right)\right)-f\left(y\left(\tau \right)\right)\parallel d\tau \le {\displaystyle \frac{L}{\Gamma \left(\lambda \right)}}{\int }_0^t{(t-\tau )}^{\lambda -1}\parallel x\left(\tau \right)-y\left(\tau \right)\parallel d\tau .$$

Taking sup over $t\in [0,T]$ and using $\parallel x\left(\tau \right)-y\left(\tau \right)\parallel \le {\parallel x-y\parallel }_{\infty }$ yields

$${\parallel \mathcal{F}x-\mathcal{F}y\parallel }_{\infty }\le {\displaystyle \frac{L}{\Gamma \left(\lambda \right)}}\left(\underset{t\in [0,T]}{sup}{\int }_0^t{(t-\tau )}^{\lambda -1}d\tau \right){\parallel x-y\parallel }_{\infty }={\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}{\parallel x-y\parallel }_{\infty }.$$

Hence, $\mathcal{F}$ is a contraction on X provided $K:={\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}<1$. By construction of $\mathcal{B}$, $\mathcal{F}\left(\mathcal{B}\right)\subseteq \mathcal{B}$, so $\mathcal{F}$ is a contraction on $\mathcal{B}$.

Step 3 (Picard iteration and convergence). Define the Picard sequence $x^{\left(0\right)}\left(t\right)\equiv x_0$ and $x^{(n+1)}=\mathcal{F}{x}^{\left(n\right)}$. Then, for $n\ge 0$,

$$\parallel x^{(n+1)}-x^{\left(n\right)}{\parallel }_{\infty }=\parallel \mathcal{F}{x}^{\left(n\right)}-\mathcal{F}{x}^{(n-1)}{\parallel }_{\infty }\le K\parallel x^{\left(n\right)}-x^{(n-1)}{\parallel }_{\infty }\le K^n{\parallel x^{\left(1\right)}-x^{\left(0\right)}\parallel }_{\infty }.$$

Thus, $\left\{x^{\left(n\right)}\right\}$ is Cauchy in X and converges (geometrically) to a unique fixed point $x\in \mathcal{B}\subset X$ with $x=\mathcal{F}x$, i.e., a solution to the integral equation (and hence to the original Caputo system). Uniqueness follows from the contraction property.

Step 4 (stability/continuous dependence). Let x and $\tilde{x}$ solve the system with initial data $x_0$ and ${\tilde{x}}_0$, respectively. By the same estimate,

$$\parallel x-\tilde{x}{\parallel }_{\infty }\le \parallel x_0-{\tilde{x}}_0\parallel +{\displaystyle \frac{L}{\Gamma \left(\lambda \right)}}\underset{t\in [0,T]}{sup}{\int }_0^t{(t-\tau )}^{\lambda -1}\parallel x\left(\tau \right)-\tilde{x}\left(\tau \right)\parallel d\tau \le \parallel x_0-{\tilde{x}}_0\parallel +K\parallel x-\tilde{x}{\parallel }_{\infty }.$$

Rearranging produces

$$\parallel x-\tilde{x}{\parallel }_{\infty }\le {\displaystyle \frac{1}{1-K}}\parallel x_0-{\tilde{x}}_0\parallel ,$$

which shows continuous dependence on initial data (Picard stability). □

Lemma 1

(non-negative Lipschitz bounds for the model). Let the state components be bounded on $[0,T]$ by $\left|S\right|\le {\ell }_1$, $|I_m|\le {\ell }_2$, $|I_s|\le {\ell }_3$, $\left|R\right|\le {\ell }_4$, $|S_r|\le {\ell }_5$, $|I_r|\le {\ell }_6$. For the right-hand sides $f_1,\dots ,f_6$ of the model, one has

$$|f_i\left(X\right)-f_i\left(Y\right)|\le L_i\parallel X-Y\parallel ,\hspace{1em}i=1,\dots ,6,$$

with non-negative constants (example for $f_1$)

$$L_1={\eta }_1{\ell }_2+{\eta }_2{\ell }_3+({\kappa }_1+{\kappa }_2){\ell }_6+{\mu }_h\ge 0,$$

and analogous expressions for $L_2,\dots ,L_6$ obtained by summing the absolute values of the relevant coefficients times the bounds ${\ell }_j$. Hence, f is globally Lipschitz on the bounded set with $L:={max}_i{L}_i\ge 0$.

Remark 1

(alignment with the Laplace-transform presentation). Using $\mathcal{L}\left\{D_t^{\lambda }x\right\}\left(s\right)=s^{\lambda }X\left(s\right)-s^{\lambda -1}{x}_0$, one can derive an equivalent fixed-point operator in the Laplace domain and, after inversion, recover the same contraction estimate ${\parallel \mathcal{F}x-\mathcal{F}y\parallel }_{\infty }\le {\displaystyle \frac{L{T}^{\lambda }}{\Gamma (\lambda +1)}}{\parallel x-y\parallel }_{\infty }$. Thus, the detailed Picard iteration above is consistent with the Laplace-based formulation while providing the required norm and contraction constant explicitly.

4. Numerical Scheme for the Lassa Fever Model

The Grünwald–Letnikov (GL) approximation of the Caputo derivative of order $\lambda \in (0,1]$ at time level $t_n=nh$ is expressed as

$$D_t^{\lambda }x\left(t_n\right)\approx {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_{k}x\left(t_{n-k}\right),$$

where the coefficients ${\omega }_k$ are defined by the generalized binomial relation

$${\omega }_0=1,\hspace{1em}{\omega }_k={(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda }{k}}\right)={(-1)}^k{\displaystyle \frac{\Gamma (\lambda +1)}{\Gamma (k+1)\Gamma (\lambda -k+1)}},\hspace{1em}k=1,2,\dots ,n.$$

These coefficients satisfy the recursive formula ${\omega }_k=\left(1-{\displaystyle \frac{1+\lambda }{k}}\right){\omega }_{k-1}$, which is convenient for numerical implementation. Throughout the discretization, the subscript n is consistently used to denote the value of a variable at time $t_n$; for example, $S_n=S\left(t_n\right)$, $I_{m,n}=I_m\left(t_n\right)$, and so on.

Let the time step be h and define the grid points as $t_n=nh$, where n is the index of time steps. For the fractional derivative at time $t_n$, the Grünwald–Letnikov formula is used to approximate the left-hand side of each equation.

Let us define the time step for each state variable as follows:

$${\mathcal{S}}_n=\mathcal{S}\left(t_n\right),\hspace{1em}{\mathcal{I}}_{m,n}={\mathcal{I}}_m\left(t_n\right),\hspace{1em}{\mathcal{I}}_{s,n}={\mathcal{I}}_s\left(t_n\right),\hspace{1em}{\mathcal{R}}_n=\mathcal{R}\left(t_n\right),\hspace{1em}{\mathcal{S}}_{r,n}={\mathcal{S}}_r\left(t_n\right),\hspace{1em}{\mathcal{I}}_{r,n}={\mathcal{I}}_r\left(t_n\right).$$

For simplicity, denote the right-hand side of each equation by a function $f_i(\mathcal{S},{\mathcal{I}}_m,{\mathcal{I}}_s,\mathcal{R},$${\mathcal{S}}_r,{\mathcal{I}}_r,t)$. Now, applying the Grünwald–Letnikov scheme for fractional derivatives to the equations:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k\mathcal{S}\left(t_{n-k}\right)& =& {\Lambda }_h-{\eta }_1{\mathcal{S}}_n{\mathcal{I}}_{m,n}-{\eta }_2{\mathcal{S}}_n{\mathcal{I}}_{s,n}-({\kappa }_1+{\kappa }_2){\mathcal{S}}_n{\mathcal{I}}_{r,n}-{\mu }_h{\mathcal{S}}_n,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k{\mathcal{I}}_m\left(t_{n-k}\right)& =& {\eta }_1{\mathcal{S}}_n{\mathcal{I}}_{m,n}+{\kappa }_1{\mathcal{S}}_n{\mathcal{I}}_{r,n}-\delta {\mathcal{I}}_{m,n}-({\mu }_h+{\sigma }_1){\mathcal{I}}_{m,n},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k{\mathcal{I}}_s\left(t_{n-k}\right)& =& {\eta }_2{\mathcal{S}}_n{\mathcal{I}}_{s,n}+{\kappa }_2{\mathcal{S}}_n{\mathcal{I}}_{r,n}+\delta {\mathcal{I}}_{m,n}-({\mu }_h+{\sigma }_2){\mathcal{I}}_{s,n},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k\mathcal{R}\left(t_{n-k}\right)& =& {\sigma }_1{\mathcal{I}}_{m,n}+{\sigma }_2{\mathcal{I}}_{s,n}-{\mu }_h{\mathcal{R}}_n,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k{\mathcal{S}}_r\left(t_{n-k}\right)& =& {\Lambda }_r-{\xi }_r{\mathcal{S}}_{r,n}{\mathcal{I}}_{r,n}-{\mu }_r{\mathcal{S}}_{r,n},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h^{\lambda }}}\sum _{k=0}^n{\omega }_k{\mathcal{I}}_r\left(t_{n-k}\right)& =& {\xi }_r{\mathcal{S}}_{r,n}{\mathcal{I}}_{r,n}-{\mu }_r{\mathcal{I}}_{r,n}.\hfill \end{array}$$

(7)

Thus, we have

$$\begin{array}{ccc}\hfill {\mathcal{S}}_n& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\Lambda }_h-{\eta }_1{\mathcal{S}}_n{\mathcal{I}}_{m,n}-{\eta }_2{\mathcal{S}}_n{\mathcal{I}}_{s,n}-({\kappa }_1+{\kappa }_2){\mathcal{S}}_n{\mathcal{I}}_{r,n}-{\mu }_h{\mathcal{S}}_n+\sum _{k=1}^n{\omega }_k\mathcal{S}\left(t_{n-k}\right)\right],\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{m,n}& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\eta }_1{\mathcal{S}}_n{\mathcal{I}}_{m,n}+{\kappa }_1{\mathcal{S}}_n{\mathcal{I}}_{r,n}-\delta {\mathcal{I}}_{m,n}-({\mu }_h+{\sigma }_1){\mathcal{I}}_{m,n}+\sum _{k=1}^n{\omega }_k{\mathcal{I}}_m\left(t_{n-k}\right)\right],\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{s,n}& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\eta }_2{\mathcal{S}}_n{\mathcal{I}}_{s,n}+{\kappa }_2{\mathcal{S}}_n{\mathcal{I}}_{r,n}+\delta {\mathcal{I}}_{m,n}-({\mu }_h+{\sigma }_2){\mathcal{I}}_{s,n}+\sum _{k=1}^n{\omega }_k{\mathcal{I}}_s\left(t_{n-k}\right)\right],\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\mathcal{R}}_n& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\sigma }_1{\mathcal{I}}_{m,n}+{\sigma }_2{\mathcal{I}}_{s,n}-{\mu }_h{\mathcal{R}}_n+\sum _{k=1}^n{\omega }_k\mathcal{R}\left(t_{n-k}\right)\right],\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\mathcal{S}}_{r,n}& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\Lambda }_r-{\xi }_r{\mathcal{S}}_{r,n}{\mathcal{I}}_{r,n}-{\mu }_r{\mathcal{S}}_{r,n}+\sum _{k=1}^n{\omega }_k{\mathcal{S}}_r\left(t_{n-k}\right)\right],\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{r,n}& =& {\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[{\xi }_r{\mathcal{S}}_{r,n}{\mathcal{I}}_{r,n}-{\mu }_r{\mathcal{I}}_{r,n}+\sum _{k=1}^n{\omega }_k{\mathcal{I}}_r\left(t_{n-k}\right)\right].\hfill \end{array}$$

(13)

In general, the discrete Grünwald–Letnikov update for each state variable $X_n\in \{{\mathcal{S}}_n,{\mathcal{I}}_{m,n},{\mathcal{I}}_{s,n},{\mathcal{R}}_n,{\mathcal{S}}_{r,n},{\mathcal{I}}_{r,n}\}$ can be written as

$$X_n={\displaystyle \frac{1}{h^{\lambda }{\omega }_0}}\left[f_i\left(X_n\right)+\sum _{k=1}^n{\omega }_k{X}_{n-k}\right],$$

where $f_i(·)$ represents the right-hand side of the corresponding fractional differential equation.

5. Numerical Simulations and Discussion

This section presents the numerical simulations of the proposed model with varying fractional orders as well as varying some crucial parameters and the effects on the model are properly discussed.

Figure 2 depicts the temporal evolution of all state variables of the proposed fractional-order Lassa fever model under varying fractional orders ($\lambda =1,0.95,0.90,0.85$). The results clearly demonstrate that the fractional order $\lambda$ strongly affects the rate of infection spread and recovery, reflecting the presence of memory and hereditary effects within the host–pathogen system. The susceptible population $\mathcal{S}$ Figure 2a declines rapidly in the early weeks as individuals move into the infected classes, with the decline becoming slower as $\lambda$ decreases, indicating that memory effects dampen transmission and delay the epidemic peak. The mildly infected class ${\mathcal{I}}_m$ Figure 2b exhibits an early sharp increase followed by an exponential decline, with lower $\lambda$ producing a smoother, more prolonged trajectory that captures biological latency and delayed immune response. The severely infected population ${\mathcal{I}}_s$ Figure 2c follows a similar trend, showing slower decay and extended persistence for smaller $\lambda$, representing prolonged disease duration and potential disability in severe cases, consistent with clinical findings in Lassa fever survivors. The recovered population $\mathcal{R}$ Figure 2d increases steadily, approaching its maximum faster for higher $\lambda$, while lower fractional orders yield gradual accumulation due to slower recovery rates. The susceptible and infected rodent populations, ${\mathcal{S}}_r$ and ${\mathcal{I}}_r$, Figure 2e,f, show damped oscillatory decay toward equilibrium, indicating the stabilizing influence of environmental and demographic memory within the reservoir species. Overall, the results highlight that reducing $\lambda$ introduces biologically realistic delays in transmission and recovery processes, reflecting immune memory, behavioral adaptation, and persistence of infection.

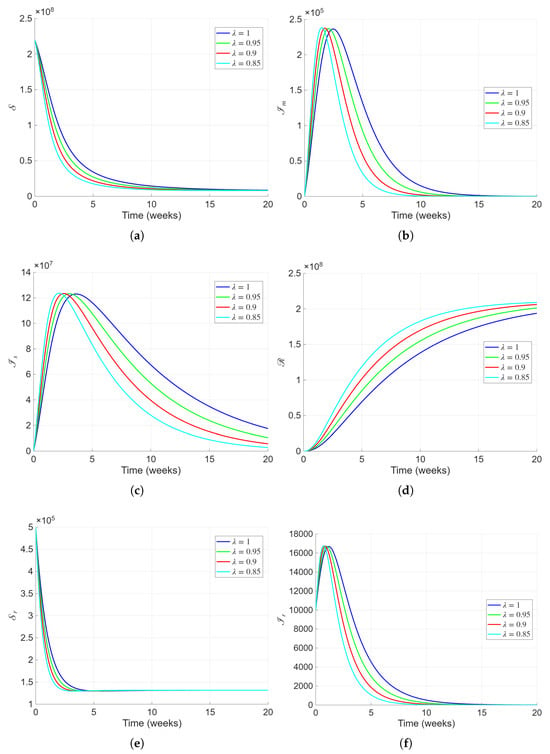
Figure 2. Numerical simulations representing the dynamics of all the state variables of the proposed model with varying fractional order and the parameters presented in Table 1.

Figure 3 presents the numerical simulations of the fractional-order Lassa fever model over a longer timescale for different fractional orders ($\lambda =1.00,0.98,0.96,0.94$). The plots clearly show the sensitivity of the disease progression to memory effects inherent in the fractional framework. In Figure 3a, the susceptible human population $\mathcal{S}$ gradually decreases as individuals become infected, with the decline being slower for smaller $\lambda$, indicating that memory-dependent contact dynamics delay transmission. The mildly infected class ${\mathcal{I}}_m$ in Figure 3b exhibits a steady rise over time, approaching a plateau as fractional order decreases, suggesting a prolonged persistence of mild infections due to slower immune activation and delayed recovery. Similarly, the severely infected population ${\mathcal{I}}_s$ (Figure 3c) and recovered population $\mathcal{R}$ (Figure 3d) show enhanced growth under lower fractional orders, capturing the biological realism of lingering infection and gradual accumulation of immune individuals. The susceptible rodent population ${\mathcal{S}}_r$ in Figure 3e decays progressively, with fractional memory prolonging the coexistence of susceptible and infected rodents. Conversely, the infected rodent population ${\mathcal{I}}_r$ (Figure 3f) rises steadily and stabilizes at a higher equilibrium when $\lambda$ is reduced, reflecting persistent infection within the reservoir species due to ecological and environmental memory. Overall, these results emphasize that fractional-order dynamics provide a biologically realistic representation of Lassa fever transmission, where smaller $\lambda$ values account for immune memory, behavioral adaptation, and delayed epidemiological responses consistent with real-world observations.

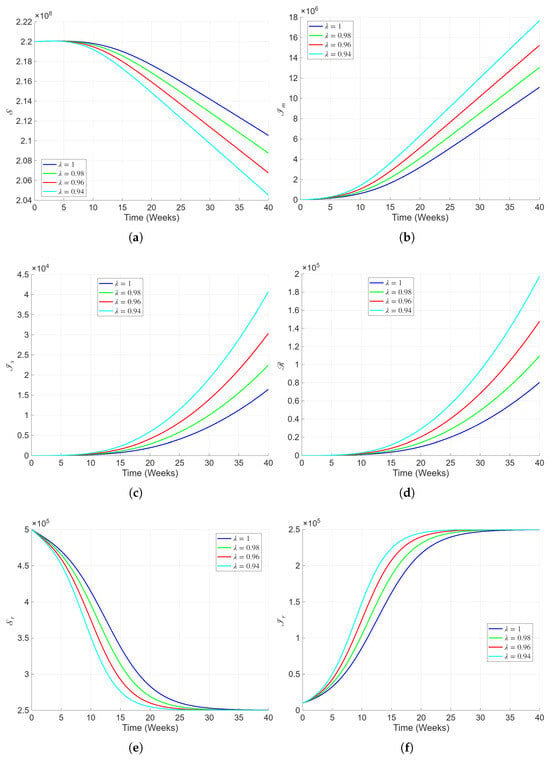
Figure 3. Numerical simulations representing the dynamics of all the state variables of the proposed model with varying fractional order and the parameters presented in Table 2.

Influence of Crucial Parameters on the Model

This part presents the influence of some key parameters on the system state variables.

Figure 4 illustrates the effect of variations in the human-to-human transmission rate ${\eta }_1$ on the dynamics of the mildly infected human population ${\mathcal{I}}_m$ and the recovered class $\mathcal{R}$ at a fixed fractional order $\lambda =0.95$. Biologically, ${\eta }_1$ quantifies the rate at which infection spreads from infected to susceptible individuals through direct or indirect human contact. As ${\eta }_1$ increases from $6.3\times {10}^{-11}$ to $9.0\times {10}^{-12}$, the trajectories of ${\mathcal{I}}_m$ (Figure 4a) exhibit a steady rise, with the mildly infected population reaching higher peak and equilibrium levels. This demonstrates that greater person-to-person transmissibility intensifies the force of infection and prolongs the persistence of Lassa fever within the community. Correspondingly, Figure 4b shows that the recovered class $\mathcal{R}$ also increases as more individuals move from infection to recovery. The delayed decline and elevated steady-state values of $\mathcal{R}$ for higher ${\eta }_1$ values suggest a longer epidemic duration and slower return to the disease-free state. These findings underscore the significant role of human-to-human transmission in sustaining Lassa fever outbreaks and emphasize the importance of interventions that limit direct contact and improve case isolation.

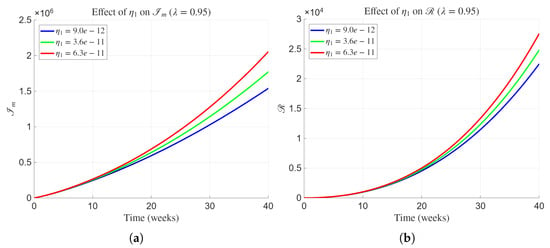
Figure 4. Influence of parameter ${\eta }_1$ on the dynamics of state variables ${\mathcal{I}}_m$ and $\mathcal{R}$ of the proposed model with fractional order $\lambda =0.95$ and parameters presented in Table 2.

Similarly, Figure 5 explores the influence of the rodent-to-human transmission rate ${\kappa }_1$ on the same state variables under $\lambda =0.95$. The parameter ${\kappa }_1$ quantifies the effective rate at which susceptible humans acquire infection through contact with infectious rodents or rodent-contaminated environments. As ${\kappa }_1$ increases from $1.1\times {10}^{-9}$ to $5.5\times {10}^{-9}$, a marked amplification in the mildly infected human population ${\mathcal{I}}_m$ is observed (Figure 5a), indicating that greater exposure to infected rodents enhances the spillover potential and sustains transmission within the human population. The steeper infection curve and delayed decline reflect an intensified epidemic momentum, where higher ${\kappa }_1$ values prolong the persistence of mild infections. The recovery trajectories shown in Figure 5b exhibit a similar pattern, with $\mathcal{R}$ rising as more individuals transition from infection to recovery. These results emphasize that increased rodent-to-human transmission substantially elevates both infection prevalence and recovery counts, underscoring the importance of effective rodent control and environmental sanitation in mitigating Lassa fever outbreaks.

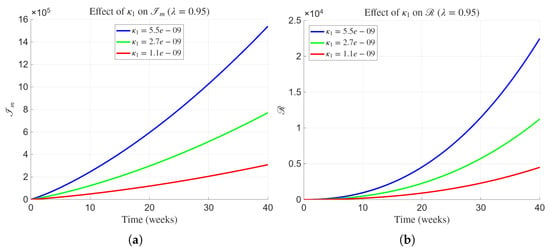
Figure 5. Influence of parameter ${\kappa }_1$ on the dynamics of state variables ${\mathcal{I}}_m$ and $\mathcal{R}$ of the proposed model with fractional order $\lambda =0.95$ and parameters presented in Table 2.

Figure 6 presents the impact of three epidemiologically significant parameters $\delta$, ${\sigma }_1$, and ${\eta }_2$ on the progression of the severely infected human population ${\mathcal{I}}_s$ at a fixed fractional order $\lambda =0.95$. The combined influence of these parameters provides important insight into the clinical and ecological transitions driving severe Lassa fever outcomes. As observed in Figure 6a, increasing $\delta$ from $3.5\times {10}^{-5}$ to $1.0\times {10}^{-4}$ substantially elevates the number of severely infected individuals ${\mathcal{I}}_s$ throughout the simulation period. The trajectories demonstrate a steeper and more persistent growth for larger $\delta$, reflecting accelerated progression of mild cases into severe forms of the disease. This behavior indicates that rapid clinical deterioration among mild patients can significantly amplify the overall disease burden and overwhelm healthcare capacity if early detection and treatment are inadequate. In Figure 6b, variations in ${\sigma }_1$ reveal an inverse relationship between recovery rate and infection prevalence. Increasing ${\sigma }_1$ from $3.2\times {10}^{-4}$ to $9.7\times {10}^{-4}$ enhances the transition of severe cases to the recovered class $\mathcal{R}$, thereby reducing the cumulative infectious pool. The nonlinear increase in $\mathcal{R}$ with higher ${\sigma }_1$ values indicates that even modest improvements in clinical recovery efficiency can markedly influence disease attenuation. Finally, Figure 6c illustrates the influence of the rodent-to-human transmission coefficient ${\eta }_2$ on ${\mathcal{I}}_s$. An increase in ${\eta }_2$ from $1.0\times {10}^{-11}$ to $7.0\times {10}^{-11}$ results in a pronounced rise in ${\mathcal{I}}_s$, with trajectories diverging progressively over time. This trend suggests that intensified exposure to infected rodents either through direct contact or contamination of food and household environments substantially increases the incidence of severe infections.

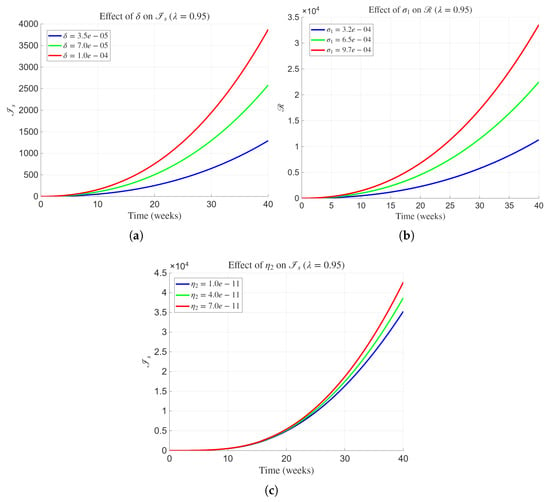
Figure 6. Influence of parameters $\delta$, ${\sigma }_1$, and ${\eta }_2$ on the dynamics of state variable ${\mathcal{I}}_s$ of the proposed model with fractional order $\lambda =0.95$ and parameters presented in Table 2.

The global sensitivity analysis summarized in Figure 7 provides quantitative insight into parameter influence across different fractional orders $\lambda =1.00,0.95,0.90,$ and $0.85$. A global sensitivity analysis was performed using the LHS–PRCC method. A total of $N=200$ samples were generated within $\pm 50\%$ of the baseline parameter values listed in Table 3. Each sampled parameter set was simulated over the interval $[0,40]$ days using the fractional Euler method with step size $h=0.005$ and fractional order $\lambda =0.85$. The outputs of interest were the peak of the mildly infected (${\mathcal{I}}_m$), the peak of the severely infected (${\mathcal{I}}_s$), and the final recovered population $\mathcal{R}\left(t_f\right)$. The PRCC values, calculated in MATLAB-version 24.1 using Spearman rank correlation, quantify the monotonic influence of each parameter on these outputs. Table 3 summarizes the numerical PRCC results.

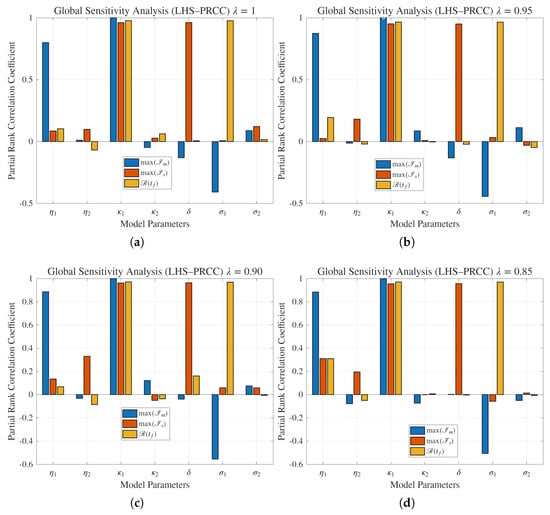
Figure 7. Global sensitivity analysis of parameters on state variables of the proposed model with fractional orders $\lambda =1.00,\lambda =0.95,\lambda =0.90$, and $\lambda =0.85$.

Table 3. PRCCs for key model parameters obtained using LHS with $N=200$ and fractional order $\lambda =0.85$. Positive values indicate parameters that increase infection prevalence, while negative values denote parameters that suppress infection.

Parameter	PRCC(max(${\mathcal{I}}_{\mathit{m}}$))	PRCC(max(${\mathcal{I}}_{\mathit{s}}$))	PRCC($\mathcal{R}\left({\mathit{t}}_{\mathit{f}}\right)$)
${\eta }_1$	0.898	0.248	0.160
${\eta }_2$	0.077	0.299	$-0.078$
${\kappa }_1$	0.999	0.970	0.954
${\kappa }_2$	$-0.072$	0.062	0.061
$\delta$	$-0.037$	0.971	$-0.071$
${\sigma }_1$	$-0.580$	$-0.066$	0.950
${\sigma }_2$	0.023	$-0.105$	0.067

In the figure, we see that the PRCCs reveal that ${\kappa }_1$ (human–rodent contact rate) and ${\eta }_1$ (human–human transmission coefficient) consistently exhibit strong positive correlations with the peak values of ${\mathcal{I}}_m$, ${\mathcal{I}}_s$, and $\mathcal{R}$, confirming them as dominant epidemic drivers. In contrast, recovery-related parameters ${\sigma }_1$ and ${\sigma }_2$ display significant negative PRCCs, indicating their mitigating role in epidemic progression. Notably, the influence of ${\kappa }_1$ remains robust across all fractional orders, whereas the sensitivity to ${\eta }_1$ and $\delta$ slightly diminishes as $\lambda$ decreases, suggesting that memory effects dampen rapid transmission amplification. As the fractional order reduces from unity to $0.85$, overall sensitivity coefficients contract, demonstrating that fractional dynamics attenuate parameter responsiveness by incorporating historical infection effects.

6. Conclusions

This study presented a fractional-order model for the transmission dynamics of Lassa fever incorporating both mild and severe infection pathways, as well as rodent and human interactions. The fractional derivative provided a flexible framework to capture the memory and hereditary characteristics inherent in Lassa virus progression and recovery. The qualitative and numerical analyses confirm that the disease-free equilibrium is locally and globally stable under realistic parameter regimes, while persistence of infection depends strongly on the human-to-human (${\eta }_1$) and rodent-to-human (${\kappa }_1$) transmission routes. The fractional order $\lambda$ significantly modulates epidemic intensity and duration, showing that memory effects can either dampen or prolong outbreaks depending on the effective transmission rates. The global sensitivity analysis identified ${\kappa }_1$, ${\eta }_1$, and ${\xi }_r$ as the most influential parameters contributing positively to infection prevalence, whereas the recovery rates ${\sigma }_1$ and ${\sigma }_2$ had the strongest negative impact. These results indicate that interventions targeting rodent control, limiting person-to-person contact, and improving treatment and recovery rates can most effectively reduce disease burden.

From a policy perspective, the findings underscore the need for integrated control measures combining environmental sanitation, community awareness, and early case detection. The model also highlights the potential of fractional-order approaches in epidemiology to better capture long-term disease memory and delayed response effects, which are often overlooked in classical models. Future work may extend this framework to include spatial heterogeneity, stochastic effects, and optimal control formulations to evaluate the cost-effectiveness of combined intervention strategies.