Existence of Solutions to Symmetric Multivalued Functional Integral Equations with Illustrative Applications in Medicine and Logistics

Abstract

This paper investigates functional integral equations with multivalued terms that appear symmetrically on both sides of the equation. We impose structural conditions on the coefficients that, while insufficient to ensure uniqueness, are adequate to guarantee the existence of at least one solution. We assumed mere continuity of the coefficients to establish a Peano-type existence theorem. The existence result was derived through the application of Schauder’s fixed-point theorem. We further highlighted that this finding for symmetric multivalued functional integral equations significantly informs the analysis of delayed multivalued functional equations, which is commonly utilized in modeling processes where both the present and past states of the system play a crucial role. To illustrate the applicability of the proposed frameworks, representative examples were formulated and numerically solved for each type of equation, highlighting potential use cases in medicine and logistics.

1. Introduction

The theory of multivalued differential equations, which was initiated in the 1960s [1], has evolved into a well-established and vibrant area of mathematical research. Over the decades, it has developed its own specialized techniques, analytical tools, and conceptual frameworks, distinct from those used in classical single-valued analysis. This branch of mathematics provides a powerful language for modeling dynamic systems in which uncertainty, imprecision, or multiplicity of states must be accounted for—particularly when the evolution of a process cannot be described by a single trajectory, but rather by a family of admissible states.

A comprehensive and foundational overview of the theory is presented in the monograph [2], which consolidates key results and methodologies developed over several decades. More recently, the relevance of multivalued differential equations has been underscored by a growing body of literature that explores their applications in various domains, including control theory, economics, engineering, and, notably, medicine. In particular, several studies have demonstrated the utility of multivalued models in the context of cancer diagnosis and treatment planning, where the inherent uncertainty in biological systems makes traditional deterministic models insufficient [3,4]. Recent developments in this field continue to attract sustained scholarly attention, underscoring both its theoretical relevance and practical applicability. For example, ref. [5] examines the existence of a unique solution by the method of successive approximations, ref. [6] explores the use of Laplace transforms in the context of fractional set-valued differential equations defined on time scales. The study [7] investigates two specific multivalued linear integral equations, providing explicit forms of their solutions. In [8], criteria for Lipschitz and practical stability of set-valued differential equations are established using a comparison principle and vector Lyapunov functions. Furthermore, ref. [9] demonstrates the globally asymptotic stability of neutral set-valued differential equations using the Banach fixed-point theorem. These developments not only affirm the theoretical richness of the field but also point to its practical potential.

The results presented in this paper—focused on existence theorems for symmetric functional multivalued integral equations—are intended to contribute to the ongoing dialogue between abstract theory and real-world applications. By relaxing classical regularity assumptions and introducing more general structural conditions, we aim to broaden the scope of solvable models and lay the groundwork for future applications in areas where uncertainty and multivalued dynamics are intrinsic features of the system under study. This paper continues the investigation initiated in [5,10,11], where the foundational directions for the development of symmetric functional multivalued integral equations were outlined. Let us mention the form of the equations considered

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X_s)ds={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds$$

(1)

with the initial condition

$$X_{t_0}={\eta }_0,$$

where ${\eta }_0\in C_{\tau }$ denotes the prescribed initial history. The functions F and G are the coefficients of the equation, depending on the time and the past trajectory of the solution

$$F,G:[t_0,t_0+T]\times C_{\tau }\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$$

and $C_{\tau }$ is a set of continuous multivalued mappings with values in ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$— the family of all nonempty, convex and compact subsets of ${\mathbb{R}}^d$. The focus of this study is on symmetric equations. In particular, if we set $F\equiv \left\{0\right\}$ in Equation (1), we obtain the following asymmetric multivalued integral equation

$$X\left(t\right)={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\mathrm{for}t\in I,$$

(2)

with the initial condition

$$X_{t_0}={\eta }_0.$$

This Equation (2) is closely related to a multivalued functional differential equation involving the Hukuhara derivative $\prime$ of multivalued mappings

$$X^{\prime }\left(t\right)=G(t,X_t)\mathrm{for}t\in I,\mathrm{with}\mathrm{initial}\mathrm{condition}{X}_{t_0}={\eta }_0,$$

(3)

which has been investigated in works such as [12,13,14,15,16], and traces back to the original formulation of multivalued differential equations in [1].

A key property of Equations (2) and (3) is that the diameter of the solution value $X\left(t\right)$ does not decrease as time progresses. Consequently, these models are inadequate for describing phenomena where uncertainty is expected to diminish over time. To address such cases, a second class of multivalued integral equations has been proposed [17], which in asymmetric functional form is given by

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X_s)ds={\eta }_0\left(0\right)\mathrm{for}t\in I,$$

(4)

with the initial condition

$$X_{t_0}={\eta }_0.$$

These equations correspond to differential equations involving the so-called Hukuhara derivative of the second kind, denoted by $*$:

$$X^{*}\left(t\right)=(-1)·F(t,X_t)\mathrm{for}t\in I,\mathrm{with}\mathrm{initial}\mathrm{condition}{X}_{t_0}={\eta }_0.$$

(5)

For this formulation, the diameter of $X\left(t\right)$ remains non-increasing over time. However, neither this type nor the previous one alone is sufficient to capture the full spectrum of dynamic behaviors and uncertainty evolution. Therefore, the general class of symmetric Equation (1) was introduced in [10], allowing for solutions whose value diameters may vary between constant, non-decreasing, non-increasing, and non-monotonic functions.

The principal results of the cited papers [5,10,11] concerning the symmetric multivalued functional integral equations were theorems establishing the existence of a unique solution. These results were obtained by successively imposing conditions on the coefficients of the equation: first, the classical Lipschitz condition with a constant; then a non-Lipschitz condition involving a single-variable function whose integral diverges; and finally a non-Lipschitz condition involving a two-variable function satisfying a specific integral inequality.

This paper advances the theory by relaxing the regularity assumptions imposed on the coefficients of the equation. Specifically, we do not impose the classical Lipschitz continuity condition, nor any of its non-Lipschitz variants. As a result, the uniqueness of the solution will not be required. Instead, we adopt weaker structural assumptions—based solely on mere continuity—in order to establish the existence of at least one solution in the form of a Peano-type theorem. This constitutes the main objective of the paper. Finally, we indicate that the obtained result has direct implications for the study of symmetric multivalued functional equations with delay, and we formulate an analogous existence theorem for this class of equations and show some potential applications.

In summary, the key contributions of this paper are as follows

• analysis of a symmetric equation that unifies two classes of asymmetric integral equations and two types of differential equations involving distinct forms of the Hukuhara derivative,
• through the introduction of symmetric equations, the class of admissible solutions is extended to include those whose value diameters may evolve in a constant, non-decreasing, non-increasing, and non-monotonic manner over time.
• adoption of continuity assumptions that are weaker than those commonly found in the literature, such as Lipschitz continuity,
• justification of the existence of solutions via a tailored version of the Schauder fixed-point theorem adapted to the framework of semilinear spaces,
• identification of hypothetical real-world domains where such equations can be applied to model the dynamics of evolving processes.

2. Preliminaries

To initiate the formal presentation of our results, we begin by outlining the fundamental mathematical structures necessary for the study of multivalued equations. Although the foundational framework has been thoroughly developed in previous work such as [5,10,11], we briefly revisit the key concepts here to ensure clarity and continuity for the reader.

Let ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ denote the family of nonempty, compact, and convex subsets of ${\mathbb{R}}^d$. We work within the metric space $({\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right),\mathcal{D})$, where $\mathcal{D}$ is the Hausdorff–Pompeiu metric defined by

$$\mathcal{D}(X,Y):=max\left\{\underset{x\in X}{sup}\underset{y\in Y}{inf}\parallel x-y\parallel ,\underset{y\in Y}{sup}\underset{x\in X}{inf}\parallel x-y\parallel \right\},X,Y\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right),$$

with $\parallel ·\parallel$ denoting the Euclidean norm in ${\mathbb{R}}^d$. The space $({\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right),\mathcal{D})$ is Polish and locally compact.

The set ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ admits addition and scalar multiplication:

$$X+Y:=\{x+y\mid x\in X,y\in Y\},\alpha ·X:=\{\alpha ·x\mid x\in X\},X,Y\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right),\alpha \in \mathbb{R},$$

yielding a semilinear structure. However, subtraction is not always well-defined, and the notion of an opposite element may not exist. In this paper, we employ the Hukuhara difference $X\ominus Y$, defined implicitly by the relation $X=Y+(X\ominus Y)$. Although such differences may not exist for all pairs, they are unique when they do.

We recall several useful properties of the Hausdorff–Pompeiu metric $\mathcal{D}$ (see [2]). For $X,Y,Z,V\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$:

(P1)

$\mathcal{D}(X+Z,Y+Z)=\mathcal{D}(X,Y)$,

(P2)

$\mathcal{D}(X+Y,Z+V)\le \mathcal{D}(X,Z)+\mathcal{D}(Y,V)$,

(P3)

If $X\ominus Y$ and $Z\ominus V$ exist, then $\mathcal{D}(X\ominus Y,Z\ominus V)\le \mathcal{D}(X,Z)+\mathcal{D}(Y,V)$.

To accommodate functional dependence, we consider the space

$$C_{\tau }:=C([-\tau ,0],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$$

of all $\mathcal{D}$-continuous multivalued mappings from $[-\tau ,0]$ to ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$, equipped with the supremum metric

$${\mathcal{D}}^{*}({\eta }_1,{\eta }_2):=\underset{t\in [-\tau ,0]}{sup}\mathcal{D}({\eta }_1\left(t\right),{\eta }_2\left(t\right)),{\eta }_1,{\eta }_2\in C_{\tau }.$$

The pair $(C_{\tau },{\mathcal{D}}^{*})$ is a complete metric space. For multivalued mappings continuous with respect to the metric $\mathcal{D}$, defined on intervals other than $[-\tau ,0]$, we shall continue to denote the supremum metric by ${\mathcal{D}}^{*}$.

The multivalued integrals in this paper are understood in the sense of Aumann (see [18]). For a multivalued mapping $X:[a,b]\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$, we define

$${\int }_a^{b}X\left(s\right)ds:=\left\{{\int }_a^{b}x\left(s\right)ds\mid x\in S\left(X\right)\right\},$$

where $S\left(X\right)$ denotes the set of integrable selections of X, which is nonempty. Key properties include (see [2]):

(P4)

${\int }_a^{b}X\left(s\right)ds\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$,

(P5)

${\int }_a^{b}X\left(s\right)ds={\int }_a^{c}X\left(s\right)ds+{\int }_c^{b}X\left(s\right)ds$ for $a\le c\le b$,

(P6)

If $X,Y$ are integrable, then

$$\mathcal{D}\left({\int }_a^{b}X\left(s\right)ds,{\int }_a^{b}Y\left(s\right)ds\right)\le {\int }_a^b\mathcal{D}(X\left(s\right),Y\left(s\right))ds,$$

(P7)

If X is integrable, then $t\mapsto {\int }_a^{t}X\left(s\right)ds$ is $\mathcal{D}$-continuous mapping.

3. Formulation of the Problem

In this paper, we investigate equations involving multivalued integrals that appear symmetrically on both sides of the equation. More precisely, we study symmetric multivalued functional integral equations of the form:

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X_s)ds={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds,t\in [t_0,t_0+T],$$

(6)

$$\mathrm{with}\mathrm{initial}\mathrm{condition}{X}_{t_0}={\eta }_0,$$

where ${\eta }_0\in C_{\tau }$ is the initial history and $F,G:[t_0,t_0+T]\times C_{\tau }\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ are the coefficients of the equation. The segment function $X_s\in C_{\tau }$ is defined by $X_s\left(u\right):=X(s+u)$ for $u\in [-\tau ,0]$.

These equations are referred to as symmetric because multivalued integrals appear on both sides of the equation, reflecting a structural balance in their formulation. Unlike classical integral equations, where the integral typically occurs on one side and can often be isolated or simplified, the presence of multivalued integrals on both sides introduces a level of complexity that prevents such reduction. In particular, due to the nature of multivalued operations—especially the lack of general invertibility and the limitations of set subtraction—the equation cannot, in general, be transformed into a form involving a single integral. This inherent symmetry is not merely a formal feature; it has significant implications for the analysis and solvability of the equation. In addition, equations with integrals on only one side—commonly referred to as asymmetric—can be viewed as special or degenerate cases of the symmetric formulation. This observation further justifies the study of symmetric equations as they encompass a broader class of models and offer a unified framework for analyzing both symmetric and asymmetric behaviors in multivalued dynamics. Below, we present the interpretation we adopt for a solution to Equation (6), specifying the structural and analytical framework within which the notion of a solution is understood. This includes the functional setting, the regularity assumptions, and the multivalued nature of the involved terms, all of which are essential for establishing existence and qualitative properties of solutions.

Definition 1. 

An element X of the space $C([t_0-\tau ,t_0+T],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$ is said to be a solution to symmetric functional multivalued integral Equation (6) if $X\left(t\right)={\eta }_0(t-t_0)$ for $t\in [t_0-\tau ,t_0]$ and $X\left(t\right)$ satisfies (6) for $t\in [t_0,t_0+T]$.

At this point, it is worth emphasizing a subtle yet important nuance arising from the nature of set-valued operations. Specifically, Equation (6) can be equivalently rewritten as

$$X\left(t\right)=\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t}F(s,X_s)ds,t\in [t_0,t_0+T],$$

$$\mathrm{with}\mathrm{initial}\mathrm{condition}{X}_{t_0}={\eta }_0.$$

This formulation, involving the Hukuhara difference, is generally irreducible to a single-integral representation—i.e., to an asymmetric equation—due to inherent difficulties in performing subtraction in the space ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$, particularly the nontrivial existence of additive inverses. Consequently, one must impose additional assumptions regarding the existence of such differences, which will be reflected in the statements of the main theorems.

This paper builds on and extends the results presented in [5,10,11] by establishing the existence of at least one solution to symmetric functional multivalued integral equations by the method of a fixed-point. We subsequently emphasize that by employing analogous reasoning, one can establish an existence theorem for symmetric multivalued integral equations with constant delay. These two existence results form the core of the paper and illustrate how weaker conditions than Lipschitz assumptions can still yield meaningful solvability within a multivalued context.

4. Existence of at Least One Continuous Solution for Functional Equations

In this part of the paper, we consider Equation (6). Our goal is to prove a Peano-type existence theorem for the given equation. The proof will rely on Schauder’s fixed-point theorem, which is a cornerstone of fixed-point theory. It asserts that every nonempty, compact, and convex subset of a normed space possesses the fixed-point property (Schauder in 1930; see Theorem 2.3.7 in [19]). This result also extends to locally convex spaces, as demonstrated by Tychonoff in 1935 (Theorem 2.3.8 in [19]). More recently, the theorem has been broadened to apply within the framework of semilinear spaces [20].

Theorem 1 

(Schauder’s Fixed-Point Theorem for Semilinear Spaces, [20]). Let B be a nonempty, closed, bounded, and convex subset of a semilinear Banach space S having the cancellation property. Suppose that $P:B\to B$ is a compact operator. Then P has at least one fixed point in B.

Since we will require the convexity of a certain set, we present a useful lemma concerning the Hausdorff–Pompeiu metric.

Lemma 1 

(see, e.g., [21]). Let $A,B$ be nonempty, convex and closed subsets of ${\mathbb{R}}^d$, C be a nonempty closed subset of ${\mathbb{R}}^d$, and let $\lambda \in [0,1]$. Then the following inequality holds

$$\mathcal{D}(\lambda ·A+(1-\lambda )·B,C)\le \lambda \mathcal{D}(A,C)+(1-\lambda )\mathcal{D}(B,C).$$

To apply Schauder’s fixed-point theorem, we will establish the relative compactness of a specific set of multivalued mappings. To this end, we invoke the Arzelà–Ascoli theorem in a form tailored to our proof. This formulation is justified by the fact that the metric space $({\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right),\mathcal{D})$ is locally compact.

Theorem 2 

(The Arzelà–Ascoli theorem for multivalued maps). A set $\mathcal{M}\subset C([t_0,t_0+T],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$ is relatively compact in the uniform convergence topology generated by the Hausdorff–Pompeiu metric $\mathcal{D}$ if and only if

(i) 

$\mathcal{M}$ is uniformly bounded, i.e., there exists a constant such that $\mathcal{D}\left(F\right(t),\{0\left\}\right)⩽K$ for all $F\in \mathcal{M}$, $t\in [t_0,t_0+T]$;

(ii) 

$\mathcal{M}$ is equicontinuous, i.e., for every $\epsilon >0$ there exists $\delta >0$ such that for all $s,t\in [t_0,t_0+T]$ with $|s-t|<\delta$, we have

$$\mathcal{D}\left(F\right(s),F(t\left)\right)<\epsilon \mathit{for}\mathit{all}F\in \mathcal{M}.$$

Within this framework, which defines the scope of the present section and the direction of our analysis, we are now in a position to formulate the main existence theorem for a symmetric functional multivalued integral equation.

Theorem 3. 

Assume that the mappings $F,G:[t_0,t_0+T]\times C_{\tau }\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ are jointly continuous, ${\eta }_0\in C_{\tau }$. Suppose that there exist $\tilde{T}\in (0,T]$ such that for every $t\in [t_0,t_0+\tilde{T}]$ and every $X\in C_{\tau }$ Hukuhara differences

$$\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X)ds\right]\ominus {\int }_{t_0}^{t}F(s,X)ds$$

exist. Then, for every initial pair $(t_0,{\eta }_0)$, there exists $\widehat{T}\in [0,\tilde{T}]$ and a multivalued mapping $X:[t_0,t_0+\widehat{T}]\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ that satisfies Equation (6).

Proof. 

Consider the space $C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$ equipped with the supremum metric ${\mathcal{D}}^{*}$. This space is a Hausdorff locally convex topological space and it is also a semilinear Banach space having the cancellation property. Choose a constant $M>0$ such that

$$\mathcal{D}\left(F\right(t,X),\{0\left\}\right)+\mathcal{D}\left(G\right(t,X),\{0\left\}\right)\le M$$

for all $(t,X)$ in the set $[t_0,t_0+\widehat{T}]\times B_R\left({\eta }_0\right)$, where $B_R\left({\eta }_0\right)$ denotes the closed ball of radius R centered at ${\eta }_0$. Select $\widehat{T}>0$ so that $\widehat{T}M\le R$.

Let us define a nonempty subset K of the considered Banach space, given by

$$K=\left\{X\in C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)):\mathcal{D}(X\left(t\right),{\eta }_0\left(0\right))\le R\mathrm{for}\mathrm{every}t\in [t_0,t_0+\widehat{T}]\right\}.$$

Let us define the integral operator

$$T\left[X\right]\left(t\right)=\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t}F(s,X_s)ds.$$

The operator T is well-defined in the set K and maps K to itself. Indeed, observe first that

$$\mathcal{D}(T\left[X\right]\left(t\right),{\eta }_0\left(0\right))=\mathcal{D}\left(\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t}F(s,X_s)ds,{\eta }_0\left(0\right)\right).$$

Applying properties (P3), (P1) and (P6) we arrive at the following

$$\mathcal{D}(T\left[X\right]\left(t\right),{\eta }_0\left(0\right))\le {\int }_{t_0}^t\left[\mathcal{D}(G(s,X_s),\left\{0\right\})+\mathcal{D}(F(s,X_s),\left\{0\right\})\right]ds\le M\widehat{T}\le R.$$

Moreover, the operator T is continuous (this follows from the continuity of F and G, together with the properties of the integral).

In the following, we prove that K is convex and compact in the metric space $(C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)),{\mathcal{D}}^{*})$.

Convexity. Let $X_1,X_2\in K$ and let $\lambda \in [0,1]$. Define the convex combination $X_{\lambda }$ as

$$X_{\lambda }\left(t\right):=\lambda X_1\left(t\right)+(1-\lambda )X_2\left(t\right),$$

where sum and scalar multiplication are understood in the sense described in Section 1.

Since ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ is closed under convex combinations, we have $X_{\lambda }\left(t\right)\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ for all t, and the mapping $X_{\lambda }$ is continuous. Applying Lemma 1, we obtain

$$\begin{array}{ccc}\hfill \mathcal{D}(X_{\lambda }\left(t\right),{\eta }_0\left(0\right))& \le & \lambda \mathcal{D}(X_1\left(t\right),{\eta }_0\left(0\right))+(1-\lambda )\mathcal{D}(X_2\left(t\right),{\eta }_0\left(0\right))\hfill \\ & \le & \lambda R+(1-\lambda )R=R.\hfill \end{array}$$

Thus, $X_{\lambda }\in K$, and K is convex.

Compactness. We prove that K is compact by showing that it is closed, bounded, and equicontinuous, and then applying the Arzelà–Ascoli theorem adapted to multivalued mappings.

(i) Closedness. Let ${\left(X_n\right)}_{n\in \mathbb{N}}\subset K$ be a sequence that converges uniformly to $X\in C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$, i.e.,

$$\underset{n\to \infty }{lim}\underset{t\in [t_0,t_0+\widehat{T}]}{sup}\mathcal{D}(X_n\left(t\right),X\left(t\right))=0.$$

Then for every $\epsilon >0$, there exists $N\in \mathbb{N}$ such that for all $n\ge N$ and all $t\in [t_0,t_0+\widehat{T}]$,

$$\mathcal{D}(X_n\left(t\right),X\left(t\right))<\epsilon .$$

Since each $X_n\in K$, we have $\mathcal{D}(X_n\left(t\right),{\eta }_0\left(0\right))\le R.$

Using the triangle inequality for $\mathcal{D}$, we obtain

$$\mathcal{D}(X\left(t\right),{\eta }_0\left(0\right))\le \mathcal{D}(X\left(t\right),X_n\left(t\right))+\mathcal{D}(X_n\left(t\right),{\eta }_0\left(0\right))\le \epsilon +R.$$

Letting $\epsilon \to 0$, we conclude that

$$\mathcal{D}(X\left(t\right),{\eta }_0\left(0\right))\le R\mathrm{for}\mathrm{all}t\in [t_0,t_0+\widehat{T}],$$

so $X\in K$. Hence, K is closed.

(ii) Boundedness. For every $X\in K$ and every $t\in [t_0,t_0+\widehat{T}]$, we have

$$\mathcal{D}(X\left(t\right),{\eta }_0\left(0\right))\le R,$$

which implies that all values $X\left(t\right)$ lie within the closed ball of radius R centered at ${\eta }_0\left(0\right)$. Hence, the set K is bounded in the supremum norm.

(iii) Equicontinuity. Let $X\in K$ be arbitrary. From the integral equation

$$X\left(t\right)=\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t}F(s,X_s)ds,$$

we estimate the Hausdorff–Pompeiu distance between $X\left(t_1\right)$ and $X\left(t_2\right)$ as follows

$$\begin{array}{cc}\hfill \mathcal{D}(X\left(t_1\right),X\left(t_2\right))& =\mathcal{D}(\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t_1}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t_1}F(s,X_s)ds,\hfill \\ & \left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t_2}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t_2}F(s,X_s)ds)\hfill \\ & \le {\int }_{min(t_1,t_2)}^{max(t_1,t_2)}\left[\mathcal{D}(G(s,X_s),\left\{0\right\})+\mathcal{D}(F(s,X_s),\left\{0\right\})\right]ds.\hfill \end{array}$$

Since $X\in K$, we know that $(s,X_s)$ belongs to the compact set $[t_0,t_0+\widehat{T}]\times B_R\left({\eta }_0\right)$, and by assumption the mappings F and G are jointly continuous and bounded in this set. Therefore, there exists a constant $M>0$ such that

$$\mathcal{D}(F(s,X_s),\left\{0\right\})+\mathcal{D}(G(s,X_s),\left\{0\right\})\le M.$$

Hence, for any $t_1,t_2\in [t_0,t_0+\widehat{T}]$, we obtain the following

$$\mathcal{D}(X\left(t_1\right),X\left(t_2\right))\le M|t_1-t_2|.$$

Now, given $\epsilon >0$, choose $\delta :=\epsilon /M$. Then, for all $X\in K$ and all $t_1,t_2$ with $|t_1-t_2|<\delta$, we have

$$\mathcal{D}(X\left(t_1\right),X\left(t_2\right))<\epsilon .$$

This proves that the family K is equicontinuous in the sense of the Hausdorff–Pompeiu metric.

(iv) Relative compactness. The Arzelà–Ascoli theorem (Theorem 2) for multivalued mappings states that a uniformly bounded and equicontinuous family of multivalued continuous functions with values in ${\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ is relatively compact in $C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$.

Since K is also closed, it is compact. Thus, the set $K\subset C([t_0,t_0+\widehat{T}],{\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right))$, defined by a uniform Hausdorff bound from a fixed set $\left\{{\eta }_0\left(0\right)\right\}$, is nonempty, closed, convex, and compact in the supremum metric ${\mathcal{D}}^{*}$.

Now, by Schauder’s fixed point theorem, the operator T admits a fixed point $Y\in K$, that is,

$$X\left(t\right)=\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds\right]\ominus {\int }_{t_0}^{t}F(s,X_s)ds.$$

Consequently,

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X_s)ds={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds,$$

which means that X is a solution to Equation (6). □

The above result confirms that under continuity assumptions alone, the symmetric multivalued functional integral equation admits at least one continuous solution. This sets the groundwork for further generalizations in the future.

We emphasize that the existence result established in this paper is not merely of theoretical interest—it plays a foundational role in validating the mathematical model and enabling further analysis. First, it guarantees that the considered equation is not vacuous: there exists at least one admissible trajectory that satisfies the imposed structural conditions. This assurance is essential in applications where ambiguity, history, and multivalued dynamics are intrinsic features of the system.

In particular, the existence of a solution allows for

—

model validation in domains such as biology, medicine, and logistics, where uncertainty and history-dependent behavior are prevalent;

—

numerical simulation, since many computational schemes rely on the mere existence of a solution, not its uniqueness;

—

formulation of control and optimization problems, where the admissibility of trajectories is a prerequisite for further analysis;

—

qualitative investigation of the solution set, including compactness, convexity, and dependence on initial data.

From a practical standpoint, the theorem may be applied to decision-making models under uncertainty (e.g., in medical treatment planning), to logistic systems with history and multiple feasible execution paths, and to economic models where agents’ responses are multivalued and history-dependent. In all such cases, the existence of a solution provides a starting point for both qualitative and quantitative exploration.

5. Numerical Example and Application Scenario for Symmetric Multivalued Functional Integral Equation

We consider an exemplary hypothetical model in logistics where the inventory level $X\left(t\right)\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$ evolves according to a symmetric multivalued functional integral equation

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X_s)ds={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X_s)ds$$

(7)

with initial history

$$X_{t_0}={\eta }_0\in C_{\tau }=C([-\tau ,0],{\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)).$$

Here,

• $X\left(t\right)$ denotes the current inventory level in the warehouse at time t.
• $X_s$ represents the inventory history over the interval $[s-\tau ,s]$, where $\tau >0$ is the delay parameter.
• $F,G:[t_0,t_0+T]\times C_{\tau }\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$ are multivalued mappings that describe the influence of historical inventory trajectories on ordering and delivery decisions, respectively.
• ${\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$ denotes the family of all nonempty, convex and compact subsets of ${\mathbb{R}}^1$, i.e., the family of intervals $A=[A_L,A^U]$, where $A_L,A^U\in {\mathbb{R}}^1$ and $A_L\le A^U$.

The equation is symmetric in structure, as the impact of ordering and delivery decisions is presented in a symmetric form on both sides of the equation. Consider specific multivalued mappings F and G with values as intervals of the form

$$F(s,X_s):=\left[sins,sins+\parallel |X_s|\parallel \right],G(s,X_s):=\left[coss-\parallel |X_s|\parallel ,coss\right],$$

where $sin\left(s\right)$ models uncertain demand forecasts, $cos\left(s\right)$ models uncertain supply forecasts, and

$$\parallel |X_s|\parallel :=\underset{\theta \in [-\tau ,0]}{sup}\mathcal{D}(X(s+\theta ),\left\{0\right\})=\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}$$

is the supremum norm over the history window, where $X\left(t\right)=\left[X_L\left(t\right),X^U\left(t\right)\right]$.

The multivalued Equation (7) with such coefficients can serve as a hypothetical example of a warehouse system where both ordering and delivery decisions depend on the historical trajectory of inventory. The multivalued nature reflects uncertainty in forecasts, and the history captures memory effects. The existence theorem ensures that at least one admissible inventory trajectory exists.

Accordingly, from Equation (7), we arrive at an equation represented in interval-valued form

$$\begin{array}{ccc}\hfill & & \left[X_L\left(t\right),X^U\left(t\right)\right]+{\int }_0^t\left[sins,sins+\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}\right]ds\hfill \\ & =& [8,10]+{\int }_0^t\left[coss-\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\},coss\right]ds.\hfill \end{array}$$

(8)

This formulation naturally leads to a representation as a system of two single-valued equations

$$\left\{\begin{array}{c}{\displaystyle X_L\left(t\right)+{\int }_0^{t}sinsds=8+{\int }_0^t\left(coss-\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}\right)ds,}\hfill \\ {\displaystyle X^U\left(t\right)+{\int }_0^t\left(sins+\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}\right)ds=10+{\int }_0^{t}cossds.}\hfill \end{array}\right.$$

In this specific case, we further obtain

$$\left\{\begin{array}{ccc}{X}_L\left(t\right)& =& {\displaystyle 7+sint+cost-{\int }_0^t\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}ds,}\\ X^U\left(t\right)& =& {\displaystyle 9+sint+cost-{\int }_0^t\underset{\theta \in [-\tau ,0]}{sup}max\left\{\right|X_L(s+\theta )|,|X^U(s+\theta )\left|\right\}ds.}\end{array}\right.$$

(9)

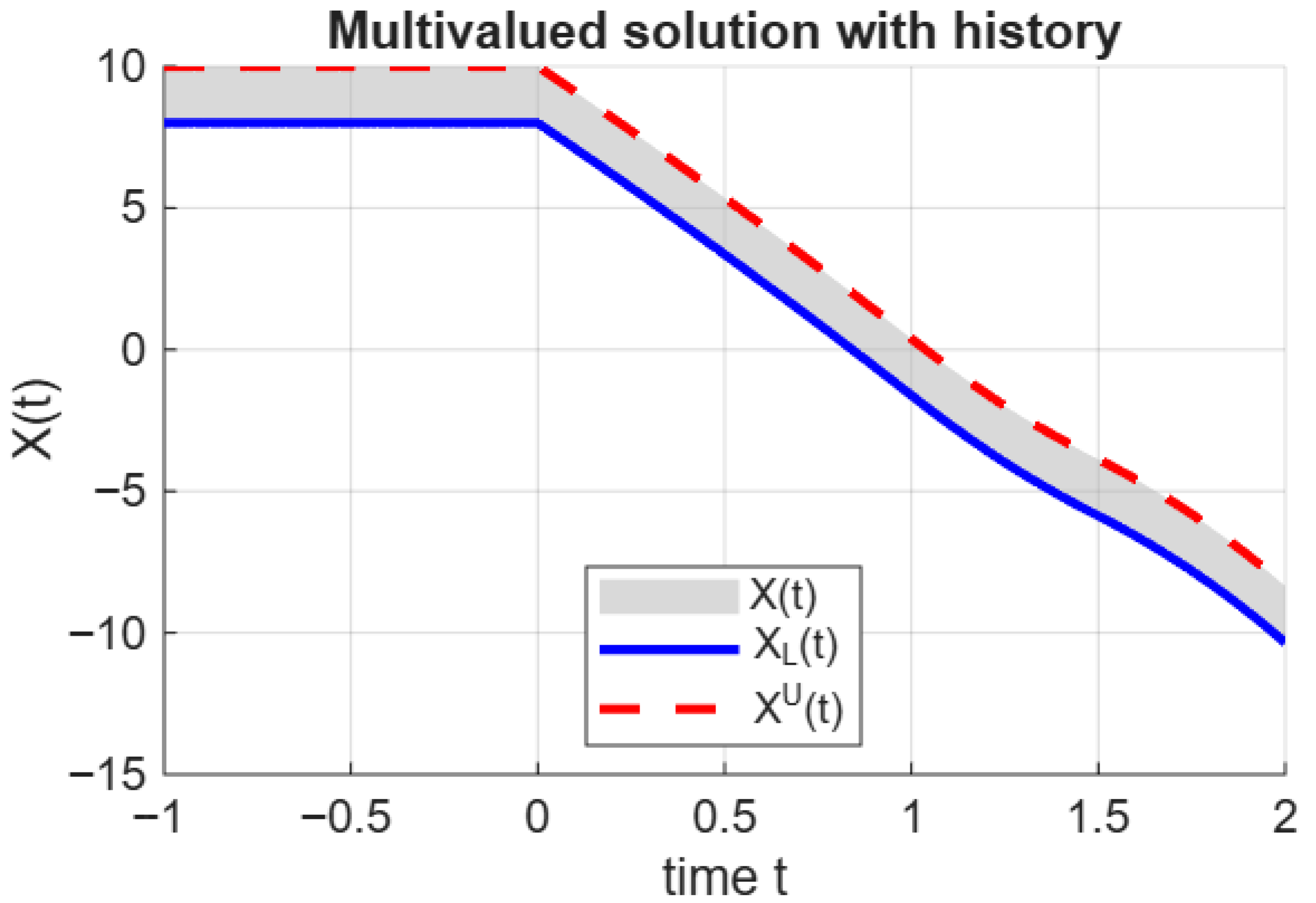
Due to this system, one can expect from the solution $X\left(t\right)$ that $X^U\left(t\right)-X_L\left(t\right)\equiv 2$. However, since a closed-form solution to this equation is not available, we present an approximate solution obtained by the use of a numerical algorithm described below, and illustrate the approximate solution using graphical and tabular representations in Figure 1 and Table 1.

Figure 1. Numerical solution X to Equation (8) represented between the boundariers $X_L$ in blue and $X^U$ in red.

Table 1. Values of the boundaries $X_L,X^U$ of the numerical solution X to (8) and the length of solution values $X^U\left(t\right)-X_L\left(t\right)$.

t	${\mathit{X}}_{\mathit{L}}\left(\mathit{t}\right)$	${\mathit{X}}^{\mathit{U}}\left(\mathit{t}\right)$	${\mathit{X}}^{\mathit{U}}\left(\mathit{t}\right)-{\mathit{X}}_{\mathit{L}}\left(\mathit{t}\right)$
0.00	8.0000	10.0000	2.0000
0.20	6.1787	8.1787	2.0000
0.40	4.3105	6.3105	2.0000
0.60	2.3900	4.3900	2.0000
0.80	0.4141	2.4141	2.0000
1.00	−1.6182	0.3818	2.0000
1.20	−3.5534	−1.5534	2.0000
1.40	−5.1720	−3.1720	2.0000
1.60	−6.5840	−4.5840	2.0000
1.80	−8.2702	−6.2702	2.0000
2.00	−10.3540	−8.3540	2.0000

The key stages of the algorithm are outlined below.

• Step 0: Grid points and initial history.

Let $h>0$ be the time step and define grid points $t_n=nh$ for $n=0,1,\dots ,N$, where $T=Nh$. Assume initial history $\eta \left(t\right)=[8,10]$ is given for $t\in [-\tau ,0]=[-1,0]$, and set

$$\left[X_L\left(t\right),X^U\left(t\right)\right]=\eta \left(t\right)\mathrm{for}t\in [-\tau ,0].$$

• Step 1: Initialization.

For $n=0$, set

$$X_L^0=7+sin\left(0\right)+cos\left(0\right),X_0^U=9+sin\left(0\right)+cos\left(0\right).$$

• Step 2: Iterative Computation.

For each $n=1,2,\dots ,N$, compute

1.

the integral approximation:

$$I_n:=h\sum _{k=0}^{n-1}\underset{\theta \in [-\tau ,0]}{sup}max\left\{|X_L(t_k+\theta )|,|X_U(t_k+\theta )|\right\},$$

where values $X_L(t_k+\theta ),X^U(t_k+\theta )$ are interpolated from known grid values or taken from history $\eta$ if $t_k+\theta <0$;

2.

update:

$$X_L\left(t_n\right)=7+sin\left(t_n\right)+cos\left(t_n\right)-I_n,$$

$$X^U\left(t_n\right)=9+sin\left(t_n\right)+cos\left(t_n\right)-I_n.$$

• Step 3: Output.

Return the sequences ${\left\{X_L\left(t_n\right)\right\}}_{n=0}^N$ and ${\left\{X^U\left(t_n\right)\right\}}_{n=0}^N$ as approximations of $X_L\left(t\right)$ and $X^U\left(t\right)$ on $[0,T]$.

The numerical simulation shown in Figure 1 corresponds to a system governed by a symmetric multivalued functional integral Equation (8), with initial history prescribed as the constant interval $\eta \left(t\right)=[8,10]$ for all $t\in [-1,0]$. This setup can model a logistic process initialized with moderate and stable inventory levels, such as a warehouse with bounded stock uncertainty or a supply chain with predictable initial conditions.

After $t=0$, both bounding trajectories $X_L\left(t\right)$ and $X^U\left(t\right)$ exhibit a monotonic downward trend, eventually crossing below zero. This behavior is driven by the cumulative effect of the history-dependent integral term, which subtracts a growing quantity from the oscillatory forcing $sin\left(t\right)+cos\left(t\right)$. The integral penalizes the system based on the supremum of past magnitudes, leading to a progressive decay in the state variable. In logistic terms, this may represent a scenario where delayed feedback — such as accumulated demand pressure or delayed replenishment — causes the system to deplete its resources over time.

Although the width of the solution interval $X^U\left(t\right)-X_L\left(t\right)=2$ remains constant, as it was expected on the basis of (9) and seen in Table 1, the entire interval $X\left(t\right)$ shifts downward, indicating that the system’s uncertainty is stable in magnitude but not in position. This translational drift reflects a structural imbalance between the replenishment and consumption dynamics encoded in the model. The symmetry of the equations ensures that the trajectories remain parallel, but the integral term dominates the sinusoidal input, resulting in net decay.

From a practical standpoint, the results highlight a critical feature of delay-driven logistic models: even with bounded initial uncertainty, the system may experience systematic degradation if historical feedback accumulates unfavorably. The fact that both trajectories fall below zero suggests that the modeled quantity—such as inventory level, production capacity, or service availability—becomes unsustainable without corrective input. This underscores the importance of incorporating active control mechanisms or adaptive policies in systems where delay and memory effects are significant.

The shaded region between $X_L\left(t\right)$ and $X^U\left(t\right)$ provides a reliable enclosure for the true trajectory $X\left(t\right)$, but its downward drift signals a need for intervention. In forecasting applications, this behavior warns against overconfidence in long-term stability based solely on initial conditions. In control contexts, it suggests that passive systems governed by delayed feedback may require external stabilization to prevent collapse or negative states. The model thus serves as a cautionary example of how history and supremum-based dynamics can erode system performance over time, even under symmetric formulations.

6. Impact on Symmetric Multivalued Integral Equations with Delay

The existence result established in the preceding sections for symmetric multivalued functional integral equations provides a foundational framework for addressing complex systems involving delay effects. In particular, we observe that the structural assumptions imposed—such as symmetry and continuity—can be suitably adapted to the delayed setting, where the solution depends not only on the present state but also on its historical states.

Motivated by this gap, we introduce and analyze a class of symmetric multivalued integral equations with delay. This formulation captures a broader range of potential applications where the system’s evolution depends symmetrically on both present and past states. Therefore, we formulate the symmetric multivalued integral equations with delay

$$X\left(t\right)+{\int }_{t_0}^{t}F(s,X\left(s\right),X(s-\tau ))ds={\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,X\left(s\right),X(s-\tau ))ds,t\in [t_0,t_0+T],$$

(10)

$$\mathrm{with}\mathrm{the}\mathrm{initial}\mathrm{condition}{X}_{t_0}={\eta }_0,$$

where ${\eta }_0:[t_0-\tau ,t_0]\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ is $\mathcal{D}$-continuous, and $F,G:I\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$.

We emphasize that such delayed multivalued equations naturally arise in the modeling of phenomena where the evolution of the system is influenced by past configurations, including applications in control theory, biological systems, and economics.

Accordingly, we formulate an analogous existence theorem for symmetric multivalued integral equations with delay. The proof strategy follows similar lines, relying on the compactness of the solution set in appropriate function spaces and the application of Schauder’s fixed-point theorem. The delayed framework requires additional care in defining the phase space and ensuring the continuity and boundedness of multivalued mappings over histories. Nevertheless, under suitable conditions, the existence of at least one solution can be guaranteed.

Theorem 4. 

Assume that the mappings $F,G:[t_0,t_0+T]\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ are jointly continuous, and let ${\eta }_0\in C_{\tau }$. Suppose that there exists a constant $\tilde{T}\in (0,T]$ such that, for every $t\in [t_0,t_0+\tilde{T}]$ and all $A,B\in {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$, the Hukuhara differences

$$\left[{\eta }_0\left(0\right)+{\int }_{t_0}^{t}G(s,A,B)ds\right]\ominus {\int }_{t_0}^{t}F(s,A,B)ds$$

are well-defined. Then, for each initial condition $(t_0,{\eta }_0)$, there exists $\widehat{T}\in [0,\tilde{T}]$ and a multivalued mapping $X:[t_0,t_0+\widehat{T}]\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^d\right)$ that satisfies Equation (10).

Proof. 

The proof of this theorem is structurally and substantively analogous to the proof of Theorem 3, with the technical distinction that we now select a constant $M>0$ such that

$$\mathcal{D}\left(F\right(t,X,Y),\{0\left\}\right)+\mathcal{D}\left(G\right(t,X,Y),\{0\left\}\right)\le M$$

for all $(t,X,Y)\in [t_0,t_0+\widehat{T}]\times B_R\left({\eta }_0\left(0\right)\right)\times B_R\left({\eta }_0\left(0\right)\right)$, where $B_R\left({\eta }_0\left(0\right)\right)$ denotes the closed ball of radius R centered at ${\eta }_0\left(0\right)$. It is important to note that this ball is not taken in the space of multivalued mappings, but rather in the space of subsets of ${\mathbb{R}}^d$. Due to the close analogy with the argumentation presented in the proof of Theorem 3, we omit the details of the present proof. □

This assertion not only broadens the applicability of the original result but also highlights the robustness of the symmetric formulation in handling temporal dependencies within multivalued dynamics.

7. Numerical Example and Application Scenario for Symmetric Multivalued Integral Equation with Delay

We consider the following symmetric multivalued integral equation with constant delay $\tau =1$

$$\begin{array}{ccc}\hfill & & X\left(t\right)+{\int }_0^{t}F(s,X\left(s\right),X(s-\tau ))ds={\eta }_0\left(0\right)+{\int }_0^{t}G(s,X\left(s\right),X(s-\tau ))ds,t\in [0,T],\hfill \\ & & \mathrm{with}\mathrm{initial}\mathrm{condition}{X}_0={\eta }_0,\hfill \end{array}$$

(11)

where ${\eta }_0:[-\tau ,0]\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$ is a constant interval $[2,5]$, and $F,G:[0,T]\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)\times {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)\to {\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$ are multivalued mappings with values that are intervals from ${\mathcal{P}}_{cc}\left({\mathbb{R}}^1\right)$.

This equation could be proposed as a hypothetical modeling of therapeutic processes that involve delayed and uncertain physiological responses, such as in immunotherapy.

Let us consider the following exemplary mappings F and G as follows

$$\begin{array}{ccc}\hfill F(s,A,B)& :=& \left[A_L+B_L,A^U+B^U+1\right],\hfill \\ & & \\ \hfill G(s,A,B)& :=& \left[A_L-B^U,A^U-B_L+2\right],\hfill \end{array}$$

(12)

where $A=[A_L,A^U]$ and $B=[B_L,B^U]$ are compact intervals that represent current and delayed physiological states, respectively. These mappings are continuous with respect to the Hausdorff–Pompeiu metric and return nonempty, convex, compact intervals. The structure of F and G reflects additive and subtractive interactions between the present and delayed immune responses, with constant offsets ensuring non-degeneracy. This formulation is particularly relevant for modeling immunotherapeutic protocols where the patient’s physiological response—such as cytokine levels or immune cell counts—is inherently uncertain and evolves with a delay. The interval-valued nature of the solution $X\left(t\right)$ captures the bounded variability in patients’ responses due to biological heterogeneity, measurement imprecision, or incomplete knowledge of the immune dynamics. Under the stated assumptions, all conditions of the existence theorem are satisfied, ensuring the well-posedness of the model. This enables further numerical simulation and analysis of treatment efficacy under uncertainty.

The problem (11) with coefficients (12), involving the unknown interval-valued process $X\left(t\right)=[X_L\left(t\right),X^U\left(t\right)]$ and the associated input data, can now be reformulated as a pair of single-valued equations representing the lower and upper bounds of the solution.

$$\left\{\begin{array}{c}{\displaystyle X_L\left(t\right)+{\int }_0^t\left(X_L\left(s\right)+X_L(s-1)\right)ds=2+{\int }_0^t\left(X_L\left(s\right)-X^U(s-1)\right)ds,}\hfill \\ {\displaystyle X^U\left(t\right)+{\int }_0^t\left(X^U\left(s\right)+X^U(s-1)+1\right)ds=5+{\int }_0^t\left(X^U\left(s\right)-X_L(s-1)+2\right)ds.}\hfill \end{array}\right.$$

This decomposition facilitates the analysis and numerical treatment of the original multivalued formulation by reducing it to a system of coupled single-valued integral equations. Further, we can rewrite this system as

$$\left\{\begin{array}{c}{\displaystyle X_L\left(t\right)=2+{\int }_0^t\left(-X_L(s-1)-X^U(s-1)\right)ds,}\hfill \\ {\displaystyle X^U\left(t\right)=5+{\int }_0^t\left(1-X_L(s-1)-X^U(s-1)\right)ds,}\hfill \end{array}\right.$$

and for $t\in [-1,0]$ we have $X_L\left(t\right)=2$ and $X^U\left(t\right)=5$.

To approximate the solution of the above system, one can use the following numerical algorithm.

• Step 0: Discretization.

Fix the time horizon $T>0$ and choose a uniform step size $h>0$. Define the grid points $t_n=nh$ for $n=0,1,\dots ,N$, where $N=\lfloor T/h\rfloor$.

• Step 1: Initialization of history.

For all grid points $t_n\in [-1,0]$, set

$$X_L\left(t_n\right):=2,X^U\left(t_n\right):=5.$$

These values are stored in arrays indexed by time.

• Step 2: Iterative computation.

For each time step $n=1,2,\dots ,N$, compute the delayed integrals using the rectangle rule

$$X_L\left(t_n\right)=2+h\sum _{k=0}^{n-1}\left(-X_L(t_k-1)-X^U(t_k-1)\right),$$

$$X^U\left(t_n\right)=5+h\sum _{k=0}^{n-1}\left(1-X_L(t_k-1)-X^U(t_k-1)\right).$$

For each summation term, the delayed arguments $t_k-1$ are evaluated by referencing previously stored values. If $t_k-1$ does not coincide with a grid point, interpolation may be used (e.g., piecewise constant or linear).

• Step 3: Storage.

After computing $X_L\left(t_n\right)$ and $X^U\left(t_n\right)$, store them in the respective arrays for use in subsequent steps.

• Step 4: Output.

The final sequences $\left\{X_L\left(t_n\right)\right\}$ and $\left\{X^U\left(t_n\right)\right\}$ contain the approximated lower and upper bounds of the interval-valued solution $X\left(t\right)$ over $[0,T]$.

The numerical solution to Equation (11) with coefficients (12), presented in Table 2 and visualized in Figure 2, describes the evolution of an interval-valued physiological response $X\left(t\right)=[X_L\left(t\right),X^U\left(t\right)]$ under delayed feedback. This formulation is relevant for modeling immunotherapeutic processes, where the patient’s immune system reacts to treatment with bounded variability and time-lagged dynamics.

Table 2. Values of the boundaries $X_L,X^U$ of the numerical solution X to (11) with coefficients (12) and the length of solution values $X^U\left(t\right)-X_L\left(t\right)$.

t	${\mathit{X}}_{\mathit{L}}\left(\mathit{t}\right)$	${\mathit{X}}^{\mathit{U}}\left(\mathit{t}\right)$	${\mathit{X}}^{\mathit{U}}\left(\mathit{t}\right)-{\mathit{X}}_{\mathit{L}}\left(\mathit{t}\right)$
0.0	2.000	5.000	3.000
0.2	−6.400	−2.200	4.200
0.4	−7.800	−3.400	4.400
0.6	−9.200	−4.600	4.600
0.9	−11.300	−6.400	4.900
1.0	−12.000	−7.000	5.000
1.2	−11.255	−6.055	5.200
1.4	−9.340	−3.940	5.400
1.6	−6.905	−1.305	5.600
1.8	−3.950	1.850	5.800
2.0	−0.475	5.525	6.000
2.2	3.312	9.512	6.200
2.4	6.488	12.888	6.400

Figure 2. Numerical solution X to Equation (11) with coefficients (12) represented between the boundariers $X_L$ in blue and $X^U$ in red.

Initially, the solution coincides with the prescribed history: $X_L\left(0\right)=2$, $X^U\left(0\right)=5$. As time progresses, both bounds deviate from their initial values due to the influence of delayed terms. The lower bound $X_L\left(t\right)$ decreases rapidly, reaching a minimum near $t=1.1$, while the upper bound $X^U\left(t\right)$ declines more gradually. This divergence reflects the asymmetric impact of past immune states on current dynamics.

The width of the interval, given by $X^U\left(t\right)-X_L\left(t\right)$, increases monotonically from $3.0$ to $6.4$ over the simulation horizon. This expansion indicates growing uncertainty in the immune response, which may correspond to inter-patient variability, heterogeneous cell activation, or delayed systemic effects. The model captures the widening therapeutic window, highlighting the need for adaptive dosing strategies.

The delay parameter $\tau =1$ models the time lag between treatment administration and physiological response. The integral terms involving $X(s-1)$ simulate how prior immune states influence current behavior—a key feature in immunotherapy, where delayed cytokine release and cellular activation are common.

The early phase ($t\le 1.0$) may represent immunosuppression or initial resistance to therapy. Beyond this point, both bounds begin to rise, suggesting recovery or effective immune activation. The increasing interval width implies that while some patients may respond strongly, others may exhibit weaker or delayed responses. This behavior supports the use of interval-valued models in personalized treatment planning and risk assessment.

The results confirm that the proposed interval-valued delayed model can yield a well-posed and biologically interpretable solution. It can effectively capture the dynamics of immune response under uncertainty and delay, making it suitable for simulating and optimizing immunotherapeutic interventions.

8. Conclusions

In this paper, we have investigated the existence of solutions to symmetric multivalued functional integral equations under minimal regularity assumptions. By employing Schauder’s fixed point theorem and carefully analyzing the structural properties of the multivalued terms, we established a Peano-type existence result under continuity conditions.

Furthermore, we demonstrated that the symmetric formulation contains equations with delay, which are particularly relevant in modeling systems whose evolution depends not only on the present state but also on the historical state. For such delayed equations, we formulated an analogous existence theorem.

For both types of equations considered, a representative example was provided to illustrate potential applications in the context of modeling processes in logistics and medicine. Each example was solved numerically to demonstrate the system’s behavior and the feasibility of the proposed approach.

The results presented here contribute to the broader theory of multivalued analysis and functional equations, offering a unified approach to both instantaneous and delayed dynamics. Future work may focus on uniqueness, stability, and numerical approximations within this framework, as well as potential applications to control systems and stochastic models.