Reflectivity Evolution and Preplasma Expansion in Front of Periodic and Flat Tilted Targets Under Laser Prepulse Influence

Abstract

In this article, we compare laser prepulse interactions with flat and periodic 1D grating aluminum targets. We describe the cases of normal and oblique radiation incidence. The choice of an appropriate radiation incidence angle and target geometry reduces back-reflection and increases the performance of laser-driven experiments due to more uniform target heating. We studied preplasma generation in front of the targets and described its temporal evolution for different angles of radiation incidence. The electron density has a symmetric periodic distribution in front of grating targets and an irregular distribution in front of flat targets. It varies from $0.3\times {10}^{22}{\mathrm{cm}}^{-3}$ to $3.5\times {10}^{22}{\mathrm{cm}}^{-3}$ for grating targets, and from $1\times {10}^{22}{\mathrm{cm}}^{-3}$ to $2.5\times {10}^{22}{\mathrm{cm}}^{-3}$ for flat targets. The generation of overcritical density regions occurs before the end of the prepulse stage. We developed a semi-analytical model based on the effective refractive index and Bloch wave approximation to describe changes in reflectivity during the simulations. During the preplasma expansion, the reflectivity varies from 0.1 to 0.8. The numerical simulation results align well with the analytically predicted behavior of the preplasma–target ensemble. Grating targets are more suitable for experiments compared with flat ones. The most convenient angle of radiation incidence is about 15°.

1. Introduction

Modern high-intensity lasers are the foundation of promising applications such as compact particle accelerators [1], high-brilliance $\gamma$-ray sources [2], the creation of environments for the observation of astrophysical phenomena [3], and new technologies for materials processing [4]. Laser-assisted materials processing can be implemented using a portion of the primary laser radiation together with secondary radiation and accelerated particles [5]. This approach allows the combination of several methods within a single experimental setup to expose samples to extreme conditions acting at different energy levels to develop novel functional materials.

Laser-driven, plasma-based accelerators offer a wide range of applications that are difficult to realize with conventional radio-frequency accelerators. In particular, high-intensity lasers can be used for compact accelerators of charged particles [6,7], high-brilliance $\gamma$-ray and X-ray sources [8,9,10], and the generation of mega-Gauss-level magnetic fields [11]. Laser-driven proton beams have proven useful for generating and probing warm dense matter states [12,13], as well as for radiography of dense plasmas [13,14]. Table-top production of rare isotopes [15] is achievable using laser acceleration of heavy-ion beams, allowing for a reduction in both the size and cost of experiments. Structured targets [13] can be employed to enhance laser-to-ion conversion efficiency and increase the temperature of laser-driven electrons.

The predictability and safety of laser-driven experiments are affected by the interference between incident and reflected radiation [16,17]. This interplay caused by back-reflection leads to the rapid growth in Rayleigh–Taylor instabilities. The focusing of reflected radiation within the preplasma, as well as its angular distribution, depends on the laser contrast and angle of incidence [18]. These considerations make the study of the influence of the angle of incidence an important topic.

The efficiency of laser energy conversion into $\gamma$-ray emission or the kinetic energy of accelerated electron beams is limited by the laser penetration depth [19]. The application of nanostructured or grating targets in laser–solid interactions not only allows for deeper laser penetration [20,21] but also increases the flux intensity of accelerated charged particles [22,23] due to the enlarged surface area of interaction. For instance, a study using nanowire targets demonstrated that more than $70\%$ of the laser energy was absorbed [24]. Moreover, the use of nanostructured targets helps to improve the energy spectra of accelerated particles [25]. In laser-driven experiments, thin foils decorated with nanocones or nanoholes [25], polystyrene spheres [20], nanostructured foams [26], nanowire arrays [26,27,28], nanoparticles [22,29], or microchannel slabs [30] are commonly used as nanostructured targets.

Sub- and near-wavelength grating targets are attractive because of their anisotropic structure. In addition, the fabrication of gratings is easier and more controllable compared to that of nanowire arrays [31]. The grating structure allows for more efficient laser radiation penetration between the protruding elements into the depth of the target. Grating targets can be produced using various crystalline or polymer materials [31,32].

Laser beam quality, together with appropriate target selection, ensures successful laser-driven experiments. The beam spectrum and the temporal evolution of the laser intensity determine the quality of the laser pulse. An ideal laser prepulse with an instantaneous rise in radiation intensity is not achievable due to the technical limitations of the chirped-pulse amplification technique [33]. As a result, the laser pulse consists of a nanosecond amplified spontaneous emission (ns-ASE) pedestal with nearly constant intensity, a picosecond (ps) ramp with exponentially increasing power, and an ultra-short, high-intensity main pulse [34,35].

A laser pulse consists of a short-duration main pulse and a long-duration prepulse. For modern PW-class lasers, the main pulse has a duration of 20–45 fs, and its radiation intensity can reach up to ${10}^{23}{\mathrm{W}/\mathrm{cm}}^2$ in the laser focus for a $10\mathrm{PW}$ laser. The laser prepulse has a duration of $500\mathrm{ps}$ to $2.5\mathrm{ns}$ and an intensity ranging from ${10}^{10}{\mathrm{W}/\mathrm{cm}}^2$ to ${10}^{14}{\mathrm{W}/\mathrm{cm}}^2$ [19,34,36], which is much lower than that of the main pulse. The prepulse power is the key parameter quantifying its impact on the target and depends on the laser contrast, defined as the prepulse-to-main-pulse power ratio. At this stage, the target surface heats above its melting point, and ablation begins. While the prepulse power is almost constant, small fluctuations and secondary peaks may be present.

The typical prepulse-to-main-pulse power ratio ranges from ${10}^{-13}$ to ${10}^{-11}$ [37,38,39,40] for high-contrast PW-class lasers. At the ELI-NP facility, a prepulse-to-main-pulse power ratio of ${10}^{-13}$ was achieved, corresponding to a prepulse power of $0.1$ kW for a 1 PW laser and 1 kW for a 10 PW laser [36]. However, the study [34] reports ultra-high contrast in the range ${10}^{-14}$ to ${10}^{-19}$, achieved by the combined use of optical parametric chirped pulse amplification (OPCPA), cross-polarized wave (XPW), and plasma mirror (PM) techniques. Other methods for improving laser contrast include nonlinear elliptical polarization rotation (NER) [41,42], double chirped-pulse amplification [43], relativistic guiding [44], and saturable absorbers [45]. During the ps-ramp stage, the laser power increases almost exponentially. At this stage, the laser power can increase by up to ${10}^3$ times over a duration of 20–$50\mathrm{ps}$. Implosion and preplasma generation continue throughout the ps-ramp stage.

Despite the considerable effort made to increase the prepulse to main pulse contrast, prepulse power at modern PW-class lasers is high enough to damage the target and impair the results of the laser-driven experiments. Because of the lengthy duration, laser prepulse transfers a significant amount of energy to the target. Studies [46,47,48] show that the increase in the prepulse duration or power affects the results of laser-driven experiments. For instance, long prepulse duration leads to a reduction in the proton energy cutoff [46]. The work [49] shows that the maximal proton energy decreases as prepulse duration increases, and it has constant power. The authors observe that the optimal results correspond to oblique laser incidence.

High-intensity laser prepulses create thick and overdense preplasma layers on nanostructured and grating targets. Such a layer prevents the penetration of the main pulse into the target. A key objective is to position the grating ridges within the primary laser interaction region. Therefore, a rigorous study of the prepulse–target interaction is essential to identify the optimal prepulse energy distribution in time and the appropriate target structure. The works [46,47,48,49] studied the interaction of different targets with laser prepulses. These studies demonstrated the influence of the prepulse on the main pulse interaction with the target. The work [35] focused on the implosion of a single nanowire under the influence of a laser prepulse, where critical density generation in front of the target was observed. In [50], the research was extended to a target with a substrate, and the influence of the angle of incidence was briefly described.

In this work, we study the influence of the laser prepulse on laser-driven experiments at PW-class laser facilities, including the ELI-NP laser facility, using flat and grating targets at different angles of incidence to determine the optimal configuration. We highlight the preplasma generation and its electron density evolution. Another topic discussed in this article is the back-reflection at different times and angles of incidence. The study was carried out numerically using the FLASH code [51] and semi-analytically using the effective refractive index model and the Bloch wave approximation.

2. Model and Method

2.1. Studied Systems Description

Let us compare a laser prepulse impact on the flat and the 1D grating aluminum targets. The flat target presents an aluminum foil with a thickness of 1 μm and a flat surface. Investigating the grating target case, we examined an aluminum foil decorated with aluminum 1D gratings. The height of the ridges is $h=5\mu \mathrm{m}$, and their width is $a=0.3\mu \mathrm{m}$. The distance between the ridges is $b=1\mu \mathrm{m}$. The aluminum density is $2.7{\mathrm{g}/\mathrm{cm}}^3$. The ridges are rectangular and are placed perpendicularly to the substrate plane. The targets are tilted to ensure the selected incidence angle of choice. The target is placed in a helium environment at a pressure of $1.6\mathrm{mbar}$.

We used the $1\mathrm{PW}$ laser experimentally reconstructed temporal profile of the laser prepulse intensity as measured at the ELI-NP facility (Figure 1a). The laser temporal profile was measured using a Tundra third-order autocorrelator by UltraFast Innovations GmbH (Garching, Germany). The Tundra autocorrelator has a temporal resolution of up to $4\mathrm{fs}$. The temporal profile was smoothed over time while conserving the laser energy, to show the general prepulse form with a timestep of $7\mathrm{ps}$. Test simulations show that secondary pulses with a maximum contrast below ${10}^{-7}$, which appear chaotic during the ASE pedestal, do not influence the preplasma expansion.

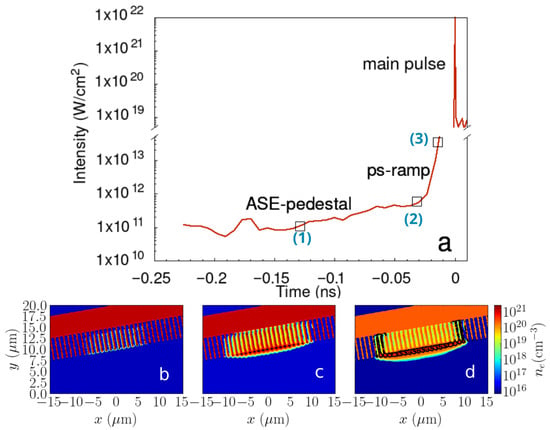
Figure 1. Laser intensity profile and electron density distribution at different times. (a) Intensity as a function of time with specified regions: ASE-pedestal, ps-ramp, and main pulse. (b) Preplasma electron density distribution at $t=-130\mathrm{ps}$ (moment (1)), where preplasma first appears in front of the targets. (c) Distribution at $t=-30\mathrm{ps}$ (moment (2)), when the ps-ramp starts. (d) Distribution at $t=-2\mathrm{ps}$ (moment (3)), corresponding to the end of the hydrodynamical simulations. The preplasma distribution is shown for the nanostructured target case with an incidence angle of $\alpha =10°$. Overcritical density regions are outlined by solid black lines.

From the start of the prepulse to point (1), the prepulse passes the ASE-pedestal stage with almost constant intensity. In regions (2)–(3), the ps-ramp has a place, and the laser power increases almost exponentially. The laser wavelength is $\lambda =800\mathrm{nm}$. The beam is focused as a spot with $2\mu \mathrm{m}$ radius. In the study, we vary the angle of radiation incidence $\alpha$ by tilting the target. During the prepulse, the radiation intensity increases from ${10}^{11}$ to ${10}^{14}{\mathrm{W}/\mathrm{cm}}^2$.

During the laser prepulse interaction with the target, the target surface heats up, and a part of the substance is ablated and ionized. Because of this process, the target is covered by a preplasma layer. The preplasma is confined by the radiation pressure, and after some point, its density increases above the critical value [35]. The ionization of Al to Al⁺ is due to both strong field phenomena (multiphoton ionization, barrier suppression ionization) and collisions between ablated atoms. Further ionization to Al⁺⁺ and beyond occurs dominantly due to collision mechanisms [35,52,53]. The laser radiation during prepulse grows above the first ionization threshold ($5.1\times {10}^{12}{\mathrm{W}/\mathrm{cm}}^2$) but is lower than the second ionization threshold ($1.26\times {10}^{14}{\mathrm{W}/\mathrm{cm}}^2$).

The preplasma critical density is calculated using the formula:

$${\varrho }_{cr}={\displaystyle \frac{{ϵ}_0{m}_e}{e^2}}{\displaystyle \frac{4{\pi }^2{c}^2}{{\lambda }^2}},$$

(1)

where ${ϵ}_0$ is vacuum dielectric permittivity, $m_e$ is electron mass, e is charge of electron, c is speed of light, and $\lambda$ is laser wavelength. If the plasma density is higher than the critical one, the laser radiation is reflected or attenuated in the preplasma. The critical density is the maximum plasma density for which the prepulse radiation can penetrate the preplasma cloud and heat the target. During the prepulse, the relativistic effects are negligible. For the non-relativistic laser intensity specific for laser prepulse, the plasma critical density is $1.74\times {10}^{21}{\mathrm{cm}}^{-3}$.

In the Results section, we describe the preplasma generation and expansion for flat and grating target surfaces and different angles of incidence.

2.2. Radiation–Hydrodynamic Simulations

We employed radiation–hydrodynamic FLASH code to implement numerical simulations of prepulse–target dynamics [51]. We chose standard hydrodynamic solvers completed with multi-temperature treatment. The solver is optimized for plasma–laser interaction simulation and high-energy-density physics experiments. The plasma components and radiation in the simulation domain are out of thermal equilibrium. The heat exchange contributes to the energy transfer between the electrons and ions. The quality of the simulation is improved by using the adaptive mesh refinement (AMR) over electron temperature and mass density.

The code implements 4–5 levels of refinement over mass density and electron temperature. The spacial resolution is up to $15.6\times 58.6$ nm. The timestep has values between $1\times {10}^{-16}\mathrm{s}$ and $3\times {10}^{-9}\mathrm{s}$, the Courant–Firderics–Lewly number has the value of $0.4$. The idea of AMR is that the computational grid automatically refines in regions where more detail is needed and coarsens where the solution is smooth. Convergence is checked by verifying that further increases in the maximum refinement level do not change the physical results significantly. The code also checks convergence with increasing refinement level by monitoring the following global physical quantities: integral reflectivity, absorbed laser energy fraction, and total mass conservation. The increase in the refinement level to 6 does not change the output density and electron temperature distribution.

The simulation program tracks the energy deposition via the inverse Bremsstrahlung effect. To reduce the computation cost, the FLASH code adopts the multi-group diffusion (MGD) theory. We choose to include in the simulation 6 groups from ${10}^{-1}$ to ${10}^5$. The suitable boundary conditions are the following: vacuum type for radiation diffusion and zero temperature gradient at the simulation boundaries. The thermal exchange is described using the Spitzer model for heat transfer. The flux coefficient is limited by $0.06$ for electron conductivity.

The radiation–hydrodynamic code requires as input the laser intensity spatial distribution, target geometry, and the equation of state for both the target material and its surrounding environment. We assumed a laser wavelength of $\lambda =800\mathrm{nm}$. The beam has Gaussian spatial distribution with the form $I\left(r_x\right)=I_{0}exp(r_x^2/R_x^2)$, where $R_x=2\mu \mathrm{m}$. The temporal intensity evolution is provided from a data file with 35 points corresponding to specific moments from experimental data.

The simulation domain has a size of $20\times 30\mu \mathrm{m}$ and is described using a Cartesian coordinate system. The target geometry is specified to ensure the correct angle of incidence and surface form. For each specified region (target and environment) are assumed the specific Z, A, specific equation of state (EOS), initial density, pressure, and temperature of $300\mathrm{K}$. EOS, transparency, and ionization levels for helium and aluminum are obtained from ionmix4 tabulated data [54]. Because the target represents a 1D grating and is invariant under translation along the grating direction (z-axis), the 2D simulations are appropriate to estimate the plasma expansion. The method inaccuracies appear only because of the laser intensity variation along the z direction. The largest divergence between the simulation results and the real distribution appears at the margins with low radiation intensity.

At the beginning of the simulation, the aluminum density is $2.7{\mathrm{g}/\mathrm{cm}}^3$. During the simulation of laser–target interaction, we preserve the form of the target by holding its boundaries until the target surface reaches the melting temperature ($925\mathrm{K}$). For greater temperatures, the preplasma expands freely. Fixing the solid target boundary by immobilizing the fluid prevents unphysical numerical expansion at low laser intensities, a typical artifact in radiation–hydrodynamic simulations [35].

The electron density $\varrho$ distribution was calculated using mass density $\rho$ and local ionization level y obtained from numerical simulation. Electron density is $\varrho =N_A\rho y/{\mu }_{Al}$, where $N_A$ is Avogadro number and ${\mu }_{Al}$ is aluminum molar mass.

2.3. Solving of Bloch Equations

To estimate the effective dielectric permittivity of the grating structure, we numerically solved the Bloch equations for the case of the incidence of normal radiation. We use the FindRoot function with standard precision in Wolfram Mathematica 11.0.3 [55] to solve the Bloch equation for the effective dielectric permittivity.

3. Results

3.1. Prepulse Target Interaction and Preplasma Generation

The laser interaction with targets depends on the laser intensity. Laser intensity increases in time from the start of the radiation emission to the main pulse (Figure 1a). At each moment of prepulse–target interaction, specific phenomena occur, and some moments are the most important. We marked, at the intensity profile line, the most important points (1–3) corresponding to the moments 130, 20, and $2\mathrm{ps}$ before the main pulse, using blue squares. The moments correspond to the plasma density distributions presented in Figure 1b–d. In Figure 1b–d, we show the electron density distribution in preplasma and target at the specified moments. At the ASE-pedestal stage, the laser radiation heats the target over the melting point and generates the preplasma (Figure 1b). After the end of the ASE-pedestal stage, the laser pulse intensity starts to increase almost exponentially. At the end of the ASE-pedestal, the preplasma in front of the target is already compressed by the radiation pressure, and the first regions with overcritical electron density appear (Figure 1c). The further evolution of preplasma leads to the growth in the overcritical density regions and the formation of the continuous overcritical density layer (Figure 1d). Laser strength parameter is given by [56]:

$$a_0^2\simeq 7.3\times {10}^{-19}{\left[\lambda (\mu \mathrm{m})\right]}^2{I}_{max}\left({\mathrm{W}/\mathrm{cm}}^2\right),$$

(2)

where $I_{max}$ is maximal prepulse intensity. Because $a_0=6.88\times {10}^{-3}\ll 1$, relativistic effects are insignificant and can be safely neglected.

Depending on the angle of laser incidence, at 10 ps before the main pulse, the overcritical density regions are already joined or close to joining (Figure 2). We studied the preplasma distribution in front of the target for different angles of incidence from 0 degrees (normal incidence) to 45 degrees. We observe that for the normal incidence (Figure 2a), the preplasma is separated into two clouds: one near the substrate and another one near the ends of the ridges. Both clouds have overcritical density islands. Such a configuration can generate difficulties in laser penetration in the depth of the array and can reduce the advantages of the nanostructured target. In the case of a 5-degree incidence angle (Figure 2b), the preplasma distribution changes, and the dense preplasma regions become concentrated close to the end of the ridges. An increase in the angle of incidence leads to the switch from the continuous overcritical density layer to separate overcritical density islands. Figure 2c shows the case of 15 degree angle of incidence. Similarly, in this case, the ridges are heated almost uniformly. In this case, the width of the overcritical preplasma is minimal. For a further increase in the angle of incidence (Figure 2d–i), the width of the overcritical density layers and the increase in the space between the overcritical density layers become more noticeable. However, further enlarging the space between the overcritical density regions does not represent an advantage for the potential experiments. The laser radiation propagates obliquely to the array and cannot penetrate the space between the overcritical density regions. As well, the heated area of the ridges switches closer to the ends of the ridges in front of the target with the increase in the angle of laser incidence. Plasma expansion width for selected angles is also presented in Table 1.

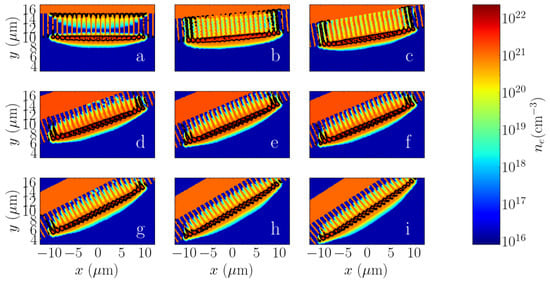
Figure 2. Preplasma electron density distribution in front of the grating target close to the end of prepulse ($t=-10\mathrm{ps}$) for different angles of laser incidence: $\alpha =0°$ (a), $\alpha =5°$ (b), $\alpha =10°$ (c), $\alpha =15°$ (d), $\alpha =20°$ (e), $\alpha =30°$ (f), $\alpha =35°$ (g), $\alpha =40°$ (h), $\alpha =45°$ (i). Overcritical density regions are outlined by solid black lines. The regions shown are those near the laser focus.

Table 1. Values such as preplasma expansion from the end of the ridges to the low-density area ($\varrho <{10}^{19}{\mathrm{W}/\mathrm{cm}}^2$) at $10\mathrm{ps}$ (${\mathit{d}}_{\mathrm{pl},-10\mathrm{ps}}$) and $2\mathrm{ps}$ ($d_{\mathrm{pl},-2\mathrm{ps}}$) before the main pulse, maximal width of the overcritical density layer ($d_{\mathrm{cr}}$), maximum and minimum electron density at $2 \mathrm{ps}$ before the main pulse, and asymmetry defined as ${\varrho }_{\max ,\mathrm{left}}/{\varrho }_{\max ,\mathrm{right}}$ for grating (G) and flat (F) targets.

$\mathit{\alpha }$		${\mathit{d}}_{\mathrm{pl},-10\mathrm{ps}}\left(\mathbf{\mu }\mathbf{m}\right)$	${\mathit{d}}_{\mathrm{pl},-2\mathrm{ps}}(\mu \mathbf{m})$	${\mathit{d}}_{\mathbf{cr}}(\mu \mathbf{m})$	${\mathit{\varrho }}_{\mathbf{max}}/{10}^{22}\left({\mathbf{W}/\mathbf{cm}}^2\right)$	${\mathit{\varrho }}_{\mathbf{min}}/{10}^{22}\left({\mathbf{W}/\mathbf{cm}}^2\right)$	Asymmetry
$0^{°}$	F	1.8	4.25	0.55	2.3	1.0	1.0
	G	1.7	4.3	0.9	3.4	0.3	1.0
${15}^{°}$	F	2.0	4.8	0.6	2.7	1.15	1.3
	G	1.8	4.7	1.15	3.2	0.33	1.1
${30}^{°}$	F	2.1	4.8	0.65	2.1	1.2	1.3
	G	1.9	4.75	1.25	3.7	0.3	1.06

In Figure 3, we compared the preplasma distribution for the flat and grating targets for normal and oblique radiation incidence. We choose the moment when the ASE-pedestal ends and the ps-pedestal starts. Figure 3a presents the normal radiation incidence and grating target case. At this stage, the overcritical density regions appear at the ends of the ridges and near the target. In the case of oblique incidence (Figure 3b), the overcritical density regions appear only at the ends of the ridges. The ends of the ridges heat above the melting point. We choose the 15-degree angle of radiation incidence as the most advantageous case. In the case of a flat target, the preplasma distribution almost does not depend on the angle of radiation incidence (Figure 3c,d). The preplasma density increases closer to the target. A continuous overcritical density layer is situated close to the target surface.

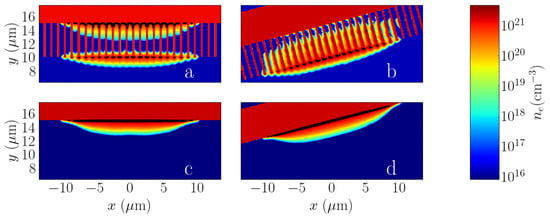
Figure 3. Preplasma electron density distribution in front of the grating (a,b) and flat (c,d) targets close to the end of prepulse ($t=-30\mathrm{ps}$) for the normal (a,c) and oblique ($\alpha =15°$) (b,d) laser incidence. The overcritical density regions are outlined by solid black lines. The regions shown are those near the laser focus.

3.2. Numerical Study of Radiation Absorption and Reflection

In this subsection, we study the energy balance during the prepulse interaction with grating (Figure 4a,b) and flat (Figure 4c,d) targets. Here, we plot the reflectivity and integral reflectivity (the ratio between the reflected and received energy). Laser–target interaction passes through the different stages.

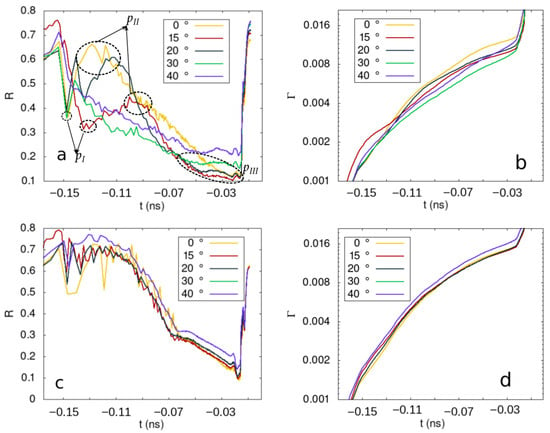
Figure 4. Reflectivity dependence on time for grating (a) and flat (c) targets.Integral reflectivity dependence on time for the case of grating (b) and flat (d) targets. The angle of radiation incidence is $\alpha =15°$.

The integral reflectivity is calculated:

$$\Gamma \left(t\right)={\displaystyle \frac{{\int }_0^t{P}_{\mathrm{out}}d\tau }{{\int }_0^{t_{\mathrm{prepulse}}}{P}_{\mathrm{laser}}d\tau }},$$

(3)

where t is the time of interaction, $P_{\mathrm{out}}$ is the power of radiation leaving the simulation domain, $P_{\mathrm{laser}}$ is the laser power, and $t_{\mathrm{prepulse}}$ is the total prepulse duration. The radiation leaving the simulation domain physically corresponds to the reflected radiation for the target configurations used.

First, the target heats up upon radiation influence until the melting point. After the ablation starts, the preplasma is generated. The preplasma generation occurs for the time $t=-140$ ps for both grating and flat targets (Figure 4a,c). At this stage, the reflectivity of the flat and grating targets is almost the same. With the increase in the preplasma amount and its density, the reflectivity decreases for both flat and grating targets; however, the reflectivity of the grating target decreases much faster. We remark that in the case of normal incidence, the reflectivity evolution of flat and grating targets is quite similar. For the case of oblique incidence, the reflectivity is less than in the case of normal incidence during almost all interaction time for the grating target case. Starting with time $t=-50$ ps, the reflectivity in the case of high angles of incidence 30°, 40° becomes greater than the reflectivity for normal incidence. Near the end of the prepulse, the overcritical density regions join, and reflectivity increases fast. After the emergence of a continuous overcritical density layer, we observe a fast increase in the ratio of reflected to the received energy. The generation of an overcritical density layer occurs approximately at the same time for grating and flat targets.

The integral reflectivity of grating targets (Figure 4b) is lower than that of flat targets (Figure 4d) for all angles of incidence. Just before the generation of a continuous overcritical density layer (at 20 ps before the main pulse), it ranges from $0.010$ to $0.013$ for grating targets, and from $0.016$ to $0.017$ for flat targets. The lowest integral reflectivity, about $0.010$–$0.011$ at 20 ps before the main pulse, was obtained for grating targets irradiated at incidence angles between 15° and 30°.

A more detailed study shows the correspondence between the electron density distribution for different angles of incidence and the reflectivity. We choose the line perpendicular to the laser propagation direction, which crosses the overcritical density region for the grating (Figure 5a) and flat (Figure 5b) targets for the moment 2 ps before the main pulse (the end of the hydrodynamic simulation).

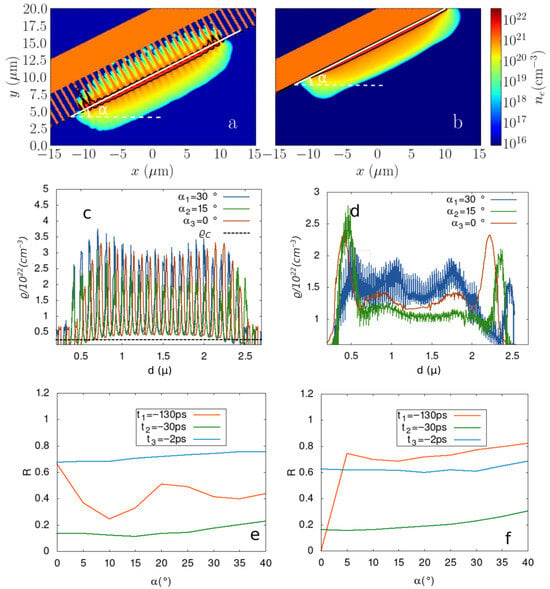
Figure 5. Electrondensity distribution along the line perpendicular to the laser propagation direction, corresponding to the maximum electron density, for grating (a) and flat (b) targets at a 25° angle of incidence, time $t=-2\mathrm{ps}$. Electron density distribution along the line of maximum density for different angles of laser incidence for grating (c) and flat (d) targets. Reflectivity as a function of the angle of incidence for different times ($t=-130$, $-30$, $-2\mathrm{ps}$) for grating (e) and flat (f) targets.

The electron density has the maximum value for the flat target along the surface of the target and, in the case of the grating target, near the ends of the ridges. In Figure 5c,d, we present the electron density profile in the region with the highest electron density. Figure 5c shows the case of the grating target, and Figure 5d depicts the case of the flat target. We observe that the maximal density along the selected line is greater for grating targets than for flat ones. However, the density in front of the grooves is much lower than the electron density in front of the flat target. The electron density profile depends on the angle of radiation incidence (Table 1). The width of the overcritical density layer has values in the range $0.55\mu \mathrm{m}$–$0.65\mu \mathrm{m}$ for flat targets and $0.9\mu \mathrm{m}$–$1.25\mu \mathrm{m}$ for grating ones. The width of the critical density layer increases with the angle of incidence.

The electron density in the preplasma varies from $0.3\times {10}^{22}{\mathrm{cm}}^{-3}$ to $3.5\times {10}^{22}{\mathrm{cm}}^{-3}$ for grating targets, and from $1\times {10}^{22}{\mathrm{cm}}^{-3}$ to $2.7\times {10}^{22}{\mathrm{cm}}^{-3}$ for flat targets. The setup with a grating target and a 15° angle of incidence is optimal, as it shows both low integral reflectivity and asymmetry. We define the asymmetry as ${\varrho }_{\max ,\mathrm{left}}/{\varrho }_{\max ,\mathrm{right}}$, where ${\varrho }_{\max ,\mathrm{left}}$ and ${\varrho }_{\max ,\mathrm{right}}$ represent the outermost left and right local maxima of electron density, respectively. In the case of $0^{°}$ incidence, the asymmetry for flat and grating targets is the same. For oblique angles of incidence (${15}^{°}$ and ${30}^{°}$), the asymmetry is greater for flat targets compared to grating ones (Table 1).

The ratio $\varrho /{\varrho }_{cr}$ has values from $1.75$ to $20.4$ for grating targets and from 5 to 14 for flat targets. With the increase in the laser intensity during the ps-ramp and main pulse, beyond the radiation–hydrodynamic simulation step, relativistic transparency occurs. The relativistic critical density is ${\varrho }_{cr,rel}=\sqrt{1+a_0^2}{\varrho }_{cr}$ [56]. Thus, we can observe the influence of relativistic transparency when the laser intensity reaches $3.5\times {10}^{17}\mathrm{W}/{\mathrm{cm}}^2$ for grating targets and $4.1\times {10}^{18}\mathrm{W}/{\mathrm{cm}}^2$ for flat targets, under the approximation that the density distribution does not change significantly during the increase in laser intensity radiation.

For a 15-degree angle of radiation incidence, the electron density is lower than for the cases of normal incidence and a 30-degrees angle of radiation incidence. The preplasma in front of the grating target has an symmetric distribution defined by the laser intensity profile and the target surface geometry. The preplasma density distribution in front of the flat target is an asymmetric one because of chaotic processes in plasma. The asymmetry becomes more observable with the increase in the angle of laser incidence.

The reflectivity for different moments also depends on the angle of incidence (Figure 5e,f). For the moment corresponding to the start of preplasma generation ($t=-130\mathrm{ps}$), the reflectivity is much lower for the grating target than for the flat one. The reflectivity from the grating targets fluctuates with the angle of incidence. Reflectivity reaches its minimal value for the 10-degrees angle of incidence. For the moments corresponding to the start of the ps-ramp ($t=-30\mathrm{ps}$) and the end of numerical simulations ($t=-2\mathrm{ps}$), the reflectivity slowly increases with the angle of incidence.

3.3. Analysis of Target–Preplasma Ensemble Optical Properties

The numerical simulations show a similar pattern of reflectivity temporal evolution for flat and grating targets. In this way, the specific reflectivity evolution is caused by the same physical phenomena. In this subsection, we analytically studied the reflectivity of grating aluminum structures before and after preplasma generation.

There are two extreme cases regarding the gratings’ periodicity: large gratings (grating period much larger than laser wavelength) and the case of deep sub-wavelength gratings (grating period much lower than laser wavelength). The target reflectivity is the same as the flat target for a large grating period. For small grating periods, the reflectivity of the structure is defined by the effective dielectric permittivity of the target. Estimation of the effective dielectric permittivity for anisotropic grating structures is given in the work [57].

Effective dielectric permittivity has the following forms:

$$1/{ϵ}_{xx}=f/{ϵ}_{Al}+(1-f)/{ϵ}_{env},$$

(4)

and

$${ϵ}_{yy}={ϵ}_{yy}=f\ast {ϵ}_{Al}+(1-f){ϵ}_{env},$$

(5)

where the fulfillment factor $f=d/(d+l)$, d is the width of the ridges, l is the width of the grooves, ${ϵ}_{Al}$ is the dielectric permitivity of aluminum, and ${ϵ}_{env}$ is the dielectric permitivity of the environment in front of the target. This approximation is suitable for $d+l\le \lambda /10$ [58].

The estimation of target reflectivity in the case of the near-wavelength period of the grating implies the Bloch wave approximation:

$${ϵ}_{xx}={(\beta /k)}^2,$$

(6)

where $\beta$ is the solution of the equation:

$$cos(K\Lambda )=cos(k_{Al}d)cos\left(k_{env}l\right)-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{ϵ}_{env}{k}_{Al}}{{ϵ}_{Al}{k}_{env}}}+{\displaystyle \frac{{ϵ}_{Al}{k}_{env}}{{ϵ}_{env}{k}_{Al}}}\right)sin(k_{Al}d)sin\left(k_{env}l\right),$$

(7)

where

$$k_{env}^2={ϵ}_{env}(\omega /c)-{\beta }^2$$

(8)

and

$$k_{Al}^2={ϵ}_{Al}(\omega /c)-{\beta }^2,$$

(9)

and $k=1/\lambda =2\pi c/\omega$, $\omega$ is laser frequency. The Bloch wave method is suitable for structures with a period of several wavelengths. The practical limitations of the Bloch wave method are related to optical decoherence and deviations from the structure periodicity.

In the case of normal incidence, the Bloch wave number is $K=0$. We obtain the equation:

$$cos(k_{Al}d)cos\left(k_{env}l\right)-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{ϵ}_{env}{k}_{Al}}{{ϵ}_{Al}{k}_{env}}}+{\displaystyle \frac{{ϵ}_{Al}{k}_{env}}{{ϵ}_{env}{k}_{Al}}}\right)sin(k_{Al}d)sin\left(k_{env}l\right),$$

(10)

which can be solved numerically. The effective optical index of the target is $n_{eff}=\sqrt{{ϵ}_{eff}}$.

To describe optical properties of the preplasma-coated target, we should take into consideration the plasma index of refraction $n_{env}=\sqrt{{ϵ}_{env}}$. The environment dielectric permittivity is:

$${ϵ}_{env}=1-{\displaystyle \frac{\varrho e^2}{{ϵ}_0{m}_e}}·{\displaystyle \frac{1}{{\omega }^2}},$$

(11)

where $\varrho$ is the electron concentration in preplasma and $\omega =2\pi c/\lambda$ is laser radiation frequency.

Let us define the relative effective index of refraction $n_t=n_{eff}/n_{env}$.

We show the relative effective index of refraction $n_t$ absolute value dependence on preplasma density in Figure 6a. The absolute value of $n_t$ for most plasma density values is much greater than 1. However, $n_t$ considerably decreases some specific resonant density values for selected target geometries. For our case $n_t$, is approximately equal to or less than 1 for $\varrho /{\varrho }_{cr}\approx \{0.4,0.85\}$.

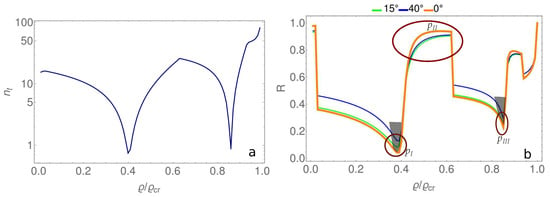
Figure 6. Relative effective index of refraction (a). Dependence of the reflectivity of a grating target on plasma density (b).

The reflection at the target-environment interface in the case of normal incidence is given by:

$$R_{t0}={\left({\displaystyle \frac{n_{eff}-n_{env}}{n_{eff}+n_{env}}}\right)}^2.$$

(12)

In the case of oblique incidence, we use the approximation formula for reflectivity [58] suitable for $|n_t|\gg 1$ and p polarization. The dependence of $n_t$ on plasma density allows us to use this formula for all density values (except resonant ones). The reflection in the case of oblique incidence is defined as:

$$R_t\approx {\displaystyle \frac{{(Re\left[n_t\right]-cos\alpha )}^2+Im\left[n_t^2\right]}{{(Re\left[n_t\right]+cos\alpha )}^2+Im\left[n_t^2\right]}},$$

(13)

where $\alpha$ is the angle of incidence.

To obtain more accurate results, we consider the radiation reflection at the vacuum–preplasma boundary, and the reflection of a part of the radiation back to the target at the preplasma–vacuum interface. For simplicity, we consider the preplasma density constant and the boundary between the preplasma and vacuum to be well-defined.

The effective plasma density is defined under the assumption that a homogeneous plasma layer of finite width and well-defined boundaries exists, exhibiting the same optical properties as the preplasma generated in front of the target. Effective plasma density represents a theoretical construct, as the preplasma generated in front of the target has the same optical properties as the homogeneous preplasma layer that covers the target. Because the preplasma density exhibits a periodic structure along the x-axis (Figure 5a,c), the Bloch wave approximation can be applied to determine its effective refractive index and establish a correspondence between the real preplasma structure and an equivalent homogeneous layer. However, this approach has several limitations:

• The preplasma density varies along the y-axis, depending on the distance from the target surface. The exact density distribution can only be obtained from simulation data or, in experimental cases, through tomographic reconstruction.
• The preplasma density also varies with distance from the center of the laser focal spot due to the non-uniform intensity profile of the laser beam. This variation becomes particularly significant in the early stages of preplasma expansion (Figure 1b), when plasma generation occurs primarily near the center of the focal spot, leaving only part of the target surface covered by preplasma.
• For high angles of incidence (above 35°), the target ridges are heated laterally, and a preplasma cloud is generated first inside the grooves. During its subsequent expansion in front of the target, it is pushed laterally by radiation pressure. In this way, regular preplasma distribution specific for low angles of incidence is perturbed Figure 2h,i.

We evaluate the reflectivity R dependence on plasma density $\varrho$ for normal incidence (orange line), oblique incidence (15° (green line), and 40° (blue line) angles of incidence) in Figure 6b. Grey areas show the regions where the formula for oblique incidence is not accurate. Brown circles mark the regions of interest for setups with different angles for comparison. The existence of resonant regions with low reflectivity is specific to near- and sub-wavelength periodic structures in optics. In metamaterials, the decrease in reflectivity occurs due to plasmon-coupled optical wave resonance at specific wavelengths. In our setup, during irradiation, the preplasma density increases, which leads to an increase in the radiation wavelength $\lambda /\sqrt{1-\varrho /{\varrho }_{cr}}$. The resonant frequencies for $\varrho =0.4{\varrho }_{cr},0.85{\varrho }_{cr},0.93{\varrho }_{cr}$ correspond to the radiation wavelengths in plasma ${\lambda }_{pl}=1.05,2.07,3.02\mu \mathrm{m}$. The resonances occur when ${\lambda }_{pl}\approx s\chi (d+l)$, where $s=1,2,3$ and $\chi =0.81$. The value of $\chi$ differs from 1 because the grating period does not correspond to the deep subwavelength regime.

The semi-analytical model predicts the same reflectivity evolution pattern during the prepulse target interaction as the numerical simulations. The plot of reflectivity deduced by solving Bloch equations repeats the principal maxima and minima of numerically evaluated reflectivity (Figure 4a). The principal inadequacies of the model are caused by the nonhomogeneous distribution of preplasma in front of the target and the continuous decrease in electron density from preplasma to vacuum. Furthermore, when making predictions based on the analytical model, we should take into account the slowing rate of increase in density of preplasma during prepulse target interaction due to preplasma expansion.

In theoretical model predictions as in numerical simulation results, we observe the decrease in reflectivity with the generation of preplasma. The minimum of reflectivity corresponds to the region $p_I$ (Table 2). In the case of numerical simulations, this gap is less pronounced due to fast and nonuniform changes in preplasma density at the beginning of its generation. The preplasma is generated first near the center of the laser spot, and after this region expands. At the moment when $\varrho /{\varrho }_{cr}>0.45$ (Figure 6b) (corresponding to the moment of $t=-120\mathrm{ps}$ (Figure 4a)), the reflectivity increases because the preplasma density increases above the resonant value. The local maximum corresponds to region $P_{II}$. In the numerical data, this feature is less pronounced due to higher preplasma density near the focal spot center and lower density toward its margins. In the numerically obtained electron density distribution for stage $P_{II}$, regions with effective densities lower than $0.45{\varrho }_{cr}$ and greater than $0.45{\varrho }_{cr}$ coexist.

Table 2. The correspondence between numerical simulation results and analytical model predictions.

Angle	Quantity	${\mathit{P}}_{\mathit{I}}$	${\mathit{P}}_{\mathit{II}}$	${\mathit{P}}_{\mathit{III}}$
$0^{°}$	$R_{\mathrm{analytic}}$	$0.04$–$0.37$	$0.82$–$0.95$	$0.2$–$0.45$
	$\varrho /{\varrho }_{cr}$	$0.03$–$0.38$	$0.42$–$0.62$	$0.63$–$0.85$
${15}^{°}$	$R_{\mathrm{analytic}}$	$0.04$–$0.31$	$0.80$–$0.90$	$0.24$–$0.43$
	$\varrho /{\varrho }_{cr}$	$0.03$–$0.38$	$0.42$–$0.62$	$0.63$–$0.85$
$0^{°}$	$R_{\mathrm{numeric}}$	$0.37$	$0.55$–$0.65$	$0.14$–$0.23$
	$\left|t\right|\left(\mathrm{ps}\right)$	147–145	135–110	48–15
${15}^{°}$	$R_{\mathrm{numeric}}$	$0.34$	$0.39$–$0.45$	$0.12$–$0.25$
	$\left|t\right|$	135–130	100–85	65–15

For the preplasma density about $\varrho /{\varrho }_{cr}\approx 0.6$, the reflectivity starts to decrease until preplasma density reaches the second resonant value $\varrho /{\varrho }_{cr}\approx 0.85$. This behavior is specific to the region $P_{III}$. Numerical simulations show the different time intervals depending on the incidence angle because preplasma density depends on the energy absorption, which changes with the angle of incidence. Starting with $\varrho /{\varrho }_{cr}\approx 0.85$ corresponding to the time $t=-15\mathrm{ps}$, the reflectivity surges fast. At this stage, the reflectivity has a minor dependence on the angle of incidence because the preplasma density increases quickly. The model and the numerical simulations show the existence of the third resonant plasma density, but the corresponding reflectivity minimum is less pronounced.

The analytical model correctly predicts that, from the first resonant density $\varrho /{\varrho }_{cr}\approx 0.45$ to the local reflectivity maximum at $\varrho /{\varrho }_{cr}\approx 0.6$, the reflectivity in the case of normal incidence is greater than in the case of oblique incidence (marked with a brown circle on the plot). From the local reflectivity maximum to the second resonant density $\varrho /{\varrho }_{cr}\approx 0.85$, the reflectivity is lower for normal incidence than for a ${15}^{°}$ angle of incidence. The reflectivity reaches its minimum value for the ${15}^{°}$ angle across all preplasma density values, making this configuration convenient for laser-driven experiments. This result is consistent with numerical simulations of reflectivity and integral reflectivity.

4. Discussion

In this article, we analyze the interaction of a laser prepulse with tilted flat and grating aluminum targets. Understanding prepulse–target interactions is crucial for PW laser-driven experiments. During irradiation, the target heats up, and a preplasma is generated. The preplasma layer changes the optical properties of the target. We studied preplasma generation and expansion for different angles of laser incidence and showed that a tilted target configuration increases radiation absorption and heats the target more uniformly.

The preplasma distribution in front of a periodic grating target has a symmetric structure with well-defined density maxima and minima. The preplasma density in front of a flat target has an asymmetric profile due to chaotic processes. In this way, the use of grating targets makes laser-driven experiments more predictable.

Numerical simulations with the FLASH code and semi-analytical methods based on the effective refractive index model and Bloch wave approximation were employed in this study. The model allows us to estimate the effective refractive index of grating targets and their reflectivity for normal and oblique laser incidence. During the investigation, the flat or grating target was tilted to angles from 0 to 45 degrees. The study was extended to targets coated with a preplasma layer caused by laser–target interaction by analyzing the reflection at the preplasma–target and preplasma–vacuum boundaries. The semi-analytical model predictions are in agreement with the numerical simulation results. The time-dependent changes in reflectivity during the prepulse–target interaction are attributed to the increasing preplasma density. The interaction of the main pulse with the target is fully determined by the preplasma distribution at the end of the prepulse stage and by the target geometry. The influence of resonances in the reflectivity curves on main pulse propagation occurs through changes in the integral reflectivity at the end of the prepulse stage.

The general pattern of reflectivity evolution in time is as follows: reflectivity is high immediately after preplasma generation, decreases until the critical density layer is formed, and then increases rapidly. Existing experimental data indirectly confirm this conclusion. In the article [59], an increase followed by a decrease in reflectivity in Au-coated glass targets is reported, due to plasma expansion after laser irradiation. The variation in reflectivity values ranges from $20\%$ to $80\%$. The laser intensity used is ${10}^{12}{\mathrm{W}/\mathrm{cm}}^2$, which is quite close to the prepulse intensity used in this work.

Analysis of preplasma extension, numerical evaluation of reflectivity, and optical property evaluation based on the effective refractive index show that grating targets exhibit symmetric and regular plasma expansion and higher radiation absorption compared to flat targets. The integral reflectivity at 20 ps before the main pulse varies from $0.010$ to $0.013$ for grating targets, and from $0.016$ to $0.017$ for flat targets, as a function of the angle of incidence. The lowest integral reflectivity at 20 ps before the main pulse, $0.010$–$0.011$, was obtained for grating targets at incidence angles between 15° and 30°. The setup with a grating target and a 15° angle of incidence is optimal, as it shows both low integral reflectivity and a symmetric preplasma distribution.