Abstract
This study investigates stochastic bifurcation in a generalized tristable Rayleigh–Duffing oscillator with fractional inertial force under both additive and multiplicative recycling noises. The system’s dynamic behavior is influenced by its inherent spatial symmetry, represented by the potential function, as well as by temporal symmetry breaking caused by fractional memory effects and recycling noise. First, an approximate integer-order equivalent system is derived from the original fractional-order model using a harmonic balance method, with minimal mean square error (MSE). The steady-state probability density function (sPDF) of the amplitude is then obtained via stochastic averaging. Using singularity theory, the conditions for stochastic P bifurcation (SPB) are identified. For different fractional derivative’s orders, transition set curves are constructed, and the sPDF is qualitatively analyzed within the regions bounded by these curves—especially under tristable conditions. Theoretical results are validated through Monte Carlo simulations and the Radial Basis Function Neural Network (RBFNN) approach. The findings offer insights for designing fractional-order controllers to improve system response control.
1. Introduction
Compared to traditional integer-order calculus, the extension of calculus to non-integer orders through fractional calculus allows for a more refined characterization of the memory effects in viscoelastic substances. A fractional derivative refers to the powerful law memory kernel from nonlocal relationships, inherently capturing both memory and long-term cumulative influences. It is effective in simulating memory effects [1,2,3,4] and has been applied in multiple areas, such as anomalous diffusion, viscoelastic mechanics, non-Newtonian fluid mechanics, and soft matter physics. Fractional calculus has also been successfully employed to explore the dynamic behaviors in ecological systems. For instance, the authors of [5] described the dynamic properties under the Grünwald–Letnikov fractional Hastings–Powell model with numerical simulations, highlighting how fractional-order parameters regulate complex ecological interactions. Similarly, Zhang et al. [6] analyzed a fractional phytoplankton–zooplankton ecological model, demonstrating that fractional derivatives effectively capture the nonlocal and memory-dependent dynamics in ecological systems. These studies, alongside work in other domains [7,8,9,10,11], collectively emphasize that various reaction dynamics can be better represented through the use of fractional derivatives than integer-order calculus. In light of the ubiquity of ambient noise throughout engineering disciplines, a thorough analysis of stochastic system dynamics, along with the effects of fractional-order parameters and noise disturbances, is of great importance.
Recently, researchers have thoroughly investigated dynamic properties in nonlinear multi-stable frameworks subjected to different types of noise excitations, resulting in important outcomes [12,13,14,15,16]. In the case of integer order, the investigations of Van der Pol–Duffing oscillators influenced by Lévy noise [14], colored noise [15], and harmonics together with random excitations [12,13,16] have attracted significant interest. A modified single-degree-of-freedom vibro-impact oscillator with a recovery factor under broadband noise excitation was examined in [17] for its random vibration performance. The researchers used the Markov approximation to calculate the sPDF for an amplitude envelope with energy, and numerical examples were used to validate the methodology. A detailed analysis of the tristable SPB in a generalized Van der Pol–Duffing oscillator exposed to multiplicative colored noise, including the derivation of an analytical sPDF expression and assessment of the parameters and noise intensity effects, was presented in [18]. Fan [19] employed He’s frequency amplitude to analyze the Duffing harmonic oscillator, demonstrating that the method is straightforward and that the results achieved are accurate across the entire solution domain. He [20] developed an enhanced amplitude frequency in nonlinear frameworks while examining the solutions of a Duffing oscillation to confirm its reliability. Zhuang et al. [21] researched event-based fuzzy control for implicit hybrid active vehicle suspension systems, embedding acceleration and Markovian jumping characteristics under random deception and denial-of-service attacks and derived the admissibility conditions under the framework of linear matrix inequalities by utilizing the piecewise Lyapunov–Krasovskii functional. Liu et al. [22] studied asynchronous admissibilization for nonlinear singular delayed hybrid hydraulic turbine governing systems with impulsive perturbations and designed the asynchronous fuzzy-state feedback controller by using parallel distributed compensation technique. Zhuang et al. [23] investigated the admissibilization for hybrid descriptor systems subject to external impulses, Markovian jumping, and fast varying delays, and employed the improved free-weight matrix technique effectively to capture the hybrid characteristics and realized the innovative conditions of admissibilization for the system. Liu et al. [24] considered the impulsive observer-based admissibilization for delayed degenerate Markovian jump systems with completely known or partly unknown transition rates and utilized the singular value decomposition technology to surmount the influence of the internal impulses of the degenerate system. Zhuang et al. [25] discussed the admissibility analysis and stabilization of stochastic singular Markovian jump systems (SSMJSs) with time delays and designed the state feedback controller to ensure the stabilization of the delayed system. The authors of [26,27] studied nonlinear tri-stable energy harvesters driven by Gaussian colored noise, and they found that the probability of jumps between potential wells increases with noise intensity; furthermore, the rectified voltage can be maximized when an appropriate rotational speed or electromechanical coupling coefficient is chosen, resulting in a symmetric tri-stable structure for the JPDF.
As for fractional-order dynamic systems, Sun and Yang [28] used the generalized-harmonic equation and random averaging approach and evaluated fractional energy harvesting frameworks subjected to Gaussian white noise, concentrating on coefficients, order, and noise intensity. The authors of [29] investigated the results of nonlinear single-DOF frameworks subjected to Gaussian white noise. Nonlinear oscillation [30] has been extensively researched due to its importance in [31,32], as well as multi-DOF systems such as six-DOF rigid body systems [33] and three-DOF auto-parametric systems [34]. The authors of [35] investigated the bistable SPB phenomenon under Van der Pol–Duffing via the fractional derivative, simultaneously excited by multiplicative and additive colored noises, showing that changes in the order of derivatives, linear damping, and noise intensity can enable SPB. He [36,37] improved a novel perturbation technique that eliminates the need for a tiny parameter in a differential formula and investigated nonlinear oscillators; then, He used examples to confirm the technique’s validity. To make all analytical techniques used in advanced calculus easily applicable to fractional calculus, the authors of [38,39] introduced a fractional complex transformation to transform a fractional differential formula into an ordinary differential formula, and examples were provided to demonstrate the efficacy of the suggested method. Golmankhaneh et al. [40] defined the fractal -velocity and -acceleration in order to obtain the Langevin equation on fractal curves and derived the Hamilton’s mechanics on fractal curves by using the Legendre transformation. He [41] developed an enhanced fractional–variational-iteration technique to more efficiently resolve fractional-order telegraph functions in space and time. Golmankhaneh et al. [42] defined the processes on totally disconnected fractal sets, suggested the random walks on fractal middle- Cantor sets, and gave the corresponding variances, which are power laws.
The fractional inertial element widely exists in nature and engineering: for instance, when an object collides into a sand pile or granular medium, its momentum is transferred in a non-local manner within the particle network, and the model that incorporates fractional inertial forces can more accurately predict the penetration depth and impact force. Due to the challenging aspects of fractional inertial elements, it is difficult to identify the specific influence of fractional inertial force, and this typically only allows for qualitative analysis of the role of parameters in shaping the vibration features of fractional-order systems [43,44,45]. However, it is crucial to identify the critical parameter conditions. Fractals are characterized by self-similarity, leading to recurring patterns at different magnifications. Additionally, fractal oscillators consistently indicate their components, such as fractal MEMS (Micro-Electromechanical Systems), which have self-similar structures that result in fractal geometry, multi-band resonance, or hierarchical frequency responses that primarily investigate the vibration framework, as thoroughly studied in [46]. Moreover, in contrast to fractals, fractional calculus models materials with complicated properties with nonlocal effects by introducing memory effects and power-law dynamics. Furthermore, fractional oscillators exhibit non-exponential decay, power-law relaxation, and response frequencies that depart from classical harmonic oscillator behaviors. They consistently represent dynamic systems described using differential functions of fractional order that involve fractional derivatives , whose order is not an integer. In this study, we primarily analyze fractional derivative-induced influence and noise excitations under nonlinear vibration. The advanced multistable Rayleigh–Duffing framework, which includes the fractional inertial item under simultaneous additive and multiplicative recycling noise, is used to describe the system’s dynamics. Utilizing singularity and the stochastic-averaging method, the SPB-related critical parametric conditions of the system are first determined, followed by an in-depth examination of the sPDF over regions enclosed by the transition set curves in the parametric plane.
This paper is organized as follows: Section 2 presents the theoretical derivation, where the original fractional-order system is equivalently transformed into an integer-order system using the harmonic balance method with minimal mean square error, and the stochastic averaging method is then applied to obtain the steady-state probability density function (sPDF) of the system’s amplitude. In Section 3, the sPDF is derived and analyzed. Section 4 deduces the critical conditions for stochastic P bifurcation (SPB) based on singularity theory. And the impact of the fractional derivative order on the system’s bifurcation behavior is investigated in Section 5, where transition sets are constructed and the qualitative changes in the sPDF across different parameter regions are discussed. Finally, Section 6 summarizes the main conclusions of this study.
2. Theoretical Derivation
Given the variety of definitions for fractional derivatives, only the most relevant ones are presented here.
The formula for the Caputo derivative about in is as follows:
where indicates the fractional order in the Caputo sense , , , and express the Euler Gamma function, while represents the -order differentiation on .
The Riemann–Liouville derivative about from is formulated as follows:
where indicates the fractional order in , , and , and represents the Euler Gamma function.
The fractal-derivative operators operating on two scales concerning the variables via under consideration are obtained following the approach in [47]:
where , displays the fractal derivative order as well as the fractal in time.
The definition for He’s fractal-order derivative operator on is as follows [48,49,50]:
In which, represents the fractal derivative order and fractal in time.
The Caputo fractional derivative’s initial conditions are consistent with integer-order differential equations and have a distinct physical interpretation. Consequently, it is utilized in this research and formulated as
In which, stands for the Caputo fractional-order derivative , , and represents the integer order derivative , while represents the Gamma function.
In determinate physical systems, where oscillators always begin motion at , the Caputo fractional derivative is frequently utilized as
where .
The advanced and multi-stable Rayleigh–Duffing oscillator framework that incorporates the fractional-order-inertia item, simultaneously driven by additive and multiplicative recycling noises, is investigated as
where stands for the linear damping coefficient and , , , and indicate the nonlinear damping coefficients in the system. The Caputo-derivative order under () can be regarded as . The recycling noises are denoted by , as , while indicates Gaussian white noise characterized by the intensity , signifies the time delay, and represents the segment corresponding to secondary noise. The self-correlation equation is indicated as
while the power spectral density of is
And is strongly correlated at time and .
When order satisfies , it encompasses damping as well as stiffness forces [51,52,53]. Furthermore, He and Liu [54] highlighted that the fractal fractional derivative contributes damping as well as inertial forces, while the order of the fractional derivative satisfies . Thus, the equivalent framework is
where the coefficients that need to be determined for the equivalent inertia and damping forces of can be denoted separately as and .
The difference between systems (8) and (11) can be represented as
In accordance with equivalent rule [55], and follow by calculating MSE under (12)
Inserting (12) into (13) results in
Assuming that the periodic form of the stationary solution in (8) is
where , then
Substituting (15) and (16) into (14) produces
For additional simplification of (17) and (18),
By substituting (15), (16), and (19) into (17) and (18) and performing integral averaging for , the ultimate forms of and are as follows:
Therefore, the isovalent oscillator for system (11) is
where
3. sPDF on Amplitude
Firstly, we examine (21) in the absence of noise excitations, and, without losing generality, the values are assumed to be , , the nonlinear damping coefficients , , , , and the natural frequency . To facilitate a detailed discussion on the parametric influence, we present the bifurcation diagram as it pertains to variations in the linear damping when , as shown in Figure 1.
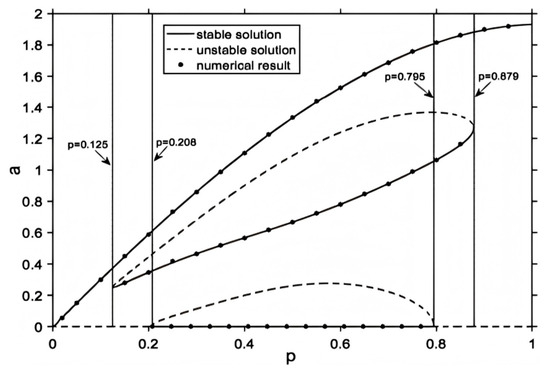
Figure 1.
Bifurcation diagram along with the fractional derivative’s order for deterministic frameworks without noise excitations.
As shown in Figure 1, the bifurcation diagram in (21) with a fractional inertial element without noise excitation is essentially different from the situation with the fractional damping element. There is only one attractor if the order varies in [0, 0.25) and (0.879, 1]: the large limit cycle. There are three attractors if the order varies in (0.208, 0.795): equilibrium and the large and small limit cycles. There is an isolated small limit cycle that is usually difficult to capture at this time, which is also fundamentally different from the van der Pol system. There are also two attractors if the order varies in the interval [0.125, 0.208] and [0.795, 0.879]: equilibrium and the small limit cycle. Suppose order is ; the phase diagram in Figure 2 indicates that the deterministic system is tristable at this moment, while belongs to the interval (0.208, 0.795).
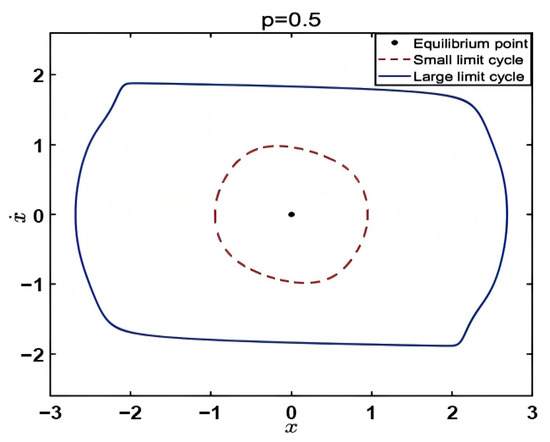
Figure 2.
Tristable phase diagram (other parameters are the same as in Figure 1).
Figure 2 shows the case without the noise excitation—the periodic orbits of the deterministic system when taken as different initial values. When the initial value of the system is taken as 0, the system exists an equilibrium point at this time, as indicated by the black dot in the figure. When the initial value of the system takes a smaller non-zero initial value, the dynamic behavior of the system is manifested as the periodic motion of the small limit cycle, as shown by the red dotted line in the figure. When the initial value of the system takes a relatively large non-zero initial value, the dynamic behavior of the system is manifested as the periodic motion of the large limit cycle, as shown by the blue solid line in the figure.
In order to calculate the sPDF, assuming (21) has a periodic solution and using the procedure described in [56], we carry out the transformation as follows:
In which and represent the magnitude and temporal alignment features. In that order, they are both random processes, while represents the fundamental frequency in (21).
Substituting (23) into (21) while applying the deterministic averaging method,
In which
Equation (24) uses the Stratonovich framework to interpret the stochastic differential equation [57]. Following the necessary Wong–Zakai correction [58], the following formulation of the consequential Itô representation is
where () refers to unit standard Wiener process, and
Utilizing the stochastic averaging method [59] and implementing averaging over (26) via ,
And
where .
Under the averaged Itô Equation (28), the amplitude has no dependence on , as demonstrated by Equation (29), indicating that is a 1D diffusion process. Consequently, the Fokker–Planck–Kolmogorov (FPK) equation for is
The boundary conditions fulfill
Based on (31), the sPDF is
Here, represents the normalized constant.
The precise equation for sPDF is achieved by applying (29) to (32) as follows:
In which
The Hamiltonian of system (21) is , and is the conservative energy.
As , the sPDF in Hamiltonian is calculated as follows:
The joint sPDF for the displacement and velocity of system (21) is
In which .
4. Derivation of the SPB Conditions
The SPB manifests through variations in the peak quantity of the sPDF profiles. To determine the threshold conditions of the system’s parameters, the parametric effects on the system’s SPB behaviors are examined.
To simplify,
where
Under [60], the sPDF in amplitude should satisfy
By substituting Equation (37) into Equation (39), the conditions can be derived as shown in [17,35]:
where signifies the critical conditions observed as peak numbers within the sPDF curve. Further, the corresponding expressions can be found as follows:
5. The Impact for Order p on a Fractional Derivative
Equations (41) and (42) demonstrate that the system’s SPB behaviors can be triggered by order , the noise intensities as well as D2, and the correlation time . Since it is challenging to illustrate and explain the effects of the three-dimensional parametric surface, to better illustrate the effects of noise intensities and , this analysis focuses on a 2D cross-section in transition sets.
In consideration of the distributions from deterministic attractors (Figure 1), we proceed by considering various data in fractional orders while maintaining all remaining items identical to those presented in Figure 1. We examine monostable, bistable, and tristable segments individually, and subsequently determine the relevant transition sets in accordance with Equations (41) and (42). Since the deterministic system only has one large limit cycle, while the order can be taken in [0, 0.125) and [0.879, 1], adding the noise excitations, the stochastic system also maintains the large-amplitude vibration. Therefore, the system’s transition sets are empty, while the order p lies in [0, 0.125) or [0.879, 1]. Without loss of generality, we only display the transition sets, while the order p can be considered as (a) , from [0.125, 0.208); (b) , from [0.208, 0.795); (c) , from [0.795, 0.879); and (d) , from [0.879, 1], as shown in Figure 3a–e, separately.
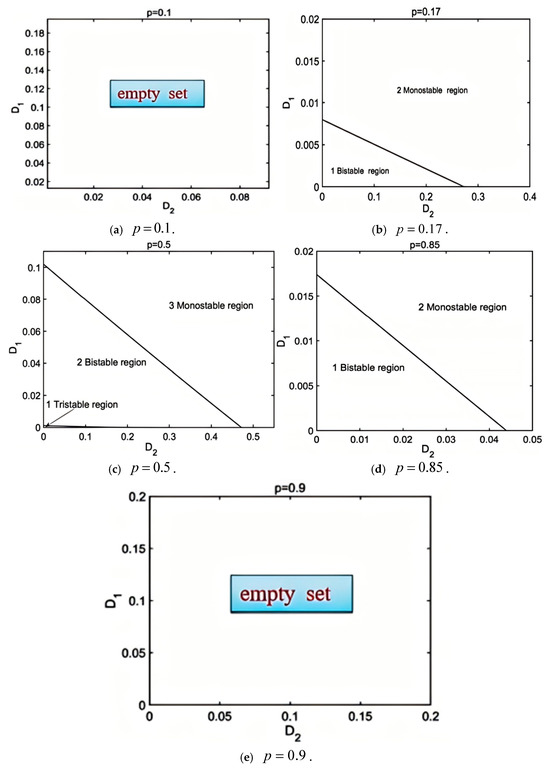
Figure 3.
Transition sets within the various values for (D2 and D1 are the unfolding parameters, and other parameters are taken with the same values as in Figure 1).
Based on Figure 1, the following conclusions are drawn:
When is within [0, 0.125) and [0.879, 1], the deterministic system associated with system (8) has a single attractor: a large limit cycle. The system’s transition set, when subjected to both multiplicative and additive noise excitations, is entirely empty, as demonstrated in Figure 3a,e. This indicates that introducing noise excitations does not lead to multi-stability in the system at this moment.
When the order is selected within the bistable intervals of [0.125, 0.208) and [0.795, 0.879] for the deterministic system (8), without loss of generality, we take and as separate examples. The system’s transition set curves driven by two noise excitations simultaneously are illustrated in Figure 3b,d. Since the deterministic system exhibits bistability at this time, and can induce the bistable phenomenon; as and increase, this system converts to a monostable state.
When is selected within [0.208, 0.795), supposing as an illustration, the system associated with (8) exhibits three attractors, an equilibrium, a small limit cycle, and a large limit cycle, with transition set curves subjected to two noise excitations depicted in Figure 3c. At this point, since the deterministic system is tristable, and can cause tristable properties; as and increase, the system initially transitions to bistability and then gradually shifts to monostability.
According to singularity theory, different kinds of the steady-state PDF in various () should be similar. Selecting () from one area, it is easy to derive that the different types in the steady-state PDF are distinct. Transition set curves divide the unfolding parametric plane into two distinct sub-areas, and, for clarity, each area (Figure 3) is labeled as one number.
To retain generality, this paper explores the steady-state PDF with joint PDF just as () within the three sub-areas, as depicted in Figure 3c. Thus, we conduct comparison with the results obtained from the Monte Carlo simulations and from the Radial Basis Function Neural Network (RBFNN) based on the original system (8) utilizing [51] (Figure 4 and Figure 5), respectively.
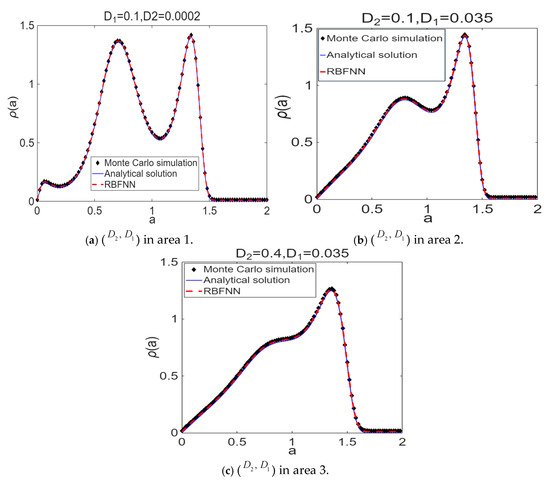
Figure 4.
PDFs for within various sub-areas from Figure 3c ( and are taken as unfolding parameters).
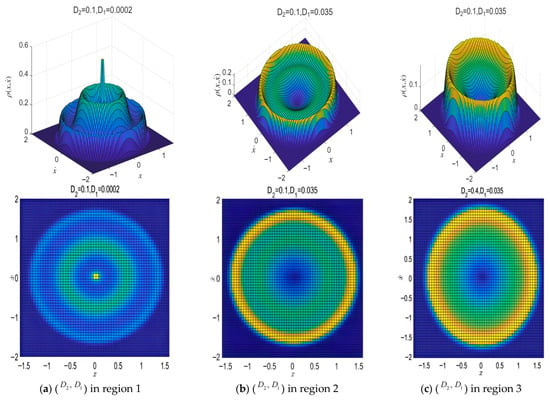
Figure 5.
Joint PDFs and the projections for in various subareas from Figure 3c ( and are unfolding parameters).
As shown in Figure 3c, in the regions holding the sPDF curve, appears to be bimodal and is encircled by two curves in the transition set. Specifically, region 1 forms the trimodal region for the system’s stationary PDF curve and is a three-peak type when parameter () is selected in region 1, showing that an equilibrium point coexists within the symmetric large-scale and small-scale limit cycles in the tristable system at this moment, as shown in Figure 4a and Figure 5a. From area 2, is a two-peak type, indicating that the system has both large and small limit cycles; see Figure 4b and Figure 5b. From area 3, is only a one-peak type and it has only one symmetric large-amplitude limit cycle at this time; see Figure 4c and Figure 5c.
Based on the analysis mentioned above, the performance indicates steady-state PDFs and that, from each area of Figure 3c, should be qualitatively distinct. Regardless of the specific unfolding parameters that intersect each curve, it will exhibit the SPB phenomenon. Therefore, these curves representing the transition sets can be identified as the key parameter thresholds required for the occurrence of the SPB. Furthermore, the explicit outcomes (Figure 4) follow the Monte Carlo simulation and RBFNN applied to (8), thereby validating the theories in this study.
6. Conclusions
This paper investigates the SPB from the tristable Rayleigh–Duffing oscillator with the fractional-order inertial force under simultaneous additive and multiplicative recycling noises, and the following conclusions can be drawn:
- (1)
- The results indicate that each of the order p in the fractional-order inertial force, the correlation time , and the noise intensities and can each induce the stochastic P bifurcation of the system, and the stationary PDF curves of the system amplitude can be switched from the unimodal to the multi-peak type by adjusting the unfolding parameters.
- (2)
- The parametric region where the system presents multi-stable behaviors is surrounded by the two transition set curves, and the transition set curves are just right for the critical parametric conditions of the stochastic P bifurcation for the system.
- (3)
- The system’s response can be retained at the monostability or a small vibration amplitude near the equilibrium by selecting the appropriate unfolding parameters, which can provide theoretical guidance on the design of such systems and prevent the damage and instability caused by nonlinear jumps or large-amplitude vibrations of the system.
- (4)
- According to the alignment of the numerical outcomes from both the MCS and RBFNN methods, the theoretical approach utilized in this study is viable to explore the stochastic P-bifurcation phenomena of nonlinear oscillators with a fractional-order derivative element.
However, the model is characterized as a single-degree-of-freedom system, while the complexity along with the state-space abstraction makes it challenging to analyze high-dimensional dynamic systems. Future research should prioritize exploration in two degrees of freedom for systems ranging from simple single-degree-of-freedom models to high-dimensional ones and coupled configurations influenced by different types of randomness, such as Lévy or Poisson noise.
Author Contributions
Conceptualization, Y.L. and Z.W.; writing—original draft preparation, Y.L.; writing—review and editing, Y.S. and G.T.; methodology, Y.L. and Z.W.; validation, Y.H.; data curation, X.Z. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 12002120, 12572034, 12072222, 11672349 and 11902287), the Natural Science Foundation of Henan Province (grant number 252300420315), and the Academic and Technical Leader of Henan University of Urban Construction (grant number YCJXSJSDTR202308).
Data Availability Statement
This article contains all relevant data. Additional queries may be directed to the corresponding author.
Acknowledgments
The authors appreciate reviewers and editors for their time; the valuable opinions of the anonymous reviewers were very helpful for the authors in improving the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, M.; Tan, W. Theoretical analysis of the velocity field, stress field and vortex sheet of generalized second order fluid with fractional anomalous diffusion. Sci. China Ser. A Math. 2001, 44, 1387–1399. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Podlubny, I. Fractional-order systems and P controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Batlleet, V.F. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Wang, X.; Zhang, H.; Wang, Y.; Li, Z. Dynamic properties and numerical simulations of the fractional Hastings-Powell model with the Grünwald-Letnikov differential derivative. Int. J. Bifurc. Chaos 2025, 35, 2550145. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; Wang, Y.; Li, Z. Dynamic properties and numerical simulations of a fractional phytoplankton-zooplankton ecological model. Netw. Heterog. Media 2025, 20, 648–669. [Google Scholar] [CrossRef]
- He, J.; Qian, M. A fractal approach to the diffusion process of red ink in a saline water. Therm. Sci. 2022, 26, 2447–2451. [Google Scholar] [CrossRef]
- Zuo, Y. Effect of SiC particles on viscosity of 3-D print paste: A fractal rheological model and experimental verification. Therm. Sci. 2021, 25, 2405–2409. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, K. A new fractal viscoelastic element: Promise and applications to Maxwell-rheological model. Therm. Sci. 2021, 25, 1221–1227. [Google Scholar] [CrossRef]
- Chen, W. An intuitive study of fractional derivative modeling and fractional quantum in soft matter. J. Vib. Control 2008, 14, 1651–1657. [Google Scholar] [CrossRef]
- Dai, D.; Ban, T.; Wang, Y.; Zhang, W. The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Therm. Sci. 2021, 25, 1261–1268. [Google Scholar] [CrossRef]
- Rong, H.; Wang, X.; Xu, W.; Meng, G.; Fang, T. On double-peak probability density functions of a Duffing oscillator under narrow-band random excitations. Acta Phys. Sin. 2005, 54, 2557–2561. [Google Scholar] [CrossRef]
- Rong, H.; Wang, X.; Meng, G.; Xu, W.; Fang, T. On double peak probability density functions of duffing oscillator to combined deterministic and random excitations. Appl. Math. Mech. 2006, 27, 1569–1576. [Google Scholar] [CrossRef]
- Xu, Y.; Gu, R.; Zhang, H.; Xu, W.; Duan, J. Stochastic bifurcations in a bistable Duffing-Vander Pol oscillator with colored noise. Phys. Rev. E 2011, 83, 056215. [Google Scholar] [CrossRef] [PubMed]
- Gu, R.; Xu, Y.; Hao, M.; Yang, Z. Stochastic bifurcations in Duffing-van der Pol oscillator with Lévy stable noise. Acta Phys. Sin. 2011, 60, 1466–1467. [Google Scholar] [CrossRef]
- Zakharova, A.; Vadivasova, T.; Anishchenko, V.; Koseska, A.; Kurths, J. Stochastic bifurcations and coherencelike resonance in a self-sustained bistable noisy oscillator. Phys. Rev. E 2010, 81, 011106. [Google Scholar] [CrossRef]
- Wu, Z.; Hao, Y. Stochastic P-bifurcations in tri-stable van der Pol-Duffing oscillator with multiplicative colored noise. Acta Phys. Sin. 2015, 64, 060501. [Google Scholar]
- Qian, J.; Chen, L. Random vibration of SDOF vibro-impact oscillators with restitution factor related to velocity under wide-band noise excitations. Mech. Syst. Signal Process. 2021, 147, 107082. [Google Scholar] [CrossRef]
- He, J. An improved amplitude-frequency formulation for nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9, 211–212. [Google Scholar] [CrossRef]
- Fan, J. He’s frequency–amplitude formulation for the Duffing harmonic oscillator. Comput. Math. Appl. 2009, 58, 2473–2476. [Google Scholar] [CrossRef]
- Zhuang, G.; Zhu, Q.; Xie, P.; Xia, J. Event-based H∞ fuzzy control for implicit hybrid AVS systems embedding acceleration characteristic under random deception and DoS attacks. IEEE Trans. Autom. Sci. Eng. 2024, 22, 6154–6167. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuang, G.; Xie, X.; Xia, J. H∞ asynchronous admissibilization for nonlinear singular delayed hybrid hydraulic turbine governing systems with impulsive perturbations. IEEE Trans. Fuzzy Syst. 2023, 31, 4220–4234. [Google Scholar] [CrossRef]
- Zhuang, G.; Ma, Q.; Zhang, B.; Xu, S.; Xia, J. Admissibility and stabilization of stochastic singular Markovian jump systems with time delays. Syst. Control Lett. 2018, 114, 1–10. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuang, G.; Xie, X.; Ma, Q. Impulsive observer-based admissibilization for delayed degenerate jump systems and application to DCM-IP device. Nonlinear Anal. Hybrid Syst. 2023, 50, 101395. [Google Scholar] [CrossRef]
- Zhuang, G.; Xu, S.; Xia, J.; Ma, Q. Double feedback control-based H∞ admissibilization for hybrid descriptor systems subject to external impulses and fast varying delays. Syst. Control Lett. 2024, 184, 105719. [Google Scholar] [CrossRef]
- Zhang, T.; Jin, Y. Enhanced DC power delivery from a rotational tristable energy harvester driven by colored noise under various constant speeds. Int. J. Non Linear Mech. 2022, 147, 104196. [Google Scholar] [CrossRef]
- Kumar, P.; Narayanan, S. Probabilistic response analysis of nonlinear tristable energy harvester under gaussian colored noise. J. Vib. Eng. Technol. 2023, 11, 2865–2879. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, Y. Stochastic averaging for the piezoelectric energy harvesting system with fractional derivative element. IEEE Access 2020, 8, 59883–59890. [Google Scholar] [CrossRef]
- Huang, Z.; Jin, X. Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. J. Sound Vib. 2009, 319, 1121–1135. [Google Scholar] [CrossRef]
- He, C.; El-Dib, Y.O. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J. Low Freq. Noise Vib. Act. Control 2022, 41, 572–603. [Google Scholar] [CrossRef]
- He, C.; Amer, T.S.; Tian, D.; Abolila, A.F.; Galal, A.A. Controlling the kinematics of a spring pendulum system using an energy harvesting device. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1234–1257. [Google Scholar] [CrossRef]
- He, C.; Tian, D.; Moatimid, G.M.; Salman, H.F.; Zekry, M.H. Hybrid rayleigh-van der pol-duffing oscillator: Stability analysis and controller. J. Low Freq. Noise Vib. Act. Control 2022, 41, 244–268. [Google Scholar] [CrossRef]
- He, J.; Amer, T.S.; El-Kafly, H.F.; Galal, A.A. Modelling of the rotational motion of 6-DOF rigid body according to the Bobylev-Steklov conditions. Results Phys. 2022, 35, 105391. [Google Scholar] [CrossRef]
- He, J.; Amer, T.S.; Abolila, A.F.; Galal, A.A. Stability of three degrees-of-freedom auto-parametric system. Alex. Eng. J. 2022, 61, 8393–8415. [Google Scholar] [CrossRef]
- Li, W.; Zhang, M.; Zhao, J. Stochastic bifurcations of generalized Duffing-van der Pol system with fractional derivative under colored noise. Chin. Phys. B 2017, 26, 62–69. [Google Scholar] [CrossRef]
- He, J. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar] [CrossRef]
- Li, Z.; He, J. Fractional complex transform for fractional differential equations. Math. Comput. Appl. 2010, 15, 970–973. [Google Scholar] [CrossRef]
- Li, Z. An extended fractional complex transform. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 335–338. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Welch, K.; Tunç, C.; Gasimov, Y.S. Classical mechanics on fractal curves. Eur. Phys. J. Spec. Top. 2023, 232, 991–999. [Google Scholar] [CrossRef]
- He, J.; Hou, W.; He, C.; Saeed, T.; Hayat, T. Variational approach to fractal solitary waves. Fractals 2021, 29, 2150199. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Tunç, C. Stochastic differential equations on fractal sets. Stochastics 2020, 92, 1244–1260. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z.; Lan, Q.; Cai, Y.; Xu, H.; Sun, Y. Stochastic transition behaviors in a tri-stable van der Pol oscillator with fractional delayed element subject to Gaussian white noise. Therm. Sci. 2022, 26, 2713–2725. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z.; Lan, Q.; Cai, Y.; Xu, H.; Sun, Y. Transition behaviors of system energy in a bistable van Ver Pol oscillator with fractional derivative element driven by multiplicative Gaussian white noise. Therm. Sci. 2022, 26, 2727–2736. [Google Scholar] [CrossRef]
- Shen, Y.; El-Dib, Y.O. A periodic solution of the fractional Sine-Gordon equation arising in architectural engineering. J. Low Freq. Noise Vib. Act. Control 2021, 40, 683–691. [Google Scholar] [CrossRef]
- He, J.; Moatimid, G.M.; Zekry, M.H. Forced nonlinear oscillator in a fractal space. Facta Univ. Ser. Mech. Eng. 2022, 20, 1–20. [Google Scholar] [CrossRef]
- He, J. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- He, J.; El-Dib, Y.O. A Tutorial Introduction to the Two-Scale Fractal Calculus and its Application to the Fractal Zhiber-Shabat Oscillator. Fractals 2021, 29, 2150268. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, X.; He, J.; Li, Z. Fractal calculus and its application to explanation of biomechanism of polar bear hairs. Fractals 2018, 26, 1850086. [Google Scholar] [CrossRef]
- He, H. A new fractal derivation. Therm. Sci. 2011, 15, 145–147. [Google Scholar] [CrossRef]
- Chen, L.; Wang, W.; Li, Z.; Zhu, W. Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int. J. Non Linear Mech. 2013, 48, 44–50. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Zhuang, Q. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. J. Vib. Control 2013, 19, 2154–2163. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, S.; Xing, H.; Ma, H. Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Int. J. Non Linear Mech. 2012, 47, 975–983. [Google Scholar] [CrossRef]
- He, C.; Liu, C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals 2022, 30, 2250046. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, W.; Sun, Y.; Gu, X. Stochastic response of van der Pol oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. Chin. Phys. B 2016, 25, 13–21. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W. Stochastic response of fractional-order van der Pol oscillator. Theor. Appl. Mech. Lett. 2014, 4, 68–72. [Google Scholar] [CrossRef]
- Xu, C.; Roberts, A.J. On the low-dimensional modelling of Stratonovich stochastic differential equations. Phys. A 1996, 225, 62–80. [Google Scholar] [CrossRef]
- Wu, Z.; Hao, Y. Three-peak P-bifurcations in stochastically excited van der Pol-Duffing oscillator. Sci. Sin. Phys. Mech. Astron. 2013, 43, 524–529. [Google Scholar] [CrossRef]
- Zhu, W. Random Vibration; Science Press: Beijing, China, 1992. [Google Scholar]
- Ling, F. Catastrophe Theory and Its Applications; Shang Hai Jiao Tong University Press: Shanghai, China, 1987. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).