Abstract
Using a relativistic mean-field model calibrated to finite-nucleus observables and bulk properties of dense nuclear matter, we investigate hyperonic neutron-star matter within an SU(3) flavor symmetry scheme. To retain SU(6)-based couplings within SU(3) flavor symmetry, we introduce a quartic self-interaction and - mixing. We demonstrate the roles of ( ratio), (mixing angle), and (singlet-to-octet coupling ratio) in SU(3)-invariant vector-meson couplings. It is found that predominantly controls the maximum mass of a neutron star, and neutron stars can be supported for . The also helps sustain large masses, whereas has a smaller effect on neutron-star properties. This SU(3) framework reconciles nuclear and astrophysical constraints and offers a plausible resolution of the hyperon puzzle.
1. Introduction
Recent multimessenger observations have significantly advanced our understanding of the dense matter equation of state (EoS). In particular, precise measurements of neutron-star radii from the Neutron star Interior Composition ExploreR (NICER) mission [1,2,3,4,5], together with the constraints on the tidal deformability from the binary neutron-star merger event, GW170817 [6,7,8], have placed stringent limits on the properties of dense matter at supranuclear densities. These astrophysical constraints, combined with the discovery of massive pulsars with masses around or above [9,10,11,12], strongly influence the theoretical modeling of neutron-star matter and provide important clues to its microscopic composition.
The possible appearance of hyperons in the core of a neutron star is a natural outcome of the Pauli exclusion principle at high densities, where the conversion of high-momentum nucleons into hyperons becomes energetically favorable. However, their onset generally softens the nuclear EoS, leading to a substantial reduction in the maximum mass of a neutron star, . This discrepancy between theoretical predictions and astrophysical observations is widely known as the hyperon puzzle.
A variety of approaches have been proposed to address this problem. In non-relativistic frameworks, repulsive three-body forces among baryons have been introduced to provide additional stiffness at high densities, as demonstrated in variational calculations and Brueckner–Hartree–Fock (BHF) studies [13,14,15,16]. In relativistic calculations, several extensions have been explored using relativistic mean-field (RMF) approaches with the additional strange mesons [17,18,19,20] and/or explicit three-baryon couplings [21,22], relativistic Hartree–Fock (RHF) models including Fock terms and tensor couplings [23,24,25,26,27], and Dirac–Brueckner–Hartree–Fock (DBHF) calculations [28,29,30].
The RMF model is a covariant energy-density functional framework that effectively describes baryonic interactions in terms of meson exchange [31,32,33], but it does not explicitly include quark and gluon degrees of freedom originating from microscopic dynamics based on quantum chromodynamics (QCD). Therefore, it should be regarded as a phenomenological realization of the strong interaction, complementary to QCD-motivated approaches such as the lattice QCD [34,35,36], chiral effective field theory (EFT) [37,38], Dyson–Schwinger equation formalism [39,40], Nambu–Jona–Lasinio (NJL) model [41,42,43], quark–meson coupling (QMC) model [44,45,46,47,48], and quarkyonic matter [49,50,51].
One of the most practical and effective approaches proposed to resolve the hyperon puzzle in RMF models is the adoption of SU(3) flavor symmetry for determining the vector-meson couplings to the baryon octet [52,53,54,55,56,57,58]. This approach enables the tuning of model parameters with empirical hypernuclear data and hyperon potentials in nuclear matter, introducing an additional repulsive force via the meson. Such flexibility can delay the onset of hyperons and maintain a sufficiently stiff EoS, which can support neutron stars. However, only a few studies have attempted to simultaneously account for both results from nuclear experiments and astrophysical observations. In particular, the nuclear EoS at high densities often shows a substantial mismatch with the constraints obtained in heavy-ion collisions [59,60,61].
The effective nucleon mass, , plays a crucial role in determining the global properties of neutron stars. As discussed in Choi et al. [62] and Li et al. [63], a lower generally leads to a stiffer EoS, thereby increasing to values exceeding . However, this reduction in also tends to enhance the dimensionless tidal deformability, , making it challenging to reproduce the constraints from GW170817 [7,8]. This dual sensitivity of the EoS to highlights its pivotal role in balancing the competing requirements from both and observations. Moreover, recent model-independent analysis suggests a much smaller than most current estimates [64]. Such a stringent constraint is particularly difficult to accommodate in the standard RMF-based EoSs, posing a serious challenge to developing a unified description of dense nuclear matter consistent with astrophysical observations.
In the present study, we extend our previous work in Miyatsu et al. [53]. We first build an RMF model that satisfies neutron-star radii and from NICER and GW170817, as well as the characteristics of finite nuclei in SU(6) spin–flavor symmetry. The SU(3) flavor symmetry approach, incorporating the effects of strange mesons, is then applied to the calibrated RMF parameters to examine how changes. We aim to clarify the role of modified vector-meson couplings in balancing the stiffness of the hyperonic neutron-star EoS under the combined constraints from both astrophysical and terrestrial data.
This paper is organized as follows. Section 2 reviews the extended RMF model based on Quantum Hadrodynamics [65]. The SU(3) extension of the vector-meson couplings is described in Section 3. Section 4 outlines the model construction and the determination of parameter sets consistent with both nuclear experiments and neutron-star observations. The properties of neutron stars in SU(3) flavor symmetry are presented in Section 5. Finally, Section 6 summarizes the main results and conclusions.
2. Lagrangian Density in SU(3) Flavor Symmetry
We extend the standard Lagrangian density in the RMF approximation to include not only the , , , and mesons but also the strange mesons, namely the isoscalar, Lorentz-scalar (), and Lorentz-vector () mesons. Since charge neutrality and equilibrium conditions are imposed in neutron-star matter, leptons are also included in the system. The total Lagrangian density is thus chosen to be [53,62,66,67]
where and denote baryon (B) and lepton (ℓ) fields, respectively, and the sum runs . The baryon fields are expressed as , , , and . The effective baryon mass is given by
with being the free mass and being the isospin matrix for B. The isospin matrix for B is defined as , , and with , , , , , and . The -B, -B, -B, -B, -B, and -B coupling constants are, respectively, denoted by , , , , , and . The covariant derivatives for the vector-meson fields are expressed as , , and . In addition, a nonlinear potential in Equation (1) is supplemented as follows:
The first and second terms in Equation (3) are introduced to provide a quantitative description of the ground-state properties of symmetric nuclear matter [68,69]. We introduce the quartic self-interaction and - mixing, which only affects the characteristics of finite nuclei and isospin-asymmetric nuclear matter [70,71,72,73,74]. Furthermore, the quartic self-interaction of the meson and the - mixing are taken into account to sustain the model parameters determined in SU(6) symmetry when the vector fields are extended to the SU(3) flavor symmetry scheme [75].
In the present study, the hadron and lepton masses in free space are taken as follows: MeV, MeV, MeV, MeV, MeV, MeV, MeV, MeV, MeV, MeV, MeV, and MeV. Note that the -meson mass, , is adjusted to reproduce the ground-state properties of several closed-shell nuclei (see Section 4).
In mean-field approximation, the meson fields are replaced by the mean-field values: , , , , , and . The equations of motion for the meson fields in uniform matter are thus given by
where the scalar density, , and the baryon density, , read
with being the Fermi momentum for . The total energy density, , and pressure, P, in neutron-star matter are expressed as
where the baryon (B), meson (M), and lepton (ℓ) contributions to and P are given by
and
3. SU(3) Symmetry in the Vector-Meson Couplings
To study the properties of neutron stars with hyperons (Y), it is important to extend SU(6) spin–flavor symmetry based on the non-relativistic quark model to the more general SU(3) flavor symmetry [19,23,24,25,26,52,53,54,55,56,57,58]. Restricting the discussion to three quark flavors (up, down, and strange), SU(3) symmetry can be regarded as a symmetry group of strong interaction. To consider combinations of the meson–baryon couplings, it is convenient to employ the SU(3)-invariant interaction Lagrangian. Using the matrix representations for the baryon octet, B, and meson nonet (singlet state, , and octet state, ), the interaction Lagrangian can be written as the sum of three terms: one arising from the coupling of the meson singlet to the baryon octet (S term) and the other two terms from the interaction of the meson octet and the baryons—one being the antisymmetric (F) term and the other being the symmetric (D) term [76,77]:
where and are, respectively, the coupling constants for the meson singlet and octet states, and () is known as the ratio.
Here we focus on the vector-meson couplings to the octet baryons, because, as usual, the other coupling constants can be determined so as to reproduce the observed properties of nuclear matter and hypernuclei. When SU(3) symmetry is applied to the isovector vector mesons, the Fock term is, in fact, necessary to reproduce the observed symmetry energy [24]. The physical and mesons are described in terms of the pure singlet, , and octet, , states as
with being the mixing angle for the vector mesons. The matrix representations for , , and B are expressed as
with () being the singlet (octet) state.
In SU(3) symmetry, all possible combinations of the couplings are then determined by four parameters: the singlet and octet coupling constants, and , the ratio for the vector mesons, , and the mixing angle, . With the coupling ratio defined by , the relations of the coupling constants for the and mesons in SU(3) symmetry can be expressed as
The -Y coupling constants are given by
Conventionally, vector couplings are taken with , under which the contribution from the D term is ignored. In the present study, by relaxing this assumption and treating as a free parameter, we are able to examine the impact of both the F and D terms. Although an additional interaction between and via the meson should be treated in SU(3) symmetry under the relation [78], we neglect its effect in the present study since our interest lies in the and interactions.
We summarize again the physical meanings of the parameters in SU(3) flavor symmetry. Specifically, represents the ratio, which controls the relative strength of the antisymmetric and symmetric couplings; is the singlet–octet mixing angle that determines the physical composition of the and mesons; and denotes the singlet-to-octet coupling ratio, which governs the overall magnitude of the vector-meson couplings.
4. Model Parameters
4.1. Model Construction and Parameters for Nucleons
Here, we construct the effective interaction that accounts not only for the characteristics of finite nuclei but also for the properties of dense nuclear matter. As a first step, model optimization is performed so as to fit the experimental data for binding energy per nucleon, , and charge radius, , of several, closed-shell nuclei in SU(6) symmetry [66,67,70]. The characteristics of several finite nuclei and the coupling constants for N are listed in Table 1 and Table 2. The bulk properties of nuclear matter at the saturation density, fm−3, are calculated as follows: the effective nucleon mass , binding energy per nucleon MeV, nuclear incompressibility MeV, nuclear symmetry energy MeV, slope parameter MeV, and curvature parameter MeV. We emphasize that the -N coupling constant, , is determined to reproduce the proton–neutron effective mass splitting, MeV, at [79,80]. Furthermore, the self-interaction of the meson is introduced to satisfy the constraints from elliptical flow data and kaon production data in heavy-ion collisions, particularly the pressure range of symmetric nuclear matter at high densities [59,60,61].

Table 1.
Theoretical predictions for ground-state properties of several closed-shell nuclei in SU(6) symmetry. Experimental data for the binding energy per nucleon, , and charge radius, , refer to Wang et al. [81] and Angeli and Marinova [82], respectively. The neutron skin thickness, , is defined as the difference between the root-mean-square radii of point neutrons and protons in a nucleus. As explained in Refs. [66,67], it is difficult to understand the PREX-2 and CREX results simultaneously in the present study [83,84].

Table 2.
Coupling constants for N in SU(6) and SU(3) symmetry. Since the meson is mainly composed of an pair, we assume that the meson does not couple to N due to the OZI rule, namely [18]. In the limit of the ideal mixing, the ratio, mixing angle, and singlet-to-octet coupling ratio are, respectively, given by , , and . In SU(3) symmetry, we present the cases for from the ideal mixing (case A) and from the Particle Data Group (PDG) (case B) [85]. The parameter is in fm−1.
As a second step, we determine the coupling constants for N in SU(3) flavor symmetry. According to Equation (29), the meson, in addition to the meson, influences the nuclear EoS in SU(3) symmetry. To preserve the same saturation properties—, , , L, and —as in the SU(6) framework, we adjust the vector-meson coupling constants, , , , and , by introducing two additional couplings, and (see Equation (3)). Several parameter sets in SU(3) symmetry are also listed in Table 2. When the quartic -meson self-interaction and - mixing terms are omitted, the extension to SU(3) flavor symmetry slightly disturbs the original SU(6) saturation conditions, particularly and L [53].
4.2. Coupling Constants for Hyperons
Using Equations (26)–(33), the hyperon coupling constants for the vector mesons, , , and , are automatically determined by , , and . On the other hand, those for the scalar mesons are fixed so as to satisfy the empirical data on potential depths. We here adopt the single-baryon potential based on the so-called Schrödinger-equivalent potential [86,87]:
where the scalar (s) and time (0) components of baryon self-energy are written as
As for the -Y couplings, we employ the recently updated values of the potential depths in symmetric nuclear matter (SNM), MeV, MeV, and MeV [88,89,90,91,92,93,94]. The - and - coupling constants, and , are calculated using the conventional relations, , with the potential from the Nagara event, MeV [17,95]. In addition, we use the potential depth in pure neutron matter (PNM), MeV, from the Lattice QCD result by the Hadrons to Atomic nuclei from Lattice QCD (HAL QCD) Collaboration to get because plays an important role in supporting a massive neutron star [96,97,98]. The other couplings are given by the relations based on the quark model: , , and . The coupling constants for Y in SU(6) and SU(3) symmetry are listed in Table 3.

Table 3.
Coupling constants for Y in SU(6) and SU(3) symmetry. We assume that , , and . For detail, see the text.
In the present RMF approach, the coupling constants are not arbitrarily chosen but are determined so as to reproduce the characteristics of finite, closed-shell nuclei and saturation properties of nuclear matter. Therefore, the uncertainties of these parameters are already strongly constrained by empirical nuclear data. Although a quantitative uncertainty analysis is beyond the scope of the present study, we have confirmed that a moderate variation in the key coupling constants does not alter qualitative conclusions regarding the equation of state and neutron star properties.
5. Neutron-Star Properties in SU(3) Flavor Symmetry
The charge neutrality and equilibrium conditions are generally imposed in the discussion of neutron-star properties. Since the neutron-star radii are remarkably sensitive to the low-density EoS that covers the crust region, we employ the realistic EoS for nonuniform matter, in which neutron-rich nuclei and neutron drips out of the nuclei are considered using the Thomas–Fermi calculation with the uniform nuclear EoS based on RHF approximation [99]. As for the crust–core phase transition, we consider the thermo-dynamical method, and it occurs at fm−3 in all cases [67], where the total baryon density is given by .
The neutron-star EoSs and mass–radius relations of neutron stars are presented in Figure 1 and Figure 2, respectively. As is well known, the appearance of hyperons softens the EoS and thereby drastically reduces in SU(6) symmetry. In the SU(3) flavor symmetry scheme, the smaller hardens the EoS and enhances , and the limit can be sufficiently satisfied for (). Note that as we set at , the neutron-star radius and dimensionless tidal deformability at the typical mass of a neutron star, and , show relatively small values ( km and ), and thus is consistent with the severe constraints from GW170817, and [7,8,64].
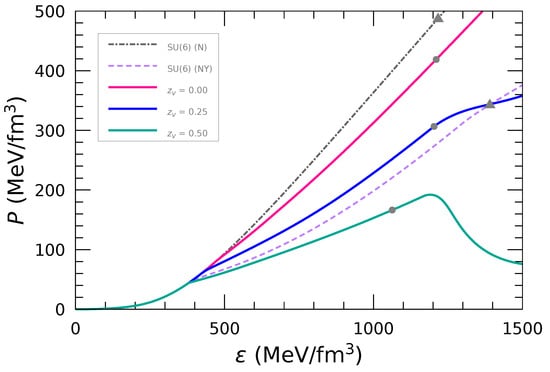
Figure 1.
Equations of state for neutron stars. The SU(6) symmetry cases are shown with and without hyperons, together with the SU(3) symmetry cases for , , and with and (case A). The filled circles and triangles denote the maximum mass points for SU(3) and SU(6) symmetry, respectively.
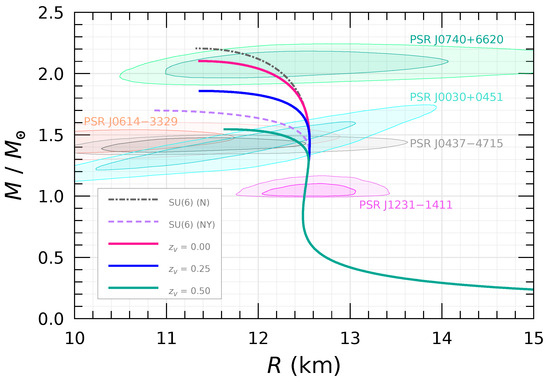
Figure 2.
Mass–radius relations of neutron stars. The observational data are supplemented by the NICER constraints [1,2,3,4,5]. We show the cases for , , and with and in SU(3) symmetry (case A).
The correlation between and in is displayed in Figure 3. We here fix the ideal mixing for . It is clearly seen that shows less impact on , while strongly affects and the smaller is favorable to support neutron stars. When is restricted by the realistic mixing angle, , the neutron stars are supported for , which is slightly smaller than the result from the Nijmegen extended-soft-core (ESC) model, [100]. The irregular contour structures observed around the central band are attributed to the rapid onset of hyperons. This behavior arises because, near the SU(6) value, the coupling becomes small, and in order to reproduce the same saturation properties as in SU(6) symmetry, in Equation (3) must increase significantly (see Table 2). Consequently, the enhanced contribution of this term leads to the sudden change in hyperon production.
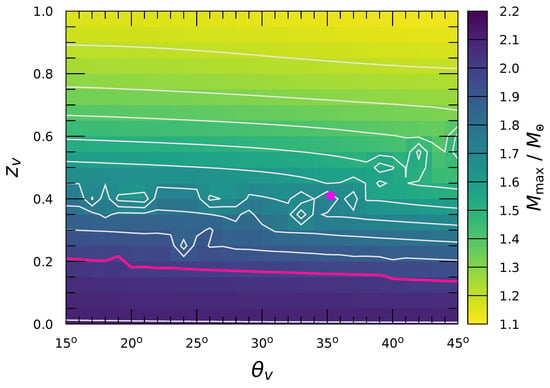
Figure 3.
Correlation between and in the maximum mass of neutron stars, , for . The red thick line is the limit, while the white lines denote contours of at intervals of 0.1. The magenta dot represents the case of SU(6) symmetry.
In Figure 4, we also show the correlation between and in with the fixed mixing angle from PDG, [85]. Similarly to the case of the fixed shown in Figure 3, mainly governs the behavior of . Nevertheless, still plays a qualitative role by setting the stiffness of the neutron-star EoS. The variation in shifts the overall magnitude of , although it is empirically indicated as . Thus, is primarily driven by , while provides a secondary but non-negligible adjustment to neutron stars.
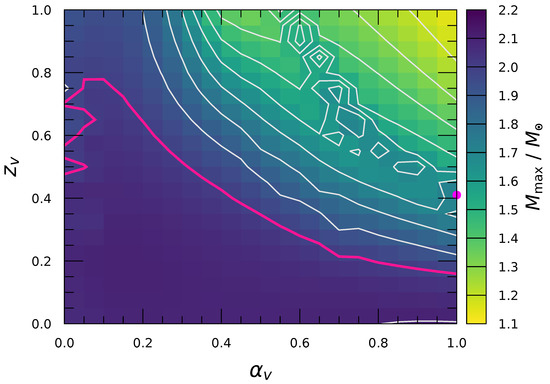
Figure 4.
Correlation between and in the maximum mass of neutron stars, , for [85]. The magenta dot represents the case of the ideal mixing. The colored lines are the same as in Figure 3.
To investigate the composition of the neutron-star core, the chemical potential, , and partial fractions, , are presented in Figure 5. As we consider the slightly deeper potentials for in SNM and PNM, MeV and MeV in the present study, appears quickly compared with the previous work in Miyatsu et al. [53]. In the cases for and , and are generated at the almost same density and their components are enhanced at high densities. Ultimately, the softening of the neutron-star EoS gives rise to the well-known hyperon puzzle. In contrast, the smaller delays the onset, and then continues to increase monotonically at high densities. Consequently, it enables supporting by preventing rapid hyperon production, although is likely to appear at lower densities through .
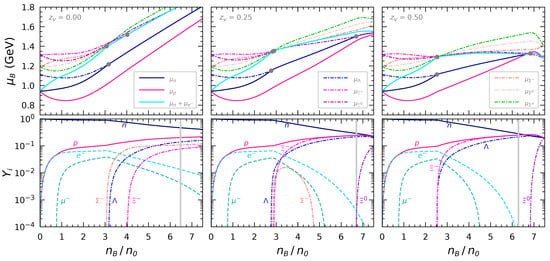
Figure 5.
Chemical potential, , and partial fractions, , in neutron-star matter as a function of . We show the cases for , , and with and in SU(3) symmetry (case A). The filled circle denotes the onset of hyperons in the upper panels. The thick vertical lines in the lower panels shows the density at which a neutron star reaches the maximum mass point by solving the TOV equation.
The effect of on the hyperon generation is demonstrated in Figure 6, showing the cases for , , and with and . As already explained in Figure 5, the constraint is satisfied in all cases by means of the small . As decreases, the onset occurs at low densities, and then appears below for . It is interesting that with decreasing , the chemical potential splitting between and is enhanced, leading to a situation in which , rather than , is produced in the core of a neutron star.

Figure 6.
Same as in Figure 5 but for , , and with and (case B).
The squared speed of sound in neutron-star matter is illustrated in Figure 7. We show two types of speed of sound: one is the adiabatic form, , and the other is the equilibrium form, [101,102,103]. Taking hyperons into account, the difference between and becomes more pronounced. As explained in Motta et al. [104] and Ye et al. [105], an abrupt decrease appears around , which corresponds to the threshold for the first hyperon (see Figure 5). Moreover, for , exhibits a sharp decline at high densities due to the rapid emergence of .
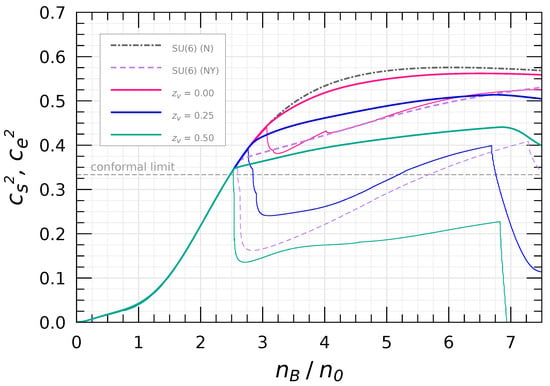
Figure 7.
Squared adiabatic and equilibrium speed of sound, (thick) and (thin), in neutron-star matter. The gray dashed lines show the conformal limit from QCD [106].
6. Summary and Conclusions
Under SU(3) flavor symmetry, we have studied the properties of neutron-star matter with hyperons using the RMF model. The model parameters are calibrated to reproduce finite-nucleus observables as well as bulk properties of dense nuclear matter. To simultaneously satisfy the astrophysical constraints on from GW170817 and the experimental data on the dense nuclear EoS from heavy-ion collisions, we have fixed a relatively large at , , and included a quartic self-interaction of the meson. The meson is incorporated to reproduce the proton–neutron effective mass splitting suggested by DBHF calculations. We further introduce the additional interactions, and , so that SU(6)-based couplings can be retained within the SU(3) scheme. The hyperon–meson couplings are determined by applying SU(3) flavor symmetry to the vector mesons and by constraining the scalar couplings with empirical potential depths in matter.
We have analyzed how , , and affect in the SU(3)-invariant vector-meson couplings. It has been found that predominantly controls , and the neutron stars are supported for . The also contributes significantly to sustaining large masses, whereas the variation in has a minor impact on neutron-star properties. Within the SU(3) framework, may become as important as, or even more significant than, and , as shown in Figure 6. This highlights the need for a more precise determination of through detailed analyses of hypernuclei. Overall, the SU(3)-based approach yields a consistent description of hyperonic neutron-star matter that reconciles nuclear data with astrophysical observations, offering a plausible resolution of the long-standing hyperon puzzle.
Author Contributions
Conceptualization, T.M.; methodology, T.M.; software, T.M.; investigation, T.M.; writing—original draft preparation, T.M.; writing—review and editing, T.M., M.-K.C., K.K., and K.S.; visualization, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) under Grant Nos. RS-2025-16066382, RS-2025-16071941, RS-2023-00242196, and RS-2021-NR060129.
Data Availability Statement
The experimental and observational data are available in the literature (references included). The numerical results presented here can be supplied upon request. Further inquiries can be directed to T.M. (tsuyoshi.miyatsu@ssu.ac.kr).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Vinciguerra, S.; Salmi, T.; Watts, A.L.; Choudhury, D.; Riley, T.E.; Ray, P.S.; Bogdanov, S.; Kini, Y.; Guillot, S.; Chakrabarty, D.; et al. An Updated Mass–Radius Analysis of the 2017–2018 NICER Data Set of PSR J0030+0451. Astrophys. J. 2024, 961, 62. [Google Scholar] [CrossRef]
- Choudhury, D.; Salmi, T.; Vinciguerra, S.; Riley, T.E.; Kini, Y.; Watts, A.L.; Dorsman, B.; Bogdanov, S.; Guillot, S.; Ray, P.S.; et al. A NICER View of the Nearest and Brightest Millisecond Pulsar: PSR J0437–4715. Astrophys. J. Lett. 2024, 971, L20. [Google Scholar] [CrossRef]
- Salmi, T.; Choudhury, D.; Kini, Y.; Riley, T.E.; Vinciguerra, S.; Watts, A.L.; Wolff, M.T.; Arzoumanian, Z.; Bogdanov, S.; Chakrabarty, D.; et al. The Radius of the High-mass Pulsar PSR J0740+6620 with 3.6 yr of NICER Data. Astrophys. J. 2024, 974, 294. [Google Scholar] [CrossRef]
- Salmi, T.; Deneva, J.S.; Ray, P.S.; Watts, A.L.; Choudhury, D.; Kini, Y.; Vinciguerra, S.; Cromartie, H.T.; Wolff, M.T.; Arzoumanian, Z.; et al. A NICER View of PSR J1231–1411: A Complex Case. Astrophys. J. 2024, 976, 58. [Google Scholar] [CrossRef]
- Mauviard, L.; Guillot, S.; Salmi, T.; Choudhury, D.; Dorsman, B.; González-Caniulef, D.; Hoogkamer, M.; Huppenkothen, D.; Kazantsev, C.; Kini, Y.; et al. A NICER view of the 1.4 solar-mass edge-on pulsar PSR J0614–3329. arXiv:2506.14883. [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nature Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Schulze, H.J.; Polls, A.; Ramos, A.; Vidana, I. Maximum mass of neutron stars. Phys. Rev. C 2006, 73, 058801. [Google Scholar] [CrossRef]
- Vidana, I.; Logoteta, D.; Providencia, C.; Polls, A.; Bombaci, I. Estimation of the effect of hyperonic three-body forces on the maximum mass of neutron stars. Europhys. Lett. 2011, 94, 11002. [Google Scholar] [CrossRef]
- Togashi, H.; Hiyama, E.; Yamamoto, Y.; Takano, M. Equation of state for neutron stars with hyperons by the variational method. Phys. Rev. C 2016, 93, 035808. [Google Scholar] [CrossRef]
- Lonardoni, D.; Lovato, A.; Gandolfi, S.; Pederiva, F. Hyperon Puzzle: Hints from Quantum Monte Carlo Calculations. Phys. Rev. Lett. 2015, 114, 092301. [Google Scholar] [CrossRef]
- Schaffner, J.; Dover, C.B.; Gal, A.; Greiner, C.; Millener, D.J.; Stoecker, H. Multiply strange nuclear systems. Ann. Phys. 1994, 235, 35–76. [Google Scholar] [CrossRef]
- Schaffner, J.; Mishustin, I.N. Hyperon rich matter in neutron stars. Phys. Rev. C 1996, 53, 1416–1429. [Google Scholar] [CrossRef]
- Sulaksono, A.; Agrawal, B.K. Existence of hyperons in the pulsar PSRJ1614-2230. Nucl. Phys. A 2012, 895, 44–58. [Google Scholar] [CrossRef]
- Tu, Z.H.; Zhou, S.G. Effects of the ϕMeson on the Properties of Hyperon Stars in the Density-dependent Relativistic Mean Field Model. Astrophys. J. 2022, 925, 16. [Google Scholar] [CrossRef]
- Tsubakihara, K.; Ohnishi, A. Three-body couplings in RMF and its effects on hyperonic star equation of state. Nucl. Phys. A 2013, 914, 438–443. [Google Scholar] [CrossRef]
- Muto, T.; Maruyama, T.; Tatsumi, T. Effects of three-baryon forces on kaon condensation in hyperon-mixed matter. Phys. Lett. B 2021, 820, 136587. [Google Scholar] [CrossRef]
- Miyatsu, T.; Katayama, T.; Saito, K. Effects of Fock term, tensor coupling and baryon structure variation on a neutron star. Phys. Lett. B 2012, 709, 242–246. [Google Scholar] [CrossRef]
- Katayama, T.; Miyatsu, T.; Saito, K. EoS for massive neutron stars. Astrophys. J. Suppl. 2012, 203, 22. [Google Scholar] [CrossRef][Green Version]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Equation of State for Neutron Stars With Hyperons and Quarks in the Relativistic Hartree–fock Approximation. Astrophys. J. 2015, 813, 135. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Sedrakian, A. Hypernuclear stars from relativistic Hartree-Fock density functional theory. Eur. Phys. J. A 2018, 54, 133. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Sammarruca, F. Effects of Lambda hyperons on the nuclear equation of state in a Dirac-Brueckner-Hartree-Fock model. Phys. Rev. C 2009, 79, 034301. [Google Scholar] [CrossRef]
- Katayama, T.; Saito, K. Properties of dense, asymmetric nuclear matter in Dirac-Brueckner-Hartree-Fock approach. Phys. Rev. C 2013, 88, 035805. [Google Scholar] [CrossRef]
- Katayama, T.; Saito, K. Hyperons in neutron stars. Phys. Lett. B 2015, 747, 43–47. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193–263. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rept. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic Continuum Hartree Bogoliubov theory for ground state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef]
- Aoki, Y.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Equation of state in lattice QCD: With physical quark masses towards the continuum limit. J. High Energy Phys. 2006, 2006, 089. [Google Scholar] [CrossRef]
- Beane, S.R.; Detmold, W.; Orginos, K.; Savage, M.J. Nuclear Physics from Lattice QCD. Prog. Part. Nucl. Phys. 2011, 66, 1–40. [Google Scholar] [CrossRef]
- Kronfeld, A.S. Twenty-first Century Lattice Gauge Theory: Results from the QCD Lagrangian. Ann. Rev. Nucl. Part. Sci. 2012, 62, 265–284. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meissner, U.G. Modern Theory of Nuclear Forces. Rev. Mod. Phys. 2009, 81, 1773–1825. [Google Scholar] [CrossRef]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral Effective Field Theory and the High-Density Nuclear Equation of State. Ann. Rev. Nucl. Part. Sci. 2021, 71, 403–432. [Google Scholar] [CrossRef]
- Roberts, C.D.; Williams, A.G. Dyson-Schwinger equations and their application to hadronic physics. Prog. Part. Nucl. Phys. 1994, 33, 477–575. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1–S103. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rept. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A Possible Quark Mechanism for the Saturation of Nuclear Matter. Phys. Lett. B 1988, 200, 235–240. [Google Scholar] [CrossRef]
- Saito, K.; Thomas, A.W. A Quark-meson coupling model for nuclear and neutron matter. Phys. Lett. B 1994, 327, 9–16. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Saito, K.; Rodionov, E.N.; Thomas, A.W. The Role of nucleon structure in finite nuclei. Nucl. Phys. A 1996, 601, 349–379. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- Nagai, S.; Miyatsu, T.; Saito, K.; Tsushima, K. Quark-meson coupling model with the cloudy bag. Phys. Lett. B 2008, 666, 239–244. [Google Scholar] [CrossRef][Green Version]
- Fujimoto, Y.; Kojo, T.; McLerran, L.D. Momentum Shell in Quarkyonic Matter from Explicit Duality: A Dual Model for Cold, Dense QCD. Phys. Rev. Lett. 2024, 132, 112701. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kojo, T.; McLerran, L. Quarkyonic matter pieces together the hyperon puzzle. arXiv:2410.22758. [CrossRef]
- Kojo, T. Stiffening of matter in quark–hadron continuity: A mini-review. J. Subat. Part. Cosmol. 2025, 4, 100088. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802, Erratum in Phys. Rev. C 2014, 90, 019904. [Google Scholar] [CrossRef]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Equation of state for neutron stars in SU(3) flavor symmetry. Phys. Rev. C 2013, 88, 015802. [Google Scholar] [CrossRef]
- Lopes, L.L.; Menezes, D.P. Hypernuclear matter in a complete SU(3) symmetry group. Phys. Rev. C 2014, 89, 025805. [Google Scholar] [CrossRef]
- Oertel, M.; Providência, C.; Gulminelli, F.; Raduta, A.R. Hyperons in neutron star matter within relativistic mean-field models. J. Phys. G 2015, 42, 075202. [Google Scholar] [CrossRef]
- Spinella, W.M.; Weber, F. Hyperonic Neutron Star Matter in Light of GW170817. Astron. Nachr. 2019, 340, 145–150. [Google Scholar] [CrossRef]
- Fu, H.R.; Li, J.J.; Sedrakian, A.; Weber, F. Massive relativistic compact stars from SU(3) symmetric quark models. Phys. Lett. B 2022, 834, 137470. [Google Scholar] [CrossRef]
- Lopes, L.L.; Marquez, K.D.; Menezes, D.P. Baryon coupling scheme in a unified SU(3) and SU(6) symmetry formalism. Phys. Rev. D 2023, 107, 036011. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Fuchs, C. Kaon production in heavy ion reactions at intermediate energies. Prog. Part. Nucl. Phys. 2006, 56, 1–103. [Google Scholar] [CrossRef]
- Lynch, W.G.; Tsang, M.B.; Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Steiner, A.W. Probing the Symmetry Energy with Heavy Ions. Prog. Part. Nucl. Phys. 2009, 62, 427. [Google Scholar] [CrossRef]
- Choi, S.; Miyatsu, T.; Cheoun, M.K.; Saito, K. Constraints on Nuclear Saturation Properties from Terrestrial Experiments and Astrophysical Observations of Neutron Stars. Astrophys. J. 2021, 909, 156. [Google Scholar] [CrossRef]
- Li, S.; Pang, J.; Shen, H.; Hu, J.; Sumiyoshi, K. Influence of Effective Nucleon Mass on Equation of State for Supernova Simulations and Neutron Stars. Astrophys. J. 2025, 980, 54. [Google Scholar] [CrossRef]
- Huang, C. Model-independent Determination of the Tidal Deformability of a 1.4 M⊙ Neutron Star from Gravitational-wave Measurements. Astrophys. J. 2025, 985, 216. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. The Relativistic Nuclear Many Body Problem. Adv. Nucl. Phys. 1986, 16, 1–327. [Google Scholar]
- Miyatsu, T.; Cheoun, M.K.; Kim, K.; Saito, K. Can the PREX-2 and CREX results be understood by relativistic mean-field models with the astrophysical constraints? Phys. Lett. B 2023, 843, 138013. [Google Scholar] [CrossRef]
- Miyatsu, T.; Cheoun, M.K.; Kim, K.; Saito, K. Novel features of asymmetric nuclear matter from terrestrial experiments and astrophysical observations of neutron stars. Front. Phys. 2024, 12, 1531475. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic Calculation of Nuclear Matter and the Nuclear Surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Konig, J.; Ring, P. A New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Sugahara, Y.; Toki, H. Relativistic mean field theory for unstable nuclei with nonlinear sigma and omega terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar] [CrossRef]
- Mueller, H.; Serot, B.D. Relativistic mean field theory and the high density nuclear equation of state. Nucl. Phys. A 1996, 606, 508–537. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J. Neutron-Rich Nuclei and Neutron Stars: A New Accurately Calibrated Interaction for the Study of Neutron-Rich Matter. Phys. Rev. Lett. 2005, 95, 122501. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, B.K.; Chatterjee, D.; Gandhi, R.; Schaffner-Bielich, J. Role of vector self-interaction in neutron star properties. Nucl. Phys. A 2023, 1030, 122578. [Google Scholar] [CrossRef]
- Malik, T.; Dexheimer, V.; Providência, C. Astrophysics and nuclear physics informed interactions in dense matter: Inclusion of PSR J0437-4715. Phys. Rev. D 2024, 110, 043042. [Google Scholar] [CrossRef]
- Wadhwa, M.; Kumari, M.; Kumar, A. Strange quark stars in modified vector MIT bag model: Role of ρ and ϕ mesons. Phys. Lett. B 2025, 868, 139707. [Google Scholar] [CrossRef]
- de Swart, J.J. The Octet model and its Clebsch-Gordan coefficients. Rev. Mod. Phys. 1963, 35, 916–939, Erratum in Rev. Mod. Phys. 1965, 37, 326. [Google Scholar] [CrossRef]
- Lichtenberg, D.B. Unitary Symmetry and Elementary Particles; Academic Press, Inc.: Cambridge, MA, USA, 1978; Available online: https://www.sciencedirect.com/book/9780124484603/unitary-symmetry-and-elementary-particles (accessed on 28 October 2025).
- Lopes, L.L. A closer look at the Yukawa interaction from a symmetry group perspective. Prog. Theor. Exp. Phys. 2023, 2023, 113D01, Erratum in Prog. Theor. Exp. Phys. 2024, 2024, 019201. [Google Scholar] [CrossRef]
- van Dalen, E.N.E.; Fuchs, C.; Faessler, A. Dirac-Brueckner-Hartree-Fock calculations for isospin asymmetric nuclear matter based on improved approximation schemes. Eur. Phys. J. A 2007, 31, 29–42. [Google Scholar] [CrossRef]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Asymmetric Nuclear Matter in Relativistic Mean-field Models with Isoscalar- and Isovector-meson Mixing. Astrophys. J. 2022, 929, 82. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K.P. Table of experimental nuclear ground state charge radii: An update. Atom. Data Nucl. Data Tabl. 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Gayoso, C.A.; Barcus, S.; Bellini, V.; Beminiwattha, R.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Gayoso, C.A.; Barcus, S.; Bellini, V.; Beminiwattha, R.; et al. Precision Determination of the Neutral Weak Form Factor of Ca48. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef] [PubMed]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Jaminon, M.; Mahaux, C.; Rochus, P. Single Particle Potential in a Relativistic Hartree-Fock Mean Field Approximation. Nucl. Phys. A 1981, 365, 371–391. [Google Scholar] [CrossRef]
- Chen, L.W.; Ko, C.M.; Li, B.A. Isospin-dependent properties of asymmetric nuclear matter in relativistic mean-field models. Phys. Rev. C 2007, 76, 054316. [Google Scholar] [CrossRef]
- Batty, C.J.; Friedman, E.; Gal, A. Strong interaction physics from hadronic atoms. Phys. Rept. 1997, 287, 385–445. [Google Scholar] [CrossRef]
- Kohno, M.; Fujiwara, Y.; Watanabe, Y.; Ogata, K.; Kawai, M. Strength of the Sigma single-particle potential in nuclei from semiclassical distorted wave model analysis of (pi-,k+) inclusive spectrum. Prog. Theor. Phys. 2004, 112, 895–900. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. In-medium nuclear interactions of low-energy hadrons. Phys. Rept. 2007, 452, 89–153. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. Constraints from Λ hypernuclei on the ΛNN content of the Λ-nucleus potential. Phys. Lett. B 2023, 837, 137669. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. Λ hypernuclear potentials beyond linear density dependence. Nucl. Phys. A 2023, 1039, 122725. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. ΛNNΛNN input to neutron stars from hypernuclear data. PoS 2025, EXA-LEAP2024, 060. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. Compatibility of recent Ξ-nuclear bound state signals. Phys. Lett. B 2025, 868, 139728. [Google Scholar] [CrossRef]
- Takahashi, H.; Ahn, J.K.; Akikawa, H.; Aoki, S.; Arai, K.; Bahk, S.Y.; Baik, K.M.; Bassalleck, B.; Chung, J.H.; Chung, M.S.; et al. Observation of a (Lambda Lambda)He-6 double hypernucleus. Phys. Rev. Lett. 2001, 87, 212502. [Google Scholar] [CrossRef] [PubMed]
- Inoue, T. Strange Nuclear Physics from QCD on Lattice. AIP Conf. Proc. 2019, 2130, 020002. [Google Scholar] [CrossRef]
- Inoue, T. Hyperon Forces from QCD and Their Applications. JPS Conf. Proc. 2019, 26, 023018. [Google Scholar] [CrossRef]
- Inoue, T. Baryon Interactions from QCD on Lattice. Few Body Syst. 2021, 62, 106. [Google Scholar] [CrossRef]
- Miyatsu, T.; Yamamuro, S.; Nakazato, K. A new equation of state for neutron star matter with nuclei in the crust and hyperons in the core. Astrophys. J. 2013, 777, 4. [Google Scholar] [CrossRef]
- Rijken, T.A.; Nagels, M.M.; Yamamoto, Y. Baryon-baryon interactions: Nijmegen extended-soft-core models. Prog. Theor. Phys. Suppl. 2010, 185, 14–71. [Google Scholar] [CrossRef]
- Jaikumar, P.; Semposki, A.; Prakash, M.; Constantinou, C. g-mode oscillations in hybrid stars: A tale of two sounds. Phys. Rev. D 2021, 103, 123009. [Google Scholar] [CrossRef]
- Aguirre, R.M. Hyperons, deconfinement, and the speed of sound in neutron stars. Phys. Rev. D 2022, 105, 116023. [Google Scholar] [CrossRef]
- Tran, V.; Ghosh, S.; Lozano, N.; Chatterjee, D.; Jaikumar, P. g-mode oscillations in neutron stars with hyperons. Phys. Rev. C 2023, 108, 015803. [Google Scholar] [CrossRef]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. On the sound speed in hyperonic stars. Nucl. Phys. A 2021, 1009, 122157. [Google Scholar] [CrossRef]
- Ye, J.T.; Wang, R.; Wang, S.P.; Chen, L.W. High-density Symmetry Energy: A Key to the Solution of the Hyperon Puzzle. Astrophys. J. 2025, 985, 238. [Google Scholar] [CrossRef]
- Bedaque, P.; Steiner, A.W. Sound velocity bound and neutron stars. Phys. Rev. Lett. 2015, 114, 031103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).