Using Sphere Symmetry Breaking to Calculate SCHENBERG’s Antenna Quadrupolar Frequencies

Abstract

Gravitational waves (GW) play an important role in the understanding of several astrophysical objects, like neutron stars and black holes. One technology used to detect them involves massive objects that vibrate as GW cross it, and the detectors built are, accordingly, of the resonant-mass type. SCHENBERG is a resonant-mass GW detector, built in Brazil, whose antenna is a spherical, 65 cm in diameter mass made of a CuAl alloy, and its quadrupole vibrational modes would be excited by GW, as predicted by general relativity. The chosen alloy can be cooled down to mK temperatures with a good mechanical quality factor. The quadrupole mode frequencies were measured at 4K, and a frequency band of about 67.5 Hz was found, but when the antenna was simulated in SolidWorks FEM software version 2010–2011 (as well as in Ansys SpaceClaim^TM), the band obtained for a free sphere was different—around 30 Hz. When the holes for the suspension were included in the simulation, the same discrepancy persisted. In this work, gravity was included in the FEM simulation, and we show that the bandwidth results are even smaller. We were then able to obtain a bandwidth close to the measured one by including a small deviation from the vertical axle, as well as variations on the sphere microstructure, which are assumptions that break the symmetry of a perfect, homogeneous free sphere. We believe that the microstructure variations are due to differences in the cooling time during the sphere casting. As for a good mechanical quality factor, the sphere was not submitted to homogenization. With these additions to the FEM simulation, a reasonable frequency distribution was found, consistent with the one measured for SCHENBERG’s antenna.

1. Introduction

Gravitational waves (GW) were theoretically predicted by A. Einstein more than a century ago as a consequence of general relativity (GR). After many decades of debates and experimental developments, the announcement of the first successful direct detection of these waves was delivered in 2015 by the LIGO-Virgo collaboration [1]. In GR, gravitational waves are modeled as space–time distortions that propagate at the speed of light. They are expected to weakly interact with matter, and in massive objects, they would excite their normal modes. This behavior led to the construction of GW detectors with resonant-mass technology long before the present interferometric GW detectors (IGD) were designed [2].

Resonant-mass GW detectors (RMD) are nowadays being investigated as a technology to pursue in collaboration with interferometric technology. RMD are cheaper to build and have narrower bandwidth, making them useful, for instance, to aid in the calibration of the large interferometers or in coincidence detection with the latter to confirm GW arrival [3].

In geometry, symmetry is the property of a shape or object that remains unchanged after a specific transformation, such as reflection, rotation, or translation. An object has symmetry if it can be divided into two or more identical pieces arranged in an organized fashion. For instance, a shape possesses rotational symmetry if it can be rotated around a fixed point (or axis in 3D) and still appear identical to its original position. A star or a circle are examples of shapes with rotational symmetry. A sphere has infinite rotational symmetry, meaning it looks the same after rotation around any axis passing through its center, and infinite reflectional symmetry, as any plane passing through its center divides it into two identical mirror images. This fundamental symmetry, where all points on the surface are equivalent relative to the center, is known as spherical symmetry.

A particularly efficient geometry for an RMD is the sphere, whose symmetry favors omnidirectionality with respect to the wave’s direction of arrival. In principle, a spherical RMD should be able to yield the direction of the arrival of a gravitational wave [4], information that is not possible to acquire from a single IGD. Indeed, in the first direct detection of GW by the LIGO-Virgo-Kagra collaboration, the direction of the source was possible to obtain because all three interferometers of the collaboration were working in coincidence [5].

A prototype of a spherical RMD has been developed, named SCHENBERG in memory of the Brazilian scientist Mario Schenberg, known for his remarkable astrophysical studies. The schematics of the detector can be seen in Figure 1. Data from this prototype was collected in a few runs, aimed at testing the technology for a possible larger detector [6]. The SCHENBERG prototype could work as a detector if GW around 3200 Hz arrived with enough intensity. The coalescence of a binary system involving a neutron star and a black hole (NS-BH merger) is expected to emit strong GW in a wide spectrum of frequencies that encompass SCHENBERG’S band. With enough sensitivity, this detector would have a significant chance of detecting NS-BH mergers of 1.4–3.0 $M_{\odot }$ [7]. The unique symmetry of this RMD could also be used to investigate whether space–time ripples could be scaled by a tiny action, for which sensitivities beyond the standard are necessary [8]. The minimum energy sensitivity of the spherical detector is one phonon at the detection frequency to allow for measurement squeezing techniques to be applied to obtain the limit with precison. In addition, SCHENBERG could also allow for the testing of alternative theories of gravitation, as in the work by de Paula et al. [9], which involves a massive graviton, implying six polarization states.

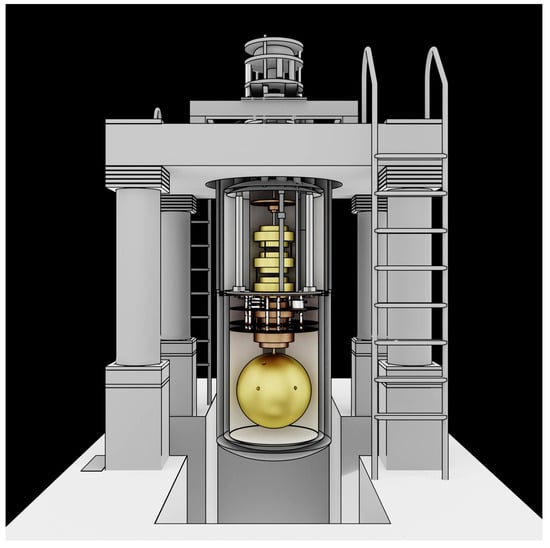
Figure 1. Schematics of the SCHENBERG gravitational wave detector prototype. The spherical antenna is suspended by a rod attached to its center through a hole. Nine small holes were drilled into its surface for transducer attachment. Source: The authors.

The geometric symmetry of the massive sphere that acts as a GW antenna in SCHENBERG is essential for its best performance. The transducers that detect the antenna’s subtle motions are also distributed throughout the surface following the symmetrical shape of a truncated icosahedron [10]. They allow for the monitoring of the sphere’s five quadrupole modes that mechanically vibrate in the presence of a GW within the band of 3.15–3.26 kHz. SCHENBERG’s antenna is made of a CuAl (6%) alloy with a high mechanical quality factor when operating at low temperatures (∼4 K), weighing 1124 kg, with a radius of 32.33 cm. Details on the transducers, suspension system, and cryogenics can be found in the literature [11,12,13,14].

In this work, we investigate how the quadrupole frequencies of SCHENBERG sphere are influenced by the breaking of symmetry due to many factors: the hole for the suspension, the presence of gravity, and the microstructure of the sphere caused by the casting process. The goal is to find the correct bandwidth of the sphere quadrupole modes. In Section 2, the SCHENBERG sensitivity curve is explained. In Section 3, a summary on the interaction of GW with matter is presented. In Section 4, the symmetry breaking processes in the spherical antenna is presented. In Section 5, the FEM modeling of the spherical antenna in the presence of gravity is presented. In Section 6, a new perspective on the importance of the sphere’s microstructure is presented. In Section 7, an FEM model for the inhomogeneous sphere and its consequences is presented. Finally, in Section 8, we present our conclusions.

2. SCHENBERG’s Sensitivity Curve with Six Transducers

The solutions of the equation of motion for the displacement vector field of a solid spherical body subjected to an external force density and to the boundary condition of zero tension at its surface are the natural modes of the sphere. The displacement vector field describes the displacements of each element of the volume of the body subjected to an external force, which is, in this case, the gravitational acceleration due the gravitational wave. This involves two families of solutions: toroidal modes and spheroidal modes [15]. Toroidal modes do not generate radial motion, and SCHENBERG’s transducers are not sensitive to them, nor are these modes excited by GW. On the other hand, in general relativity, GW are quadrupolar, implying that only the five spheroidal quadrupolar modes of the antenna couple to a GW, allowing for the detection of the latter through the antenna’s mechanical response. For SCHENBERG’s physical characteristics, these five degenerate modes have a frequency of around 3.2 kHz.

The mechanical oscillations of SCHENBERG’s antenna are monitored by transducers positioned on its surface. Johnson and Merkowitz [16] showed how the output of six transducers distributed on the antenna’s surface could be mathematically related to the quadrupolar modes of the sphere. This relation allows for the determination of the parameters that characterize the incident GW from the measured data [4,17].

SCHENBERG had nine transducers attached to the surface of its antenna, six of which were distributed according to the truncated icosahedron configuration proposed by Johnson and Merkowitz [10]. The other three transducers performed auxiliary functions [13,14,18,19]. Those six transducers introduced new resonant frequencies to the detector and enlarged its band. The mathematical model of the detector when the six transducers are added show the presence of eleven modes: five from the antenna and six from the transducers [7].

In general, a complex detector like SCHENBERG is subject to various kinds of noise that were extensively studied in order to be minimized and increase the detector’s sensitivity [7]. The noises that significantly influenced the detector’s performance were thermal noise (from the antenna and the suspension system), noises from the dilution refrigerator and the mixing chamber, and external noises.

One method to determine the influence of the noise on the detector’s sensitivity is to calculate its GW-equivalent signal, i.e., to determine its intensity as if it was a gravitational wave hitting the detector [7]. Figure 2 shows a typical sensitivity curve for SCHENBERG in the presence of noise, with six transducers distributed according to the truncated icosahedron geometry in one of the antenna’s hemispheres [7]. The curve basically shows the energy spectrum in the output of the detector (in a convenient unit) as a function of the frequency when no gravitational wave is present, thus presenting how the coupled system behaves in the frequency domain in view of its physical characteristics. Particularly important for this study are the three lowest dips of this figure, between 3080 Hz and 3170 Hz. They indicate the frequencies of the antenna’s quadrupole modes for a perfect sphere coupled with the transducer, which we will discuss in detail below.

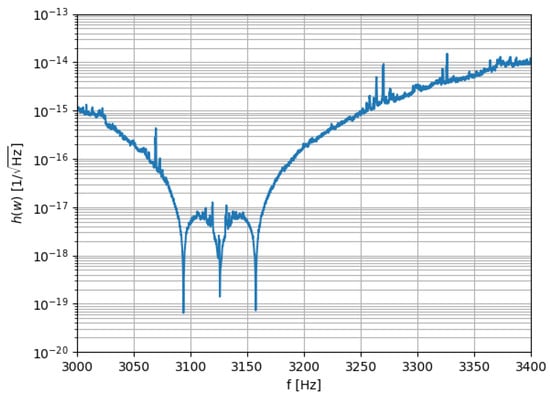
Figure 2. Example of a theoretical sensitivity curve of SCHENBERG’s antenna coupled to six transducers attached to its surface in the presence of noise. The three lowest dips shown are related to the antenna’s quadrupole modes. Source: [7].

3. Summary on the Interaction of GW with Matter

A GW generates a tidal force on any matter located at time t and at position x [20]. This tidal force density is given by

$$f_i^{GW}(x,t)={\displaystyle \frac{1}{2}}\rho {\ddot{h}}_{ij}\left(t\right)x_j,$$

(1)

where a sum over repeated indices is implied and $i,j=1,2,3$. The letter $\rho$ represents the mass density of the matter, and $\ddot{h}$ is the second time derivative of the GW amplitude, $h_{ij}$.

Since SCHENBERG’S antenna should resonate with GW with frequencies of about 3 kHz, the wavelength of such detectable GW is about 100 km since in GR, these waves are expected to travel at the speed of light in a vacuum (c). Therefore, the antenna can be considered small enough relative to the wave’s wavelength to allow for its use in the calculations of the value of $h_{ij}\left(t\right)$ only at the center of the sphere.

The solution of (1) introduces spherical harmonics, from which only quadrupole modes remain for GW given by GR [21]. This simplification allows for the modeling of the action of a gravitational wave on SCHENBERG’S antenna, both analytically and computationally, for many cases of interest.

We now focus on the mechanical response of SCHENBERG to external forces, which includes forces due to GW. The equation of motion for the displacement vector field $u(x,t)$ of a solid subjected to an external force density $f(x,t)$ is given by [22]

$$\rho {\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}-({\lambda }_L+{\mu }_L)\nabla \left(\nabla ·u\right)-{\mu }_L{\nabla }^{2}u=f,$$

(2)

where ${\lambda }_L$ and ${\mu }_L$ are, respectively, the tangential and volumetric Lamé coefficients of the material, with initial conditions $u(x,0)=0$ and $\dot{u}(x,0)=0$. This problem has been solved in the literature [23]. In particular, in the description of the motion of the surface of an uncoupled sphere (free of tension on its surface), spheroidal modes are found to be the relevant ones considering the kind of transducers used in SCHENBERG, which detect radial motions only. For this reason, these are the modes used in this work to monitor the sphere’s motion.

The solution of (2) is obtained, expanding the displacement vector $u(x,t)$ in a series of the eigenfunctions ${\Psi }_N\left(x\right)$ of the equation

$$({\lambda }_L+{\mu }_L)\nabla \left(\nabla ·\Psi \left(x\right)\right)+{\mu }_L{\nabla }^2\Psi \left(x\right)=-{\rho }^2\Psi \left(x\right)$$

(3)

subjected to the boundary condition of tension free at the surface of the sphere [20].

$${\lambda }_L\left(\nabla ·u\right)\widehat{r}+2{\mu }_L\left(\widehat{r}·\nabla \right)u+{\mu }_L\widehat{r}\times \left(\nabla \times u\right)=0.$$

(4)

The displacement vector field can be expanded as

$$u(x,t)=\sum _N{a}_N\left(t\right){\Psi }_N\left(x\right),$$

(5)

where N is a set of indices, $a_N\left(t\right)$ is the time-dependent mode amplitude, and ${\Psi }_N$ obeys the normalization condition.

$${\int }_V\rho \left(x\right){\Psi }_N\left(x\right)·{\Psi }_{N^{\prime }}\left(x\right)d^{3}x=M_S{\delta }_{N{N}^{\prime }}.$$

(6)

The integration is over the volume V of the sphere. After substituting (3) and (5) in (2), multiplying by ${\Psi }_{N^{\prime }}$, and integrating over the volume of the sphere using (6), we obtain

$$M_S{\ddot{a}}_N\left(t\right)+{\kappa }_S{a}_N\left(t\right)={\int }_V{\Psi }_N\left(x\right)·f(x,t)d^{3}x$$

(7)

with ${\kappa }_S$ being the elastic constant.

At this point, it is convenient to introduce a damping term in Equation (7)

$${\int }_V{\Psi }_N\left(x\right)·f(x,t)d^{3}x,$$

(8)

where $C_S=w_N/Q_N$, $w_N$ is the natural angular frequency of mode N, and $Q_N$ is the mechanical quality factor Q for mode N.

The physical parameters of SCHENBERG are listed in Table 1, following the experimental setup and results given by Aguiar et al. [24] and the other references presented in this table.

Table 1. Parameters of the Schenberg antenna. Source: Adapted from [7].

Description	Value	Method
3 Quadrupole frequencies at 2 K	3172.485, 3213.623, 3222.900 ± 0.001 Hz	measured
2 Quadrupole frequencies at 2 K	3183, 3240 ± 0.5 Hz	measured
Quadrupole frequencies at 300 K	3045, 3056, 3086, 3095, 3102 ± $0.5\mathrm{Hz}$	measured
Monopole frequency at 300 K	$f_{10}=6443.0\pm 0.5\mathrm{Hz}$	measured
Antenna’s radius at 300 K	$R_0=0.3233\mathrm{m}$	measured
Antenna mass	$M_S=1124\mathrm{kg}$	measured
Antenna’s density at 300 K	$\rho =7938.523\pm 19\mathrm{kg}/{\mathrm{m}}^3$	measured
Transducer first stage mass	$M_1=59.7100\pm 0.5\mathrm{mg}$	measured
Transducer second stage mass	$M_2=12.0\pm 0.5\mathrm{mg}$	measured
Monopole frequency at 4 K	$f_{10}=6713.42\mathrm{Hz}$	calculated
Mean quadrupole frequency at 4 K	${\overline{f}}_{12}=3205.94\mathrm{Hz}$	calculated
Longitudinal sound velocity at 4 K	$c_l=4937.6\mathrm{m}/\mathrm{s}$	[7]
Transversal sound velocity at 4 K	$c_t=2448.2\mathrm{m}/\mathrm{s}$	[7]
Linear therm. expans. coef at 273.15 K	${\alpha }_0=1.75\times {10}^{-5}{\mathrm{K}}^{-1}$	[25]
Weight average of CuAl6 Debye temp.	${\Theta }_D=319.74\mathrm{K}$	[26]
Weight average of CuAl6 Fermi temp.	$T_F=84449.46\mathrm{K}$	[26]
Weight average CuAl6 Gruneisen coef.	$\gamma =1.912$	[27]
Sound velocities ratio	$r=2.016847$	[7]
Poisson ratio	$\sigma =0.337010$	[7]
Sphere radius as 4 K	$R=0.32213\mathrm{m}$	[7]
Sphere density at 4 K	$\rho =8025.04\mathrm{kg}/{\mathrm{m}}^3$	calculated
Volumetric Lamé coefficient	${\mu }_L=48.100\mathrm{GPa}$	[7]
Tangential Lamé coefficient	${\lambda }_L=99.455\mathrm{GPa}$	[7]
Young’s modulus	$E=128.621\mathrm{GPa}$	[7]
Bulk modulus	$B=131.522\mathrm{GPa}$	[7]
Chi factor	$\chi =-0.6004$	[7]
Radial component factor at $r=R$	$\alpha =2.88345$; $\alpha =A_{12}\left(R\right)$
Antenna equivalent mass	$M_{\mathrm{eq}}=340\mathrm{kg}$; $M_{\mathrm{eq}}=\frac{4\pi }{5{\alpha }^2}{M}_S$
Antenna effective mass	$M_{\mathrm{eff}}=283\mathrm{kg}$; $M_{\mathrm{eff}}=\frac{5}{6}{M}_{\mathrm{eq}}$
Transducer amplification factor	$\mathrm{amp}=$ 4740; $\mathrm{amp}=\sqrt{\frac{M_{\mathrm{eff}}}{M_2}}$

4. Symmetry Breaking in the Spherical Antenna

Although SCHENBERG’s antenna was designed with a symmetric, very-well-studied geometry (the sphere), the need for suspension resulted in changes in the geometry. One important modification was the drilling of a hole through one axis of the sphere to host the suspension at its center, which caused the antenna to no longer be a perfect sphere, and resulted in more complex calculations.

For a perfect sphere, the frequencies of the five quadrupole vibrational modes are degenerate, all having the same value of ∼3.2 KHz. Regarding mode vibration, one of the modes ($l_{20}$) is called prolate–oblate because its vibration causes the sphere to change from a prolate to an oblate shape. The other four modes are rotations of a motion in which the poles that move the most in the prolate–oblate mode stay still. These four modes resemble a tangerine with four segments, where two opposite segments vibrate in phase, while the other two segments vibrate in phase opposition. Two of these modes ($l_{21}$ and $l_{22}$) differ only by a 45-degree rotation relative to the poles. The other two modes ($l_{23}$ and $l_{24}$) behave similarly, but the axis through the poles is rotated by 45 degrees in one direction plus another 45 degrees in a different direction. These modes are displayed in Figure 3.

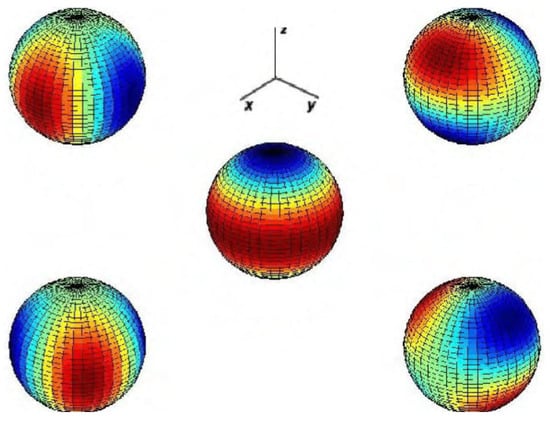
Figure 3. Vibrations of the quadrupole modes of the spherical antenna. The red areas vibrate in phase opposition to the blue areas. On the right is mode $l_{20}$ (prolate–oblate). On the left is mode $l_{21}$, and a 45-degree rotation of it relative to the vertical axis yields mode $l_{22}$. In the middle is mode $l_{23}$, and a 45-degree rotation of it relative to the horizontal axis yields mode $l_{24}$. The colors represents vibrations on the sphere surface, red and blue represents opposite radial movements. Source: From the authors.

As the hole is machined in the sphere, there is a break in the spherical symmetry. Suppose the hole was machined in the direction of the two poles that vibrate in the prolate–oblate mode. It breaks the spherical symmetry, and the prolate–oblate mode has its frequency changed in a way that is different from the frequency change in modes $l_{21}$ and $l_{22}$, which also differs from modes $l_{23}$ and $l_{24}$. The five modes shift from a quintuplet configuration to a configuration with two doublets and a singlet.

The spherical symmetry is also broken by machining nine small holes to house the transducers in the upper hemisphere. The study and evaluation of the new frequencies is no longer analytical, and it is performed through simulations with finite element modeling (FEM); in this work, the FEM program used was SolidWorks and Ansys SpaceClaim^TM. Using this method, several sets of definitions can be adopted, like the mesh size or the presence of gravity, normally affecting the results obtained and having a great impact on the simulation running time. The two programs obtained the same results for the sphere quadrupole modes of a homogeneous sphere, not a symmetrical sphere.

Using FEM SolidWorks and Ansys SpaceClaim^TM, a simulation considering all the details of a sphere in the absence and presence of gravity was performed, while in an experiment with the sphere [24], the quadrupole frequencies were identified. As can be seen in Table 2, a significant difference in the bandwidth of the quadrupole modes was found between both results: the simulation yielded a bandwidth of 35 Hz, while the experiment yielded a bandwidth of 67.5 Hz.

Table 2. The first column displays the frequencies obtained experimentally, with the detector cooled down to 5K; the second column displays the frequencies obtained by simulation without gravity; the third column shows the simulated frequencies considering the effect of gravity; and in the fourth columnm a twist of 5 degrees in the direction of gravity was assumed in the simulation to include some misalignment.

Experimental Frequency	Frequencies	Frequencies (Gravity)	Frequency (Gravity and Twist)
3172.5 Hz [24]	3173.6 Hz	3183.2 Hz	3183.2 Hz
3183.0 Hz [24]	3173.7 Hz	3183.3 Hz	3183.3 Hz
3213.6 Hz [24]	3193.4 Hz	3200.3 Hz	3200.3 Hz
3222.0 Hz [24]	3193.4 Hz	3200.4 Hz	3200.4 Hz
3240.0 Hz [24]	3208.6 Hz	3212.4 Hz	3212.4 Hz
Band 67.5 Hz	Band 35.0 Hz	Band 29.2 Hz	Band 29.2 Hz

Also, a small twist in gravity was tested (5 degrees from the vertical direction) to simulate a misalignment in the sphere suspension, but again, the results do not reproduced the measured quadrupole frequencies.

5. FEM Model of the Spherical Antenna in the Presence of Gravity

In a study carried out previously [28], the GW antenna was isolated from the rest of the experiment and free from the influence of gravity, which greatly simplified the problem and required a reasonable computer processing time.

In this work, gravity is taken into account in the simulation to try and explain the quadrupole frequencies previously measured in the detector. This is done also by introducing a constraint in the location where the sphere is connected to the suspension [12]. Also, a small misalignment in the suspension mounting is included by considering gravity inclined by a small angle. This work was possible due the interdisciplinary research group involved.

In order to make the sphere a GW detector, nine holes were drilled into its surface to house the transducers, six of which would specifically monitor the quadrupolar modes, positioned according to a half-dodecahedron distribution. Another transducer would act as a calibration device, and two others would monitor monopolar vibrations (to aid in vetoing spurious signals). All these holes were included in the simulation, as well as an axial hole that contains, in its center, a conical shape surface where the suspension central rod is connected. Figure 4 displays the model containing the surface holes and the central conical surface where the sphere is connected to the suspension rod.

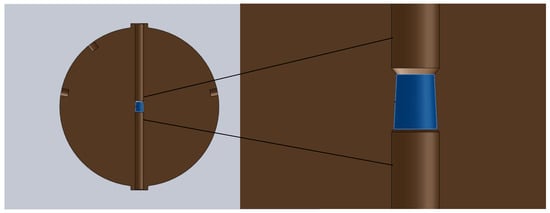
Figure 4. Antenna modeling used in the simulations to obtain the frequency modes with and without gravity. Source: The authors.

The study of the effect of gravity on SCHENBERG’s quadrupolar frequencies starts with a static analysis of the effect of gravity on its sphere. The gravitational force is applied vertically, and the displacements caused by it are identified. In Figure 5, the result of the static simulation applying gravity to the sphere can be seen, including the iso-displacements of the spherical antenna due to its own weight. Iso-displacements belong to surfaces where the displacements have the same magnitude. We found that the surface of the sphere drops by 0.8977 micrometers under the influence of gravity.

Figure 5. Results of the simulations showing the surfaces where the displacements have the same magnitude (iso-displacements). The final result is the sphere dropping 0.8977 micrometers. Source: The authors.

The same procedure was used to evaluate if some misalignment in the mounting of the suspension could be responsible for the scattering of the antenna mode frequencies. For this evaluation, the direction of gravity was tilted by 5 degrees, which was the maximum angle that could be attained in the mounting of the suspension without being detected in the mounting. This emulated a misalignment in the mounting.

We found (see Table 2) that the effect of gravity on the quadrupole frequencies was to increase the frequencies as a whole while reducing the bandwidth. We also noted that the increase in frequency was smaller the higher the doublet frequency. The absolute value of the frequencies is not important as it can be caused by differences in the material properties, but the decrease found in this case for the bandwidth does not solve the problem of the mismatch between the theoretical value of the bandwidth and the measured one.

Furthermore, no frequency change due to the tilted gravity was obtained. Therefore, we found that no change in frequency due to small misalignment problems should be expected in actual detectors.

In both cases where gravity was included in the simulations, it is possible that the change in the antenna’s shape due to gravity might be responsible for the narrower bandwidth. Indeed, gravity is likely to make the sphere more prolate in the vertical direction, possibly favoring the oscillations of the quadrupole modes towards a dominant frequency. As a consequence of this part of our study, it seems that the gravitational pull is not responsible for the wider bandwidth found in the real detector. Therefore, we proceeded to investigate another aspect, as follows.

The the drilling of the central hole, the two collars (in the top and in the bottom), the holes for the transducers, and the presence of gravity breaks the symmetry of the sphere, leaving only the rotational symmetry in $\phi$ untouched. This breaking of symmetry is not enough to explain the bandwidth. Therefore, a new approach was applied to break the remaining symmetry (rotation around $\phi$), as is explained in the next section.

6. A New Perspective: The Importance of the Sphere’s Microstructure

As the bandwidth of the measured frequencies seemed to have no explanation in terms of the gravitational pull, we hypothesized problems resulting from the FEM simulation program (two different programs were used, yielding the same results) and problems due to the microstructure of the sphere (the quality factor of the sphere was too high to for allow any large discontinuities in the sphere macrostructure). However, we suspect that the main cause could lie in the microstructure.

Figure 6 shows the ingot from which SCHENBERG’s sphere was machined. The sphere was produced from the lower part of the ingot as the mechanical quality factor of this part should be higher since the defects in the metal should move to the upper part during solidification when the ingot was casted.

Figure 6. Ingot from which the sphere was machined. Image courtesy of Odylio D. Aguiar.

During casting, the ingot solidified faster on the sides and on the bottom. When the ingot was ready, the sphere was machined from its lower part in the region of the circle in Figure 7. It is important to note that because of the need for a high mechanical quality factor, the ingot was not homogenized.

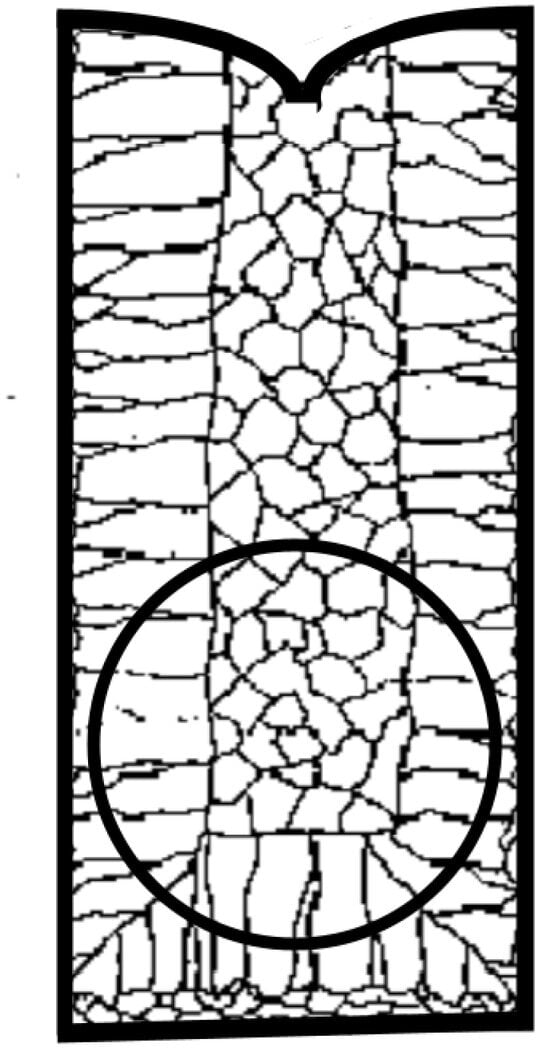
Figure 7. Representation of the possible internal microstructure of the ingot and the region from which the sphere was machined. Source: The authors.

The regions of the ingot on its side and on its bottom, which solidify faster, are known in the literature to become harder depending on the speed of the cooling process. Figure 8 shows an example of how the Brinell Hardness changes with the cooling speed for Cu Al the alloy. Equation (9) shows how the hardness of the material changes with the cooling speed [29]. According to [29], the hardness and the Young’s modulus of the CuAl alloy can vary by 20%.

$$HB=187.38F^{0.016}$$

(9)

where HB is the Brinell Hardness and F is the cooling speed in K/s.

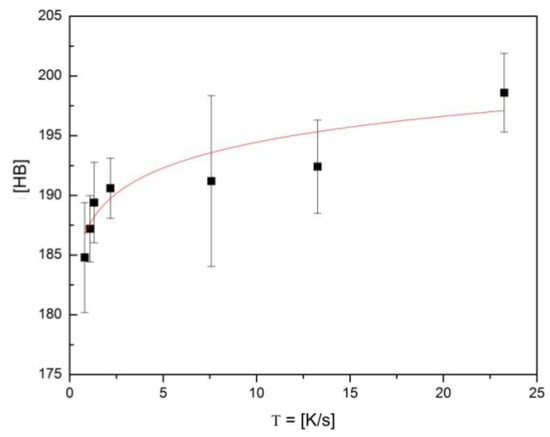
Figure 8. Graphic of the Brinell hardness of CuAl as a function of the cooling speed. Source: [29].

7. The FEM Model for the Inhomogeneous Sphere

Given this new physical model that we devised for the sphere’s internal structure, the idea behind the FEM model was to separate the sphere’s volume in two parts, in which the external one was made of a material 20% harder than that of the internal part, as seen in Figure 9. To allow for a small difference in the cooling distribution according to the directions, a mismatch of 5 cm was created for the vertical symmetry axis of the internal part relative to the vertical symmetry axis of the external part. This mismatch is essential to break the supposes a duplet from modes $l_{21}$ and $l_{2s}$; this mismatch will break it, as appears in the measurements.

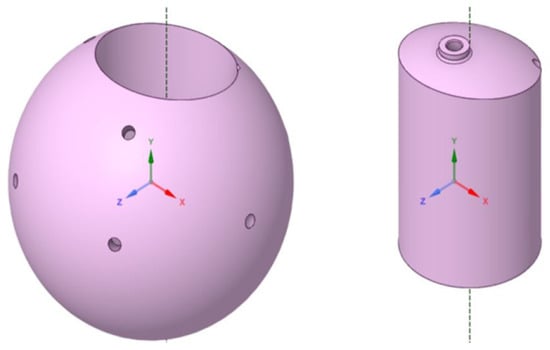
Figure 9. Drawing of the simulated antenna model, showing its two parts. The spherical, external part was considered harder than the internal, cylindrical part by 20%. Source: The authors.

Using this model, three different simulations were performed as there is no access to the actual internal structure of the material. The idea was to perform the three simulations and to check if any of the results yielded the measured bandwidth. The dimensions used in each case are presented in Table 3. The cylinder’s diameter was kept constant as the microstructure model of Figure 7 indicates that this diameter is central enough to basically not change in the casting.

Table 3. For the model displayed in Figure 9, this table presents the three simulated cases, called Sphere I, Sphere II and Sphere III. The dimensions shown in columns 2 and 3 refer to the diameter of the internal part and the bottom thickness of the external part of the model that were assumed in each case.

	Internal Part’s Diameter (mm)	Bottom Thickness (mm)
Sphere I	325	162.5
Sphere II	325	200
Sphere III	325	100

Once the dimensions were chosen for each case, then, the Young’s modulus of the parts were determined, aiming at a total variation from 20% to 30%, as argued above. The values that yielded the best bandwidth results for each case are presented in Table 4. The Sphere II case demanded a larger variation between the Young’s modulus of each part in order to yield an interesting bandwidth.

Table 4. For the model displayed in Figure 9, this table presents the three simulated cases (Sphere I, Sphere II and Sphere III). The letter E represents the Young’s modulus for the material in each part of the model, shown in columns 2 and 3. Column 4 shows the approximate variations of E relative to the Young’s modulus of the antenna (128.621 GPa; see Table 1), the plus sign refers to the external part, and the minus signal refers to the internal one.

	E of the External Part (GPa)	E of Internal Part (GPa)	Variation (%)
Sphere I	143	117	±10
Sphere II	149	110	±15
Sphere III	143	117	±10

Figure 10, Figure 11 and Figure 12 show the results of the FEM simulations. In Figure 10, the vibrational shapes of the five quadrupolar modes are shown with their respective frequencies for the Sphere I case, which has a bottom thickness of intermediate width, chosen to be equal to the radius of the internal cylinder for symmetry. Also, the internal part is softer than the external one by $20\%$. The bandwidth obtained from this simulation was 52.5 Hz, a value 22.2% smaller than the experimental value presented in Table 2 (67.5 Hz) but notably better than the bandwidth of 35.0 Hz obtained from the simulation of a homogeneous sphere. The antenna’s vibrations are clearly less symmetric than those of the homogeneous sphere, as shown in Figure 3.

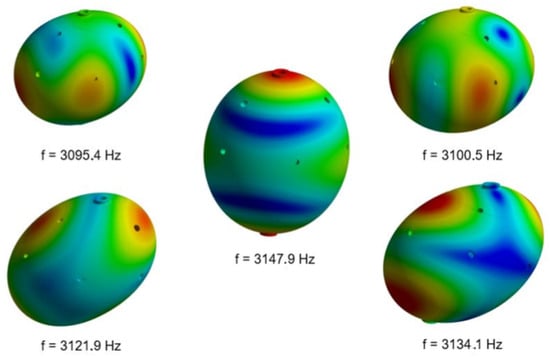
Figure 10. For the Sphere I case (with an intermediate bottom width of the external part and a 20% difference in the Young’s modulus), these are the mode shapes, with their respective frequencies and a bandwidth of 52.5 Hz. The colors represents radials oscillations of the surface, being red the opposite of blue. Source: The authors.

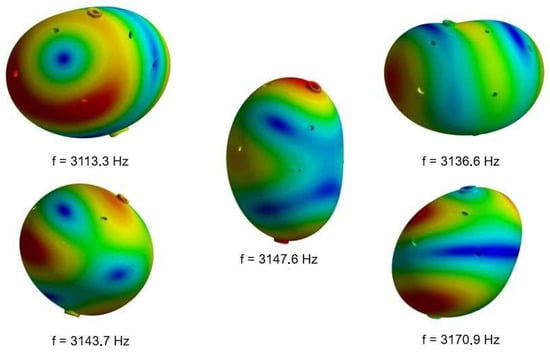
Figure 11. For the Sphere II case (with the largest bottom width of the external part and a 30% difference in the Young’s modulus), these are the mode shapes, with their respective frequencies and a bandwidth of 57.6 Hz. The colors represents radials oscillations of the surface, being red the opposite of blue. Source: The authors.

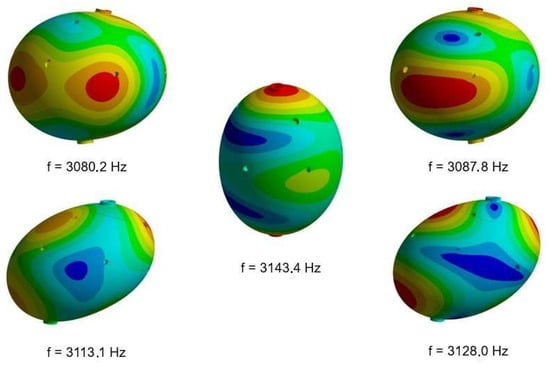
Figure 12. For the Sphere III case (with the narrowest bottom width of the external part and a 20% difference in the Young’s modulus), these are the mode shapes, with their respective frequencies and a bandwidth of 63.2 Hz. The colors represents radials oscillations of the surface, being red the opposite of blue. Source: The authors.

Figure 11 shows the vibrational shapes and their respective frequencies for the Sphere II case, which has the widest bottom thickness. The internal part is even softer than the external one (by 30%) compared to the Sphere I case. The bandwidth obtained from this simulation was 57.6 Hz, 14.7% smaller than the experimental one (67.5 Hz), and a better result than the bandwidth of the homogeneous sphere. The antenna’s vibrations are notably less symmetric compared to those of the homogeneous sphere, shown in Figure 3. This result is better but as the difference in the Young’s modulus is too big, another simulation set up was constructed.

Figure 12 shows the vibrational shapes and their respective frequencies for the Sphere III case, which has the narrowest bottom thickness. The relationships between the Young’s modulus of each part are the same as those in the Sphere I case. The bandwidth obtained from this simulation was 63.2 Hz, a value smaller than the experimental one by ∼6%, and a much better result than the bandwidth of the homogeneous sphere. The antenna’s vibrations are less symmetric compared to those of the homogeneous sphere, as shown in Figure 3.

Table 5 summarizes the results for these bandwidths.

Table 5. This table summarizes the results for the bandwidths.

	Bandwidth (Hz)
Sphere I	$52.5$
Sphere II	$57.5$
Sphere III	$63.2$

8. Conclusions

In this work, we analyzed the spherical, resonant-mass gravitational wave antenna of the SCHENBERG detector under new physical circumstances, i.e., in the presence of gravity (with and without suspension tilt) and considering the effects of the material microstructure on the antenna’s quadrupole mode frequencies. We accomplished these investigations by simulating the antenna using FEM.

When analyzing the effect of the action of gravity on the frequencies of the quadrupole modes of SCHENBERG’s antenna, an increase in the frequency values was noted, as well as a reduction in its bandwidth relative to the free sphere case. It was also noted that the increase in frequency was larger for doublets with lower frequency. This was an interesting result which, however, could not explain the experimental bandwidth. It confirmed numerically, on the other hand, that the effect of Earth’s gravitational pull on the antenna is not expected to significantly influence the detector’s signal.

Through an unprecedented analysis of the antenna’s microstructure resulting from the casting process, we created an original numerical model to be applied in the FEM study of three cases. The cases also included different hardness values throughout the sphere’s volume. The best bandwidth found among these cases was 63.5 Hz (Sphere III), the closest to the measured bandwidth of 67.5 Hz. This case involved an external part harder than the internal part and with a relatively thin bottom.

On the other hand, it is possible that more accurate measurements of the detector bandwidth could result in a narrower bandwidth for SCHENBERG’s quadrupole frequencies. In this case, the Sphere III model would be even more precise in describing the antenna’s physical model. Consequently, better theoretical models could be developed in regard to GW characterization from SCHENBERG’s data.

The simulations performed in this research show that the microstructure of the metal that constitutes the spherical antenna plays a significant role in the determination of the quadrupole modes’ bandwidth of the SCHENBERG GW detector. This microstructure is, in general, not symmetrically distributed when the antenna is casted, a feature that enhances its influence on the detector’s performance.

In the continuation of this work, all the quadrupole frequencies will be analyzed in detail to obtain a better description of the system. In the future, it is possible that the analysis of the vibrational frequencies can be used to identify the internal microstructure.