Abstract
Patterned fabrics are characterized by strong periodic and symmetric structures, and defect detection in such materials is essentially the task of identifying local disruptions of global texture symmetry. Conventional low-rank decomposition methods separate defect-free regions as low-rank and defects as sparse components, yet singular value decomposition (SVD)-based formulations inevitably lose structural details, hindering faithful recovery of symmetric background patterns. Autoencoder (AE)-based reconstruction provides nonlinear modeling capacity but tends to over-reconstruct defective areas, thereby reducing the separability between anomalies and symmetric textures. To address these challenges, this study proposes WOT-AE (Weighted Optimal Transport Autoencoder), a unified framework that exploits the inherent symmetry of patterned fabrics for robust defect detection. The framework integrates three key components: (1) AE-based low-rank modeling, which replaces SVD to preserve fine-grained repetitive patterns; (2) weighted sparse isolation guided by pixel-level priors, which suppresses false positives in symmetric but defect-free regions; and (3) optimal transport alignment in the encoder feature space, which enforces distributional consistency of symmetric textures while allowing deviations caused by asymmetric defects. Through extensive experiments on benchmark patterned fabric datasets, WOT-AE demonstrates superior performance over six state-of-the-art methods, achieving more accurate detection of symmetry-breaking defects with improved robustness.
1. Introduction
Fabric defect detection is an essential task in textile quality control, as surface imperfections such as broken yarns, stains, or holes can significantly reduce the usability and market value of products. Manual inspection is still widely practiced in the industry, yet it is inefficient, subjective, and error-prone. Automatic inspection [1] has attracted increasing attention, but patterned fabrics (shown in Figure 1) remain challenging due to their highly repetitive background structures and the subtle differences between true defects and normal textures.

Figure 1.
Samples of patterned fabrics: (a) star pattern, (b) dot pattern, and (c) box pattern.
Several approaches have been investigated for this task. Traditional methods based on handcrafted features, frequency analysis, or filtering often fail to distinguish defects from repetitive motifs under varying illumination [2,3,4]. Low-rank decomposition has emerged as a principled alternative, representing defect-free regions as low-rank components and defects as sparse anomalies [5,6,7]. Nevertheless, SVD-based low-rank approximation discards high-frequency weave patterns, making the reconstructed background suboptimal. At the same time, sparsity modeling alone often treats normal repetitive textures as anomalies, leading to high false-positive rates [5,7]. Deep autoencoder (AE)-based reconstruction alleviates the problem of information loss by capturing nonlinear fabric structures [8,9,10], but its strong reconstruction capacity tends to overfit, frequently reconstructing defective regions along with the background. Nonetheless, conventional AEs are typically trained with mixed data and may absorb defective regions into the background, reducing anomaly separability [8,9,10].
In contrast, the proposed framework leverages the fact that defects correspond to local disruptions of global textile symmetry [11]. To capture this property, the autoencoder [12,13,14] is trained exclusively on defect-free samples, enabling it to learn the intrinsic periodic and symmetric structures of fabrics. When defective samples are passed through the trained model, regions that break the learned symmetry cannot be faithfully reconstructed and thus emerge in the residual map as anomalies.
These observations motivate a decomposition framework that explicitly models both structured backgrounds and sparse anomalies, a principle that has been widely applied in low-rank based methods [5,6,7,15,16]. Specifically, the observed image can be represented as the sum of a background term and a defect term, but the decomposition must address three critical challenges: (1) recovering periodic and structured backgrounds without SVD-induced information loss [5,6]; (2) isolating defects while suppressing false positives in repetitive but defect-free regions [7,15,16]; and (3) preventing autoencoders from absorbing defective patterns into the reconstructed background [8,10,17,18].
Although several AE-based and OT-based methods have been explored for fabric defect detection, most approaches either reconstruct defects together with normal regions or perform global feature alignment that blurs defect boundaries. To address these limitations, this study develops WOT-AE, a unified decomposition framework combining AE-based low-rank modeling, prior-weighted sparsity, and selective OT alignment.
To address these challenges, a unified framework termed WOT-AE (Weighted Optimal Transport Autoencoder) was developed. The framework consists of three complementary modules. First, an AE-based low-rank modeling module replaces SVD, thereby preserving fine-grained textile patterns while suppressing noise. Second, a weighted sparse isolation mechanism introduces pixel-level priors derived from reconstruction errors, which penalize clean repetitive regions more heavily while preserving suspected defective regions. Third, an optimal transport (OT) alignment module enforces feature-level consistency between the input and reconstruction only in defect-free areas while allowing deviations in defective regions to remain distinguishable. The three modules are integrated into a joint objective function and optimized alternately, forming an efficient and scalable framework for patterned fabric defect detection.
The main contributions of this study are summarized as follows:
- Unified decomposition framework. We propose WOT-AE (Weighted Optimal Transport Autoencoder), a unified unsupervised framework that integrates AE-based low-rank modeling, prior-weighted sparsity, and selective OT alignment to jointly address information loss, false positives, and feature misalignment in patterned fabric defect detection.
- Learnable low-rank background modeling. The proposed AE replaces the SVD used in classical RPCA, capturing nonlinear periodic and symmetric structures while reducing reconstruction loss of fine textile patterns.
- Pixel-level prior-weighted sparsity. A reconstruction-derived prior adaptively weights the sparsity term to suppress false activations in clean repetitive areas and emphasize truly defective regions.
- Selective OT feature alignment. Entropy-regularized OT is applied only to defect-free regions in the encoder feature space, maintaining feature consistency for normal textures while preserving separability of anomalies.
- Comprehensive evaluation. Extensive experiments on three benchmark patterned textile datasets (Box, Star, and Dot) demonstrate that WOT-AE consistently outperforms nine state-of-the-art baselines in both accuracy and robustness while maintaining high computational efficiency.
2. Related Work
2.1. Fabric Defect Detection Methods
Fabric defect detection has been approached using traditional image processing techniques, matrix decomposition, and more recently deep learning models. Early methods employed handcrafted descriptors and frequency-domain analysis such as Gabor filters, Fourier transforms, and local binary patterns (LBPs) to highlight texture irregularities [19,20]. Although effective for simple fabrics, these approaches are highly sensitive to illumination and fail in the presence of complex periodic patterns, often leading to unstable detection performance.
Low-rank decomposition, inspired by robust principal component analysis (RPCA) [21], provides a more principled solution by modeling defect-free regions as low-rank components and defects as sparse anomalies. Principal Component Pursuit (PCP) and related variants have demonstrated promising results in separating structured backgrounds from irregular patterns [22,23,24,25]. However, singular value decomposition (SVD) used in these models discards fine-grained weaving details, making reconstructed backgrounds suboptimal, while sparsity without structural priors frequently misclassifies repetitive motifs as defects, resulting in false positives.
2.2. Autoencoder and Feature Alignment Approaches
With the emergence of deep learning, autoencoders (AEs) have been applied to fabric inspection by reconstructing defect-free textures and detecting anomalies through reconstruction errors. Convolutional AEs are more effective than linear decomposition in capturing nonlinear, repetitive structures, yet their strong reconstruction capacity often leads to defect over-reconstruction, reducing anomaly separability.
Recent studies have further explored autoencoder-based frameworks trained predominantly or exclusively on defect-free samples, aiming to improve the separability of normal and abnormal regions. Variants of stacked convolutional autoencoders and unsupervised reconstruction networks have been applied to fabric and surface defect detection, showing that residual maps derived from clean training can highlight anomalies more reliably [26,27]. Extensions have also investigated improvements in the latent space of autoencoders to enhance anomaly sensitivity and robustness [28]. While these methods demonstrate the advantage of leveraging defect-free training data, they still struggle with repetitive or symmetric textile structures, often leading to defect leakage into the reconstructed background. Moreover, none of them explicitly incorporate prior-guided sparsity or optimal transport-based alignment, leaving open the challenge of balancing sensitivity with robustness in highly structured textures.
To enhance robustness, feature alignment techniques have been widely explored in broader vision tasks [29,30,31]. Optimal transport (OT), in particular, provides a principled means of aligning feature distributions and has demonstrated success in domain adaptation and generative modeling [32,33,34,35]. In the context of fabric inspection, OT can ensure consistency of encoder features in defect-free regions while allowing defective ones to remain distinguishable. Nevertheless, the integration of OT into AE-based decomposition frameworks remains largely unexplored, as existing fabric detection methods typically rely on low-rank decomposition and sparsity modeling without OT [7,22,36]. Unlike these existing approaches [27,37,38,39], our proposed WOT-AE combines AE-based low-rank background modeling, pixel-level prior-weighted sparsity, and selective OT alignment into a unified unsupervised decomposition framework. This design allows WOT-AE to maintain interpretability and robustness under limited defect-free training data, overcoming the defect-leakage and global-alignment limitations of prior AE and OT methods.
Recently, Transformer architectures have been explored for anomaly detection due to their strong capability in modeling long-range dependencies. For instance, some studies introduce Vision Transformers (ViTs) [40,41,42] into industrial surface inspection and demonstrate promising results when trained or fine-tuned on large-scale datasets. These approaches highlight the potential of attention mechanisms in capturing global contextual information beyond local convolutional features. However, most Transformer-based solutions rely heavily on supervised training or large-scale pretraining, which limits their applicability in small-sample, unsupervised scenarios such as patterned fabric inspection. Our work differs by focusing on a lightweight autoencoder with prior-guided sparsity and OT alignment, designed to remain effective with only a few defect-free samples.
3. The Proposed WOT-AE Method
To the best of our knowledge, this is the first framework that unifies autoencoder-based low-rank modeling, prior-weighted sparsity, and optimal transport alignment into a decomposition scheme tailored for patterned fabric inspection. Unlike a simple aggregation of existing modules, each component was carefully adapted to address specific challenges: (i) AE-based low-rank modeling preserves fine-grained repetitive textures without the information loss inherent to SVD; (ii) the weighted sparsity term exploits pixel-level priors to suppress false positives in repetitive yet defect-free regions; (iii) OT alignment is constrained to defect-free areas using , ensuring that anomalies are not absorbed into the reconstructed background. This synergistic design distinguishes our method from prior works and provides a principled solution to the three key challenges of fabric defect detection: over-reconstruction, false positives, and background information loss.
3.1. Problem Definition and Challenges
Fabric defect detection can be formulated as the decomposition of an observed image into a background representation and a sparse anomaly map:
where A denotes the low-rank background corresponding to defect-free textures, and E encodes sparse defects.
Even when training with defect-free samples, introducing a sparse term E remains necessary, as real images inevitably contain noise, illumination variations, and reconstruction residuals. The sparse component provides a buffer to absorb these unpredictable deviations, allowing the autoencoder to concentrate on capturing the symmetric background structure.
This problem is non-trivial due to several challenges:
- Information loss in low-rank approximation. Traditional robust PCA methods rely on singular value decomposition (SVD), which inevitably discards fine-grained background details, leading to suboptimal reconstruction of defect-free textures.
- Over-reconstruction by autoencoders. Deep autoencoders (AEs) can model complex textures but often reconstruct defects as well, reducing defect–background separability.
- False positives in sparse modeling. Conventional -based sparsity regularization may mistakenly activate pixels in clean regions due to local variations or residual noise.
- Distributional inconsistency. Even when backgrounds are well reconstructed, misalignment between encoder features of input and reconstruction can cause background leakage into the sparse component.
To address these issues, we propose a novel decomposition framework (as shown in Figure 2) that integrates autoencoder-based low-rank modeling, weighted sparse defect isolation, and optimal transport alignment in the encoder feature space.
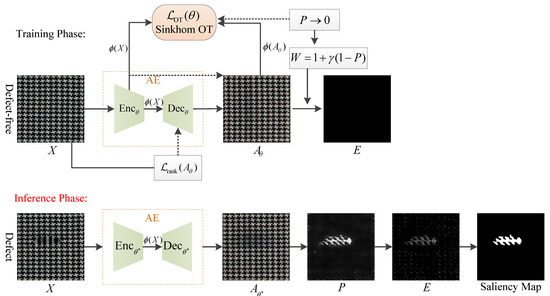
Figure 2.
Framework of the proposed WOT-AE model for patterned fabric defect detection. In the training phase, an autoencoder (AE) is trained on defect-free samples to reconstruct the low-rank background , and the reconstruction residual is used to generate a pixel-wise prior P. The prior further guides weighted sparse decomposition, while an optimal transport (OT) module aligns encoder features of input and reconstructed backgrounds to suppress residual errors in defect-free regions. In the inference phase, test images are decomposed into a clean background and sparse anomalies E, from which a saliency map is obtained to locate fabric defects.
3.2. Autoencoder-Based Low-Rank Modeling
Motivation. To overcome the information loss induced by SVD, we parameterized the low-rank background using an AE [9]. The bottleneck structure of AEs captures repetitive fabric patterns while suppressing noise.
Design. Let the encoder and decoder be parameterized by . The reconstructed background is the following:
Objective. Reconstruction consistency was enforced by the following:
To enhance regularity, we further applied a smooth rank surrogate on unfolded background matrices:
where denotes singular values, and avoids instability.
3.3. Weighted Sparse Defect Isolation
Motivation. Pure -regularization does not consider spatial structure and may lead to false positives in clean regions.
Design. We designed a pixel-level prior based on reconstruction differences:
where the operators and were computed over all pixels of the residual map for the current test image, so that P is scaled to the range .
This prior was used to weight the sparsity term:
where controls the balance. Intuitively, clean regions (low P) were heavily penalized to suppress false activations [6,22], while suspected defective regions (high P) were encouraged to remain sparse.
Remark on the prior in training vs. inference. Since only defect-free images were used during training, the reconstruction error was expected to be small, and the corresponding prior map approached zero almost everywhere. In this stage, the role of P is primarily to absorb minor reconstruction residuals or sensor noise, preventing the autoencoder from overfitting to such variations. During inference, however, defective images were provided as input. In regions that violate the learned symmetric structures, the reconstruction error becomes significant, resulting in high prior responses. Consequently, P highlights defects while remaining close to zero in background areas, enabling the weighted sparsity term to suppress false positives and isolate true anomalies.
3.4. Optimal Transport Feature Alignment
Motivation. Although AE reconstructions are effective, they tend to mistakenly reconstruct defect patterns as part of the background. To mitigate this, we enforced feature-level alignment between input and reconstructed backgrounds only in defect-free regions.
Design. Let and . These were reshaped into token sets , , where . The cost matrix is as follows:
To emphasize defect-free alignment, we defined probability weights from the prior:
Objective. The OT loss was computed as an entropy-regularized Wasserstein distance [34]:
This loss encourages encoder features of X and to align in defect-free regions while allowing discrepancies in defective ones, pushing anomalies into the sparse component. In essence, the OT module enforced strong feature-level alignment in defect-free regions while relaxing this constraint in defective ones, ensuring that true anomalies were not absorbed into the reconstructed background but instead remaiedn isolated in the sparse component.
3.5. Joint Objective
The overall loss integrates all modules:
During training on defect-free data, the sparse component E mainly captured random noise and reconstruction residuals, preventing the model from overfitting these variations. This design ensures that, during inference, genuine defects that strongly violate the learned symmetry were naturally isolated into the sparse channel.
Remark on the Noise Term. Unlike traditional RPCA frameworks that explicitly model Gaussian noise via an additional variable N, we omit the noise term here. The AE bottleneck naturally suppresses random noise, while OT alignment absorbs residual variations in defect-free regions. Ablation studies confirm that explicit noise modeling provides negligible benefit, so the simplified formulation is adopted.
3.6. Optimization Strategy
3.6.1. Training Phase
During training, only defect-free samples were used so that the autoencoder learns the intrinsic symmetric and repetitive background structures. The optimization was performed in an alternating manner between the sparse component E and the autoencoder parameters . Given a training image X, the background reconstruction is . The sparse component was updated in closed form via weighted soft-thresholding:
where and .
Subsequently, the autoencoder parameters were updated by minimizing
using backpropagation with the Adam optimizer [43]. The OT loss was approximated with Sinkhorn iterations (–10 steps). This alternating procedure enables the AE to focus on capturing low-rank symmetric patterns, while E absorbs noise and residual variations during training.
3.6.2. Inference Phase
Once the autoencoder parameters are learned from defect-free samples, inference proceeds in a feed-forward manner without iterative optimization. Given a test image X, the background was reconstructed, and a prior map was derived as
The sparse component was then obtained by a single weighted soft-thresholding update:
The resulting E serves as the defect map, highlighting regions that violate the learned symmetry while suppressing noise and repetitive clean patterns. This design ensures that inference is efficient and scalable for real-world fabric inspection, requiring only a single forward pass through the trained autoencoder and one closed-form sparse update.
Note that OT alignment was used only during training to enforce feature consistency. During inference, the model applied a single forward pass and sparse update without any OT iterations.
4. Results
4.1. Experimental Setup
4.1.1. Datasets
This study employs three patterned textile databases [44,45] provided by the Industrial Automation Research Laboratory, Department of Electrical and Electronic Engineering, Hong Kong (Figure 1). Each database (Dot-patterned, Box-patterned, and Star-patterned fabrics) consists of images with a spatial resolution of pixels. In total, 75 defect-free images are used to train the autoencoder for background reconstruction, while 81 defective images are reserved for performance evaluation. The defective samples cover six representative types of textile flaws: Broken End, Hole, Netting Multiple, Thick Bar, Thin Bar, and Knots. This experimental design closely reflects realistic industrial inspection settings, where defect-free samples are utilized for model learning, and defective ones serve as benchmarks for detection evaluation.
4.1.2. Implementation Details
All experiments were conducted on a workstation equipped with an NVIDIA RTX 3080Ti GPU (12 GB memory). The proposed WOT-AE framework was implemented in PyTorch 1.2.1 support.
In this study, a per-pattern training protocol is adopted. In total, 75 defect-free images are available, with 25 per database (Box, Star, Dot). The three patterns are trained independently. For each pattern, we use 20 defect-free images to train the autoencoder and 5 defect-free images for validation; all defective images (81 in total) are held out for testing only. Each fabric image has a spatial resolution of pixels, with a background pattern period smaller than 32 pixels. To ensure that each training sample contained multiple repetitions of the symmetric structure, images were divided into patches of size with a stride of 32. This resulted in 49 overlapping patches per image. With 20 defect-free training images, a total of 980 patches were obtained. To further enlarge the training set and improve robustness, standard symmetry-preserving data augmentation techniques were applied, including horizontal and vertical flipping as well as 90° rotations. This yielded several thousand effective training samples while maintaining the periodicity of fabric patterns.
The autoencoder backbone consists of nine convolutional layers in both encoder and decoder, with kernels and ReLU activations. Batch normalization was applied after each convolutional layer to stabilize training. The latent space dimension was set to 128 to balance compactness and representational capacity. We use the Adam optimizer with a maximum of 150 training epochs and an early-stopping patience of 15 epochs. The Sinkhorn algorithm for the OT loss runs for 10 iterations with a convergence tolerance of . All implementations are based on PyTorch 1.12.1.
Hyperparameters in the objective function were set as for weighted sparsity, for rank regularization, and for OT alignment. The Sinkhorn iterations in OT alignment were fixed at with a regularization parameter . The sparsity weighting factor was set to to balance false suppression and defect preservation.
Optimization was performed using the Adam optimizer with an initial learning rate of and weight decay of . The learning rate decayed by a factor of 0.1 after 50 epochs. The batch size was set to 16, and the maximum number of epochs was 150 with early stopping (patience of 15 epochs).
4.1.3. Evaluation Metrics
To comprehensively assess detection quality, we report pixel-wise classification metrics and curve-based criteria. Let TP, FP, TN, and FN denote the numbers of true positives, false positives, true negatives, and false negatives, respectively, obtained from the binarized defect map.
Basic metrics:
F-measure. We further report the F-measure to summarize the trade-off between precision and recall. The standard score [46] (harmonic mean) is
More generally, the score weights recall times as much as precision:
where reduces to . Unless otherwise specified, we report at the default operating point; we also set to emphasize precision in diagnostic experiments, which is called Weighted F-measure (WF) [47].
Curve-based criteria. Receiver Operating Characteristic (ROC) and Precision–Recall (PR) curves are plotted by sweeping the decision threshold on the continuous defect map. The Area Under the Curve (AUC) is used as a threshold-independent summary; higher AUC indicates stronger discriminative ability across operating points.
4.1.4. Comparative Methods
To evaluate the effectiveness of the proposed WOT-AE framework, we compared it with representative methods from two categories: (1) an autoencoder-based method, AE-SSIM, and (2) a series of low-rank decomposition methods, including PN-RPCA, G-NLR, T-LRSD, S-LRSD, and AS-LRSD. Together, these approaches encompass both deep learning-based reconstruction and classical low-rank decomposition, providing a comprehensive benchmark for fabric defect detection. All baseline methods were implemented following their original papers, and hyperparameters were tuned with recommended settings on the validation set to ensure a fair comparison.
4.2. Detection Performance of WOT-AE
Table 1 presents the detection performance of WOT-AE across six defect categories on three patterned fabrics. Overall, the model achieves high TPR values (mostly above 85%) and competitive scores, demonstrating a good balance between sensitivity and precision.

Table 1.
Per-defect performance (TPR and ) on three patterned fabric categories (Box, Star, Dot).
Bar-type defects (Thick Bar and Thin Bar) are the easiest to detect, with TPR consistently above 90% and up to 94.36% (Dot-Thick Bar). For Broken End and Hole, performance remains stable with average TPR above 85% and between 55–83%. More challenging defects such as Netting Multiple show lower on Box (48.57%) but improve significantly on Star and Dot (above 74%). Knots, only present in Dot patterns, are detected with TPR of 88.41% and of 66.82%.
In summary, WOT-AE performs strongly across all categories, excelling on bar-type defects and maintaining robustness on irregular types, validating the effectiveness of its design.
Table 2 summarizes the average detection results of WOT-AE across the three patterned fabrics. Overall, bar-type defects (Thick Bar and Thin Bar) are the easiest to detect, achieving the highest average TPR values above 91% and scores up to 86.03%. Broken End and Hole also reach stable detection performance, with average TPR around 89% and between 64–68%. In contrast, Netting Multiple remains the most challenging defect, with a lower average TPR of 80.60% and of 66.13%, due to its similarity to regular background textures. For Knots, which only appear in Dot-patterned fabrics, the model still achieves reliable performance (TPR = 88.41%, = 66.82%), demonstrating robustness even for underrepresented categories.

Table 2.
Average detection performance of WOT-AE across three patterned fabrics (Box, Star, Dot).
4.3. Comparison with SOTA
4.3.1. Quantitative Comparison
Table 3 reports the detection performance of WOT-AE and six representative methods on Box, Star, and Dot patterned fabrics. Across all three patterns, WOT-AE consistently achieves the highest or near-highest scores on most metrics, demonstrating its effectiveness in balancing sensitivity and precision.

Table 3.
Detection performance comparison on Box, Star, and Dot-patterned fabrics.
For the Box pattern, WOT-AE achieves the best overall performance with a TPR of 86.78% and an of 62.39%, outperforming the strongest low-rank baseline (T-LRSD, = 54.94%). Notably, WOT-AE reduces the FPR to 1.27%, which is significantly lower than most low-rank methods, showing its robustness in suppressing false alarms in repetitive textures.
On the Star pattern, WOT-AE further improves detection reliability, achieving the highest score of 67.51% and the lowest FPR of 0.74%. This indicates superior sensitivity (TPR = 89.32%) combined with strong precision (PPV = 55.22%), whereas other methods exhibit a notable trade-off between recall and precision.
For the Dot pattern, WOT-AE achieves the best performance of 80.47% with balanced TPR (89.37%) and PPV (73.93%). While AE-SSIM reports a slightly higher TPR (94.03%), its low precision (44.14%) leads to inferior (58.79%). Similarly, G-NLR yields the second-best TPR (92.21%) but sacrifices precision, highlighting the advantage of WOT-AE in maintaining both sensitivity and precision simultaneously.
Overall, WOT-AE surpasses all competing methods across Box, Star, and Dot fabrics, delivering the highest scores and stable performance in terms of TPR, FPR, and PPV. These results confirm the benefit of combining autoencoder-based low-rank modeling, prior-guided sparsity, and optimal transport alignment for defect detection in patterned fabrics.
4.3.2. Qualitative Comparison
Figure 3 illustrates representative detection results on the Box, Star, and Dot patterned fabrics. Overall, the proposed WOT-AE consistently achieves clearer and more accurate defect localization than existing approaches. Classical low-rank decomposition methods such as PN-RPCA, T-LRSD, S-LRSD, and AS-LRSD often fail to suppress repetitive background textures, leading to spurious detections along fabric lattices or stripes. Similarly, the autoencoder-based AE-SSIM tends to over-reconstruct defective regions, causing incomplete localization and blurred defect boundaries.

Figure 3.
Qualitative comparison of defect detection results on three patterned fabrics: Box, Star, and Dot. Each row shows the original image, ground-truth annotations, and detection results from PN-RPCA, AE-SSIM, T-LRSD, S-LRSD, AS-LRSD, and the proposed WOT-AE. Compared with competing methods, WOT-AE produces clearer and more accurate defect localization with fewer false alarms, particularly in complex repetitive textures.
In contrast, WOT-AE effectively reconstructs the repetitive background and isolates true anomalies. As shown in the figure, defect regions such as Thick Bar and Thin Bar are highlighted with sharper contours, while complex cases such as Netting Multiple and Knots are detected with minimal background interference. Importantly, WOT-AE substantially reduces false positives in highly repetitive textures, which are prevalent in Box and Star patterns, and maintains high precision even in Dot patterns where defects are visually similar to normal motifs. These qualitative results complement the quantitative comparisons and demonstrate the robustness of WOT-AE under diverse fabric structures.
4.3.3. Per-Class Detection Comparison
The TPR–FPR scatter plots provide an intuitive view of how different methods balance sensitivity and false alarms across defect categories. Points closer to the upper-left indicate stronger performance. Figure 4 shows that WOT-AE consistently lies near the upper-left region, achieving high recall with low false alarms across all defect types. In contrast, AE-SSIM tends to sacrifice precision for recall, and low-rank baselines either miss challenging defects or trigger excessive false positives. These results confirm that WOT-AE provides the most balanced trade-off among sensitivity and specificity.
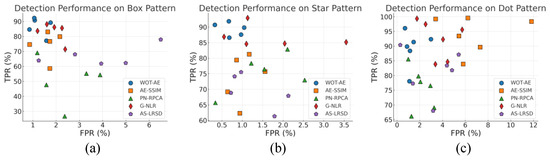
Figure 4.
Per-class comparison of different detection methods using TPR–FPR scatter plots on (a) Box, (b) Star, and (c) Dot patterned fabrics. Each point corresponds to a specific defect type, with higher TPR and lower FPR indicating superior detection quality.
4.4. Ablation Studies
4.4.1. Effectiveness of Model Components: ROC and PR Analysis
Figure 5 further illustrates the effect of different modules through ROC and PR curves. The full WOT-AE consistently produces curves closer to the upper-left boundary in ROC space and the upper-right boundary in PR space, corresponding to superior AUC and AUPR values. When the weighted sparsity term is removed, both ROC and PR curves shift significantly downward, indicating a higher rate of false alarms and reduced defect separability. Excluding the OT alignment also leads to a noticeable decline, particularly in PR curves, reflecting reduced stability in precision–recall trade-offs. In contrast, the complete model combines both modules to achieve the most balanced and robust performance, thereby validating the complementary roles of weighted sparsity and OT feature alignment in fabric defect detection.
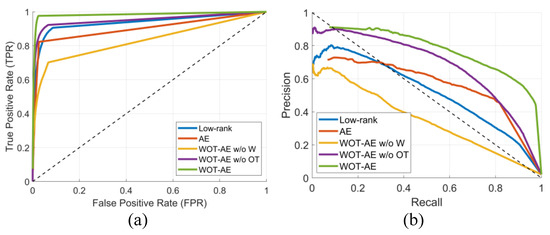
Figure 5.
ROC and PR curves of different ablation settings on the patterned fabric dataset: (a) ROC curve, (b) PR curve. Removing the weighted sparsity module (w/o W) or the OT alignment (w/o OT) degrades performance, confirming that both components contribute to robust and accurate defect detection.
Table 4 presents the ablation results of different modules in the proposed WOT-AE. The low-rank baseline achieves relatively high AUC (91.97%) but a poor WF (28.11%), indicating limited robustness in capturing repetitive textures. The AE baseline obtains better WF (50.40%) but lower AUC (89.31%), reflecting its tendency to over-reconstruct defects. Removing the weighted sparsity module (WOT-AE w/o W) causes the most severe degradation, with both AUC (79.39%) and WF (24.44%) dropping sharply, which confirms the essential role of prior-guided sparsity in suppressing false positives. Without OT alignment (WOT-AE w/o OT), AUC remains competitive (93.51%), but WF decreases to 37.35%, showing that OT alignment primarily contributes to enhancing feature consistency and stabilizing defect localization. The full WOT-AE achieves the best overall results (AUC = 96.84%, WF = 58.73%), validating that the integration of weighted sparsity and OT alignment provides complementary benefits and leads to robust performance improvements.

Table 4.
Ablation study of different modules in the proposed WOT-AE framework. Performance is reported in terms of AUC and WF on the patterned fabric dataset.
4.4.2. Parameter Sensitivity Analysis
The three-dimensional surface plot in Figure 6 illustrates the sensitivity of WF scores to the hyperparameters and . Overall, WF increases steadily as grows from 0.01 to 0.05, reaching a peak of 58.73 at . Beyond this point, further enlarging leads to a gradual decline, suggesting that excessively strong weighting may suppress not only false positives but also true defect responses. Similarly, moderate values of (1.0–2.0) yield consistently higher WF than very small or very large values, indicating that balanced sparsity weighting is critical for reliable detection. The broad plateau observed around and demonstrates that the model is robust to parameter variation, while the default choice lies near the optimum, ensuring both accuracy and stability.
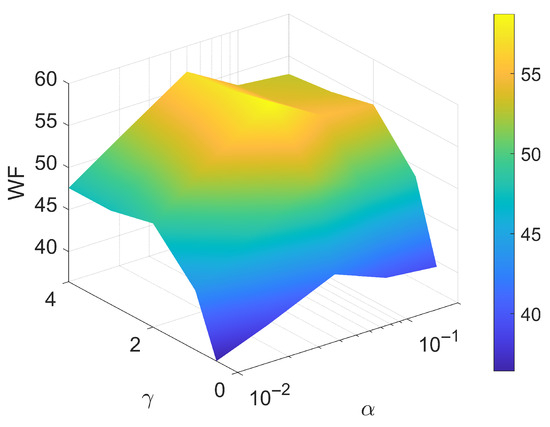
Figure 6.
Three-dimensional sensitivity analysis of WF with respect to and . The score peaks at , while a broad plateau is observed for and , confirming both optimality and robustness of the default parameter setting.
4.4.3. Comparison of the Defect Prior and Saliency Map
As shown in Figure 7, the visualization of the prior map P and its complementary background confidence demonstrates how reconstruction errors are transformed into spatial guidance for subsequent modules. Specifically, the prior P highlights regions with strong deviations between the input and reconstructed background, which correspond to potential defect areas. Conversely, emphasizes the repetitive background regions with high confidence, serving as the basis for constructing transport weights in the OT module and for regulating sparsity in the defect map E. This complementary relationship ensures that defects are enhanced, while intact background patterns are preserved, thereby reducing false alarms in repetitive textures.
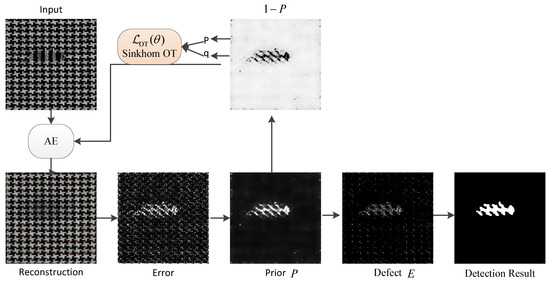
Figure 7.
Visualization of the prior map P and its complementary background confidence . The prior P highlights potential defect regions based on reconstruction errors, while emphasizes defect-free textures with high confidence. This complementary representation provides spatial guidance for both OT weighting and sparse defect separation.
5. Discussion
The proposed WOT-AE framework demonstrates the effectiveness of combining autoencoder-based background modeling, prior-guided sparsity, and optimal transport alignment for patterned fabric defect detection. Several insights can be drawn from the experimental results.
First, the introduction of prior maps P and their complementary confidence plays a pivotal role in addressing the unique challenges of repetitive fabric textures. By explicitly weighting sparse separation with , the framework effectively suppresses false alarms in highly structured regions while maintaining high sensitivity to subtle defects. The visualizations confirm that this mechanism provides interpretable spatial guidance for defect localization.
Second, the OT-based alignment enhances the consistency between encoder features of defect-free regions, preventing defects from being reconstructed as background. Ablation studies reveal that, while weighted sparsity is critical for reducing false positives, OT alignment stabilizes feature learning and further improves sensitivity. Their complementary effect explains the superior performance of the full WOT-AE.
Third, sensitivity analysis on the hyperparameters and shows that the framework maintains a broad plateau of high performance around the default setting . This indicates robustness to parameter selection, which is particularly valuable in real-world industrial inspection scenarios where extensive hyperparameter tuning is impractical.
Finally, comparison with classical low-rank decomposition methods and existing deep learning approaches highlights the unique advantages of WOT-AE. While low-rank models often fail to preserve high-frequency weave patterns, and vanilla autoencoders over-reconstruct defects, WOT-AE balances background fidelity, defect sensitivity, and robustness against repetitive noise.
These findings suggest that the proposed strategy not only advances patterned fabric inspection but may also be extended to other structured anomaly detection problems, such as wafer defect detection or surface quality assessment, where repetitive patterns and subtle defects coexist. On the other hand, it is worth noting that the proposed WOT-AE is not restricted to the six defect categories used in this study. By learning only from defect-free samples of a new patterned fabric, the framework can be readily extended to detect unseen defect types, demonstrating scalability toward practical industrial deployments.
Although our framework demonstrates strong performance under the small-sample unsupervised setting, there remains room for improvement. In particular, Transformer-based backbones offer a promising direction, as their attention mechanisms can naturally capture global periodicity and irregular structures in fabrics. However, directly training or fine-tuning Transformers is prone to overfitting under the limited data regime used in this study. Future work will therefore focus on exploring hybrid architectures that combine the generative low-rank autoencoder with Transformer modules, aiming to leverage their complementary strengths for domain-generalized fabric defect detection.
6. Conclusions
In this work, we proposed WOT-AE, a Weighted Optimal Transport Autoencoder for patterned fabric defect detection. By combining autoencoder-based low-rank background modeling, prior-guided weighted sparsity, and optimal transport feature alignment, the framework effectively preserves repetitive textures, suppresses false alarms, and prevents defect leakage into the background. Extensive experiments demonstrated that WOT-AE consistently outperforms both low-rank decomposition and deep learning baselines across multiple defect types, achieving superior accuracy and robustness. Ablation and sensitivity analyses further validated the complementary roles of weighted sparsity and OT alignment, as well as the stability of the default parameter settings. These results highlight the potential of WOT-AE not only for fabric inspection but also for broader anomaly detection tasks involving structured backgrounds and localized defects. Recent advances in domain generalization research have also highlighted the importance of disentangling invariant and variant features across domains. For example, a domain feature decoupling network has been proposed for rotating machinery fault diagnosis under unseen operating conditions [48]. Although targeting a different application, this line of work reinforces the need for explicitly modeling domain shifts in real-world deployments. Inspired by such perspectives, our WOT-AE framework can be further extended toward domain-generalized fabric defect detection, enabling reliable performance under varying manufacturing conditions and unseen fabric patterns.
Author Contributions
Conceptualization, T.Y. and H.Y.; methodology, H.Y.; software, T.Y.; validation, T.Y., H.Y., and L.K.; formal analysis, T.Y.; investigation, H.Y.; resources, H.Y.; data curation, H.Y. and L.K.; writing—original draft preparation, H.Y.; writing—review and editing, T.Y.; visualization, T.Y.; supervision, T.Y.; project administration, H.Y. and L.K.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Dot-patterned, Box-patterned and Star-patterned fabric databases are available at https://ytngan.wordpress.com/codes/ (accessed on 27 November 2015).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Srinivasan, K.; Dastoor, P.H.; Radhakrishnaiah, P.; Jayaraman, S. FDAS: A knowledge-based framework for analysis of defects in woven textile structures. J. Text. Inst. 1992, 83, 431–448. [Google Scholar] [CrossRef]
- Ngan, H.Y.; Pang, G.K.; Yung, S.P.; Ng, M.K. Wavelet based methods on patterned fabric defect detection. Pattern Recognit. 2005, 38, 559–576. [Google Scholar] [CrossRef]
- Wen, Z.; Cao, J.; Liu, X.; Ying, S. Fabric defects detection using adaptive wavelets. Int. J. Cloth. Sci. Technol. 2014, 26, 202–211. [Google Scholar] [CrossRef]
- Tong, L.; Wong, W.K.; Kwong, C.K. Differential evolution-based optimal Gabor filter model for fabric inspection. Neurocomputing 2016, 173, 1386–1401. [Google Scholar] [CrossRef]
- Li, C.; Gao, G.; Liu, Z.; Huang, D.; Xi, J. Defect detection for patterned fabric images based on GHOG and low-rank decomposition. IEEE Access 2019, 7, 83962–83973. [Google Scholar] [CrossRef]
- Liu, G.; Li, F. Fabric defect detection based on low-rank decomposition with structural constraints. Vis. Comput. 2022, 38, 639–653. [Google Scholar] [CrossRef]
- Shi, B.; Liang, J.; Di, L.; Chen, C.; Hou, Z. Fabric defect detection via low-rank decomposition with gradient information. IEEE Access 2019, 7, 130423–130437. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Su, H.; Du, B.; Tao, D. Multistage GAN for fabric defect detection. IEEE Trans. Image Process. 2019, 29, 3388–3400. [Google Scholar] [CrossRef]
- Bergmann, P.; Löwe, S.; Fauser, M.; Sattlegger, D.; Steger, C. Improving unsupervised defect segmentation by applying structural similarity to autoencoders. arXiv 2018, arXiv:1807.02011. [Google Scholar]
- Soukup, D.; Pinetz, T. Reliably decoding autoencoders’ latent spaces for one-class learning image inspection scenarios. In Proceedings of the OAGM Workshop, Hall/Tyrol, Austria, 15–17 May 2018; pp. 90–93. [Google Scholar]
- Kahraman, Y.; Durmuşoğlu, A. Deep learning-based fabric defect detection: A review. Text. Res. J. 2023, 93, 1485–1503. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Lu, S.; Yao, L.; Li, P. A mixed-attention-based multi-scale autoencoder algorithm for fabric defect detection. Color. Technol. 2024, 140, 451–466. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Wang, C.; Lu, S.; Xiong, W. Color-patterned fabric defect detection algorithm based on triplet attention multi-scale U-shape denoising convolutional auto-encoder. J. Supercomput. 2024, 80, 4451–4476. [Google Scholar] [CrossRef]
- Xiang, J.; Pan, R.; Gao, W. eYarn-dyed fabric defect detection based on an improved autoencoder with Fourier convolution. Text. Res. J. 2023, 93, 1153–1165. [Google Scholar] [CrossRef]
- Cao, Q.; Han, Y.; Xiao, K. Fabric defect detection based on low-rank decomposition with factor group-sparse regularizer. Text. Res. J. 2023, 93, 3509–3526. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, J.; Li, C.; Liu, P.; Yang, R. Fabric defect detection via feature fusion and total variation regularized low-rank decomposition. Multimed. Tools Appl. 2024, 83, 609–633. [Google Scholar] [CrossRef]
- Guo, Y.; Kang, X.; Li, J.; Yang, Y. Automatic fabric defect detection method using AC-YOLOv5. Electronics 2023, 12, 2950. [Google Scholar] [CrossRef]
- Huang, H.; Yang, J.; Zeng, H.; Wang, Y.; Xiao, L. Self-Organizing Maps-Assisted Variational Autoencoder for Unsupervised Network Anomaly Detection. Symmetry 2025, 17, 520. [Google Scholar] [CrossRef]
- Hu, G.H.; Wang, Q.H.; Zhang, G.H. Unsupervised defect detection in textiles based on Fourier analysis and wavelet shrinkage. Appl. Opt. 2015, 54, 2963–2980. [Google Scholar] [CrossRef]
- Jia, L.; Chen, C.; Liang, J.; Hou, Z. Fabric defect inspection based on lattice segmentation and Gabor filtering. Neurocomputing 2017, 238, 84–102. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Shi, B.; Liang, J.; Di, L.; Chen, C.; Hou, Z. Fabric defect detection via low-rank decomposition with gradient information and structured graph algorithm. Inf. Sci. 2021, 546, 608–626. [Google Scholar] [CrossRef]
- Di, L.; Long, H.; Shi, B.; Xia, Y.; Liang, J. Fabric defect detection via low-rank decomposition with multi-priors and visual saliency features. J. Frankl. Inst. 2024, 361, 107150. [Google Scholar] [CrossRef]
- Shi, W.; Chen, Z.; Liang, J.; Jiang, D. Adaptive optimization of low rank decomposition and its application on fabric defect detection. Pattern Anal. Appl. 2025, 28, 4. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, Z.; Zhang, S.; Li, Y.; Zhao, L. Sparse adaptive optimization based on low rank decomposition for image defect detection. IEEE Access 2025, 13, 139433–139444. [Google Scholar] [CrossRef]
- Han, Y.J.; Yu, H.J. Fabric defect detection system using stacked convolutional denoising auto-encoders trained with synthetic defect data. Appl. Sci. 2020, 10, 2511. [Google Scholar] [CrossRef]
- Getachew Shiferaw, T.; Yao, L. Autoencoder-based unsupervised surface defect detection using two-stage training. J. Imaging 2024, 10, 111. [Google Scholar] [CrossRef]
- Walczyna, T.; Jankowski, D.; Piotrowski, Z. Enhancing Anomaly Detection Through Latent Space Manipulation in Autoencoders: A Comparative Analysis. Appl. Sci. 2024, 15, 286. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 1180–1189. [Google Scholar]
- Sun, B.; Saenko, K. Deep CORAL: Correlation alignment for deep domain adaptation. In Proceedings of the 14th European Conference on Computer Vision (ECCV) Workshops, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 443–450. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Courty, N.; Flamary, R.; Tuia, D.; Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1853–1865. [Google Scholar] [CrossRef]
- Cao, J.; Wang, N.; Zhang, J.; Wen, Z.; Li, B.; Liu, X. Detection of varied defects in diverse fabric images via modified RPCA with noise term and defect prior. Int. J. Cloth. Sci. Technol. 2016, 28, 516–529. [Google Scholar] [CrossRef]
- Hu, C.; Lai, S. A lightweight reconstruction network for surface defect inspection. In Proceedings of the 2023 International Conference on Machine Vision, Image Processing and Imaging Technology (MVIPIT), Hangzhou, China, 22–24 September 2023; pp. 43–50. [Google Scholar]
- Zhao, H.; Zi, C.; Liu, Y.; Zhang, C.; Zhou, Y.; Li, J. Weakly supervised anomaly detection via knowledge-data alignment. In Proceedings of the ACM Web Conference, Singapore, 13–17 May 2024; pp. 4083–4094. [Google Scholar]
- Blanchet, J.; Li, J.; Pelger, M.; Zanotti, G. Automatic outlier rectification via optimal transport. Adv. Neural Inf. Process. Syst. 2024, 37, 35313–35357. [Google Scholar]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.H.; Tay, F.E.; Feng, J.; Yan, S. Tokens-to-token vit: Training vision transformers from scratch on imagenet. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 558–567. [Google Scholar]
- Wang, J.; Xu, G.; Yan, F.; Wang, J.; Wang, Z. Defect transformer: An efficient hybrid transformer architecture for surface defect detection. Measurement 2023, 211, 112614. [Google Scholar] [CrossRef]
- Jiang, X.; Guo, K.; Lu, Y.; Yan, F.; Liu, H.; Cao, J.; Xu, M.; Tao, D. CINFormer: Transformer network with multi-stage CNN feature injection for surface defect segmentation. arXiv 2023, arXiv:2309.12639. [Google Scholar]
- Adam, K.D.P.B.J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ng, M.K.; Ngan, H.Y.; Yuan, X.; Zhang, W. Patterned fabric inspection and visualization by the method of image decomposition. IEEE Trans. Autom. Sci. Eng. 2014, 11, 943–947. [Google Scholar] [CrossRef]
- Tsang, C.S.C.; Ngan, H.Y.T.; Pang, G.K.H. Fabric inspection based on the Elo rating method. Pattern Recognit. 2016, 51, 378–394. [Google Scholar] [CrossRef]
- Lazarevic-McManus, N.; Renno, J.; Jones, G.A. Performance evaluation in visual surveillance using the F-measure. In Proceedings of the 4th ACM International Workshop on Video Surveillance and Sensor Networks, Santa Barbara, CA, USA, 7 October 2006; pp. 45–52. [Google Scholar]
- Margolin, R.; Zelnik-Manor, L.; Tal, A. How to evaluate foreground maps? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 248–255. [Google Scholar]
- Gao, T.; Yang, J.; Wang, W.; Fan, X. A domain feature decoupling network for rotating machinery fault diagnosis under unseen operating conditions. Reliab. Eng. Syst. Saf. 2024, 252, 110449. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).