Reexamining Key Applications of the Poisson Distribution

Abstract

The Poisson distribution is a discrete probability model, widely used in science and engineering to describe various natural and man-made phenomena. It possesses an important feature, namely being inherently asymmetric, but as its parameter becomes large, the distribution becomes approximately symmetric. To broaden its use, multiple extensions and variations have been developed. Determining whether a data set follows a Poisson distribution involves hypothesis testing at a chosen significance level. When sampling from a Poisson distribution, confidence intervals provide an estimated range instead of a single value. Due to the discrete nature of the Poisson distribution, confidence intervals cannot be derived from a simple formula, and are therefore computed using specialized algorithms. In this paper, three alternatives are given and discussed.

1. Introduction

A common approach to approximate the value of a function at a point is to express it as a (typically infinite) series called the Taylor series [1]:

$$f\left(x\right)=\sum _{y=0}^{\infty }{\displaystyle \frac{{(x-a)}^y}{y!}}{f}^{\left(y\right)}\left(a\right)$$

(1)

where $f^{\left(y\right)}$ denotes the $y^{\mathrm{th}}$ derivative of f. A special case arises when $a=0$, which is known as the Maclaurin series [2], although Euler examined similar expansions around the same period [3]. A notable property of the exponential function is that it equals its own derivative. Applying Equation (1) to $f\left(x\right)=e^x$ with $a=0$ yields:

$$e^x=\sum _{y=0}^{\infty }{\displaystyle \frac{x^y}{y!}}$$

(2)

Using Equation (2), it is straightforward to verify that the function $\mathrm{Poisson}(x;z)$ in Equation (3) describes an infinite series over $x=0,1,\dots$ whose sum equals 1:

$$\mathrm{Poisson}(x;z)={\displaystyle \frac{z^x}{x!}}{e}^{-z}$$

(3)

This defines the Poisson distribution [4]. For a Poisson process with an expected number x of events occurring in a given interval, the probability of observing z events in that interval is given by $\mathrm{Poisson}(x;z)$.

The skewness of the Poisson distribution is $z^{-1}$, meaning the distribution becomes more symmetric as z increases, but it is never perfectly symmetric as long as it has support only on non-negative integers. In other words, since probabilities for negative values are zero, the exact symmetry around a center is broken.

2. Literature Survey

Simon Newcomb [5] applied the Poisson distribution in 1860 to model the number of stars observed within a unit of space. Later, in 1898, Ladislaus Bortkiewicz [6] demonstrated that the occurrence of soldiers in the Prussian army accidentally killed by horse kicks followed a Poisson distribution closely.

One of the simplest methods to generate Poisson-distributed values relies on the uniform distribution. Various algorithms exist for this purpose, with two examples being presented in this paper, in Algorithms 1 and 2.

Algorithm 1: Knuth’s [7] algorithm on generating a Poisson-distributed series

Input: z  //Real value, see Equation (3) $L\leftarrow e^{-z};k\leftarrow 0;p\leftarrow 1;$ $\mathrm{Repeat}$ $u\leftarrow \mathrm{Rand}(0,1);p\leftarrow p·u;\mathrm{If}(p<L)\mathrm{Break};k\leftarrow k+1$ $\mathrm{Until}\left(\mathrm{False}\right);$ $\mathrm{Return}\left(k\right);$

Algorithm 2: Devroye’s [8] algorithm on generating a Poisson-distributed series

Input:  z //Real value, see Equation (3) $k\leftarrow 0;p\leftarrow e^{-\lambda };s\leftarrow p;u\leftarrow \mathrm{Rand}(0,1)$ $\mathrm{Repeat}$ $\mathrm{If}(u>s)\mathrm{Break};k\leftarrow k+1;p\leftarrow p·\lambda /k;s\leftarrow s+p$ $\mathrm{Until}\left(\mathrm{False}\right);$ $\mathrm{Return}\left(k\right);$

  Applications of the Poisson distribution are across several fields.

2.1. Physics and Engineering

Particle Physics and Quantum Mechanics are addressed with particle collision events in Brownian motion [9], asteroid impacts [10], particle clusters [11], electron–positron pair creation in relativistic heavy-ion collisions [12], and other various quantum phenomena [13]. In quantum systems, it describes photocurrent zero-axis crossings in Cassinian oscillators [14], particle dwell times in low-temperature defects [15], and virtual charged pair counts in mesoscopic capacitor theory [16]; the distribution also applies to quantum eigenstate level spacing analysis when uncertainty is sufficiently small [17].

Electromagnetic radiation and Photon Counting Light scattering applications include modeling photon bounces from Earth’s surface in laser altimetry systems [18], particularly in Multiple Altimeter Beam Experimental Lidar operations [19]. The distribution describes photon counts in various detection systems [20], UV background measurements [21], and stellar occultation events [22]. For radiation emission, it models X-ray photon emission patterns [23] and photon numbers in weak coherent light pulses [24].

Radioactive Decay and Cosmic Phenomena are subject to modeling too. Even if radioactive particle emission technically follows the Ruark–Devol distribution [25,26,27], it is commonly approximated using Poisson distributions for practical applications [28]. In cosmic ray physics, the distribution models particle density [29], flux measurements through detectors [30], and air shower observations [31]; it also describes cosmic ray cluster multiplicities at ultrahigh energies [32], and emission patterns from luminous sources over time [25,26,27].

Astronomical Object Counting is addressed with counting of various celestial objects, including halos per mass bin in cosmic surveys [33], primordial black holes [34], galaxies within dark matter halos [35], and even hypothetical artificial broadcasts from extraterrestrial intelligences [36].

Signal Processing and Manufacturing is addressed with spatio-temporal backhopping in magnetic memory arrays [37], sensor surface binding events in magnetic bead detectors [38], and quantum noise in optical transmission [39]. Manufacturing is covered with spatially uncorrelated defect distribution analysis [40,41], component volume defects classified by size and type [42], and new product development counts across firms [43].

2.1.1. A First Case Study of Poisson Distribution Use in Physics

In [10], it is assumed that a potential target object, such as a planet or a specific asteroid, is in a heliocentric orbit in which it can collide with other asteroids or with comets. The assumption is that the orbit of this target passes through a region of space which can be characterized as having a constant spatial density $\delta$ of objects with which the target can collide. For such a Poisson ensemble of objects, it follows that a model based on the Poisson distribution is constructed and describes the probability of a collision. Following particle-in-a-box modeling, it is assumed that the target and surrounding asteroids are all simply points rather than extended objects. Spatial distribution of asteroids with respect to the target at a random instant of time is characterized by the Poisson distribution and the probability of finding no asteroids in a sphere of volume V centered at the target is given by Equation (3) with $x=0$ and $z=\delta V$.

2.1.2. A Second Case Study of Poisson Distribution Use in Physics

In [33], a differentiable and physics-informed neural network is introduced, which can generate a computationally generated catalog of dark matter halos designed to simulate observations of the universe’s large-scale structure. In doing that, $N_{i,M}^{halo}$, the number of halos per mass bin and per cubic element (where i is the index of the cubic element and $[M,M+\Delta M]$ is the mass bin) is assumed to be distributed by Poisson law, model identified by fixing $x=N_{i,M}^{halo}$ and $z={\lambda }_{i,M}$ in Equation (3), and with ${\lambda }_{i,M}$ denoting the Poisson intensity.

2.1.3. A Case Study of Poisson Distribution Use in Engineering

Spin-transfer-torque magnetic random-access memory is used for embedded non-volatile memory applications. At high biases, these memories can anomalously increase owing to the switching back or flipping of the magnetization phenomenon commonly referred to as backhopping, undesirable for memory applications. However, the phenomenon gained attention for its potential in spiking neural network applications. In [37], it was found that the probability of backhopping follows a Poisson distribution (Equation (3)) characterized by the rate of backhopping ($\lambda =z$).

2.2. Transportation and Network Systems

In Vehicle and Aircraft Movement, Poisson distribution effectively models irregular arrival patterns for aircrafts [44], cars [45], and sea ships [46,47,48,49,50] at various transportation hubs. It is particularly useful for analyzing flight delays [51,52], cancellations [53], and service desk operations [54]; the memoryless property makes it ideal for modeling unpredictable arrival scenarios [55,56].

Traffic Flow Analysis is included with highway traffic analysis, when Poisson distribution is applied to vehicles moving in infinitely long lines without traffic controls [57], when predicting overtaking probabilities over time. However, its validity depends on traffic density remaining below critical thresholds, ranging from 600 to 800 vehicles per hour [58,59,60]; the distribution also models inter-vehicle spacing [61] and serves as the foundation for traditional telephony network traffic analysis [62].

Communication systems applications include network traffic with user session arrivals [63], legitimate internet traffic patterns [64,65], and packet reception counts [66]; the distribution proves valuable for capacity planning and server load management in web systems [67]. Email spam retrieval rates also follow Poisson patterns when spammer lists are large and retrieval rates remain constant [68,69]. Phone call modeling includes both incoming switchboard calls [70] and bidirectional calling patterns with variable frequencies [71]; mobile communication applications cover GSM signal paging [72], call logging with time quantization [73], active phone counts per cell area [74], and base station traffic analysis [75].

2.2.1. A Case Study of Poisson Distribution Use in Transportation

The problem of determining the optimal number of berths is addressed in [46], considering both service and waiting costs for ships. When the ship arrival rate at the seaport is lower than the service rate (the number of ships handled per unit time), some berths remain idle, reducing the overall service efficiency. Conversely, if the arrival rate exceeds the service rate, ships will form a queue, modeled probabilistically by Equation (3), with z the average number of arrivals and x the number of ships arriving in a seaport in specific time.

2.2.2. A Case Study of the Poisson Distribution Use in Network Systems

Considering that uplink Global System for Mobile Communication power is dependent on the number of nearby mobile phones in an active call, in [74], a nearby approach with mobile phones only in a 10m radius is considered. In this instance, the number of active mobile phones was modeled using the Poisson distribution (Equation (3)), with a mean value $z=3$, where three mobile phones talking in the 10 m radius were used. Consideration was given to typical places where Radio Frequency Identification systems can be used, such as schools and universities, hospitals, supermarkets, public transportation, and sports events. In this instance, $x=n$ was the number of mobile phones in the selected area.

2.3. Biology and Medicine

Safety and Risk Assessment is addressed by accident modeling when areas are divided into grid patterns where accident counts per quadrat follow the Poisson distribution [76]; however, careful application is required, since the distribution assumes constant hazard rates and does not account for changing risk factors following incidents or seasonal variations in accident-producing conditions [77].

Genetic and Cellular Processes are addressed with DNA mutation analysis using Poisson modeling for mutagenesis rate [78] and mutation frequency data [79], though actual mutant distributions often follow the Luria–Delbrück pattern [80,81,82,83]; the distribution models DNA lesion counts [84] and HPRT gene mutations in lymphocyte cultures, using 96-well plate assays with colony formation analysis [85].

Healthcare System Operations are well addressed, since hospital systems extensively use Poisson modeling for emergency department arrivals [86], obstetric patient flow [87], and disease-specific admission patterns like asthma hospitalizations [88] and annual expected number of amyotrophic lateral sclerosis cases by town [89]; the distribution’s appropriateness stems from arrivals representing independent medical incidents from many individuals, each using services infrequently [90].

Disease Surveillance and Outbreaks are addressed with epidemic modeling, employing distributed lag models with Poisson-weighted parameters corresponding to disease-specific incubation periods [91,92], space–time permutation scan statistics, which use Poisson assumptions for early outbreak detection through hospital visit monitoring [93], and modeling case numbers for specific diseases, such as amyotrophic lateral sclerosis across geographic regions [89].

Medical Error Analysis is addressed with healthcare quality assessments, applying the Poisson distribution to model the intensive care unit medical errors [94], adverse event frequencies [95], emergency department visit patterns, and prescription error rates [96]; models for healthcare worker burnout and depression rates when analyzing workplace safety factors are also reported [97,98,99].

Environmental Health is addressed through natural disaster impacts analysis when Poisson patterns were reported for meteorological threshold exceedances [100], post-disaster suicide rates [101], and catastrophic event frequencies [102], providing frameworks for public health emergency planning.

2.3.1. A Case Study of Poisson Distribution Use in Biology

The time evolution of deoxyribonucleic acid damage was placed under scrutiny in [84]. With the Microdosimetric Kinetic Model, the initial distribution of lethal lesions was Poissonian (Equation (3)). When given a cell nucleus, composed by $N_d$ domains, the probability that events deposit an energy z obeys a Poissonian distribution of mean ${\displaystyle \frac{z_n}{z_F}}$, $z_n$ being the mean energy deposition on the nucleus, and $z_F$ the first moment of the single event distribution, either computed numerically via Monte Carlo or by experimental microdosimetric measurements.

2.3.2. A Case Study of Poisson Distribution Use in Medicine

In [94], medical error rates were calculated as the number of medical errors divided by patient-days and number of admissions, when the overall medical error rates were compared between the preintervention (traditional fluorescent) and postintervention (blue-enriched) lighting conditions, assuming that the number of medical errors followed a Poisson distribution (Equation (3)), given the length of stay.

2.4. Economics and Commerce

Customer Behavior Analysis is included with commercial applications modeling transaction item counts [103,104], customer purchase frequencies over time periods [105], and website visitor arrivals for online businesses [106]; the distribution also describes demand patterns for spare parts [107], customer churn prediction [108], and unplanned category purchases during shopping trips [109].

Retail Operations is included with store traffic modeling for online retailing patterns [110], standard product demand at retail locations [111], and shopping intensity, measured by store visit counts in mall environments [112]; these applications help optimize staffing, inventory, and facility management.

Product Lifecycle Management is included with return product analysis using Poisson modeling for reusable product demand and return streams [113,114], return timing patterns [115], and customer-to-customer non-returned item counts [116]; this supports reverse logistics planning and warranty cost estimation.

Service Industry Applications is addressed through call center operations, relying heavily on Poisson modeling for daily and hourly call volume prediction [104,117], banking customer service arrival patterns [86], and capacity planning [67]; the distribution’s memoryless property aligns well with independent customer service needs arising from separate individual circumstances.

2.4.1. A Case Study of Poisson Distribution Use in Economics

In [104] is considered an inhomogeneous Poisson model with arrival rate incorporating both strong within-day patterns and day-to-day dynamics, modelled separately and combined in a multiplicative model. If $N_{jk}$ is the number of arrivals to the queue on day $j=1,\dots ,J$ during the time interval $[t_k-1,t_k]$, with $k=1,\dots ,K$ the kth period in the day, the model is obtained by substituting ${\lambda }_{jk}$ in Equation (3), where ${\lambda }_{jk}$ is the arrival rate for day j and period k.

2.4.2. A Case Study of Poisson Distribution Use in Commerce

In [116], it is assumed that customers arrive according to a Poisson process with rate ${\lambda }_t$ during $[t,t+1)$ time interval for $t\in \{0,1,\dots ,T-1\}$, and the demand is satisfied at the end of the period, generating a quantifiable revenue per customer. Meanwhile, for items purchased in $[t-i,t-i+1)$ time period, the number of returns follows a binomial distribution.

3. Testing for Poisson Distribution

A variety of tests is available for testing whether a sample of observations comes from a Poisson distribution. An additional test based on variance stabilizing transformation from [118] is as follows.

If $X_1$, …, $X_n$ are independent non-negative integer valued random variables with $P(X=x_i)=Poisson({\lambda }_i;x_i)$, the basic null hypothesis of interest is that

$$\begin{array}{cc}\hfill H_0& :{\lambda }_1=\cdots ={\lambda }_n\hfill \\ \hfill & \mathrm{against}\hfill \\ \hfill H_a& :\sum _{i=0}^n{({\lambda }_i-\overline{\lambda })}^2>0\hfill \end{array}$$

(4)

where $\overline{\lambda }={\displaystyle \frac{{\sum }_{i=0}^n{\lambda }_i}{n}}$.

With $\overline{X}={\displaystyle \frac{{\sum }_{i=0}^n{X}_i}{n}}$ and $\overline{Y}={\displaystyle \frac{{\sum }_{i=0}^n{Y}_i}{n}}$, the statistic for testing $H_0$ vs. $H_a$ can be [119]:

$$\begin{array}{ccc}& T_{CC}=& \sum _{i=1}^n{\displaystyle \frac{{(X_i-\overline{X})}^2}{\overline{X}}}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& T_{LR}=& 2\sum _{i=1}^n{X}_i\ln {\displaystyle \frac{X_i}{\overline{X}}}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& T_{BA}=& 4\sum _{i=1}^n{(Y_i-\overline{Y})}^2,Y_i=\sqrt{X_i+3/8}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& T_{NS}=& \sqrt{{\displaystyle \frac{n-1}{2}}}\left({\displaystyle \frac{{(X_i-\overline{X})}^2}{\overline{X}}}-1\right)\hfill \end{array}$$

(8)

where:

• $T_{CC}$ is conditional ${\chi }^2$ (chi-squared) statistic, relying on the fact that, under null hypothesis, the conditional distribution of $X_1$, …, $X_n$ given ${\sum }_{i=1}^n{X}_i=n\overline{X}$ is multinomial (each of the draws having $1/n$ chance);
• $T_{LR}$ has an approximately non-central ${\chi }^2$ distribution with non-centrality parameter ${\sum }_{i=1}^n{\displaystyle \frac{{({\lambda }_i-\overline{\lambda })}^2}{\overline{\lambda }}}$;
• $T_{BA}$ is based on the Bartlett–Anscombe statistic [118,120];
• $T_{NS}\sim N({\sum }_{i=1}^n{\displaystyle \frac{{({\lambda }_i-\overline{\lambda })}^2}{\overline{\lambda }}}/\sqrt{2n},1)$, or, even better, $T_{NS}\sim t_{n-1}$, with N being the normal distribution and t being the student distribution.

Summarizing, with Equations (5)–(7), either of the statistics rejects $H_0$ when $T_{CC},T_{LR},T_{BA}>{\chi }_{n-1;1-\alpha }^2$, while, with Equation (8), $H_0$ is rejected when $T_{NS}>t_{n-1,1-\alpha }$.

4. Working with the Poisson Distribution for Unique Observations

Since Poisson is a discrete distribution, one cannot (in general) find values of $x_L$ and $x_U$ such that the probability $\mathrm{Prob}(x_L\le x\le x_U)=95\%$ exactly (or any other coverage). The median $\nu$ is defined as the infimum value for $\nu$ such that $\mathrm{Prob}(x\le \nu )\ge 50\%$, since the probability will generally not equal 50% exactly  [121]. One can see this as a 50% confidence interval, with $x_L=0$ and $x_U=\nu$. It is known that there is no closed-form expression for the median of the Poisson distribution, but there are upper and lower bounds [122].

In a Poisson distribution (see Equation (3)), a certain number of events (let y be that number) are observed over a time interval (an arbitrary value: let us say 1 year). What is the probability of observing $y+1$ events? Or more specifically, with $\alpha =0.05$ being set (what follows works with any arbitrary level of significance), what is the range of possible observations with $100(1-\alpha )$% (95%) probability? In this section, the paper will try to provide an answer to this question.

Before proceeding with math, note the following remarks:

• The working hypothesis (what is known) is that the observed number of events follows the Poisson distribution;
• It is not a repeated experiment; more precisely, the repetition of the experiment was not performed;
• As stated in the Poisson experiment, the population (of the occurring events) is infinite, but even so, only one observation was made (the occurrence of y events was observed);
• The parameter of the distribution (z in Equation (3)) is unknown and we need to estimate it.

One would think to estimate z from the formula of the population mean, while another would try to maximize the likelihood. The truth is that the same result will be obtained:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}z}}\ln \left(\mathrm{Poisson}(y;z)\right)={\displaystyle \frac{y-z}{z}}=0\Rightarrow z=y$$

(9)

The likelihood (Equation (9)) shows that $z\leftarrow y$. So the problem is expressing the confidence interval around y having $100(1-\alpha )$% probability coverage.

The main issue is that, just as with the first observation, any further observation will also obtain a non-negative integer as the number of events in the specified timeframe (of 1 year). Thus, the boundaries of the (closed) confidence interval should also be non-negative integers. Let $y_{\mathrm{Low}}$ and $y_{\mathrm{Upp}}$ be the boundaries of the confidence interval. This means that:

$$\sum _{x=y_{\mathrm{Low}}}^{y_{\mathrm{Upp}}}\mathrm{Poisson}(x;z))\mathrm{near}\mathrm{to}0.95$$

(10)

Equation (10) expresses the fact that a simple, obvious solution to the problem exists, since the sum is built up from discrete quantities; adding some may obtain a value below 0.95, and adding something more may result in a value above 0.95, with no implicit criteria of which solution to be retained. The following example is used to clarify the issue:

It makes sense to express the 95% CI for x from Poisson(x;2) as [0, 4] (the true coverage of [0, 4] is about 0.94735) or [0, 5] (the true coverage of [0, 5] is 0.98334). However, without additional information or constraint, one cannot decide which interval best expresses the expected 95% CI. In some instances, an interval of at least 95% coverage is needed (and then [0, 5] is the solution), while in other instances, the nearest solution is preferred (and then [0, 4] is the solution).

However, one should note that Table 1 is (just an example and) a simplified case in which investigating the lower CI boundary was not necessary because $\alpha <$ Poisson(0;2).

Table 1. PMF for Poisson(x;2) and its CDF and 1−CDF.

x	0	1	2	3	4	5	…
PMF	0.13534…	0.27067…	0.27067…	0.18045…	0.09022…	0.03609…	…
CDF	0.13534…	0.40601…	0.67668…	0.85612…	0.94735…	0.98334…	…
1−CDF	0.86466…	0.59399…	0.32332…	0.14288…	0.05265…	0.01656…	…

4.1. Algorithm for CI

The algorithms reported for binomial distribution [123] were adapted to obtain boundaries for the Poisson distribution too (Algorithms 3–5). Since there is no upper limit for the value of a variable from Poisson distribution, the following algorithms are using a special construction, a finite representation of the CDF, which have contained the expected coverage interval in it. This is possible all the time for any imposed level, since the Poisson distribution diminishes its probability with the increasing value of the variate (Equation (11)).

$$\begin{array}{cc}\hfill & \mathrm{FPoisson}(x,\alpha )=\left\{\mathrm{CDF}\right(0;x),\mathrm{CDF}(1;x),\dots ,\mathrm{CDF}(y;x\left)\right\},\hfill \\ \hfill & \mathrm{with}1-\mathrm{CDF}(y;x)<{\displaystyle \frac{\alpha }{10}}\mathrm{or}\mathrm{CDF}(y;x)<\mathrm{CDF}(0;x)\hfill \\ \hfill & \mathrm{and}\mathrm{CDF}(y;x)={\sum }_{k=0}^y\mathrm{Poisson}(k;x)\hfill \end{array}$$

(11)

Algorithm 3:  Algorithm for minimal effort (adapted from A1 in [123])

Input data: x, α //$x\in {\mathbb{N}}^{*}$ the Poisson parameter, $\alpha \in (0,0.5)$ the significance level Output data: nl, nu, ne  //$nl,nu\in {\mathbb{N}}^{*}$ the CI boundaries, $ne$ the true coverage $r\leftarrow \mathrm{FPoisson}(x,\alpha );m\leftarrow \mathrm{Count}\left(r\right);$   //See Equation (11) $nl\leftarrow x;nu\leftarrow x;er\leftarrow r\left[x\right];$ //Always $x\in CI$ $\mathrm{repeat}$ $\mathrm{If}(er\ge 1-\alpha )\mathrm{Break};$ $\mathrm{If}\left(\right(nl=0\left)\mathrm{and}\right(nu=m\left)\right)\mathrm{Break};$ $\mathrm{If}(nl=0)nu+=1;er+=r\left[nu\right];\mathrm{Continue}\mathrm{EndIf};$ $\mathrm{If}(nu=m)nl-=1;er-=r\left[nl\right];\mathrm{Continue}\mathrm{EndIf};$ $\mathrm{If}\left(r\right[nl-1]=r[nu+1\left]\right)nl-=1;nu+=1;er+=r\left[nl\right]+r\left[nu\right];\mathrm{Continue}\mathrm{EndIf};$ $\mathrm{If}\left(r\right[nl-1]>r[nu+1\left]\right)nl-=1;er+=r\left[nl\right];\mathrm{Continue}\mathrm{EndIf};$ $\mathrm{If}\left(r\right[nl-1]<r[nu+1\left]\right)nu+=1;er+=r\left[nu\right];\mathrm{Continue}\mathrm{EndIf};$ $\mathrm{until}\left(\mathrm{false}\right);$ $ne\leftarrow 1-er;$

Algorithm 4:  Algorithm for minimal departure (adapted from A2 in [123])

$\mathit{Input}\mathit{data}:x,\alpha$ //$x\in {\mathbb{N}}^{*}$ the Poisson parameter, $\alpha \in (0,0.5)$ the significance level $\mathit{Output}\mathit{data}:nl,nu,ne$ //$nl,nu\in {\mathbb{N}}^{*}$ the CI boundaries, $ne$ the true coverage $r\leftarrow \mathrm{FPoisson}(x,\alpha );m\leftarrow \mathrm{Count}\left(r\right);$ //See Equation (11) $(nl,nu,ne)\leftarrow \mathrm{Algorithm\; 3}(x,\alpha );er=1-ne;$ $\mathrm{repeat}$ $\mathrm{If}(nu\le nl)\mathrm{Break};$ $\mathrm{If}\left(\right(r\left[nl\right]=r\left[nu\right]\left)\mathrm{and}\right(|1-\alpha -er|>|1-\alpha -er+r[nl]+r[nu\left]\right|\left)\right)$ $er+=r\left[nl\right]+r\left[nu\right];nl+=1;nu-=1;\mathrm{Break};$ $\mathrm{EndIf}$ $\mathrm{If}\left(\right(r\left[nl\right]<r\left[nu\right]\left)\mathrm{and}\right(|1-\alpha -er|>|1-\alpha -er+r[nl\left]\right|\left)\right)$ $er+=r\left[nl\right];nl+=1;\mathrm{Break};$ $\mathrm{EndIf}$ $\mathrm{If}\left(\right(r\left[nl\right]>r\left[nu\right]\left)\mathrm{and}\right(|1-\alpha -er|>|1-\alpha -er+r[nu\left]\right|\left)\right)$ $er+=r\left[nu\right];nu-=1;\mathrm{Break};$ $\mathrm{EndIf}$ $\mathrm{until}\left(\mathrm{false}\right);$ $ne\leftarrow 1-er;$

Algorithm 5:  Algorithm for the closest but not greater significance (adapted from A3 in [123])

$\mathit{Input}\mathit{data}: x,\alpha$ //$x\in {\mathbb{N}}^{*}$ the Poisson parameter, $\alpha \in (0,0.5)$ the significance level $\mathit{Output}\mathit{data}:nl,nu,ne$ //$nl,nu\in {\mathbb{N}}^{*}$ the CI boundaries, $ne$ the true coverage $r\leftarrow \mathrm{FPoisson}(x,\alpha );m\leftarrow \mathrm{Count}\left(r\right);$ //See Equation (11) $(nl,nu,ne)\leftarrow \mathrm{Algorithm\; 4}(x,\alpha );er=1-ne;$ $\mathrm{repeat}$ $\mathrm{If}(er\ge 1-\alpha )\mathrm{Break};$ $\mathrm{If}\left(\right(nl=0\left)\mathrm{and}\right(nu=m\left)\right)\mathrm{Break};$ $\mathrm{If}(nl=0)nu+=1;er+=r\left[nu\right];\mathrm{Continue};$ $\mathrm{If}(nu=m)nl-=1;er+=r\left[nl\right];\mathrm{Continue};$ $\mathrm{If}\left(r\right[nl-1]=r[nu+1\left]\right)nl-=1;nu+=1;er+=r\left[nl\right]+r\left[nu\right];\mathrm{Continue};$ $\mathrm{If}\left(r\right[nl-1]<r[nu+1\left]\right)nl-=1;er+=r\left[nl\right];\mathrm{Continue};$ $\mathrm{If}\left(r\right[nl-1]>r[nu+1\left]\right)nu+=1;er+=r\left[nu\right];\mathrm{Continue};$ $\mathrm{until}\left(\mathrm{false}\right);$ $ne\leftarrow 1-er;$

4.2. Theoretical Analysis of Algorithms 3–5

Algorithms 3–5 were designed to compute CIs for the Poisson distribution parameter with a range of significance levels $\alpha \in [0,0.5]$. Each algorithm adapts classical approaches to find minimal coverage or significance departure, ensuring the constructed intervals meet desired confidence levels effectively.

The algorithm for minimal effort (Algorithm 3, adapted from A1 of [123]) begins with the exact Poisson cumulative probabilities $r=\mathrm{FPoisson}(x,\alpha ))$ for a Poisson parameter x and significance level $\alpha$. It iteratively adjusts the lower $nl$ and upper $nu$ bounds of the CI to maintain the coverage probability $ne=1-er$ (where $er$ is the summation of the tail probabilities outside the interval) just reaching or exceeding $1-\alpha$. The routine balances the interval symmetrically by comparing probabilities at the boundaries, and expands or contracts the interval with minimal effort to achieve nominal coverage. This approach ensures continuous intervals without gaps, and enlarges the interval only to the minimal extent necessary to achieve the required coverage. The loop terminates when coverage is adequate or when boundaries reach the global range. The complexity is proportional to the number of counts m in r, ensuring accuracy with efficient trimming.

The algorithm for minimal departure (Algorithm 4, adapted from A2 of [123]) refines the output of the minimal effort algorithm (Algorithm 3) by iteratively testing whether removing extreme values from the interval (either from $nl$ or from $nu$) reduces the departure of the coverage from the nominal $1-\alpha$ level. It prioritizes moves that reduce the absolute difference $|1-\alpha -err|$. By minimizing the absolute coverage error, this algorithm can produce intervals closer to the nominal coverage, but may stop early if further improvements are not beneficial. This strategy gives a local search for minimal deviation, providing potentially tighter intervals than minimal effort by balancing under- and over-coverage considerations.

The algorithm for closest but not greater significance (Algorithm 5, adapted from A3 of [123]) further adjusts the interval found by the minimal departure algorithm (Algorithm 4), expanding it if the current coverage $er$ is less than the nominal $\alpha$, stopping as soon as coverage reaches or exceeds $1-\alpha$, but never exceeding it. Algorithm 5 tries to obtain coverage as close as possible to the intended confidence level without going beyond it, thus strictly controlling type I error under the nominal level, being useful in hypothesis testing where exact control of the significance level is critical, and ensuring the CI is not overly conservative.

Algorithms 3–5 provide iterative optimization routines for discrete distributions since exact coverage calculation and discrete steps pose challenges, relying on cumulative probabilities and carefully adding or removing points to minimize coverage error, length, or deviation from the significance threshold.

Lower and upper boundaries ($nl$ and $nu$ in Algorithms 3–5 as integers), as well as true coverage ($ne$, as probability), are collected by the algorithms. Each algorithm is given as a refinement of the solution proposed by the previous one.

An important behavior is related to monotony. All algorithms provide monotonic increases in the boundaries. To show this fact, the first nine confidence intervals are provided in Table 2.

Table 2. CI for Poisson(x; x) with Algorithms 3–5 and their true coverages for $\alpha =5\%$.

For	Algorithm 3			Algorithm 4			Algorithm 5
$\mathit{x}$	${\mathit{CI}}_{\mathrm{Low}}$	${\mathit{CI}}_{\mathrm{Upp}}$	${\mathit{\alpha }}_{\mathrm{True}}$	${\mathit{CI}}_{\mathrm{Low}}$	${\mathit{CI}}_{\mathrm{Upp}}$	${\mathit{\alpha }}_{\mathrm{True}}$	${\mathit{CI}}_{\mathrm{Low}}$	${\mathit{CI}}_{\mathrm{Upp}}$	${\mathit{\alpha }}_{\mathrm{True}}$
2	0	5	1.7	0	4	5.3	0	5	1.7
3	0	6	3.4	0	6	3.4	0	6	3.4
4	1	8	4.0	1	8	4.0	1	8	4.0
5	1	9	3.9	1	9	3.9	1	9	3.9
6	2	11	3.7	2	10	6.0	1	10	4.5
7	2	12	3.4	3	12	5.7	3	13	4.2
8	3	13	4.8	3	13	4.8	3	13	4.8
9	4	15	4.3	4	15	4.3	4	15	4.3
10	4	16	3.7	5	16	5.6	5	17	4.4

The monotonicity in the $C{I}_{\mathrm{Low}}$ and $C{I}_{\mathrm{Upp}}$ series is visible for all three algorithms for the first nine confidence intervals expressed in Table 2. Furthermore, the $C{I}_{\mathrm{Low}}$ and $C{I}_{\mathrm{Upp}}$ series are monotone for the values of x till 500, where this simulation ended. The same monotony applies to the width of the confidence interval—all proposed solutions provide monotonic increases in the width of the confidence interval till 500, where this simulation ended. It is thus very likely that the monotonies are to be kept for any arbitrary value of x.

However, the solutions proposed by Algorithms 3–5 are different in general. Therefore, for $x=6$, Algorithm 3 proposes [2, 11] (with a true coverage of 3.7%), Algorithm 4 proposes [2, 10] (with a true coverage of 6.0%), and Algorithm 3 proposes [1, 10] (with a true coverage of 4.5%).

The solutions proposed by Algorithms 3–5 are related to one another. Thus, ${CI}_{\mathrm{Alg}.4}\subseteq {CI}_{\mathrm{Alg}.3}$ and ${CI}_{\mathrm{Alg}.4}\subseteq {CI}_{\mathrm{Alg}.5}$ for any x from the studied range (2 to 500). Therefore, ${CI}_{\mathrm{Alg}.4}$ is the shortest from all three, and the intersection of the other two (Equation (12)).

$${CI}_{\mathrm{Alg}.4}={CI}_{\mathrm{Alg}.3}\cap {CI}_{\mathrm{Alg}.5}$$

(12)

4.3. Graphical Representations of the Confidence Intervals

Figure 1 depicts the confidence intervals relative to the mean (x). Despite appearances, these intervals are not symmetric (see as examples ${CI}_{\mathrm{Alg}.3}$(6;6) = [2, 11], ${CI}_{\mathrm{Alg}.4}$(7;7) = [2, 12], and ${CI}_{\mathrm{Alg}.5}$(7;7) = [3, 13] in Table 2).

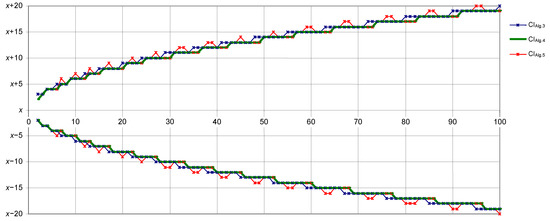
Figure 1. Poisson distribution 95% confidence intervals for $x=2,\dots ,100$.

It is visible how the upper boundary of the solutions proposed by Algorithm 3 and by Algorithm 5 jumps up and returns back to the green line expressing the solution proposed by Algorithm 4. Notably, the jumps are not simultaneous. Similarly, the lower boundary interval of the solutions proposed by Algorithm 3 and by Algorithm 5 jumps down and returns back to the green line expressing the solution proposed by Algorithm 4. Additionally, the jumps are not simultaneous with the jumps from the upper boundary and not simultaneous from one algorithm to another. It is an expected behavior, since each algorithm is seeking for boundaries providing true coverages near the imposed $\alpha$ level.

Another remark is about the tendency of the boundaries, made by irregular but monotonic steps (upper are increasing, lower are decreasing). The tendency in the $x=2,\dots ,100$ range is approximated by a linear function of the square root of the Poisson parameter (for instance, ${CI}_{\mathrm{Low},\mathrm{Alg}.3}(x;\alpha =0.05)\approx x+0.553-1.960\sqrt{x}$ for $x=2,\dots ,100$). However, this is only a tendency observed for small x, and the dependency is slightly more complicated. For instance, ${CI}_{\mathrm{Low},\mathrm{Alg}.3}(x;\alpha =0.05)$ for $x=100,\dots ,200$ is better approximated by $x+1-{\left({\displaystyle \frac{a}{x+a}}\right)}^b$, with $a\approx 0.231$ and $b\approx -0.494$ (see Figure 2).

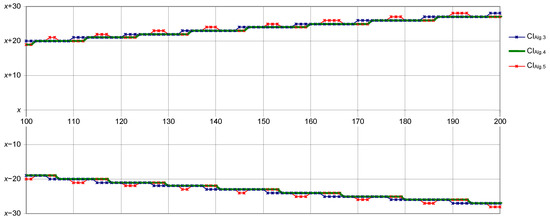
Figure 2. Poisson distribution 95% confidence intervals for $x=100,\dots ,200$.

A good approximation for ${CI}_{\mathrm{Low},\mathrm{Alg}.4}(x;\alpha =0.05)$ (with $r^2\approx 0.999$ in the range of $x=2,\dots ,500$) is $x+0.759-1.960\sqrt{x}$ while for ${CI}_{\mathrm{Upp},\mathrm{Alg}.4}(x;\alpha =0.05)$ (with $r^2\approx 0.999$ in the range of $x=2,\dots ,500$) is $x-0.295+1.962\sqrt{x}$.

The obtained values of the confidence boundaries for $x=2,\dots ,500$ with Algorithms 3–5 are given in Appendix A (Table A1).

The width of the 95% confidence interval is about $4\sqrt{x}-1$.

4.4. Graphical Representations of the Error Bounds

True significance levels (or errors, Er (%) = 100% − True coverage (%)) of the confidence intervals obtained with Algorithms 3–5 are depicted in the following three figures (Figure 3, Figure 4 and Figure 5).

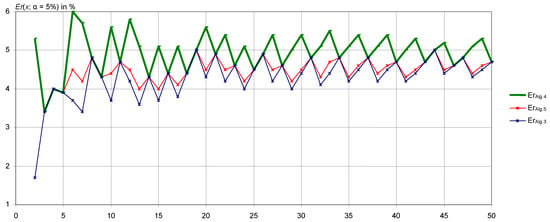
Figure 3. True coverage of 95% confidence intervals for $x=2,\dots ,50$.

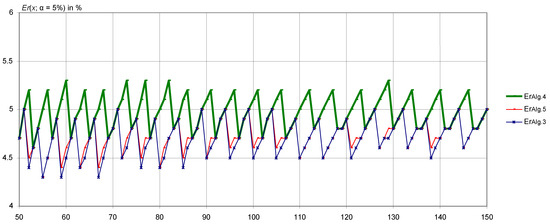
Figure 4. True coverage of 95% confidence intervals for $x=50,\dots ,150$.

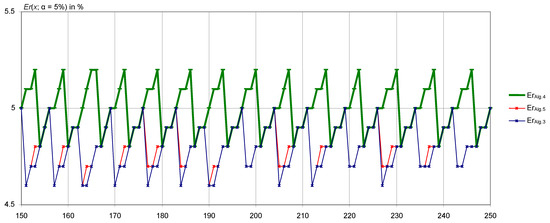
Figure 5. True coverage of 95% confidence intervals for $x=150,\dots ,250$.

The blue line (${\mathrm{Er}}_{\mathrm{Alg}.4}$) and the green line (${\mathrm{Er}}_{\mathrm{Alg}.4}$) alternate around a middle line located near the red line in a nearly symmetrical reflection. There are a few exceptions breaking the symmetry, which are visible in all three figures (Figure 3, Figure 4 and Figure 5).

The true significance level (and the true coverage) calculated by Algorithm 4 oscillates on both sides of the imposed level of 5% (and of the expected coverage of 95%), while the true significance level (and the true coverage) calculated by Algorithms 3 and 5 are always below the imposed level of 5% (and true coverages are above the expected coverage of 95%).

When comparing the solution proposed by Algorithm 3 with the solution proposed by Algorithm 5, the coverage of Algorithm 5 is better, closer to the imposed level at all times.

In any instance, representations of the true significance levels for larger values of the Poisson parameter (Figure 4 and especially Figure 5) show that the solutions proposed by Algorithms 3 and 5 tend (with increasing Poisson parameter x) to overlap and to mirror with the solution proposed by Algorithm 4.

There is no limit for the value of the Poisson parameter. In the case of typical statistics of the Poisson distribution, their value is calculable exactly, by knowing the parameter of the distribution, but the quality of coverage of the confidence intervals can be obtained only for the values for which Algorithms 3–5 were executed. Thus, having an image of the tendency is useful. The tendencies for the true significance levels, provided by the alternatives Algorithms 3–5 for confidence intervals, are expressed as averages and deviations in Table 3.

Table 3. Tendencies in the true coverages (in %) for $\alpha =5\%$ for Algorithms 3–5, expressed with averages and deviations.

	$\mathit{Avg}\left(\mathit{x}\right)$			$\mathit{StD}\left(\mathit{x}\right)$			$\mathit{Dev}\left(\mathit{x}\right)$
$\mathit{x}$	Alg. 3	Alg. 4	Alg. 5	Alg. 3	Alg. 4	Alg. 5	Alg. 3	Alg. 4	Alg. 5
5	3.25	4.15	3.25	1.07	0.81	1.07	1.98	1.10	1.98
10	3.66	4.78	3.91	0.86	0.92	0.92	1.57	0.90	1.39
50	4.29	4.95	4.42	0.56	0.50	0.50	0.90	0.50	0.76
100	4.48	4.96	4.56	0.46	0.38	0.40	0.69	0.38	0.59
500	4.76	4.99	4.78	0.27	0.20	0.23	0.36	0.20	0.32

Alg.: Algorithm, $Avg\left(x\right)={\displaystyle \frac{{\displaystyle \sum _{k=2}^x}Er(k;\alpha )}{x-2}}$, $StD\left(x\right)=\sqrt{{\displaystyle \sum _{k=2}^x}{\displaystyle \frac{{(Er(k;\alpha )-Avg\left(k\right))}^2}{x-3}}}$, $Dev\left(x\right)=\sqrt{{\displaystyle \sum _{k=2}^x}{\displaystyle \frac{{(Er(k;\alpha )-\alpha )}^2}{x-2}}}$.

The desire to always have a confidence level with at least the imposed significance is implemented in Algorithms 3 and 5, and it comes with a cost in terms of the closeness to the imposed level.

Inspecting the $Avg$, $StD$, and $Dev$ values from Table 3, one can appreciate the solution proposed by Algorithm 3 as the poorest one. It performs the worst at all indicators and its behavior is systematic. In the same series of indicators, one can appreciate the (accelerated) tendency in $Avg$ for Algorithm 4 to the imposed level, as well as the fact that it performs the best at all indicators. The only disadvantage of the solution proposed by Algorithm 4 remains that it oscillates (above and below) around the imposed level, being unsuited for the applications requiring strict coverage of at least $1-\alpha$.

5. Modifications to the Poisson Distribution

5.1. Zero-Inflated Poisson (ZIP) Distribution

ZIP [124,125,126,127,128] is a model for count data with excess zeros; it assumes with a probability that the only possible observation is 0, and the alternate event is a Poisson random variable—when manufacturing equipment is properly aligned, defects may be nearly impossible, but when it is misaligned, defects may occur, according to a Poisson distribution (Equation (13)).

$$\mathrm{ZIP}(x;z,\nu )=\left\{\begin{array}{cc}1-\nu +\nu \mathrm{Poisson}(0;z),\hfill & \mathrm{for}x=0\hfill \\ \nu \mathrm{Poisson}(x;z),\hfill & \mathrm{for}x>0\hfill \end{array}\right.$$

(13)

5.2. Conway–Maxwell–Poisson (CMP) Distribution

CMP distribution [129] generalizes the Poisson distribution [4] by adding a parameter ($\nu$ in Equation (14)) to model overdispersion and underdispersion, having Poisson distribution and geometric distribution as special cases, and the Bernoulli distribution as a limiting case [130,131,132]. Equation (14) provides the PMF for this distribution:

$$\mathrm{CMP}(y;z,\nu )={\displaystyle \frac{z^y}{{(y!)}^{\nu }}}{\left(\sum _{j=0}^{\infty }{\displaystyle \frac{z^j}{{(j!)}^{\nu }}}\right)}^{-1}$$

(14)

When $\nu =1$, ordinary Poisson distribution results in (${\displaystyle \frac{z^y}{y!}}{\mathrm{e}}^{-z}$); when $\nu =0$ and $z<1$, the distribution is geometric ($z^y(1-z)$); and as $\nu \to \infty$, the distribution is Bernoulli ($z{(1+z)}^{-1}$).

5.3. Consul–Jain–Poisson (CJP) Distribution

CJP distribution [133] generalizes (with $\theta$ in Equation (15)) the Poisson distribution [4] as a limit case from generalized negative binomial distribution [134], while multivariate distributions for count data derived from the Poisson distribution are reviewed in [135]. Equation (15) provides the PMF for this distribution:

$$\mathrm{CJP}(y;z,\nu )={\displaystyle \frac{\nu {(\nu +yz)}^{y-1}}{y!}}{\mathrm{e}}^{-\nu -yz}$$

(15)

describing an event that occurs rarely in a short period, but having its occurrence for longer periods of time [136].

5.4. Pólya–Aeppli–Poisson (PAP) Distribution

PAP distribution, or geometric extension of Poisson distribution (Equation (16)), was introduced in [137] and further reported in [138] and in [139].

$$\mathrm{PAP}(x;z,\nu )=\left\{\begin{array}{cc}{\mathrm{e}}^{-z},\hfill & \mathrm{for}x=0\hfill \\ \sum _{k=1}^x\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{k-1}}\right){(1-\nu )}^{x-k}{\nu }^k\mathrm{Poisson}(k;z),\hfill & \mathrm{for}x>0\hfill \end{array}\right.$$

(16)

It is used for describing objects that come in clusters (groups of students may apply here), where the number of clusters follows a Poisson distribution and the number of objects within a cluster follows a geometric distribution, as noted in [140]. It is referred to as geometric Poisson distribution in [141,142,143,144].

5.5. Snyder–Ord–Beaumont (SOB) Distribution

SOB distribution, or hurdle-shifted Poisson distribution (Equation (17)), was introduced in [145].

$$\mathrm{SOB}(x;z,\nu )=\left\{\begin{array}{cc}\nu ,\hfill & \mathrm{for}x=0\hfill \\ (1-\nu )\mathrm{Poisson}(x-1;z),\hfill & \mathrm{for}x>0\hfill \end{array}\right.$$

(17)

When evaluations take place in a particular period, their combined size is assumed to follow a shifted Poisson distribution (Equation (17)) defined by Y = X + 1, where X follows the classical Poisson distribution (Equation (3)). This shift to the right leaves the probability of a zero to be defined by a new parameter ($\nu$ in Equation (17)).

5.6. Other Modifications

Before proceeding, it is helpful to establish a skeleton for defining the PMF via CDF:

$${\mathrm{PMF}}_f(x;pars)=\left\{\begin{array}{cc}{\mathrm{CDF}}_f(0;pars),\hfill & \mathrm{for}x=0\hfill \\ {\mathrm{CDF}}_f(x;pars)-{\mathrm{CDF}}_f(x-1;pars),\hfill & \mathrm{for}x>0\hfill \end{array}\right.$$

(18)

where f is the selected discrete distribution and $pars$ are its parameters.

Please note that the definition of Equation (18) is valid only for discrete distributions having $x=0$ as the first value of their domain.

Exponentiated Poisson (EP) distribution [146,147,148] is defined by Equation (19).

$$\begin{array}{cc}\hfill & {\mathrm{CDF}}_{\mathrm{EP}}(x;z,\nu )={\left(\mathrm{Poisson}(x,z)\right)}^{\nu },\hfill \\ \hfill & \mathrm{EP}(x;z,\nu )={\mathrm{PMF}}_{\mathrm{EP}}(x;z,\nu )\hfill \end{array}$$

(19)

with PMF from Equation (18).

EP (from Equation (19)) is a typical example from a more general case. Imagine a distribution (continuous or discrete) having a certain cumulative distribution function (CDF). Let it be $f_{\mathrm{CDF}}(x;pars)$. Then, with one more parameter (let $\gamma$ be the new parameter), a new distribution can be imagined (let it be $g_{\mathrm{CDF}}(x;\gamma ,pars)$), having the CDF be the previous one raised to an arbitrary power ($\gamma$): $g_{\mathrm{CDF}}(x;\gamma ,pars)\leftarrow {\left(f_{\mathrm{CDF}}(x;\gamma ,pars)\right)}^{\gamma }$. Such a definition of a distribution is consistent in all instances except $\gamma \le 0$, since, at the limit of the domain: $f_{\mathrm{CDF}}(\underset{x\in X}{sup}x;pars)=1$, $1^{\gamma }=1$, and thus $g_{\mathrm{CDF}}(\underset{x\in X}{sup}x;\gamma ,pars)=1$.

Transmutated Poisson (TP) distribution [149] is defined by Equation (20).

$$\begin{array}{cc}\hfill & {\mathrm{CDF}}_{\mathrm{TP}}(x;z,\nu )=(1+\nu )\mathrm{Poisson}(x,z)-\nu {\left(\mathrm{Poisson}(x,z)\right)}^2,\hfill \\ \hfill & \mathrm{TP}(x;z,\nu )={\mathrm{PMF}}_{\mathrm{TP}}(x;z,\nu )\hfill \end{array}$$

(20)

with PMF from Equation (18).

TP (from Equation (20)) is also a typical example from a more general case. Consider the function $f(u,v)=(1+u)v-u{v}^2$. Using its derivatives, one can prove that $f(u,v)$ is increasing from $v=0$ (where is 0) to $v=1$ (where is 1). Thus, any such construction is suited to define a distribution from any other distribution.

Another modification to the Poisson distribution is zero-modified Poisson (ZMP), with yet another limit case, zero-truncated Poisson (ZTP) [150,151,152,153,154] as in Equations (21) and (22).

$$\mathrm{ZMP}(x;z,\nu )=(1-\nu )\mathrm{Poisson}(x;0)+\nu \mathrm{Poisson}(x;z)$$

(21)

A particular case of ZMP (from Equation (21)) is when $\nu =1$, leading to the classical Poisson from Equation (3), while another particular case is $\nu ={\displaystyle \frac{e^z}{e^z-1}}$, leading to zero-truncated Poisson of Equation (22).

$$\mathrm{ZTP}(x;z)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for}x=0\hfill \\ {(1-e^{-z})}^{-1}\mathrm{Poisson}(\mathrm{x};\mathrm{z}),\hfill & \mathrm{for}x>0\hfill \end{array}\right.$$

(22)

Modified Poisson distributions arise as adaptations or extensions of the classical Poisson distribution to address limitations such as overdispersion, heterogeneity in counts, or clustering effects. To sum up, the above listed distributions extend the classical Poisson model to handle features like excess zeros, dispersion changes, or truncation, each useful in different applied contexts. Thus, ZIP (Equation (13)) models count data with more zeros than a standard Poisson would predict. By mixing a point mass at zero with a Poisson, CMP (Equation (14)) adds a dispersion parameter to handle overdispersion or underdispersion relative to Poisson, CJP (Equation (15)) introduces an extra parameter to accommodate variability and skewness, connected to queueing models, PAP (Equation (16)) mixes geometric and Poisson processes, being useful in clustering or batch arrival contexts, and SOB (Equation (17)) was designed for counting time series with autocorrelation and variable mean. EP (Equation (19)) applies an exponentiation transformation to the Poisson CDF to produce flexible tails and shapes, TP (Equation (20)) adds a skewing parameter via transmutation to adjust shape and kurtosis, ZMP (Equation (21)) alters the Poisson’s zero probability independently, allowing probability mass at zero to differ from a standard Poisson, and ZTP (Equation (22)) is a Poisson distribution conditioned to exclude zero counts, often used when zero observations are impossible or unrecorded.

In the light of the above-given generalizations, one should recognize that there are other modifications to the Poisson distribution too (such as Gamma–Poisson local level [155,156], and linear transformation of the Poisson distribution [157]), which will not be covered here.

5.7. Alternatives to the Poisson Distribution

Poisson distribution have a simple expression, depending only on one parameter, giving great parsimony [158]. This is a great advantage which does have limitations, namely the strict assumption that the mean equals the variance (equidispersion). Real-world count data may exhibit overdispersion (variance greater than the mean) or underdispersion (variance less than the mean), which the standard Poisson model cannot handle. From another point of view, even if it is not a common known fact, the Poisson distribution was originally derived as a limit of the negative binomial distribution [4,159]. Knowing this, it is no longer surprising that, in many instances, including [160,161,162,163], negative binomial distribution has been reported as a better alternative to Poisson distribution for modeling the populations of the sampled data. Other considered alternatives for certain instances were geometric distribution in [164], Gaussian distribution in [165], and Weibull and hyperexponential in [166].

5.8. Connections with Other Distributions

Poisson arrivals with the rate z imply exponentially distributed waiting times between arrivals with the same rate z and vice versa, making these distributions tightly linked in modeling random event arrivals over time, so if one records arrival times and identifies a Poisson distribution, then another will identify inter-arrival times as exponentially distributed [167,168,169]. The key property is that the inter-arrival times between consecutive arrivals in a Poisson process are independent and identically distributed exponential random variables. If the Poisson process has rate z, then each inter-arrival time follows an exponential distribution with parameter z. This means the expected time between arrivals is $1/z$. Intuitively, the memoryless property of the exponential distribution aligns with the independent increments property of the Poisson process: the waiting time until the next arrival does not depend on when previous arrivals occurred.

6. Conclusions

The Poisson distribution finds extensive application across diverse fields. It is used for studying and characterizing phenomena such as Brownian motion collisions, quantum states, electromagnetic radiation scattering, radiation emission and particle decay, cosmic rays, distribution of stars in space, signal errors, manufacturing defects, and new product development. Additionally, the literature reports numerous simulations and models for a variety of processes including ship arrivals, flight delays, traffic flow, network traffic, email spam, phone calls, website traffic, GSM signals, various types of accidents, mutations in nucleic acids and cells, natural disasters, hospital arrivals and disease outbreaks, medical errors, customer service call volumes, purchasing and sales activities, store traffic, and product returns.

To determine if a data sample follows a Poisson distribution, statistical tests are recommended. Four such tests summarized here are the conditional chi-squared, likelihood ratio, Bartlett–Anscombe, and normality statistics.

For estimation, confidence intervals should be used. Due to the discrete nature of the Poisson distribution, no closed-form formula exists for confidence intervals, and algorithms must be employed for their computation. Three algorithms are presented here, of which one algorithm (Algorithm 4) achieves coverage closest to the desired level, and another (Algorithm 5) provides the closest approach for at least the prescribed coverage.

The many extensions of the Poisson distribution, such as the Zero-Inflated Poisson (ZIP), Conway–Maxwell–Poisson (CMP), Compound Poisson (CJP), Poisson Autoregressive Process (PAP), and others (SOB, EP, TP, ZMP, ZTP), highlight the model’s simplicity, but also its inherent limitations.

Alternatives and extensions to Poisson distribution provide more flexibility by relaxing the strict Poisson assumption of equal mean and variance, leading to better fit and more accurate modeling of count data. Poisson distribution serves as a key limiting and building-block distribution that links to the binomial, multinomial, negative binomial, gamma, and several other distributions.