The λ-Fold Spectrum Problem for the Oriented Pentagons

Abstract

A D-decomposition of a directed graph G is a collection of arc-disjoint subgraphs of G, each isomorphic to D, such that every arc of G belongs to exactly one subgraph. The $\lambda$-fold spectrum problem for a directed graph D asks for the set of all integers v such that the $\lambda$-fold complete symmetric directed graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a D-decomposition. A five-cycle (pentagon) has 4 non-isomorphic orientations. The $\lambda$-fold spectrum problem has been solved for one of these oriented pentagons. In this paper, we provide a complete solution for each of the remaining three orientations, proving that the necessary and sufficient condition is $5\mid \lambda v(v-1)$ in all cases.

1. Introduction

Let m and n be positive integers with $m\le n$. We denote by $[m,n]$ the set of all integers from m to n, inclusive. For a graph or directed graph G with vertex set $V\left(G\right)$ and edge (or arc) set $E\left(G\right)$, the order and size of G are $\left|V\right(G\left)\right|$ and $\left|E\right(G\left)\right|$, respectively. We write ${\phantom{G}}^{\lambda }G$ for the multigraph (or directed multigraph) obtained from G by replacing each edge (or arc) in $E\left(G\right)$ with $\lambda$ parallel copies. Here, $\lambda$ represents the multiplicity of each edge/arc, meaning that in ${\phantom{G}}^{\lambda }G$, each unordered pair $\{x,y\}$ (or ordered pair $(x,y)$ in the directed case) is connected by exactly $\lambda$ distinct edges (or arcs). This construction generalizes the underlying graph G to a uniform multigraph where all edge multiplicities equal $\lambda$. The graph $K_{a\times b}$ denotes the complete equipartite graph with a parts of size b each. In addition, we use the notation $K_{a\times b,c}$ to refer to the complete multipartite graph with a parts of size b and one part of size c.

In the undirected setting, a decomposition of a graph G is a collection of subgraphs $\mathcal{H}=\{H_1,H_2,\dots ,H_t\}$ such that $E\left(G\right)={\bigcup }_{i\in [1,t]}E\left(H_i\right)$ and $E\left(H_i\right)\cap E\left(H_j\right)=\varnothing$ for all $i\ne j$. In other words, the edge sets of these subgraphs form a partition of the edge set of G. If each subgraph $H_i$ is isomorphic to a fixed graph H, then $\mathcal{H}$ is called an H-decomposition of G. The spectrum of H is the set of all positive integers v for which the complete graph $K_v$ admits an H-decomposition. Similarly, the λ-fold spectrum of H is the set of all v for which the $\lambda$-fold complete multigraph ${\phantom{K}}^{\lambda }{K}_v$ admits an H-decomposition. The spectrum problem for $\lambda =1$ has been extensively studied and settled for various classes of simple graphs, including cycles, paths, and stars (see [1] for a survey).

Analogous concepts to those introduced above for undirected graphs can naturally be extended to directed graphs. Throughout this work, we use curly braces (e.g., $\{x,y\}$) to denote undirected edges, and parentheses (e.g., $(x,y)$) to denote directed arcs. Given an undirected simple graph G, we define its symmetric directed graph $G^{*}$ as the directed graph with vertex set $V\left(G^{*}\right)=V\left(G\right)$ and arc set $E\left(G^{*}\right)={\bigcup }_{\{x,y\}\in E\left(G\right)}\{(x,y),(y,x)\}$; that is, each undirected edge $\{x,y\}$ is replaced with a pair of symmetric arcs $(x,y)$ and $(y,x)$. Using this construction, we define ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ as the $\lambda$-fold complete symmetric directed graph on v vertices, and ${\phantom{K^{*}}}^{\lambda }{K}_{a\times b}^{*}$ as the $\lambda$-fold complete symmetric equipartite directed graph with a parts, each of size b.

Let G be a digraph. A D-decomposition of G is a collection $\mathcal{D}=\{D_1,D_2,\dots ,D_t\}$ of pairwise arc-disjoint subgraphs of G, each isomorphic to a fixed directed graph D, such that $E\left(G\right)={\bigcup }_{i\in [1,t]}E\left(D_i\right)$. As with the undirected setting, a D-decomposition of G is also referred to as a $(G,D)$-design. The spectrum of D is defined as the set of all positive integers v for which the complete symmetric directed graph $K_v^{*}$ admits a D-decomposition. Similarly, the λ-fold spectrum of D is the set of all v for which the $\lambda$-fold complete symmetric directed graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a D-decomposition.

The number of non-isomorphic orientations of a cycle of order n, denoted by $o\left(C_n\right)$, is given by a known formula (see [2]). In particular, $o\left(C_3\right)=2$, $o\left(C_4\right)=o\left(C_5\right)=4$, $o\left(C_6\right)=9$, $o\left(C_7\right)=10$, and $o\left(C_8\right)=22$. The spectrum problem for all bipartite directed graphs on four vertices containing up to five arcs was determined in [3]. Certain subgraphs of $K_4^{*}$, both bipartite and non-bipartite, have also been studied in this context [4,5,6,7,8]. The two non-isomorphic orientations of $C_3$ are known as the cyclic and transitive orientations. If D is the cyclic orientation, a $(K_v^{*},D)$-design is called a Mendelsohn triple system, whose spectrum was independently determined by Mendelsohn [7] and Bermond [4]. For the transitive orientation of $K_3$, the corresponding $(K_v^{*},D)$-design is referred to as a transitive triple system, and its spectrum was found by Hung and Mendelsohn [6]. Hartman and Mendelsohn [9] determined the spectra of all other simple connected subgraphs of $K_3^{*}$. The spectrum problem for the cyclic orientation of a four-cycle (also called a quadrilateral) was completely solved in [8], while the remaining three orientations were addressed in [5]. Alspach et al. [10] showed that each of the four orientations of a five-cycle (also known as a pentagon) can decompose $K_v^{*}$ under certain congruence conditions on v. In [11], it was proved that for any positive integers m and v with $2\le m\le v$, the directed graph $K_v^{*}$ can be decomposed into directed cycles of length m (i.e., with all arcs oriented in the same direction), except for a few specific pairs $(m,v)$. The spectrum problem for all ten non-isomorphic orientations of a seven-cycle (heptagon) was completely solved in [12]. The $\lambda$-fold spectrum problem was determined for all orientations of the six-cycle in [13], and later for all orientations of the eight-cycle in [14].

Graphs, directed graphs, and multigraphs are fundamental mathematical structures that play a crucial role in various fields, including computer science, logistics, chemistry, and biology. In particular, directed graphs have numerous real-world applications, such as modeling social networks, communication systems, electrical circuit design, network flow analysis, and biological interactions (see [15]). In this context, graph decomposition, an essential concept in both graph theory and combinatorial design theory, focuses on breaking down complex structures into simpler, well-organized components. Many problems in these areas can be formulated in terms of decomposing graphs into specified subgraphs. Beyond its theoretical importance, graph decomposition has practical applications in areas such as graph similarity and matching [16], as well as parallel computation on large-scale graphs [17], among others.

Among all graph classes, cycles have been extensively studied in the context of the spectrum problem, which naturally extends to oriented cycles in directed graphs. Determining the spectrum for odd cycles is generally more challenging than for even cycles, and this difficulty is further amplified when considering multigraphs.

As previously mentioned, there are four non-isomorphic orientations of a pentagon, which we denote by $D_1,D_2,D_3$, and $D_4$, as illustrated in Figure 1. The $\lambda$-fold spectrum problem for the directed pentagon ($D_1$ in Figure 1) was completely settled in [18], where it was proved that $\lambda v(v-1)\equiv 0(mod5)$ is both necessary and sufficient for the existence of a $D_1$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ for all $\lambda \ge 1$. Subsequently, in [11], all four orientations were considered, but only in the simple case $\lambda =1$, and it was shown that $K_v^{*}$ admits a decomposition into copies of each orientation precisely when $v\equiv 0\mathrm{or}1(mod5)$. The general $\lambda$-fold spectrum problem for the remaining three orientations ($D_2,D_3,D_4$) has remained open. In this paper, we close this gap by proving that the same divisibility condition suffices for all $\lambda$, thereby providing a complete solution for each oriented pentagon.

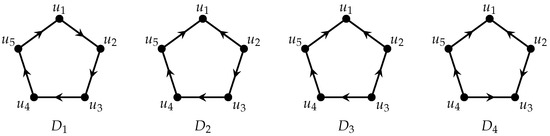
Figure 1. The four oriented pentagons. The $\lambda$-fold spectrum problem for the directed pentagon ($D_1$) has previously been settled.

Notably, oriented pentagons share the basic divisibility requirement with oriented $C_6$ and $C_8$ [13,14]: $\lambda v(v-1)$ must be divisible by the number of arcs. However, while antidirected orientations of even cycles require $\lambda (v-1)$ to be even, all four oriented pentagons are governed solely by this condition. Our work thus extends this simplified characterization from the directed case to all orientations of $C_5$. Let us now state the main result of this paper, which is proved in Section 5.

Theorem 1 

(Main Theorem). Let D be an oriented pentagon (i.e., $D\in \{D_1,D_2,D_3,D_4\}$), and let λ and v be positive integers with $v\ge 5$. There exists a D-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ if and only if $\lambda v(v-1)\equiv 0(mod5)$.

2. Preliminaries and Necessary Conditions

We begin by establishing the necessary conditions for the existence of a D-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$. These conditions follow from elementary counting arguments and will guide our constructive proofs in subsequent sections.

Lemma 1 

(Necessary Conditions). Let D be a directed graph and let $\lambda ,v$ be positive integers. If ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a D-decomposition, then the following must hold:

1. 

(Order Condition) $\left|V\right(D\left)\right|\le v$

2. 

(Size Condition) $\left|E\right(D\left)\right|$ divides $\lambda v(v-1)$

3. 

(Degree Condition) both $gcd\{d^{+}\left(x\right):x\in V\left(D\right)\}$ and $gcd\{d^{-}\left(x\right):x\in V\left(D\right)\}$ divide $\lambda (v-1)$,

where $d^{+}\left(x\right)$ and $d^{-}\left(x\right)$ denote the outdegree and indegree of vertex x in D, respectively. In particular, for any oriented pentagon $D\in \{D_1,D_2,D_3,D_4\}$ with $v\ge 5$, these conditions reduce to:

$$\lambda v(v-1)\equiv 0(mod5)$$

Proof. 

The order condition is immediate. For the size condition, observe that ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ contains exactly $\lambda v(v-1)$ arcs, while each copy of D contains $\left|E\right(D\left)\right|$ arcs. Since the decomposition partitions the arc set, we must have that $\left|E\right(D\left)\right|$ divides $\lambda v(v-1)$. For the degree conditions, note that each vertex in ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ has indegree and outdegree equal to $\lambda (v-1)$. In any D-decomposition, the indegree (respectively, outdegree) at each vertex must be expressible as a nonnegative integer combination of the indegrees (respectively, outdegrees) of vertices in D. This is possible only if the stated divisibility conditions hold.

For oriented pentagons specifically, we have $\left|E\right(D\left)\right|=5$, so the size condition requires $5\mid \lambda v(v-1)$. The degree conditions are automatically satisfied since the indegrees and outdegrees in any oriented pentagon are either 1 or 2. □

Bermond and Sotteau [18] established in 1977 that this necessary condition is also sufficient for the directed pentagon $D_1$.

Theorem 2 

([18]). Let $v\ge 5$ and $\lambda \ge 1$ be integers. Then, a $D_1$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ exists if and only if $\lambda v(v-1)\equiv 0(mod5)$.

Alspach et al. [10] showed in 1979 that each of the four orientations of a pentagon admits a decomposition of $K_v^{*}$ whenever the necessary condition is satisfied.

Theorem 3 

([10]). Let $v\ge 5$ be an integer. Then, a $D_i$-decomposition of $K_v^{*}$ exists for all $i\in [1,4]$ if and only if $v\equiv 0\mathrm{or}1(mod5)$.

We observe that any $({\phantom{G}}^{\mu }G,D)$-design can be extended to a $({\phantom{G}}^{\lambda }G,D)$-design for all positive integers $\lambda$ divisible by $\mu$, as established in the following lemma.

Lemma 2.

Let G and D be graphs or directed graphs, and let λ and μ be positive integers with $\mu \mid \lambda$. If a $({\phantom{G}}^{\mu }G,D)$-design exists, then so does a $({\phantom{G}}^{\lambda }G,D)$-design.

Proof. 

Let $k=\lambda /\mu$. View ${\phantom{G}}^{\mu }G$ (resp. ${\phantom{G}}^{\lambda }G$) as the (directed)multigraph obtained from G by replacing with $\mu$ (resp. $\lambda$) parallel copies. Let $\mathcal{D}=\{D_1,D_2,\dots ,D_t\}$ be a $({\phantom{G}}^{\mu }G,D)$-design, i.e., the arc sets $E\left(D_t\right)$ form a partition of $E\left({\phantom{G}}^{\mu }G\right)$. For each block $D_i$ and for each index $j\in [1,k]$, construct a copy $D_i^{\left(j\right)}$ isomorphic to $D_i$ on the same vertex set as G. When forming $D_i^{\left(j\right)}$, every arc $(u,v)\in E\left(D_i\right)$ of ${\phantom{G}}^{\mu }G$ is replaced by one of the k distinct parallel copies of $(u,v)$ in ${\phantom{G}}^{\lambda }G$ that correspond to the same base arc in G but belong to the j-th group of multiplicity. Since each arc of ${\phantom{G}}^{\mu }G$ is replicated exactly k times in ${\phantom{G}}^{\lambda }G$, the k families $\{D_i^{\left(j\right)}:1\le i\le t\}$ are pairwise arc-disjoint and together cover all arcs of ${\phantom{G}}^{\lambda }G$. Consequently,

$${\mathcal{D}}^{\prime }=\{D_i^{\left(j\right)}:1\le i\le t,1\le j\le k\}$$

forms a $({\phantom{G}}^{\lambda }G,D)$-design. Thus, whenever a $({\phantom{G}}^{\mu }G,D)$-design exists and $\mu \mid \lambda$, a $({\phantom{G}}^{\lambda }G,D)$-design also exists. □

The remainder of this paper is dedicated to proving the sufficiency of the necessary condition stated in Lemma 1. We achieve this by exhibiting constructions for the desired decompositions (see Section 4) using certain small examples (see Section 3.1). Henceforth, each of the graphs in Figure 1, with vertices labeled as in the figure, will be represented by $D_i[u_1,u_2,\dots ,u_5]$. For instance, $D_4[u_1,u_2\dots ,u_5]$ refers to the directed graph with vertex set $\{u_1,u_2\dots ,u_5\}$ and arc set $\{(u_2,u_1),(u_2,u_3),(u_4,u_3),(u_4,u_5),(u_5,u_1)\}$.

The following result establishes the existence of 5-cycle decompositions of complete equipartite graphs with an odd number of parts, each of size 5. We will use this result to construct a decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{(2a+1)\times 5}^{*}$ into oriented pentagons.

Lemma 3 

([10]). For every integer $a\ge 1$, there exists a $C_5$-decomposition of $K_{(2a+1)\times 5}$.

For any directed graph D, we denote by $\mathrm{Rev}\left(D\right)$ its reverse orientation, defined by $\mathrm{Rev}\left(D\right)=\left(V\right(D),\{(v,u):(u,v)\in E\left(D\right)\left\}\right)$. A key observation for our constructions is that each oriented pentagon $D_i$ (see Figure 1) is isomorphic to its reverse orientation, i.e., $\mathrm{Rev}\left(D_i\right)\cong D_i$ for all $i\in [1,4]$. This property ensures that the pair $\{D_i,\mathrm{Rev}\left(D_i\right)\}$ naturally forms a $D_i$-decomposition of $C_5^{*}$ (the symmetric directed graph whose underlying simple graph is a 5-cycle). To see this, note that $C_5^{*}$ contains exactly 10 arcs (5 edges × 2 directions), while the union $D_i\cup \mathrm{Rev}\left(D_i\right)$ contains all 10 arcs of $C_5^{*}$ exactly once, since each arc $(u,v)$ in $D_i$ corresponds to $(v,u)$ in $\mathrm{Rev}\left(D_i\right)$.

This fundamental property allows us to transition from undirected $C_5$-decompositions to directed $D_i$-decompositions, as exploited in Corollary 1 and subsequent constructions. Specifically, since an H-decomposition of a graph G induces an $H^{*}$-decomposition of $G^{*}$, we proceed as follows: First, Lemma 3 guarantees a $C_5$-decomposition of $K_{(2a+1)\times 5}$, which induces a $D_i$-decomposition of $K_{(2a+1)\times 5}^{*}$. Then, applying Lemma 2 with $\mu =1$ and $G=K_{(2a+1)\times 5}$, we obtain that $\lambda$ disjoint copies of this decomposition yield a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{(2a+1)\times 5}^{*}$.

Corollary 1.

For all positive integers a and λ, and for each $i\in [1,4]$, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{(2a+1)\times 5}^{*}$.

We also make use of the following result in Section 4; this result can be found in the Handbook of Combinatorial Designs [19].

Theorem 4.

A $K_3$-decomposition of the complete equipartite graph $K_{a\times b}$ exists if and only if the following conditions are satisfied:

1. 

$a\ge 3$,

2. 

$(a-1)b$ is even, and

3. 

$a(a-1)b^2\equiv 0(mod6)$.

One key result from [18] provides $C_5$-decompositions of the 5-fold complete tripartite graph ${\phantom{K}}^5{K}_{2\times 2,a}$, where a is either 2 or 4.

Lemma 4 

([18]). Let $a\in \{2,4\}$. There exists a $C_5$-decomposition of ${\phantom{K}}^5{K}_{2\times 2,a}$.

Using this as a base, we now present a general product-type construction, which we will prove in the following lemma, that allows such decompositions to be extended to larger graphs.

Lemma 5.

Let m and λ be positive integers, and let n be an integer with $0\le n\le m$. If ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,c}^{*}$ and ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,d}^{*}$ each admit a decomposition into subgraphs isomorphic to H, then ${\phantom{K^{*}}}^{\lambda }{K}_{ma,mb,nc+(m-n)d}^{*}$ can also be decomposed into subgraphs isomorphic to H.

Proof. 

By Theorem 4 (applied with $a=3$ and $b=m$), $K_{3\times m}$ admits a $K_3$-decomposition, since all conditions are readily verified. Let the vertex set of $K_{3\times m}$ be $X\cup Y\cup Z$ with the obvious partition into three parts of size m each. We now blow up the vertices as follows: replace each vertex in X by a set of a vertices, each vertex in Y by a set of b vertices, n vertices of Z by sets of c vertices each, and the remaining $m-n$ vertices of Z by sets of d vertices each. Each copy of $K_3$ in the $K_3$-decomposition of $K_{3\times m}$ is then replaced by a copy of $K_{a,b,c}$ (if its vertex from Z was replaced by c vertices) or by $K_{a,b,d}$ otherwise. This yields a decomposition of $K_{ma,mb,nc+(m-n)d}$ into copies of $K_{a,b,c}$ and $K_{a,b,d}$. Next, we pass to the directed setting by replacing each edge $\{u,v\}$ of $K_{ma,mb,nc+(m-n)d}$ with a pair of symmetric arcs $(u,v)$ and $(v,u)$. In this way, the decomposition of $K_{ma,mb,nc+(m-n)d}$ into $K_{a,b,c}$ and $K_{a,b,d}$ naturally extends to its symmetric directed counterpart $K_{ma,mb,nc+(m-n)d}^{*}$, which is accordingly decomposed into subgraphs isomorphic to $K_{a,b,c}^{*}$ and $K_{a,b,d}^{*}$. Finally, by applying Lemma 2, we extend this to the $\lambda$-fold setting: that lemma (with $\mu =1$) yields a decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{ma,mb,nc+(m-n)d}^{*}$ into subgraphs isomorphic to ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,c}^{*}$ and ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,d}^{*}$. Since ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,c}^{*}$ and ${\phantom{K^{*}}}^{\lambda }{K}_{a,b,d}^{*}$ each decompose into copies of H, we obtain a decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{ma,mb,nc+(m-n)d}^{*}$ into subgraphs isomorphic to H. □

Applying Lemma 4, we obtain $C_5$-decompositions of small multipartite graphs. By setting $a=b=c=2$ and $d=4$ in Lemma 5, these base cases are extended to an infinite family of larger graphs. As in the transition from $C_5$-decompositions to $D_i$-decompositions described earlier, each $C_5$-decomposition naturally induces a $D_i$-decomposition of the corresponding symmetric directed graph. Repeating this argument with multiple copies (while leveraging the index condition $\lambda \equiv 0(mod5)$), we obtain the following result.

Corollary 2.

Let m and λ be positive integers, and let n be an integer with $0\le n\le m$ and $\lambda \equiv 0(mod5)$. Then, for each $i\in [1,4]$, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{2\times 2m,4m-2n}^{*}$.

3. Small Designs

In this section, we concentrate on the constructions of small orders that facilitate the establishment of necessary base cases. These constructions, presented in Examples 1–11, were obtained via computational search conducted by the first author. Furthermore, these decompositions are extensively employed in the general constructions described in Section 4.

Given a directed graph represented by the notation $D[u_1,u_2,\dots ,u_5]$ and for $i\in {\mathbb{Z}}_n$, we define $D[u_1,u_2,\dots ,u_5]+i=D[u_1+i,$$u_2+i,$$\dots ,$$u_5+i]$, where all addition is performed modulo n. Furthermore, by convention, $\infty +i$ is interpreted as simply ∞.

3.1. Designs with $\lambda =5$

Here, we present decompositions of small 5-fold complete directed graphs found by exhaustive computer searches, which are essential for our general constructions. Please note that for any $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_v^{*}$, the number of blocks must be $5v(v-1)/5=v(v-1)$, since ${\phantom{K^{*}}}^5{K}_v^{*}$ contains $5v(v-1)$ arcs and each oriented pentagon $D_i$ contains exactly five arcs.

In each example below, we provide $(v-1)$ base blocks whose orbits under the cyclic group ${\mathbb{Z}}_v$ yield exactly $v(v-1)$ distinct $D_i$-blocks, forming the desired decomposition. The arc-disjointness of these blocks follows from the difference properties of the base blocks, while exact coverage is ensured by the fact that each nonzero difference in ${\mathbb{Z}}_v$ appears exactly five times across all base blocks and their cyclic shifts. For instance, in the $D_2$-decomposition of ${\phantom{K^{*}}}^5{K}_7^{*}$ (Example 1), the base blocks have difference multisets

$$\{6,1,3,5,4\}(\times 4),\{2,3,2,6,5\}(\times 1),\{2,4,2,2,1\}(\times 1),$$

which collectively cover each nonzero difference in ${\mathbb{Z}}_7$ exactly five times, thereby generating all required arcs when developed modulo 7.

Example 1.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_7^{*}$ be ${\mathbb{Z}}_7$ and let

$$\begin{array}{cc}\hfill & {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_7}\left\{4(D_2[0,1,2,5,3]+i),D_2[0,5,1,3,2]+i,D_2[0,5,2,4,6]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_7}\left\{4(D_3[0,1,6,2,3]+i),D_3[0,1,3,4,2]+i,D_3[0,3,1,4,2]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_7}\left\{3(D_4[0,4,2,1,3]+i),D_4[0,1,4,2,3]+i,D_4[0,3,4,2,1]+i,D_4[0,4,2,3,1]+i\right\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_7^{*}$ for $i\in \{2,3,4\}$.

Example 2.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_8^{*}$ be ${\mathbb{Z}}_8$ and let

$$\begin{array}{cc}\hfill & {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_8}\left\{4(D_2[0,3,1,2,4]+i),D_2[0,4,3,2,5]+i,D_2[0,1,3,2,5]+i,D_2[0,1,2,5,3]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_8}\left\{4(D_3[0,5,4,2,6]+i),D_3[0,1,7,4,3]+i,D_3[0,1,2,6,3]+i,D_3[0,2,1,4,3]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_8}\left\{4(D_4[0,2,3,1,4]+i),D_4[0,1,6,4,3]+i,D_4[0,1,5,6,3]+i,D_4[0,2,1,4,5]+i\right\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_8^{*}$ for $i\in \{2,3,4\}$.

Example 3.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_9^{*}$ be ${\mathbb{Z}}_9$ and let

$$\begin{array}{cc}\hfill & {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_9}\left\{4(D_2[0,6,1,2,4]+i),2(D_2[0,1,7,4,2]+i),D_2[0,7,6,5,8]+i,D_2[0,3,1,5,4]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_9}\left\{4(D_3[0,7,6,1,4]+i),2(D_3[0,2,5,4,1]+i),D_3[0,2,8,6,7]+i,D_3[0,1,3,7,4]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_9}\left\{4(D_4[0,7,2,1,4]+i),2(D_4[0,2,1,4,3]+i),D_4[0,2,4,1,8]+i,D_4[0,1,5,7,3]+i\right\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_9^{*}$ for $i\in \{2,3,4\}$.

Example 4.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_{12}^{*}$ be ${\mathbb{Z}}_{12}$ and let

$$\begin{array}{cc}\hfill & {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_{12}}\left\{5(D_2[0,10,1,2,6]+i),4(D_2[0,4,1,6,5]+i),D_2[0,1,8,4,2]+i,D_2[0,2,7,5,3]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_{12}}\left\{5(D_3[0,6,4,5,8]+i),4(D_3[0,1,4,9,5]+i),D_3[0,2,9,7,5]+i,D_3[0,2,6,3,1]+i\right\},\hfill \\ \hfill & {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_{12}}\left\{5(D_4[0,6,7,5,8]+i),4(D_4[0,1,6,9,4]+i),D_4[0,1,11,4,2]+i,D_4[0,2,10,5,3]+i\right\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{12}^{*}$ for $i\in \{2,3,4\}$.

Example 5.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_{13}^{*}$ be ${\mathbb{Z}}_{13}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_{13}}\{& 5(D_2[0,1,2,4,7]+i),4(D_2[0,2,6,1,8]+i),D_2[0,2,11,7,3]+i,\hfill \\ \hfill & D_2[0,6,2,12,3]+i,D_2[0,5,1,6,3]+i\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_{13}}\{& 5(D_3[0,10,8,7,12]+i),4(D_3[0,2,8,1,5]+i),D_3[0,3,12,8,4]+i,\hfill \\ \hfill & D_3[0,3,10,7,4]+i,D_3[0,4,10,5,2]+i\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_{13}}\{& 5(D_4[0,10,9,7,8]+i),4(D_4[0,2,6,12,5]+i),D_4[0,3,12,8,4]+i,\hfill \\ \hfill & D_4[0,4,1,7,3]+i,D_4[0,3,1,8,5]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{13}^{*}$ for $i\in \{2,3,4\}$.

3.2. Designs with a Hole

If H is a subgraph of the directed graph G, then $G\setminus H$ denotes the directed graph obtained from G by deleting all arcs of H. The directed graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_u^{*}$ is called the λ-fold complete symmetric directed graph of order v with a hole of size u, and the vertices of ${\phantom{K^{*}}}^{\lambda }{K}_u^{*}$ are referred to as the hole vertices.

The holey decompositions (Examples 6–11) were also obtained by computational search, using the same framework described in Section 3.1. The main modification was that the hole vertices ${\infty }_1,{\infty }_2,\dots ,{\infty }_u$ were fixed throughout the search, thereby ensuring that no arc of ${\phantom{K^{*}}}^5{K}_u^{*}$ was generated. Please note that any $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_v^{*}\setminus {\phantom{K^{*}}}^5{K}_u^{*}$ must contain exactly $v(v-1)-u(u-1)$ blocks, since the graph contains $5\left[v\right(v-1)-u(u-1\left)\right]$ arcs and each $D_i$ has five arcs. Each resulting base block was then developed under the cyclic group ${\mathbb{Z}}_{v-u}$ acting only on the non-hole vertices, and the difference conditions were verified analogously to those in the full designs.

Example 6.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_7^{*}\setminus {\phantom{K^{*}}}^5{K}_2^{*}$ be ${\mathbb{Z}}_5\cup \{{\infty }_1,{\infty }_2\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 4(D_2[0,1,{\infty }_1,2,{\infty }_2]+i),2(D_2[0,3,1,2,4]+i),D_2[0,1,3,4,2]+i,D_2[0,2,{\infty }_1,1,{\infty }_2]+i\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 3(D_3[0,{\infty }_1,1,4,{\infty }_2]+i),2(D_3[0,{\infty }_1,1,2,{\infty }_2]+i),2(D_3[0,1,3,2,4]+i),D_3[0,3,2,4,1]+i\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 2(D_4[0,{\infty }_1,1,2,{\infty }_2]+i),2(D_4[0,4,{\infty }_1,1,{\infty }_2]+i),2(D_4[0,1,4,2,3]+i),D_4[0,1,2,4,{\infty }_1]+i,\hfill \\ \hfill & D_4[0,2,4,1,{\infty }_2]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_7^{*}\setminus {\phantom{K^{*}}}^5{K}_2^{*}$ for $i\in \{2,3,4\}$.

Example 7.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_8^{*}\setminus {\phantom{K^{*}}}^5{K}_3^{*}$ be ${\mathbb{Z}}_5\cup \{{\infty }_1,{\infty }_2,{\infty }_3\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_2[0,2,{\infty }_1,1,{\infty }_2]+i),5(D_2[0,1,2,4,{\infty }_3]+i)\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_3[0,{\infty }_1,1,3,{\infty }_2]+i),5(D_3[0,1,3,4,{\infty }_3]+i)\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_4[0,1,2,4,{\infty }_1]+i),2(D_4[0,{\infty }_2,1,{\infty }_3,2]+i),D_4[{\infty }_2,0,{\infty }_3,1,4]+i,D_4[0,2,{\infty }_2,1,{\infty }_3]+i,\hfill \\ \hfill & D_4[0,2,{\infty }_3,1,{\infty }_2]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_8^{*}\setminus {\phantom{K^{*}}}^5{K}_3^{*}$ for $i\in \{2,3,4\}$.

Example 8.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_9^{*}\setminus {\phantom{K^{*}}}^5{K}_4^{*}$ be ${\mathbb{Z}}_5\cup \{{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_2[0,2,{\infty }_1,1,{\infty }_2]+i),5(D_2[0,3,{\infty }_3,1,{\infty }_4]+i),D_2[0,1,2,3,4]+i,D_2[0,4,3,2,1]+i\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_3[0,{\infty }_1,1,3,{\infty }_2]+i),5(D_3[0,{\infty }_3,1,4,{\infty }_4]+i),D_3[0,1,2,3,4]+i,D_3[0,4,3,2,1]+i\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 4(D_4[0,1,2,4,{\infty }_1]+i),2(D_4[0,{\infty }_2,1,{\infty }_3,3]+i),D_4[0,1,{\infty }_4,2,{\infty }_1]+i,\hfill \\ \hfill & D_4[0,2,{\infty }_2,1,{\infty }_4]+i,D_4[0,{\infty }_4,1,4,{\infty }_2]+i,D_4[0,{\infty }_4,1,4,{\infty }_3]+i,D_4[{\infty }_2,0,{\infty }_3,1,2]+i,\hfill \\ \hfill & D_4[{\infty }_3,0,{\infty }_4,1,3]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_9^{*}\setminus {\phantom{K^{*}}}^5{K}_4^{*}$ for $i\in \{2,3,4\}$.

Example 9.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_{12}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*}$ be ${\mathbb{Z}}_5\cup {\bigcup }_{1\le i\le 7}\left\{{\infty }_i\right\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_2[0,1,{\infty }_1,2,{\infty }_2]+i),5(D_2[0,2,{\infty }_3,1,{\infty }_4]+i),3(D_2[0,3,{\infty }_5,1,{\infty }_6]+i),\hfill \\ \hfill & 2(D_2[0,4,{\infty }_5,1,{\infty }_7]+i),2(D_2[0,4,{\infty }_6,1,{\infty }_7]+i),D_2[0,3,4,1,{\infty }_7]+i\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_3[0,{\infty }_1,1,2,{\infty }_2]+i),5(D_3[0,{\infty }_3,1,3,{\infty }_4]+i),3(D_3[0,{\infty }_5,1,4,{\infty }_6]+i),\hfill \\ \hfill & 2(D_3[0,{\infty }_5,2,{\infty }_7,1]+i),2(D_3[0,{\infty }_6,2,{\infty }_7,1]+i),D_3[0,2,3,1,{\infty }_7]+i\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 2(D_4[0,{\infty }_1,1,{\infty }_2,2]+i),2(D_4[0,{\infty }_3,1,{\infty }_4,2]+i),2(D_4[0,{\infty }_5,1,{\infty }_6,3]+i),\hfill \\ \hfill & 2(D_4[{\infty }_1,0,{\infty }_2,1,2]+i),2(D_4[{\infty }_3,0,{\infty }_4,1,2]+i),D_4[0,1,{\infty }_5,2,{\infty }_1]+i,\hfill \\ \hfill & D_4[0,1,{\infty }_5,2,{\infty }_2]+i,D_4[0,1,{\infty }_6,2,{\infty }_3]+i,D_4[0,1,{\infty }_7,2,{\infty }_4]+i,\hfill \\ \hfill & D_4[0,1,{\infty }_7,2,{\infty }_5]+i,D_4[0,3,{\infty }_6,1,{\infty }_7]+i,D_4[0,{\infty }_7,1,3,{\infty }_6]+i,\hfill \\ \hfill & D_4[0,{\infty }_7,4,2,3]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{12}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*}$ for $i\in \{2,3,4\}$.

Example 10.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_{13}^{*}\setminus {\phantom{K^{*}}}^5{K}_8^{*}$ be ${\mathbb{Z}}_5\cup {\bigcup }_{1\le i\le 8}\left\{{\infty }_i\right\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_2[0,1,{\infty }_1,2,{\infty }_2]+i),5(D_2[0,2,{\infty }_3,1,{\infty }_4]+i),5(D_2[0,3,{\infty }_5,1,{\infty }_6]+i),\hfill \\ \hfill & 5(D_2[0,4,{\infty }_7,1,{\infty }_8]+i)\},\hfill \\ \hfill {\mathcal{D}}_3={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 5(D_3[0,{\infty }_1,1,{\infty }_2,2]+i),5(D_3[0,{\infty }_3,1,{\infty }_4,3]+i),5(D_3[0,{\infty }_5,1,{\infty }_6,4]+i),\hfill \\ \hfill & 5(D_3[0,{\infty }_7,2,{\infty }_8,1]+i)\},\hfill \\ \hfill {\mathcal{D}}_4={\bigcup }_{i\in {\mathbb{Z}}_5}\{& 2(D_4[0,{\infty }_1,1,{\infty }_2,2]+i),2(D_4[0,{\infty }_3,1,{\infty }_4,3]+i),2(D_4[0,{\infty }_5,1,{\infty }_6,4]+i),\hfill \\ \hfill & 2(D_4[0,{\infty }_7,2,{\infty }_8,1]+i),D_4[{\infty }_1,0,{\infty }_2,1,2]+i,D_4[{\infty }_3,0,{\infty }_4,1,2]+i,\hfill \\ \hfill & D_4[{\infty }_5,0,{\infty }_6,1,2]+i,D_4[{\infty }_7,0,{\infty }_8,1,3]+i,D_4[0,1,{\infty }_2,2,{\infty }_1]+i,\hfill \\ \hfill & D_4[0,1,{\infty }_3,2,{\infty }_2]+i,D_4[0,1,{\infty }_4,2,{\infty }_3]+i,D_4[0,2,{\infty }_5,1,{\infty }_4]+i,\hfill \\ \hfill & D_4[0,2,{\infty }_6,1,{\infty }_5]+i,D_4[0,2,{\infty }_7,1,{\infty }_6]+i,D_4[0,3,{\infty }_8,1,{\infty }_7]+i,\hfill \\ \hfill & D_4[0,3,{\infty }_1,1,{\infty }_8]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{13}^{*}\setminus {\phantom{K^{*}}}^5{K}_8^{*}$ for $i\in \{2,3,4\}$.

Example 11.

Let the vertex set of ${\phantom{K^{*}}}^5{K}_{14}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*}$ be ${\mathbb{Z}}_7\cup {\bigcup }_{1\le i\le 7}\left\{{\infty }_i\right\}$ and let

$$\begin{array}{cc}\hfill {\mathcal{D}}_2=& {\bigcup }_{i\in {\mathbb{Z}}_7}\left\{5(D_2[0,1,2,4,{\infty }_1]+i),5(D_2[0,2,{\infty }_2,1,{\infty }_3]+i),5(D_2[0,3,{\infty }_4,1,{\infty }_5]+i),5(D_2[0,4,{\infty }_6,1,{\infty }_7]+i)\right\},\hfill \\ \hfill {\mathcal{D}}_3=& {\bigcup }_{i\in {\mathbb{Z}}_7}\left\{5(D_3[0,1,3,4,{\infty }_1]+i),5(D_3[0,{\infty }_2,1,3,{\infty }_3]+i),5(D_3[0,{\infty }_4,1,4,{\infty }_5]+i),5(D_3[0,{\infty }_6,1,5,{\infty }_7]+i)\right\},\hfill \\ \hfill {\mathcal{D}}_4=& {\bigcup }_{i\in {\mathbb{Z}}_7}{\bigcup }_{1\le j\le 3}\{5(D_4[0,1,2,4,{\infty }_1]+i),2(D_4[{\infty }_{2j},0,{\infty }_{2j+1},1,j+2]+i),D_4[0,{\infty }_{2j},1,{\infty }_{2j+1},j+2]+i,\hfill \\ \hfill & D_4[0,{\infty }_{2j},1,j+3,{\infty }_{2j+1}]+i,D_4[0,{\infty }_{2j+1},1,j+3,{\infty }_{2j}]+i\}.\hfill \end{array}$$

Then, ${\mathcal{D}}_i$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{14}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*}$ for $i\in \{2,3,4\}$.

4. General Constructions

The union $G\cup H$ of two edge-disjoint graphs (or directed graphs) G and H is defined as the graph with vertex set $V\left(G\right)\cup V\left(H\right)$ and edge (or arc) set $E\left(G\right)\cup E\left(H\right)$. Given a positive integer $\alpha$, we denote by $\alpha G$ the edge-disjoint union of $\alpha$ copies of G, which are not necessarily vertex-disjoint.

In the subsequent lemmas, we provide constructions for decomposing ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$, covering all cases based on the congruence class of v modulo 5. These constructions culminate in the statement of our main result in Theorem 1.

Lemma 6.

Let λ and v be positive integers such that $\lambda \equiv 0(mod5)$, $v\equiv 2(mod5)$, and $v\ge 7$. Then, for each $i\in \{2,3,4\}$, ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a $D_i$-decomposition.

Proof. 

Let x be a positive integer and set $v=5x+2$. Examples 1 and 4 provide $D_i$-decompositions of ${\phantom{K^{*}}}^5{K}_7^{*}$ and ${\phantom{K^{*}}}^5{K}_{12}^{*}$, respectively, for each $i\in \{2,3,4\}$. Therefore, for the base cases $x\in \{1,2\}$, Lemma 2 (with $\mu =5$ and $G=K_{5x+2}^{*}$) directly yields $D_i$-decompositions of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ when $5\mid \lambda$. Hence, we may assume that $x\ge 3$. The remainder of the proof is divided into two cases.

Case 1: (x is odd with $x\ge 3$).

• Let ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ have vertex partition $\{H_j:0\le j\le x\}$, where $\left|H_j\right|=5$ for each $j\in [1,x]$, and $\left|H_0\right|=2$. First, Corollary 1 gives a $D_i$-decomposition $B^{\prime }$ of ${\phantom{K^{*}}}^{\lambda }{K}_{x\times 5}^{*}$ with vertex set ${\bigcup }_{j=1}^x{H}_j$ and the obvious vertex partition. Second, Example 1 combined with Lemma 2 (with $\mu =5$) provides a $D_i$-decomposition $B_0$ of ${\phantom{K^{*}}}^{\lambda }{K}_7^{*}$ on $H_0\cup H_x$ for each $i\in \{2,3,4\}$. Finally, for each $1\le j\le x-1$, we obtain a $D_i$-decomposition $B_j$ of ${\phantom{K^{*}}}^{\lambda }{K}_7^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_2^{*}$ with vertex set $H_j\cup H_0$ (where $H_0$ forms the hole) through the Example 6 and Lemma 2. Then $(V,\mathcal{B})$, where $V={\bigcup }_{j=0}^x{H}_j$ and $\mathcal{B}=B^{\prime }\cup B_0\cup {\bigcup }_{j=1}^{x-1}{B}_j$, forms a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$.

Case 2: (x is even with $x\ge 4$).

• Let ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ have vertex partition $\{H_j:0\le j\le x-1\}$, where $\left|H_j\right|=5$ for each $j\in [1,x-1]$ and $\left|H_0\right|=7$. First, Corollary 1 provides a $D_i$-decomposition $B^{\prime }$ of ${\phantom{K^{*}}}^{\lambda }{K}_{(x-1)\times 5}^{*}$ on ${\bigcup }_{j=1}^{x-1}{H}_j$ with the natural vertex partition. Second, applying Lemma 2 to Example 4 yields a $D_i$-decomposition $B_0$ of ${\phantom{K^{*}}}^{\lambda }{K}_{12}^{*}$ with vertex set $H_0\cup H_{x-1}$. Finally, for each $1\le j\le x-2$, Example 9 combined with Lemma 2 gives a $D_i$-decomposition $B_j$ of ${\phantom{K^{*}}}^{\lambda }{K}_{12}^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_7^{*}$ on $H_j\cup H_0$, where $H_0$ forms the hole. Thus, $(V,\mathcal{B})$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$, where $V={\bigcup }_{j=0}^{x-1}{H}_j$, and $\mathcal{B}=B^{\prime }\cup B_0\cup {\bigcup }_{j=1}^{x-2}{B}_j$. □

Lemma 7.

Let λ and v be positive integers such that $\lambda \equiv 0(mod5)$, $v\equiv 3(mod5)$, and $v\ge 8$. Then, for each $i\in \{2,3,4\}$, ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a $D_i$-decomposition.

Proof. 

Let x be a positive integer and set $v=5x+3$. By Examples 2 and 5, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_8^{*}$ and ${\phantom{K^{*}}}^5{K}_{13}^{*}$ for each $i\in \{2,3,4\}$, respectively. Therefore, if $x=1$ or $x=2$, the result follows from Lemma 2. Hence, we may assume that $x\ge 3$. The remainder of the proof is divided into two cases.

Case 1: (x is odd with $x\ge 3$).

• Let ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ have vertex partition $\{H_j:0\le j\le x\}$, where $\left|H_j\right|=5$ for each $j\in [1,x]$, and $\left|H_0\right|=3$. First, Corollary 1 gives a $D_i$-decomposition $B^{\prime }$ of ${\phantom{K^{*}}}^{\lambda }{K}_{x\times 5}^{*}$ with vertex set ${\bigcup }_{j=1}^x{H}_j$ and the obvious vertex partition. Second, Example 2 combined with Lemma 2 provides a $D_i$-decomposition $B_0$ of ${\phantom{K^{*}}}^{\lambda }{K}_8^{*}$ on $H_0\cup H_x$. Finally, for each $1\le j\le x-1$, we obtain a $D_i$-decomposition $B_j$ of ${\phantom{K^{*}}}^{\lambda }{K}_8^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_3^{*}$ with vertex set $H_j\cup H_0$, where $H_0$ represents the hole, by applying Example 7 together with Lemma 2. Then $(V,\mathcal{B})$, where $V={\bigcup }_{j=0}^x{H}_j$ and $\mathcal{B}=B^{\prime }\cup B_0\cup {\bigcup }_{j=1}^{x-1}{B}_j$, forms a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$.

Case 2: (x is even with $x\ge 4$).

• Let ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ have vertex partition $\{H_j:0\le j\le x-1\}$, where $\left|H_j\right|=5$ for each $j\in [1,x-1]$ and $\left|H_0\right|=8$. First, Corollary 1 provides a $D_i$-decomposition $B^{\prime }$ of ${\phantom{K^{*}}}^{\lambda }{K}_{(x-1)\times 5}^{*}$ on ${\bigcup }_{j=1}^{x-1}{H}_j$ with the natural vertex partition. Second, applying Lemma 2 to Example 5 yields a $D_i$-decomposition $B_0$ of ${\phantom{K^{*}}}^{\lambda }{K}_{13}^{*}$ with vertex set $H_0\cup H_{x-1}$. Finally, for each $1\le j\le x-2$, Example 10 combined with Lemma 2 gives a $D_i$-decomposition $B_j$ of ${\phantom{K^{*}}}^{\lambda }{K}_{13}^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_8^{*}$ on $H_j\cup H_0$, where $H_0$ forms the hole. Thus, $(V,\mathcal{B})$ forms a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$, where $V={\bigcup }_{j=0}^{x-1}{H}_j$, and $\mathcal{B}=B^{\prime }\cup B_0\cup {\bigcup }_{j=1}^{x-2}{B}_j$. □

Lemma 8.

Let λ and v be positive integers such that $\lambda \equiv 0(mod5)$, $v\equiv 4(mod5)$, and $v\ge 9$. Then, for each $i\in \{2,3,4\}$, ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a $D_i$-decomposition.

Proof. 

Let x be a positive integer and set $v=5x+4$. For each $i\in \{2,3,4\}$, Example 3 provides a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_9^{*}$. For ${\phantom{K^{*}}}^5{K}_{14}^{*}$, we employ the decomposition ${\phantom{K^{*}}}^5{K}_{14}^{*}=({\phantom{K^{*}}}^5{K}_{14}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*})\cup {\phantom{K^{*}}}^5{K}_7^{*}$, where Example 11 yields a $D_i$-decomposition of ${\phantom{K^{*}}}^5{K}_{14}^{*}\setminus {\phantom{K^{*}}}^5{K}_7^{*}$ and Example 1 provides one for ${\phantom{K^{*}}}^5{K}_7^{*}$. For the initial cases, Lemma 2 yields a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_9^{*}$ when $x=1$ and of ${\phantom{K^{*}}}^{\lambda }{K}_{14}^{*}$ when $x=2$. We therefore focus on $x\ge 3$ in the remainder.

Case 1: (x is odd with $x\ge 3$).

• Let ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ have vertex partition $\{H_j:0\le j\le x\}$, where $\left|H_j\right|=5$ for each $j\in [1,x]$, and $\left|H_0\right|=4$. First, Corollary 1 gives a $D_i$-decomposition $B^{\prime }$ of ${\phantom{K^{*}}}^{\lambda }{K}_{x\times 5}^{*}$ with vertex set ${\bigcup }_{j=1}^x{H}_j$ and the obvious vertex partition. Second, Example 3 combined with Lemma 2 provides a $D_i$-decomposition $B_0$ of ${\phantom{K^{*}}}^{\lambda }{K}_9^{*}$ on $H_0\cup H_x$. Finally, for each $1\le j\le x-1$, we obtain a $D_i$-decomposition $B_j$ of ${\phantom{K^{*}}}^{\lambda }{K}_9^{*}\setminus {\phantom{K^{*}}}^{\lambda }{K}_4^{*}$ with vertex set $H_j\cup H_0$, where $H_0$ represents the hole, by applying Example 8 together with Lemma 2. Then $(V,\mathcal{B})$, where $V={\bigcup }_{j=0}^x{H}_j$ and $\mathcal{B}=B^{\prime }\cup B_0\cup {\bigcup }_{j=1}^{x-1}{B}_j$, forms a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$.

Case 2: (x is even with $x\ge 4$).

• To handle this case, we proceed by considering separate subcases based on the congruence class of x modulo 6.

Subcase 2.1: ($x\equiv 0(mod6)$).

• Let $x=6y$ for some integer $y\ge 1$; hence $v=30y+4$. It can be seen that ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}={\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y-2),10y+8}^{*}\cup 2{\phantom{K^{*}}}^{\lambda }{K}_{10y-2}^{*}\cup {\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$. This follows from a vertex partition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ into $X_1,X_2$ (each of size $10y-2$) and Y (size $10y+8$), where ${\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y-2),10y+8}^{*}$ covers all arcs between different parts, and $2{\phantom{K^{*}}}^{\lambda }{K}_{10y-2}^{*}$, ${\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$ cover arcs within $X_1\cup X_2$ and Y, respectively. By Corollary 2, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y-2),10y+8}^{*}$ (which corresponds to the parameters $m=5y-1$ and $n=5y-2$ satisfying $0<n\le m$). For the graph ${\phantom{K^{*}}}^{\lambda }{K}_{10y-2}^{*}$ and ${\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$, a $D_i$-decomposition exists by Lemma 7 since $10y-2\equiv 10y+8\equiv 3(mod5)$. Thus, the union of these decompositions gives a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$.

Subcase 2.2: ($x\equiv 2(mod6)$).

• Let $x=6y+2$ for some integer $y\ge 1$; hence $v=30y+14$. Observe that the graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ is isomorphic to the disjoint union ${\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y+2),10y+10}^{*}\cup 2{\phantom{K^{*}}}^{\lambda }{K}_{10y+2}^{*}\cup {\phantom{K^{*}}}^{\lambda }{K}_{10y+10}^{*}$. This follows from a vertex partition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ into $X_1,X_2$ (each of size $10y+2$) and Y (size $10y+10$), where ${\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y+2),10y+10}^{*}$ covers all arcs between different parts, and $2{\phantom{K^{*}}}^{\lambda }{K}_{10y+2}^{*}$, ${\phantom{K^{*}}}^{\lambda }{K}_{10y+10}^{*}$ cover arcs within $X_1\cup X_2$ and Y, respectively. By Corollary 2, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{2\times (10y+2),10y+10}^{*}$ (which corresponds to the parameters $m=5y+1$ and $n=5y-3$ satisfying $0<n\le m$). For the graph ${\phantom{K^{*}}}^{\lambda }{K}_{10y+2}^{*}$, a $D_i$-decomposition exists by Lemma 6. For the graph ${\phantom{K^{*}}}^{\lambda }{K}_{10y+10}^{*}$, a $D_i$-decomposition exists by Theorem 3 (for $\lambda =1$) and is extended to general $\lambda$ by Lemma 2, since $10y+10\equiv 0(mod5)$ and the necessary conditions are satisfied. Consequently, combining these decompositions gives a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$.

Subcase 2.3: ($x\equiv 4(mod6)$).

• Let $x=6y+4$ for some integer $y\ge 0$; hence $v=30y+24$. Observe that the graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ is isomorphic to the disjoint union ${\phantom{K^{*}}}^{\lambda }{K}_{3\times (10y+8)}^{*}\cup 3{\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$. This follows from a vertex partition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ into $X_1,X_2,X_3$ (each of size $10y+8$), where ${\phantom{K^{*}}}^{\lambda }{K}_{3\times (10y+8)}^{*}$ covers all arcs between different parts, and $3{\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$ cover arcs within each $X_i$. By Corollary 2, there exists a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_{3\times (10y+8)}^{*}$. Moreover, by Lemma 7, ${\phantom{K^{*}}}^{\lambda }{K}_{10y+8}^{*}$ admits a $D_i$-decomposition. Thus, taking the union of these decompositions results in a $D_i$-decomposition of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$. □

5. Main Results

By Theorem 3 and Lemma 2, we have the following result for the cases where $v\equiv 0$ or $1(mod5)$.

Corollary 3.

Let λ and v be positive integers such that $v\equiv 0\mathrm{or}1(mod5)$ and $v\ge 5$. Then, for each $i\in [1,4]$, ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a $D_i$-decomposition.

Lemmas 6–8 establish the existence of $D_i$-decompositions of ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ for each $i\in \{2,3,4\}$, when $\lambda \equiv 0(mod5)$ and $v\equiv 2,3,$ or $4(mod5)$, respectively. Combining these results with Corollary 3 and Theorem 2 (which covers $D_1$ for all $\lambda$), we obtain the complete solution to the $\lambda$-fold spectrum problem for all oriented pentagons.

Proof of Theorem 1.

The necessity of the condition is given by Lemma 1.

For sufficiency, assume $\lambda v(v-1)\equiv 0(mod5)$. We consider cases based on the directed graph D and the residue of v modulo 5.

• If $D=D_1$, the result holds by Theorem 2.
• If $D\in \{D_2,D_3,D_4\}$:

  −

  If $v\equiv 0$ or $1(mod5)$, then a decomposition exists by Corollary 3.

  −

  If $v\equiv 2,3,$ or $4(mod5)$, then $5\mid \lambda$. The existence of a decomposition in these cases is provided by Lemmas 6–8, respectively.

This exhausts all possibilities, thus proving the theorem. □

To enhance the readability and traceability of our constructions, we include Figure 2, which illustrates the logical flow from the base examples through intermediate lemmas, corollaries, and theorems to the final result, Theorem 1. At the foundation lie the explicit constructions in Examples 1–11, establishing decompositions for small orders and holey designs. These base cases feed into intermediate results (Lemmas 2–5 and Corollaries 1–2) that extend the constructions through various product-type and lifting arguments. The main case analysis is organized by the residue of v modulo 5: Lemmas 6–8 handle the cases $v\equiv 2,3,4(mod5)$, respectively, while Corollary 3 covers $v\equiv 0,1(mod5)$ by combining Theorem 2 (which settles $D_1$ for all $\lambda$) and Theorem 3 (the known $\lambda =1$ case). All paths ultimately converge to Theorem 1, our main result, which provides the complete solution to the $\lambda$-fold spectrum problem for all oriented pentagons.

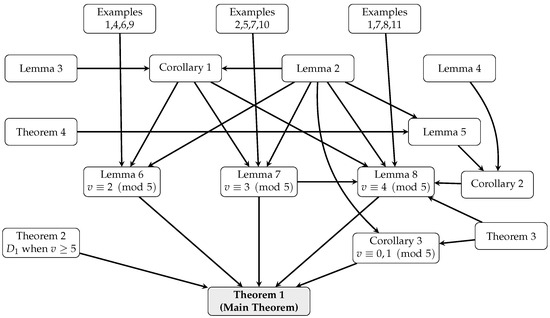
Figure 2. Dependency graph illustrating how small designs, lemmas, corollaries, and theorems interconnect to establish Theorem 1, confirming full coverage for all $v\ge 5$.

6. Conclusions

In this paper, we have completely solved the $\lambda$-fold spectrum problem for all non-isomorphic orientations of the 5-cycle (pentagon). Our main result (Theorem 1) establishes that for any oriented pentagon $D_i$ ($i\in [1,4]$) and for any positive integers $\lambda$ and $v\ge 5$, the $\lambda$-fold complete symmetric directed graph ${\phantom{K^{*}}}^{\lambda }{K}_v^{*}$ admits a decomposition into copies of $D_i$ if and only if $\lambda v(v-1)\equiv 0(mod5)$.

The structural properties of odd cycles, particularly those lacking arc-direction regularity, present distinctive challenges that require specialized constructions, as in the proof of Lemma 8 for the case $v\equiv 4(mod5)$. By overcoming these obstacles, we provide a complete solution to the problem of decomposing the $\lambda$-fold complete symmetric directed graph into all orientations of the pentagon, thereby solving a long-standing problem in graph theory and design theory.

Building upon the complete solution of the $\lambda$-fold spectrum problem for oriented pentagons presented in this work, several natural directions for future research emerge. A direct extension would be to investigate the $\lambda$-fold spectrum problem for the ten non-isomorphic orientations of the 7-cycle (heptagon). Furthermore, we plan to explore the more general problem of decomposing $\lambda$-fold complete symmetric directed graphs into antidirected cycles (where consecutive arcs have opposite directions) of arbitrary length.

The constructive approach employed here—combining holey designs with blow-up constructions—could potentially be adapted to antidirected cycles and other mixed-orientation cycles beyond lengths 5, 6, and 8. While the computational search for base designs becomes more challenging with increasing cycle length, this framework provides a promising starting point for these broader decomposition problems.