Error-Driven Varying-Gain in Zeroing Neural Networks for Solving Time-Varying Quadratic Programming Problems

Abstract

Convergence is a critical performance metric when zeroing neural networks (ZNNs) are employed to solve time-varying problems. As an effective strategy to enhance the convergence of ZNN models, gain adjustment is widely adopted to accelerate convergence speed, with the core objective of enabling the residual error to converge to zero rapidly and accurately. However, existing gain-tuning methods are decoupled from the residual error. This decoupling may lead to oscillation when the residual error approaches zero. To address this limitation, this paper proposes a novel error-driven varying-gain scheme. In this scheme, the gain value dynamically adapts to the residual error; a large residual error triggers a large gain, while a small residual error corresponds to a small gain, ensuring the gain changes synchronously with the residual error. Theoretical analyses and experimental results collectively demonstrate that integrating this error-driven varying-gain into ZNNs yields superior convergence performance, providing a more reliable solution for time-varying problem solving with ZNNs.

1. Introduction

In the practical engineering applications and scientific research, many problems can be synthesized into a quadratic programming (QP) problem to be solved [1,2,3,4,5]. For example, in [1,2], the trajectory tracking of the robot manipulator can be expressed as a solution to a time-varying QP (TVQP) mathematical problem. An improved sequential quadratic programming (ISQP) algorithm is proposed to solve the receding horizon optimization problem by the authors in [6]. Note that, during the solution the robot manipulator [1,7,8], by making full use of the symmetry characteristics, the performance index can be formulated into a symmetric mathematical model, which is convenient for the computing [9]. As for its solution of the QP problem, there are also many methods, mainly including the numerical solutions and the neural network models [1,2,10,11]. As an effective parallel computing method during the hardware realization, recently, neural networks have been drawing increasing attention due to their outstanding performance in image recognition and natural language processing [12,13].

Inspired by Zhang’s design method [14], a zeroing neural network (ZNN) is also used for solutions to TVQP problems [1,2,7]. In [15], the authors presented a discrete sliding-mode reaching-raw ZNN model to solve the TVQP problem. In [7], since the nonlinear complementary method would expend the dimensions of the matrix, to overcome this deficiency, the authors proposed a lower ZNN model to solve the TVQP problem. In fact, many ZNN models are developed and have already been widely used in many other fields, e.g., robot control [2,7], unmanned aerial vehicle (UAV) control [8,16,17], and noise control [18,19]. During the solutions of these practical problems, convergence is a performance index used for neural networks. To accelerate the convergence of the neural network models, many authors have presented activation functions to enhance the convergence performance [20,21,22,23,24]. Based on the fuzzy logic strategy, a fuzzy activation function-based ZNN model was proposed and used for dynamic Arnold map image cryptography [21]. In [20], an activation function based on the super-twisting algorithm (STA) was encapsulated with the ZNN models to solve the time-variant Sylvester equation with the superior finite time convergence and noise tolerance. This is one way to accelerate the convergence speed for ZNN models.

Another way to improve the convergence is to change the value of the gain [25,26,27,28,29,30,31]. For instance, the authors in [25] presented a changing-parameter complex-valued ZNN model to solve the linear time-varying complex matrix equation with the finite time convergence. Evidently, this varying-gain scheme can achieve better convergence performance than fixed parameters [25,26,27,28,29], since the value of the varying gain would increase over time. However, this value would continue to increase even if the residual error is already very small. This would lead to oscillation of the residual error. In addition, with a varying gain, it is difficult to control a suitable value. In other words, if the gain value is set too small, the convergence performance may be unsatisfactory, which would result in slow error reduction that fails to meet the real-time requirements of time-varying problems. Conversely, if the gain value is set too high, it may exceed the voltage-bearing capacity of the circuit components used to implement the neural network, potentially causing component malfunctions or even irreversible burnout. This trade-off between convergence speed and hardware safety is a critical limitation of fixed or improperly designed varying-gain schemes [29]. Moreover, the gain setting has nothing to do with the residual error.

Considering these issues, in this paper, we present a varying gain driven by the residual error, which includes a constant item and an exponential item. Generally speaking, In the initial stage of the iterative solution, the residual error is typically much larger than in subsequent phases of the process. At this stage, the exponential term dominates, resulting in a sufficiently large gain value to rapidly reduce the residual error. Therefore, the initial gain value derived from the error-driven varying-gain scheme is also sufficiently large, which facilitates the rapid reduction of the residual error. As the iterative solution progresses, the residual error gradually decreases. At this point, the constant term takes over to further minimize the small residual error. Through this adaptive gain-tuning mechanism, the ZNN model integrated with the error-driven varying gain can solve the TVQP problem effectively and accurately. Both theoretical analysis and experimental results further validate the effectiveness of the proposed error-driven varying gain.

The remainder of this paper is organized as follows. Section 2 presents the mathematical formulations of existing varying-gain schemes and the proposed error-driven gain for ZNN models. Section 3 provides rigorous theoretical analyses of the proposed model. Section 4 conducts simulations, comparisons, and analyses of an illustrative example to validate the scheme’s performance. Section 5 concludes the paper with final remarks. The main contributions of this work are summarized as follows.

(i)

An error-driven varying-gain scheme is proposed for the ZNN model. The initial gain is large due to the large initial residual error, which facilitates the rapid reduction of the large initial residual error.

(ii)

Rigorous theoretical analysis, along with detailed proofs, is presented for the varying gain zeroing neural network (VGZNN) model. These analyses demonstrate that the VGZNN model achieves superior convergence performance when integrated with the proposed error-driven varying-gain scheme.

(iii)

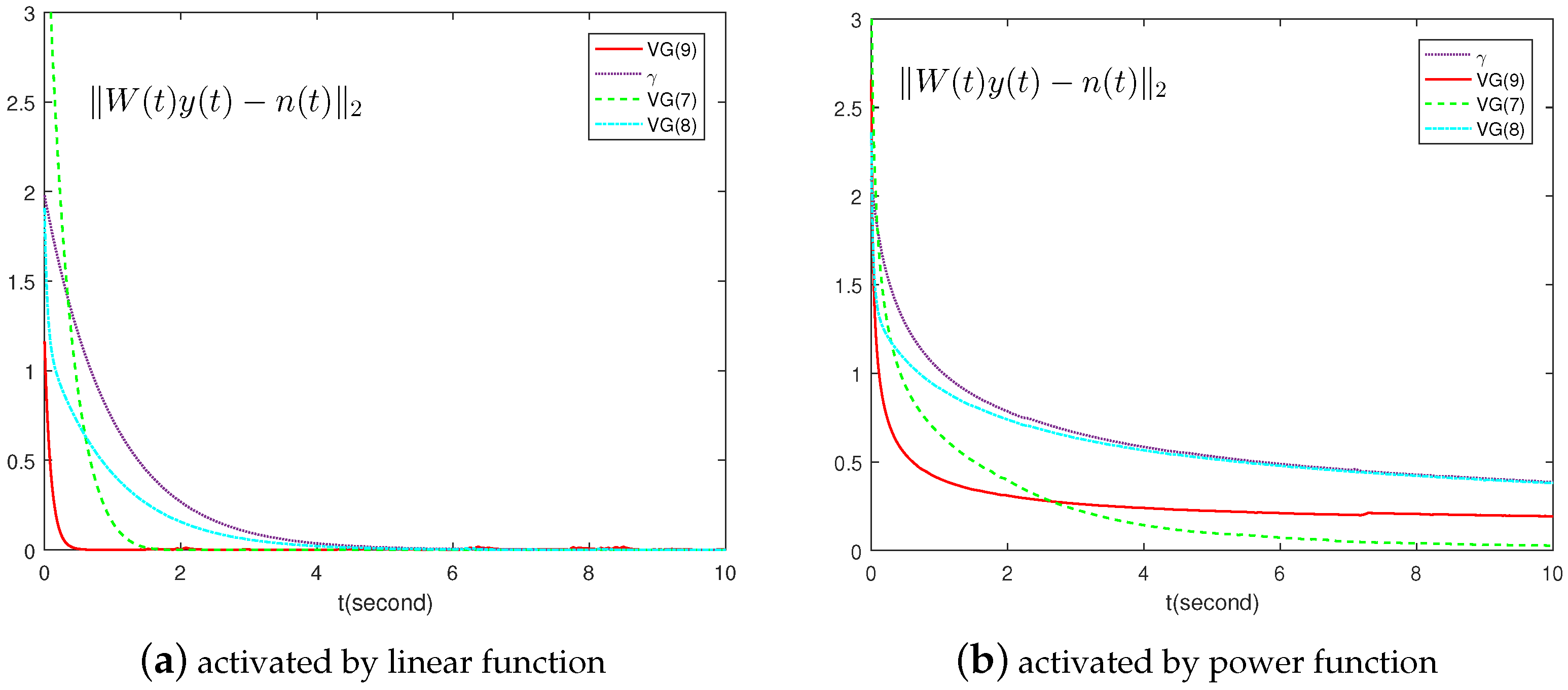
In the experimental section, a numerical TVQP example is simulated, analyzed, and compared with existing methods. These results further validate that the proposed error-driven varying-gain scheme outperforms the other three varying-gain schemes, making it the optimal choice.

2. Varying Gain for Solving TVQP Problems

Suppose that the TVQP problem subjected to non-stationary linear equality constraints can be formulated as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\min \hfill & x^T\left(t\right)Q\left(t\right)x\left(t\right)/2+p^T\left(t\right)x\left(t\right),\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & A\left(t\right)x\left(t\right)=b\left(t\right),\hfill \end{array}\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in R^n$ is an unknown state to be solved to satisfy the TVQP problem (1), and all of the known time-varying coefficients $Q\left(t\right)\in R^{n\times n}$, $p\left(t\right)\in R^n$, $A\left(t\right)\in R^{m\times n}$, and $b\left(t\right)\in R^m$ are assumed to be smooth, which ensures their time derivatives can be computed during the solution process. Moreover, TVQP (1) is supposed to have a unique solution.

Then, by the Karush–Kuhn–Tucker conditions [32], we can define a Lagrangian function for TVQP (1) as follows:

$$L(x\left(t\right),\nu \left(t\right),t)=x^T\left(t\right)Q\left(t\right)x\left(t\right)/2+p^T\left(t\right)x\left(t\right)+{\nu }^T\left(t\right)(A\left(t\right)x\left(t\right)-b\left(t\right)),$$

where $\nu \left(t\right)\in R^m$ is expressed as a Lagrange multiplier. As a result, the time-varying solution to the TVQP problem can be obtained by solving the following system of coupled equations:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial L\left(x\right(t),\nu (t),t)}{\partial x\left(t\right)}}=Q\left(t\right)x\left(t\right)+p\left(t\right)+A^T\left(t\right)\nu \left(t\right)=0,\hfill \\ {\displaystyle \frac{\partial L\left(x\right(t),\nu (t),t)}{\partial \nu \left(t\right)}}=A\left(t\right)x\left(t\right)-b\left(t\right)=0,\hfill \end{array}\right.$$

which can be further re-written as the following linear time-varying matrix-vector equation:

$$W\left(t\right)y\left(t\right)=n\left(t\right),$$

(2)

with the following defined time-varying coefficients:

$$\begin{array}{c}W\left(t\right):=\left[\begin{array}{cc}Q\left(t\right)& A^T\left(t\right)\\ A\left(t\right)& {\mathbf{0}}_{m\times m}\end{array}\right]\in R^{(n+m)\times (n+m)},\\ y\left(t\right):=\left[\begin{array}{c}x\left(t\right)\\ \nu \left(t\right)\end{array}\right]\in R^{n+m},n\left(t\right):=\left[\begin{array}{c}-p\left(t\right)\\ b\left(t\right)\end{array}\right]\in R^{n+m}.\end{array}$$

As for the solution of Problem (2), inspired by Zhang et al.’s design idea in [14], an indefinite (i.e., negative or positive) error function $e\left(t\right)=W\left(t\right)y\left(t\right)-n\left(t\right)$ is set as follows:

$$\dot{e}\left(t\right)=-\gamma \varphi \left(e\left(t\right)\right).$$

(3)

By extending the design Formula (3), we can derive the following fixed-gain zeroing neural network (FGZNN) model:

$$W\left(t\right)\dot{x}\left(t\right)=-\gamma \varphi (W\left(t\right)x\left(t\right)-n\left(t\right))-\dot{W}\left(t\right)x\left(t\right)+\dot{n}\left(t\right).$$

(4)

where $\gamma$ generally is a constant (i.e., time-invariant) parameter used to regulate the convergence speed, and $\varphi (·)$ is referred to as an activation function array, which serves to enhance the convergence performance [28,29]. In this study, the following activation functions are investigated [28,29]:

(1)

the linear activation function: $\varphi \left(u\right)=u$;

(2)

the power function: $\varphi \left(u\right)=u^{\xi }$ with $\xi \ge 3$;

(3)

and the sign-bi-power activation function:

$$\varphi \left(u\right)=\left(\right|u{|}^{ϵ}+\left|u{|}^{1/ϵ}\right)\mathrm{sgn}\left(u\right)/2,0<ϵ<1$$

(5)

with $\mathrm{sgn}(·)$ denoting the following signum function:

$$\mathrm{sgn}\left(u\right)\left\{\begin{array}{c}=1,\mathrm{if}u>0,\hfill \\ =0,\mathrm{if}u=0,\hfill \\ =-1,\mathrm{if}u<0.\hfill \end{array}\right.$$

Generally speaking, assuming all other parameters remain identical, the sigmoid function and power-sigmoid function, two widely adopted and extensively investigated activation functions in existing studies, enable the model to achieve favorable convergence performance. In contrast, under the same conditions of other parameters, the linear activation function and the power function yield the poorest convergence performance, which is consistent with the findings reported in [14]. Therefore, to achieve significantly much better convergence performance even when using the latter two activation functions, the authors of [28] proposed a varying-gain scheme (i.e., $\gamma \to \gamma \left(t\right)$) to enhance convergence performance. The FGZNN model with a varying gain can thus be transformed into the following varying gain ZNN (VGZNN):

$$W\left(t\right)\dot{y}\left(t\right)=-\gamma \left(t\right)\varphi (W\left(t\right)y\left(t\right)-n\left(t\right))-\dot{W}\left(t\right)y\left(t\right)+\dot{n}\left(t\right).$$

(6)

In this paper, the primary object is to find a neural solution $y\left(t\right)$ that converges to the theoretical solution $y^{*}\left(t\right)$ of (2). That is, we can find $x\left(t\right)$ from $y\left(t\right)$, and ensure that $x\left(t\right)$ converges to the theoretical solution $x^{*}\left(t\right)$ of TVQP (1), where $x^{*}\left(t\right)$ is obtained from $y^{*}\left(t\right)$. When a varying-gain scheme is used, the convergence performance of the model can be enhanced. For example, in [28], the authors presented the following varying-gain expression:

$$\gamma \left(t\right)=t^k+k,k>0,$$

(7)

As shown in Figure 4 of [28], the convergence performance is significantly improved when the gain is changed from a constant $\gamma$ to a varying gain $\gamma \left(t\right)$ defined in Equation (7). Meanwhile, another varying-gain scheme incorporating $exp\left(t\right)$ was proposed in [29] to enhance the convergence performance of the model; this scheme is repeated as follows:

$$\gamma \left(t\right)={\gamma }_0+{\gamma }_{1}exp(-{\gamma }_{2}t),$$

(8)

where ${\gamma }_0>0$, ${\gamma }_1>0$, and ${\gamma }_2>0$ are the known constant parameters, which are used to adjust the value of the varying-gain defined in (8). As for the varying-gain scheme (8), a large initial varying gain (at $t=0$) can be achieved by setting a large value for ${\gamma }_1$; ${\gamma }_0$ is configured to determine the steady-state gain, while ${\gamma }_2$ is used to regulate the decay rate of the varying gain $\gamma \left(t\right)$. In this way, the network model can achieve a superior convergence performance, as illustrated in Figure 3 in [29].

Remark 1.

In practical applications, the initial computational error is generally relatively large. Therefore, a relatively large design parameter should be set to reduce the computational error rapidly. At this moment, if the varying parameter is designed as a linear-power function, e.g., Equation (7), or an exponential function $exp\left(t\right)$, e.g, Equation (8), the varying-gain will be relatively small due to their inherent characteristics of these functions. of this paper. Since the time t is extremely small at the initial stage (e.g., $t={10}^{-5}$ s), this will result in an extremely slow convergence speed.

Therefore, to address this issue, we propose an error-driven varying-gain scheme, which is expressed as follows:

$$\gamma \left(t\right)={\gamma }_0+{\gamma }_{1}exp(-\parallel e\left(t\right)\parallel t),$$

(9)

where $\parallel ·\parallel$ is defined as the Frobenius norm [28,29], ${\gamma }_0$ and ${\gamma }_1$ have the same definitions and values in this paper.

Remark 2.

It is evident that the varying-gain defined in (9) is driven by the computation error. At the initial stage, the computational error is extremely large. As a result, a large gain is required to reduce the error rapidly. By following the function’s characteristics, the value of $exp(-\parallel e(t)\parallel t)$ will be very large initially (i.e., as $t\to 0$), given that the norm error $\parallel e\left(t\right)\parallel$ is large at this stage. Moreover, as time $t\to \infty$, the error will become extremely small, and the varying gain should be small to ensure the error reduction is smooth. It is worth noting that, if the varying gain remains relatively large at this stage, the residual error will exhibit an oscillation phenomenon.

Remark 3.

As for the VGZNN model (6), under the same conditions, in general, the larger the gain value, the faster the convergence speed that can be achieved. As a result, compared to the scheme (8), when ${\parallel e\left(t\right)\parallel }_2\ge {\gamma }_2$, a faster convergence performance can be achieved by using the scheme (9) because of the different item $exp(·)$. Compared to the scheme (7), since t is small at the beginning, the scheme (6) can achieve a faster convergence. However, as $t\to \infty$, the gain value of Scheme (7) will become larger than that of Scheme (9), and the resulting convergence will be faster than that of Scheme (9).

3. Theoretical Analysis

In this section, we would like to present the theoretical analysis on the VGZNN model (6) when integrated with the error-driven varying gain specified in Equation (9).

Theorem 1.

We take as given that ${\gamma }_0>0$ and ${\gamma }_1>0$. If the VGZNN model (6) is activated by an arbitrary monotonically increasing odd function, the neural solution $y\left(t\right)$ would globally and asymptotically converge to the theoretical solution $y^{*}\left(t\right)$ of (2).

Proof. 

Let $\tilde{y}\left(t\right)=y\left(t\right)-y^{*}\left(t\right)$ denote the difference of the neural state $y\left(t\right)$ and $y^{*}\left(t\right)$. Then

$$W\left(t\right)\dot{\tilde{y}}\left(t\right)=-\gamma \left(t\right)\varphi \left(W\left(t\right)\tilde{y}\left(t\right)\right)-\dot{W}\left(t\right)\tilde{y}\left(t\right).$$

(10)

Additionally, from $W\left(t\right)y\left(t\right)-n\left(t\right)=0$ and $W\left(t\right)y^{*}\left(t\right)-n\left(t\right)=0$, we would have $W\left(t\right)\tilde{y}\left(t\right)=0$. Since the error function $e\left(t\right)=W\left(t\right)y\left(t\right)-n\left(t\right)$ and $W\left(t\right)y^{*}\left(t\right)-n\left(t\right)=0$, $e\left(t\right)=W\left(t\right)\tilde{y}\left(t\right)$ and $\dot{e}\left(t\right)=\dot{W}\left(t\right)\tilde{y}\left(t\right)+W\left(t\right)\dot{\tilde{y}}\left(t\right)$. By following the design Formula (3), Model (10) can be also expressed as $\dot{e}\left(t\right)=-\gamma \left(t\right)\varphi \left(e\left(t\right)\right)$, which can be further transformed into the following $n+m$ element-wise form:

$${\dot{e}}_i\left(t\right)=-\gamma \left(t\right){\varphi }_i\left(e_i\left(t\right)\right),\forall i\in \{0,1,2,3,\cdots ,n+m\}$$

(11)

where ${\varphi }_i(·)$ denotes the ith element of the activation function array $\varphi (·)$. Therefore, as for the model (11), a candidate Lyapunov function can be defined as $v_i\left(t\right)=e_i^2\left(t\right)/2$, so ${\dot{v}}_i\left(t\right)=e_i\left(t\right){\dot{e}}_i\left(t\right)=-\gamma \left(t\right)e_i\left(t\right){\varphi }_i\left(e_i\left(t\right)\right)$. Given that ${\varphi }_i(·)$ is a monotonically increasing odd activation function. Then

$$e_i\left(t\right){\varphi }_i\left(e_i\left(t\right)\right)\left\{\begin{array}{c}>0\mathrm{if}{e}_i\left(t\right)>0,\hfill \\ =0\mathrm{if}{e}_i\left(t\right)=0,\hfill \\ <0\mathrm{if}{e}_i\left(t\right)<0.\hfill \end{array}\right.$$

It is evident that the Lyapunov function $v_i\left(t\right)$ satisfies $v_i\left(t\right)\ge 0$ for all t, and its time derivative ${\dot{v}}_i\left(t\right)$ satisfies ${\dot{v}}_i\left(t\right)\le 0$ for all t. By the Lyapunov stability [28,29], each error element $e_i\left(t\right)$ from $e\left(t\right)$ would globally and asymptotically converge to zero; that is, $e\left(t\right)=W\left(t\right)\tilde{y}\left(t\right)$ would converge to zero. In turn, this implies that $\tilde{y}\left(t\right)=y\left(t\right)-y^{*}\left(t\right)$ (the difference between the neural solution and the theoretical solution) would also converge to zero. In other words, the neural solution $y\left(t\right)$ will converge to $y^{*}\left(t\right)$ when time $t\to \infty$. Theorem 1 is thus proved. □

Theorem 2.

We take as given that ${\gamma }_0>0$ and ${\gamma }_1>0$. If linear activation $\varphi \left(e\right(t\left)\right)=e\left(t\right)$ is adopted for the VGZNN model (6), then the neural state $y\left(t\right)$ will exponentially converge to $y^{*}\left(t\right)$ with the exponential rate is 2${\gamma }_0$ or so when time $t\to \infty$.

Proof. 

From the proof of Theorem 1, we know that ${\dot{v}}_i\left(t\right)=e_i\left(t\right){\dot{e}}_i\left(t\right)=-\gamma \left(t\right)e_i\left(t\right){\varphi }_i\left(e_i\left(t\right)\right)$. If the linear function $\varphi \left(e\right(t\left)\right)=e\left(t\right)$ is used, then ${\dot{v}}_i\left(t\right)=-\gamma \left(t\right)e_i^2\left(t\right)=-2\gamma \left(t\right)v_i\left(t\right)$ since $v_i\left(t\right)=e_i^2\left(t\right)/2$ is defined in Theorem 1. Therefore, we have

$${\dot{v}}_i\left(t\right)=-2\gamma \left(t\right)v_i\left(t\right)$$

(12)

Recall the error-driven varying gain (9). When time $t\to \infty$, $\gamma \left(t\right)$ would be approximately equal to ${\gamma }_0$. Therefore, solving Equation (12), we have the following inequality:

$$\begin{array}{c}\hfill v_i\left(t\right)\le \kappa exp(-2{\gamma }_{0}t)\end{array}$$

with $\kappa =v_i\left(0\right)=e_i^2\left(0\right)/2$.

By leveraging Lyapunov stability theory, the energy function $v_i\left(t\right)$ will converge to zero at an exponential rate of $2{\gamma }_0$; this exponential convergence property is also applied to the error element $e_i\left(t\right)$. It implies that the neural solution $y\left(t\right)$ converge to the theoretical solution $y^{*}\left(t\right)$ at the same exponential rate $2{\gamma }_0$ as $t\to \infty$. The proof is thus completed. □

Theorem 3.

We take as given that ${\gamma }_0\ge 0$ and ${\gamma }_1>0$, and power function $\varphi \left(u\right)=u^{\xi }$ is used with $\xi \ge 3$ used to govern the nonlinearity of the activation function. When the fixed gain $\gamma ={\gamma }_0$ is used for the FGZNN (4) and the varying gain (9) is used for VGZNN (6), the convergence speed of VGZNN (6) would be faster than that of FGZNN (4).

Proof. 

Let $V_F\left(t\right)$ and $V_V\left(t\right)$ denote the Lyapunov function for the FGZNN (4) and VGZNN (6), respectively. By Theorem 1, it is known that $\dot{V}\left(t\right)=-\gamma e\left(t\right)\varphi \left(e\left(t\right)\right)$, so we have

$$\begin{array}{cc}\hfill {\dot{V}}_V\left(t\right)-{\dot{V}}_F\left(t\right)& =(-\gamma \left(t\right)+{\gamma }_0)e^{p+1}\hfill \\ \hfill & =-{\gamma }_{1}exp(-{\gamma }_2\parallel e\left(t\right)\parallel )\hfill \\ \hfill & \le 0.\hfill \end{array}$$

That is, ${\dot{V}}_V\left(t\right)$ descends faster than ${\dot{V}}_F\left(t\right)$ in the negative direction. This further substantiates that the sufficiently large gain can accelerate the decay rate of the residual error $e\left(t\right)$. As a result, numerous researchers have adopted sufficiently large gain values to achieve superior convergence performance for neural network models [28,29]. However, if the power function $\varphi \left(u\right)=u^{\xi }$ (with $\xi$≥ 3) is adopted, the convergence performance of the neural network model is difficult to improve, even if the gain is set to a sufficiently large value. Moreover, it is not allowed in piratical circuit realization if the gain is set too large, which will result in the instability or even irreversible burnout of circuit components. Fortunately, if the error-driven varying gain specified in Equation (9) is adopted, the model can automatically obtain a sufficiently large initial gain to significantly enhance the convergence performance of the neural network. □

Theorem 4.

We take as given that ${\gamma }_0>0$ and ${\gamma }_1>0$. If the sign-bi-power activation function (5) is adopted, the state solution $y\left(t\right)$ will be globally convergent to the theoretical solution $y^{*}\left(t\right)$ for Model (6) with the following finite convergence time t expressed as

$$t\le {\displaystyle \frac{2\parallel e_i{\left(t\right)\parallel }^{1-ϵ}}{(1-ϵ)({\gamma }_0+{\gamma }_1)}}.$$

(13)

Proof. 

By following Theorem 1, it is known that $v_i\left(t\right)=e_i^2\left(t\right)/2$ and ${\dot{v}}_i\left(t\right)=-\gamma \left(t\right)e_i\left(t\right){\varphi }_i\left(e_i\left(t\right)\right)$. Therefore, when the activation function (5) is exploited, we have

$$\begin{array}{cc}\hfill {\dot{v}}_i\left(t\right)& =-{\displaystyle \frac{1}{2}}\gamma \left(t\right)e_i\left(t\right)(\parallel e_i{\left(t\right)\parallel }^{ϵ}+\parallel e_i\left(t\right){\parallel }^{{\displaystyle \frac{1}{ϵ}}})\mathrm{sgn}\left(e_i\left(t\right)\right)\hfill \\ \hfill & =\left\{\begin{array}{c}-{\displaystyle \frac{1}{2}}\gamma \left(t\right))e_i\left(t\right)(\parallel e_i{\left(t\right)\parallel }^{ϵ}+\parallel e_i\left(t\right){\parallel }^{{\displaystyle \frac{1}{ϵ}}}),e_i\left(t\right)\ge 0\hfill \\ {\displaystyle \frac{1}{2}}\gamma \left(t\right))e_i\left(t\right)(\parallel e_i{\left(t\right)\parallel }^{ϵ}+\parallel e_i\left(t\right){\parallel }^{{\displaystyle \frac{1}{ϵ}}}),e_i\left(t\right)\le 0\hfill \end{array}\right.\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\gamma \left(t\right)\left({\left(e_i^2\left(t\right)\right)}^{{\displaystyle \frac{1+ϵ}{2}}}+{\left(e_i^2\left(t\right)\right)}^{{\displaystyle \frac{1+ϵ}{2ϵ}}}\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\gamma \left(t\right)\left({\left(2v_i\left(t\right)\right)}^{{\displaystyle \frac{1+ϵ}{2}}}+{\left(2v_i\left(t\right)\right)}^{{\displaystyle \frac{1+ϵ}{2ϵ}}}\right)\hfill \end{array}$$

(14)

Therefore, by considering the value range of $v_i\left(t\right)$ and recalling the error-driven varying gain specified in Equation (9) for (14), we can derive the following inequality:

$${\dot{v}}_i\left(t\right)\le -{\displaystyle \frac{1}{2}}\gamma \left(t\right){\left(2v_i\left(t\right)\right)}^{{\displaystyle \frac{1+ϵ}{2}}}.$$

(15)

Based on Equation (15) with $0<ϵ<1$, we have the following analytical solution:

$$0\le {\left(2v_i\left(t\right)\right)}^{{\displaystyle \frac{1-ϵ}{2}}}\le {\left(2v_0\left(t\right)\right)}^{{\displaystyle \frac{1-ϵ}{2}}}-{\displaystyle \frac{1-ϵ}{2}}({\gamma }_0+{\gamma }_1)t.$$

(16)

By following Theorem 1 and Lyapunov stability, $v_i\left(t\right)$ would converge to zero along with time $t\to \infty$. Thus, Equation (16) can be further transformed into the following:

$${\displaystyle \frac{1-ϵ}{2}}({\gamma }_0+{\gamma }_1)t\le {\left(2v_0\left(t\right)\right)}^{{\displaystyle \frac{1-ϵ}{2}}}.$$

Therefore, the convergence time t is satisfied with the following expression:

$$t\le {\displaystyle \frac{2\parallel e_i{\left(t\right)\parallel }^{1-ϵ}}{(1-ϵ)({\gamma }_0+{\gamma }_1)}}.$$

(17)

The proof is thus completed. □

4. Illustrative Examples

In the previous sections, we have already presented the different varying-gain schemes and active functions tailored for the VGZNN model (6), along with a comprehensive theoretical analysis of the model’s convergence behavior. To demonstrate the superior convergence performance of the VGZNN model when adopting the error-driven varying gain specified in Equation (9), we conduct comparative simulations with benchmarks including other varying-gain schemes and different activation functions.

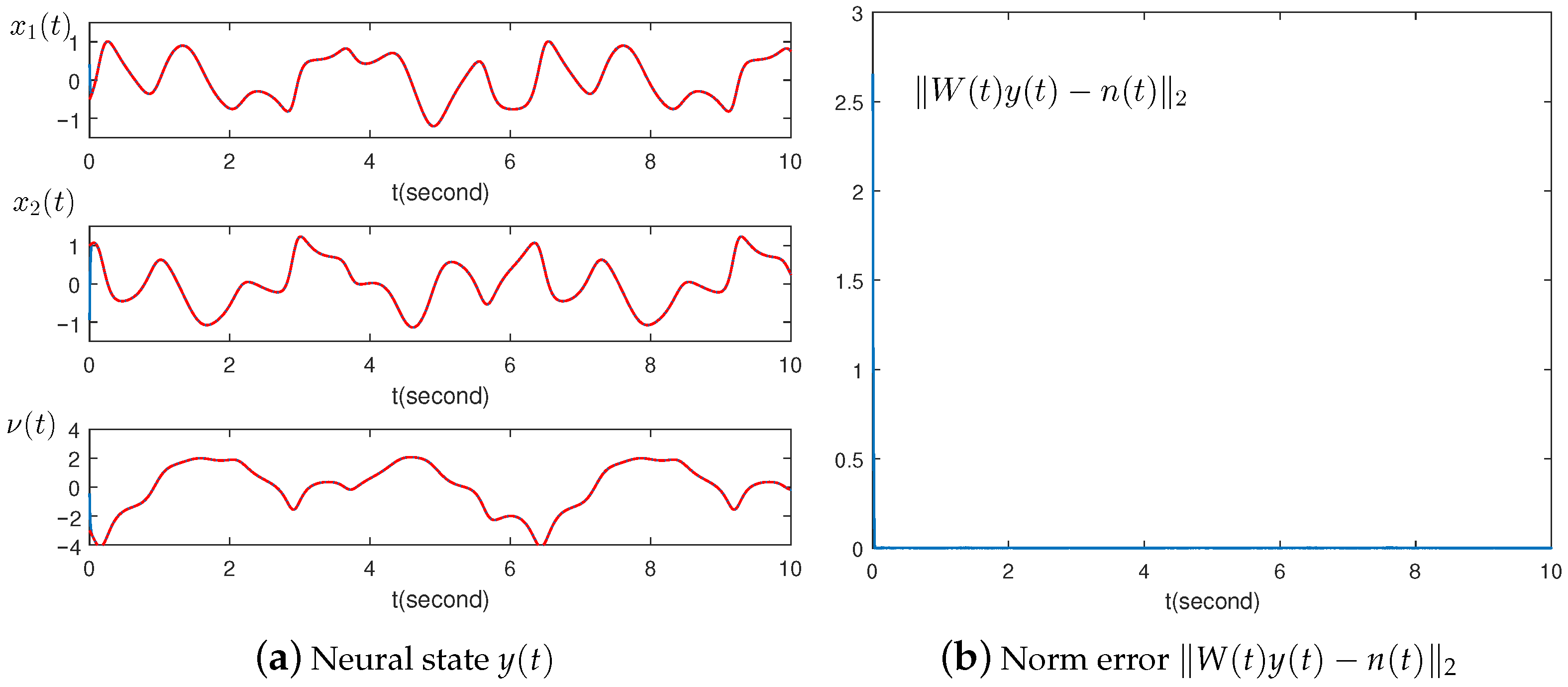
4.1. Example 1: Numerical Example

To verify the effectiveness of the proposed varying-gain scheme, we investigate and compare the following illustrative time-varying quadratic programming (TVQP) problem. The coefficients of this TVQP problem are consistent with those used in [1], ensuring the realism of the experimental setup and the comparability of the results.

$$\left\{\begin{array}{c}\begin{array}{cc}\min \hfill & (1+{\displaystyle \frac{1}{4}}sint){\mathsf{x}}_1^2\left(t\right)+(1+{\displaystyle \frac{1}{4}}cost){\mathsf{x}}_2^2\left(t\right)+(cost){\mathsf{x}}_1\left(t\right){\mathsf{x}}_2\left(t\right)+(sin3t){\mathsf{x}}_1\left(t\right)+(cos3t){\mathsf{x}}_2\left(t\right),\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & (sin4t){\mathsf{x}}_1\left(t\right)+(cos4t){\mathsf{x}}_2\left(t\right)=cos2t,\hfill \end{array}\hfill \end{array}\right.$$

(18)

which can be expressed as the standard form like (1) with the following time-varying coefficients for (18)

$$Q\left(t\right)=\left[\begin{array}{cc}0.5sint+2& cost\\ cost& 0.5cost+2\end{array}\right],p\left(t\right)=\left[\begin{array}{c}sin3t\\ cos3t\end{array}\right],A\left(t\right)=\left[\begin{array}{c}sint\\ cos4t\end{array}\right],b\left(t\right)=cos2t.$$

Then the above TVQP problem can be easily transformed into the linear time-varying Equation (2) with the time-varying coefficients expressed nearby (2). For the comparison and analysis purposes, by using the MATLAB R2016a tools, we can obtain the theoretical solution $y^{*}\left(t\right)={[{x^{*}}^T\left(t\right),{{\nu }^{*}}^T\left(t\right)]}^T:=W^{-1}\left(t\right)n\left(t\right)\in R^{n+m}$.

When the sign-bi-power activation function (5) with $ϵ=1/3$ is exploited for the VGZNN model (6) to solve the TVQP problem (18), together with ${\gamma }_0=10$ and ${\gamma }_1=100$ in the error-driven gain (9), the convergence performance is as shown in Figure 1. The neural state $y\left(t\right)$, denoted by the blue curve, is fast overlapped with the theoretical solution $y^{*}\left(t\right)=W^{-1}\left(t\right)n\left(t\right)$, which can be easily computed by the MATLAB tool and is denoted by the red curve. As shown in Figure 1a, $x_1\left(t\right)$ and $x_2\left(t\right)$ are the neural solution of (18), and $\nu \left(t\right)$ is a Lagrangian factor designed for the construction from TVQP problem (1) to the linear time-varying Equation (2). In addition, the residual norm error ${\parallel W\left(t\right)y\left(t\right)-n\left(t\right)\parallel }_2$ also quickly converges to zero within 0.025 s. This indicates that, as the neural state $y\left(t\right)$ approaches the theoretical solution $y^{*}\left(t\right)$, the residual error is convergent to zero accordingly.

In addition, different parameters and activation functions will also affect the convergence of the VGZNN model (6). As shown in Figure 2a and

Table 1. Comparisons of the convergence performance of the VGZNN (6) integrated with Scheme (9) using different parameters.

${\mathit{\gamma }}_0$	${\mathit{\gamma }}_1$	Time (s)	Residual Error $\mathit{e}\left(\mathit{t}\right)$
10	10	$0.293$	$7.909\times {10}^{-3}$
10	1	$0.5222$	$8.889\times {10}^{-3}$
1	1	$3.148$	$9.813\times {10}^{-3}$
1	10	$0.5829$	$4.446\times {10}^{-3}$

Note: time (s) is the time when the residual error arrives at ${10}^{-3}$ at the first time.

, when the error-driven varying gain (9) and linear activation function $\varphi \left(u\right)=u$ are used for the VGZNN model (6) under the same experimental conditions, the residual error $\parallel W\left(t\right)y\left(t\right)-n\left(t\right)\parallel$ would converge to zero at a much faster rate if the parameters are set much larger; for example, when ${\gamma }_0={\gamma }_1=1$, the residual error is convergent to $9.813\times {10}^{-3}$ at $t=3.148$ s; in contrast, when ${\gamma }_0={\gamma }_1=10$, the residual error is $7.909\times {10}^{-3}$ at $t=0.293$ s. The activation function is another important factor influencing the convergence performance of the VGZNN model. It can be seen in Figure 2b that the best convergence can be achieved when the sign-bi-power activation function is exploited for the VGZNN model (6) among the three functions (i.e., linear, sign-bi-power (which is denoted by sgn), and power function).

As for the VGZNN model (6) used to solve the TVQP problem (18), if we utilize the different varying-gain schemes, then we can obtain a different convergence effect, which can be seen in Figure 3 and

Table 2. Comparisons of the convergence performance of the VGZNN (6) for solving the TVPQ problem (18) with different gain schemes.

Gain Scheme	Activation Function	Time (s)	Residual Error $\mathit{e}\left(\mathit{t}\right)$
$\gamma =10$	linear function	$5.286$	$9.999\times {10}^{-3}$
	power function	10	$0.3868$
$VG$ (7) with $k=3$	linear function	$1.566$	$8.132\times {10}^{-3}$
	power function	10	$0.02478$
$VG$ (8) with ${\gamma }_0=1$, ${\gamma }_1=10$ and ${\gamma }_2=20$	linear function	$4.829$	$9.418\times {10}^{-3}$
	power function	10	$0.3804$
$VG$ (9) with ${\gamma }_0=1$, ${\gamma }_1=10$	linear function	$0.4601$	$8.263\times {10}^{-3}$
	power function	10	$0.193$

. Under the same simulation conditions, as shown in Figure 3a, the same linear function and the same parameters ($\gamma =10,$ ${\gamma }_0=1$, ${\gamma }_1=10$ and ${\gamma }_2=20$) are adopted, and it is evident that the best convergence effect is achieved for the error-driven varying gain (9) (denoted by VG (9) in Figure 3) among the four cases (i.e., the constant case $\gamma$, varying gain (7), denoted by VG (7), and varying gain (8), denoted by VG (8)). It is noted that the residual errors are finally convergent to zero in all cases. However, if the power function is encapsulated in the VGZNN model (6), the residual errors do not converge to zero in all cases within 10 s. Certainly, if given enough time, the residual error would converge to zero finally. Or, in another case, if the parameters are set large enough to accelerate the convergence speed, the residual error would finally converge to zero [28,29]. Furthermore, in most cases, the power activation function is generally not investigated because of its poor convergence performance. This issue is also discussed in [14] and a power-extension function is also presented for the superior convergence. It is worth noting that, as shown in Table 2, when the power function is used, the convergence performance with VG (7) is superior to that with $VG$ (9). This is because the value of VG (7) increases progressively as time elapses.

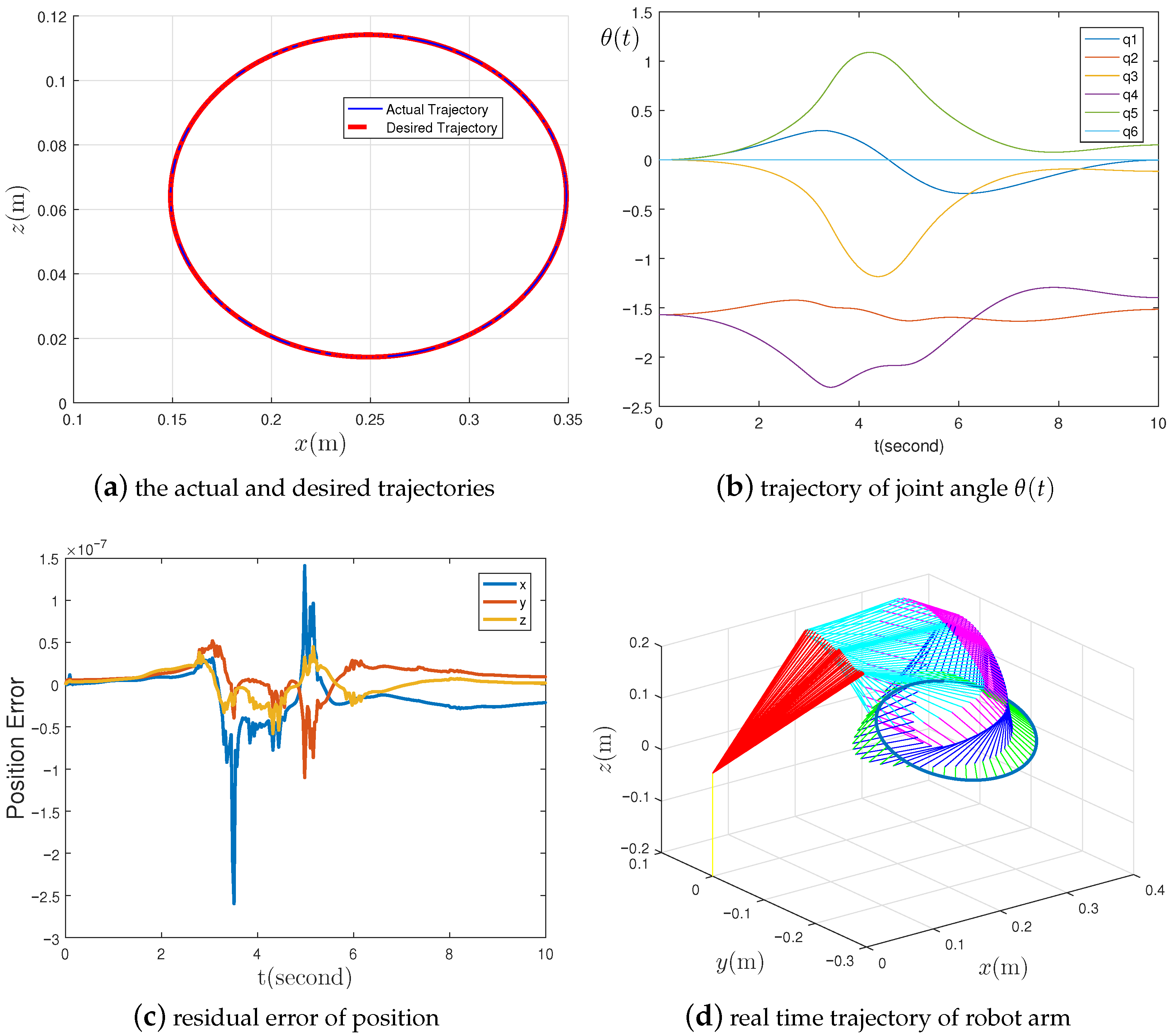
4.2. Example 2: TVQP Problem Solution for a Robot Manipulator

As described in the Introduction section, robot arm manipulation can be synthesized as a solution to a TVQP problem. In this section, the VGZNN model (6) integrated with the varying-gain scheme (9) is used for the robot arm PUMA560 for tracking [19]. If the robot end-effector position $d\left(t\right)\in R^m$ and the joint angle $\theta \left(t\right)\in R^n$, then the forward kinematics dynamical equation in Cartesian space can be modeled as the following mathematical expression:

$$d\left(t\right)=\psi \left(\theta \right(t\left)\right)$$

(19)

where $\psi (·)$ denotes the continuous nonlinear mapping with the known structure parameters of the robot arm. Evidently, Equation (19) is difficult to solve directly. Therefore, a TVQP-based scheme at velocity level is presented in [1], as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\min \hfill & {\displaystyle \frac{1}{2}}\dot{\theta }\left(t\right){\dot{\theta }}^T\left(t\right),\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & J\left(\theta \left(t\right)\right)\dot{\theta }\left(t\right)=\dot{d}\left(t\right).\hfill \end{array}\hfill \end{array}\right.$$

(20)

where $J\left(\theta \left(t\right)\right)=\partial f\left(\theta \right(t\left)\right)/\partial \theta \left(t\right)\in R^{m\times n}$ is a Jacobian matrix. Then Equation (20) can be transformed into a standard TVQP problem (1), where $x\left(t\right):=\dot{\theta }\left(t\right)\in R^n$, $Q\left(t\right):=I\in R^{n\times n}$, $A\left(t\right):=J\left(\theta \left(t\right)\right)\in R^{m\times n}$, $b\left(t\right):=\dot{d}\left(t\right)\in R^m$, and $p\left(t\right):=0\in R^n$. Therefore, we can adopt the same transformation method to convert the time-varying quadratic programming (TVQP) problem defined in Equation (1) into a linear time-varying equation, as shown in Equation (2).

In this example, the VGZNN model (6) integrated with our proposed error-driven varying scheme (9) is adopted to control the PUMA560 to track a circle. As shown in Figure 4, the actual trajectory of the robot arm coincides with the desired circular trajectory, as illustrated in Figure 4a. The real time trajectory of $\theta \left(t\right)$ is drawn in Figure 4b. Moreover, as shown in Figure 4c, the position error can reach ${10}^{-7}$. The real time control trajectory can be seen in Figure 4d.

5. Conclusions

This study focuses on enhancing the convergence performance of zeroing neural networks (ZNNs) for the online solution of time-varying matrix equation problems, with a particular emphasis on time-varying quadratic programming (TVQP) problems. Two core strategies for improving network convergence are systematically investigated and validated through theoretical analyses and experimental simulations. The selection of the activation functions significantly impacts the convergence behavior of ZNN models. Among the three typical functions, i.e., the linear function, power function (with $\xi =3$), and sign-bi-power function (with $0<ϵ<1$), the sign-bi-power activation function demonstrates superior performance in accelerating convergence. As verified by comparative simulations (Table 2 and Figure 3), when integrated with the varying-gain ZNN (VGZNN) model, this function enables faster convergence to the theoretical solution compared to linear and power functions, confirming its effectiveness as a priority choice for optimizing ZNN convergence.

In another way, the design of gain adjustment schemes is identified as a critical factor in determining ZNN performance. In this paper, to address the limitations of existing varying-gain schemes, such as decoupling from residual errors, potential oscillation when errors approach zero, and trade-offs between convergence speed and hardware safety, we propose an error-driven varying-gain scheme for the VGZNN model. Unlike traditional schemes that adjust gain independently of residual errors, the proposed scheme dynamically adapts the gain value to the real-time residual error. A large initial residual error triggers a sufficiently large gain to rapidly reduce errors, while a decreasing residual error corresponds to a reduced gain to avoid oscillation and ensure hardware safety. This adaptive mechanism ensures synchronous variation between gain and residual error, fundamentally overcoming the drawbacks of conventional gain-tuning methods.

Experimental results further validate the superiority of the proposed scheme. In numerical simulations of TVQP problems (i.e., Example 1), the error-driven varying-gain scheme reduces the time to reach a residual error of ${10}^{-3}$ to 0.4601 s (with linear activation functions), outperforming fixed-gain ($\gamma =10$, 5.286 s) and other varying-gain schemes (e.g., VG (7), 1.566 s; VG (8), 4.829 s). In practical applications (i.e., Example 2), applying the scheme to the trajectory tracking control of the PUMA560 redundant robot arm results in a position error as low as ${10}^{-7}$, and the actual trajectory of the robot end-effector perfectly matches the desired circular trajectory, demonstrating the scheme’s practical engineering value.

Future research will focus on two directions: (1) further optimizing the error-driven varying-gain scheme to enhance its robustness against external noise and complex time-varying characteristics, which is also the limitations in this article, and (2) expanding the application scope of the scheme to more fields involving solutions to time-varying problems, such as unmanned aerial vehicle (UAV) control and real-time signal processing, to fully exploit its potential in practical engineering scenarios.