Symmetric Equilibrium Bagging–Cascading Boosting Ensemble for Financial Risk Early Warning
Abstract
1. Introduction
- (1)
- Existing ensemble methods typically rely on either bagging (variance reduction) or boosting (bias reduction) in isolation, limiting their ability to address the complex trade-offs in financial risk modeling. This study pioneers a bagging–cascading–boosting tripartite architecture, where LightGBM’s sequential residual fitting minimizes bias, bagging aggregates multiple outputs to suppress variance, and the cascading framework dynamically adjusts model depth. This integration outperforms traditional single-strategy ensembles by simultaneously optimizing prediction performance and stability.
- (2)
- Existing ensemble frameworks often suffer from rigid structures that cannot adapt to evolving data complexity. The proposed cascading strategy overcomes this limitation by dynamically adjusting model depth based on the complexity of datasets. Unlike static architectures, this design enables seamless incorporation of new risk indicators, ensuring scalability without compromising performance.
- (3)
- While prior studies have explored bagging or boosting in isolation, this work pioneers their synergistic integration. The LightGBM–bagging combination not only enhances prediction stability but also mitigates overfitting risks, a common issue in financial risk modeling. The cascading layer further refines this robustness by allowing iterative feature selection. This triple innovation—hybrid architecture, adaptive scaling, and robust optimization—sets this work apart from existing ensemble approaches.
2. Literature Review
2.1. Statistical Methods and Individual ML-Based Algorithms
2.2. Ensemble Approaches
2.3. Other Related Research
3. Methodology
3.1. LightGBM as Base Learner
3.2. Base Learner Training Based on the Cascade Framework
3.3. Aggregate Multiple Base Learners for Financial Risk Early Warning
| Algorithm 1: Training of the proposed method |
| Input: A training set for financial risk early warning; ; ; Round T for Bagging; Output: the proposed method
|
4. Experimental Settings
4.1. Sample Selection
4.2. Implementation Details of the Proposed Method
4.3. Evaluation Metrics
- (1)
- Precision (Pre)
- (2)
- Recall (Rec)
- (3)
- F1-score (F1)
- (4)
- Brier Score (BS)
- (5)
- ROC curve and AUC
5. Experimental Results
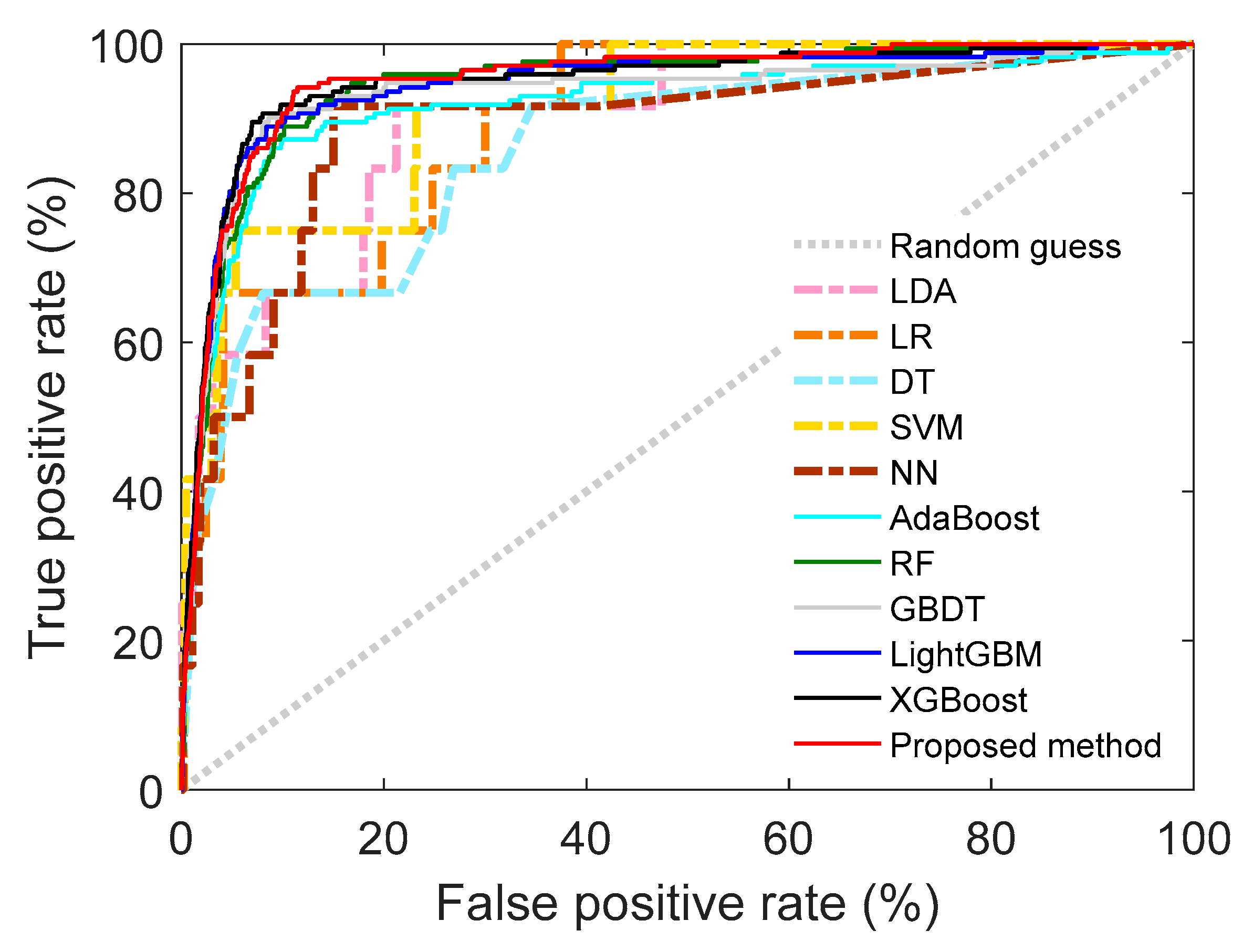
5.1. Performance Comparison and Analysis
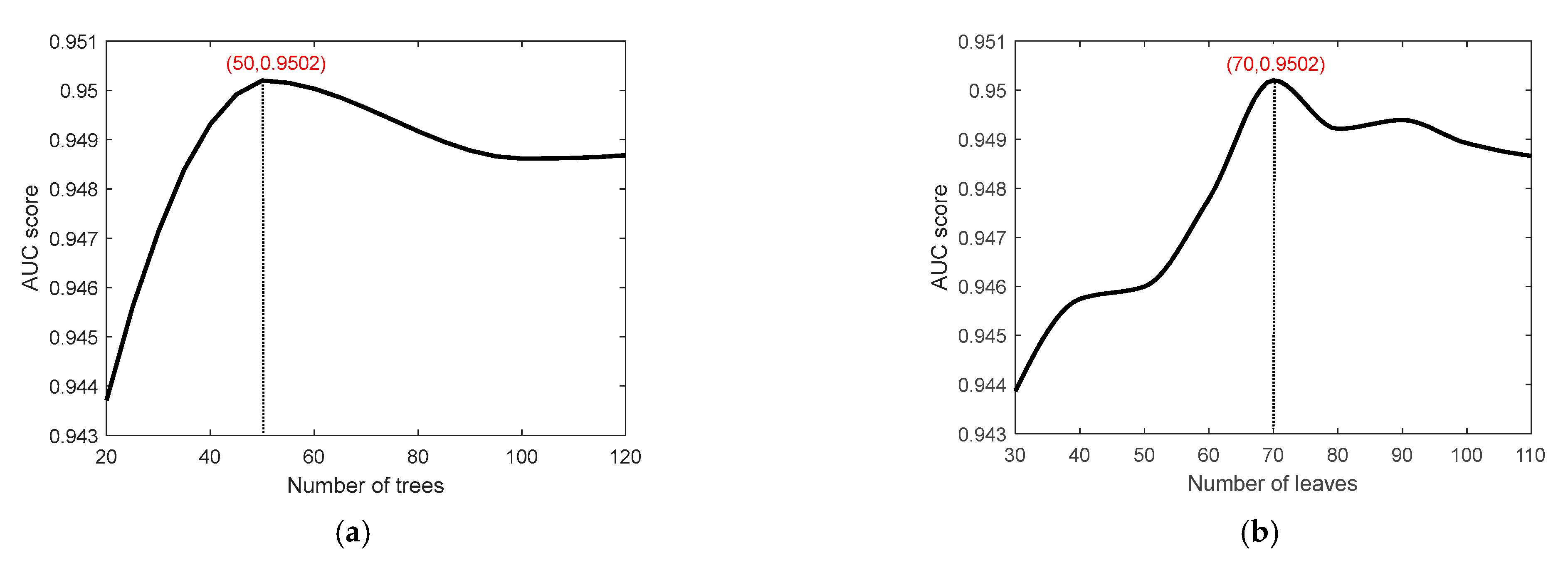
5.2. Sensitivity Analysis
6. Discussion
6.1. Limitations
6.2. Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wanke, P.; Barros, C.P.; Faria, J.R. Financial Distress Drivers in Brazilian Banks: A Dynamic Slacks Approach. Eur. J. Oper. Res. 2015, 240, 258–268. [Google Scholar] [CrossRef]
- Altman, E.I. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. J. Financ. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- Ohlson, J.A. Financial Ratios and the Probabilistic Prediction of Bankruptcy. J. Account. Res. 1980, 18, 109–131. [Google Scholar] [CrossRef]
- West, R.C. A Factor-Analytic Approach to Bank Condition. J. Bank. Financ. 1985, 9, 253–266. [Google Scholar] [CrossRef]
- Chen, N.; Ribeiro, B.; Chen, A. Financial Credit Risk Assessment: A Recent Review. Artif. Intell. Rev. 2016, 45, 1–23. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Yang, C. Risk Prediction in Financial Management of Listed Companies Based on Optimized BP Neural Network under Digital Economy. Neural Comput. Appl. 2023, 35, 2045–2058. [Google Scholar] [CrossRef]
- Shin, K.-S.; Lee, T.S.; Kim, H. An Application of Support Vector Machines in Bankruptcy Prediction Model. Expert Syst. Appl. 2005, 28, 127–135. [Google Scholar] [CrossRef]
- Olson, D.L.; Delen, D.; Meng, Y. Comparative Analysis of Data Mining Methods for Bankruptcy Prediction. Decis. Support Syst. 2012, 52, 464–473. [Google Scholar] [CrossRef]
- Wolpert, D.H. The Lack of a Priori Distinctions between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Beaver, W.H. Financial Ratios as Predictors of Failure. J. Account. Res. 1966, 4, 71–111. [Google Scholar] [CrossRef]
- Martin, D. Early Warning of Bank Failure: A Logit Regression Approach. J. Bank. Financ. 1977, 1, 249–276. [Google Scholar] [CrossRef]
- Jones, S.; Hensher, D.A. Predicting Firm Financial Distress: A Mixed Logit Model. Account. Rev. 2004, 79, 1011–1038. [Google Scholar] [CrossRef]
- Odom, M.D.; Sharda, R. A Neural Network Model for Bankruptcy Prediction. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; IEEE: Piscataway, NJ, USA, 1990; pp. 163–168. [Google Scholar]
- Wu, D.; Ma, X.; Olson, D.L. Financial Distress Prediction Using Integrated Z-Score and Multilayer Perceptron Neural Networks. Decis. Support Syst. 2022, 159, 113814. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, J.; Huang, J.; Lin, B. A Novel Method for Financial Distress Prediction Based on Sparse Neural Networks with L 1/2 Regularization. Int. J. Mach. Learn. Cybern. 2022, 13, 2089–2103. [Google Scholar] [CrossRef]
- Chen, M.-Y. Predicting Corporate Financial Distress Based on Integration of Decision Tree Classification and Logistic Regression. Expert Syst. Appl. 2011, 38, 11261–11272. [Google Scholar] [CrossRef]
- Xie, C.; Luo, C.; Yu, X. Financial Distress Prediction Based on SVM and MDA Methods: The Case of Chinese Listed Companies. Qual. Quant. 2011, 45, 671–686. [Google Scholar] [CrossRef]
- Xu, W.; Xiao, Z.; Yang, D.; Yang, X. A Novel Nonlinear Integrated Forecasting Model of Logistic Regression and Support Vector Machine for Business Failure Prediction with All Sample Sizes. J. Test. Eval. 2015, 43, 681–693. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Li, X.; Zhang, J. Classifier Selection and Ensemble Model for Multi-Class Imbalance Learning in Education Grants Prediction. Appl. Artif. Intell. 2021, 35, 290–303. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.; Abe, N. A Short Introduction to Boosting. J. Soc. Artif. Intell. 1999, 14, 1612. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Heo, J.; Yang, J.Y. AdaBoost Based Bankruptcy Forecasting of Korean Construction Companies. Appl. Soft Comput. 2014, 24, 494–499. [Google Scholar] [CrossRef]
- Yao, G.; Hu, X.; Song, P.; Zhou, T.; Zhang, Y.; Yasir, A.; Luo, S. AdaFNDFS: An AdaBoost Ensemble Model with Fast Nondominated Feature Selection for Predicting Enterprise Credit Risk in the Supply Chain. Int. J. Intell. Syst. 2024, 2024, 5529847. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L. A Study on Forecasting the Default Risk of Bond Based on Xgboost Algorithm and Over-Sampling Method. Theor. Econ. Lett. 2021, 11, 258–267. [Google Scholar] [CrossRef]
- Wang, W.; Liang, Z. Financial Distress Early Warning for Chinese Enterprises from a Systemic Risk Perspective: Based on the Adaptive Weighted XGBoost-Bagging Model. Systems 2024, 12, 65. [Google Scholar] [CrossRef]
- Tan, B.; Gan, Z.; Wu, Y. The Measurement and Early Warning of Daily Financial Stability Index Based on XGBoost and SHAP: Evidence from China. Expert Syst. Appl. 2023, 227, 120375. [Google Scholar] [CrossRef]
- Huang, C.; Cai, Y.; Cao, J.; Deng, Y. Stock Complex Networks Based on the GA-LightGBM Model: The Prediction of Firm Performance. Inf. Sci. 2025, 700, 121824. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, T.; Wu, Y.; Li, S.; Li, Z. Research on Optimization of an Enterprise Financial Risk Early Warning Method Based on the DS-RF Model. Int. Rev. Financ. Anal. 2022, 81, 102140. [Google Scholar] [CrossRef]
- Liang, D.; Tsai, C.-F.; Lu, H.-Y.R.; Chang, L.-S. Combining Corporate Governance Indicators with Stacking Ensembles for Financial Distress Prediction. J. Bus. Res. 2020, 120, 137–146. [Google Scholar] [CrossRef]
- Chen, X.; Wu, C.; Zhang, Z.; Liu, J. Multi-Class Financial Distress Prediction Based on Stacking Ensemble Method. Int. J. Financ. Econ. 2025, 30, 2369–2388. [Google Scholar] [CrossRef]
- Wang, S.; Chi, G. Cost-Sensitive Stacking Ensemble Learning for Company Financial Distress Prediction. Expert Syst. Appl. 2024, 255, 124525. [Google Scholar] [CrossRef]
- Nguyen, M.; Nguyen, B.; Liêu, M. Corporate Financial Distress Prediction in a Transition Economy. J. Forecast. 2024, 43, 3128–3160. [Google Scholar] [CrossRef]
- Ekinci, A.; Sen, S. Forecasting Bank Failure in the US: A Cost-Sensitive Approach. Comput. Econ. 2024, 64, 3161–3179. [Google Scholar] [CrossRef]
- Lee, M.-J.; Choi, S.-Y. The Impact of Financial Statement Indicators on Bank Credit Ratings: Insights from Machine Learning and SHAP Techniques. Financ. Res. Lett. 2025, 85, 107758. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Z. Corporate ESG Rating Prediction Based on XGBoost-SHAP Interpretable Machine Learning Model. Expert Syst. Appl. 2026, 295, 128809. [Google Scholar] [CrossRef]
- He, K.; Yang, Q.; Ji, L.; Pan, J.; Zou, Y. Financial Time Series Forecasting with the Deep Learning Ensemble Model. Mathematics 2023, 11, 1054. [Google Scholar] [CrossRef]
- Mochurad, L.; Dereviannyi, A. An Ensemble Approach Integrating LSTM and ARIMA Models for Enhanced Financial Market Predictions. R. Soc. Open Sci. 2024, 11, 240699. [Google Scholar] [CrossRef]
- Ding, Y.; Song, X.; Zen, Y. Forecasting Financial Condition of Chinese Listed Companies Based on Support Vector Machine. Expert Syst. Appl. 2008, 34, 3081–3089. [Google Scholar] [CrossRef]
| Indicator Category | Specific Indicators | Indicator Category | Specific Indicators |
|---|---|---|---|
| solvency | current ratio | Profitability | Return on equity |
| quick ratio | Earnings Before Interest and Tax (EBIT) | ||
| cash ratio | Return on invested capital | ||
| working capital | Long-term capital return rate | ||
| Asset liability ratio | Operating cost ratio | ||
| Tangible asset liability ratio | Operating margin | ||
| Equity multiplier | Total operating cost ratio | ||
| Business capability | Accounts receivable turnover rate | Asset impairment loss/operating income | |
| Inventory turnover rate | EBIT margin | ||
| Operating Cycle | Return on assets | ||
| Accounts payable turnover ratio | Net profit margin of total assets | ||
| Operating capital turnover rate | Net profit margin of current assets | ||
| Inventory turnover days | Per share indicator | Earnings per share | |
| receivables | Net asset value per share | ||
| Development capability | Capital accumulation rate | Revenue per share | |
| Growth rate of owner’s equity | Operating profit per share | ||
| Growth rate of net assets per share | Capital reserve per share | ||
| Relative Value Index | Price-sales ratio | Earnings reserve per share | |
| market-to-book ratio | Undistributed profit per share | ||
| market value | Retained earnings per share | ||
| Market rate | Net cash flow per share | ||
| book-to-market | Earnings per share before interest and tax | ||
| Price-to-Earnings Ratio | Net cash flows from operating activities per share |
| Hyper-Parameters | Description | Searching Space | Stride |
|---|---|---|---|
| N_estimators | The number of DTs | [100, 500] | 50 |
| Learning_rate | Learning rate that control the optimization step | [0.001, 0.2] | Dichotomy |
| Max_depth | Maximum depth of DT in each | [3, 11] | 1 |
| subsample | Subsample ratio to undersample the training set | [0.6, 1] | 0.05 |
| Colsample_bytree | Subsample ratio to undersample the feature set | [0.6, 1] | 0.05 |
| Parameter that specifies the minimum loss function drop required for node splitting | [0, 0.5] | 0.10 | |
| A coefficient for the L1 regularization term | [10−5, 10−1] | Dichotomy | |
| A coefficient for the L2 regularization term | [10−5, 10−1] | Dichotomy | |
| T | The number of rounds for Bagging | [10, 50] | 10 |
| Actual | |||
|---|---|---|---|
| ST | Non-ST | ||
| Predicted | ST | TP | FP |
| Non-ST | FN | TN | |
| Algorithm | AUC | Precision | Recall | F1 | BS |
|---|---|---|---|---|---|
| LR | 0.8932 | 0.25 | 0.1667 | 0.2 | 0.0104 |
| LDA | 0.8991 | 0.375 | 0.25 | 0.3 | 0.0104 |
| DT | 0.8579 | 0 | 0 | 0 | 0.0088 |
| SVM | 0.9119 | 0 | 0 | 0 | 0.0090 |
| KNN | 0.8722 | 0 | 0 | 0 | 0.0087 |
| NN | 0.8880 | 0.1429 | 0.1667 | 0.1538 | 0.0142 |
| RF | 0.9448 | 0.6735 | 0.1919 | 0.2986 | 0.0304 |
| AdaBoost | 0.9191 | 0.5833 | 0.3256 | 0.4179 | 0.2444 |
| XGBoost | 0.9478 | 0.6538 | 0.2965 | 0.4080 | 0.0323 |
| LightGBM | 0.9446 | 0.6812 | 0.2733 | 0.3900 | 0.0373 |
| Proposed method | 0.9502 | 0.6974 | 0.3081 | 0.4274 | 0.0287 |
| Algorithm | AUC | Precision | Recall | F1 | BS |
|---|---|---|---|---|---|
| Cascade LR | 0.7611 | 0.5217 | 0.0698 | 0.1231 | 0.0472 |
| Cascade LDA | 0.8638 | 0.5179 | 0.1686 | 0.2544 | 0.0394 |
| Cascade KNN | 0.7730 | 0.5263 | 0.0581 | 0.1047 | 0.0404 |
| Cascade DT | 0.9160 | 0.4946 | 0.2674 | 0.3472 | 0.0327 |
| Cascade RF | 0.9477 | 0.6471 | 0.1919 | 0.2960 | 0.0302 |
| Cascade AdaBoost | 0.9350 | 0.5694 | 0.2384 | 0.3361 | 0.1913 |
| Cascade XGBoost | 0.9508 | 0.5733 | 0.25 | 0.3482 | 0.0333 |
| Cascade LightGBM | 0.9502 | 0.6974 | 0.3081 | 0.4274 | 0.0287 |
| Proportion of Training Set | Algorithm | AUC | Precision | Recall | F1 | BS |
|---|---|---|---|---|---|---|
| 0.8 | Cascade forest | 0.9477 | 0.6471 | 0.1919 | 0.2960 | 0.0302 |
| Cascade XGBoost | 0.9508 | 0.5733 | 0.25 | 0.3482 | 0.0333 | |
| Cascade LightGBM | 0.9502 | 0.6974 | 0.3081 | 0.4274 | 0.0287 | |
| 0.7 | Cascade forest | 0.9468 | 0.6327 | 0.1802 | 0.2805 | 0.0303 |
| Cascade XGBoost | 0.9462 | 0.5595 | 0.2733 | 0.3672 | 0.0347 | |
| Cascade LightGBM | 0.9435 | 0.6452 | 0.3488 | 0.4528 | 0.0303 | |
| 0.6 | Cascade forest | 0.9465 | 0.6327 | 0.1802 | 0.2805 | 0.0303 |
| Cascade XGBoost | 0.9443 | 0.6098 | 0.2907 | 0.3937 | 0.0335 | |
| Cascade LightGBM | 0.9479 | 0.5625 | 0.2616 | 0.3571 | 0.0314 | |
| 0.5 | Cascade forest | 0.9435 | 0.6304 | 0.1686 | 0.2661 | 0.0304 |
| Cascade XGBoost | 0.9441 | 0.6420 | 0.3023 | 0.4111 | 0.0332 | |
| Cascade LightGBM | 0.9409 | 0.5641 | 0.2558 | 0.3520 | 0.0321 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Yuan, Y.; Zhu, C.; Yu, C. Symmetric Equilibrium Bagging–Cascading Boosting Ensemble for Financial Risk Early Warning. Symmetry 2025, 17, 1779. https://doi.org/10.3390/sym17101779
Zou Y, Yuan Y, Zhu C, Yu C. Symmetric Equilibrium Bagging–Cascading Boosting Ensemble for Financial Risk Early Warning. Symmetry. 2025; 17(10):1779. https://doi.org/10.3390/sym17101779
Chicago/Turabian StyleZou, Yao, Yuan Yuan, Chen Zhu, and Chenhui Yu. 2025. "Symmetric Equilibrium Bagging–Cascading Boosting Ensemble for Financial Risk Early Warning" Symmetry 17, no. 10: 1779. https://doi.org/10.3390/sym17101779
APA StyleZou, Y., Yuan, Y., Zhu, C., & Yu, C. (2025). Symmetric Equilibrium Bagging–Cascading Boosting Ensemble for Financial Risk Early Warning. Symmetry, 17(10), 1779. https://doi.org/10.3390/sym17101779





