Abstract
This study focuses on the analysis of the simultaneous impact of inclined magnetohydrodynamic Carreau hybrid nanofluid flow over a stretching sheet, including microorganisms with the effects of chemical reactions in the presence and absence of slip conditions for dilatant and quasi-elastic hybrid nanofluid limitations. Meanwhile, the transfer of energy is strengthened through the employment of heat sources and bioconvection. The analysis incorporates nonlinear thermal radiation, chemical reactions, and Arrhenius activation energy effects on different profiles. Numerical simulations are conducted using the efficient Bvp5c solver. Motile concentration profiles decrease as the density slip parameter of the motile microbe and Lb increase. The Weissenberg number exhibits a distinct nature depending on the hybrid nanofluid; the velocity profile, skin friction, and Nusselt number fall when and increase when . For small values of inclination, the 3D surface plot is far the surface, while it is close to the surface for higher values of inclination but has the opposite behavior for the 3D plot of the Nusselt number. A detailed numerical investigation on the effects of important parameters on the thermal, concentration, and motile profiles and the Nusselt number reveals a symmetric pattern of boundary layers at various angles . Results are presented through tables, graphs, contour plots, and streamline and surface plots, covering both shear-thinning cases and shear-thickening cases .
1. Introduction
Nano-fluids, first introduced in [1], are produced by suspending metallic or non-metallic nanoparticles in traditional heat transfer fluids to significantly enhance their thermal performance. The thermal conductivity of the nanofluid with copper nanophase materials was investigated, and the findings showed that one benefit of employing nanofluids is a significant decrease in heat exchanger pumping power. In recent years, extensive studies have examined slip effects in hybrid nanofluid flows over stretching or shrinking sheets. Thermal radiation, chemical reactions, and magnetohydrodynamics (MHD) were among the factors taken into consideration in these experiments, as explained by Sharma et al. [2].
Eid et al. [3] explored Carreau nanofluid’s boundary-layer flow across a nonlinearly stretched sheet, as well as chemical reactions and heat generation in porous media. Regarding the effects of chemical reaction against magnetohydrodynamics, Carreau–Yasudab investigated nanofluid flow caused by a nonlinear stretched surface under zero normal flux, slip, and convective boundary conditions [4]. The effect of a magnetic field and effects on a generalized Carreau fluid’s flow over a porous cylindrical surface without a slip requirement was investigated in the presence of thermal radiation, thermal stratification, and heat generation [5]. Reddy et al. [6] conducted a numerical investigation on Carreau nanofluid’s unsteady three-dimensional hydromagnetic flow over a sheet with the influences of velocity slip, thermal slip, solutal slip, Soret, and Dufour. The behavior of Newtonian, Maxwell, and Casson fluids in the existence of an induced MHD influence was compared using the slip effect and the bioconvective phenomenon in a study by Gautam et al. [7]. The decrease in the thicknesses of the momentum profile, thermal distribution, and concentration boundary layers when velocity, thermal, and mass slips are included was studied in hybrid nanofluid flow with various slips over stretching or shrinking sheets in recent research [8,9].
The role of microorganisms in bioconvective nanofluids has also received attention. Abdeen et al. [10] demonstrated that gyrotactic microorganisms enhance nanoparticle stability, and Rehman et al. [11] incorporated chemical reactions, MHD, and heat radiation into bioconvection models. These studies often use advanced numerical techniques such as the homotopy analysis method and the bvp4c function [12].
Bilal [13] identified the activation energy factors influencing the flow of Carreau fluid over a nonlinear stretching surface, including heat transfer and the Arrhenius relation.
Hayat et al. [14] looked at the melting heat transfer of nanofluid flow toward an extended surface in the presence of heat generation, a nonlinear thermal radiation parameter, and a magnetic field. The irreversibility of the Fe3O4-CO Kerosene hybrid nanofluid flow beyond a wedge with a heat source and radiation parameter was explained by Mabood et al. [15]. The Carreau fluid model was significantly increased by a high-volume-fraction parameter of hybrid particles more than in the Casson fluid model [16]. The theoretical and mathematical discussion of nanofluids, with the effects of the heat absorption parameter and Joule parameter of Carreau nanofluids in a magnetohydrodynamic flow with viscous dissipation, was provided by Rehman et al. [17]. It was found that the fluid characteristics and magnetic field have opposing effects on the flow [18].
Prasad et al. [19] investigated the influence of magnetic fields, radiation, heat sources, and porosity on hybrid nanofluid flow characteristics. Kathuroju et al. [20] observed that increasing the Jeffrey fluid parameter enhanced the Nusselt number and skin friction but reduced the Sherwood number. Vijaya et al. [21] reported that exponential heat source parameters increased temperature profiles, while variable viscosity decreased fluid velocity. These effects significantly influence heat and mass transfer in hybrid nanofluids, which consist of multiple nanoparticles dispersed in a base fluid [22,23]. For shear-thickening fluids, the radiation factor raised the fluid heat, while the chemical reaction factor lowered the flow concentration. In contrast, the local Weissenberg number had the opposite impact on the Sherwood and Nusselt numbers for shear-thinning fluids [24].
The magnetic parameter significantly increases shear stress and fluid velocity, while decelerating temperature and concentration curves [25]. The study of thermophoresis and Brownian motion effects on inclined MHD nanofluid flow with multiple slip conditions by Patel and Nanda [26] shows that while the inclination parameter and magnetic field parameter tend to reduce fluid motion, thermophoresis and Brownian motion improve the heat transfer process. The effects of an inclined magnetic field and a constant chemical reaction on the tri-hybrid Carreau nanofluid slip flow of blood across a porous inclined stenosed artery with viscous dissipation were studied by Kumar et al. [27]. Using a wedge-shaped artery and thermal radiation, the study examined the thermal transport properties of a tri-hybrid Carreau nanofluid (blood) containing copper (Cu), titanium dioxide (TiO2), and aluminum oxide (Al2O3) nanoparticles with an inclined magnetic field [28].
Notwithstanding the expanding literature, considerable research gaps endure. A comprehensive analysis that integrates inclined MHD, multiple slip conditions, nonlinear thermal radiation, and Arrhenius activation energy within a Carreau hybrid nanofluid framework is notably absent. Furthermore, the confluence of nonlinear thermal conductivity and bioconvection phenomena in hybrid nanofluids comprising multiple nanoparticles has received scant attention. While the individual influences of parameters like slip, activation energy, and inclined magnetic fields have been investigated, their collective effect on heat and mass transfer dynamics is still poorly understood.
This study investigates the flow of a Carreau hybrid nanofluid, comprising Al2O3-Fe2O3 nanoparticles, over a nonlinear stretching sheet. The analysis incorporates the effects of inclined magnetohydrodynamics (MHD), multiple slip boundary conditions, nonlinear thermal radiation, Arrhenius activation energy, and non-uniform thermal conductivity for both dilatant and quasi-elastic fluid regimes. Furthermore, the model includes Brownian motion, thermophoresis, and bioconvection of motile microorganisms. The governing partial differential equations (PDEs) are converted into a system of ordinary differential equations (ODEs) through appropriate similarity transformations. This system is then solved numerically using the Bvp5c solver in MATLAB. The results are comprehensively presented through velocity, temperature, concentration, and microorganism profiles, alongside the variations in the skin friction coefficient, Nusselt number, and Sherwood number across a range of physical parameters.
2. Physical Pattern and Interpretation
This section presents a two-dimensional mathematical model for heat and mass transfer. The analysis encompasses the flow of a Carreau-type hybrid nanofluid containing microorganisms over a nonlinear stretching surface. The model incorporates inclined magnetohydrodynamics (MHD), chemically reactive species, thermal radiation, surface chemical reaction (kr), activation energy (Ea), and a multi-slip boundary condition. These elements are included to enhance the comprehensiveness and applicability of the research.
Assumption 1.
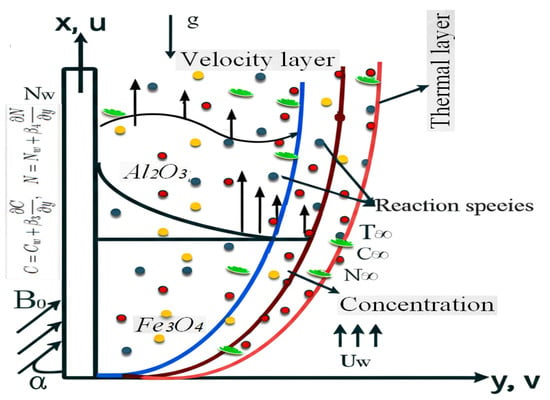
Consider a laminar, two-dimensional, incompressible, water-based hybrid nanofluid (see [Figure 1]) containing and nanoparticles. The flow is induced by a stretching surface with a velocity defined as , where b and r are positive constants. The model incorporates the effects of Brownian motion, thermophoresis, and a magnetic field. Heat transfer is governed by a convective boundary condition, where a hot working fluid at temperature with a heat transfer coefficient heats the nanofluidic medium. The ambient temperature and concentration, attained as y approaches infinity, are denoted by and , respectively.

Figure 1.
Graphical representation of the model.
Governing equations [29,30,31]
Boundary conditions [32,33]:
Here, the velocity components along the x and y axes are denoted by u and v, respectively; is the kinematic viscosity; is the base fluid’s density; is the coefficient of dimensional heat production/absorption; denotes the Brownian diffusion coefficient; and is the thermophoretic diffusion coefficient. Other parameters include the thermal relaxation time , the chemical reaction parameter , the magnetic field strength [34], the activation energy , and the relaxation parameter . The fluid properties are assumed constant except for the density variation, which induces a thermal buoyancy force.
The following non-dimensional variables are introduced to simplify the problem:
Ordinary differential equations (ODEs) are derived by applying the similarity transformations and substituting Equation (6) into the governing partial differential Equations (2)–(7):
Moreover, the controlled limitations at the boundary are
3. Physical Quantities
The many contributing elements and involving factors are similarly described by Equations (7) through (10). The following parameters are considered: Péclet number , Lewis number , heat source , microorganism difference parameter , thermal slip factor , concentration slip factor , density slip factor , Prandtl number , magnetic parameter , Weissenberg number , and parameter .
4. Engineering Quantities
Key engineering parameters of interest include the skin friction factor , the local Sherwood number , and the local Nusselt number .
Applying the aforementioned similarity transformations allows for the computation of the wall shear stress , the wall heat flux , and the wall mass flux .
Here, is the local Reynold’s number.
5. Execution of Methodology
By considering the effects of significant active physical factors, this work employs the Bvp5c method to solve the fundamental flow equations for MHD Carreau hybrid nanofluid flow across a stretched surface. Computational simulations were performed using MATLAB-2021. The highly nonlinear coupled ordinary differential equation (ODE) system, represented by Equations (8)–(11) along with boundary conditions (12), was solved using the built-in bvp5c solver in MATLAB. This technique is particularly well-suited for solving ODEs when the problem’s precise behavior is not known a priori, as it provides a flexible approach that effectively balances computational accuracy and efficiency. The solution process involves continually refining the initial guess for the unknown boundary limits based on the model’s residual. The initial guess strategy and solver setup are as follows:
For all dependent variables—, , , and —an initial mesh of 200 uniformly spaced points is generated across the computational domain . These initial guesses are iteratively refined by the Bvp5c solver until the solution residuals fall within a predefined tolerance. The initial profiles are constructed according to physically expected trends, such as a linear variation for velocity and an exponential decay for temperature, concentration, and motile microorganism density.
Tolerance and convergence criteria:
High numerical precision is achieved by setting both the relative and absolute error tolerances to . The solver iteratively updates the solution until the maximum residual norm, , is reduced below throughout the entire domain. Additionally, it was verified that further mesh refinement (up to 200 points) resulted in changes of less than 0.01.
Choice of = 7 and asymptotic verification:
The far-field boundary, , was selected based on a series of sensitivity tests where was varied from 6 to 10. The results showed that for values beyond , the velocity, temperature, concentration, and motile microorganism profiles all asymptotically approached their ambient values (, ), with subsequent computed variations being negligible (in the order of ). This value ensures computational efficiency without compromising accuracy. The asymptotic convergence of the profiles was confirmed by visually comparing plots for progressively larger values until no discernible difference was observed in the curves.
The rescaled infinity condition is now = 7. The thermal and physical properties of the hybrid nanofluid are provided in Table 1 and Table 2. Numerical results obtained using the Bvp5c and Rk45 methods are compared with each other, and and results obtained using the Bvp5c and Rk45 methods is shown in Table 3 and Table 4.

Table 1.
The physical properties [35,36].

Table 2.
Physical properties [37,38].

Table 3.
Assessment of for different values of n, where We and other parameters are constant.

Table 4.
Validation of at for different values of .
6. Results and Discussion
The effects of the physical parameters—M, , , , , , , , and —on the velocity profile , temperature distribution , hybrid nanofluid concentration profile , and motile microorganism profile , along with the Nusselt number , skin friction coefficient , and non-dimensional Sherwood number , are illustrated using various graphical profiles and condition tables for both dilatant and pseudo-plastic fluids.
The variation in the velocity profile with the local Weissenberg number (), under the combined influence of velocity slip () and the magnetic parameter (), is depicted in Figure 2a,b for both shear-thinning () and shear-thickening () fluids. It is observed that the fluid velocity responds differently to changes in depending on the fluid behavior: it decreases for shear-thickening fluids () but increases for shear-thinning fluids (). Physically, the Weissenberg number represents the ratio of the fluid’s relaxation time to a characteristic process time. An increase in signifies a dominant elastic response, which enhances the effective viscosity and consequently reduces the fluid velocity. Furthermore, the figure shows that the dimensionless velocity decreases as increases. This occurs because the magnetic parameter is directly related to the Lorentz force, which opposes flow. A higher strengthens this resistive magnetic effect, thereby decelerating the flow. The velocity slip parameter () quantifies the interaction between the fluid and a solid boundary. An increase in implies greater slip, creating a larger effective gap between the fluid and the wall. This reduces momentum transfer from the boundary, resulting in a lower fluid velocity. Thus, the velocity profile declines as the slip parameter increases. This behavior of the velocity profile with the Weissenberg number is consistent across both shear-thinning and shear-thickening cases, which aligns with the findings of Sabu et al. [39].
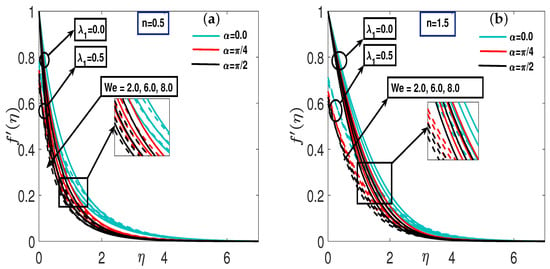
Figure 2.
(a,b) A pictorial representation of the velocity profile using parameter for both shear thinning instances and shear thickening .
Figure 3a,b demonstrate the influence of the Weissenberg number on the temperature profile for dilatant and pseudo-plastic fluids, respectively. The presence of thermal slip () at the boundary, alongside parameter , exhibits a concurrent effect on the profile. It is observed that the temperature profile for dilatant fluids intensifies with an increasing Weissenberg number (), whereas pseudo-plastic fluids display the opposite trend. This temperature rise is attributed to extended particle relaxation times and a higher frequency of inter-particle collisions. Furthermore, the results indicate that the dimensionless temperature profile increases with higher values of . This correlation is due to an enhanced magnetic effect, which grows with . The transverse magnetic field acts to decelerate the fluid’s velocity, thereby significantly diminishing the rate of energy transmission. This increased flow resistance is a result of the strengthening Lorentz force associated with a higher magnetic parameter (M). Consequently, the thermal boundary layer thickens for both fluid types. Conversely, an increase in the thermal slip parameter () reduces the size of the thermal boundary layer and decreases the susceptibility of the fluid flow within it.
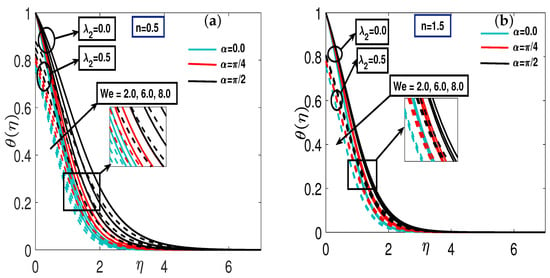
Figure 3.
(a,b) A pictorial representation of the temperature profile using parameter for both shear thinning instances and shear thickening .
The radiation factor is influenced by the simultaneous effects of thermal slip () and on the temperature profile of the Carreau fluid for both dilatant and pseudo-plastic hybrid nanofluids, as shown in Figure 4a,b. In both cases, an increase in the radiation factor corresponds to a rise in the nanofluid’s temperature profile. From a physical perspective, an increase in the radiation parameter enhances the emission of heat energy from the flow region. This process elevates the temperature of the nanofluid, thereby cooling the system. A higher radiation parameter introduces more heat into the system, and a thicker thermal boundary layer further contributes to this heating effect. The thermal field is also enhanced as K1 increases, due to a reduction in the mean absorption coefficient. Consequently, to achieve a more efficient cooling process, radiative heat transfer should be minimized. Furthermore, an increase in the thermal slip parameter () raises the temperature at the surface by inhibiting heat exchange between the fluid and the wall. This effect causes the fluid to retain more thermal energy, reduces the rate of heat transfer, and diminishes the thermal gradient. The overall temperature profile is consequently elevated due to the thickening of the thermal boundary layer.
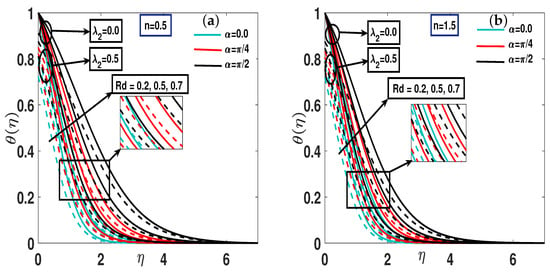
Figure 4.
(a,b) A pictorial representation of the temperature profile using parameter for both shear thinning instances and shear thickening .
Figure 5a,b show trends of over the temperature field for and . The angle of inclination and the exponentially space-dependent heat source affect the temperature profile, improving the thermal boundary layer profiles and corresponding thickness by raising for both scenarios. In practical systems, Qe models effects such as volumetric heating from chemical reactions, nuclear or electrical heating, and radiative absorption. It directly influences the energy balance by altering temperature gradients, modifying convection strength, and impacting overall heat transfer characteristics between the surface and the surrounding fluid. Figure 6a,b demonstrate the positive change in the temperature ratio parameter and temperature profile for dilatant and quasi-elastic liquids, respectively, with the parallel effect of in the presence of thermal slip at the boundary. Figure 7a,b illustrate the effects of the parameter and concentration slip on the concentration profile for both dilatant and pseudo-plastic fluids with the angle of inclination . Increasing and leads to a decline in the profile in both scenarios.
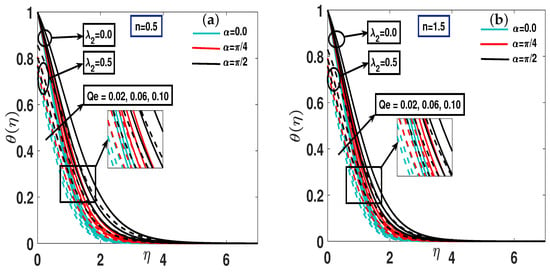
Figure 5.
(a,b) A pictorial representation of the temperature profile for and .
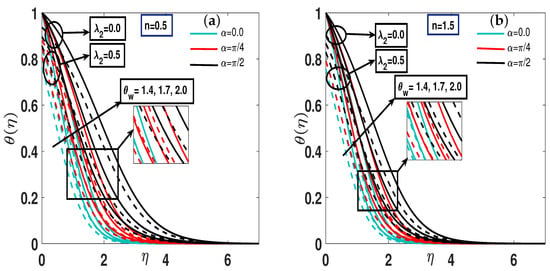
Figure 6.
(a,b) A pictorial representation of the temperature profile for both shear thinning instances and shear thickening .
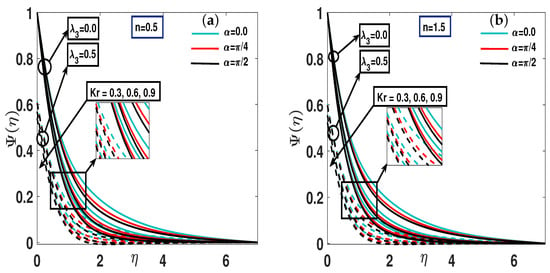
Figure 7.
(a,b) A pictorial representation of the concentration profile using parameter for both shear thinning instances and shear thickening .
Figure 8a,b illustrate the characteristics of the concentration field under the influence of the Eckart number (), the inclination angle (), and the parallel effects of the concentration slip parameter . The concentration profile is shown to increase with both the Eckart number and . Physically, activation energy () critically influences reaction rates in reactive flows according to the Arrhenius law; a lower or a higher temperature accelerates reactions. A high slows species consumption, resulting in elevated concentration levels, whereas a lower enhances reaction rates, causing sharper declines in species concentration. This makes its inclusion vital for accurately modeling mass transfer and conversion in reactive systems. Consequently, higher-dimensional activation energy () leads to an increase in the concentration profile for both dilatant () and pseudo-plastic () hybrid nanofluids.
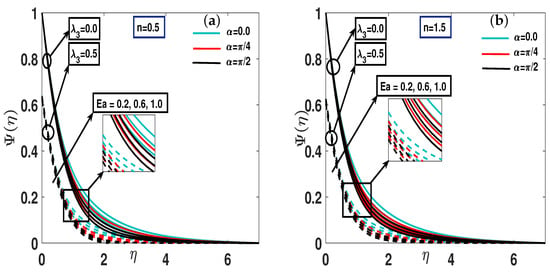
Figure 8.
(a,b) A pictorial representation of the concentration profile using parameter for both shear thinning instances and shear thickening .
The influence of the bioconvective Lewis parameter () on the profile of gyrotactic motile microorganisms is shown in Figure 9a,b for both thinning () and thickening () cases, under the simultaneous effects of the microorganism slip parameter () and inclined MHD (). It is observed that an increase in the bioconvective Lewis number reduces the fluid motility in both scenarios. The parameter , which represents the ratio of thermal to microorganism diffusivity, determines the relative rates of heat and microbe diffusion. A higher value sharpens the concentration gradients and thins the microorganism boundary layer, whereas a lower promotes smoother profiles through enhanced microbial dispersion. Furthermore, Lorentz forces generated by the inclined magnetic field impede fluid motion, thereby reducing convection and mitigating excessive microbial accumulation. The interplay between and the magnetic field collaboratively governs the stability and behavior of the bioconvective flow by shaping the microorganism distribution, altering the boundary layer thickness, and modulating the associated transport of heat, mass, and microbes.
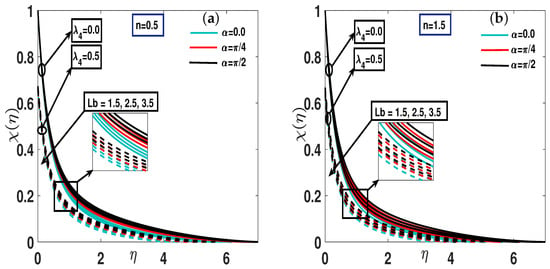
Figure 9.
(a,b) Motile concentration profile fluctuation with simultaneous effect of parameter for and .
The influence of on the motile profiles are displayed in Figure 10a,b for both dilatant and pseudo-plastic hybrid nanofluids , with a parallel effect of as the microbe slip parameter is present at the boundary. It has been noted that for both dilatant and pseudo-plastic hybrid nanofluids , the interpretation of the profile decreases as the parameter increases.
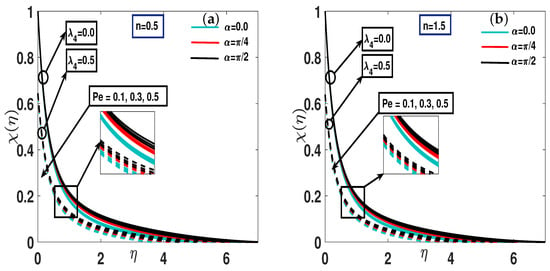
Figure 10.
(a,b) Motile concentration profile fluctuation with simultaneous effect of parameter for both shear thinning instances and shear thickening .
The streamlined graphs illustrate how fluid flow is simultaneously influenced by the magnetic parameter M and an angled magnetic field, as depicted in Figure 10a,b and Figure 11a,b. Asymmetric streamline patterns emerge when the flow direction is skewed by the magnetic field’s inclination. This inclination alters the balance between inertial and magnetic forces, redirecting the flow and causing the boundary layer to thicken on one side. Higher values of M enhance damping effects, resulting in a smoother flow field and reduced velocity. In MHD flow management and heat transfer optimization, the combined influence of magnetic strength and angle dictates the flow behavior. In contrast, a higher depletes the solute, thickens the concentration boundary layer, and diminishes the diffusive driving force at the wall, collectively causing a decline in . As illustrated in Figure 12b, a larger suppresses convective transport. This effect lowers the absolute levels and flattens the concentration surface.
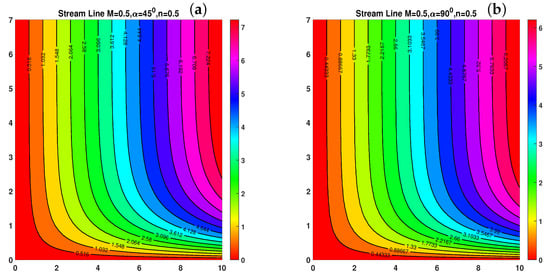
Figure 11.
(a,b) Stream line with M and inclined MHD at and for shear thinning instances .
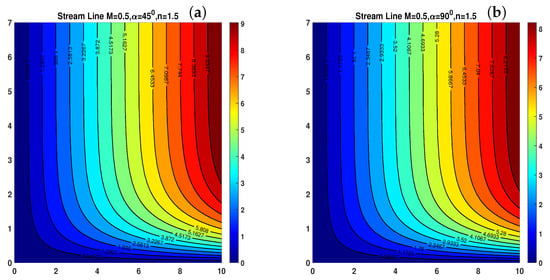
Figure 12.
(a,b) Stream line with M and inclined MHD at and for shear thickening .
This analysis suggests that MHD (magnetohydrodynamics) dampens the sensitivity of mass transfer to parameters and . These pictorial results validate that the same trend holds for different parameter values involving an inclined magnetic field and slip effect [42,43]. Furthermore, the response of the microorganism slip parameter and the Peclet number to the local motile–microorganism transfer measure is mapped for various inclined MHD angles in Figure 13a.
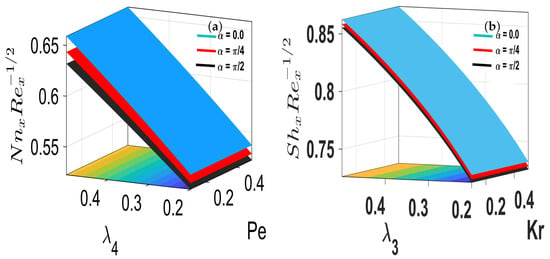
Figure 13.
(a,b) A pictorial representation of and using parameters , , , and with inclined MHD for both shear thinning instances and shear thickening .
The Peclet number () decrease corresponds to enhanced advective cell sweeping. This weakens wall-normal diffusion, resulting in flattened near-wall number-density gradients. Consistent with the observed reduction at high , a lower further diminishes the relative mobility of microorganisms near the surface. This reduces the wall flux and pushes the surface concentration lower. Conversely, a higher combined with a smaller elevates and steepens the near-wall slopes. Figure 13b plots the local Sherwood number against the reaction parameter and the solutal slip parameter . An increase in raises by intensifying wall-normal concentration gradients and relaxing the wall’s constraint on species transport. Figure 14 presents a contour map demonstrating how the radiation parameter (Rd), thermophoresis (Nt), Brownian motion (Nb), and inclined MHD interact collectively to influence the local Nusselt number. This number serves as a measure of heat transport at the surface for both dilatant and pseudo-plastic hybrid nanofluids. Maximum heat transfer is achieved in both cases with higher values of Rd and Nt coupled with a lower value of Nb. Although the introduction of inclined MHD slightly diminishes convection and the overall Nusselt number due to Lorentz forces that oppose fluid motion, the overarching trends of the parameter interactions confirm that Rd and Nt play a dominant role in enhancing thermal transport.
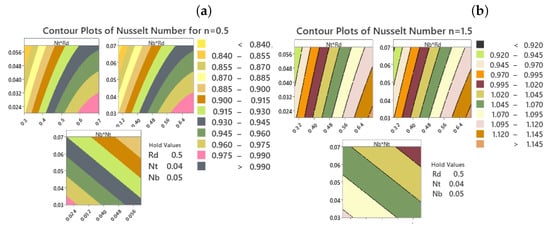
Figure 14.
(a,b) Contour plots for for both shear thinning instances and shear thickening .
The combined effects of the radiation parameter (Rd), Brownian motion parameter (Nb), and thermophoresis parameter (Nt) on heat transfer in both dilatant and pseudo-plastic hybrid nanofluids are illustrated in the 3D surface plots in Figure 15a,b. The Nusselt number increases with higher Nt values. This occurs because the thermophoretic force, which drives nanoparticles from hotter to cooler regions, intensifies, thereby enhancing energy transmission and steepening the wall temperature gradient. Similarly, a larger Rd enhances radiative heat transfer, which reduces thermal resistance and further accelerates the rate of heat transfer. Conversely, a higher Nb increases the random motion of nanoparticles. This random Brownian diffusion disrupts the directed transport caused by thermophoresis, thickens the thermal boundary layer, and ultimately reduces the Nusselt number, despite also promoting local thermal mixing. The surface plots effectively capture this complex, nonlinear interplay among the parameters, revealing optimal ranges for heat transfer optimization. Prominent peaks occur at high combinations of Nt and Rd with low Nb, while troughs are observed where Nb is high or Rd is low.
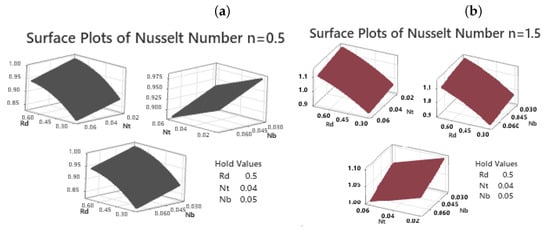
Figure 15.
(a,b) Surface plots for for both shear thinning instances and shear thickening .
The residual versus fitted plot in Figure 16 is used to assess the reliability of the estimated model. This plot, which indicates a maximum error of 0.01001, further confirms the model’s accuracy. This section presents the numerical results for the skin friction and Nusselt number with respect to various parameters and the inclination angle (). Table 5 displays the corresponding calculated numerical values. An increase in the radiation parameter (Rd) within the range leads to a decrease in skin friction. Higher radiation enhances energy transfer via thermal radiation, which thickens the thermal boundary layer. This reduces the momentum boundary layer gradient, resulting in lower wall shear stress and consequently lower skin friction. Conversely, an increase in the Weissenberg number within the range raises the skin friction values. Furthermore, as the inclination angle increases from , the buoyant driving force diminishes. This slows the fluid motion near the surface, reducing wall shear stress and thus skin friction.
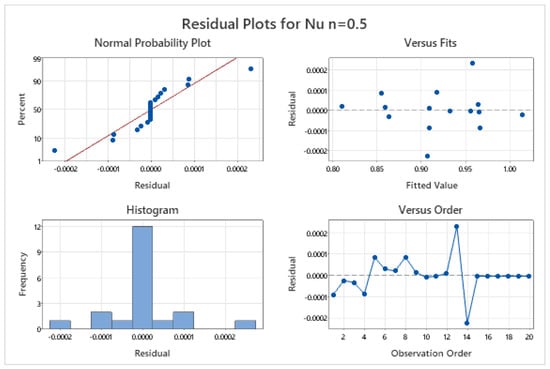
Figure 16.
Residual plot for .

Table 5.
The variation in the skin friction coefficient and the Nusselt number for different values of and while other parameters remain fixed in active and passive cases.
As the inclination angle increases within the range , the component of surface gravity tangential to the slope decreases. This reduction diminishes the buoyant driving force, weakens the flow velocity, and consequently lowers the Nusselt number, impairing convective heat transfer in both active and passive scenarios. A higher Biot number signifies that surface convection is more dominant relative to internal conduction within the fluid, which enhances overall heat transfer and raises the Nusselt number. The Nusselt number increases for both cases as the radiation parameter Rd grows from . Conversely, the Nusselt number declines for all cases with rising values of the Brownian motion parameter Nb , the thermophoresis parameter Nt , and the Weissenberg number We . The decrease associated with a higher Weissenberg number is attributed to heightened elastic effects, which reduce the thermal efficiency of the flow.
7. Concluding Remarks
This study numerically investigates the magnetohydrodynamic flow of a two-dimensional, incompressible Carreau hybrid nanofluid over a nonlinear stretching sheet, incorporating microorganisms. The model accounts for the simultaneous effects of nonlinear thermal radiation, chemical reactions, and multiple slip boundary conditions for both dilatant () and pseudo-plastic () fluid behaviors. The governing partial differential equations (PDEs) were transformed into ordinary differential equations (ODEs) via similarity transformations and solved numerically using the Bvp5c solver in MATLAB. The major findings of this research are the following:
- A magnetic field promotes higher temperature and elevates the motile concentration profiles. However, it induces a reversing character in the velocity and concentration profiles
- The physical parameters of heat sources, nonlinear radiation, and the Weissenberg number intensify the temperature field, and the structure of the boundary layers exhibits symmetry as a result of parameters acting at various angles .
- The Weissenberg number affects heat transfer, skin friction, and the velocity profile differently at various angles , with effects intensifying when and weakening when .
- The hybrid nanofluid concentration is effectively affected by activation energy, whereas a significant decrease is noted upon increasing the chemical reaction parameter with the simultaneous effect of concentration slip and inclined magnetohydrodynamic for shear thinning and shear thickening .
- The motile profile shrinks with increasing and in dilatant and quasi-elastic liquids, showing a parallel effect from , under the presence of the boundary slip parameter for microorganisms.
- Increasing the inclination angle () causes the skin friction surface to shift toward the base plane; conversely, the Nusselt number surface shows an opposite trend.
- The maximum heat transfer rate occurs at larger radiation parameter values. An increase in the inclination angle within the range of to () results in a reduction in the Nusselt number.
- The hybrid nanofluid model enhances cooling efficiency in applications like solar panels and electronic equipment. It is also highly effective in industries such as coating and polymer extrusion, where precise control of mass and heat transfer under magnetic fields is essential.
Author Contributions
Conceptualization, S., P.K., P.S.M. and M.A.; methodology, S., P.K. and M.A.; software, S., P.K., P.S.M. and M.A.; validation, S., P.K., P.S.M. and M.A.; formal analysis, S., P.K., P.S.M. and M.A.; writing—original draft, S., P.K., P.S.M. and M.A.; project administration, M.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The first author acknowledges the School of Basic and Applied Sciences for their technical support at KR Mangalam University, India.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Sharma, R.P.; Badak, K.; Khan, U.; Ishak, A.; Sherif, E.S.M.; Wróblewski, P. Dynamics of variable thermal conductivity and multiple slip conditions in a Carreau hybrid nanofluid flow past a stretching sheet. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, e202400388. [Google Scholar] [CrossRef]
- Eid, M.R.; Mahny, K.; Dar, A.; Muhammad, T. Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. Phys. A Stat. Mech. Its Appl. 2020, 540, 123063. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.; Salahuddin, T. Chemical reaction for Carreau-Yasuda nanofluid flow past a nonlinear stretching sheet considering Joule heating. Results Phys. 2018, 8, 1124–1130. [Google Scholar] [CrossRef]
- Gopal, D.; Naik, S.H.S.; Kishan, N.; Raju, C. The impact of thermal stratification and heat generation/absorption on MHD carreau nano fluid flow over a permeable cylinder. SN Appl. Sci. 2020, 2, 639. [Google Scholar] [CrossRef]
- Reddy, R.R.; Reddy, P.B.A.; Chamkha, J. Influence of Soret and Dufour effects on unsteady 3D MHD slip flow of Carreau nanofluid over a slendering stretchable sheet with chemical reaction. Nonlinear Anal. Model. Control 2019, 24, 853. [Google Scholar] [CrossRef]
- Gautam, A.K.; Rajput, S.; Bhattacharyya, K.; Pandey, A.K.; Chamkha, A.J.; Begum, M. Comparative study of two non-Newtonian fluids with bioconvective induced MHD flow in presence of multiple slips, heat source/sink and nonlinear thermal radiation. Chem. Eng. J. Adv. 2022, 12, 100365. [Google Scholar] [CrossRef]
- Jiann, L.Y.; Isa, S.M.; Rawi, N.A.; Mohamad, A.Q.; Shafie, S. Investigating the effects of Wu’s slip and Smoluchowski’s slip on hybrid TiO2/Ag nanofluid performance. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 107, 236–252. [Google Scholar] [CrossRef]
- Shamshuddin, M.; Raizah, Z.; Akkurt, N.; Patil, V.S.; Eldin, S.M. Case study of thermal and solutal aspects on non-Newtonian Prandtl hybrid nanofluid flowing via stretchable sheet: Multiple slip solution. Case Stud. Therm. Eng. 2023, 49, 103186. [Google Scholar] [CrossRef]
- Abdeen, W.S.; Rashad, A.M.; Mahdy, A.; Elshehabey, H.M. Bio-Convection Eyring-Powell Hybrid Nanofluid Flow Over an Extended Sheet in the Existence of Chemical Reaction and Motile Microorganisms. J. Nanofluids 2024, 13, 973–984. [Google Scholar] [CrossRef]
- Rehman, S.; Hashim; Boujelbene, M.; Waqas, M. On the augmentation of heat transfer with hybrid nanofluid containing microorganisms on flat plate under thermal radiation, using mixtures models. Energy Environ. 2024, 0958305X241244487. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Shah, N.A.; Kumar, M.; Eldin, S.M. Ternary hybrid nanofluid flow containing gyrotactic microorganisms over three different geometries with Cattaneo–Christov model. Mathematics 2023, 11, 1237. [Google Scholar] [CrossRef]
- Bilal, S.; Shah, I.A.; Rashid, M.; Khan, I. Impact of activation energy on carreau nanofluid flow over non-linear stretching surface. Heliyon 2024, 10, e23934. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Shafiq, A. Inclined magnetic field and heat source/sink aspects in flow of nanofluid with nonlinear thermal radiation. Int. J. Heat Mass Transf. 2016, 103, 99–107. [Google Scholar] [CrossRef]
- Mabood, F.; Shafiq, A.; Khan, W.A.; Badruddin, I.A. MHD and nonlinear thermal radiation effects on hybrid nanofluid past a wedge with heat source and entropy generation. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 120–137. [Google Scholar] [CrossRef]
- Chalavadi, S.; Madde, P.; Naramgari, S.; Gangadhar Poojari, A. Effect of variable heat generation/absorption on magnetohydrodynamic Sakiadis flow of Casson/Carreau hybrid nanoliquid due to a persistently moving needle. Heat Transf. 2023, 50, 8354–8377. [Google Scholar] [CrossRef]
- Rehman, S.; Hashim, A.; Shah, S.I.; Galal, A.M. Multiple aspects of heat generation/absorption on the hydromagnetic flow of Carreau nanofluids via nonuniform channels. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 237, 1961–1975. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Fatima, K.; Prasad, J. Effect of Inclined Magnetic Field and Chemical Reaction on Radiative Hybrid Nanofluid Flow Through an Exponentially Stretched Porous Surface in the Presence of Heat Source. J. Mech. Contin. Math. Sci 2025, 20, 38–53. [Google Scholar] [CrossRef]
- Kathuroju, S.K.; Prashar, P.; Ojjela, O. Asymptotic analysis of MHD chemically reacting boundary layer flow of Jeffrey hybrid nanofluid. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, 104, e202300770. [Google Scholar] [CrossRef]
- Sreenivasulu, M.; Bhuvana Vijaya, R. Influence of exponential heat source, variable viscosity and shape factor on a hybrid nanofluid flow over a flat plate when thermal radiation and chemical reaction are significant. Mod. Phys. Lett. B 2024, 38, 2450102. [Google Scholar] [CrossRef]
- Jat, K.; Sharma, K.; Soni, P.; Choudhary, P. Numerical analysis of heat and mass transport of hybrid nanofluid over a nonlinear stretchable sheet with magnetic field in presence of Soret and dufour Effect. In Proceedings of the 5th National Conference on Recent Advancement in Physical Sciences, Uttarakhand, India, 19–20 December 2023; Journal of Physics: Conference Series. IOP Publishing: Bristol, UK, 2024; Volume 2844, p. 012019. [Google Scholar]
- Rafique, K.; Mahmood, Z.; Ansari, M.A.; Kumar, A.; Khan, U. Investigating Soret–Dufour effects and discharge concentration on accelerating hybrid nanofluid flow over radiative disk embedded in porous media under convective conditions. Can. J. Phys. 2025, 103, 860–878. [Google Scholar] [CrossRef]
- Kumar, S.; Prasad, P.; Raju, C.; Shehzad, S.; Bashir, M.; Varma, S. Three-dimensional magnetized slip flow of Carreau non-Newtonian fluid flow through conduction and radiative chemical reaction. Indian J. Phys. 2021, 96, 491–501. [Google Scholar]
- Khan, M.; Hashim. Effects of multiple slip on flow of magneto-Carreau fluid along wedge with chemically reactive species. Neural Comput. Appl. 2018, 30, 2191–2203. [Google Scholar] [CrossRef]
- Nanda, G.; Patel, H. Thermophoresis and brownian motion effects on inclined mhd nano-fluid flow with multi slip condition. J. Comput. Anal. Appl. 2025, 34, 795. [Google Scholar]
- Deshwal, J.; Chaudhary, S.; Kumar, R. Chemical reaction and inclined magnetic field effects on tri-hybrid Carreau nanofluid slip flow of blood past a porous inclined stenosed artery with viscous dissipation. Phys. Scr. 2025, 100, 035216. [Google Scholar] [CrossRef]
- Shah, S.Z.H.; Ayub, A.; Bhatti, S.; Khan, U.; Ishak, A.; Sherif, E.S.M.; Pop, I. Aspects of inclined magnetohydrodynamics and heat transfer in a non-Newtonian tri-hybrid bio-nanofluid flow past a wedge-shaped artery utilizing artificial neural network scheme. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, 104, e202400278. [Google Scholar] [CrossRef]
- Mohamed, R.; Abo-Dahab, S.; Soliman, M. Effects of nonlinear thermal radiation and heat generation/absorption on magnetohydrodynamic (MHD) Carreau nanofluid flow on a nonlinear stretching surface through a porous medium. J. Nanofluids 2022, 11, 845–856. [Google Scholar] [CrossRef]
- Yasmin, H. Numerical investigation of heat and mass transfer study on MHD rotatory hybrid nanofluid flow over a stretching sheet with gyrotactic microorganisms. Ain Shams Eng. J. 2024, 15, 102918. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; ul Huda, N.; Chung, J.D.; Farooq, U. Nonlinear radiation effect on MHD Carreau nanofluid flow over a radially stretching surface with zero mass flux at the surface. Sci. Rep. 2018, 8, 3709. [Google Scholar] [CrossRef]
- Yahaya, R.I.; Arifin, N.M.; Ali, F.M.; Isa, S. Hybrid Nanofluid Flow with multiple slips over a Permeable Stretching/Shrinking sheet embedded in a porous medium. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 106, 143–152. [Google Scholar] [CrossRef]
- Das, M.; Nandi, S.; Kumbhakar, B.; Shanker Seth, G. Soret and Dufour effects on MHD nonlinear convective flow of tangent hyperbolic nanofluid over a bidirectional stretching sheet with multiple slips. J. Nanofluids 2021, 10, 200–213. [Google Scholar] [CrossRef]
- Alrehili, M. Improvement for engineering applications through a dissipative Carreau nanofluid fluid flow due to a nonlinearly stretching sheet with thermal radiation. Case Stud. Therm. Eng. 2023, 42, 102768. [Google Scholar] [CrossRef]
- Raju, S.S.K.; Babu, M.J.; Raju, C. Irreversibility analysis in hybrid nanofluid flow between two rotating disks with activation energy and cross-diffusion effects. Chin. J. Phys. 2021, 72, 499–529. [Google Scholar] [CrossRef]
- Neethu, T.S.; Areekara, S.; Mathew, A. Statistical approach on 3D hydromagnetic flow of water-based nanofluid between two vertical porous plates moving in opposite directions. Heat Transf. 2021, 50, 5170–5197. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Gholinia, M.; Hoseini, M.; Ganji, D. Natural convection MHD flow due to MoS2–Ag nanoparticles suspended in C2H6O2H2O hybrid base fluid with thermal radiation. J. Taiwan Inst. Chem. Eng. 2019, 97, 12–23. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D. Investigation on thermophysical properties of Tio2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Sabu, A.S.; Areekara, S.; Mathew, A. Effects of multislip and distinct heat source on MHD Carreau nanofluid flow past an elongating cylinder using the statistical method. Heat Transf. 2021, 50, 5652–5673. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Wang, C. Free convection on a vertical stretching surface. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 1989, 69, 418–420. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Shah, N.A.; Chung, J.D. Significance of Weissenberg number, Soret effect and multiple slips on the dynamic of biconvective magnetohydrodynamic carreau nanofuid flow. Mathematics 2023, 11, 1685. [Google Scholar] [CrossRef]
- Kumari, P.; Poonia, H.; Kumar, P.; Aquib, M. Inclined MHD Flow of Carreau Hybrid Nanofluid over a Stretching Sheet with Nonlinear Radiation and Arrhenius Activation Energy Under a Symmetry-Inspired Modeling Perspective. Symmetry 2025, 17, 1330. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).