A Multistage Algorithm for Phase Load Balancing in Low-Voltage Electricity Distribution Networks Operated in Asymmetrical Conditions
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Motivation and Contributions
| Approach | Method | Advantages | Limitations |
|---|---|---|---|
| Limitation of neutral wire current | Hardware solution [8] | Scalability | Lack of optimization |
| Multi-agent deep reinforcement learning [28] | Use of distributed single-phase storage | Small test system | |
| PV inverter management [31] | Distributed and local PV inverter control | HIL model | |
| Management of battery storage and electric vehicle charging | Simulation [10] | Multiple scenario analysis | No individual phase analysis |
| Mixed-integer linear optimization [20] | Simultaneous optimization of EV charging, PV output, and LVDN management | Small test system and no individual phase analysis | |
| Local peer-to-peer electricity trading and communication | Gale–Shapley algorithm [16] | DSO-independent network congestion solving | No individual phase analysis, trading based solely on distance |
| Stratified optimization and control [27] | Usable in real-time operation | Complex model, requiring multiple concurrent tools and the need for forecasted data | |
| Phase load balancing | Benders decomposition (MILP and LP) [21] | Phase identification of individual consumers | High number of iterations |
| Whale optimization algorithm [29] | The detailed three-phase model of the LVDN is considered | Small test system and consumers modeled as typical load profiles | |
| Deterministic crowding algorithm (genetic algorithm variant) [30] | Efficient even with a low count of measured consumers | No explicit diagram of the LVDN and consumers modeled as typical load profiles | |
| Particle swarm optimization [36] | Initial and continuous optimization | ||
| Mixed-integer second-order optimization [37] | Works with partial information from the LVDN | Needs accurate control of phase-switching devices | |
| Simulation [38] | Can outperform the use of energy storage | Uses a theoretical active asymmetry energy-absorbing device | |
| Estimation of phase peak current | Statistical method, cluster-wise probability assessment [24] | Minimal input data | Lack of precision |
| Reactive power compensation using capacitor banks | Mathematical computation [25] | Flexible capacitor bank configurations | Small, theoretical test system and restrictive initial assumptions |
| Interior-point nonlinear optimization [39] | Consideration of special types of loads | Small test system | |
| PV generation management | Custom PV inverter simulation [26] | Flexible scenario generation | Small, theoretical test system |
| Particle swarm optimization [40] | DG optimization | Small test system | |
| Demand response, on-load transformer tap changers | Particle swarm optimization [41] | Voltage symmetry optimization | User comfort settings can reduce the efficiency of the approach |
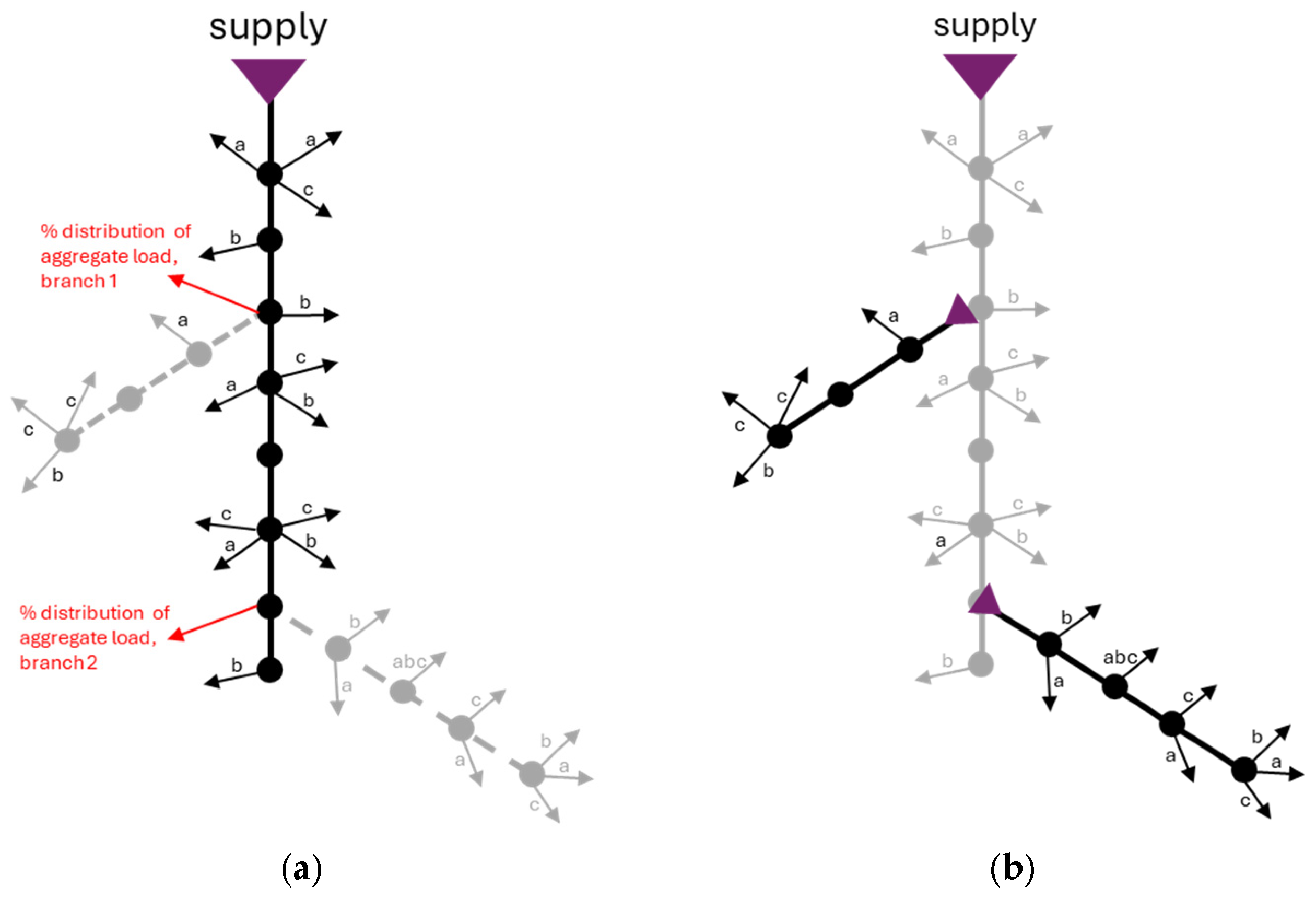
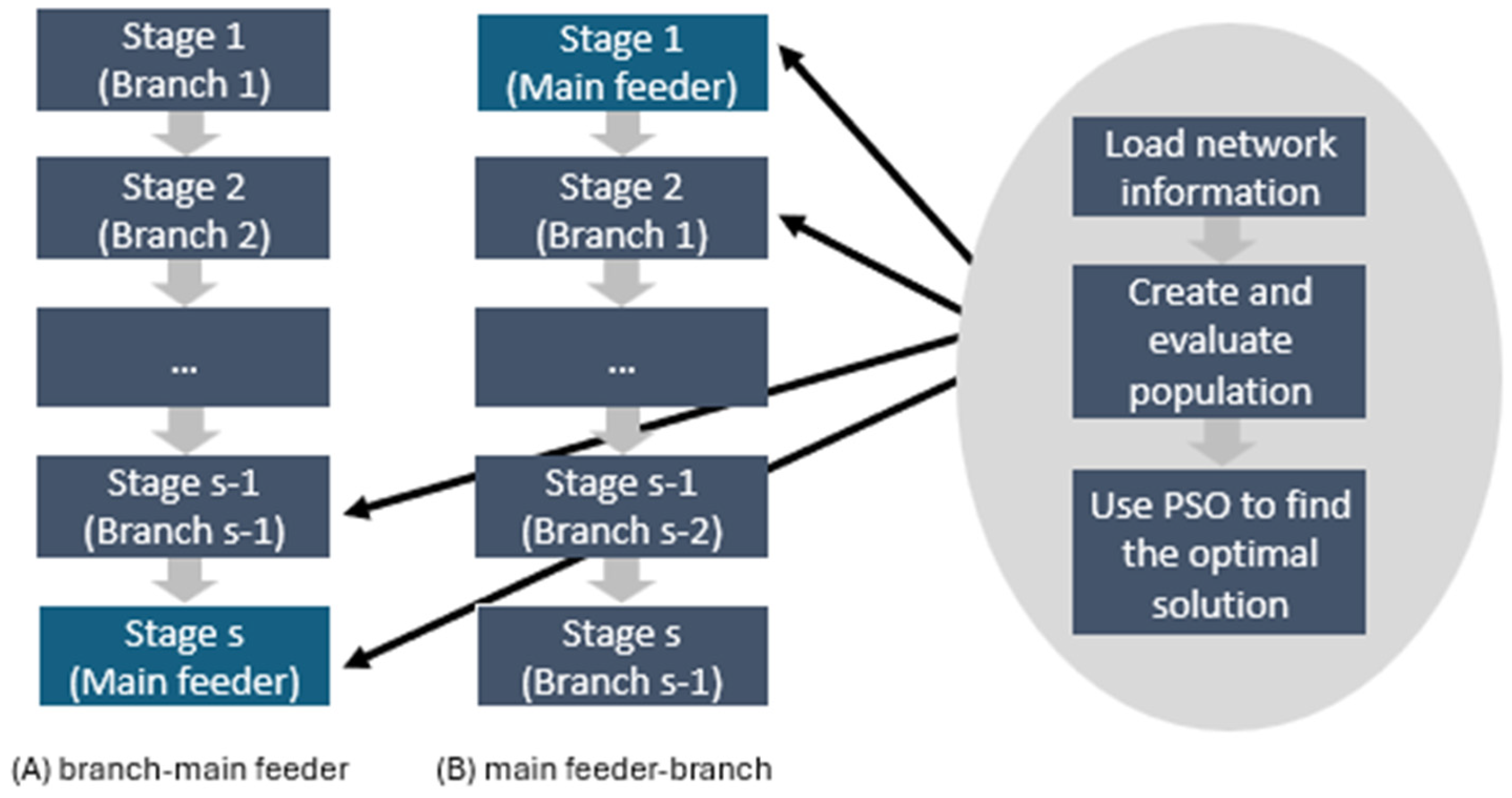
- A multistage swapping approach where the swapping is performed first separately on each branch, and then their aggregate load is used subsequently to optimize the main feeder (the branch–main feeder multistage method).
- A multistage swapping approach where the phase swapping is performed first on the main feeder and the branches are considered as aggregate three-phase loads, and the phase distribution of these aggregated loads is used subsequently as reference for swapping the loads on the branches (the main feeder–branch multistage method).
2. Materials and Methods
2.1. Theoretical Considerations
- Balance of the end-users at the level of LVDN in the PLB process, which can be represented as follows:
- Balance of the phase currents at the level of the control nodes (poles/lateral branches), which can be represented as follows:
- Thermal limit currents of phase conductors from each section of the LVDN, which are as follows:
2.2. Methodology
- (A)
- Consumer phase swap is performed first on each branch separately (the branch–main feeder multistage method).
- (B)
- Consumer phase swap is performed first on the main feeder (the main feeder–branch multistage method).
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MV | Medium Voltage |
| LV | Low Voltage |
| DNO | Distribution Network Operator |
| LVDN | Low Voltage Distribution Network |
| EV | Electric Vehicle |
| DG | Distributed Generation |
| PLB | Phase Load Balancing |
| PV | Photovoltaic |
| PSO | Particle Swarm Optimization |
References
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Ramasubbareddy, S.; Babu, T.S.; Kumar, N.M.; Elavarasan, R.M.; Mihet-Popa, L. A Comprehensive Survey on Different Control Strategies and Applications of Active Power Filters for Power Quality Improvement. Energies 2021, 14, 4589. [Google Scholar] [CrossRef]
- Shabalov, M.Y.; Zhukovskiy, Y.L.; Buldysko, A.D.; Gil, B.; Starshaia, V.V. The influence of technological changes in energy efficiency on the infrastructure deterioration in the energy sector. Energy Rep. 2021, 7, 2664–2680. [Google Scholar] [CrossRef]
- Gitelman, L.; Magaril, E.; Kozhevnikov, M. Energy security: New threats and solutions. Energies 2023, 16, 2869. [Google Scholar] [CrossRef]
- CEER. CEER Report on Power Losses; C17-EQS-80-03; Council of European Energy Regulators: Brussels, Belgium, 2017. [Google Scholar]
- Kazymov, I.; Kompaneets, B. Definition of fact and place of losses in low voltage electric networks. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019. [Google Scholar] [CrossRef]
- Carr, D.; Thomson, M. Non-technical electricity losses. Energies 2022, 15, 2218. [Google Scholar] [CrossRef]
- Diahovchenko, I.; Petrichenko, L. Assessment of energy losses in power distribution systems with individual prosumers and energy communities. J. Eng. 2023, 2023, e12243. [Google Scholar] [CrossRef]
- Naumov, I. Additional power losses in low-voltage electrical networks and their influence on people. In Research Paradigms Transformation in Social Sciences; Ardashkin, I.B., Iosifovich, B.V., Martyushev, N.V., Eds.; European Proceedings of Social and Behavioural Sciences; Future Academy: Cairo, Egypt; London, UK, 2018; Volume 50, pp. 844–853. [Google Scholar] [CrossRef]
- Matanov, N.; Angelov, I.; Stoev, P. A study of load unbalance on low voltage grid. In Proceedings of the 16th Electrical Engineering Faculty Conference (BulEF), Varna, Bulgaria, 19–22 September 2024. [Google Scholar] [CrossRef]
- Reibsch, R.; Blechinger, P.; Kowal, J. The importance of battery storage systems in reducing grid issues in sector-coupled and renewable low-voltage grids. J. Energy Storage 2023, 72, 08726. [Google Scholar] [CrossRef]
- Pandraju, T.K.S.; Samal, S.; Saravanakumar, R.; Yaseen, S.M.; Nandal, R.; Dhabliya, D. Advanced metering infrastructure for low voltage distribution system in smart grid based monitoring applications. Sustain. Comput. Inform. Syst. 2022, 35, 100691. [Google Scholar] [CrossRef]
- Gatta, F.M.; Geri, A.; Maccioni, M.; Palazzoli, A.; Sancioni, P. Low voltage electric distribution network planning with demand control. Electr. Power Syst. Res. 2024, 226, 109950. [Google Scholar] [CrossRef]
- Ahmadi Kamarposhti, M.; Ghandour, R.; Abdel-Aty, M.; Hafez, M.; Alfiras, M.; Alkhazaleh, S.; Colak, I.; Solyman, A. Optimizing capacitor bank placement in distribution networks using a multi-objective particle swarm optimization approach for energy efficiency and cost reduction. Sci. Rep. 2025, 15, 12332. [Google Scholar] [CrossRef]
- Musaruddin, M.; Tambi, T.; Zulkaidah, W.; Masikki, G.A.N.; Lolok, A.; Djohar, A.; Marwan, M. Optimizing network reconfiguration to reduce power loss and improve the voltage profile in the distribution system: A practical case study. E-Prime-Adv. Electr. Eng. Electron. Energy 2024, 8, 100599. [Google Scholar] [CrossRef]
- Werkie, Y.G.; Kefale, H.A. Optimal allocation of multiple distributed generation units in power distribution networks for voltage profile improvement and power losses minimization. Cogent Eng. 2022, 9, 2091668. [Google Scholar] [CrossRef]
- Guerrero, J.; Sok, B.; Chapman, A.C.; Verbič, G. Electrical-distance driven peer-to-peer energy trading in a low-voltage network. Appl. Energy 2021, 287, 116598. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elattar, E.E.; Nagem, N.A.; Nasef, A.F. Allocation of PV systems with Volt/Var control based on automatic voltage regulators in active distribution networks. Sustainability 2023, 15, 15634. [Google Scholar] [CrossRef]
- Wu, X.; Yang, C.; Han, G.; Ye, Z.; Hu, Y. Energy loss reduction for distribution networks with energy storage systems via loss sensitive factor method. Energies 2022, 15, 5453. [Google Scholar] [CrossRef]
- Sadat, S.M.; Shourkaei, H.M.; Soleymani, S. Electrical vehicles impact on unbalanced distribution networks considering different loads and energy prices. Heliyon 2024, 10, e39233. [Google Scholar] [CrossRef]
- Grammenou, C.V.; Dragatsika, M.; Bouhouras, A.S. Optimal EV charging and PV siting in prosumers towards loss reduction and voltage profile improvement in distribution networks. World Electr. Veh. J. 2024, 15, 462. [Google Scholar] [CrossRef]
- Heidari-Akhijahani, A.; Safdarian, A.; Aminifar, F. Phase identification of single-phase customers and PV panels via smart meter data. IEEE Trans. Smart Grid 2021, 12, 4543–4552. [Google Scholar] [CrossRef]
- Routray, A.; Mistry, K.D.; Arya, S.R.; Chittibabu, B. Applied machine learning in wind speed prediction and loss minimization in unbalanced radial distribution system. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 3790–3810. [Google Scholar] [CrossRef]
- Ghatak, S.R.; Sannigrahi, S.; Acharjee, P. Multiobjective framework for optimal integration of solar energy source in three-phase unbalanced distribution network. IEEE Trans. Ind. Appl. 2020, 56, 3068–3078. [Google Scholar] [CrossRef]
- Fang, L.; Ma, K.; Zhang, Z. A statistical methodology to identify imbalance-induced capacity wastes for LV networks. Electr. Power Syst. Res. 2021, 199, 107388. [Google Scholar] [CrossRef]
- Blasco, P.A.; Montoya-Mira, R.; Diez, J.M.; Montoya, R. Algorithm for passive reactive power compensation of an unbalanced three-phase four-wire system using capacitors ensuring minimum line losses. Electr. Power Syst. Res. 2024, 227, 109972. [Google Scholar] [CrossRef]
- Fernão Pires, V.; Cordeiro, A.; Foito, D.; José Pires, A.; Hao, C.; Francisco Martins, J.; Castro, R. Compensation of unbalanced low-voltage grids using a photovoltaic generation system with a dual four-leg, two-level inverter. Electronics 2022, 11, 320. [Google Scholar] [CrossRef]
- Rao, B.V.; Stefan, M.; Schwalbe, R.; Karl, R.; Kupzog, F.; Kozek, M. Stratified control applied to a three-phase unbalanced low voltage distribution grid in a local peer-to-peer energy community. Energies 2021, 14, 3290. [Google Scholar] [CrossRef]
- Pinthurat, W.; Hredzak, B. Multi-agent deep reinforcement learning for mitigation of unbalanced active powers using distributed batteries in low voltage residential distribution system. Electr. Power Syst. Res. 2025, 245, 111599. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, X.D.; Shi, H.R.; Yang, C.; Zhou, S.Q.; Hao, T. Research on three-phase unbalance control of low-voltage distribution network based on load commutation. J. Electr. Eng. Technol. 2024, 19, 4027–4043. [Google Scholar] [CrossRef]
- Jimenez, V.A.; Will, A.L.E.; Lizondo, D.F. Phase reassignment for load balance in low-voltage distribution networks. Int. J. Electr. Power Energy Syst. 2022, 137, 107691. [Google Scholar] [CrossRef]
- Feng, Q.; Xia, Y.; Yang, P.; Wei, W. Unbalance compensation for PV-dominated 3P-4W distribution networks. IEEE Trans. Power Deliv. 2024, 39, 1983–1996. [Google Scholar] [CrossRef]
- Ji, B.-X.; Liu, H.-H.; Cheng, P.; Ren, X.-Y.; Pi, H.-D.; Li, L.-L. Phased optimization of active distribution networks incorporating distributed photovoltaic storage system: A multi-objective coati optimization algorithm. J. Energy Storage 2024, 91, 112093. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.J. Low voltage distribution networks modeling and unbalanced (optimal) power flow: A comprehensive review. IEEE Access 2021, 9, 143026–143084. [Google Scholar] [CrossRef]
- Toma, N.; Ivanov, O.; Neagu, B.; Gavrilas, M. A PSO algorithm for phase load balancing in low voltage distribution networks. In Proceedings of the 2018 International Conference and Exposition on Electrical And Power Engineering (EPE), Iasi, Romania, 18–19 October 2018. [Google Scholar] [CrossRef]
- Ivanov, O.; Neagu, B.C.; Gavrilas, M.; Grigoras, G.; Sfintes, C.V. Phase load balancing in low voltage distribution networks using metaheuristic algorithms. In Proceedings of the 2019 International Conference on Electromechanical and Energy Systems (SIELMEN), Craiova, Romania, 9–11 October 2019. [Google Scholar] [CrossRef]
- Zhong, K.; Tang, Y.; Zhang, S.; Zhang, Y.; Deng, W. A predictive rolling optimization method of load balancing in low-voltage active distribution network. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021. [Google Scholar] [CrossRef]
- Liu, B.; Meng, K.; Dong, Z.Y.; Wong, P.K.C.; Li, X. Load balancing in low-voltage distribution network via phase reconfiguration: An efficient sensitivity-based approach. IEEE Trans. Power Deliv. 2020, 36, 2174–2185. [Google Scholar] [CrossRef]
- Xiao, M.; Wang, S.; Ullah, Z. D-PMU and 5G-Network-Based Coordination Control Method for Three-Phase Imbalance Mitigation Units in the LVDN. Energies 2021, 14, 2754. [Google Scholar] [CrossRef]
- Yanghua, L.I.U.; Shunjiang, L.I.N. Optimal allocation of distributed reactive power compensation for low voltage distribution network considering pump loads’ characteristics. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018. [Google Scholar] [CrossRef]
- Majeed, A.A.; Abderrahim, M.; Alkhazraji, A.A. Optimal allocation of photovoltaic-green distributed generation for maximizing the performance of electrical distribution networks. Energies 2024, 17, 1376. [Google Scholar] [CrossRef]
- Rahman, M.M.; Arefi, A.; Shafiullah, G.M.; Hettiwatte, S. A new approach to voltage management in unbalanced low voltage networks using demand response and OLTC considering consumer preference. Int. J. Electr. Power Energy Syst. 2018, 99, 11–27. [Google Scholar] [CrossRef]
- Grigoraș, G.; Noroc, L.; Chelaru, E.; Scarlatache, F.; Neagu, B.-C.; Ivanov, O.; Gavrilaș, M. Coordinated control of single-phase end-users for phase load balancing in active electric distribution networks. Mathematics 2021, 9, 2662. [Google Scholar] [CrossRef]
- Toader, C.; Porumb, R.; Bulac, C.; Tristiu, I. A perspective on current unbalance in low voltage distribution networks. In Proceedings of the 2015 9th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 7–9 May 2015. [Google Scholar] [CrossRef]
- Nour, A.M.; Helal, A.A.; El-Saadawi, M.M.; Hatata, A.Y. Voltage imbalance mitigation in an active distribution network using decentralized current control. Prot. Control Mod. Power Syst. 2023, 8, 20. [Google Scholar] [CrossRef]
- Calin. Single Phase STS Prepaid Meter. Available online: https://www.prepayment-meter.com/supplier-109289-sts-prepaid-meters (accessed on 27 August 2025).
- Londian. Smart Prepaid Meter. Available online: https://londianglobal.com/product-category/prepaid-electricity-meter (accessed on 27 August 2025).
- Novatek-Electro. Universal Automatic Electronic Phase Switch Pef-319. Available online: https://novatek-electro.in/pef-319/ (accessed on 27 August 2025).
- Yongxia, L.; Yulei, G. Design of three phase load unbalance automatic regulating system for low voltage power distribution grids. In Proceedings of the 2018 International Conference on Smart Materials, Intelligent Manufacturing and Automation (SMIMA 2018), Nanjing, China, 24–26 May 2018; Volume 173, p. 02040. [Google Scholar] [CrossRef]
- Haq, S.U.; Arif, B.; Khan, A.; Ahmed, J. Automatic three phase load balancing system by using fast switching relay in three phase distribution system. In Proceedings of the 1st International Conference on Power, Energy and Smart Grid (ICPESG), Mirpur, Pakistan, 9–10 April 2018. [Google Scholar] [CrossRef]
- Iyappan, M.; Karpagam, M.; Raviram, P. Automatic load sharing in industrial plant with monitoring system using microcontroller. Int. J. App. Eng. Res. 2015, 10, 114–120. [Google Scholar]
- Ofualagba, G.; Udoha, E.E. Design and simulation of automatic phase selector and changeover switch for 3-phase supply. Int. J. Nov. Res. Electr. Mech. Eng. 2017, 4, 28–35. [Google Scholar]
- Rashid, A.T.; Rashid, M.T. Design and implementation of load balancing system for a smart home. In Proceedings of the International Scientific Conference for Renewable Energy (ISCRE’ 2018), Basrah, Iraq, 14–15March 2018; pp. 1–6. [Google Scholar]
- Shakeel, M.O.B.; Jaffar, S.A.; Ali, M.F.; Zaidi, S.S. LV three phase automatic load balancing system. In Proceedings of the International Conference on Energy, Environment and Sustainable Development 2016 (EESD 2016), Jamshoro, Pakistan, 1–3 November 2016. [Google Scholar]
- Bao, G.; Ke, S. Load transfer device for solving a three-phase unbalance problem under a low-voltage distribution network. Energies 2019, 12, 2842. [Google Scholar] [CrossRef]
- Homaee, O.; Mirzaei, M.J.; Najafi, A.; Leonowicz, Z.; Jasinski, M. A practical probabilistic approach for load balancing in data-scarce LV distribution systems using Discrete PSO and 2 m + 1 PEM. Int. J. Electr. Power Energy Syst. 2022, 135, 107530. [Google Scholar] [CrossRef]
- Zanjani, P.N.; Javadi, S.; Aliabadi, M.H.; Gharehpetian, G. A novel approach for mitigating electrical losses and current unbalance in low voltage distribution networks. IET Gener. Transm. Distrib. 2025, 19, e70072. [Google Scholar] [CrossRef]
- Hassan, M.; Najjar, M.; Tohme, R. A practical way to balance single phase loads in a three phase system at distribution and unit level. In Proceedings of the 20th International Conference on Renewable Energies and Power Quality (ICREPQ’22), Vigo, Spain, 27–29 July 2022; pp. 173–177. [Google Scholar] [CrossRef]
- Grigoras, G.; Gavrilas, M.; Neagu, B.C.; Ivanov, O.; Triștiu, I.; Bulac, C. An efficient method to optimal phase load balancing in low voltage distribution network. In Proceedings of the 2019 International Conference on ENERGY and ENVIRONMENT (CIEM), Timisoara, Romania, 17–18 October 2019; pp. 323–327. [Google Scholar] [CrossRef]
- Grigoraș, G.; Gavrilaș, M.; Scarlatache, F.; Cazacu, M.; Cosarca, M. Assessing energy losses in unbalanced low voltage electric distribution networks. Energetica 2016, 64, 53–59. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE Press: Piscataway, NJ, USA, 1995; pp. 1942–1947. [Google Scholar] [CrossRef]





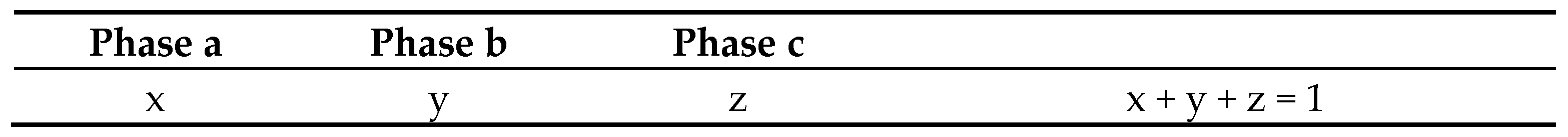
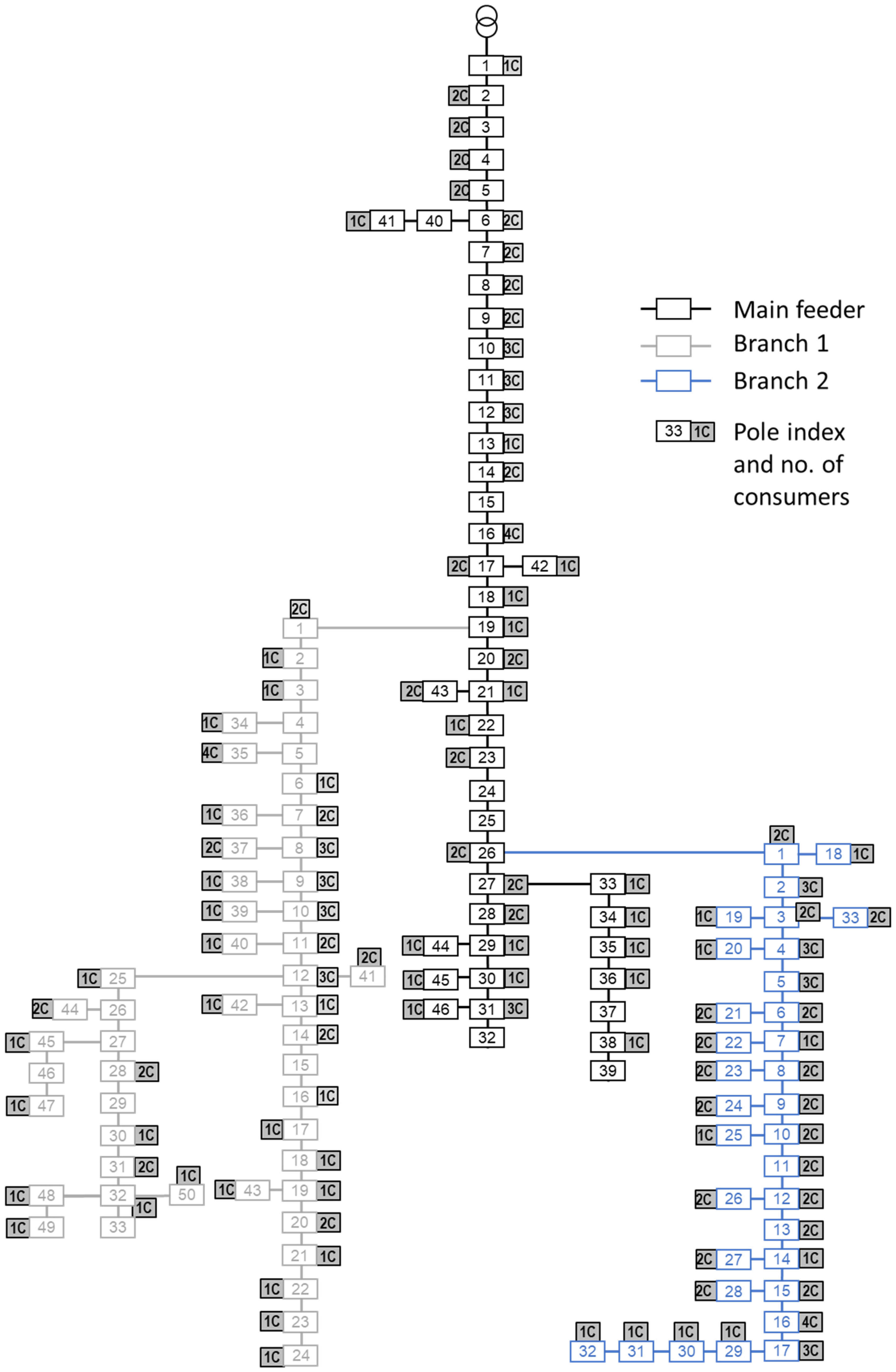




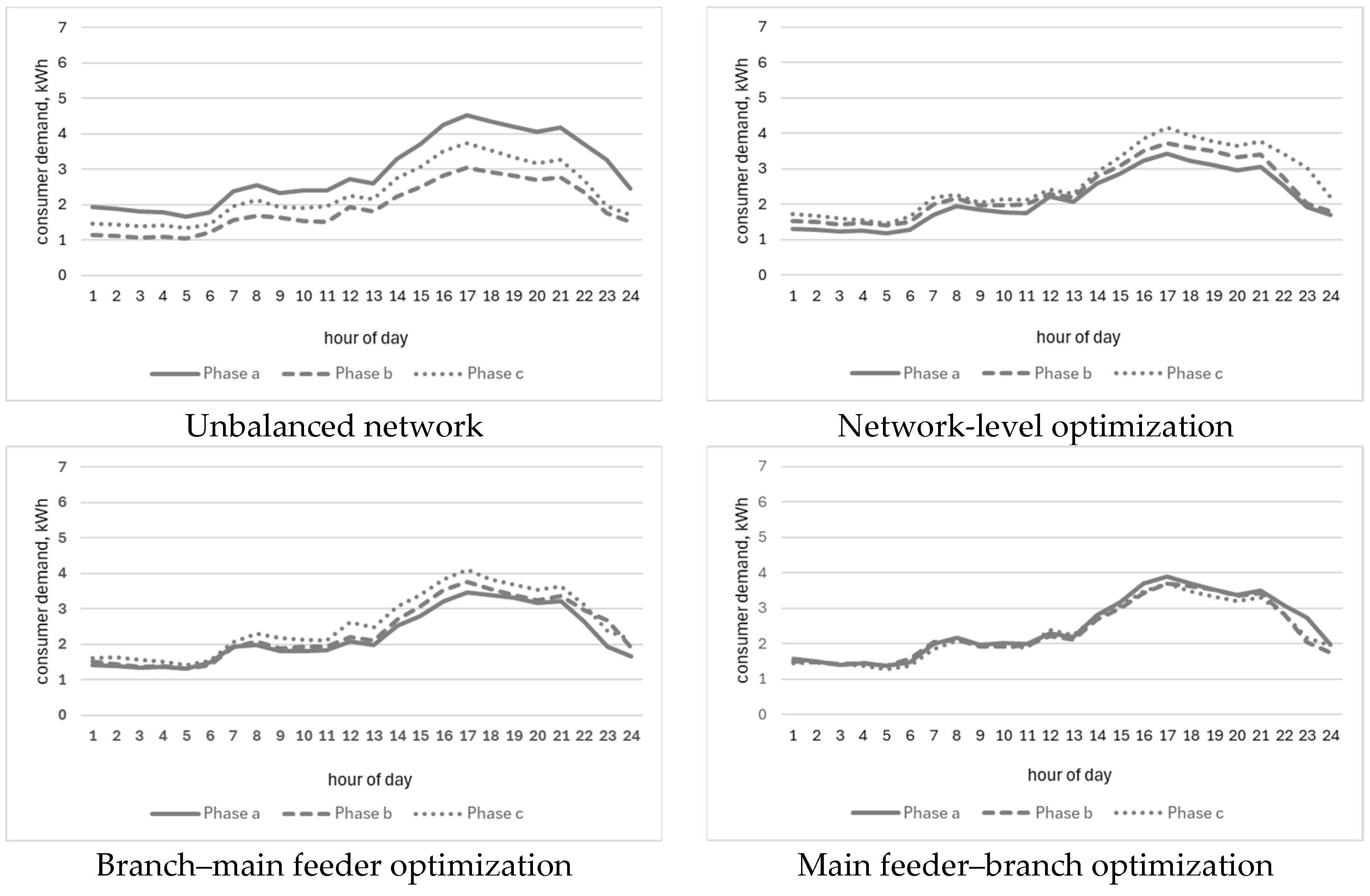
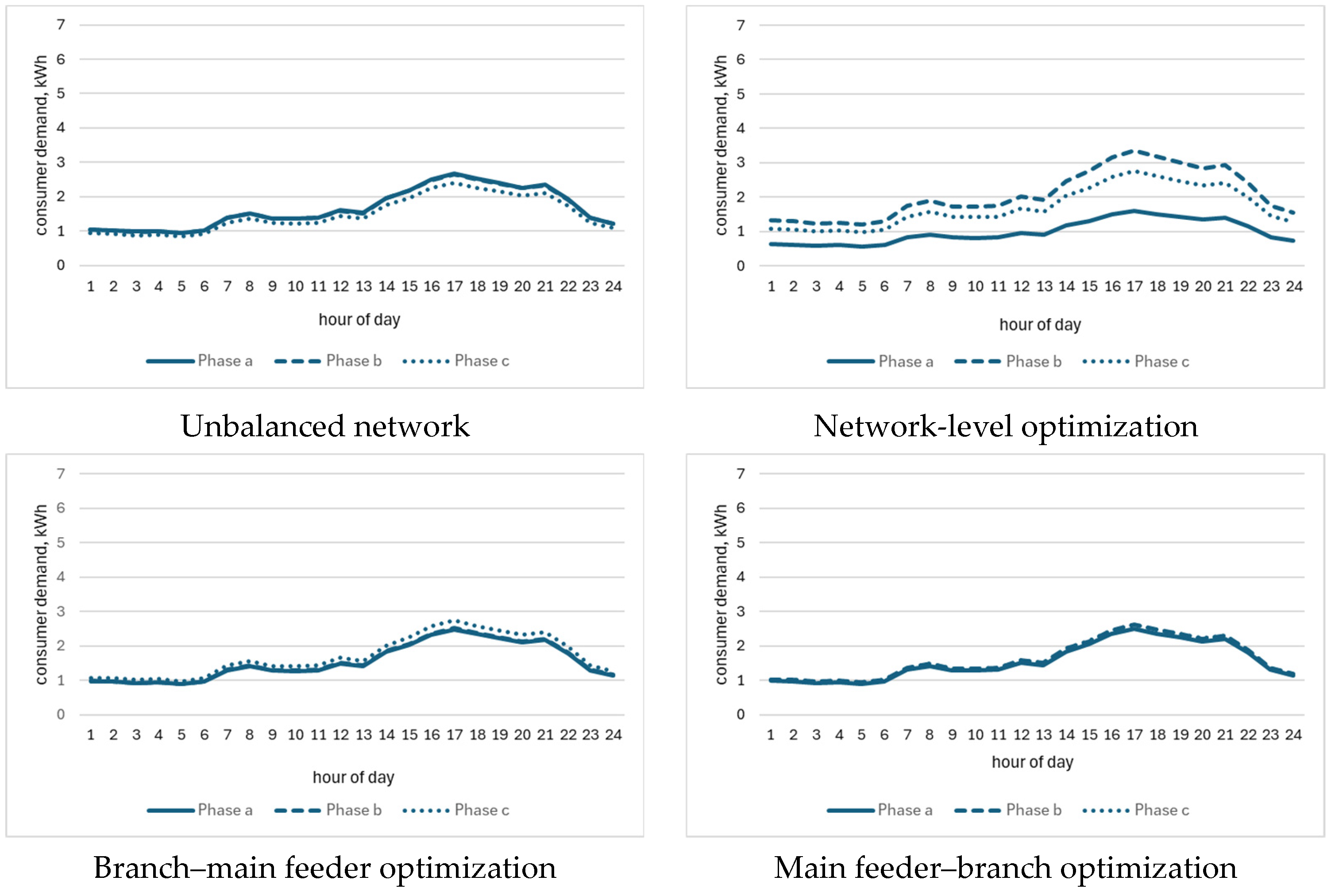
| Parameter | Entire Network | Main Feeder (Cons. 1–68) | Branch 1 (Cons.69–129) | Branch 2 (Cons.130–190) |
|---|---|---|---|---|
| No. of poles | 128 | 46 | 49 | 33 |
| No. of consumers | 190 | 68 | 61 | 61 |
| Phase a | 68 | 26 | 21 | 21 |
| Phase b | 62 | 24 | 21 | 17 |
| Phase c | 60 | 18 | 19 | 23 |
| Active energy demand, kWh | 486.89 | 201 | 171.26 | 114.63 |
| Phase a | 192.69 | 82.87 | 70.14 | 39.68 |
| Phase b | 159.89 | 74.77 | 45.75 | 39.37 |
| Phase c | 134.31 | 43.36 | 55.37 | 35.58 |
| Active energy losses, kWh | 36.149 | 32.641 | 2.775 | 0.734 |
| Feeder length, km | 5.16 | 1.84 | 2 | 1.32 |
| Wire type | OHL 3 × 50 mm2 + 50 mm2 | |||
| <0.5 kWh | 0.5–1 kWh | 1–5 kWh | 5–10 kWh | >10 kWh |
|---|---|---|---|---|
| 54 | 8 | 106 | 18 | 4 |
| Parameter | Entire Network | Main Feeder | Branch 1 | Branch 2 |
|---|---|---|---|---|
| No. of poles | 128 | 46 | 49 | 33 |
| No. of consumers | 190 | 68 | 61 | 61 |
| Phase a | 38 | 15 | 12 | 11 |
| Phase b | 76 | 30 | 26 | 20 |
| Phase c | 76 | 23 | 23 | 30 |
| Active energy demand, kWh | 486.89 | 201 | 171.26 | 114.63 |
| Phase a | 161.05 | 85.89 | 51.38 | 23.78 |
| Phase b | 161.11 | 54.49 | 56.79 | 49.83 |
| Phase c | 164.73 | 60.61 | 63.10 | 41.02 |
| Active energy losses, kWh | 32.888 | 30.283 | 1.941 | 0.665 |
| Feeder length, km | 5.16 | 1.84 | 2 | 1.32 |
| Parameter | Entire Network | Main Feeder | Branch 1 | Branch 2 |
|---|---|---|---|---|
| No. of poles | 128 | 46 | 49 | 33 |
| No. of consumers | 190 | 68 | 61 | 61 |
| Phase a | 33 | 10 | 10 | 13 |
| Phase b | 65 | 21 | 19 | 25 |
| Phase c | 92 | 37 | 32 | 23 |
| Active energy demand, kWh | 486.89 | 201 | 171.26 | 114.63 |
| Phase a | 159.74 | 70.07 | 52.93 | 36.74 |
| Phase b | 162.96 | 69.09 | 56.53 | 37.34 |
| Phase c | 164.19 | 61.84 | 61.80 | 40.55 |
| Active energy losses, kWh | 33.037 | 30.635 | 1.845 | 0.557 |
| Feeder length, km | 5.16 | 1.84 | 2 | 1.32 |
| Parameter | Entire Network | Main Feeder | Branch 1 | Branch 2 |
|---|---|---|---|---|
| No. of poles | 128 | 46 | 49 | 33 |
| No. of consumers | 190 | 68 | 61 | 61 |
| Phase a | 38 | 9 | 15 | 14 |
| Phase b | 61 | 22 | 22 | 17 |
| Phase c | 91 | 37 | 24 | 30 |
| Active energy demand, kWh | 486.89 | 201 | 171.26 | 114.63 |
| Phase a | 160.73 | 64.77 | 58.87 | 37.09 |
| Phase b | 161.81 | 66.68 | 56.38 | 38.75 |
| Phase c | 164.36 | 69.56 | 56.01 | 38.79 |
| Active energy losses, kWh | 33.312 | 30.643 | 2.074 | 0.595 |
| Feeder length, km | 5.16 | 1.84 | 2 | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, O.; Băiceanu, F.-C.; Nemeș, C.-M.; Grigoraș, G.; Țuchendria, B.-E.; Gavrilaș, M. A Multistage Algorithm for Phase Load Balancing in Low-Voltage Electricity Distribution Networks Operated in Asymmetrical Conditions. Symmetry 2025, 17, 1589. https://doi.org/10.3390/sym17101589
Ivanov O, Băiceanu F-C, Nemeș C-M, Grigoraș G, Țuchendria B-E, Gavrilaș M. A Multistage Algorithm for Phase Load Balancing in Low-Voltage Electricity Distribution Networks Operated in Asymmetrical Conditions. Symmetry. 2025; 17(10):1589. https://doi.org/10.3390/sym17101589
Chicago/Turabian StyleIvanov, Ovidiu, Florin-Constantin Băiceanu, Ciprian-Mircea Nemeș, Gheorghe Grigoraș, Bianca-Elena Țuchendria, and Mihai Gavrilaș. 2025. "A Multistage Algorithm for Phase Load Balancing in Low-Voltage Electricity Distribution Networks Operated in Asymmetrical Conditions" Symmetry 17, no. 10: 1589. https://doi.org/10.3390/sym17101589
APA StyleIvanov, O., Băiceanu, F.-C., Nemeș, C.-M., Grigoraș, G., Țuchendria, B.-E., & Gavrilaș, M. (2025). A Multistage Algorithm for Phase Load Balancing in Low-Voltage Electricity Distribution Networks Operated in Asymmetrical Conditions. Symmetry, 17(10), 1589. https://doi.org/10.3390/sym17101589










