Symmetry Analysis in Construction Two Dynamic Lightweight S-Boxes Based on the 2D Tinkerbell Map and the 2D Duffing Map

Abstract

The lack of an S-Box in some lightweight cryptography algorithms, like Speck and Tiny Encryption Algorithm, or the presence of a fixed S-Box in others, like Advanced Encryption Standard, makes them more vulnerable to attacks. This proposal presents a novel approach to creating two dynamic 8-bit S-Boxes (16 × 16). The generation process for each S-Box consists of two phases. Initially, the number initialization phase involves generating sequence numbers 1, sequence numbers 2, and shift values for S-Box1 using the 2D Tinkerbell map. Additionally, sequence numbers 3, sequence numbers 4, and shift values for S-Box2 are generated using the 2D Duffing map. Subsequently, the S-Box construction phase involves the construction of S-Box1 and S-Box2. The effectiveness of the newly proposed S-Boxes was evaluated based on various criteria, including the bijective property, balance, fixed points, and strict avalanche criteria. It was observed that S-Box1 achieved a remarkable linear and differential branch number of 4, surpassing any previous studies. Furthermore, it exhibited a non-linearity of 105.50, a differential uniformity of 12, and an algebraic degree of 7. Similarly, S-Box2 also achieved a linear and differential branch number of 4, a non-linearity of 105.25, a differential uniformity of 14, and an algebraic degree of 7. Moreover, the reduction in the number of linear and nonlinear operations for both S-Boxes makes them suitable for lightweight algorithms. The architecture of the proposed S-Boxes demonstrates robustness, with a total of 3.35 × 10⁵⁰⁴ possible S-Boxes, providing protection against algebraic attacks.

1. Introduction

Lightweight cryptographic algorithms, like lightweight block ciphers designed for use in limited resource environments such as radio-frequency identification (RFID), sensor networks, and healthcare systems, rely heavily on the substitution box (S-Box) [1]. The S-Box, as the only nonlinear component in modern block ciphers, plays a key role in creating a complex relationship between plaintext and ciphertext. This role is also known as confusion [2]. This relationship has a significant impact on both hardware consumption and the critical path delay of a block cipher, making an efficiently structured S-Box crucial for optimal implementation performance [3].

The security of a block cipher depends on the confusion in the ciphertext caused by an S-Box. Therefore, researchers are developing new S-Box designs and assessing their strength using common benchmarks [4]. The advanced encryption standard (AES) utilizes a highly secure 8-bit S-Box based on perfect nonlinear transformation, but it is static and requires a minimum of 35 nonlinear operations for implementation [5]. In 2021, Kim, H. et al. proposed various methods for constructing S-Boxes from smaller S-Boxes, establishing criteria for ensuring a minimum linear and differential branch number of 3. However, some of these S-Boxes exhibit high fixed points and high differential uniformity and still demand a high number of linear operations for implementation, all while remaining static [6]. Block ciphers such as Fantomas [7], Robin [7], Scream v3 [8], FLY [9], and PIPO [10] employ 8-bit S-Boxes composed of three smaller S-Boxes but also demonstrate a static nature requiring numerous linear operations for implementation, with a linear and differential branch number of 2. M. Sajjad et al. [11] proposed designing a pair of nonlinear components of a block cipher over quaternion integers. Jassim, S. A. and Farhan, A. K. [12] proposed designing a novel efficient substitution box by using a flower pollination algorithm and chaos system. Sajjad, M. et al. [13] proposed designing a pair of nonlinear components of a block cipher over gaussian integers. Zahid, A. H. and Arshad, M. J. [14] proposed an innovative design of substitution boxes using cubic polynomial mapping. Sajjad, M. et al. [15] proposed a novel approach for constructing substitution boxes (S-boxes) over Gaussian integers, which are complex numbers with integer coefficients.

This paper introduces a new method for constructing two dynamic, lightweight 8-bit S-Boxes (16 × 16) in HEX format, based on the 2D Tinkerbell map and the 2D Duffing map. The process of generating each S-Box has two phases. First is the initialization phase. This involves generating sequence numbers 1, sequence numbers 2, and shift values (buffer 1 and buffer 2) for S-Box1 using the 2D Tinkerbell map and generating sequence numbers 3, sequence numbers 4, and shift values (buffer 3 and buffer 4) for S-Box2 using the 2D Duffing map. Second is the S-Box construction phase. This involves constructing S-Boxes’ values depending on the results from the number initialization phase. This methodology enables both linear and differential branch numbers of at least four, and this enhances security. In addition, high non-linearity, low fixed points, a high algebraic degree, high strict avalanche criteria, low differential uniformity, and reducing the number of linear and nonlinear operations required to implement the S-Boxes.

The paper is organized as follows: Section 2 introduces an overview; Section 3 presents the proposed method of constructing a new S-Box; Section 4 assesses the proposed S-Boxes and provides a comparison of our proposed S-Box and existing S-Boxes; and Section 5 presents the conclusions and directions for future work. Appendix A shows a complete example.

2. Overview of Chaotic Systems (the 2D Tinkerbell Map and the 2D Duffing Map) and Deoxyribose Nucleic Acid (DNA)

2.1. Chaotic Systems

A mathematical behavior that is both nonlinear and deterministic is the foundation of the chaos theory [16]. It has a higher sensitivity to any change in initial conditions, including the control parameters and initial values. Consequently, a slight alteration to the beginning values or control settings causes a large alteration in the chaotic outputs [17]. The properties of a good cipher in cryptography, such as confusion and diffusion, are linked to those of chaotic systems, aiding researchers in improving the security of cryptographic systems [18]. In this study, two chaotic maps are used: the 2D Tinkerbell map and the 2D Duffing map.

✓

The 2D Tinkerbell map. Equation (1) shows the formal definition of the 2D Tinkerbell map iterator [19]:

$$\left\{\begin{array}{c}{\mathrm{x}}_{\mathrm{n}+1}={\mathrm{x}}_{\mathrm{n}}^2-{\mathrm{y}}_{\mathrm{n}}^2+\mathrm{a}\times {\mathrm{x}}_{\mathrm{n}}+{\mathrm{b}\times \mathrm{y}}_{\mathrm{n}}\\ {\mathrm{y}}_{\mathrm{n}+1}=2\times {\mathrm{x}}_{\mathrm{n}}\times {\mathrm{y}}_{\mathrm{n}}+{\mathrm{c}\times \mathrm{x}}_{\mathrm{n}}+{\mathrm{d}\times \mathrm{y}}_{\mathrm{n}}\end{array}\right.$$

(1)

There are four parameters: a, b, c, and d. The range of parameters is unbounded. The typical values of a, b, c, and d are: a = 0.9, b = 0.6013, c = 2, and d = 0.5, or a = 0.3, b = 0.6, c = 2, and d = 0.27. The range of the initial values is between x₀ and y₀ [−1, 1].

✓

The 2D Duffing map. Equation (2) shows the formal definition of the 2D Duffing map iterator [20]:

$$\left\{\begin{array}{c}{\mathrm{x}}_{\mathrm{n}+1}={\mathrm{y}}_{\mathrm{n}}\\ {\mathrm{y}}_{\mathrm{n}+1}=-\mathrm{b}\times {\mathrm{x}}_{\mathrm{n}}+{\mathrm{a}\times \mathrm{y}}_{\mathrm{n}}-{\mathrm{y}}_{\mathrm{n}}^3\end{array}\right.$$

(2)

There are two parameters: a and b. The range of parameters is unbounded. The range of the initial values is between x₀ and y₀ [−1, 1].

2.2. Deoxyribose Nucleic Acid (DNA)

The DNA sequence consists of four main nucleic acid cores: A (adenine), C (cytosine), G (guanine), and T (thymine). A and T correspond to each other, as do G and C [21]. When applying encoded function on the combinations 00, 01, 10, and 11 using the four cores A, C, G, and T, there are 24 different coding manners [22]. However, only eight coding manners adhere to the Watson–Crick complement law, which can be seen in Table 1.

Table 1. Eight map rules.

	1	2	3	4	5	6	7	8
0	A	A	C	C	G	G	T	T
1	C	G	A	T	A	T	C	G
2	G	C	T	A	T	A	G	C
3	T	T	G	G	C	C	A	A

The binary string is transformed into a DNA sequence by taking the intersection of the row and column for every 2 bits from Table 1 as shown in Algorithm 1.

Algorithm 1 Present DNA codes

Input: String. Output: DNA codes.  begin Read the string. Convert each character of the string into ASCII code. Convert the ASCII code of each character of the string into an 8-bit binary. Compare every 2 bits with Table 1 by taking the intersection of the bits value with its location. Represent the DNA codes. End

For example, if the user inputs the string “book”, here are the detailed steps of how to convert the string into DNA codes.

String	book
Binary string	01100010011011110110111101101011
Split into 2 bits	01	10	00	10	01	10	11	11	01	10	11	11	01	10	10	11
Value of each 2 bits	1	2	0	2	1	2	3	3	1	2	3	3	1	2	2	3
Location	1	2	3	4	5	6	7	8	1	2	3	4	5	6	7	8
DNA codes	C	C	C	A	A	A	A	A	C	C	G	G	A	A	G	A

3. The Proposed Method

This paper presents a novel approach to constructing two dynamic S-Boxes that are responsible for creating confusion in block ciphers. The generation process of the two S-Boxes goes through two stages.

A. 

The initialization phase includes generating sequence numbers 1, sequence numbers 2, and shift values (buffer 1, buffer 2) based on the 2D Tinkerbell map for S-Box1 by using Equation (1), as shown in Figure 1 and Algorithm 2.

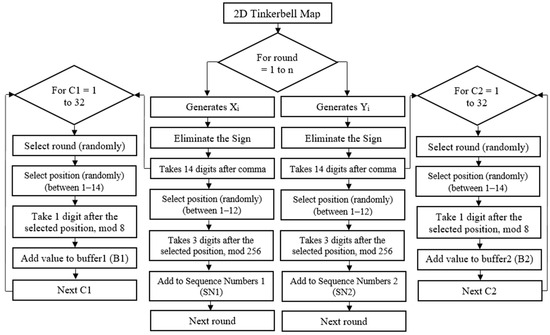Figure 1. Generating sequence numbers 1, 2, and shift values using the 2D Tinkerbell map.

Algorithm 2 Generating sequence numbers 1, 2, and buffers 1 and 2 based on the 2D Tinkerbell map

Input: Initial conditions for the 2D Tinkerbell map (a, b, c, d, X0, and Y0) Output: Generates sequence numbers 1, sequence numbers 2 and shift values (buffer 1 and buffer 2) Begin Read the initial conditions. For round = 1 to n          // n is a dynamic value, defined by the user randomly 2.1: Generates Xi and Yi using Equation (1) // The 2D Tinkerbell map 2.2: Next round Generates sequence numbers 1 (768 bits) depending on Xi values 3.1: For j = 1 to 96 3.2: Read Xi, remove the Sign and takes 14 digits after comma 3.3: Select position randomly (not exceed 12), takes 3 digits after it, takes mod 256, convert to 8-bit binary format and store the result in sequence numbers 1. 3.4: Next j Generates sequence numbers 2 (768 bits) depending on Yi values 4.1: For k = 1 to 96 4.2: Read Yi, remove the Sign and takes 14 digits after comma 4.3: Select position randomly (not exceed 12), takes 3 digits after it, takes mod 256, convert to 8 bits binary and store the result in sequence numbers 2. 4.4: Next k Generates shift values (buffer 1) depending on Xi 5.1: For C1 = 1 to 32 5.2: Select Xi randomly, read its value, remove the Sign, and takes 14 digits after comma 5.3: Select position randomly (not exceed 14), read its value and store result in buffer 1 5.4: Next C1 Generates shift values (buffer 2) depending on Yi 6.1: For C2 = 1 to 32 6.2: Select Yi randomly, read its value, remove the Sign, and takes 14 digits after comma 6.3: Select position randomly (not exceed 14), read its value and store result in buffer 2 6.4: Next C2 End

The same steps of Algorithm 2 can be followed to generate sequence numbers 3, sequence numbers 4, and shift values (buffer 3, buffer 4) based on the 2D Duffing map for S-Box2 by using Equation (2), as shown in Figure 2.

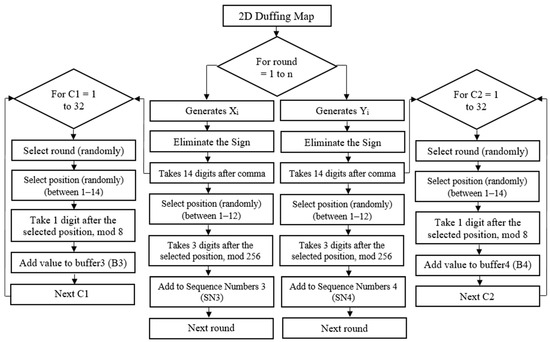
Figure 2. Generating sequence numbers 3, 4, and shift values using the 2D Duffing map.

B. 

The construction phase includes the construction of the two dynamic S-Boxes. To construct S-Box1 (16 × 16), the user randomly inputs secret key1 and secret key2, each consisting of 24 symbols. These secret keys are then transformed into a binary strings of 192 bits. The binary strings are then converted into a DNA coding of 768 bits. The DNA coding of secret key1 is XORed with sequence number 1 and shifted by buffer 1; each value is converted into HEX format, eliminating duplicate values, and adding the values to S-Box1 in the order of their appearance. On the other hand, the DNA coding of secret key2 is XORed with sequence numbers 2 and shifted by buffer 2; each value is converted into HEX format, eliminating duplicate values, and adding only values not already present in S-Box1. In cases where values ranging from 00 to FF are missing, they are identified and added accordingly, as illustrated in Figure 3 and Algorithm 3.

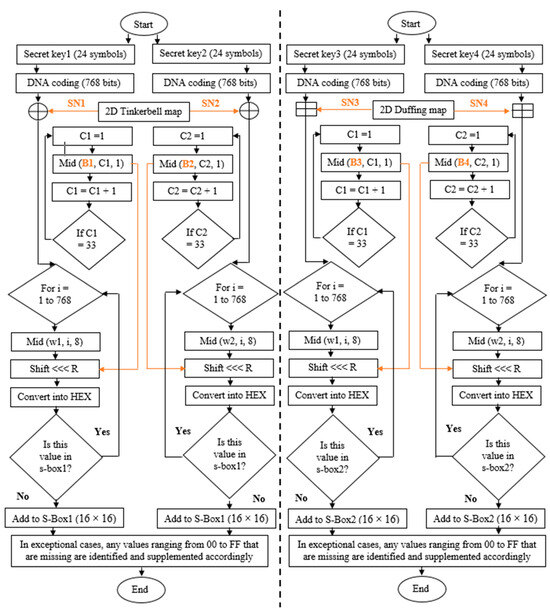Figure 3. Construction phase of S-Box1 and S-Box2.

Algorithm 3 Construction of S-Box1

Input: Secret key1 (24 symbols), secret key2 (24 symbols), buffer 1, buffer 2. Output: S-Box1 (16 × 16). Begin Convert the secret key1 and secret key2 to DNA codes and store the results in D1 and D2 // D1 (result of secret key1) and D2 (result of secret key2). Do the following: 2.1: XOR operation between sequence numbers 1and bits value of D1 and store the results in W1 // W1 is binary string (768 bits), // in first, W1 = “ ”. 2.2: XOR operation between sequence numbers 2 and bits value of D2 and store the results in W2 // W2 is binary string (768 bits), in first, W2 = “ ”. For i = 1 to 768 3.1: Mid (W1, i, 8) 3.2: Mid (buffer 1, C1, 1) mod 8 and store the result in U1 // in first, C1 = 1 3.3: Shift the result of step 3.1 by U1 value, convert to HEX format and store the result in S-Box1 if value not already presented in S-Box1 3.4: C1 = C1 + 1 3.5: if C1 = 33 then C1 = 1 3.6: Next i For j = 1 to 768 4.1: Mid (W2, j, 8) 4.2: Mid (buffer 2, C2, 1) mod 8 and store the result in U2 //in first, C2 = 1 4.3: Shift the result of step 4.1 by U2 value, convert to HEX format and store the result in S-Box1 if value not already presented in S-Box1 4.4: C2 = C2 + 1 4.5: if C2 = 33 then C2 = 1 4.6: Next j. In cases where values ranging from 00 to FF are missing, they are identified and added accordingly. End

The construction process of S-Box2 (16 × 16) involves the user randomly inputting secret key3 and secret key4, each consisting of 24 symbols. These secret keys are then converted into a binary string of 192 bits. Subsequently, the binary strings are transformed into a DNA coding of 768 bits. The DNA coding of secret key3 is additive with sequence number 3, shifted by buffer 3, converting each value into HEX format, eliminating duplicate values, and adding the values to S-Box2 in the order of their appearance. Similarly, the DNA coding of secret key4 is additive with sequence numbers 4, shifted by buffer 4, converting each value into HEX format, eliminating duplicate values, and adding only values that are not already presented in S-Box2. In exceptional cases, any values ranging from 00 to FF that are missing are identified and supplemented accordingly. Depending on the inputs provided, the construction of S-Box2 can follow the same steps as algorithm 3, with the only difference being that in step 2, the XOR process is replaced by the additive process, as depicted in Figure 3.

4. Performance Evaluation

This section demonstrates the security strength of the proposed 8-bit S-Box, measured over balanced, bijective property, strict avalanche criteria, linear branch number, differential branch number, differential uniformity, non-linearity, fixed points, linear and nonlinear operations, algebraic degree, and algebraic attacks. It also compares the cryptanalysis of the proposed 8-bit S-Box with other 8-bit S-Box such as AES [5], Kim, H. et al. [6], Fantomas [7], Robin [7], Scream v3 [8], FLY [9], and Sajjad, M. et al [11,13,15].

A.

Balanced

The obtained S-Box is balanced since it contains an equal number of 1s and 0s in the corresponding truth table of Galois field (GF) (2⁸).

B.

Bijective property

The obtained S-Box is bijective by balancing 0s and 1s. The Hamming weight of all Boolean functions is [128 128 128 128 128 128 128 128].

C.

Strict Avalanche Criteria (SAC)

If any individual input bit is altered, it should affect approximately half of the output bits [23]. An SAC score of around 0.5 is considered sufficient. Table 2 and Table 3 illustrate the dependency matrix of SAC scores for the proposed S-Boxes. Our S-Box1 has an average SAC score of 0.57645, while our S-Box2 has an average SAC score of 0.57227. Table 4 compares the average SAC score of our proposed S-Boxes with other S-Boxes in the literature.

Table 2. Dependency matrix of proposed S-Box1.

0.5	0.515625	0.515625	0.546875	0.515625	0.53125	0.484375	0.40625
0.5	0.5	0.59375	0.46875	0.546875	0.5625	0.46875	0.5625
0.484375	0.484375	0.546875	0.59375	0.515625	0.5625	0.515625	0.453125
0.46875	0.453125	0.46875	0.453125	0.546875	0.5	0.515625	0.46875
0.5	0.53125	0.5625	0.515625	0.53125	0.421875	0.53125	0.46875
0.484375	0.546875	0.453125	0.484375	0.515625	0.515625	0.484375	0.5
0.46875	0.5625	0.46875	0.53125	0.46875	0.5	0.515625	0.484375
0.5	0.484375	0.46875	0.546875	0.53125	0.5	0.453125	0.484375

Table 3. Dependency matrix of proposed S-Box2.

0.4375	0.515625	0.546875	0.484375	0.5	0.421875	0.53125	0.484375
0.484375	0.5	0.5	0.46875	0.453125	0.484375	0.5	0.484375
0.453125	0.515625	0.453125	0.515625	0.5	0.484375	0.53125	0.453125
0.546875	0.546875	0.46875	0.546875	0.515625	0.484375	0.453125	0.4375
0.46875	0.5625	0.46875	0.46875	0.4375	0.515625	0.515625	0.5
0.53125	0.53125	0.5	0.5625	0.5	0.484375	0.421875	0.5
0.59375	0.53125	0.53125	0.515625	0.625	0.5	0.515625	0.4375
0.515625	0.5	0.484375	0.546875	0.46875	0.578125	0.484375	0.546875

Table 4. Constituent Boolean functions and NL scores.

Boolean Function	B1	B2	B3	B4	B5	B6	B7	B8
NL (B), S-Box1	108	106	102	104	106	104	108	106
NL (B), S-Box2	104	106	106	106	104	106	106	104

D.

Linear Branch Number

The linear branch number (LBN) of an S-Box [24] is defined as

$$\underset{\mathrm{a},\mathrm{b},\mathsf{\Phi }(\mathrm{a},\mathrm{b})\ne 0}{\min }\left(\mathrm{w}\mathrm{t}\right(\mathrm{a})+\mathrm{w}\mathrm{t}(\mathrm{b}\left)\right).$$

(3)

The upper bound of LBN ≤ n − 1, where n is input bits. A higher LBN enhances the system’s resistance against linear attacks [25]. The proposed S-Box1 and S-Box2 have an LBN of 4, as shown in Table 4, a milestone not attained by any other research to date.

E.

Differential Branch Number

The differential branch number (DBN) of an S-Box [26] is defined as

$$\underset{\mathrm{a},\mathrm{b}\ne \mathrm{a}}{\min }\left(\mathrm{w}\mathrm{t}\right(\mathrm{a}\oplus \mathrm{b})+\mathrm{w}\mathrm{t}(\mathrm{S}\left(\mathrm{a}\right)\oplus \mathrm{S}\left(\mathrm{b}\right)\left)\right).$$

(4)

The user calculates all possible XORs between the Galois field (GF) (2ⁿ) entries and then all possible XORs between the S-Box entries. Finally, the user calculates their Hamming weights and compute the minimum value. The upper bound of DBN is [$\frac{2n}{3}$], where n is input bits. A higher DBN enhances the resistance of the system against differential attacks [27]. The proposed S-Box1 and S-Box2 have a DBN of 4, as shown in Table 4, a milestone not attained by any other research to date.

F.

Differential Uniformity

The differential uniformity (DU) of an S-Box [28] is defined as

$$\underset{∆\mathsf{\alpha }\ne 0,∆\mathsf{\beta }}{\max }\#\{\mathrm{x}\in {\mathrm{F}}_{\mathrm{n}}^2\mathrm{S}(\mathrm{x})\oplus \mathrm{S}(\mathrm{x}\oplus ∆\mathsf{\alpha })=∆\mathsf{\beta }\}.$$

(5)

The lower the DU, the better the resistance to differential attack [29]. The lowest possible DU is two [30]. The proposed S-Box1 achieved a maximum DU score of 12, while S-Box2 achieved a score of 14. This low score affirms the potential of the proposed S-Boxes to resist differential cryptanalysis effectively. Furthermore, Table 4 compares the DU scores of the proposed S-Boxes with those found in the existing literature. This comparison underscores the efficacy of our S-Boxes in thwarting attempts at differential cryptanalysis.

G.

Non-Linearity

The non-linearity (NL) of an S-Box [26] is defined as

$$2^{n-1}-2^{-1}\times \underset{\mathsf{\lambda }\mathsf{\alpha },\mathsf{\lambda }\mathsf{\beta }\ne 0}{\max }\left|\mathsf{\Phi }\right(\mathsf{\lambda }\mathsf{\alpha },\mathsf{\lambda }\mathsf{\beta }\left)\right|,\mathrm{where}\mathsf{\Phi }(\mathsf{\lambda }\mathsf{\alpha },\mathsf{\lambda }\mathsf{\beta })={\sum }_{\mathrm{x}\in {\mathrm{F}}_{\mathrm{n}}^2}{\left(-1\right)}^{\mathsf{\lambda }\mathsf{\beta }•\mathrm{S}\left(\mathrm{x}\right)\oplus \mathsf{\lambda }\mathsf{\alpha }•\mathrm{x}}$$

(6)

where “·” is the inner product in the respective Galois field. A higher NL implies greater complexity and unpredictability in the relationship between inputs and outputs, which enhances the resistance of the cryptographic algorithm against various attacks, including differential cryptanalysis and linear cryptanalysis [31]. The maximum NL in the GF (2ⁿ) is (a) for n = even is $2^{n-1}$−$2^{\frac{n}{2}-1}$ and (b) for n = odd is $2^{n-1}$−$2^{\frac{n-1}{2}}$. The proposed S-Box1 attained an NL of 105.50, while the proposed S-Box2 attained an NL of 105.25, as demonstrated in Table 4 and Table 5. However, it is worth noting that some S-Boxes have higher non-linearity but are static, which poses a significant weakness.

Table 5. Comparison of the cryptographic characteristics and operation counts of 8-bit S-Boxes.

Reference	Differential Branch Number	Linear Branch Number	Differential Uniformity	Non-Linearity	Algebraic Degree	Fixed Points	Nonlinear Operations	Linear Operations	Strict Avalanche Criteria
Proposed S-Box1	4	4	12	105.50	7	1	0	2	0.57645
Proposed S-Box2	4	4	14	105.25	7	0	2	0	0.57227
[6], Listing1	3	3	16	96	6	16	12	30	0.5444
[6], Listing2	3	3	16	96	5	1	12	32	0.5234
[6], Listing3	3	3	16	96	5	0	11	24	0.5103
[10], PIPO	3	3	16	96	5	0	11	23	0.5469
[9], FLY	3	3	16	96	5	1	12	24	0.5400
[7], Fantomas	2	2	16	96	5	0	11	27	0.4858
[7], Robin	2	2	16	96	6	16	12	24	0.5188
[8], Scream v3	2	2	8	96	6	0	12	27	0.4985
[5], AES	2	2	4	112	7	0	35	93	0.5049
[11], S-Box A	2	2	10	107	7	0	30	45	0.504
[11], S-Box B	2	2	10	107	7	0	30	45	0.504
[13], S-Box A	3	3	12	107.50	7	1	12	24	0.5
[13], S-Box B	3	3	12	106.50	7	0	12	24	0.5
[13], S-Box C	3	3	12	106.75	7	0	12	24	0.5
[13], S-Box D	2	2	12	106.75	7	2	12	24	0.508
[15], S-Box1	3	3	12	107.50	7	1	20	32	0.57896
[15], S-Box2	3	3	12	106.50	7	2	20	32	0.56948

H.

Fixed Points (FP)

If an S-Box returns the same value as its input (S-Box (m) = m), it is said to contain an FP [31]. An S-Box with fewer FPs is more resistant to attacks. The proposed S-Box1 possesses one FP, while the proposed S-Box2 is free of any FP. Table 4 compares the FP of the proposed S-Boxes with other S-Boxes in the literature.

I.

Linear and Nonlinear Operations

The fewer linear (XOR, NOT) and nonlinear (AND, OR) operations, the better. In this method, the proposed S-Box1 does not utilize nonlinear operations but employs two linear operations, whereas the proposed S-Box2 utilizes two nonlinear operations and no linear operations, as shown in Table 4.

J.

Algebraic Degree

The algebraic degree is the number of variables in the highest order term with non-zero coefficients. The maximum algebraic degree can be denoted as deg (f) = n − 1. A higher algebraic degree is preferable [30]. The proposed S-Box1 and S-Box2 achieved a favorable algebraic degree of 7, as evidenced in Table 4.

K.

Algebraic Attacks

The structure of the proposed S-Box is robust. The total number of possible S-Boxes is 3.35 × 10⁵⁰⁴, which is massive and noticeably greater than the 6-bit S-Box (63! ≈ 1.98 × 10⁸⁷), 5-bit S-Box (31! ≈ 8.22 × 10³³), and 4-bit S-Box (15! ≈ 1.3 × 10¹²). Furthermore, the proposed 8-bit S-Box uses a dynamic chaotic system to introduce randomness into the S-Box’s elements, making it difficult to break through.

5. Conclusions

This research introduces a novel approach to constructing dynamic S-Boxes by utilizing the 2D Tinkerbell map and the 2D Duffing map. The resulting S-Boxes, namely S-Box1 and S-Box2, achieved a remarkable linear and differential branch number of four, surpassing any previous studies. In the symmetry analysis, the reduction in the number of linear and nonlinear operations for both S-Boxes makes them suitable for lightweight algorithms. This increased robustness improves resistance against various attacks, especially linear and differential attacks. The generation of any S-Box1 value relies on the initial values of the 2D Tinkerbell map, secret keys 1 and 2, the rounds, and the selected positions to generate shift values. Similarly, the generation of any S-Box2 value depends on the initial values of the 2D Duffing map, secret keys 3 and 4, the rounds, and the selected positions to generate shift values. Consequently, any straightforward manipulation could potentially result in a collapse of the S-Box values. Subsequent studies might incorporate these S-Boxes into lightweight algorithms that currently lack S-Boxes, such as Tiny Encryption Algorithm, Lightweight Encryption Algorithm, etc., or into algorithms with static S-Boxes. Subsequently, they can compare the algorithmic results before and after the incorporation of these S-Boxes.