Abstract
In this paper, a novel approach to design a photonic crystal exclusive-OR (XOR) gate with high performance using recurrent neural network (RNN) is proposed, integrating the principles of symmetry and asymmetry inherent in photonic structures. The proposed model realizes the nonlinearities and dispersion properties in photonic systems, optimizing the waveguide paths and interference patterns to improve the performance of the logic gate. Simulation results demonstrate that the presented RNN design not only achieves high fidelity in the logical operation but also significantly enhances the functionality of the all-optical gate. This integration of machine learning with photonic crystal technology opens a new era for developing compact, energy-efficient photonic circuits for high-speed optical computing. Finally, the performance of the designed all-optical gate is compared with other related methods, which shows that the proposed gate outperforms other works. The results show that the obtained output power of the proposed all-optical XOR gate is 0, 0.813, 0.82, and 1 × 10−7 in the logical states.
1. Introduction
According to Moore’s law, every few years the number of transistors inside processors doubles in the same volume, but today we have reached a point where this is no longer possible due to many reasons, such as the interaction of electrons and the complexity of manufacturing [1]. However, day by day the need for higher processing speed and more and faster data transfer is increasing, taking into account that today data transfer is mostly conducted by photons rather than electrons because they have higher efficiency and wider bandwidth, and also because processing by electronic systems reduces the speed so much and this problem can be solved by optical processing [2]. According to this, the need for optical processing is unavoidable, which justifies the necessity of using optical gates, but unlike electrons, the movement of light cannot be controlled in very small structures; due to the diffraction limit, light cannot be controlled in dimensions. It is less than the focused wavelength, so the optical parts have a larger size than the corresponding electronic parts, and photonic crystals can be used to solve this problem [3]. Although older photonic systems, especially those relying on bulk optics, were larger than electronic systems, with the development of integrated photonic circuits and photonic crystals, the size gap between photonic and electronic systems has significantly narrowed. The small wavelength at photonic operational frequency can lead to very small devices in optics applications versus microwave applications. Simply, photonic crystals can be considered repeating structures in one, two, or three dimensions, made of materials such as insulators and semiconductors. The structures with air voids in the dielectric substrate pass a certain range of wavelengths according to the refractive index of the materials used and the type of placement, and act like a filter [4]. Photonic crystals have become increasingly popular for creating all-optical processors and communication systems. The symmetrical and asymmetrical arrangements in photonic crystals are fundamental to their ability to control light propagation and enable high-performance optical computing. The presented work in [5] explores numerous design approaches that have led to diverse structures capable of performing logical operations. Techniques such as self-collimated beams [6], multi-mode interference [7], interference-based defect methods [8], and logic gates employing nonlinear Kerr effect [9] and ring resonators [10,11] are common methods to design all-optical gates.
Artificial Neural Networks (ANNs) are computational models inspired by the human brain’s neural networks. ANNs are used for a variety of tasks in which pattern recognition, prediction, and optimization are crucial. Neural network and machine learning methods can find the patterns and nonlinearity behind the structures in various problems. In the field of photonics, specifically in the design of photonic crystal structures, ANNs can play a pivotal role by optimizing the complex geometrical and material parameters required to achieve specific optical properties. The application of ANNs in the design of photonic crystal gates is particularly significant. Photonic crystals are used to control the flow of light in optical devices, acting similarly to how electronic gates control electron flow in semiconductor devices. Designing these structures requires precise control over their photonic bandgaps, which determine the wavelengths of light that they can block or transmit. Traditionally, designing these structures involves extensive simulations and iterative adjustments, which can be computationally expensive and time-consuming. However, by using ANNs, the process can be significantly accelerated.
In [12], a two-dimensional photonic crystal-based XOR gate is designed. The presented approach in [12] aimed to optimize the output such that it maximized optical power for the specific logical states. To achieve this, simulations were conducted on four defect rods, varying the rod radii, to analyze their effects on the output. Furthermore, the K-Nearest Neighbors algorithm, a method derived from machine learning, was employed to fine-tune the configurations, ensuring optimal output for both logical states. However, the optical power can be still improved [12]. The performance of a three-input all-optical XOR gate modeled with ANNs is examined in [13], which elaborates on how trained ANNs serve as an effective and accurate rapid modeling technique for optical digital gates. ANNs are used to design photonic crystal fiber polarization filters in [14], which has used a feed forward network. In [15], a generative adversarial network (GAN) is utilized to train an ANN model for a surface plasmon resonance sensor based on photonic crystal fiber. A physics-guided neural network is introduced in [16] using coupled-mode theory for optical waveguides.
As mentioned, artificial intelligence methods have been recently used in the design of optical devices. However, none of the mentioned works has used artificial intelligence as a design method, which is proposed in this work. By using the proposed recurrent neural network (RNN) model, the circuit parameters can be predicted to enhance the all-optical gate performance. In this work, a recurrent neural network (RNN) model is used to enhance the performance of a photonic crystal XOR gate, utilizing the symmetry and asymmetry in the crystal design to optimize waveguide paths and interference patterns. The XOR gate is one of the fundamental building blocks in digital logic design and can be used in arithmetic circuits or used as a benchmark in the study of new computational technologies. The proposed approach allows for precise control over photonic bandgaps, improving the functionality and efficiency of the all-optical gate.
2. Suggested Structure for XOR Gate
A structure consisting of silicon rods in air is considered for the design of the optical XOR gate. The lattice constant in this structure is chosen equal to a = 600 nm. The radius of the rods is also considered to be r = 0.2a. The TM photonic bandgap structure of the proposed XOR optical gate with photonic crystals is shown in Figure 1. According to calculations, the bandgap structure is in the normalized range of 0.28 < a/λ < 0.42, which is a wide bandgap. The equivalent wavelength of this range is 1.42 < λ < 2.14 micrometers. The working wavelength of the presented gate is 1.55 micrometers, which is the telecommunication wavelength.
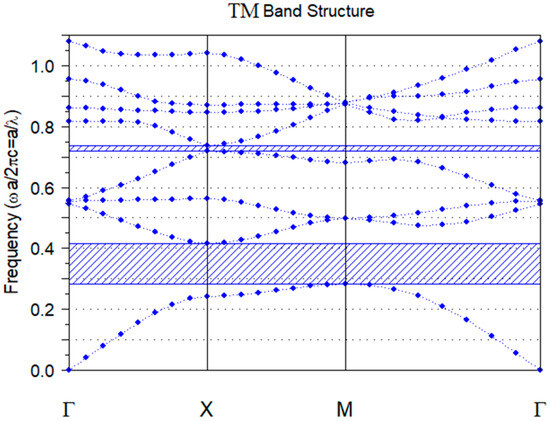
Figure 1.
Bandgap structure of the proposed prototype.
The initial structure of the all-optical XOR gate is shown in Figure 2. In this structure, Si rods with a refractive index of 3.46 were used in the air; this layout was created by completely removing a row of rods in the vertical direction and removing a number of rods in the horizontal direction, which created waveguides for inputs 1 and 2. As can be seen from Figure 2, a defect bar is created, whose dimensions can be obtained using the results and determined by the machine learning method, providing the most optimal value. Also, the phi parameter is assumed to be optimized using the proposed neural network model.
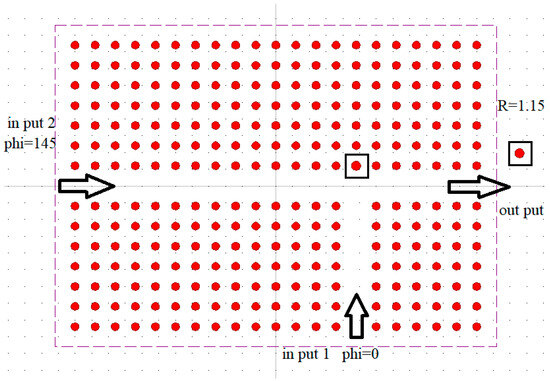
Figure 2.
Initial presented structure of the all-optical XOR gate. The dimensions of the indicated defect rod in the figure (indicated with a square) are used to optimize the output of the XOR gate by using RNN.
3. Design of the Crystal Photonic XOR Gate Using RNN
In this section, we employ a recurrent neural network (RNN) model to design and enhance the performance of the proposed crystal photonic XOR gate. At first, an initial structure of the XOR gate is designed, which is described in the previous section. Then, the important design parameters of the structure are considered as the neural network inputs. Therefore, the parameters of radius ‘r’ and phase ‘phi’ are considered as the input parameters of the ANN, where ‘r’ parameter is the radius of the defect rod and ‘phi’ is the phase of the input laser. Also, the output powers of the all-optical XOR gate in digital situations are considered as the network outputs. So, the output powers in logical situations of F1 (A = 0, B = 1), F2 (A = 1, B = 0), and F3 (A = 1, B = 1) are assumed as the output parameters of the model.
The structure of the proposed RNN model is depicted in Figure 3. Three hidden layers are considered with numbers of 20, 20, 15, and 3 neurons in hidden layers and the output layer. The activation functions used in the network layers are ‘tansig’ (hyperbolic tangent sigmoid transfer function), ‘logsig’ (logarithmic sigmoid transfer function), and ‘purelin’ (linear transfer function). This configuration of activation functions allows for a mix of nonlinear and linear transformations across the network, enabling it to capture complex relationships between the inputs and outputs. This neural network is presented to learn from and adapt to the intricate dynamics of the photonic system, by using the recurrent connections inherent in the applied RNN.
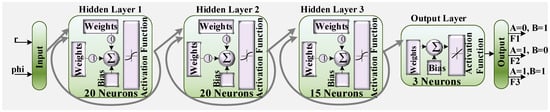
Figure 3.
Structures of the proposed RNN model with three hidden layers.
Figure 4 shows a plot of the Mean Squared Error (MSE) versus the number of training epochs for the presented RNN model. The plot indicates a trend of decreasing error, where the MSE starts at a higher value and gradually reduces as the number of epochs increases, eventually reaching a value of 0.00486 after 2000 epochs. The MSE measures the average of the squares of the errors, which is the average squared difference between the estimated values and the actual value. A decreasing MSE over epochs signifies that the network is effectively learning from the training data, refining its weights and biases to better predict the output powers of the XOR gate under various digital conditions. The applied MSE for the presented model is written in Equation (1).
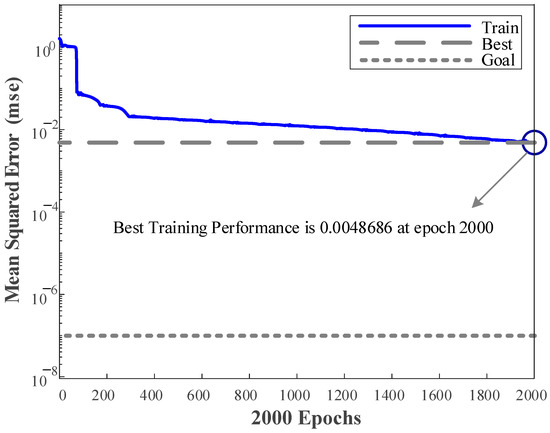
Figure 4.
Mean Squared Error (MSE) versus the number of training epochs for the presented RNN model.
The performances of the presented RNN model are depicted in Figure 5. As seen, the predicted values of the F1, F2, and F3 outputs are predicted accurately. From the 92 obtained samples, 77 samples are used for training the model and 12 samples are used for testing the model. Also, three samples are selected for verification of the presented model, which is also shown in Figure 5. The obtained results shown in Figure 5a indicate the accuracy of the RNN model in learning from the training data. The real output powers (actual values) and the predicted output powers (values estimated by the RNN model) are plotted against the number of samples. The close alignment between the real and predicted values demonstrates the model’s effectiveness in capturing the relationship between input parameters and output powers during training. The results shown in Figure 5b, which is plotted for the test data, reveal how well the RNN model generalizes to unseen data. The consistency between the real and predicted values in the test data indicates the robustness and reliability of the model. Also, the regression plots in Figure 5c,d, which are plotted for the train and test data, include regression lines that show the correlation between the predicted and actual output powers. The closer the points are to the regression line, the higher the accuracy of the model. Overall, the results shown in Figure 5 indicate the obtained high accuracy of the proposed RNN model in predicting the output powers of the XOR gate, in both the training and test phases.
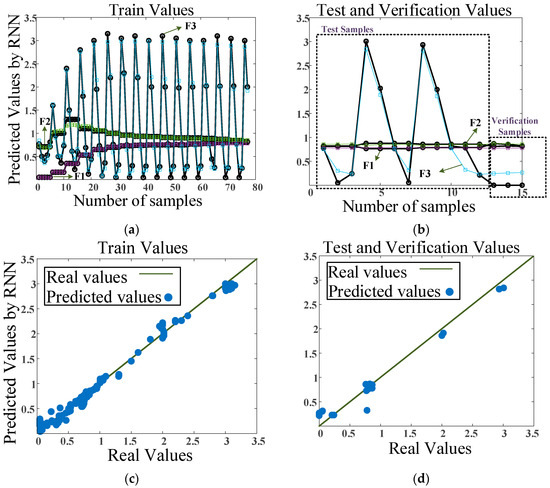
Figure 5.
Performances of the presented RNN model. The real and predicted results versus number of samples for (a) train and (b) test data. Results of the regression plots for (c) train and (d) test data.
The results show high accuracy for the proposed RNN model. After training and testing of the presented model, the values of 0.004 and 0.01 are obtained for the train MSE and test MSE, which show high accuracy of the model in predicting the output power of the proposed XOR gate in different logical situations.
4. Results of the Final Structure
The simulation results obtained from the recurrent neural network (RNN) model demonstrate a high level of precision in predicting the output powers for various configurations of the crystal photonic XOR gate. The consistency in performance across different test cases, as evidenced by the outputs F1, F2, and F3, proves that the RNN model has effectively captured the nonlinear relationships inherent in the photonic crystal configurations. As mentioned, three data samples are used to verify the proposed RNN model, as shown later in Table A1. These verification samples show the efficiency of the proposed model, which can optimize the performance of the proposed XOR all-optical gate. The best structure of the presented gate is selected according to the last verification sample with radius of 1.15 and ‘phi’ of 145 degrees; the result of this structure is explained in this section.
The power distributions for all logical states of the proposed XOR gate are shown in Figure 6. As seen, in the case of A = 0, B = 0, both sources are off and the output power is zero as expected. In the case of different inputs, where A = 1, B = 0 and A = 0, B = 1, the high power at the output is obtained, which can be considered as the logical state of 1. Also, in the A = 1, B = 1 state, no power reaches the output, which is desired. Therefore, the desired logical conditions of the XOR gate are obtained in the proposed structure.
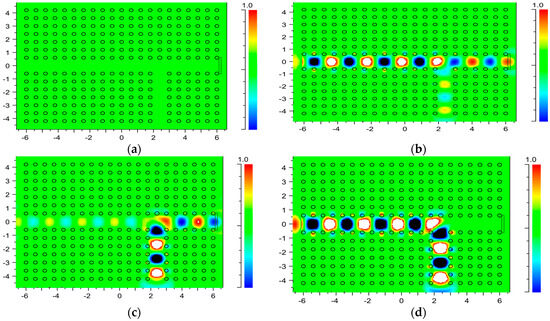
Figure 6.
Power distribution in the proposed XOR gate structure for the (a) A = 0, B = 0; (b) A = 0, B = 1; (c) A = 1, B = 0; and (d) A = 1, B = 1 states.
The output normalized powers for all logical states of the proposed XOR gate are shown in Figure 7. As seen, the output power is near 1 at the conditions with different inputs, while it is near 0 at the conditions with similar inputs, which shows the desired performance for the designed all-optical gate.
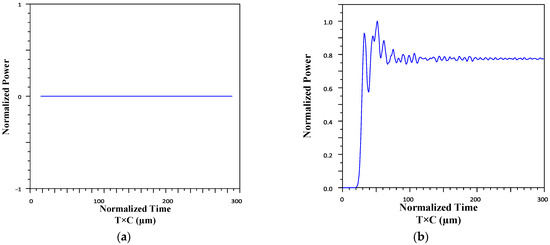
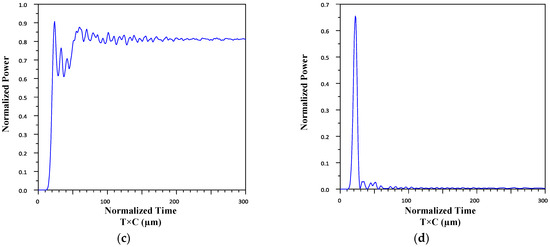
Figure 7.
Normalized output power for the (a) A = 0, B = 0; (b) A = 0, B = 1; (c) A = 1, B = 0; and (d) A = 1, B = 1 states.
Polar diagrams of the output normalized power for three logical states of the proposed XOR gate are shown in Figure 8. The correct performance of the proposed all-optical gate can be observed in these polar diagrams. In the polar diagrams, the radial axes show the normalized values of the output power, while the angular axes show the normalized time parameter.
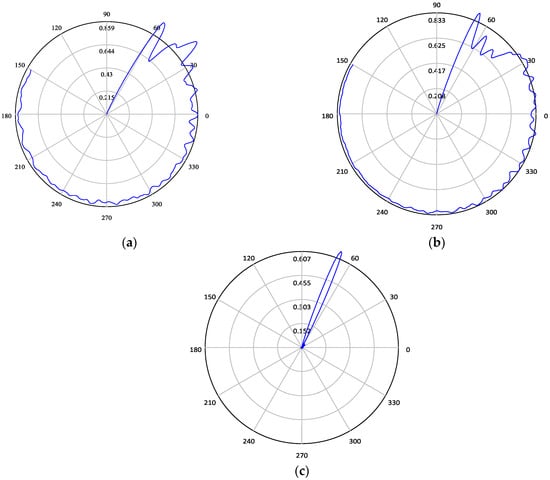
Figure 8.
Polar diagram of the normalized output power for the (a) A = 0, B = 1; (b) A = 1, B = 0; and (c) A = 1, B = 1 states.
According to the obtained results, in the case of A = 0, B = 0, where both sources are off, the output power is zero. In the case of A = 0, B = 1, the second state, the first source is off and the second source is on. In this state, the normalized output power is equal to 0.813, which can be considered to be 1, i.e., logical. Also, when A = 1, B = 0, the first source is on and the second source is off. In this case, the normalized power of the output is equal to 0.82, which we consider to be a logical 1. Moreover, in the fourth state of A = B = 0, both sources are on, but the second source has a phase difference of 145 degrees, compared to the first source, which causes the output power to be 1 × 10−7, which can be considered to be a logical 0.
A comparison between the proposed XOR gate and other related works is presented in Table 1. As seen, four logical states are compared in this table, which shows the all-optical gate performances. According to the results, the proposed gate, by helping the recurrent neural network in the design process, outperforms other related work.

Table 1.
A comparison between the proposed XOR gate and other related works.
5. Conclusions
This study presents a new approach to the design of a crystal photonic XOR gate through the application of recurrent neural networks (RNNs), highlighting a significant advancement in the field of optical computing. By integrating RNNs into the design process, we have successfully demonstrated the optimization of waveguide paths and interference patterns in the photonic crystal structure, resulting in enhancing the performance and reliability of the XOR gate. Our findings indicate that the proposed RNN model effectively captures the complex interdependencies between design parameters and operational characteristics, leading to a robust and high-fidelity photonic logic gate. Furthermore, the model demonstrates significant improvements in the XOR gate’s functionality, particularly in terms of power efficiency, which is critical for photonic circuits applications.
Author Contributions
Conceptualization, P.K., S.R. (Saeed Roshani), S.I.Y., F.P. and S.R. (Sobhan Roshani); Formal analysis, S.I.Y. and M.A.C.; Methodology, S.I.Y. and M.A.; Software, F.H., M.A. and S.R. (Saeed Roshani); Validation, M.A.C., M.A.; Writing—original draft, S.R. (Saeed Roshani), S.I.Y., P.K., F.P., F.H. and S.R. (Sobhan Roshani); Writing—review & editing, M.A.C., P.K., F.P., F.H. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the material conducted in the study is mentioned in article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Results of the ANN Models
Table A1 provides a comprehensive overview of the input and output parameters used in the training and testing of the recurrent neural network models developed for the design of the crystal photonic XOR gate. The table lists distinct configurations defined by the radius (‘r’) and phase (‘phi’) of the rods in the photonic crystal structure, alongside their corresponding output powers for the different logical states of the XOR gate (F1, F2, and F3). Additionally, the predicted outputs (F1_N, F2_N, F3_N) are included to facilitate the comparison and evaluation of performance across varying configurations. Each row in Table A1 represents a unique train or test case, detailing the specific conditions under which the XOR gate was simulated. The parameters were carefully selected to span a wide range of potential operational scenarios, thereby ensuring that the neural network model was robustly trained to handle diverse and dynamically changing optical properties. These data played a crucial role in optimizing the gate design, enabling the neural network to learn and adapt to the intricate dynamics of photon manipulation within the crystal structure, ultimately enhancing the gate performance and efficiency.

Table A1.
The RNN data samples and the predicted outputs in train and test procedures.
Table A1.
The RNN data samples and the predicted outputs in train and test procedures.
| Inputs | Outputs | |||||||
|---|---|---|---|---|---|---|---|---|
| r | phi | F1 | F2 | F3 | F1_N | F2_N | F3_N | |
| Train Samples | ||||||||
| 1 | 0.1 | 0 | 0.05 | 0.71 | 0.77 | 0.048703 | 0.725087 | 0.840357 |
| 2 | 0.1 | 45 | 0.05 | 0.71 | 0.5 | 0.044245 | 0.696264 | 0.430668 |
| 3 | 0.1 | 90 | 0.05 | 0.71 | 0.4 | 0.04944 | 0.685025 | 0.355217 |
| 4 | 0.1 | 135 | 0.05 | 0.71 | 0.53 | 0.040208 | 0.692503 | 0.460609 |
| 5 | 0.1 | 180 | 0.05 | 0.71 | 0.81 | 0.039657 | 0.704879 | 0.732037 |
| 6 | 0.2 | 0 | 0.16 | 1 | 1.6 | 0.17565 | 1.034929 | 1.623758 |
| 7 | 0.2 | 45 | 0.16 | 1 | 0.95 | 0.165447 | 1.037405 | 0.901435 |
| 8 | 0.2 | 90 | 0.16 | 1 | 0.5 | 0.164945 | 1.047788 | 0.509344 |
| 9 | 0.2 | 135 | 0.16 | 1 | 0.36 | 0.158725 | 1.057031 | 0.512875 |
| 10 | 0.2 | 180 | 0.16 | 1 | 0.73 | 0.164291 | 1.05619 | 0.776896 |
| 11 | 0.3 | 0 | 0.35 | 1.3 | 2.4 | 0.347985 | 1.159138 | 2.35868 |
| 12 | 0.3 | 45 | 0.35 | 1.3 | 1.5 | 0.340205 | 1.176915 | 1.448436 |
| 13 | 0.3 | 90 | 0.35 | 1.3 | 0.61 | 0.341899 | 1.184247 | 0.601161 |
| 14 | 0.3 | 135 | 0.35 | 1.3 | 0.22 | 0.34218 | 1.181005 | 0.439065 |
| 15 | 0.3 | 180 | 0.35 | 1.3 | 0.6 | 0.345998 | 1.170237 | 0.660624 |
| 16 | 0.4 | 0 | 0.53 | 1.1 | 2.8 | 0.528477 | 1.145395 | 2.760477 |
| 17 | 0.4 | 45 | 0.53 | 1.1 | 1.8 | 0.535769 | 1.161787 | 1.886814 |
| 18 | 0.4 | 90 | 0.53 | 1.1 | 0.69 | 0.544598 | 1.159038 | 0.554956 |
| 19 | 0.4 | 135 | 0.53 | 1.1 | 0.12 | 0.545089 | 1.149767 | 0.211226 |
| 20 | 0.4 | 180 | 0.53 | 1.1 | 0.44 | 0.536442 | 1.144298 | 0.410893 |
| 21 | 0.5 | 0 | 0.65 | 1.05 | 3 | 0.646117 | 1.073815 | 2.916234 |
| 22 | 0.5 | 45 | 0.65 | 1.05 | 1.95 | 0.658307 | 1.081247 | 2.149869 |
| 23 | 0.5 | 90 | 0.65 | 1.05 | 0.73 | 0.66373 | 1.071693 | 0.541235 |
| 24 | 0.5 | 135 | 0.65 | 1.05 | 0.08 | 0.662209 | 1.064574 | 0.073404 |
| 25 | 0.5 | 180 | 0.65 | 1.05 | 0.36 | 0.652106 | 1.071571 | 0.241112 |
| 26 | 0.6 | 0 | 0.7 | 1 | 3.15 | 0.70526 | 1.004799 | 2.971069 |
| 27 | 0.6 | 45 | 0.7 | 1 | 2.2 | 0.714413 | 1.005661 | 2.257516 |
| 28 | 0.6 | 90 | 0.7 | 1 | 0.76 | 0.715375 | 0.998003 | 0.590222 |
| 29 | 0.6 | 135 | 0.7 | 1 | 0.05 | 0.71446 | 0.99465 | 0.071354 |
| 30 | 0.6 | 180 | 0.7 | 1 | 0.32 | 0.708783 | 1.006017 | 0.191008 |
| 31 | 0.7 | 0 | 0.73 | 0.96 | 3.05 | 0.736537 | 0.956136 | 2.985825 |
| 32 | 0.7 | 45 | 0.73 | 0.96 | 2.3 | 0.742093 | 0.95499 | 2.262889 |
| 33 | 0.7 | 90 | 0.73 | 0.96 | 0.75 | 0.740706 | 0.950752 | 0.644085 |
| 34 | 0.7 | 135 | 0.73 | 0.96 | 0.05 | 0.740677 | 0.948829 | 0.122652 |
| 35 | 0.7 | 180 | 0.73 | 0.96 | 0.3 | 0.738588 | 0.958362 | 0.196426 |
| 36 | 0.75 | 0 | 0.74 | 0.935 | 3.1 | 0.747006 | 0.93751 | 2.984985 |
| 37 | 0.75 | 45 | 0.74 | 0.935 | 2.2 | 0.751016 | 0.936482 | 2.242006 |
| 38 | 0.75 | 90 | 0.74 | 0.935 | 0.75 | 0.74894 | 0.933592 | 0.665985 |
| 39 | 0.75 | 135 | 0.74 | 0.935 | 0.045 | 0.749161 | 0.93189 | 0.151956 |
| 40 | 0.75 | 180 | 0.74 | 0.935 | 0.29 | 0.748275 | 0.939849 | 0.20528 |
| 41 | 0.8 | 0 | 0.75 | 0.93 | 3 | 0.755375 | 0.921402 | 2.980135 |
| 42 | 0.8 | 45 | 0.75 | 0.93 | 2 | 0.758019 | 0.921026 | 2.211023 |
| 43 | 0.8 | 90 | 0.75 | 0.93 | 0.75 | 0.755434 | 0.919257 | 0.684144 |
| 44 | 0.8 | 135 | 0.75 | 0.93 | 0.05 | 0.755757 | 0.917662 | 0.179841 |
| 45 | 0.8 | 180 | 0.75 | 0.93 | 0.28 | 0.755735 | 0.924074 | 0.214256 |
| 46 | 0.85 | 0 | 0.75 | 0.91 | 3.1 | 0.762207 | 0.907152 | 2.971812 |
| 47 | 0.85 | 45 | 0.75 | 0.91 | 2 | 0.763647 | 0.907849 | 2.173121 |
| 48 | 0.85 | 90 | 0.75 | 0.91 | 0.77 | 0.760671 | 0.907037 | 0.698948 |
| 49 | 0.85 | 135 | 0.75 | 0.91 | 0.045 | 0.760962 | 0.905529 | 0.205125 |
| 50 | 0.85 | 180 | 0.75 | 0.91 | 0.29 | 0.761522 | 0.910573 | 0.221935 |
| 51 | 0.9 | 0 | 0.76 | 0.9 | 3.05 | 0.767874 | 0.894312 | 2.960354 |
| 52 | 0.9 | 45 | 0.75 | 0.9 | 1.98 | 0.768263 | 0.896394 | 2.130935 |
| 53 | 0.9 | 90 | 0.75 | 0.9 | 0.77 | 0.764971 | 0.896436 | 0.710967 |
| 54 | 0.9 | 135 | 0.75 | 0.9 | 0.043 | 0.76512 | 0.895039 | 0.227393 |
| 55 | 0.9 | 180 | 0.75 | 0.9 | 0.286 | 0.766026 | 0.898959 | 0.227667 |
| 56 | 0.95 | 0 | 0.77 | 0.9 | 3 | 0.772636 | 0.88258 | 2.946013 |
| 57 | 0.95 | 45 | 0.77 | 0.9 | 2 | 0.772115 | 0.88626 | 2.086684 |
| 58 | 0.95 | 90 | 0.77 | 0.9 | 0.765 | 0.768558 | 0.887093 | 0.720841 |
| 59 | 0.95 | 135 | 0.77 | 0.9 | 0.0447 | 0.768476 | 0.885853 | 0.246692 |
| 60 | 0.95 | 180 | 0.77 | 0.9 | 0.293 | 0.769532 | 0.8889 | 0.231307 |
| 61 | 1 | 0 | 0.78 | 0.89 | 3 | 0.776683 | 0.871746 | 2.929027 |
| 62 | 1 | 45 | 0.78 | 0.89 | 2.02 | 0.775382 | 0.877145 | 2.042231 |
| 63 | 1 | 90 | 0.78 | 0.89 | 0.78 | 0.771595 | 0.878735 | 0.72922 |
| 64 | 1 | 135 | 0.78 | 0.89 | 0.444 | 0.771215 | 0.877698 | 0.263333 |
| 65 | 1 | 180 | 0.78 | 0.89 | 0.26 | 0.77226 | 0.880109 | 0.233027 |
| 66 | 1.05 | 0 | 0.81 | 0.87 | 3.1 | 0.780155 | 0.861651 | 2.909667 |
| 67 | 1.05 | 45 | 0.81 | 0.87 | 2.016 | 0.778194 | 0.868814 | 1.999104 |
| 68 | 1.05 | 90 | 0.81 | 0.87 | 0.78 | 0.774201 | 0.871145 | 0.736726 |
| 69 | 1.05 | 135 | 0.81 | 0.87 | 0.046 | 0.773476 | 0.870358 | 0.277765 |
| 70 | 1.05 | 180 | 0.81 | 0.87 | 0.253 | 0.774381 | 0.87233 | 0.233185 |
| 71 | 1.1 | 0 | 0.82 | 0.845 | 3.045 | 0.783164 | 0.852166 | 2.888267 |
| 72 | 1.1 | 45 | 0.82 | 0.845 | 2.02 | 0.78065 | 0.861082 | 1.958514 |
| 73 | 1.1 | 90 | 0.82 | 0.845 | 0.78 | 0.776469 | 0.864151 | 0.743932 |
| 74 | 1.1 | 135 | 0.82 | 0.845 | 0.045 | 0.775369 | 0.863651 | 0.29049 |
| 75 | 1.1 | 180 | 0.82 | 0.845 | 0.245 | 0.776032 | 0.865348 | 0.23223 |
| 76 | 1.15 | 0 | 0.813 | 0.82 | 3 | 0.785795 | 0.843181 | 2.865224 |
| 77 | 1.15 | 45 | 0.813 | 0.82 | 2 | 0.782825 | 0.853798 | 1.921365 |
| Test Samples | ||||||||
| 1 | 1.15 | 90 | 0.813 | 0.82 | 0.775 | 0.778469 | 0.85761 | 0.751347 |
| 2 | 1.15 | 135 | 0.813 | 0.82 | 0.05 | 0.776976 | 0.857431 | 0.302017 |
| 3 | 1.15 | 180 | 0.813 | 0.82 | 0.24 | 0.777322 | 0.858978 | 0.230634 |
| 4 | 1.2 | 0 | 0.875 | 0.765 | 3.008 | 0.788119 | 0.834598 | 2.840994 |
| 5 | 1.2 | 45 | 0.875 | 0.765 | 2.025 | 0.784775 | 0.846844 | 1.888279 |
| 6 | 1.2 | 90 | 0.875 | 0.765 | 0.8 | 0.780254 | 0.851406 | 0.759408 |
| 7 | 1.2 | 135 | 0.875 | 0.765 | 0.054 | 0.778363 | 0.851576 | 0.312827 |
| 8 | 1.25 | 0 | 0.855 | 0.788 | 2.935 | 0.790189 | 0.826333 | 2.816065 |
| 9 | 1.25 | 45 | 0.855 | 0.788 | 2 | 0.786543 | 0.840122 | 1.859629 |
| 10 | 1.25 | 90 | 0.855 | 0.788 | 0.82 | 0.781866 | 0.845447 | 0.768478 |
| 11 | 1.25 | 135 | 0.855 | 0.788 | 0.78 | 0.779579 | 0.84599 | 0.323364 |
| 12 | 1.25 | 180 | 0.855 | 0.788 | 0.214 | 0.779143 | 0.847508 | 0.227289 |
| Verification Samples | ||||||||
| 1 | 1.05 | 145 | 0.81 | 0.87 | 0 | 0.773607 | 0.870574 | 0.245186 |
| 2 | 1.1 | 145 | 0.82 | 0.854 | 0 | 0.77542 | 0.863846 | 0.255531 |
| 3 | 1.15 | 145 | 0.813 | 0.82 | 0 | 0.776938 | 0.857623 | 0.26475 |
References
- Waldrop, M.M. The chips are down for Moore’s law. Nat. News 2016, 530, 144. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.A. Device requirements for optical interconnects to silicon chips. Proc. IEEE 2009, 97, 1166–1185. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Meade, R.; Winn, J.N. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Sakoda, K.; Sakoda, K. Optical Properties of Photonic Crystals; Springer: Berlin/Heidelberg, Germany, 2005; Volume 2. [Google Scholar]
- Jindal, P.; Abou Houran, M.; Goyal, D.; Choudhary, A. A review of different techniques used to design photonic crystal-based logic gates. Optik 2023, 282, 170794. [Google Scholar] [CrossRef]
- Jiang, Y.-C.; Liu, S.-B.; Zhang, H.-F.; Kong, X.-K. Realization of all optical half-adder based on self-collimated beams by two-dimensional photonic crystals. Opt. Commun. 2015, 348, 90–94. [Google Scholar] [CrossRef]
- Liu, W.; Yang, D.; Shen, G.; Tian, H.; Ji, Y. Design of ultra compact all-optical XOR, XNOR, NAND and OR gates using photonic crystal multi-mode interference waveguides. Opt. Laser Technol. 2013, 50, 55–64. [Google Scholar] [CrossRef]
- Shaik, E.H.; Rangaswamy, N. Interference-Based All-Optical Photonic Crystal Logic Gates. In Advances in Photonic Crystals and Devices; CRC Press: Boca Raton, FL, USA, 2019; pp. 283–311. [Google Scholar]
- Danaie, M.; Kaatuzian, H. Design and simulation of an all-optical photonic crystal AND gate using nonlinear Kerr effect. Opt. Quantum Electron. 2012, 44, 27–34. [Google Scholar] [CrossRef]
- Naghizade, S.; Sattari-Esfahlan, S. An optical five channel demultiplexer-based simple photonic crystal ring resonator for WDM applications. J. Opt. Commun. 2019, 41, 37–43. [Google Scholar] [CrossRef]
- Naghizade, S.; Sattari-Esfahlan, S. Loss-less elliptical channel drop filter for WDM applications. J. Opt. Commun. 2019, 40, 379–384. [Google Scholar] [CrossRef]
- Parandin, F.; Mohamadi, A. Design and Optimization of a Photonic Crystal-Based All-Optical XOR Gate Using Machine Learning. Majlesi J. Electr. Eng. 2024, 18, 1–8. [Google Scholar]
- Hamedi, S.; Jahromi, H.D. Performance analysis of all-optical logical gate using artificial neural network. Expert Syst. Appl. 2021, 178, 115029. [Google Scholar] [CrossRef]
- Yang, D.; Qin, H.; Li, Y.; Tang, C.; Xu, B.; Cheng, T. A hybrid method for photonic crystal fiber polarization filter based on artificial neural network and genetic algorithms. Opt. Fiber Technol. 2023, 80, 103426. [Google Scholar] [CrossRef]
- Zelaci, A.; Yasli, A.; Kalyoncu, C.; Ademgil, H. Generative adversarial neural networks model of photonic crystal fiber based surface plasmon resonance sensor. J. Light. Technol. 2020, 39, 1515–1522. [Google Scholar] [CrossRef]
- Liang, B.; Xu, D.; Yu, N.; Xu, Y.; Ma, X.; Liu, Q.; Asif, M.S.; Yan, R.; Liu, M. Physics-guided neural-network-based inverse design of a photonic–plasmonic nanodevice for superfocusing. ACS Appl. Mater. Interfaces 2022, 14, 27397–27404. [Google Scholar] [CrossRef] [PubMed]
- Swarnakar, S.; Rathi, S.; Kumar, S. Design of all optical XOR gate based on photonic crystal ring resonator. J. Opt. Commun. 2019, 41, 51–56. [Google Scholar] [CrossRef]
- Rao, D.G.S.; Swarnakar, S.; Palacharla, V.; Raju, K.S.R.; Kumar, S. Design of all-optical AND, OR, and XOR logic gates using photonic crystals for switching applications. Photonic Netw. Commun. 2021, 41, 109–118. [Google Scholar] [CrossRef]
- Parandin, F.; Reza Malmir, M. Reconfigurable all optical half adder and optical XOR and AND logic gates based on 2D photonic crystals. Opt. Quantum Electron. 2020, 52, 56. [Google Scholar] [CrossRef]
- Hussein, H.M.; Ali, T.A.; Rafat, N.H. New designs of a complete set of photonic crystals logic gates. Opt. Commun. 2018, 411, 175–181. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).