Calibrated Empirical Neutrosophic Cumulative Distribution Function Estimation for Both Symmetric and Asymmetric Data

Abstract

The traditional stratification weight is widely used in survey sampling for estimation under stratified random sampling (StRS). A neutrosophic calibration approach is proposed under neutrosophic statistics for the first time with the aim of improving conventional stratification weight. This addresses the challenge of estimating the empirical cumulative distribution function (CDF) of a finite population using the neutrosophic technique. The neutrosophic technique extends traditional statistics, dealing with indeterminate, vague, and uncertain values. Thus, using additional information, we are able to obtain an effective estimate of the neutrosophic CDF. The suggested estimator yields an interval range in which the population empirical CDF is likely to exist rather than a single numerical value. The proposed family of neutrosophic estimators will be defined under suitable calibration constraints. A simulation study is also computed in order to assess the effectiveness of the suggested and adapted neutrosophic estimators using real-life symmetric and asymmetric datasets.

1. Introduction

Datasets can consist of numerical or categorical variables in classical statistics. Numerous writers have developed a variety of estimators for calculating the countable population mean under classical statistics when additional data are present. In survey studies, supplementary information on a finite population is typically obtainable from census databases or from previous experience. Research on survey sampling has illustrated a vast range of techniques for employing supplementary data in order to improve the sampling design and also obtain progressively more accurate estimates [1]. It is noteworthy that the ratio, regression, and product procedures are appealing when auxiliary information is presented [2]. Therefore, many scholars have combined their efforts to increase the efficiency of these methods in the hopes of developing increasingly skilled estimators of measures of central tendency, measures of dispersion, and CDF, etc.

Neutrosophic statistics are used when there is some degree of indeterminacy in the data. When the data contain neutrosophy, this statistical methodology, which goes beyond the conventional approach, is used. According to [3], neutrosophic statistics are especially helpful when data within the population or sample are unclear, indeterminate, or indefinite.

Ref. [3] referred to a variety of neutrosophic values, including quantitative data that suggest that a given value might lie inside the interval range $\left[L, U\right]$ even while the precise value is unknown. The neutrosophic observation is composed of $Z_N=Z_L+Z_U{I}_N$, where $I_N\in \left[I_L,I_U\right]$. As a result, we developed a notation scheme for neutrosophic data representation that uses the interval type $Z_N\in Z_L,Z_U$, where $“L”$ stands for the lower value and $“U”$ for the upper value.

In the literature, the researchers have estimated the neutrosophic statistics and utilized information on one or more supplementary variables. In simple random sampling (SRS), [4] created neutrosophic ratio-type estimation methods. Ref. [5] developed generalized ratio and product-type estimation methods under neutrosophic ranked set sampling (RSS). Ref. [6] created a two-phase process loss index utilizing the neutrosophic statistical interval technique. Refs. [7,8] developed generalized classes of neutrosophic ratio and exponential estimation methods. Ref. [9] has suggested a generalized neutrosophic exponential robust ratio-type estimation method. Using neutrosophic robust regression, [10] introduced a new family of Hartley–Ross-type estimation techniques for estimating the population parameter. Ref. [11] suggested a neutrosophic predictive estimation method of countable population mean utilizing kernel regression.

Suppose we are interested in a population’s proportion of unclear or indeterminate $y_{iN}$ values. When utilizing sample data from a survey, users often need to estimate the population neutrosophic CDF. Alternatively, they may need to estimate the proportion of population units whose elements are not more than or equal to a specific number $t_{yN}$. For instance, we could be curious to know how many filtration facilities have lower levels of arsenic in their water than zero or how much agricultural area has fewer consequences of pesticide poisoning than zero. Such a proportion is a certain value of the population’s neutrosophic CDF.

$$F_{YN}\left(t_{yN}\right)=\frac{1}{M}\sum _{i=1}^M\mathrm{I}\left(y_{iN}\le t_{yN}\right),$$

where $\mathrm{I}\left(y_{iN}\le t_{yN}\right)=1$ for $y_{iN}\le t_{yN}$ and $\mathrm{I}\left(y_{iN}\le t_{yN}\right)=0,$ for $y_{iN}>t_{yN}$. Frequently, when conducting survey sampling, the research variable can only be measured for the units in a sample; thus, the traditional technique of the CDF is based only on the chosen sampling methodology and the sampling ratio of the population. Estimating $F_{YN}\left(t_{yN}\right)$ can be undertaken as follows:

$${\widehat{F}}_{yN}\left(t_{yN}\right)=\frac{1}{m}\sum _{i=1}^m\mathrm{I}\left(y_{iN}\le t_{yN}\right).$$

Several authors have computed the CDF utilizing information on sole or various supplementary symmetric and asymmetric data. Firstly, [12] created a technique for evaluating the countable population CDF. Ref. [13] developed both traditional and predictive techniques for estimating the CDF using survey information. Ref. [14] use the model-calibrated pseudo-empirical probability methodology to propose an estimation technique for the population CDF. Ref. [15] examined the problem of CDF and quantiles estimators for a population utilizing extra information. Ref. [16] develop a new class of estimation methods in order to estimate the CDF using extra information. Ref. [17] proposed two new estimation methods that make use of the mean and ranks of the supplemental data to estimate the limited population CDF under SRS and StRS. Ref. [18] created a novel type of exponential estimation technique for evaluating the population CDF with additional data in the form of the rank and average of the additional data under StRS. Ref. [19] also created a novel class of estimation techniques for the population CDF utilizing dual additional information under StRS.

The calibration approach has been a priority as a field of study for survey sampling in recent years. The calibration approach modifies the initial design weights to improve the precision of estimation by utilizing extra data. The calibration approach uses modified weights to minimize the difference between modified and original weights while performing a set of conditions with supplementary variables. See the pioneers in this discipline for more details [20]. Ref. [21] created a calibrated technique for mean estimation. Ref. [22] presented a calibration technique for computing the population parameter in StRS with a variety of calibrated conditions constructed with additional data. Ref. [23] suggested calibrated mean estimation methods based on a stratified RSS method along with calibration variance of the estimator. Ref. [24] creates a calibration technique for the population mean of the research information utilizing novel calibrated weights that use two additional sources of information under StRS. Ref. [25] extended the study by utilizing the properties of linear moments. Refs. [26,27,28] proposed a novel robust calibrated technique for computing the population parameter under StRS. Ref. [29] proposed a calibration CDF estimator using robust measures under StRS. It is important to note that [29] uses $\sum _{i=0}^m\left(.\right)$ mistakenly, instead of $\sum _{i=1}^m\left(.\right)$ in ${\widehat{F}}_{yN}\left(t_{yN}\right)$ and $F_{YN}\left(t_{yN}\right)$. However, this is merely a typing error. The calibration technique proposed by Tracy et al. [21] and utilized by many researchers, as discussed above, has not yet to receive much attention in terms of neutrosophic CDF estimation.

Research Gap of Neutrosophic Calibrated Estimation of CDF

All earlier studies on survey sampling have employed only certain, clear, and unambiguous symmetric and asymmetric data. These methods yield a single, clean result, which can occasionally be problematic because it has a probability of being overstated, inaccurate, or overlooked. However, under certain conditions, data are often of a neutrosophic type; this is the moment at which traditional classical methods are ineffective and a neutrosophic approach is used. Neutrosophic data include uncertain, partially unknown, inconsistent, incomplete, and other indeterminate data. Consequently, interval-valued neutrosophic numbers (INN) may be observed in data from populations or experiments. It had been thought that the actual data, which were unknown at the time of collection, belonged to that interval. In reality, there are more unclear facts available than certain information. As a result, more neutrosophic methods are required.

In life, various research data are available, and the collection of data is very costly, particularly when the data are unclear. As a result, using the outdated traditional methods to calculate the population’s actual value for ambiguous data will be costly and risky. When the research and additional information are of the neutrosophic type, there is no technique accessible that is able to resolve the issue using the calibration approach. We now switch to a new approach, known as neutrosophic calibrated estimation of CDF, which offers an entirely new viewpoint on survey techniques. Therefore, this paper proposes a neutrosophic calibrated estimator of CDF.

However, to our knowledge, no work has been undertaken so far on the type of calibrated estimators of neutrosophic CDF under StRS considered by [21]. Thus, we are motivated to suggest the neutrosophic calibration estimators of CDF by adapting the idea of [10]. Because all the authors, under conventional statistics, rely on certain, single-valued numbers to estimate the empirical CDF when additional variable is accessible. These forms of estimations offer biased outcomes. Finding the best estimate for the uncertain empirical CDF value with an optimal (lowest) MSE is our main objective.

The article’s remaining sections are arranged as follows: the adapted neutrosophic CDF calibration estimators are introduced in Section 2. The suggested estimators are given in Section 3. A simulation study is conducted in Section 4, and, in Section 5, the article comes to an end.

2. Adapted Neutrosophic Calibration Estimators of CDF Using Supplementary Information

Neutrosophic calibration-based estimate techniques involve neutrosophic calibrated or adjusted weights that are designed with the use of auxiliary data and are designed to minimize a specific measure of distance from the original stratum weights. Neutrosophic statistics are used to analyze datasets, or neutrosophic data, that have some uncertainty interval in them. By using this method, researchers may deal with inconsistent or incomplete data and draw more accurate conclusions from the sampled data. Assume that $Y_N\in \left[Y_L,Y_U\right]$ and $X_N\in \left[X_L,X_U\right]$ are the research and supplementary neutrosophic variables related with $\mathsf{\Omega }=\left\{\mathrm{1,2},\dots ,N\right\}$, which is a countable population of size $N$ that is divided into $\zeta$ strata, with the ${\zeta }^{th}$ stratum incorporating $N_{\zeta }$ elements, $\zeta =\mathrm{1,2},\dots ,\omega$, and $\sum _{\zeta =1}^{\omega }{N}_{\zeta }=N$. The weight of each stratum is defined as $W_{\zeta }=\frac{N_{\zeta }}{N}$. The traditional neutrosophic calibration estimator of CDF, under StRS is as follows:

$$H_{AN}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}(t_{yN}),$$

where ${\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)=\frac{1}{m}\sum _{i=1}^m{\rm I}\left(y_{iN}\le t_{yN}\right)$ is the sample neutrosophic CDF estimation for $Y_N$ in the ${\zeta }^{th}$ stratum. We consider the following terms, where $y_{iN}\in \left[y_{iL},y_{iU}\right]$ and $x_{iN}\in \left[x_{iL},x_{iU}\right]$ are the $i^{th}$ sample observation of our neutrosophic study variable $Y_N$ and supplementary variable $X_N$, respectively. $t_{yN}\in \left[t_{yL},t_{yU}\right]$ and $t_{xN}\in \left[t_{xL},t_{xU}\right]$ are the sample specific value neutrosophic of our study variable $Y_N$ and additional variable $X_N$, respectively. ${\widehat{\mathcal{F}}}_{\zeta yN}\in \left[{\widehat{\mathcal{F}}}_{\zeta yL},{\widehat{\mathcal{F}}}_{\zeta yU}\right]$ and ${\mathcal{F}}_{\zeta yN}\in \left[{\mathcal{F}}_{\zeta yL},{\mathcal{F}}_{\zeta yU}\right]$ are the ${\zeta }^{th}$ stratum sample and population neutrosophic CDF of the study variable $Y_N$, respectively. ${\widehat{\mathcal{F}}}_{\zeta xN}\in \left[{\widehat{\mathcal{F}}}_{\zeta xL},{\widehat{\mathcal{F}}}_{\zeta xU}\right]$ and ${\mathcal{F}}_{\zeta xN}\in \left[{\mathcal{F}}_{\zeta xL},{\mathcal{F}}_{\zeta xU}\right]$ are the ${\zeta }^{th}$ stratum sample and population neutrosophic CDF, respectively, of the additional variable $X_N.c_{\zeta xN}\in \left[c_{\zeta xL},c_{\zeta xU}\right]$ and $C_{\zeta xN}\in \left[C_{\zeta xL},C_{\zeta xU}\right]$ are the ${\zeta }^{th}$ stratum sample and population neutrosophic coefficient of variation (CV), respectively, of the additional variable $X_N.$ ${\psi }_{\zeta N}\in \left[{\psi }_{\zeta L},{\psi }_{\zeta U}\right]$ are wisely selected neutrosophic weights, determining the estimator’s shape. The traditional neutrosophic calibration estimator of CDF under StRS is $H_{AN}\in \left[H_{AL},H_{AU}\right].$

Adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ Family of Neutrosophic CDF Estimators

Taking inspiration from [25], the adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ family of estimators is as follows in Equation (1):

$$H_{A_i{\left(N\right)}_1}=\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right),$$

(1)

where ${\mathsf{\Omega }}_{{\zeta A}_{1}N}\in \left[{\mathsf{\Omega }}_{{\zeta A}_{1}L}, {\mathsf{\Omega }}_{{\zeta A}_{1}U}\right]$ is the neutrosophic calibrated weight. Using the chi-square distance function we obtain the following:

$$\sum _{\zeta =1}^{\omega }\frac{{\left({\mathsf{\Omega }}_{{\zeta A}_{1}N}-W_{\zeta }\right)}^2}{{\psi }_{\zeta N}{W}_{\zeta }},$$

(2)

and satisfy the calibrated constraints, as follows:

$$\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right) ,$$

(3)

$$\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}{c}_{\zeta xN}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{C}_{\zeta xN} ,$$

(4)

$$\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}=\sum _{\vartheta =1}^{\omega }{W}_{\zeta } .$$

(5)

Hence, the function of Lagrange using Equations (2)–(5) with multipliers ${\lambda }_{A_{1}N}\in \left[{\lambda }_{A_{1}L},{\lambda }_{A_{1}U}\right]$, ${\lambda }_{A_{2}N}\in \left[{\lambda }_{A_{2}L},{\lambda }_{A_{2}U}\right]$ and ${\lambda }_{A_{3}N}\in \left[{\lambda }_{A_{3}L},{\lambda }_{A_{3}U}\right]$, denoted by $∆\left({\mathsf{\Omega }}_{{\zeta A}_{1}N},W_{\zeta }\right)$, is given by

$$\begin{gathered} ∆\left({\mathsf{\Omega }}_{{\zeta A}_{1}N},W_{\zeta }\right)=\sum _{\zeta =1}^{\omega }\frac{{\left({\mathsf{\Omega }}_{{\zeta A}_{1}N}-W_{\zeta }\right)}^2}{{\psi }_{\zeta N}{W}_{\zeta }}-2{\lambda }_{A_{1}N}\left(\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right.\left.-\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)\right) \\ -2{\lambda }_{A_{2}N}\left(\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}{c}_{\zeta xN}-\sum _{\zeta =1}^{\omega }{W}_{\zeta }{C}_{\zeta xN}\right)-2{\lambda }_{A_{3}N}\left(\sum _{\zeta =1}^{\omega }{\mathsf{\Omega }}_{{\zeta A}_{1}N}-\sum _{\zeta =1}^{\omega }{W}_{\zeta }\right) . \end{gathered}$$

(6)

setting Equation (6) $\frac{\partial ∆({\mathsf{\Omega }}_{{\zeta A}_{1}N},W_{\zeta })}{\partial {\mathsf{\Omega }}_{{\zeta A}_{1}N}}=0$, we obtain the following:

$${\mathsf{\Omega }}_{{\zeta A}_{1}N}=W_{\zeta }+W_{\zeta }{\psi }_{\zeta N}\left({\lambda }_{A_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)+{\lambda }_{A_{2}N}{c}_{\zeta xN}+{\lambda }_{A_{3}N}\right) .$$

(7)

Substituting Equation (7) in Equations (3)–(5), we obtain the following:

$$\begin{gathered} \left[\begin{array}{ccc}\left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\\ \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\\ \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)& \left({\displaystyle \sum _{\zeta =1}^{\omega }}{\psi }_{\zeta N}{W}_{\zeta }\right)\end{array}\right]\left[\begin{array}{c}{\lambda }_{A_{1}N}\\ {\lambda }_{A_{2}N}\\ {\lambda }_{A_{3}N}\end{array}\right] \\ =\left[\begin{array}{c}{\displaystyle \sum _{\zeta =1}^{\omega }}{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\\ {\displaystyle \sum _{\zeta =1}^{\omega }}{W}_{\zeta }\left(C_{\zeta xN}-c_{\zeta xN}\right)\\ 0\end{array}\right] \end{gathered}$$

When we solve the system of equations, the expressions of lambdas are as follows:

$${\lambda }_{A_{1}N}=\frac{A_{1N}}{B_N}, {\lambda }_{A_{2}N}=\frac{A_{2N}}{B_N}, {\lambda }_{A_{3}N}=\frac{A_{3N}}{B_N} ,$$

$$\begin{gathered} A_{1N}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)\right.\left.-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)}^2\right] \\ +\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left(C_{\zeta xN}-c_{\zeta xN}\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\right.\left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\right] , \end{gathered}$$

$$\begin{gathered} A_{2N}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left(C_{\zeta xN}-c_{\zeta xN}\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\right.\left.-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)}^2\right] \\ -\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\right.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\left.-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\right] , \end{gathered}$$

$$\begin{gathered} A_{3N}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\right.-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)\right] \\ +\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left(C_{\zeta xN}-c_{\zeta xN}\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\right.\left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\right] , \end{gathered}$$

$$\begin{gathered} B_N=\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)}^2\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)}^2 \\ \left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)}^2\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)+2\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right) . \end{gathered}$$

Substituting these values in Equations (7) and (1), we obtain the neutrosophic calibrated estimators of CDF, as given below:

$$H_{A_i{\left(N\right)}_1}=H_{AN}+{\lambda }_{A_{1}N}\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right){\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right)+{\lambda }_{A_{2}N}\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)c_{\zeta xN}\right)+{\lambda }_{A_{3}N}\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right),$$

$$H_{A_i{\left(N\right)}_1}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)+{\widehat{\beta }}_{A_{1}N}\left(\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\right)+{\widehat{\beta }}_{A_{2}N}\left(\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left(C_{\zeta xN}-c_{\zeta xN}\right)\right) .$$

where neutrosophic betas ${\widehat{\beta }}_{A_{1}N}\in \left[{\widehat{\beta }}_{A_{1}L},{\widehat{\beta }}_{A_{1}U}\right]$ and ${\widehat{\beta }}_{A_{2}N}\in \left[{\widehat{\beta }}_{A_{2}L},{\widehat{\beta }}_{A_{2}U}\right]$ are given by

$${\widehat{\beta }}_{A_{1}N}=\frac{A_{4N}}{B_N} , {\widehat{\beta }}_{A_{2}N}=\frac{A_{5N}}{B_N} ,$$

where

$$\begin{gathered} A_{4N}=\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right){\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)}^2\right] \\ -\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)c_{\zeta xN}\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\right.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right) \\ \left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\right]+\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\right. \\ \left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}^2\right)\right] , \end{gathered}$$

$$\begin{gathered} A_{5N}=\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right){\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\right.-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right) \\ \left.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\right]+\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }\right)\right.\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right) \\ \left.-{\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)}^2\right]+\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)\right)\left[\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)c_{\zeta xN}\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)\right. \\ \left.-\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)\right)\left(\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{c}_{\zeta xN}\right)\right] . \end{gathered}$$

The family members of $H_{A_i{\left(N\right)}_1}$ are provided in Table 1.

Table 1. Adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ family of neutrosophic CDF estimators.

$\mathit{i}$	${\mathit{H}}_{{\mathit{A}}_{\mathit{i}}{\left(\mathit{N}\right)}_1}$	${\mathit{\psi }}_{\mathit{\zeta }\mathit{N}}$
1	$H_{A_1{\left(N\right)}_1}$	1
2	$H_{A_2{\left(N\right)}_1}$	$\frac{1}{{\overline{x}}_{\zeta N}}$
3	$H_{A_3{\left(N\right)}_1}$	$\frac{1}{s_{\zeta xN}}$
4	$H_{A_4{\left(N\right)}_1}$	$\frac{1}{s_{\zeta xN}^2}$
5	$H_{A_5{\left(N\right)}_1}$	$\frac{1}{c_{\zeta xN}}$

The neutrosophic estimators are developed based on different values of ${\psi }_{\zeta N}$, such as ${\psi }_{\zeta N}=1,\frac{1}{{\overline{x}}_{\zeta N}},\frac{1}{s_{\zeta xN}},\frac{1}{s_{\zeta xN}^2},\frac{1}{c_{\zeta xN}}$, where ${\overline{x}}_{\zeta N}\in \left[{\overline{x}}_{\zeta L},{\overline{x}}_{\zeta U}\right],s_{\zeta xN}\in \left[s_{\zeta xL},s_{\zeta xU}\right],s_{\zeta xN}^2\in \left[s_{\zeta xL}^2,s_{\zeta xU}^2\right]$ and $c_{\zeta xN}\in \left[c_{\zeta xL},c_{\zeta xU}\right],$ are the sample neutrosophic mean, sample neutrosophic standard deviation, sample neutrosophic variance, sample neutrosophic CV, of the supplementary information of $X_N$ in the ${\zeta }^{th}$ stratum, respectively.

3. Proposed Class of Neutrosophic CDF Estimators

Proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ Family of Neutrosophic CDF Estimators

Taking motivation from adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators, we proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ the following class of neutrosophic CDF estimators in Equation (8)

$$H_{P_i{\left(N\right)}_1}=\sum _{\zeta =1}^{\omega }{\Omega }_{{\zeta P}_{1}N}{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right) ,$$

(8)

where ${\Omega }_{{\zeta P}_{1}N}\in \left[{\Omega }_{{\zeta P}_{1}L},{\Omega }_{{\zeta P}_{1}U}\right]$ is the neutrosophic calibrated weight. Using the chi-square distance function we obtain the following:

$$\sum _{\zeta =1}^{\omega }\frac{{\left({\Omega }_{{\zeta P}_{1}N}-W_{\zeta }\right)}^2}{{\psi }_{\zeta N}{W}_{\zeta }} ,$$

(9)

and satisfy the calibrated constraint, as follows:

$$\sum _{\zeta =1}^{\omega }{\Omega }_{{\zeta P}_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right) ,$$

(10)

where $\left({\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right), {\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)\right)$ are the ${\zeta }^{th}$ stratum sample and population neutrosophic CDF, respectively, of the auxiliary variable $X_N$ and, ${\psi }_{\zeta N}$ are wisely selected neutrosophic weights, determining the estimator’s shape. Different values of ${\psi }_{\zeta N}$ are available in Table 2. Hence, the function of Lagrange using Equations (9) and (10), with multipliers ${\lambda }_{P_{1}N}\in \left[{\lambda }_{P_{1}L},{\lambda }_{P_{1}U}\right]$ and denoted by $∆\left({\Omega }_{{\zeta P}_{1}N},W_{\zeta }\right)$, is given as follows:

$$∆\left({\Omega }_{{\zeta P}_{1}N},W_{\zeta }\right)=\sum _{\zeta =1}^{\omega }\frac{{\left({\Omega }_{{\zeta P}_{1}N}-W_{\zeta }\right)}^2}{{\psi }_{\zeta N}{W}_{\zeta }}-2{\lambda }_{P_{1}N}\left(\sum _{\zeta =1}^{\omega }{\Omega }_{{\zeta P}_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right.\left.-\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)\right) .$$

(11)

Table 2. Proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ family of neutrosophic CDF estimators.

$\mathit{i}$	${\mathit{H}}_{{\mathit{P}}_{\mathit{i}}{\left(\mathit{N}\right)}_1}$	${\mathit{\psi }}_{\mathit{\zeta }\mathit{N}}$
1	$H_{P_1{\left(N\right)}_1}$	1
2	$H_{P_2{\left(N\right)}_1}$	$\frac{1}{{\overline{x}}_{\zeta N}}$
3	$H_{P_3{\left(N\right)}_1}$	$\frac{1}{s_{\zeta xN}}$
4	$H_{P_4{\left(N\right)}_1}$	$\frac{1}{s_{\zeta xN}^2}$
5	$H_{P_5{\left(N\right)}_1}$	$\frac{1}{c_{\zeta xN}}$

Setting Equation (11),$\frac{\partial ∆({\Omega }_{{\zeta P}_{1}N},W_{\zeta })}{\partial {\Omega }_{{\zeta P}_{1}N}}=0$, we obtain the neutrosophic calibrated weight as follows:

$${\Omega }_{{\zeta P}_{1}N}=W_{\zeta }+{\lambda }_{P_{1}N}{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right){\psi }_{\zeta N}{W}_{\zeta } .$$

(12)

Substituting Equation (12) in Equation (10), and solving for neutrosophic lambda, we obtain the following:

$${\lambda }_{P_{1}N}=\frac{\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)}{\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)} .$$

(13)

Substituting Equation (13) in Equation (12), we obtain the neutrosophic calibration weight, as follows:

$${\Omega }_{{\zeta P}_{1}N}=W_{\zeta }+\frac{\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)}{\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)}{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right) .$$

(14)

Substituting Equation (14) in Equation (8), we obtain the neutrosophic calibrated estimator of CDF, as given below:

$$H_{P_i{\left(N\right)}_1}=\sum _{\zeta =1}^{\omega }{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right)+\frac{\sum _{\zeta =1}^{\omega }{W}_{\zeta }\left({\mathcal{F}}_{\zeta xN}\left(t_{xN}\right)-{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right)\right)}{\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}^2\left(t_{xN}\right)}\sum _{\zeta =1}^{\omega }{\psi }_{\zeta N}{W}_{\zeta }{\widehat{\mathcal{F}}}_{\zeta xN}\left(t_{xN}\right){\widehat{\mathcal{F}}}_{\zeta yN}\left(t_{yN}\right) .$$

The family members of $H_{P_i{\left(N\right)}_1}$ are provided in Table 2.

4. Simulation Study

To the best of the authors’ knowledge, no research has been undertaken on the neutrosophic calibration estimation of CDF thus far. This is because, the idea of evaluating the effectiveness of the suggested neutrosophic calibration estimation of CDF using supplementary information is still a novel idea. Thus, we examined the mean square error (MSE) of the developed family of neutrosophic estimators given in Table 2 with the adapted family of neutrosophic estimators given in Table 1 in order to evaluate the most effective estimators by identifying the neutrosophic estimators. We perform the simulation study steps for MSE and percentage relative efficiency (PRE) estimates by following [25], as stated below:

• Step 1: Using simple random sampling without replacement (SRSWOR) from stratum $\zeta$, choose a random sample of size $n_{\zeta }$.
• Step 2: Find the CDF estimate value, for instance ${\tau }_Q=H_{A_i{\left(N\right)}_1}, H_{P_i{\left(N\right)}_1}$
• Step 3: Repeat the previous steps $R=5000$ times to achieve ${\tau }_{Q1}, {\tau }_{Q2}, \dots , {\tau }_{QR}$.
• Step 4: Evaluate the MSE, as follows:

  $$MSE\left({\tau }_{QN}\right)=\frac{1}{R}\sum _{i=1}^R{\left({\tau }_Q-{\mathcal{F}}_{YN}\left(t_{yN}\right)\right)}^2 .$$
• Step 5: Compute the PRE, as follows:

  $$PRE\left({\tau }_{QN}\right)=\frac{MSE\left(H_{A_i{\left(N\right)}_1}\right)}{MSE\left(H_{P_i{\left(N\right)}_1}\right)}\times 100 .$$

The MSEs and PREs are provided in Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, Table 24, Table 25 and Table 26 based on three quantile points i.e., $(t=0.25, 0.50, 0.75)$.

Table 3. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.12550700, 0.09495555\right]$	$\left[0.07372283, 0.03183353\right]$	$\left[0.01307641, 0.01275580\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.10600970, 0.07969699\right]$	$\left[0.05155015, 0.02133777\right]$	$\left[0.01260893, 0.01200653\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.11414690, 0.06854242\right]$	$\left[0.04894732, 0.02054492\right]$	$\left[0.01233337, 0.01194092\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.11769560, 0.07805772\right]$	$\left[0.05129713, 0.02270461\right]$	$\left[0.01273243, 0.01196914\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.13526440, 0.10382170\right]$	$\left[0.06075261, 0.02671161\right]$	$\left[0.01261490, 0.01244723 \right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00043587, 0.00107817\right]$	$\left[0.00069142, 0.00182162\right]$	$\left[0.00127275, 0.00111091\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00043552, 0.00107847\right]$	$\left[0.00069379, 0.00182357\right]$	$\left[0.00127149, 0.00111071\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00043422, 0.00107233\right]$	$\left[0.00068692, 0.00179739\right]$	$\left[0.00127309, 0.00111534\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00043474, 0.00106791\right]$	$\left[0.00068392, 0.00177883\right]$	$\left[0.00127401, 0.00112097\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00043513, 0.00107207\right]$	$\left[0.00068482, 0.00179573\right]$	$\left[0.00127456, 0.00111567\right]$

Table 4. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.09938451, 0.07907769\right]$	$\left[0.06012644, 0.04282329\right]$	$\left[0.01116777, 0.01742282\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.08471047, 0.06887898\right]$	$\left[0.04339170, 0.03047215\right]$	$\left[0.01013658, 0.01639673\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.07956097, 0.06311932\right]$	$\left[0.04244550, 0.03046902\right]$	$\left[0.00999788, 0.01630728\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.08444315, 0.06629178\right]$	$\left[0.04221479, 0.03115415\right]$	$\left[0.00993667, 0.01708019\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[\mathrm{0.09192286,0.07363932}\right]$	$\left[0.05034084, 0.03660268\right]$	$\left[0.01077619, 0.01742002\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00055561, 0.00084529\right]$	$\left[0.00073901, 0.00106629\right]$	$\left[0.00071978, 0.00329068\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00055524, 0.00084509\right]$	$\left[0.00073910, 0.00106812\right]$	$\left[0.00071974, 0.00328824\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00055210, 0.00083945\right]$	$\left[0.00073793, 0.00106376\right]$	$\left[0.00071935, 0.00329016\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00055121, 0.00083560\right]$	$\left[0.00073726, 0.00106182\right]$	$\left[0.00071909, 0.00328999\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00055307, 0.00084024\right]$	$\left[0.00073794, 0.00106213\right]$	$\left[0.00071937, 0.00329285\right]$

Table 5. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.16533400, 0.12493000\right]$	$\left[0.10604800, 0.03462509\right]$	$\left[0.01699839, 0.02947149\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.14090010, 0.10346060\right]$	$\left[0.07543888, 0.02562175\right]$	$\left[0.01530376, 0.02928658\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.14371760, 0.10536490\right]$	$\left[0.07553381, 0.02339384\right]$	$\left[0.01523818, 0.02893875\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.13801410, 0.10476130\right]$	$\left[0.07562968, 0.02466783\right]$	$\left[0.01603289, 0.02895724\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.16912520, 0.11837020\right]$	$\left[0.09032016, 0.02998409\right]$	$\left[0.01754146, 0.02905653\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00025958, 0.00093281\right]$	$\left[0.00038758, 0.00166299\right]$	$\left[0.00043079, 0.00428377\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00025913, 0.00093546\right]$	$\left[0.00038773, 0.00166369\right]$	$\left[0.00043080, 0.00428058\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00025825, 0.00092476\right]$	$\left[0.00038684, 0.00166057\right]$	$\left[0.00043079, 0.00428438\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00025804, 0.00092036\right]$	$\left[0.00038640, 0.00165903\right]$	$\left[0.00043083, 0.00428603\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00025890, 0.00092286\right]$	$\left[0.00038676, 0.00166006\right]$	$\left[0.00043081, 0.00428734\right]$

Table 6. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[12659.18000000, 52.95105000\right]$	$\left[9848.06500000, 34.80282000\right]$	$\left[1390.32900000, 43.79722000\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[12848.09000000, 52.90249000\right]$	$\left[9937.59300000, 34.83687000\right]$	$\left[1393.63900000, 43.87352000\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[12878.36000000, 52.75121000\right]$	$\left[9804.92700000, 35.03531000\right]$	$\left[1378.85400000, 43.62861000\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[13396.63000000, 52.73636000\right]$	$\left[8401.08800000, 35.32916000\right]$	$\left[1354.67600000, 43.55621000\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[12652.08000000, 52.79689000\right]$	$\left[9867.90100000, 35.00586000\right]$	$\left[1376.04100000, 43.56635000\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00235515, 0.00254313\right]$	$\left[0.00225229, 0.00328725\right]$	$\left[0.00273807, 0.00295161\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00236679, 0.00254399\right]$	$\left[0.00225184, 0.00328669\right]$	$\left[0.00273411, 0.00295103\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00239635, 0.00253732\right]$	$\left[0.00231006, 0.00329569\right]$	$\left[0.00275508, 0.00295577\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00241799, 0.00253049\right]$	$\left[0.00232416, 0.00329873\right]$	$\left[0.00275984, 0.00295528\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00239698, 0.00253698\right]$	$\left[0.00231220, 0.00329621\right]$	$\left[0.00275649, 0.00295604\right]$

Table 7. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[28794.92000000, 8807.07900000\right]$	$\left[10662.49000000, 1747.53700000\right]$	$\left[1027.41400000, 1148.22900000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[24340.81000000, 7389.79700000\right]$	$\left[7430.19800000, 1170.10700000\right]$	$\left[991.65840000, 1080.97800000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[26287.65000000, 6391.93400000\right]$	$\left[7125.59300000, 1143.04200000\right]$	$\left[968.77530000, 1070.61100000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[27072.90000000, 7309.39900000\right]$	$\left[7500.47400000, 1276.38200000\right]$	$\left[999.39660000, 1067.75100000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[31086.07000000, 9684.18600000\right]$	$\left[8871.29900000, 1487.51100000\right]$	$\left[989.74450000, 1115.67000000\right]$

Table 8. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[\mathrm{17887.42000000,9354.99300000}\right]$	$\left[8135.97600000, 4016.08000000\right]$	$\left[1551.54900000, 529.45880000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[15256.49000000, 8150.48500000\right]$	$\left[5870.84100000, 2852.85700000\right]$	$\left[1408.35400000, 498.64720000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[14410.60000000, 7519.11700000\right]$	$\left[5751.94100000, 2864.25400000\right]$	$\left[1389.8400000, 495.63750000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[15319.61000000, 7933.41400000\right]$	$\left[5725.91500000, 2934.01700000\right]$	$\left[1381.83600000, 519.15620000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[16620.42000000, 8764.01800000\right]$	$\left[6821.77200000, 3446.14300000\right]$	$\left[1498.00100000, 529.02580000\right]$

Table 9. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[63693.23000000,13392.82000000\right]$	$\left[27361.67000000,2082.10100000\right]$	$\left[3945.78400000,687.98060000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[54373.39000000,11059.91000000\right]$	$\left[19456.74000000,1540.04800000\right]$	$\left[3552.39400000,684.17400000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[55650.08000000,11393.73000000\right]$	$\left[19525.93000000,1408.78300000\right]$	$\left[3537.18500000,675.44740000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[53484.81000000,11382.60000000\right]$	$\left[19572.67000000,1486.88000000\right]$	$\left[3721.41100000,675.61890000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[65323.39000000,12826.46000000\right]$	$\left[23353.06000000,1806.20600000\right]$	$\left[4071.70300000,677.72930000\right]$

Table 10. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 5%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[537510420.10000000, 2082123.10000000\right]$	$\left[437247684.10000000, 1058722.10000000\right]$	$\left[50777790.10000000, 1483841.10000000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[542848807.10000000, 2079502.10000000\right]$	$\left[441309532.10000000, 1059936.10000000\right]$	$\left[50972385.10000000, 1486719.10000000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[537415642.10000000, 2079013.10000000\right]$	$\left[424445080.10000000, 1063066.10000000\right]$	$\left[50047658.10000000, 1476051.10000000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[554039427.10000000, 2084033.10000000\right]$	$\left[361467699.10000000, 1070992.10000000\right]$	$\left[49085369.10000000, 1473845.10000000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[527835504.10000000, 2081090.10000000\right]$	$\left[426775100.10000000, 1062002.10000000\right]$	$\left[49920017.10000000, 1473811.10000000\right]$

Table 11. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.05278514, 0.03103824\right]$	$\left[0.02293561, 0.00863221\right]$	$\left[0.00452109, 0.00408159\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.04556192, 0.02622204\right]$	$\left[0.01839788, 0.00727704\right]$	$\left[0.00445757, 0.00394331\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.04738312, 0.02172956\right]$	$\left[0.01941909, 0.00664607\right]$	$\left[0.00445610, 0.00388231\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.04985967, 0.02567838\right]$	$\left[0.01922507, 0.00742291\right]$	$\left[0.00446277, 0.00393611\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.05599423, 0.03178389\right]$	$\left[0.02329781, 0.00880282\right]$	$\left[0.00461344, 0.00406053\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00029686, 0.00085081\right]$	$\left[0.00038942, 0.00148873\right]$	$\left[0.00072948, 0.00059511\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00029691, 0.00085084\right]$	$\left[0.00039149, 0.00149078\right]$	$\left[0.00072966, 0.00059520\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00029594, 0.00085053\right]$	$\left[0.00038628, 0.00146474\right]$	$\left[0.00072864, 0.00059438\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00029552, 0.00085090\right]$	$\left[0.00038371, 0.00144341\right]$	$\left[0.00072797, 0.00059382\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00029603, 0.00085054\right]$	$\left[0.00038423, 0.00146279\right]$	$\left[0.00072849, 0.00059430\right]$

Table 12. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[\begin{array}{c}0.03201772, 0.02207009\end{array}\right]$	$\left[\begin{array}{c}0.01571671, 0.00894583\end{array}\right]$	$\left[\begin{array}{c}0.00344596, 0.00730504\end{array}\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[\begin{array}{c}0.02698789, 0.01722464\end{array}\right]$	$\left[\begin{array}{c}0.01417302, 0.00769259\end{array}\right]$	$\left[\begin{array}{c}0.00334932, 0.00728080\end{array}\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[\begin{array}{c}0.02530204, 0.01732694\end{array}\right]$	$\left[\begin{array}{c}0.01295956, 0.00786451\end{array}\right]$	$\left[\begin{array}{c}0.00328828, 0.00701269\end{array}\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[\begin{array}{c}0.02508618, 0.01825600\end{array}\right]$	$\left[\begin{array}{c}0.01440447, 0.00717085\end{array}\right]$	$\left[\begin{array}{c}0.00326247, 0.00699018\end{array}\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[\begin{array}{c}0.03044012, 0.02105985\end{array}\right]$	$\left[\begin{array}{c}0.01630019, 0.00899331\end{array}\right]$	$\left[\begin{array}{c}0.00343424, 0.00720987\end{array}\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00034510, 0.00065756\end{array}\right]$	$\left[\begin{array}{c}0.00046213, 0.00065388\end{array}\right]$	$\left[\begin{array}{c}0.00039188, 0.00250048\end{array}\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00034504, 0.00065742\end{array}\right]$	$\left[\begin{array}{c}0.00046220, 0.00065570\end{array}\right]$	$\left[\begin{array}{c}0.00039229, 0.00249942\end{array}\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00034320, 0.00065497\end{array}\right]$	$\left[\begin{array}{c}0.00046140, 0.00065368\end{array}\right]$	$\left[\begin{array}{c}0.00039276, 0.00249928\end{array}\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00034189, 0.00065279\end{array}\right]$	$\left[\begin{array}{c}0.00046087, 0.00065372\end{array}\right]$	$\left[\begin{array}{c}0.00039366, 0.00249803\end{array}\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00034337, 0.00065530\right]$	$\left[0.00046139, 0.00065199\right]$	$\left[0.00039234, 0.00250031\right]$

Table 13. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[\begin{array}{c}0.07023669, 0.05348943\end{array}\right]$	$\left[\begin{array}{c}0.03667399, 0.00787167\end{array}\right]$	$\left[\begin{array}{c}0.00542214, 0.01255324\end{array}\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[\begin{array}{c}0.05989029, 0.04451275\end{array}\right]$	$\left[\begin{array}{c}0.03216543, 0.00717289\end{array}\right]$	$\left[\begin{array}{c}0.00468516, 0.01254090\end{array}\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[\begin{array}{c}0.05978501, 0.04081650\end{array}\right]$	$\left[\begin{array}{c}0.02805722, 0.00701938\end{array}\right]$	$\left[\begin{array}{c}0.00480273, 0.01252107\end{array}\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[\begin{array}{c}0.05903541, 0.04616470\end{array}\right]$	$\left[\begin{array}{c}0.03090341, 0.00770717\end{array}\right]$	$\left[\begin{array}{c}0.00469045, 0.01256707\end{array}\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[\begin{array}{c}0.07292860, 0.05298113\end{array}\right]$	$\left[\begin{array}{c}0.03687221, 0.00815749\end{array}\right]$	$\left[\begin{array}{c}0.00587575, 0.01261741\end{array}\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00015005, 0.00079295\end{array}\right]$	$\left[\begin{array}{c}0.00021372, 0.00116272\end{array}\right]$	$\left[\begin{array}{c}0.00025309, 0.00353636\end{array}\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00014986, 0.00079444\end{array}\right]$	$\left[\begin{array}{c}0.00021384, 0.00116275\end{array}\right]$	$\left[\begin{array}{c}0.00025297, 0.00353541\end{array}\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00014969, 0.00079034\right]$	$\left[\begin{array}{c}0.00021347, 0.00116161\end{array}\right]$	$\left[\begin{array}{c}0.00025333, 0.00353626\end{array}\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00014952, 0.00078854\end{array}\right]$	$\left[\begin{array}{c}0.00021325, 0.00116067\end{array}\right]$	$\left[\begin{array}{c}0.00025358, 0.00353625\end{array}\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00014988, 0.00078909\end{array}\right]$	$\left[\begin{array}{c}0.00021338, 0.00116164\end{array}\right]$	$\left[\begin{array}{c}0.00025344, 0.00353711\end{array}\right]$

Table 14. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[\begin{array}{c}18.26232000, 17.38877000\end{array}\right]$	$\left[\begin{array}{c}21.55961000, 33.46750000\end{array}\right]$	$\left[\begin{array}{c}0.10202770, 33.07366000\end{array}\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[\begin{array}{c}17.55407000, 17.3972\end{array}0000\right]$	$\left[\begin{array}{c}21.54354000, 33.44364000\end{array}\right]$	$\left[\begin{array}{c}0.10302250, 33.18657000\end{array}\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[\begin{array}{c}17.55962000, 17.48267000\end{array}\right]$	$\left[\begin{array}{c}21.54388000, 33.35970000\end{array}\right]$	$\left[\begin{array}{c}0.10314110, 33.06412000\end{array}\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[\begin{array}{c}16.89388000, 17.62576000\end{array}\right]$	$\left[\begin{array}{c}21.52976000, 33.28332000\end{array}\right]$	$\left[\begin{array}{c}0.10612860, 33.12167000\end{array}\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[\begin{array}{c}18.26487000, 17.47264000\end{array}\right]$	$\left[\begin{array}{c}21.56045000, 33.38678000\end{array}\right]$	$\left[\begin{array}{c}0.10213000, 32.95957000\end{array}\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00160199, 0.00186467\end{array}\right]$	$\left[\begin{array}{c}0.00146192, 0.00209583\end{array}\right]$	$\left[\begin{array}{c}0.00175950, 0.00187631\end{array}\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00160980, 0.00186595\end{array}\right]$	$\left[\begin{array}{c}0.00146069, 0.00209569\end{array}\right]$	$\left[\begin{array}{c}0.00175860, 0.00187565\end{array}\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00159285, 0.00186075\end{array}\right]$	$\left[\begin{array}{c}0.00148106, 0.00209416\end{array}\right]$	$\left[\begin{array}{c}0.00176694, 0.00188578\end{array}\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00159198, 0.00185844\end{array}\right]$	$\left[\begin{array}{c}0.00148989, 0.00209369\end{array}\right]$	$\left[\begin{array}{c}0.00176976, 0.00188666\end{array}\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[\begin{array}{c}0.00159077, 0.00186014\end{array}\right]$	$\left[\begin{array}{c}0.00148256, 0.00209447\end{array}\right]$	$\left[\begin{array}{c}0.00176760, 0.00188607\end{array}\right]$

Table 15. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[17780.95000000, 3648.09100000\right]$	$\left[5889.61800000, 579.83620000\right]$	$\left[619.77080000, 685.85570000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[15345.24000000, 3081.90500000\right]$	$\left[4699.33200000, 488.13630000\right]$	$\left[610.91250000, 662.51650000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[16011.10000000, 2554.82500000\right]$	$\left[5027.23400000, 453.73750000\right]$	$\left[611.56170000, 653.16850000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[16872.02000000, 3017.79000000\right]$	$\left[5010.33400000, 514.26390000\right]$	$\left[613.04340000, 662.84210000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[18914.78000000, 3736.89500000\right]$	$\left[6063.45400000, 601.78430000\right]$	$\left[633.28420000, 683.23970000\right]$

Table 16. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[9277.77100000, 3356.37900000\right]$	$\left[3400.92700000, 1368.12000000\right]$	$\left[879.34680000, 292.14510000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[7821.72800000, 2620.05100000\right]$	$\left[3066.40300000, 1173.18100000\right]$	$\left[853.79040000, 291.30000000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[7372.31400000, 2645.43700000\right]$	$\left[2808.72600000, 1203.11100000\right]$	$\left[837.22350000, 280.58850000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[7337.58200000, 2796.57100000\right]$	$\left[3125.48500000, 1096.93700000\right]$	$\left[828.76440000, 279.82740000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[8865.21700000, 3213.75900000\right]$	$\left[3532.78700000, 1379.35400000\right]$	$\left[875.31730000, 288.35920000\right]$

Table 17. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[46810.30000000, 6745.63900000\right]$	$\left[17160.10000000, 677.00780000\right]$	$\left[2142.41100000, 354.97660000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[39963.99000000, 5603.04500000\right]$	$\left[15041.75000000, 616.89100000\right]$	$\left[1852.07800000, 354.72230000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[39939.96000000, 5164.40000000\right]$	$\left[13143.36000000, 604.27990000\right]$	$\left[1895.80800000, 354.07640000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[39482.56000000, 5854.48500000\right]$	$\left[14491.48000000, 664.02660000\right]$	$\left[1849.66100000, 355.37810000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[48659.02000000, 6714.22000000\right]$	$\left[17280.26000000, 702.23720000\right]$	$\left[2318.41100000, 356.71520000\right]$

Table 18. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimator’s w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 10%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[1139971.10000000, 932538.90000000\right]$	$\left[1474744.10000000, 1596858.10000000\right]$	$\left[5798.66700000, 1762694.10000000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[1090450.10000000, 932351.20000000\right]$	$\left[1474892.10000000, 1595827.10000000\right]$	$\left[5858.19800000, 1769333.10000000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[1102405.10000000, 939549.20000000\right]$	$\left[1454625.10000000, 1592991.10000000\right]$	$\left[5837.26300000, 1753342.10000000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[1061188.10000000, 948418.10000000\right]$	$\left[1445049.10000000, 1589694.10000000\right]$	$\left[5996.78200000, 1755568.10000000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[1148177.10000000, 939318.10000000\right]$	$\left[1454269.10000000, 1594042.10000000\right]$	$\left[5777.89300000, 1747524.10000000\right]$

Table 19. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.02423724, 0.02521752\right]$	$\left[0.01013707, 0.00436531\right]$	$\left[0.00423744, 0.00318711\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.02032192, 0.02182145\right]$	$\left[0.01035944, 0.00410658\right]$	$\left[0.00405645, 0.00317238\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.02256156, 0.02226276\right]$	$\left[0.00977304, 0.00435874\right]$	$\left[0.00420122, 0.00311620\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.02388722, 0.02348978\right]$	$\left[0.00978326, 0.00443506\right]$	$\left[0.00428133, 0.00309671\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.02541181, 0.02641287\right]$	$\left[0.01217725, 0.00453425\right]$	$\left[0.00430458, 0.00325799\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00024404, 0.00084491\right]$	$\left[0.00028227, 0.00138944\right]$	$\left[0.00061685, 0.00050901\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00024416, 0.00084417\right]$	$\left[0.00028367, 0.00139088\right]$	$\left[0.00061677, 0.00050904\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00024361, 0.00085899\right]$	$\left[0.00028035, 0.00137184\right]$	$\left[0.00061657, 0.00050933\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00024327, 0.00087593\right]$	$\left[0.00027869, 0.00135528\right]$	$\left[0.00061634, 0.00050985 \right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00024349, 0.00086004\right]$	$\left[0.00027892, 0.00137041\right]$	$\left[0.00061668, 0.00050933\right]$

Table 20. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.01217292, 0.00915546\right]$	$\left[0.00574358, 0.00473178\right]$	$\left[0.00190995, 0.01581105\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.01133602, 0.00925104\right]$	$\left[0.00587575, 0.00454565\right]$	$\left[0.00183164, 0.01569076\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.01050344, 0.00782591\right]$	$\left[0.00539212, 0.00472929\right]$	$\left[0.00186089, 0.01565197\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.01188887, 0.00812091\right]$	$\left[0.00578986, 0.00430275\right]$	$\left[0.00176988, 0.01585948\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.01490505, 0.00945394\right]$	$\left[0.00692203, 0.00508339\right]$	$\left[0.00171219, 0.01582575\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00029955, 0.00058966\right]$	$\left[0.00039184, 0.00052005\right]$	$\left[0.00029563, 0.00233310\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00029933, 0.00058969\right]$	$\left[0.00039191, 0.00052105\right]$	$\left[0.00029581, 0.00233216\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00029846, 0.00058849\right]$	$\left[0.00039124, 0.00051958\right]$	$\left[0.00029598, 0.00233165\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00029754, 0.00058745\right]$	$\left[0.00039072, 0.00051922\right]$	$\left[0.00029634, 0.00233019\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00029871, 0.00058853\right]$	$\left[0.00039119, 0.00051865\right]$	$\left[0.00029579, 0.00233258\right]$

Table 21. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[0.03657191, 0.02439917\right]$	$\left[0.01808088, 0.00722918\right]$	$\left[0.00316343, 0.02164782\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[0.03463097, 0.02389522\right]$	$\left[0.01817396, 0.00702091\right]$	$\left[0.00248699, 0.02219127\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[0.03279962, 0.02120182\right]$	$\left[0.01759832, 0.00715856\right]$	$\left[0.00295482, 0.02050702\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[0.03333753, 0.02501256\right]$	$\left[0.01829039, 0.00744975\right]$	$\left[0.00288229, 0.01942301\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[0.04454848, 0.02675314\right]$	$\left[0.02226382, 0.00736752\right]$	$\left[0.00354308, 0.02002272\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00013042, 0.00076973\right]$	$\left[0.00017573, 0.00109067\right]$	$\left[0.00020431, 0.00271852\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00013036, 0.00077070\right]$	$\left[0.00017576, 0.00109061\right]$	$\left[0.00020429, 0.00271754\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00013023, 0.00076896\right]$	$\left[0.00017562, 0.00109000\right]$	$\left[0.00020435, 0.00271849\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00013009, 0.00076839\right]$	$\left[0.00017553, 0.00108942\right]$	$\left[0.00020439, 0.00271853\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00013029, 0.00076808\right]$	$\left[0.00017559, 0.00109009\right]$	$\left[0.00020436, 0.00271937\right]$

Table 22. MSE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ and adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$H_{A_1{\left(N\right)}_1}$	$\left[1.07473400, 30.53655000\right]$	$\left[0.02329777, 13.03802000\right]$	$\left[11.04803000, 191.03530000\right]$
$H_{A_2{\left(N\right)}_1}$	$\left[1.08310400, 30.64574000\right]$	$\left[0.02184079, 13.03078000\right]$	$\left[10.55876000, 191.62410000\right]$
$H_{A_3{\left(N\right)}_1}$	$\left[1.08276600, 30.45685000\right]$	$\left[0.02201946, 13.02999000\right]$	$\left[12.62746000, 191.98260000\right]$
$H_{A_4{\left(N\right)}_1}$	$\left[1.09153000, 30.40495000\right]$	$\left[0.02110268, 13.04988000\right]$	$\left[14.70891000, 193.06520000\right]$
$H_{A_5{\left(N\right)}_1}$	$\left[1.07416700, 30.35368000\right]$	$\left[0.02333948, 13.03710000\right]$	$\left[13.33633000, 191.40170000\right]$
$H_{P_1{\left(N\right)}_1}$	$\left[0.00153637, 0.00148698\right]$	$\left[0.00112341, 0.00169163\right]$	$\left[0.00144035, 0.00183146\right]$
$H_{P_2{\left(N\right)}_1}$	$\left[0.00154792, 0.00148857\right]$	$\left[0.00112126, 0.00169154\right]$	$\left[0.00143918, 0.00183071\right]$
$H_{P_3{\left(N\right)}_1}$	$\left[0.00151023, 0.00147533\right]$	$\left[0.00113311, 0.00168989\right]$	$\left[0.00144614, 0.00184546\right]$
$H_{P_4{\left(N\right)}_1}$	$\left[0.00149851, 0.00147402\right]$	$\left[0.00113987, 0.00168964\right]$	$\left[0.00144949, 0.00184714\right]$
$H_{P_5{\left(N\right)}_1}$	$\left[0.00150502, 0.00147458\right]$	$\left[0.00113491, 0.00169020\right]$	$\left[0.00144707, 0.00184578\right]$

Table 23. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimators w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 1 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[9931.80600000, 2984.63400000\right]$	$\left[3591.28400000, 314.17690000\right]$	$\left[686.94460000, 626.13370000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[8323.19100000, 2584.96200000\right]$	$\left[3651.99500000, 295.25020000\right]$	$\left[657.68740000, 623.21460000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[9261.49500000, 2591.70800000\right]$	$\left[3486.00200000, 317.72880000\right]$	$\left[681.38970000, 611.82030000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[9819.03300000, 2681.69900000\right]$	$\left[3510.33800000, 327.24400000\right]$	$\left[694.63330000, 607.37980000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[10436.12000000, 3071.13900000\right]$	$\left[4365.88600000, 330.86760000\right]$	$\left[698.02840000, 639.65900000\right]$

Table 24. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimators w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 2 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[4063.80300000, 1552.66600000\right]$	$\left[1465.80900000, 909.87520000\right]$	$\left[646.06990000, 677.68400000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[3787.15100000, 1568.79300000\right]$	$\left[1499.25900000, 872.40520000\right]$	$\left[619.19780000, 672.80020000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[\mathrm{3519.26900000,1329.81700000}\right]$	$\left[1378.22800000, 910.21660000\right]$	$\left[628.72390000, 671.28430000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[3995.67100000, 1382.40400000\right]$	$\left[1481.84800000, 828.69940000\right]$	$\left[597.24690000, 680.60890000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[4989.83700000, 1606.35900000\right]$	$\left[1769.48300000, 980.11500000\right]$	$\left[578.86400000, 678.46490000\right]$

Table 25. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimators w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 3 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[28041.68000000, 3169.83400000\right]$	$\left[10289.24000000, 662.82300000\right]$	$\left[1548.33800000, 796.30850000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[26566.22000000, 3100.44000000\right]$	$\left[10339.93000000, 643.75970000\right]$	$\left[1217.35200000, 816.59290000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[25185.16000000, 2757.19500000\right]$	$\left[10020.47000000, 656.74930000\right]$	$\left[1445.97100000, 754.35340000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[25627.92000000, 3255.18800000\right]$	$\left[10420.04000000, 683.82710000\right]$	$\left[1410.20400000, 714.46790000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[34192.70000000, 3483.14700000\right]$	$\left[12679.06000000, 675.86270000\right]$	$\left[1733.71500000, 736.29930000\right]$

Table 26. PRE of proposed $\left(H_{P_i{\left(N\right)}_1}\right)$ estimators w.r.t adapted $\left(H_{A_i{\left(N\right)}_1}\right)$ estimators for population 4 when sample size is 15%.

Estimators	$0.25$	$0.50$	$0.75$
$\left(H_{P_1{\left(N\right)}_1},H_{A_1{\left(N\right)}_1}\right)$	$\left[69953.01000000, 2053589.10000000\right]$	$\left[2073.83700000, 770736.30000000\right]$	$\left[767040.50000000, 10430743.10000000\right]$
$\left(H_{P_2{\left(N\right)}_1},H_{A_2{\left(N\right)}_1}\right)$	$\left[69971.57000000, 2058739.10000000\right]$	$\left[1947.87600000, 770349.50000000\right]$	$\left[733666.60000000, 10467204.10000000\right]$
$\left(H_{P_3{\left(N\right)}_1},H_{A_3{\left(N\right)}_1}\right)$	$\left[71695.46000000, 2064414.10000000\right]$	$\left[1943.28000000, 771053.10000000\right]$	$\left[873186.30000000, 10402960.10000000\right]$
$\left(H_{P_4{\left(N\right)}_1},H_{A_4{\left(N\right)}_1}\right)$	$\left[72841.01000000, 2062729.10000000\right]$	$\left[1851.32000000, 772345.70000000\right]$	$\left[1014767.10000000, 10452121.10000000\right]$
$\left(H_{P_5{\left(N\right)}_1},H_{A_5{\left(N\right)}_1}\right)$	$\left[71372.46000000, 2058464.10000000\right]$	$\left[2056.50600000, 771333.50000000\right]$	$\left[921611.10000000, 10369700.10000000\right]$

4.1. Weather Data Sets

We performed a numerical study utilizing interval/ambiguous values with indeterminate values from the weather datasets in Pakistani cities like Karachi, Lahore, Multan, and Peshawar. The data are composed of uncertain neutrosophic values that fall into a specific range. One reason to consider weather datasets contain neutrosophic data is that their values diverge in an interval form, with the recorded weather data for the day potentially being the highest, lowest, or any value in between. For the purposes of this article, we have considered four populations—temperature, dew point, humidity, and pressure datasets. The symmetric and asymmetric data are taken from a website (https://www.wunderground.com, accessed on 20 June 2023) that was open to the public.

4.1.1. Temperature Data (Population 1)

We have considered the temperature data of four cities in Pakistan—stratum I: Karachi temperature data with 365 days; stratum II: Lahore temperature data with 365 days; stratum III: Peshawar temperature data with 365 days; and stratum-IV: Multan temperature data with 365 days—from 1 January 2021, to 31 December 2022. Each stratum’s size is represented by the number of days. We select various neutrosophic samples of sizes 5%, 10% and 15%, as given below:

$$N_1=365, N_2=365, { N}_3=365, { N}_4=365$$

➢

For 5% sample size:

$$n_1=18, n_2=18, n_3=18, n_4=18$$

➢

For 10% sample size:

$$n_1=37, n_2=37, n_3=37, n_4=37$$

➢

For 15% sample size:

$$n_1=55, n_2=55, n_3=55, n_4=55$$

For population 1, we take the following factors into consideration:

• $x_N$ = Neutrosophic temperature 1 January 2021 to 31 December 2021
• $y_N$ = Neutrosophic temperature 1 January 2022 to 31 December 2022

4.1.2. Dew Point Temperature Data (Population 2)

We have considered the dew point temperature data of four (cities) in Pakistan—stratum I: Karachi dew point temperature data with 365 days; stratum II: Lahore dew point temperature data with 365 days; stratum III: Peshawar dew point temperature data with 365 days; and stratum IV: Multan dew point temperature data with 365 days—from 1 January 2021, to 31 December 2022. Each stratum’s size is represented by the number of days. We select various neutrosophic samples of sizes 5%, 10% and 15%, as given below:

➢

For 5% sample size:

$$n_1=18, n_2=18, n_3=18, n_4=18$$

➢

For 10% sample size:

$$n_1=37, n_2=37, n_3=37, n_4=37$$

➢

For 15% sample size:

$$n_1=55, n_2=55, n_3=55, n_4=55$$

For population 2, we take the following factors into consideration:

• $x_N$ = Neutrosophic dew-point 1 January 2021 to 31 December 2021
• $y_N$ = Neutrosophic dew-point 1 January 2022 to 31 December 2022

4.1.3. Humidity Data (Population 3)

We have considered the humidity data of four (cities) in Pakistan—stratum I: Karachi humidity data with 365 days; stratum-II: Lahore humidity data with 365 days; stratum-III: Peshawar humidity data with 365 days; and stratum-IV: Multan humidity data with 365 days—from 1 January 2021, to 31 December 2022. Each stratum’s size is represented by the number of days. We select various neutrosophic samples of sizes 5%, 10% and 15%, as given below:

$$N_1=365, N_2=365, { N}_3=365, { N}_4=365$$

➢

For 5% sample size:

$$n_1=18, n_2=18, n_3=18, n_4=18$$

➢

For 10% sample size:

$$n_1=37, n_2=37, n_3=37, n_4=37$$

➢

For 15% sample size:

$$n_1=55, n_2=55, n_3=55, n_4=55$$

For population 3, we take the following factors into consideration:

• $x_N$ = Neutrosophic humidity 1 January 2021 to 31 December 2021
• $y_N$ = Neutrosophic humidity 1 January 2022 to 31 December 2022

4.1.4. Pressure Data (Population 4)

We have considered the pressure temperature data of four (cities) in Pakistan—stratum I: Karachi pressure data with 365 days; stratum II: Lahore pressure data with 365 days; stratum III: Peshawar pressure data with 365 days; and stratum IV: Multan pressure data with 365 days—from 1 January 2021, to 31 December 2022. Each stratum’s size is represented by the number of days. We select various neutrosophic samples of sizes 5%, 10% and 15% as given below:

$$N_1=365, N_2=365, { N}_3=365, { N}_4=365$$

➢

For 5% sample size:

$$n_1=18, n_2=18, n_3=18, n_4=18$$

➢

For 10% sample size:

$$n_1=37, n_2=37, n_3=37, n_4=37$$

➢

For 15% sample size:

$$n_1=55, n_2=55, n_3=55, n_4=55$$

For population 4, we take the following factors into consideration:

• $x_N$ = Neutrosophic pressure 1 January 2021 to 31 December 2021
• $y_N$ = Neutrosophic pressure 1 January 2022 to 31 December 2022

4.2. Interpretations and Figures

4.2.1. When Sample Size Is 5%

The results for 5% sample size are mentioned in Table 3, Table 4, Table 5 and Table 6 and indicate the following:

➢

For population 1, the lower and upper values of adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(L\right)}_1}=0.01233337$ at quantile ($t=0.75$), while $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=0.01194092$ at quantile ($t=0.75$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{P_3{\left(L\right)}_1}=0.00043422$ at quantile ($t=0.25$), while $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00106791$ at quantile ($t=0.25$).

➢

For population 2, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{A_4{\left(L\right)}_1}=0.00993667$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=0.01630728$ at quantile ($t=0.75$). The lower and upper values of proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00055121$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00083560$ at quantile ($t=0.25$).

➢

For population 3, the lower and upper values of adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=3$ have a minimum value of MSE for $H_{A_3{\left(L\right)}_1}=0.01523818$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=0.02339384$ at quantile ($t=0.50$). The lower and upper values of proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00025804$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00092036$ at quantile ($t=0.25$).

➢

For population 4, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{A_4{\left(L\right)}_1}=1354.67600000$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=1$ has a minimum value of MSE for $H_{A_1{\left(U\right)}_1}=34.80282000$ at quantile ($t=0.50$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{P_2{\left(L\right)}_1}=0.00225184$ at quantile ($t=0.50$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00253049$ at quantile ($t=0.25$).

➢

The same pattern of the proposed neutrosophic estimators PRE’s for a 5% sample size can be seen in Table 7, Table 8, Table 9 and Table 10 for all $i=1,2,3,4,5$.

➢

The visual representation of MSE’s results based on a 5% sample size is provided in Figure 1, Figure 2, Figure 3 and Figure 4.

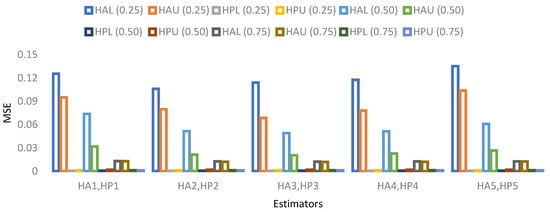Figure 1. MSE for population 1 when sample size is 5%.

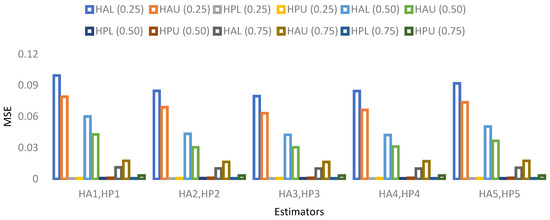Figure 2. MSE for population 2 when sample size is 5%.

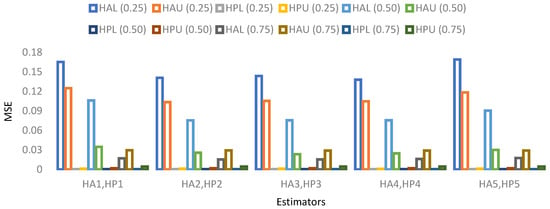Figure 3. MSE for population 3 when sample size is 5%.

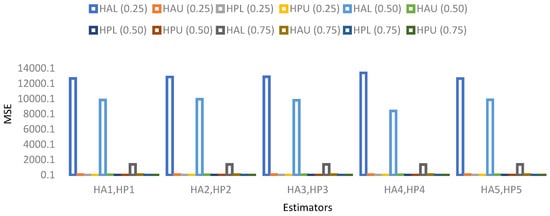Figure 4. MSE for population 4 when sample size is 5%.

4.2.2. When Sample Size Is 10%

The results for 10% sample size are mentioned in Table 11, Table 12, Table 13 and Table 14 and indicate that:

➢

For population 1, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=3$ have a minimum value of MSE for $H_{A_3{\left(L\right)}_1}=0.00445610$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=0.00388231$ at quantile ($t=0.75$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00029552$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00059382$ at quantile ($t=0.75$).

➢

For population 2, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{A_4{\left(L\right)}_1}=0.00326247$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{A_4{\left(U\right)}_1}=0.00699018$ at quantile ($t=0.75$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00034189$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=5$ has a minimum value of MSE for $H_{P_5{\left(U\right)}_1}=0.00065199$ at quantile ($t=0.50$).

➢

For population 3, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{A_2{\left(L\right)}_1}=0.00468516$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=0.00701938$ at quantile ($t=0.50$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00014952$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00078854$ at quantile ($t=0.25$).

➢

For population 4, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=1$ have a minimum value of MSE for $H_{A_1{\left(L\right)}_1}=0.10202770$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=1$ has a minimum value of MSE for $H_{A_1{\left(U\right)}_1}=17.38877000$ at quantile ($t=0.25$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{P_2{\left(L\right)}_1}=0.00146069$ at quantile ($t=0.50$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00185844$ at quantile ($t=0.25$).

➢

The same pattern of the proposed neutrosophic estimators PRE’s for a 10% sample size can be seen in Table 15, Table 16, Table 17 and Table 18 for all $i=1,2,3,4,5$.

➢

A visual representation of MSE’s results based on a 10% sample size is provided in Figure 5, Figure 6, Figure 7 and Figure 8.

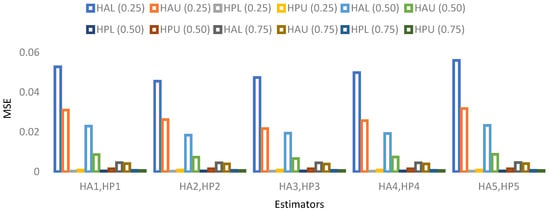Figure 5. MSE for population 1 when sample size is 10%.

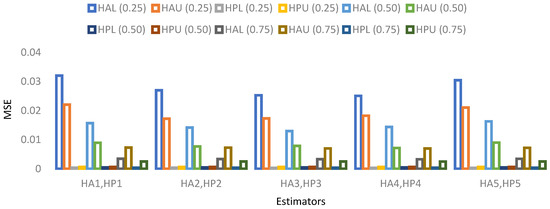Figure 6. MSE for population 2 when sample size is 10%.

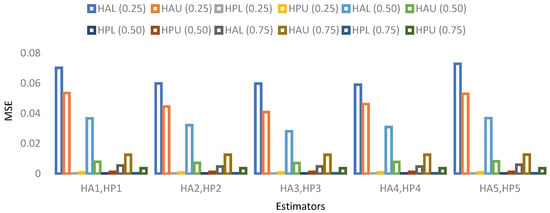Figure 7. MSE for population 3 when sample size is 10%.

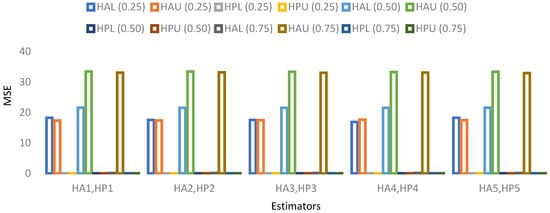Figure 8. MSE for population 4 when sample size is 10%.

4.2.3. When Sample Size Is 15%

The results for 15% sample size are mentioned in Table 19, Table 20, Table 21 and Table 22 and indicate that:

➢

For population 1, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{A_2{\left(L\right)}_1}=0.00405645$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{A_4{\left(U\right)}_1}=0.00309671$ at quantile ($t=0.75$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00024327$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=1$ has a minimum value of MSE for $H_{P_1{\left(U\right)}_1}=0.00050901$ at quantile ($t=0.25$).

➢

For population 2, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=5$ have a minimum value of MSE for $H_{A_5{\left(L\right)}_1}=0.00171219$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{A_4{\left(U\right)}_1}=0.00430275$ at quantile ($t=0.50$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=1$ have a minimum value of MSE for $H_{P_1{\left(L\right)}_1}=0.00029563$ at quantile ($t=0.75$) and $H_{P_i{\left(U\right)}_1}$ for $i=5$ has a minimum value of MSE for $H_{P_5{\left(U\right)}_1}=0.00051865$ at quantile ($t=0.50$).

➢

For population 3, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{A_2{\left(L\right)}_1}=0.00248699$ at quantile ($t=0.75$) and $H_{A_i{\left(U\right)}_1}$ for $i=2$ has a minimum value of MSE for $H_{A_2{\left(U\right)}_1}=0.00702091$ at quantile ($t=0.50$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{P_4{\left(L\right)}_1}=0.00013009$ at quantile ($t=0.25$) and $H_{P_i{\left(U\right)}_1}$ for $i=5$ has a minimum value of MSE for $H_{P_5{\left(U\right)}_1}=0.00076808$ at quantile ($t=0.25$).

➢

For population 4, the lower and upper values of the adapted neutrosophic estimator $H_{A_i{\left(L\right)}_1}$ for $i=4$ have a minimum value of MSE for $H_{A_4{\left(L\right)}_1}=0.02110268$ at quantile ($t=0.50$) and $H_{A_i{\left(U\right)}_1}$ for $i=3$ has a minimum value of MSE for $H_{A_3{\left(U\right)}_1}=13.02999000$ at quantile ($t=0.50$). The lower and upper values of the proposed neutrosophic estimator $H_{P_i{\left(L\right)}_1}$ for $i=2$ have a minimum value of MSE for $H_{P_2{\left(L\right)}_1}=0.00112126$ at quantile ($t=0.50$) and $H_{P_i{\left(U\right)}_1}$ for $i=4$ has a minimum value of MSE for $H_{P_4{\left(U\right)}_1}=0.00147402$ at quantile ($t=0.25$).

➢

The same pattern of the proposed neutrosophic estimators PRE’s for a 15% sample size can be seen in Table 23, Table 24, Table 25 and Table 26 for all $i=1,2,3,4,5$.

➢

A visual representation of MSE’s results based on a 15% sample size is provided in Figure 9, Figure 10, Figure 11 and Figure 12.

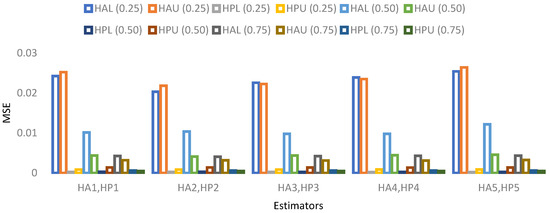Figure 9. MSE for population 1 when sample size is 15%.

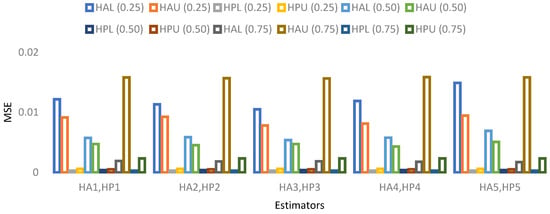Figure 10. MSE for population 2 when sample size is 15%.

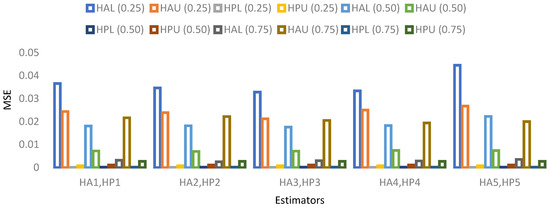Figure 11. MSE for population 3 when sample size is 15%.

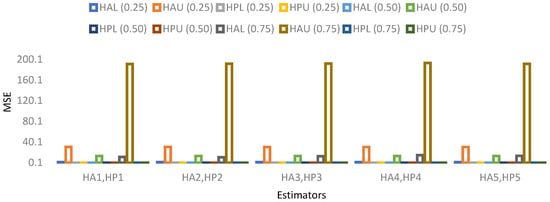Figure 12. MSE for population 4 when sample size is 15%.

After analyzing the performance of all the neutrosophic estimators, it can be concluded that the proposed neutrosophic class outperforms the adapted neutrosophic estimators in all four symmetric and asymmetric populations, with the lowest MSEs and the highest PREs values.

5. Conclusions

This work aims to adapt the neutrosophic calibration estimation of CDF derived by StRS when supplementary information and neutrosophic studies are present. The distinctive feature of neutrosophic outcomes is the presence of values that are ambiguous, unclear, or uncertain. The traditional CDF approach gives single-valued outcomes, which are often not accurate, mostly in neutrosophic value. In this paper, a novel calibration estimation of CDF using a neutrosophic approach is suggested under StRS. We performed simulation research utilizing real-world symmetric and asymmetric datasets to evaluate the effectiveness of the proposed neutrosophic calibrated estimators with the adapted neutrosophic calibrated estimators. For the neutrosophic calibration estimators, we calculate the PREs and MSEs. The outcomes show that the recommended estimators outperform the adapted estimators in terms of effectiveness. In future research, the study can be built to incorporate other sampling methodologies, and novel ideas can be contrasted to past techniques. In future studies, the work can be extended under ranked set sampling, as suggested by [30].