A 3D Descriptive Geometry Problem-Solving Methodology Using CAD and Orthographic Projection

Abstract

In solving descriptive geometry (DG) problems, board (i.e., hand drawing) methods are frequently used, despite this discipline is still very important to enhance spatial vision. These methods are very different from CAD tools which are used in the field of design. CAD facilitates the realization of geometric constructions and transformations (i.e., rotation, translation, copying, scaling, alignment, and symmetry, among others) are performed analytically. For this reason, a 3D DG problem-solving methodology using CAD and orthographic projection (CADOP) is introduced. Once the principles of DG, orthographic projection, and CAD fundamentals and tools are described, CADOP is applied to obtain (i) orthogonal views; (ii) principal lines of a plane; (iii) true-size view of a plane; (iv) parallelism, perpendicularity, and distance, and (v) angles. Considering the user coordinate system in CADOP allows one to place the horizontal plane in the suitable position to solve DG problems directly in one step. In the traditional methods, the use of auxiliary views must be carried out in several steps instead. The dynamic management of the 3D view of the scene is facilitated in CADOP, improving its understanding, and achieving the precision inherent in analytical calculations.

1. Introduction

Currently, the contents of technical graphics in engineering are plane geometry and construction, descriptive geometry, analytic geometry, standards and conventions, and CAD. These contents provide the engineer with the necessary ability to represent and interpret the information contained in the plans. In addition, knowledge of all these subjects helps students to reach the necessary skills that allow them to have spatial vision and solve 2D and 3D problems.

This article focuses on descriptive geometry (DG). DG is the graphical representation of plane, solid, and analytical geometry used to describe real or imagined devices and technical objects. It is the science of graphic representation in engineering design that forms the basis of technical drawings [1]. DG comprises a set of geometric techniques that allow 3D space to be represented on a plane. Therefore, it is possible to solve spatial problems in 2D in such a way that the reversibility of the process is guaranteed.

The French mathematician Gaspard Monge (1746–1818) organized and developed the foundations of DG in his book Géométrie Descriptive (1798). It is considered the first DG exposition and formalization of orthographic projection (OP) which is a direct view method, sometimes called the natural method. When using OP, the observer is placed at an infinite distance from the object, with their parallel lines of sight perpendicular to the plane of projection. Monge used methods of revolution and orthographic projection to solve design problems associated with complex star-shaped military fortifications in France. Monge’s reference system consisted of a vertical plane (V) and a horizontal plane (H) that intersected at a ground line. At the beginning of the 20th century, in the USA, the direct method was developed by Adam V. Millar. He exposed this method at the University of Wisconsin in 1908. Since then, it has been widely used. Here, the reference planes do not have a fixed position and therefore the ground line is not used. The first book on the direct method was written in 1913 by Millar and Maclin, although without including auxiliary projections, which were added in the second edition published in 1919 in collaboration with Marguardf. Professor G.J. Hood published Geometry of Engineering Drawing in 1926, a work in which this modality of exposition of Monge’s system was named for the first time as a direct method.

The fundamentals of technical graphics have not significantly changed since Monge’s time. However, the methods and tools, as well as the standards and conventions, have changed in the past two centuries, using CAD instead of drafting tools such as the T-square and compass. Until CAD technology was developed and widely adopted as a graphical tool, three traditional methods were used to solve spatial design problems through the application of DG: the direct view method, the revolution method, and the fold-line method. In certain cases, one method may be preferred over another because of its ease in determining the solution to the problem.

Although DG is a very important discipline in enhancing spatial vision [2], the growing development of CAD software has made its classical hand-drawing methods outdated [3,4,5,6,7]. CAD programs have several commands that allow one to perform location and identification procedures without building elaborated geometric constructions. To solve DG problems using CAD, a 3D model is created, and the appropriate commands applied on it. This fact has some advantages comparing to hand-drawing methods traditionally used. Thus, CAD facilitates the conversion of a shape defined in the projective space of a computer in digitized coordinate form via transformations to give parallel projections perspective views. According to [8], these are all carried out in terms of the real spatial geometry, referred to as the primary geometry, and not in terms of vanishing points, or the general secondary geometry. The application of the spatial manipulation of primary geometry, called constructional graphics by [9], in engineering computer graphics is stressed by the need to exploit spatial constructions in engineering graphics problem solving. On the other hand, geometric transformations such as rotation, translation, copying, scaling, alignment, and symmetry are easily carried out with CAD, which performs these operations analytically [10].

The learning process in engineering is constantly reconsidered [11] to improve the educational results of students, selecting and applying new methods that make the subjects more attractive. In the teaching of DG, Virtual Reality (VR) and Augmented Reality (AR) have been used as innovations to facilitate spatial vision. In the case of VR, the works that describe the use of Anaglyphs for this purpose are especially interesting [12,13]. The interactivity, the 2D and 3D visualization of the same object, and the low cost of executing the project [14,15] make the use of VR through CAD suitable for teaching DG. Furthermore, VR is easily adaptable to the remote teaching of DG in engineering [16]. The introduction of 3D virtual models in CAD has increased student interest in DG and assimilation indicators have improved [17,18]. Research on the use of AR in education has received much attention in recent years [19,20]. Its effectiveness for the visualization of spatial objects is promising in disciplines whose assimilation requires a complex spatial representation [21,22]. These disciplines include the engineering graphics used in DG [23], facilitating a favorable evolution in their understanding [24,25].

VR and AR have helped to acquire spatial vision and understand theoretical content [26], but they are not efficient in solving DG problems. In addition, these methods require the laborious preparation of teaching material and need advanced technology that, despite offering fully immersive and collaborative interaction, is very expensive [27]. On the other hand, these methods are very different from the CAD tools that the future engineer will use in the field of design and technical drawings. This fact has been the main reason why the combined use of CAD and OP is proposed in this work to solve the different problems that arise in DG, having as target users people involved in engineering graphics learning. In addition, the methodology introduced here connects knowledge about the fundamentals of DG and the use of CAD. This fact may help to overcome the lack in the understanding of the principles of descriptive geometry sometimes found in CAD users.

2. Materials and Methods

Before developing this section, the theoretical principles of DG [1] that will be addressed with CAD and orthographic projection (CADOP) are exposed:

• Orthogonal views.
• Three-dimensional definition and creation of the plane main lines.
• Defining and creating views to show the true magnitude of lines and plane figures.
• Identifying, defining, and creating lines: intersecting, parallel, and perpendicular.
• Determining the angle between two coplanar lines, line and plane, and two planes.

The basic elements used in these principles are the point, line, and plane. Next, brief conceptual definitions of these geometric primitives are exposed.

Point is defined as (i) a specific position in space, (ii) the end of a line, and (iii) the intersection of two lines.

Line has no thickness, only length and direction. A line can graphically represent (i) the intersection of two planes, (ii) the limiting element of a surface, or (iii) the edge view of a plane surface. Theoretically it is unlimited, and it is common to define it by two points (straight segment).

Plane is, theoretically, unlimited. In practice, to work with planes, the elements that define them are used: (i) three non-aligned points, (ii) two intersecting lines, (iii) two parallel lines, and (iv) a line and a point outside it.

CAD allows the use of the direct view and revolution methods. In direct view, the user can specify the desired view and the lines of sight will be placed perpendicular to the geometry in question. This is the orthographic projection. The revolution method can be easily applied with CAD, unlike traditional and manual methods, by keeping the reference system fixed and rotating the geometry to the desired position. The CADOP methodology uses both methods. This section ends by explaining the combination of the tools available in CAD with OP that gives rise to the CADOP methodology proposed to solve DG problems. The CAD system used in this work is Autodesk AutoCAD 2024. A reason for working with this graphic design tool is because it is highly demanded in the development of the professional activity of an engineer. Thus, the knowledge of AutoCAD is widely spread. In addition, access to these tools is guaranteed thanks to the educational versions available.

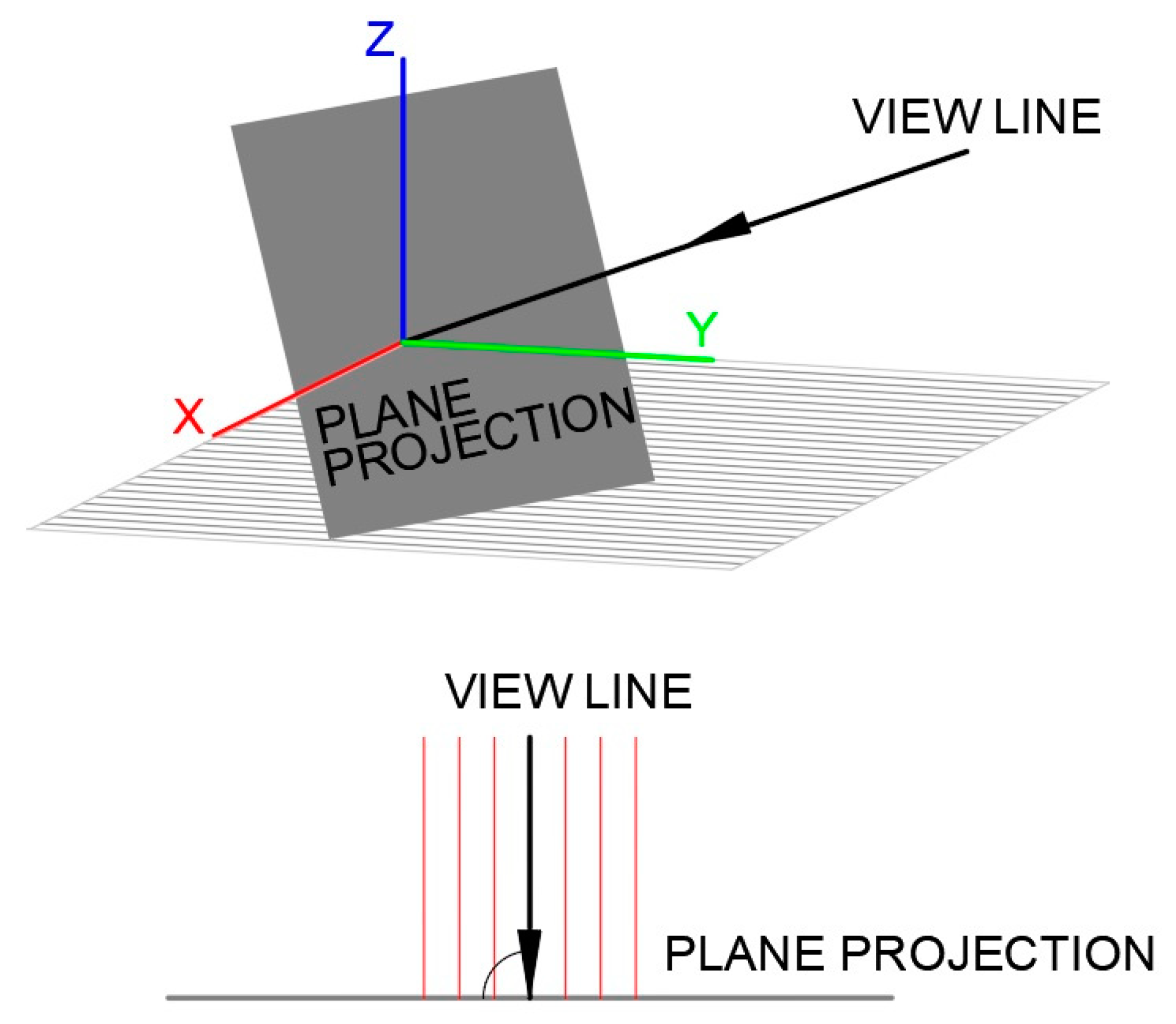
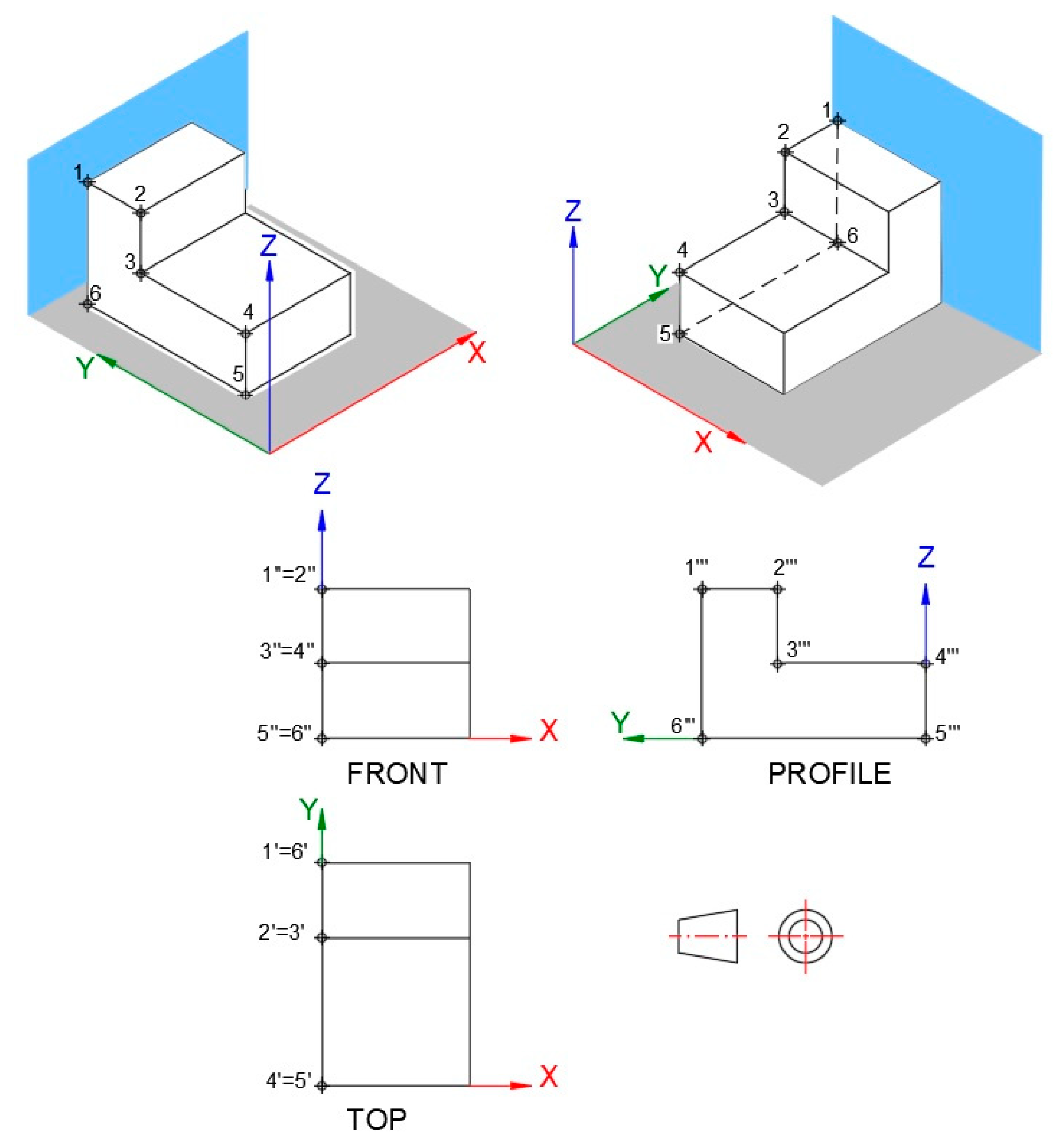
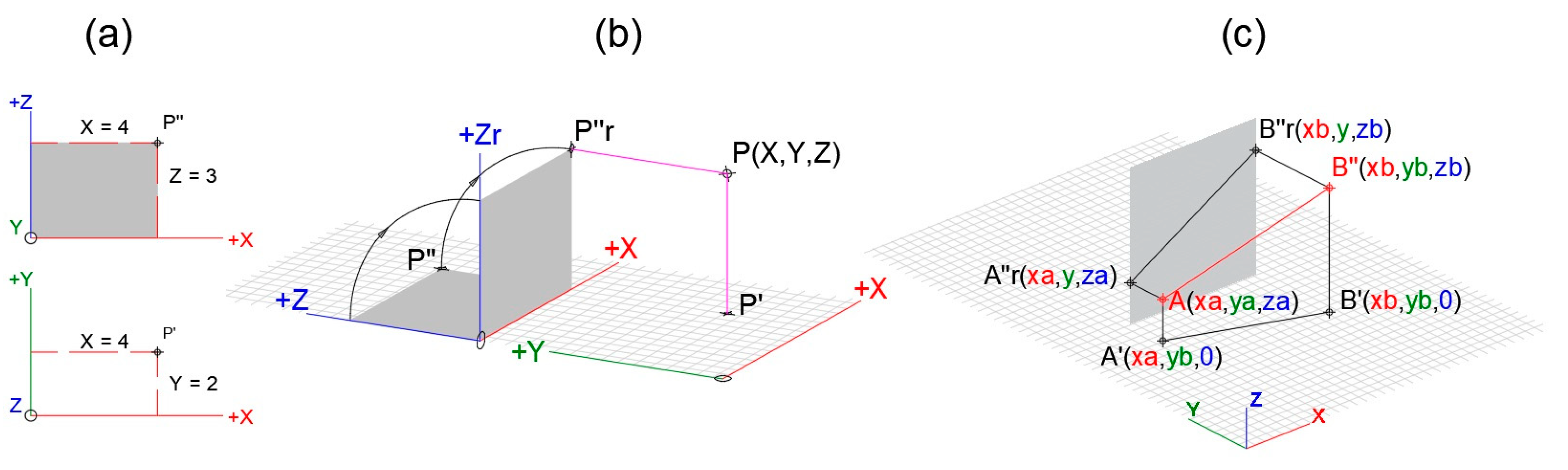
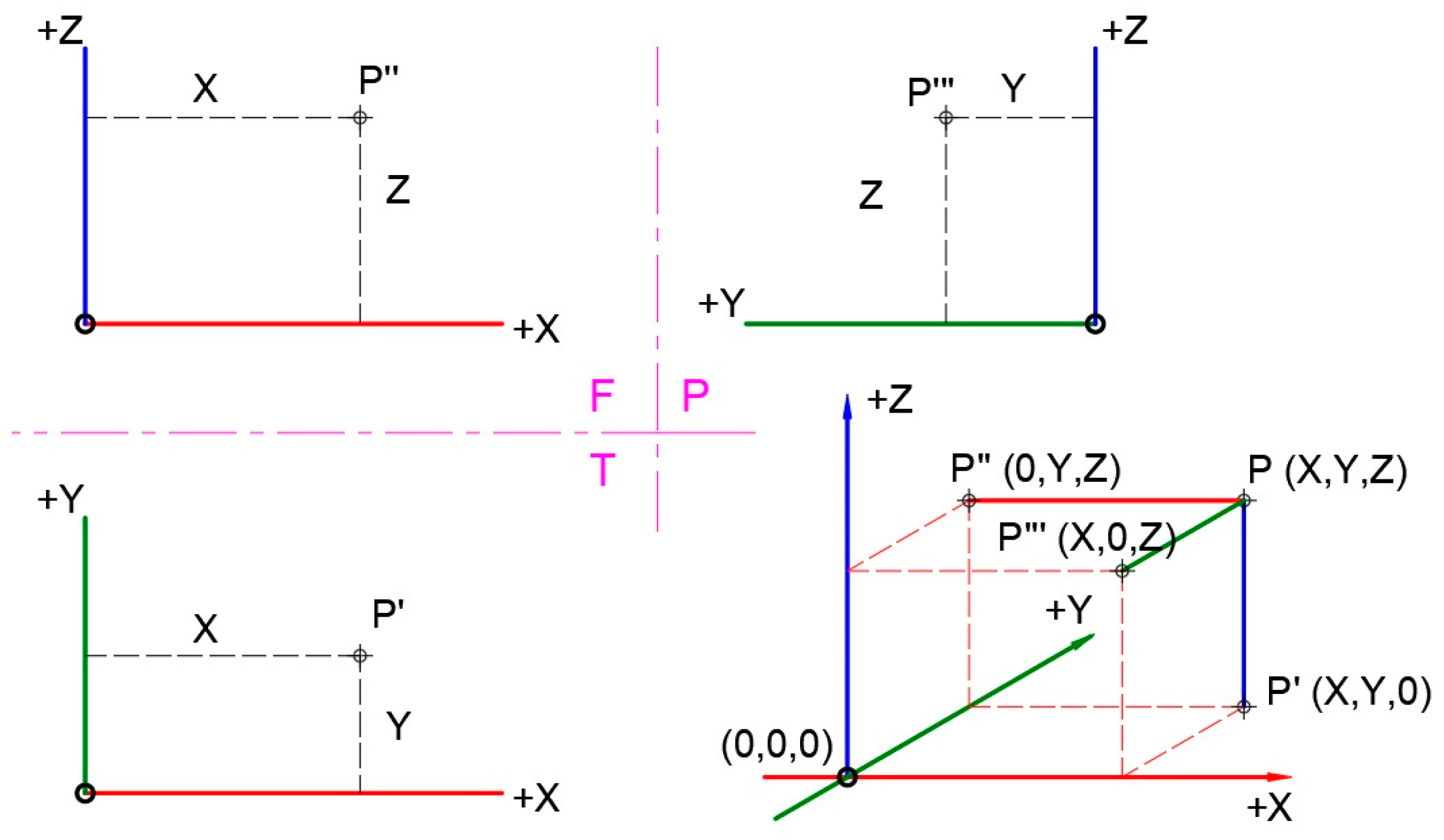
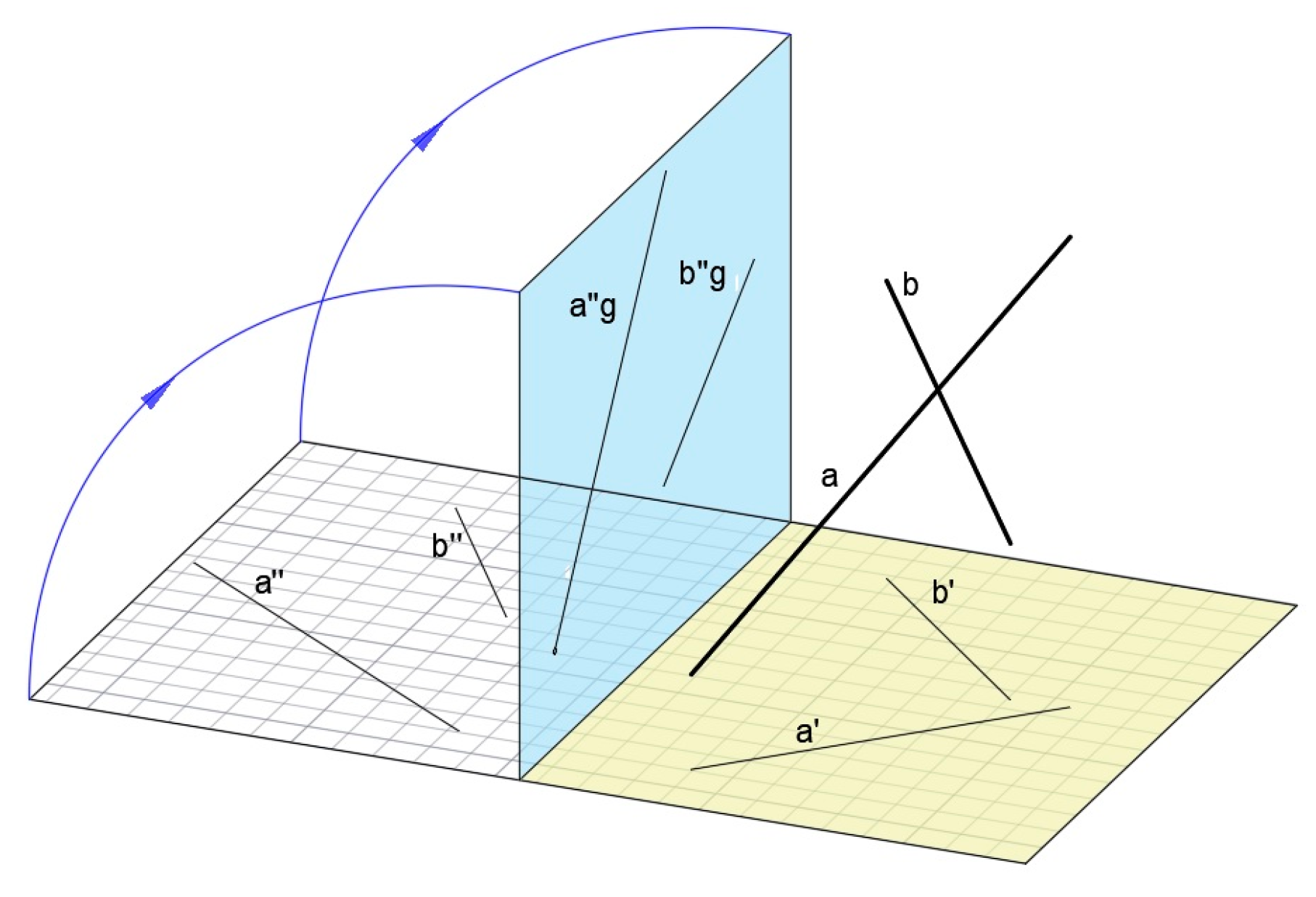
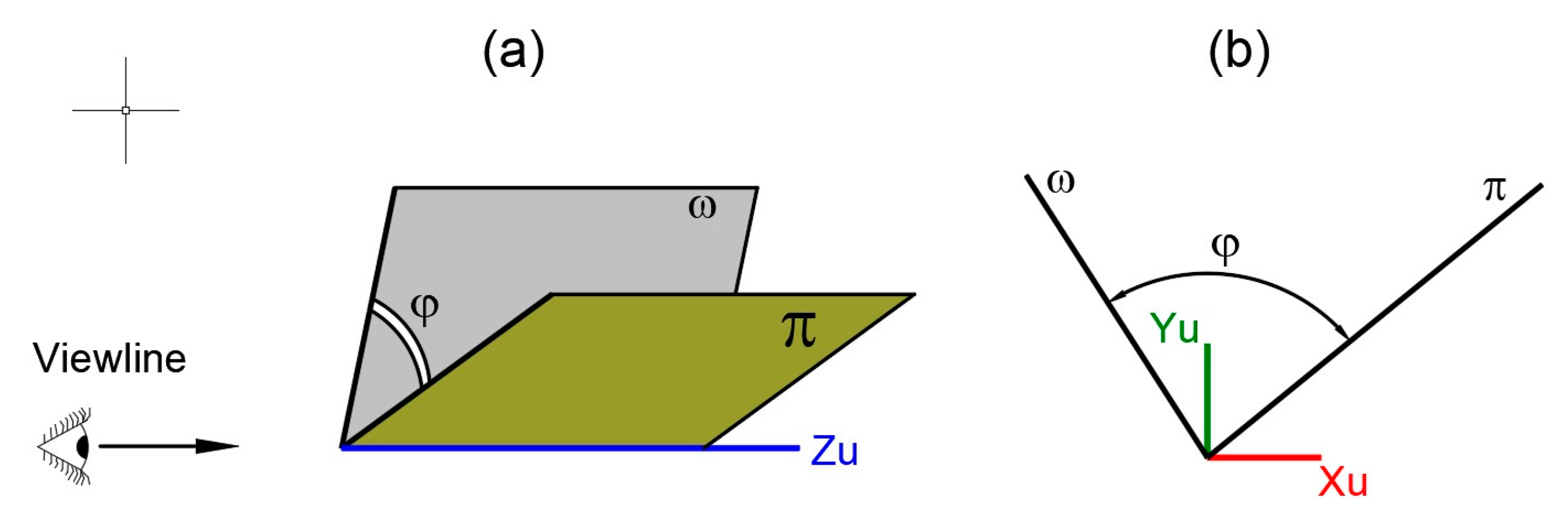
2.1. Orthographic Projection Fundamentals

For OP, the horizontal or top view, the front view, and the profile or side view correspond to X, Y (Z = 0), X, Z (Y = 0), and Y, Z (X = 0) coordinates, respectively. For example, Figure 1 shows the views of the face with n vertices defined by coordinates (X_n, Y_n, Z_n), n ∈ [1, 6]. Thus, the top view corresponds to the X_n, Y_n, the front view to X_n, Z_n, and the side view to the Y_n, Z_n coordinates.

2.2. CAD Fundamentals

The CAD fundamentals used here to solve 2D and 3D DG problems are the following: (i) reference system; (ii) point of view; (iii) change of coordinate system; and (iv) graphic windows.

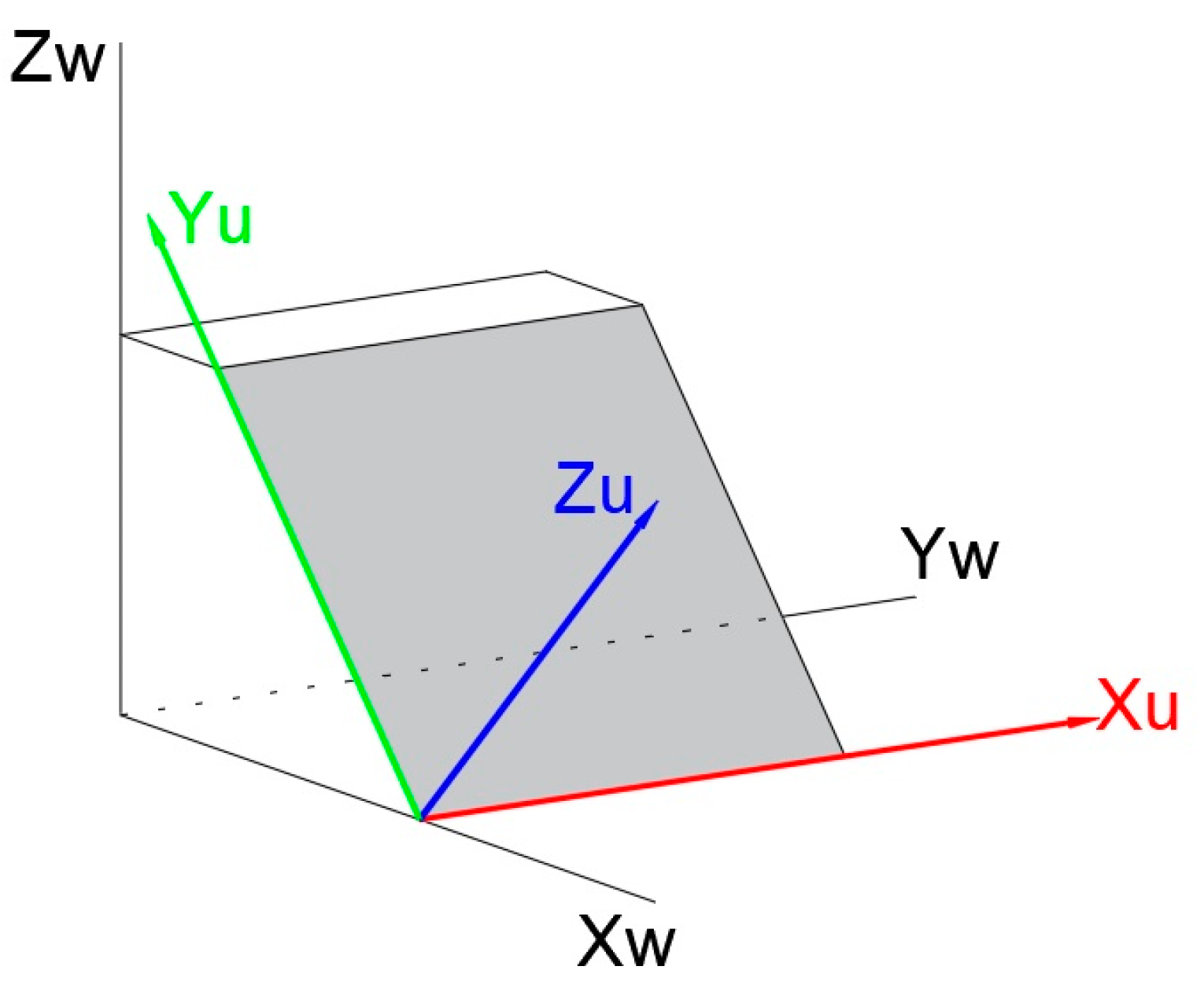
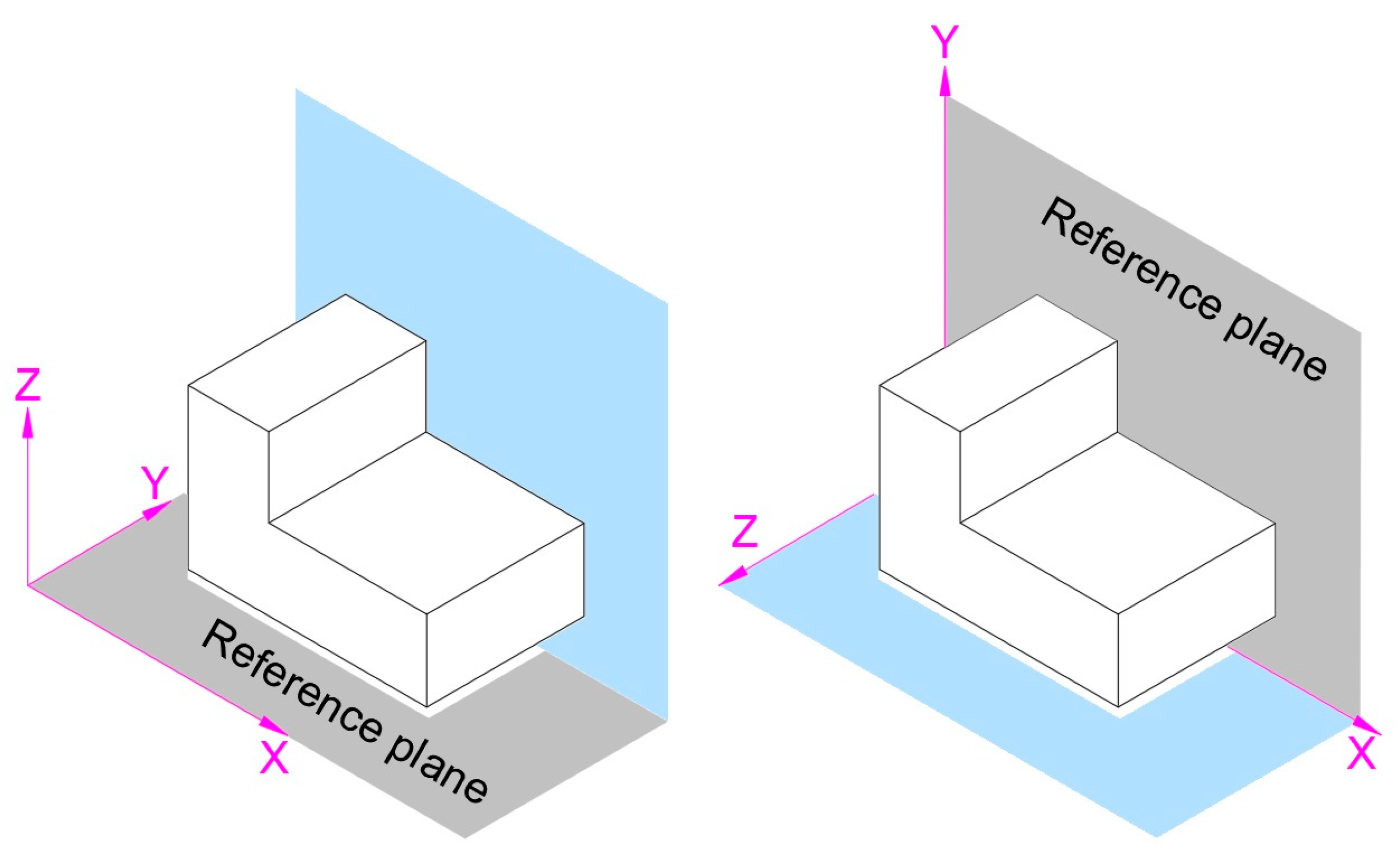
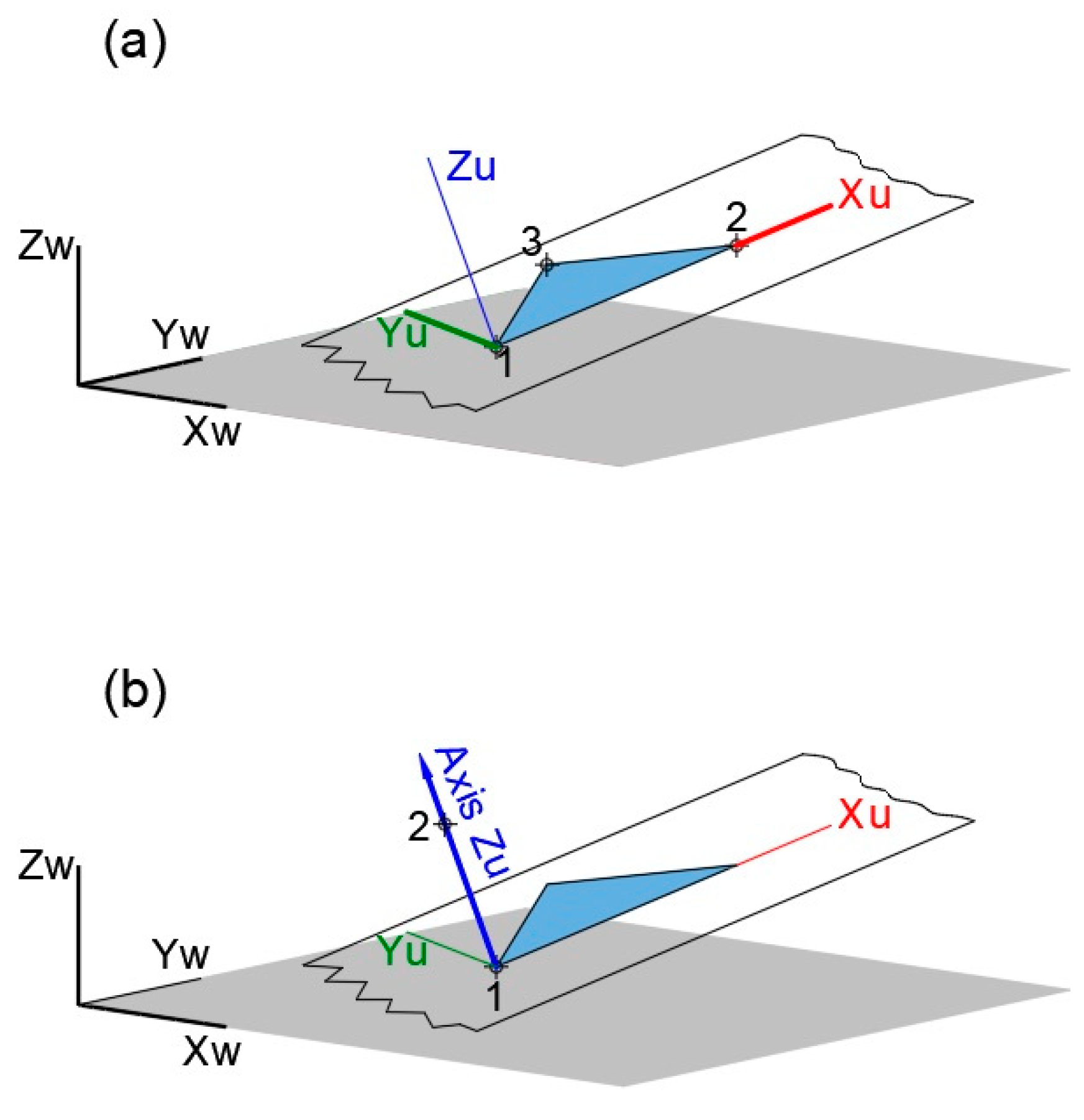
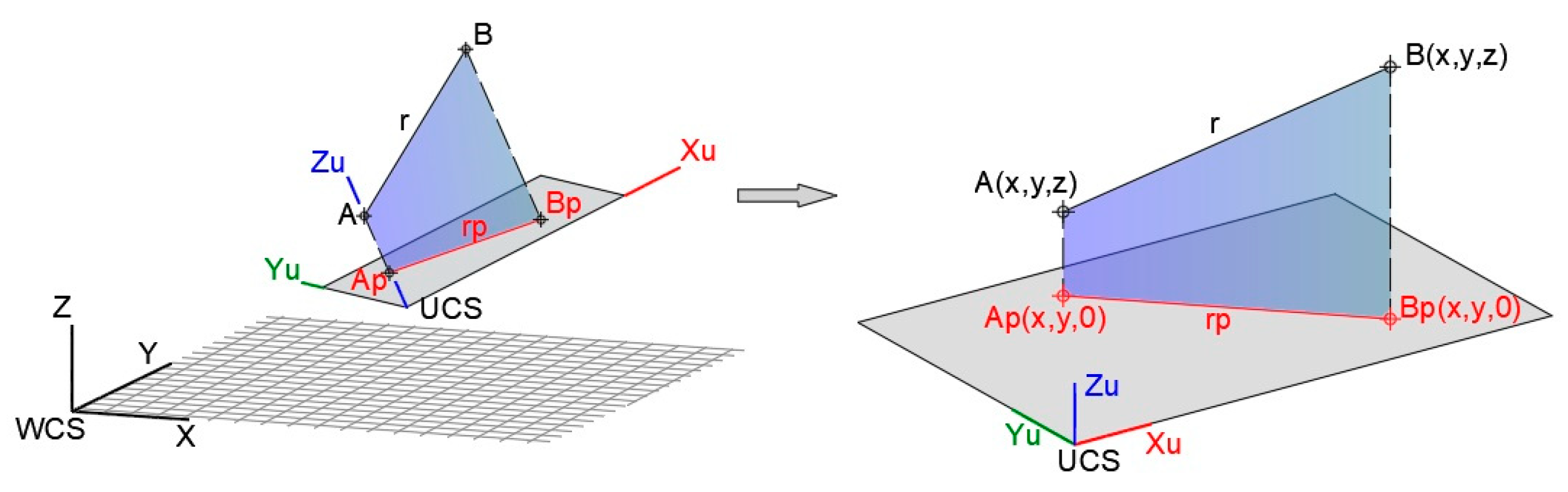
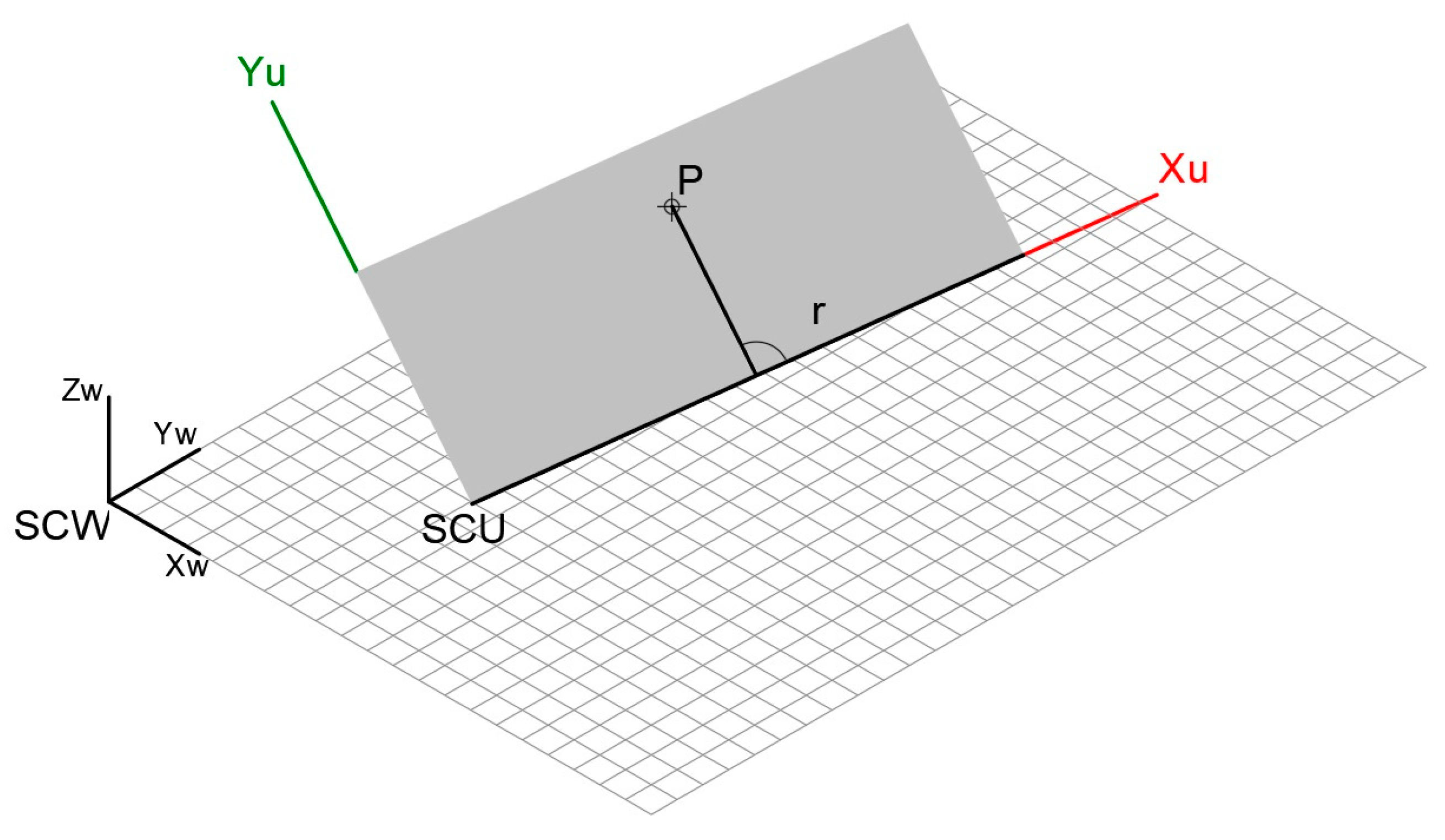
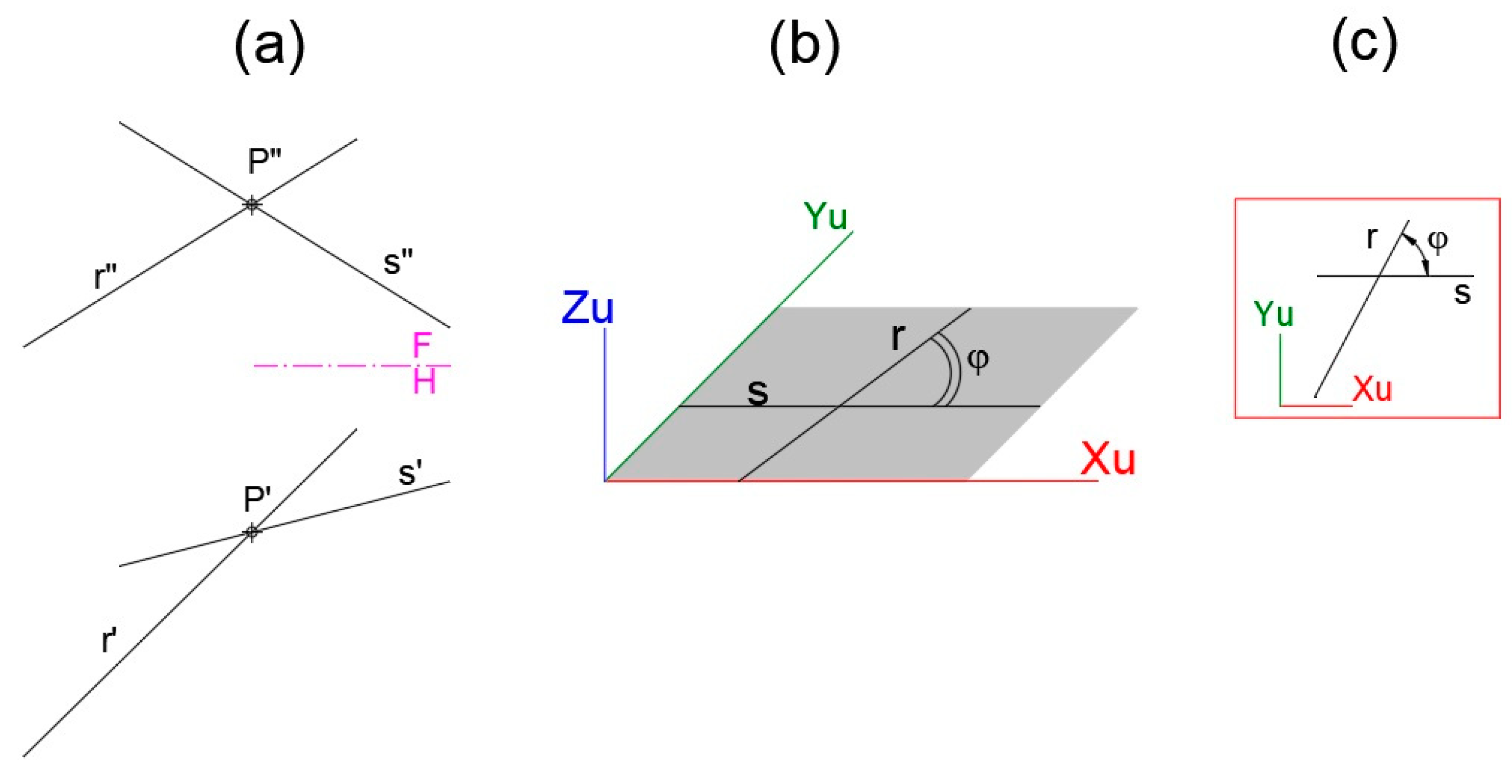
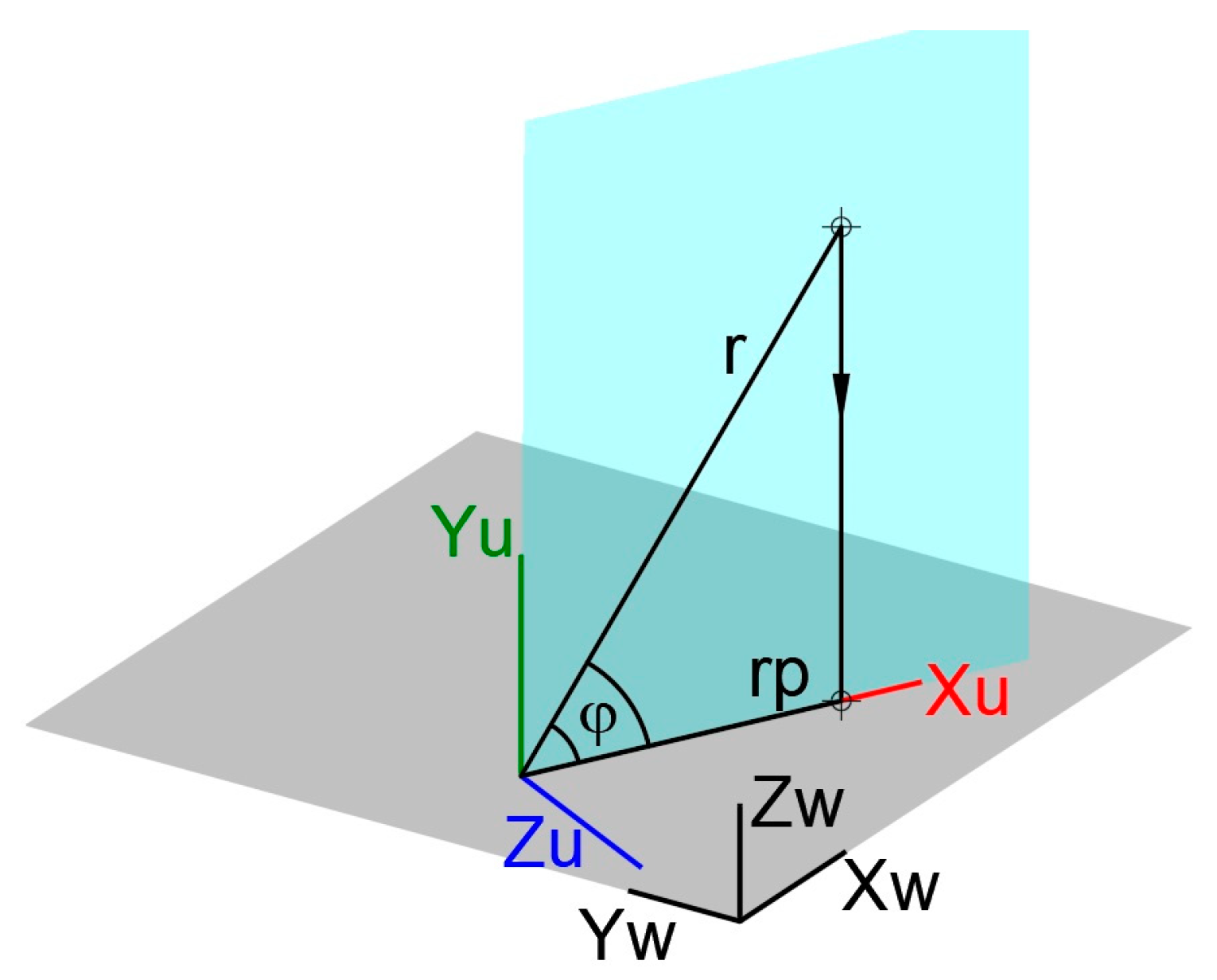
2.2.1. Reference System

Defining the reference system is the first step to obtaining the OP views. This reference system consists of the following components: world coordinate system (WCS), user coordinate system (UCS), reference plane, and coordinate system.

• World and User Coordinate Systems

WCS is a fixed Cartesian coordinate system which is the reference for any other UCS. The latter is a mobile Cartesian coordinate system that establishes the XY reference plane, horizontal and vertical directions, and rotation axes (Figure 2).

Once the reference plane is defined, the Z axis is determined by applying the right-hand rule. This rule is also used to specify the direction of positive rotation about each axis.

• Reference Plane

A reference plane is considered for solving 3D problems with CAD. It can be placed anywhere, and all the coordinates are determined with respect to this plane. Figure 3 shows reference planes for two different positions. Frequently, the position of the reference plane is chosen to facilitate DG troubleshooting.

• Coordinate system

The Cartesian coordinate system is used as a reference for the WCS and UCS in CAD. Any point can be located by describing its location with respect to the three axes X, Y, Z. These axes have the coordinate system origin (0, 0, 0) as their intersection point. Figure 4 shows the Cartesian representation of a point P (4, 2, 3), that is, find 4 units on the X axis, 2 on the Y axis, and 3 on the Z axis.

2.2.2. Viewpoint

The point of view defines the line of sight or line of projection of a 3D visualization. The 2D view from a 3D scene is obtained by means of orthographic projection. It is created on a plane perpendicular to the viewing direction (Figure 5).

Figure 6 shows different points of view for the same orientation of the object with respect to the WCS. As can be seen, the projection on the horizontal, vertical, and profile planes does not change, since the WCS remains fixed in both cases.

2.2.3. User Coordinate System

A new UCS can be defined in a simple way to attain suitable objects’ position to solve DG problems. As mentioned before, the reference plane is the XY. Therefore, a change in coordinate system implies a new definition of this plane. One frequent way to define the XY reference plane of the UCS is by means of three non-aligned points, in which the first point is the origin of coordinates, the second indicates the Xu axis positive direction and the third determines the Yu axis positive direction; the Zu axis is perpendicular to the reference plane according to the right-hand rule (Figure 7a). The XY reference plane can also be defined by using the Zu axis in such a way that the first point is the origin of the UCS, and its direction is determined by a second point. The XuYu reference plane is perpendicular to this Zu axis (Figure 7b).

2.2.4. Viewports

CAD allows one to create different viewports. Each viewport can have different display settings, making it easy to find different viewpoints, projections, and scales of the same model. Thus, the necessary views in a single work plane can be shown. Three viewports with different views and scales are shown for the same model in Figure 8.

2.3. CAD Tools

2.3.1. Rotation

Once the point of view is set, CAD helps to obtain different projections of an object by rotating it. Figure 9 shows the initial (a) and rotated (b) positions of a solid with respect to the WCS for the same point of view. This rotation implies different orthographic projections on the coordinate planes.

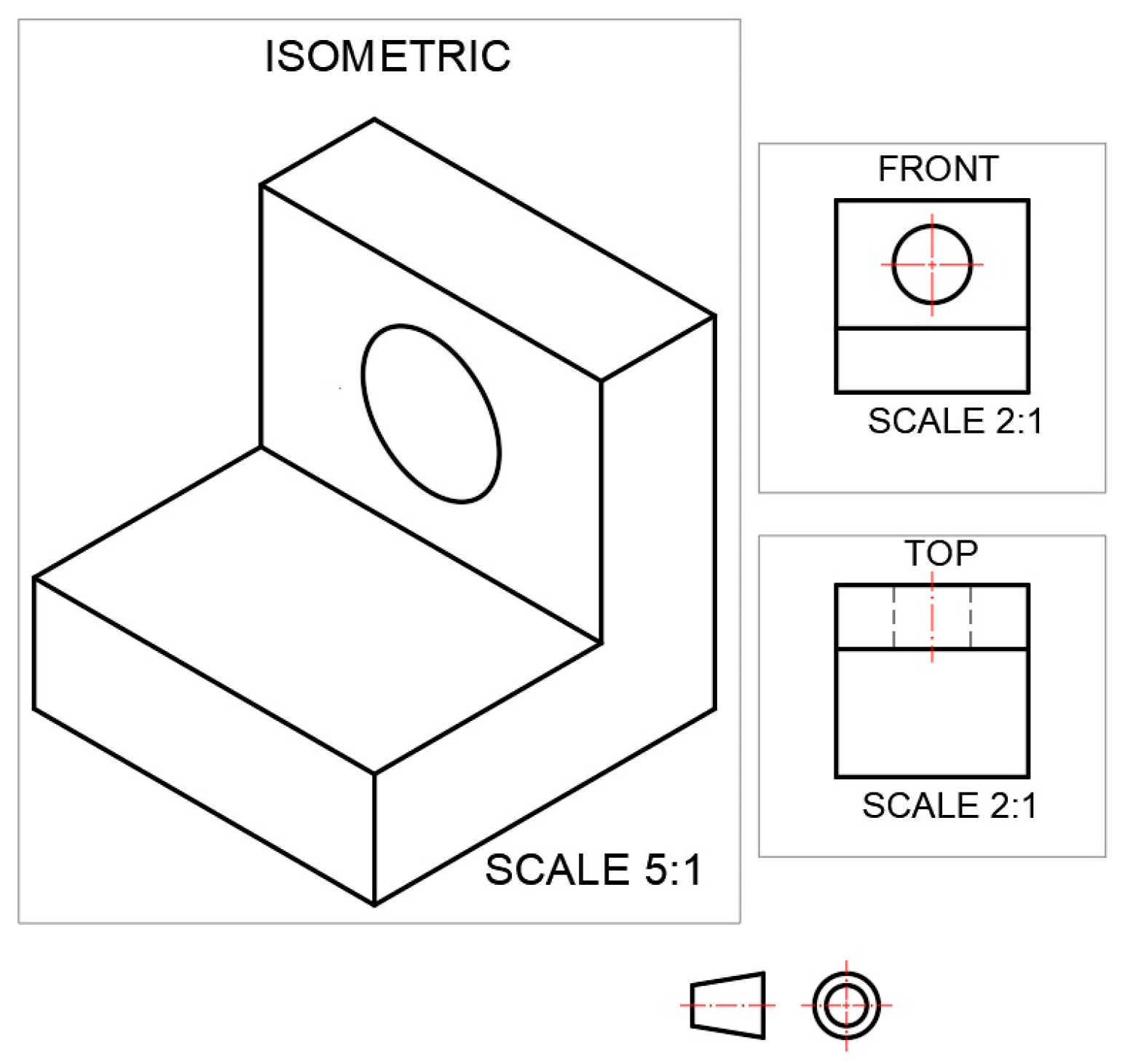
2.3.2. First-Angle and Third-Angle Projection

Once the problem has been solved in 3D, CAD allows one to obtain standard views. There are two types of view layouts, called first-angle projection (used in Europe and other countries), shown in Figure 10 top, and third-angle projection (used in the USA and Canada), shown in Figure 10 bottom.

2.3.3. Point Filters

CAD point filters are very useful when requesting the location of a point, as the software allows one to combine X, Y, Z values from different point projections to specify a single point. It is possible to obtain the point 3D position from at least two orthographic projections. The orthographic projection of a point is shown in Figure 11a where the X, Y, Z coordinates with respect to the WSC are indicated. The 3D position of the point can be obtained using the point filters. To do this, a 90° rotation must be carried out around the X axis (or an axis parallel to it) of the front projection (Figure 11b). This allows the spatial coordinates of the point to be known. The X, Y coordinates are obtained from the top projection and the Z coordinate from the rotated front projection. Figure 11c shows the use of filters to obtain the spatial position of an oblique line, applying the procedure described above to the points that define it.

3. Results

The application of CADOP is shown in this section to verify the theoretical principles of DG mentioned before.

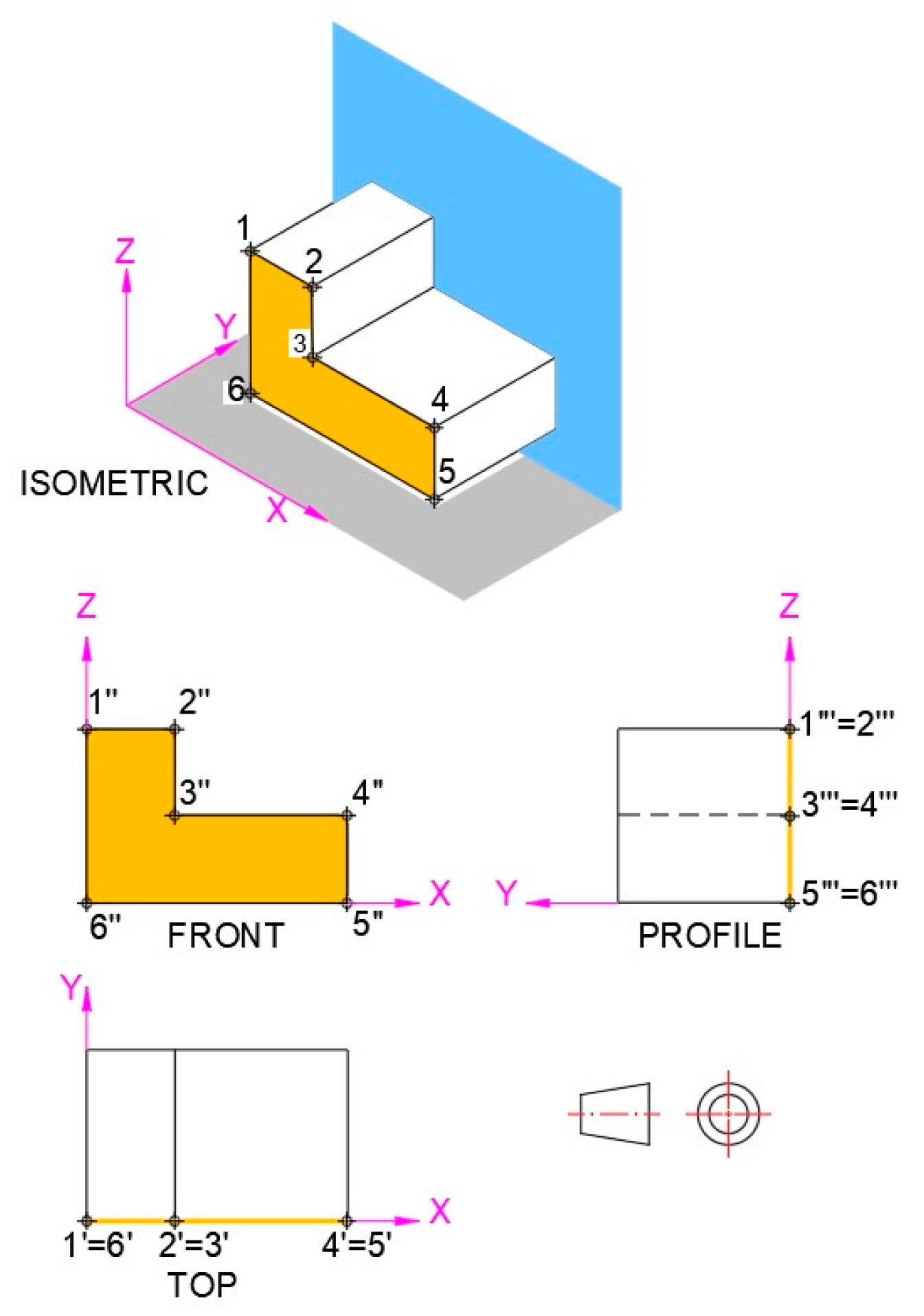
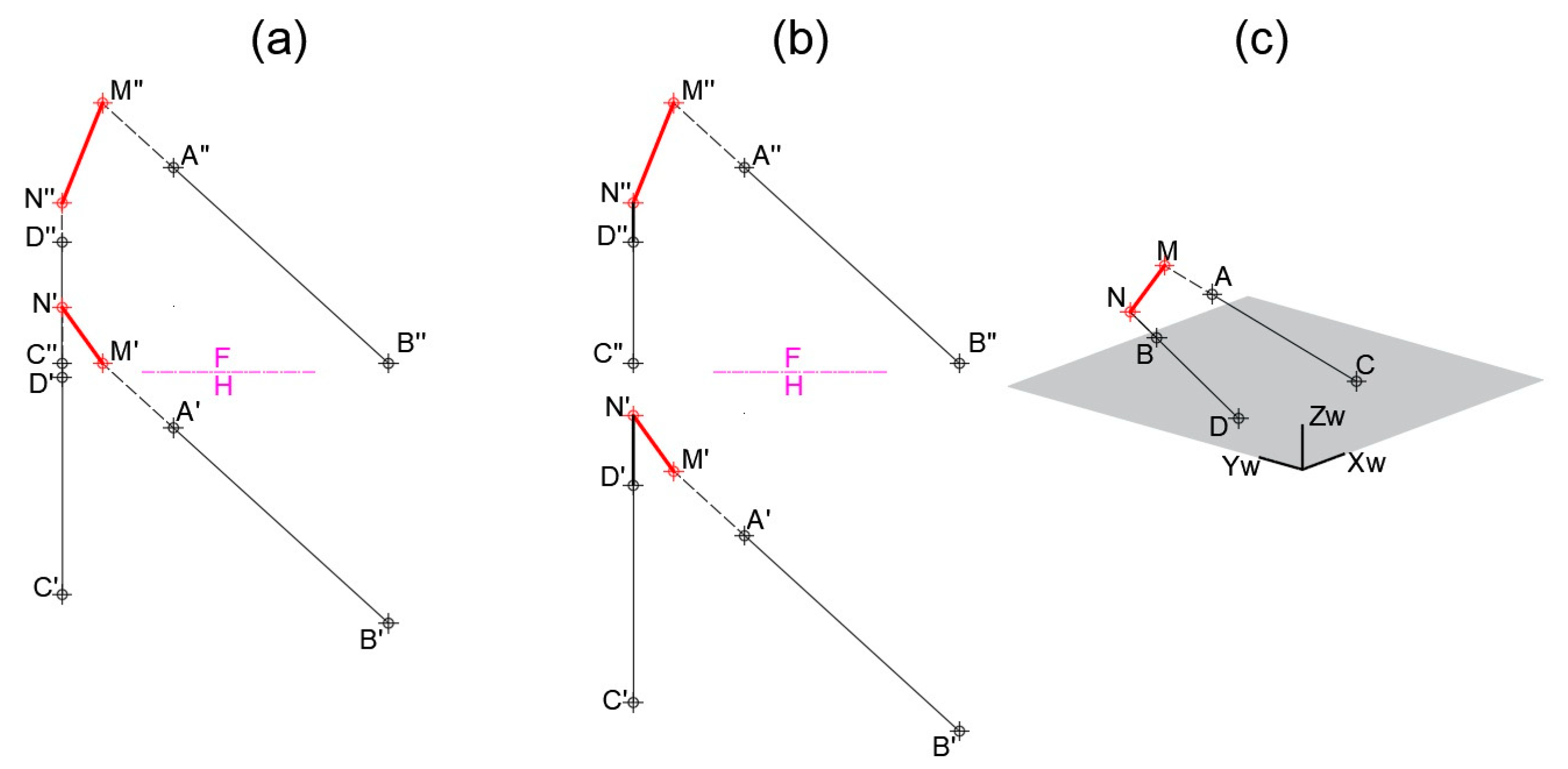
3.1. Orthogonal Views

The projection on the XY, XZ, YZ coordinate planes, which correspond to the standard top, front, and profile views, is an application of the orthogonal views. Setting the corresponding coordinate to 0 is enough. In this way, a point with coordinates (X, Y, Z), would have the coordinates (X, Y, 0) as its top view, the front view would be (X, 0, Z), and the profile (0, Y, Z), as shown in Figure 12.

The determination of the line projection on an oblique plane with respect to the WCS is another orthogonal view application. The oblique plane must be set as the XY plane of the new UCS. After that, the Zu coordinates of the segment ends are 0. Figure 13 shows the procedure.

The reversibility of the system allows the spatial position of a geometric element from two views to be determined. As is shown in Figure 14, the spatial position of an object can be restored from the top and front views by using the coordinate filters and 3D rotation. Figure 14a shows the projections of line AB. By rotating the front view 90° around the X axis and applying the coordinate filters, the line spatial position can be easily obtained (Figure 14b).

This procedure is essential, since it allows the spatial position of the objects represented in 2D to be obtained before solving the 3D problem with CADOP. Once solved, the solution views can be obtained.

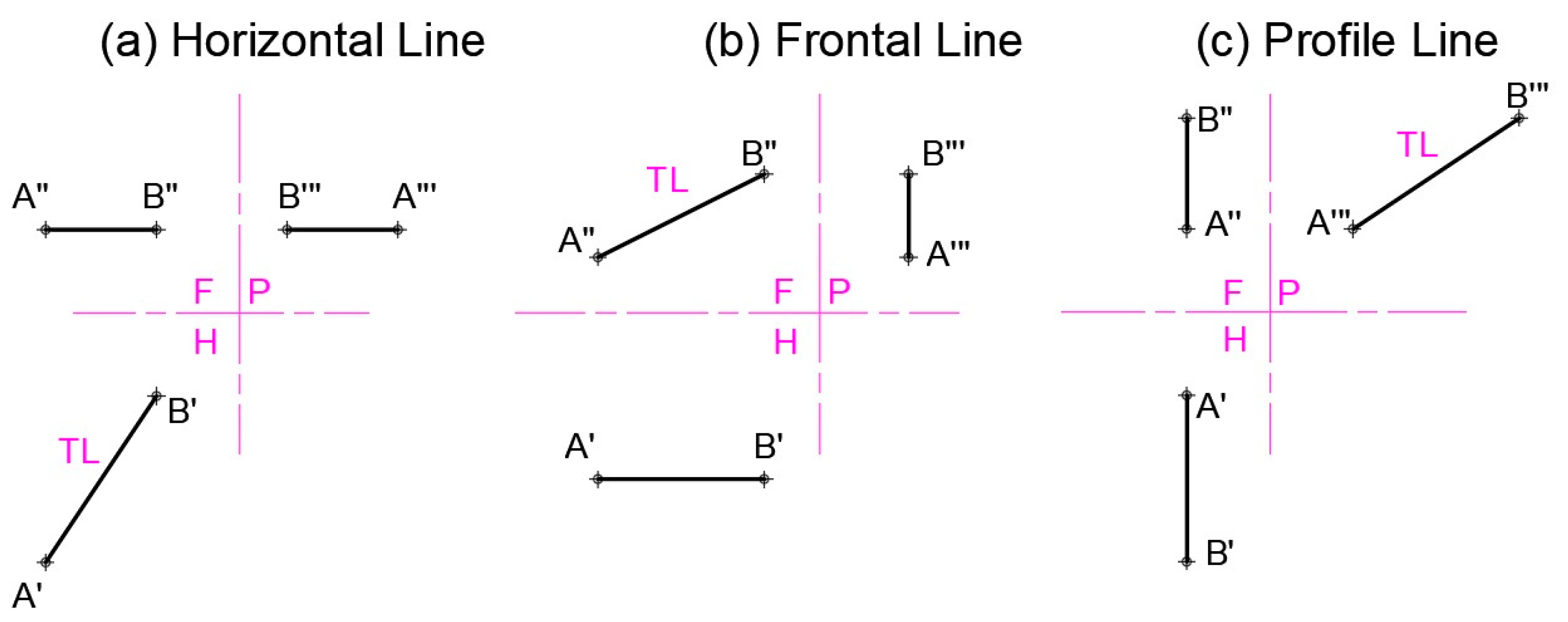
3.2. Identifying, Defining, and Creating Principal Lines of a Plane

Depending on their orientation with respect to the WCS, the lines can be horizontal (parallel to the XY plane), frontal (parallel to the XZ plane), and profile (parallel to the YZ plane). When they are not in any of these positions, they are called oblique lines. The horizontal, frontal, and profile lines are important since they allow us to know the true length (TL) and coordinate angles (angles formed by the line with the UCS reference planes). It is described below how to obtain a horizontal, frontal, and profile line from an oblique line using CADOP. To set it as horizontal line, it is enough to rotate the front view until the line is horizontal, as can be seen in Figure 15a. As its spatial position is rotated, its top and profile views are automatically updated. The front line (Figure 15b) is obtained by rotating the top view until it is horizontal. The profile line (Figure 15c) is obtained from the horizontal or frontal line; in this case, the horizontal line shown in Figure 15a has been considered.

Next, the determination of the principal lines through a point belonging to an oblique plane is described. With this aim, the intersection of surfaces is calculated applying CADOP. Thus, Figure 16a shows the horizontal line of the plane obtained through point A. To do this, a flat surface parallel to the XY plane is created through the point; the intersection of the plane and this surface determines the horizontal line h. By drawing surfaces parallel to the XZ and ZY planes, the frontal and profile lines are obtained, respectively. Figure 16b shows the frontal line f through point B yielded by this procedure.

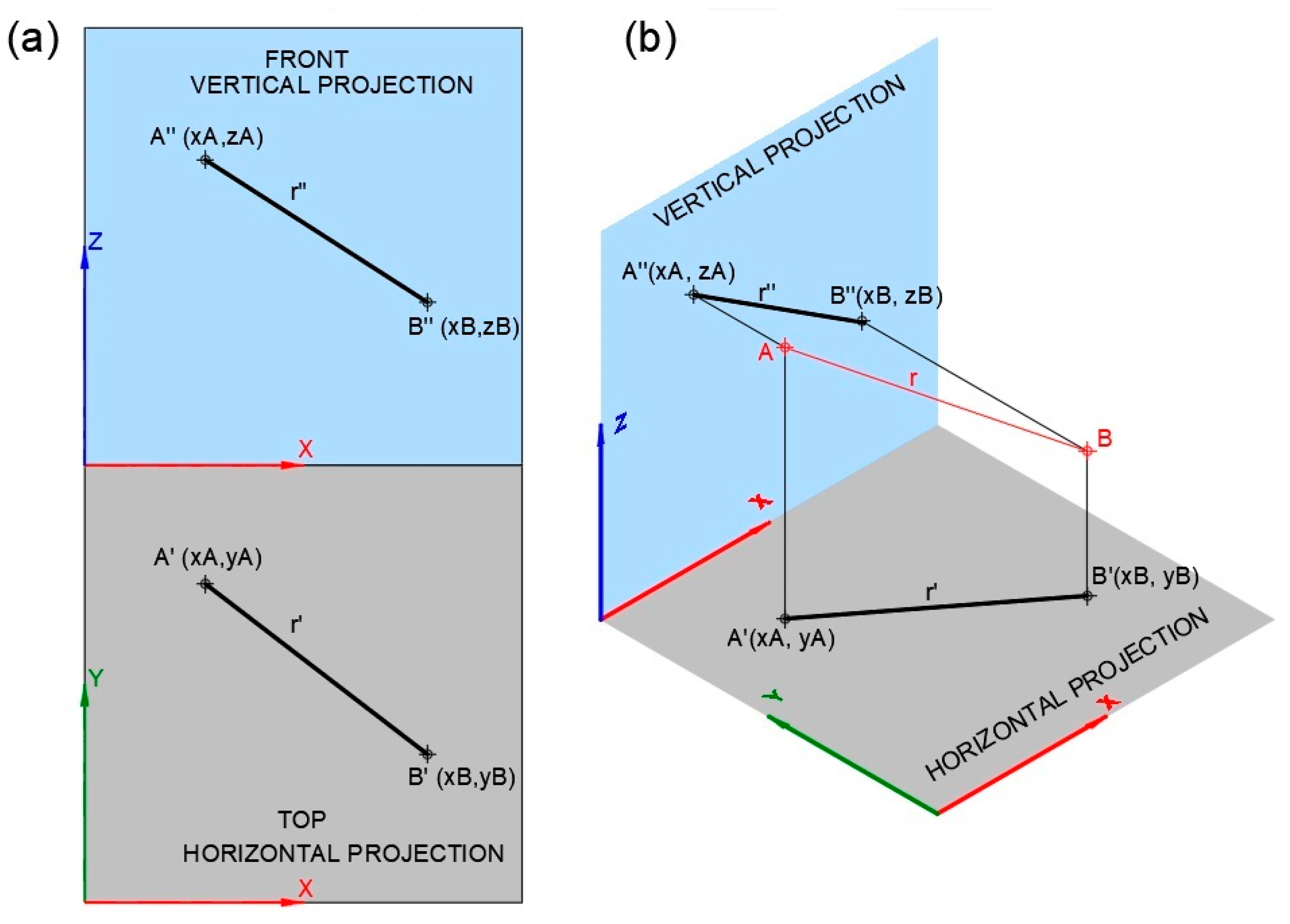
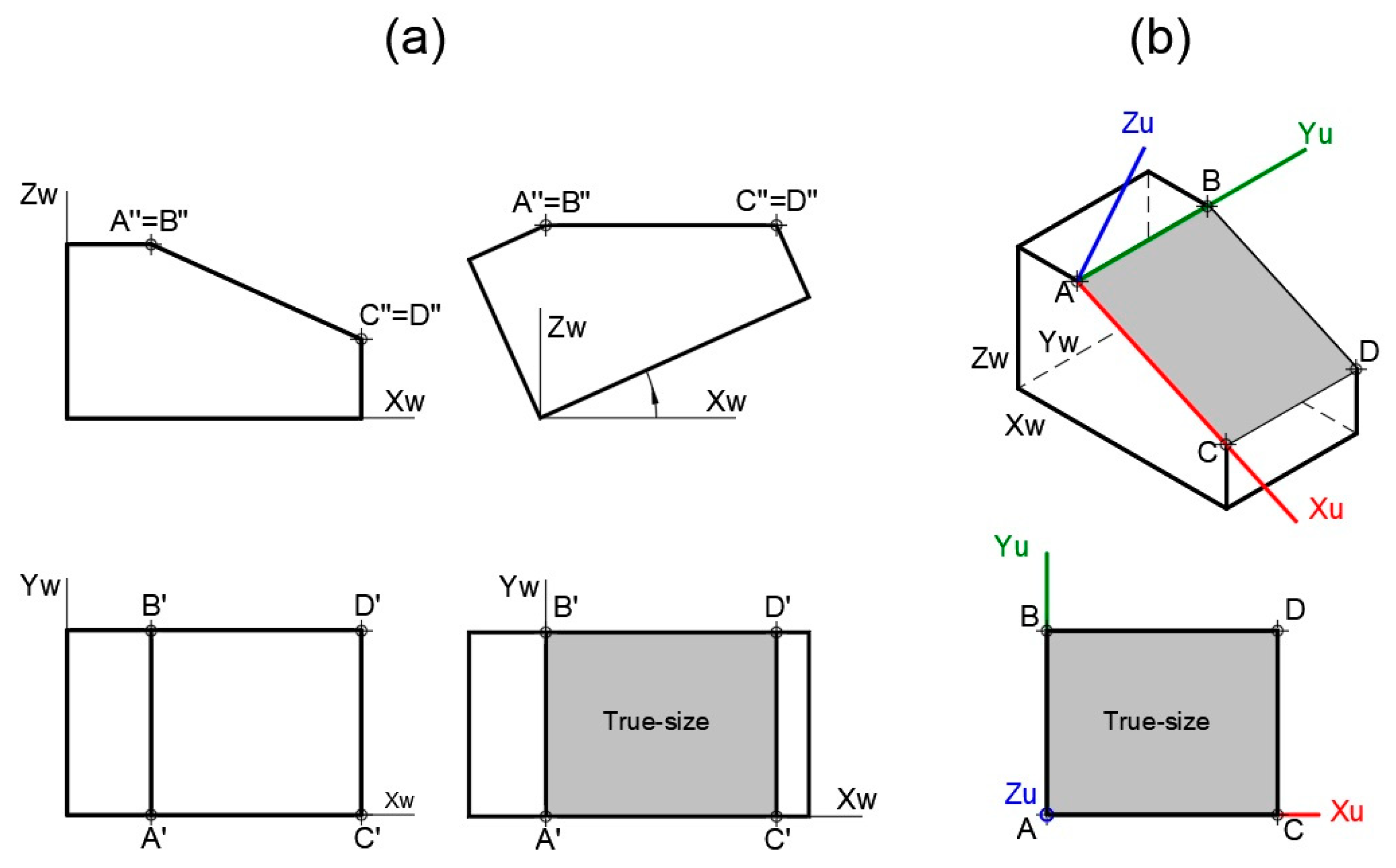
3.3. True Length of a Line and True Size of a Plane

The following describes how to determine the true length of an oblique line and the true size of a plane. Figure 17a shows the result by using the object rotation, without modifying the coordinate system. In the case of Figure 17b, a UCS is considered, in such a way that the true size view can be obtained from the top view.

3.4. Parallelism and Perpendicularity

In this section, the distance calculation between geometric elements will not be explicitly addressed. This is because the procedures for solving problems of parallelism and perpendicularity are the ones used to determine distances.

3.4.1. Parallelism between Lines

If two lines are parallel in space, their orthographic projections are parallel too. This condition must be fulfilled with respect to at least two projection planes. As can be seen in Figure 18a, the lines are parallel; therefore, their projections on any plane of the dihedral will also be parallel. Figure 18b shows two skew lines. Parallelism is not maintained in all projections for this case.

It is very easy to determine the parallelism of two lines with CADOP since, once their spatial positions are known, the views are obtained directly, as is shown in Figure 18.

In addition, two lines are parallel it they define a plane. It can be checked whether two lines are coplanar by using the UCS, defined by three non-aligned points. In Figure 19, lines m and t are not parallel while lines r and s are parallel because they define a plane.

This procedure can also be used to check whether two non-parallel lines intersect. If they define a plane, they intersect, determining a UCS. Otherwise, they are skew lines.

3.4.2. Parallelism between Line and Plane

For testing whether a line is parallel to a plane, it is enough to check that they do not intersect. Figure 20 shows how to do this. First, the line is projected onto the given plane. Next, it is checked whether the line intersects with its projection. If so, the line and the plane are not parallel.

3.4.3. Parallelism between Planes

To determine whether two planes are parallel, a line from one of them is considered and copied through any point on the other. Next, the UCS is matched to this latter plane. If two points belonging to this copied line have Z = 0 in the UCS, the planes are parallel.

3.4.4. Perpendicularity between Lines

If two lines intersect, they are coplanar. Therefore, in the plan view of the UCS that they define, it will be possible to check its perpendicularity.

For two skew lines, an additional line is drawn parallel to one of them at any point of the other. Next, the described procedure is applied to determine the perpendicularity of two intersecting lines.

3.4.5. Perpendicular Line from a Point to a Line

The UCS is matched to the plane defined by point P and line r (Figure 21). The perpendicular line is drawn from the point to the line in the top view. The true length of this perpendicular line is the distance from the point to the line.

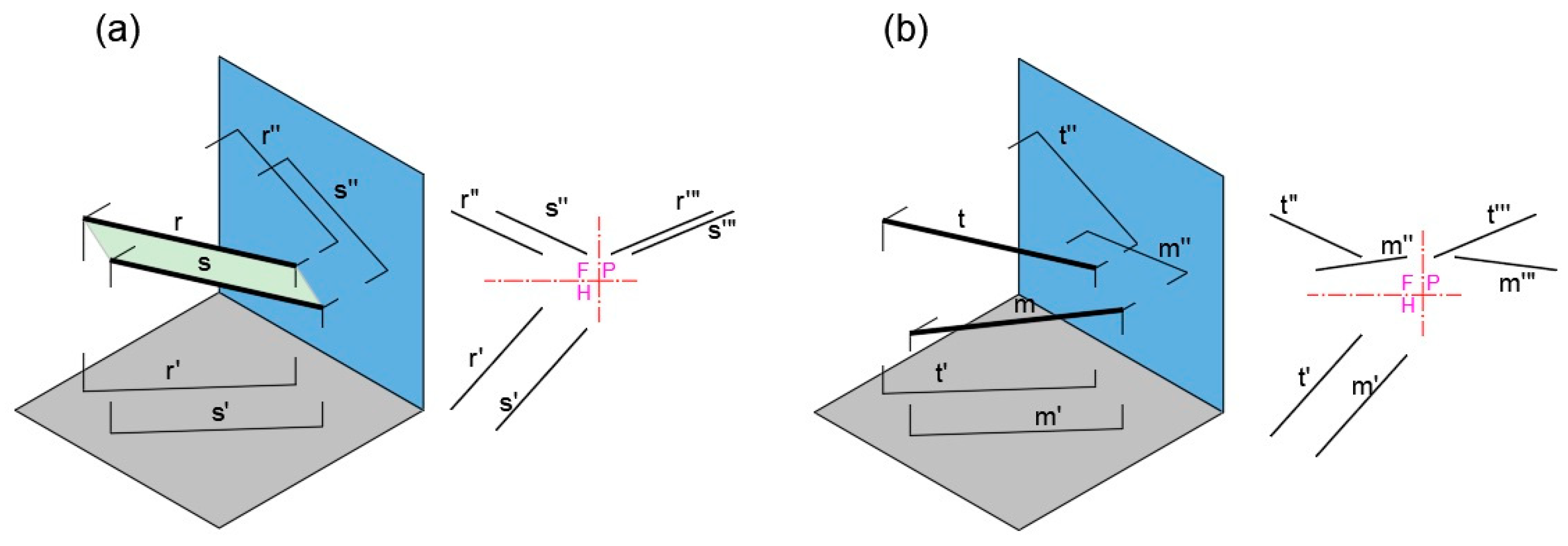
3.4.6. Perpendicular Line and Shortest Distance between Two Skew Lines

The determination of the perpendicular line and shortest distance between two skew lines is shown below as an example, applying CADOP.

• CADOP vs. traditional method.

Solving this problem using the traditional method is very tedious due to the number of lines that must be drawn. In addition, the relative position of the lines with respect to the dihedral can further complicate its resolution. Figure 22 shows the solution if one of the lines is parallel to the profile plane. Therefore, it is necessary to consider the profile projection to solve the problem. The true length of the shortest distance between two skew lines, r and s (profile line), is determined using auxiliary procedures such as rotation and views.

Figure 23 shows the result obtained with CADOP. As can be seen, the drawing complexity dismisses thanks to the use of layers that allow the results to be shown by hiding the intermediate procedures (Figure 23a). In addition, CADOP makes it possible to arrange the views at the suitable distance to avoid projections overlapping (Figure 23b). All this facilitates a better understanding of the graphic information transmitted. On the other hand, when working in 3D, the problem solution is reached faster and more intuitively (Figure 23c). Finally, another important factor to consider is the CADOP precision, which cannot be achieved in the traditional method as it is conditioned by the human factor.

• CADOP solving procedure step by step.

Figure 24 shows the top and front views of skew lines a and b. They are in the problem statement.

The first step is to determine the position of the lines in space. For the restitution, the procedure previously described in Figure 14 is followed, as is shown in Figure 25.

Once the lines are restored, the resolution of the problem is described in the following steps.

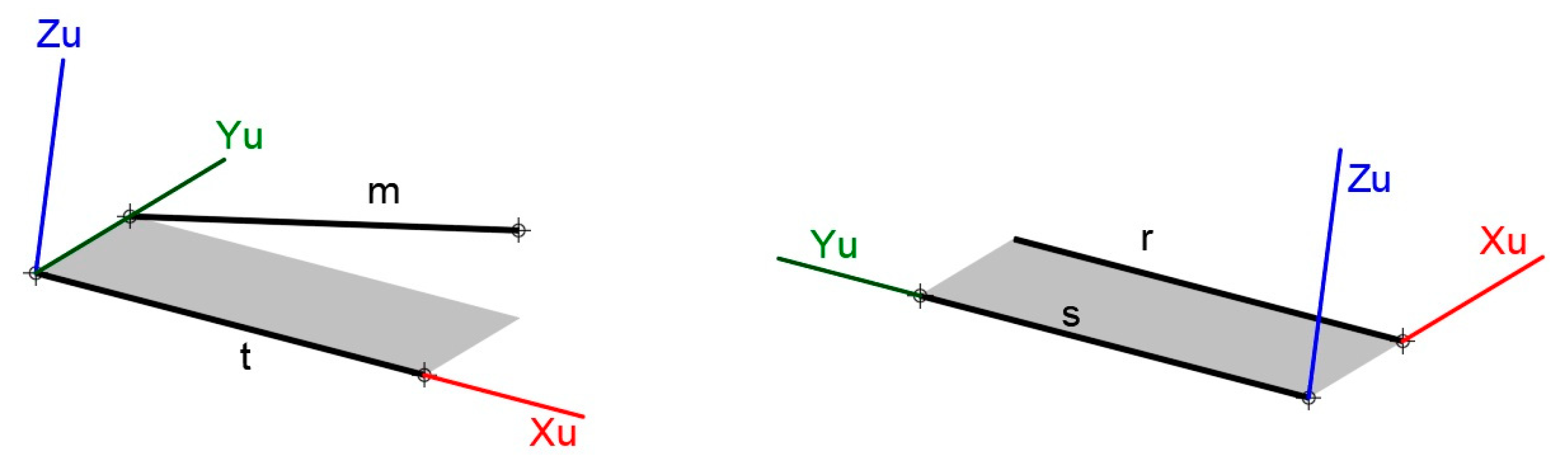
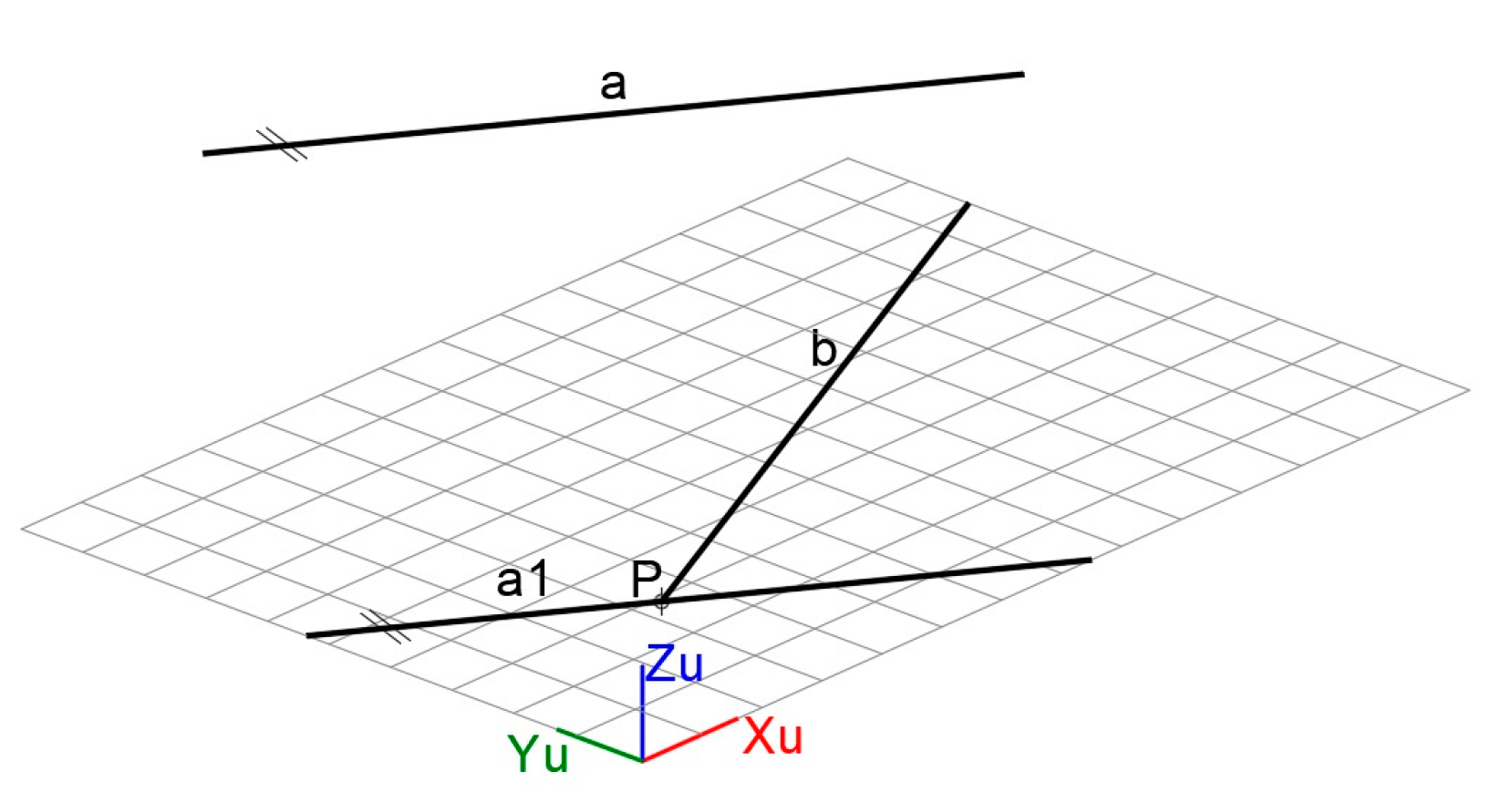
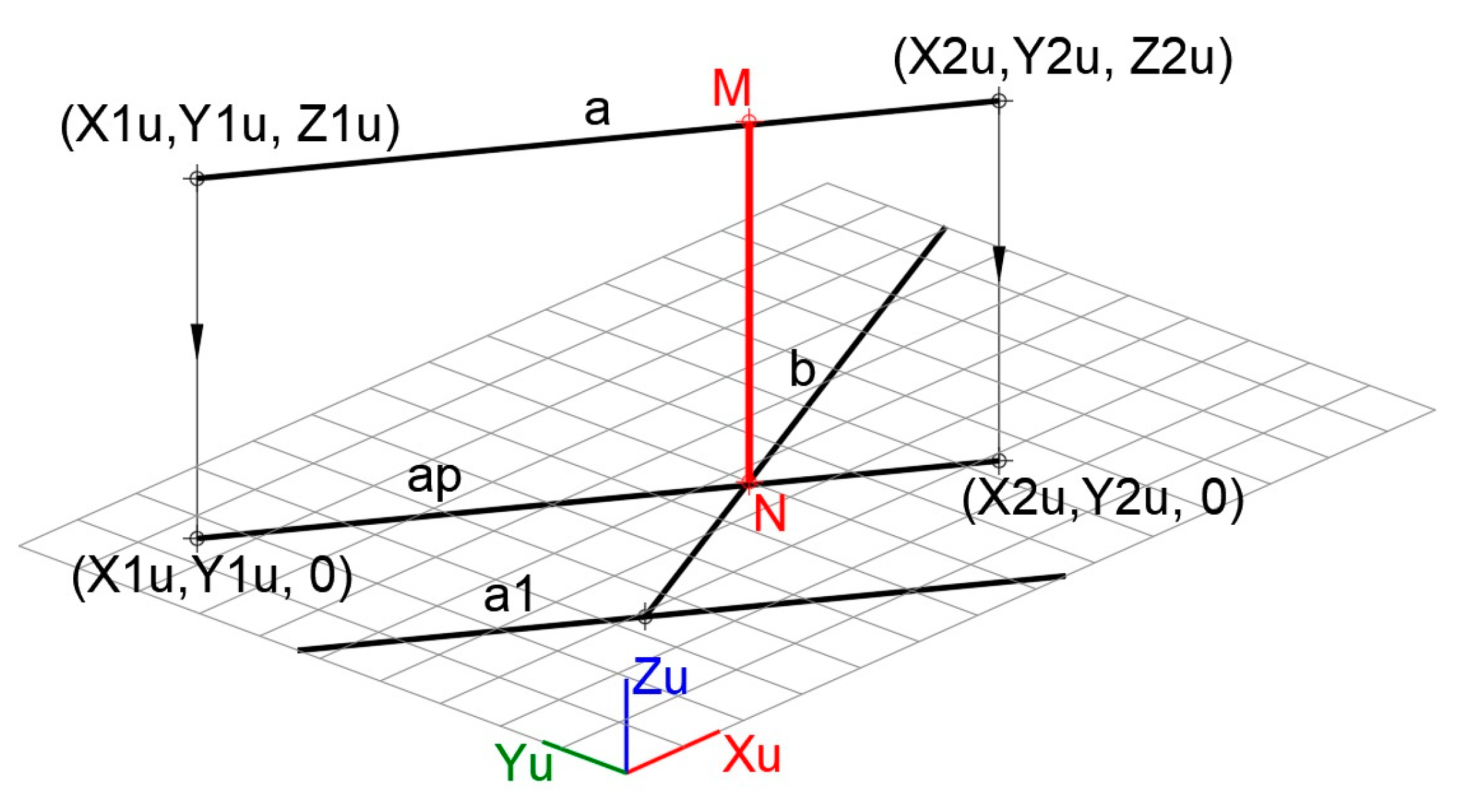
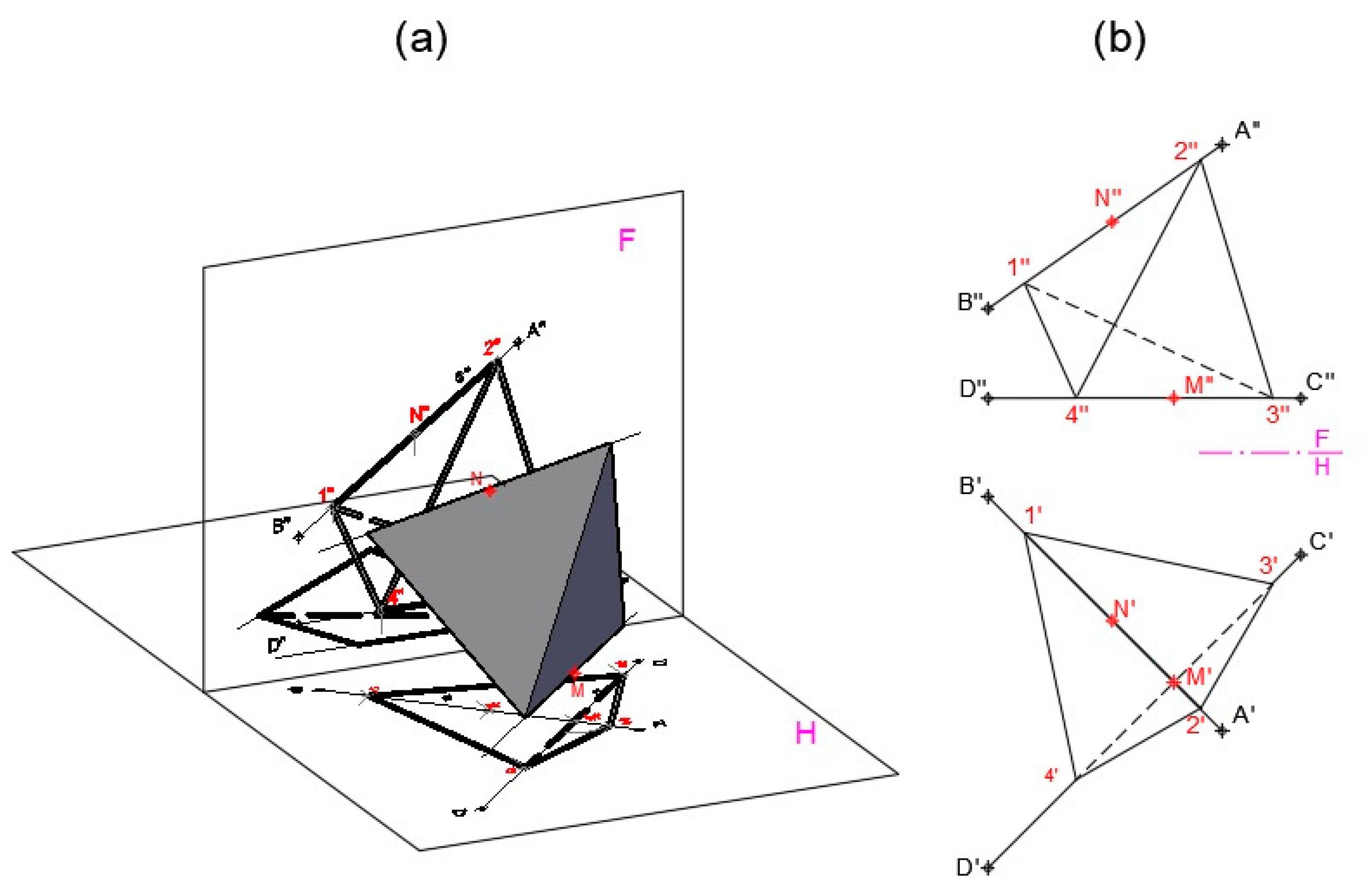
• The plane is defined through line b parallel to line a (Figure 26). Line a1 is a copy of line a through any point P on line b. The plane is determined by obtaining the UCS formed by line a1 and b.

2.

Making Zu = 0 for any two points on line a results in a projection onto the UCS defined before. Figure 27 shows line ap resulting from the projection.

3.

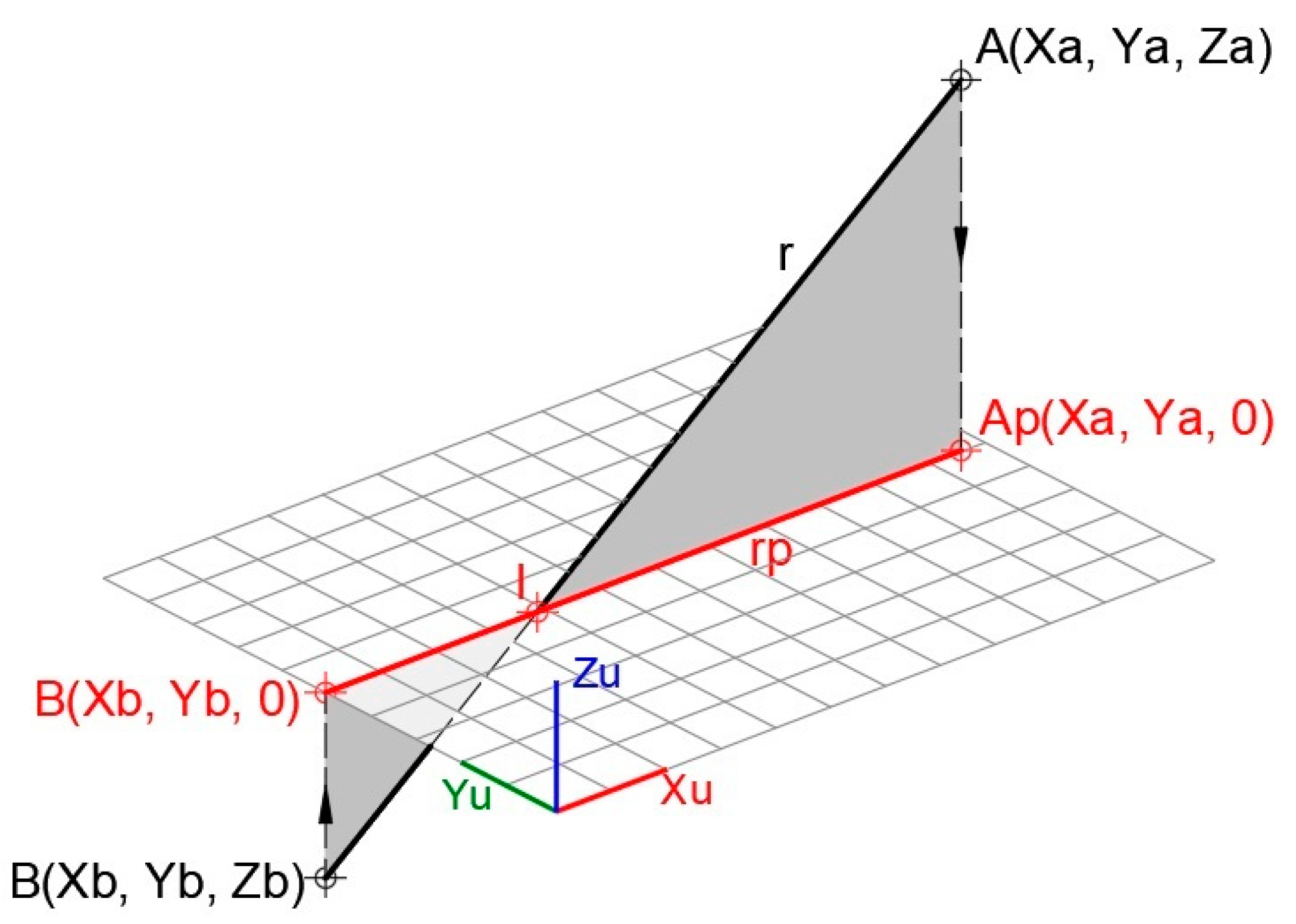
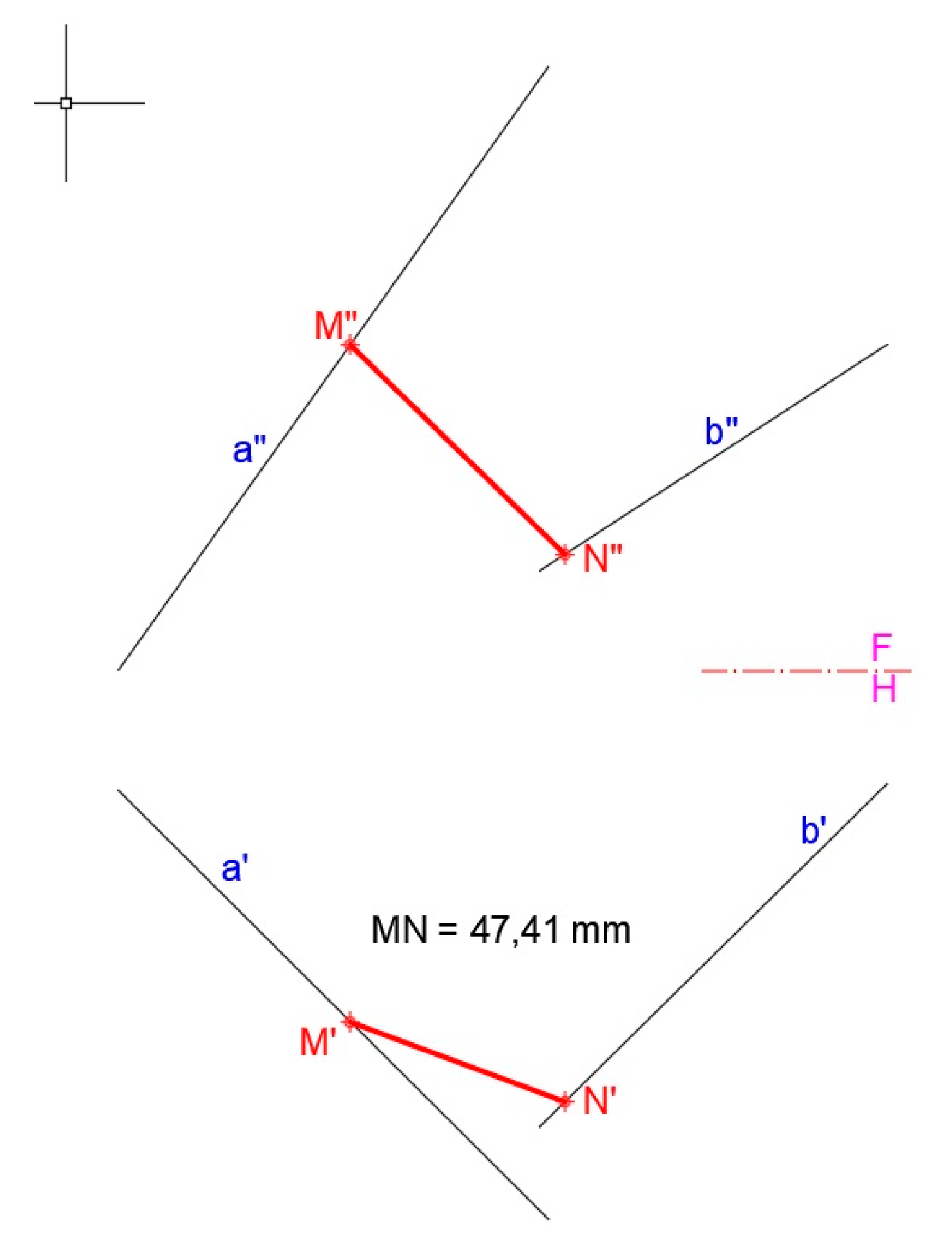
The perpendicular line and shortest distance segment MN between lines a and b are obtained. As shown in Figure 28, the intersection of the projected line ap and line b determines point N which is one of the ends of the solution segment. The other end, point M, is the intersection of line a with the line that, drawn through N, is perpendicular to the plane defined by the UCS. Segment MN is parallel to the Z axis of this UCS, and its true length is obtained directly from the information provided by CAD.

The MN segment’s 3D position obtained with CADOP as a solution to the proposed problem is shown in Figure 29.

4.

Finally, the top and front views and true length dimension of segment MN are obtained. Figure 30 shows the solution provided by applying CADOP.

The procedure followed to solve this problem can be seen in more detail in the Video S1: Shortest distance between two skew lines, provided as Supplementary Material.

3.5. Angles

This section focuses on determining the position and true value of angles between lines and planes.

3.5.1. Angle between Two Coplanar Lines

The measure of an angle between two coplanar lines (Figure 31a) is determined by matching the UCS to the plane defined by them (Figure 31b). Therefore, the top view allows the true angle to be obtained (Figure 31c).

When considering skew lines, one of them is copied through any point of the other and the angle formed by these two coplanar lines is determined with the previous procedure.

3.5.2. Angle between Line and Plane

This angle corresponds to the one between the line and its projection on the plane (Figure 32). The line is projected onto the plane according to the procedure shown in Figure 13. The angle measurement is determined as described above.

3.5.3. Angle between Two Planes

Two non-parallel planes intersect according to a line that is determined using surface intersection with CADOP. By matching the Z axis of the UCS to the line of intersection of the planes (Figure 33a), the top view will show the angle measurement (Figure 33b).

3.6. Regular Polyhedra

Regular or Platonic polyhedra have some features that facilitate DG understanding by applying the previously described concepts. It is easy to solve these 3D bodies with CADOP. As an example, Figure 34a shows the tetrahedron obtained in 3D, knowing that two of its opposite edges are located on two perpendicular skew lines. To solve this problem, it is necessary to determine the position and true length of the perpendicular line and shortest distance segment between them. The ends of this segment are the midpoints of the edges. Next, a tetrahedron of arbitrary edge and orientation is drawn. Thus, the similarity between regular polyhedra is applied to obtain the tetrahedron solution. With this aim, the distance between the opposite edges of a tetrahedron of arbitrary edge length is matched to the shortest distance segment of the two given lines. The corresponding top and front views of the polyhedron solution can be seen in Figure 34b.

4. Conclusions

In this paper, a methodology, called CADOP, is proposed to solve DG problems based on the combined use of CAD and orthographic projection. To the best of the authors’ knowledge, this work describes how to solve some of the DG problems by using this methodology for the first time. In this way, 3D problems can be solved from the 2D dihedral projections of their statement, to finally obtain the solution top, front, and profile views.

The use of UCS in CADOP allows DG problems to be solved in a more straightforward way compared to the traditional and direct hand-drawing methods of the dihedral system. CADOP is focused on the representation of geometric solutions than on the mechanics of geometric construction. The spatial solution to geometrical problems is found by placing the work plane to define the suitable projecting direction. In the traditional and direct methods, the use of auxiliary views must be carried out in several steps, modifying in each of them the position of one of the dihedral planes and keeping the other fixed. Nevertheless, all these operations are carried out in a single step in CADOP. Consequently, this fact makes it easier to understand the resolution of the problem, by focusing on the concepts required to solve it instead of the procedure. The calculations are performed analytically, and reference modes are used that provide maximum precision in CADOP. By contrast, the hand drawing used in the traditional and direct methods has an intrinsic lack of accuracy. Thus, for example, the rotation method is easily and accurately executed in CADOP by the CAD software, which has a copy of the initial position of the geometric elements. This fact overcomes the difficulties of manually performing this useful operation. The same applies to scale, copy, translate, align (move plus rotate and scale), and symmetry operations. These are very powerful tools in DG troubleshooting and are easy to run with the CAD software. The plane shapes are defined by three non-aligned points in DG, and they are considered as surfaces in CADOP. Boolean operations can be performed on them to determine, for example, their intersection. Once the 3D problem is solved, the required 2D views are obtained directly from CADOP. These views can be in any position and conveniently scaled to avoid their overlapping. In addition, it is possible to select different visual styles that allow one to easily distinguish seen and hidden elements. On the other hand, the dynamic management of the 3D scene point of view facilitates the understanding of the problem resolution and the acquisition of spatial vision capacity. Finally, the advantages of having the model and paper spaces at the same time must be highlighted. It is possible to obtain several paper spaces from the model. Each one of these paper spaces is configured with the suitable views, scale, formats, and any other required option.