Abstract
In this paper, we present two new classes of fuzzy negations. They are an extension of a well-known class of fuzzy negations, the Sugeno Class. We use it as a base for our work for the first two construction methods. The first method generates rational fuzzy negations, where we use a second-degree polynomial with two parameters. We investigate which of these two conditions must be satisfied to be a fuzzy negation. In the second method, we use an increasing function instead of the parameter δ of the Sugeno class. In this method, using an arbitrary increasing function with specific conditions, fuzzy negations are produced, not just rational ones. Moreover, we compare the equilibrium points of the produced fuzzy negation of the first method and the Sugeno class. We use the equilibrium point to present a novel method which produces strong fuzzy negations by using two decreasing functions which satisfy specific conditions. We also investigate the convexity of the new fuzzy negation. We give some conditions that coefficients of fuzzy negation of the first method must satisfy in order to be convex. We present some examples of the new fuzzy negations, and we use them to generate new non-symmetric fuzzy implications by using well-known production methods of non-symmetric fuzzy implications. We use convex fuzzy negations as decreasing functions to construct an Archimedean copula. Finally, we investigate the quadratic form of the copula and the conditions that the coefficients of the first method and the increasing function of the second method must satisfy in order to generate new copulas of this form.
1. Introduction
In recent years, there has been a growing body of research on fuzzy sets, systems, and fuzzy logic and their applications in practice, as well as the construction of new fuzzy negations, implications, and copulas. The production of a new fuzzy implication and copula is required. Fuzzy implications are the generalization of classical (Boolean) inference in the interval of [0, 1]. They are widely known to play an important role in the fields of fuzzy logic, decision theory, and fuzzy control. For this reason, the generation of new fuzzy implications has created the need to generate new fuzzy negations. Extensive research has been conducted in the literature on the production of fuzzy negations [1,2,3,4,5,6]. We know that we can generate fuzzy implications from aggregation functions and fuzzy negations [7,8,9,10,11,12,13,14,15]. Other methods of generating fuzzy implications can be achieved using additive generating functions or by some initial implications [16,17,18,19,20,21,22]. Thus, fuzzy implications are useful in fuzzy relational equations and fuzzy mathematical morphology, fuzzy measures and image processing [23], data mining [24], and computing with words and fuzzy partitions. On the other hand, functions with two variables, named copulas, have attracted the interest of many researchers because they are used in many fields. Copulas [25,26,27,28] are functions of two variables with specific properties based on probability theory and are often used in statistics and economics. In recent decades, the interest of many researchers in copulas has been very intense, as is evident from the large number of different copula constructions. Moreover, copulas introduce a new way to model multivariable data by considering the type of structure of these variables.
Although they come from different backgrounds, copulas and fuzzy implications have much in common with each other. The literature testifies that there have been many in-depth studies analyzing the relationship aggregation functions in general, and references have been made to them [29,30]. In recent years, new ways of constructing implications and copula functions have appeared, and their properties have been extensively studied. Fuzzy implications are studied in many areas. The construction of new fuzzy implications requires the construction of new fuzzy negations. The goal of this paper is to continue to construct rational fuzzy functions and, this time, fuzzy negations.
This paper is partially inspired by Sugeno-class fuzzy implication. Here, we present two new classes of fuzzy negations, the first of which generates rational fuzzy negations and the second of which generates rational negations assuming that the function is polynomial. The first one is a parametric, with two parameters which satisfy various conditions. We kept parameter δ from the Sugeno class and added another parameter γ just to generalize it to a second-degree polynomial. The second method is fuzzy negation, which is a generalization of the well-known fuzzy negation Sugeno class, replacing the parameter with an increasing function . Some conditions, like turn into . Compared to previous works, herein, a new function is used in place of the parameter δ, and this creates a large range of fuzzy negations where the choice of an appropriate function creates new implications that satisfy specific conditions. Imagine that g can be any polynomial function of any degree, which means that the denominator can have a degree higher than two, as the first method has. On the other hand, g can be also any other type of function, and the produced negation is a composition of trigonometric functions or a root function. Using all these new fuzzy negations and in combination with known methods of constructing fuzzy implications, many new implications are produced.
A new method which produces strong fuzzy negations is presented. Strong negations produce S-implications and satisfy some basic properties of fuzzy implications, like the exchange principle, ordering property, and identity principle. We generalize an old method by using the equilibrium point ε of the new fuzzy negation and two decreasing functions with specific conditions. We compare the equilibrium points of the new negations of the two first methods. Also, we investigate which conditions the coefficients of the produced negation of the first method and the function g of the second method must satisfy in order to be convex. We use this convexity to produce Archimedean copulas using a well-known method. Finally, we investigate another category of copula, the quadratic section, which has the form . We give another proof of condition that the function a must satisfy. Function has at least two roots: the numbers 0 and 1. Using root 1, and because it is also a root of the fuzzy negations, we can give it the following form: where N is a fuzzy negation. Choosing the Sugeno class or its extension of the second method, we investigate which conditions the parameter δ or the function g must satisfy in order for the function a to be the appropriate for the quadratic section of the copula. With the help of fuzzy negations, we produce fuzzy implications which we can customize into an application. They fit better because, here, we use a function in place of a parameter δ. Thus, we can choose an appropriate inference. We have a plethora of implications, and, therefore, we can choose the most appropriate implication to simulate the data we have.
The paper is organized as follows. In Section 2, we recall the basic concepts and definitions used in the paper. In Section 3, we study the newly constructed methods of fuzzy negations, strong fuzzy negations, and their convexity. We present many examples of the produced negations. Also, we give some examples of the new fuzzy implications that are produced when two or more new negations are combined. Finally, we investigate the quadratic form of the copula, and we combine the new fuzzy negations, giving extra conditions to produce the copula. We present examples of the quadratic form of the copula and Archimedean copulas.
2. Preliminaries
To help the reader to become familiar with the theory, here, we outline some of the concepts and results employed in the rest of the paper.
Definition 1.
(see [30] Definition 1.4.1). The function is a fuzzy negation if the following properties are applied:
N: is decreasing.
Definition 2.
(see [30] Definition 1.4.2 (i)). A fuzzy negation N is called strict if the following properties are applied:
N is strictly decreasing.
N is continuous.
Definition 3.
(see [30] Definition 1.4.2 (ii)). A fuzzy negation N is called strong if
Definition 4.
(see [30] Definition 1.4.2 (ii)). The solution of the equation is called the equilibrium point of N. If the function N is continuous, the equilibrium point is unique.
Table 1 below shows some basic fuzzy negations used in this article.

Table 1.
Examples of basic fuzzy negations.
Fuzzy implications have probably become the most important operations in fuzzy logic, approximate reasoning, and fuzzy control. These operators not only model fuzzy conditionals, but also make inferences in any fuzzy rule-based system. These operators are defined as follows.
Definition 5.
(see [30] Definition 1.1.1). A function is called a fuzzy implication, if it satisfies, for all the following conditions:
Definition 6.
(see [30] Definition 1.4.15 (ii)). If I is a fuzzy implication, then the function with the form
is called a natural negation of I.
Definition 7.
(see [30] Definitions 1.3.1, 1.5.1). A fuzzy implication is said to satisfy:
- i.
- the left neutrality property if:
- ii.
- the exchange principle if:
- iii.
- the identity principle if:
- iv.
- the ordering property if:
- v.
- the law of contraposition with respect to N if:
- vi.
- the law of left contraposition with respect to N if:
- vii.
- the law of right contraposition with respect to N if:
Definition 8.
Let I be a nonempty interval of R. A function f from I to R is convex if and only if
Definition 9.
([28]). A function is called a copula if it satisfies the following properties:
The C-volume of a rectangle must be not negative, e.g.,
for each and where ,
Definition 10.
([28]). If the function C is a copula, then the function in form
Definition 11.
([30]). If f is a decreasing function where , then we define the pseudo-inverse of function f as:
Definition 12.
([30]). Let be a continuous, strictly decreasing, and convex function such that , and let be the pseudo-inverse. Let defined by:
Then, C is an Archimedean copula.
3. Results
In this section, we give definitions and proofs of the newly generated fuzzy negations. The utility of fuzzy negations is known because, with the help of a new negation, we can construct a family of fuzzy implications. Also, we give examples of the new negations and the new fuzzy implications that are produced. Using the above equilibrium points and generalizing a known formula, we construct the branching functions and we generate strong fuzzy negations. Moreover, we combine the new fuzzy negations with the quadratic form of the copula.
3.1. New Fuzzy Negations
Theorem 1.
The function with the following form:
is a fuzzy negation if the condition is satisfied, where and .
Proof.
The boundary conditions (1) are satisfied: .
Also, the monotony condition (2):
If and then so the monotony condition is satisfied.
If and then
□
Proposition 1.
The fuzzy negation of the Theorem 1 is strong if and only if γ = 0, which means it is the Sugeno class.
Remark 1.
If then the produced negation is the well-known Sugeno class where .
Remark 2.
If then the produced negation is the well-known classical (standard) fuzzy negation.
Remark 3.
The fuzzy negation of Theorem 1 is a strict fuzzy negation.
Theorem 2.
Let an increasing function. Then, the function with the following form:
is a fuzzy negation.
Proof.
Boundary conditions (1) are satisfied: .
Monotony condition (2):
□
Because is an increasing function, for every and .
Remark 4.
The function of Theorem 2 is a strict fuzzy negation.
Remark 5.
The function of Theorem 2 is an evolution if and only if g is a constant function.
Remark 6.
If we choose , then the fuzzy negation that is produced from Theorem 2 is a well-known .
Proposition 2.
Let the increasing function of the Theorem 2. We define the following increasing function, given by:
If K is a concave function, then the fuzzy negation of the Theorem 2 is a convex function.
Proof.
If K is an increasing function, then . If K is a concave function, then . We will calculate the second partial derivate of K.
We know from Theorem 3 that is a strictly decreasing function, so:
□
Proposition 3.
If and are the equilibrium points of respectively, then
Proof.
If then . Let be the equilibrium points of , respectively. Suppose that then which is a contradiction. Therefore, . □
Example 1.
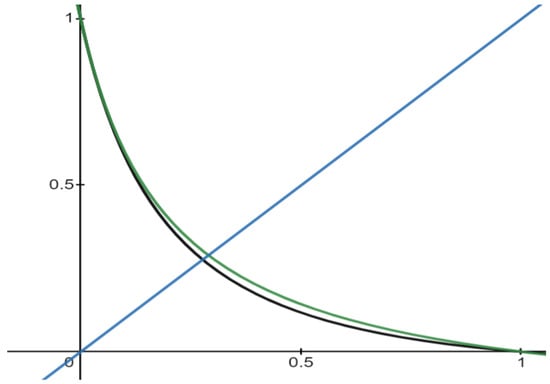
In Figure 1 we present the graphs of three functions, (the black one), (the green one), and the identity function (the blue one). belongs to fuzzy negations of Theorem 1 and belongs to fuzzy negation of the Table 1.

Figure 1.
Fuzzy negations of Example 1.
As we can see, the equilibrium point of ( is to the left of the point of the function.
The distance between these two equilibrium points is where are the equilibrium points of functions , , respectively.
We can produce strong branching fuzzy negations [1] where one branch is a rational function. If N is a fuzzy negation, which is not necessary, there is a strong negation, and where ε is the equilibrium point of . Thus, if is any continuous fuzzy negation in the interval [0, 1], then the following form [12] produces strong fuzzy negations and, in our case, rational fuzzy negations.
Below, in Figure 2 we present the graph of the function
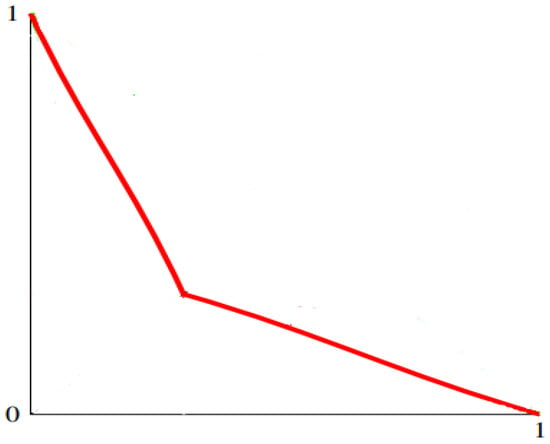
Figure 2.
Fuzzy negation .
We will generalize the above formula using two decreasing functions,
Theorem 3.
Let ε be the equilibrium point of . and two decreasing functions with the following conditions:
, and . Then the following form is a strong fuzzy negation:
Proof.
For we have
For we have
Monotony condition:
For we have
For every where
Thus, we conclude that is decreasing when .
For we have
For every where
Thus, we conclude that is decreasing when . □
Now, we will present some examples of new fuzzy negations. We will define some values for parameters γ and δ of Theorem 1, and we will produce new fuzzy negations.
Example 2.
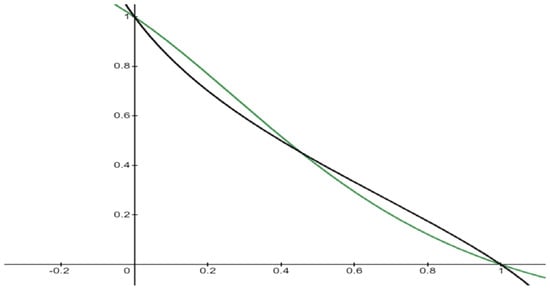
If we define the produced negation is (the green graph), and the inverse function is (the black one).
In Figure 3 we present the graphs of the function , .

Figure 3.
Fuzzy negations and .
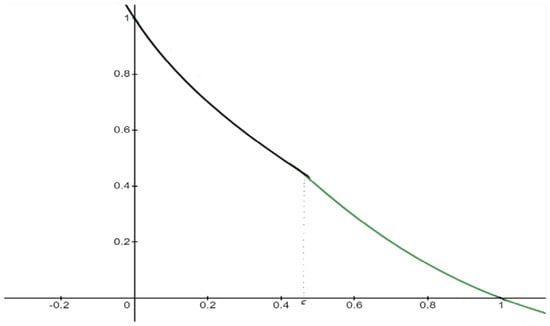
Then, the produced strong fuzzy negation has the following form and graph:
where is the equilibrium point of .
In the Figure 4 we present the graph of function . Particularly, the black graph is the first branch of and the green graph is the second branch of .

Figure 4.
Fuzzy negation .
Example 3.
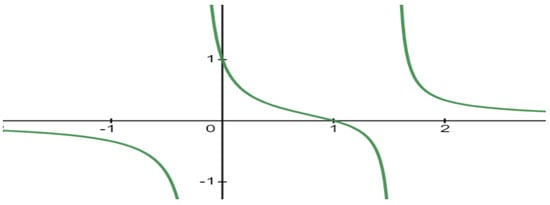
For the produced negation is
In the Figure 5 the graph of function is presented.

Figure 5.
Fuzzy negation .
3.2. Fuzzy Implications Generated from Fuzzy Negations of Theorems 1 and 2
Fuzzy negations are very useful in the construction of both fuzzy implications and copulas. Firstly, we will use fuzzy negations that were generated from the above methods for the construction of fuzzy implications.
Example 4.
According to the formula [8] are two fuzzy negations and is an increasing and continuous function with . From Theorem 1, if we set and from Theorem 3, if then the produced negations are and . If we set , and we generate the following fuzzy implication:
And its natural negation is
Moreover, we can construct parametric fuzzy implications using the produced fuzzy negations of Theorems 1 and 2.
Remark 7.
If we choose a strong fuzzy negation from relation (32), then the produced fuzzy implication satisfies the neutrality property.
Proposition 4.
Let be two fuzzy negations of Theorems 1, 2 with the form . If we set , , then, according to formula [8], and the produced implication has the form:
Proof.
Proof is obvious. □
With this combination, we can make many rational fuzzy implications. We can make a family of them. Also, we can use fuzzy negations as decreasing functions to construct copulas. The following form helps us to understand this.
In the literature, various methods of manufacturing copulas have been presented. Here, we will deal with the Archimedean copulas.
Example 5.
According to Theorem 1, if we choose for then we take the fuzzy negation:
Fuzzy negation is strict and convex. Its inverse function has the form:
And its pseudoinverse has the form:
If we define:
then, by the form (18), a new copula is generated.
Proposition 5.
If or and , then the fuzzy negation of Theorem 1 is a convex function.
Proof.
If we calculate the second derivate of we have the following:.
We define then:
And the discriminant of the polynomial
If we examine the case, then, , which means that is a decreasing function, so we have .
In this case (γ < 0), we already know that . So, .
In the case that and we have the following:
which means that is an increasing function. Thus, . □
3.3. Copulas with Quadratic Sections
We will analyze one of the linear sections of copulas, the quadratic form of the copula. In the book of Nelsen [28], we can find the quadratic and cubic sections of copulas.
The quadratic section of the copula is defined by the form:
And the cubic section of the copula is defined by the form:
Before that, we present a proof of the equivalency and the last condition of the copula. We will use the main value theorem twice.
Proposition 6.
We know that, for a function to be 2-increasing, it must satisfy the inequality . This inequality is equivalent to
when C is a differentiable function.
Proof.
We apply the mean value theorem for the function in the interval :
We apply the mean value theorem for the function in the interval :
Let us suppose that then:
The other implication is analogous, but proceeds in reverse order. □
Proposition 7.
Function with quadratic form
is a copula if , and .
Proof.
Employing the boundary conditions, we have the following:
After the boundary conditions, the quadratic form of the copula takes the following form
We know that, in order for a function to be 2-increasing, it must satisfy the following inequality:
This inequality is equivalent to when the function C is differentiable. We will use this inequality to set some conditions for the function .
In the case of we have:
In the case of we have:
We conclude that the function must satisfy the following condition:
□
Function has at least two roots: the numbers 0 and 1. Using root 1, and because it is also a root of the fuzzy negations, we can give it the following form: where N is a fuzzy negation. Here, we can make combinations with the above generated fuzzy negations. If we choose the Sugeno fuzzy negation, we will study what conditions must be satisfied by coefficient δ.
Theorem 4.
Let the Sugeno class fuzzy negation and with the form .
Proof.
Function must satisfy the inequality .
For we have which is always true.
For we have .
If we set then .
If then . Thus, , (6) is true.
If then . Thus, .
We therefore conclude that inequality is satisfied when . □
As follows, if we choose the fuzzy negation of Theorem 2, we will study what conditions must be established by the function g in order to satisfy the inequality . We recall that the function g is an increasing function and .
Theorem 5.
Let the fuzzy negation of the Theorem 2 and function defined by .
Proof.
Function must satisfy the inequality .
For
For
□
Example 6.
If we take the quadratic section of the copula for we can set , then the produced copula is:
The survival copula (15) is defined by:
Example 7.
If we choose which is true for every . Thus, we can produce another copula if we set . Then, the produced copula is
The survival copula is defined by:
3.4. A Presentation of a Hypothetical Scenario
Let X, Y represented linguistic variables, i.e., fuzzy sets. Let us also suppose that . For each, and correspond to a value pair . If we collect a “good sample” then we have:
But since we have a “good sample”,
Then, using our implication, which is produced by a convex negation with a parameter a, we have the parametric implication .
Thus, we have:
Now, we can select the “best implication” as that which has the shortest distance from 1. That is, we see this when the number
becomes the minimum.
For further reading and other research applications, the development method in [31,32] could also be applied.
4. Conclusions
The main goal of our construction of fuzzy negations is the generation of fuzzy implications. The symmetry or lack thereof of the generated fuzzy implications plays a key role in the application. For example, if the generated implications are symmetric, then the cause and the causality are mixed. In our construction, the cause and the causality are distinct. Moreover, new fuzzy implications give us new copulas. In this work, we have proposed some novel construction methods of fuzzy negations. Firstly, we presented a new class of rational fuzzy negations inspired by the Sugeno class fuzzy negation. Secondly, we replaced the parameter δ of the Sugeno class with an increasing function g with specific conditions. We generalized a form which generates strong fuzzy negations by using two decreasing functions . Also, we gave some extra conditions so that the new fuzzy negations would be convex and we gave many examples of the new generated fuzzy negations (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5). Finally, we dealt with the quadratic section of the copula, trying to find the appropriate function using the new fuzzy negations of the Theorems 1 and 2. As a future work, we can investigate some other methods that produce copulas. We will produce parametric copulas and research what conditions the coefficients must satisfy. At this point, we must emphasize the fact that our suggested method could also be applied by using a method that is amazing, in our opinion, on the cubic section of the copula:
which we can find in the book of Nelsen [28]. With this method, the case of the cubic section of the copula, which has two functions, a and b, with common roots of the numbers 0 and 1, is investigated. Using the new fuzzy negation of the first method, we can find which conditions its coefficients must satisfy in order to produce a copula. We could accomplish the same result using the extension of the Sugeno class. In this class, we investigate a function g in which we must determinate properties to be satisfied such that a cubic copula can be produced. On the other hand, we can continue to extend other well-known fuzzy negations by using appropriate functions instead of parameters. In addition to this, we can investigate the extension of the Yager class of fuzzy negation, where instead of the parameter w, we can use a function with the appropriate properties.
The more new negations are produced, the more fuzzy implications and copulas can be generated. In research, we need many such functions of two variables in order to be able to choose the best one for each case every time.
Author Contributions
Conceptualization, M.N.R. and B.K.P.; methodology, M.N.R. and B.K.P.; software, M.N.R.; validation, M.N.R., A.K. and B.K.P.; formal analysis, M.N.R. and A.K.; investigation, M.N.R., A.K. and B.K.P.; resources, M.N.R. and A.K.; data curation, M.N.R.; writing—original draft preparation, M.N.R.; writing—review and editing, M.N.R. and A.K.; visualization, M.N.R.; supervision, A.K and B.K.P.; project administration, A.K. and B.K.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bustince, H.; Campión, M.J.; De Miguel, L.; Induráin, E. Strong negations and restricted equivalence functions revisited: An analytical and topological approach. Fuzzy Sets Syst. 2022, 441, 110–129. [Google Scholar] [CrossRef]
- Bedregal, B.C. On interval fuzzy negations. Fuzzy Sets Syst. 2010, 161, 2290–2313. [Google Scholar] [CrossRef]
- Gupta, V.K.; Massanet, S.; Vemuri, N.R. Novel construction methods of interval-valued fuzzy negations and aggregation functions based on admissible orders. Fuzzy Sets Syst. 2023, 473, 108722. [Google Scholar] [CrossRef]
- Grabowski, A. On Fuzzy Negations Generated by Fuzzy Implications. Formaliz. Math. 2020, 28, 121–128. [Google Scholar] [CrossRef]
- De Lima, A.A.; Bedregal, B.; Mezzomo, I. Ordinal Sums of the Main Classes of Fuzzy Negations and the Natural Negations of t-Norms, t-Conorms and Fuzzy Implications; Elsevier: Amsterdam, The Netherlands, 2020; Volume 116, pp. 19–32. [Google Scholar]
- Grabowski, A. On Fuzzy Negations and Laws of Contraposition. Lattice of Fuzzy Negations. Formaliz. Math. 2023, 31, 151–159. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B. QL-implications: Some properties and intersections. Fuzzy Sets Syst. 2010, 161, 158–188. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B. (U, N)-implications and their characterizations. Fuzzy Sets Syst. 2009, 160, 2049–2062. [Google Scholar] [CrossRef]
- Durante, F.; Klement, E.P.; Meriar, R.; Sempi, C. Conjunctors and their residual implicators: Characterizations and construction methods. Mediterr. J. Math. 2007, 4, 343–356. [Google Scholar] [CrossRef]
- Massanet, S.; Torrens, J. An Overview of Construction Methods of Fuzzy Implications. In Advances in Fuzzy Implication Functions; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2013; Volume 300, pp. 1–30. [Google Scholar] [CrossRef]
- Rapti, M.; Papadopoulos, B. A Method of Generating Fuzzy Implications from n Increasing Functions and n + 1 Negations. Mathematics 2020, 8, 886. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B.; Massanet, S.; Torrens, J. Fuzzy implications: Past, present, and future. In Springer Handbook of Computational Intelligence. Springer Handbooks; Springer: Berlin/Heidelberg, Germany, 2015; pp. 183–202. [Google Scholar] [CrossRef]
- Sainio, E.; Turunen, E.; Mesiar, R. A characterization of fuzzy implications generated by generalized quantifiers. Fuzzy Sets Syst. 2008, 159, 491–499. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B. On the characterization of (S, N)-implications. Fuzzy Sets Syst. 2007, 158, 1713–1727. [Google Scholar] [CrossRef]
- Massanet, S.; Torrens, J. Threshold generation method of construction of a new implication from two given ones. Fuzzy Sets Syst. 2012, 205, 50–75. [Google Scholar] [CrossRef]
- Balasubramanian, J. Yager’s new class of implications Jf and some classical tautologies. Inf. Sci. 2007, 177, 930–946. [Google Scholar] [CrossRef]
- Daniilidou, A.; Konguetsof, A.; Souliotis, G.; Papadopoulos, B. Generator of Fuzzy Implications. Algorithms 2023, 16, 569. [Google Scholar] [CrossRef]
- Massanet, S.; Vicente, J.; Clapes, R.; Aguilera, D.R. On fuzzy polynomials implications. In Proceedings of the 2015 Conference of the International Fuzzy Systems Association and the European Society for Fuzzy Logic and Technology (IFSA-EUSFLAT-15), Montpellier, France, 15–19 July 2014. [Google Scholar] [CrossRef]
- Torrens, S.M.J. A new method of generating fuzzy implications from given ones. In Proceedings of the 7th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-11), Aix-les-Bains, France, 18–22 July 2011. [Google Scholar]
- Mas, M.; Monserrat, M.; Torrens, J.; Trillas, E. A survey on fuzzy implication functions. IEEE Trans. Fuzzy Syst. 2007, 15, 1107–1121. [Google Scholar] [CrossRef]
- Grzerorzewski, P. Probabilistic Implications. In Proceedings of the 7th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-11), Aix-les-Bains, France, 18–22 July 2011. [Google Scholar] [CrossRef][Green Version]
- Bustince, H.; Pagola, M.; Barrenechea, E. Construction of fuzzy indices from fuzzy DIsubsethood measures: Application to the global comparison of images. Inf. Sci. 2007, 177, 906–929. [Google Scholar] [CrossRef]
- Chaira, T. Fuzzy Measures in Image Processing. In Fuzzy Sets and Their Extensions: Representation, Aggregation and Models; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Jayaram, B.; Mesiar, R. I-fuzzy equivalence relations and i-fuzzy partitions. Inf. Sci. 2009, 179, 1278–1297. [Google Scholar] [CrossRef]
- Morillas, P.M. A method to obtain new copulas from a given one. Metrika 2005, 61, 169–184. [Google Scholar] [CrossRef]
- Mesiar, R.; Kolesarova, A. Copulas and fuzzy implications. Int. J. Approx. Reason. 2020, 117, 52–59. [Google Scholar] [CrossRef]
- Durante, F.; Sempi, C. Principles of Copula Theory; Chapman and Hall/CRC: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Baczynski, M.; Jayaram, B. (S, N)-and R-implications; a state-of-the-art survey. Fuzzy Sets Syst. 2008, 159, 1836–1859. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B. Fuzzy Implications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Javadpour, A.; Sangaiah, A.K.; Zaviyeh, H.; Ja’fari, F. Enhancing Energy Efficiency in IoT Networks Through Fuzzy Clustering and Optimization. In Mobile Networks and Applications; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Botzoris, G.N.; Papadopoulos, K.; Papadopoulos, B.K. A method for the evaluation and selection of an appropriate fuzzy implication by using statistical data. Fuzzy Econ. 2015, 20, 19–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).