Applications of a q-Integral Operator to a Certain Class of Analytic Functions Associated with a Symmetric Domain

Abstract

In this article, our objective is to define and study a new subclass of analytic functions associated with the q-analogue of the sine function, operating in conjunction with a convolution operator. By manipulating the parameter q, we observe that the image of the unit disc under the q-sine function exhibits a visually appealing resemblance to a figure-eight shape that is symmetric about the real axis. Additionally, we investigate some important geometrical problems like necessary and sufficient conditions, coefficient bounds, Fekete-Szegö inequality, and partial sum results for the functions belonging to this newly defined subclass.

1. Introduction

Let $\mathcal{A}$ denote the class of all analytic functions $\psi \left(r\right)$ defined in the open unit disk $\mathsf{\Omega }=\{r:r\in \mathbb{C}$ and $\left|r\right|<1\},$ and having the Taylor series representation at $r=0$ given as

$$\psi \left(r\right)=r+\sum _{t=2}^{\infty }{a}_t{r}^t,r\in \mathsf{\Omega },$$

(1)

with conditions of normalization $\psi \left(0\right)=0$ and $\psi \prime \left(0\right)=1$. A subclass $\mathcal{S}$ of $\mathcal{A}$ contains all the functions which are univalent (one-to-one) in $\mathsf{\Omega }$. The fundamental and important subclasess of $\mathcal{S}$ are ${\mathcal{S}}^{*}$ and $\mathcal{C}$, which represent the classes of starlike and convex functions, respectively.

Let $\psi \left(r\right)$ and $\delta \left(r\right)$ be two analytic functions in $\mathsf{\Omega }$, then $\psi \left(r\right)$ can be said to subordinate $\delta \left(r\right)$ (written as $\psi \left(r\right)\prec \delta \left(r\right)),$ if there exists a Schwarz function $x\left(r\right)$ which is also analytic and satisfies the conditions $x\left(0\right)=0$, $\left|x\left(r\right)\right|<1$, and $\psi \left(r\right)=\delta \left(x\left(r\right)\right).$ In addition, if the function $\delta \left(r\right)$ is univalent in $\mathsf{\Omega }$, then

$$\psi \left(r\right)\prec \delta \left(r\right)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\psi \left(0\right)=\delta \left(0\right)\mathrm{and}\psi \left(\mathsf{\Omega }\right)\subset \delta \left(\mathsf{\Omega }\right),$$

see [1].

The convolution of two functions $\psi$ and $\varsigma$ that are analytic in $\mathsf{\Omega },$ with the series representation of $\psi$, is provided in (1) and $\varsigma \left(r\right)=r+{\displaystyle \sum _{t=2}^{\infty }}{b}_t{r}^t$ is defined as

$$(\psi \ast \varsigma )\left(r\right)=r+\sum _{t=2}^{\infty }{a}_t{b}_t{r}^t,r\in \mathsf{\Omega }.$$

It is worth mentioning that the convolution operator has emerged as an important and attractive tool in the field of Geometric Function Theory. This mathematical technique has not only opened a new direction to introduce new operators but also to define interesting subclasses of analytic functions. Important geometrical problems like necessary and sufficient conditions, coefficient bounds, growth and distortion results can also be explored by the applications of convolution technique.

Quantum calculus is the study of ordinary calculus without the notation of limit. Due to vast applications in the fields of mathematics, quantum physics, hyper-geometric functions, mechanics and operator theory, quantum calculus has gained significant interest among researchers, leading to rapid advancement in this field.

Jackson [2,3] was the first who provided the q-analogue of differential and integral operators. In the field of Geometric Function Theory, Ismail et al. [4] introduced the idea of q-calculus and made transformations of starlike functions to q-starlike functions. On the other hand, in [5] this concept is discussed in order terminology. Ashis and Sarasvati [6] used q-trigonometric functions along with q-hyper geometric series to derive the recursion formulas. Amini et al. [7] made an important contribution to the field by using the q-Salagean operator to investigate important differential subordination results for a certain subclass of univalent functions.

More recently, Noor et al. [8] demonstrated important geometrical problems for a q-generalized subclass of close-to-convex functions connected with a parabolic domain. Meanwhile, Shaikh et al. [9] gave some applications of analogues of differential and integral operators for new subclasses of q-starlike and q-convex functions. Similarly, by generalizing a class of close-to-convex functions using the q-Srivastava–Attiya operator, Barez et al. [10] made considerable developments in this field. In a similar manner, Cotîrlâ et al. [11] and Mahmood et al. [12] investigated a number of geometric problems related to the subclasses of analytic functions using the Ruscheweyh q-differential operator associated with Janowksi and conical domains, respectively. Sokól and Stankiewicz [13] also defined and studied a new subclass of analytic functions in a specific domain.

Furthermore, Saliu et al. [14] introduced a new subclass related to the lemniscate of Bernoulli, which are connected to q-Janowski type functions. Alsoboh et al. [15] advanced this field of study by presenting a new class of analytic functions, which is defined by making use of the q-differential operator with respect to $k$—symmetric points. The role of q-operators and their consequences on analytic functions has extended the limits of our understanding.

To put our findings in a clear perspective, we present the following preliminaries.

Definition 1

([2]). For $q\in \left(0,1\right),$ the q-difference operator of a function $\psi \left(r\right)$ is defined as

$${\partial }_q\psi \left(r\right)={\displaystyle \frac{\psi \left(qr\right)-\psi \left(r\right)}{r(q-1)}},(r\ne 0),$$

(2)

and we can also observe that $\underset{q⟶1^{-}}{lim}{\partial }_q\psi \left(r\right)={\psi }^{\prime }\left(r\right).$

For $q\in \left(0,1\right),t\in \mathbb{N}$ and $r\in \mathsf{\Omega }$, we can see that

$${\partial }_q\left\{\sum _{t=1}^{\infty }{a}_t{r}^t\right\}=\sum _{t=1}^{\infty }[t,q]a_t{r}^{t-1},$$

where $[t,q]$ is the q-number and is defined as

$$[t,q]={\displaystyle \frac{1-q^t}{1-q}}=1+\sum _{l=1}^{t-1}{q}^l.$$

Definition 2

([16]). For $t\ge 0,$ the q-generalization of factorial notation is defined as

$$[t,q]!=\left\{\begin{array}{cc}1,\hfill & t=0,\hfill \\ [1,q][2,q][3,q]\dots [t,q]\hfill & t\in \mathbb{N}.\hfill \end{array}\right.$$

Definition 3.

For $x\in \mathbb{C},$ the q-generalization of the Pochammar symbol is defined as

$${[x,q]}_t=\left\{\begin{array}{cc}1,\hfill & t=0,\hfill \\ [x,q][x+1,q]\dots [x+t-1,q]\hfill & t\in \mathbb{N}.\hfill \end{array}\right.$$

Definition 4

([17]). For $0<q<1$, the q-logarithmic function is defined as

$${ln}_{q}u={\displaystyle \frac{u^{1-q}-1}{1-q}},u\in \mathsf{\Omega }.$$

It can be easily observed that $\underset{q⟶1}{lim}{ln}_{q}u=lnu$.

Definition 5

([18]). For $0<q<1$, the q-exponential function is defined as

$$e_q\left(u\right)=\sum _{t=0}^{\infty }{\displaystyle \frac{u^t}{[t,q]!}},u\in \mathsf{\Omega },$$

and we can see that $\underset{q⟶1}{lim}{e}_q\left(u\right)=e^u$; also,

$${ln}_q\left(e_q\left(u\right)\right)=u.$$

Definition 6.

For a function $\psi \in \mathcal{A}$, Jackson [3] was the first to introduce the q-integral operator as

$$\underset{0}{\overset{r}{\int }}\psi \left(u\right)d_q\left(u\right)=u\left(1-q\right)\sum _{j=0}^{\infty }{q}^j\psi \left(u{q}^j\right).$$

For a function $\psi \left(u\right)=u^t$, we have

$$\underset{0}{\overset{r}{\int }}\psi \left(u\right)d_q\left(u\right)=\underset{0}{\overset{r}{\int }}{u}^t{d}_q\left(u\right)={\displaystyle \frac{1}{{[t+1]}_q}}{r}^{t+1},t\ne -1,$$

also

$$\int {\displaystyle \frac{{\partial }_q\psi \left(u\right)}{\psi \left(u\right)}}{d}_q\left(u\right)={ln}_q\psi \left(u\right),$$

and

$${\int }_a^b{\displaystyle \frac{{\partial }_q\psi \left(u\right)}{\psi \left(u\right)}}{d}_q\left(u\right)={ln}_q\psi \left(b\right)-{ln}_q\psi \left(b\right)={ln}_q\left({\displaystyle \frac{\psi \left(b\right)}{\psi \left(a\right)}}\right).$$

(3)

Let $\mu >-1$, and then the function ${\mathcal{F}}_{q,\mu +1}\left(r\right)$ is defined as

$${\mathcal{F}}_{q,\mu +1}\left(r\right)=r+\sum _{t=2}^{\infty }{\displaystyle \frac{{[\mu +1,q]}_{t-1}}{[t-1,q]!}}{r}^t,r\in \mathsf{\Omega },$$

(4)

also, let ${\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)$ be defined as

$${\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)\ast {\mathcal{F}}_{q,\mu +1}\left(r\right)=r{\partial }_q\psi \left(r\right).$$

For $\psi \in \mathcal{A}$, consider the q-integral operator $I_q^{\mu }\psi \left(r\right)$ : $\mathcal{A}⟶\mathcal{A}$, given as

$$I_q^{\mu }\psi \left(r\right)={\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)\ast \psi \left(r\right)=r+\sum _{t=2}^{\infty }{\phi }_{t-1}{a}_t{r}^t,(r\in \mathsf{\Omega }).$$

(5)

The q-integral operator $I_q^{\mu }\psi \left(r\right)$ and ${\phi }_{t-1}$ are defined in [19], where

$${\phi }_{t-1}={\displaystyle \frac{[t,q]!}{{[\mu +1,q]}_{t-1}}}.$$

(6)

When $q⟶1^{-}$, the operator $I_q^{\mu }\psi \left(r\right)$ reduces to the well-known operator defined in [20]. From (5), it can easily be seen that

$$[\mu +1,q]I_q^{\mu }\psi \left(r\right)=[\mu ,q]I_q^{\mu +1}\psi \left(r\right)+q^{\mu }r{\partial }_q{I}_q^{\mu +1}\psi \left(r\right).$$

It can also be noted that

$$I_q^0\psi \left(r\right)=r{\partial }_q\psi \left(r\right)\mathrm{and}{I}_q^1\psi \left(r\right)=\psi \left(r\right).$$

Ma and Minda [21] defined a general form of a family of starlike functions ${\mathcal{S}}^{*}\left(\varphi \right)$ as

$${\mathcal{S}}^{*}\left(\varphi \right)=\left\{\psi \in \mathcal{A}:{\displaystyle \frac{r\psi \prime \left(r\right)}{\psi \left(r\right)}}\prec \varphi \left(r\right),r\in \mathsf{\Omega }\right\},$$

(7)

with $Re\left(\varphi \right)>0$ in $\mathsf{\Omega }$. Geometrically, the function $\varphi$ maps $\mathsf{\Omega }$ onto a star-shaped region whose image domain is also starlike with respect to $\varphi \left(0\right)=1,$$\varphi \prime \left(0\right)>0$ and symmetric about the real axis.

Seoudy and Aouf [22] extended the work of [21] and introduced a generic form of q-starlike functions associated with the q-difference operator, which is defined as

$${\mathcal{S}}_q^{*}\left(\varphi \right)=\left\{\psi \in \mathcal{A}:{\displaystyle \frac{r{\partial }_q\psi \left(r\right)}{\psi \left(r\right)}}\prec \varphi \left(r\right),r\in \mathsf{\Omega }\right\}.$$

(8)

Several authors have defined and investigated new subclasses of analytic and univalent functions by applying different q-operators and setting generalized domains $\varphi \left(r\right)$ in ${\mathcal{S}}_q^{*}\left(\varphi \right)$. For the most recent work on certain q-subclasses of analytic functions, see [23,24,25,26].

Motivated by the above cited work, we define a new q-subclass ${\mathcal{SL}}_s^{*}(\mu ,q)$ of starlike functions by using the q-analogue of the sine function, that is, $\left(sin\right(qr\left)\right)$ and q-integral operator $I_q^{\mu }\psi \left(r\right)$, as follows:

Definition 7.

Let $q\in \left(0,1\right)$ and $\psi \in \mathcal{A}$ be as given in (1). Then, $\psi \in {\mathcal{SL}}_s^{*}(\mu ,q)$ if

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}\prec 1+sin\left(qr\right)(r\in \mathsf{\Omega }),$$

(9)

and equivalently,

$$\psi \in {\mathcal{SL}}_s^{*}(\mu ,q)\iff \left|{sin}^{-1}\left({\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}-1\right)\right|<q.$$

(10)

Geometrically, the class ${\mathcal{SL}}_s^{*}(\mu ,q)$ contains all the functions $\psi \in \mathcal{A}$ such that the image domain of $\mathsf{\Omega }$ under ${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}$ is contained in the image domain of $\mathsf{\Omega }$ under $1+sin\left(qr\right)$. For different values of q, the image domains of unit disk $\mathsf{\Omega }$ under $1+sin\left(qr\right)$ are shown below (see Figure 1, Figure 2 and Figure 3):

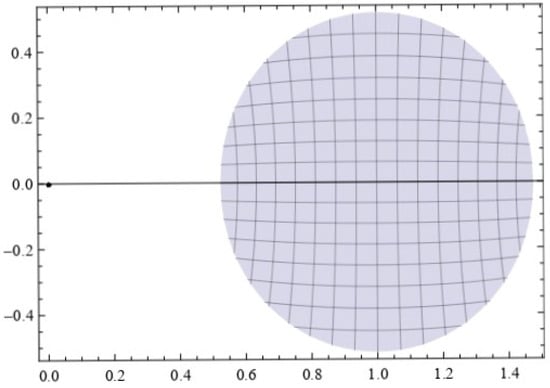
Figure 1. $q=0.5$.

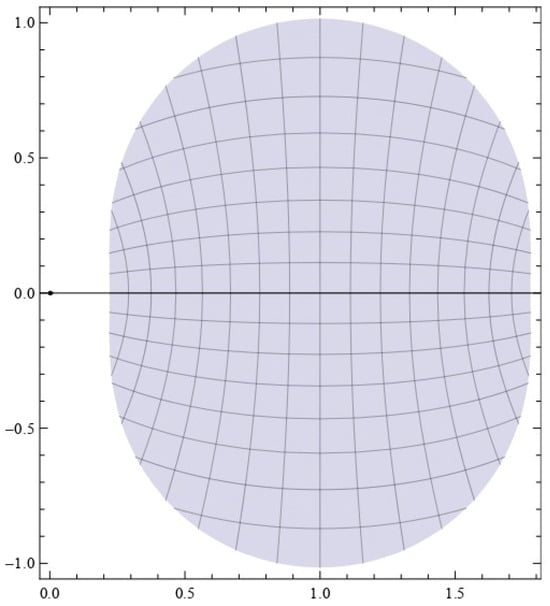
Figure 2. $q=0.9$.

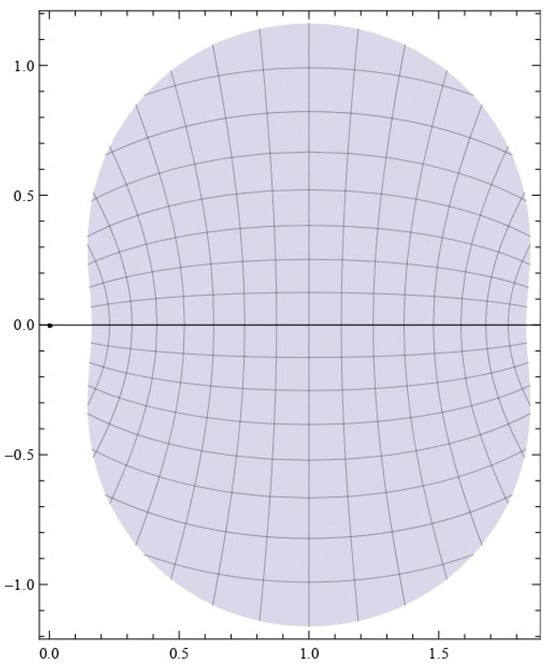
Figure 3. $q=1$.

It can be noted that as $q⟶1^{-}$, the image domain of the unit disk under $1+sin\left(qr\right)$ takes the shape of a curve with an eight-shaped geometry.

Example 1.

Let

$$\psi =r+{\displaystyle \frac{1}{2}}{r}^2,r\in \mathsf{\Omega },$$

(11)

then $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right).$

Proof. 

Let $\psi \in$$\mathcal{A}$ be given in (11). Then, according to (5), we have

$$I_q^{\mu }\psi \left(r\right)=r+{\displaystyle \frac{1}{2}}{\phi }_1{r}^2.$$

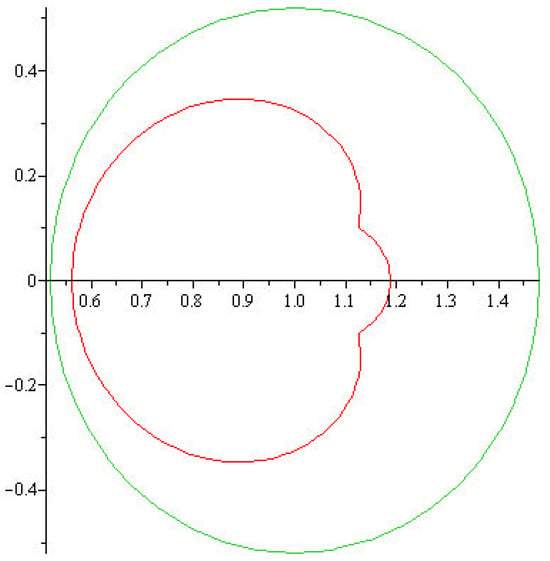
For $\mu =1$ and $q=0.5$, we can see that

$$I_{0.5}^1\psi \left(r\right)=r+{\displaystyle \frac{1}{2}}{r}^2,{\phi }_1=1.$$

After some simple calculations, we have

$$\xi \left(r\right)={\displaystyle \frac{r{\partial }_{0.5}{I}_{0.5}^1\psi \left(r\right)}{I_{0.5}^1\psi \left(r\right)}}=1+0.25r-0.125r^2+0.0625r^3+\dots .$$

Also for $q=0.5$, we have

$$\chi \left(r\right)=1+sin\left(0.5r\right)=1+0.5r-0.020r^3+\dots .$$

By the univalance of “$\chi$” along with the fact that $\xi \left(0\right)=\chi \left(0\right)$ and $\xi \left(\mathsf{\Omega }\right)\subset \chi \left(\mathsf{\Omega }\right)$, as shown in the Figure 4,

Figure 4. The inner and outer curves show the image of unit disc $\mathsf{\Omega }$ under the $\xi$ and $\chi$ functions, respectively.

Then by definition of subordination, we have

$$\xi \left(r\right)\prec \chi \left(r\right),$$

which implies $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(1,0.5\right).$ This example shows that class $\mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$ is non-empty. □

2. A Set of Lemmas

Let $\mathcal{P}$ represent the class of analytic functions $g\left(r\right)$ with $Reg\left(r\right)>0$, $r\in \mathsf{\Omega }$ and meeting the constraint $g\left(0\right)=1$, with the series forming

$$g\left(r\right)=1+\sum _{t=1}^{\infty }{c}_t{r}^t,r\in \mathsf{\Omega }.$$

(12)

Let us have $\psi \in$$\mathcal{A}$ and $g\in \mathcal{P}$ with the series representation given in (1) and (12), respectively. Then, the class $\mathcal{W}\left(\chi ,\xi ,g\right)$ is defined in [27] as

$${\displaystyle \frac{\chi \ast \psi }{\xi \ast \psi }}\prec g,$$

(13)

where

$$\xi \left(r\right)=r+\sum _{t=2}^{\infty }{d}_t{r}^t\mathrm{and}\chi \left(r\right)=r+\sum _{t=2}^{\infty }{e}_t{r}^t.$$

The following Lemmas will be useful in demonstrating our key findings.

Lemma 1

([21]). Let us have $g\in \mathcal{P}$, of the form given in (12). Then,

$$\left|c_2-\eta c_1^2\right|\le \left\{\begin{array}{cc}-4\eta +2\hfill & for(\eta <0),\hfill \\ 2\hfill & for(0\le \eta \le 1),\hfill \\ 4\eta -2\hfill & for(\eta >1).\hfill \end{array}\right.$$

For $\eta =0,$ the given inequality gives sharp bounds if

$$g\left(r\right)=\left({\displaystyle \frac{1-\delta }{2}}\right)\left({\displaystyle \frac{1-r}{1+r}}\right)+\left({\displaystyle \frac{1+\delta }{2}}\right)\left({\displaystyle \frac{1+r}{1-r}}\right),r\in \mathsf{\Omega },\mathrm{and}0\le \delta \le 1.$$

In the case of $\eta <0$ or $\eta >0$, equality holds for the function $g\left(r\right)={\displaystyle \frac{1+r}{1-r}}$ or one of its rotation. For $0<\eta <1,$ the inequality is sharp for $g\left(r\right)={\displaystyle \frac{1+r^2}{1-r^2}}$ or one of its rotation. For $\eta =1,$ sharpness exists if and only if $g\left(r\right)$ is reciprocal of the functions that give equality for $\eta =0.$

Lemma 2

([27]). Let $\psi \in \mathcal{W}\left(\chi ,\xi ,g\right)$ and $e_k\ne d_k$ for (k = 2, 3). Then,

$$\left|a_2\right|\le {\displaystyle \frac{\left|g_1\right|}{\left|e_2-d_2\right|}},\left|a_3\right|\le {\displaystyle \frac{\left|g_1\right|}{\left|e_3-d_3\right|}}max\left\{1,\left|\rho \right|\right\},$$

and

$$\left|a_3-\eta a_2^2\right|\le {\displaystyle \frac{\left|g_1\right|}{\left|e_3-d_3\right|}}max\left\{1,\left|\mu \right|\right\},\eta \in \mathbb{C},$$

where

$$\rho ={\displaystyle \frac{g_2}{g_1}}+{\displaystyle \frac{d_2{g}_1}{e_2-u_2}}\mathrm{and}\mu ={\displaystyle \frac{e_3-d_3}{{\left(e_2-d_2\right)}^2}}{g}_1\eta -\rho .$$

3. Main Results

Theorem 1.

Let $\psi \in \mathcal{A}$. Then,

$$\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)\iff {\displaystyle \frac{1}{r}}\left[I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r-\vartheta q{r}^2}{\left(1-r\right)\left(1-qr\right)}}\right]\ne 0,r\in \mathsf{\Omega },$$

(14)

for $\vartheta ={\vartheta }_{\theta }={\displaystyle \frac{1+sin\left(q{e}^{i\theta }\right)}{sin\left(q{e}^{i\theta }\right)}},$$0\le \theta <2\pi$ as well as $\vartheta =1$.

Proof. 

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$. Then, $\psi \left(r\right)$ is an analytic in $\mathsf{\Omega }$ and $I_q^{\mu }\psi \left(r\right)\ne 0$ for all $r\in {\mathsf{\Omega }}^{*}=\mathsf{\Omega }\setminus \left\{0\right\}$, so it follows that ${\displaystyle \frac{I_q^{\mu }\psi \left(r\right)}{r}}\ne 0$ for all r in $\mathsf{\Omega }$, which shows that the condition in (14) is true for $\vartheta =1.$ On the other hand, according to (9) and using the definition of subordination, we have

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}=1+sin\left(qw\left(r\right)\right),$$

where $w\left(r\right)$ is the Schwarz function with $w\left(0\right)=0$ and $\left|w\left(r\right)\right|<1.$ Consider $w\left(r\right)=e^{i\theta }$, $0\le \theta <2\pi$, and then

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}\ne 1+sin\left(q{e}^{i\theta }\right),$$

(15)

that is,

$${\displaystyle \frac{1}{r}}\left(I_q^{\mu }\psi \left(r\right)\left(1+sin\left(q{e}^{i\theta }\right)\right)-r{\partial }_q{I}_q^{\mu }\psi \left(r\right)\right)\ne 0.$$

(16)

Using the relations

$$I_q^{\mu }\psi \left(r\right)=I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{1-r}},\mathrm{and}r{\partial }_q{I}_q^{\mu }\psi \left(r\right)=I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{\left(1-r\right)\left(1-qr\right)}},$$

(17)

then (16) becomes

$${\displaystyle \frac{1}{r}}\left(\left(I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{1-r}}\right)\left(1+sin\left(q{e}^{i\theta }\right)\right)-\left(I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{\left(1-r\right)\left(1-qr\right)}}\right)\right)\ne 0.$$

After some simple calculations, we obtain

$${\displaystyle \frac{1}{r}}\left(I_q^{\mu }\psi \left(r\right)\ast \left({\displaystyle \frac{sin\left(q{e}^{i\theta }\right)r-\left(1+sin\left(q{e}^{i\theta }\right)\right)q{r}^2}{\left(1-r\right)\left(1-qr\right)}}\right)\right)\ne 0,$$

and this expression can be written as

$${\displaystyle \frac{sin\left(q{e}^{i\theta }\right)}{r}}\left(I_q^{\mu }\psi \left(r\right)\ast \left({\displaystyle \frac{r-\frac{\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}q{r}^2}{\left(1-r\right)\left(1-qr\right)}}\right)\right)\ne 0,$$

which leads to (14).

Conversely, suppose that the condition (14) holds. Let $\xi \left(r\right)={\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}$ be analytic in $\mathsf{\Omega }$ along with $\xi \left(0\right)=1$, and additionally suppose that $\chi \left(r\right)=1+sin\left(q{e}^{i\theta }\right)$, $r\in \mathsf{\Omega }$. Since the conditions given in (14) and (15) are identical, then from (15), we can say that $\chi \left(\partial \mathsf{\Omega }\right)\cap \xi \left(\mathsf{\Omega }\right)=\varphi$. Therefore, the simply connected component $\mathbb{C}\setminus \chi \left(\partial \mathsf{\Omega }\right)$ contains the domain $\xi \left(\mathsf{\Omega }\right)$, which is also connected. Now, according to the univalence of “$\chi$”, together with the assumption $\xi \left(0\right)=\chi \left(0\right)=1$, it is clear that $\xi \prec \chi$, which means that $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$. □

Corollary 1.

Let $\psi \in \mathcal{A}$, then the necessary and sufficient condition for a function $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$ is

$$1-\sum _{t=2}^{\infty }\left\{{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right\}{\phi }_{t-1}{a}_t{r}^{t-1}\ne 0,r\in \mathsf{\Omega },$$

(18)

where ${\phi }_{t-1}$ is given in (6).

Proof. 

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$, then according to Theorem 1, we have

$${\displaystyle \frac{1}{r}}\left[I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r-\vartheta q{r}^2}{\left(1-r\right)\left(1-qr\right)}}\right]\ne 0,$$

which is equivalent to

$$\begin{array}{ccc}& =& {\displaystyle \frac{1}{r}}\left[I_q^{\mu }\psi \left(r\right)\ast \left({\displaystyle \frac{r}{\left(1-r\right)\left(1-qr\right)}}\right)-I_q^{\mu }\psi \left(r\right)\ast \left({\displaystyle \frac{\vartheta q{r}^2}{\left(1-r\right)\left(1-qr\right)}}\right)\right]\ne 0,\hfill \\ & =& {\displaystyle \frac{1}{r}}\left[I_q^{\mu }\psi \left(r\right)\ast \left({\displaystyle \frac{r}{\left(1-r\right)\left(1-qr\right)}}\right)-\vartheta \left(I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{\left(1-r\right)\left(1-qr\right)}}-I_q^{\mu }\psi \left(r\right)\ast {\displaystyle \frac{r}{\left(1-r\right)}}\right)\right]\ne 0.\hfill \end{array}$$

Now, using the properties of convolution given in (17), we have

$$\left(1-\vartheta \right){\partial }_q{I}_q^{\mu }\psi \left(r\right)+\vartheta {\displaystyle \frac{I_q^{\mu }\psi \left(r\right)}{r}}\ne 0.$$

(19)

Since

$$I_q^{\mu }\psi \left(r\right)=r+\sum _{t=2}^{\infty }{\phi }_{t-1}{a}_t{r}^t\mathrm{and}{\partial }_q{I}_q^{\mu }\psi \left(r\right)=1+\sum _{t=2}^{\infty }\left[t,q\right]{\phi }_{t-1}{a}_t{r}^{t-1}.$$

Putting these values in (19), we have

$$\left(1-\vartheta \right)\left(1+\sum _{t=2}^{\infty }\left[t,q\right]{\phi }_{t-1}{a}_t{r}^{t-1}\right)+\vartheta \left(1+\sum _{t=2}^{\infty }{\phi }_{t-1}{a}_t{r}^{t-1}\right)\ne 0.$$

Using the value of ${\vartheta }_{\theta }$ from Theorem 1, we obtain

$$1-\sum _{t=2}^{\infty }\left\{{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right\}{\phi }_{t-1}{a}_t{r}^{t-1}\ne 0.$$

□

Corollary 2.

Let $\psi \in \mathcal{A}$, as given in (1), which satisfies the condition

$$\sum _{t=2}^{\infty }\left|{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right|\left|{\phi }_{t-1}\right|\left|a_t\right|<1,$$

(20)

then $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right).$

Proof. 

Consider

$$\begin{array}{ccc}& & \left|1-\sum _{t=2}^{\infty }\left\{{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right\}{\phi }_{t-1}{a}_t{r}^{t-1}\right|\hfill \\ & \ge & 1-\sum _{t=2}^{\infty }\left|{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right|\left|{\phi }_{t-1}\right|\left|a_t\right|.\hfill \end{array}$$

According to (20), we have

$$1-\sum _{t=2}^{\infty }\left|{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right|\left|{\phi }_{t-1}\right|\left|a_t\right|>0.$$

(21)

Hence, according to Corollary 1, we have $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$. □

Theorem 2.

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right),$ then the integral representation of $I_q^{\mu }\psi \left(r\right)$ is given as

$$I_q^{\mu }\psi \left(r\right)=I_q^{\mu }\psi \left(r_0\right)\times {exp}_q\underset{r_0}{\overset{r}{\int }}\left({\displaystyle \frac{1+sinq\left(w\left(t\right)\right)}{t}}\right)d_{q}t.$$

(22)

with $\left|w\left(r\right)\right|<1$ and $r$, $r_0\in \mathsf{\Omega }$ such that $r_0⟶0$.

Proof. 

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right),$ then according to (9), we have

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}=1+sin\left(qw\left(r\right)\right),$$

(23)

where $w\left(r\right)$ is the Schwarz function with $w\left(0\right)=0$ and $\left|w\left(r\right)\right|<1.$ By taking q-integration, we have

$$\underset{r_0}{\overset{r}{\int }}{\displaystyle \frac{{\partial }_q{I}_q^{\mu }\psi \left(t\right)}{I_q^{\mu }\psi \left(t\right)}}{d}_{q}t=\underset{r_0}{\overset{r}{\int }}{\displaystyle \frac{\left(1+sinqw\left(t\right)\right)}{t}}{d}_{q}t.$$

By using the property of q-integration, we have

$${ln}_q\left({\displaystyle \frac{I_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r_0\right)}}\right)=\underset{r_0}{\overset{r}{\int }}{\displaystyle \frac{\left(1+sinqw\left(t\right)\right)}{t}}{d}_{q}t.$$

After some simplifications, we obtain

$$I_q^{\mu }\psi \left(r\right)=I_q^{\mu }\psi \left(r_0\right)\times {exp}_q\underset{r_0}{\overset{r}{\int }}\left({\displaystyle \frac{1+sinq\left(w\left(t\right)\right)}{t}}\right)d_{q}t.$$

□

3.1. Coefficient Estimates and the Fekete–Szegö Problem

Let $\psi \in \mathcal{A}$, with the series representation given in (1). Then, for any parameter $\lambda$ (real or complex), the factor $\left|a_3-\lambda a_2^2\right|$ is known as the Fekete–Szegö problem. As a special case, that is, for $\lambda =1$, this functional plays an important role in the study of the sharp coefficient problems of Hankel and Toeplitz determinants, as well as generalized Zalcman conjectures and more useful inequalities. In the recent past, many authors have studied this inequality for various classes of analytic functions; see ([28,29,30]). In this section, we find the bounds of the Fekete–Szegö inequality for functions belonging to the class ${\mathcal{SL}}_s^{*}(\mu ,q)$.

Theorem 3.

Let $\psi \in$${\mathcal{SL}}_s^{*}(\mu ,q)$ of the form given in (1). Then,

$$\left|a_3-\lambda a_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{-\lambda (1+q){\phi }_2+{\phi }_1^2}{(1+q){\phi }_1^2{\phi }_2}}\hfill & \mathrm{for}\lambda <0,\hfill \\ {\displaystyle \frac{1}{(1+q){\phi }_2}},\hfill & \mathrm{for}0\le \lambda \le {\displaystyle \frac{2{\phi }_1^2}{(1+q){\phi }_2}},\hfill \\ {\displaystyle \frac{\lambda (1+q){\phi }_2-{\phi }_1^2}{(1+q){\phi }_1^2{\phi }_2}},\hfill & \mathrm{for}\lambda >{\displaystyle \frac{2{\phi }_1^2}{(1+q){\phi }_2}}.\hfill \end{array}\right.$$

where ${\phi }_1$ and ${\phi }_2$ are obtained from (6).

Proof. 

Let $\psi \in$${\mathcal{SL}}_s^{*}(\mu ,q)$. Then, according to (9), we have

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}=1+sin\left(qw\left(r\right)\right),$$

(24)

where $w\left(r\right)$ is a Schwarz function. Let $g\in \mathcal{P}$, and then

$$g\left(r\right)={\displaystyle \frac{1+w\left(r\right)}{1-w\left(r\right)}}=1+c_{1}r+c_2{r}^2+c_3{r}^3+\dots ,$$

which implies

$$\begin{array}{ccc}\hfill w\left(r\right)& =& {\displaystyle \frac{1}{2}}{c}_{1}r+\left({\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{4}}{c}_1^2\right)r^2+\left({\displaystyle \frac{1}{8}}{c}_1^3-{\displaystyle \frac{1}{2}}{c}_1{c}_2+{\displaystyle \frac{1}{2}}{c}_3\right)r^3\hfill \\ & & +\left({\displaystyle \frac{1}{2}}{c}_4-{\displaystyle \frac{1}{2}}{c}_1{c}_3-{\displaystyle \frac{1}{4}}{c}_2^2-{\displaystyle \frac{1}{16}}{c}_1^4+{\displaystyle \frac{3}{8}}{c}_1^2{c}_2\right)r^4+\dots .\hfill \end{array}$$

As

$$1+sin\left(qr\right)=1+qr-{\displaystyle \frac{1}{6}}{q}^3{r}^3+{\displaystyle \frac{1}{120}}{q}^5{r}^5-{\displaystyle \frac{1}{5040}}{q}^7{r}^7+\dots .$$

(25)

Using the value of $w\left(r\right)$ in (25), and after some simplifications, we obtain

$$1+sin\left(qw\left(r\right)\right)=1+q{\displaystyle \frac{c_1}{2}}r+q\left({\displaystyle \frac{c_2}{2}}-{\displaystyle \frac{c_1^2}{4}}\right)r^2+\left(-{\displaystyle \frac{q^3{c}_1^3}{48}}+q(-{\displaystyle \frac{c_1{c}_2}{4}}+{\displaystyle \frac{c_3}{2}}-{\displaystyle \frac{c_1{c}_2}{4}}+{\displaystyle \frac{c_1^3}{8}})\right)r^3+\dots .$$

(26)

Similarly,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}& =& 1+\left(([2,q]-1)a_2{\phi }_1\right)r+\left((1-[2,q])a_2^2{\phi }_1^2+([3,q]-1)a_3{\phi }_2\right)r^2\hfill \\ & & +\left(([4,q]-1)a_4{\phi }_3+(2-[2,q]-[3,q]){\phi }_1{\phi }_2{a}_2{a}_3\right)r^3+\dots .\hfill \end{array}$$

(27)

From (26) and (27), we have

$$a_2={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{q}{{\phi }_1([2,q]-1)}}{c}_1\right),$$

(28)

and

$$a_3={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{q}{{\phi }_2([3,q]-1)}}{c}_2\right).$$

(29)

Therefore,

$$\left|a_3-\lambda a_2^2\right|={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{q}{{\phi }_2([3,q]-1)}}\right)\left|c_2-\lambda {\displaystyle \frac{{\phi }_2([3,q]-1)}{2q{\phi }_1^2}}{c}_1^2\right|.$$

Using the definition of q-number and by applying Lemma 1, we have

$$\left|a_3-\lambda a_2^2\right|\le {\displaystyle \frac{1}{2(1+q){\phi }_2}}\left\{\begin{array}{cc}-4\left({\displaystyle \frac{\lambda {\phi }_2([3,q]-1)}{2q{\phi }_1^2}}\right)+2\hfill & \mathrm{for}{\displaystyle \frac{\lambda {\phi }_2([3,q]-1)}{2q{\phi }_1^2}}<0,\hfill \\ 2\hfill & \mathrm{for}0\le {\displaystyle \frac{\lambda {\phi }_2([3,q]-1)}{2q{\phi }_1^2}}\le 1,\hfill \\ 4\left({\displaystyle \frac{\lambda {\phi }_2([3,q]-1)}{2q{\phi }_1^2}}\right)-2\hfill & \mathrm{for}{\displaystyle \frac{\lambda {\phi }_2([3,q]-1)}{2q{\phi }_1^2}}>1.\hfill \end{array}\right.$$

This is equivalent to

$$\left|a_3-\lambda a_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{-\lambda (1+q){\phi }_2+{\phi }_1^2}{(1+q){\phi }_1^2{\phi }_2}}\hfill & \mathrm{for}\lambda <0,\hfill \\ {\displaystyle \frac{1}{(1+q){\phi }_2}},\hfill & \mathrm{for}0\le \lambda \le {\displaystyle \frac{2{\phi }_1^2}{(1+q){\phi }_2}},\hfill \\ {\displaystyle \frac{\lambda (1+q){\phi }_2-{\phi }_1^2}{(1+q){\phi }_1^2{\phi }_2}},\hfill & \mathrm{for}\lambda >{\displaystyle \frac{2{\phi }_1^2}{(1+q){\phi }_2}}.\hfill \end{array}\right.$$

□

In our next result, we will discuss the Fekete–Szegö problem for a complex parameter $\lambda$. Before proving the Fekete–Szegö result, it is important to mention that for $\psi \in \mathcal{A},$ having the series representation given in (1), along with

$$\begin{array}{ccc}\hfill {\xi }_1& =& {\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)=r+\sum _{t=2}^{\infty }{\phi }_{t-1}{r}^t=r+{\phi }_1{r}^2+{\phi }_2{r}^3+{\phi }_3{r}^4+\dots ,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\chi }_1& =& r{\partial }_q{\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)=r+\sum _{t=2}^{\infty }[t,q]{\phi }_{t-1}{r}^t=r+[2,q]{\phi }_1{r}^2+[3,q]{\phi }_2{r}^3+\dots ,\hfill \end{array}$$

(31)

also

$$g_q\left(r\right)=1+sin\left(qr\right)=1+qr-{\displaystyle \frac{1}{6}}{q}^3{r}^3+{\displaystyle \frac{1}{120}}{q}^5{r}^5-\dots ,$$

(32)

and

$$I_q^{\mu }\psi \left(r\right)=r+\sum _{t=2}^{\infty }{\phi }_{t-1}{a}_t{r}^t=\left(r+\sum _{t=2}^{\infty }{\phi }_{t-1}{r}^t\right)\ast \left(r+\sum _{t=2}^{\infty }{a}_t{r}^t\right)={\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)\ast \psi \left(r\right),r\in \mathsf{\Omega },$$

(33)

$$r{\partial }_q{I}_q^{\mu }\psi \left(r\right)=\left(r+\sum _{t=2}^{\infty }[t,q]{\phi }_{t-1}{r}^t\right)\ast \left(r+\sum _{t=2}^{\infty }{a}_t{r}^t\right)=r{\partial }_q{\mathcal{F}}_{q,\mu +1}^{-1}\left(r\right)\ast \psi \left(r\right),r\in \mathsf{\Omega }.$$

(34)

From (30)–(34), we have

$${\displaystyle \frac{r{\partial }_q{I}_q^{\mu }\psi \left(r\right)}{I_q^{\mu }\psi \left(r\right)}}={\displaystyle \frac{{\chi }_1\left(r\right)\ast \psi \left(r\right)}{{\xi }_1\left(r\right)\ast \psi \left(r\right)}},$$

thus, we conclude that the newly defined class $\mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$ is a particular case of the class $\mathcal{W}\left(\xi ,\chi ,g\right)$, that is,

$$\mathcal{W}\left({\xi }_1,{\chi }_1,g_q\right)=\mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right).$$

(35)

Moreover, by applying Lemma 2 on (35), we have the following corollary.

Corollary 3.

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$ be of the form given in (1). Then,

$$\left|a_2\right|\le {\displaystyle \frac{1}{\left|{\phi }_1\right|}},\left|a_3\right|\le {\displaystyle \frac{1}{\left(1+q\right)\left|{\phi }_2\right|}},$$

and

$$\left|a_3-\lambda a_2^2\right|\le {\displaystyle \frac{1}{\left(1+q\right)\left|{\phi }_2\right|}}max\left\{1,\left|\eta \right|\right\},\lambda \in \mathbb{C},$$

where ${\phi }_1$ and ${\phi }_2$ are from (6), and

$$\eta ={\displaystyle \frac{\left(e_3-d_3\right)}{{\left(e_2-d_2\right)}^2}}{g}_1\lambda -{\displaystyle \frac{g_2}{g_1}}-{\displaystyle \frac{d_2{g}_1}{e_2-d_2}}.$$

Proof. 

Let $\psi \in \mathcal{S}{\mathcal{L}}_s^{*}\left(\mu ,q\right)$ then by Equations (30)–(32), we have

$$d_2={\phi }_1,d_3={\phi }_2,e_2=[2,q]{\phi }_1,e_3=[3,q]{\phi }_2,$$

and

$$\begin{array}{c}\hfill g_1=q,g_2=0.\end{array}$$

Now by Lemma $2,$ we can see that

$$\left|a_2\right|\le {\displaystyle \frac{1}{\left|{\phi }_1\right|}}.$$

Since by Lemma $2,$

$$\left|a_3\right|\le {\displaystyle \frac{\left|g_1\right|}{\left|e_3-d_3\right|}}max\left\{1,\left|\rho \right|\right\},$$

where

$$\rho ={\displaystyle \frac{g_2}{g_1}}+{\displaystyle \frac{d_2{g}_1}{e_2-d_2}},$$

using the values of $g_1$, $g_2$, $d_2$ and $e_2$ and simplifying, we get $\left|\rho \right|$ = 1. Hence

$$\left|a_3\right|\le {\displaystyle \frac{1}{\left(1+q\right)\left|{\phi }_2\right|}}.$$

Similarly,

$$\left|a_3-\lambda a_2^2\right|\le {\displaystyle \frac{\left|g_1\right|}{\left|e_3-d_3\right|}}max\left\{1,\left|\eta \right|\right\},$$

where

$$\eta ={\displaystyle \frac{\left(e_3-d_3\right)}{{\left(e_2-d_2\right)}^2}}{g}_1\lambda -\rho .$$

□

3.2. Partial Sums Results

In Geometric Function Theory, the partial sum of the series form of analytic and univalent functions plays a crucial role in our understanding of the behaviour of these functions, especially convergence and divergence. In terms of geometric properties, partial sums are used to study coefficient bounds, distortion and growth problems, and radius problems, as well as subordination and superordination results.

Silverman [31] was the first who found the sharp bounds for the ratio of a function to its partial sums for the subclasses of analytic functions. In this portion, we find some lower bound results of the function defined in (1) to its partial sum, which is defined as

$${\psi }_t\left(r\right)=r+\sum _{k=2}^t{a}_k{r}^k(r\in \mathsf{\Omega }).$$

(36)

Theorem 4.

Let $\psi \in \mathcal{A}$ of the form given in (1), and assume that the coefficients of ψ are so small that they satisfy the condition (21). Then,

$$Re\left({\displaystyle \frac{\psi \left(r\right)}{{\psi }_t\left(r\right)}}\right)\ge 1-{\displaystyle \frac{1}{{\epsilon }_{t+1}}}(r\in \mathsf{\Omega }),$$

(37)

and

$$Re\left({\displaystyle \frac{{\psi }_t\left(r\right)}{\psi \left(r\right)}}\right)\ge {\displaystyle \frac{{\epsilon }_{t+1}}{1+{\epsilon }_{t+1}}}(r\in \mathsf{\Omega }),$$

(38)

where

$${\epsilon }_t=\left|{\displaystyle \frac{\left[t,q\right]-\left(1+sin\left(q{e}^{i\theta }\right)\right)}{sin\left(q{e}^{i\theta }\right)}}\right|\left|{\phi }_{t-1}\right|.$$

(39)

The inequalities (37) and (38) are sharp for the function

$$\psi \left(r\right)=r+{\displaystyle \frac{1}{{\epsilon }_{t+1}}}{r}^{t+1}.$$

(40)

Proof. 

Consider

$$w\left(r\right)={\epsilon }_{t+1}\left[{\displaystyle \frac{\psi \left(r\right)}{{\psi }_t\left(r\right)}}-(1-{\displaystyle \frac{1}{{\epsilon }_{t+1}}})\right],$$

and after some simple calculations, we have

$$w\left(r\right)={\displaystyle \frac{1+{\displaystyle \sum _{t=2}^k}{a}_t{r}^{t-1}+{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}{a}_t{r}^{t-1}}{1+{\displaystyle \sum _{t=2}^k}{a}_t{r}^{t-1}}}={\displaystyle \frac{1+{\varsigma }_1\left(r\right)}{1-{\varsigma }_1\left(r\right)}},$$

which gives

$${\varsigma }_1\left(r\right)={\displaystyle \frac{w\left(r\right)-1}{w\left(r\right)+1}}={\displaystyle \frac{{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}{a}_t{r}^{t-1}}{2+2{\displaystyle \sum _{t=2}^k}{a}_t{r}^{t-1}+{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}{a}_t{r}^{t-1}}}.$$

By taking the modulus and applying the triangular inequality, we obtain

$$\left|{\varsigma }_1\left(r\right)\right|=\left|{\displaystyle \frac{w\left(r\right)-1}{w\left(r\right)+1}}\right|\le {\displaystyle \frac{{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}\left|a_t\right|}{2-2{\displaystyle \sum _{t=2}^k}\left|a_t\right|-{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}\left|a_t\right|}}.$$

To prove the required result, that is, $Rew\left(r\right)\ge 0$ in $\mathsf{\Omega },$ we just need to show $\left|{\varsigma }_1\left(r\right)\right|\le 1$ in $\mathsf{\Omega }$. Therefore, $\left|{\varsigma }_1\left(r\right)\right|\le 1$ gives

$$\sum _{t=2}^k\left|a_t\right|+{\epsilon }_{t+1}\sum _{t=k+1}^{\infty }\left|a_t\right|\le 1.$$

(41)

Since $\psi \left(r\right)$ satisfies (21), then to prove (37), it would be enough to show that the left-hand side of (41) is bounded above by ${\displaystyle \sum _{t=2}^{\infty }}{\epsilon }_t\left|a_t\right|$ and is equal to

$$\sum _{t=2}^k\left({\epsilon }_t-1\right)\left|a_t\right|+\sum _{t=k+1}^{\infty }\left({\epsilon }_t-{\epsilon }_{t+1}\right)\left|a_t\right|\ge 0.$$

(42)

On account of inequality (42), we can obtain the required result.

Similarly, to prove assertion (38), let

$$w\left(r\right)=\left(1+{\epsilon }_{t+1}\right)\left({\displaystyle \frac{{\psi }_t\left(r\right)}{\psi \left(r\right)}}-{\displaystyle \frac{{\epsilon }_{t+1}}{1+{\epsilon }_{t+1}}}\right),$$

which implies

$$w\left(r\right)={\displaystyle \frac{1+{\displaystyle \sum _{t=2}^k}{a}_t{r}^{t-1}-{\epsilon }_{t+1}{\displaystyle \sum _{t=k+1}^{\infty }}{a}_t{r}^{t-1}}{1+{\displaystyle \sum _{t=2}^k}{a}_t{r}^{t-1}}}.$$

Therefore,

$$\left|{\displaystyle \frac{w\left(r\right)-1}{w\left(r\right)+1}}\right|\le {\displaystyle \frac{(1+{\epsilon }_{t+1}){\displaystyle \sum _{t=k+1}^{\infty }}\left|a_t\right|}{2-2{\displaystyle \sum _{t=2}^k}\left|a_t\right|-\left({\epsilon }_{t+1}-1\right){\displaystyle \sum _{t=k+1}^{\infty }}\left|a_t\right|}}.$$

Now, one can see that $\left|{\displaystyle \frac{w\left(r\right)-1}{w\left(r\right)+1}}\right|\le 1,$ if and only if

$$\sum _{t=2}^k\left|a_t\right|+{\epsilon }_{t+1}\sum _{t=k+1}^{\infty }\left|a_t\right|\le 1.$$

(43)

The inequality in (38) follows if the left-hand side of (43) is bounded above by ${\displaystyle \sum _{t=2}^{\infty }}{\epsilon }_t\left|a_t\right|$.

To ensure that the function defined in (40) gives sharp bounds, we set $r=\rho e^{\iota {\displaystyle \frac{\pi }{t}}}$, and then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\psi \left(r\right)}{{\psi }_t\left(r\right)}}& =& 1+{\displaystyle \frac{1}{{\epsilon }_{t+1}}}{r}^t\hfill \\ & =& 1+{\displaystyle \frac{1}{{\epsilon }_{t+1}}}{\rho }^t{e}^{\iota \pi .}\hfill \end{array}$$

This implies

$${\displaystyle \frac{\psi \left(r\right)}{{\psi }_t\left(r\right)}}=1-{\displaystyle \frac{1}{{\epsilon }_{t+1}}},\mathrm{when}\rho ⟶1.$$

Similarly, the sharpness for (38) can be proved. □

Theorem 5.

Let $\psi \in \mathcal{A}$ of the form given in (1), which satisfies the condition (21). Then,

$$Re\left({\displaystyle \frac{{\psi }^{\prime }\left(r\right)}{{\psi }_t^{\prime }\left(r\right)}}\right)\ge 1-{\displaystyle \frac{t+1}{{\epsilon }_{t+1}}},(r\in \mathsf{\Omega })$$

(44)

and

$$Re\left({\displaystyle \frac{{\psi }_t^{\prime }\left(r\right)}{{\psi }^{\prime }\left(r\right)}}\right)\ge {\displaystyle \frac{{\epsilon }_{t+1}}{t+1+{\epsilon }_{t+1}}},(r\in \mathsf{\Omega }),$$

(45)

where ${\epsilon }_t$ is given in (39).

Proof. 

The proof follows by working on similar lines as in Theorem 4. □

4. Conclusions

In this article, considering the importance and applications of q-calculus, we used the q-trigonometric function and q-integral operator to define and investigate a new subclass ${\mathcal{SL}}_s^{*}(\mu ,q)$ of normalized analytic functions in the open unit disc $\mathsf{\Omega }$. We obtained several interesting results of analytic functions belonging to this newly defined class. In this article, our findings include necessary and sufficient conditions for a function $\psi \in \mathcal{A}$ to be in the class ${\mathcal{SL}}_s^{*}(\mu ,q)$. Moreover, we drew the image domains of unit disc under different functions, and found the integral representation, coefficient estimates, Fekete–Szegö problems and partial sum results for the function satisfying certain condition in the class ${\mathcal{SL}}_s^{*}(\mu ,q)$. Hopefully, the research carried out in this article will be beneficial for researchers working in GFT, quantum calculus and related areas.