Stochastic Dynamics Analysis of Epidemic Models Considering Negative Feedback of Information

Abstract

In this article, we mainly consider the dynamic analysis of a stochastic infectious disease model with negative feedback, a symmetric and compatible distribution family. Based on the sir epidemic model taking into account the isolation (y) and the death (v), we consider adding a new variable (w) to control the information of non-drug interventions, which measures transformations in isolation performance that determine the epidemic, and establish a new model. We have demonstrated various properties of the model solution using Lyapunov functions for this model. To begin with, we demonstrate the existence and uniqueness of the global positive solution. After that, we obtained the conditions that need to be met for the extinction of the disease and verified the correctness of the conclusion by simulating numerical values. Afterwards, we prove the stochastic boundedness and stationary distribution of the model solution.

1. Introduction

Infectious diseases are still a significant issue that seriously endangers human health and life safety, and the harm of contagious diseases is a global public health problem that needs to be addressed. From smallpox, cholera, SARS, AIDS, and H1N1 to COVID-19, infectious diseases have greatly threatened people’s physical and mental health. Therefore, preventing and treating infectious diseases has always been an essential aspect of building a good living environment, and researchers from various disciplines use different methods to study infectious diseases. In the field of biomathematics, Tillett and Ruan et al. [1,2,3] applied mathematical modeling methods to study infectious diseases. Through dynamic analysis of infectious disease models, they dynamically simulate the development of infectious diseases, make predictions based on actual infection data, and based on the conclusions drawn from the research, corresponding recommendations for infectious disease prevention and control are proposed. Many infectious disease models are deterministic [4,5,6,7,8,9], including various features such as time delay, immunity, multi-group, network, etc., making the established mathematical models close to the natural propagation process. However, deterministic models have to some extent simplified the model of transmission process of infectious diseases. Because in actual living environments, various environmental factors can interfere with the spread of infectious diseases, thereby affecting their development. Therefore, considering stochastic Brownian motion [10,11,12,13,14] in the deterministic system will help the model to more accurately predict the dynamic behavior of infectious diseases and provide help for the precaution and containment of infectious diseases.

With the advancement of science, vaccination has been widely applied, and for some diseases, vaccination is an effective means of prevention and control. However, when a newly emerging infectious disease begins to spread in a region, vaccines cannot quickly control the spread of the disease. Furthermore, some non-drug interventions (such as isolation, media promotion, etc.) are very important. Isolation is an incipient precaution measure, while treatment is a later means of treating patients who have already fallen ill. Even if effective medications can be used to treat infectious diseases, a large patient population can never be treated without causing the emergence of new cases. And because isolation and anti-epidemic measures are considerably more crucial in the absence of specific treatments and vaccinations, prevention will save hundreds or even thousands of lives more often. Taking China’s COVID-19 epidemic as an example. Since COVID-19 broke out in 2019, China always adhered to the concept of “people first and life first”, actively, scientifically, and orderly formulated epidemic prevention policies, and constantly optimized and adjusted policies based on the development and changes of the epidemic. So as to win a window period for vaccine drug research and development, and ensure people’s life safety to the greatest extent. Isolation and control are also key measures to block the hidden spread of the epidemic and achieve “social zero”. For isolated personnel, exact health examination and NAT during isolation can realize earlier investigation, estimation, and settlement to avoid illness delay. For others, isolating close contacts of infectious diseases can prevent further spread of the virus and contain the spread of the outbreak.

However, since the COVID-19 epidemic in Europe and the US, protests against quarantine laws, pleas for freedom, and rallies have persisted from Italy to the US to Australia and Brazil. The main reasons for people’s collective protests are: first, in terms of the economy, many enterprises were forced to lay off workers due to the outbreak of the epidemic, resulting in continuously high unemployment rates. Many people had no source of income and no savings and could only hope for government relief. Even though the government has offered pandemic subsidies to the populace, they are insufficient to address long-term living issues. The best solution is to resume work and restore income as soon as possible, so some people are also unwilling to quarantine at home. Second, in terms of culture, some citizens’ values of freedom and democracy have become deeply ingrained. They interpret the epidemic prevention and control measures taken by various states, such as home quarantine and maintaining social distancing, as violating their human rights and causing them to lose their freedom. Thirdly, in terms of hygiene, many people are concerned that inadequate disinfection and other measures during quarantine may further increase the risk of infection. This negative information will affect the implementation of quarantine measures. In light of the aforementioned factors, we present and investigate an infectious illness stochastic differential equation model in this study, taking into account the impact of information exponential function and negative feedback on non-drug treatment parameters (such as isolation and quarantine).

Some literature has analyzed the impact of negative feedback on disease occurrence [15,16,17,18,19]. D’Onof Rio et al. [15] investigated the SIR model, while Vargas and D’Onof Rio [16] discussed the SEIR model. At the same time, they all considered negative feedback factors. They proposed three descriptions of information linear indexes and analyzed the model through ordinary differential equations. Due to factors such as the ecological environment, various antiviral drugs, and biological evolution, the variation of pathogens is more frequent. The variation of pathogens increases the duration of host infection. Therefore, the mutation of pathogens can have a huge impact on the prevention and reign of infectious diseases. Establishing a mathematical model for the spread of infectious diseases based on the actual situation, analyzing the modifies in the number of infected persons, and simulating the development and epidemic trend of infectious diseases should play a positive guiding role in the precaution and containment of infectious diseases, and the mathematical model can aid us to understand and analyze the transmission behavior of infectious diseases from a broader perspective. In addition, considering the effect of different individual immunizations on the incubation period of infectious diseases, this will take some time for the susceptible to become infectious after being infected. The delay of infectious diseases is generally 2–14 days, such as cholera in about 2 days, and COVID-19 in 14 days [20,21]. These all indicate that the infection of a disease exhibits hysteresis and is continuous during the infection period [22,23], so the distribution delay can better reflect its hysteresis. In this article, we think about a stochastic distributed time-delay infectious disease model with a negative feedback isolation rate based on a nonlinear information index.

Due to Roxana López-Cruz and Alberto D’Onofrio’s insightful work [15,24], we have now established a stochastic infectious disease model with negative information feedback. Firstly, on account of the sir infectious disease model, we think about the divided population (y) and the demised population (v) and find an infectious disease model with temporary isolation for a period of time.

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\lambda (1-x(t\left)\right)-\delta z\left(t\right)x\left(t\right)+\eta y\left(t\right)-\rho x\left(t\right)\hfill \\ \hfill \dot{y}\left(t\right)& =\rho x\left(t\right)-(\eta +\lambda )y\left(t\right)\hfill \\ \hfill \dot{z}\left(t\right)& =\delta z\left(t\right)x\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)\hfill \\ \hfill \dot{u}\left(t\right)& =\gamma z\left(t\right)-\lambda u\left(t\right)\hfill \\ \hfill \dot{v}\left(t\right)& =\omega z\left(t\right).\hfill \end{array}\right.$$

(1)

This system can better describe the epidemic trend of a class of infectious diseases requiring isolation measures, such as COVID-19. During the epidemic of COVID-19, due to the interference of various factors, people have some concerns. In this article, we call these concerns negative information feedback. Then, adding negative feedback variables of information index to the model, which reflects how incorrect information affects non-drug (segregation, etc.) or drug steps (immunization, etc.). We incorporate these factors into the pandemic dynamics caused by infectious diseases and set up a new infectious disease model with a temporary isolation period and negative feedback.

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\lambda (1-x(t\left)\right)-\delta z\left(t\right)x\left(t\right)+\eta y\left(t\right)-\rho \left(w\right)x\left(t\right)\hfill \\ \hfill \dot{y}\left(t\right)& =\rho \left(w\right)x\left(t\right)-(\eta +\lambda )y\left(t\right)\hfill \\ \hfill \dot{z}\left(t\right)& =\delta z\left(t\right)x\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)\hfill \\ \hfill \dot{u}\left(t\right)& =\gamma z\left(t\right)-\lambda u\left(t\right)\hfill \\ \hfill \dot{v}\left(t\right)& =\omega z\left(t\right)\hfill \\ \hfill w\left(t\right)& ={\int }_{-\infty }^{t}f(x\left(\tau \right),z\left(\tau \right))K_{a_1}(t-\tau )d\tau .\hfill \end{array}\right.$$

(2)

Among them, $x\left(t\right)$, $y\left(t\right)$, $z\left(t\right)$, $u\left(t\right)$, and $v\left(t\right)$ are the number of susceptible, divided, infected, recovered, and demised populations at time t, respectively, and $w\left(t\right)$ is the information index at time t (regarding the corresponding disease), $\lambda$ is the birth rate or natural mortality rate of each individual, $\delta$ is the effective contact rate, and $\eta$ is the desertion of a non-pharmaceutical intervention rate, $\gamma$ is recovery rate, $\omega$ is the mortality rate caused by infection, $\tau$ is a delay in the feedback effect of information in the isolation policy for susceptible populations to avoid the transmission of diseases, $K_{a_1}(t-\tau )$ is a delayed selection kernel. In this study, we apply the weak delay kernel $K_{a_1}(t-\tau )=a_1{e}^{a_{1}t}$, where $a_1$ is a constant, representing the reciprocal of the average delay of the collected information about the disease. $\rho \left(w\right)x$ is the impact of information feedback on disease isolation rate, where $\rho \left(w\right)$ is a positive function for modeling isolated susceptible populations, $\rho \left(w\right)={\rho }_0+{\rho }_1\left(w\right)$, ${\rho }_0$ is existing and historical information independent of the prevalence level in the relevant disease population, ${\rho }_1\left(w\right)$ is a modeling of the proportion of isolated susceptible populations based on social alerts caused by diseases, $f(x,z)$ represents the impact of susceptibility and the number of infected individuals in information dynamics, considering information variable $w\left(t\right)$ as the state function $f(x,z)=kz$, $(k>0)$ [15] of the past values of state variables x and z, and propose the following assumptions [15]:

(1):

$f\left(0\right)\ge 0$, $f^{\prime }\left(z\right)>0$ for ∀$z>0$,

(2):

$\rho \left(0\right)>0$, $\rho \left(w\right)>0$, ${\rho }^{\prime }\left(w\right)>0$ for ∀$w>0$, ${\rho }_1\left(w\right):=\frac{c_{1}w}{1+c_{2}w}$, $(c_1,c_2>0)$.

Due to the fact that the dynamic behavior of the population density of recovered (u) and deceased individuals (v) does not affect other populations, through this selection and assumption, the system (2) is equivalent to the following nonlinear differential systems:

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\lambda (1-x\left(t\right))-\delta x\left(t\right)z\left(t\right)+\eta y\left(t\right)-({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)\hfill \\ \hfill \dot{y}\left(t\right)& =({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)-(\eta +\lambda )y\left(t\right)\hfill \\ \hfill \dot{z}\left(t\right)& =\delta x\left(t\right)z\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)\hfill \\ \hfill \dot{w\left(t\right)}& =a_{1}kz\left(t\right)-a_{1}w\left(t\right).\hfill \end{array}\right.$$

(3)

In addition, Øksendal’s research [25] indicates that environmental changes have a big influence on the spread of infectious diseases. For the spread of infectious diseases, due to the unpredictability caused by humankind, the variation and transmission of diseases are essentially random, resulting in continuous interference with population size [26,27]. Therefore, the stochastic differential Equation (SDE) model is more practical in modeling infectious diseases in infectious disease dynamics. At the same time, a deterministic system can evolve into a stochastic epidemic model. Brownian motion is essentially a continuous stochastic process. A stochastic process is a group of random variables that appear sequentially in the time or space domain. It represents a random fluctuation phenomenon, and its theory has important applications in other fields. Symmetry is an important property of Brownian motion. When we study stochastic differential equations, we can use symmetry to solve some simple problems, which is conducive to the study of stochastic processes. Presuming that the coefficient of model (3) is effected by Brownian motion, then model (3) changes into a random model:

$$\left\{\begin{array}{cc}\hfill dx\left(t\right)& =[\lambda (1-x\left(t\right))-\delta x\left(t\right)z\left(t\right)+\eta a\left(t\right)-({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)]dt+{\alpha }_{1}x\left(t\right)d{A}_1\left(t\right)\hfill \\ \hfill dy\left(t\right)& =[({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)-(\eta +\lambda )y\left(t\right)]dt+{\alpha }_{2}y\left(t\right)d{A}_2\left(t\right)\hfill \\ \hfill dz\left(t\right)& =[\delta x\left(t\right)z\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)]dt+{\alpha }_{3}z\left(t\right)d{A}_3\left(t\right)\hfill \\ \hfill dw\left(t\right)& =[a_{1}kz\left(t\right)-a_{1}w\left(t\right)]dt+{\alpha }_{4}w\left(t\right)d{A}_4\left(t\right),\hfill \end{array}\right.$$

(4)

among ${\alpha }_j(j=1,2,3,4)$ represent the intensities of the white noises, $A_j\left(t\right)(j=1,2,3,4)$ are mutually independent standard Brownian motions. Nevertheless, in practical situations, the populations of x, y, z, and w are usually affected by random factors. Therefore, in non-general cases, it is assumed that these five types of random disturbance noise are uncorrelated. We make $A_j\left(t\right)=A\left(t\right)(j=1,2,3,4)$, then model (4) changes into:

$$\left\{\begin{array}{c}dx\left(t\right)=[\lambda (1-x\left(t\right))-\delta x\left(t\right)z\left(t\right)+\eta y\left(t\right)-({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)]dt+{\alpha }_{1}x\left(t\right)dA\left(t\right)\hfill \\ dy\left(t\right)=[({\rho }_0+\frac{c_{1}w\left(t\right)}{1+c_{2}w\left(t\right)})x\left(t\right)-(\eta +\lambda )y\left(t\right)]dt+{\alpha }_{2}y\left(t\right)dA\left(t\right)\hfill \\ dz\left(t\right)=[\delta x\left(t\right)z\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)]dt+{\alpha }_{3}z\left(t\right)dA\left(t\right)\hfill \\ dw\left(t\right)=[a_{1}kz\left(t\right)-a_{1}w\left(t\right)]dt+{\alpha }_{4}w\left(t\right)dA\left(t\right).\hfill \end{array}\right.$$

(5)

Let $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ be a complete probability space with the filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfying the usual condition (i.e., ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ is increasing and right continuous while ${\mathcal{F}}_0$ contains all $\mathbb{P}$-null sets). To simplify the description, we denote $R_{+}^4:=\{(x_0,y_0,z_0,w_0):x_0,y_0,z_0,w_0>0\}$.

This article provides a detailed discussion on the existence and uniqueness of global solutions, disease extinction, random ultimate boundedness and stationary distribution of the model (5). The analysis model (5) has two random reproduction numbers $R_1$ and $R_2$, if $R_1<0$, the disease vanishes. If $R_2>0$, the system (5) is evenly distributed, meaning that the disease will persist. We believe that non-drug control can strain the spread of infectious diseases and the effect of index formation on the decision to isolate susceptible populations. This is crucial for understanding the characteristics of the disease. This will help people analyze the development process of infectious diseases, predict transmission trends, and analyze key factors such as the medium of disease transmission.

The primary compositions of this article are as below: In Section 2, we have verified the existence and uniqueness of global positive solutions for model (5). In Section 3, we are committed to proving extinction and providing an example to support our discovery. In Section 4, we demonstrate the stochastic boundedness of the solution. In Section 5, we are committed to proving the stationary distribution. In Section 6, we briefly discussed and summarized the main results.

2. The Existence and Uniqueness of Global Positive Solutions

Thanks to Lan et al. [28] for their fruitful research results on Theorem 3.1. Since system (5) is an infectious disease model, where variables represent various populations, we first need to ensure the existence and uniqueness of the positive solution of system (5). This property also lays the foundation for us to study more properties of the system further (5) in $R_{+}^4$.

Theorem 1.

For initial value $\forall (x_0,y_0,z_0,w_0)\in R_{+}^4$, the system (5) has a unique positive solution, that is $\left(x\right(t),y(t),z(t),w(t\left)\right)$, for any $t\ge 0$, $(x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right))\in R_{+}^4$ is true almost everywhere.

Proof. 

For initial value $\forall (x_0,y_0,z_0,w_0)\in R_{+}^4$, it is obvious that the coefficients of model (5) satisfy the local Lipschitz condition. Hence, there exists a unique local solution $\left(x\right(t),y(t),z(t),w(t\left)\right)$ for system (5) on $t\in [0,{\tau }_a)$, where ${\tau }_a$ is the blowup time. To demonstrate the globality of the solution, we just need to prove that ${\tau }_a=\infty$ a.s. Let $b_0\in N$ is a adequately large positive integer, then making $x_0\in (\frac{1}{b_0},b_0)$, $y_0\in (\frac{1}{b_0},b_0)$, $z_0\in (\frac{1}{b_0},b_0)$, $w_0\in (\frac{1}{b_0},b_0)$, for any integer $b\ge b_0$, defining downtime:

$${\tau }_b:=inf\{t\in [0,{\tau }_a):x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right)\notin (\frac{1}{b},b)\}.$$

(6)

Here we define Ø as an empty set and $infØ=\infty$.

Therefore, it is likely to obtain that ${\tau }_b$ as $b\to \infty$ monotonic increase. Permitting ${\tau }_{\infty }=\underset{b\to +\infty }{\lim }{\tau }_b$, there is ${\tau }_{\infty }\le {\tau }_b$, a.s. we only demand proving ${\tau }_{\infty }=\infty$. Otherwise, there are two constants $T>0$, $\epsilon \in (0,1)$, so that $\rho ({\tau }_{\infty }\le T)\ge \epsilon ,\forall b\ge b_0$. So there is an integer $b_1\ge b_0$, that holds

$$P({\tau }_b\le T)\ge \epsilon ,forallb\ge b_1.$$

(7)

First, we define a $C^2-$function V:$R_{+}^4\to R_{+}$:

$$V\left(n\right)=n\left(t\right)-1-lnn\left(t\right),$$

where $n\left(t\right)=x\left(t\right)+y\left(t\right)+z\left(t\right)+w\left(t\right)$.

Allowing $It{\widehat{o}}^{\prime }s$ formula [29], it can be concluded that

$$dV\left(n\right)=LV\left(n\right)dt+(1-\frac{1}{n})({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w)dA\left(t\right),$$

where

$$\begin{array}{cc}\hfill LV& =(1-\frac{1}{n})[\lambda (1-x\left(t\right))-\lambda y\left(t\right)-(\gamma +\omega +\lambda )z\left(t\right)+a_{1}kz\left(t\right)-a_{1}w\left(t\right)]\hfill \\ \hfill & +\frac{{\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2}{2n^2}\hfill \\ \hfill & =(1-\frac{1}{n})[\lambda -(\gamma +\omega )z\left(t\right)+a_{1}kz\left(t\right)-(a_1-\lambda )w\left(t\right)-\lambda n]\hfill \\ \hfill & +\frac{{\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2}{2n^2}\hfill \\ \hfill & =\lambda (1-\frac{1}{n})(1-n)-(\gamma +\omega -a_{1}k)z\left(t\right)(1-\frac{1}{n})-(a_1-\lambda )w\left(t\right)(1-\frac{1}{n})\hfill \\ \hfill & +\frac{{\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2}{2n^2}\hfill \\ \hfill & =\frac{-\lambda {(n-1)}^2}{n}-(\gamma +\omega -a_{1}k)z\left(t\right)+\frac{(\gamma +\omega -a_{1}k)z}{n}-(a_1-\lambda )w\left(t\right)+\frac{(a_1-\lambda )w\left(t\right)}{n}\hfill \\ \hfill & +\frac{{\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2}{2n^2}\hfill \\ \hfill & \le \gamma +\omega -a_{1}k+a_1-\lambda +\frac{{\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2}{2}:=B,\hfill \end{array}$$

therefore, we can obtain

$$dV\left(n\right)\le Bdt+(1-\frac{1}{n})({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w)dA\left(t\right).$$

(8)

Integrate from 0 to $min\{{\tau }_b,T\}$ both sides of Equation (8) simultaneously, taking expectations and obtaining

$$EV\left(n({\tau }_b\wedge T)\right)\le V\left(n\left(0\right)\right)+BE({\tau }_b\wedge T)\le V\left(n\left(0\right)\right)+BT.$$

(9)

Setting ${\Omega }_b=\{{\omega }_0:{\tau }_b\le T\}$, for any $\omega \in {\Omega }_b$, by (7), we have $P\left({\Omega }_b\right)\ge \epsilon$, then at least one of $x(min\{{\tau }_b\left({\omega }_0\right),T\})$, $y(min\{{\tau }_b\left({\omega }_0\right),T\})$, $z(min\{{\tau }_b\left({\omega }_0\right),T\})$, $w(min\{{\tau }_b\left({\omega }_0\right),T\})$ is equal to $\frac{1}{b}$ or equal to b, thus

$$V\left(n({\tau }_b,{\omega }_0)\right)\ge min\{b+1-lnb,\frac{1}{b}+1+lnb\}.$$

(10)

By (9) and (10), there is

$$V\left(n\left(0\right)\right)+BT\ge E\left[1_{{\Omega }_b}\left({\omega }_0\right)V\left(N\left({\omega }_0\right)\right)\right]\ge \epsilon min\{b+1-lnb,\frac{1}{b}+1+lnb\},$$

where $1_{{\Omega }_b}$ is the indicator function of ${\Omega }_b$. Let $b\to \infty$, then $\underset{b\to \infty }{lim}min\{b+1-lnb,\frac{1}{b}+1+lnb\}=\infty$, so, we encountered a conflict

$$V\left(n\right(0\left)\right)+B\left(T\right)\ge \infty .$$

Furthermore, we obtain ${\tau }_{\infty }=\infty$, a.s. system (5) has a unique global positive solution $(x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right))\in R_{+}^4$ for ∀$t\ge 0$. □

3. Extinction of Disease

3.1. The Extinction of Diseases

Thanks to the research results of Tan et al. in Section 3 of [30], Dieu et al. in Section 2 of [31] and Liu et al. in Theorem 3.3 of [32]. This section, demonstrates that when the noise ${\alpha }_3$ is large enough to satisfy $R_1<0$, the infected population $z\left(t\right)$ will become extinct exponentially.

To further earn the properties of the solution, we prove the bounds of the first equation of model (5):

$$\begin{array}{cc}\hfill d\overline{x}\left(t\right)& =[\lambda (1-\delta \overline{x}\left(t\right))-{\rho }_0\overline{x}\left(t\right)]dt+{\alpha }_1\overline{x}\left(t\right)dA\left(t\right)\hfill \\ \hfill & =[\lambda -(\lambda +{\rho }_0)\overline{x}\left(t\right)]dt+{\alpha }_1\overline{x}\left(t\right)dA\left(t\right).\hfill \end{array}$$

(11)

According to the research results of Theorem 1.16 in P.C. Kiessler [33], we have,

$${\displaystyle \frac{1}{t}}{\int }_0^t\overline{x}\left(\tau \right)d\tau ={\displaystyle \frac{\overline{x}\left(0\right)-\overline{x}\left(t\right)}{(\lambda +{\rho }_0)t}}+{\displaystyle \frac{\lambda }{\lambda +{\rho }_0}}+{\displaystyle \frac{{\alpha }_1}{(\lambda +{\rho }_0)t}}{\int }_0^t\overline{x}\left(\tau \right)dA\left(\tau \right).$$

Let $\overline{x}\left(t\right)$ be the solution of model (11) and have an initial value of $x_0$. In the light of the comparison theorem that $x\left(t\right)\le \overline{x}\left(t\right)$ for all $t\ge 0$. By resolving the Fokker–Planck equation, the solution $\overline{x}\left(t\right)$ has a unique stationary distribution and the probability density is $g^{*}\left(x\right)$. Then, according to the law of strong numbers, we obtain

$$\underset{t\to \infty }{lim}{\displaystyle \frac{1}{t}}{\int }_0^t\overline{x}\left(\tau \right)d\tau ={\int }_0^{\infty }x{g}^{*}\left(x\right)dx=\frac{\lambda }{\lambda +{\rho }_0}.$$

(12)

Theorem 2.

If $\gamma +\omega +\lambda -a_{1}k\ge 0$ and $R_1:=\frac{\lambda }{\lambda +{\rho }_0}-a<0$, then $M\left(t\right)$ almost certainly converges to 0 at an exponential rate. This means that both the infected population $z\left(t\right)$ and the information index $w\left(t\right)$ will tend to become extinct, i.e.,

$$\underset{t\to \infty }{limsup}\frac{1}{t}lnM\left(t\right)\le R_1<0,$$

which implies the disease and the negative feedback of information disappears.

Proof. 

Let $M\left(t\right)=z\left(t\right)+w\left(t\right)$. For $lnM\left(t\right)$ using $It{\widehat{o}}^{\prime }s$ formula, then we gain,

$$\begin{array}{cc}\hfill dlnM\left(t\right)& =\left\{\frac{1}{M\left(t\right)}\left[\delta x\left(t\right)z\left(t\right)-\left(\gamma +\omega +\lambda \right)z\left(t\right)+a_{1}kz\left(t\right)-a_{1}w\left(t\right)\right]-\frac{{\alpha }_3^2{z}^2\left(t\right)+{\alpha }_4^2{w}^2\left(t\right)}{2M^2\left(t\right)}\right\}dt\hfill \\ \hfill & +\frac{{\alpha }_{3}z\left(t\right)+{\alpha }_{4}w\left(t\right)}{M\left(t\right)}dA\left(t\right)\hfill \\ \hfill & =\left[\frac{\delta x\left(t\right)z\left(t\right)}{M\left(t\right)}-\frac{\left(\gamma +\omega +\lambda \right)z\left(t\right)}{M\left(t\right)}+\frac{a_{1}kz\left(t\right)}{M\left(t\right)}-\frac{a_{1}w\left(t\right)}{M\left(t\right)}-\frac{{\alpha }_3^2{z}^2\left(t\right)+{\alpha }_4^2{w}^2\left(t\right)}{2M^2\left(t\right)}\right]dt\hfill \\ \hfill & +\frac{{\alpha }_{3}z\left(t\right)+{\alpha }_{4}w\left(t\right)}{M\left(t\right)}dA\left(t\right)\hfill \\ \hfill & =\left[\frac{\delta x\left(t\right)z\left(t\right)}{M\left(t\right)}-\frac{\left(\gamma +\omega +\lambda -a_{1}k\right)z\left(t\right)+a_{1}w\left(t\right)}{M\left(t\right)}-\frac{{\alpha }_3^2{z}^2\left(t\right)+{\alpha }_4^2{w}^2\left(t\right)}{2M^2\left(t\right)}\right]dt\hfill \\ \hfill & +\frac{{\alpha }_{3}z\left(t\right)+{\alpha }_{4}w\left(t\right)}{M\left(t\right)}dA\left(t\right)\hfill \\ \hfill & \le \left[\delta \overline{x}\left(t\right)-a\right]dt+\alpha dA\left(t\right),\hfill \end{array}$$

where $\gamma +\omega +\lambda -a_{1}k\ge 0$ and $a=min\{\gamma +\omega +\lambda -a_{1}k,a_1\}$.

After that, simultaneously integrating both ends of the inequality from 0 to t and dividing by t at the same time, we receive

$$\frac{lnM\left(t\right)}{t}\le \frac{ln{M}_0}{t}+\frac{\delta }{t}{\int }_0^t\overline{x}\left(\tau \right)d\tau -a+\frac{\alpha A\left(t\right)}{t}.$$

On the basis of the strong law of large numbers $\underset{t\to \infty }{limsup}\frac{\alpha A\left(t\right)}{t}=0$, we obtain

$$\underset{t\to \infty }{limsup}\frac{1}{t}lnM\left(t\right)\le \frac{\lambda }{\lambda +p_0}-a:=R_1<0.$$

(13)

For ∀$\epsilon >0$, from (13), it can be seen that there is a condition where $t_0>0$ causes $P\left({\Omega }_{\epsilon }\right)>1-\epsilon$, among

$${\Omega }_{\epsilon }=\{lnM\left(t\right)\le R_{1}t\}=\{M\left(t\right)\le e^{R_{1}t},\forall t\ge t_0\}.$$

Therefore, $M\left(t\right)$ can almost certainly converge to 0 at an exponential rate. □

3.2. Numerical Simulation

Thanks to the Milstein method mentioned in Higham [34], model (5) can be reworked as the following discretization equation:

$$\left\{\begin{array}{cc}\hfill x_{n+1}& =x_n+(\lambda (1-x_n)-\delta x_n{z}_n+\eta y_n-({\rho }_0+\frac{c_1{w}_n}{1+c_2{w}_n})x_n)\Delta t+{\alpha }_1{x}_n\sqrt{\Delta t}\xi n+{\displaystyle \frac{{\alpha }_1^2}{2}}{x}_n(\Delta t{\xi }_n^2-\Delta t)\hfill \\ \hfill y_{n+1}& =y_n+(({\rho }_0+\frac{c_1{w}_n}{1+c_2{w}_n})x_k-(\eta +\lambda )y_n)\Delta t+{\alpha }_2{y}_n\sqrt{\Delta t}\xi n+{\displaystyle \frac{{\alpha }_2^2}{2}}{y}_n(\Delta t{\xi }_n^2-\Delta t)\hfill \\ \hfill z_{n+1}& =z_n+(\delta x_n{z}_n-(\gamma +\omega +\lambda )z_n)\Delta t+{\alpha }_3{z}_n\sqrt{\Delta t}\xi n+{\displaystyle \frac{{\alpha }_3^2}{2}}{z}_n(\Delta t{\xi }_n^2-\Delta t)\hfill \\ \hfill w_{n+1}& =w_n+(a_{1}k{z}_n-a_1{w}_n)\Delta t+{\alpha }_4{w}_n\sqrt{\Delta t}\xi n+{\displaystyle \frac{{\alpha }_4^2}{2}}{w}_n(\Delta t{\xi }_n^2-\Delta t),\hfill \end{array}\right.$$

where ${\xi }_n,n=1,2,\cdots ,n$ are gaussian random variables. The following graph was drawn using a numerical example using a MATLAB program.

Example 1.

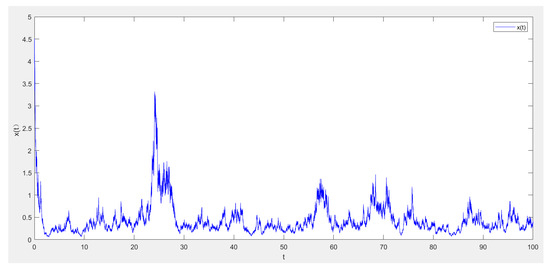
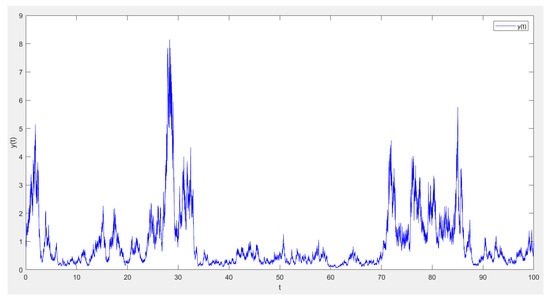
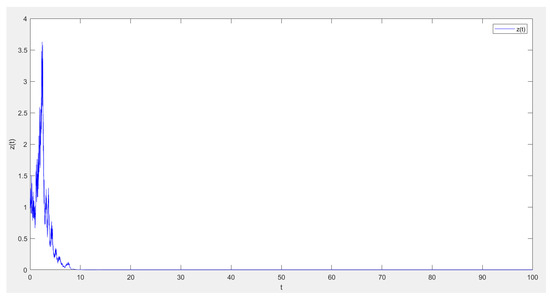
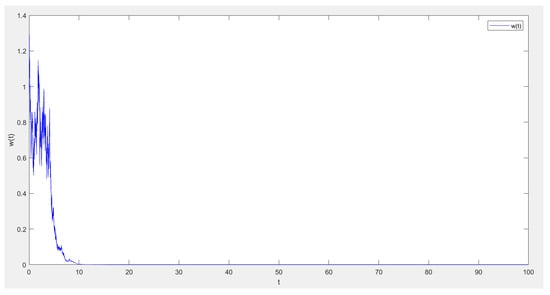
Theorem 2 indicates that when the parameters satisfy the above conditions, the population of the system (5) will become extinct. In order to prove the validity of the theorem, the parameter set is taken $\lambda =0.3,\delta =0.95,\eta =0.00001,{\rho }_0=0.1,\gamma =0.143,\omega =0.28,a_1=0.5,k=0.8$, $c_1=0.5,c_2=0.3,{\alpha }_1=0.7,{\alpha }_2=0.5,{\alpha }_3=0.8,{\alpha }_4=0.5$, and the condition satisfies Theorem 2. And the time interval $[0,t]$ is discretized into $0=t_0<t_1<\cdots <t_n=t=100$, where the time step $\Delta T={10}^{-4}$ is a constant. The numerical simulation is shown in Figure 1, Figure 2, Figure 3 and Figure 4.

Figure 1. The sample path of x(t).

Figure 2. The sample path of y(t).

Figure 3. The sample path of z(t).

Figure 4. The sample path of w(t).

4. Random Ultimate Boundedness

The previous reasoning indicates that the solution of the system (5) will not explode to infinity in a finite time. Referencing Cai’s fruitful research results [35], we can derive the solution of the system is bounded randomly, and under certain conditions is ultimately bounded.

Theorem 3.

Assuming $\gamma +\omega -a_{1}k>0$ and $a_1-\lambda >0$ holding, then for any initial value $f_0=(x_0,y_0,z_0,w_0)\in R_{+}^4$, the solution $f\left(t\right)=(x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right))\in R_{+}^4$ of system (5) is random and ultimately bounded for ∀$t\ge 0$.

Proof. 

For $f\left(t\right)=(x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right))\in R_{+}^4$, defining

$$V\left(t\right)=n\left(t\right)+\frac{1}{n\left(t\right)},$$

where $n\left(t\right)=x\left(t\right)+y\left(t\right)+z\left(t\right)+w\left(t\right)$.

In line with the $It{\widehat{o}}^{\prime }s$ formula has

$$dV\left(t\right)=LVdt+(1-\frac{1}{n^2})\left({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w\right)dA\left(t\right),$$

(14)

and there are

$$\begin{array}{cc}\hfill LV& =\left(1-\frac{1}{n^2}\right)\left[\lambda \left(1-x\right)-\lambda y-\left(\gamma +\omega +\lambda \right)z+a_{1}kz-a_{1}w\right]+\frac{1}{n^3}\left({\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2\right)\hfill \\ \hfill & \le \left(1-\frac{1}{n^2}\right)\left[\lambda \left(1-x\right)-\lambda y-\left(\gamma +\omega +\lambda -a_{1}k\right)z-a_{1}w\right]+\frac{{\alpha }^2{n}^2}{n^3}\hfill \\ \hfill & \le \left(1-\frac{1}{n^2}\right)\left(\lambda -\lambda n\right)+\frac{{\alpha }^2}{n}\hfill \\ \hfill & =\lambda -\lambda n-\frac{\lambda }{n^2}+\frac{\alpha }{n}+\frac{{\alpha }^2}{n}\hfill \\ \hfill & =-\lambda n-\frac{\lambda }{n}+\alpha -\frac{\lambda }{n^2}+\frac{2\lambda +{\alpha }^2}{n},\hfill \end{array}$$

where $\alpha =max\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\}$, let $c_0=\lambda -\frac{\lambda }{n^2}+\frac{2\lambda +{\alpha }^2}{n}$, obviously, $c_0$ has a supremum, so making $c=\underset{\left(x,y,z,w\right)\in R_{+}^4}{sup}{c}_0$, we can obtain

$$LV\le -\lambda \left(n+\frac{1}{n}\right)+c=-\lambda V+c.$$

By (14), we can obtain

$$dV\le \left(-\lambda V+c\right)dt+\left(1-\frac{1}{n^2}\right)\left({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w\right)dA\left(t\right).$$

Let $G\left(t\right)=e^{\lambda t}V\left(t\right)$, by the $It{\widehat{o}}^{\prime }s$ formula has

$$\begin{array}{cc}\hfill d\left(e^{\lambda t}V\left(t\right)\right)& =\lambda e^{\lambda t}V\left(t\right)dt+e^{\lambda t}dV\left(t\right)\hfill \\ \hfill & \le \lambda e^{\lambda t}V\left(t\right)dt+e^{\lambda t}\left(-\lambda V\left(t\right)+c\right)dt+e^{\lambda t}\left(1-\frac{1}{n^2}\right)\left({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w\right)dA\left(t\right)\hfill \\ \hfill & =c{e}^{\lambda t}+e^{\lambda t}\left(1-\frac{1}{n^2}\right)\left({\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_{3}z+{\alpha }_{4}w\right)dA\left(t\right).\hfill \end{array}$$

(15)

By integrating both sides of Equation (15) from 0 to t and taking the mean, we obtain:

$$e^{\lambda t}EV\left(t\right)-V\left(0\right)\le c{e}^{\lambda t}-c.$$

Accordingly, there are

$$\underset{t\to \infty }{lim}EV\left(t\right)<c,$$

then

$$\underset{t\to \infty }{lim}E\left(n+\frac{1}{n}\right)<c.$$

For ∀$\epsilon >0$, let us obtain $H=\frac{\sqrt{c}}{\sqrt{\epsilon }}$ from the Chebyshev inequality, we have

$$P\left\{|x\left(t\right)|>H\right\}\le \frac{E\left({\left|X\left(t\right)\right|}^2\right)}{H^2},$$

so that

$$\underset{t\to \infty }{limsup}\rho \left\{\left|x\left(t\right)\right|>H\right\}<\frac{c}{H^2}=\epsilon .$$

So the solution of system (5) is random and ultimately bounded. □

5. Stationary Distribution

Inspired by the research results of Han and Zuo et al. [36,37], in this section, we investigate the existence of stationary distributions in the system (5). Next, we consider Theorem 3.3 and Theorem 3.4 in integral Equation [38]:

$$F\left(t\right)=F\left(t_0\right)+{\int }_{t_0}^{t}b(x,F\left(x\right))dx+\sum _{r=1}^k{\int }_{t_0}^t{\alpha }_r(x,F\left(x\right))d{B}_r\left(x\right),t\ge t_0\ge 0.$$

(16)

Lemma 1.

Let the vectors $\left(x,f\right),{\alpha }_1(x,f),\cdots ,{\alpha }_k(x,f)\left(x\in \left[t_0,T\right],f\in R^k\right)$ be continuous functions of $(x,f)$, such that for some constant B the following conditions hold in the entire domain of definition [38]:

$$\left|h(x,f)-h(x,g)\right|+\sum _{r=1}^k|{\alpha }_r(x,f)-{\alpha }_r(x,g)|\le \left|f-g\right|,$$

(17)

$$\left|h(x,f)\right|+\sum _{r=1}^k|{\alpha }_r(x,f)| \le A\left(1+\left|f\right|\right).$$

(18)

In addition, there exists a non-negative function $V\left(x\right)$, such that

$$LV\left(f\right)\le -1,foranyf\in R^k\backslash D:=D^c,$$

where D is a compact subset defined on $R^k$.

Afterwards the Markov process (16) on $R^k$ has at least one stationary solution $F\left(t\right)$.

Theorem 4.

Assuming $R_2=2\sqrt{\lambda \delta }-3\alpha -\eta -\gamma -\omega -a_1-\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)>0$, the model (5) is a Markov process, which means that the disease persists.

Proof. 

By Lemma 1 and Theorem 1, we found a $C^2-$function $V(x,y,z,w)$:

$$V=H{V}_1+V_2+V_3,$$

where $V_1=V_2=-lnx-lny-lnz-lnw$, $V_3=\frac{1}{\theta +1}{(x+y+z+w)}^{\theta +1}$, with D, $\theta$ are determined later, using ${\rho }_0+\frac{c_{1}w}{1+c_{2}w}$ to replace with $\rho \left(w\right)$. Employing the $It{\widehat{o}}^{\prime }s$ formula to $V_1$, we can obtain

$$\begin{array}{cc}\hfill L{V}_1& =-\frac{1}{x}[\lambda (1-x)-\delta xz+\eta a_1-\rho \left(w\right)x]-\frac{1}{y}[\rho \left(w\right)x-(\eta +\lambda )a_1]-\frac{1}{z}(\delta xz-\hfill \\ \hfill & (\gamma +\omega +\lambda )z)-\frac{1}{w}(a_{1}kz-a_{1}w)+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & =-\frac{\lambda }{x}+\lambda +\delta z-\frac{\eta y}{x}+\rho \left(w\right)-\frac{\rho \left(w\right)x}{y}+(\eta +\alpha )-\delta x+\gamma +\omega +\lambda -\frac{a_{1}kz}{w}\hfill \\ \hfill & +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & =-(\frac{\lambda }{x}+\delta x)-(\frac{\eta y}{x}+\frac{\rho \left(w\right)x}{y})+\beta z+3\lambda +\eta +\gamma +\omega +a_1+\rho \left(w\right)-\frac{a_{1}kz}{w}\hfill \\ \hfill & +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & \le -2\sqrt{\lambda \delta }-2\sqrt{\eta \rho \left(w\right)}+\rho \left(w\right)+\delta z+3\lambda +\eta +\gamma +\omega +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2\hfill \\ \hfill & +{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & =-2\sqrt{\lambda \delta }+{(\sqrt{\rho \left(w\right)}-\sqrt{\eta })}^2+\delta z+3\lambda +\gamma +\omega +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2).\hfill \end{array}$$

(19)

Because $\rho \left(w\right)\le 1$, so ${(\sqrt{\rho \left(w\right)}-\sqrt{\eta })}_{max}^2=\eta$, by (19) we have

$$\begin{array}{cc}\hfill L{V}_1& \le -2\sqrt{\lambda \delta }+\eta +\delta z+3\lambda +\gamma +\omega +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & =-R_2+\delta z,\hfill \end{array}$$

where $R_2:=2\sqrt{\lambda \delta }-\eta -3\lambda -\gamma -\omega -a_1-\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)>0$, and similarly

$$\begin{array}{cc}\hfill L{V}_2& =-\frac{\lambda }{x}+\lambda +\delta z-\frac{\eta y}{x}-\frac{\rho \left(w\right)x}{y}+\rho \left(w\right)+\eta +\lambda -\delta x+\gamma +\omega +\lambda -\frac{a_{1}kz}{w}\hfill \\ \hfill & +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & \le -\frac{\lambda }{x}-\frac{\rho \left(w\right)x}{a}-\frac{a_{1}kz}{w}+\delta z+3\alpha +\eta +\gamma +\omega +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)\hfill \\ \hfill & =-\frac{\lambda }{x}-\frac{\rho \left(w\right)x}{y}-\frac{a_{1}kz}{w}+\delta z+{\lambda }_2,\hfill \end{array}$$

where ${\lambda }_2:=3\lambda +\eta +\gamma +\omega +a_1+\frac{1}{2}({\alpha }_1^2+{\alpha }_2^2+{\alpha }_3^2+{\alpha }_4^2)$,

$$\begin{array}{cc}\hfill L{V}_3& ={(x+y+z+w)}^{\theta }[\lambda (1-x)-\lambda y-(\gamma +\omega +\lambda )z+a_{1}kz-a_{1}w]\hfill \\ \hfill & +\frac{\theta }{2}{(x+y+z+w)}^{\theta -1}({\alpha }_1^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2)\hfill \\ \hfill & =n^{\theta }[\lambda (1-x)-\lambda y-(\gamma +\omega +\lambda -a_{1}k)z-a_{1}w]+\frac{\theta n^{\theta +1}}{2}({\alpha }_z^2{x}^2+{\alpha }_2^2{y}^2+{\alpha }_3^2{z}^2+{\alpha }_4^2{w}^2)\hfill \\ \hfill & \le n^{\theta }[\lambda -\lambda x-\lambda y-(\gamma +\omega +\lambda -a_{1}k)z-a_{1}w]+\frac{\theta n^{\theta +1}}{2}({\alpha }_1^2\vee {\alpha }_2^2\vee {\alpha }_3^2\vee {\alpha }_4^2)\hfill \\ \hfill & =n^{\theta }[\lambda -\lambda n-(\gamma +\omega -a_{1}k)z-(a_1-\lambda )w]+\frac{\theta n^{\theta +1}}{2}({\alpha }_1^2\vee {\alpha }_2^2\vee {\alpha }_3^2\vee {\alpha }_4^2)\hfill \\ \hfill & \le n^{\theta }[\lambda -\lambda n]+\frac{\theta n^{\theta +1}}{2}({\alpha }_1^2\vee {\alpha }_2^2\vee {\alpha }_3^2\vee {\alpha }_4^2)\hfill \\ \hfill & =\lambda n^{\theta }-\lambda n^{\theta +1}+\frac{\theta n^{\theta +1}}{2}({\alpha }_1^2\vee {\alpha }_2^2\vee {\alpha }_3^2\vee {\alpha }_4^2)\hfill \\ \hfill & =\lambda n^{\theta }-(\lambda -\frac{\theta }{2}({\alpha }_1^2\vee {\alpha }_2^2\vee {\alpha }_3^2\vee {\alpha }_4^2)n^{\theta +1}\hfill \\ \hfill & =\lambda n^{\theta }-\frac{\lambda }{2}{n}^{\theta +1}\hfill \\ \hfill & \le H_1-\frac{\lambda }{4}(x^{\theta +1}+y^{\theta +1}+z^{\theta +1}+w^{\theta +1}),\hfill \end{array}$$

where $H_1={sup}_{(x,y,z,w)\in R_{+}^4}\{\lambda n^{\theta }-\frac{\lambda }{2}{n}^{\theta +1}\}$.

As a result

$$\begin{array}{cc}\hfill LV& \le H(-R_2+\beta z)-\frac{\lambda }{x}-\frac{\rho \left(w\right)x}{y}-\frac{a_{1}kz}{w}+\delta z+{\lambda }_2+H_1-\frac{\alpha }{4}(x^{\theta +1}+y^{\theta +1}+z^{\theta +1}+w^{\theta +1})\hfill \\ \hfill & =-R_{2}H+{\lambda }_3+(H+1)\delta z-\frac{\lambda }{x}-\frac{\rho \left(w\right)x}{y}-\frac{a_{1}kz}{w}-\frac{\lambda }{4}(x^{\theta +1}+y^{\theta +1}+z^{\theta +1}+w^{\theta +1}),\hfill \end{array}$$

where ${\lambda }_3={\lambda }_2+H_1$.

Making H big enough to make $-\lambda H+{\lambda }_3\le -2$, then

$$LV\le \left\{\begin{array}{c}-2+c-\frac{\lambda }{x}-\frac{\rho \left(w\right)x}{y}\to -\infty .asx\to 0^{+},y\nrightarrow 0^{+}\hfill \\ -2+(H+1)\delta z\to -2.asz\to 0^{+}\hfill \\ -2+c-\frac{a_{1}kz}{w}\to -\infty .asw\to 0^{+}\hfill \\ -2+c-\frac{\lambda }{8}{x}^{\theta +1}\to -\infty .asx\to +\infty \hfill \\ -2+c-\frac{\lambda }{8}{y}^{\theta +1}\to -\infty .asy\to +\infty \hfill \\ -2+c-\frac{\lambda }{8}{z}^{\theta +1}\to -\infty .asz\to +\infty \hfill \\ -2+c-\frac{\lambda }{8}{w}^{\theta +1}\to -\infty .asw\to +\infty ,\hfill \end{array}\right.$$

where $c=\underset{z\in (0,+\infty )}{max}\{(H+1)z-\frac{\lambda }{8}{z}^{\theta +1}\}$.

It only needs $\epsilon$ to be small enough for any $(x,y,z,w)\in R_{+}^4\backslash D$, where $D=[\epsilon ,\frac{1}{\epsilon }]\times [\epsilon ,\frac{1}{\epsilon }]\times [\epsilon ,\frac{1}{\epsilon }]\times [\epsilon ,\frac{1}{\epsilon }]$, we have $LV<-1$. This completes the proof. □

6. Conclusions and Discussion

Starting from the practical issues of warning and government of infectious diseases, and considering the lag of disease infection, the negative impact of negative media reports, forced isolation, and environmental impacts, this article establishes a model that can depict susceptible (non-isolated) populations (x), divided populations (y), infected populations (z), recovered populations (u), and demised populations (v), as well as the stochastic infectious disease model with the distributed delay that the information index (about the aspect of the corresponding disease) variable (w) interacts with each other, using the existing stochastic differential equation theory, develop new qualitative analysis methods and numerical simulation skills of the model, and apply the obtained theory and numerical results to the precaution and reign of infectious diseases. The details are as follows:

First, we analyze the existence and uniqueness of positive global solutions of the model, and focys on the application of the Lyapunov function, $It{\widehat{o}}^{\prime }s$ lemma, local solution existence and uniqueness theorem, strong law of large numbers, etc. in stochastic differential systems. Second, the analysis model has two random reproduction numbers $R_1$, $R_2$, which proves that when $R_1<0$, the disease tends to extinct and develop corresponding numerical simulation methods to supply a basis for the precaution and reign of infectious diseases; when $R_2>0$, the system is evenly distributed, meaning that the disease will persist. Finally, we prove the stochastic ultimate boundedness of the solution of the model (5).

The precaution and settlement of infectious diseases, as well as the lag in disease infection, have driven the development of this article. In view of the previous work, we will further use the existing infectious disease models, stochastic differential equation, distributed delay and other theories to develop a new class of stochastic infectious disease models with distributed delay and theoretical analysis methods, reveal the dynamic laws of infectious disease transmission and prevention, and provide new ideas and the theoretical foundation of the precaution and settlement of infectious diseases.