Scaled-Invariant Extended Quasi-Lindley Model: Properties, Estimation, and Application

Abstract

In many research fields, statistical probability models are often used to analyze real-world data. However, data from many fields, such as the environment, economics, and health care, do not necessarily fit traditional models. New empirical models need to be developed to improve the fit. In this study, we investigated a further extension of the quasi-Lindley model. This extension was asymmetrically distributed on the positive real number line. Maximum likelihood, least square error, Anderson–Darling, and expectation maximization algorithms were used to estimate the parameters studied. All techniques provided accurate and reliable estimates of the parameters. However, the mean square error of the expectation-maximization approach was lower. The usefulness of the proposed model was demonstrated by analyzing a reliability data set, and the analysis showed that it outperformed all other alternative models.

1. Introduction

Probability models can be classified as symmetric and asymmetric models. An asymmetric model is a type of model in which the probability density or mass function is symmetric about its mean. The shape of the asymmetric model is not symmetric. Both symmetric and asymmetric models have received considerable attention in the probability and statistics literature. A Lindley model, which is simple and remarkably flexible in application, was proposed by [1]. It is characterized by the probability density function (pdf):

$$f(x)=\frac{{\xi }^2}{\xi +1}(1+x)e^{-\xi x}, \xi >0, x\ge 0$$

(1)

which is a mixture of two gamma models $G(1,\xi )$ and $G(2,\xi )$ with weights $\xi /\xi +1$ and $1/\xi +1,$ respectively. Numerous studies have been conducted on the Lindley model. For example, many properties, extensions, and applications of the model have been studied in [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. A scale-invariant version of the Lindley model, namely the quasi-Lindley (QL), with the pdf:

$$f\left(x\right)=\frac{\xi }{\alpha +1}\left(\alpha +\xi x\right)e^{-\xi x}, \alpha >0 ,\xi >0, x\ge 0,$$

(2)

was proposed by [22]. It is a mixture of two gamma models $G(1,\xi )$ and $G(2,\xi )$ with weights $\alpha /\alpha +1$ and $1/\alpha +1$, respectively.

A family of models characterized by $f_{\theta }\left(x\right)$ is said to be scale-invariant if the transformation from $x$ to $kx$ lies within the family. In other words, $f_{\theta }\left(kx\right)=J{f}_{\tilde{\theta }}(x)$ for every $x$ where $J$ is the transformation Jacobian. Thus, if you change the scale of measurement or the unit of $x$, the fit remains invariant. For instance, a lifetime can be measured in days, hours, or minutes, and the unit of measurement does not affect inferences about lifetimes. Since scale invariance is an essential property of lifetime models, this model has attracted considerable interest. A comparison of the maximum likelihood estimator (MLE) and the expectation-maximization (EM) algorithm for estimating the parameters of the QL model was studied by [23] and new scale-invariant extensions of the Lindley model were proposed by [24,25].

Many data sets are composed of multiple populations or sources, and the subpopulation associated with each data point is usually unknown or not recorded. For example, the lifetime of a device or system may be available, but the manufacturer is unknown or an event associated with a living being lacks its geographic location. Such data sets are mixtures because information about some covariates, such as the manufacturer or geographic location, that significantly affect the observations is unknown. For detailed information on mixture models, see [26,27]. The Lindley model and its extensions are examples of mixture models of the gamma distribution that can be useful for describing many real-world applications.

The various needs for mixture models motivate us to propose a new extension of the scaled-invariant QL model, a mixture of three gamma models. Some statistical and reliability properties, such as failure rate (FR), mean residual life (MRL), and p-quantile residual life (p-QRL) functions, are discussed. The problem of estimating the parameters are discussed using the maximum likelihood (ML) method, the least-squares error (LSE) method, the weighted LSE method, and one innovative (EM) algorithm. It is examined that all methods provide consistent and efficient estimates of the parameters. However, the EM algorithm yields a lower mean square error.

The rest of this article is organized as follows. The scaled-invariant extended quasi-Lindley (EQL) model is explained in Section 2 along with some of its basic properties. In Section 3, an innovative EM algorithm is presented for estimating the model parameters, along with ML, LSE, and weighted LSE methods. In Section 4, a simulation study is conducted to investigate and compare the behavior of the estimators. In Section 5, the proposed model is fitted to a reliability data set of intervals between successive air conditioning failures in a Boeing 720 aircraft to demonstrate the usefulness of the model in practice. Finally, Section 6 concludes this paper.

2. Scaled-Invariant Extended QL Model

In this section, a new model is proposed and some of its basic statistical properties are examined. A random variable $X$ follows from $EQL(\alpha ,\xi )$ if its PDF is

$$f\left(x\right)=\frac{\xi }{1+\alpha +{\alpha }^2}\left(1+\alpha \xi x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2\right)e^{-\xi x}, \alpha \ge 0, \xi >0, x\ge 0.$$

(3)

It is a mixture of $G(1,\xi )$, $G(2,\xi )$, and $G(3,\xi )$ with weights $1/(1+\alpha +{\alpha }^2)$, $\alpha /\left(1+\alpha +{\alpha }^2\right)$, and ${\alpha }^2/\left(1+\alpha +{\alpha }^2\right)$, respectively, and presents an asymmetric form on the positive real line. When $\alpha =0$, it reduces to the exponential model. The reliability function is an important yet very simple measure in reliability theory and survival analysis. For the EQL model, it is

$$R(x)=\frac{1}{1+\alpha +{\alpha }^2}\left(1+\alpha +{\alpha }^2+\alpha \xi x+{\alpha }^2\xi x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2\right)e^{-\xi x}.$$

(4)

The distribution function is simply related to the reliability function by $F\left(x\right)=1-R\left(x\right)$ and the quantile function, which is in fact the inverse of the distribution function:

$$q\left(p\right)=F^{-1}\left(p\right)=\min \left\{x:F\left(x\right)=p\right\}, 0<p<1.$$

The quantile function could be used for simulating random samples, estimating the parameters, and computing the skewness of the model.

In addition, for the EQL, the k-th moment is finite and equal to

$$E(X^k)=\frac{1}{1+\alpha +{\alpha }^2}\frac{1}{{\xi }^k}\left[\mathsf{\Gamma }(k+1)+\alpha \mathsf{\Gamma }(k+2)+\frac{{\alpha }^2}{2}\mathsf{\Gamma }(k+3)\right].$$

(5)

Reliability Properties

The proposed model represents a lifetime model. Thus, it is important to study the main reliability measures, such as the FR, MRL, and p-QRL functions, for the proposed model. The FR function at time $x$ expresses the instantaneous risk of fail at $x$ given survival up to $x$. Mathematically, it is defined by

$$\lambda \left(x\right)=\underset{\delta \to 0}{\lim }P\left(x<X<x+\delta \right| X>x)=\frac{f\left(x\right)}{R\left(x\right)}.$$

For more information about the FR function, refer to Lai and Xie [28]. In the case of the EQL model, we have

$$\lambda (x)=\frac{1+\alpha \xi x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2}{1+\alpha +{\alpha }^2+\alpha \xi x+{\alpha }^2\xi x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2}\xi .$$

(6)

Using simple algebra, we can see that the FR function increases from $\lambda \left(0\right)=\xi /(1+\alpha +{\alpha }^2)$ to ${\mathrm{l}\mathrm{i}\mathrm{m}}_{x\to \mathrm{\infty }}\lambda \left(x\right)=\xi$. Figure 1 shows the shape of the pdf and the FR function for some parameter values.

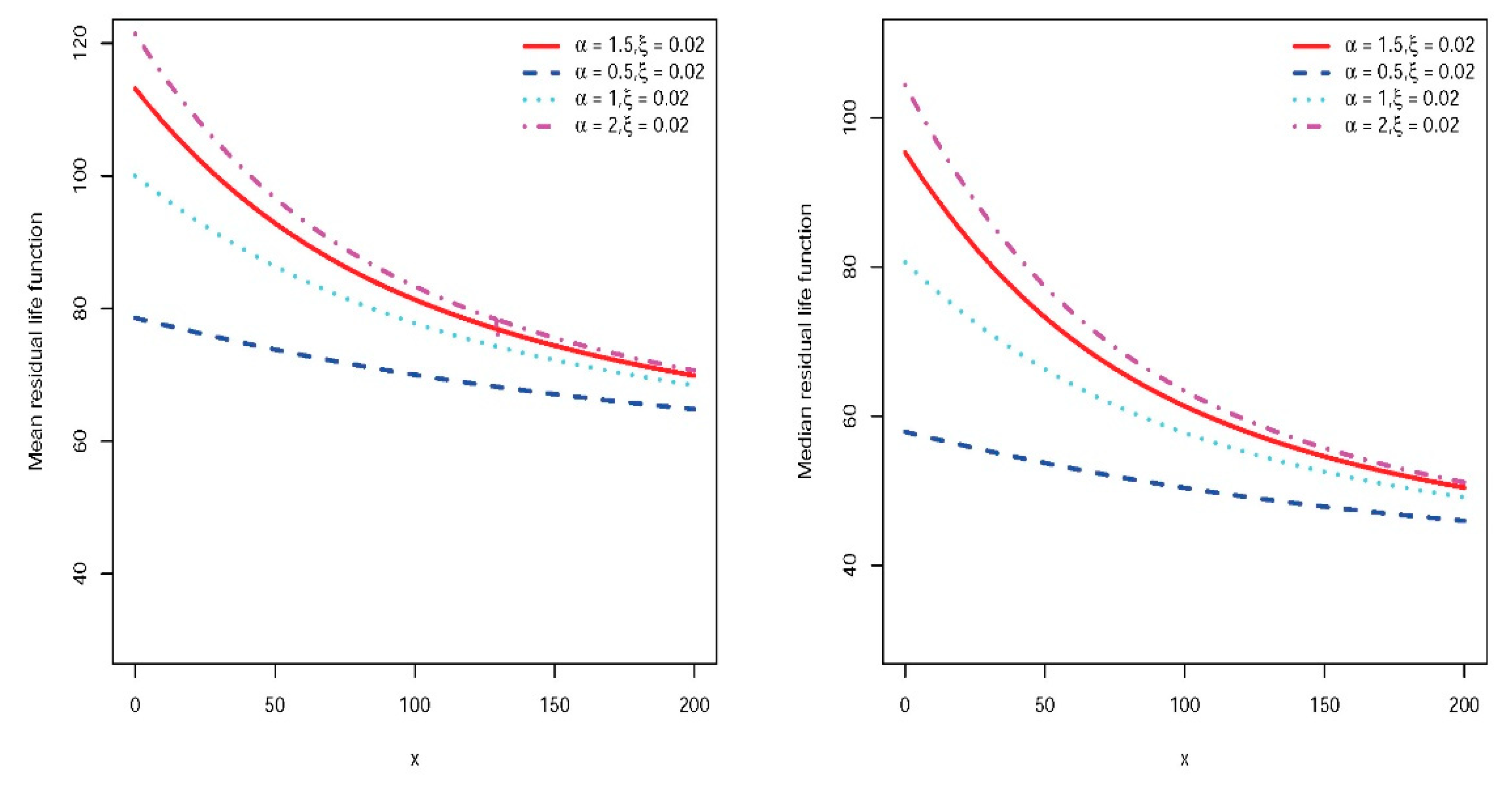
Two other useful and well-known measures in reliability theory and survival analysis are the MRL and p-QRL functions. At time $x$, they describe the mean and p-quantile of the remaining life for survival to $x$. In practice, the MRL function is an attractive alternative to the survival or hazard function of survival. It provides the remaining life expectancy of a subject surviving up to time $x$. For EQL, the MRL is obtained by

$$m(x)=\frac{1+2\alpha +3{\alpha }^2+(\alpha \xi +2{\alpha }^2\xi )x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2}{1+\alpha +{\alpha }^2+(\alpha \xi +{\alpha }^2\xi )x+\frac{1}{2}{\alpha }^2{\xi }^2{x}^2}\frac{1}{\xi }.$$

(7)

Since the FR function is increasing, it follows that the MRL function decreases from

$$m(0)=\frac{1+2\alpha +3{\alpha }^2}{1+\alpha +{\alpha }^2}\frac{1}{\xi } \mathrm{to} \frac{1}{\xi } \mathrm{at} \mathrm{infinity}.$$

The $p$-QRL reads

$$q_p(x)=R^{-1}((1-p)R(x))-x,$$

(8)

which can be calculated numerically (refer to Lai and Xie [28] for more details). Like the MRL, this measure is a decreasing function of $x$. When $p=0.5$, it is called the median residual life, which is a good alternative to the MRL. In Figure 2, the MRL and the median residual lifetime are plotted for some parameter values and show their similar behavior.

An important concept in reliability theory and survival analysis is orderings between lifetimes. For two lifetimes $X_1$ and $X_2$ following reliability functions $R_1$ and $R_2$, respectively, we say that $X_2$ is greater than $X_1$, $X_2\ge X_1$, in stochastic if $R_2\left(x\right)\ge R_1\left(x\right)$ for every $x$ (refer to Lai and Xie [28] for more details about lifetime orderings). Equivalently, we may write $R_2\ge R_1$ in stochastic. There are other useful orderings, e.g., by means of the FR function, $X_2\ge X_1$ in FR if $h_1\left(x\right)\ge h_2\left(x\right)$ for every $x$. Moreover, $X_2\ge X_1$ in MRL and $p$-QRL if $m_2\left(x\right)\ge m_1\left(x\right)$ and $q_{p,2}\left(x\right)\ge q_{p,1}\left(x\right)$ for every $x$, respectively. The following result shows that EQL is internally ordered in terms of $\alpha$.

Proposition 1. 

Let $X_i$, $i=\mathrm{1,2}$ follow from $EQL(\alpha , \xi )$ and ${\alpha }_2\ge {\alpha }_1$; then, $X_2\ge X_1$ in stochastic, FR, MRL, and $p$-QRL.

Proof. 

See Appendix A. □

3. Estimation

In this section, to estimate the model parameters, three well-known methods, ML, LSE, and weighted LSE, are first discussed. Then, an innovative EM algorithm for this purpose is presented.

3.1. ML Method

Let $x_1,x_2,\dots ,x_n$ represent independent and identically distributed (iid) instances from$EQL(\alpha ,\xi )$. Then, the log-likelihood function is

$$l(\alpha ,\xi ;\mathbf{x})=n\mathrm{l}\mathrm{n}\xi -n\mathrm{l}\mathrm{n}(1+\alpha +{\alpha }^2)+{\displaystyle {\sum }_{i=1}^n}\mathrm{ }\mathrm{l}\mathrm{n}(1+\alpha \xi x_i+\frac{1}{2}{\alpha }^2{\xi }^2{x}_i^2)-\xi {\sum }_{i=1}^n\mathrm{ }{x}_i.$$

(9)

The ML estimator of $(\alpha ,\xi )$ denoted by $(\widehat{\alpha },\widehat{\xi })$ maximizes the log-likelihood function and can be computed directly using numerical methods or by solving the following likelihood equations.

$$\frac{\partial }{\partial \alpha }l(\alpha ,\xi ;\mathbf{x})=-n\frac{1+2\alpha }{1+\alpha +{\alpha }^2}+\sum _{i=1}^n\mathrm{ }\frac{\xi x_i+\alpha {\xi }^2{x}_i^2}{1+\alpha \xi x_i+\frac{1}{2}{\alpha }^{2}x{\xi }^2{x}_i^2}=0,$$

and

$$\frac{\partial }{\partial \xi }l(\alpha ,\xi ;\mathbf{x})=\frac{n}{\xi }+\sum _{i=1}^n\mathrm{ }\frac{\alpha x_i+{\alpha }^2\xi x_i^2}{1+\alpha \xi x_i+\frac{1}{2}{\alpha }^2{\xi }^2{x}_i^2}-\sum _{i=1}^n\mathrm{ }{x}_i=0.$$

The observed Fisher information matrix can be calculated by replacing $\widehat{\alpha }$ and $\widehat{\xi }$ for $\alpha$ and $\xi$ in the following Fisher information matrix.

$$O=\left[\begin{array}{ll}-\frac{{\partial }^2}{\partial {\alpha }^2}& -\frac{{\partial }^2}{\partial \alpha \partial \xi }\\ -\frac{{\partial }^2}{\partial \xi \partial \alpha }& -\frac{{\partial }^2}{\partial {\xi }^2}\end{array}\right]l(\alpha ,\xi ;\mathbf{x}).$$

(10)

Then, the asymptotic distribution of $(\widehat{\alpha },\widehat{\xi })$ is approximately the bivariate normal distribution with mean $(\alpha ,\xi )$ and variance-covariance matrix $O^{-1}$.

3.2. LSE Method

Suppose that $x_1\le x_2\le \dots \le x_n$ represents the ordered sample. In this approach, we search for parameter values that minimize the sum of squared distances between the empirical distribution and the estimated distribution functions. More precisely, we minimize the following expression in terms of the parameters.

$$S^2=\sum _{i=1}^n\mathrm{ }(F\left(x_i\right)-\widehat{F}\left(x_i\right){)}^2,$$

where $\widehat{F}\left(x_i\right)=\frac{i}{n}$ is the well-known empirical distribution function at $x_i$ and provides a common estimate of $F\left(x_i\right)$. By substituting the distribution function, we have

$$S^2=\sum _{i=1}^n\mathrm{ }{\left(\frac{1}{\left(1+\alpha +{\alpha }^2\right)}\left(1+\alpha +{\alpha }^2+\alpha \xi x_i+{\alpha }^2\xi x_i+\frac{1}{2}{\alpha }^2{\xi }^2{x}_i^2\right)e^{-\xi x_i}-\frac{i}{n}\right)}^2.$$

Then, the estimates could be computed as follows:

$$(\widehat{\alpha },\widehat{\xi })=\mathrm{a}\mathrm{r}\mathrm{g}\underset{(\alpha ,\beta ,\lambda )}{\mathrm{m}\mathrm{i}\mathrm{n}}\sum _{i=1}^n\mathrm{ }{\left(\frac{1}{1+\alpha +{\alpha }^2}\left(1+\alpha +{\alpha }^2+\alpha \xi x_i+{\alpha }^2\xi x_i+\frac{1}{2}{\alpha }^2{\xi }^2{x}_i^2\right)e^{-\xi x_i}-\frac{i}{n}\right)}^2.$$

3.3. Weighted LSE Method

A well-known weight that could improve the LSE estimate is $\frac{1}{F\left(x_i\right)(1-F(x_i\left)\right)}$. With this idea, the weighted LSE estimate is computed by minimizing the following expression in terms of the parameters.

$$S^2=\sum _{i=1}^n\mathrm{ }\frac{1}{F\left(x_i\right)(1-F(x_i))}(F\left(x_i\right)-\widehat{F}\left(x_i\right){)}^2.$$

This method is well known as the Anderson–Darling (AD) method.

3.4. EM Algorithm

The EM algorithm takes advantage of the fact that we have a mixed model and creates a more informative likelihood function. The parameters are then estimated iteratively. Suppose that $X_i$, $i=1,2,\dots ,n$ is an iid sample from $EQL(\alpha ,\xi )$. For a short exposition, take $\theta =(\alpha ,\xi )$. Since EQL is a mixture of three gamma models $G(j,\xi )$, $j=\mathrm{1,2},3$, we consider a latent random variable $V_i$ such that $V_i=j$ when $X_i$ comes from $G(j,\xi )$. Thus, $\left(X_i\right|V_i=j,\theta )\sim G(j,\xi )$ and $P(V_i=j|\theta )=\frac{{\alpha }^{j-1}}{1+\alpha +{\alpha }^2}$, $j=\mathrm{1,2},3$. However, the latent variable $V_i$ will not be observed, but applying it helps to improve the estimation of the parameters in an iterative process. With the evidence $X_i$ and $V_i$, $i=1,2,\dots ,n$, the likelihood function can be written as follows:

$$L(\theta ;\mathbf{x},\mathbf{v})={\prod }_{i=1}^n\mathrm{ }{\prod }_{j=1}^3\mathrm{ }{\left(g\left(x_i\right|\theta \left)P\right(V_i=j\left|\theta \right)\right)}^{I(v_i=j)},$$

(11)

where $I(v_i=j)$ equals $1$ when $v_i=j$ and $0$ otherwise, and $g_j\left(x_i\right|\theta )$ represents the PDF of gamma $G(j,\xi )$. Then, the log-likelihood function is

$$l\left(\theta ;\mathbf{x},\mathbf{v}\right)={\sum }_{i=1}^n\mathrm{ }{\sum }_{j=1}^3\mathrm{ }I\left(V_i=j\right)\mathrm{l}\mathrm{n}\left(\frac{{\xi }^j{x}_i^{j-1}}{\mathsf{\Gamma }\left(j\right)}{e}^{-\xi x_i}\frac{{\alpha }^{j-1}}{1+\alpha +{\alpha }^2}\right).$$

(12)

Since this function depends on the unobserved random variable $V_i$, we cannot estimate the parameters by maximizing them directly. One approach is to implement an iterative process with expectation (E) and maximization (M) steps. In the E step, the expected log-likelihood function is constructed with respect to the conditional latent variable. In the M step, the expected log-likelihood function is maximized to estimate the parameters. See Appendix B for the implementations of the E-step and M-step.

4. Simulations

The goal of this section is to investigate and compare the behavior of the discussed estimators through simulations. To this end, we calculate the empirical bias (B) and mean square error (MSE) of the estimators. We generate a random sample of $EQL(\alpha ,\xi )$ using the following steps:

• First, drive one random instance from a multinomial model with parameters $(p_1,p_2,p_3,n)$, where $p_1=1/(1+\alpha +{\alpha }^2)$, $p_2=\alpha /(1+\alpha +{\alpha }^2)$, and $p_3=1-p_1-p_2$. Assume the derived instance is $(k_1,k_2,k_3)$.
• Generate and mix three identical and independent (iid) random samples from $G(1,\xi )$, $G(2,\xi )$, and $G(3,\xi )$ with sizes $k_1$, $k_2$, and $k_3$ respectively.

In each simulation run, $r=1000$ samples are generated with a size of $n=80$ or $150$. Then, the parameters are estimated for each instance using the ML, LSE, and AD methods or EM algorithm. For the calculation of the optimum values of the parameters, the integrated function “optim” of R is used. The initial values needed for computing all estimators are randomly generated from a uniform distribution, e.g., the initial values for $\alpha$ are randomly and uniformly derived from the interval ($0.9\alpha$, $1.1\alpha$).

Table 1. Simulation results for ML, LSE, AD, and EM algorithm. The first and second lines of every cell correspond to $\alpha$ and $\xi$.

		$\mathit{n}$
Method		80		150
	α,$\xi$	B	MSE	B	MSE
MLE	0.1, 0.1	0.2093 0.0221	0.1413 0.0015	0.1486 0.0166	0.0853 0.0010
	0.3, 0.5	0.1009 0.0415	0.1222 0.0209	0.0466 0.0168	0.0771 0.0133
	0.8, 1	0.0598 0.0029	0.1716 0.0326	0.0273 −0.0043	0.0948 0.0201
EM	0.1, 0.1	0.0833 0.0097	0.0377 0.0004	0.0463 0.0054	0.0126 0.0002
	0.3, 0.5	0.1346 0.0530	0.1095 0.0181	0.0807 0.0329	0.0554 0.0100
	0.8, 1	0.1023 0.0223	0.1856 0.0299	0.0281 0.0015	0.0728 0.0156
LSE	0.1, 0.1	0.2350 0.0306	0.1970 0.0026	0.1734 0.0230	0.1185 0.0016
	0.3, 0.5	0.0906 0.0523	0.1726 0.0315	0.0466 0.0287	0.1083 0.0206
	0.8, 1	0.0609 0.0075	0.2960 0.0500	0.0143 −0.0038	0.1085 0.0270
Weighted LSE (AD)	0.1, 0.1	0.0283 0.0097	0.0592 0.0009	0.0249 0.0084	0.0392 0.0006
	0.3, 0.5	−0.1116 −0.0233	0.1157 0.0211	−0.1373 −0.0367	0.0778 0.0121
	0.8, 1	−0.3220 −0.1497	0.2795 0.0700	−0.2426 −0.1230	0.1963 0.0466

shows the bias (B) and mean square error (MSE) for estimators and for some parameter values calculated using the following relations:

$$B_{\alpha }=\frac{1}{r}\sum _{i=1}^n\mathrm{ }({\widehat{\alpha }}_i-\alpha ),$$

and

$$MS{E}_{\alpha }=\frac{1}{r}\sum _{i=1}^n\mathrm{ }({\widehat{\alpha }}_i-\alpha {)}^2,$$

with a similar approach for $\xi$. Small values of MSE reported in Table 1 show that all estimators are consistent and sufficiently efficient but the EM algorithm outperforms others for all selected parameters.

5. Application

In this section, the EQL and some alternative models are fitted to a data set of air conditioning systems of a Boeing 720 aircraft to verify the usefulness of the proposed model. Alternative models include gamma, exponentiated gamma (EG), Lehmann gamma (LG), Marshal–Olkin gamma (MOG), and QL.

Table 2. Time interval, in terms of hours, between successive failures of air conditioner system of Boeing 720 aircraft.

59	20	68	67	25	13	5	79	76
127	117	100	52	189	398	60	117	263
143	39	194	128	160	88	74	66	199
180	156

shows 29 time intervals, in terms of hours, between successive air conditioning failures in a Boeing 720 aircraft. For more details about the experiment and the data, see Proschan [29].

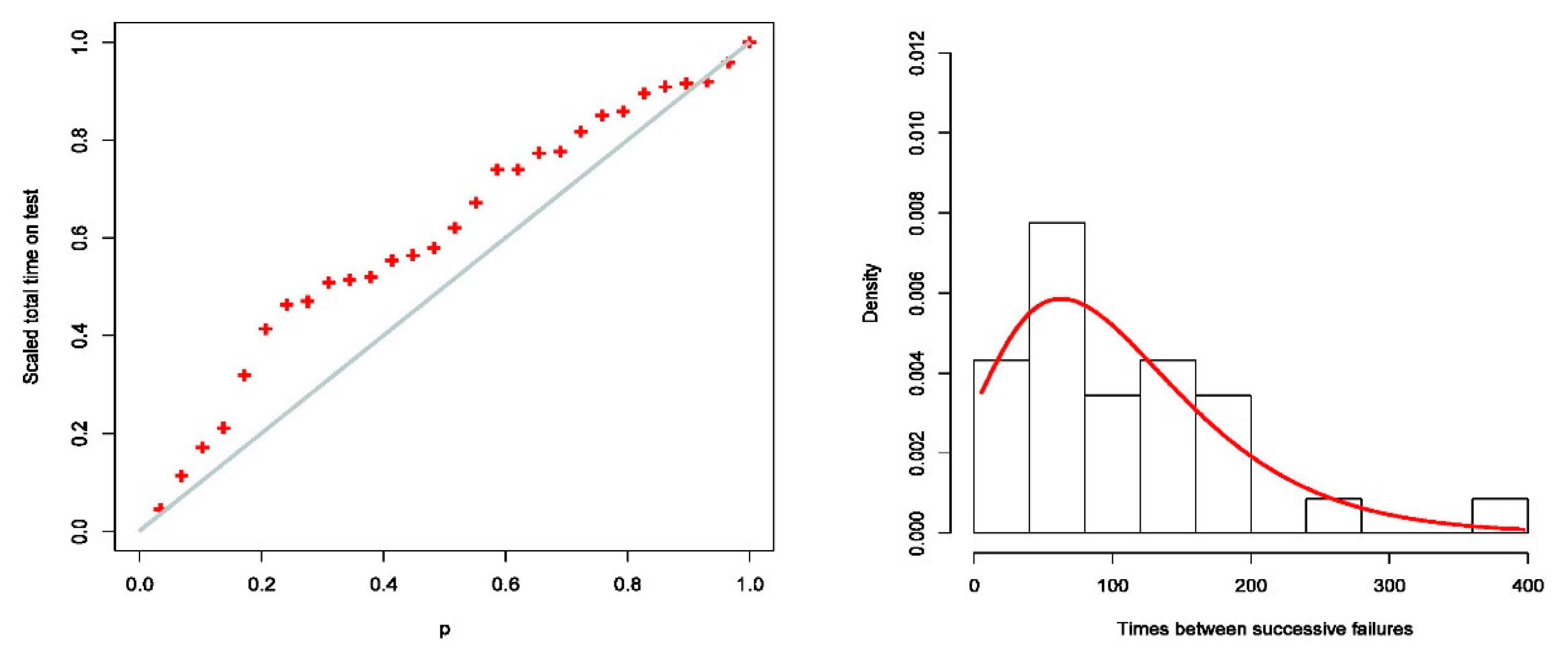
For this data set, the total time on test (TTT) is plotted in Figure 3 (left), which shows an increasing FR function. The TTT plot is really a nonparametric plot, which is very useful for determining the FR form of the data. Figure 3 (right) draws the histogram of the data and the calculated PDF of the EQL and gives a graphical investigation.

For each model, parameters were estimated using ML. In addition, the parameters of the EQL were estimated using the ML method and the EM algorithm, and because the results were approximately the same, only the EM estimates are reported in

Table 3. Fitting the successive times between failures.

Model	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{\xi }}$	AIC	CVM	AD	KS
					p-Value	p-Value	p-Value
EQL	1.9668	—	0.0215	331.22	0.0278 0.9843	0.1833 0.9944	0.0801 0.9923
Gamma	1.7195	—	0.0153	331.55	0.0363 0.9539	0.2399 0.9754	0.1028 0.9190
EG	2.8250	0.0823	0.1459	334.57	0.0647 0.7882	0.3836 0.8638	0.1308 0.7037
LG	1.4504	1.1997	0.0142	333.59	0.0373 0.9682	0.2454 0.9727	0.1041 0.9120
MOG	1.6439	1.2563	0.0161	333.37	0.0322 0.9705	0.2169 0.9851	0.0965 0.9498
QL	0.1382	—	0.0167	331.35	0.0320 0.9712	0.2057 0.9888	0.0965 0.9499

. The Akaike information criterion (AIC), Cramer–von Mises (CVM) statistics, Anderson–Darling (AD) statistics, and Kolmogorov–Smirnov (KS) statistics were also calculated and are summarized in Table 3.

In Figure 4, the empirical and fitted distribution functions for EQL and some alternatives are plotted, providing a graphical investigation.

Considering Table 3, a smaller AIC indicates a better fit to the data. Here, the AIC of the proposed EQL model is smaller than that of all other selected models, indicating that it is preferred over the other models. In addition, the model with a smaller CVM (AD and KS) statistic better describes the data. Fortunately, the value of the CVM (AD and KS) statistic for EQL is smallest among all the selected models. This shows that EQL is preferred in terms of CVM, AD, and KS statistics.

6. Conclusions

For data modeling and analysis, an appropriate statistical model must be used to draw more accurate conclusions. The EQL model, which combines three gamma distributions, is an extension of QL, which can be used in various scientific disciplines. In the context of reliability theory and survival analysis, it could be useful for data with increasing FR and decreasing MRL functions, for example, for modeling the lifetime of devices subject to depletion. The model can be useful in practice, as shown by the analysis of a data set consisting of the intervals between successive failures of the air conditioning system of a Boeing 720 aircraft. Based on the simulation results, the ML and EM algorithms provide accurate and consistent parameter estimates. However, the EM algorithm provides a more accurate approximation than the MLE. Some future research related to this study can be considered as follows:

• Estimate the unknown parameters of the proposed model, along with the reliability and hazard rate functions under different types of censoring schemes, such as progressive type II, hybrid, general progressive, and adaptive censoring schemes.
• Consider the maximum likelihood and maximum product-of-spacing methods to determine the point estimates and approximate confidence intervals of the various model parameters.
• Provide Bayesian estimates based on the likelihood function and product of the distance function of the unknown parameters using the quadratic error loss function with independent gamma priors.
• The methods investigated in this study can be extended to study estimation problems in more complex cases.