Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications

Abstract

In manufacturing sectors, product performance evaluation is crucial. The lifetime performance index, denoted as $C_L$, is widely used in product evaluation, where L signifies the lower specification limit. This study aims to refine the estimation of $C_L$ by employing maximum-likelihood and Bayesian methodologies, where symmetric and asymmetric loss functions are utilized. The analysis is conducted on progressive type II censored data, a requirement often imposed by budgetary constraints or the need for expedited testing. The data are assumed to follow the Ishita distribution, whose conforming rate is also evaluated. Furthermore, a hypothesis testing framework is employed to validate whether component lifetimes meet predefined standards. The theoretical findings are corroborated using real data collected from glass strength in aircraft windows. The numerical analysis emphasizes the goodness of fit of the Ishita distribution to model the data, thereby demonstrating the applicability of the proposed distribution.

1. Introduction

The manufacturing capability index of the process (CIP) serves as a gauge for its level of quality and is used to assess the lifetime performance of electronic components. Ref. [1] explained the lifetime of electronic components as demonstrating the larger-the-better quality characteristic of time orientation. Kaneh [2] developed the $C_L$ (or PCI), for which L refers to the lowest specific limit. Three different types of process capability indexes are available. The first quality is “the target the better kind”. The second is “the larger the better kind”, which is one of the most recommended PCIs and is used when a specific goal is desired. The third is “the smaller the better type”; it is applied in industries like a product’s testing period and radiation exposure. Numerous studies have been conducted on the statistical inference for the lifetime performance index using the conventional type II and the progressive type II censoring methods with a wide class of lifetime models. For example; see Hong et al. [3,4,5], and Lee et al. [6,7,8]. Furthermore, the latter [9] used Bayesian estimation to obtain a credible interval for $C_L$, then suggested an assessing procedure for the products’ lifetime performance. Depending on the Weibull distribution with a progressive first-failure censored sample, Ahmadi et al. [10] produced a confidence interval for $C_L$ using the maximum-likelihood estimation. At the same time, Mahmoud et al. [11] accomplished the same for the Lomax distribution and constructed a maximum-likelihood estimator and Bayesian estimator for $C_L$ using a progressive type II censored sample. Amal et al. [12] develop a lifetime performance index estimation using the Burr type III distribution under type II censoring. Hybrid censoring samples were created by Majdah et al. [13] to assess the performance lifetime index of Chen distribution. The performance index under a weighted Lomax distribution’s lifetime with progressive type II censoring samples was introduced by Dina [14].

A progressive censoring scheme permits the removal of particularly unsafe individual subjects from the trial at every ordered failure time. For more related works, one may refer to Howlader and Hossain [15], Cohen [16,17], Fernandez [18], Sen [19], AL-Hussaini and Ahmad [20,21], and Asgharzadeh [22].

The censoring scheme used in this work can be summarized as follows: Assume that n independent items are placed through a life test with $X_1,X_2,\dots ,X_n$ failure times that are continuous and identically distributed. Assume that a censoring scheme $(R_1,R_2,\dots ,R_m)$ is predetermined so that immediately after the first failure $X_1,R_1$ surviving items are removed from the experiment at random, and immediately after the second failure $X_2,R_2$ surviving items are removed from the experiment at random. When the $mth$ observed failure occurs, the remaining $R_m$ surviving items are removed from the test, or $X_m$. The order statistics of size m that have been gradually type II right-censored from a sample of size n using a progressive censoring scheme $(R_1,R_2,\dots ,R_m)$ are the m ordered observed failure times represented by $X_{1:m:n}^{(R_1,R_2,\dots ,R_m)},X_{2:m:n}^{(R_1,R_2,\dots ,R_m)},\dots ,X_{m:m:n}^{(R_1,R_2,\dots ,R_m)}$. There is no doubt that $n=m+R_1+R_2+\dots +R_m$. The particular situation of traditional type II right-censored sampling occurs when $R_1=R_2=\dots =R_{m-1}=0$ and $R=n-m$. Additionally, the gradual type II right-censoring method is due to the absence of censoring when $R_1=R_2=\dots =R_{m-1}=0$; (ordinary order statistics), see [23,24,25].

Shukla and Shanker [26] used the Ishita distribution in quality control, reliability analysis, and failure time modeling. The probability density function (PDF) and the cumulative density function (CDF) of the Ishita distribution are written respectively as

$$f\left(x;\theta \right)=\frac{{\theta }^3}{{\theta }^3+2}\left(\theta +x^2\right)e^{-\theta x},x>0,\theta >0$$

(1)

and

$$F\left(x;\theta \right)=1-\left[1+\frac{\theta x\left(\theta x+2\right)}{{\theta }^3+2}\right]e^{-\theta x},x>0,\theta >0.$$

(2)

With mean

$$\mu =\frac{{\theta }^3+6}{\theta ({\theta }^3+2)}$$

(3)

and standard deviation

$$\sigma =\frac{\sqrt{{\theta }^6+16{\theta }^3+12}}{\theta ({\theta }^3+2)}.$$

(4)

Modeling Ishita distribution lifetimes from biomedical data and engineering have been studied by [26], in which its various statistical and mathematical properties were introduced and the rules of over-, equi-, and under-dispersed for Ishita distribution were presented in addition to Akash, Lindley, and exponential distributions. Recently, Kariema et al. [27] introduced statistical inference for the inverse power Ishita distribution with a progressive type II censored scheme and applied it to COVID-19 data.

The purpose of this study is to create a maximum-likelihood estimation (MLE) of $C_L$ under a progressive type II censoring sample with Ishita lifetimes using transformation technology data. The development of a novel method started from testing hypotheses under the assumption of known L and then making use of the MLE of $C_L$. The new testing method is to determine if a unit’s lifetime follows the standard under known L conditions.

This work is written as follows: the lifetime index and conforming rate are presented in Section 2. Suggested methods of estimation and testing hypotheses are performed in Section 3, including the maximum-likelihood approach as well as the Bayes estimator of $C_L$ for a parameter following the Ishita distribution. In Section 4, a numerical example is offered; hence, the theoretical framework is applied to a real-world lifetime dataset, thereby substantiating its practical utility in engineering areas.

2. The Performance Index and Conforming Rate of the Ishita Distribution

In this section, two important values are evaluated, namely the performance index and the conforming rate, in which the product’s lifetime X following the Ishita distribution with PDF and CDF that were represented by Equations (1) and (2). In order to fulfill the needs of customers, the lifetime must exceed the lowest L units. To assess the larger-the-better quality feature, $C_L$ was presented by Montgomery [1], which refers to the process capability index. So, $C_L$ is defined as follows:

$$C_L=\frac{\mu -L}{\sigma },$$

(5)

such that $\mu$ and $\sigma$ represent the mean and the standard deviation of the process, respectively, and L is the lower specification limit, where the lifetime is desired to surpass L unit times to have success and customer satisfaction.

Following that, the Ishita distribution’s lifetime performance index is

$$C_L=\frac{(6+{\theta }^3)-\theta (2+{\theta }^3)L}{\sqrt{{\theta }^6+16{\theta }^3+12}},$$

(6)

where

$$-\infty <C_L<\frac{6+{\theta }^3}{\sqrt{{\theta }^6+16{\theta }^3+12}},$$

(7)

when $\frac{6+{\theta }^3}{\sqrt{{\theta }^6+16{\theta }^3+12}}>L$, $\theta >0$, and $C_L>0$.

The hazard rate (failure rate) function of the Ishita distribution is given as

$$h\left(x\right)=\frac{{\theta }^3(\theta +x^2)}{\theta x(\theta x+2)+({\theta }^3+2)};x>0,\theta >0.$$

(8)

The hazard rate function has an increasing curve with respect to x when $\theta \le 1$ and $x\ge 1$, while it has a decreasing curve for $\theta >1$ and $0<x<1$; see Figure 1.

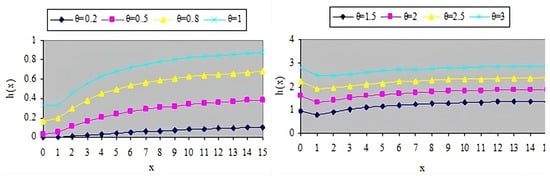
Figure 1. Hazard rate function for the Ishita distribution.

If the product’s lifetime X is greater than L, then as a result, the conforming rate (CR), also known as the conforming product ratio, is given as follows:

$$p_r=p(X\ge L)={\int }_L^{\infty }f\left(x\right)dx=\left[1+\frac{\theta L}{{\theta }^3+2}(\theta L+2)\right]e^{-\theta L}$$

$$\begin{array}{cc}\hfill =& \left[1+\frac{{\theta }^3+6-\sqrt{{\theta }^6+16{\theta }^3+12}}{{\theta }^3+2}{C}_L\left(\frac{{\theta }^3+6-\sqrt{{\theta }^6+16{\theta }^3+12}}{{\theta }^3+2}{C}_L+2\right)\right]\hfill \\ \hfill & \times Exp\left[-\frac{{\theta }^3+6-\sqrt{{\theta }^6+16{\theta }^3+12}}{{\theta }^3+2}{C}_L\right],\hfill \end{array}$$

(9)

where $-\infty <C_L<\frac{6+{\theta }^3}{\sqrt{{\theta }^6+16{\theta }^3+12}},\theta >0,x>0$.

It is clear that there is a strictly increasing relationship between the two values of $C_L$ and $P_r$ for the specified parameter $\theta$. The idea in Table 1 is based on the calculated parameter estimations using the maximum-likelihood estimator, which is discussed in the next section; this helps in obtaining the related values for $C_L$ that meet the necessary example of CR in Section 4.

Table 1. The lifetime performance index $C_L$ vs. the CR $P_r$ with $(\widehat{\theta }=1.20329)$.

${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$
−11	$7.34341\times {10}^{-8}$	−0.25	0.327713	0.499	0.611436
−7	0.0000382405	0	0.410495	0.513	0.617739
−6.5	0.0000816901	0.1	0.447049	0.534	0.627266
−6	0.000173278	0.2	0.485503	0.556	0.63734
−5.75	0.000251629	0.25	0.505425	0.589	0.65264
−5	0.000760398	0.3	0.525805	0.618	0.666279
−4	0.0032004	0.32	0.534084	0.634	0.673885
−3	0.0127309	0.34	0.542436	0.758	0.73503
−2.5	0.0246903	0.35	0.546639	0.897	0.809544
−2	0.0467506	0.353	0.547903	0.95	0.840259
−1	0.152262	0.412	0.573104	1	0.870775
−0.5	0.257434	0.478	0.602053	1.1818996	1

3. Parameter Estimation and Testing Hypothesis

The parameter $\theta$ of $C_L$ is estimated using the MLE and Bayesian estimation (BE) methods.

3.1. Maximum-Likelihood Estimation

Let X indicate the product’s lifetime and X has the one parameter Ishita distribution with the PDF as in Equation (1). Assume n products (or items) are subject to progressive type II censoring with censored sample $X_{1:m:n},X_{2:m:n},\dots ,X_{m:m:n}$ and a censoring scheme $R=(R_1,R_2,\dots ,R_m)$. Balakrishnan et al. [28] combined the PDF of all m progressive type II censored as

$$L\left(\theta \right|\underline{x})=C\prod _{i=1}^{m}f\left(x_{i:m:n}\right){[1-F\left(x_{i:m:n}\right)]}^{R_i},$$

(10)

where $C=n(n-R_1-1)\dots (n-\sum (R_i+1)),f\left(x_{i:m:n}\right)$ is the PDF of X in Equation (1) and $F\left(x_{i:m:n}\right)$ is the CDF in Equation (2). As a result, the likelihood function for the Ishita distribution is written as

$$L\left(\theta \right|\underline{x})\propto \prod _{i=1}^m\frac{{\theta }^3}{{\theta }^3+2}\left(\theta +x_{i:m:n}^2\right)e^{-\theta x_{i:m:n}}{\left[\left(1+\frac{\theta x_{i:m:n}\left(\theta x_{i:m:n}+2\right)}{{\theta }^3+2}\right)e^{-\theta x_{i:m:n}}\right]}^{R_i}.$$

(11)

The log-likelihood function can be specified by

$$\begin{array}{cc}\hfill l=& 3mlog\theta -mlog({\theta }^3+2)-\theta \sum _{i=1}^m{x}_i+\sum _{i=1}^{m}log(\theta +x_{i:m:n}^2)-\theta \sum _{i=1}^m{R}_i{x}_{i:m:n}\hfill \\ \hfill & +\sum _{i=1}^m{R}_{i}log\left[1+\frac{\theta x_{i:m:n}\left(\theta x_{i:m:n}+2\right)}{{\theta }^3+2}\right]e^{-\theta x_{i:m:n}}.\hfill \end{array}$$

(12)

The given equation can be solved to produce the Ishita distribution’s MLE for the parameter $\theta$ under the progressive type II censored sample:

$$\frac{\partial l}{\partial \theta }=\frac{3m}{\theta }-\frac{3m{\theta }^2}{{\theta }^3+2}-\sum _{i=1}^m{x}_i(1+R_i)+\sum _{i=1}^m\frac{1}{\theta +x_i^2}+\sum _{i=1}^m{R}_i\frac{2x_i({\theta }^3+2)(\theta x_i+1)-3{\theta }^3{x}_i(\theta x_i+2)}{{({\theta }^3+2)}^2+\theta x_i(\theta x_i+2)}.$$

(13)

Equation (13) has no closed-form solutions; hence, the estimator can be derived using the numerical Newton–Raphson iteration algorithm. Hence, Mathematica 13 is used for performing the numerical analysis. For more details, refer to Essam [29].

According to Zehan [30], if the MLE’s invariant property is content, the $C_L$ MLE has the following form.

$$\widehat{C_L}=\frac{(6+{\widehat{\theta }}^3)L}{\sqrt{{\widehat{\theta }}^6+16{\widehat{\theta }}^3+12}}.$$

(14)

The elements of the Fisher information matrix’s inverse $I=E[-\frac{{\partial }^{2}l\left(\theta \right)}{\partial {\theta }^2}]$ are the basis for the asymptotic variances and covariances of the MLEs. Therefore, it is difficult to find the exact closed forms for the given expectations. To create confidence intervals (CIs) for the parameter, the Fisher information matrix $\widehat{I}=(-\frac{{\partial }^{2}l\left(\theta \right)}{\partial {\theta }^2})$, which is derived by removing the expectation operator E, would be applied. Consequently, the observed information matrix is represented by

$$\widehat{I}\left(\widehat{\theta }\right)={(-\frac{{\partial }^{2}l}{\partial {\theta }^2})}_{(\theta =\widehat{\theta })},$$

(15)

where $\frac{{\partial }^{2}l}{\partial {\theta }^2}$ is the second partial derivative with respect to $\theta$. For the approximate asymptotic variance–covariance matrix $\left[\widehat{V}\right]$, with inverting the viewed information matrix $\widehat{I}\left(\theta \right)$, the MLEs are produced:

$$\left[\widehat{V}\right]={\widehat{I}}^{-1}(\widehat{\theta })=(var(\widehat{\theta })).$$

(16)

It is widely considered that $\left(\widehat{\theta }\right)$ approximates a multivariate normal distribution with the following parameter $\theta$ for the mean and $I^{-1}\left(\theta \right)$ for the covariance matrix; see Lawless [31]. Then, the $100(1-\gamma )\%$ CI for $\theta$ can be provided by

$$\widehat{\theta }\pm Z_{\frac{\gamma }{2}}\sqrt{\widehat{\theta }}$$

(17)

where $Z_{\frac{\gamma }{2}}$ denotes the percentile of the right-tail probability $\frac{\gamma }{2}$ of the standard normal distribution.

Using the Delta technique [32], we can obtain the asymptotic distribution for $C_L\equiv h\left(\theta \right)$ as

$${\widehat{C}}_L=h(\widehat{\theta })\sim N(C_L,\sum _{\theta }),$$

(18)

where the asymptotic normal distribution of $h(\widehat{\theta })$ with asymptotic variance is

$$\sum _{\theta }=\left(\frac{\partial h\left(\theta \right)}{\partial \theta }\right)I^{-1}\left(\theta \right){\left(\frac{\partial h\left(\theta \right)}{\partial \theta }\right)}_{\theta =\widehat{\theta }}.$$

(19)

3.2. Bayes Estimation

The BE approach is employed in this subsection to estimate the $\theta$, where $\theta \sim Gamma(a,b).$

The gamma prior density function is expressed as

$$\pi \left(\theta \right)\propto {\theta }^{a-1}{e}^{-b\theta },\theta >0,a,b>0,$$

(20)

where the hyper-parameters a and b were considered to be similar, and their values are chosen to reflect the preceding assumption on the unknown parameters.

By Bayes’ theorem, the posterior distribution of the parameter $\theta$ indicated by ${\pi }^{*}(\theta \mid \underline{x})$ is combined by Equations (11) and (20):

$${\pi }^{*}(\theta \mid \underline{x})=\frac{\pi \left(\theta \right)L(\theta \mid \underline{x})}{{\int }_0^{\infty }\pi \left(\theta \right)L(\theta \mid \underline{x})d\theta }.$$

(21)

The square error loss (SEL) function for $\theta$ is defined as follows:

$$L(\theta ,\widehat{\theta })={(\widehat{\theta }-\theta )}^2,$$

(22)

where the SEL function is a symmetric loss function that equals overestimation and underestimating losses and is a frequently employed loss function. As a result, the SEL function Equation (22) allows for the BE of the parameter of $\theta$ to be calculated as

$${\widehat{g}}_{BS}(\theta \mid \underline{x})=E_{\theta \mid \underline{x}}\left(g\left(\theta \right)\right),$$

(23)

and

$$E_{\theta \mid \underline{x}}\left(g\left(\theta \right)\right)=\frac{{\int }_0^{\infty }g\left(\theta \right)\pi \left(\theta \right)L(\theta \mid \underline{x})d\theta }{{\int }_0^{\infty }\pi \left(\theta \right)L(\theta \mid \underline{x})d\theta }.$$

(24)

Also, we utilize an asymmetrical loss function, the LINEX loss function. It is considered to be more comprehensive in many respects; see Varian [33]. It is defined as

$$L\left(▵\right)=\left(e^{\epsilon ▵}-\epsilon ▵-1\right),\epsilon \ne 0,▵=\widehat{\varphi }-\varphi ,$$

(25)

where $\epsilon$ is a loss function scale parameter. The LINEX loss function is almost the same as the SEL function for the characteristic of positive or negative values of $\epsilon$; in other words, it is close to zero.

The Bayesian estimate of a function of $\theta$, say $k\left(\theta ,\right)$ under the LINEX function can be calculated by

$${\widehat{k}}_{BL}\left(\theta ,\mid \mathrm{data}\right)=-\frac{1}{\epsilon }log\left[E\left(e^{-\epsilon k\left(\theta ,\right)}\mid \mathrm{data}\right)\right],\epsilon \ne 0,$$

(26)

and

$$E\left(e^{-\epsilon \left(\theta ,\right)}\mid \mathrm{data}\right)=\frac{\underset{0}{\overset{\infty }{\int }}{e}^{-\epsilon k\left(\theta ,\right)}\pi \left(\theta \right)L(\theta ,\mid \mathrm{data})d\theta }{\underset{0}{\overset{\infty }{\int }}\pi \left(\theta \right)L(\theta ,\mid \mathrm{data})d\theta }.$$

(27)

It should be noted that the likelihood function has a complicated structure, making it impossible to perform the analytical calculation of multiple integrals. Because of this, to generate samples from the joint posterior density function, the Markov chain Monte Carlo (MCMC) approximation approach used for those samples calculates the BE of $\theta$ and any functions derived from it, like $C_L$. To apply the MCMC approach, use the Gibbs within the Metropolis sampler for the creation of conditional posterior distributions. Equation (21) can be used to compute the joint posterior up to proportionality.

$${\pi }^{*}(\theta \mid data)\propto \prod _{i=1}^m{\theta }^{a-1}{e}^{-b\theta }\frac{{\theta }^3}{{\theta }^3+2}\left(\theta +x_{i:m:n}^2\right)e^{-\theta x_{i:m:n}}{\left[\left[1+\frac{\theta x_{i:m:n}\left(\theta x_{i:m:n}+2\right)}{{\theta }^3+2}\right]e^{-\theta x_{i:m:n}}\right]}^{R_i}.$$

(28)

It is clear that the conditional posteriors of $\theta$ in Equation (28) do not exhibit standard forms, making the employment of the Metropolis–Hasting (M-H) sampler necessary for the implementation of the MCMC approach sampler. The method using M-H update steps $\theta$ is shown below given these conditional distributions in Equation (28).

• Begin with the first suggestion ${\theta }^{\left(0\right)}$.
• Specify $j=1$.
• Generate ${\theta }^{\left(j\right)}$ from ${\pi }^{*}({\theta }^{j-1}\mid \underline{x})$ using the M-H method with the normal distribution

  $$N({\theta }^{j-1},var\left(\theta \right)).$$

  (a)

  Produce a proposal ${\theta }^{*}$ from $N({\theta }^{j-1},var\left(\theta \right))$.

  (b)

  Determine the probability of acceptance

  $${\eta }_{\theta }=min\left[1,\frac{{\pi }^{*}({\theta }^{*}\mid \underline{x})}{{\pi }^{*}({\theta }^{j-1}\mid \underline{x})}\right].$$

  (c)

  Produce a u from a uniform $(0,1)$ distribution.

  (d)

  Accept the proposal and set ${\theta }^{\left(j\right)}={\theta }^{*}$ if $u<{\eta }_{\theta }$; otherwise set ${\theta }^{\left(j\right)}={\theta }^{(j-1)}$.

• Calculate the $C_{LBS}$ as

  $$C_{LBS}^{\left(j\right)}=\frac{6+{\theta }^{3\left(j\right)}-{\theta }^{\left(j\right)}(2+{\theta }^{3\left(j\right)})L}{\sqrt{{\theta }^{6\left(j\right)}+16{\theta }^{3\left(j\right)}+12}}.$$

  (29)
• Let $j=j+1$.
• Steps (3)–(5) are repeated N times to obtain ${\theta }^{\left(i\right)}$ and $C_{LBS}^{\left(i\right)},i=1,2,\dots ,N.$
• Evaluate the credible intervals of $\theta$ and $C_L$ order ${\theta }^{\left(i\right)}$ and $C_{LBS}^{\left(i\right)},i=1,‥,N$ as ${\theta }_{\left(1\right)}<{\theta }_{\left(2\right)}<‥<{\theta }_{\left(N\right)}$ and $C_{L_{\left(1\right)}}<C_{L_{\left(2\right)}}<‥<C_{L_{\left(N\right)}}$. Then, the $100(1-\eta )\%$ credible intervals of $\theta$ be $\left(\varphi \right(N(\eta /2)),\varphi (N(1-\eta /2)\left)\right)$.

In this section, a one-sided technique for testing hypotheses is built into a one-sided confidence interval. They are designed to demonstrate whether the lifetime performance index, $C_L$, remains at the desired level, L. Let $c^{*}$ define the selected destination or the wanted value; thus, the null hypothesis $H_0$ versus the alternative hypothesis $H_1$ is

$$H_0:C_L\le c^{*},$$

(30)

against

$$H_1:C_L>c^{*}.$$

(31)

Wu et al. [34] state that the required rejection area can be computed using the formula ${\widehat{C}}_L$ where ${\widehat{C}}_L>C_0$, where $C_0$ is the critical value, and ${\widehat{C}}_L$ has an asymptotic normal distribution. The formula can be used to calculate it at a certain significance level

$$P\left(\frac{{\widehat{C}}_L-C_L}{\sqrt{{\sum }_{\widehat{\theta }}}}=\frac{C_0-c^{*}}{\sqrt{{\sum }_{\widehat{\theta }}}}\right)=1-\gamma ,$$

(32)

as $\frac{{\widehat{C}}_L-C_L}{\sqrt{{\sum }_{\widehat{\theta }}}}\sim N(0,1)$; then, $\frac{C_0-c^{*}}{\sqrt{{\sum }_{\widehat{\theta }}}}=z_{\gamma }$ and the critical value is

$$C_0=c^{*}+z_{\gamma }\sqrt{\sum _{\widehat{\theta }}}.$$

(33)

Furthermore, $100(1-\gamma )\%$ is the one-sided CI for the value of $C_L$

$$C_L\ge {\widehat{C}}_L-z_{\gamma }\sqrt{\sum _{\widehat{\theta }}},$$

(34)

Also, the lower confidence bound for $C_L$ of $100(1-\gamma )\%$ is

$$\underline{LB}={\widehat{C}}_L-z_{\gamma }\sqrt{\sum _{\widehat{\theta }}}.$$

(35)

The following steps summarize the testing procedure:

• Using the progressive type II censoring sample $X_{1:m:n},X_{2:m:n},\dots ,X_{m:m:n}$ and the censoring scheme $R=(R_1,R_2,\dots ,R_m)$, find the MLE of the $\theta$ of the Ishita distribution.
• The L is predetermined; therefore, calculate the $c^{*}$. The statistical test for lifetime performance is thus constructed as: $H_0:C_L\le c^{*}$ against $H_1:C_L>c^{*}$.
• Set the $\gamma$ significance level.
• Determine the $C_L$’s lower bound as the $100(1-\gamma )\%$ lower confidence interval, $[\underline{LB},\infty )$.
• Lastly, the choice is made as if $c^{*}\notin [\underline{LB},\infty )$, and $H_0$ is rejected.

4. Real Data

The glass strength data provided by [26] for the aircraft window are investigated. The goodness of fit measures are helpful in checking the suitability of the Ishita distribution to the real data, and this can be achieved by using Mathematica 13 suitable codes. The Kolmogorov–Smirnov (K–S) value of the Ishita distribution is $0.297$. As a result, the Ishita distribution fits the presented data well. Using a progressive type II censored scheme, 31 failed observations were chosen at random to create a progressive type II censored sample with an effective size of $m=16$ and $R=(10,5,1,0,0,0,0,0,0,0,0,0,0,0,0,0)$. Table 2 contains the observations.

Table 2. Progressive type II censored sample for the strength data.

${\mathit{x}}_{\mathit{i}}:$	18.83	20.80	21.657	23.03	23.23	24.05	24.321	25.50
$R_i$	10	5	1	0	0	0	0	0
$x_i:$	25.52	25.80	26.69	26.77	26.78	27.05	27.67	29.90
$R_i$	0	0	0	0	0	0	0	0

Next, the suggested testing method for $C_L$ based on a CI is given:

Step 1:

With the current scheme, take into account the progressive type II censoring in Table 2, and use Equation (13) to determine the MLE estimates of the Ishita distribution’s $\widehat{\theta }=0.0973$ is the outcome of the parameter estimates.

Step 2:

It is expected that the L is $1.73125$; i.e., when the lifetime of the strength data for an aircraft window exceeds $1.73125$, the strength data are considered to be a conforming product. The $C_L$ of items must be greater than $90\%$ in order to address concerns raised by product buyers regarding lifetime performance. The $C_L$ value must exceed 1 according to Table 3. As a result, the $C_L$ is set at $c^{*}=0.897$, and the following is tested: $H_0:C_L\le 0.897$ vs. $H_1:C_L>0.897$.

Step 3:

Choose a level of significance of $\gamma =0.05$.

Step 4:

Apply Equations (15) and (17) and the bounds of the lower CI in Equation (35).

$$\underline{LB}={\widehat{C}}_L-z_{\gamma }\sqrt{\sum _{\widehat{\theta }}}=1.9643-\left(1.645\right)\sqrt{0.00059}=1.9243.$$

As a result, the $95\%$ one-sided CI for $C_L$ is $[\underline{LB},\infty )=[1.9243,\infty )$.

Step 5.

As a result of the $c^{*}=0.897\notin [\underline{LB},\infty )=[1.9243,\infty ),H_0:C_L\le 0.897$ is refused.

Therefore, the $C_L$ of the aircraft window’s 31 strengths has reached the required level. In addition, from Equations (19) and (34), we observe

$${\widehat{C}}_L=1.9643>c^{*}-z_{\gamma }\sqrt{\sum _{\widehat{\theta }}}=0.897-\left(1.645\right)\sqrt{0.00059}=0.857.$$

Consequently, we refuse $H_0:C_L\le 0.897$, and the glass strength measurements for the aircraft window exceed the required level. Point and interval estimation for the $C_L$ are presented in Table 4 and Table 5 respectively.

Table 4. Point estimates for the parameter $\theta$ and $C_L$ for the strength data.

Parameter	MLE	SEL	LINEX
			${\mathbf{c}}_{\mathbf{1}}=-\mathbf{2}$	${\mathbf{c}}_{\mathbf{2}}=\mathbf{2}$	${\mathbf{c}}_{\mathbf{3}}=\mathbf{0}.\mathbf{0001}$
$\theta$	0.089449	4.52857	10.0237	1.47632	4.52819
$C_L$	0.99997	1.09643	2.20227	1.01326	1.09641

Table 5. The $95\%$ asymptotic and credible intervals for $\theta$ and $C_L$ for the strength data.

Parameter	MLE	MCMC
$\theta$	(−136.364, 136.543)	(0.291955, 10.1095)
$C_L$	(0.99997, 1.22154)	(0.965014, 3.22197)

Table 3. $C_L$ vs. the $P_r$ for the Ishita distribution with $(\widehat{\theta }=0.0973)$.

${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$
−11	$7.0295\times {10}^{-8}$	−0.25	0.333439	0.499	0.640043
−7	0.0000352065	0	0.423224	0.513	0.646582
−6.5	0.000749944	0.1	0.463129	0.534	0.656405
−6	0.000158733	0.2	0.505102	0.556	0.66671
−5.75	0.000230328	0.25	0.526791	0.589	0.682179
−5	0.000695385	0.3	0.548898	0.618	0.695765
−4	0.00293547	0.32	0.557848	0.634	0.703252
−3	0.0117921	0.34	0.566855	0.758	0.760654
−2.5	0.0230645	0.35	0.571378	0.897	0.822204
−2	0.0441834	0.353	0.572738	0.95	0.844379
−1	0.014911	0.412	0.599694	1	0.864429
−0.5	0.258413	0.478	0.630253	1.73215	1

Note: $C_L\to \frac{6+{\theta }^3}{\sqrt{{\theta }^6+16{\theta }^3+12}}\approx 1.73125⟹P_r\to 1$.

Table 3. $C_L$ vs. the $P_r$ for the Ishita distribution with $(\widehat{\theta }=0.0973)$.

${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{r}}$
−11	$7.0295\times {10}^{-8}$	−0.25	0.333439	0.499	0.640043
−7	0.0000352065	0	0.423224	0.513	0.646582
−6.5	0.000749944	0.1	0.463129	0.534	0.656405
−6	0.000158733	0.2	0.505102	0.556	0.66671
−5.75	0.000230328	0.25	0.526791	0.589	0.682179
−5	0.000695385	0.3	0.548898	0.618	0.695765
−4	0.00293547	0.32	0.557848	0.634	0.703252
−3	0.0117921	0.34	0.566855	0.758	0.760654
−2.5	0.0230645	0.35	0.571378	0.897	0.822204
−2	0.0441834	0.353	0.572738	0.95	0.844379
−1	0.014911	0.412	0.599694	1	0.864429
−0.5	0.258413	0.478	0.630253	1.73215	1

Note: $C_L\to \frac{6+{\theta }^3}{\sqrt{{\theta }^6+16{\theta }^3+12}}\approx 1.73125⟹P_r\to 1$.

5. Conclusions

To determine the level of quality for service industry items, the $C_L$ is introduced. The progressive type II censored sample is used to save resources where the lifetime distribution follows the Ishita distribution. To estimate $C_L$, the ML and Bayesian estimators are used in addition to confidence interval estimation of the model parameters. A hypothesis test and real data example are used and all support the suitability of our model and guarantee that the glass strength measurements for aircraft windows exceed the required level. In future works, we will estimate the Ishita distribution’s parameters using adaptive progressive type II censored data and also compare it to all types of censored algorithms that we will apply and determine the level of quality for service industry items.