Abstract
In the present paper, we discuss a nonlocal modification of the Kerr metric. Our starting point is the Kerr–Schild form of the Kerr metric . Using Newman’s approach, we identify a shear free null congruence with the generators of the null cone with apex at a point p in the complex space. The Kerr metric is obtained if the potential is chosen to be a solution of the flat Laplace equation for a point source at the apex p. To construct the nonlocal modification of the Kerr metric, we modify the Laplace operator by its nonlocal version . We found the potential in such an infinite derivative (nonlocal) model and used it to construct the sought-for nonlocal modification of the Kerr metric. The properties of the rotating black holes in this model are discussed. In particular, we derived and numerically solved the equation for a shift of the position of the event horizon due to nonlocality. AlbertaThy 5–23.
1. Introduction
The Kerr metric discovered by Roy Kerr [1] is the most general vacuum solution of the Einstein equations describing a stationary rotating black hole in an asymptotically flat spacetime. It is widely used in astrophysics both for the description of the gravitational field of stellar mass and supermassive black holes as well as in the study of the coalescence of black holes. The properties of the Kerr metric are well known and are described in a number of books (see, e.g., [2,3,4,5,6,7] and references therein). The Kerr metric, besides two commuting Killing vectors generating time translation and rotation, possesses a hidden symmetry. Namely, it has a so-called closed conformal Killing–Yano tensor which generates a second rank Killing tensor [8,9]. As a result, the geodesic equations of motion of a particle in the Kerr spacetime are completely integrable and the additional quadratic in momentum integral of motion (Carter’s constant [10]) is constructed by using the Killing tensor. (A comprehensive discussion of the hidden symmetries in black hole spacetimes and further references can be found in [11]).
Another remarkable property of the Kerr metric (as well as of its charged version, the Kerr–Newman metric [12,13]) is that it can be written in the Kerr–Schild form [14]
where is a flat metric, is a scalar field, and is a tangent vector to a shear-free geodesic null congruence. It has been shown that these solutions of the Einstein equations can be obtained by complex coordinate transformations from the Schwarzschild metric [15,16]. In particular, the potential for the Kerr metric can be obtained as a solution of the Laplace equation in flat coordinates
with a point-like source j located at the complex coordinate , where a is the rotation parameter of the Kerr black hole [17,18]. A comprehensive review of the Kerr–Schild metrics and complex space approaches can be found in [19].
More recently, the Kerr–Newman representation of the spacetime geometry received further development and modifications in the so-called double copy formalism. The main idea of this approach is based on the observation that for the metrics which allow the Kerr–Schild representation, the non-linear Einstein equations can be reduced to the linear equations for Maxwell and scalar fields. This observation can be used to simplify calculations of gravity scattering amplitudes by reducing this problem to the calculation of the Yang–Mills amplitudes with a subsequent double copy prescription [20,21,22,23]. At the moment, there exist dozens of publications on this subject. Related references can be found, e.g., in the following review articles [24,25,26,27].
In this paper, we propose a model of a nonlocal modification of the Kerr metric and discuss its properties. The main idea of this approach is the following. We use the Kerr–Schild ansatz for the metric but modify Equation (2) for the potential and write it in the form
with a specially chosen form factor function . In particular, we assume that the form factor is chosen such that it does not vanish in the complex plane of z; hence, it has a unique inverse. As a result, no new unphysical degrees of freedom are present (at least at tree level). For this reason, such nonlocal (infinite derivative) theories are sometimes referred to as “ghost-free”. Quite often, the form factor satisfying these conditions is chosen in the form
Here, N is a positive integer number, and ℓ plays the role of the fundamental length specifying a length scale at which the effects of nonlocality become important. One refers to this kind of nonlocality as a model.
These kinds of models have been studied in many publications starting with the papers [28,29,30,31,32]. The main motivation for studying such models is the following. It is well known that the standard Einstein gravity theory is ultraviolet incomplete. In the classical theory, this incompleteness manifests itself in the inevitable presence of singularities both in cosmology and in the black hole interior. One can try to improve the ultraviolet behavior of the theory by adding higher orders in the derivatives of the curvature terms of the action. However, this usually results in new unphysical degrees of freedom (ghosts) arising. The interest in the infinite derivative (nonlocal) modifications of Einstein’s gravity is partially motivated by the hope of overcoming this difficulty.
Solutions for the gravitational field of point-like sources in linearized ghost-free gravity were obtained and studied in many papers, references to which can be found, e.g., in [33]. A solution of these equations when the source is a rotating infinitely thin massive ring was found in [34]. Cosmology in the nonlocal stringy models was studied in [35,36]. Exact pp-wave and gyraton type solutions in the infinite derivative gravity were discussed in [37,38,39]. Additional references can be found in the reviews [40,41,42,43,44,45].
In this paper, we consider the following modification of the Kerr solution, which for briefness we call the “nonlocal Kerr metric”. We start with the Kerr–Schild form (1) of the metric. We keep the same shear-free, geodesic null congruence and the same point-like source j in the complex space as for the Kerr solution. However, we modify the potential and choose it to be a solution of Equation (3) with a specially chosen (ghost-free) form factor. Our goal is to obtain such a nonlocal Kerr metric and to study its properties.
Let us stress that such a metric certainly is not a solution to the exact infinite derivative equations, which are highly non-linear [46]. At the same time, the obtained nonlocal Kerr metric, written in coordinates similar to the Boyer–Lindquist coordinates, is non-linear in the mass parameter. It describes a stationary axisymmetric black hole which differs in several aspects from the Kerr spacetime. Written in the Kerr–Schild form, (1) this metric, similarly to the Kerr solution, looks like a linear perturbation of the flat spacetime. However, the coordinate transformation, required to present the metric in Boyer–Lindquist form non-linearly depends on the scalar function . For this reason, even for the weak nonlocality, the nonlocal Kerr metric cannot be obtained by a small change of the mass parameter M in the Kerr metric, for example, by taking its slight dependence on the radial and angle coordinates.
The paper is organized as follows. In Section 2, we discuss the Kerr–Schild form of the metric and describe different coordinates which are used later in the paper. Section 3 discusses a definition of the delta function in the complex space and contains the derivation of the potential , which is a solution of the Poisson equation with a complex delta function. A similar solution for an infinite derivative modification of the Poisson equation with the same point-like source in the complex space is derived in Section 4. This section also contains a discussion of the properties of the nonlocal potential. In Section 5, we use the obtained nonlocal potential to recover the nonlocal modification of the Kerr metric. The spacetime structure of such a black hole, including the shift of the event horizon due to nonlocality, is also discussed in Section 5. In Section 6, we discuss a limiting case of a non-rotating nonlocal black hole. Section 7 contains a discussion of the obtained results. Technical details and calculations required for the derivation of the equation for the event horizon shift are discussed in the Appendix A.
2. Kerr Metric and Its Kerr–Schild Form
2.1. Kerr Metric
The Kerr metric describing a vacuum stationary rotating black hole written in the Boyer–Lindquist coordinates is
Here, M is the black hole mass, and a is its rotation parameter. This metric has two commuting Killing vectors and (Many useful relations for the Kerr metric and its Kerr–Schild form can be found in [47]).
The projection of the metric (5) along the orbits of the Killing vectors determines a smooth two-dimensional space S with metric [48]
The Killing vectors and satisfy the following circularity condition (see, e.g., [2,5,6])
These relations are necessary and sufficient conditions for the 2-flats orthogonal to and to be integrable. Let us denote by the two-dimensional span of the Killing vectors and . Then, the circularity condition implies that is orthogonal to S.
2.2. Coordinates
In what follows, we shall use several different coordinate systems. Let us describe them in this section.
Let us first note that for , the Riemann curvature of the Kerr metric vanishes and the metric (5) takes the form
In this limit, the metric (8) is nothing but the Minkowski metric and its spatial part is flat as well. We denote by standard Cartesian coordinates in this 3D space. Then, it is easy to check that the coordinates are related to these Cartesian coordinates as follows
The coordinates are nothing but standard oblate spheroidal coordinates taking the following values , , . For the surfaces const are oblate ellipsoids. Figure 1 shows the coordinate lines of the oblate spheroidal coordinates in the plane ().
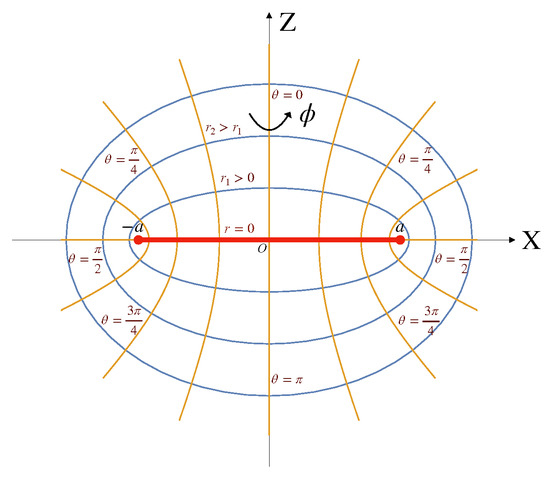
Figure 1.
Coordinate lines of the oblate spheroidal coordinates in the plane ().
For and , one has a disc of radius a located in the plane. The coordinate is discontinuous on the disc. For , the coordinate covers the upper part of the disc, while for , it covers the lower part of it. The boundary of this disc is a ring of radius a. Equations and describe the axis of symmetry . For , is positive, while for , is negative.
The third type of coordinates in the flat 3D space which will be also used in the paper are the cylindrical coordinates related to Cartesian coordinates as
In these coordinates, the flat 3D metric is
The cylindrical coordinates are related to the oblate spheroidal coordinates as follows
The equation of the ring in cylindrical coordinates is , .
Finally, let us introduce the fourth type of the coordinates. For this purpose, we define a new coordinate, y, related to the angle as follows
The equation of the disc in coordinates is , , and . The equations , describe its boundary, the ring , see Figure 2. This figure also shows a sphere of radius a. On its surface, and . Inside the sphere (in the region ), one has , while outside (in the region ) one has .
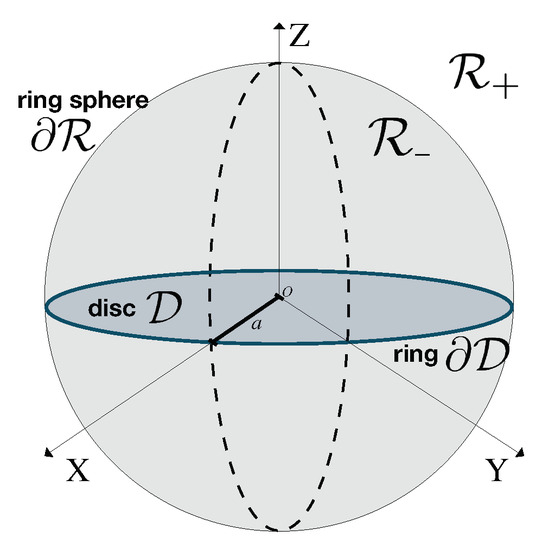
Figure 2.
The ring , the disc , and the ring sphere .
The flat metric in the coordinates is
One can see that the metric coefficients in (14) are simple rational functions of r and y and the coordinates r and y enter this metric in a quite symmetric way (These coordinates and their generalizations in the higher dimensions are naturally connected with the hidden symmetries of the black hole metrics. In fact, they are eigenvalues of the rank two Killing tensor generating the hidden symmetry. For more details, see e.g., [11,49]).
2.3. Kerr-Schild Form
Let us consider the following 1-form
where . We define a metric
where is some function. Then, the following statements are valid for each of the metrics and . In other words, these statements are valid for an arbitrary function , including :
- The contravariant components of the vector in coordinates are ;
- is a null vector ;
- Vectors are tangent vectors to incoming (for ) or outgoing (for ) null geodesics in the affine parameterization, .
- ;
- .
The last property implies that the congruence of null vectors is shear-free (for more details, see e.g., [50,51]). Such a null geodesic congruence is related to the light cones with apex on the world-line in the complex space. The twist is a measure of how far the complex world-line is from the real slice [52].
It is easy to check that for a special choice of the function
the metric given by (16) is Ricci flat, and in fact, it coincides with the Kerr metric. In order to prove this, it is sufficient to make the following coordinate transformation
where is defined in (5). These coordinates are chosen so that the non-diagonal components and of the metric vanish. One can check that the metric written in the coincides with the Kerr metric , provided one identifies the coordinates and in with the standard Boyer–Lindquist coordinates t and in the metric (5) (Let us emphasize that there exists quite an important difference between and coordinates. Namely, the Boyer–Lindquist coordinates cover only the exterior of the black hole, that is, the domain outside the event horizon, while coordinates can “penetrate” into the interior of the black and white holes).
Carter [2] showed that if the circularity conditions (7) are satisfied, the event horizon of an arbitrary stationary axially symmetric black hole coincides with the Killing horizon. The latter is the set of points where
For the Kerr metric, this condition implies that
This relation determines the position of the event horizon of the Kerr black hole.
3. Potential and a Point Charge in Complex Space
3.1. Complex Delta Function
Let us consider the scalar function given by (19) in flat spacetime with the metric (8). It is easy to check that it satisfies the Laplace equation
where is the standard 3D flat Laplace operator which takes the following form in Cartesian coordinates
In fact, is a very special solution of (23) which has a point-like source in the complex space. Namely, it can be written in the following form
where is an analytical extension in the complex domain of the fundamental solution of the Laplace equation [18].
To obtain the solution , let us, following [18,53], define a delta function in the complex plane. Here and later, we denote
A generalized delta function of a complex argument is defined as [53]
Here, is constant. The Gaussian exponent containing is introduced to provide convergence of the integral over p. The prescription means that the limit should be taken at the end of the calculations. It should be mentioned that this expression is divergent in the quadrants and converges to zero everywhere else. However, if both endpoints of the integration contour are in the convergent sector, the definition (27) can be used.
Let be a test function of the complex variable z, which is analytic throughout the complex plane and decreases sufficiently rapidly at large distances along the real axis. Then, as it is shown in [18,53], the following relation is valid
Using expression (27), it easy to check that .
In what follows, we shall be using the real part of the complex delta function
It is easy to check that . Hence, this object is an even function of z. Other properties of the generalized delta function and its application can be found in [18,53,54,55,56].
3.2. Potential of a Point Source in Complex Space
Using the definition of the complex delta-function, one can define as a solution of the following equation
Here, we use the notation introduced in (26).
Denote and . Then,
We use the following representation for the function
Then, using Equation (30), one finds the Fourier transform of the Green function
Here,
Combining these results, one gets
Here, . Let and , then the integration over in the range yields
Thus,
This expression shows that written in the cylindrical coordinates, the Green function does not depend on the angle . For this reason, instead of the arguments X and Y of the Green function, we use a polar radius in the cylindrical coordinates .
The integral over p for can be taken with the following result
Here, is the error function of a complex variable z. Its definition and properties can be found in [57].
The limit can be easily taken and one gets
Using this result and expression, (36) one gets
which finally gives
It is easy to check that
The square root has a branch point. In what follows, we use the following prescription
Here, are oblate spheroidal coordinates (9).
Hence, we can write relation (40) as
This relation implies that
which correctly reproduces the expression (19).
Let us note that similar solutions for a point source in the complex space can be found in the Maxwell theory. Such an electromagnetic field and its properties were studied in [58]. Potential (44) was also used in [59] to construct the Newtonian analogue of the Kerr metric.
4. Potential in an Infinite Derivative Model
4.1. Integral Representation of the Nonlocal Green Function
In order to obtain the nonlocal modification of the Kerr metric, we proceed as follows. At first, we calculate a nonlocal version of the potential function . To achieve this, we consider the following modification of the Equation (30)
Here, f is a form factor that is chosen so that it does not produce new (unphysical) poles. For example, one can take it in the form
where N is a positive integer number. Quite often, one refers to this choice of the form factor as the model.
After solving Equation (45), we define the nonlocal potential as follows
To find the nonlocal Green function , we proceed in the same way as in the previous section. Namely, we use again the Fourier transform in variables
and the following representation for the function
Then, using Equation (45) one finds
Here, is the Fourier transform of the Green function (45). It depends on the parameters and p of this transform with . It looks quite similar to the expression (33) with the only difference that now it contains an extra factor in the denominator associated with the form factor.
Combining these results, one gets
Using (35), we can write the expression for in the form
For the model, the integral in contains an exponentially decreasing factor which provides the convergence of the integral. For this reason, one can simply put in the integrand (This remark is valid for any sufficiently fast decreasing at form factors).
In the simplest case when , the form factor takes the form
and one has
For this case, the Green function can be found exactly in an explicit form. In what follows, we shall focus on this case.
4.2. Nonlocal Green Function
Relations (52) and (54) give the required integral representation for the nonlocal Green function. In fact, this function depends on the polar coordinates and z, so we write it as . For the model, this Green function can be found in an explicit form. For this purpose, we use the following relation
where
Differentiating (52) with respect to , one gets
Taking this integral, one finds
Integration over and putting gives
Let us note that
Thus, one has
In what follows, we shall use the following properties of the error function
Let us discuss the properties of the obtained nonlocal Green function. It is a function of the complex variable
and can be written in the form
The function has the following properties
The potential is obtained by taking the real part of G. One can write
In the domain where , the error function remains finite at infinity. For fixed values of r and y, one has
Thus,
This means that in the local limit, that is, when , the constructed nonlocal Green function correctly reproduces the local Green function (43).
However, this property is violated in where . In this domain, the Green function does not properly reproduce the local Green function in the limit . Let us discuss this point in more detail.
At the boundary surface separating the and domains, one has . Calculating the value of on , one gets
where . Let us denote
Using (65), it is easy to check that the value of restricted to the sphere coincides with a similar value of
We use to define the potential in the domain . As a result, we obtain the following expression for the potential which is valid in both domains (see Figure 3)
Here, and
This so-defined potential is continuous at and has a correct local limit when . Using the definition of the complementary error function
one can write the potential in the form
Here, is the potential for the local theory given by (44)
and
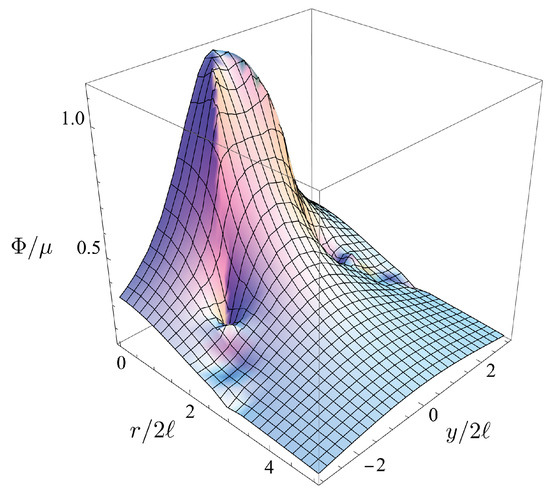
Figure 3.
Plot of a potential as a function of .
The function describes the nonlocality contribution to the potential . The complex variable is defined by (73).
Before we discuss properties of the nonlocal potential , let us make the following remark. The function K which enters the Equation (58) has the form
It is easy to check that this function obeys the following heat equation
where is the standard flat Laplacian. Thus, K can be considered as a heat kernel in a space with the interval . Let us mention that the method of the heat kernels has been used earlier for the study of solutions of higher and infinite derivative linearized gravity equations [40,44,60,61].
The real part of this interval is positive in the domain and negative in the domain. The problem with the definition of the Green function in is similar to the problem of defining the heat kernel in the Minkowski space with the Lorentzian signature of the metric. This problem is solved by using the complex parameter and choosing a proper branch of the corresponding complex function. For more details see e.g., [62,63].
4.3. Properties of the Potential
Let us discuss now some of the properties of the potential defined by (72).
4.3.1. Potential at the Ring
To obtain the value of the potential at the ring, , it is sufficient to use the following expansion of the error function [57,64]
One has
Hence, the potential at the ring is finite and independent of the rotation parameter a.
4.3.2. Potential at the Symmetry Axis
Let us consider the value of the potential at the symmetry axis . For its value is the same. One has
where
The plot of is shown in Figure 4.
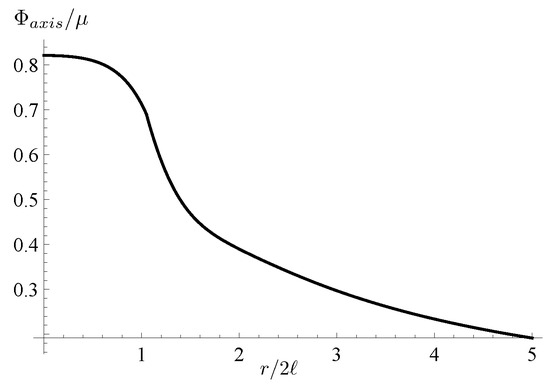
Figure 4.
Plot of the potential along the axis as a function of for .
4.3.3. Potential on the Disc
The disc is defined by the equation , while and are the coordinates on the disc. The potential evaluated on the disc is
where . The plot of is shown in Figure 5.
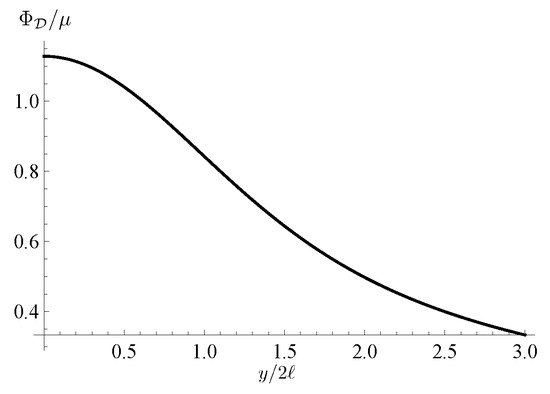
Figure 5.
Plot of the potential on the disc as a function of .
The point corresponds to the ring and the value of at this point coincides with (81). For the disc of the radius a the part of the plot in Figure 5 with should be omitted. At the center of the disc of radius a, that is for , the value of coincides with the limit of the potential on the symmetry axis (82).
4.3.4. Potential on the Sphere
At the sphere one has and the potential is
The plot of is shown in Figure 6. For , that is, on the ring , the potential coincides with (81).
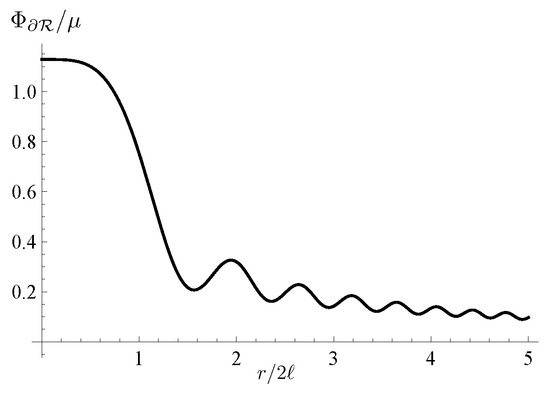
Figure 6.
Plot of the potential on the surface as a function of .
4.3.5. Small ℓ Limit
One can expect that when ℓ is small, then is small as well. Let us discuss this regime in more detail.
For small ℓ, the argument of the function defined by (77) becomes large. In both cases, that is when and when , one can use the following asymptotic form of the complementary error function [64]
The nonlocal contribution to the potential for small ℓ is
5. Nonlocal Modification of the Kerr Metric
5.1. Ergoregion and Its Inner Boundary
We use the Kerr–Schild ansatz and write the nonlocal modification of the Kerr metric in the form (16), where is the nonlocal potential described in the previous section. Let us notice that the quantity depends not only on the “radial” coordinate r, but also on the “angle” coordinate y. This difference from the standard (local) Kerr metric has several important consequences
- In a general case, by using transformations similar to (20), one cannot restore the Boyer–Lindquist form of the metric with only one non-vanishing non-diagonal component of the metric ;
- The nonlocal version of the metric still has two Killing vectors, and , but these vectors do not satisfy the circularity conditions (7);
- As a result of the violation of the circularity conditions, in the general case the surface is not the event horizon.
Let us discuss the last point in more detail. The function V vanishes when the following equation is satisfied
Calculations give
On the surface , where , the second term in the square brackets vanishes, while the first one is . If and , then . This means that in a general case, the surface outside the symmetry axis is timelike and hence it cannot be the event horizon.
For the metric (16), a surface where is defined by the relation
This is an infinite red-shift surface. Outside it, a particle can be at rest with respect to infinity, so that its 4-velocity
is timelike.
The domain between and is the ergoregion. In this domain, a particle can move along a circular orbit so that its 4-velocity is proportional to a linear combination of the Killing vectors
where is a constant angular velocity. The vector is timelike when , where
For the vector is null. At
This quantity is known as the angular velocity of the black hole. We call the surface the inner boundary of the ergoregion.
In the Kerr metric, the surface coincides with the horizon and hence is null. It plays the role of a one-way membrane. For the metric (16), with a more general potential function , the situation is quite different. The surface is timelike, and it can be penetrated by the outgoing particles and light rays.
The inner boundary of the ergoregion, where is defined by the equation
where is defined by (77). Let us emphasize that this relation is valid for an arbitrary function .
For small the surface is located close to the unperturbed Kerr horizon,
Let us write
Then,
5.2. Shift of the Event Horizon
For a stationary black hole, the event horizon coincides with the outer trapped surface. A useful formalism for finding such surfaces was developed by Senovilla [65]. In this section, we follow this work and apply its results to find the event horizon for the nonlocal modification of the Kerr metric.
Let us assume that in the vicinity of the horizon, the potential differs from its unperturbed (classical) value only slightly. Hence, defined by (75) is small, and one can expect that the displacement of the horizon for the nonlocal modification of the Kerr metric from the Kerr horizon is also small and write
where is small. At the moment, we do not specify the function . We only assume that it is an even function of y. In Appendix A, it is shown that the function obeys the following linear second order ordinary differential equation which is valid in the leading order of the smallness parameter
Here, .
5.3. Numerical Results
To find a solution for the horizon shift, it is convenient to write the equation (102) in dimensionless form by using , and (100)
Since is an even function of x, it satisfies the following condition
Both and are regular at the symmetry axis and near it they can be expanded as
Substituting these expansions in (103), one obtains the following relation
Equation (103) with boundary conditions (104) and (106) is a well-posed boundary value problem which can be solved numerically.
Let us first show that for , the corresponding homogeneous Equation (103) does not have a regular solution. Since this equation is invariant under the reflection , it is sufficient to consider only the case when . Using the initial condition (104), one has
This relation implies that is a positive monotonically growing function of x and, as a result, infinitely grows at . (Let us note that for , Equation (103) has a form of the equation for the oblate spheroidal angle functions [66]. For a given , it has a regular solution only for special values of , which are the eigenvalues of this problem. For an adopted form of the coefficients and , this homogeneous equation has a only trivial regular solution, ).
In order to find a numerical solution, it is convenient to use a function where for . One can write (103) in the following form
We are looking for a solution satisfying the condition
and which is regular at and .
We chose now the function in the form (77). Then, the function which enters the right-hand side of (103) takes the form
where and is given by (99). To find a regular solution with the boundary condition (109), we used a specially designed solver (This boundary value problem was solved with pseudo-spectral method, with basis functions and Gauss collocation grid (corresponding to Type II discrete cosine transform). The authors are grateful to Andrei Frolov for the help). Figure 7, Figure 8 and Figure 9 show plots of and for some selected values of the parameters and .
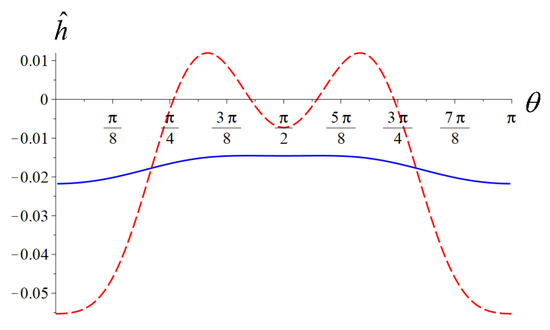
Figure 7.
Plots of (solid line) and (dash line) as a function of the angle for parameters and ().
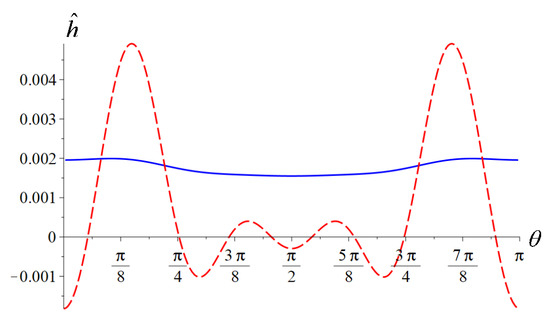
Figure 8.
Plots of (solid line) and (dash line) as a function of the angle for parameters and ().
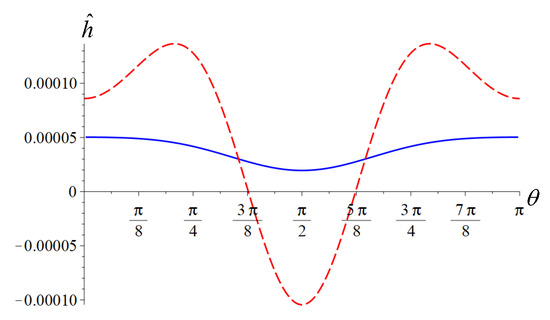
Figure 9.
Plots of (solid line) and (dash line) as a function of the angle for parameters and ().
6. Non-Rotating Black Holes
Let us discuss now the limiting case of a non-rotating black hole when the rotation parameter vanishes. In this case, the metric is spherically symmetric and all the related expressions are greatly simplified.
The metric (8) takes the form
This is a flat metric in spherical coordinates. The null vector has components
Here, for the incoming radial null rays, and for the outgoing ones. We define a metric
Herem is some function. Written in an explicit form, this metric is
One can exclude the non-diagonal term of the metric by making the following coordinate transformation
The metric (113) written in the coordinates is
Let us note that the time coordinate differs from time t in the metric (111). In fact, for one has
Here, v is the standard advanced time coordinate. Let us notice that relation (117) is similar to (20) for the Kerr metric and coincides with the latter in the absence of the rotation. The coordinates which are used in the Kerr–Schild form of the metric (113) cover not only the black hole’s exterior but also its interior, remaining regular at the horizon.
One can easily recover the Schwarzschild metric by taking the potential to be a solution of the equation
Here, both the Laplacian and delta function are taken in the real flat space with metric . The solution is
so that the metric (116) is nothing but the Schwarzschild metric.
In order to obtain the nonlocal modification of the Schwarzschild metric, it is sufficient to choose the potential to be a solution of the equation
This equation for the nonlocal models with the form factor of the form (4) has been studied in several publications. For and , the potential can be found in an explicit analytic form [33,40]
Here, is the hypergeometric function [67].
For all N, the potentials are finite at and they have the following asymptotic form [40]
Let us note that for all models, the coefficients are finite and positive. For the non-rotating black hole, the inner boundary of the ergosphere coincides with the event horizon and its equation is . For the model, this equation can be written in the form
7. Discussion
In this paper, we discussed the nonlocal modification of the Kerr geometry. Our starting point is the Kerr–Schild form of the Kerr metric. The potential which enters this representation is a solution of the 3D flat Poisson equation with a point-like source shifted to the complex space. We considered a modification of this equation obtained by changing the Laplace operator by its infinite derivative analog . The function is chosen so that it does not have zeroes in the complex plane z, so that the form factor operator has an inverse. We focus on the study of the simplest case, namely, when the form factor has the form . In this case, the potential can be obtained in an explicit analytic form. We discussed the properties of a rotating black hole in such a nonlocal model.
Let us notice that in order to reconstruct the Kerr metric in Boyer–Lindquist coordinates, one should make a coordinate transformation that contains dependence on the black-hole’s mass M. As a result, this parameter enters the Kerr metric in the Boyer–Lindquist coordinates non-linearly. It is easy to check that a simple linearization of the Kerr metric, by expanding it in terms of the mass parameter and keeping only its zero and first order in M terms, produces a metric that is singular and does not have a horizon. One can also check that the nonlocal modification of the Kerr metric presented in this paper, like the Kerr metric, is regular at the horizon.
The main difference of the nonlocal modification of the Kerr metric discussed in this paper is that besides the mass M and the rotation parameter a which specify the Kerr solution, it contains a new parameter ℓ which controls the nonlocality effects. We did not specify its value. However, recent experiments showed that Newtonian gravity gave an excellent fit to the data at least up to the length µm [68]. This means that ℓ at least should be less than . This implies that for astrophysical stellar mass and supermassive black holes, . One can expect that the corresponding nonlocal effects for these objects are extremely small and exponentially suppressed. The effects of the nonlocality discussed in this paper might be important when , that is, for mini black holes. In particular, the nonlocality may change the properties of its Hawking evaporation, such as its temperature and anisotropy. One can also expect that the effects of the nonlocality becomes important at the final stage of the mini black hole evaporation.
An important property of the Kerr–Schild form of the Kerr metric is that there exists a coordinate transformation that allows one to recover the Kerr metric which has only one non-diagonal component, . This property is not valid for the nonlocal modification of the Kerr metric discussed in this paper. This property makes this metric quite different from models of a regular rotating black hole discussed in the papers [69,70,71,72,73].
The modified metric described in this paper still has two commuting Killing vectors. However, these vectors do not satisfy the circularity condition which plays an important role in proving the uniqueness theorems for the rotating black hole solutions of the Einstein equations. One of the interesting consequences of the violation of the circularity condition is that the event horizon does not coincide with the inner boundary of the ergoregion, where the invariant V, (17), constructed from the Killing vectors, vanishes.
When the “fundamental length” parameter ℓ, which defines the scale of nonlocality, tends to zero, the obtained nonlocal potential has the limit , and the metric takes the form of the standard Kerr metric. Corrections to the metric in the black hole exterior are controlled by the dimensionless parameter . When this parameter is small, the event horizon of the nonlocal black hole is slightly shifted from the Kerr horizon. In this approximation, we derived and numerically solved the equation that describes this shift. These results are illustrated by Figure 7, Figure 8 and Figure 9. Solid and dashed lines represent the deviation of the modified event horizon and the position of the inner boundary of the ergoregion with respect to the Kerr horizon.
In the absence of the rotation, that is, in the limit , the modified metric contains two parameters, the mass M and the scale of the nonlocality ℓ. This metric and its properties are discussed in Section 6. Let us emphasize that in the Kerr–Schild representation, the potential enters as a perturbation of the flat metric and it is a solution of the linearized infinite derivative gravity equations. The standard “Schwarzschild”-type form of the metric (116) is obtained after making the coordinate transformation (117) which depends on the mass parameter in the non-linear form.
Let us emphasize that the obtained nonlocal Kerr metric is not a solution to the fundamental nonlocal gravity equations. However, one can expect that it might properly reproduce some important features of the (unknown at the moment) solution for a rotating black hole in the consistent nonlocal (infinity derivative) models of gravity.
Author Contributions
Conceptualization, methodology, investigation, writing and editing, V.P.F. and J.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Sciences and Engineering Research Council of Canada and the Killam Trust.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council of Canada. The authors are also grateful to the Killam Trust for its financial support. The authors thank Andrei Frolov for his help with finding the numerical solutions of the equation for the horizon shift.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Marginally Trapped Surface
The explicit form of the metric (16) in coordinates for an arbitrary function is
The contravariant components of this metric are
To find the event horizon in this metric, we follow the recipe described by Senovilla [65]. Because of the symmetry of the metric (16), the horizon surface equation can be written in the form
Denote
and consider a set of 2D surfaces
where and are constant parameters. A 2D surface with is the intersection of the event horizon by the 3D surface . This implies that is a marginally trapped surface. To find the function which determines , we proceed as follows.
First, we change to the coordinates by using the relations
and then present the metric (A1) in the form
Indices take values while stand for , and we denote
The condition that the coordinates are constant specifies a 2D surface , with coordinates on it. The metric (A7) in these new coordinates is
Let us denote by a two dimensional metric on and by its inverse. Following [65], we also introduce the following objects
A necessary condition for a 2D surface to be marginally trapped is that [65], where
Using the GRTensor package in Maple we calculated for the metric (A7), (A9) with an arbitrary potential function . However, the obtained expression is rather long, so we do not reproduce it here.
Instead of this, we consider an approximation where the potential is close to its local limit
In this case, the horizon surface differs only slightly from the Kerr horizon
We denote
where we have introduced a dimensionless parameter which we assume to be small. This parameter is used to control the order of “smallness" of the different terms that enter the equations. We restrict our calculations by keeping the zero and first order expressions in the decomposition over . At the end of the calculations, we put . For simplicity purposes, we proceed as follows: First, we omit in the metric coefficients all of the terms which contain , and other similar expressions, which are evidently of second order in . After calculating the quantity for an arbitrary we use (A14) and omit all of the terms in the final expression.
In the adopted approximation, after omitting quadratic in f terms, one obtains the following expression for the part of the metric (A7)
and one has
Let us note that the metric coefficients in (A1) and (A9) are functions of coordinates. In order to calculate their partial derivatives with respect to variables, one should use the relations
The —component of vanishes, while the other component is
One also gets
After substituting these expressions in defined by (A10), we calculated the quantity . In these calculations, we use the following truncated version of in which only the zero and first order in f is preserved
Following our approximation, we use again relations (A14) in the obtained expression for while retaining solely the leading-order terms with respect to . In particular, this means that it is sufficient to use the quantity instead of since itself is already is of the first order in .
As is expected, the contribution to of the order vanishes since is the horizon of the unperturbed Kerr metric. In the first order in , the condition gives the following differential equation for the function which describes the displacement of the horizon for the perturbed metric.
Here, .
References
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Carter, B. Black holes equilibrium states. In Les Houches Summer School of Theoretical Physics: Black Holes; Les Astres Occlus: Les Houches, France, 1973; pp. 57–214. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman, W.H., Ed.; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Frolov, V.P.; Novikov, I.D. Black Hole Physics: Basic Concepts and New Developments; Kluwer Academic Publishers: New York, NY, USA, 1998. [Google Scholar]
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- O’Neill, B. The Geometry of Kerr Black Holes, Dover Books on Physics; Dover Publications: Mineola, NY, USA, 2014. [Google Scholar]
- Penrose, R. Naked singularities. Ann. N. Y. Acad. Sci. 1973, 224, 125. [Google Scholar] [CrossRef]
- Floyd, R. The Dynamics of Kerr Elds. Ph.D. Thesis, University of London, London, UK, 1973. [Google Scholar]
- Carter, B. Global structure of the kerr family of gravitational elds. Phys. Rev. 1968, 174, 1559–1571. [Google Scholar] [CrossRef]
- Frolov, V.P.; Krtous, P.; Kubiznak, D. Black holes, hidden symmetries, and complete integrability. Living Rev. Rel. 2017, 20, 6. [Google Scholar] [CrossRef] [PubMed]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918–919. [Google Scholar] [CrossRef]
- Debney, G.C.; Kerr, R.P.; Schild, A. Solutions of the einstein and einstein-maxwell equations. J. Math. Phys. 1969, 10, 1842–1854. [Google Scholar] [CrossRef]
- Kerr, R.P.; Schild, A. Republication of: A new class of vacuum solutions of the Einstein eld equations. Gen. Gravit. 2009, 41, 2485–2499. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.I. Note on the Kerr spinning particle metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Newman, E.T. Complex coordinate transformations and the Schwarzschild-Kerr metrics. J. Math. Phys. 1973, 14, 774. [Google Scholar] [CrossRef]
- Israel, W. Source of the kerr metric. Phys. Rev. D 1970, 2, 641–646. [Google Scholar] [CrossRef]
- Kaiser, G. Physical wavelets and their sources: Real physics in complex spacetime. J. Phys. A Mathematical Gen. 2003, 36, R291–R338. [Google Scholar] [CrossRef]
- Adamo, T.; Newman, E.T. The Kerr-Newman metric: A Review. Scholarpedia 2014, 9, 31791. [Google Scholar]
- Bern, Z.; Carrasco, J.J.M.; Johansson, H. Perturbative quantum gravity as a double copy of gauge theory. Phys. Rev. Lett. arXiv 2010. [Google Scholar] [CrossRef]
- Monteiro, R.; O’Connell, D.; White, C.D. Black holes and the double copy. J. High Energy Phys. 2014, 2014. [Google Scholar] [CrossRef]
- Luna, A.; Monteiro, R.; O’Connell, D.; White, C.D. The classical double copy for taub-NUT spacetime. Phys. Lett. 2015, 750, 272–277. [Google Scholar] [CrossRef]
- Bah, I.; Dempsey, R.; Weck, P. Kerr-Schild Double Copy and ComplexWorldlines. JHEP 2020, 02, 180. [Google Scholar] [CrossRef]
- White, C.D. The double copy: Gravity from gluons. Contemp. Phys. 2018, 59, 109–125. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.; Chiodaroli, M.; Johansson, H.; Roiban, R. The duality between color and kinematics and its applications. arXiv 2019, arXiv:1909.01358. [Google Scholar]
- Bern, Z.; Carrasco, J.J.; Chiodaroli, M.; Johansson, H.; Roiban, R. The sagex review on scattering amplitudes, chapter 2: An invitation to color-kinematics duality and the double copy. arXiv 2022, arXiv:2203.13013. [Google Scholar]
- Netto, T.d.; Giacchini, B.L.; Burzillá, N.; Modesto, L. Regular black holes from higher-derivative and nonlocal gravity: The smeared delta source approximation. arXiv 2023, arXiv:2308.12251. [Google Scholar]
- Tomboulis, E.T. Superrenormalizable gauge and gravitational theories. arXiv 1997. [Google Scholar] [CrossRef]
- Moát, J.W. Ultraviolet Complete Quantum Gravity. Eur. Phys. J. Plus 2011, 126, 43. [Google Scholar]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Biswas, T.; Gerwick, E.; Koivisto, T.; Mazumdar, A. Towards singularity- and ghostfree theories of gravity. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Biswas, T.; Conroy, A.; Koshelev, A.S.; Mazumdar, A. Generalized ghost-free quadratic curvature gravity. Class. Quantum Gravity 2013, 31, 015022. [Google Scholar] [CrossRef]
- Boos, J.; Frolov, V.P.; Zelnikov, A. Gravitational eld of static branes in linearized ghost-free gravity. Phys. Rev. 2018, 97, 080421. [Google Scholar] [CrossRef]
- Buoninfante, L.; Cornell, A.S.; Harmsen, G.; Koshelev, A.S.; Lambiase, G.; Marto, J.A.; Mazumdar, A.A. Towards nonsingular rotating compact object in ghost-free innite derivative gravity. Phys. Rev. D 2018, 98, 084041. [Google Scholar] [CrossRef]
- Aref’eva, I.Y.; Joukovskaya, L.V.; Vernov, S.Y. Bouncing and accelerating solutions in nonlocal stringy models. JHEP 2007, 07, 087. [Google Scholar] [CrossRef]
- Koshelev, A.S.; Vernov, S.Y. Cosmological Solutions in Nonlocal Models. Phys. Part. Nucl. Lett. 2014, 11, 960–963. [Google Scholar] [CrossRef]
- Kilicarslan, E. pp-waves as exact solutions to ghostfree innite derivative gravity. Phys. Rev. D 2019, 99, 124048. [Google Scholar] [CrossRef]
- Dengiz, S.; Kilicarslan, E.; Koláŕ, I. Anupam Mazumdar Impulsive waves in ghost free innite derivative gravity in antide Sitter spacetime. Phys. Rev. D 2020, 102, 044016. [Google Scholar] [CrossRef]
- Kolář, I.; Málek, T.; Dengiz, S. Ercan Kilicarslan Exact gyratons in higher and innite derivative gravity. Phys. Rev. D 2022, 105, 044018. [Google Scholar] [CrossRef]
- Boos, J. Effects of Non-locality in Gravity and Quantum Theory. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2020. [Google Scholar]
- Modesto, L.; Rachwa, L. Nonlocal quantum gravity: A review. Int. J. Mod. Phys. D 2017, 26, 1730020. [Google Scholar] [CrossRef]
- Buoninfante, L. Nonlocal Field theories: Theoretical and Phenomenological Aspects. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2019. [Google Scholar]
- Heredia, C.; Kolář, I.; Llosa, J.; Torralba, F.M.; Mazumdar, A. Innite-derivative linearized gravity in convolutional form. Class. Quant. Grav. 2022, 39, 085001. [Google Scholar] [CrossRef]
- Kolář, I. Nonlocal scalar elds in static spacetimes via heat kernels. Phys. Rev. D 2022, 105, 084026. [Google Scholar] [CrossRef]
- Buoninfante, L.; Giacchini, B.L.; Netto, T.P. Black holes in non-local gravity. arXiv 2022, arXiv:2211.03497. [Google Scholar]
- Kolář, I.; Málek, T.; Mazumdar, A. Exact solutions of nonlocal gravity in a class of almost universal spacetimes. Phys. Rev. D 2021, 103, 124067. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A Brief introduction. in Kerr Fest: Black Holes in Astrophysics, General Relativity and Quantum Gravity. arXiv 2007, arXiv:0706.0622. [Google Scholar]
- Geroch, R.P. A Method for generating new solutions of Einstein’s equation. 2. J. Math. Phys. 1972, 13, 394–404. [Google Scholar] [CrossRef]
- Frolov, V.P.; Zelnikov, A. Introduction to Black Hole Physics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Sommers, P. Properties of shear-free congruences of null geodesics. Proc. R. Soc. London A. Math. Phys. Sci. 1976, 349, 309–318. [Google Scholar]
- Frolov, V.P. The newman-penrose method in the theory of general relativity. In Problems in the General Theory of Relativity and Theory of Group Representations; Basov, N.G., Ed.; Springer: Boston, MA, USA, 1979; pp. 73–185. [Google Scholar]
- Newman, E.T. Maxwell elds and shear-free null geodesic congruences. Class. Quantum Gravity 2004, 21, 3197–3221. [Google Scholar] [CrossRef]
- Brewster, R.A.; Franson, J.D. Generalized delta functions and their use in quantum optics. J. Math. Phys. 2018, 59, 012102. [Google Scholar] [CrossRef]
- Lindell, I. Delta function expansions, complex delta functions and the steepest descent method. Am. J. Phys. 1993, 61, 438–442. [Google Scholar] [CrossRef]
- Smagin, V.A. Complex delta function and its information application. Autom. Control Comput. Sci. 2014, 48, 10–16. [Google Scholar] [CrossRef]
- Berry, M. Faster than fourier. In A Half-Century of Physical Asymptotics and Other Diversions; World Scientific: Singapore, 2017; pp. 483–493. [Google Scholar]
- Oldham, K.B.; Myland, J.; Spanier, J. An Atlas of Functions: With Equator, the Atlas Function Calculator, an Atlas of Functions; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kaiser, G. Distributional sources for newman’s holomorphic coulomb eld. J. Phys. Math. Gen. 2004, 37, 8735–8745. [Google Scholar] [CrossRef][Green Version]
- Eleni, A.; Apostolatos, T.A. Newtonian analogue of a kerr black hole. Phys. Rev. 2020, 101, 044056. [Google Scholar] [CrossRef]
- Frolov, V.P. Mass-gap for black hole formation in higher derivative and ghost free gravity. Phys. Rev. Lett. 2015, 115, 051102. [Google Scholar] [CrossRef]
- Boos, J.; Soto, J.P.; Frolov, V.P. Ultrarelativistic spinning objects in nonlocal ghostfree gravity. Phys. Rev. D 2020, 101, 124065. [Google Scholar] [CrossRef]
- DeWitt, B.S. Dynamical Theory of Groups and Fields; Documents on Modern Physics; Gordon and Breach: Philadelphia, PA, USA, 1965. [Google Scholar]
- DeWitt, B.S. Quantum Field Theory in Curved Space-Time. Phys. Rept. 1975, 19, 295–357. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series; Dover Publications: Mineola, NY, USA, 1965. [Google Scholar]
- Senovilla, J.M.M. Trapped surfaces. Int. J. Mod. Phys. D 2011, 20, 2139. [Google Scholar] [CrossRef]
- Flammer, C. Spheroidal Wave Functions; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. The NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Lee, J.G.; Adelberger, E.G.; Cook, T.S.; Fleischer, S.M.; Heckel, B.R. New Test of the Gravitational 1/r2 Law at Separations down to 52 µm. Phys. Rev. Lett. 2020, 124, 101101. [Google Scholar] [CrossRef] [PubMed]
- Gurses, M.; Feza, G. Lorentz Covariant Treatment of the Kerr-Schild Metric. J. Math. Phys. 1975, 16, 2385. [Google Scholar] [CrossRef]
- Babichev, E.; Charmousis, C.; Cisterna, A.; Hassaine, M. Regular black holes via the Kerr-Schild construction in DHOST theories. JCAP 2020, 6, 49. [Google Scholar] [CrossRef]
- Torres, R. Regular rotating black holes: A review. arXiv 2022, arXiv:2208.12713. [Google Scholar]
- Baines, J.; Visser, M. Killing Horizons and Surface Gravities for a Well-Behaved Three-Function Generalization of the Kerr Spacetime. Universe 2023, 9, 223. [Google Scholar] [CrossRef]
- Zhou, T.; Modesto, L. On the analytic extension of regular rotating black holes. arXiv 2023, arXiv:2303.11322. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).