Current Status and Prospects on High-Precision Quantum Tests of the Weak Equivalence Principle with Cold Atom Interferometry
Abstract
1. Introduction
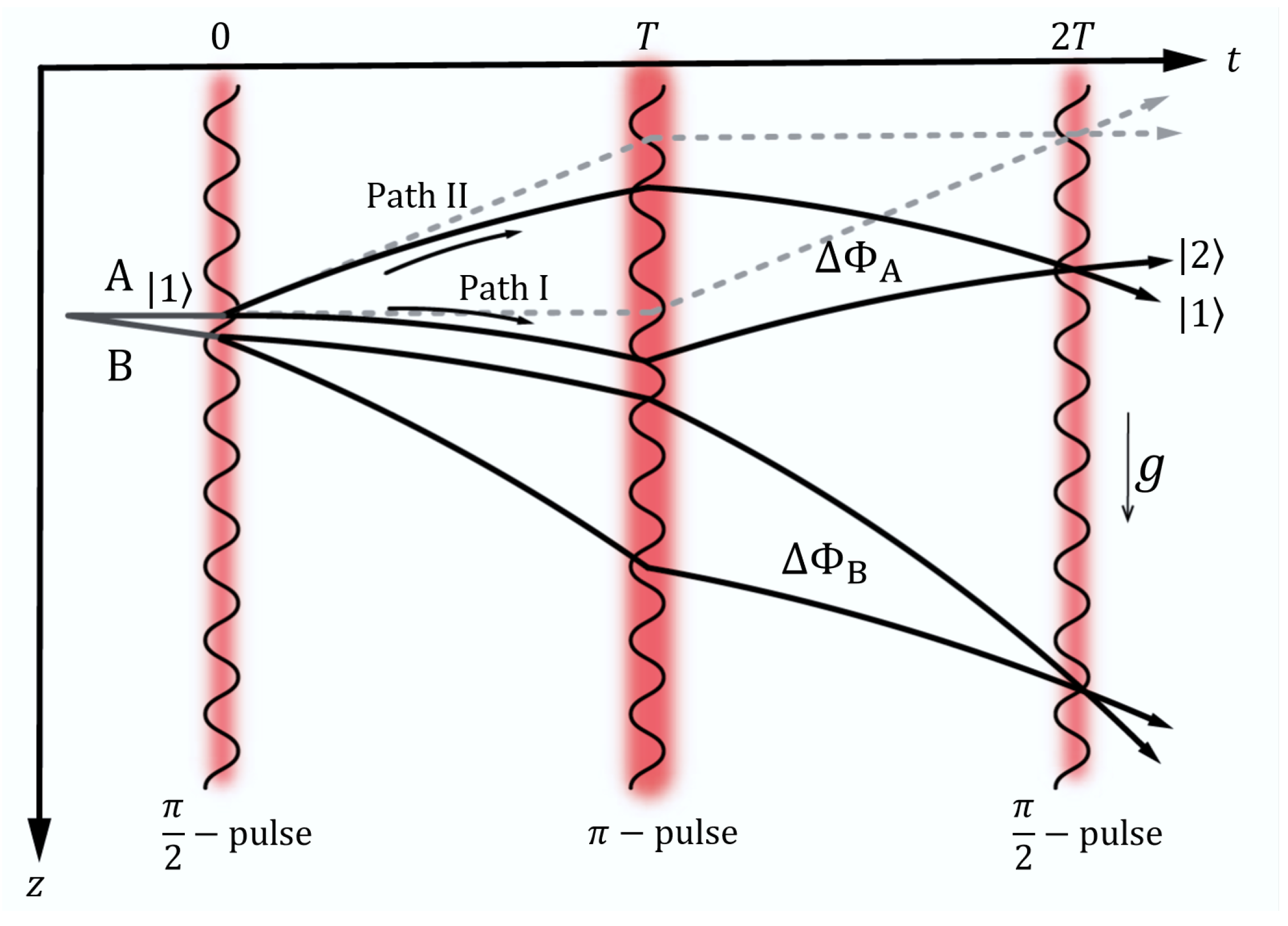
2. Basic Theory
3. Developments and State of the Art
3.1. Dual Atomic Species
3.2. Dual Atomic Isotopes
3.3. Dual Atomic Internal States
4. Key Techniques and Systematic Effects
4.1. Preparation and Control of Laser Pulse
4.2. Atom Trajectory and Signal Detection
4.3. Major Systematic Effects
4.3.1. Gravity Gradient and Coriolis Effect
4.3.2. Wavefront Aberrations
4.3.3. Stark and Zeeman Effects
4.3.4. Atoms Interaction and Self-Attraction Effect
4.4. Noise Suppression
4.5. Integrated Packages
5. Prospect and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Meaning | Section |
| AI | atom interferometry | 2 |
| AOM | acousto-optic modulation | 4 |
| BEC | Bose–Einstein condensate | 4, 5 |
| CAL | Cold Atom Lab | 5 |
| EEP | Einstein equivalence principle | 1 |
| EOM | electro-optic modulation | 4 |
| FWDR | four-wave double-diffraction Raman transition | 3, 4 |
| GR | general relativity | 1, 5 |
| HUST | Huazhong University of Science and Technology | 3, 4 |
| I/Q | in-phase/quadrature | 4 |
| LLI | local Lorentz invariance | 1, 5 |
| LMT | large momentum transfer | 4, 5 |
| LPI | local position invariance | 1, 5 |
| LP2N | The Photonics, Numerical and Nanosciences Laboratory | 3 |
| LUH | Leibniz Universität Hannover | 3 |
| LENS | European Laboratory for Non Linear Spectroscopy | 3 |
| MICROSCOPE | Micro-Satellite a traînée Compensée pour l’Observation du Principe d’Equivalence | 1 |
| MPIQ | Max-Planck-Institut für Quantenoptik | 3 |
| MSLC | microgravity scientific laboratory cabinet | 5 |
| OPLL | optical phase lock-loop | 4 |
| ONERA | The French Aerospace Lab | 3, 5 |
| QTEST | Quantum Test of the Equivalence Principle in Space | 5 |
| QUANTUS | QUANTen Gase Unter Schwerelosigkeit | 5 |
| SM | Standard Model | 1 |
| STE-QUEST | Space–Time Explorer and Quantum Equivalence principle Space Test | 5 |
| UFF | University of Free Fall | 1 |
| WEP | weak equivalence principle | 1, 2, 3, 4, 5 |
| WIPM | Wuhan Institute of Physics and Mathematics | 3, 4 |
| ZAIGA | The Zhaoshan Long-Baseline Atom Interferometer Gravitation Antenna | 5 |
References
- Kragh, H.; Smith, R.W. Who discovered the expanding universe? Hist. Sci. 2003, 41, 141–162. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Alves, M.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Aussel, H.; Baccigalupi, C.; et al. Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 2014, 571, A1. [Google Scholar] [CrossRef]
- Bell, J.S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Mintert, F.; Kuś, M.; Buchleitner, A. Concurrence of Mixed Multipartite Quantum States. Phys. Rev. Lett. 2005, 95, 260502. [Google Scholar] [CrossRef]
- Yang, C.N.; Mills, R.L. Conservation of Isotopic Spin and Isotopic Gauge Invariance. Phys. Rev. 1954, 96, 191–195. [Google Scholar] [CrossRef]
- Dicke, R. Republication of: The theoretical significance of experimental relativity. Gen. Relativ. Gravit. 2019, 51, 1–31. [Google Scholar] [CrossRef]
- Whitrow, G.J. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Phys. Bull. 1974, 25, 65. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University: Cambridge, UK, 2018. [Google Scholar]
- Ciufolini, I.; Wheeler, J.A. Gravitation and Inertia; Princeton University Press: Princeton, NJ, USA, 1995; Volume 101. [Google Scholar]
- Damour, T.; Polyakov, A.M. String theory and gravity. Gen. Relativ. Gravit. 1994, 26, 1171–1176. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J. Dual models and the geometry of space-time. Phys. Lett. B 1974, 52, 347–350. [Google Scholar] [CrossRef]
- Chiou, D.W. Loop quantum gravity. Int. J. Mod. Phys. D 2015, 24, 1530005. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Damour, T. Theoretical aspects of the equivalence principle. Class. Quantum Gravity 2012, 29, 184001. [Google Scholar] [CrossRef]
- Fayet, P. A new long-range force? Phys. Lett. B 1986, 171, 261–266. [Google Scholar] [CrossRef]
- Fayet, P. The fifth interaction in grand-unified theories: A new force acting mostly on neutrons and particle spins. Phys. Lett. B 1986, 172, 363–368. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. General relativistic effects in atom interferometry. Phys. Rev. D 2008, 78, 042003. [Google Scholar] [CrossRef]
- Graham, P.W.; Kaplan, D.E.; Mardon, J.; Rajendran, S.; Terrano, W.A. Dark matter direct detection with accelerometers. Phys. Rev. D 2016, 93, 075029. [Google Scholar] [CrossRef]
- Hees, A.; Minazzoli, O.; Savalle, E.; Stadnik, Y.V.; Wolf, P. Violation of the equivalence principle from light scalar dark matter. Phys. Rev. D 2018, 98, 064051. [Google Scholar] [CrossRef]
- Sondag, A.; Dittus, H. Electrostatic Positioning System for a free fall test at drop tower Bremen and an overview of tests for the Weak Equivalence Principle in past, present and future. Adv. Space Res. 2016, 58, 644–677. [Google Scholar] [CrossRef]
- Potter, H.H.; Richardson, O.W. Some experiments on the proportionality of mass and weight. Proc. R. Soc. Lond. Ser. A 1923, 104, 588–610. [Google Scholar] [CrossRef]
- Carusotto, S.; Cavasinni, V.; Mordacci, A.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. Test of g universality with a Galileo type experiment. Phys. Rev. Lett. 1992, 69, 1722–1725. [Google Scholar] [CrossRef] [PubMed]
- Carusotto, S.; Cavasinni, V.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. g-Universality test with a Galileo’s type experiment. Nuov. Cim. B 1996, 111, 1259–1275. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Q.; Zhao, H.H.; Gong, Q.L.; Yang, S.Q.; Luo, P.; Shao, C.G.; Wang, Q.L.; Tu, L.C.; Luo, J. Test of the Equivalence Principle with Chiral Masses Using a Rotating Torsion Pendulum. Phys. Rev. Lett. 2018, 121, 261101. [Google Scholar] [CrossRef]
- Viswanathan, V.; Fienga, A.; Minazzoli, O.; Bernus, L.; Laskar, J.; Gastineau, M. The new lunar ephemeris INPOP17a and its application to fundamental physics. Mon. Not. R. Astron. Soc. 2018, 476, 1877–1888. [Google Scholar] [CrossRef]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quantum Gravity 2018, 35, 035015. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; Bergé, J.; Robert, A.; Baghi, Q.; André, Y.; Bedouet, J.; Boulanger, D.; Bremer, S.; et al. MICROSCOPE Mission: Final Results of the Test of the Equivalence Principle. Phys. Rev. Lett. 2022, 129, 121102. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; Bergé, J.; Robert, A.; Baghi, Q.; André, Y.; Bedouet, J.; Boulanger, D.; Bremer, S.; et al. Result of the MICROSCOPE weak equivalence principle test. Class. Quantum Gravity 2022, 39, 204009. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. Testing General Relativity with Atom Interferometry. Phys. Rev. Lett. 2007, 98, 111102. [Google Scholar] [CrossRef] [PubMed]
- Miffre, A.; Jacquey, M.; Büchner, M.; Trénec, G.; Vigué, J. Atom interferometry. Phys. Scr. 2006, 74, C15. [Google Scholar] [CrossRef]
- Khoury, J. Chameleon field theories. Class. Quantum Gravity 2013, 30, 214004. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J.; Hinds, E. Probing dark energy with atom interferometry. J. Cosmol. Astropart. Phys. 2015, 2015, 042. [Google Scholar] [CrossRef]
- Hamilton, P.; Jaffe, M.; Haslinger, P.; Simmons, Q.; Müller, H.; Khoury, J. Atom-interferometry constraints on dark energy. Science 2015, 349, 849–851. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J. Using atom interferometry to detect dark energy. Contemp. Phys. 2016, 57, 164–176. [Google Scholar] [CrossRef]
- Elder, B.; Khoury, J.; Haslinger, P.; Jaffe, M.; Müller, H.; Hamilton, P. Chameleon dark energy and atom interferometry. Phys. Rev. D 2016, 94, 044051. [Google Scholar] [CrossRef]
- Puetzfeld, D.; Obukhov, Y.N. Propagation equations for deformable test bodies with microstructure in extended theories of gravity. Phys. Rev. D 2007, 76, 084025. [Google Scholar] [CrossRef]
- Yasskin, P.B.; Stoeger, W.R. Propagation equations for test bodies with spin and rotation in theories of gravity with torsion. Phys. Rev. D 1980, 21, 2081–2094. [Google Scholar] [CrossRef]
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Shapiro, I. Physical aspects of the space–time torsion. Phys. Rep. 2002, 357, 113–213. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Silenko, A.J.; Teryaev, O.V. Spin-torsion coupling and gravitational moments of Dirac fermions: Theory and experimental bounds. Phys. Rev. D 2014, 90, 124068. [Google Scholar] [CrossRef]
- Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599. [Google Scholar] [CrossRef]
- Bong, K.; Holynski, M.; Vovrosh, J.; Bouyer, P.; Condon, G.; Rasel, E.; Schubert, C.; Schleich, W.P.; Roura, A. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat. Rev. Phys. 2019, 1, 731–739. [Google Scholar] [CrossRef]
- Geiger, R.; Landragin, A.; Merlet, S.; Pereira Dos Santos, F. High-accuracy inertial measurements with cold-atom sensors. AVS Quantum Sci. 2020, 2, 024702. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Ander, M.E.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Pearson, W.C.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. Historical development of gravity method in exploration. Geophysics 2005, 70, 63ND–89ND. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Blanchard, C.; Bonnin, A.; Cadoret, M.; Bresson, A.; Rouxel, D.; Lequentrec-Lalancette, M.F. Absolute marine gravimetry with matter-wave interferometry. Nat. Commun. 2018, 9, 627. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Bresson, A.; Blanchard, C.; Cadoret, M.; Olesen, V.A.; Forsberg, R. Absolute airborne gravimetry with a cold atom sensor. J. Geod. 2020, 94, 20. [Google Scholar] [CrossRef]
- Boddice, D.; Metje, N.; Tuckwell, G. Capability assessment and challenges for quantum technology gravity sensors for near surface terrestrial geophysical surveying. J. Appl. Geophy 2017, 146, 149–159. [Google Scholar] [CrossRef]
- Stray, B.; Lamb, A.; Kaushik, A.; Vovrosh, J.; Rodgers, A.; Winch, J.; Hayati, F.; Boddice, D.; Stabrawa, A.; Niggebaum, A.; et al. Quantum sensing for gravity cartography. Nature 2022, 602, 590–594. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Pálinkáš, V.; Arias, F.E.; Liard, J.; Merlet, S.; Wilmes, H.; Vitushkin, L.; Robertsson, L.; Tisserand, L.; Santos, F.P.D.; et al. The 8th International Comparison of Absolute Gravimeters 2009: The first Key Comparison (CCM.G-K1) in the field of absolute gravimetry. Metrologia 2012, 49, 666. [Google Scholar] [CrossRef]
- Stock, M.; Davis, R.; de Mirandés, E.; Milton, M.J.T. The revision of the SI—the result of three decades of progress in metrology. Metrologia 2019, 56, 022001. [Google Scholar] [CrossRef]
- Wu, S.; Feng, J.; Li, C.; Su, D.; Wang, Q.; Hu, R.; Mou, L. The results of 10th International Comparison of Absolute Gravimeters (ICAG-2017). J. Geod. 2021, 95, 63. [Google Scholar] [CrossRef]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G.M. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef]
- Fixler, J.B.; Foster, G.T.; McGuirk, J.M.; Kasevich, M.A. Atom Interferometer Measurement of the Newtonian Constant of Gravity. Science 2007, 315, 74–77. [Google Scholar] [CrossRef]
- Bouchendira, R.; Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef]
- Parker, R.H.; Yu, C.; Zhong, W.; Estey, B.; Müller, H. Measurement of the fine-structure constant as a test of the Standard Model. Science 2018, 360, 191–195. [Google Scholar] [CrossRef]
- Morel, L.; Yao, Z.; Clade, P.; Guellati-Khelifa, S. Determination of the fine-structure constant with an accuracy of 81 parts per trillion. Nature 2020, 588, 61–65. [Google Scholar] [CrossRef]
- Herrmann, S.; Dittus, H.; Lämmerzahl, C.; (for the QUANTUS and PRIMUS teams). Testing the equivalence principle with atomic interferometry. Class. Quantum Gravity 2012, 29, 184003. [Google Scholar] [CrossRef]
- Tino, G.; Cacciapuoti, L.; Capozziello, S.; Lambiase, G.; Sorrentino, F. Precision gravity tests and the Einstein Equivalence Principle. Prog. Part. Nucl. Phys. 2020, 112, 103772. [Google Scholar] [CrossRef]
- Tino, G.M. Testing gravity with cold atom interferometry: Results and prospects. Quantum Sci. Technol. 2021, 6, 024014. [Google Scholar] [CrossRef]
- Hohensee, M.; Lan, S.Y.; Houtz, R.; Chan, C.; Estey, B.; Kim, G.; Kuan, P.C.; Müller, H. Sources and technology for an atomic gravitational wave interferometric sensor. Gen. Relativ. Gravit. 2011, 43, 1905–1930. [Google Scholar] [CrossRef]
- Graham, P.W.; Hogan, J.M.; Kasevich, M.A.; Rajendran, S. New Method for Gravitational Wave Detection with Atomic Sensors. Phys. Rev. Lett. 2013, 110, 171102. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lu, X.Y.; Qin, C.G.; Tan, Y.J.; Shao, C.G. Modeling gravitational wave detection with atom interferometry. Class. Quantum Gravity 2021, 38, 145025. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Moosbrugger, D. An Update on the Impact of Schiff’s Conjecture on Tests of the Einstein Equivalence Principle Today. Master’s Thesis, ETH Zürich, Zürich, Switzerland, 2018. [Google Scholar]
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25–61. [Google Scholar] [CrossRef]
- Giltner, D.M.; McGowan, R.W.; Lee, S.A. Atom Interferometer Based on Bragg Scattering from Standing Light Waves. Phys. Rev. Lett. 1995, 75, 2638–2641. [Google Scholar] [CrossRef]
- Siemß, J.N.; Fitzek, F.; Abend, S.; Rasel, E.M.; Gaaloul, N.; Hammerer, K. Analytic theory for Bragg atom interferometry based on the adiabatic theorem. Phys. Rev. A 2020, 102, 033709. [Google Scholar] [CrossRef]
- Béguin, A.; Rodzinka, T.; Vigué, J.; Allard, B.; Gauguet, A. Characterization of an atom interferometer in the quasi-Bragg regime. Phys. Rev. A 2022, 105, 033302. [Google Scholar] [CrossRef]
- Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. Large Momentum Beam Splitter Using Bloch Oscillations. Phys. Rev. Lett. 2009, 102, 240402. [Google Scholar] [CrossRef] [PubMed]
- Müller, H.; Chiow, S.; Herrmann, S.; Chu, S. Atom Interferometers with Scalable Enclosed Area. Phys. Rev. Lett. 2009, 102, 240403. [Google Scholar] [CrossRef]
- McAlpine, K.E.; Gochnauer, D.; Gupta, S. Excited-band Bloch oscillations for precision atom interferometry. Phys. Rev. A 2020, 101, 023614. [Google Scholar] [CrossRef]
- Poli, N.; Wang, F.Y.; Tarallo, M.G.; Alberti, A.; Prevedelli, M.; Tino, G.M. Precision Measurement of Gravity with Cold Atoms in an Optical Lattice and Comparison with a Classical Gravimeter. Phys. Rev. Lett. 2011, 106, 038501. [Google Scholar] [CrossRef] [PubMed]
- Charrière, R.; Cadoret, M.; Zahzam, N.; Bidel, Y.; Bresson, A. Local gravity measurement with the combination of atom interferometry and Bloch oscillations. Phys. Rev. A 2012, 85, 013639. [Google Scholar] [CrossRef]
- Dunning, A.; Gregory, R.; Bateman, J.; Cooper, N.; Himsworth, M.; Jones, J.A.; Freegarde, T. Composite pulses for interferometry in a thermal cold atom cloud. Phys. Rev. A 2014, 90, 033608. [Google Scholar] [CrossRef]
- Berg, P.; Abend, S.; Tackmann, G.; Schubert, C.; Giese, E.; Schleich, W.P.; Narducci, F.A.; Ertmer, W.; Rasel, E.M. Composite-Light-Pulse Technique for High-Precision Atom Interferometry. Phys. Rev. Lett. 2015, 114, 063002. [Google Scholar] [CrossRef]
- Xu, V.; Jaffe, M.; Panda, C.D.; Kristensen, S.L.; Clark, L.W.; Müller, H. Probing gravity by holding atoms for 20 seconds. Science 2019, 366, 745–749. [Google Scholar] [CrossRef]
- Zhou, L.; Long, S.; Tang, B.; Chen, X.; Gao, F.; Peng, W.; Duan, W.; Zhong, J.; Xiong, Z.; Wang, J.; et al. Test of Equivalence Principle at 10−8 Level by a Dual-Species Double-Diffraction Raman Atom Interferometer. Phys. Rev. Lett. 2015, 115, 013004. [Google Scholar] [CrossRef]
- Geiger, R.; Trupke, M. Proposal for a Quantum Test of the Weak Equivalence Principle with Entangled Atomic Species. Phys. Rev. Lett. 2018, 120, 043602. [Google Scholar] [CrossRef]
- Viola, L.; Onofrio, R. Testing the equivalence principle through freely falling quantum objects. Phys. Rev. D 1997, 55, 455–462. [Google Scholar] [CrossRef]
- Kajari, E.; Harshman, N.; Rasel, E.; Stenholm, S.; Süssmann, G.; Schleich, W.P. Inertial and gravitational mass in quantum mechanics. Appl. Phys. B 2010, 100, 43–60. [Google Scholar] [CrossRef]
- Orlando, P.J.; Mann, R.B.; Modi, K.; Pollock, F.A. A test of the equivalence principle(s) for quantum superpositions. Class. Quantum Gravity 2016, 33, 19LT01. [Google Scholar] [CrossRef]
- Zych, M.; Brukner, C. Quantum formulation of the Einstein equivalence principle. Nat. Phys. 2018, 14, 1027–1031. [Google Scholar] [CrossRef]
- Chu, S.; Hollberg, L.; Bjorkholm, J.E.; Cable, A.; Ashkin, A. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure. Phys. Rev. Lett. 1985, 55, 48–51. [Google Scholar] [CrossRef] [PubMed]
- Lett, P.D.; Watts, R.N.; Westbrook, C.I.; Phillips, W.D.; Gould, P.L.; Metcalf, H.J. Observation of Atoms Laser Cooled below the Doppler Limit. Phys. Rev. Lett. 1988, 61, 169–172. [Google Scholar] [CrossRef]
- Aspect, A.; Arimondo, E.; Kaiser, R.; Vansteenkiste, N.; Cohen-Tannoudji, C. Laser Cooling below the One-Photon Recoil Energy by Velocity-Selective Coherent Population Trapping. Phys. Rev. Lett. 1988, 61, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated Raman transitions. Phys. Rev. Lett. 1991, 67, 181–184. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.; Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 1999, 400, 849–852. [Google Scholar] [CrossRef]
- Clauser, J.F. Ultra-high sensitivity accelerometers and gyroscopes using neutral atom matter-wave interferometry. Physica B+C 1988, 151, 262–272. [Google Scholar] [CrossRef]
- Walz, J.; Hansch, T. A proposal to measure antimatter gravity using ultracold antihydrogen atoms. Gen. Relativ. Gravity 2004, 36, 561–570. [Google Scholar] [CrossRef]
- Hamilton, P.; Zhmoginov, A.; Robicheaux, F.; Fajans, J.; Wurtele, J.S.; Müller, H. Antimatter Interferometry for Gravity Measurements. Phys. Rev. Lett. 2014, 112, 121102. [Google Scholar] [CrossRef]
- Rodewald, J.; Dörre, N.; Grimaldi, A.; Geyer, P.; Felix, L.; Mayor, M.; Shayeghi, A.; Arndt, M. Isotope-selective high-order interferometry with large organic molecules in free fall. New J. Phys. 2018, 20, 033016. [Google Scholar] [CrossRef]
- Amoretti, M.; Amsler, C.; Bonomi, G.; Bouchta, A.; Bowe, P.; Carraro, C.; Cesar, C.; Charlton, M.; Collier, M.; Doser, M.; et al. Production and detection of cold antihydrogen atoms. Nature 2002, 419, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.J.; Bertsche, W.; Capra, A.; Cesar, C.L.; Charlton, M.; Mathad, A.C.; Eriksson, S.; Evans, A.; Evetts, N.; Fabbri, S.; et al. Sympathetic cooling of positrons to cryogenic temperatures for antihydrogen production. Nat. Commun. 2021, 12, 6139. [Google Scholar] [CrossRef]
- Pedalino, S.; Galindo, B.R.; de Sousa, T.; Fein, Y.Y.; Geyer, P.; Gerlich, S.; Arndt, M. Experimental challenges for high-mass matter-wave interference with nanoparticles. In Proceedings of the Quantum Sensing, Imaging, and Precision Metrology; Scheuer, J., Shahriar, S.M., Eds.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2023; Volume 12447, p. 124470K. [Google Scholar] [CrossRef]
- Fray, S.; Diez, C.A.; Hänsch, T.W.; Weitz, M. Atomic Interferometer with Amplitude Gratings of Light and Its Applications to Atom Based Tests of the Equivalence Principle. Phys. Rev. Lett. 2004, 93, 240404. [Google Scholar] [CrossRef]
- Altin, P.A.; Johnsson, M.T.; Negnevitsky, V.; Dennis, G.R.; Anderson, R.P.; Debs, J.E.; Szigeti, S.S.; Hardman, K.S.; Bennetts, S.; McDonald, G.D.; et al. Precision atomic gravimeter based on Bragg diffraction. New J. Phys. 2013, 15, 023009. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Z.; Cheng, B.; Wang, Q.; Xu, A.; Lin, Q. The investigation of a μGal-level cold atom gravimeter for field applications. Metrologia 2014, 51, 452–458. [Google Scholar] [CrossRef]
- Zhou, L.; Xiong, Z.Y.; Yang, W.; Tang, B.; Peng, W.C.; Wang, Y.B.; Xu, P.; Wang, J.; Zhan, M.S. Measurement of local gravity via a cold atom interferometer. Chin. Phys. Lett. 2011, 28, 013701. [Google Scholar] [CrossRef]
- Dickerson, S.M.; Hogan, J.M.; Sugarbaker, A.; Johnson, D.M.S.; Kasevich, M.A. Multiaxis Inertial Sensing with Long-Time Point Source Atom Interferometry. Phys. Rev. Lett. 2013, 111, 083001. [Google Scholar] [CrossRef]
- Zhou, L.; Yan, S.T.; Ji, Y.H.; He, C.; Jiang, J.J.; Hou, Z.; Xu, R.D.; Wang, Q.; Li, Z.X.; Gao, D.F.; et al. Toward a high-precision mass–energy test of the equivalence principle with atom interferometers. Front. Phys. 2022, 10, 1039119. [Google Scholar] [CrossRef]
- Bodart, Q.; Merlet, S.; Malossi, N.; Dos Santos, F.P.; Bouyer, P.; Landragin, A. A cold atom pyramidal gravimeter with a single laser beam. Appl. Phys. Lett. 2010, 96, 134101. [Google Scholar] [CrossRef]
- Bidel, Y.; Carraz, O.; Charrière, R.; Cadoret, M.; Zahzam, N.; Bresson, A. Compact cold atom gravimeter for field applications. Appl. Phys. Lett. 2013, 102, 144107. [Google Scholar] [CrossRef]
- Hauth, M.; Freier, C.; Schkolnik, V.; Senger, A.; Schmidt, M.; Peters, A. First gravity measurements using the mobile atom interferometer GAIN. Appl. Phys. B 2013, 113, 49–55. [Google Scholar] [CrossRef]
- Wang, S.K.; Zhao, Y.; Zhuang, W.; Li, T.C.; Wu, S.Q.; Feng, J.Y.; Li, C.J. Shift evaluation of the atomic gravimeter NIM-AGRb-1 and its comparison with FG5X. Metrologia 2018, 55, 360–365. [Google Scholar] [CrossRef]
- Huang, P.W.; Tang, B.; Chen, X.; Zhong, J.Q.; Xiong, Z.Y.; Zhou, L.; Wang, J.; Zhan, M.S. Accuracy and stability evaluation of the 85 Rb atom gravimeter WAG-H5-1 at the 2017 International Comparison of Absolute Gravimeters. Metrologia 2019, 56, 045012. [Google Scholar] [CrossRef]
- Fu, Z.; Wu, B.; Cheng, B.; Zhou, Y.; Weng, K.; Zhu, D.; Wang, Z.; Lin, Q. A new type of compact gravimeter for long-term absolute gravity monitoring. Metrologia 2019, 56, 025001. [Google Scholar] [CrossRef]
- Schlippert, D.; Hartwig, J.; Albers, H.; Richardson, L.L.; Schubert, C.; Roura, A.; Schleich, W.P.; Ertmer, W.; Rasel, E.M. Quantum Test of the Universality of Free Fall. Phys. Rev. Lett. 2014, 112, 203002. [Google Scholar] [CrossRef]
- Barrett, B.; Antoni-Micollier, L.; Chichet, L.; Battelier, B.; Gominet, P.A.; Bertoldi, A.; Bouyer, P.; Landragin, A. Correlative methods for dual-species quantum tests of the weak equivalence principle. New J. Phys. 2015, 17, 085010. [Google Scholar] [CrossRef]
- Barrett, B.; Antoni-Micollier, L.; Chichet, L.; Battelier, B.; Leveque, T.; Landragin, A.; Bouyer, P. Dual matter-wave inertial sensors in weightlessness. Nat. Commun. 2016, 7, 13786. [Google Scholar] [CrossRef]
- Albers, H.; Herbst, A.; Richardson, L.L.; Heine, H.; Nath, D.; Hartwig, J.; Schubert, C.; Vogt, C.; Woltmann, M.; Laemmerzahl, C.; et al. Quantum test of the Universality of Free Fall using rubidium and potassium. Eur. Phys. J. D 2020, 74, 145. [Google Scholar] [CrossRef]
- Barrett, B.; Condon, G.; Chichet, L.; Antoni-Micollier, L.; Arguel, R.; Rabault, M.; Pelluet, C.; Jarlaud, V.; Landragin, A.; Bouyer, P.; et al. Testing the universality of free fall using correlated 39K-87Rb atom interferometers. AVS Quantum Sci. 2022, 4, 014401. [Google Scholar] [CrossRef]
- Bonnin, A.; Zahzam, N.; Bidel, Y.; Bresson, A. Simultaneous dual-species matter-wave accelerometer. Phys. Rev. A 2013, 88, 043615. [Google Scholar] [CrossRef]
- Tarallo, M.G.; Mazzoni, T.; Poli, N.; Sutyrin, D.V.; Zhang, X.; Tino, G.M. Test of Einstein Equivalence Principle for 0-Spin and Half-Integer-Spin Atoms: Search for Spin-Gravity Coupling Effects. Phys. Rev. Lett. 2014, 113, 023005. [Google Scholar] [CrossRef]
- Overstreet, C.; Asenbaum, P.; Kovachy, T.; Notermans, R.; Hogan, J.M.; Kasevich, M.A. Effective Inertial Frame in an Atom Interferometric Test of the Equivalence Principle. Phys. Rev. Lett. 2018, 120, 183604. [Google Scholar] [CrossRef]
- Asenbaum, P.; Overstreet, C.; Kim, M.; Curti, J.; Kasevich, M.A. Atom-Interferometric Test of the Equivalence Principle at the 10−12 Level. Phys. Rev. Lett. 2020, 125, 191101. [Google Scholar] [CrossRef]
- Zhou, L.; He, C.; Yan, S.T.; Chen, X.; Gao, D.F.; Duan, W.T.; Ji, Y.H.; Xu, R.D.; Tang, B.; Zhou, C.; et al. Joint mass-and-energy test of the equivalence principle at the 10−10 level using atoms with specified mass and internal energy. Phys. Rev. A 2021, 104, 022822. [Google Scholar] [CrossRef]
- Duan, X.C.; Deng, X.B.; Zhou, M.K.; Zhang, K.; Xu, W.J.; Xiong, F.; Xu, Y.Y.; Shao, C.G.; Luo, J.; Hu, Z.K. Test of the Universality of Free Fall with Atoms in Different Spin Orientations. Phys. Rev. Lett. 2016, 117, 023001. [Google Scholar] [CrossRef]
- Rosi, G.; D’Amico, G.; Cacciapuoti, L.; Sorrentino, F.; Prevedelli, M.; Zych, M.; Brukner, C.; Tino, G.M. Quantum test of the equivalence principle for atoms in coherent superposition of internal energy states. Nat. Commun. 2017, 8, 15529. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, M.K.; Cheng, Y.; Chen, L.L.; Luo, Q.; Xu, W.J.; Cao, L.S.; Duan, X.C.; Hu, Z.K. Testing the Universality of Free Fall by Comparing the Atoms in Different Hyperfine States with Bragg Diffraction. Chin. Phys. Lett. 2020, 37, 043701. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Deng, X.B.; Duan, X.C.; Cao, L.S.; Zhou, M.K.; Shao, C.G.; Hu, Z.K. de-Broglie wavelength enhanced weak equivalence principle test for atoms in different hyperfine states. arXiv 2022, arXiv:2210.08533. [Google Scholar]
- Damour, T. Testing the equivalence principle: Why and how? Class. Quantum Gravity 1996, 13, A33. [Google Scholar] [CrossRef]
- Hartwig, J.; Abend, S.; Schubert, C.; Schlippert, D.; Ahlers, H.; Posso-Trujillo, K.; Gaaloul, N.; Ertmer, W.; Rasel, E.M. Testing the universality of free fall with rubidium and ytterbium in a very large baseline atom interferometer. New J. Phys. 2015, 17, 035011. [Google Scholar] [CrossRef]
- Tinsley, J.N.; Bandarupally, S.; Chiarotti, M.; Manzoor, S.; Salvi, L.; Poli, N. Prospects for a simultaneous atom interferometer with ultracold cadmium and strontium for fundamental physics tests. In Proceedings of the Optical and Quantum Sensing and Precision Metrology II; Scheuer, J., Shahriar, S.M., Eds.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2022; Volume 12016, p. 1201602. [Google Scholar] [CrossRef]
- Altschul, B.; Bailey, Q.G.; Blanchet, L.; Bongs, K.; Bouyer, P.; Cacciapuoti, L.; Capozziello, S.; Gaaloul, N.; Giulini, D.; Hartwig, J.; et al. Quantum tests of the Einstein Equivalence Principle with the STE–QUEST space mission. Adv. Space Res. 2015, 55, 501–524. [Google Scholar] [CrossRef]
- Williams, J.; wey Chiow, S.; Yu, N.; Müller, H. Quantum test of the equivalence principle and space-time aboard the International Space Station. New J. Phys. 2016, 18, 025018. [Google Scholar] [CrossRef]
- Cacciapuoti, L.; de Angelis, M.; Fattori, M.; Lamporesi, G.; Petelski, T.; Prevedelli, M.; Stuhler, J.; Tino, G.M. Analog+digital phase and frequency detector for phase locking of diode lasers. Rev. Sci. Instrum. 2005, 76, 053111. [Google Scholar] [CrossRef]
- Tackmann, G.; Gilowski, M.; Schubert, C.; Berg, P.; Wendrich, T.; Ertmer, W.; Rasel, E.M. Phase-locking of two self-seeded tapered amplifier lasers. Opt. Express 2010, 18, 9258–9265. [Google Scholar] [CrossRef] [PubMed]
- Lenef, A.; Hammond, T.D.; Smith, E.T.; Chapman, M.S.; Rubenstein, R.A.; Pritchard, D.E. Rotation Sensing with an Atom Interferometer. Phys. Rev. Lett. 1997, 78, 760–763. [Google Scholar] [CrossRef]
- Müller, H.; Chiow, S.W.; Long, Q.; Herrmann, S.; Chu, S. Atom Interferometry with up to 24-Photon-Momentum-Transfer Beam Splitters. Phys. Rev. Lett. 2008, 100, 180405. [Google Scholar] [CrossRef]
- Weitz, M.; Young, B.C.; Chu, S. Atomic Interferometer Based on Adiabatic Population Transfer. Phys. Rev. Lett. 1994, 73, 2563–2566. [Google Scholar] [CrossRef]
- Shahriar, M.; Turukhin, A.; Liptay, T.; Tan, Y.; Hemmer, P. Demonstration of injection locking a diode laser using a filtered electro-optic modulator sideband. Opt. Commun. 2000, 184, 457–462. [Google Scholar] [CrossRef]
- Yim, S.H.; Lee, S.B.; Kwon, T.Y.; Park, S.E. Optical phase locking of two extended-cavity diode lasers with ultra-low phase noise for atom interferometry. Appl. Phys. B 2014, 115, 491–495. [Google Scholar] [CrossRef]
- Wang, K.; Yao, Z.; Li, R.; Lu, S.; Chen, X.; Wang, J.; Zhan, M. Hybrid wide-band, low-phase-noise scheme for Raman lasers in atom interferometry by integrating an acousto-optic modulator and a feedback loop. Appl. Opt. 2016, 55, 989–992. [Google Scholar] [CrossRef] [PubMed]
- Weitz, M.; Young, B.C.; Chu, S. Atom manipulation based on delayed laser pulses in three- and four-level systems: Light shifts and transfer efficiencies. Phys. Rev. A 1994, 50, 2438–2444. [Google Scholar] [CrossRef]
- Li, R.B.; Zhou, L.; Wang, J.; Zhan, M.S. Measurement of the quadratic Zeeman shift of 85Rb hyperfine sublevels using stimulated Raman transitions. Opt. Commun. 2009, 282, 1340–1344. [Google Scholar] [CrossRef][Green Version]
- Zhu, L.; Lien, Y.H.; Hinton, A.; Niggebaum, A.; Rammeloo, C.; Bongs, K.; Holynski, M. Application of optical single-sideband laser in Raman atom interferometry. Opt. Express 2018, 26, 6542–6553. [Google Scholar] [CrossRef]
- Rammeloo, C.; Zhu, L.; Lien, Y.H.; Bongs, K.; Holynski, M. Performance of an optical single-sideband laser system for atom interferometry. J. Opt. Soc. Am. B 2020, 37, 1485–1493. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, H.; Zhang, K.; Duan, X.C.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. A compact laser system for a portable atom interferometry gravimeter. Rev. Sci. Instrum. 2019, 90, 043104. [Google Scholar] [CrossRef]
- McGuirk, J.M.; Snadden, M.J.; Kasevich, M.A. Large Area Light-Pulse Atom Interferometry. Phys. Rev. Lett. 2000, 85, 4498–4501. [Google Scholar] [CrossRef]
- Hu, L.; Poli, N.; Salvi, L.; Tino, G.M. Atom Interferometry with the Sr Optical Clock Transition. Phys. Rev. Lett. 2017, 119, 263601. [Google Scholar] [CrossRef]
- Hamilton, P.; Jaffe, M.; Brown, J.M.; Maisenbacher, L.; Estey, B.; Müller, H. Atom Interferometry in an Optical Cavity. Phys. Rev. Lett. 2015, 114, 100405. [Google Scholar] [CrossRef] [PubMed]
- Nourshargh, R.; Lellouch, S.; Hedges, S.; Langlois, M.; Bongs, K.; Holynski, M. Circulating pulse cavity enhancement as a method for extreme momentum transfer atom interferometry. Commun. Phys. 2021, 4, 257. [Google Scholar] [CrossRef]
- Yao, Z.W.; Lu, S.B.; Li, R.B.; Luo, J.; Wang, J.; Zhan, M.S. Calibration of atomic trajectories in a large-area dual-atom-interferometer gyroscope. Phys. Rev. A 2018, 97, 013620. [Google Scholar] [CrossRef]
- Zhu, L.; Zhong, J.; Zhang, X.; Lyu, W.; Liu, W.; Xu, W.; Chen, X.; Wang, J.; Zhan, M. Feedback control of atom trajectories in a horizontal atom gravity gradiometer. Opt. Express 2022, 30, 10071–10083. [Google Scholar] [CrossRef]
- Rocco, E.; Palmer, R.N.; Valenzuela, T.; Boyer, V.; Freise, A.; Bongs, K. Fluorescence detection at the atom shot noise limit for atom interferometry. New J. Phys. 2014, 16, 093046. [Google Scholar] [CrossRef]
- Biedermann, G.W.; Wu, X.; Deslauriers, L.; Takase, K.; Kasevich, M.A. Low-noise simultaneous fluorescence detection of two atomic states. Opt. Lett. 2009, 34, 347–349. [Google Scholar] [CrossRef]
- Song, H.; Zhong, J.; Chen, X.; Zhu, L.; Wang, Y.; Wang, J.; Zhan, M. Normalized detection by using the blow-away signal in cold atom interferometry. Opt. Express 2016, 24, 28392–28399. [Google Scholar] [CrossRef]
- Foster, G.T.; Fixler, J.B.; McGuirk, J.M.; Kasevich, M.A. Method of phase extraction between coupled atom interferometers using ellipse-specific fitting. Opt. Lett. 2002, 27, 951–953. [Google Scholar] [CrossRef]
- Stockton, J.K.; Wu, X.; Kasevich, M.A. Bayesian estimation of differential interferometer phase. Phys. Rev. A 2007, 76, 033613. [Google Scholar] [CrossRef]
- Varoquaux, G.; Nyman, R.A.; Geiger, R.; Cheinet, P.; Landragin, A.; Bouyer, P. How to estimate the differential acceleration in a two-species atom interferometer to test the equivalence principle. New J. Phys. 2009, 11, 113010. [Google Scholar] [CrossRef]
- Chen, X.; Zhong, J.; Song, H.; Zhu, L.; Wang, J.; Zhan, M. Proportional-scanning-phase method to suppress the vibrational noise in nonisotope dual-atom-interferometer-based weak-equivalence-principle-test experiments. Phys. Rev. A 2014, 90, 023609. [Google Scholar] [CrossRef]
- Wang, Y.P.; Zhong, J.Q.; Chen, X.; Li, R.B.; Li, D.W.; Zhu, L.; Song, H.W.; Wang, J.; Zhan, M.S. Extracting the differential phase in dual atom interferometers by modulating magnetic fields. Opt. Commun. 2016, 375, 34–37. [Google Scholar] [CrossRef][Green Version]
- Hu, J.G.; Chen, X.; Wang, L.Y.; Liao, Q.H.; Wang, Q.N. Systematic error suppression scheme of the weak equivalence principle test by dual atom interferometers in space based on spectral correlation. Chin. Phys. B 2020, 29, 110305. [Google Scholar] [CrossRef]
- Antoine, C.; Bordé, C.J. Quantum theory of atomic clocks and gravito-inertial sensors: An update. J. Opt. B Quantum Semiclass. Opt. 2003, 5, S199. [Google Scholar] [CrossRef]
- Roura, A. Circumventing Heisenberg’s Uncertainty Principle in Atom Interferometry Tests of the Equivalence Principle. Phys. Rev. Lett. 2017, 118, 160401. [Google Scholar] [CrossRef]
- D’Amico, G.; Rosi, G.; Zhan, S.; Cacciapuoti, L.; Fattori, M.; Tino, G.M. Canceling the Gravity Gradient Phase Shift in Atom Interferometry. Phys. Rev. Lett. 2017, 119, 253201. [Google Scholar] [CrossRef]
- Chiow, S.; Williams, J.; Yu, N.; Müller, H. Gravity-gradient suppression in spaceborne atomic tests of the equivalence principle. Phys. Rev. A 2017, 95, 021603. [Google Scholar] [CrossRef]
- Duan, W.T.; He, C.; Yan, S.T.; Ji, Y.H.; Zhou, L.; Chen, X.; Wang, J.; Zhan, M.S. Suppression of Coriolis error in weak equivalence principle test using 85Rb–87Rb dual-species atom interferometer. Chin. Phys. B 2020, 29, 070305. [Google Scholar] [CrossRef]
- Lan, S.Y.; Kuan, P.C.; Estey, B.; Haslinger, P.; Müller, H. Influence of the Coriolis Force in Atom Interferometry. Phys. Rev. Lett. 2012, 108, 090402. [Google Scholar] [CrossRef]
- Louchet-Chauvet, A.; Farah, T.; Bodart, Q.; Clairon, A.; Landragin, A.; Merlet, S.; Santos, F.P.D. The influence of transverse motion within an atomic gravimeter. New J. Phys. 2011, 13, 065025. [Google Scholar] [CrossRef]
- Schkolnik, V.; Leykauf, B.; Hauth, M.; Freier, C.; Peters, A. The effect of wavefront aberrations in atom interferometry. Appl. Phys. B 2015, 120, 311–316. [Google Scholar] [CrossRef]
- Hu, J.; Chen, X.; Fang, J.; Zhou, L.; Zhong, J.; Wang, J.; Zhan, M. Analysis and suppression of wave-front-aberration phase noise in weak-equivalence-principle tests using dual-species atom interferometers. Phys. Rev. A 2017, 96, 023618. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, T.; Wang, X.; Zhang, Z.; Xu, Y.; Lin, Q. A precision analysis and determination of the technical requirements of an atom interferometer for gravity measurement. Front. Phys. China 2009, 4, 174–178. [Google Scholar] [CrossRef]
- Zhou, M.; Luo, Q.; Chen, L.; Duan, X.; Hu, Z. Observing the effect of wave-front aberrations in an atom interferometer by modulating the diameter of Raman beams. Phys. Rev. A 2016, 93, 043610. [Google Scholar] [CrossRef]
- Trimeche, A.; Langlois, M.; Merlet, S.; Pereira Dos Santos, F. Active Control of Laser Wavefronts in Atom Interferometers. Phys. Rev. Appl. 2017, 7, 034016. [Google Scholar] [CrossRef]
- Karcher, R.; Imanaliev, A.; Merlet, S.; Santos, F.P.D. Improving the accuracy of atom interferometers with ultracold sources. New J. Phys. 2018, 20, 113041. [Google Scholar] [CrossRef]
- Chamakhi, R.; Ahlers, H.; Telmini, M.; Schubert, C.; Rasel, E.M.; Gaaloul, N. Species-selective lattice launch for precision atom interferometry. New J. Phys. 2015, 17, 123002. [Google Scholar] [CrossRef]
- Hu, Q.Q.; Freier, C.; Leykauf, B.; Schkolnik, V.; Yang, J.; Krutzik, M.; Peters, A. Mapping the absolute magnetic field and evaluating the quadratic Zeeman-effect-induced systematic error in an atom interferometer gravimeter. Phys. Rev. A 2017, 96, 033414. [Google Scholar] [CrossRef]
- Wodey, E.; Tell, D.; Rasel, E.M.; Schlippert, D.; Baur, R.; Kissling, U.; Kölliker, B.; Lorenz, M.; Marrer, M.; Schläpfer, U.; et al. A scalable high-performance magnetic shield for very long baseline atom interferometry. Rev. Sci. Instrum. 2020, 91, 035117. [Google Scholar] [CrossRef]
- Ji, Y.H.; Zhou, L.; Yan, S.T.; He, C.; Zhou, C.; Barthwal, S.; Yang, F.; Duan, W.T.; Zhang, W.D.; Xu, R.D.; et al. An actively compensated 8 nT-level magnetic shielding system for 10-m atom interferometer. Rev. Sci. Instrum. 2021, 92, 083201. [Google Scholar] [CrossRef]
- Hobson, P.; Vovrosh, J.; Stray, B.; Packer, M.; Winch, J.; Holmes, N.; Hayati, F.; McGovern, K.; Bowtell, R.; Brookes, M.; et al. Bespoke magnetic field design for a magnetically shielded cold atom interferometer. Sci. Rep. 2022, 12, 10520. [Google Scholar] [CrossRef] [PubMed]
- Jannin, R.; Cladé, P.; Guellati-Khélifa, S. Phase shift due to atom-atom interactions in a light-pulse atom interferometer. Phys. Rev. A 2015, 92, 013616. [Google Scholar] [CrossRef]
- Horikoshi, M.; Nakagawa, K. Dephasing due to atom-atom interaction in a waveguide interferometer using a Bose-Einstein condensate. Phys. Rev. A 2006, 74, 031602. [Google Scholar] [CrossRef]
- Yao, Z.; Solaro, C.; Carrez, C.; Cladé, P.; Guellati-Khelifa, S. Local phase shift due to interactions in an atom interferometer. Phys. Rev. A 2022, 106, 043312. [Google Scholar] [CrossRef]
- Burchianti, A.; D’Errico, C.; Marconi, L.; Minardi, F.; Fort, C.; Modugno, M. Effect of interactions in the interference pattern of Bose-Einstein condensates. Phys. Rev. A 2020, 102, 043314. [Google Scholar] [CrossRef]
- Zhang, H.; Mao, D.K.; Luo, Q.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. The self-attraction effect in an atom gravity gradiometer. Metrologia 2020, 57, 045011. [Google Scholar] [CrossRef]
- D’Agostino, G.; Merlet, S.; Landragin, A.; Santos, F.P.D. Perturbations of the local gravity field due to mass distribution on precise measuring instruments: A numerical method applied to a cold atom gravimeter. Metrologia 2011, 48, 299. [Google Scholar] [CrossRef]
- Hensley, J.M.; Peters, A.; Chu, S. Active low frequency vertical vibration isolation. Rev. Sci. Instrum. 1999, 70, 2735–2741. [Google Scholar] [CrossRef]
- Tang, B.; Zhou, L.; Xiong, Z.; Wang, J.; Zhan, M. A programmable broadband low frequency active vibration isolation system for atom interferometry. Rev. Sci. Instrum. 2014, 85, 093109. [Google Scholar] [CrossRef]
- Zhou, M.K.; Xiong, X.; Chen, L.L.; Cui, J.F.; Duan, X.C.; Hu, Z.K. Note: A three-dimension active vibration isolator for precision atom gravimeters. Rev. Sci. Instrum. 2015, 86, 046108. [Google Scholar] [CrossRef]
- Bonnin, A.; Zahzam, N.; Bidel, Y.; Bresson, A. Characterization of a simultaneous dual-species atom interferometer for a quantum test of the weak equivalence principle. Phys. Rev. A 2015, 92, 023626. [Google Scholar] [CrossRef]
- Lévèque, T.; Gauguet, A.; Michaud, F.; Pereira Dos Santos, F.; Landragin, A. Enhancing the Area of a Raman Atom Interferometer Using a Versatile Double-Diffraction Technique. Phys. Rev. Lett. 2009, 103, 080405. [Google Scholar] [CrossRef] [PubMed]
- Malossi, N.; Bodart, Q.; Merlet, S.; Lévèque, T.; Landragin, A.; Santos, F.P.D. Double diffraction in an atomic gravimeter. Phys. Rev. A 2010, 81, 013617. [Google Scholar] [CrossRef]
- Deng, X.B.; Duan, X.C.; Mao, D.K.; Zhou, M.K.; Shao, C.G.; Hu, Z.K. Common-mode noise rejection using fringe-locking method in WEP test by simultaneous dual-species atom interferometers. Chin. Phys. B 2017, 26, 043702. [Google Scholar] [CrossRef]
- Abend, S.; Allard, B.; Arnold, A.S.; Ban, T.; Barry, L.; Battelier, B.; Bawamia, A.; Beaufils, Q.; Bernon, S.; Bertoldi, A.; et al. Technology roadmap for cold-atoms based quantum inertial sensor in space. AVS Quantum Sci. 2023, 5, 019201. [Google Scholar] [CrossRef]
- Schuldt, T.; Schubert, C.; Krutzik, M.; Bote, L.G.; Gaaloul, N.; Hartwig, J.; Ahlers, H.; Herr, W.; Posso-Trujillo, K.; Rudolph, J.; et al. Design of a dual species atom interferometer for space. Exp. Astron. 2015, 39, 167–206. [Google Scholar] [CrossRef]
- Hinton, A.; Perea-Ortiz, M.; Winch, J.; Briggs, J.; Freer, S.; Moustoukas, D.; Powell-Gill, S.; Squire, C.; Lamb, A.; Rammeloo, C.; et al. A portable magneto-optical trap with prospects for atom interferometry in civil engineering. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160238. [Google Scholar] [CrossRef]
- Lee, J.; Ding, R.; Christensen, J.; Rosenthal, R.R.; Ison, A.; Gillund, D.P.; Bossert, D.; Fuerschbach, K.H.; Kindel, W.; Finnegan, P.S.; et al. A compact cold-atom interferometer with a high data-rate grating magneto-optical trap and a photonic-integrated-circuit-compatible laser system. Nat. Commun. 2022, 13, 5131. [Google Scholar] [CrossRef]
- Fang, J.; Hu, J.; Chen, X.; Zhu, H.; Zhou, L.; Zhong, J.; Wang, J.; Zhan, M. Realization of a compact one-seed laser system for atom interferometer-based gravimeters. Opt. Express 2018, 26, 1586–1596. [Google Scholar] [CrossRef]
- Mazon, M.J.; Iyanu, G.H.; Wang, H. A Portable, Compact Cold Atom Physics Package for Atom Interferometry. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Kovachy, T.; Asenbaum, P.; Overstreet, C.; Donnelly, C.A.; Dickerson, S.M.; Sugarbaker, A.; Hogan, J.M.; Kasevich, M.A. Quantum superposition at the half-metre scale. Nature 2015, 528, 530–533. [Google Scholar] [CrossRef]
- He, C.; Yan, S.; Zhou, L.; Barthwal, S.; Xu, R.; Zhou, C.; Ji, Y.; Wang, Q.; Hou, Z.; Wang, J.; et al. All acousto-optic modulator laser system for a 12 m fountain-type dual-species atom interferometer. Appl. Opt. 2021, 60, 5258–5265. [Google Scholar] [CrossRef] [PubMed]
- Zhan, M.S.; Wang, J.; Ni, W.T.; Gao, D.F.; Wang, G.; He, L.X.; Li, R.B.; Zhou, L.; Chen, X.; Zhong, J.Q.; et al. ZAIGA: Zhaoshan long-baseline atom interferometer gravitation antenna. Int. J. Mod. Phys. D 2020, 29, 1940005. [Google Scholar] [CrossRef]
- Müntinga, H.; Ahlers, H.; Krutzik, M.; Wenzlawski, A.; Arnold, S.; Becker, D.; Bongs, K.; Dittus, H.; Duncker, H.; Gaaloul, N.; et al. Interferometry with Bose-Einstein Condensates in Microgravity. Phys. Rev. Lett. 2013, 110, 093602. [Google Scholar] [CrossRef] [PubMed]
- Battelier, B.; Berge, J.; Bertoldi, A.; Blanchet, L.; Bongs, K.; Bouyer, P.; Braxmaier, C.; Calonico, D.; Fayet, P.; Gaaloul, N.; et al. Exploring the foundations of the physical universe with space tests of the equivalence principle. Exp. Astron. 2021, 51, 1695–1736. [Google Scholar] [CrossRef]
- Koenemann, T.; Brinkmann, W.; Goeklue, E.; Laemmerzahl, C.; Dittus, H.; Van Zoest, T.; Rasel, E.M.; Ertmer, W.; Lewoczko-Adamczyk, W.; Schiemangk, M.; et al. A freely falling magneto-optical trap drop tower experiment. Appl. Phys. B 2007, 89, 431–438. [Google Scholar] [CrossRef]
- Stern, G.; Battelier, B.; Geiger, R.; Varoquaux, G.; Villing, A.; Moron, F.; Carraz, O.; Zahzam, N.; Bidel, Y.; Chaibi, W.; et al. Light-pulse atom interferometry in microgravity. Eur. Phys. J. D 2009, 53, 353–357. [Google Scholar] [CrossRef]
- Elsen, M.; Piest, B.; Adam, F.; Anton, O.; Arciszewski, P.; Bartosch, W.; Becker, D.; Böhm, J.; Boles, S.; Döringshoff, K.; et al. A dual-species atom interferometer payload for operation on sounding rockets. arXiv 2023, arXiv:2305.08634. [Google Scholar] [CrossRef]
- Aguilera, D.N.; Ahlers, H.; Battelier, B.; Bawamia, A.; Bertoldi, A.; Bondarescu, R.; Bongs, K.; Bouyer, P.; Braxmaier, C.; Cacciapuoti, L.; et al. STE-QUEST—test of the universality of free fall using cold atom interferometry. Class. Quantum Gravity 2014, 31, 115010. [Google Scholar] [CrossRef]
- Tino, G.M.; Bassi, A.; Bianco, G.; Bongs, K.; Bouyer, P.; Cacciapuoti, L.; Capozziello, S.; Chen, X.; Chiofalo, M.L.; Derevianko, A.; et al. SAGE: A proposal for a space atomic gravity explorer. Eur. Phys. J. D 2019, 73, 228. [Google Scholar] [CrossRef]
- van Zoest, T.; Gaaloul, N.; Singh, Y.; Ahlers, H.; Herr, W.; Seidel, S.T.; Ertmer, W.; Rasel, E.; Eckart, M.; Kajari, E.; et al. Bose-Einstein Condensation in Microgravity. Science 2010, 328, 1540–1543. [Google Scholar] [CrossRef]
- Aveline, D.C.; Williams, J.R.; Elliott, E.R.; Dutenhoffer, C.; Kellogg, J.R.; Kohel, J.M.; Lay, N.E.; Oudrhiri, K.; Shotwell, R.F.; Yu, N.; et al. Observation of Bose-Einstein condensates in an Earth-orbiting research lab. Nature 2020, 582, 193–197. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Chen, X.; Fang, J.; Chen, Q.; Sun, H.; Wang, Y.; Zhong, J.; Zhou, L.; He, C.; Li, J.; et al. The space cold atom interferometer for testing the equivalence principle in the China Space Station. NPJ Microgravity 2023, 9, 58. [Google Scholar] [CrossRef] [PubMed]
- Belenchia, A.; Carlesso, M.; Bayraktar, Ö.; Dequal, D.; Derkach, I.; Gasbarri, G.; Herr, W.; Li, Y.L.; Rademacher, M.; Sidhu, J.; et al. Quantum physics in space. Phys. Rep. 2022, 951, 1–70. [Google Scholar] [CrossRef]
- Chiow, S.W.; Kovachy, T.; Chien, H.C.; Kasevich, M.A. 102ℏk Large Area Atom Interferometers. Phys. Rev. Lett. 2011, 107, 130403. [Google Scholar] [CrossRef]
- Plotkin-Swing, B.; Gochnauer, D.; McAlpine, K.E.; Cooper, E.S.; Jamison, A.O.; Gupta, S. Three-Path Atom Interferometry with Large Momentum Separation. Phys. Rev. Lett. 2018, 121, 133201. [Google Scholar] [CrossRef]
- Hensel, T.; Loriani, S.; Schubert, C.; Fitzek, F.; Abend, S.; Ahlers, H.; Siemss, J.N.; Hammerer, K.; Rasel, E.M.; Gaaloul, N. Inertial sensing with quantum gases: A comparative performance study of condensed versus thermal sources for atom interferometry. Eur. Phys. J. D 2021, 75, 108. [Google Scholar] [CrossRef]
- Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Anders, F.; Idel, A.; Feldmann, P.; Bondarenko, D.; Loriani, S.; Lange, K.; Peise, J.; Gersemann, M.; Meyer-Hoppe, B.; Abend, S.; et al. Momentum Entanglement for Atom Interferometry. Phys. Rev. Lett. 2021, 127, 140402. [Google Scholar] [CrossRef]
- Overstreet, C.; Asenbaum, P.; Curti, J.; Kim, M.; Kasevich, M.A. Observation of a gravitational Aharonov-Bohm effect. Science 2022, 375, 226–229. [Google Scholar] [CrossRef]
- Nobili, A.M. Fundamental limitations to high-precision tests of the universality of free fall by dropping atoms. Phys. Rev. A 2016, 93, 023617. [Google Scholar] [CrossRef]
- Hohensee, M.A.; Müller, H.; Wiringa, R.B. Equivalence Principle and Bound Kinetic Energy. Phys. Rev. Lett. 2013, 111, 151102. [Google Scholar] [CrossRef] [PubMed]
- Shaniv, R.; Ozeri, R.; Safronova, M.S.; Porsev, S.G.; Dzuba, V.A.; Flambaum, V.V.; Häffner, H. New Methods for Testing Lorentz Invariance with Atomic Systems. Phys. Rev. Lett. 2018, 120, 103202. [Google Scholar] [CrossRef] [PubMed]
- Fortier, T.M.; Ashby, N.; Bergquist, J.C.; Delaney, M.J.; Diddams, S.A.; Heavner, T.P.; Hollberg, L.; Itano, W.M.; Jefferts, S.R.; Kim, K.; et al. Precision Atomic Spectroscopy for Improved Limits on Variation of the Fine Structure Constant and Local Position Invariance. Phys. Rev. Lett. 2007, 98, 070801. [Google Scholar] [CrossRef] [PubMed]
- Bauch, A.; Weyers, S. New experimental limit on the validity of local position invariance. Phys. Rev. D 2002, 65, 081101. [Google Scholar] [CrossRef]
- Zhou, Z. Quantum Test of the Local Position Invariance with Internal Clock Interferometry. arXiv 2023, arXiv:2301.11258. [Google Scholar]
- Guéna, J.; Abgrall, M.; Rovera, D.; Rosenbusch, P.; Tobar, M.E.; Laurent, P.; Clairon, A.; Bize, S. Improved Tests of Local Position Invariance Using 87Rb and 133Cs Fountains. Phys. Rev. Lett. 2012, 109, 080801. [Google Scholar] [CrossRef]
- Lange, R.; Huntemann, N.; Rahm, J.M.; Sanner, C.; Shao, H.; Lipphardt, B.; Tamm, C.; Weyers, S.; Peik, E. Improved Limits for Violations of Local Position Invariance from Atomic Clock Comparisons. Phys. Rev. Lett. 2021, 126, 011102. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, L.L.; Shu, Y.B.; Xu, W.J.; Cheng, Y.; Luo, Q.; Hu, Z.K.; Zhou, M.K. Ultrahigh-Sensitivity Bragg Atom Gravimeter and its Application in Testing Lorentz Violation. Phys. Rev. Appl. 2023, 20, 014067. [Google Scholar] [CrossRef]


| Properties of the Test Bodies | Year | Accuracy () | Group & Reference | |
|---|---|---|---|---|
| Dual-species | 2014 | LUH [112] | ||
| 2015 | per shot | LP2N [113] | ||
| 2016 | @ | LP2N [114] | ||
| 2020 | LUH [115] | |||
| 2022 | LP2N [116] | |||
| Dual-isotopes | 2004 | MPIQ [100] | ||
| 2013 | ONERA [117] | |||
| 2014 | LENS [118] | |||
| 2015 | WIPM [82] | |||
| 2018 | per shot | Stanford [119] | ||
| 2020 | Stanford [120] | |||
| 2021 | WIPM [121] | |||
| Dual-states | 2004 | MPIQ [100] | ||
| 2016 | HUST [122] | |||
| 2017 | LENS [123] | |||
| 2020 | HUST [124] | |||
| 2022 | HUST [125] | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Wu, J.; Yang, S.-J. Current Status and Prospects on High-Precision Quantum Tests of the Weak Equivalence Principle with Cold Atom Interferometry. Symmetry 2023, 15, 1769. https://doi.org/10.3390/sym15091769
Yuan L, Wu J, Yang S-J. Current Status and Prospects on High-Precision Quantum Tests of the Weak Equivalence Principle with Cold Atom Interferometry. Symmetry. 2023; 15(9):1769. https://doi.org/10.3390/sym15091769
Chicago/Turabian StyleYuan, Liang, Jizhou Wu, and Sheng-Jun Yang. 2023. "Current Status and Prospects on High-Precision Quantum Tests of the Weak Equivalence Principle with Cold Atom Interferometry" Symmetry 15, no. 9: 1769. https://doi.org/10.3390/sym15091769
APA StyleYuan, L., Wu, J., & Yang, S.-J. (2023). Current Status and Prospects on High-Precision Quantum Tests of the Weak Equivalence Principle with Cold Atom Interferometry. Symmetry, 15(9), 1769. https://doi.org/10.3390/sym15091769






