Shape Preserving Properties of Parametric Szász Type Operators on Unbounded Intervals

Abstract

The B$\acute{e}$zier-type operator has become a powerful tool in operator theory, neural networks, curve and surface design and representation because of its good shape-preserving properties. Motivated by the improvements of the operator in computational disciplines, we investigate some elementary properties of two kinds of modified Sz$\acute{a}$sz type basis functions, depending on non-negative parameters. Using the derivative, the symmetry of variables, the modulus of continuity and the concave continuous modulus, we study some shape preserving properties of these operators concerning monotonicity, convexity, starshapedness, semi-additivity and the preservation of smoothness. Moreover, some illustrative examples are provided to demonstrate the approximation behavior of the proposed operators and the classical ones.

1. Introduction

As parametric operators, B$\acute{e}$zier operators are described by the Bernstein’s basis polynomials and are the elements of a computer-aided geometric design (CAGD) [1,2,3,4,5,6]. The basis functions of these type of operators have many good properties suitable for modeling, such as shape-preserving properties, convex hull constraints, symmetry, etc. There has been a lot of research on parametric operators [7,8,9,10,11]. Due to their controllable shape parameters, these operators have potential applications in fields such as computer graphics, engineering problems and industrial applications. In recent years, the shape-preserving properties of various operators have been deeply studied [12,13,14,15,16,17,18,19,20,21,22,23].

From this point of view, studying the shape preserving properties of operators is a very important part of the function approximation theory. In order to be more effectively applied to CAGD on infinite intervals, some kinds of Sz$\acute{a}$sz operators based on non-negative parameters were introduced [7,8,9,10,11,24,25,26]. In 1998, Carbone et al. obtained the shape preserving properties of the Sz$\acute{a}$sz operators by probabilistic methods [16,17,18]. In 2005, Zhang Chungou [23] studied the shape preserving properties of the classical Sz$\acute{a}$sz-Kantorovich operators. In 2022, Huang Jieyu and Qi Qiulan [26] constructed Sz$\acute{a}$sz-type operators that hold the functions of $f\left(x\right)=1$ and $f\left(x\right)=e^{-\mu x}(\mu >0)$ and studied their uniform approximation and statistical approximation properties. Through reading the above references, we have found that most of them only study the monotonicity and convexity preservation of classical operators. However, research on shape preserving properties of semi-additivity, starshapedness and smoothness is not in-depth enough. Few people have used analytical methods to study the shape preserving properties of Sz$\acute{a}$sz operators in semi-additivity, starshapedness and smoothness, etc. Motivated by the work of Huang Jieyu et al. [26], in this paper, we conduct more in-depth research on the Sz$\acute{a}$sz type operators which preserve the functions $e^{-\mu x},e^{2\mu x}(\mu >0)$ with the help of the method of analysis. First of all, we discuss some important properties of the basis functions and the corresponding operators, such as the endpoint properties, the maximum value of the basis functions, the endpoint interpolation, the linearity of the operators and so on. We also show the change tendency of the basis functions with the change of the shape parameters. The methods of proving shape preserving properties, such as starshapedness, semi-addivability and smoothness are relatively novel. We apply the derivative and the symmetry of variables to obtain these conclusions. The preservation of smoothness is proved by combining the relationship between the ordinary modulus and concave modulus.

The aim of this paper is to show some shape-preserving properties of these parametric Sz$\acute{a}$sz type operators. The complete structure of the manuscript constitutes six sections. The rest of this paper is constructed as follows. In Section 2, the fundamental facts are summarized for use in the sequel. In Section 3, we shall prove that the operators preserve monotonicity, convexity, starshapedness and semi-additivity. In Section 4, we investigate the preservation of smoothness. In Section 5, we will demonstrate some numerical experiments which verify the validity of the theoretical results and the potential superiority of these new operators. Finally, in Section 6, some conclusions are provided.

2. Fundamental Properties of the Basis Functions and the Operators

In this section, some basic facts that will be used in the following sections are given.

Let $C[0,\infty )$ denote the space of continuous functions on $[0,\infty )$, and $C_B[0,\infty )$ be the space of bounded functions in the space of $C[0,\infty )$ endowed with the norm: $\parallel f\parallel ={sup}_{x\in [0,\infty )}\left|f\left(x\right)\right|$. Let $A_i(i=0,1,2,3)$ denote the subclasses of $C[0,\infty ):$

$$A_0:=\{f\in C[0,\infty ):f\left(0\right)=0\};$$

$$A_1:=\{f\in A_0:f\left(x\right)\mathrm{is}\mathrm{a}\mathrm{convex}\mathrm{on}[0,\infty )\};$$

$$A_2:=\{f\in A_0:x^{-1}f\left(x\right)\mathrm{is}\mathrm{increasing}\mathrm{on}(0,\infty )\};$$

$$A_3:=\{f\in A_0:f\left(x\right)\mathrm{is}\mathrm{the}\mathrm{super}-\mathrm{additive}\mathrm{on}[0,\infty )\},$$

where $f\left(x\right)$ is said to be the super-additive on $[0,\infty )$, if for any $x_1,x_2\in [0,\infty )$, $f(x_1+x_2)\ge f\left(x_1\right)+f\left(x_2\right)$. In addition, by ([20] Theorem 5), we find that $A_1\subset A_2\subset A_3$.

On the other hand, $A_i^{*}(i=1,2,3)$stand for the other three subsets:

$$A_1^{*}:=\{f\in A_0:f\left(x\right)\mathrm{is}\mathrm{the}\mathrm{concave}\mathrm{on}[0,\infty )\};$$

$$A_2^{*}:=\{f\in A_0:x^{-1}f\left(x\right)\mathrm{is}\mathrm{decreasing}\mathrm{on}(0,\infty )\};$$

$$A_3^{*}:=\{f\in A_0:f\left(x\right)\mathrm{is}\mathrm{semi}-\mathrm{additive}\mathrm{on}[0,\infty )\},$$

where $f\left(x\right)$ is said to be the semi-additive on $[0,\infty )$, if for any $x_1,x_2\in [0,\infty )$, $f(x_1+x_2)\le f\left(x_1\right)+f\left(x_2\right)$.

Remark 1.

If $f\in A_2\left(or{A}_2^{*}\right)$, we say that $f\left(x\right)$ is a star-shapedness function with respect to the origin.

The parametric Sz$\acute{a}$sz type operators are defined by [7,26]:

$$S_n^{\mu }(f;x)=\sum _{k=0}^{\infty }f\left(\frac{k}{n}\right)s_{n,k}\left(x\right)$$

where

$$s_{n,k}\left(x\right)=e^{-n\alpha \left(x\right)}\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!}.$$

(1)

For $\alpha \left(x\right)={\alpha }_1\left(x\right)=\frac{\mu x}{n(1-e^{-\frac{\mu }{n}})}$, the operators $S_n^{\mu }(f;x)$ preserve $f\left(x\right)=1$ and $f\left(x\right)=e^{-\mu x}(\mu >0)$;

(2)

For $\alpha \left(x\right)={\alpha }_2\left(x\right)=\frac{2\mu x}{n(e^{\frac{2\mu }{n}}-1)}$, the operators $S_n^{\mu }(f;x)$ preserve $f\left(x\right)=1$ and $f\left(x\right)=e^{2\mu x}(\mu >0)$.

Remark 2

([7] Lemma 3; [26] Remark 1). $\underset{n\to \infty }{lim}\alpha \left(x\right)=x.$

Remark 3

([7] Lemma 2; [26] Lemma 2.1, Lemma 2.2). For $x\in [0,\infty ),\mu >0,S_n^{\mu }(1;x)=1,S_n^{\mu }(t;x)=\alpha \left(x\right).$

Remark 4

([7] Theorem 3; [26] Theorem 3.1). For $f\left(x\right)\in C^{*}[0,\infty ):=\{f\in C[0,\infty ):\underset{n\to \infty }{lim}f\left(x\right)$ exists and is finite}, one has the sequence $\left\{S_n^{\mu }(f;x)\right\}$ and converges to $f\left(x\right)$ uniformly.

For $\mu >0$, the new basis functions $s_{n,k}\left(x\right)$ are defined by

$$s_{n,k}\left(x\right)=e^{-n\alpha \left(x\right)}\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!},k=0,1,\cdots .$$

Figure 1 shows the Sz$\acute{a}$sz type basis functions with $\alpha \left(x\right)={\alpha }_1\left(x\right)$ of degree three, and Figure 2 shows the Sz$\acute{a}$sz type basis functions with $\alpha \left(x\right)={\alpha }_2\left(x\right)$ of degree three. We can observe the variation of the basis functions with parameters $\mu$.

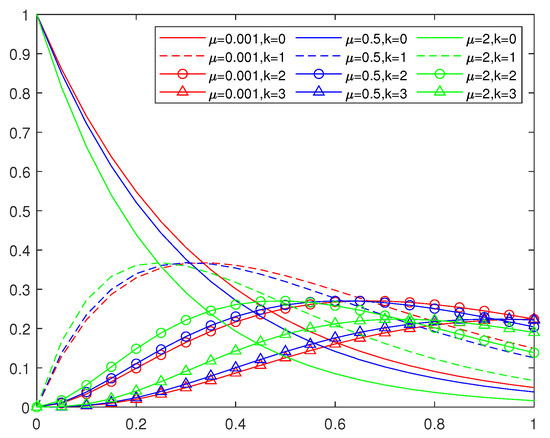
Figure 1. The cubic Sz$\acute{a}$sz basis functions with $\alpha \left(x\right)={\alpha }_1\left(x\right)$,$k=0,1,2,3$.

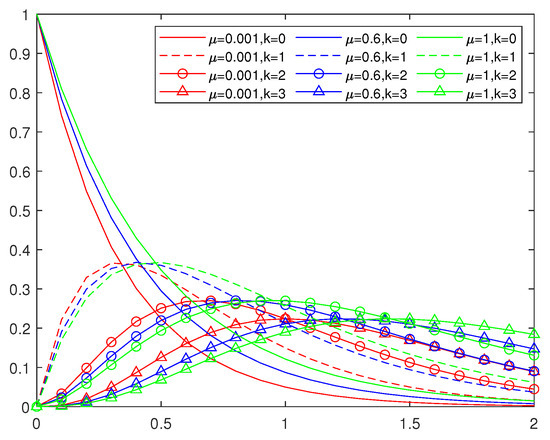
Figure 2. The cubic Sz$\acute{a}$sz basis functions with $\alpha \left(x\right)={\alpha }_2\left(x\right)$,$k=0,1,2,3$.

The new basis functions $s_{n,k}\left(x\right)$ hold the following properties:

Lemma 1.

$\left(1\right).$ Non-negativity: For $x\in [0,\infty ),\mu >0,s_{n,k}\left(x\right)\ge 0.$

$\left(2\right).$ Partition of unity: ${\displaystyle \sum _{k=0}^{\infty }}{s}_{n,k}\left(x\right)=1.$

$\left(3\right).$ Properties at the endpoint:

$$s_{n,k}\left(0\right)=\left\{\begin{array}{ccc}\hfill 1,& & k=0;\hfill \\ \hfill 0,& & k\ne 0.\hfill \end{array}\right.$$

$\left(4\right).$ Integrals:

$${\int }_0^{\infty }{s}_{n,k}\left(x\right)dx=\left\{\begin{array}{ccc}\hfill \frac{1-e^{-\frac{\mu }{n}}}{\mu },& & \alpha \left(x\right)={\alpha }_1\left(x\right);\hfill \\ \hfill \frac{e^{\frac{2\mu }{n}}-1}{2\mu },& & \alpha \left(x\right)={\alpha }_2\left(x\right).\hfill \end{array}\right.$$

$\left(5\right).$ Derivative: $s_{n,k}^{{}^{\prime }}\left(x\right)=\frac{n\alpha \left(x\right)}{x}[s_{n,k-1}\left(x\right)-s_{n,k}\left(x\right)],x\in (0,\infty ).$

$\left(6\right).$ Maximum value: $s_{n,k}\left(x\right)$ has only one local maximum at $x=\frac{k(1-e^{-\frac{\mu }{n}})}{\mu }$ and $\frac{k(e^{\frac{2\mu }{n}}-1)}{2\mu }$ for ${\alpha }_1\left(x\right)$ and ${\alpha }_2\left(x\right)$, respectively.

For the operators $S_n^{\mu }(f;x)$, we can deduce the following geometric properties from those of the Sz$\acute{a}$sz basis functions.

Lemma 2.

$\left(1\right).$ Normativity and boundedness: $S_n^{\mu }(1;x)=1.$

$\left(2\right).$ Endpoint interpolation: $S_n^{\mu }(f;0)=f\left(0\right).$

$\left(3\right).$ Linearity: For all real numbers ${\lambda }_1$, ${\lambda }_2$ and functions $f\left(x\right)$, $g\left(x\right)$, one has

$$S_n^{\mu }({\lambda }_{1}f+{\lambda }_{2}g;x)={\lambda }_1{S}_n^{\mu }(f;x)+{\lambda }_2{S}_n^{\mu }(g;x).$$

3. Shape Preservation

First, let us consider the monotonicity and convexity for the operators $S_n^{\mu }(f;x).$

Theorem 1

(Monotonicity). Let $f\in C[0,\infty )$; if $f\left(x\right)$ is monotonically increasing (or decreasing) on $[0,\infty )$, for $n\in N,$ so are all the operators $S_n^{\mu }(f;x).$

Proof. 

We write

$$\frac{d}{dx}{S}_n^{\mu }(f;x)=\frac{n\alpha \left(x\right)}{x}{e}^{-n\alpha \left(x\right)}\sum _{k=0}^{\infty }\left[f\left(\frac{k+1}{n}\right)-f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!}.$$

(1)

Noting that if $f\left(x\right)$ is monotonically increasing, then the derivative of the operators $S_n^{\mu }(f;x)$ is non-negative on $[0,\infty )$, and so $S_n^{\mu }(f;x)$ is monotonically increasing.

Similarly, we see that if $f\left(x\right)$ is monotonically decreasing on $[0,\infty )$, so are the operators $S_n^{\mu }(f;x)$. □

Theorem 2

(Convexity). Let $f\left(x\right)\in C[0,\infty )$; if $f\left(x\right)$ is convex (or concave), so are all the operators $S_n^{\mu }(f;x)$.

Proof. 

Now let us take the second order derivative of $S_n^{\mu }(f;x)$. It follows from (1) that

$$\frac{d^2}{d{x}^2}{S}_n^{\mu }(f;x)={\left(\frac{n\alpha \left(x\right)}{x}\right)}^2{e}^{-n\alpha \left(x\right)}\sum _{k=0}^{\infty }\left[f\left(\frac{k+2}{n}\right)-2f\left(\frac{k+1}{n}\right)+f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!}.$$

(2)

If $f\left(x\right)$ is the convex on $[0,\infty )$, all second order derivatives of $S_n^{\mu }(f;x)$ in (2) are non-negative, which implies the convexity of $S_n^{\mu }(f;x)$.

Similarly, we see that if $f\left(x\right)$ is the concave on $[0,\infty )$, so are the operators $S_n^{\mu }(f;x)$. □

Next, we turn to the starshapedness and semi-additivity.

Theorem 3

(starshapedness). If $f\left(x\right)\in A_2^{*}$ (or $A_2$), then for $n\in N$, $S_n^{\mu }(f;x)\in A_2^{*}$ (or $A_2$).

Proof. 

We shall use the representation

$$\begin{array}{ccc}\hfill \frac{d}{dx}\left(x^{-1}{S}_n^{\mu }(f;x)\right)& =& -x^{-2}{S}_n^{\mu }(f;x)+x^{-1}\frac{d}{dx}{S}_n^{\mu }(f;x)\hfill \\ & =& -x^{-2}{S}_n^{\mu }(f;x)+x^{-2}\alpha \left(x\right)e^{-n\alpha \left(x\right)}\sum _{k=0}^{\infty }n\left[f\left(\frac{k+1}{n}\right)-f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!},\hfill \end{array}$$

noting that

$$\begin{array}{ccc}& \sum _{k=0}^{\infty }& n\left[f\left(\frac{k+1}{n}\right)-f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!}\hfill \\ & =& \left[nf\left(\frac{1}{n}\right)-nf\left(\frac{0}{n}\right)\right]+\left[nf\left(\frac{2}{n}\right)-nf\left(\frac{1}{n}\right)\right]n\alpha \left(x\right)+\left[nf\left(\frac{3}{n}\right)-nf\left(\frac{2}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^2}{2!}+\cdots \hfill \\ & =& nf\left(\frac{1}{n}\right)+\left[\frac{n}{2}f\left(\frac{2}{n}\right)-nf\left(\frac{1}{n}\right)\right]n\alpha \left(x\right)+\frac{n}{2}f\left(\frac{2}{n}\right)n\alpha \left(x\right)\hfill \\ & +& 2\left[\frac{n}{3}f\left(\frac{3}{n}\right)-\frac{n}{2}f\left(\frac{2}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^2}{2!}+\frac{n}{3}f\left(\frac{3}{n}\right)\frac{{\left(n\alpha \left(x\right)\right)}^2}{2!}+\cdots ,\hfill \end{array}$$

let

$$I=x^{-2}\alpha \left(x\right)e^{-n\alpha \left(x\right)}k\sum _{k=1}^{\infty }\left[\frac{n}{k+1}f\left(\frac{k+1}{n}\right)-\frac{n}{k}f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!},$$

which yields,

$$\begin{array}{ccc}\hfill \frac{d}{dx}\left(x^{-1}{S}_n^{\mu }(f;x)\right)& =& -x^{-2}{S}_n^{\mu }(f;x)+x^{-2}\alpha \left(x\right)e^{-n\alpha \left(x\right)}\sum _{k=1}^{\infty }\frac{n}{k}f\left(\frac{k}{n}\right)\frac{{\left(n\alpha \left(x\right)\right)}^{k-1}}{(k-1)!}+I\hfill \\ & =& -x^{-2}{S}_n^{\mu }(f;x)+x^{-2}{e}^{-n\alpha \left(x\right)}\sum _{k=1}^{\infty }f\left(\frac{k}{n}\right)\frac{{\left(n{\alpha }_n\left(x\right)\right)}^k}{k!}+I\hfill \\ & =& -x^{-2}{S}_n^{\mu }(f;x)+x^{-2}{S}_n^{\mu }(f;x)-x^{-2}{e}^{-n\alpha \left(x\right)}f\left(\frac{0}{n}\right)+I\hfill \\ & =& x^{-2}\alpha \left(x\right)e^{-n\alpha \left(x\right)}k\sum _{k=1}^{\infty }\left[\frac{n}{k+1}f\left(\frac{k+1}{n}\right)-\frac{n}{k}f\left(\frac{k}{n}\right)\right]\frac{{\left(n\alpha \left(x\right)\right)}^k}{k!}.\hfill \end{array}$$

If $x^{-1}f\left(x\right)$ is decreasing on $(0,\infty )$, then $I\le 0$, i.e., the derivative of $x^{-1}{S}_n^{\mu }(f;x)$, is negative on $(0,\infty )$, and so $x^{-1}{S}_n^{\mu }(f;x)$ is decreasing.

Similarly, we see that if $x^{-1}f\left(x\right)$ is increasing on $(0,\infty )$, then $I\ge 0$, and so is $x^{-1}{S}_n^{\mu }(f;x)$. □

Theorem 4

(Semi-additivity). If $f\left(x\right)\in A_3^{*}$ (or $A_3$), then for $n\in N$, $S_n^{\mu }(f;x)\in A_3^{*}$ (or $A_3$).

Proof. 

We only take $\alpha \left(x\right)={\alpha }_1\left(x\right)$ as an example to prove the semi-additivity; the case $\alpha \left(x\right)={\alpha }_2\left(x\right)$ is similar. $\forall x,y\in [0,\infty )$, $\forall n\in N$,

$$\begin{array}{ccc}\hfill S_n^{\mu }(f;x+y)& =& e^{-\frac{\mu (x+y)}{1-e^{-\frac{\mu }{n}}}}\sum _{k=0}^{\infty }f\left(\frac{k}{n}\right)\frac{{\left(\frac{\mu (x+y)}{1-e^{-\frac{\mu }{n}}}\right)}^k}{k!}\hfill \\ & =& e^{-\frac{\mu (x+y)}{1-e^{-\frac{\mu }{n}}}}\sum _{k=0}^{\infty }f\left(\frac{k}{n}\right)\frac{{\left(\frac{\mu }{1-e^{-\frac{\mu }{n}}}\right)}^k}{k!}\sum _{j=0}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right)x^j{y}^{k-j}\hfill \\ & =& e^{-\frac{\mu (x+y)}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{k=j}^{\infty }f\left(\frac{k}{n}\right){\left(\frac{\mu }{1-e^{-\frac{\mu }{n}}}\right)}^k\frac{x^j{y}^{k-j}}{j!(k-j)!},\hfill \end{array}$$

let $K=k-j$, $k=K+j$, then

$$S_n^{\mu }(f;x+y)=e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}·e^{-\frac{\mu y}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{K=0}^{\infty }f\left(\frac{K+j}{n}\right)\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}·\frac{{\left(\frac{\mu y}{1-e^{-\frac{\mu }{n}}}\right)}^K}{K!}.$$

(3)

If $f\left(x\right)$ is the semi-additive on $[0,\infty )$, one has

$$\begin{array}{ccc}\hfill S_n^{\mu }(f;x+y)& \le & e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}·e^{-\frac{\mu y}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{K=0}^{\infty }f\left(\frac{K}{n}\right)\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}·\frac{{\left(\frac{\mu y}{1-e^{-\frac{\mu }{n}}}\right)}^K}{K!}\hfill \\ & & +e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}·e^{-\frac{\mu y}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{K=0}^{\infty }f\left(\frac{j}{n}\right)\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}·\frac{{\left(\frac{\mu y}{1-e^{-\frac{\mu }{n}}}\right)}^K}{K!}\hfill \\ & =& S_n^{\mu }(f;x)+S_n^{\mu }(f;y),\hfill \end{array}$$

which implies $S_n^{\mu }(f;x)$ is the semi-additive on $[0,\infty )$. Similarly, if $f\left(x\right)$ is the super-additive on $[0,\infty )$, so is $S_n^{\mu }(f;x)$, and thus, the proof is completed. □

Remark 5.

When applying binomial expansion, it does not affect the proof process due to the symmetry between x and y.

4. Preservation of Smoothness

For $t>0$, the continuous modulus is defined as [27]:

$$\omega (f;t)=sup\left\{\right|f\left(x\right)-f\left(y\right)|:|x-y|\le t,x,y\in [0,\infty \left)\right\}.$$

A function $\omega \left(t\right)$ on $[0,1]$ is called a modulus of continuity if $\omega \left(t\right)$ is continuous, nondecreasing, semi-additive and $\underset{t\to 0^{+}}{lim}\omega \left(t\right)=\omega \left(0\right)=0$ [28].

Lemma 3

([28]). For any continuous $\omega \left(t\right)$ (not identical to 0), there exists a concave continuous modulus ${\omega }^{*}\left(t\right)$ such that for $t>0$ and one has $\omega \left(t\right)\le {\omega }^{*}\left(t\right)\le 2\omega \left(t\right)$, where the constant 2 can not be any smaller.

Lemma 4.

Let $\left\{L_n(f;x)\right\}$ be a sequence of linear positive operators from $C\left(I\right)$ to $C\left(I\right)$, where I is a finite or infinite interval, and $L_n(1;x)=1$, $L_n(t;x)=C_n\left(x\right)x,0\le C_n\left(x\right)\le 1$. If $g\left(x\right)$ is a concave, monotonically increasing and continuous function on I, then $L_n(g;x)\le g\left(x\right)$.

Remark 6.

We can obtain Lemma 4 by imitating the proof of the Lemma in ref. [21]. Here, we omit the details.

Theorem 5.

For $f\left(x\right)\in C_B[0,\infty )$, $h>0,\forall n\in N$, one has $\omega (S_n^{\mu };h)\le S_n^{\mu }(\omega ;h)$.

Proof. 

As before, we only prove the case $\alpha \left(x\right)={\alpha }_1\left(x\right)$; the case $\alpha \left(x\right)={\alpha }_2\left(x\right)$ is similar. Since

$$e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}=1,$$

for $h>0$, from (3), we write

$$\begin{array}{cc}& \left|S_n^{\mu }(f;x+h)-S_n^{\mu }(f;x)\right|\hfill \\ \hfill & \le e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}·e^{-\frac{\mu h}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}·\frac{{\left(\frac{\mu h}{1-e^{-\frac{\mu }{n}}}\right)}^k}{k!}\left|f\left(\frac{k+j}{n}\right)-f\left(\frac{j}{n}\right)\right|\hfill \\ \hfill & \le e^{-\frac{\mu x}{1-e^{-\frac{\mu }{n}}}}·e^{-\frac{\mu h}{1-e^{-\frac{\mu }{n}}}}\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }\frac{{\left(\frac{\mu x}{1-e^{-\frac{\mu }{n}}}\right)}^j}{j!}·\frac{{\left(\frac{\mu h}{1-e^{-\frac{\mu }{n}}}\right)}^k}{k!}\omega (f;\frac{k}{n}),\hfill \end{array}$$

(4)

and then the desired result is obtained. □

Due to the use of Lemma 4 in Theorems 6 and 7 below, noting that $1<{\alpha }_1\left(x\right)<2$, $0<{\alpha }_2\left(x\right)<1$, the following two theorems thus only hold for the case $\alpha \left(x\right)={\alpha }_2\left(x\right)$.

Theorem 6.

(i) For $f\in H_{\omega }\left(A\right)=\{f:\omega (f;x)\le A\omega \left(x\right)\}$, then $S_n^{\mu }(f;x)\in H_{\omega }\left(2A\right),\forall n\in N;$

(ii) If $\underset{n\to \infty }{lim}{S}_n^{\mu }(f;x)=f\left(x\right)$, then $f\in H_{\omega }\left(A\right)\iff S_n^{\mu }(f;x)\in H_{\omega }\left(A\right)$; here, n is big enough.

Proof. 

(i) For the case $\alpha \left(x\right)={\alpha }_2\left(x\right)$, $\forall x_1,x_2\in I$, $x_1>x_2$, from (4), and using Lemma 3, we have

$$\begin{array}{ccc}\hfill \left|S_n^{\mu }(f;x_1)-S_n^{\mu }(f;x_2)\right|& \le & e^{-\frac{\mu (x_1-x_2)}{e^{\frac{2\mu }{n}}-1}}\sum _{j=0}^{\infty }\omega (f;\frac{j}{n})\frac{{\left(\frac{\mu (x_1-x_2)}{e^{\frac{2\mu }{n}}-1}\right)}^j}{j!}\le A{S}_n^{\mu }(\omega ;x_1-x_2)\hfill \\ & \le & A{S}_n^{\mu }({\omega }^{*};x_1-x_2)\le A{\omega }^{*}(x_1-x_2)\le 2A\omega (x_1-x_2),\hfill \end{array}$$

and here, we use Lemma 4 for ${\omega }^{*}\left(t\right)$.

(ii) If ${lim}_{n\to \infty }{S}_n^{\mu }(f;x)=f\left(x\right)$, then

$$\underset{n\to \infty }{lim}\left|S_n^{\mu }(f;x_1)-S_n^{\mu }(f;x_2)\right|=\left|f\left(x_1\right)-f\left(x_2\right)\right|.$$

We have $f\in H_{\omega }\left(A\right)\iff S_n^{\mu }(f;x)\in H_{\omega }\left(A\right)$; here, n is big enough. □

Remark 7.

If $f\in {Lip}_K^{\alpha }=\{f:\omega (f;h)\le K{h}^{\alpha },K\ge 0,\alpha \in (0,1]\}$, then $S_n^{\mu }(f;x)\in {Lip}_K^{\alpha }$, here, n is big enough.

Theorem 7.

For any modulus of continuity $\omega \left(t\right)$, $S_n^{\mu }(\omega ;t)$ is also a modulus of continuity; here, only $\alpha \left(x\right)={\alpha }_2\left(x\right)$ is considered.

Proof. 

For any modulus of continuity, $\omega \left(t\right)$, $S_n^{\mu }(\omega ;t)$ is continuous, non-decreasing and

$$\underset{t\to 0^{+}}{lim}{S}_n^{\mu }(\omega ;t)=S_n^{\mu }(\omega ;0)=\omega \left(0\right)=0.$$

Combining the semi-additivity of $\omega \left(t\right)$ and $S_n^{\mu }(\omega ;t)$, we deduce that $S_n^{\mu }(\omega ;t)$ is a modulus of continuity. □

5. Illustrative Examples

In order to more intuitively understand the approximation effect of classic Sz$\acute{a}$sz operators and several new Sz$\acute{a}$sz operators acting on functions, in this section, we will draw some graphs of different values of $\mu$ and different values of n with the help of Matlab software. Figure 3 and Figure 4 show the approximation of $\alpha \left(x\right)={\alpha }_1\left(x\right)$, i.e., the Sz$\acute{a}$sz operators of preserving $e^{-\mu x}$ to the function $e^{-\frac{x}{2}}$, where $\mu$ and n take different values; Figure 5 and Figure 6 show the approximation of $\alpha \left(x\right)={\alpha }_2\left(x\right)$, i.e., the Sz$\acute{a}$sz operators of preserving $e^{2\mu x}$ to the function $(x^3+1){10}^x$, where $\mu$ and n take different values; Figure 7 and Figure 8 show the approximation of the classic Sz$\acute{a}$sz operators, the new Sz$\acute{a}$sz operators of preserving $e^{-\mu x}$, $e^{2\mu x}$ to the functions $e^{-\frac{x}{2}}$ and $(x^3+1){10}^x$. At the same time, the root mean square errors of their approximation are calculated (See Table 1 and Table 2).

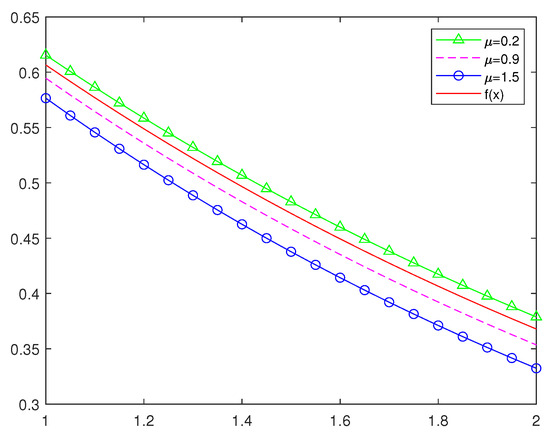
Figure 3. The approximation of the Sz$\acute{a}$sz operators of preserving $e^{-\mu x}$ to the function $e^{-\frac{x}{2}}$, where $\mu =0.2,0.9,1.5,n=5$.

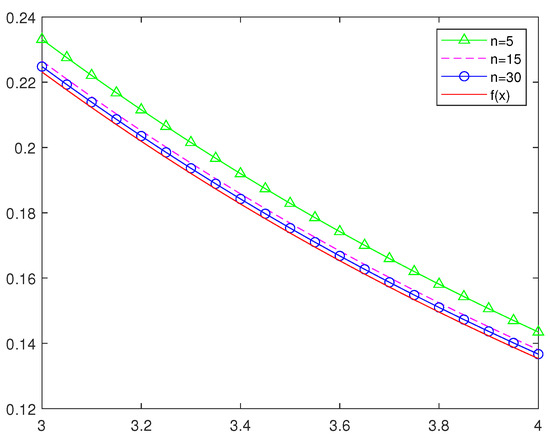
Figure 4. The approximation of the Sz$\acute{a}$sz operators of preserving $e^{-\mu x}$ to the function $e^{-\frac{x}{2}}$, where $n=5,15,30,\mu =0.2$.

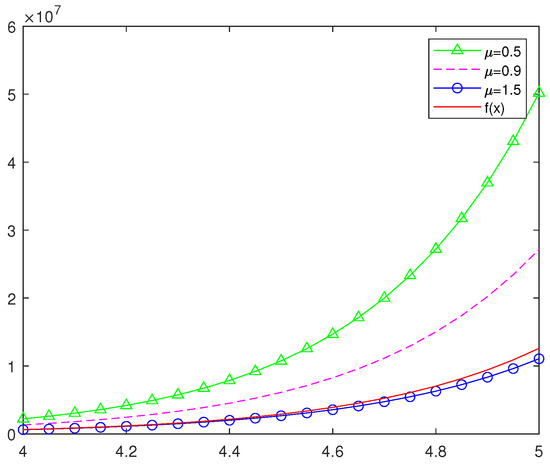
Figure 5. The approximation of the Sz$\acute{a}$sz operators of preserving $e^{2\mu x}$ to the function $(x^3+1){10}^x$, where $\mu =0.5,0.9,1.5,n=10$.

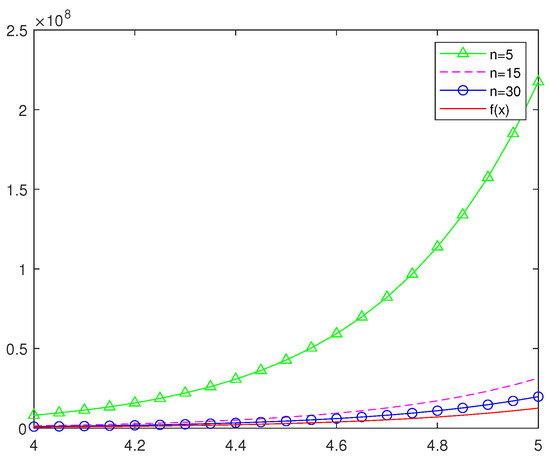
Figure 6. The approximation of the Sz$\acute{a}$sz operators of preserving $e^{2\mu x}$ to the function $(x^3+1){10}^x$, where $n=5,15,30,\mu =0.5$.

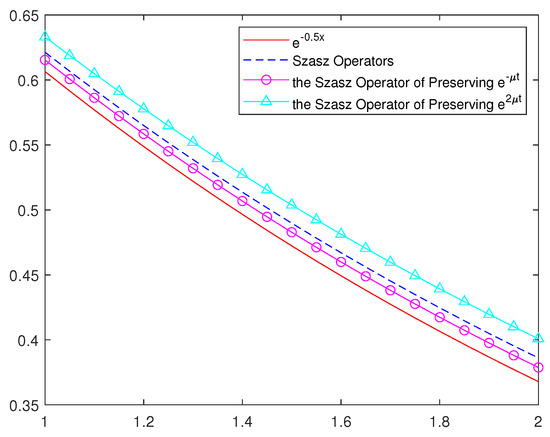
Figure 7. The approximation of the classic Sz$\acute{a}$sz operators, the Sz$\acute{a}$sz operator of preserving $e^{-\mu x}$ and the Sz$\acute{a}$sz operator of preserving $e^{2\mu x}$ to the function $e^{-\frac{x}{2}}$, where $\mu =0.2,n=5$.

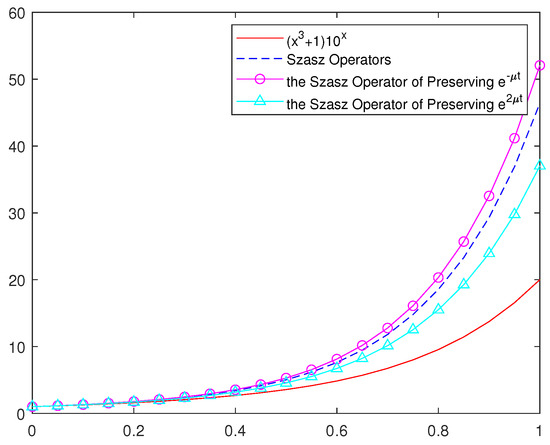
Figure 8. The approximation of the classic Sz$\acute{a}$sz operators, the Sz$\acute{a}$sz operator of preserving $e^{-\mu x}$ and the Sz$\acute{a}$sz operator of preserving $e^{2\mu x}$ to the function $(x^3+1){10}^x$, where $\mu =0.5,n=10$.

Table 1. Root mean square errors of approximation of four classes of operators to the function $e^{-\frac{x}{2}}$, $\mu =0.2$.

n	Sz$\acute{\mathit{a}}$sz Operators	the Sz$\acute{\mathit{a}}$sz Operator of Preserving ${\mathit{e}}^{-\mathit{\mu }\mathit{t}}$	the Sz$\acute{\mathit{a}}$sz Operator of Preserving ${\mathit{e}}^{2\mathit{\mu }\mathit{t}}$
5	1.7151 × 10−2	1.0282 × 10−2	3.0914 × 10−2
15	5.7728 × 10−3	3.4626 × 10−3	1.0397 × 10−2
30	2.8933 × 10−3	1.7357 × 10−3	5.2096 × 10−3

Table 2. Root mean square errors of approximation of four classes of operators to the function $(x^3+1){10}^x$, $\mu =0.5$.

n	Sz$\acute{\mathit{a}}$sz Operators	the Sz$\acute{\mathit{a}}$sz Operator of Preserving ${\mathit{e}}^{-\mathit{\mu }\mathit{t}}$	the Sz$\acute{\mathit{a}}$sz Operator of Preserving ${\mathit{e}}^{2\mathit{\mu }\mathit{t}}$
50	1.1574 × 100	1.3176 × 100	8.4766 × 10−1
150	3.6112 × 10−1	4.0779 × 10−1	2.6880 × 10−1
300	1.7765 × 10−1	2.0022 × 10−1	1.3275 × 10−1

6. Conclusions

In this paper, some fundamental facts of two kinds of parametric Sz$\acute{a}$sz type operators are presented. The shape preserving properties, such as linearity, monotonicity, convexity, starshapedness and semi-additivity are examined. Furthermore, with the help of the continuous modulus, the preservation of smoothness is discussed. Finally, illustrative examples are used to verify the validity of the theoretical results and some potential superiorities of our new operators. If we look on future work of the above-defined operators, we can see towards some converse theorems. The results are so beneficial that these can be used in other fields, such as mathematical physics, automobile industry, etc.