Delay-Aware Intelligent Asymmetrical Edge Control for Autonomous Vehicles with Dynamic Leading Velocity

Abstract

The integration of Connected Cruise Control (CCC) and wireless Vehicle-to-Vehicle (V2V) communication technology aims to improve driving safety and stability. To enhance CCC’s adaptability in complex traffic conditions, in-depth research into intelligent asymmetrical control design is crucial. In this paper, the intelligent CCC controller issue is investigated by jointly considering the dynamic network-induced delays and target vehicle speeds. In particular, a deep reinforcement learning (DRL)-based controller design method is introduced utilizing the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm. In order to generate intelligent asymmetrical control strategies, the quadratic reward function, determined by control inputs and vehicle state errors acquired through interaction with the traffic environment, is maximized by the training that involves both actor and critic networks. In order to counteract performance degradation due to dynamic platoon factors, the impact of dynamic target vehicle speeds and previous control strategies is incorporated into the definitions of Markov Decision Process (MDP), CCC problem formulation, and vehicle dynamics analysis. Simulation results show that our proposed intelligent asymmetrical control algorithm is well-suited for dynamic traffic scenarios with network-induced delays and outperforms existing methods.

1. Introduction

In recent years, the challenges of road safety and traffic congestion have grown increasingly urgent [1,2,3,4]. The Advanced Driver Assistance System (ADAS) has been widely studied as a solution to ease driving burdens and enhance road safety [5]. As an innovative ADAS technology, Connected Cruise Control (CCC) employs Vehicle-to-Vehicle (V2V) communication to develop perception ability and maintain stable traffic flow within a diverse vehicle platoon [6]. In particular, CCC has a flexible network topology and asymmetrical control ability, enabling platoon members to communicate with each other to share their motion information. Through the received information, the CCC controller empowers autonomous vehicles to achieve adaptive longitudinal control, thereby boosting safety, comfort, and fuel efficiency [7,8,9,10].

Safe, robust, and asymmetrical controller design is a crucial challenge in CCC research. Various factors induced by V2V communication, such as network-induced delays and connection topology, can significantly reduce system stability and security [11,12,13]. In [14], in order to reduce the system performance degradation introduced by network-induced delays, a predictive feedback control method is introduced based on the system state estimation. In [15], a semi-constant time gap policy is adopted to compensate for delays by utilizing historical information from the preceding vehicle rather than current states. However, works [14,15] assume a fixed constant delay, whereas network-induced delays should be considered stochastic and time-varying due to the complexity of vehicle communication networks [16,17,18,19]. In [20], the impact of stochastic time latency on string stability in connected vehicles is explored by evaluating the mean and covariance features of system dynamics. In [21], an optimal control strategy incorporating stochastic network-induced delays is derived as a two-step iteration. Although these studies address the influence of uncertain factors in wireless communication, they focus on static traffic situations or deterministic system models. In fact, the CCC system faces various disturbances, such as unpredictable acceleration or deceleration of the leading vehicle [22]. In other words, in order to adapt to dynamic traffic conditions, the expected state of the platoon must also exhibit time-varying features. Therefore, it is essential to develop a robust asymmetrical controller capable of compensating for these system disturbances and uncertainties.

According to the dynamic and unpredictable nature of traffic environments, reinforcement learning (RL) and deep reinforcement learning (DRL) have emerged as promising solutions [23,24,25]. Unlike most traditional model-based optimization techniques, RL agents learn control strategies directly from their interaction experiences within environments based on training parameter models. One of the earliest works to apply the RL approach to the design of safe controllers for longitudinal tracking is [26]. In [27], an automated driving framework employing Deep Q Networks (DQN) is presented and tested in a simulation environment. However, vehicle acceleration regulation falls within the realm of continuous action space [28]. In the research mentioned above, it is challenging to identify every action through discrete action design, which unavoidably results in behavior vibration and performance degradation. Subsequently, the Deterministic Policy Gradient (DPG) [29] is proposed to enable learning in a continuous action domain, along with several further developed algorithms such as Deep Deterministic Policy Gradient (DDPG), Soft Actor Critic (SAC), Advantage Actor Critic (A2C), and Twin Delayed DDPG (TD3) [30,31,32].

Unfortunately, intelligent approaches addressing the CCC controller issues in dynamic traffic situations are seldom explored. In addition, existing DRL-based algorithms focus on cases with no network-induced delays. Even if the delay is investigated, its impact on the Markov Decision Process (MDP) definition for CCC is also missed. Actually, as a real-time control application, the network-induced delay is one of most crucial factors influencing system control stability. Consequently, this article proposes an innovative DRL-based algorithm to address the asymmetrical cruise control optimization problem for dynamic vehicle scenarios in the presence of network-induced delays. The key contributions are outlined below.

• A novel DRL-based intelligent controller is designed for dynamic traffic conditions with network-induced delays. Through interaction with the traffic environment, the intelligent asymmetrical control strategy is updated via self-learning to meet the emerging requirements of cruise control systems.
• To account for the inevitable network-induced delays caused by wireless V2V communication, the effects of previous control strategies are analyzed in optimization problem formulation, dynamics analysis, and MDP definition for CCC. This approach effectively mitigates performance degradation due to network-induced delays and helps ensure the stability of the CCC system.
• A CCC algorithm employing the Twin Delayed Deep Deterministic Policy Gradient (TD3) is proposed to improve the asymmetrical adaptability of CCC systems in dynamic traffic conditions with varying desired velocities. By completing two stages of sampling and training, optimal control schemes can be generated through the maximization of a quadratic reward function, which is defined by state errors and control inputs.

The rest of this article is structured as follows. The system modeling and optimization problem formulation is described in Section 2. Section 3 proposes a DRL-based controller design. Finally, the performance comparisons and conclusions are given in Section 4 and Section 5, respectively.

2. System Modeling and Optimization Problem Formulation

As depicted in Figure 1, the CCC system, based on the Internet of Vehicles, primarily comprises the vehicles, Roadside Units (RSUs), and the cloud. Specifically, this work focuses on a heterogeneous platoon of multiple vehicles traveling on a single lane. The CCC vehicle with the edge controller is in the tail, and the remaining vehicles are human-driven vehicles following the target vehicle m + 1 at the front of the platoon. Through V2V communication, the cruise control vehicle can obtain motion information from preceding vehicles, such as acceleration, velocity, and headway. Based on these information, the controller generates suitable real-time control strategies to ensure asymmetrical control stability.

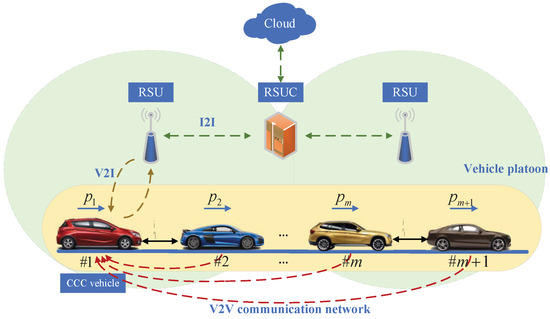
Figure 1. The CCC system architecture based on the Internet of Vehicles.

Considering human-driven vehicles, i, the system dynamics can be described using the classic car-following model [6]

$$\begin{array}{cc}\hfill & {\dot{p}}_i\left(t\right)={\gamma }_i(f\left(l_i\left(t\right)\right)-p_i\left(t\right))+{\mu }_i(p_{i+1}\left(t\right)-p_i\left(t\right)),\hfill \\ \hfill & {\dot{l}}_i\left(t\right)=p_{i+1}\left(t\right)-p_i\left(t\right),i=2,3,\cdots ,m,\hfill \end{array}$$

(1)

where $l_i\left(t\right)$ denotes the headway, $p_i\left(t\right)$ represents the velocity, dot $\dot{p}$ represents the time-dependent derivative t, ${\gamma }_j$ and ${\mu }_j$ are system parameters determined by the behavior of the driver, and $f\left(l\right)$ is the function of the velocity policy that

$$f\left(l\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}0<l<l_{min},\hfill \\ p_g,\hfill & \mathrm{if}l>l_{max},\hfill \\ \frac{p_g}{2}(1-cos\left(\pi \frac{l-l_{min}}{l_{max}-l_{min}}\right)),\hfill & \mathrm{if}{l}_{min}\le l\le l_{max},\hfill \end{array}\right.$$

(2)

where $p_g$ is the maximum velocity, $l_{min}$ and $l_{max}$ are the minimum and maximum headway, respectively.

For a CCC vehicle, the dynamics are given by [11]

$$\begin{array}{cc}\hfill & {\dot{p}}_1\left(t\right)=c(t-d\left(t\right)),\hfill \\ \hfill & {\dot{l}}_1\left(t\right)=p_2\left(t\right)-p_1\left(t\right),\hfill \end{array}$$

(3)

where $d\left(t\right)$ represents the time-varying delay, and $c\left(t\right)$ refers to the control strategy, namely, the acceleration.

In the vehicle platoon, each vehicle aims to achieve the leader velocity $p^{*}\left(t\right)=p_{m+1}\left(t\right)$ and corresponding desired headway $l^{*}\left(t\right)$, the dynamics of desired states are given by

$$\begin{array}{c}\hfill {\dot{p}}^{*}\left(t\right)=g\left(p^{*}\left(t\right),l^{*}\left(t\right)\right),\end{array}$$

(4)

where $g\left(p^{*}\left(t\right),l^{*}\left(t\right)\right)$ denotes the acceleration of the leading vehicle, which is time-varying due to the dynamic target vehicle velocity.

As a result, the velocity and headway errors can be represented as $\Delta p\left(t\right)=p\left(t\right)-p^{*}\left(t\right)$ and $\Delta l\left(t\right)=l\left(t\right)-l^{*}\left(t\right)$. Based on (1) and (3), and the first-order approximation of the policy $f\left(l\right)=f\left(l^{*}\right)+f^{\prime }\left(l^{*}\right)(l-l^{*})$, the error dynamics for the vehicles can be expressed as follows.

$$\begin{array}{cc}\hfill & \Delta {\dot{p}}_i\left(t\right)=\left\{\begin{array}{cc}c\left(t-d\left(t\right)\right),& i=1,\\ {\gamma }_m\left(f^{*}\Delta l_m\left(t\right)-\Delta p_m\left(t\right)\right)+{\mu }_m\left(g\left(p^{*}\left(t\right),l^{*}\left(t\right)\right)-\Delta p_m\left(t\right)\right),& i=m,\\ {\gamma }_i\left(f^{*}\Delta l_i\left(t\right)-\Delta p_i\left(t\right)\right)+{\mu }_i\left(\Delta p_{i+1}\left(t\right)-\Delta p_i\left(t\right)\right),& others,\end{array}\right.\hfill \\ \hfill & {\Delta \dot{l}}_i\left(t\right)=\Delta p_{i+1}\left(t\right)-\Delta p_i\left(t\right),\hfill \end{array}$$

(5)

where $f^{*}=\dot{f}\left(l^{*}\right)$.

Construct the state vector

$$y\left(t\right)={\left[\Delta p_1\left(t\right),\Delta l_1\left(t\right),\Delta p_2\left(t\right),\Delta l_2\left(t\right),\cdots ,\Delta p_m\left(t\right),\Delta l_m\left(t\right)\right]}^T\in {\mathbb{R}}^{2m},$$

(6)

and rewrite (5) as

$$\dot{y}\left(t\right)=Cy\left(t\right)+Dc(t-d\left(t\right))+Gw\left(t\right),$$

(7)

where

$$\begin{array}{c}C=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& \cdots & 0& 0\\ 0\hfill & -1& 0& 1& 0& 0& \cdots & 0& 0\\ 0\hfill & 0& {\beta }_2& {\alpha }_2& 0& {\gamma }_2& \cdots & 0& 0\\ 0\hfill & 0& 0& -1& 0& 1& \cdots & 0& 0\\ ⋮\hfill & ⋮& \ddots & \ddots & \ddots & \ddots & \ddots & ⋮& ⋮\\ 0\hfill & 0& \cdots & \cdots & 0& {\beta }_{m-1}& {\alpha }_{m-1}& 0& {\gamma }_{m-1}\\ 0\hfill & 0& \cdots & \cdots & 0& 0& -1& 0& 1\\ 0\hfill & 0& \cdots & \cdots & 0& 0& 0& {\beta }_m& {\alpha }_m\\ 0\hfill & 0& \cdots & \cdots & 0& 0& 0& 0& -1\end{array}\right],\hfill \\ D={\left[\begin{array}{ccccc}1,& 0,& 0,& \cdots ,& 0\end{array}\right]}^T,G={\left[\begin{array}{cccccc}0,& 0,& 0,& \cdots ,& {\mu }_m,& 1\end{array}\right]}^T,\hfill \\ w\left(t\right)=g(p*(t),l*(t\left)\right),\hfill \end{array}$$

and ${\beta }_i={\gamma }_i{f}^{*},{\alpha }_i=-{\gamma }_i-{\mu }_i,i=2,3,...,m.$

Then, based on (7), the dynamics in the k-th sampling interval in the discrete-time domain can be deduced as

$$y_{k+1}=C_k{y}_k+D_{1,k}{c}_{k-n}+D_{2,k}{c}_{k-n-1}+w_k,$$

(8)

where

$$\begin{array}{cc}& y_k=y(k\Delta T),D_{1,k}={\int }_0^{(n+1)\Delta T-d_k}{e}^{Ct}dtD,C_{2,k}={\int }_{(n+1)\Delta T-d_k}^{\Delta T}{e}^{Ct}dtD,\hfill \\ & C_k=e^{C\Delta T},w_k=-\underset{k\Delta T}{\overset{\left(k+1\right)\Delta T}{\int }}{e}^{C\left[\left(k+1\right)\Delta T-t\right]}g\left(p^{*}\left(t\right),l^{*}\left(t\right)\right)dt{\mu }_m,\hfill \end{array}$$

and $d_k\in [n\Delta T,(n+1)\Delta T)$ is the time-varying delay in the k-th sampling interval, which is commonly taken to be stochastic, n is a non-negative integer, $\Delta T$ is the sampling interval, and $c_i$ is the relevant control signal.

Note that, due to the complexity of the traffic environment and the dynamics of driving vehicles, the network-induced delay causes the time-varying features of $D_{1,k}$ and $D_{2,k}$, and the variable desired state also introduces the uncertain item $w_k$.

The objective of the cruise control is to minimize the velocity and headway errors, namely, to achieve the equilibrium $y^{*}\equiv 0$. the optimization control issue of the CCC system can be expressed as follows using the common quadratic cost function:

$$\begin{array}{c}\underset{\left\{c_i\right\}}{min}\mathbb{E}\left[y_N^{T}A{y}_N+{\displaystyle \sum _{k=0}^{N-1}}\left(y_k^{T}A{y}_k+c_k^{T}B{c}_k\right)\right]\hfill \\ s.t.y_{k+1}=C_k{y}_k+D_{1,k}{c}_{k-n}+D_{2,k}{c}_{k-n-1}+w_k,\hfill \end{array}$$

(9)

where N represents the time length of cruise control, the term $y_k^{T}A{y}_k$ denotes the errors, $c_k^{T}B{c}_k$ represents the effect of control inputs, the expectation operator, $\mathbb{E}$, accounts for the stochastic nature of the desired state and time delays, and $A⪰0$ and $B\succ 0$ denote pre-determined system parameters.

3. Drl-Based Controller Design

Considering the time-varying communication delay and desired states, the intelligent DRL-based asymmetrical control is designed to address the cruise control problem. Since the CCC’s actions are within the continuous-value range, utilizing discrete action strategies will result in a considerable increase in computational complexity and system performance degradation. A DRL algorithm known as TD3 has recently demonstrated promising results in the area of continuous control and has been validated in various applications. Next, on the basis of MDP analysis, the application of TD3 algorithm is proposed to learn CCC policy.

3.1. MDP Definition of CCC

MDP, typically used to define the DRL problem, can be described as the tuple $M(S,A_c,P,R)$, where $A_c,S,R,P$ represents the action space, state space, reward function, and transition dynamics, respectively. At each slot, the agent, which serves as the core brain of the DRL, detects the environment state $s_k\in S$ in real time, executes action $a_k\in A_c$ based on policy ${\pi }^{*}\left(s\right)$, and receives a reward. The aim of DRL is to derive ${\pi }^{*}\left(s\right)$ to maximize $R={\sum }_{k=0}^{\infty }{\lambda }^k{r}_k$, with $\lambda \in \left[0,1\right]$ being the discount factor. In the following, the MDP for the intelligent cruise control is defined in conjunction with the analysis in Section 2.

(1) State: Similar to (6), the state of the CCC system can be expressed as

$$\begin{array}{cc}\hfill s_k=& [y_k^T,c_{k-1},\cdots ,c_{k-n-1}]\hfill \\ \hfill =& \left[\Delta p_{1,k},\Delta l_{1,k},\cdots ,\Delta p_{m,k},\Delta l_{m,k},c_{k-1},\cdots ,c_{k-n-1}\right]\in {\mathbb{R}}^{2m+n+1},\hfill \end{array}$$

(10)

where the first $2m$ items of the state vector indicate the velocity and headway errors, while comparable from the typical state design, in order to resolve for the influence of network-induced delays, the state vector is supplemented with delayed control inputs $\left\{c_{k-1},\cdots ,c_{k-n-1}\right\}$.

In accordance with (3), the state space can be further specified as follows:

$$\begin{array}{c}0\le p\le p_g,\hfill \\ l_{min}\le l\le l_{max},\hfill \\ c_{min}\le c\le c_{max},\hfill \end{array}$$

(11)

where $c_{max}$ and $c_{min}$ are the acceleration and deceleration limits, respectively.

(2) Action: The objective of the agent is to form the cruise control policy. Therefore, the action can be given by

$$\begin{array}{c}{a}_k=c_k.\hfill \end{array}$$

(12)

(3) Transition dynamics: The transition dynamics take action $a_k$ and current state $s_k$ as inputs, yielding the subsequent state $s_{k+1}$ as output. Thus, based on (8), (10), and (12), the transition dynamics can be formulated as

$$s_{k+1}=s_k{E}_k+a_k{F}_k+W_k,$$

(13)

where

$$\begin{array}{c}{E}_k=\left[\begin{array}{cccccc}{C}_k^T& 0& 0& 0& \cdots & 0\\ 0& 0& I& 0& \cdots & 0\\ 0& 0& 0& I& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ D_{1,k}^T& 0& 0& 0& \cdots & I\\ D_{2,k}^T& 0& 0& 0& \cdots & 0\end{array}\right],F_k={\left[\begin{array}{c}0\\ I\\ 0\\ ⋮\\ 0\end{array}\right]}^T,\hfill \\ W_k=\left[\begin{array}{ccccc}{w}_k& 0& 0& \cdots & 0\end{array}\right].\hfill \end{array}$$

(4) Reward function: Similar to (9), the headway error, velocity error, and control input serve as the principal components of the reward design. In distinction to optimization theory, where the objective is to minimize the cost function, DRL seeks to maximize the cumulative rewards. Consequently, the reward is defined using a negative value representation as follows

$$r_k=-\left(s_k\overline{A}{s}_k^T+a_{k}B{a}_k^T\right),$$

(14)

where

$$\overline{A}=\left[\begin{array}{cc}A& 0_{2m\times \left(n+1\right)}\\ 0_{\left(n+1\right)\times 2m}& 0_{\left(n+1\right)\times \left(n+1\right)}\end{array}\right].$$

In relation to the CCC design employing control length N, the return for a specific number of trainings can be determined by using

$$\begin{array}{c}\hfill R_N=-\sum _{k=1}^N{\lambda }^k\left(s_k\overline{A}{s}_k^T+a_{k}B{a}_k^T\right).\end{array}$$

(15)

3.2. Td3-Based CCC Algorithm

Figure 2 illustrates the structure of the TD3-based CCC algorithm, which primarily comprises a sensor layer and a controller layer. The sensor layer is specifically tasked with monitoring surrounding traffic conditions and gathering vehicle state data utilizing wireless network. The controller layer stores platoon data obtained from the sensor and trained within the TD3 framework. Subsequently, after gaining sufficient experience, the controller generates the near-optimal asymmetrical control strategies for the cruise control vehicle in real time.

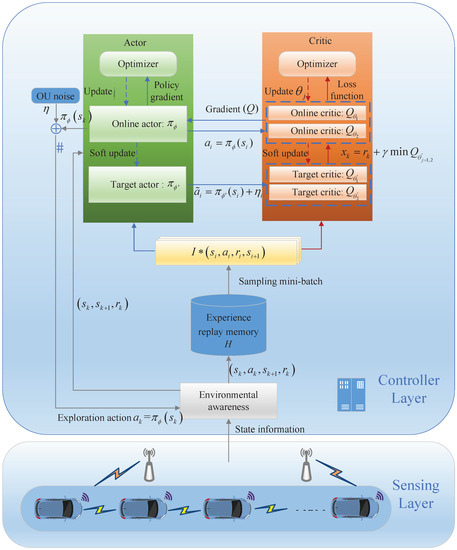
Figure 2. The architecture of TD3-based CCC algorithm.

TD3 is an algorithm belonging to the actor–critic network family, primarily consisting of six deep neural networks: the online actor ${\pi }_{\varphi }$, the target actor ${\pi }_{{\varphi }^{\prime }}$, two online critics $Q_{{\theta }_1},Q_{{\theta }_2}$, and two target critics $Q_{{\theta }_1^{\prime }},Q_{{\theta }_2^{\prime }}$. Here, Q denotes evaluation function, $\pi$ represents actor policy, and $\varphi$ and $\theta$ are network parameters. The proposed TD3-based cruise control method typically trains to learn a near-optimal control strategy, while training the critic network to find appropriate Q value for evaluating the effectiveness of the control strategy.

TD3-based algorithm consists of two phases: sampling and training.

(1) Sampling: Initially, the velocity and headway information gathered as starting states through V2V communication. In the k-th time slot, the action policy ${\pi }_{\varphi }\left(s_k\right)$ can be generated using the state $s_k$ by the online actor. Considering the continuous action space, the exploration policy is designed as follows

$$a_k={\pi }_{\varphi }\left(s_k\right)+{\eta }_k,$$

(16)

where ${\eta }_k$ is a temporally correlated disturbance induced by an Ornstein–Uhlenbeck (OU) process.

Upon taking action as in (16), the subsequent state $s_{k+1}$ can be observed through the transition dynamics in (13), and the feedback reward $r_k$ can be obtained as in (14). The transition tuple $(s_k,a_k,r_k,s_{k+1})$, is stored in the experience replay memory buffer. Through interaction with the environment, a sufficient number of samples can be generated.

(2) Training: Actually, the training process involves optimizing both critic and actor components. In each episode, the mini-batch $(s_i,a_i,r_i,s_{i+1})$, including I samples, is randomly selected from the experience buffer H for training. Prior to updating the critic, the target action is smoothed and regularized to minimize the variance caused by function approximation errors, which is achieved by

$$\begin{array}{c}{\tilde{a}}_i={\pi }_{{\varphi }^{\prime }}\left(s_i\right)+{\eta }_i,\hfill \\ {\eta }_i\sim clip({\eta }_i,-b,b),\hfill \end{array}$$

(17)

where ${\eta }_i$ is clipped to keep the target in a small range.

The online critics are trained to update their parameters ${\theta }_j,j=1,2$ by minimizing a mean square error loss function given as

$$arg\underset{{\theta }_j}{min}{I}^{-1}\sum {(x_i-Q_{{\theta }_j}(s_i,a_i))}^2,$$

(18)

where $Q_{{\theta }_j}(s_i,a_i)$ represents the output of the online critics when the input state $s_i$ and action $a_i$ are introduced into the online critics. Meanwhile, $x_i$ denotes the target Q value, which is defined as

$$x_i=r_i+\lambda \underset{j=1,2}{min}{Q}_{{{\theta }^{\prime }}_j}(s_i^{\prime },{\tilde{a}}_i).$$

(19)

In (19), $r_i$ represents the current reward as determined by (14), while $Q_{{{\theta }^{\prime }}_j}(s_i^{\prime },{\tilde{a}}_i)$ denotes the subsequent Q value obtained through the target critics, and ${\tilde{a}}_i$ corresponds to the next action policy (17). To address the potential overestimation of the Q value, the minimum value from the assessments of two reviewers is chosen.

In order to decrease the accumulation of errors during training, the actor and target networks are updated after e times of updating critics. Specifically, the online actor is trained to update its parameter $\varphi$ by the policy gradient algorithm as follows

$${\nabla }_{\varphi }J\left(\varphi \right)=I^{-1}\sum {\nabla }_a{Q}_{{\theta }_1}(s_i,a_i){|}_{a_i={\pi }_{\varphi }\left(s_i\right)}{\nabla }_{\varphi }{\pi }_{\varphi }\left(s_i\right),$$

(20)

where ∇ is the gradient operator.

The objective of policy gradient is to assist the online actor network in selecting the appropriate action that can yield the higher Q value by increasing or decreasing the probability of a given action.

Next, for the target networks, their parameters are updated using a soft update method, which can be expressed as

$$\begin{array}{c}{\theta }_j^{\prime }\leftarrow \delta {\theta }_j+\left(1-\delta \right){\theta }_j^{\prime },\hfill \\ {\varphi }^{\prime }\leftarrow \delta \varphi +\left(1-\delta \right){\varphi }^{\prime },\hfill \end{array}$$

(21)

where $0<\delta \ll 1$ is a constant.

Finally, after enough training, the optimal CCC policy can be obtained as follows

$$a^{*}={\pi }_{{\varphi }^{*}}\left(s\right),$$

(22)

where ${\varphi }^{*}$ is the applicable online actor parameters.

The comprehensive TD3-based CCC algorithm is outlined in Algorithm 1.

Algorithm 1 TD3-based CCC algorithm

1: % Sampling 2: Initialize system parameters $\overline{A},B,E_0,F_0$ and the experience replay buffer H. 3: Randomly initialize online critics $Q_{{\theta }_1},Q_{{\theta }_2}$ and online actor ${\pi }_{\varphi }$ with parameters ${\theta }_1$, ${\theta }_2$, and $\varphi$. 4: Initialize target networks ${\theta }_1^{\prime }\leftarrow {\theta }_1,{\theta }_2^{\prime }\leftarrow {\theta }_2,{\varphi }^{\prime }\leftarrow \varphi$. 5: for k = $1:1:K$ do 6:    Select and execute action $a_k$ by (16). 7:    Observe $s_{k+1}$ by (13). 8:    Obtain reward $r_k$ by (14). 9:    Store transition $(s_k,a_k,r_k,s_{k+1})$ in H. 10:    % Training 11:    Sample a random mini-batch of i transitions $(s_i,a_i,r_i,s_{i+1})$ from H. 12:    Select target action ${\tilde{a}}_i$ with random noise by (17). 13:    Update critics ${\theta }_j$ by minimizing the loss function using (18). 14:     15:    if k mod e then 16:      Update actor $\varphi$ by the deterministic policy gradient by (20). 17:      Update the target networks by (21). 18:    end if 19: end for

4. Simulations

In this section, simulations are presented to show the performance comparisons of the proposed intelligent asymmetrical control algorithm. A platoon consisting of 5 vehicles is analyzed, where the tail vehicle operates under CCC, while the remaining vehicles are human driven. Similar to [11,20], the following constraint parameters are used that $p_g$ = 30 [m/s], $l_{max}$ = 35 [m], $l_{min}$ = 5 [m], $c_{max}$ = 5 [m/s${}^2$], $c_{min}$ = −5 [m/s${}^2$], $\gamma$ = 0.6, $\mu$ = 0.6. The sampling interval is $\Delta T$ = 0.1 s, and the time-varying communication delay is specified as a constrained random variable $d_k\in [0,0.5\mathrm{s}]$. The simulation parameters setting can be summarized as in Table 1.

Table 1. Simulation parameters setting.

Symbol	Description	Setting
m	Number of vehicles	5
$p_{min},p_{max}$	Velocity space	$[0,30]$ m/s
$l_{min},l_{max}$	Headway space	$[5,35]$ m
$c_{min},c_{max}$	Acceleration space	$[-5,5]$ m/s${}^2$
$\gamma ,\mu$	Driver parameters	$0.6,0.6$
$\Delta T$	Sampling interval	$0.1$ s
$d_k$	Network-induced delay	$[0,0.4]$ s
K	Time step	$2\times {10}^5$
b	Noise clip	$0.5$
e	Policy delay	2
$\lambda$	Discount factor	$0.99$
$l_a,l_c$	Learning rates	$0.001,0.001$
I	Mini-batch size	64

We evaluate the learning performance of the designed algorithm in relation to those of other classical DRL algorithms (i.e., DQN in [27] and DDPG in [30]) that do not consider time-varying factors. The hyper-parameters are set as follows: total training step $K={10}^5$, mini-bactch size 64, learning rates $l_a=0.001,l_c=0.001$, discount factor $\lambda =0.99$, noise clip $b=0.5$, policy delay $e=2$. Figure 3 shows the normalized reward against the training step. The findings demonstrate that the proposed algorithm learns the most efficiently and converges before $1.2\times {10}^5$ steps. The learning efficiency of DDPG is second, but it still fluctuates after convergence. However, algorithm DQN has the lowest learning efficiency and fails to converge within limited training. This indicates that it is challenging to learn CCC strategy in a complex dynamic environment, and the proposed algorithm may help learning by the MDP design considering the time-varying communication delay and desired state.

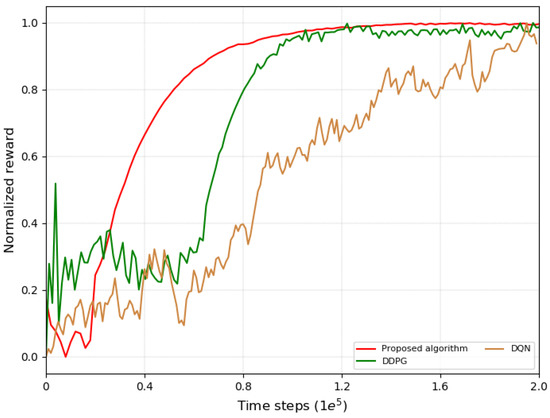
Figure 3. Normalized rewards.

Next, a real-world dataset named DACT [33] is used to validate the effectiveness of proposed DRL-based intelligent control algorithm. The DACT data are a collection of driving trajectory data from Columbus and Ohio, and can be divided into multiple segments marked according to operation modes, such as acceleration and deceleration. In particular, three traffic scenarios are selected from the DACT dataset: a case with significant speed drop represents the harsh brake in an emergency situation, the speed variations around zero represent stop-and-go traffic in congestion, and the change in average speed represents the change in the speed limit in the road work area. As shown in Figure 4, Figure 5 and Figure 6, the proposed controller can accurately execute control decisions and track the desired states under three traffic scenarios. However, when using a controller trained by the DRL algorithm that does not consider time-varying factors, it may face greater speed variations and headway errors. For example, as shown in Figure 4, in order to achieve a harsh brake, the proposed algorithm provides fast control response and constant deceleration, while the other two algorithms respond slowly, which will cause too small of a headway and traffic safety problems. In the traffic congestion and road work areas of Figure 5 and Figure 6, the other two algorithms have obvious tracking errors, and the speed adjustment methods are more radical, which will not only reduce the driving comfort, but also endanger following and preceding vehicles. Therefore, the proposed controller has significant advantages in accurate tracking, comfort, and safety. In addition, using the real dataset DACT indicates that the proposed intelligent delay-aware control method has potential practical applications, such as urban driving control.

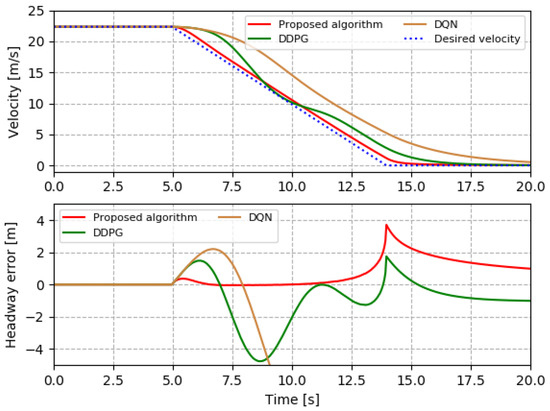
Figure 4. Harsh brake in emergency situation.

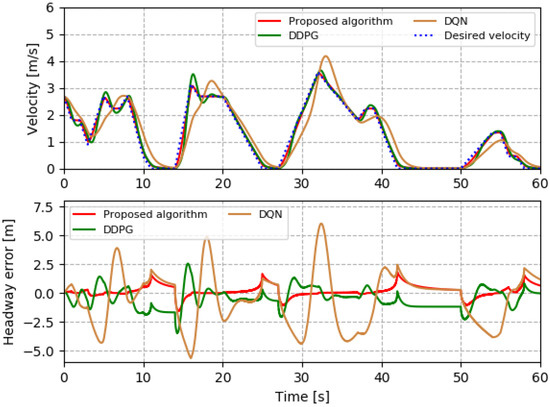
Figure 5. Stop-and-go traffic in congestion.

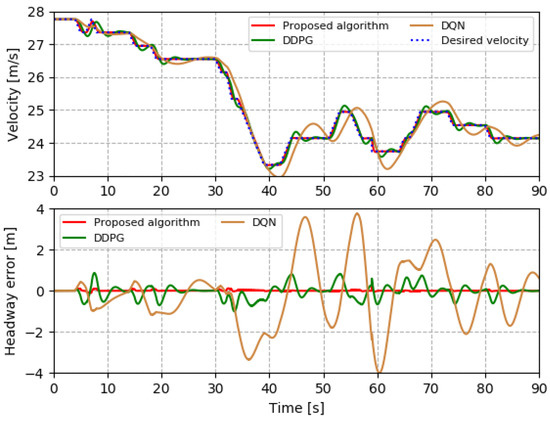
Figure 6. Speed limit changes in work zone.

5. Conclusions

In this study, we propose a DRL-based asymmetric control algorithm for longitudinal control in CCC vehicles. This strategy considers time-varying traffic conditions and dynamic network-induced delays to improve traffic flow stability. Real-time movement information of a vehicle platoon is gathered through V2V wireless communication. As the vehicle’s action space is continuous, a TD3-based method for intelligent cruise control is introduced. Upon training completion, the CCC strategy for the cruise control system, defined by headway and velocity errors, as well as control input, is proposed by the cost function maximization. Simulation results indicate that the developed controller effectively minimizes the impact of communication delays and adapts to dynamic traffic conditions. Furthermore, the proposed asymmetrical control algorithm outperforms existing methods in terms of control performance. In the proposed intelligent control design, the dynamic target vehicle velocity and network-induced delays are investigated. However, other potential system constraints, such as bandwidth restriction and unreliable transmission, and much more complicated traffic scenarios with multiple CCC vehicles, are left for future works.