Abstract
In this article, the aim was to obtain kink soliton solutions of the (2+1)-dimensional integro-differential Jaulent–Miodek equation (IDJME), which is a prominent model related to energy-dependent Schrödinger potential and is used in fluid dynamics, condensed matter physics, optics and many engineering systems. The IDJME is created depending on the parameters and with constant coefficients, and two efficient methods, the generalized Kudryashov and a sub-version of an auxiliary equation method, were applied for the first time. Initially, the traveling wave transform, which comes from Lie symmetry infinitesimals and , was applied, and a nonlinear ordinary differential equation (NODE) form was derived. In order to make physical interpretations, appropriate solution sets and soliton solutions were obtained by performing systematic operations in line with the algorithm of the proposed methods. Then, 3D, 2D and contour simulations were made. Interpretations of different kink soliton solutions were made by obtaining results that are consistent with previous studies in the literature. The obtained results contribute to the studies in this field, though the contribution is small.
Keywords:
smooth-kink soliton; generalized Kudryashov method; a sub-version of auxiliary equation method; energy-dependent Schrödinger potential; Lie symmetry MSC:
37K40
1. Introduction
Nonlinear partial differential equations (NLPDEs) are very important in modeling and solving complex physical occurrences and problems in the world. Researchers have used partial differential equations to understand many complex problems in solid-state physics, quantum mechanics, fluid mechanics and plasma physics. Therefore, analytical solutions of NLPDEs play a very important role in understanding and explaining one or more phenomena, especially dispersion, scattering, propagation, reaction and convection problems. For this reason, searching for numerical and exact solutions to NLPDEs is a concern of many scientists. Researchers have used various solution methods to obtain exact solutions of many important NLPDEs. Some of these methods are the Kudryashov method [1,2,3], tanh–coth method [4,5,6], new Kudryashov method [7,8,9], modified F-expansion method [10,11], extended tanh method [12,13,14,15], generalized projective Riccati equations method [16,17,18], expansion method [19,20,21], extended rational sine–cosine method [22,23,24,25], extended Kudryashov method [26,27,28,29], inverse scattering transform method [30], Hirota’s bilinear method [31], Darboux transformation [32], the ansatz methods [33] and the Lie symmetry or Lie group method [34].
The fractional forms of this equation are among the titles of work carried out in recent years regarding the Jaulent–Miodek equation. For example, Sahoo et al. investigated the JM system by using fractional Lie symmetry analysis unified with symmetry analysis and used the conservation laws of the system in order to derive new conserved vectors [35]; Zadeh et al. analyzed the fractional-order JME with the help of Laplace decomposition and Laplace variational iteration methods [36]; Veeresha et. al. investigated the numerical solution of the time-fractional JME with the help of thr coupled fractional reduced differential transform method (CFRDTM) and homotopy analysis transform method (HATM) [37]; and Alshammari et al. studied the numerical solution of the fractional JME with the help of the coupled fractional variational iteration transformation technique and the Adomian decomposition transformation technique [38].
One of the important NLPDEs is the Jaulent–Miodek equation (JME), which is used to model many important problems in optics, condensed matter physics and fluid dynamics [39].
The Jaulent–Miodek equation was first introduced by M. Jaulent and I. Miodek in 1976 [40] as a coupled Jaulent–Miodek equation by using inverse scattering transform with the help of energy-dependent Schrödinger potentials. Since the source of the JM equation is energy-dependent Schrödinger potentials [41,42], it has also been the subject of different studies as a coupled JM system [43,44]. In particular, the (2+1)-dimensional JME gives information about the energy-dependent Schrödinger potential [45]. In the literature, the following four models are called the Jaulent–Miodek hierarchy [46]:
where is the inverse of with and . When the literature is scanned, it is seen that there are many studies related to both the Jaulent–Miodek equation and the Jaulent–Miodek hierarchy depending on the importance of the Jaulent–Miodek equation: Ruan and Lou investigated the new symmetries of the JM hierarchy [47]; Feng and Li derived many explicit expressions by using the theory of the plane dynamic system for studying the existence of solitary and periodic waves of the coupled JME [48]; Gang et al. derived a hierarchy of generalized JM equations and their explicit solutions [49]; MA Hong-Cai et al. applied the Hereman–Nuseir method to the model in Equation (2) and obtained kink, multiple singular and multiple kink-singular solitons [46]; Wafaa M. Taha et al. applied the tanh method and method to the model in Equation (3) and produced kink and bright solitons [50]; Kaplan et al. applied the generalized Kudryashov method to the model in Equation (3) and obtained singular and bright solitons [51]; Apranti et al. applied the extended simple equation method and produced a periodic soliton [52]. For the model in Equation (4), Liu et al. obtained anti-bell-shape and two bell-shape solitons with the help of Bell polynomials [53]. In previous studies, scientists investigated analytical solutions of Jaulent–Miodek equations in different forms and obtained a kink-type soliton, periodic-type soliton and bell-type soliton [54,55,56]. In addition, the following recent studies should be mentioned: Mbusi et al. investigated the the exact solutions and conservation laws of a generalized (1+2)-dimensional JME with power-law nonlinearity [57]; Motsepa et al. investigated the conservation law and gained the traveling wave solutions of the (2+1)-JME [58]; Gu utilized the complex method in order to obtain the exact solutions of the (2+1)-dimensional JME [45]; Iqbal et al. studied the JM system with the modified exponential rational function method [59]; Guiping et al. derived the new solitary solutions to the time-fractional coupled JME [60]; Sadat and Kassem gained explicit solutions for the (2+1) JME using the integrating factors method in an unbounded domain [61]; Kaewta et al. studied the (2+1) conformable time partial integro-differential JM equation using the exp-function [62] and transformed the (2+1)-dimensional JME into a fourth-order partial differential equation by having the exact solution [63]; Pei and Bai investigated the Lie symmetries, conservation laws and exact solutions for JME [64]. Furthermore, the space–time fractional form of the coupled JME by Chao and Qilong [65], the JME with positive dispersion by Jing et al. [66] and dozens of other studies like these can be listed as studies emphasizing the importance of the JM equation.
The (2+1)-dimensional integro differential Jaulent–Miodek equation is given as follows [67]:
where , and are real constants and . Here, the model in Equation (2) is obtained for , the model in Equation (3) is obtained for and the model in Equation (4) is obtained for . In order to obtain the traveling wave solutions of the nonlinear integrable evolution equations, the decomposition of nonlinear partial differential equations has its own importance and difficulty. The decomposition method is basically based on transforming or reducing a nonlinear partial differential equation into a system of double ordinary differential equations, either from a theoretical or practical point of view. Therefore, with this approach, it is possible to obtain solutions of soliton equations by converting soliton equations to finite dimensional Hamiltonian systems, with the aim of integrating decomposition, or to make the calculations required for this purpose much easier. Li is among the first researchers to make these applications to prove the existence of kink, periodic and solitary wave solutions of different, singular nonlinear propagating soliton wave equations [68,69]. Such approximations make it possible to obtain integrable equations such as the equation given by Equation (5). In Equation (5), by substituting and by getting rid of the integral term, we obtain the equivalent form of Equation (5), which we will study in this manuscript as follows:
Exact solutions of NLEEs have crucial importance in adding an elite point of view. Numerical methods, calculations and simulations are important but they also always give a pictorial view and, generally, the results obtained are fuzzy for evaluation. At this point, analytical or exact solutions add extra flavor to this research. This is one of the main factors underlying the choice of an analytical method as a method in this study.
Although different forms of the kink soliton solutions have been obtained by various techniques related to the JM and IDJMEs before, there are a lack of studies that focus on kink soliton shapes (parabolic or smooth) and show that the utilized approaches are easily applicable and effective, which are positive aspects of this work.
The remainder of the article is structured as follows: Section 2 is devoted to obtaining the NODE form of Equation (6). In Section 3, basic algorithms of the generalized Kudryashov method and a sub-version of auxiliary methods are presented. Section 4 includes the soliton solutions and their interpretations, and Section 5 is the conclusions.
2. Mathematical Analysis of the Investigated Problem
Let us consider Equation (6) and follow the traveling wave transform, which comes from Lie symmetry infinitesimals and :
where are spatial coordinates and t is temporal variable. In addition, and w are nonzero arbitrary constants, where w stands for velocity. Inserting Equation (7) into Equation (6) presents the following equation:
3. Proposed Methods and Their Applications
In this section, the proposed methods are briefly explained and applied to Equation (9).
3.1. Generalized Kudryashov Method and Its Implementatiton
Step-1: Let us assume that Equation (9) has the solution in the following form [70]:
where and are real constants such that , should not be zero simultaneously. Here, r and s are balancing constants that are positive integers and is the solution of the following equation [70]:
in which Equation (11) has the following well-known solution [70]:
where is a nonzero constant.
Step-2: We determine the positive integers r and s using the homogeneous balance principle between the highest-order derivative term and the highest-degree nonlinear term in Equation (9) by considering Equations (10) and (11). The result is ; then, . If we select , then . Thus, Equation (10) takes the following form:
3.2. A Sub-Version of Auxiliary Method and Its Implementatiton
Step-1: Let us assume that Equation (9) has a solution in the following form [70]:
where are real values, r is a balancing constant and is the solution of the following formula:
It is easy to ascertain that:
Step-2: Applying the homogeneous balance principle between the highest-order derivative term and the highest-degree term in Equation (9) by taking into account Equations (21) and (22), we calculate the balancing constant as . The calculation of r as 1 generates the following structure of Equation (21):
4. Results and Discussion
In this section, we illustrate some graphical simulations of the (2+1)-dimensional IDJME in Equations (18)–(20), (28) and (29). We demonstrate 3D, contour and 2D graphics to present soliton models of the solution functions. In addition, we interpret the state of movement of solitons with respect to time via 2D graphics.
In Figure 1, can be seen in Equation (18) for and . This soliton is a kink soliton. We examine the behavior of this soliton with the help of 3D, contour and 2D graphics in Figure 1a, Figure 1b and Figure 1c, respectively. In Figure 1c, the direction of the parabolic kink soliton for the values of is shown. The soliton moves to the right on the x-axis.
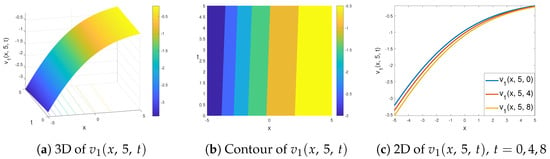
Figure 1.
The 3D (a), contour (b) and 2D (c) view of parabolic kink soliton solution of in Equation (18) for and .
In Figure 2, we visualize in Equation (28) for the and parameter values. This soliton model is a kink soliton. We investigate the physical orientation of the kink soliton via 3D, contour and 2D graphs in Figure 2a, Figure 2b and Figure 2c, respectively. In Figure 2c, we show the movement of the flat–kink soliton for the values of . It can be observed that this kink soliton maintains its form and goes to the left along the x-axis.
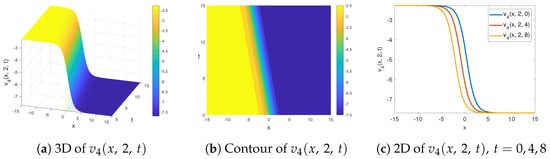
Figure 2.
The 3D (a), contour (b) and 2D (c) view of flat kink soliton solution of in Equation (28) for and .
In Figure 3, we plot the solution of in Equation (29) by assigning and values to the parameters. This figure represents the smooth kink soliton model. We analyze the physical orientation of this soliton via 3D, contour and 2D graphs in Figure 3a, Figure 3b and Figure 3c, respectively. In Figure 3c, it can be understood that, when using the values assigned to the view, which are , the soliton moves to the right on the x-axis while maintaining its form.
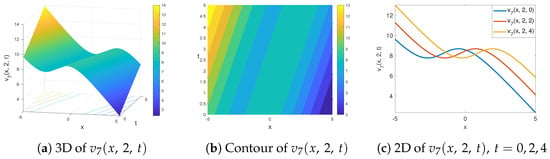
Figure 3.
The 3D (a), contour (b) and 2D (c) view of smooth kink soliton solution of in Equation (29) for and .
Figure 4 is another scenario of in Equation (19) for and . Figure 4a, Figure 4b and Figure 4c belong to 3D, contour and 2D scenarios, respectively. In Figure 4c, the direction of the soliton for the values of is shown, where the soliton migrates to the right on the x-axis. If a little more attention is paid to the soliton graph presented in Figure 4, it will be seen that this presentation is different from the previous graphical simulations. The soliton, in general, is like a combination of two planar behaviors (the junction is curved). In a sense, it reflects the kink soliton appearance in terms of the general image, but not in terms of the lower skirt part of the soliton. It has a large flat area at the top. In Figure 4, there is a situation similar to the observation that we made beforehand in Figure 2; that is, the wave is below the neutral level. However, unlike Figure 2, it is seen that there is no skirt formation belonging to the lower part of the wave. In addition, as another difference, it is seen that the slope of the waterfall part of the wave occurs more. It is also possible to make a physical observation regarding Figure 4 as follows. If the graph represented by Figure 4 is considered as a water wave in the sea or ocean, then we can say that the wave representation is below the sea or ocean surface (if the sea or ocean surface is considered as a neutral or zero level). Therefore, in this respect, the entire wave is formed below the neutral level. While the entire wave is below its neutral level, the bottom skirt of the wave (bottom right), in a sense, forms or runs parallel to the bottom.
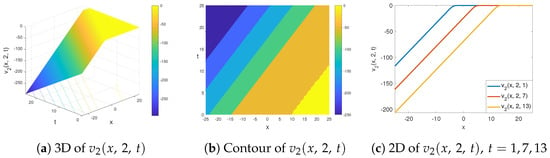
Figure 4.
The 3D (a), contour (b) and 2D (c) view of soliton solution of in Equation (19) for and .
Figure 5 simulates the projection of in Equation (20) for and . The 3D, contour and 2D graphics are presented in Figure 5a, Figure 5b and Figure 5c, respectively. In addition, Figure 5c depicts the direction of the soliton for a specific t of .
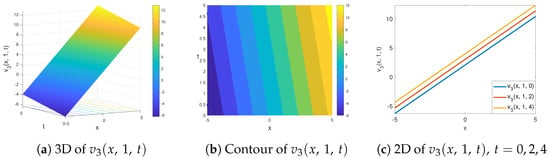
Figure 5.
The 3D (a), contour (b) and 2D (c) view of soliton solution of in Equation (20) for and .
Figure 5 also represents a behavior that draws our attention and needs to be emphasized. Here, the same soliton solution function is used (as in Equations (18) and (19)) but another solution set is used as in the previous graphs. The bottom and top skirts are not visible in the scenarios of Equation (20). In a sense, it can be taken into account as the form of the graph in Figure 4, in which the upper skirt also disappears. In general, such soliton behaviors are called plane solutions. If Figure 2, Figure 4 and Figure 5 are considered separately, these graphs are graphical representations of the solution functions obtained by applying the same solution method as the generalized Kudryashov scheme. Therefore, it is seen that solution functions with the same character represent different soliton behaviors with different solution sets. While there are lower and upper skirts of the soliton in Figure 2, the lower skirt of the soliton cannot be observed in Figure 4 and both the lower and upper skirts in Figure 5. In addition, except for the skirt parts of the soliton (i.e., the waterfall part), it turns into an additional inclined physical structure. Beyond the fact that this kind of behavior is presented as a rare case for IDJME, it is important in terms of showing how important and effective the solution sets and parameter selection obtained in such NLPDE solutions are.
5. Conclusions
In this article, the soliton solutions of the (2+1)-dimensional IDJME, which gives information about the energy-dependent Schrödinger potential, were investigated using two different efficient analytical methods: the generalized Kudryashov method and a sub-version of an auxiliary method. We derived the IDJME and different forms of kink solitons in accordance with the structure of the IDJME. Although different forms of the kink soliton type have been obtained by using different methods related to the JM and IDJM equations in the literature, there is a lack of studies that focus on the kink soliton types presented in Figure 4 and Figure 5 and that show that the methods used are easily applicable and effective, which are the positive aspects of this study. Examining the behavior of different nonlinear forms of JM equations with different dimensions under the effect of perturbation due to the effect of various parameters, examining the forms under the effect of different nonlinearity forms, considering these studies also for fractional forms and examining multiple wave solutions and bifurcation states can be given as future projects that await detailed investigation. The solutions and interpretations that were obtained in this work could contribute to the analysis of problems in solid-state and plasma physics, fluid mechanics and other fields for the understanding of wave propagation.
Author Contributions
Conceptualization, H.C. and M.O.; methodology, A.S.; software, A.S.; validation, M.B., H.C., M.O. and A.S.; formal analysis, A.S. and M.O.; investigation, M.B.; resources, A.S.; data curation, H.C. and M.O.; writing—original draft preparation, H.C. and M.B.; writing—review and editing, H.C., M.B. and M.O.; visualization, M.B.; supervision, A.S.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive solitary wave solutions of perturbed nonlinear Schrödinger equations. Appl. Math. Comput. 2020, 371, 124972. [Google Scholar] [CrossRef]
- Aksoy, E.; Bekir, A.; Çevikel, A.C. Study on fractional differential equations with modified riemann-liouville derivative via kudryashov method. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 511–516. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations. Appl. Math. Comput. 2007, 188, 1467–1475. [Google Scholar] [CrossRef]
- Gozukizil, O.F.; Salhi, A. New travelling wave solutions of two nonlinear physical models by using a modified tanh-coth method. J. Algorithms Comput. Technol. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Gozukizil, O.F.; Akcagil, S. The tanh-coth method for some nonlinear pseudoparabolic equations with exact solutions. Adv. Differ. Equ. 2013, 2013, 143. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2022, 206, 163550. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Ullah, N.; Akinyemi, L.; Shah, A.; Mirhosseini, A.; Seyed, M.; Chu, Y.M.; Ahmad, H. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Results Phys. 2021, 24, 104179. [Google Scholar] [CrossRef]
- Arnous, A.H.; Biswas, A.; Kara, A.H.; Yildirim, Y.; Alshehri, H.M.; Belic, M.R. Highly dispersive optical solitons and conservation laws in absence of self–phase modulation with new Kudryashov’s approach. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2022, 431, 128001. [Google Scholar] [CrossRef]
- Inc, M.; Aliyu, A.I.; Yusuf, A.; Baleanu, D.; Nuray, E. Complexiton and solitary wave solutions of the coupled nonlinear Maccari’s system using two integration schemes. Mod. Phys. Lett. B 2018, 32, 1850014. [Google Scholar] [CrossRef]
- Patel, P.M.; Pradhan, V.H. Exact Travelling Wave Solutions of Richards’ Equation by Modified F-expansion Method. Procedia Eng. 2015, 127, 759–766. [Google Scholar] [CrossRef]
- Shukri, S.; Al-Khaled, K. The extended tanh method for solving systems of nonlinear wave equations. Appl. Math. Comput. 2010, 217, 1997–2006. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The extended tanh method for the Zakharov-Kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1039–1047. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Abundant solitons solutions for several forms of the fifth-order KdV equation by using the tanh method. Appl. Math. Comput. 2006, 182, 283–300. [Google Scholar] [CrossRef]
- Mbusi, S.O.; Muatjetjeja, B.; Adem, A.R. Exact Lagrangian Formulation, Conservation Laws, Travelling Wave Solutions: A Generalized Benney-Luke Equation. Mathematics 2021, 9, 1480. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Korkmaz, A.; Eslami, M.; Vahidi, J.; Asghari, R. Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt. Quantum Electron. 2018, 50, 1–13. [Google Scholar] [CrossRef]
- Shahoot, A.M.; Alurrfi, K.A.E.; Hassan, I.M.; Almsri, A.M. Solitons and Other Exact Solutions for Two Nonlinear PDEs in Mathematical Physics Using the Generalized Projective Riccati Equations Method. Adv. Math. Phys. 2018, 2018, 6870310. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Arshed, S.; Sameen, F. Bright, dark, kink, singular and periodic soliton solutions of Lakshmanan–Porsezian–Daniel model by generalized projective Riccati equations method. Optik 2021, 241, 167051. [Google Scholar] [CrossRef]
- Kudryashov, N.A. A note on the (G′/G)-expansion method. Appl. Math. Comput. 2010, 217, 1755–1758. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J. Generalized (G′/G)-expansion method and exact traveling wave solutions of the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity in optical fiber materials. Opt. Quantum Electron. 2017, 49, 52. [Google Scholar] [CrossRef]
- Javadi, S.; Moradi, E.; Fardi, M.; Abbasian, S. Solving Equal-width Wave-burgers Equation By (G′/G)-expansion Method. J. Math. Comput. Sci. 2014, 11, 246–251. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Yusuf, A.; Sulaiman, T.A.; Bayram, M.; Aydin, H. Soliton Solutions of (2+1) Dimensional Heisenberg Ferromagnetic Spin Equation by the Extended Rational sine-cosine and sinh-cosh Method. Int. J. Appl. Comput. Math. 2021, 7, 1–17. [Google Scholar] [CrossRef]
- Mahak, N.; Akram, G. Application of extended rational trigonometric techniques to investigate solitary wave solutions. Opt. Quantum Electron. 2021, 53, 1–14. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H.; Wu, J. Soliton solutions to the Fokas system arising in monomode optical fibers. Optik 2022, 251, 168319. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Jadallah, H. New topological and non-topological unidirectional-wave solutions for the modified-mixed KdV equation and bidirectional-waves solutions for the Benjamin Ono equation using recent techniques. J. Ocean Eng. Sci. 2022, 7, 163–169. [Google Scholar] [CrossRef]
- Hassan, M.M.; Abdel-Razek, M.A.; Shoreh, A.A.H. New Exact Solutions of some (2+1)-Dimensional Nonlinear Evolution Equations Via Extended Kudryashov Method. Rep. Math. Phys. 2014, 74, 347–358. [Google Scholar] [CrossRef]
- Yasar, E.; Yildirim, Y.; Adem, A.R. Perturbed optical solitons with spatio-temporal dispersion in (2+1)-dimensions by extended Kudryashov method. Optik 2018, 158, 1–14. [Google Scholar] [CrossRef]
- El-Borai, M.M.; El-Owaidy, H.M.; Ahmed, H.M.; Arnous, A.; Moshokoa, S.; Biswas, A.; Belic, M. Topological and singular soliton solution to Kundu–Eckhaus equation with extended Kudryashov’s method. Optik 2017, 128, 57–62. [Google Scholar] [CrossRef]
- Fu, L.; Yang, H. An Application of (3+1)-Dimensional Time-Space Fractional ZK Model to Analyze the Complex Dust Acoustic Waves. Complexity 2019, 2019, 2806724. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto—Sivashinsky equation. Int. J. Geom. Methods Mod. Phys. 1990, 147, 287–291. [Google Scholar] [CrossRef]
- Hietarinta, J. Hirota’s Bilinear Method and its Generalization. Int. J. Mod. Phys. 1997, 12, 43–51. [Google Scholar] [CrossRef]
- Shuwei, X.; Jingsong, H.; Lihong, W. The Darboux transformation of the derivative nonlinear Schrödinger equation. J. Phys. Math. Theor. 2011, 44, 305203. [Google Scholar] [CrossRef]
- Elsayed, M.E.Z.; Abdul-Ghani, A.-N. The solitary wave ansatz method for finding the exact bright and dark soliton solutions of two nonlinear Schrödinger equations. J. Assoc. Arab. Univ. Basic Appl. Sci. 2016, 24, 184–190. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Niwas, M.; Baleanu, D. The Lie symmetry analysis and exact Jacobi elliptic solutions for the Kawahara–KdV type equations. Results Phys. 2021, 23, 2211–3797. [Google Scholar] [CrossRef]
- Sahoo, S.; Saha Ray, S.; Abdou, M.A.M.; Inc, M.; Chu, Y.-M. New Soliton Solutions of Fractional Jaulent-Miodek System with Symmetry Analysis. Symmetry 2020, 12, 1001. [Google Scholar] [CrossRef]
- Zadeh, A.H.; Jacob, K.; Shah, N.A.; Chung, J.D. Fractional-View Analysis of Jaulent-Miodek Equation via Novel Analytical Techniques. J. Funct. Spaces 2022, 2022, 11. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Magesh, N.; Nandeppanavar, M.M.; John Christopher, A.J. Numerical simulation for fractional Jaulent–Miodek equation associated with energy-dependent Schrödinger potential using two novel techniques. Waves Random Complex Media 2021, 31, 1141–1162. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M.; Shah, R. Approximate Analytical Methods for a Fractional-Order Nonlinear System of Jaulent–Miodek Equation with Energy-Dependent Schrödinger Potential. Waves Random Complex Media 2023, 7, 140. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Xin, X. Explicit solutions, conservation laws of the extended (2+1)-dimensional jaulent-miodek equation. arXiv 2015, arXiv:1512.09196. [Google Scholar] [CrossRef]
- Jaulent, M.; Miodek, I. Nonlinear evolution equations associated with ‘enegry-dependent Schrödinger potentials’. Lett. Math. Phys. 1976, 1, 243–250. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Arshad, M.; Lu, D. The weakly nonlinear wave propagation of the generalized third-order nonlinear Schrödinger equation and its applications. Waves Random Complex Media 2022, 32, 819–831. [Google Scholar] [CrossRef]
- Kamimura, Y. Energy-Dependent Reflectionless Inverse Scattering. Publ. Res. Inst. Math. Sci. 2022, 58, 379–440. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Bayram, M.; Sulaiman, A.T.; Yusuf, A. Solving the fractional Jaulent–Miodek system via a modified Laplace decomposition method. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.S. Exotic wave patterns in Riemann problem of the high-order Jaulent–Miodek equation: Whitham modulation theory. Stud. Appl. Math. 2022, 149, 12513. [Google Scholar] [CrossRef]
- Ma, H.C.; Deng, A.P.; Yu, Y.D. Lie symmetry group of (2+1)-dimensional Jaulent-Miodek equation. Therm. Sci. 2014, 18, 1547–1552. [Google Scholar] [CrossRef]
- Ma, H.C.; Qin, Z.Y.; Deng, A.P. Symmetry transformation and new exact multiple kink and singular kink solutions for (2+1)-dimensional nonlinear models generated by the Jaulent-Miodek Hierarchy. Commun. Theor. Phys. 2013, 59, 141–145. [Google Scholar] [CrossRef]
- Hang-yu, R.; Sen-yue, L. New Symmetries of the Jaulent-Miodek Hierarchy. J. Phys. Soc. Jpn. 1993, 62, 1917–1921. [Google Scholar] [CrossRef]
- Yongyi, G.; Bingmao, D.; Jianming, L. Exact Traveling Wave Solutions to the (2+1)-Dimensional Jaulent-Miodek Equation. Adv. Math. Phys. 2018, 2018, 5971646. [Google Scholar] [CrossRef]
- Geng, X.; Guan, L.; Xue, B. A hierarchy of generalized Jaulent-Miodek equations and their explicit solutions. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850002. [Google Scholar] [CrossRef]
- Taha, W.M.; Noorani, M.S.M. Exact solutions of equation generated by the jaulent-miodek hierarchy by (G′/G)-expansion method. Math. Probl. Eng. 2013, 2013, 392830. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Apeanti, W.O.; Lu, D.; Yaro, D.; Akuamoah, S.W. Dispersive traveling wave solutions of nonlinear optical wave dynamical models. Mod. Phys. Lett. B 2019, 33, 1950120. [Google Scholar] [CrossRef]
- Liu, D.Y.; Tian, B.; Jiang, Y.; Sun, W.R. Soliton solutions and Bäcklund transformations of a (2+1)-dimensional nonlinear evolution equation via the Jaulent–Miodek hierarchy. Nonlinear Dyn. 2014, 78, 2341–2347. [Google Scholar] [CrossRef]
- Feng, D.; Li, J. Bifurcations of travelling wave solutions for Jaulent-Miodek equations. Appl. Math. Mech. (Engl. Ed.) 2007, 28, 999–1005. [Google Scholar] [CrossRef]
- Ji-Huan, H.; Li-Na, Z. Generalized solitary solution and compacton-like solution of the Jaulent–Miodek equations using the Exp-function method. Phys. Lett. A 2008, 372, 1044–1047. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple kink solutions and multiple singular kink solutions for (2+1)-dimensional nonlinear models generated by the Jaulent-Miodek hierarchy. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2009, 373, 1844–1846. [Google Scholar] [CrossRef]
- Mbusi, S.; Muatjetjeja, B.; Adem, A.R. On the exact solutions and conservation laws of a generalized (1+2)-dimensional Jaulent-Miodek equation with a power law nonlinearity. Int. J. Nonlinear Anal. Appl. 2022, 13, 1721–1735. [Google Scholar] [CrossRef]
- Motsepa, T.; Abudiab, M.; Khalique, C. A Study of an Extended Generalized (2+1)-dimensional Jaulent–Miodek Equation. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 391–395. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Seadawy, A.R.; Baber, M.Z.; Qasim, M. Application of modified exponential rational function method to Jaulent–Miodek system leading to exact classical solutions. Chaos Solitons Fractals 2022, 164, 112600. [Google Scholar] [CrossRef]
- Guiping, S.; Jalil, M.; Syed, M.Z.; Dinh, T.N.H.; Trung-Hieu, L. The New Solitary Solutions to the Time-Fractional Coupled Jaulent–Miodek Equation. Discret. Dyn. Nat. Soc. 2021, 2021, 2429334. [Google Scholar] [CrossRef]
- Sadat, R.; Kassem, M. Explicit Solutions for the (2+1)-Dimensional Jaulent–Miodek Equation Using the Integrating Factors Method in an Unbounded Domain. Math. Comput. Appl. 2018, 23, 15. [Google Scholar] [CrossRef]
- Kaewta, S.; Sirisubtawee, S.; Sungnul, S. Application of the exp-function and generalized kudryashov methods for obtaining new exact solutions of certain nonlinear conformable time partial integro-differential equations. Computation 2021, 2021, 52. [Google Scholar] [CrossRef]
- Kaewta, S.; Sirisubtawee, S.; Khansai, N. Explicit Exact Solutions of the (2+1)-Dimensional Integro-Differential Jaulent–Miodek Evolution Equation Using the Reliable Methods. Int. J. Math. Math. Sci. 2020, 2020, 2916395. [Google Scholar] [CrossRef]
- Pei, J.T.; Bai, Y.S. Lie symmetries, conservation laws and exact solutions for Jaulent-Miodek equations. Symmetry 2019, 11, 1319. [Google Scholar] [CrossRef]
- Li, C.; Guo, Q. On the solutions of the space–time fractional coupled Jaulent–Miodek equation associated with energy-dependent Schrödinger potential. Appl. Math. Lett. 2021, 121, 107517. [Google Scholar] [CrossRef]
- Chen, J.; Li, E.; Xue, Y. Evolution of initial discontinuities in the Riemann problem for the Jaulent–Miodek equation with positive dispersion. Appl. Math. Comput. 2022, 419, 126869. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Liu, X.Q.; Wang, G.W. Symmetry reductions and exact solutions of the (2+1)-dimensional Jaulent-Miodek equation. Appl. Math. Comput. 2012, 219, 911–916. [Google Scholar] [CrossRef]
- KLi, J.; Chen, G. On a Class of Singular Nonlinear Traveling Wave Equations. Int. J. Bifurc. Chaos 2007, 17, 4049–4065. [Google Scholar] [CrossRef]
- Li, J.; Chen, F. Exact travelling wave solutions and their dynamical behavior for a class coupled nonlinear wave equations. Discret. Contin. Dyn.-Syst.-D 2013, 18, 163–172. [Google Scholar] [CrossRef]
- Ozisik, M.; Cinar, M.; Secer, A.; Bayram, M. Optical solitons with Kudryashov’s sextic power-law nonlinearity. Optik 2022, 261, 169202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).