Abstract
We seek a simple but physically motivated model of strongly interacting matter applicable in atomic nuclei and the dense matter in the core of neutron stars. For densities below and somewhat above normal nuclear density, energy density functional (EDF) theory based on nucleonic degrees of freedom is the ideal candidate. We have explored that direction within the KIDS (Korea-IBS-Daegu-SKKU) framework, which we review in this contribution. The formalism for the KIDS-EoS and microscopic KIDS-EDF and optimization options for the EDF are described in a practical way to facilitate further applications. At densities higher than one nucleon per single-nucleon volume, i.e., roughly fm, nucleonic degrees of freedom are no longer appropriate. The pseudo-conformal symmetry emergent in dense, topologically altered nuclear matter provides a simple expression for the energy per baryon in terms of the baryonic density. Besides resembling a simple EDF for dense matter, the expression has the appeal that it predicts a converged speed of sound at high densities. It can thus be implemented as a special case of the constant speed of sound (CSS) model. Here we consider a matching between representative nucleonic KIDS-EoSs and the CSS model, including the pseudo-conformal EoS, and apply the unified model to describe the mass–radius relation of neutron stars and examine the compatibility of CSS cores with heavy neutron stars. Although an abrupt transition to the pseudo-conformal regime at low densities does not favor heavy neutron stars, intermediate scenarios including a cusp in the speed of sound are not ruled out, while some appear more favorable to heavy stars than purely nucleonic matter.
1. Introduction
Multi-messenger astronomy and laboratory experiments together with ab initio nuclear structure and the concept of quantified theoretical uncertainties have revolutionized studies of the nuclear equation of state (EoS). Photonic, neutrino, and gravitational detectors on Earth and in space reveal the composition and dynamics of dense celestial objects and thereby the EoS of dense baryonic matter, cold and hot [,,,]. Information on the EoS of nucleonic matter is also obtained, at least indirectly, by studying the shapes and sizes of atomic nuclei and the nature and properties of their excited states through electromagnetic, weak, and hadronic probes [,,,,]. Heavy-ion collisions further sharpen our knowledge of the EoS across densities, temperatures, and isospin asymmetries [,,]. Microscopic calculations with controlled approximations offer valuable additional gauges [,], while Bayesian analyses and machine learning translate the findings into meaningful constraints for the EoS of baryonic matter [,]. The availability of exotic beams at new rare-isotope facilities such as RAON [] could generate even more opportunities to constrain the EoS.
Much of what we know about the EoS in cold matter at subsaturation densities we owe to nuclear data. Connections between measured nuclear masses, sizes, and collective motion are most directly facilitated by energy density functional (EDF) theory at the mean-field level [,,]. The procedure has traditionally been as follows: one first defines a phenomenological in-medium effective interaction (non-relativistic EDF models) or Lagrangian (relativistic models). The Hartree or Hartree–Fock equations, or, for superfluid nuclei, the Hartree–Bogolyubov or Hartree–Fock–Bogolyubov equations are solved for that interaction or Lagrangian. The coupling strength parameters may be density-dependent in order to take into account many-body interactions and correlations beyond mean-field. The parameters of the model are fitted to selected nuclear data. The EoS can then be obtained for infinite matter at the mean-field level as well. Thus the EDF model has served traditionally as an extrapolation tool from nuclei to infinite or dense nuclear matter. The EDF approach is justified in terms of the Hohenberg–Kohn and Kohn–Sham theorems. Linear response theory allows for applications also in excited states within the random-phase approximation.
As additional information is gathered regarding the EoS, especially from heavy-ion collisions and astronomy, EDF models are adjusted accordingly. In the past ten years or so, it was realized that the majority of EDF models fitted to nuclear data extrapolate to unrealistic EoSs and, conversely and more seriously, that imposing realistic EoS parameters to EDFs can lead to very strange results for nuclei [,,,]. Recently, the problem has been overcome in the so-called Korea-IBS-Daegu-SKKU or KIDS framework (named after the locale and institutes of the original developers []) by the use of functionals of extended type. These accommodate realistically the density dependence of the EoS, as dictated by the theory of interacting Fermi systems while decoupling it from largely phenomenological parameters relevant for finite nuclei, namely the in-medium effective mass and gradient terms [,,].
EDF models remain applicable at densities above saturation as long as the nucleonic degrees of freedom remain relevant. The nucleonic picture can be extended to accommodate the change in baryon structure, resulting in additional repulsion and hyperons [,,]. As more hyper-nuclear data accumulate, it will become possible to fit EDF models in the same spirit as nucleonic EDFs. However, the hadronic picture will break down eventually at high densities where quarks may be deconfined or percolate among tightly packed baryons. Whether there is a phase transition or a crossover between hadronic and quark matter is not currently known. Possible phase transitions and the existence of hybrid stars can be investigated by analyzing the products of heavy ion collisions and astronomical data [,].
For describing dense matter, as it might exist in compact stars, and the phase transition or crossover, a number of theoretical scenarios are under investigation [,]. Quark models include most prominently the bag model and extensions [,,] and (Polyakov–) Nambu–Jona–Lasinio models [,,,,]. Also employed are quark mass scaling [], quantum Skyrmion crystals [], the related pseudo-conformal model stemming from a chiral-scale symmetric effective field theory [], the isospin-dependent confining quark matter (ICQM), and confined-isospin and density-dependent mass (CIDDM) models []. Lattice calculations are also applied []. A useful constraint for the validity of any model at high densities is provided by the predicted speed of sound u, which must remain lower than the speed of light in vacuum c, and eventually approach the conformal limit of . For modeling purposes, one may assume a constant speed of sound in some density regime []. The possibility to infer the quark-hadron crossover from merger and postmerger observations of binary neutron stars has been discussed in [].
In this work we are exploring the constant speed of sound (CSS) modeling of dense matter, of which the pseudo-conformal model also discussed in this issue [] can be considered a special case. Simplicity and versatility as well as a good physical grounding are important reasons for adopting the CSS and pseudo-conformal models. Like the nucleonic KIDS model, we need not make a priori assumptions about what constitutes a “physical” parameter space for the model itself, only a sound physical motivation for the formalism and respect of certain generic physical principles. The physical motivation here lies in the scale and local symmetries hidden in the QCD vacuum but emergent at high scales and leading to the pseudo-conformal regime [,], while the generic principles are causality or conformality.
Confrontation even of simple models with observations can lead to new insights. For example, although KIDS was formulated as a nucleonic model, confrontation with astronomical data revealed the need for the symmetry energy, which is generally predicted moderately soft at saturation density, to stiffen at high density, showing an inflection point in the vicinity of twice the saturation density. The stiffening may be attributed to beyond-nucleonic degrees of freedom, following a phase transition or crossover. It is consistent with the findings of some of the quark models mentioned above as well as more agnostic statistical or model-independent approaches [,], while a cusp in the speed of sound associated with stiffening followed by softening has also been discussed [,,,,]. Our purpose here is to extend our modeling, without compromising its simplicity at this point, so as to examine this consistency further.
The manuscript is organized as follows. In Section 2, we review the formalism required in the description of cold non-rotating neutron stars. In Section 3, we provide a comprehensive overview of the KIDS formalism for the EoS and EDF and a summary of existing applications. This material has only been published in a fragmentary manner before and we hope that the present exposition will facilitate further applications. We provide the formalism for the CSS model in Section 4. In Section 5, we specify the parameter sets used in this work and we present and discuss our results. We conclude in Section 6.
2. Description of Cold Static Neutron Stars
In order to obtain the macroscopic structure of a non-rotating neutron star under the assumption of spherical symmetry, we solve numerically the Tolman-Oppenheimer-Volkoff (TOV) equations [,],
resulting from the general relativistic hydrostatic equations. In the above, G is Newton’s gravitational constant, is the amount of mass enclosed by a sphere of radius r around the star’s center, is the pressure at distance r from the center, and is the energy density at distance r. In practice, what is required is a tabulation of the baryonic density , pressure , and energy density , across a broad density regime from practically zero to several times the saturation density and assuming charge-neutral matter in equilibrium. The tabulated values are to be input into a numerical code that solves the above TOV equations. At each possible central density (density at the center of the star), the code yields the radius and total mass of the star []. The relation between the latter two quantities defines the neutron star mass–radius (NSMR) relation and is a major point of comparison with observations.
For calculating and tabulating the input quantities, an EoS model for stable matter is required. The composition of stable matter, for example, the proton fraction and the lepton content in homogeneous matter, depends on the density. The density and composition in turn determine the pressure and energy density according to the given model.
We will distinguish three density regimes and match the corresponding EoSs: the dilute, non-homogeneous regime in the crust, the homogeneous primarily nucleonic matter in the saturation regime (potentially up to a few times the saturation density), and the putative homogeneous quark matter in dense stellar cores. The description of the first regime, involving lattice structures, nuclear clusters, and pasta phases, goes beyond the scope of the present work, so for the EoS at low densities relevant to the crust, we will adopt existing models from the literature, specifically tabulations of the SLy [], BPS [], and D1M* [] EoSs. For the homogeneous phase in the saturation regime, we will employ the KIDS EoS, which is extensively presented in Section 3. It provides analytical expressions for the energy per particle as a function of the density and isospin asymmetry. For possible quark matter in dense stellar cores, we employ the CSS model, which is analytical. We will not make explicit assumptions about the precise composition of matter, which instead is encoded in the parameters. The expressions are presented in Section 4.
For the homogeneous nucleonic regime, it remains to numerically determine the predicted composition of matter and from that the total energy density and pressure of stable matter as follows. We define the total nucleon density in homogeneous nucleonic matter, the asymmetry density , and the isospin asymmetry ,
so that
and assume that a nucleonic EoS is given, such as KIDS, characterized by the energy per particle . Let us also introduce the nuclear symmetry energy, which is defined as the difference between the energy of pure neutron matter (PNM) and symmetric nuclear matter (SNM),
or, more commonly, from the second derivative with respect to the asymmetry at the saturation point of SNM,
The numerical difference is marginal for KIDS models. In the numerical applications of Section 5 we use , but for the sake of completeness, in Section 3 we will provide expressions for both cases. There will also be leptons present, specifically electrons and beyond a certain density also muons, whose number densities , we can calculate based on the conditions of charge neutrality and equilibrium. We first define the proton fraction , the electron fraction , and the muon fraction . We also define the chemical potential of each type of particle i (we trust that there will be no confusion between as a symbol for the chemical potential of particle i and as a symbol for the muon). We assume the state of the electron or muon gas to be that of a cold relativistic non-interacting Fermi gas characterized by a respective Fermi momentum . The chemical potentials are given by
where the electron mass is considered negligibly small. For the chemical potentials of protons and neutrons, whose mass we denote m, and by virtue of
we have
Charge neutrality dictates that
The following reactions, which also involve the electron and muon neutrinos, , are assumed to be in chemical equilibrium (the first pair of reactions give these conditions the name β equilibrium):
In equilibrium, the above lead to the following relations among the chemical potentials,
where we have used . The above also implies
The last two equations define the conditions for equilibrium and are routinely solved in cold neutron star matter calculations. The key EoS quantity is clearly the symmetry energy.
For a given symmetry energy model and at given density , Equations (15) and (16) can be solved for the proton and lepton fractions and, therefore, also for the asymmetry . Then we can obtain the total energy density as the sum of the nuclear, electron, and muon energy densities,
where m is the nucleon mass and is the mass of lepton . The nucleon is treated non-relativistically, while the electron is considered ultra-relativistic. Finally, we obtain the pressure as
The speed of sound u through the nuclear medium can also be calculated,
The matching of the KIDS EoS with the dilute-matter EoS is done at the density where the KIDS model gives mechanically unstable matter. For the matching with CSS at high density, see Section 4.
3. KIDS Framework for the EoS and EDF of Nucleonic Matter and CSS Extension
The KIDS theoretical framework for the nuclear EoS and EDF [,] is based on a power expansion of the nuclear matter energy per particle in terms of the Fermi momentum—equivalently, the cubic root of the density. An expansion in powers of is justified with arguments from effective field theories and the theory of interacting Fermi systems as discussed in Ref. []. The reader is encouraged to turn to that publication for quantitative details. We summarize here the qualitative points for the sake of completeness.
Following a textbook example [], let us assume a local interaction between nucleons with an infinitely repulsive core and a longer-range attractive part of finite depth. Let us label the ranges of the core and attraction and , respectively. The contribution of the repulsive core to the potential energy per particle in infinite nuclear matter is given by Brueckner’s theory as a sum of terms proportional to , , etc., slowly converging to . The contribution of the attractive part is given in closed analytical form involving trigonometric functions and integrals of and , which can also be expanded in ascending odd powers of with expansion coefficients which quickly diminish for higher powers. This basic approach [] already suggests a expansion for the energy per particle of nuclear matter. The importance of the and terms, in particular, for obtaining the empirical saturation regime of symmetric matter has been shown explicitly in the three-loop approximation of chiral perturbation theory [].
Indeed, another way to justify the Fermi momentum expansion is via effective field theories. In the particular case of very dilute Fermi systems, the expression for the energy per particle is also obtained as a polynomial expansion in plus logarithmic functions arising from three-fermion forces []. The expansion coefficients depend on the scattering lengths and effective ranges of the interaction terms. Nuclear matter near saturation densities is arguably far from dilute. However, certain arguments can be made that it is dilute in terms of relevant physics, for instance in an effective theory without pions. The one-pion-exchange potential vanishes in nuclear matter and its mean field potential does not appear in the nucleonic fluid. Pionic contributions through loops and multipion exchanges will have an effect that can perhaps be absorbed in the in-medium couplings among nucleons and heavier mesons. The next heavier meson is , whose mass (775 MeV or 4 fm) can be treated as a large scale within some effective Lagrangian expressed in powers of applicable to matter not too far from the saturation point (where fm). Of course, the coefficients of such a Lagrangian would have to be fitted a posteriori.
The KIDS approach originates from such an idea. In Ref. [], expansions in including a logarithmic term were fitted to pseudodata from ab initio calculations in nuclear matter and the fits were analyzed statistically to determine the type and number of terms that capture the relevant physics without risking overfitting. Thus, the optimal number of low-order expansion terms for describing normal and neutron star matter was found to be four terms (three for symmetric matter) with no need for a logarithmic term. In addition, the naturalness of the coefficients was confirmed by defining corresponding dimensionless coefficients, inspecting their values after the optimal fit, and finding them to be of the order of one []. The power expansion was further explored with the aid of more pseudodata in Ref. [].
The KIDS EoS can easily be transposed to an EDF for finite nuclei in the form of a Skyrme functional with extended density dependence. Of course, in addition to the EoS coefficients, for nuclei, one needs to determine also the gradient terms of the functional, represented by the isoscalar (IS) and isovector (IV) coupling parameters and , the IS and IV in-medium effective mass, and , represented by the coupling parameters and , and at least one spin-orbit coupling term (see, e.g., Ref. []). A crucial novelty is that in the KIDS framework, unlike traditional Skyrme models, the above EDF parameters are determined without altering the EoS of homogeneous matter at all: any density dependence introduced to the EDF through the effective mass choice, for the purpose of describing nuclei or dynamic phenomena, is compensated for in the EoS of homogeneous matter by an equal and opposite density-dependent term of the same form , while the gradient and spin-orbit terms leave no contribution to the EoS of infinite matter. The purpose is to be able to test any given EoS in nuclei as it is. Conversely, a KIDS-type EDF, viewed as an extended Skyrme functional, leads to a homogeneous-matter EoS in a straightforward manner.
We would like to stress that in this framework, the density dependence of the SNM EoS and of the symmetry energy is completely agnostic with respect to the momentum-dependent terms introduced for the description of nuclei: it would be the same whether there were momentum-dependent terms or not. This versatility makes it possible to reconcile homogeneous matter and nuclei and is absent from traditional functionals.
Next, we provide the formalism of the KIDS EoS and EDF and summarize recent applications.
3.1. General Expression for the KIDS Equation of State (KIDS EoS)
We consider homogeneous, unpolarized nuclear matter at zero temperature and without strangeness (extensions are possible in Ref. []). The proton or neutron Fermi momentum is given by
Recall that the kinetic energy per particle of a non-interacting Fermi gas consisting of protons and neutrons with equal masses m is given by
where . Let us also define for later use
In the KIDS ansatz, the potential energy per particle is expanded in powers of the Fermi momentum or equivalently of the cubic root of the density so that the energy per particle is given by
where the isospin dependence of the interaction contribution to is absorbed in the coefficients . The quadratic approximation for the isospin dependence is expressed as
More precisely, taking into account the momentum dependence of an EDF of Skyrme type, an exception must be made for :
where , , as well as and are constants, which we will relate to Skyrme-type parameters on the one hand and standard parameters of the equation of state (EoS) on the other. We also defined for brevity
Note that
Equations (22)–(24), define the KIDS EoS. The necessary EoS parameters are , , , and , and we may call them the KIDS-EoS parameters. Their connections with the standard EoS parameters defined at the saturation point are analytical and straightforward. As mentioned earlier, and determine the IS and IV in-medium effective masses, and . At saturation density we have
Setting implies and simplifies the expression for to the exactly quadratic form.
For most purposes, it suffices to consider three expansion terms, for symmetric nuclear matter (SNM) and four expansion terms , for pure neutron matter (PNM) [,]. In other words, we usually consider four expansion terms () but set . The only reason is that for most purposes additional terms in SNM or PNM have been found inconsequential. Generally, depending on the application (e.g., exploring the role of high-order EoS terms in various observables) any number of terms can be considered (see also the next section, where we provide the general expressions). In addition, if deemed necessary or potentially interesting, one can extend the formalism to include higher-order momentum-dependent terms.
3.2. Standard EoS Parameters in the KIDS Framework
As already described, the KIDS EoS is based on an expansion in . The corresponding expansion coefficients suffice to proceed to further studies and calculations. However, most practitioners for decades have compared and benchmarked their results in terms of Taylor expansion coefficients of around the saturation density [,,,,,,,]. For the purpose of comparison and easier communication, we must calculate those coefficients as well. In addition, to the extent that the lowest-order Taylor expansion coefficients are relatively well known, such coefficients also provide a good starting point for explorations with KIDS. Therefore, here we provide the expressions needed to “translate” the KIDS language to the Taylor-expansion language and vice versa. The expansions will of course become unusable outside the nucleonic fluid phase.
First, let us review the relevant parameters. For SNM, let us consider the saturation density , the saturation energy per particle , the compression modulus , and optionally the skewness parameters ,
Higher-order parameters can also be considered at will.
The symmetry energy as a function of the density, , was defined in Section 2, Equations (3) (difference) or (4) (derivative). The numerical difference between the two definitions is minor for all density domains (e.g., typical nuclear densities) where the quadratic approximation can be considered good. The KIDS ansatz gives
where, depending on the definition used,
Standard parameters describing the density dependence of the symmetry energy are also defined by convention as Taylor-expansion coefficients around the saturation density. Thus, we can define, besides the value J at saturation density, the slope parameter L, the curvature , the skewness parameter ,
and higher-order parameters . In order to determine the KIDS-EoS parameters giving a specific set of standard EoS parameters, we differentiate the KIDS EoS as necessary, obtain the standard coefficients as linear functions of the KIDS coefficients multiplied by the respective powers of , and invert the resulting algebraic system. For SNM, the system reads
where
The expressions for the symmetry energy parameters are completely analogous. For 3–4 SNM terms and 4 PNM or terms, we next provide the expressions obtained after the matrix inversion.
Suppose we are given the values for the SNM parameters , , and and optionally , and for the symmetry-energy the parameters J, L, , . What is the corresponding KIDS EoS? In order to answer uniquely, we need also the values for the effective masses, and . If we are unconcerned about them, we may set them equal to one. That would mean and the quadratic approximation holding exactly. However, in the general case, we have, inverting Equation (28),
and we find:
- For symmetric matter: if is unspecified, and the inversion of the system givesIf is also specified (), inversion of the system gives
- For the symmetry energy, the inversion of the system giveswhere and depend on the definition used for the symmetry energy, see Equation (32).
3.3. KIDS EoS and Skyrme-Like Functional
The utility of the KIDS-EoS is that it can be generated by an extended Skyrme-type effective interaction in the Hartree–Fock (HF) approximation and thus can be applied to nuclear structure and response like any microscopic EDF. The Skyrme interaction is of zero range and here it is extended to include more than one density-dependent term,
The notation used is standard except that we have made the substitution
The interaction includes momentum-dependent terms (parameters ) and a spin-orbit term (parameter ). The corresponding energy per particle in HF, which defines the corresponding KIDS EDF, is given by
where we have introduced also the IS and IV current densities. Let us also denote the contribution of the gradient terms in the shorthand
where
Matching with Equation (22) and taking into account that , we obtain the transformations from the KIDS parameters to the Skyrme parameters. In the next subsection, we wrap up the procedure. The inverse procedure, from a KIDS-EDF to an EoS, according to Equation (42) is of course straightforward.
For applications to open-shell nuclei within HF-Bogoliubov and quasiparticle RPA models, pairing parameters can also be considered [].
3.4. From EoS to EDF in Practice
In practice, when we want to test a specific set of EoS parameters in nuclei, we need to solve the following problem: Given the EoS parameters including the effective masses (see Equations (28) and (37)) and the gradient coefficients of Equation (43), what are the corresponding extended-Skyrme parameters of Equation (41), which we can employ in standard HF or RPA codes? (Note that the EoS parameters may be given as such [] or determined from a fit of the KIDS ansatz, Equation (22), to pseudodata from ab initio calculations [,,].) Once this procedure is set up, it can be used, for example, to find the optimal gradient parameters and/or for a given EoS, or it could be used to actually fit the EoS, effective mass, or gradient terms to nuclei—directly, without the use of the Skyrme-type parameters , etc. The spin-orbit parameter does not enter the EoS of homogeneous matter, so it does not need special consideration in the transformation from EoS to EDF. Of course, it is necessary for describing nuclei and it may be found correlated with the gradient terms when all are optimized. The same holds for pairing parameters necessary for open-shell nuclei.
First, let us assume we have selected the SNM parameters and the IS effective mass . Then Equation (37) provides , Equation (38) provides , and finally
We can also specify if we wish, use Equation (39) instead of (38), and obtain . Next, we consider the isovector quantities. We specify , and , solve Equation (40) for with given by Equation (37), and finally obtain
As in standard Skyrme, for and we need both and the gradient coefficients of Equation (43):
Note that the minus sign in the transformation of the gradient terms is because we write the contribution in the form
instead of . The expressions of and in terms of are given in Equation (44). The spin-orbit coupling decouples from all equations. Its value can be set independently or fitted to data. Note that the gradient terms and are not active in homogeneous matter, so we may fit them to nuclear data for any given EoS of homogeneous matter and effective mass values, without affecting the homogeneous EoS at all.
As regards the kinetic and gradient terms and the spin-orbit parameter, three methods have been in use to determine them for a given EoS:
- The most rudimentary option is to split the EoS term into a term , which will provide the parameters of the Skyrme-type functional (for ), and the rest, , which will provide a genuine density-dependent term. The optimal values of the constant k and at the same time are determined by a fit to a minimal amount of data (masses and radii of three nuclei). This simple procedure, first explored in [], typically leads to a close to one. It is good enough for inspecting bulk nuclear and neutron-star properties [,,], but is quite restrictive when looking at, e.g., single-particle spectra and collective excitations.
- A second option is to select, besides the EoS parameters, the desired values for the effective masses; and then, determine by a fit to nuclei. This method has been used, e.g., in the proof-of-concept study of Ref. [] and in additional applications in Ref. []. Once spectroscopic or dynamic properties are considered, the in-medium effective mass should also come into play [,,,,,] and it can be fitted as well. It may be also relevant for a precision fit to nuclear masses, which is underway.
- A third option is to choose, besides the EoS and the effective masses, the values of , , and from the beginning. This is useful for inspecting trends [] (by independently varying each variable) or to reduce the parameter space [].
Next, we summarize the various applications of KIDS so far.
3.5. Summary of Applications
KIDS was introduced in Ref. [] in order to carry over what we know from quantum many-body theory and from effective field theories about the static, cold, homogeneous Fermi system of nuclear matter, namely that its energetics are expressed in terms of the Fermi momentum or the cubic root of the density, into a model for homogeneous matter and eventually for nuclei. Fits to EoS pseudodata from ab initio calculations revealed the naturalness of the power expansion and its convergeness [,]. It was also realized that any density dependence of the EoS can be generated by a Skyrme-type EDF with extended density dependence. The reverse engineering of the EDF for nuclei from the EoS of homogeneous matter was first demonstrated in Ref. [] and carried out more fully in Ref. [] and finally in Ref. [], where the APR EoS was converted to a Skyrme-type functional and was shown to give realistic results for closed-shell nuclei regardless of what we assumed for the effective mass. Noting that such a model, closely resembling the Skyrme functional, can be very easily implemented in existing nuclear structure codes (Hartree Fock, RPA, etc.), it is obvious that the framework offers enormous versatility in different directions, for example in exploring homogeneous matter or the influence of the effective mass in dynamic properties, as shown in subsequent applications. It can also be extended for application to hypernuclei, as shown in Ref. [].
Having demonstrated in Refs. [,] that four terms in the expansion suffice for many applications in nuclei and neutron stars and taking advantage of the framework’s flexibility, we have used it to constrain the curvature parameter of the symmetry energy [,,]. Binding energies and radii of closed-shell nuclei and the Sn isotopic chain as well as the NSMR relation and deformability were used to constrain the parameter space. Pairing parameters were introduced for this purpose in Ref. []. Thus we were able to conclude that must be negative (possibly below MeV) and no lower than MeV (possibly higher than MeV). Also shown was that traditional EoS/EDF models (more explicitly, Skyrme models) are overly restrictive, imposing extremely tight artificial correlations between EoS parameters, for instance between and []. This insight was conclusively confirmed by a Bayesian analysis of both isoscalar and isovector nuclear properties, including giant resonances and the neutron skin thickness, within KIDS and Skyrme models []. There, it was also shown that cannot be constrained from nuclear properties alone but requires input from higher densities as well, such as those offered by astronomical observations and heavy-ion collisions.
A related observation in Ref. [] was that the neutron-skin thickness of nuclei and the properties of neutron stars are not correlated within KIDS, i.e., the properties of dilute matter and dense matter decouple, suggesting that varying degrees of freedom come into play. Preliminary studies devoted to the neutron skin thickness and aiming to help resolve the PREX-CREX discrepancy seem to confirm this view [] and further work is in progress. We note that predictions for the neutron skin thickness coming from KIDS EoSs as constrained in Ref. [], offer predictions in line with other EDFs [].
Besides these developments on the EoS front, the KIDS model has recently also been applied to lepton-nucleus scattering, especially in view of the role that the effective nucleon mass plays in the cross-section predictions. Both inclusive and exclusive electron scattering were considered in the quasi-elastic regime. Comparisons of KIDS predictions with exclusive electron scattering data were found to favor models with a high IS effective mass, i.e., close to one []. The exploration was extended to inclusive electron scattering in Ref. [] which considers also variations in the symmetry energy slope parameter. Comparisons with data also seem to favor an effective mass close to the free nucleon mass. Neutrino-nucleus scattering was investigated in Ref. []. The total cross section was found independent from the effective mass, so the axial mass could be determined independently. Recently, the effect of the nucleon effective mass and symmetry energy on the neutrino mean free path in a neutron star was examined [] with important consequences for cooling and neutrino trapping.
4. Constant Speed of Sound Model and Pseudo-Conformal Dense Matter
An interesting finding of the KIDS analyses is the apparent necessity for the EoS to stiffen at high density in order to support a heavy neutron star [,]. Specifically, the symmetry energy is predicted to have an inflection point below or at roughly and signifies a possible phase transition or the activation of new degrees of freedom. An early example is the Akmal–Pandharipande–Ravenhal (APR) EoS [], where pion condensation gives rise to an inflection point at . Currently, it is conjectured that hadronic matter might cross over to quarkyonic matter at high densities and support very heavy neutron stars [,] or very compact (small) third-family neutron stars [,]. The crossover density could be inferred from measurements by next-generation gravitational wave detectors []. In Ref. [], the mechanism of parity doubling is proposed to be activated at about two times saturation density and lead to the onset of a pseudo-conformal state with . This result which is discussed also in Ref. [] in this issue, was the motivation for the present study.
A common prediction of hybrid EoSs is that the speed of sound is not a monotonic function of the density, but peaks at some density well above the saturation regime, reaching roughly , and then drops and stabilizes at the conformal limit of . In that case, the upper limit for the central density of a neutron star could increase considerably. The conformal limit is not expected to be reached abruptly, so in principle, we need to model the crossover regime between nucleonic and conformal matter in a smooth way. Here we will explore a much simpler scenario: up to some density, where an as yet unspecified value is reached for the speed of sound, we will use the nucleonic EoS; above that density, a constant speed of sound (CSS) is assumed. The value of the CSS may be either the conformal one or a different one. The purpose of this exercise is to examine the trends and possibilities and gain guidance for future realistic parameterizations of unified EoSs.
If we assume a priori that is constant, and given that , we readily obtain that the energy density and pressure must be given by
The constants B and D remain to be determined. In the special case of , we have
The following values are suggested in Ref. [] for the coefficients B and D (based on Equation (53) therein and the associated density fm):
For matching the KIDS EoS and the CSS EoS, a number of scenarios can be considered. For , we could employ the parameter set already obtained in Ref. [] and interpolate at some high density, e.g., at about two times saturation density as suggested in that work. Here we will rather take advantage of the observation that the relations (49) remain valid for equilibrium matter (at least if one adopts the quadratic approximation for the dependence on isospin asymmetry, which is not necessarily valid, but is made here lacking a better option). Then the isospin degree of freedom need not be considered explicitly. Let us then simply assume that, up to some onset density , matter is described by KIDS, while beyond that, the total energy density and the pressure are given by Equation (49). Further assuming that at both P and are continuous (also not necessarily true in the presence of a phase transition), we can determine B and D from the values, according to the KIDS model, at the onset density, , . We get
As matching density we will choose the density at which the speed of sound in the KIDS model reaches a specific maximal value . The constant at higher densities will be
The values we will consider to explore for are from to .
5. Results and Discussion
We will now apply the standard KIDS EoS and different extensions to dense matter in the description of stable matter and the NSMR relation. As already mentioned, for the dilute, clusterized phase, which has not yet been modeled consistently within KIDS but is necessary for describing the neutron star crust, we employ three different EoSs from the literature, specifically the SLy [], BPS [], and D1M* [] EoSs. Since the crust EoS affects predictions for the neutron star radius in particular, the use of three different models will give us some measure of model uncertainty in this respect. For the homogeneous regime, we will use three representative KIDS EoS sets, labeled here KIDS-P4, KIDS-46, and KIDS-65. For SNM, all three of them are characterized by the same parameters,
For KIDS-P4, the EoS of pure neutron matter was obtained by a fit to the APR EoS [,]. The KIDS-46 and KIDS-65 sets, labeled here for convenience according to their L value, were obtained by adjusting to gross nuclear properties as well as the NSMR relation []. The corresponding symmetry energy parameters are given in Table 1.

Table 1.
Analytical EoS parameters used in this work. The numbers tabulated under “Symm. Energy” correspond to in units of MeV. The numbers tabulated under “Extension()” correspond to the values of in units of (fm, MeV fm, MeV/fm), respectively, where is the assumed onset condition for the CSS EoS, at which point the baryonic density is , while or is the speed of sound at higher densities. The density, energy per particle, and compression modulus of symmetric nuclear matter are set to the respective values, fm, MeV, and 240 MeV, at saturation.
The energy per particle in SNM, stable matter, and PNM, the symmetry energy, and the speed of sound in stable matter as functions of the density are shown in Figure 1. Also shown are the basic properties of nuclei calculated with respective EDFs. Specifically, shown are the energy per particle and charge radius for the closed-shell nuclei
For the purposes of this illustration, the effective mass and gradient terms of the EDFs are kept fixed to , , MeV fm, and MeV fm. Only the spin-orbit coupling strength is fitted to the shown data (19 data), resulting in the following values in units of MeV fm: 114 for KIDS-46, 111 for KIDS-65, and 128 for KIDS-P4. The average relative deviation per experimental datum for these values is of the order of . We note that for all three models, reaches at a density about fm and it does not reach the causality limit until very high densities. We point out again the stiffening of the EoSs at high densities. The three EoSs can support a two-solar-mass neutron star [,].
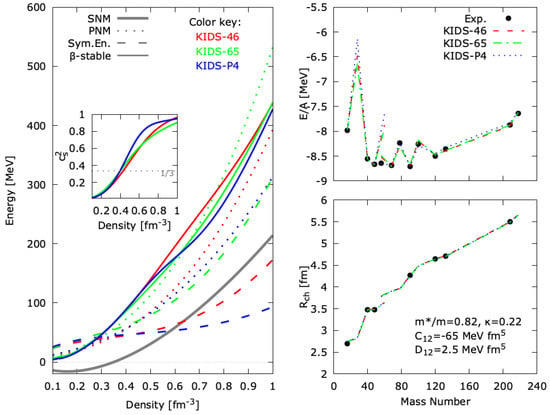
Figure 1.
The three nucleonic EoSs used in this work and corresponding results for selected nuclei. The EoS of symmetric nuclear matter (SNM) is the same for all three. For KIDS-P4, the EoS of pure nuclear matter (PNM) was obtained by a fit to the APR EoS [,]. The KIDS-46 ( MeV) and KIDS-65 ( MeV) sets were obtained by adjusting to gross nuclear properties as well as the NSMR relation []. Left: energy per particle for SNM, PNM, and stable matter and the symmetry energy as a function of nucleon density. Inset: speed of sound for stable matter. Right: nuclear masses (top) and charge radii (bottom) for the nuclei O, Ca, Ni, Zr, Sn, Pb, U. Lines are drawn to guide the eye. For the purposes of this illustration, the effective mass and gradient terms of the EDFs are kept fixed to the values shown, while the spin-orbit coupling strength is fitted to the shown data, resulting in the following values in units of MeV fm: 114 for KIDS-46, 111 for KIDS-65, and 128 for KIDS-P4.
Next, we consider different matches with the CSS model and examine the resulting NSMR relation. First, we find the density at which the speed of sound in stable matter according to the KIDS model reaches a given value, . We also calculate the pressure and energy density at that density according to the KIDS model. Assuming that at densities higher than the speed of sound is steady, we then determine the CSS parameters B and D from Equations (53).
The resulting total unified EoSs and the NSMR relations for are shown in Figure 2 while the results for are shown in Figure 3. Specifically, regarding EoS, we show the pressure as a function of the baryonic density and of the energy density. We also show the speed of sound as a function of the density.
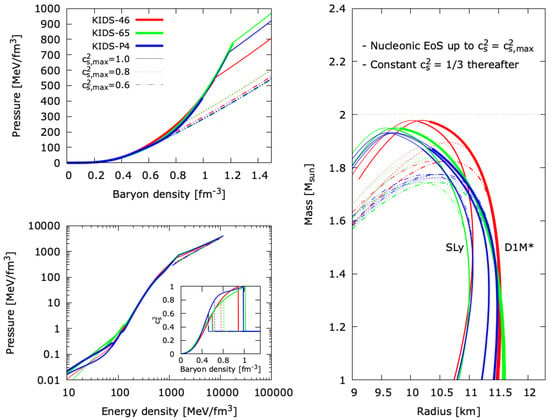
Figure 2.
Pressure as a function of the baryonic density and of the energy density and speed of sound as a function of the baryonic density (left), and neutron star mass–radius relations (right) for the EoSs considered in this work, specifically: the KIDS-46, KIDS-65, and KIDS-P4 nucleonic EoSs (see Figure 1) are adopted up to the density where the speed of sound reaches the indicated maximum value (thick continuous lines); thereafter, the constant speed of sound, pseudo-conformal EoS for is adopted (thin lines), assuming an abrupt crossover (see text). The EoSs are matched at low densities to the crustal EoSs SLy, BPS, or D1M* models, leading to the lowest, middle, and highest radius for a canonical star, respectively.
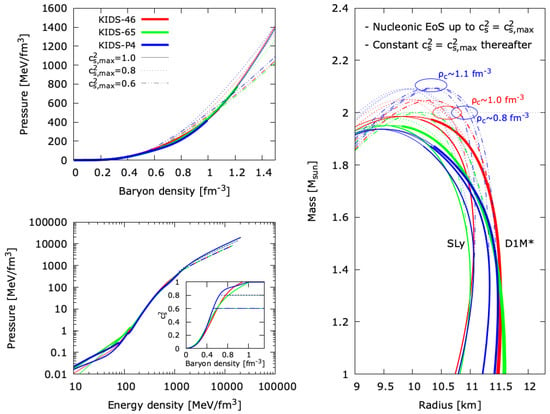
Figure 3.
Pressure as a function of the baryonic density and of the energy density and speed of sound as a function of the baryonic density (left), and neutron star mass–radius relations (right) for the EoSs considered in this work, specifically: the KIDS-46, KIDS-65, and KIDS-P4 nucleonic EoSs (see Figure 1) are adopted up to the density where the speed of sound reaches the indicated maximum value (thick continuous lines); thereafter, the constant speed of sound EoS for is adopted (thin lines), assuming a smooth crossover (see text). Also indicated are characteristic values of a heavy neutron star’s central baryonic density. The EoSs are matched at low densities to the crustal EoSs SLy, BPS, or D1M* models, leading to the lowest, middle, and highest radius for a canonical star, respectively.
From Figure 2, we conclude that such an abrupt crossover to the conformal limit does not easily support a heavy star unless we allow the speed of sound to approach the causality limit . The softening of the EoS is visible in the pressure plots. We should comment at this point that, possibly owing to different computational details such as the very simplistic matchings used here between the crust and core EoSs, the present calculations predict somewhat lower maximal solar masses than those of Refs. [,]. The uncertainty for the radius of a canonical star is of the order of half a kilometer.
From Figure 3, we observe that if the speed of sound is permitted to reach a relatively high value such as those considered here and remain steady for a broader density regime, rather than drop quickly to the conformal limit, the EoS can support even heavier stars than with only a nucleonic EoS. In the present simplistic calculations, a maximal mass is found for an intermediate value . A scenario where the speed of sound peaks around is consistent with other studies. We observe also that the radius of a massive star can be comparable with, i.e., not much smaller than the radius of a canonical star. Finally, in all scenarios, very dense stars are predicted to be viable.
6. Conclusions
We have reviewed the KIDS framework for the nuclear EoS and EDF and sought a physically motivated extension to dense matter, where the nucleonic degrees of freedom are not necessarily justified. As physical motivation, we have considered the pseudo-conformal symmetry emergent in dense, topologically altered nuclear matter, which leads to a converged speed of sound at high densities and thus provides a simple expression for the energy per baryon in terms of the baryonic density as a special case of the CSS model. Here we resorted to a simple matching between representative nucleonic KIDS-EoSs and the CSS model, including the pseudo-conformal EoS, and applied the unified model to describe the mass–radius relation of neutron stars and examine the compatibility of CSS cores with heavy neutron stars. Although an abrupt transition to the pseudo-conformal regime at low densities does not favor heavy neutron stars, intermediate scenarios including a cusp in the speed of sound are not ruled out, while some appear more favorable to heavy stars than purely nucleonic matter. Improvements are needed in the EoS interpolations between the dense, near-saturated, and dilute regimes for more accurate results, but we expect our conclusions to remain valid.
Author Contributions
Conceptualization, P.P. and C.H.H.; Calculation and visualization, P.P.; Writing, P.P. and C.H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Rare Isotope Science Project of the Institute for Basic Science funded by the Ministry of Science, ICT and Future Planning and the National Research Foundation (NRF) of Korea (2013M7A1A1075764) and by the NRF grants of the Korean government No. 2018R1A5A1025563 and No. 2020R1F1A1052495. The APC was funded by the National Research Foundation (NRF) of Korea, grant number 2018R1A5A1025563.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Mannque Rho for suggesting such a study and Taehyun Kim for sharing his numerical code for solving the TOV equations [].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSS | Constant Speed of Sound |
| EDF | Energy Density Functional |
| EoS | Equation of State |
| NSMR | Neutron Star Mass–Radius |
| PNM | Pure Neutron Matter |
| SNM | Symmetric Nuclear Matter |
| TOV | Tolman–Oppenheimer–Volkoff |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Pang, P.T.; Dietrich, T.; Coughlin, M.W.; Bulla, M.; Tews, I.; Almualla, M.; Barna, T.; Kiendrebeogo, W.; Kunert, N.; Mansingh, G.; et al. NMMA: A nuclear-physics and multi-messenger astrophysics framework to analyze binary neutron star mergers. arXiv 2022, arXiv:2205.08513. [Google Scholar]
- Aumann, T.; Bertulani, C.A.; Schindler, F.; Typel, S. Peeling Off Neutron Skins from Neutron-Rich Nuclei: Constraints on the Symmetry Energy from Neutron-Removal Cross Sections. Phys. Rev. Lett. 2017, 119, 262501. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Paar, N. Nuclear equation of state from ground and collective excited state properties of nuclei. Prog. Part. Nucl. Phys. 2018, 101, 96–176. [Google Scholar] [CrossRef]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55–95. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; Benesch, J.F.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; Benesch, J.F.; et al. Precision Determination of the Neutral Weak Form Factor of 48Ca. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: Experiment, theory, and observation. J. Phys. G 2014, 41, 093001. [Google Scholar] [CrossRef]
- Lynch, W.; Tsang, M. Decoding the density dependence of the nuclear symmetry energy. Phys. Lett. B 2022, 830, 137098. [Google Scholar] [CrossRef]
- Drischler, C.; Bogner, S.K. A Brief Account of Steven Weinberg’s Legacy in ab initio Many-Body Theory. Few-Body Syst. 2021, 62, 109. [Google Scholar] [CrossRef]
- Gezerlis, A.; Tews, I.; Epelbaum, E.; Gandolfi, S.; Hebeler, K.; Nogga, A.; Schwenk, A. Quantum Monte Carlo Calculations with Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2013, 111, 032501. [Google Scholar] [CrossRef] [PubMed]
- Newton, W.G.; Crocombe, G. Nuclear symmetry energy from neutron skins and pure neutron matter in a Bayesian framework. Phys. Rev. C 2021, 103, 064323. [Google Scholar] [CrossRef]
- Xu, J.; Papakonstantinou, P. Bayesian inference of finite-nuclei observables based on the KIDS model. Phys. Rev. C 2022, 105, 044305. [Google Scholar] [CrossRef]
- Jeong, S.; Papakonstantinou, P.; Ishiyama, H.; Kim, Y. A Brief Overview of RAON Physics. J. Korean Phys. Soc. 2018, 73, 516–523. [Google Scholar] [CrossRef]
- Colò, G. Nuclear density functional theory. Adv. Phys. X 2020, 5, 1740061. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Sá Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Stevenson, P.D.; Goddard, P.M.; Stone, J.R.; Dutra, M. Do Skyrme forces that fit nuclear matter work well in finite nuclei? AIP Conf. Proc. 2013, 1529, 262–268. [Google Scholar]
- Papakonstantinou, P.; Park, T.S.; Lim, Y.; Hyun, C.H. Density dependence of the nuclear energy-density functional. Phys. Rev. C 2018, 97, 014312. [Google Scholar] [CrossRef]
- Gil, H.; Kim, Y.M.; Hyun, C.H.; Papakonstantinou, P.; Oh, Y. Analysis of nuclear structure in a converging power expansion scheme. Phys. Rev. C 2019, 100, 014312. [Google Scholar] [CrossRef]
- Motta, T.F.; Thomas, A.W. The role of baryon structure in neutron stars. Mod. Phys. Lett. A 2022, 37, 2230001. [Google Scholar] [CrossRef]
- Kochankovski, H.; Ramos, À.; Vidaña, I. An analytic parametrization of the hypernuclear matter equation of state. Eur. Phys. J. A 2022, 58, 31. [Google Scholar] [CrossRef]
- Choi, S.; Hiyama, E.; Hyun, C.H.; Cheoun, M.K. Effects of many-body interactions in hypernuclei with Korea-IBS-Daegu-SKKU functionals. Eur. Phys. J. A 2022, 58, 161. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, 88, 083013. [Google Scholar] [CrossRef]
- Li, A.; Yong, G.C.; Zhang, Y.X. Testing the phase transition parameters inside neutron stars with the production of protons and lambdas in relativistic heavy-ion collisions. arXiv 2022, arXiv:2211.04978. [Google Scholar] [CrossRef]
- Kojo, T. Phenomenological neutron star equations of state. Eur. Phys. J. A 2016, 52, 51. [Google Scholar] [CrossRef]
- Kojo, T. QCD equations of state and speed of sound in neutron stars. AAPPS Bull. 2021, 31, 11. [Google Scholar] [CrossRef]
- Kutschera, M.; Kotlorz, A. Maximum quark core in a neutron star for realistic equations of state. Astrophys. J. 1993, 419, 752–757. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28. [Google Scholar] [CrossRef]
- Joshi, S.; Sau, S.; Sanyal, S. Quark cores in extensions of the MIT bag model. J. High Energy Astrophys. 2021, 30, 16–23. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Fukushima, K. Critical surface in hot and dense QCD with the vector interaction. Phys. Rev. D 2008, 78, 114019. [Google Scholar] [CrossRef]
- Hell, T.; Weise, W. Dense baryonic matter: Constraints from recent neutron star observations. Phys. Rev. C 2014, 90, 045801. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Ángeles Pérez-García, M.; Sagun, V.; Albertus, C. Second look to the Polyakov loop Nambu–Jona-Lasinio model at finite baryonic density. Phys. Rev. D 2019, 100, 103020. [Google Scholar] [CrossRef]
- Pinto, M.B. EoS for strange quark matter: Linking the NJL model to pQCD. arXiv 2022, arXiv:2211.11071. [Google Scholar]
- Peng, G.X.; Li, A.; Lombardo, U. Deconfinement phase transition in hybrid neutron stars from the Brueckner theory with three-body forces and a quark model with chiral mass scaling. Phys. Rev. C 2008, 77, 065807. [Google Scholar] [CrossRef]
- Adam, C.; Martín-Caro, A.G.; Huidobro, M.; Vázquez, R.; Wereszczynski, A. Quantum Skyrmion crystals and the symmetry energy of dense matter. arXiv 2022, arXiv:2202.00953. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. Towards the hadron–quark continuity via a topology change in compact stars. Prog. Part. Nucl. Phys. 2020, 113, 103791. [Google Scholar] [CrossRef]
- Chu, P.C.; Zhou, Y.; Qi, X.; Li, X.H.; Zhang, Z.; Zhou, Y. Isospin properties in quark matter and quark stars within isospin-dependent quark mass models. Phys. Rev. C 2019, 99, 035802. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E. Velocity of Sound beyond the High-Density Relativistic Limit from Lattice Simulation of Dense Two-Color QCD. 2022. arXiv 2022, arXiv:2207.01253. [Google Scholar]
- Huang, Y.J.; Baiotti, L.; Kojo, T.; Takami, K.; Sotani, H.; Togashi, H.; Hatsuda, T.; Nagataki, S.; Fan, Y.Z. Merger and Postmerger of Binary Neutron Stars with a Quark-Hadron Crossover Equation of State. Phys. Rev. Lett. 2022, 129, 181101. [Google Scholar] [CrossRef] [PubMed]
- Rho, M. Pseudo-Conformal Sound Speed in the Core of Compact Stars. Symmetry 2022, 14, 2154. [Google Scholar] [CrossRef]
- Paeng, W.G.; Kuo, T.T.S.; Lee, H.K.; Ma, Y.L.; Rho, M. Scale-invariant hidden local symmetry, topology change, and dense baryonic matter. II. Phys. Rev. D 2017, 96, 014031. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Altiparmak, S.; Ecker, C.; Rezzolla, L. On the Sound Speed in Neutron Stars. Astrophys. J. Lett. 2022, 939, L34. [Google Scholar] [CrossRef]
- McLerran, L.; Reddy, S. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef]
- Lee, H.K.; Ma, Y.L.; Paeng, W.G.; Rho, M. Cusp in the symmetry energy, speed of sound in neutron stars and emergent pseudo-conformal symmetry. Mod. Phys. Lett. A 2022, 37, 2230003. [Google Scholar] [CrossRef]
- Braun, J.; Geißel, A.; Schallmo, B. Speed of sound in dense strong-interaction matter. arXiv 2022, arXiv:2206.06328. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Lim, Y.; Kim, T.; Oh, Y. Nuclear Equation of State and the Structure of Neutron Stars. New Phys. (Sae Mulli) 2016, 66, 1571–1577. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151–167. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Viñas, X.; Gonzalez-Boquera, C.; Centelles, M.; Mondal, C.; Robledo, L.M. Unified Equation of State for Neutron Stars Based on the Gogny Interaction. Symmetry 2021, 13, 1613. [Google Scholar] [CrossRef]
- Gil, H.; Papakonstantinou, P.; Hyun, C.H.; Oh, Y. From homogeneous matter to finite nuclei: Role of the effective mass. Phys. Rev. C 2019, 99, 064319. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Dover Publications: New York, NY, USA, 1971. [Google Scholar]
- Kaiser, N.; Fritsch, S.; Weise, W. Chiral dynamics and nuclear matter. Nucl. Phys. A 2002, 697, 255. [Google Scholar] [CrossRef]
- Hammer, H.-W.; Furnstahl, R.J. Effective field theory for dilute Fermi systems. Nucl. Phys. A 2000, 678, 277. [Google Scholar] [CrossRef]
- Gil, H.; Kim, Y.M.; Papakonstantinou, P.; Hyun, C.H. Constraining the density dependence of the symmetry energy with nuclear data and astronomical observations in the Korea-IBS-Daegu-SKKU framework. Phys. Rev. C 2021, 103, 034330. [Google Scholar] [CrossRef]
- Gil, H.; Papakonstantinou, P.; Hyun, C.H.; Park, T.S. Nuclear energy density functional for KIDS. Acta Phys. Pol. B 2017, 48, 537. [Google Scholar] [CrossRef]
- Gil, H.; Hyun, C.H. Compression modulus and symmetry energy of nuclear matter with KIDS density functional. New Phys. (Sae Mulli) 2021, 71, 242–248. [Google Scholar] [CrossRef]
- Gil, H.; Hyun, C.H.; Kim, K. Quasielastic electron scattering with the KIDS nuclear energy density functional. Phys. Rev. C 2021, 104, 044613. [Google Scholar] [CrossRef]
- Gil, H.; Hyun, C.H.; Kim, K. Inclusive electron scattering in the quasielastic region with the Korea-IBS-Daegu-SKKU density functional. Phys. Rev. C 2022, 105, 024607. [Google Scholar] [CrossRef]
- Kim, K.; Gil, H.; Hyun, C.H. Quasielastic charged-current neutrino-nucleus scattering with nonrelativistic nuclear energy density functionals. Phys. Lett. B 2022, 833, 137273. [Google Scholar] [CrossRef]
- Hutauruk, P.T.P.; Gil, H.; Nam, S.i.; Hyun, C.H. Effect of nucleon effective mass and symmetry energy on the neutrino mean free path in a neutron star. Phys. Rev. C 2022, 106, 035802. [Google Scholar] [CrossRef]
- Papakonstantinou, P. Density dependence of the nuclear symmetry energy and neutron skin thickness in the KIDS framework. HNPS Adv. Nucl. Phys. 2022, 28, 36–41. [Google Scholar] [CrossRef]
- Gil, H.; Oh, Y.; Hyun, C.; Papakonstantinou, P. Skyrme-Type Nuclear Force for the KIDS Energy Density Functional. New Phys. (Sae Mulli) 2017, 67, 456–461. [Google Scholar] [CrossRef]
- Gil, H.; Papakonstantinou, P.; Hyun, C.H. Constraints on the curvature of nuclear symmetry energy from recent astronomical data within the KIDS framework. Int. J. Mod. Phys. E 2022, 31, 2250013. [Google Scholar] [CrossRef]
- Papakonstantinou, P. Nuclear symmetry energy and the PREX-CREX neutron skin puzzle within the KIDS framework. Nucl. Theory 2022, 39, 36. [Google Scholar]
- Hyun, C.H. Neutron Skin Thickness of 48Ca, 120Sn, and 208Pb with KIDS Density Functional. New Phys. (Sae Mulli) 2022, 72, 371–375. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Brandes, L.; Weise, W.; Kaiser, N. Inference of the sound speed and related properties of neutron stars. Phys. Rev. D 2023, 107, 014011. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Kettner, C. Possible third family of compact stars more dense than neutron stars. Astron. Astrophys. 2000, 353, L9–L12. [Google Scholar]
- Alvarez-Castillo, D.E.; Blaschke, D.B.; Grunfeld, A.G.; Pagura, V.P. Third family of compact stars within a nonlocal chiral quark model equation of state. Phys. Rev. D 2019, 99, 063010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).