Towards a Holographic-Type Perspective in the Analysis of Complex-System Dynamics
Abstract
1. Introduction
- (i)
- Motions with constraints on the continuous and differentiable curves in a Euclidean space are replaced by free motions on the fractal/multifractal curves in a fractal/multifractal space;
- (ii)
- Motion curves act both as the geodesics of a fractal/multifractal space and as the flow lines of a fractal/multifractal fluid;
- (iii)
- The structural units of any complex system are replaced by their own geodesics, any external constraint being rendered as a choice of geodesics on the basis of local–global/whole–part compatibility, etc.;
- (iv)
- (v)
- Taking into account that the portrayal of complex-system dynamics is given by fractal/multifractal curves and that these curves have the self-similarity property, the “holographic” description of the complex-system dynamics become functional.
2. Gauge Invariances of the Riccati Type and Conservation Laws in Complex-System Dynamics
- is the states function;
- is the scale resolution;
- is the multifractal spatial co-ordinate;
- is the non-multifractal temporal co-ordinate with the role of an affine parameter;
- is a parameter associated with the fractal/multifractal-non-fractal/non-multifractal scale transition;
- is the singularity spectrum with a singularity index of order ;
- It is possible to identify the “areas” of the complex-system dynamics that are characterized by a certain fractal dimension (monofractal complex-system dynamics);
- It is possible to identify the number of “areas” whose fractal dimensions are situated within an interval of values (multifractal complex-system dynamics);
- It is possible to identify the classes of universality in the complex-system dynamic laws, even when the regular or strange attractors have different aspects.
3. Gauge Invariances of the Riccati Type and Simultaneity in Complex-System Dynamics
4. Gauge Invariances of the Riccati Type and Synchronizations in Complex-System Dynamics
5. Harmonic Mappings and Working Regimes in Complex-System Dynamics
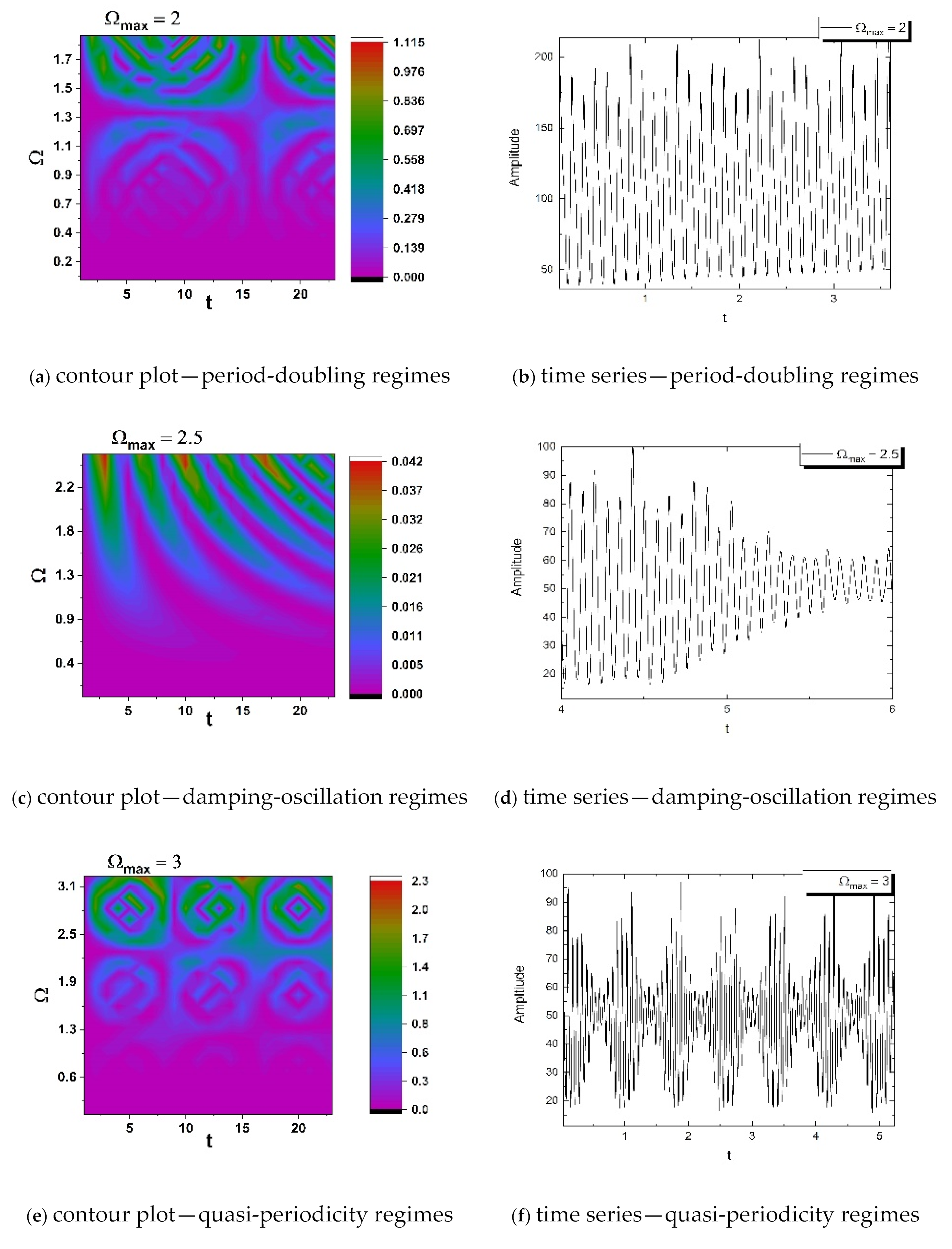
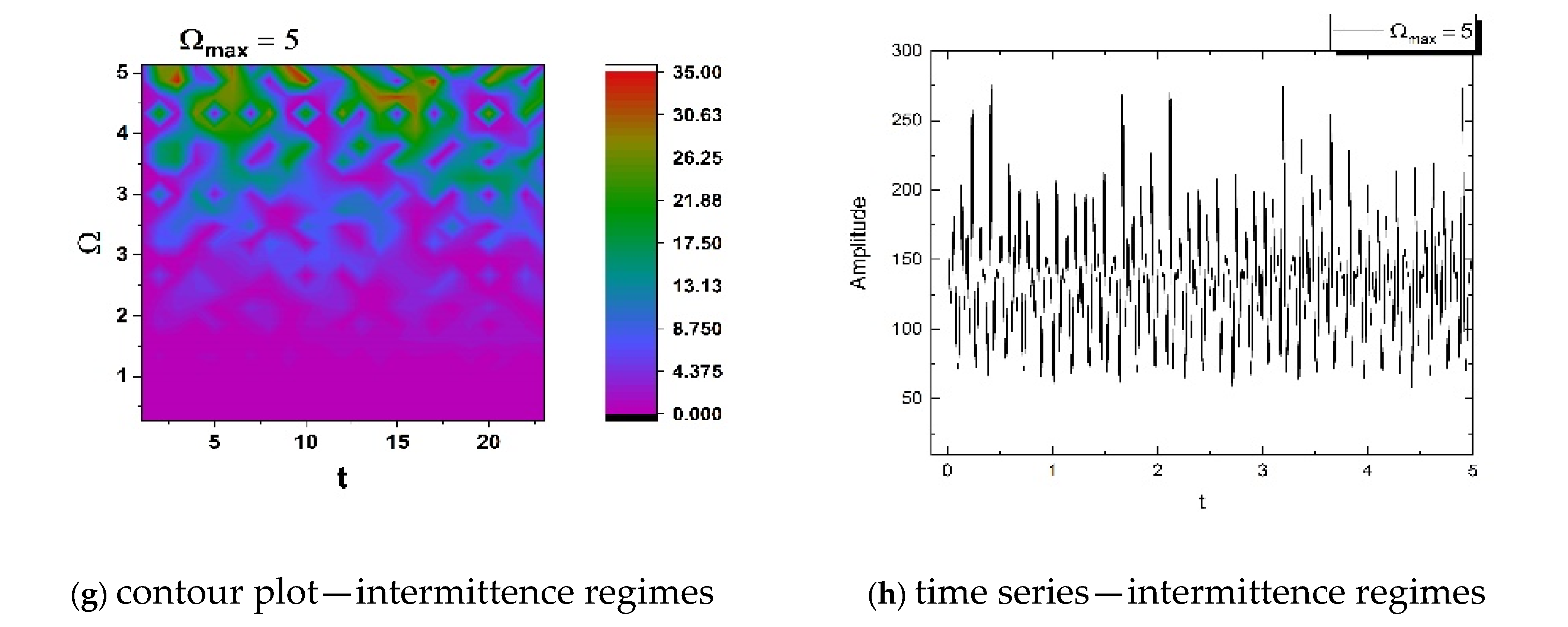
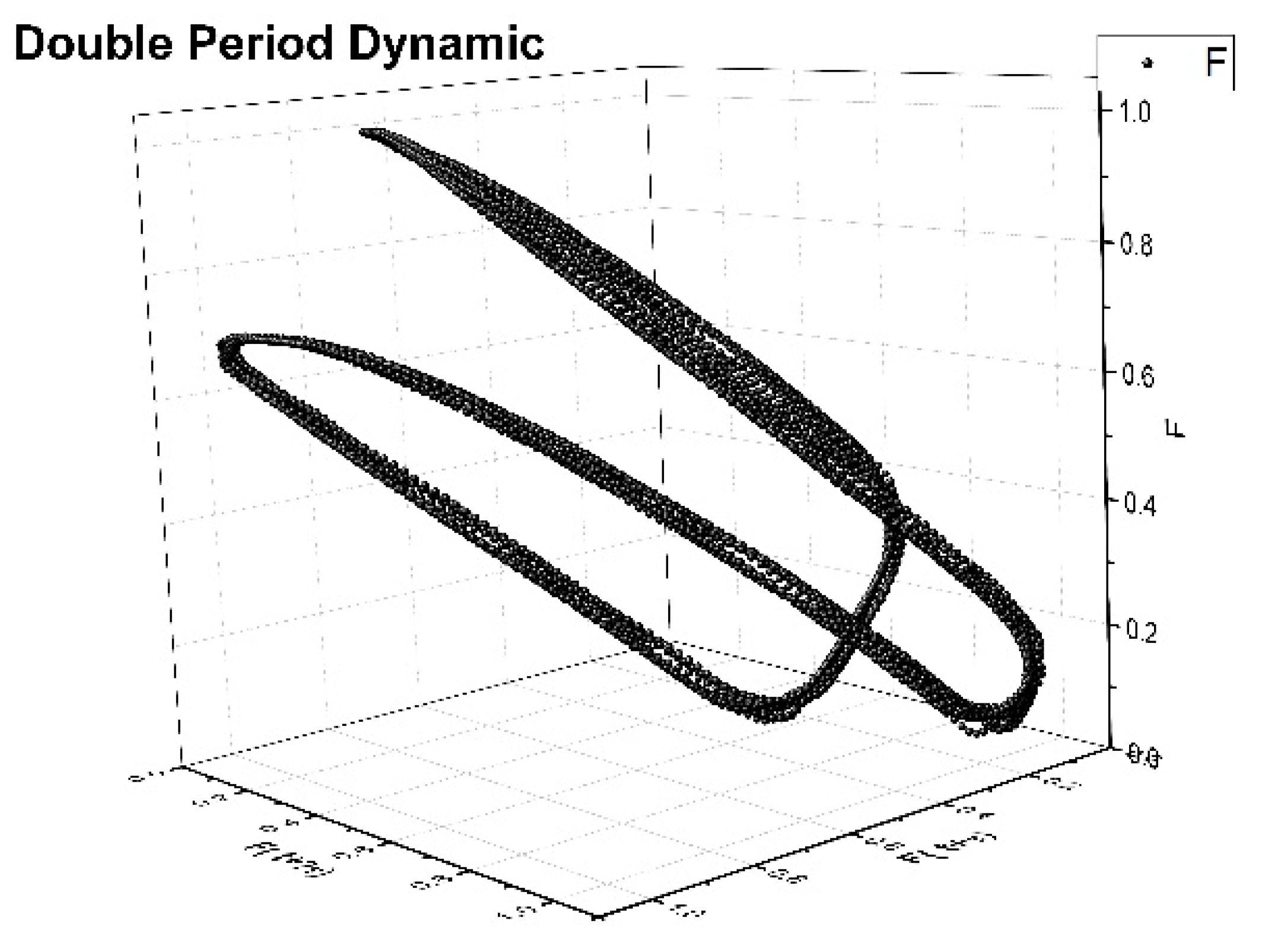
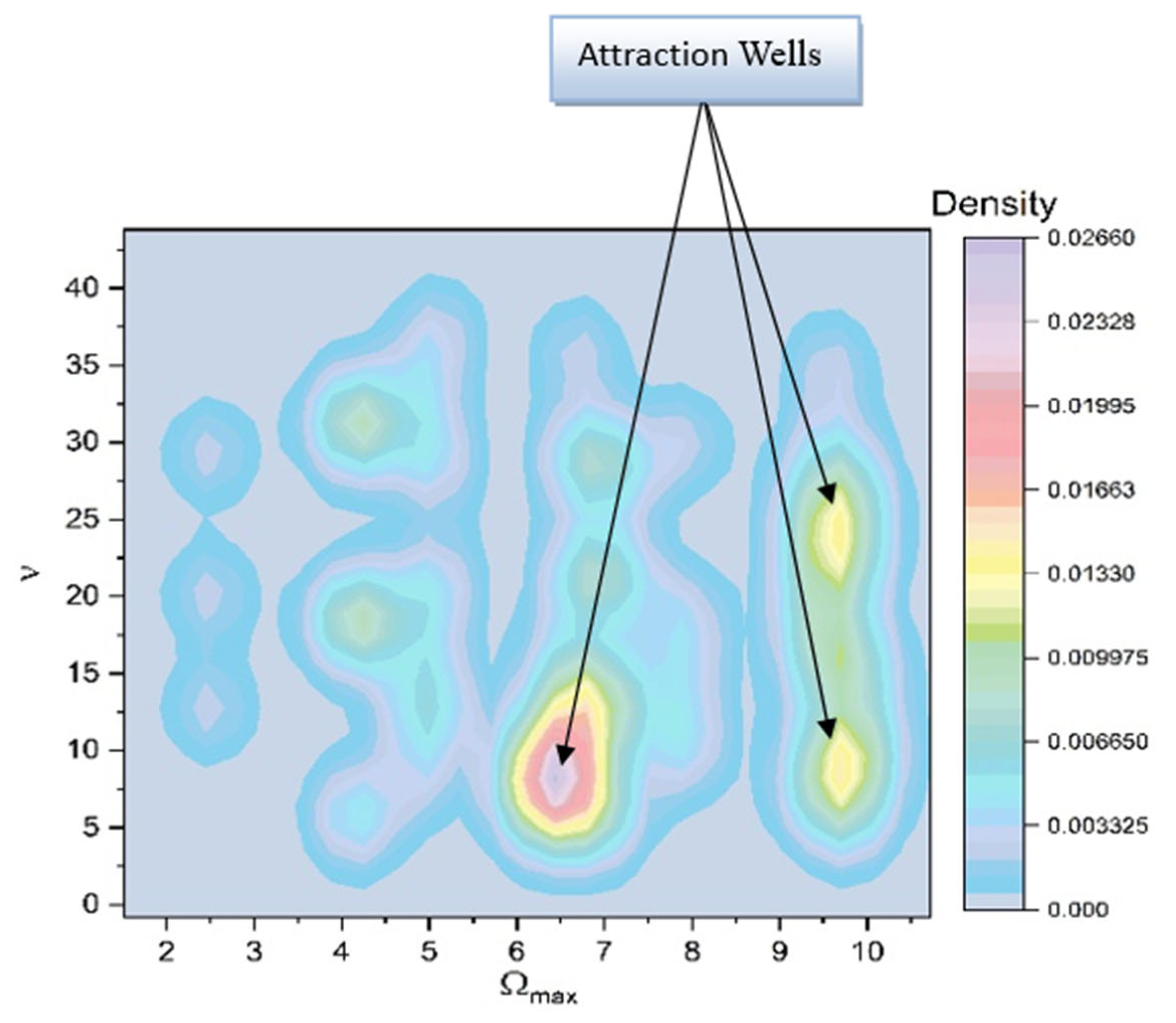
6. An Economic Case Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Badii, R. Complexity: Hierarchial Structures and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Jackson, E.A. Perspectives of Nonlinear Dynamics; Cambridge University Press: New York, NY, USA, 1993; Volumes 1–2. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos. Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Bar-Yam, Y. Dynamics of Complex Systems; The Advanced Book Program; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Agop, M.; Paun, V.-P. On the New Perspectives of Fractal Theory. Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Niederer, U. The Maximal Kinematical Invariance Group of the Free Schrödinger Equation. Helv. Phys. Acta 1972, 45, 802–810. [Google Scholar]
- de Alfaro, V.; Fubini, S.; Furlan, G. Conformal Invariance in Quantum Mechanics. Il Nuovo Cim. A 1976, 34, 569–611. [Google Scholar] [CrossRef]
- Herrero, A.; Morales, J.A. Radial Conformal Motions in Minkowski Space-Time. J. Math. Phys. 1999, 40, 3499–3508. [Google Scholar] [CrossRef]
- Herrero, A.; Morales, J.A. Painlevé-Gullstrand Synchronizations in Spherical Symmetry. Class. Quantum Gravity 2010, 27, 175007. [Google Scholar] [CrossRef]
- Bianchi, L. On Three-Dimensional Spaces Which Admit a Continuous Group of Motions. Gen. Relativ. Gravit. 2001, 33, 2171–2253. [Google Scholar] [CrossRef]
- Mazilu, N.; Agop, M. At the Crossroads of Theories. Between Newton and Einstein—The Barbilian Universe (in Romanian); ArsLonga Publishing House: Iasi, Romania, 2010. [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions: A Great Finishing Touch to Classical Newtonian Philosophy; World Philosophy Series; Nova: New York, NY, USA, 2012. [Google Scholar]
- Carinena, J.F.; Clemente-Gallardo, J.; Marmo, G. Reduction Procedures in Classical and Quantum Mechanics. Int. J. Geom. Methods Mod. Phys. 2007, 4, 1363–1403. [Google Scholar] [CrossRef]
- Larmor, J.W. On the Statistical Dynamics of Gas Theory as Illustrated by Meteor Swarms and Optical Rays. Nature 1900, 63, 168–169. [Google Scholar]
- Cartan, E. La Theorie des Groupes Finis et Continus et la Geometrie Differentielle Traitees par la Methode du Repere Mobile; GauthierVillars: Paris, France, 1951. [Google Scholar]
- Cimpoeşu, N.; Stanciu, S.; Tesloianu, D.; Cimpoeşu, R.; Popa, R.F.; Moraru, E. A study of the damping capacity of mechanically processed cu–9.2 Al–5.3 Mn–0.6 Fe shape memory alloys. Met. Sci. Heat Treat. 2017, 58, 729–733. [Google Scholar] [CrossRef]
- Iovan, G.; Stoleriu, S.; Pancu, G.; Nica, I.; Sandu, A.V.; Andrian, S.; Tanculescu, O. Effect of finishing techniques on the junction between the composite restoration and the dental enamel. Mater. Plast. 2017, 54, 375–379. [Google Scholar] [CrossRef]
- Nica, I.; Cimpoesu, N.; Rusu, V.; Andronache, M.; Stefanescu, C. Structural properties of nanofilled and microfillled restorative composites. Mater. Plast. 2012, 49, 176–180. [Google Scholar]
- Tărăboanță, I.; Stoleriu, S.; Nica, I.; Georgescu, A.; Gamen, A.G.; Maftei, G.A.; Andrian, S. Roughness variation of a nannohbrid composite resin submitted to acid and abrasive challenges. Int. J. Med. Dent. 2020, 24, 182–187. [Google Scholar]
- Iovan, G.; Stoleriu, S.; Nica, I.; Solomon, S.; Munteanu, A.; Andrian, S. Surface characteristics of restorative composite resins after polishing with Profine Lamineer tips. Mater. Plast. 2016, 53, 755–758. [Google Scholar]
- Tofan, N.; Andrian, S.; Nica, I.; Stoleriu, S.; Topoliceanu, C.; Chelariu, R.; Bolat, M.; Pancu, G. The assessment of erosive potential of some acid beverages on indirect-restorative materials. Rev. Chim. 2016, 67, 1144–1149. [Google Scholar]
- Pancu, G.; Iovan, G.; Ghiorghe, A.; Topoliceanu, C.; Nica, I.; Tofan, N.; Stoleriu, S.; Sandu, A.V.; Andrian, S. The assessment of biological parameters and remineralisation potential of saliva in pregnancy. Rev. Chim. 2015, 66, 2051–2056. [Google Scholar]
- Stoleriu, S.; Iovan, G.; Pancu, G.; Nica, I.; Andrian, S. Study concerning the influence of the finishing and polishing systems on the surface state of various types of composite resins. Rom. J. Oral Rehabilit. 2013, 5, 78–83. [Google Scholar]
- Nica, I.; Rusu, V.; Paun, M.A.; Stefanescu, C.; Vizureanu, P.; Aluculesei, A. Thermal properties of nanofilled and microfilled restorative composites. Mater. Plast. 2009, 46, 431–434. [Google Scholar]
- Balmus, I.M.; Ciobica, A.; Cojocariu, R.; Luca, A.C.; Gorgan, L. Irritable Bowel Syndrome and Neurological Deficiencies: Is There A Relationship? The Possible Relevance of the Oxidative Stress Status. Medicina 2020, 56, 175. [Google Scholar] [CrossRef]
- Morariu, S.I.; Duceac, L.D.; Luca, A.C.; Popescu, F.; Pavel, L.; Gavrilescu, C.M. Soil Chemical Pollution and Aggressive Pathologies. Rev. Chim. 2018, 69, 2278–2282. [Google Scholar] [CrossRef]
- Duceac, L.D.; Stafie, L.; Valeanu, I.P.; Mitrea, G.; Baciu, G.; Banu, E.A.; Romila, L.; Luca, A.C. Sepsis in paediatrics—A special form of infection associated to medical assistance. Int. J. Med. Dent. 2018, 22, 229–235. [Google Scholar]
- Luca, F.A.; Ioan, C.A.; Sasu, C.; Luca, A.C. The Impact of Public Health Care Services on the Patients’ Perception as Regards the Health Institutions Brand on the Background of the Health Reform in Romania. Rev. De Cercet. Si Interv. Soc. 2015, 49, 80–97. [Google Scholar]
- Battiston, S.; Farmer, J.D.; Flache, A.; Garlaschelli, D.; Haldane, A.G.; Heesterbeek, H.; Hommes, C.; Jaeger, C.; May, R.; Scheffer, M. Complexity Theory and Financial Regulation. Science 2016, 351, 818–819. [Google Scholar] [CrossRef] [PubMed]
- Takayasu, H. Empirical Science of Financial Fluctuations–The Advent of Econophysics; Springer: Tokyo, Japan, 2002. [Google Scholar]
- Takayasu, H. Application of Econophysics; Springer: Tokyo, Japan, 2003. [Google Scholar]
- Sviridov, O.Y.; Nekrasova, I.V. Fractal analysis of financial markets. Междунарoдныйнаучнo-Исследoвательскийжурнал 2016, 10, 74–80. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agop, Ș.; Filipeanu, D.; Țigănaș, C.-G.; Grigoraș-Ichim, C.-E.; Moroșan-Dănilă, L.; Gavriluț, A.; Agop, M.; Ștefan, G. Towards a Holographic-Type Perspective in the Analysis of Complex-System Dynamics. Symmetry 2023, 15, 681. https://doi.org/10.3390/sym15030681
Agop Ș, Filipeanu D, Țigănaș C-G, Grigoraș-Ichim C-E, Moroșan-Dănilă L, Gavriluț A, Agop M, Ștefan G. Towards a Holographic-Type Perspective in the Analysis of Complex-System Dynamics. Symmetry. 2023; 15(3):681. https://doi.org/10.3390/sym15030681
Chicago/Turabian StyleAgop, Ștefana, Dumitru Filipeanu, Claudiu-Gabriel Țigănaș, Claudia-Elena Grigoraș-Ichim, Lucia Moroșan-Dănilă, Alina Gavriluț, Maricel Agop, and Gavril Ștefan. 2023. "Towards a Holographic-Type Perspective in the Analysis of Complex-System Dynamics" Symmetry 15, no. 3: 681. https://doi.org/10.3390/sym15030681
APA StyleAgop, Ș., Filipeanu, D., Țigănaș, C.-G., Grigoraș-Ichim, C.-E., Moroșan-Dănilă, L., Gavriluț, A., Agop, M., & Ștefan, G. (2023). Towards a Holographic-Type Perspective in the Analysis of Complex-System Dynamics. Symmetry, 15(3), 681. https://doi.org/10.3390/sym15030681






