Target-Network Update Linked with Learning Rate Decay Based on Mutual Information and Reward in Deep Reinforcement Learning

Abstract

In this study, a target-network update of deep reinforcement learning (DRL) based on mutual information (MI) and rewards is proposed. In DRL, updating the target network from the Q network was used to reduce training diversity and contribute to the stability of learning. If it is not properly updated, the overall update rate is reduced to mitigate this problem. Simply slowing down is not recommended because it reduces the speed of the decaying learning rate. Some studies have been conducted to improve the issues with the t-soft update based on the Student’s-t distribution or a method that does not use the target-network. However, there are certain situations in which using the Student’s-t distribution might fail or force it to use more hyperparameters. A few studies have used MI in deep neural networks to improve the decaying learning rate and directly update the target-network by replaying experiences. Therefore, in this study, the MI and reward provided in the experience replay of DRL are combined to improve both the decaying learning rate and the target-network updating. Utilizing rewards is appropriate for use in environments with intrinsic symmetry. It has been confirmed in various OpenAI gymnasiums that stable learning is possible while maintaining an improvement in the decaying learning rate.

1. Introduction

The high-function approximation capabilities of deep neural networks (DNNs) have increased, and their popularity is growing [1]. Continuous research has revealed the hidden relationships between data, which are black boxes, and has many applications in various academic fields, such as engineering [2] and economics [3]. Deep reinforcement learning (DRL) is one of the most promising methods for solving various control problems because it uses DNNs to approximate the policy and value functions of reinforcement learning [4]. The deep Q-network (DQN) [5] is the first instantiation to successfully show this combination, resulting in remarkable performance in Atari video games. However, owing to high non-linearity, using DNNs only as an estimated function for problems might make the learning process quite unstable [6,7,8]. Thus, various techniques for reducing the variance of the learning signal have been developed to ensure stable training of the optimal DRL. For this purpose, experience replay using minibatch learning [6], ensemble value functions [7], and regularization techniques [8] have been developed.

One such method involves the use of a target-network for learning stabilization [5]. The target network updates “slowly” the estimated parameters (weights and biases) with respect to the reference signals of the main paired Q network [5]. This essentially reduces the learning speed of the model using the Q-network; however, it can learn more stably because the reference signals do not fluctuate frequently [5,9]. However, several drawbacks of target networks have been reported. These move away from online reinforcement learning [4], and the value function update may be delayed, which may slow the learning speed. Initially, the “hard” update strategy of copying the main Q-network to the target-network after a certain period of time was used [5]. Since then, the “soft” update strategy has been used by interpolating the parameters of the target-network using a fixed ratio between the current parameters of the target-network and the parameters of the main Q-network [10,11,12,13,14].

However, these methods exhibit several limitations. In addition to their slow learning speed, they are sensitive to noise and outliers in parameter updates for the main Q-network [11,12,13]. A simple solution to this problem is to reduce the copy size; however, the learning speed is considerably slower. As a result, a t-soft update based on the Student’s t-distribution, a well-known distribution that is robust to outliers [12,13], and Mellowmax [14], a softmax operator that does not use target-network updates, were proposed. However, these studies might force us to use more hyperparameters in addition to hyper-parameters, such as the learning rate (LR) used in existing DQN, to use these methods [12,13,14]. Recent research shows how well-known algorithms are highly sensitive to the setting of hyperparameters and the details of implementation [15]. Therefore, state-of-the-art (SOTA) optimization methods are introduced [16,17]. Although Mellowmax uses more hyperparameters provided by a grid-search method or adaptive methods for applying hyperparameters to various domains, this is a topic for future research [14]. According to t-soft updates [12,13], this could deliberately affect the training process depending on the design of the reinforcement learning reward; therefore, it would be forced to be a very large reward. Such criteria may make it difficult to demonstrate Student’s t-distribution performance, and a more sophisticated method should be used because it cannot easily reach the global optimum [11]. Moreover, depending on the design of the reward, the t-soft update is very likely to fall into the exploration-exploitation dilemma [11]. Although Student’s t-distribution is used, if the data size becomes extremely large, it approaches the normal distribution and is difficult to use.

Therefore, in this study, among the existing hyperparameters, the LR, which is significantly related to the target-network update, was also considered. We propose a method for updating the target-network in accordance with the method [18], which uses mutual information (MI) to adaptively update the learning rate. In the study [18], MI provided the upper and lower bounds of LR, such as a measure of LR, through conditional classification accuracy. In this study, the MI and reward of DRL were used as performance metrics to adjust the LR and update the target-network through the training of DRL agents. The reason for using MI and rewards together is that in DRL, rewards can be received by agents through mini-batch training; therefore, the advantage of using mini-batches in DNNs can be acquired through rewards.

In most studies, Maximum Likelihood Estimation (MLE), KL-Divergence, or Maximum A Posterior (MAP) are used as the basic loss function theory when doing deep learning or machine learning [19,20]. In particular, MAP is used from a Bayesian perspective, and when a prior is available, MAP shows better results than MLE. In this study, from a Bayesian perspective, MI uses the posterior generated by every training as the prior for the next learning process. Therefore, using MI, learning progresses gradually with the help of the prior, and uncertainty decreases as model learning progresses. However, since the prior is almost random from the beginning, if the learning continues, the effectiveness of using MI might increase as it is used for the next learning. In that sense, MI might represent the loss function effect during learning and is used for updating the target network in this study.

The selection and adaptation of hyperparameters through training is one of the main issues that must be addressed for the successful use of DNNs [21]. Hyperparameter selection in DNNs is mostly performed through a training process on different datasets and models and is implemented using various forms of searches, such as grid search, random search, and Bayesian optimization. Stochastic gradient descent (SGD) optimization using mini-batches of data [22] are an efficient approach to optimizing the weights of DNNs, where hyperparameter selection and adaptation may yield robust results on SGD-based training. SGD is also widely used in DRL training through mini-batches, called experience replay. In the study [12], it was also reported that the target network may be directly updated by mini-batches of experience replay for the optimal target network to affect the LR. In addition, in the study [23], reward shaping was performed in an environment with symmetric information. However, only rewards are used in this study. Redesigning the reward might not be applicable to all environments. Rewards by themselves are quite suitable for use in environments with intrinsic symmetry. Therefore, in this study, to use mini-batch experiential replay, the rewards of DRL agents affected by the experience replay are also used for updating the target-network.

The contribution of this study is to alleviate the degradation of learning due to LR, which is a disadvantage when updating the target-network, in conjunction with research [18] on how to use MI as a metric to realize the goal of gradient descent-based adaptive LR that strongly influences the DNN training process. In addition, when using MI, the reward via minibatches is used as a metric, particularly for improved DRL learning. The method proposed in this study shows that even if the target network is updated, the training of the agents is extremely stable when compared to the existing, well-known DQN. Experiments were conducted in various OpenAI gyms [24], such as CartPole v1. [25,26,27], MountainCar v0. [28,29,30], and LunarLander V2. [31,32,33].

2. Related Works

2.1. Studies of Deep Neural Networks Using Mutual Information

In the study [18], MI-based LR and SGD were used to train DNNs. The MI between the output of the neural network and the results was used to adaptively set the LR for the neural network at every training epoch. Because MI provides layer-wise performance metrics, it was used to determine the operating range of the LR. The gradient descent-based adaptive LR has been applied to various gradient descent-based optimization algorithms used for DNNs [34]. These include SOTA algorithms such as RMSprop [35] and Adam [36]. In these cases, careful initial selection of the LR might be required because the LR was set at the individual parameter level by considering the current gradients of the past gradients. Various types of LR decay have been used, such as time decay and exponential decay. In general, in all these cases, the decay rate parameter and LR bounds (MAX or the starting value of LR) are required. Although adaptive gradient descent-based optimization provides excellent options for several applications, traditional minibatch SGD is preferred for complex models such as RL [20]. The study in [37] used training loss to adapt LR to train neural network models. The method in [37] was based on linearizing the loss function at each epoch. The results of the method in this study showed that the loss was minimized at each step for the stabilization of training, which showed that LR was well adapted to training, as implemented in [37], and was almost the same as minimizing loss. Meyen [36] demonstrated a technique that linked MI to classification accuracy using conditional classification accuracy. In the study [38], MI was used as a performance metric for applying LR through training. The method proposed by Tishby et al. [39] was an MI-based signal compression formula that attempted to determine the maximally compressed signal abstraction, where the signal was the data being modeled, such as the input denoted by X, output denoted by Y, and abstraction layer of the neural network denoted by T. The method in Shamir et al. [40] showed that the MI between the neural network layer and input (MI(T, X)) was denoted by ITX, and the MI between the neural network layer and output (MI(T, Y)) was denoted by ITY, which are functions of performance metrics.

2.2. Deep Reinforcement Learning with Target-Network Update

Reinforcement learning [4] is a formula for Markov decision processes (MDP) [41] for tuples $(S,A,T,R,\gamma )$. $S$ represents the state set, and $A$ represents the action set. The function $T:S\times A\times S\to \left[\mathrm{0,1}\right]$ is the transition dynamics of the process. The probability of moving to state $s\prime$ after selecting an action $a$ in a state $s$ is denoted by $T(s,a,s^{\prime })$. In the same manner, $R:S\times A\times S\to R$ is the reward function, where $R(s,a,s^{\prime })$ is the expected reward when moving from state $s$ to state $s\prime$ when considering an action $a$. Finally, the discount rate $\gamma \in \left[\mathrm{0,1}\right)$ determines the importance of immediate rewards over long-term rewards. In reinforcement learning, the agent tries to identify a policy π. $\pi :S\to \mathrm{Pr}\left(A\right)$ can obtain high long-term rewards. The long-term value of taking action $a$ in state $s$ is defined as follows:

$$Q^{\pi }\left(s,a\right)=E\left[\sum _{t=0}^{\infty }{\gamma }^{t}R\left(s_t,a_t,s_{t+1}\right)|s_0=s,a_0=a,\pi \right]$$

Defining the optimal Q, we can express it as a state-action pair under the optimal policy ${\pi }^{*}$ as follows:

$$Q^{*}\left(s,a\right)=E\left[\sum _{t=0}^{\infty }{\gamma }^{t}R\left(s_t,a_t,s_{t+1}\right)|s_0=s,a_0=a,{\pi }^{*}\right]$$

According to the Bellman equation [41], as a fundamental result of MDP, Q* can be written recursively as follows:

$$Q^{*}\left(s,a\right)=\sum _{s^{\prime }ϵS}{\rm T}(s,a,s^{\prime })\left[R\left(s,a,s^{\prime }\right)+\gamma {max}_{a^{\prime }}{Q}^{*}(s^{\prime },a^{\prime })\right]$$

Given the samples $<s,a,r,s^{\prime }>$, Q-learning attempts to improve the approximate solution to the Bellman equation by performing the following update:

$$Q\left(s,a\right)\leftarrow Q\left(s,a\right)+\alpha (r+\gamma {max}_{a^{\prime }}{Q}^{*}\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right))$$

Instead of representing Q-learning as the value of each state-action pair in a domain with large state spaces, the algorithm uses a parameterized function approximator to represent the Q-function. DQN [5] may use DNNs, which are parameterized by weights $\theta$. In this case, the value function estimate is updated as follows:

$$Q\leftarrow Q+\alpha (r+\gamma {max}_{a^{\prime }}Q\left(s^{\prime },a^{\prime };\theta \right)-Q\left(s,a;\theta \right)){\nabla }_{\theta }Q\left(s,a;\theta \right)$$

Because DNNs are used for learning DQN, learning is significantly unstable owing to non-linearity [6,7,8]. Therefore, it uses two additional techniques: experience replay buffers and a target-network [5]. Experience randomly replays samples in a mini-batch in a buffer and performs an update based on the sampling. This could significantly reduce the correlations between consecutive samples, which can negatively affect gradient-based learning. The target-network maintains a separate weight vector ${\theta }^{\wedge }$ to make a temporal interval between the target action-value function and the main action-value function. Thus, the update changes as follows:

$$Q\leftarrow Q+\alpha (r+\gamma {max}_{a^{\prime }}{Q}^{\wedge }\left(s^{\prime },a^{\prime };{\theta }^{\wedge }\right)-Q\left(s,a;\theta \right)){\nabla }_{\theta }Q\left(s,a;\theta \right)$$

The weight vector ${\theta }^{\wedge }$ of the target-network $Q^{\wedge }$ is synchronized with the main network’s weight vector $\theta$ after a period of time selected as a hyper-parameter. Using a separate target-network eliminates the possibility of divergence, because it adds a delay between the time the $Q$ value is changed and the time the target $Q^{\wedge }$ value is updated.

Mellowmax [14] proposed that DQNs could achieve stable learning in high-dimensional domains while reducing the requirement for a target-network. This guaranteed the convergence of learning. However, it must be used in addition to the hyperparameter fundamentally used for the well-known DQN, called DeepMellow’s temperature parameter. If the temperature parameter is considerably large or close to zero, it can still exhibit near-random update behavior. Therefore, it is necessary to adjust the hyperparameters further to suit each domain. Studies [11,12,13] use soft update rules, such as

$${\theta }^{\wedge }\leftarrow \left(1-\tau \right){\theta }^{\wedge }+\tau \theta$$

where $\tau$ represents smoothness, and $\tau =1$ is a hard update. They enable the target-network to be directly updated by replaying the experience to achieve optimal learning. The target-network, which only follows the main network, is expected to present more appropriate targets and accelerate learning. Studies [11,12,13] provided insights into using the experience reply method proposed in this study. When the target-networks were first introduced, a hard update technique was used in the study [5]. Since then, the soft update has been proposed, where $\tau \in \left(\mathrm{0,1}\right]$ represents the update rate. To fine-tune $\tau$, studies [11,12,13] have proposed replacing it with the Student’s t-distribution, which is more robust to noise. The method in [13] was a more robust heuristic consolidation that secured the method in [12] so that the outliers would not occur when $\tau$ was well-adjusted. However, these methods required a redesign of the reward to use the Student’s t-distribution, and depending on the design of the designed reward, the Student’s t-distribution was likely to fall into an exploration-exploitation dilemma.

The study [19] uses MLE as a basic loss function and uses supervision learning called advantage-weighted regression as a subroutine to derive the advantages of off-policy. This algorithm is based on expectation maximization (EM), which solves the supervised regression problem at each iteration. It has two supervised regression steps: one is to train the value function baseline through regression on accumulated rewards, and the other is to train the policy through weighted regression. This study [20] shows the practical possibility of performing online distributional reinforcement learning by applying the Wasserstein Metric to a stochastic approximation setting rather than KL-Divergence, which is widely used as a loss function in reinforcement learning. It focuses on how to practically apply already-well-known theories. In particular, the Wasserstein Metric has been shown to be applicable for research areas where the basic similarity of results is more important than the likelihood of an exact match. This study deals with [42] user identity linkages across social networks. They set up a multi-level attribute embedding for semi-conductive user ID connections to find common user IDs across social networks by covering a full set of different attribute features or capturing high-level semantic features of attribute text. They proved that it could be more suitable for real-world data sets.

3. Proposed Algorithm

In this section, the proposed algorithm is described. Because it is based on the DQN model [5], DNN training is performed using minibatches. The algorithm approach, as in the study [18], requires LR ranges and thresholds by changing MI. It is based on the gradient descent of mini-batches of DRL and uses MI and reward as metrics for adapting LR and updating the target-network in each mini-batch. The proposed algorithm shows that the maximum value of MI and the reward of DRL provide the upper and lower bounds of LR and the update timing of the target-network. In the study [18], MI and classification were the performance metrics of adaptive LR through training, which provided the upper and lower bounds of LR. However, in the proposed algorithm, the MI and reward of DRL are combined to adjust the LR through training as performance metrics and simultaneously decide when to update the target-network.

Based on the method described by Shamir et al. [40], in this study, the MI between the layer of the main Q-network and the reward of emulation is $I{T}^{\wedge }\theta R^{\wedge }\theta$, and the MI between the layer of the target-network is $I{T}^{\wedge }{\theta }^{\wedge }{R}^{\wedge }{\theta }^{\wedge }$, where the neural network layer is denoted by $T$, reward is denoted by $R$, parameters of the Q-network are denoted by $\theta$, and parameters of the target-network are denoted by ${\theta }^{\wedge }$. As in the study [18], the use of MI as a metric for LR adaptation is intended for further work towards a deeper understanding of DNNs learning [40]. In particular, for DRL, rewards are also used in accordance with MI through minibatches.

Therefore, the calculation measurements and reference upper limits of the MI were performed using mini-batches. The initialization ${LR}_t$ of the proposed algorithm is similar to the “LR Range Test” in [18]. In every epoch, the method records the loss, accuracy, and MI and calculates the qualification for all possible LR candidates. The method set a threshold based on the maximum LR value, ${LR}_{min}$ and ${LR}_{max}$ as values smaller than the threshold, and $ϵ$ as the median of the minimum values of all recorded measures of the relative change in the MI between epochs. In this study, we do not suggest a separate “LR Range Test”, and if prior knowledge can be obtained by the study [43], the system designer defines ${LR}_{min}$ and ${LR}_{max}$. The study [18] suggested that the components were known to fit the data a priori; therefore, we might remove them based on prior experience. Therefore, in this study, the initial LR was determined by repeating the experiment several times in advance to be similar to the “LR Range Test.” Subsequently, LR adaptation based on MI was applied. Computing MI is extremely expensive, and accurate MI estimation was not an essential goal of this study. Therefore, the proposed algorithm also used MI estimators [44,45,46,47], as in the study [18]. In particular, for DRL, minibatches are used to estimate the MI.

In the proposed algorithm, two metrics are calculated during the training of the mini-batches. $d_p$ is a measure of the distance from the maximum value that the model of the best MI might have, and $d_s$ is a measure of the relative change in MI in every mini-batch. Because agent training through mini-batches is performed in DRL, MI can also be calculated effectively. $d_s$ sets the LR for each episode, ds sets when the LR changes, and updates the target-network. LR is set to $\max (d_p·(1-\frac{t}{T})·{LR}_{max},{LR}_{min})$, and the range of LR becomes (${LR}_{min}$, ${LR}_{max}$), as in the study [18]. When the change of $d_s$ by mini-batch training is less than $ϵ$, which is determined in step 6, the LR change occurs, and the update of the target-network occurs. Therefore, the proposed Algorithm 1 replaces the fixed-parameter-based decay LR SGD with the variable-performance-based decay LR SGD, enabling the selection of the LR for DRL.

Algorithm 1: Algorithm DQN Combined with Mutual Information and the Reward for Target-Network Update and Learning Rate

Initialize replay memory $D$ to capacity $N$   Initialize the main action-value $Q$ with $\theta$   Initialize the target action-value $Q^{^}$ with ${\theta }^{^}=\theta$   Initialize $MI$ for ${\mathrm{I}\mathrm{T}}^{\mathsf{\theta }}{\mathrm{R}}^{\mathsf{\theta }}$ and ${\mathrm{I}\mathrm{T}}^{\mathsf{\theta }^}{\mathrm{R}}^{\mathsf{\theta }^}$   Initialize R by theoretical MI upper bound of the reward of the emulation   Initialize ${LR}_t$ between ${LR}_{max}$ and ${LR}_{min}$ and $ϵ$ by system designers   Initialize $d_p$ = $1-\frac{I{T}^{\theta }{R}^{\theta }}{I{T}^{\theta ^}{R}^{\theta ^}}$ and $d_s$ = 1.0   for e = 1, M do      Initialize sequence $s_1$ = $\left\{x_1\right\}$ and ${\Phi }_1$ = $\Phi \left(s_1\right)$      for t = 1, T do          With probability ε, select a random action $a_t$          Otherwise, select $a_t={argmax}_{a}Q(\Phi \left(s_t\right),a;\theta )$          Execute action $a_t$ and observe reward $r_t$ and sequence $x_{t+1}$          Set $s_{t+1}$ = $s_t$ and ${\Phi }_{t+1}$ = $\Phi \left(s_{t+1}\right)$          Store transition (${\Phi }_t$, $a_t$, $r_t$, ${\Phi }_{t+1}$) in $D$          Sample random mini-batch of transitions (${\Phi }_j$, $a_j$, $r_j$, ${\Phi }_{j+1}$) from $D$              Compute $d_p$  = $1-\frac{{{IT}^{\theta }{R}^{\theta }}_{0:t-1}}{I{T}^{\theta ^}{R}^{\theta ^}}$       #how far from the value it achieves              Compute $d_s$  = $\frac{{{(IT}^{\theta }{R}^{\theta }}_{t-1})-{{(IT}^{\theta }{R}^{\theta }}_{t-2})}{{{IT}^{\theta }{R}^{\theta }}_{t-1}}$         #MI between mini-batch              If $d_s$ < ϵ then,                          Set ${LR}_t$ to $\mathrm{m}\mathrm{a}\mathrm{x}(d_p·(1-\frac{t}{T})·{LR}_{max},{LR}_{min})$                          Set Update-Target to TRUE          Set $y_j$ = $r_j$                                                        if it terminates at step j + 1          Set $y_j$ = $r_j$ + ${\gamma max}_{a\prime }{Q}^{^}({\Phi }_{j+1},a\prime ;{\theta }^{^})$             otherwise          Perform a gradient descent step on ($y_j$ − ${Q({\Phi }_j,a_j;\theta ))}^2$ with respect to θ          If Update-Target is True then,              Set ${\theta }^{^}=\theta$              ${\mathrm{I}\mathrm{T}}^{\mathsf{\theta }^}{\mathrm{R}}^{\mathsf{\theta }^}$ = ${\mathrm{I}\mathrm{T}}^{\mathsf{\theta }}{\mathrm{R}}^{\mathsf{\theta }}$              Set Update-Target to False     End for End for

4. Results

In this experiment, it is demonstrated that the stable use of basic parameters, especially LR in DQN [5], has improved performance. We attempt to show that performance improvement has been achieved not by newly proposing the deep learning structure but by DRL. Cart-Pole [25,26,27] and MountainCar [28,29,30] are mostly used with DQN in “Classic Control” environment of OpenAI Gym [24]. In particular, MountainCar [28] is a sparse environment and is quite difficult to handle if approached only with DRL. Moreover, in the “Box2D” environment of the OpenAI gym [24], LunarLander [31,32,33] is mostly used with DQN. In the comparison between the method of fixing the update of the target-network and the method proposed in this study, the final rewards were obtained in the fastest possible period. However, the most important goal of this study was to pursue the stable learning of the agents. Figure 1 shows cart-pole [25], MountainCar [28], and LunarLander [31].

Figure 1. The environment of Cart-Pole V1 [25], MountainCar [28], and LunarLander [31].

4.1. Cart-Pole

The cart pole [25] is part of a classic control environment. A cart pole was proposed in an environment that could solve the research control problem [48]. The poles were attached with nonactuated joints to carts that moved along frictionless tracks. The pendulum was placed perpendicular to the cart, and the goal was to balance the pole by applying forces to the left and right sides of the cart. As shown in Figure 2, action can have {0, 1} values representing the direction of the fixed force pushing the cart. The observed values correspond to position and speed. During an episode, the cart x-position (index 0) can have values between (−4.8 and 4.8), and the polar angle can be observed between (−0.418 and 0.418) radians (or ±24°). The reward was to keep the pole upright for as long as possible, and a reward of +1 was acquired. The reward threshold was 500 for cart-pole v1. Initially, all observations were assigned a uniform random value of (−0.05, 0.05). An episode was terminated when one of the following conditions was satisfied: (1) the polar angle was greater than ±12°; (2) the cart position was greater than ±2.4 (the cart center reached the edge of the display); and (3) the episode length was greater than 500. In particular, for the cart pole, the state action space is symmetric with respect to the plane perpendicular to the cart’s direction of movement. So, utilizing rewards is appropriate for environments such as cart poles.

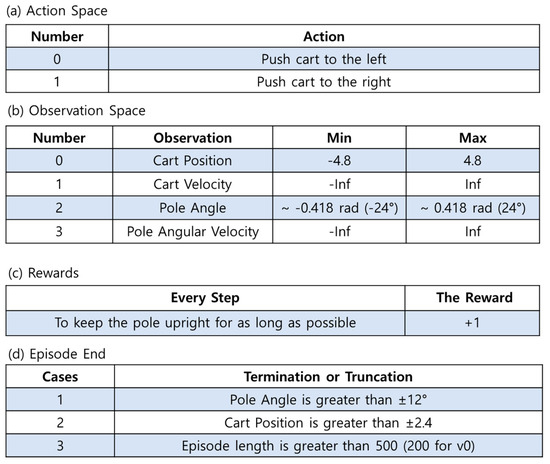
Figure 2. The environment of Cart-Pole V1 [25].

For a better solution, we considered certain requirements, such as recent implementation studies [25,26,27], such as reducing the number of steps in an episode. In one case, if the episode does not reach its maximum and the pole ends in the middle, a reward of −1 is received; in the other case, if the average reward is 400 or more, the episode is terminated. Figure 3 shows the best case in which the reward is reached. We can observe that the results of the method proposed in this study are almost similar to the previously well-known DQN that updates the target-network after setting “a certain period of time”, such as the hyper-parameter for the update. It can be observed that if the hyperparameter setting is performed well in the beginning, good results can be obtained, even if the target-network is updated in a fixed manner. Figure 4 compares the worst cases in a manner similar to that of the best cases. In addition, the participants did not complete the maximum number of steps. This implies that the goal of reinforcement learning is to maximize future rewards and not ensure future rewards. Figure 5 shows the average of the best and worst cases by adjusting the fine-tuned hyperparameter settings, even if the target-network is updated in a fixed manner. It can be observed that even if the target-network is updated in a fixed manner, the result can be quite different depending on the settings of the hyperparameters.

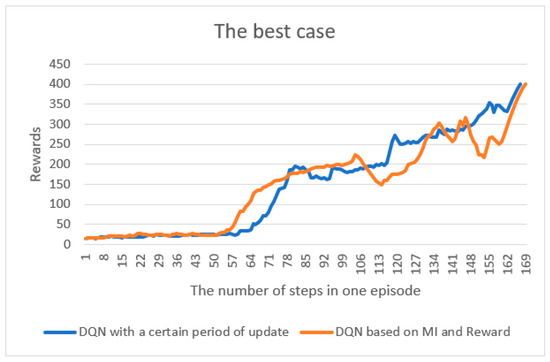
Figure 3. The best case comparison between the previous model (DQN with a certain period of update) and the proposed model (DQN based on MI and Reward), which finished in the average reward of +400.

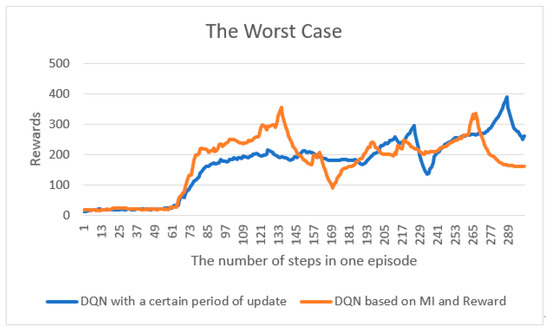
Figure 4. The worst-case comparison between the previous model (DQN with a certain period of update) and the proposed model (DQN based on MI and Reward), which finished in the maximum number of steps in one episode without reaching the average reward.

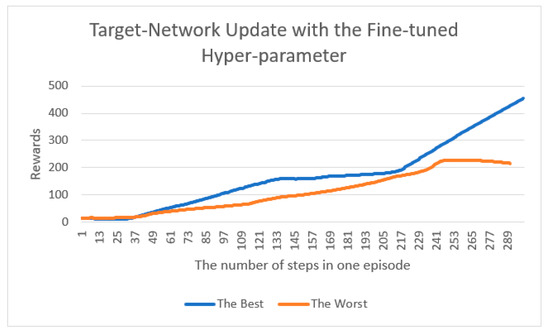
Figure 5. The best-case and worst-case comparisons were made by adjusting the fine-tuned hyper-parameter settings in DQN.

4.2. LunarLander

LunarLander is an environment with discrete or continuous actions in Box2D of the OpenAI Gym [24]. Discrete actions are considered in this implementation. As shown in Figure 6, there are four action spaces, which is a classic rocket trajectory optimization problem. Action spaces and reward rules exist, and when the score ranges from 0 to approximately +200, one episode is considered to have obtained a solution. In this comparison, because the reward of approximately −200 is at the start, it would be approximately +100 at the end. The reward was nothing when the lander moved away from the landing pad. If the lander crashes, the agent receives −100 at the end of the episode, or +100 if it lands properly. The landing pad is at coordinates (0, 0). The coordinates represent the first two state vectors. External landings are possible, and fuel is infinite; thus, agents can learn how to fly and land on their first attempt. The lander starts at the top center of the viewport by applying a random initial force to its center of mass. Figure 7 shows the average number of cases until the reward reaches approximately +100. As shown in the cart-pole results, the results of the method proposed in this study are similar to those of the previously well-known DQN with a certain update period.

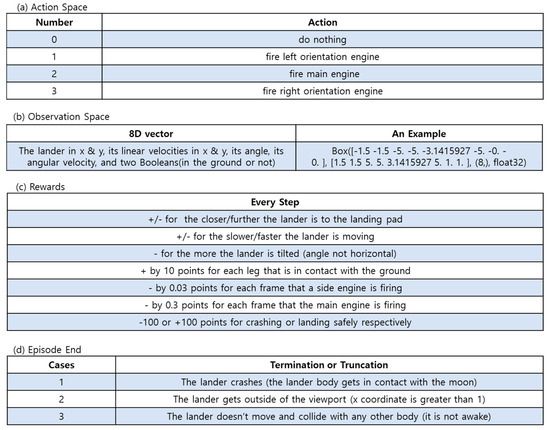
Figure 6. The environment of LunarLander V2 [31].

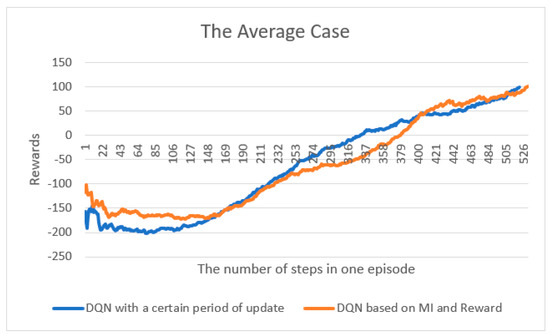
Figure 7. Average case comparison between the previous model (DQN with a certain period of update) and the proposed model (DQN based on MI and Reward), which finished in +100.

4.3. MountainCar

Generally, it is difficult to experiment with DRL in an environment in which sparse rewards are provided. Therefore, MountainCar [28], which is a representative example of an extremely sparse reward environment, was considered. MountainCar, such as cart-pole [25], is part of the representative environment for classic control in OpenAI Gym [24]. As shown in Figure 8, MountainCar had a discrete action space. Continuous action spaces also exist. In this study, only discrete action spaces were considered. MountainCar was a deterministic Markov decision process (MDP) [41] consisting of cars stochastically placed at the bottom of a sinusoidal valley. The only possible operation was acceleration, which could be applied to the car in the other direction. The goal of MountainCar was to strategically accelerate the car to reach the target condition on top of a hill on the right. However, the engine of a car was not strong enough to climb a mountain at once. The only method to achieve this goal was to drive back and forth to build momentum. The car started each episode from a standstill on the valley floor between the hills (at approximately −0.5 of the position). The episode ended when the car reached the flag (at a position greater than 0.5) or moved 200 steps. For each move, the car performed three actions (push left, push right, or do nothing). A penalty of 1 unit was applied for each move (doing nothing or reaching a half-point). In contrast to Cart-Pole [25] and LunarLander [31], MountainCar [28] followed the transition dynamics when given a motion.

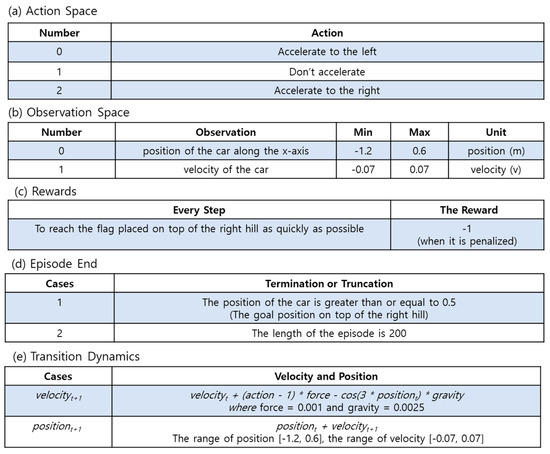
Figure 8. The environment of MountainCar V0 [28].

For a more qualitative comparison, the average loss was compared with a previously well-known DQN, which updates the target-network after setting a certain update period using the method proposed in this study. As shown in Figure 9, the box plot of the average loss showed a small but significant difference. Figure 10 shows a box plot of the differences in the change process for the rewards. When comparing the average losses, the loss of the method proposed in this study had a small loss range (the difference between the minimum and maximum), and the position of the box was relatively lower, which implies that the variability of the losses was smaller than that of the well-known DQN. Moreover, the number of outliers was relatively small. In the box plot of the reward changes, the variance (difference between the minimum and maximum) was significantly smaller than that of the well-known DQN. Moreover, the outliers were relatively small, similar to the shape of the box plot of the average losses. To obtain these results, the length of the episodes was increased from 200 to 1000, and only the results with a similar number of episodes reaching the top of the hill on the right were selected. These results showed that the method proposed in this study was much more stable in terms of agent learning. In particular, because the car in MountainCar was rewarded when it reached the top of the mountain, the method proposed in this study worked stably in an environment where there were sparse rewards, even when the car approached the top.

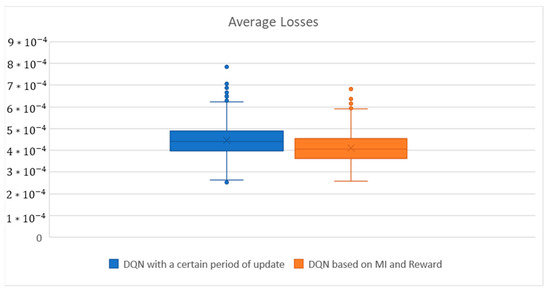
Figure 9. Average Losses comparison between the previous model (DQN with a certain period of update) and the proposed model (DQN based on MI and Reward), which has a 1000-length of episodes.

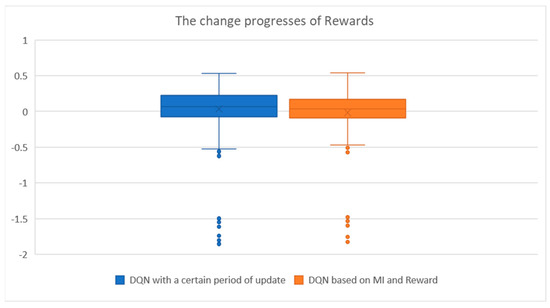
Figure 10. Comparison of the change in rewards between the previous model (DQN with a certain period of update) and the proposed model (DQN based on MI and Reward), which has results with a similar number of reaching the top of the hill on the right.

The method proposed in this study applied MI, which has been used to increase the accuracy of deep learning classification, to DRL. Deep learning can be viewed as a problem in determining a functional relationship between the input and output. The DNN parameters are determined when a DNN with a relationship is determined. In DNNs, all weights between the input and output layers become model parameters that are estimated for a more accurate prediction. In order to estimate these parameters, there should be a criterion for determining “good or bad”. This determines the loss function. In [18], MI was used to increase the accuracy of the DNN parameter estimation, which eventually affected the loss function. Therefore, the results shown in Figure 9 and Figure 10 indicate that the loss can be improved. That is, if the reward of DRL determines “how quickly the agent’s learning can be accomplished in the expected period”, the loss is that it determines “how reliably and accurately the agent’s learning process can be achieved”. This indicated that the target-network could perform in a stable manner. Depending on how the loss function is defined, the evaluation of the parameters, that is, learning orientation, changes.

Moreover, if a certain period of update, such as a hyperparameter for the update, is set from the beginning and the hyperparameter settings are fairly well conducted, it might not be necessary to use the methods [12,13,14], including the ones proposed in this study. However, in a field where the training time is less rigorous and the stable learning of the agent is more important, the method proposed in this study is recommended. The method proposed in this study requires more training time than the existing DQN. However, because Google Colab’s GPU [49] was used in the implementations in this study and it does not train a large number of parameters, such as a super-giant AI [50], the difference was not significant. The t-soft update [12,13] and Mellowmax [14] are both proposed methods for solving issues related to target-network updates. The method proposed in this study is a technique to overcome the criteria of additional hyperparameters used in these studies [12,13,14]. Therefore, if a method for adapting the hyperparameters well to each domain could be proposed, much better results could be obtained. It appears that no matter what method is used, there is no such thing as a “panacea” that is perfectly applied to all domains.

5. Conclusions

We propose a method of using MI for training DNNs together with rewards that can take advantage of mini-batches in DRL, particularly in DQN, for updating the target-network. In deep learning, hyperparameter selection and adaptation are important for the successful training of an agent. Existing methods for updating target-networks use more hyperparameters than the previously used hyperparameters in DQN. In this study, we used MI, one of the methods used to adjust the LR in DNNs, to utilize the LR of the original DQN. The proposed method uses minibatches of DRLs to calculate the MI and rewards. The results of the experiment conducted in this study confirmed that the loss was lower in a sparse environment than in the existing DQN. Moreover, if the hyperparameters were well applied for each domain, the existing DQN with a certain update period would work appropriately. However, identifying well-adapted hyperparameters for each domain is difficult. Therefore, methods for improving target-network updates are required, as in this study.