Abstract
We introduce a systematic way to obtain expressions for computing the amount of fundamental quantities such as helicity and angular momentum contained in static matter, given its charge and magnetization densities. The method is based on a scalar product that we put forward which is invariant under the ten-parameter conformal group in three-dimensional Euclidean space. This group is obtained as the static restriction (frequency ) of the symmetry group of Maxwell equations: The fifteen-parameter conformal group in 3+1 Minkowski spacetime. In an exemplary application, we compute the helicity and angular momentum squared stored in a magnetic Hopfion.
1. Introduction and Summary
Research in light–matter interactions benefits from theoretical tools whose generality allows one to treat light and matter in similar ways. Symmetries and conservation laws are prominent examples of such generic tools [1]. For example, linear and angular momentum are physical quantities that are tied to symmetry transformations and that apply to both light and matter. These quantities have in common that they are the generators of transformations in symmetry groups that are relevant in physics, such as the Poincaré group of special relativity [2].
In classical electrodynamics, light and matter are treated in a rather similar way, namely, as continuous fields, such as the electric and magnetic fields and representing radiation, and the densities of charge , current , polarization , and magnetization , representing matter. Light can be treated by using the tools of Hilbert spaces [3,4,5,6,7], facilitating the consideration of material symmetries and their consequences for light upon light–matter interaction [7]. The conformal invariance of Maxwell equations [8,9,10] and the corresponding conformally invariant scalar product between free electromagnetic fields [3,5,6] play an important role in such algebraic approach to electrodynamics. In particular, the scalar product allows one to obtain expressions for computing the amount of quantities such as angular momentum, energy, and helicity contained in a given radiation field [5,6,11]. For the radiation field, helicity is essentially its polarization handedness.
In this article, we extend the algebraic approach towards the matter side and introduce a way to obtain expressions for computing the amount of fundamental quantities contained in static material objects from their charge and magnetization densities, and , respectively. The densities are assumed to be spatially confined and real-valued. The expressions are obtained as a scalar product , where represents , and is the self-adjoint (Hermitian) operator representing the particular quantity of interest. The expression of the scalar product for static matter is derived for the static fields that are bijectively connected to and . To this end, the largest group of transformations that leave Maxwell equations with sources invariant, that is, the fifteen-parameter conformal group in 3+1 Minkowski spacetime [8,9] is considered first, then the transformations that would not preserve the frequency condition of static fields are excluded. The remaining transformations also form a group, the ten-parameter conformal group in three-dimensional Euclidean space ([12], Chapter 24). We put forward an expression for a scalar product and show that it is invariant under . In particular, it allows for explicit numerical computations of . We discuss the importance of invariant scalar products for the consistent definition of measurements and quantities such as , which provides the motivation for finding a relevant group of transformations and an invariant scalar product for the static case.
In an exemplary application, we set to focus on magnetization textures and compute the helicity and total angular momentum squared stored in a Hopfion [13,14,15,16,17] hosted inside a FeGe disk under zero external field. The definition of helicity that we use in this article Equation (5) is the one commonly used in optics and field theory, and can be understood as the sense of screw. This is not the same as the definition often used for magnetic solitons [18]. One important difference is that the latter can be defined for two-dimensional objects, while the former needs three spatial dimensions. With the definition in Equation (5), the helicity of the Hopfion is equal to −129.1. This number is a lower bound for the number of circularly polarized photons of positive helicity that would be needed in a helicity–dependent all–optical switching of the Hopfion to its mirror image of opposite-handedness: . The number −129.1ℏ also bounds the helicity that can be radiated from the Hopfion as it loses its chirality, for example by the action of a large magnetic bias aligning its magnetization density vector along the same direction at all points in the magnet.
More generally, we find that the net angular momentum and linear momentum of any along any given axis vanishes, which is consistent with the assumption of static matter.
The rest of this article is organized as follows. Section 2 introduces the setting and context of the work. The relevance of invariant scalar products for the consistent definition of measurements and quantities such as is discussed in Section 3. The scalar product for matter in static equilibrium is presented in Section 4, where its conformal invariance under is shown, providing the basis for a new approach to computing the properties of static material objects of finite volume from their charge and magnetization densities. In Section 5, we provide explicit formulas for computing the helicity, angular momentum, and angular momentum squared of a static magnetization texture and show that the net angular momentum vanishes along any given axis. In Section 5.2, we use the presented formalism for a quantitative study of a Hopfion in a FeGe disk. Section 6 concludes the article.
The approach presented here makes the computation of fundamental quantities in matter very similar to the corresponding computations for the electromagnetic fields, and can be readily applied to analytically derived [13], numerically obtained [19], or experimentally measured three-dimensional charge [20] and magnetization density distributions [21]. We foresee that the methodology will particularly be useful for the design and analysis of experiments involving the switching between stable states of a material system, such as, for example, when using circularly polarized light to switch the magnetization direction in magnetic films [22], which indicates a path towards much faster and more energy efficient computer memories, and whose underlying mechanisms are under intense scrutiny.
2. Motivation and Problem Setting
Figure 1 depicts a light–matter interaction sequence. A beam of electromagnetic radiation approaches a material object of finite size. Before the start of the interaction the object is in equilibrium with the radiation field. Then, the beam and the object interact for a finite period of time. When the interaction stops and equilibrium is reached again, both the beam and the object may have changed. For example, the energy, momentum, and angular momentum contained in the radiation field before and after the interaction may be different. The same can be said about the material system.
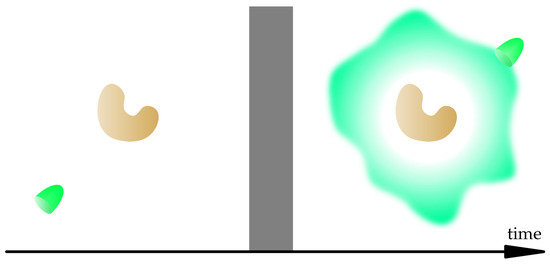
Figure 1.
A beam of electromagnetic radiation interacts with a material object of finite size during the grayed-out period. Before and some time sfter the interactiob the object is in static equilibrium, where the time derivatives of all macroscopic quantities vanish. The interaction typically changes fundamental quantities of the field such as its energy or momentum. Well known formulas exist for computing such quantities for the electromagnetic field. In this article, we develop a method to compute them for the material object in static equilibrium.
There are well-known expressions for computing the amount of a fundamental quantity such as energy or momentum contained in a given electromagnetic field. For example, in SI units which are used throughout this article, and with and respectively denoting the permittivity and permeability of vacuum, we have
as the energy and momentum of the field, respectively. The fields and are real-valued. As is explained later, we will use complex fields with positive frequencies to describe the dynamic electromagnetic field, which we denote by and , and for which the relation with the real-valued fields is .
Expressions such as those in Equation (1) can be derived in several different ways. For example, using conservation laws as in [23] (Chapter 3), or integrating the electromagnetic stress tensor as in [24] (Chapter 12.10). An alternative approach uses the tools of Hilbert spaces. In such a framework, the fields are vectors in the Hilbert space of free solutions of Maxwell equations, that is, electromagnetic fields that are not interacting with matter. Each particular solution corresponds to a ket . The fundamental quantities are represented by self-adjoint operators that act on the kets. Then, the total amount of a given fundamental quantity contained in a given electromagnetic field can be written as the scalar product of and :
The expression of the scalar product for the free radiation fields, which in particular is used for obtaining explicit expressions from Equation (2), reads [3,6]:
where , and the two kets and are represented by their plane wave components of well-defined helicity and , and and , respectively, which correspond to their left– and right–handed circular polarizations:
with , and, importantly, the angular frequency is restricted here to positive values . The exclusion of is possible in electromagnetism because both sides of the spectrum contain the same information [6] (§3.1) and [25]. The point is also excluded from the domain of the dynamic fields.
The [] are the eigenstates of the helicity operator . Helicity is the projection of the angular momentum onto the direction of the linear momentum . The -space representation of is particularly simple:
The defining property of the scalar product in Equation (3) is that it is conformally invariant [3]. That is, the value of is identical to the scalar product between and , for any transformation X in the conformal group in 3+1 Minkowski spacetime. This group is the largest group of invariance of Maxwell equations including sources as spacetime densities [8,9]. In particular, free Maxwell fields transform into free Maxwell fields under the conformal group [3]. The group consists of spacetime scalings, four special conformal transformations, and the Poincaré group, which consists of four spacetime translations, three Lorentz boosts, and three spatial rotations [26,27].
The quantity under the integral sign in Equation (3) is unitless. This can be verified by the direct computation of its units, where it should be taken into account that, according to Equation (4), the units of are equal to the units of times . A conformally invariant scalar product must be unitless, because spacetime scalings and special conformal transformations can be interpreted as changes of units [28,29,30]. In the case of the spacetime scalings, the change of units is the same for all spacetime points, while in the case of the special conformal transformations the change varies with space and time.
Together, Equations (2) and (3) are a general and convenient way of computing the amount of any fundamental quantity in the field. This motivates the following question: Can this algebraic approach be used for the material object?
An affirmative answer to this question requires an appropriate mathematical representation of matter, an appropriate group of transformations, and a scalar product that is invariant under all the group transformations. These latter two requirements are explained in the following section.
3. The Importance of Invariant Scalar Products in the Consistent Definition of Measurements
The conformal invariance of in Equation (3) is crucial for a consistent interpretation of measurements [31,32] which, besides quantum mechanics, can also be used in wave mechanics. In this interpretation, an observable property is represented by a self-adjoint operator , and the value of the property in a ket is computed by the trace rule, which for a pure state such as leads to the “sandwiches” in Equation (2) that we consider in this paper
The fact that Equation (6) is useful for Maxwell fields is clearly seen in e.g., [6]. For example, it is there shown that the result of for the energy operator H and of for the momentum operator vector are equivalent to the corresponding integrals in Equation (1). Besides reproducing results typically obtained by other means, the algebraic approach for new ones to be derived, such as the content of the generators of Lorentz boosts in a given field [6] ([Equation (4.16)), as well as for an alternative expression for the optical helicity [11].
In order to better appreciate the importance of an invariant scalar product, let us now examine its role in the consistent definition of projective measurements. Consider a setup such as the one in Figure 2, where the field is measured. We can imagine, for example, that is the outgoing field in the right hand side of Figure 1, although the exact way in which the field is produced is not important. At a certain point far away from the material object, that is, in the far field, we place a measurement device consisting of an analyzer that selects a particular frequency and polarization , followed by a photo-detector. The number of clicks in the detector will be equal to , where is essentially a -polarized plane wave with momentum lying in the direction connecting the origin of coordinates (assumed to be in or nearby the object) and the location of the measurement device.
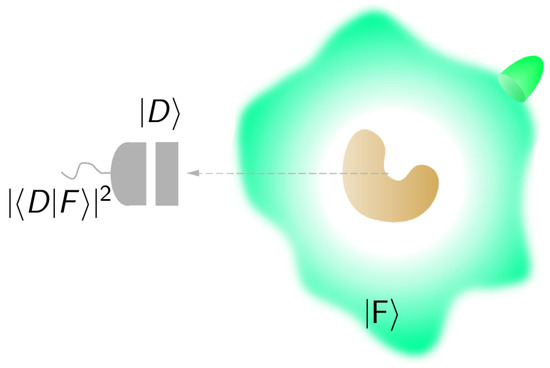
Figure 2.
In a projective measurement, the outcome of an apparatus for measuring the field can be modeled as , that is, the modulus square of the projection of onto an electromagnetic mode .
Let us now consider the effects of a global transformation X applied to the whole physical system, including both the field and the measurement apparatus:
In order for the measurement outcome to be meaningful, we must require that for any X in the largest symmetry group of Maxwell equations, i.e., the conformal group . Measurement outcomes should not change under the allowed changes of reference frame or changes of units. Similarly, we must also require that quantities such as , which can be interpreted as the average value of the measurements of on , are also invariant under any X in the conformal group: .
All such invariance requirements are fulfilled because any X in the conformal group is unitary with respect to the scalar product in Equation (3) [3], and hence, is the identity.
Thus, it is clear that the extension of the algebraic approach to matter requires a group of transformations and an invariant scalar product for the static case.
4. Conformally Invariant Scalar Product for Static Matter
4.1. Representation of Matter
With respect to electromagnetism, matter in static equilibrium can be represented by its electric charge density and its magnetization density . We assume that the time derivatives of macroscopic quantities vanish and that there are no static currents []. Moreover, we also assume that and are contained in a finite volume.
The choice of and for representing matter in static equilibrium is motivated by the existence of electric charge and magnetic spin as fundamental properties of elementary particles. In sharp contrast, while the search continues [33,34], there is no experimental evidence of isolated magnetic charges or static electric dipole moments. We therefore exclude magnetic charge densities and static polarization densities from the description of matter in static equilibrium. We note that the static electric dipoles that are present in certain molecules can be described by the dipole moment of their electric charge density, and that the dynamic polarization density can be understood as arising from a nonstatic magnetization density. In such model and are the space–space and time–space components of a totally anti-symmetric tensor, respectively, and vanishes in static equilibrium (). Such a totally antisymmetric tensor is a common model for point particles in relativistic electrodynamics [35] (Chapter II, Section 4), and has been used in studies of the effect of electron spin on the atomic nucleus [36], and of relativistic spin precession [37].
The densities and are equivalent to the static fields that they generate, as per the equations of electrostatics and magnetostatics. The scalar charge density generates the Coulomb field, which is a longitudinal (zero-curl) electric field:
The vectorial magnetization density generates the and fields. Outside the material object, both fields are proportional to each other and transverse (i.e., have zero divergence). Inside the object, where , the field is transverse, and the field is longitudinal:
Equation (8) and the second line of Equation (9) can be obtained as the limit of Maxwell equations in static equilibrium [38] (Section III), and the first line of Equation (9) is the definition of . The expressions in Equation (9) can alternatively be obtained by imposing our assumption onto the typical magnetostatic equations found in, e.g., [39] ([Equations (2.37), (2.40) and (2.41)]) or in [24] ([Equations (5.80)–(5.82)). Effectively, the equations in (9) are identifications of the transverse and longitudinal parts of with the other fields, and we may as well use only instead of both and together. Equation (8) implies that and determine each other bijectively. We choose to use here because it shares some transformation properties with the magnetization , allowing us to avoid different derivations in some cases should we use instead. We can therefore represent matter in static equilibrium by means of and , or alternatively by means of their Fourier transforms and , which can be obtained by integrals in the finite volume V occupied by the object:
where the first equality in the second line of Equation (10) follows from Equation (8).
We note that both and are real–valued.
4.2. Group of Transformations and Invariant Scalar Product for the Static Case
In this section, we define an appropriate scalar product for static matter, which, in particular, allows one to use Equation (2) for computing the amount of fundamental quantities stored in matter. With such scalar product, each corresponds to a ket in the Hilbert space of static matter. This Hilbert space is different from the one containing the radiation fields. One salient difference is the frequency , which is equal to zero for static matter and strictly larger than zero in radiation fields. Another difference is that there are helicity zero (longitudinal) components in static matter, while the radiation fields are always transverse.
Motivated by the requirement of invariant measurements formulated in Section 3, we pursue the idea of a group invariance for the scalar product by starting with the full conformal invariance of Maxwell equations with the sources shown by Bateman [8], Cunningham [9] and Dirac [10], among others [30]. While in Dirac’s work the sources were electric charge-current densities, both Bateman and Cunningham additionally included magnetization and polarization densities.
The conformal invariance including sources deserves further discussion. On the one hand, the invariance of Maxwell equations with sources under the 15 parameter conformal group in Minkowski spacetime is often explicitly recognized in the literature; e.g., see [27] (Section 3.1) or the review by Kastrup [30], where the conformal symmetry, its role in theoretical physics, and their historical evolution are comprehensively explained. On the other hand, the fact that fixed mass parameters break the scale invariance, and consequently the conformal invariance, could suggest the incorrect conclusion that Maxwell equations are conformally invariant only in the source-free case. In this respect, it is important to note that Maxwell equations including electric charge-current densities and magnetization and polarization densities do not feature any fixed mass parameter. The invariance under conformal transformations follows from the way in which the sources transform. The transformations of can be found in [27] ([Equations 3.40ab). A simple illustration is the transformation law of the electric charge density under a scaling : in the static case, which is readily shown to preserve the total charge in a volume. The bottom line is that when both fields and sources are transformed, the form of the dynamic Maxwell equations with sources remains invariant. This is what we use below as the starting point for obtaining the sought after expression of a scalar product for the static case. Incidentally, even equations with a mass parameter, such as the Dirac equation, can be shown to be conformally invariant if one allows for a particular re-scaling of the mass [30] (Section 5.1).
Let us now return to the idea of invariance for the scalar product. Since we are considering matter in static equilibrium, we need to remove all the transformations of that do not preserve the condition. Lorentz boosts change and mix it with the components of . The time component of the special conformal transformations four-vector also changes [26] (Section 3). We remove all these transformations. We also remove time translations because, while preserving the condition, any time–translations will, for the static case, just degenerate into the identity operator. We are then left with a ten-parameter group consisting of spatial translations, spatial rotations, the spatial scaling ( with ), and three special conformal transformations: The the ten-parameter conformal group in three-dimensional Euclidean space [12] (Chapter 24). It is interesting to see that the static restriction of the conformal group in 3+1 spacetime dimensions results in the conformal group in three spatial dimensions. Accordingly, along with the discussion in Section 3, our sought-after scalar product must be invariant under all the transformations in .
We now proceed by considering the -invariant scalar product expression in Equation (3). We first perform a unitary change of basis, going from the to the basis by using Equation (4) to express the latter as linear combinations of the former:
where is the 3×3 identity matrix. We now replace by . Both quantities have the same units. This replacement is necessary in order to include the longitudinal degree of freedom that can contain, which is always absent in :
Equations (3), (11), and (12) motivate us to write the following scalar product expression for the fields.
As is the case in Equation (3), the quantity under the integral sign in Equation (13) is unitless. This is readily seen with the following equalities between the units of different fields:
When written in the equivalent form in Equation (28), Equation (13) coincides with the invariant scalar product for the relevant representations of the scale-Euclidean group in Equation (29) in [40]; the extra in Equation (29) of [40] with respect to Equation (28) in this paper is compensated by the extra factor in the plane wave decomposition in Equation (57) in [40], as compared to Equation (10). That in Equation (57) in ([40], follows from the definition of N in Equation (25a) in [40], and the transformation properties of and under spatial scalings. Therefore, the scalar product in Equation (13) is invariant under the scale-Euclidean group, which is a seven–parameter sub–group of composed by translations, rotations, and spatial scalings. These transformations act hence unitarily with respect to the scalar product. The invariance of the scalar product in Equation (13) under the rest of , that is, under special conformal transformations, xan be seen as below.
The special conformal transformations act on the coordinate vector as ([12], Equation (24.4)):
where is a real-valued 3-vector: . To prove that Equation (13) is invariant under such transformations one must show that the special conformal transformations are unitary. This unitary character is shown by considering that the special conformal transformation along axis l with parameter can be obtained from the spatial translation along such axis by the same parameter and the inversion operation ([12], below Equation (24.4)):
The action of on the coordinate vector is
Since we already known that the translations act unitarily, Equation (15) implies that and if is unitary, then is unitary as well. The unitary character of is shown in Appendix A by extending a result contained in Section II of [41].
Once known to be unitary, the conclusion that the scalar product in Equation (13) is invariant under can also be reached directly without using its invariance under the scale-Euclidean group. First, we establish that the action of spatial translations leaves Equation (13) invariant, which is obvious when substituting the known action of arbitrary translations by a displacement vector on the Fourier transforms and
onto Equation (13), where the acquired phases cancel.
Since the translations are unitary, their generators are self-adjoint, and so are the generators of the special conformal transformations , because of Equation (15). The other generators of , that is, the angular momentum operators and the generator of dilations D, can be obtained as commutators of and [41] (Equation (20)):
Then, because the adjoint of the commutator of two self-adjoint operators is minus itself, it follows, noting that when taking the adjoint of the right hand side of Equation (18), that and must be self-adjoint, and hence, the transformations that they generate must be unitary. We recall that , , , , and .
We adopt Equation (13) as the -invariant scalar product for . This provides a new way of obtaining expressions for computing the amount of fundamental quantities stored in matter.
Conveniently, the very similar functional form of the expressions for the scalar products in the dynamic and static cases, Equations (3) and (13), respectively, implies that known -space expressions of fundamental operators for the case [5,6,42] can be also used for the case. The same is true for the corresponding -space expressions.
We note that, while the scalar products for the dynamic case in Equation (3) and for the static case in Equation (13) are invariant under and , respectively, the dynamic fields and static densities are not required to exhibit specific symmetries.
In the rest of the article, we will focus on fundamental quantities stored in the magnetization density, for which we set in Equation (13):
Nevertheless, the methodology that we use applies to the case with as well. For example, the representations of using three scalar complex functions in the domain of linear momentum , or angular momentum , where is the helicity, have their counterparts for representing , except that contains only the component. The counterpart of Equation (25) is
and Equations (30) and (32)–(34) apply, with the difference that the helicity takes only the value .
5. Helicity and Angular Momentum in Magnetization
We start with the helicity stored in . At each point, can be decomposed into the three eigenstates of the helicity operator for vectorial fields:
The longitudinal component corresponds to non-vanishing . While a net magnetic charge in an isolated object has not been observed, complicated magnetization textures are expected to contain pairs of monopoles of opposite charge [14], and pairs of singularities have indeed been experimentally imaged [21]. The longitudinal term in the magnetization is crucial for their description. In contrast, the free dynamic electromagnetic field is divergenceless, and the component vanishes.
For the explicit decomposition into plane waves we use
where are complex-valued functions, and
where and . The meet [5,6]
The last equation in (24) implies that
Other choices for the helicity eigenvectors exist in the literature. In particular, the used by Bialynicki-Birula [5,6] are related to the vectors used by Moses [40,43] in the following way: .
Using the expression of the helicity operator in Equation (5), the helicity stored in can then be written:
We note that the charge density cannot store helicity, because .
As shown in [38], the result of Equation (26) is proportional to the definition of the static magnetic helicity [44,45,46]:
where , and hence .
More generally, Equations (21), (24) and (25) can be used to write the expression of the scalar product in Equation (19) as a function of the
which allows one to compute from the , as long as the action of on is known.
Let us now turn our attention to angular momentum. Rather than using , the computation of is more conveniently performed in the angular momentum basis:
where denotes a simultaneous eigenstate of , , , and with eigenvalues , , , and , respectively, and
where the Wigner D-matrices for spatial rotations [47] (Chapter 4) enter as follows:
where are the Wigner small d-matrices as defined in [47] (Chapter 4.3), and . The publicly available EasySpin computer code contains a convenient implementation of the Wigner matrices [48].
As we show in Appendix B, the scalar product can also be written as:
The action of angular momenta operators on is [49] (Equations (2.1)–(2.3)):
with which we can write:
Appendix C shows that the angular momenta and the linear momenta both vanish. The origin of this vanishing can be found in the following restrictions, which follow from assuming :
For example, for the proof is straightforward because the sum over m vanishes since the second line of Equation (35) implies that , and hence, for all .
Derivations similar to those in Appendix C show that the linear and angular momenta in [] vanish as well since, for :
The vanishing of linear and angular momenta for the whole is consistent with the static equilibrium condition under zero external fields. In contrast, the squared linear and angular momenta and , do not vanish (see, e.g., the last line of Equation (34)). We note that the non-zero mean value of the square of a property simultaneously with zero mean value of such property can easily occur, and should not be taken as a sign of a quantum effect. Since the eigenvalues of self-adjoint operators are real numbers, the eigenvalues of squares of self-adjoint operators are non-negative real numbers. Then, the value of a property measured as the average of a self-adjoint operator for a given state can be zero, while, simultaneously, the average of the squared operator is non-zero. For example: The average joint linear momentum of two counterpropagating plane-waves is zero in any direction, yet the linear momentum squared () is not.
The and for a given can be readily obtained with the following sequence of computations:
which can be applied to analytically derived, numerically obtained, or experimentally measured three-dimensional magnetization textures confined to finite volumes.
We note that, given , the and corresponding to can be obtained similarly.
5.1. Discrepancies with Existing Results
The computation of the linear and angular momenta of magnetic solitons [50,51,52,53,54,55] remains an active field of research [56,57,58,59]. Starting from the Landau–Lifshitz (LL) equation, different integral expressions have been proposed, mostly for predicting the dynamics of topologically non-trivial magnetization textures inside an unbounded magnetic medium under, for example, an external magnetic field. Nevertheless, such integrals are assumed to also be valid for the static case without external fields. Using one of the latest versions of such integrals, even a completely static domain wall has a finite linear momentum [58]. With our methodology, as shown in Appendix C.2, a static magnetization density has a vanishing value of average linear momentum and angular momentum along any given axis. The difference in the results can be attributed to the fact that the two approaches are applied to systems meeting quite different assumptions. In this article, we consider a bounded three-dimensional domain containing a given static three-dimensional magnetization. In contrast, the LL-based approaches consider a two or three-dimensional domain of infinite size where the magnetization is allowed to vary, as for example when three-dimensional topological textures are stabilized by endless motion with constant velocity [53].
5.2. Helicity and Angular Momentum of a Hopfion
As an exemplary application, we will now compute the helicity and angular momentum squared stored in a Hopfion.
A convenient analytical approximation of the magnetization density of a Hopfion has been provided by P. Sutcliffe in [13], where the Hopfion is hosted in a disk of FeGe of height L = 70 and diameter 3L, and is numerically stabilized to a cylindrically symmetric configuration using the Dzyaloshinskii–Moriya interaction of the chiral magnet and a strong anisotropy perpendicular to the flat ends of the cylinder. With good approximation to the numerical results, the Cartesian components of unit magnetization density vector of the Hopfion are given in [13] (Equation (3.3)) as a function of the cylindrical coordinates of the position vector . The magnitude of is assumed to be constant: . A value of M = 384 / is assumed here.
For the numerical calculations, the cylindrical domain of the Hopfion was discretized with [107, 65, 71] points in cylindrical coordinates and the space with 950 points for between 0 and 20 L, and with 2592 points for at each . The multipolar orders from to were considered.
All the expected outcomes such as the conditions in Equation (35), or the vanishing of the momenta and angular momenta, are numerically verified for the Hopfion up to numerical inaccuracies at the level of the fifth significant digit.
Table 1 contains the values for the helicity and angular momentum squared stored in the Hopfion computed with the last lines of Equations (26) and (34), respectively. The stored helicity is equivalent to ≈129 right-handed circularly polarized photons, which is about ten orders of magnitude smaller than the number of photons in a circularly polarized femtosecond laser pulse of 10 −2 fluence at a central wavelength of 800 .

Table 1.
Helicity , and angular momentum squared stored in a Hopfion computed using the last lines of Equations (26) and (34), respectively. An analytical approximation of the Hopfion in a chiral FeGe magnet of cylindrical shape [13] was used in the calculations. The height of the cylinder is equal to the magnetic helical period L, and the diameter is equal to 3L. A magnetization density saturation value of M = 384 kA/ is assumed.
The value of helicity, equal to −129.1 implies a lower bound for the number of circularly polarized photons that would be needed in a helicity–dependent all optical switching of the Hopfion onto its mirror image of opposite helicity: . Additionally, −129.1 also bounds the helicity that can be radiated by the Hopfion as it loses its chirality, for example, by the action of a large magnetic bias aligning its magnetization density vector along the same direction at all points.
Appendix D contains further analysis of the angular momentum content of the Hopfion. In particular, we show that the Hopfion is an eigenstate of with angular momentum zero.
6. Conclusions
We have introduced a new way to obtain expressions for the computation of the fundamental quantities in static matter from its charge and magnetization densities. The method is based on a scalar product obtained from requirements of invariance under the ten-parameter conformal group in three-dimensional Euclidean space . This group is obtained as the static () restriction of the symmetry group of Maxwell equations with sources, namely, the fifteen-parameter conformal group in 3+1 Minkowski spacetime.
In an exemplary application, we have used the formalism to compute the angular momentum squared and helicity stored in a Hopfion inside a FeGe disk.
We foresee that this methodology will in particularly be useful for the design and analysis of experiments involving the switching between stable states of a material system.
Author Contributions
Conceptualization, I.F.-C.; Methodology, I.F.-C. and M.V.; Formal analysis, I.F.-C.; Writing—original draft, I.F.-C.; Writing—review & editing, M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project ID 258734477, SFB 1173, and by the Helmholtz Association via the Helmholtz program “Materials Systems Engineering” (MSE).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Inversion R Is Unitary
In this appendix, we extend some of the results in [41] to prove that the inversion operation is unitary under the scalar product of Equation (13) (Equation (28)) for meeting:
We first summarize the results in [41] (Section II).
While [41] deals mainly with solutions of the scalar wave equation, the results in its Section II apply in general to functions such that
where, instead of the four-momentum , we just use as the argument since the time component is equal to for the functions considered in [41].
Since the inversion commutes with all rotations, the expansion in spherical harmonics
is convenient because the inversion leaves unchanged. This is a consequence of the preservation of angles by conformal transformations. Only the radial parts are affected by . Radial eigenfunctions
are identified in [41] (Equation (11)). They are a complete orthonormal system for functions defined on the positive real line .
The authors of [41] then constructed a basis of eigenstates of defined by three integers , which allows one to expand any meeting Equation (A2) as:
The unitary character of under the scalar product
follows then readily from the third line of Equation (A5) and from .
The result that is unitary can be extended to the functions used in this article as follows.
The angular momentum basis is again convenient for the task. The properties of the Wigner D-matrices imply that the relation inverse to Equation (30) is
We see that Equation (A7) is very similar to Equation (A3). Importantly, the angular and radial dependences are separated into and , respectively.
Let us now define the functions:
The angular functions are, as the , a complete orthonormal system on the sphere (see the solution of the boxed integral in Equation (A11) of Appendix B). Actually, for we have that [60] (Equation 8.5–10). Since the radial functions are orthonormal and complete on the real positive line, it follows that the in Equation (A8) are a basis of the eigenstates of with eigenvalue , and hence can be readily shown to act unitarily on the spaces of functions by repeating the above considerations around Equations (A5) and (A6).
Appendix B. The Scalar Product in the Angular Momentum Basis
The properties of the Wigner D-matrices imply that the relation inverse to Equation (30) is
which we substitute into Equation (28):
After splitting the d integral into its radial and angular parts
we solve the angular integral in the box by substituting (Equation (31)), solving the integral in , and using the orthogonality properties of the small Wigner d-matrices [60] (Equation (8.3-2)), whose elements are real-valued:
Substituting this result in the box of Equation (A11) results in Equation (32).
Appendix C. The Linear and Angular Momenta Vanish
In this appendix, we will show that the angular momenta and the linear momenta vanish by using , and its consequences of this for the and coefficients.
The well-known consequence of for its Fourier transform is that
which, together with the complex conjugation transformations of the in Equation (23)
and the decomposition in Equation (22), readily leads to
Showing that
is somewhat more involved. We start by using Equation (A9) to write:
and manipulate the last term
using the change of angular variables upon spatial inversion in the first equality, a formula in [47] (Equation (1), p. 79) in the second, and that the fact that the small Wigner d-matrices are real valued in the third.
After substituting Equation (A18) into Equation (A17)
and re-labeling the summation variable
comparing Equation (A20) with Equation (A9) makes it clear that the condition in Equation (A15) implies Equation (A16).
Appendix C.1. Angular Momentum
The proof that can be found in the main text, just below Equation (35).
Let us now consider in Equation (34), and show that
which implies that .
The summation in m contains an even number of terms since is not defined for . The summing can be done pairwise, where one of the terms has and the other is the term. Dropping elements from the notation, their sum reads:
We now substitute
and find that the sum vanishes after applying Equation (A16) to the two factors of the second line of Equation (A23):
The steps for the corresponding proof that = 0 in the second line of Equation (34) are very similar.
Appendix C.2. Linear Momentum
In -space, the action of the momentum operator is . Then, the momentum of in direction can be written:
Appendix D. Angular Momentum Content of the Hopfion
This appendix contains further analysis of the angular momentum content of the Hopfion. Some insight can be gained even without having the at hand. For example, we show that the Hopfion magnetization density is an eigenstate of with eigenvalue zero.
We start by slightly rewriting the expression in [13] (Equation (3.3)) with the help of a rotation matrix:
where the last equality contains the definition of and
We now apply the of [61] (Equation (5.43)) to the Hopfion. In cylindrical coordinates for but Cartesian components for the vector, has the following expression:
Since does not depend on , we can just apply to :
The result of Equation (A29) is faithfully reproduced by the amplitudes obtained from the sequence of computations indicated in Equation (37). Figure A1 shows the distribution of the different helicities across the values of m. We highlight that the values for are not suppressed from the plot, but they are not visible in this scale. The sign of the helicity of the Hopfion in Table 1 can be deduced from the larger value of the negative helicity component in Figure A1.
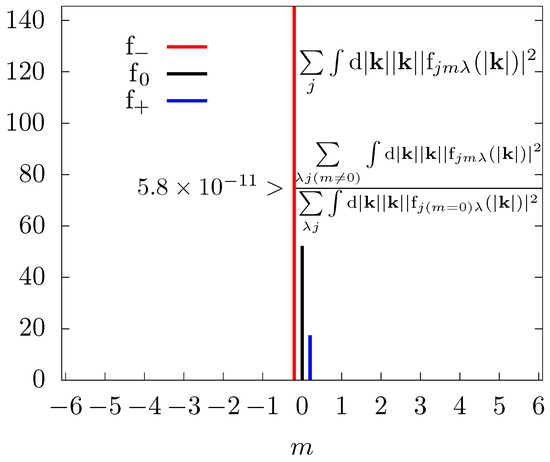
Figure A1.
Angular momentum content of the Hopfion for each helicity computed with the formula on the top right corner. Such expression gives the partial norm squared of the Hopfion in each subspace, and is therefore a conformally invariant unitless number. While the numerical errors in the calculations produce components, they are not visible in this scale because they are much smaller than the components, as indicated by the inequality. For clarity, two of the color bars are horizontally offset from the point.
References
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Wigner, E. On Unitary Representations of the Inhomogeneous Lorentz Group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Gross, L. Norm Invariance of Mass-Zero Equations under the Conformal Group. J. Math. Phys. 1964, 5, 687–695. [Google Scholar] [CrossRef]
- Moses, H.E. Photon Wave Functions and the Exact Electromagnetic Matrix Elements for Hydrogenic Atoms. Phys. Rev. A 1973, 8, 1710–1721. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. Quantum Electrodynamics; Pergamon: Oxford, UK, 1975. [Google Scholar]
- Bialynicki-Birula, I. Photon Wave Function. Prog. Opt. 1996, 36, 245–294. [Google Scholar]
- Fernandez-Corbaton, I.; Rockstuhl, C. Unified theory to describe and engineer conservation laws in light-matter interactions. Phys. Rev. A 2017, 95, 053829. [Google Scholar] [CrossRef]
- Bateman, H. The Transformation of the Electrodynamical Equations. Proc. Lond. Math. Soc. 1910, s2-8, 223–264. [Google Scholar] [CrossRef]
- Cunningham, E. The Principle of Relativity in Electrodynamics and an Extension Thereof. Proc. Lond. Math. Soc. 1910, s2-8, 77–98. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Wave Equations in Conformal Space. Ann. Math. 1936, 37, 429–442. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I. A Conformally Invariant Derivation of Average Electromagnetic Helicity. Symmetry 2019, 11, 1427. [Google Scholar] [CrossRef]
- Grafarend, E.W.; Krumm, F.W. Map Projections; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Sutcliffe, P. Hopfions in chiral magnets. J. Phys. A Math. Theor. 2018, 51, 375401. [Google Scholar] [CrossRef]
- Liu, Y.; Lake, R.K.; Zang, J. Binding a hopfion in a chiral magnet nanodisk. Phys. Rev. B 2018, 98, 174437. [Google Scholar] [CrossRef]
- Tai, J.S.B.; Smalyukh, I.I. Static Hopf Solitons and Knotted Emergent Fields in Solid-State Noncentrosymmetric Magnetic Nanostructures. Phys. Rev. Lett. 2018, 121, 187201. [Google Scholar] [CrossRef] [PubMed]
- Kent, N.; Reynolds, N.; Raftrey, D.; Campbell, I.T.G.; Virasawmy, S.; Dhuey, S.; Chopdekar, R.V.; Hierro-Rodriguez, A.; Sorrentino, A.; Pereiro, E.; et al. Creation and observation of Hopfions in magnetic multilayer systems. Nat. Commun. 2021, 12, 1562. [Google Scholar] [CrossRef] [PubMed]
- Khodzhaev, Z.; Turgut, E. Hopfion dynamics in chiral magnets. J. Phys. Condens. Matter 2022, 34, 225805. [Google Scholar] [CrossRef]
- Verba, R.V.; Navas, D.; Bunyaev, S.A.; Hierro-Rodriguez, A.; Guslienko, K.Y.; Ivanov, B.A.; Kakazei, G.N. Helicity of magnetic vortices and skyrmions in soft ferromagnetic nanodots and films biased by stray radial fields. Phys. Rev. B 2020, 101, 064429. [Google Scholar] [CrossRef]
- Peralta, J.E.; Scuseria, G.E.; Frisch, M.J. Noncollinear magnetism in density functional calculations. Phys. Rev. B 2007, 75, 125119. [Google Scholar] [CrossRef]
- Coppens, P. Charge Densities Come of Age. Angew. Chem. Int. Ed. 2005, 44, 6810–6811. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, C.; Guizar-Sicairos, M.; Scagnoli, V.; Gliga, S.; Holler, M.; Raabe, J.; Heyderman, L.J. Three-dimensional magnetization structures revealed with X-ray vector nanotomography. Nature 2017, 547, 328–331. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-Optical Magnetic Recording with Circularly Polarized Light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Schwinger, J.; Deraad, L.L.J.; Milton, K.A. Classical Electrodynamics; Westview Press: Boulder, CO, USA, 1998. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Bialynicki-Birula, I.; Newman, E.T.; Porter, J.; Winicour, J.; Lukacs, B.; Perjes, Z.; Sebestyen, A. A note on helicity. J. Math. Phys. 1981, 22, 2530–2532. [Google Scholar] [CrossRef]
- Budinich, P.; Raczka, R. Global properties of conformally flat momentum space and their implications. Found. Phys. 1993, 23, 599–615. [Google Scholar] [CrossRef]
- Fuschchich, W.; Nikitin, A. Symmetries of Equations of Quantum Mechanics; Allerton Press: New York, NY, USA, 1994. [Google Scholar]
- Kastrup, H.A. Zur physikalischen Deutung und darstellungstheoretischen Analyse der konformen Transformationen von Raum und Zeit. Ann. Der Phys. 1962, 464, 388–428. [Google Scholar] [CrossRef]
- Barut, A.; Haugen, R.B. Theory of the conformally invariant mass. Ann. Phys. 1972, 71, 519–541. [Google Scholar] [CrossRef]
- Kastrup, H. On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics. Ann. Der Phys. 2008, 520, 631–690. [Google Scholar] [CrossRef]
- Sorkin, R.D. Quantum mechanics as a quantum measure theory. Mod. Phys. Lett. A 1994, 9, 3119–3127. [Google Scholar] [CrossRef]
- Hardy, L. Quantum theory from five reasonable axioms. arXiv 2001, arXiv:quant-ph/0101012. [Google Scholar]
- Rajantie, A. The search for magnetic monopoles. Phys. Today 2016, 69, 40–46. [Google Scholar] [CrossRef]
- Fortson, N.; Sandars, P.; Barr, S. The Search for a Permanent Electric Dipole Moment. Phys. Today 2003, 56, 33–39. [Google Scholar] [CrossRef]
- Barut, A.O. Electrodynamics and Classical Theory of Fields & Particles; Dover: New York, NY, USA, 1980. [Google Scholar]
- Frenkel, J. Die Elektrodynamik des rotierenden Elektrons. Z. Für Phys. 1926, 37, 243–262. [Google Scholar] [CrossRef]
- Bargmann, V.; Michel, L.; Telegdi, V.L. Precession of the Polarization of Particles Moving in a Homogeneous Electromagnetic Field. Phys. Rev. Lett. 1959, 2, 435–436. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I. Total helicity of electromagnetic fields and matter. Phys. Rev. B 2021, 103, 054406. [Google Scholar] [CrossRef]
- Brown, W.F. Magnetostatic Principles in Ferromagnetism; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962; Volume 1. [Google Scholar]
- Moses, H.E.; Quesada, A.F. The expansion of physical quantities in terms of the irreducible representations of the scale-euclidean group and applications to the construction of scale-invariant correlation functions. Arch. Ration. Mech. Anal. 1973, 50, 194–221. [Google Scholar] [CrossRef]
- Kastrup, H.A.; Mayer, D.H. On Some Classes of Solutions of the Wave Equation. J. Math. Phys. 1970, 11, 1041–1047. [Google Scholar] [CrossRef]
- Moses, H.E. Transformation from a Linear Momentum to an Angular Momentum Basis for Particles of Zero Mass and Finite Spin. J. Math. Phys. 1965, 6, 928–940. [Google Scholar] [CrossRef]
- Moses, H.E. The role of the irreducible representations of the Poincaré group in solving Maxwell’s equations. J. Math. Phys. 2004, 45, 1887–1918. [Google Scholar] [CrossRef]
- Woltjer, L. A theorem on force-free magnetic fields. Proc. Natl. Acad. Sci. USA 1958, 44, 489–491. [Google Scholar] [CrossRef]
- Moffatt, H.K. The degree of knottedness of tangled vortex lines. J. Fluid Mech. 1969, 35, 117–129. [Google Scholar] [CrossRef]
- Ranada, A.F. On the magnetic helicity. Eur. J. Phys. 1992, 13, 70–76. [Google Scholar] [CrossRef]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Lomont, J.S.; Moses, H.E. The Representations of the Inhomogeneous Lorentz Group in Terms of an Angular Momentum Basis. J. Math. Phys. 1964, 5, 294–298. [Google Scholar] [CrossRef]
- Dzyloshinskii, I.; Ivanov, B. Localized topological solitons in a ferromagnet. Sov. J. Exp. Theor. Phys. Lett. 1979, 29, 540. [Google Scholar]
- Volovik, G.E. Linear momentum in ferromagnets. J. Phys. C Solid State Phys. 1987, 20, L83–L87. [Google Scholar] [CrossRef]
- Papanicolaou, N.; Tomaras, T. Dynamics of magnetic vortices. Nucl. Phys. B 1991, 360, 425–462. [Google Scholar] [CrossRef]
- Papanicolaou, N. Dynamics of magnetic vortex rings. In Singularities in Fluids, Plasmas and Optics; Springer: Berlin/Heidelberg, Germany, 1993; pp. 151–158. [Google Scholar]
- Cooper, N.R. Propagating Magnetic Vortex Rings in Ferromagnets. Phys. Rev. Lett. 1999, 82, 1554–1557. [Google Scholar] [CrossRef]
- Kosevich, A.; Ivanov, B.; Kovalev, A. Magnetic Solitons. Phys. Rep. 1990, 194, 117–238. [Google Scholar] [CrossRef]
- Borisov, A.B.; Rybakov, F.N. Stationary precession topological solitons with nonzero Hopf invariant in a uniaxial ferromagnet. JETP Lett. 2008, 88, 264–267. [Google Scholar] [CrossRef]
- Borisov, A.B.; Rybakov, F.N. Dynamical toroidal Hopfions in a ferromagnet with easy-axis anisotropy. JETP Lett. 2009, 90, 544–547. [Google Scholar] [CrossRef]
- Yan, P.; Kamra, A.; Cao, Y.; Bauer, G.E.W. Angular and linear momentum of excited ferromagnets. Phys. Rev. B 2013, 88, 144413. [Google Scholar] [CrossRef]
- Tchernyshyov, O. Conserved momenta of a ferromagnetic soliton. Ann. Phys. 2015, 363, 98–113. [Google Scholar] [CrossRef]
- Tung, W.K. Group Theory in Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; Wiley: New York, NY, USA, 1957. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).