A Study on a Spacelike Line Trajectory in Lorentzian Locomotions

Abstract

In this study, we establish a novel Lorentzian interpretation of the Euler–Savary ($\mathcal{E}-\mathcal{S}$) and Disteli ($\mathcal{D}is$) formulae. Subsequently, we proceed to establish a theoretical structure for a Lorentzian torsion line congruence which is the spatial symmetry of the Lorentzian circling-point dual curve, in accordance with the principles of the kinematic theory of spherical locomotions. Further, a timelike ($\mathcal{T}like$) torsion line congruence is defined and its spatial equivalence is examined. The findings contribute to an enhanced comprehension of the interplay between axodes and Lorentzian spatial movements, which has possible significance in various disciplines, such as the fields of robotics and mechanical engineering.

1. Introduction

The concept of the instantaneous screw axis ($\mathbb{ISA}$) of a moving body is well-established. This axis gives rise to two distinct ruled surfaces, known as the mobile and immobile axodes, with $\mathbb{ISA}$ as their creating line in the movable space and in the steady space, respectively. The axodes exhibit both sliding and rolling motion relative to each other along a defined trajectory, which ensures that the tangential contact between the axodes remains constant throughout the entire length of the two matting rulings (one being in all axodes), which simultaneously motivate the $\mathbb{ISA}$ at any instant. at any given moment. It is appreciable that not only does a certain suitable locomotion lead to a unique set of axodes but the opposite also occurs. This designates that, should the axodes of any locomotion be recognized, the private locomotion can be recreated without awareness of the physical constituents of the mechanism, their organization, distinct dimensions, or the designates by which they are attached [1,2,3,4,5]. The recruitment of axodes in the execution of composition is enhanced as manifest by examination showing that the axodes are central within the physical mechanism and the actual locomotion of its constituents. For instance: Garnier [6] was the first to address the issue of the kinematics ownership of the instantaneous locomotion created by the axodes up to the second order. Then, he gave the $\mathcal{E}-\mathcal{S}$ formulae for the spherical locomotion by appointing the spherical polodes. A procedure for appointing and finding its characteristics was advanced by Phillips and Hunt [7]. Skreiner [8] assigned the intermediate modification of the $\mathbb{ISA}$ by the intermediary of a spatial locomotion and researched numerous distinct cases. Diziogly [9] suggested that the $\mathcal{E}-\mathcal{S}$ action be utilized to determine the $\mathcal{D}is$-axis, taking into consideration the local characteristics of the axodes. Abdel-Baky and Al-Solamy [10] proposed a novel geometric-kinematic approach to one-parameter locomotion based on facts describing the locomotion of the axodes. A significant amount of research exists concerning the $\mathbb{ISA}$ and the axode invariants [11,12,13,14,15,16,17,18,19].

The discovery of dual numbers is attributed to W. Clifford, who was the first to identify their existence. Subsequently, E. Study employed dual numbers as a tool to investigate the properties of locomotions and line geometry. The theorist attracted attention to the performance of straight lines through the utilization of dual unit vectors. Additionally, he identified and established the mapping that is commonly associated with his name, known as the E. Study map. The collection of all oriented lines in Euclidean 3-space ${\mathbb{E}}^3$ is in bijection with a set of points on the dual unit sphere ($\mathcal{DUS}$) in the dual 3-space ${\mathbb{D}}^3$. Further characteristics of the E. Study map and screw calculus can be found in [8,9,20,21,22]. By utilizing these works, if we adopt the Minkowski 3-space ${\mathbb{E}}_1^3$ as an alternative of ${\mathbb{E}}^3$, the situation frequently has more features than the Euclidean case. In ${\mathbb{E}}_1^3$, the distance $⟨,⟩$ can be positive, negative or zero, while the distance in ${\mathbb{E}}^3$ is strictly limited to positive values. Thus, it is necessary to differentiate oriented lines based on the value of distance $⟨,⟩$ determining whether it is positive, negative, or zero. Oriented lines with $⟨,⟩<0$ ($⟨,⟩>0)$ are named timelike ($\mathcal{T}like$) (spacelike ($\mathcal{S}like$)) oriented lines and oriented lines with $⟨,⟩=0$ are named null lines [23,24,25,26].

In this paper, the invariants of the axodes are utilized for extracting new Lorentzian proofs of the $\mathcal{E}-\mathcal{S}$ and $\mathcal{D}is$ formulae. Symmetrical to the kinematic theory of spherical movement, the well known cubic of the steady curvature is discovered on a Lorentzian dual unit sphere. Afterward, a $\mathcal{S}like$ torsion line congruence is elucidated and its spatial synonym is scrutinized. The advanced statements degenerate into a quadratic form, which can readily enable evident understanding into the geometric estates of the $\mathcal{S}like$ torsion line congruence.

2. Preliminaries

An outline of dual numbers theory and the dual Lorentzian vectors is specified in [23,24,25,26,27,28]. If $\xi ,$ and ${\xi }^{*}$ are real numbers, then a dual number can be designed as: $\widehat{\xi }=\xi +\epsilon {\xi }^{*}$, such that $\epsilon \ne 0$ and ${\epsilon }^2=0$. This is, in fact, quite analogous to the notion of a complex number, the prime singularity being in a complex number ${\epsilon }^2=-1$. Then, the set

$${\mathbb{D}}^3=\{\widehat{\mathit{\xi }}:=\mathit{\xi }+\epsilon {\mathit{\xi }}^{*}=({\widehat{\xi }}_1,{\widehat{\xi }}_2,{\widehat{\xi }}_3)\},$$

shared with the Lorentzian metric

$$⟨\widehat{\mathit{\xi }},\widehat{\mathit{\xi }}⟩=-{\widehat{\xi }}_1^2+{\widehat{\xi }}_2^2+{\widehat{\xi }}_3^2,$$

is a dual Lorentzian 3-space ${\mathbb{D}}_1^3$. A dual vector $\widehat{\mathit{\xi }}\in {\mathbb{D}}_1^3$ is a $\mathcal{S}like$ dual if $⟨\widehat{\mathit{\xi }},\widehat{\mathit{\xi }}⟩>0$ or $\widehat{\mathit{\xi }}=\mathbf{0}$, a $\mathcal{T}like$ dual if $⟨\widehat{\mathit{\xi }},\widehat{\mathit{\xi }}⟩<0$, and a lightlike ($\mathcal{L}like$) or null dual if $⟨\widehat{\mathit{\xi }},\widehat{\mathit{\xi }}⟩=0$ and $\widehat{\mathit{\xi }}\ne \mathbf{0}$. If $\mathit{\xi }$$\ne \mathbf{0}$, the norm of $\widehat{\mathit{\xi }}$ is

$$∥\widehat{\mathit{\xi }}∥=\sqrt{\left|⟨\widehat{\mathit{\xi }},\widehat{\mathit{\xi }}⟩\right|}=∥\mathit{\xi }∥(1+\epsilon \frac{⟨\mathit{\xi },{\mathit{\xi }}^{*}⟩}{{∥\mathit{\xi }∥}^2}).$$

then, the vector $\widehat{\mathit{\xi }}$ is a $\mathcal{S}like$ ($\mathcal{T}like$) dual unit vector if ${∥\widehat{\mathit{\xi }}∥}^2=1$ (${∥\widehat{\mathit{\xi }}∥}^2=-1$). It is uncomplicated that

$${∥\widehat{\mathit{\xi }}∥}^2=\pm 1⟺{∥\mathit{\xi }∥}^2=\pm 1,⟨\mathit{\xi },{\mathit{\xi }}^{*}⟩=0.$$

The 6-components ${\xi }_i,$ and ${\xi }_i^{*}(i=1,2,3)$ of $\mathit{\xi }$$,$ and $\mathit{\xi }$${}^{*}$ are the normed Plücker coordinates. For any two dual vectors $\widehat{\mathit{\xi }}=\left({\widehat{\xi }}_1,{\widehat{\xi }}_2,{\widehat{\xi }}_3\right)$ and $\widehat{\mathit{\psi }}=({\widehat{\psi }}_1,{\widehat{\psi }}_2,{\widehat{\psi }}_3)$ of ${\mathbb{D}}_1^3$, the vector product is

$$\widehat{\mathit{\xi }}\times \widehat{\mathit{\psi }}=\left|\begin{array}{ccc}-{\widehat{\mathbf{e}}}_1& {\widehat{\mathbf{e}}}_2& {\widehat{\mathbf{e}}}_3\\ {\widehat{\xi }}_1& {\widehat{\xi }}_2& {\widehat{\xi }}_3\\ {\widehat{\psi }}_1& {\widehat{\psi }}_2& {\widehat{\psi }}_3\end{array}\right|,$$

where ${\widehat{\mathbf{e}}}_1$, ${\widehat{\mathbf{e}}}_2$, ${\widehat{\mathbf{e}}}_3$ is the canonical dual basis of ${\mathbb{D}}_1^3$. The hyperbolic and Lorentzian (de Sitter space) dual unit ($\mathcal{DU}$) spheres, respectively, are

$${\mathbb{H}}_{+}^2=\{\widehat{\mathit{\xi }}\in {\mathbb{D}}_1^3\mid {∥\mathit{\xi }∥}^2:=-{\widehat{\xi }}_1^2+{\widehat{\xi }}_2^2+{\widehat{\xi }}_3^2=-1\},$$

and

$${\mathbb{S}}_1^2=\{\widehat{\mathit{\xi }}\in {\mathbb{D}}_1^3\mid {∥\mathit{\xi }∥}^2:=-{\widehat{\xi }}_1^2+{\widehat{\xi }}_2^2+{\widehat{\xi }}_3^2=1\}.$$

Through this, we are presented with the map provided by E. Study. The $\mathcal{DU}$ spheres are formulated as a couple of integrate hyperboloids. The shared asymptotic cone illustrates the set of null lines, the ring constituted hyperboloid illustrates the set of $\mathcal{S}like$ lines, and the oval constituted hyperboloid illustrates the set of $\mathcal{T}like$ lines The reverse points of each hyperboloid illustrate the couple of reverse vectors on a non-null line (see Figure 1).

Figure 1. The dual hyperbolic and dual Lorentzian unit spheres.

Via the E. Study map, a smooth curve $\widehat{\mathit{\xi }}:t\in \mathbb{R}\mapsto \widehat{\mathit{\xi }}\left(t\right)\in {\mathbb{H}}_{+}^2$ is a $\mathcal{T}like$ ruled surface $(\widehat{\xi })$ in Minkowski 3-space ${\mathbb{E}}_1^3$. Correspondingly, a smooth curve $\widehat{\mathit{\xi }}:t\in \mathbb{R}\mapsto \widehat{\mathit{\xi }}\left(t\right)\in {\mathbb{S}}_1^2$ is a $\mathcal{S}like$ or $\mathcal{T}like$ ruled surface in ${\mathbb{E}}_1^3$. $\widehat{\mathit{\xi }}$ are distinguished by their rulings, and we no longer differentiate between a ruled surface and its dual curve image.

Lorentzian Dual Spherical Locomotion

Let us assume that ${\mathbb{S}}_{1m}^2$ and ${\mathbb{S}}_{1f}^2$ are two Lorentzian $\mathcal{DU}$ spheres centered at the origin $\widehat{\mathbf{0}}$ in ${\mathbb{D}}_1^3$. Let the orthonormal dual frames $\left\{\widehat{\mathbf{e}}\right\}=\{\widehat{\mathbf{0}}$;${\widehat{\mathbf{e}}}_1$($\mathcal{T}like$)$,{\widehat{\mathbf{e}}}_2,{\widehat{\mathbf{e}}}_3$} and $\{\widehat{\mathbf{f}}\}=\{\widehat{\mathbf{0}}$;${\widehat{\mathbf{f}}}_1$($\mathcal{T}like$),${\widehat{\mathbf{f}}}_2$,${\widehat{\mathbf{f}}}_3$} be rigidly linked to ${\mathbb{S}}_{1m}^2$ and ${\mathbb{S}}_{1f}^2$, respectively. We set that $\{\widehat{\mathbf{f}}\}$ is fixed, whereas the components of the set $\left\{\widehat{\mathbf{e}}\right\}$ are functions of a real parameter $t\in \mathbb{R}$. Then, we contemplate that ${\mathbb{S}}_{1m}^2$ is movable with respect to ${\mathbb{S}}_{1f}^2.$ The explication of this is as follows: the $\mathcal{DUS}$${\mathbb{S}}_{1m}^2$ rigidly correlated with $\left\{\widehat{\mathbf{e}}\right\}$ movable over the $\mathcal{DUS}$ ${\mathbb{S}}_{1f}^2$ is rigidly correlated with $\{\widehat{\mathbf{f}}\}$. This locomotion is a one-parameter dual spherical locomotion and is represented by ${\mathbb{S}}_{1m}^2/{\mathbb{S}}_{1f}^2$. If ${\mathbb{S}}_{1f}^2$ and ${\mathbb{S}}_{1f}^2$ correlate with the Lorentzian line spaces ${\mathbb{L}}_m$ and ${\mathbb{L}}_f$, respectively, then ${\mathbb{S}}_{1m}^2/{\mathbb{S}}_{1f}^2$ correlate with the one-parameter Lorentzian spatial locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f.$ Therefore, ${\mathbb{L}}_m$ is the movable Lorentzian space with respect to the unmovable Lorentzian space ${\mathbb{L}}_f$ [23,24,25,26,27,28].

We will now locate the auxiliary dual frame $\left\{\widehat{\mathbf{g}}\right\}=\{\mathbf{s}\left(t\right);{\widehat{\mathbf{g}}}_1,{\widehat{\mathbf{g}}}_2,{\widehat{\mathbf{g}}}_3\}$ by the first order instantaneous assets of the locomotion. We locate ${\widehat{\mathbf{g}}}_1\left(t\right)=$g${}_1\left(t\right)+\epsilon$g${}_1^{*}\left(t\right)$ as the $\mathbb{ISA}$, ${\widehat{\mathbf{g}}}_2\left(t\right):=$g${}_2\left(t\right)+\epsilon$g${}_2^{*}\left(t\right)=\frac{d{\widehat{\mathbf{g}}}_1}{dt}{∥\frac{d{\widehat{\mathbf{g}}}_1}{dt}∥}^{-1}$, and ${\widehat{\mathbf{g}}}_3\left(t\right)={\widehat{\mathbf{g}}}_1\times {\widehat{\mathbf{g}}}_2$. The set $\left\{\widehat{\mathbf{g}}\right\}$ so specified will be an auxiliary Blaschke frame. Hence, via the E. Study map, one can generate two $\mathcal{T}like$ ruled surfaces: one is in ${\mathbb{L}}_f$-space and the other is in ${\mathbb{L}}_m$-space. The first $\mathcal{T}like$ ruled surface is called the steady $\mathcal{T}like$ axode ${\pi }_f$, whereas the second is called the movable $\mathcal{T}like$ axode ${\pi }_m$. Steady or movable $\mathcal{T}like$ axodes have, at all times, a shared tangent over the $\mathbb{ISA}$ and slide on each other. The origin $\mathbf{s}$ is the shared central point of the movable axode ${\pi }_m$ and the steady axode ${\pi }_f$ created by the $\mathcal{T}like$$\mathbb{ISA}$ of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$. Thus, ${\widehat{\mathbf{g}}}_1\times {\widehat{\mathbf{g}}}_2={\widehat{\mathbf{g}}}_3,{\widehat{\mathbf{g}}}_1\times {\widehat{\mathbf{g}}}_3=-{\widehat{\mathbf{g}}}_2,{\widehat{\mathbf{g}}}_2\times {\widehat{\mathbf{g}}}_3=-{\widehat{\mathbf{g}}}_1.$ The dual arc length of the axodes is $d{\widehat{s}}_i=d{s}_i+\epsilon d{s}_i^{*}=∥\frac{d{\widehat{\mathbf{r}}}_1}{dt}∥dt=\widehat{p}\left(t\right)dt$. We let $d\widehat{s}=ds+\epsilon d{s}^{*}$ to confirm $d{\widehat{s}}_i$, since they are equal to each other. The shared distribution parameter ($\mathcal{D}-\mathcal{P}ar$) of the axodes is

$$\mu \left(s\right):=\frac{p^{*}}{p}=\frac{d{s}^{*}}{ds}.$$

In light of the E. Study map, in every location of the locomotion, the axodes have the $\mathbb{ISA}$ of the situation shared; that is, the movable axode touches the steady axode over the $\mathbb{ISA}$ in the first order at any instant t (compared with [6]).

If dash is designated differentiation with respect to $\widehat{s}$, then the Blaschke formula of $\left\{\widehat{\mathbf{r}}\right\}$ with respect to ${\mathbb{L}}_i$ is

$$\left(\begin{array}{c}{\widehat{\mathbf{g}}}_1^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{g}}}_2^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{g}}}_3^{{}^{\prime }}\hfill \end{array}\right){\mid }_i=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ 1\hfill & 0\hfill & {\widehat{\beta }}_i\hfill \\ 0\hfill & -{\widehat{\beta }}_i\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\widehat{\mathbf{g}}}_1\hfill \\ {\widehat{\mathbf{g}}}_2\hfill \\ {\widehat{\mathbf{g}}}_3\hfill \end{array}\right)={\widehat{\mathit{\eta }}}_i\times \left(\begin{array}{c}{\widehat{\mathbf{g}}}_1\hfill \\ {\widehat{\mathbf{g}}}_2\hfill \\ {\widehat{\mathbf{g}}}_3\hfill \end{array}\right),$$

(1)

where ${\widehat{\mathit{\eta }}}_i={\mathit{\eta }}_i+\epsilon {\mathit{\eta }}_i^{*}={\widehat{\beta }}_i{\widehat{\mathbf{g}}}_1-{\widehat{\mathbf{g}}}_3$ is the Darboux vector, and ${\widehat{\beta }}_i={\beta }_i+\epsilon {\beta }_i^{*}$$(i=m,$$f)$ is the dual geodesic curvatures of the axodes ${\pi }_i$; that is, ${\widehat{\beta }}_i={\beta }_i+\epsilon ({\mathsf{\Gamma }}_i-\mu {\beta }_i)=det({\widehat{\mathbf{g}}}_1,{\widehat{\mathbf{g}}}_1^{{}^{\prime }},{\widehat{\mathbf{g}}}_1^{{}^{″}}).$ Then, the $\mathcal{D}is$-axis (evolute or curvature axis) is

$${\widehat{\mathbf{b}}}_i\left(\widehat{s}\right)={\mathbf{b}}_i+\epsilon {\mathbf{b}}_i^{*}=\frac{{\widehat{\mathit{\eta }}}_i}{∥{\widehat{\mathit{\eta }}}_i∥}=\frac{{\widehat{\beta }}_i}{\sqrt{\left|1-{\widehat{\beta }}_i^2\right|}}{\widehat{\mathbf{g}}}_1-\frac{1}{\sqrt{\left|1-{\widehat{\beta }}_i^2\right|}}{\widehat{\mathbf{g}}}_3.$$

Under the hypothesis that $\left|{\widehat{\beta }}_i\right|<1$, let ${\widehat{\varphi }}_i\left(\widehat{s}\right)={\varphi }_i+\epsilon {\varphi }_i^{*}$ be the radius of curvature through ${\widehat{\mathbf{g}}}_1$ and ${\widehat{\mathbf{b}}}_i$. Then,

$${\widehat{\mathbf{b}}}_i\left(\widehat{s}\right)=sinh{\widehat{\varphi }}_i{\widehat{\mathbf{g}}}_1-cosh{\widehat{\varphi }}_i{\widehat{\mathbf{g}}}_3,$$

(2)

is a $\mathcal{T}like$ dual unit vector, and

$${\widehat{\beta }}_i={\beta }_i+\epsilon ({\mathsf{\Gamma }}_i-\mu {\beta }_i)=tanh{\widehat{\varphi }}_i.$$

The invariants ${\beta }_i\left(s\right)$, ${\mathsf{\Gamma }}_i\left(s\right)$ and $\mu \left(s\right)$ are the construction (curvature) functions of the axodes. Let us suppose that the auxiliary Blaschke frame $\left\{\widehat{\mathbf{r}}\right\}$ is steady in ${\mathbb{L}}_m$-space. Then, its locomotion with respect to ${\mathbb{L}}_f$-space is

$$\left(\begin{array}{c}{\widehat{\mathbf{g}}}_1^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{g}}}_2^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{g}}}_3^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ 1\hfill & 0\hfill & \widehat{\mathit{\eta }}\hfill \\ 0\hfill & -\widehat{\mathit{\eta }}\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\widehat{\mathbf{g}}}_1\hfill \\ {\widehat{\mathbf{g}}}_2\hfill \\ {\widehat{\mathbf{g}}}_3\hfill \end{array}\right)=\widehat{\mathit{\eta }}\times \left(\begin{array}{c}{\widehat{\mathbf{g}}}_1\hfill \\ {\widehat{\mathbf{g}}}_2\hfill \\ {\widehat{\mathbf{g}}}_3\hfill \end{array}\right),$$

(3)

where $\widehat{\mathit{\eta }}:= {\widehat{\mathit{\eta }}}_f-{\widehat{\mathit{\eta }}}_m=\widehat{\eta }{\widehat{\mathbf{g}}}_1$ is the auxiliary Darboux vector and $∥\widehat{\mathit{\eta }}∥=\eta +\epsilon {\eta }^{*}={\beta }_r+\epsilon \left({\mathsf{\Gamma }}_r-\mu {\beta }_r\right)$ is the auxiliary dual geodesic curvature. It follows that $\eta ={\beta }_f-{\beta }_m$ and ${\eta }^{*}={\mathsf{\Gamma }}_f-{\mathsf{\Gamma }}_m-\mu \left({\beta }_f-{\beta }_m\right)$ are the rotational angular speed and translational angular speed of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, and they are both also invariants, respectively. In this work, we set ${\eta }^{*}\ne 0$ to remove the pure translational locomotions. Moreover, we remove zero divisors $\eta =0$. Therefore, we set that the $\mathcal{T}like$ axodes are non-developable ruled surfaces ($\mu \ne 0$). Hence, the following corollary can be given (compared with [1,2,3,4,5]):

Corollary 1.

Through the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, the pitch $h\left(s\right)$ is reported by

$$h\left(s\right):=\frac{{\eta }^{*}\times \eta }{{∥\eta ∥}^2}=\frac{{\mathsf{\Gamma }}_f-{\mathsf{\Gamma }}_m}{{\beta }_f-{\beta }_m}-\mu .$$

3. Spacelike Lines with Special Trajectories

For the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, any steady $\mathcal{S}like$ line $\widehat{\mathbf{x}}$ in the movable ${\mathbb{L}}_m$-space mostly create a $\mathcal{T}like$ or $\mathcal{S}like$ ruled surface ($\widehat{x}$) in $\mathbb{L}$${}_f$-space. It will be presumed to be a $\mathcal{T}like$ ruled surface. Then, we may write

$$\widehat{\mathbf{x}}\left(\widehat{s}\right)={\widehat{x}}^t\widehat{\mathbf{g}},\widehat{x}=\left(\begin{array}{c}{\widehat{x}}_1\hfill \\ {\widehat{x}}_2\hfill \\ {\widehat{x}}_3\hfill \end{array}\right)=\left(\begin{array}{c}{x}_1+\epsilon x_1^{*}\hfill \\ x_2+\epsilon x_2^{*}\hfill \\ x_3+\epsilon x_3^{*}\hfill \end{array}\right),\widehat{\mathbf{g}}=\left(\begin{array}{c}{\widehat{\mathbf{g}}}_1\hfill \\ {\widehat{\mathbf{g}}}_2\hfill \\ {\widehat{\mathbf{g}}}_3\hfill \end{array}\right),$$

where

$$\begin{array}{c}-x_1^2+x_2^2+x_3^2=1,\\ -x_1{x}_1^{*}+x_2{x}_2^{*}+x_3{x}_3^{*}=0.\end{array}$$

The velocity and acceleration vectors of $\widehat{\mathbf{x}}\in {\mathbb{S}}_{1m}^2$, respectively, are

$${\widehat{\mathbf{x}}}^{{}^{\prime }}:=\widehat{\mathit{\eta }}\times \widehat{\mathbf{x}}=-{\widehat{x}}_3{\widehat{\mathbf{g}}}_2+{\widehat{x}}_2{\widehat{\mathbf{g}}}_3,$$

(4)

and

$${\widehat{\mathbf{x}}}^{{}^{{}^{″}}}=-{\widehat{x}}_3\widehat{\eta }{\widehat{\mathbf{g}}}_1-({\widehat{x}}_2{\widehat{\eta }}^2+{\widehat{x}}_3{\widehat{\eta }}^{{}^{\prime }}){\widehat{\mathbf{g}}}_2+(-{\widehat{x}}_1\widehat{\eta }+{\widehat{x}}_2{\widehat{\eta }}^{{}^{\prime }}-{\widehat{x}}_3{\widehat{\eta }}^2){\widehat{\mathbf{g}}}_3.$$

(5)

Then,

$${\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{{}^{″}}}={\widehat{\eta }}^2\left[(1+{\widehat{x}}_1^2)\widehat{\eta }{\widehat{\mathbf{g}}}_1-{\widehat{x}}_3\widehat{\mathbf{x}}\right].$$

(6)

From Equation (4), the dual arc length $d\widehat{\xi }=d\xi +\epsilon d{\xi }^{*}$ of $\widehat{\mathbf{x}}\left(\widehat{s}\right)$ is

$$d\widehat{\xi }=∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥d\widehat{s}=\widehat{\eta }\sqrt{1+{\widehat{x}}_1^2}d\widehat{s}.$$

(7)

The $\mathcal{D}-\mathcal{P}ar$ $\lambda \left(\xi \right)$ of $\left(\widehat{x}\right)$ is

$$\lambda \left(\xi \right):=\frac{d{\xi }^{*}}{d\xi }=\frac{x_2{x}_2^{*}+x_3{x}_3^{*}+h(x_2^2+x_3^2)}{(x_2^2+x_3^2)}.$$

(8)

Equation (8) can be utilized to discriminate the coupled steady $\mathcal{S}like$ lines in ${\mathbb{L}}_m$-space, creating $\mathcal{T}like$ ruled surfaces with the same distribution parameter in ${\mathbb{L}}_f$-space. This set of $\mathcal{S}like$ lines is a $\mathcal{S}like$ line complex and is fulfilled by

$$x_2{x}_2^{*}+x_3{x}_3^{*}+(h-\lambda )(x_2^2+x_3^2)=0,$$

(9)

Equation (9) characterizes a quadratic $\mathcal{S}like$ line complex. Consequently, we have:

Theorem 1.

Through the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, a meditate set of steady $\mathcal{S}like$ lines followed with the movable $\mathcal{T}like$ axode; these steady $\mathcal{S}like$ lines are rulings of $\mathcal{T}like$ ruled surfaces with the same $\mathcal{D}-\mathcal{P}ar$ in ${\mathbb{L}}_f$-space. Then, this set of $\mathcal{S}like$ lines belongs to a quadratic $\mathcal{S}like$ line complex.

Furthermore, let $\mathbf{q}(x,y,z)$ be a random point on $\widehat{\mathbf{x}}$, then

$${\mathbf{x}}^{*}=\mathbf{q}\times \mathbf{x},$$

or

$$x_1^{*}=x_{3}y-x_{2}z,x_2^{*}=x_{1}z-x_{3}x,x_3^{*}=-x_{2}x+x_{1}y.$$

Then, Equation (9) takes the form

$$-x_1{x}_{3}y+x_1{x}_{2}z+(h-\lambda )(x_2^2+x_3^2)=0.$$

(10)

Equation (10) shows that the steady $\mathcal{S}like$ lines $\widehat{\mathbf{x}}$ of the movable $\mathcal{T}like$ axode that create $\mathcal{S}like$ ruled surfaces with the same $\mathcal{D}-\mathcal{P}ar$ lie on a $\mathcal{T}like$ plane parallel to the $\mathbb{ISA}$. From Equation (10), we also have two conditions: In the case of $\lambda =h$, the $\mathcal{D}-\mathcal{P}ar$ is coupled with the constant $\mathcal{S}like$ lines in planes passing through the $\mathbb{ISA}$. In the case of $\lambda =0$, the steady $\mathcal{S}like$ line $\widehat{\mathbf{x}}$ of the movable $\mathcal{T}like$ axode, at instant t, creates a $\mathcal{T}like$ developable ruled surface, and Equation (10) becomes

$$-x_1{x}_{3}y+x_1{x}_{2}z+h(x_2^2+x_3^2)=0.$$

(11)

In this condition, the steady $\mathcal{S}like$ line $\widehat{\mathbf{x}}$ and its neighboring $\widehat{\mathbf{x}}(\widehat{\xi }+d\widehat{\xi })$ meet at the edge of regression on the $\mathcal{T}like$ ruled surface; that is, the tangent $\mathcal{S}like$ lines of the edge of regression are those lines. Thus, we have:

Theorem 2.

Through the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, if steady, $\mathcal{S}like$ lines of the movable $\mathcal{T}like$ axode create $\mathcal{T}like$ developable ruled surfaces in ${\mathbb{L}}_f$-space. Then, these steady $\mathcal{S}like$ lines are included in a special quadratic $\mathcal{S}like$ line complex, which is identical to the $\mathcal{S}like$ line complex of the tangent lines of edge points in ${\mathbb{L}}_f$.

To investigate the geometrical properties of ($\widehat{x}$), the Blaschke frame is produced as:

$$\widehat{\mathbf{x}}=\widehat{\mathbf{x}}\left(\widehat{s}\right),\widehat{\mathbf{t}}\left(\widehat{s}\right)={\widehat{\mathbf{x}}}^{{}^{\prime }}{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥}^{-1},\widehat{\mathbf{g}}\left(\widehat{s}\right)=\widehat{\mathbf{x}}\times \widehat{\mathbf{t}},$$

(12)

where

$$\left.\begin{array}{c}\widehat{\mathbf{x}}\times \widehat{\mathbf{t}}=\widehat{\mathbf{g}},\widehat{\mathbf{x}}\times \widehat{\mathbf{g}}=\widehat{\mathbf{t}},\widehat{\mathbf{t}}\times \widehat{\mathbf{g}}=\widehat{\mathbf{x}},\hfill \\ \\ ⟨\widehat{\mathbf{x}},\widehat{\mathbf{x}}⟩=⟨\widehat{\mathbf{t}},\widehat{\mathbf{t}}⟩=-⟨\widehat{\mathbf{g}},\widehat{\mathbf{g}}⟩=1.\hfill \end{array}\right\}$$

(13)

Here, $\widehat{\mathbf{x}}$, $\widehat{\mathbf{t}}$, and $\widehat{\mathbf{g}}$ are intersected orthogonal lines at a point $\mathbf{c}$ on $\widehat{\mathbf{x}}$ named the striction (or central) point. The locus of $\mathbf{c}$ is the striction curve on $\left(\widehat{x}\right)\in {\mathbb{L}}_f$. Then,

$$\frac{d}{d\widehat{\xi }}\left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ -1\hfill & 0\hfill & \widehat{\chi }\hfill \\ 0\hfill & \widehat{\chi }\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right),$$

(14)

where

$$\widehat{\chi }(\widehat{\xi })=det(\widehat{\mathbf{x}},{\widehat{\mathbf{x}}}^{{}^{\prime }},{\widehat{\mathbf{x}}}^{{}^{{}^{″}}}){∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥}^{-3}=\frac{\widehat{\eta }{\widehat{x}}_1({\widehat{x}}_1^2+1)-{\widehat{x}}_3}{\widehat{\eta }{({\widehat{x}}_1^2+1)}^{\frac{3}{2}}},$$

(15)

is the dual spherical curvature of $\widehat{\mathbf{x}}(\widehat{\xi })$. The tangent of $\mathbf{c}\left(\xi \right)$ is [24]:

$$\frac{d\mathbf{c}}{d\xi }=-\mathsf{\Gamma }\mathbf{x}\left(\xi \right)+\lambda \mathbf{g}\left(\xi \right),$$

(16)

which is a $\mathcal{S}like$ (a $\mathcal{T}like$) curve if $\left|\lambda \right|<\left|\mathsf{\Gamma }\right|$ ($\left|\lambda \right|>\left|\mathsf{\Gamma }\right|)$. $\gamma \left(\xi \right)$, $\mathsf{\Gamma }\left(\xi \right)$, and $\lambda \left(\xi \right)$ are the construction functions of ($\widehat{x}$). By the hypothesis that $\left|\widehat{\chi }\right|<1$, the $\mathcal{S}like$ $\mathcal{D}is$-axis is:

$$\widehat{\mathbf{b}}=\mathbf{b}+\epsilon {\mathbf{b}}^{*}=\frac{\widehat{\chi }}{\sqrt{{\widehat{\chi }}^2-1}}\widehat{\mathbf{x}}-\frac{1}{\sqrt{{\widehat{\chi }}^2-1}}\widehat{\mathbf{g}}.$$

(17)

Let $\widehat{\varphi }=\varphi +\epsilon {\varphi }^{*}$ be the radius of curvature through $\widehat{\mathbf{b}}$ and $\widehat{\mathbf{x}}$. Then,

$$\widehat{\mathbf{b}}=cosh\widehat{\varphi }\widehat{\mathbf{x}}-sinh\widehat{\varphi }\widehat{\mathbf{g}},$$

(18)

where

$$\widehat{\chi }:=\chi +\epsilon {\chi }^{*}=\chi +\epsilon (\mathsf{\Gamma }-\lambda \chi )=coth\widehat{\varphi }.$$

(19)

Equations (15) and (19) lead to

$$coth\widehat{\varphi }=\frac{\widehat{\eta }{\widehat{x}}_1({\widehat{x}}_1^2+1)-{\widehat{x}}_3}{\widehat{\eta }{({\widehat{x}}_1^2+1)}^{\frac{3}{2}}}.$$

(20)

Furthermore, we have

$$\left.\begin{array}{c}\hfill \widehat{\kappa }:=\kappa +\epsilon {\kappa }^{*}=∥{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{{}^{″}}}∥{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥}^{-3}=\sqrt{{\widehat{\chi }}^2-1}=\frac{1}{sinh\widehat{\varphi }},\\ \hfill \widehat{\tau }:=\tau +\epsilon \tau =det({\widehat{\mathbf{x}}}^{{}^{\prime }},{\widehat{\mathbf{x}}}^{{}^{{}^{″}}},{\widehat{\mathbf{x}}}^{{}^{‴}}){∥{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{{}^{″}}}∥}^{-2}=\pm \frac{{\widehat{\chi }}^{{}^{\prime }}}{{\widehat{\chi }}^2-1}=\pm {\widehat{\varphi }}^{{}^{\prime }},\end{array}\right\}$$

(21)

where $\widehat{\kappa }\left(\widehat{\xi }\right)$ is the dual curvature, and $\widehat{\tau }\left(\widehat{\xi }\right)$ is the dual torsion, respectively.

Since $\widehat{\mathbf{x}}$ is a $\mathcal{S}like$ dual unit vector, we can write out the coordinates of $\widehat{\mathbf{x}}$ in the form

$$\widehat{\mathbf{x}}=sinh\widehat{\vartheta }{\widehat{\mathbf{g}}}_1+cosh\widehat{\vartheta }\widehat{\mathbf{m}},\mathrm{with}\widehat{\mathbf{m}}=cos\widehat{\phi }{\widehat{\mathbf{g}}}_2+sin\widehat{\phi }{\widehat{\mathbf{g}}}_3.$$

(22)

This option is such that $\widehat{\phi }$ is the dual angle through the central normal $\widehat{\mathbf{t}}$ of $\widehat{\mathbf{x}}$ and ${\widehat{\mathbf{g}}}_2$ metrical on the $\mathbb{ISA}$. This implies that there is a screw movement of angle $\phi$ on the $\mathbb{ISA}$ and distance ${\phi }^{*}$ on it which carries ${\widehat{\mathbf{g}}}_2$ to be the central normal $\widehat{\mathbf{t}}$. The dual angle $\widehat{\vartheta }=\vartheta +\epsilon {\vartheta }^{*}$ provides an interpretation of $\widehat{\mathbf{x}}$ relative to the $\mathbb{ISA}$ of the movement ${\mathbb{L}}_m/{\mathbb{L}}_f$.

Similarly, we may write the $\mathcal{S}like$$\mathcal{D}is$-axis as:

$$\widehat{\mathbf{b}}=sinh\widehat{\alpha }{\widehat{\mathbf{g}}}_1+cosh\widehat{\alpha }\widehat{\mathbf{m}},\mathrm{with}\widehat{\alpha }=\mathit{\alpha }+\epsilon {\mathit{\alpha }}^{*}.$$

(23)

Notice that the striction point $\mathbf{s}$ is the origin of the auxiliary Blaschke frame; that is, $\mathbf{s}=\mathbf{0}$ (see Figure 2) (compared with [1,2,3,4,5]). This means that $\vartheta =c_1(realconst.)$, and ${\vartheta }^{*}=c_2(realconst.).$

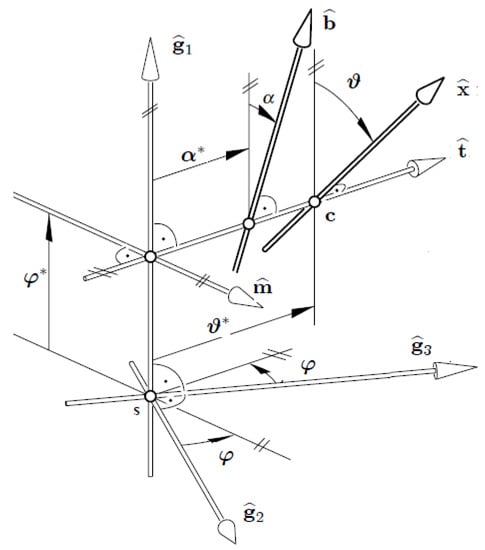
Figure 2. $\widehat{\mathit{x}}$ and its Disteli-axis $\widehat{\mathit{b}}$.

3.1. Disteli Formulae for a Spacelike Line Trajectory

The $\mathcal{D}is$ formula confirms the connections through the $\mathcal{D}is$-axis of the line trajectories for one-parameter spatial locomotion [1,2,3,4,5]. There are many works which consider the $\mathcal{D}is$ formulae and geometric invariants of ruled surfaces [9,10,11,12,13,14,15,24,25,26,27,28]. The Lorentzian $\mathcal{D}is$ formulae may be gained immediately from the dual spherical curvature of $\widehat{\mathbf{x}}\left(\widehat{\xi }\right)$ as follows: Substituting the Equation (22) into Equation (20), we have

$$tanh\widehat{\vartheta }-coth\widehat{\varphi }=\frac{sin\widehat{\phi }}{\widehat{\eta }{sinh}^2\widehat{\vartheta }}.$$

(24)

Equation (24) is the Lorentzian dual version of the $\mathcal{E}-\mathcal{S}$ equation for a point trajectory in planar and spherical locomotions in form (see [1,2,3,4]). From the real and the dual parts, respectively, we get:

$$tanh\vartheta -coth\varphi =\frac{sin\phi }{\eta {sinh}^2\vartheta }.$$

(25)

and

$${\varphi }^{*}=\{\frac{{\phi }^{*}\eta }{cos\phi }-\frac{{\vartheta }^{*}}{{cosh}^2\vartheta }+[h{sinh}^2\vartheta +{\vartheta }^{*}sinh2\vartheta ]\frac{sin\phi }{\eta {sinh}^2\vartheta }\}{sinh}^2\varphi .$$

(26)

Equation (25) simultaneously with (26) are the $\mathcal{D}is$ formulae of a $\mathcal{S}like$ line trajectory in spatial Lorentzian locomotions. Its geometrical importance is shown in Figure 2. Equation (25) offers the connection among the attitudes of $\widehat{\mathbf{x}}$ in the ${\mathbb{L}}_m$-space and its $\mathcal{S}like$$\mathcal{D}is$ -axis $\widehat{\mathbf{b}}$. Equation (26) offers the distance from $\widehat{\mathbf{x}}$ to $\widehat{\mathbf{b}}$. The sign of ${\varphi }^{*}$(+ or −) in the above expression indicates that the attitudes of the $\mathcal{S}like$$\mathcal{D}is$ -axis $\widehat{\mathbf{b}}$ are situated on the positive or negative direction of the central normal $\widehat{\mathbf{t}}$ of $\widehat{\mathbf{x}}$ at $\mathbf{c}$, while the direction of $\widehat{\mathbf{t}}$ is located by

$$\widehat{\mathbf{t}}\left(\widehat{s}\right)={\widehat{\mathbf{x}}}^{{}^{\prime }}{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥}^{-1}=-sin\widehat{\phi }{\widehat{\mathbf{g}}}_2+cos\widehat{\phi }{\widehat{\mathbf{g}}}_3.$$

However, we can express a second dual version of the $\mathcal{E}-\mathcal{S}$ equation by applying dual angle estimations. This means we seek the steady $\mathcal{S}like$ line $\widehat{\mathbf{x}}\in {\mathbb{L}}_m$, which is at a steady dual angle from a steady $\mathcal{S}like$ line $\widehat{\mathbf{y}}\in {\mathbb{L}}_f$. So, we set the central dual angle $\widehat{\theta }=\vartheta +\epsilon {\theta }^{*}$ of the $\mathcal{S}like$ dual unit vectors $\widehat{\mathbf{x}}$, and $\widehat{\mathbf{y}}$

$$\widehat{\theta }={cosh}^{-1}\left(⟨\widehat{\mathbf{x}},\widehat{\mathbf{y}}⟩\right),$$

such that $\widehat{\mathbf{y}}$ and $\widehat{\theta }$ stay steady up to the second order at $\widehat{s}={\widehat{s}}_0$; that is,

$${\widehat{\theta }}^{{}^{\prime }}\mid \widehat{s}={\widehat{s}}_0=0,{\widehat{\mathbf{y}}}^{{}^{\prime }}\mid \widehat{s}={\widehat{s}}_0=\mathbf{0},$$

and

$${\widehat{\theta }}^{{}^{{}^{″}}}\mid \widehat{s}={\widehat{s}}_0=0,{\widehat{\mathbf{y}}}^{{}^{{}^{″}}}\mid \widehat{s}={\widehat{s}}_0=\mathbf{0}.$$

We have for the first order, steady

$$⟨{\widehat{\mathbf{x}}}^{{}^{\prime }},\widehat{\mathbf{y}}⟩=0,$$

and, for the second order, steady

$$⟨{\widehat{\mathbf{x}}}^{{}^{{}^{″}}},\widehat{\mathbf{y}}⟩\mid =0.$$

Then, $\widehat{\theta }$ will be invariant in the second estimation if, and only if, $\widehat{\mathbf{y}}$ is the $\mathcal{S}like$$\mathcal{D}is$-axis $\widehat{\mathbf{b}}$ of $\left(\widehat{x}\right)$; that is,

$${\widehat{\theta }}^{{}^{\prime }}={\widehat{\theta }}^{{}^{″}}=0\iff \widehat{\mathbf{y}}=\frac{{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{″}}}{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{″}}∥}=\pm \widehat{\mathbf{b}}.$$

(27)

Substituting Equation (6) into Equation (27), we have

$$\pm \widehat{\mathbf{b}}=\frac{(1+{\widehat{x}}_1^2)\widehat{\eta }{\widehat{\mathbf{r}}}_1-{\widehat{x}}_3\widehat{\mathbf{x}}}{∥(1+{\widehat{x}}_1^2)\widehat{\eta }{\widehat{\mathbf{r}}}_1-{\widehat{x}}_3\widehat{\mathbf{x}}∥}.$$

(28)

From Equations (23) and (28), one finds that:

$$\frac{\widehat{\eta }{\widehat{x}}_1({\widehat{x}}_1^2+1)-{\widehat{x}}_3{\widehat{x}}_1}{sinh\widehat{\alpha }}=\frac{-{\widehat{x}}_2{\widehat{x}}_3}{cosh\widehat{\alpha }cos\widehat{\phi }}=\frac{-{\widehat{x}}_3^2}{cosh\widehat{\alpha }sin\widehat{\phi }}.$$

(29)

Substituting Equation (22) into Equation (29), we may express the $\mathcal{E}-\mathcal{S}$ equation as:

$$tanh\widehat{\vartheta }-tanh\widehat{\alpha }=\frac{\widehat{\eta }sinh\widehat{\vartheta }}{sin\widehat{\phi }}.$$

(30)

By considering the real and dual parts, we obtain the following:

$$tanh\vartheta -tanh\alpha =\frac{\eta sinh\vartheta }{sin\phi },$$

(31)

and

$$(\frac{{\vartheta }^{*}}{{cosh}^2\vartheta }-\frac{{\alpha }^{*}}{{cosh}^2\alpha })+\frac{{\phi }^{*}}{sin\phi }(\frac{\eta sinh\vartheta }{sin\phi })=\frac{\eta ({\vartheta }^{*}cosh\vartheta +hsinh\vartheta )}{sin\phi }$$

(32)

The Equations (31) with (32) are the $\mathcal{D}is$ formulae of a $\mathcal{S}like$ line trajectory in spatial Lorentzian locomotions. Via Figure 2, the sign of ${\alpha }^{*}$ (+ or −) in Equation (32) references that the attitudes of the $\mathcal{S}like$$\mathcal{D}is$ axis $\widehat{\mathbf{b}}$ are settled on the positive or negative direction on the shared $\widehat{\mathbf{t}}$. Since the central points of the line’s trajectories are on the normal plane, when the direction of their rulings are settled by $(\widehat{\vartheta },\widehat{\phi })$, the $\mathcal{D}is$-formulae can be settled in the $\mathcal{T}like$ plane $Sp\{{\widehat{\mathbf{g}}}_1,\widehat{\mathbf{t}}\}$. Hence, any arbitrary point $\mathbf{c}({\phi }^{*},{\vartheta }^{*})$ on this $\mathcal{T}like$ plane is the central point of the $\mathcal{S}like$ oriented line $\widehat{\mathbf{x}}$ and the radius can be acquired by Equation (31). However, the central point $\mathbf{c}({\phi }^{*},{\vartheta }^{*})$ may be on $\widehat{\mathbf{b}}$ if ${\vartheta }^{*}={\alpha }^{*}$, and on the $\mathbb{ISA}$ if ${\vartheta }^{*}=0$. In the second condition the point $\mathbf{c}({\phi }^{*},{\theta }^{*})$ can be gained by putting ${\vartheta }^{*}=0$ in Equation (31), which can be reduced as follows:

$$L:{\phi }^{*}=\left(\frac{cos\phi }{\eta sinh\vartheta {cosh}^2\alpha }\right){\alpha }^{*}++hsin\phi .$$

(33)

Equation (33) represents a linear equation in the ${\phi }^{*}$ and ${\alpha }^{*}$ of the $\mathcal{S}like$$\mathcal{D}is$-axis $\widehat{\mathbf{b}}$. The position of line L will change if the parameter ${\alpha }^{*}$ is assigned a different value, while keeping $\phi =$ steady. However, if a pencil of the steady $\mathcal{S}like$ line envelope is a $\mathcal{S}like$ curve on the $\mathcal{T}like$ plane $Sp\{{\widehat{\mathbf{g}}}_1,\widehat{\mathbf{t}}\}$, then, the subspace $Sp\{{\widehat{\mathbf{g}}}_1,\widehat{\mathbf{t}}\}$ modifies if the parameter $\phi$ of a $\mathcal{S}like$ line has distinct values, but ${\alpha }^{*}=$ steady. Therefore, the pencil of all steady $\mathcal{S}like$ lines L shown by Equation (33) is a $\mathcal{S}like$ line congruence for all values of $({\phi }^{*},{\alpha }^{*})$. The results indicate a straightforward geometric illustration of the properties of the $\mathcal{D}is$ formulae for a steady $\mathcal{S}like$ linear trajectory.

At the conclusion of this subsection, we are able to consider the $\mathcal{E}-\mathcal{S}$ equation for the axodes, in the following manner: Substituting $\widehat{\vartheta }={\widehat{\phi }}_m$, $\widehat{\alpha }={\widehat{\phi }}_f$, and $\phi =\frac{\pi }{2}$, and ${\phi }^{*}=0$ into Equation (30), after simplification, it may be deduced that we obtain,

$$tanh{\widehat{\phi }}_m-tanh{\widehat{\phi }}_f=\widehat{\eta }sinh\widehat{\vartheta }.$$

(34)

3.2. Spacelike Torsion Line Congruence

We now locate the $\mathcal{S}like$ torsion line congruence, which is the spatial symmetry of the Lorentzian circling-point dual curve (cubic of steady curvature) [1,2,3,4,5].

Definition 1.

The trajectory of the dual points, whose trajectories have a vanishing dual torsion in ${\mathbb{S}}_{1f}^2$, is named the Lorentzian circling-point curve or the cubic of steady curvature.

The dual curve in ${\mathbb{S}}_{1f}^2$ with zero torsion is a planar section of ${\mathbb{S}}_{1f}^2$. The Lorentzian cone with steady curvature can be defined as the trace of dual points in ${\mathbb{S}}_{1f}^2$ that possess trajectories with a steady osculating dual plane. By utilizing Definition 1 and Equation (21), we obtain

$$\widehat{\tau }(\widehat{\xi })=\tau +\epsilon {\tau }^{*}=det({\widehat{\mathbf{x}}}^{{}^{\prime }},{\widehat{\mathbf{x}}}^{{}^{{}^{″}}},{\widehat{\mathbf{x}}}^{{}^{‴}})=0\iff \widehat{\chi }=const.$$

(35)

Therefore, the spatial symmetry of the torsion dual cone with steady curvature is defined by: (1) The $\mathcal{S}like$ line complex pointed by the $\mathcal{S}like$ torsion cone $c:$$\tau \left(\xi \right)=0$, and (2) the $\mathcal{S}like$ line complex pointed by the linked plane of $\mathcal{S}like$ lines $\pi :$${\tau }^{*}\left(\xi \right)=0$. All the pencil of $\mathcal{S}like$ lines $\widehat{\mathbf{x}}\in {\mathbb{L}}_m$-space and also in the $\mathcal{S}like$ plane satisfy $\pi :$${\tau }^{*}\left(\xi \right)=0$ initiating the $\mathcal{S}like$ torsion line congruence. Therefore, the $\mathcal{S}like$ torsion line congruence is traced by a pencil of $\mathcal{S}like$ planes $\pi$, each of which is coupled with an orientation of the torsion cone c. Therefore, we present the following theorem:

Theorem 3.

Through the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, set the pencil of steady $\mathcal{S}like$ lines of the movable $\mathcal{T}like$ axode, such that each one of these $\mathcal{S}like$ lines has symmetry of a torsion dual cone with steady curvature. Then, this pencil of $\mathcal{S}like$ lines defines a $\mathcal{S}like$ torsion line congruence, which are the shared $\mathcal{S}like$ lines of the two line complexes $\tau \left(\xi \right)=0$ and ${\tau }^{*}\left(\xi \right)=0$.

Furthermore, from Equation (21), we have:

$$\widehat{\tau }\left(\widehat{\xi }\right)=\tau +\epsilon {\tau }^{*}=0\iff \widehat{\varphi }\left(\widehat{\xi }\right)=\varphi +\epsilon {\varphi }^{*}=\widehat{c}(dualconst.).$$

(36)

This shows that $\varphi =c(realconst.)$, and ${\varphi }^{*}=c^{*}(realconst.)$. In this case, the $\mathcal{S}like$$\mathcal{D}is$-axis is steady up to the second order, and the $\mathcal{S}like$ line $\widehat{\mathbf{x}}$ moves over it with steady pitch. Hence, the $\mathcal{T}like$ ruled surface $\widehat{x}$ is formed by a $\mathcal{S}like$ line $\widehat{\mathbf{x}}$ that exists at a steady Lorentzian distance ${\varphi }^{*}$ and a steady Lorentzian angle $\varphi$ relative to the $\mathcal{S}like$$\mathcal{D}is$-axis $\widehat{\mathbf{b}}$.

Theorem 4.

A $\mathcal{S}like$ torsion line congruence is a steady $\mathcal{S}like$$\mathcal{D}is$-axis if, and only if, $\chi \left(\xi \right)$ = steady, and $\mathsf{\Gamma }\left(\xi \right)-\chi \left(\xi \right)\lambda \left(\xi \right)$ = steady.

However, if we set Equations (21) and (22), we attain the spatial symmetry of the torsion dual cone with steady curvature as

$$\widehat{\tau }\left(\widehat{u}\right)=0\iff \widehat{\omega }\left[3sinh\widehat{\vartheta }sin\widehat{\phi }+(\widehat{\omega }-\widehat{\chi })cosh\widehat{\vartheta }\right]cos\widehat{\phi }-{\widehat{\omega }}^{{}^{\prime }}cosh\widehat{\vartheta }sin\widehat{\phi }=0.$$

(37)

We solve Equation (37) for $\widehat{\vartheta }$ as

$$tanh\widehat{\vartheta }=\widehat{a}csc\widehat{\phi }+\widehat{b}sec\widehat{\phi },$$

(38)

where

$$\widehat{a}=a+\epsilon a^{*}=\frac{\widehat{\gamma }-\widehat{\omega }}{3},\widehat{b}\left(u\right)=b+\epsilon b^{*}=\frac{{\widehat{\omega }}^{{}^{\prime }}}{3\widehat{\omega }}.$$

(39)

The real part of Equation (38) characterizes the Lorentzian cone for the spherical part of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$ and is

$$\left.\begin{array}{c}\vartheta ={tanh}^{-1}\left(acsc\phi +bsec\phi \right),\hfill \\ a\left(\upsilon \right)=\frac{\chi -\omega }{3},\mathrm{and}b\left(\upsilon \right)=b+\epsilon b^{*}=\frac{{\omega }^{{}^{\prime }}}{3\omega }.\hfill \end{array}\right\}$$

(40)

A Lorentzian spherical curve is produced by the intersection of the torsion cone with a Lorentzian unit sphere fixed at the cone’s apex. Associated with the orientation of a $\mathcal{S}like$ line L in the $\mathcal{S}like$ torsion cone, there exists a $\mathcal{S}like$ plane $\pi$ defined by the dual part of Equation (38). This plane is

$$a^{*}csc\phi +b^{*}sec\phi +{\phi }^{*}\left(bsec\phi tan\phi -acsc\phi cot\phi \right)+{\vartheta }^{*}{sinh}^2\vartheta =0.$$

(41)

For any orientation of a $\mathcal{S}like$ line L within the $\mathcal{S}like$ torsion cone, there exists a corresponding plane consisting of lines that are parallel to L. The torsion cone and the plane of lines is used to define the torsion line congruence.

3.3. Line Geometry of the Spacelike Torsion Line Congruence

In order to recognize the $\mathcal{S}like$ torsion line congruence, from the real and the dual parts of Equation (22), respectively, we get:

$$\mathbf{x}\left(\phi \right)=\left(sinh\vartheta ,cosh\vartheta cos\phi ,cosh\vartheta sin\phi \right),$$

(42)

and

$${\mathbf{x}}^{*}(\phi ,{\phi }^{*})=\left(\begin{array}{c}{\vartheta }^{*}cosh\vartheta \hfill \\ {\vartheta }^{*}sinh\vartheta cos\phi -{\phi }^{*}cosh\vartheta sin\phi \hfill \\ {\vartheta }^{*}sinh\vartheta sin\phi +{\phi }^{*}cosh\vartheta cos\phi \hfill \end{array}\right).$$

(43)

Let $\mathbf{p}(\phi ,{\phi }^{*})$ be the director surface of the congruence; that is, $\mathbf{x}(\phi ,{\phi }^{*})=\mathbf{p}(\phi ,{\phi }^{*})\times \mathbf{x}\left(\phi \right)$. After some algebraic manipulations, it can be determined that

$$\mathbf{p}(\phi ,{\phi }^{*})=\left({\phi }^{*},-{\vartheta }^{*}sin\phi ,{\vartheta }^{*}cos\phi \right).$$

(44)

Let $\mathbf{y}$ be a point on the directed $\mathcal{S}like$ line $\widehat{\mathbf{x}}$. We can write:

$$\left(\widehat{x}\right):\mathbf{y}(\phi ,{\phi }^{*},v)=\mathbf{p}(\phi ,{\phi }^{*})+v\mathbf{x}(\phi ,{\phi }^{*}),v\in \mathbb{R}.$$

(45)

If we set ${\phi }^{*}=h\phi$ and $\phi$ as the locomotion parameter, then $\left(\widehat{x}\right)$ is a $\mathcal{T}like$ ruled in ${\mathbb{L}}_f$-space. By substituting the Equation (40) into the Equation (42), we find

$$\mathbf{x}\left(\phi \right)=\frac{1}{\sqrt{1-{(acsc\phi +bsec\phi )}^2}}\left(acsc\phi +bsec\phi ,cos\phi ,sin\phi \right),$$

(46)

which is the Lorentzian spherical torsion curve. From Equations (44)–(46), we also obtain that:

$$\left(\widehat{x}\right):\mathbf{y}(\phi ,v)=\left(\begin{array}{c}h\phi +\frac{v\left(a csc \phi +b sec \phi \right)}{\sqrt{1-{(a csc \phi +b sec \phi )}^2}}\\ -{\vartheta }^{*}sin\phi +\frac{v cos \phi }{\sqrt{1-{(a csc \phi +b sec \phi )}^2}}\\ {\vartheta }^{*}cos\phi +\frac{v sin \phi }{\sqrt{1-{(a csc \phi +b sec \phi )}^2}}\end{array}\right),v\in \mathbb{R}.$$

(47)

According to Equations (46) and (47), we have:

(1)

Lorentzian spherical torsion curve with its $\mathcal{T}like$ torsion ruled surface: for $a=0.6$, $b=0.3$, $h=0,$${\vartheta }^{*}=0.6$, $0\le \phi \le 2\pi$, $-4\le v\le 4$ (Figure 3 and Figure 4).

Figure 3. Lorentzian torsion curve.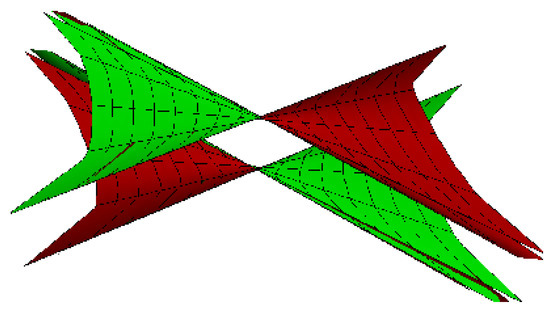

Figure 4. $\mathcal{T}like$ torsion ruled surface.

(2)

Lorentzian spherical torsion curve with its $\mathcal{T}like$ torsion ruled surface: for $a=0$, $b=0.1$, $h=0,$${\vartheta }^{*}=0.6$, $0\le \phi \le 2\pi$, $-4\le v\le 4$ (Figure 5 and Figure 6).

Figure 5. Lorentzian torsion curve.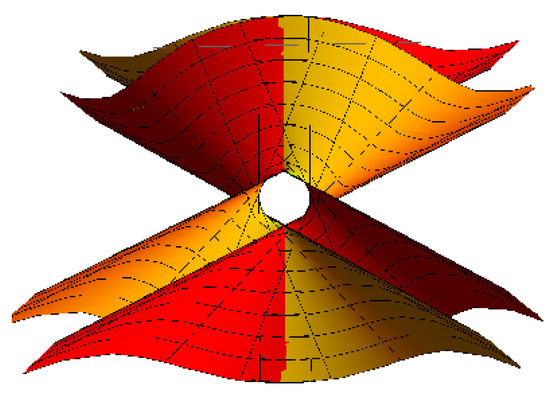

Figure 6. $\mathcal{T}like$ torsion ruled surface.

(3)

Lorentzian spherical torsion curve with its $\mathcal{T}like$ torsion ruled surface: for $a=0.6$, $b=0$, $h=0,$${\vartheta }^{*}=0.6$, $0\le \phi \le 2\pi$, $-4\le v\le 4$ (Figure 7 and Figure 8).

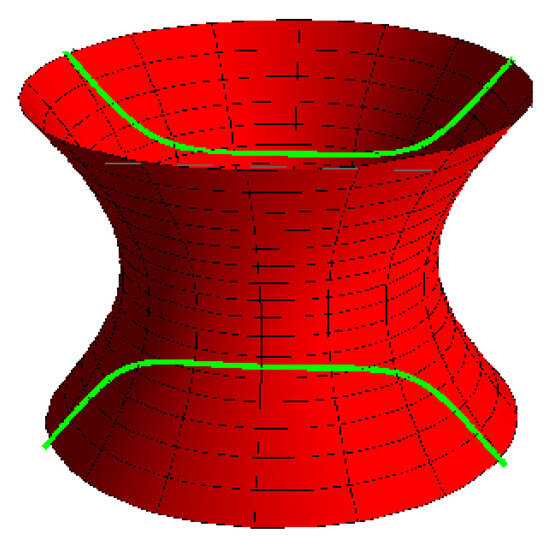Figure 7. Lorentzian torsion curve.

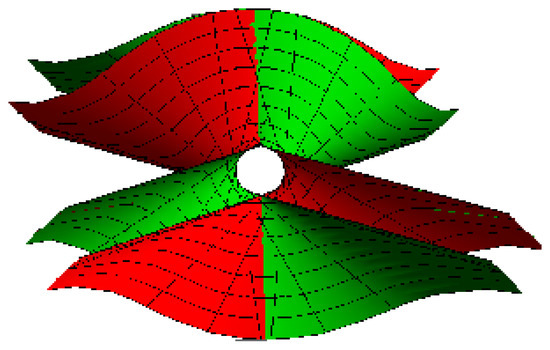Figure 8. $\mathcal{T}like$ torsion ruled surface.

4. Conclusions

The main outcome of the paper is generalization of the $\mathcal{E}-\mathcal{S}$ and $\mathcal{D}is$ formulae in the Lorentzian motion. On the basis of the E. Study map, formulae for the velocity and acceleration of a $\mathcal{S}like$ dual curve are obtained by applying the invariants of relative locomotion through two Lorentzian $\mathcal{DU}$ spheres. The torsion and curvature of this $\mathcal{S}like$ curve are related to the invariants. The $\mathcal{E}-\mathcal{S}$ equation and the $\mathcal{D}is$ equation are then given novel proofs using the axode invariants. Additionally, the well-known torsion cone with a constant spherical kinematic curvature is investigated in dual space. Further, we defined and studied $\mathcal{T}like$ torsion line congruence. Then, a detailed examination of a Lorentzian torsion line congruence and its spatial equivalent was performed using the E. Study map. It is possible to discuss specific issues and develop new implementations using the E. Study map to describe spatial kinematics in Minkowski 3-space (${\mathbb{E}}_1^3$). As seen in [9,12,17,20,21,26], in the future, our primary focus will be on the development of $\mathcal{T}like$ ruled surfaces to serve as tooth edges for gears with skew axes.